Кинематика все определения: Кинематика - основные определения и формулы - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Основные понятия кинематики. Относительность движения

С данной темы приступаем к повторению первого раздела физики, который называется «Кинематика». И в начале вспомним основные понятия, относящиеся к данному разделу, а также поговорим об относительности движения.

Кинематика, как часть механики, была известна еще со времен Аристотеля. Однако впервые раздел кинематики был четко выделен в курсе «Физической и экспериментальной механики» генерала Жана-Виктора Понселе, который читал его в Парижском университете с 1837 по 1848 годы.

Кинематика — это раздел механики, в котором изучают движение тел, без рассмотрения причин, вызвавших это движение.

Основной задачей кинематики является нахождение положения тела в произвольный момент времени, если известны его положение, скорость и ускорение в начальный момент времени.

Наиболее простым видом движения в природе является механическое движение. Под механическим движением понимают изменение положения тел (или частей одного тела) друг относительно друга в пространстве с течением времени.

Простым примером механического движения может служить лодка, плывущая по реке. Она меняет свое положение относительно берега, деревьев и человека, находящихся на берегу. И таких примеров можно привести достаточно много.

Чтобы изучать движение тела, нужно прежде всего уметь определять это положение. Здесь важно помнить, что положение тела можно задать только относительно какого-либо другого тела, которое, обычно, называют телом отсчета. И так, тело отсчета — это тело (или группа тел), принимаемое в данном случае за неподвижное, относительно которого рассматривается движение других тел.

Тело отсчета можно выбрать совершенно произвольно. В рассмотренном примере, им может служить рыбак, стоящий на берегу реки, или деревья, кусты, береговая линия.

Для описания движения мало выбрать тело отсчета, необходимо еще указать и систему координат, связав ее с телом отсчета, и способ измерения времени. Так вот, совокупность тела отсчета, системы координат и способа измерения времени создают систему отсчета, относительно которой и рассматривают движение тела.

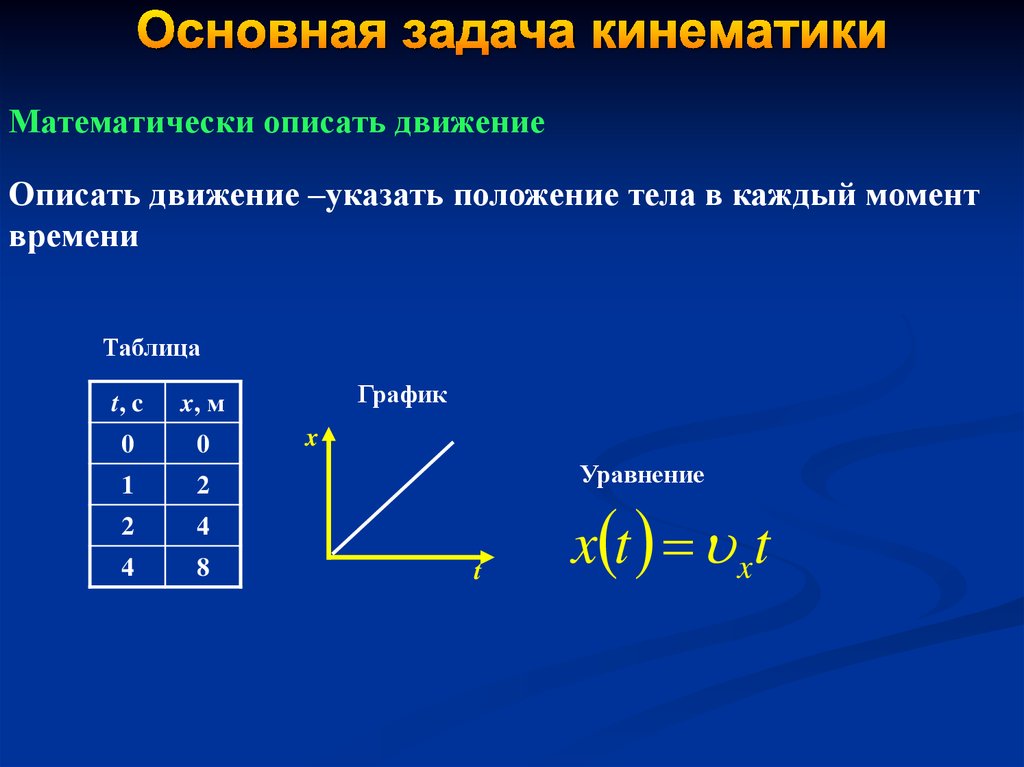
Положение тела в пространстве можно определить с помощью радиус-вектора или при помощи координат. Радиус-вектор — это вектор, который соединяет исследуемую точку и начало координат. Радиус-вектор обозначается латинской буквой и, как и любой другой вектор, имеет длину и направление.

Под координатой точки понимают проекцию конца радиус-вектора на выбранную координатную ось.

Таким образом, для того, чтобы в рассмотренном примере определить координату точки М, необходимо опустить с конца радиус-вектора два перпендикуляра — на ось Ox и ось Oy. Тогда найденные значения

x и y и будут являться координатами точки M.

Еще одно затруднение, с которым можно столкнуться, при изучении движения тела, это то, что каждое тело имеет определенные размеры, следовательно, разные его части, разные точки тела находятся в разных местах пространства.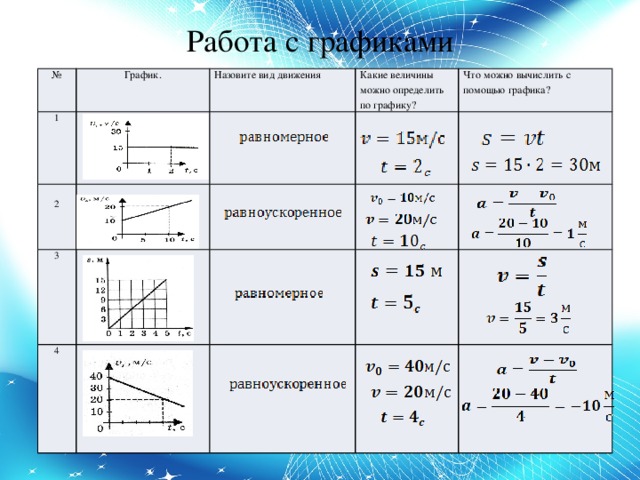 Так как же определить положение всего тела? В общем случае это сделать трудно. Но оказывается, во многих случаях нет необходимости указывать положение каждой точки движущегося тела.

Зачем, например, описывать движение каждой точки самолета, если эти движения ничем не различаются между собой?

Движение тела, при котором все его точки движутся одинаково, называют поступательным.

Не нужно описывать движение каждой точки тела и тогда, когда размеры тела малы по сравнению с расстоянием, которое оно проходит, или по сравнению с расстояниями от него до других тел.

Например, сидя в автомобиле, его нельзя считать точкой, по отношению к водителю или пассажиру, но, например, автомобиль мал по сравнению с протяженностью расстояния, которое ему предстоит преодолеть, и поэтому автомобиль считают точкой при описании его движения.

Так же поступают в астрономии при изучении движений небесных тел.

Планеты, звезды и Солнце, конечно, не малые тела.

Но, например, в сравнении с масштабами нашей галактики «Млечный путь» и Землю и Солнце мы можем принимать за точку, которая движется вокруг другой точки — центра галактики.

А можно ли галактику принять за точку? Конечно же да, но только в случаях рассмотрения ее движения относительно других галактик или всей Вселенной.

Поэтому говоря в дальнейшем о движении тела, в действительности будем иметь в виду движение какой-нибудь точки этого тела. Не надо забывать при этом, что эта точка материальна, то есть она отличается от обычных тел лишь тем, что она не имеет размеров.

Таким образом, материальная точка — это тело, размерами которого в данных условиях движения можно пренебречь.

Линия, которую описывает движущееся тело в определенной системе координат, называется траекторией. Например, в идеализированной модели движения Луны вокруг Земли, в системе отсчета, связанной с Землей, траекторией движения Луны будет являться окружность.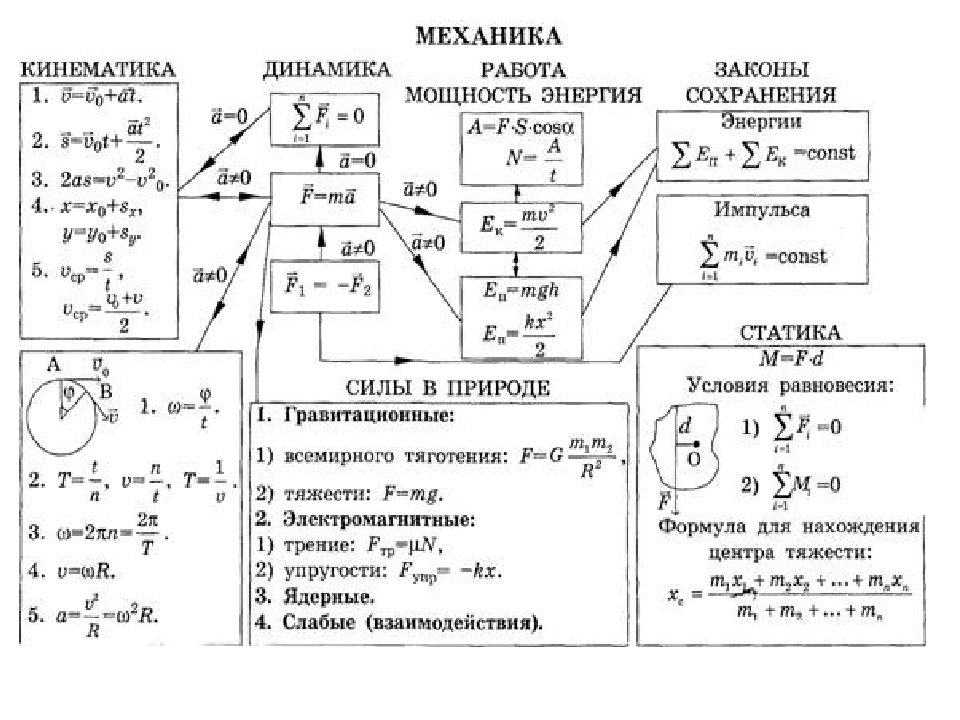

А в системе отсчета, связанной с Солнцем это кривая, чем-то напоминающая лепестки цветка (такую кривую еще называют циклоидой).

Если можно найти длину траектории, которую описало тело за некоторый промежуток времени, то можно определить путь, пройденный телом. Обозначается путь малой латинской буквой s. Следует также помнить, что путь — величина скалярная и всегда положительная.

В тех случаях, когда траектория движения не известна, определить положение тела, то есть его координаты, в конце пути нельзя, даже если известны начальное положение тела и длина пройденного им пути.

Допустим, известно, что некоторое тело начинает двигаться из точки

О и за один час проходит 20 км.

Для ответа на вопрос, где будет находиться тело спустя один час после его выхода из точки О, не хватает информации о его движении. Ведь тело могло, например, двигаться прямолинейно в северном направлении и оказаться в точке А, находящейся на расстоянии 20 км. А могло также, дойдя до точки B, находящейся на расстоянии 10 км от точки О, повернуть на восток и вернуться в точку О. При этом пройденный путь также окажется равным 20 км. При заданном значении пути, тело могло оказаться в любой точке пространства, ограниченного окружностью, радиуса 20 км.

Чтобы избежать такой неопределенности, для нахождения положения тела в пространстве в заданный момент времени, была введена физическая величина, называемая перемещением.

Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением.

Как видно из рисунка, перемещение тела равно геометрической разности радиус-векторов тела в начальный и конечный моменты времени.

Для того, чтобы определить проекцию перемещения на выбранную координатную ось, необходимо найти координаты тела в начальный и конечный моменты времени, и найти их разность.

Необходимо отметить, что модуль перемещения не может быть больше пути.

Знак равенства относится только к случаю прямолинейного движения, если направление движения не изменяется.

Скорость — это мера механического состояния тела, которая характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной.

Известно, что тело в редких случаях движется с неизменной скоростью, поэтому для характеристики такого движения было введено понятие средней скорости. И так,

средняя скорость — это векторная физическая величина, численно равная отношению перемещения к промежутку времени, за который оно произошло, и направленная вдоль перемещения.

Так же в физике различают понятие мгновенной скорости, то есть скорости тела в данный момент времени или в данной точке траектории. Она равна пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени.

– это производная от радиус-вектора по времени.

Следует помнить, что

мгновенная скорость всегда направлена по касательной к траектории движения тела, а в случае прямолинейного движения совпадает с ней.

Следующей важной характеристикой движения является ускорение. Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости. Оно показывает, на какую величину изменяется скорость тела за единицу времени.

Среднее ускорение — векторная физическая величина, численно равная отношению изменения скорости ко времени, за который оно произошло.

где — это производная от скорости по времени.

Для того, чтобы найти направление вектора среднего ускорения, необходимо найти направление вектора изменения скорости. Для этого параллельным переносом совмещают начало вектора начальной скорости с началом вектора конечной скорости и строят их разность.

Вектор среднего ускорения направлен параллельно вектору скорости в сторону вогнутости траектории.

Важно запомнить, что, зная траекторию движения тела, можно определить направление вектора его скорости, но не ускорения. Ведь направление ускорения определяется направлением равнодействующей сил, действующих на тело.

На рисунке изображен автомобиль. Что можно сказать о данном автомобиле: движется он или покоится? Однозначного ответа нет. Ведь не известно, относительно чего рассматривать его движение.

А вот так?

Здесь можно сказать, что автомобиль движется относительно дороги.

А что можно сказать о водителе данного автомобиля: он движется или покоится?

В данном примере оба ответа будут правильными, ведь относительно дороги водитель действительно движется вместе с автомобилем, а относительно автомобиля он покоится.

А что можно сказать о траектории его движения? И опять здесь нет однозначного ответа.

Так как в разных системах отсчета будут различны вид траектории, значение скорости и других величин! В этом и заключается относительность движения.

Вот еще один пример. Два велосипедиста на велосипеде-тандеме движутся по проселочной дороге. Движутся ли они относительно друг друга?

Правильный ответ — «нет», так как положение их тел относительно друг друга не меняется с течением времени.

А вот еще один классический пример. Мальчик переходит с кормы на нос лодки, которая сама движется по течению реки. Когда мальчик доходит до носа лодки, отсчет времени прекращают. Каково перемещение мальчика относительно берега реки?

Для ответа на этот вопрос необходимо определить перемещение мальчика, относительно лодки.

И перемещение лодки относительно берега, за этот промежуток времени.

Тогда очевидно, что перемещение мальчика относительно берега будет равно геометрической сумме перемещений мальчика относительно лодки, и лодки, относительно берега.

Таким образом, если тело одновременно участвует в нескольких движениях, то результирующее перемещение точки равно векторной сумме перемещений, совершаемых ею в каждом из движений. В этом состоит установленный экспериментально принцип независимости движений.

Основные выводы:

В рамках данной темы были повторены основные понятия кинематики, поговорили о механическом движении тел и способах его описания. А также разобрались с понятием относительности механического движения.

1. Основные понятия

Лекция 10

Кинематика

Вопросы

2. Основные задачи кинематики

3. Способы задания движения точки

1. Кинематикой называется раздел теоретической механики, в котором изучаются геометрические свойства механического движение тел, без учета их масс и действующих на них сил.

Под механическим движением понимается изменение с течением времени положение тела в пространстве по отношению к другим телам. Для того чтобы определить изменение положения тела по отношению к другому телу, с последним связывают какую-либо систему координатных осей, называемую системой отсчета. В зависимости от тела, с которым она связана, система отсчета может быть как подвижной, так и неподвижной. Тело движется по отношению к выбранной системой отсчета, если с течением времени изменяются координаты хотя бы одной из его точек; в противном случае тело по отношению к данной системе отсчета будет находиться в состоянии покоя. Таким образом, покой и движение – понятия относительные, зависящие от выбора системы отсчета.

Механическое движение происходит в пространстве и во времени. При этом пространство считается трехмерным евклидовым пространством. Все измерения в нем производятся на основании методов евклидовой геометрии. За единицу длины при измерении расстояния принят 1 метр. Время в механике считается универсальным, т.е. протекающем одинаково во всех системах отсчета. За единицу времени принимается 1 секунда.

В задачах кинематики время t принимается за независимое переменное (аргумент). Все другие переменные величины (расстояние, скорость, ускорение и т.д. ) рассматриваются как функции времени t. Отсчет времени ведется от некоторого начального момента (t = 0), о выборе которого в каждом случае уславливаются. Всякий данный момент времени t определяется числом секунд, прошедшим от начального момента; разность между какими-нибудь двумя моментами времени называется промежутком времени.

Для решения задач кинематики необходимо, чтобы изучаемое движение было как-то задано (описано). Движение тела считается заданным, если известно положение всех его точек (относительно выбранной системы отсчета) в любой момент времени.

2. Две основные задачи кинематики

Основными задачами кинематики являются:

а) установление математических способов задания движения тел в произвольно выбранной системе отсчета,

б) определение по заданному движению тела всех основных кинематических характеристик (траектории, скорости, ускорения) любой из его точек. Рассмотрим решение этих задач для одной точки.

Кинематика точки

Способы задания движения точки

Для задания движения в кинематике используются три способа: векторный, координатный и естественный.

а) Векторный способ задания движения точки.

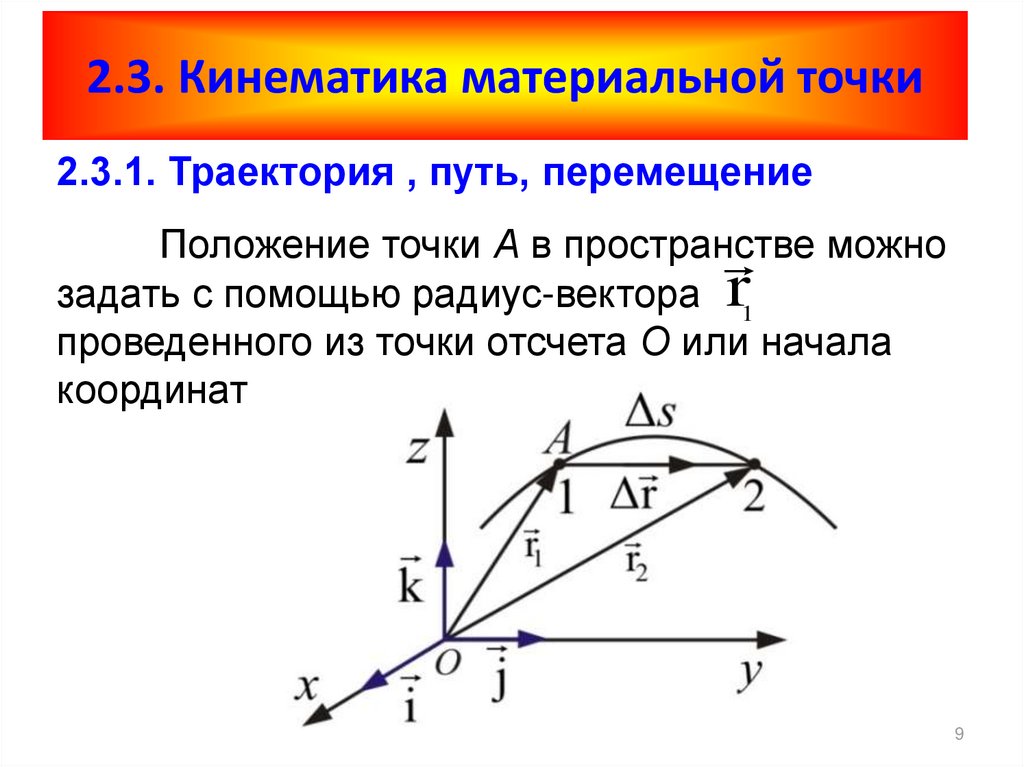
Пусть точка М движется по некоторой кривой АВ. Положение точки M относительно начала некоторой системы координат можно однозначно определить с помощью радиус-вектора , начало которого неизменно связано с точкойО.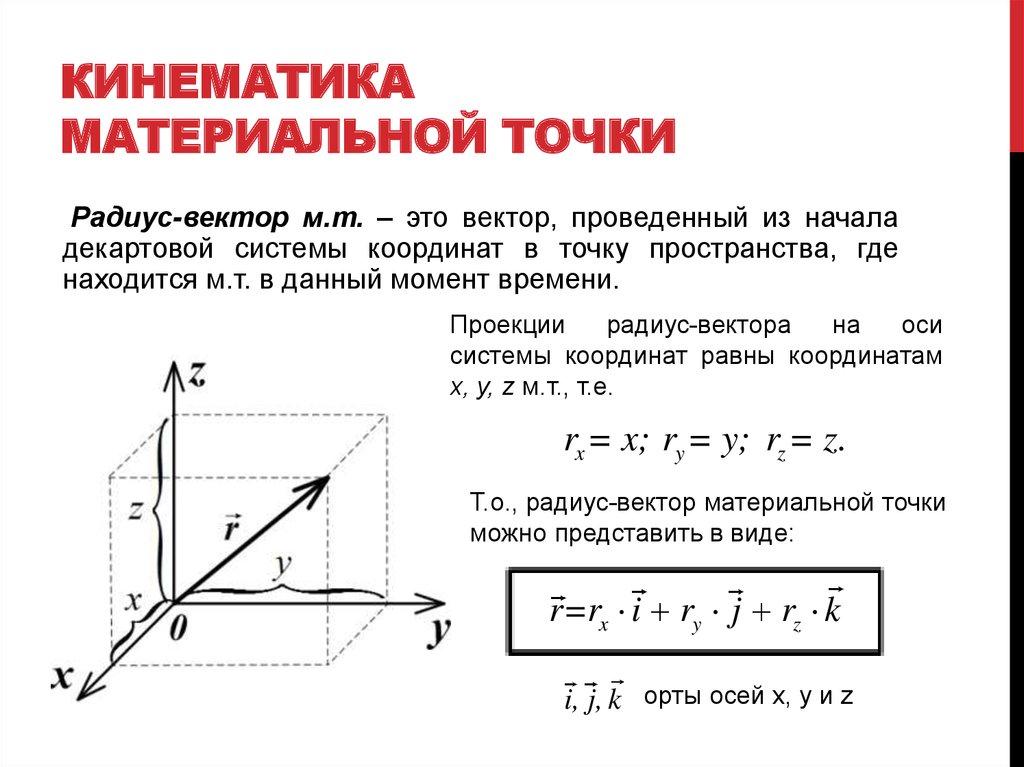 Движение точки М будет полностью определено, если ее радиус вектор задан как функция времени. Векторное равенство:

(2.1)

называется векторным уравнением движения или законом движения точки в векторной форме.

Рис. 2.1. Векторный способ задания движения точки

При движении точки М длина и ориентация вектора будет меняться, а его конец будет вычерчивать в пространстве линию называемую годографом радиуса – вектора или траекторией движения точки М (рис. 2.1).

Выражая в (1) вектор через его проекции, получим:

или учитывая, что проекции радиуса-вектора равны координатам точки М:

r_x = x, r_y = y, r_z = z,

, (2. 2)

где x(t), y(t), z(t) – текущие координаты движущейся точки М.

б) Координатный способ задания движения точки.

С векторным способом тесно связан координатный способ задания движения точки. Очевидно, что положение движущейся точки в пространстве будет однозначно определено, если будут известны текущие координаты точки, фигурирующие в выражении (1.2):

x = x(t), y = y(t), z = z(t). (2.3)

Уравнения (2.3) называются уравнениями движения или законом движения точки в координатной форме. Эти же уравнения можно трактовать как параметрические уравнения траектории, в которых роль параметра играет время t. Чтобы получить уравнение траектории в координатной форме, нужно из уравнений (3) исключить время t.

Пример 1.

Пусть движение точки задано уравнениями:

x = t², y = t,

где t измеряется в секундах, x и y в метрах. Определить уравнение траектории.

Исключая из уравнений движения t, получим уравнение траектории

t = y, x = y².

Поскольку время t >0, координата y в исходных уравнениях движения не может быть отрицательной. Следовательно, траекторией движения будет лишь верхняя ветвь параболы x = y² .

Рис. 2.2. Вид траектории точки в примере 1

Пример 2.

Движение точки в плоскости xOy описывается уравнениями:

x = 3 sin 4t , y = 4 cos 4t .

Найти уравнение траектории в координатной форме.

Решение: Перепишем исходные уравнения движения в виде:

x/3 = sin4t , y/4 = cos4t

возводя оба уравнения в квадрат и складывая их почленно, получим уравнение траектории в координатной форме: .

Рис. 2.3. Вид траектории движения точки в примере 2

в) Естественный способ задания движения точки.

Рассмотрим естественный способ задания движения точки, когда отдельно задается:

– траектория движения;

– начало и положительное направление отсчета;

– закон движения точки по траектории: S = S(t),

где S – дуговая координата (расстояние, измеренное от выбранного на траектории начала отсчета до текущего положение точки на траектории).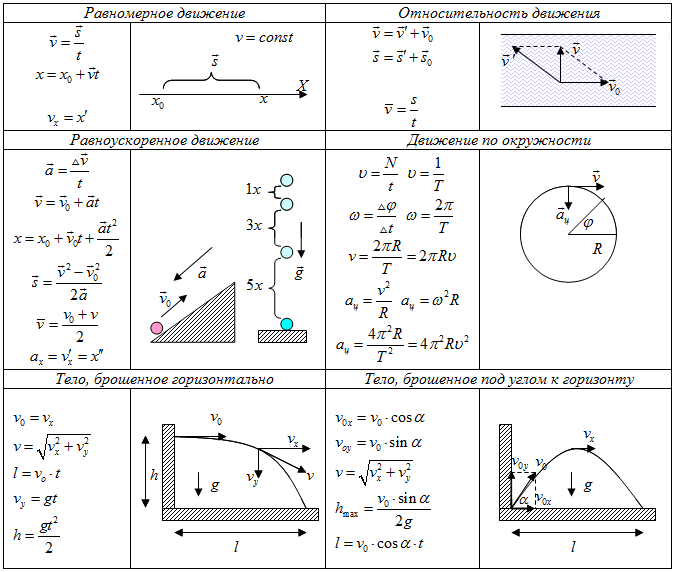

Рис. 2.4. Естественный способ движения точки

Поскольку одно и то же движение точки может задаваться тремя различными способами, между ними должна существовать связь и от одного способа задания можно переходить к другому. Такой переход от векторного способа к координатному и наоборот очевиден (формулы 2.2, 2.3). Рассмотрим пример перехода от естественного способа задания движения к координатному:

Пусть точка движется по окружности x² + y² = a² по закону S = Vt, где a и V заданные константы (рис. 2.5). Начало отсчета – точка М(а,0). Положительное направление отсчета координаты S – против хода часовой стрелки. Определить уравнения движения точки в координатной форме: x = x(t), y = y(t).

Рис. 2.5. Траектория, начало отсчета и положительное направление движения

Для обратного перехода к естественному способу задания движения нужно исключив время t из полученных уравнений движения, получить уравнение траектории , а затем по формулеи закон движения точки по траектории:.

Лекция 11

Вопросы

Скорость точки.

Что такое кинематика? | Определение из TechTarget

Участник TechTarget

Кинематика — это изучение движения механических точек, тел и систем без учета связанных с ними физических свойств и сил, действующих на них. Это исследование часто называют геометрией движения, и оно математически моделирует эти движения с помощью алгебры.

Системы в кинематике моделируются для расчета таких вещей, как скорости и отношения. Примером модели тел в системе являются шестерни в трансмиссии автомобиля. Эти модели используются для проектирования всех видов механических устройств и для моделирования движений существующих физических тел, включая жесткую, шарнирно закрепленную механику человеческого скелета или движение небесных тел в астрофизике, также известное как звездное движение. кинематика.

Кинематика очень полезна при концептуальном проектировании механических систем. Начальные геометрии и скорости тел являются частью модели. Хотя кинематика может помочь определить, возможен ли дизайн теоретически, при разработке чего-либо для реального мира возникает больше сложностей. Без учета материалов и сил, действующих на них, многие теоретически возможные конструкции могут выйти из строя.

Кинетика, в отличие от кинематики, не учитывает физические свойства, такие как масса тел или движущие их силы. Кинетика логически выводится из кинематики путем алгебраического расчета физических свойств и сил. Кинетика учитывает физические силы и свойства, включая свойства материалов, такие как жесткость массы и прочность на растяжение или сжатие. Эти свойства в сочетании с физикой и термодинамикой могут взять теоретическую модель из кинематики и помочь определить, как спроектировать жизнеспособную, надежную и функционирующую реальную систему.

Последнее обновление: май 2018 г.

Продолжить чтение О кинематике
Как построить успешную стратегию цифрового производства
Узнайте больше об основах кинематики
Зачем геопространственным инженерам нужны облака
3D-технологии, аддитивное производство ускоряют производство
Использование супергероев, таких как Соколиный Глаз, Чудо-женщина и Женщина-невидимка, на уроках физики
враждебный ML
Состязательное машинное обучение — это метод, используемый в машинном обучении для обмана или введения в заблуждение модели с помощью злонамеренных входных данных.
Сеть
межсоединение центра обработки данных (DCI)
Технология соединения центров обработки данных (DCI) объединяет два или более центров обработки данных для совместного использования ресурсов.
Протокол маршрутной информации (RIP)
Протокол маршрутной информации (RIP) — это дистанционно-векторный протокол, в котором в качестве основной метрики используется количество переходов.
доступность сети
Доступность сети — это время безотказной работы сетевой системы в течение определенного интервала времени.
Безопасность
кража учетных данных
Кража учетных данных — это тип киберпреступления, связанный с кражей удостоверения личности жертвы.
суверенная идентичность
Самостоятельная суверенная идентификация (SSI) — это модель управления цифровой идентификацией, в которой отдельные лица или предприятия владеют единолично . ..
Сертифицированный специалист по безопасности информационных систем (CISSP)
Certified Information Systems Security Professional (CISSP) — это сертификат информационной безопасности, разработанный …
ИТ-директор
рассказывание историй о данных
Рассказывание историй о данных — это процесс перевода анализа данных в понятные термины с целью повлиять на деловое решение…
оншорный аутсорсинг (внутренний аутсорсинг)
Оншорный аутсорсинг, также известный как внутренний аутсорсинг, — это получение услуг от кого-то вне компании, но в пределах …
FMEA (анализ видов и последствий отказов)
FMEA (анализ видов и последствий отказов) представляет собой пошаговый подход к сбору сведений о возможных точках отказа в …
HRSoftware
самообслуживание сотрудников (ESS)
Самообслуживание сотрудников (ESS) — это широко используемая технология управления персоналом, которая позволяет сотрудникам выполнять множество связанных с работой . ..
платформа обучения (LXP)
Платформа обучения (LXP) — это управляемая искусственным интеллектом платформа взаимного обучения, предоставляемая с использованием программного обеспечения как услуги (…
Поиск талантов
Привлечение талантов — это стратегический процесс, который работодатели используют для анализа своих долгосрочных потребностей в талантах в контексте бизнеса …
Служба поддержки клиентов
виртуальный помощник (помощник ИИ)
Виртуальный помощник, также называемый помощником ИИ или цифровым помощником, представляет собой прикладную программу, которая понимает естественный язык …
интерактивный голосовой ответ (IVR)
Интерактивный голосовой ответ (IVR) — это автоматизированная система телефонии, которая взаимодействует с вызывающими абонентами, собирает информацию и маршрутизирует . ..
жизненный цикл клиента
В управлении взаимоотношениями с клиентами (CRM) жизненный цикл клиента — это термин, используемый для описания последовательности шагов, которые проходит клиент…
Кинематика Определение и значение | Dictionary.com
Основные определения
Викторина
Примеры
Британский
Научный
Показывает уровень сложности слова.
[ kin-uh-mat-iks, kahy-nuh- ]
/ ˌkɪn əˈmæt ɪks, ˌkaɪ nə- /
Сохранить это слово!
Показывает уровень оценки в зависимости от сложности слова.
существительное (используется с глаголом в единственном числе)Физика.
Раздел механики, изучающий чистое движение без учета вовлеченных в него масс или сил.
Также называется прикладной кинематикой. теория механического устройства для преобразования одного вида движения в другой.
ВИКТОРИНА
ВЫ ПРОЙДЕТЕ ЭТИ ГРАММАТИЧЕСКИЕ ВОПРОСЫ ИЛИ НАТЯНУТСЯ?
Плавно переходите к этим распространенным грамматическим ошибкам, которые ставят многих людей в тупик. Удачи!
Вопрос 1 из 7
Заполните пропуск: Я не могу понять, что _____ подарил мне этот подарок.
Происхождение кинематики
18:30–40; <греческое kīnēmat- (основа движения kī́nēma; см. кино) + -ics
ДРУГИЕ СЛОВА ИЗ кинематики
kin·e·mat·ic, kin·e·mat·i·al, прилагательноеkin·e·mat·i· кал·лы, наречие
Слова рядом кинематика
родственная душа, кинду, кинды, кинэ, кинематическая пара, кинематика, кинематическая вязкость, кинематограф, кинескоп, кинешма, -кинезия
Dictionary.com Полный текст На основе Random House Unabridged Dictionary, © Random House, Inc. 2023
Как использовать кинематику в предложении
Должна ли геометрия рассматриваться как раздел кинематики и как раздел оптики?
Основы науки: наука и гипотеза, ценность науки, науки и метода|Анри Пуанкаре
Этот экземпляр, вероятно, представляет собой первый учебник по кинематике.
Кинематика механизмов времен Уатта | Юджин С. Фергюсон
Роботы были достаточно просты — на самом деле, просто готовые вещи, — но костюмы и кинематика были чем-то другим.
В волшебном королевстве|Кори Доктороу
Доказательство аналогично доказательству соответствующей теоремы плоской кинематики ( 3).
Британская энциклопедия, 11-е издание, том 17, часть 8|Разное
Кинематика, кин-э-матикс, н. наука, изучающая движение без ссылки на силу.
Chambers’s Twentieth Century Dictionary (part 2 of 4: E-M)|Various
British Dictionary definitions for kinematics
kinematics
/ (ˌkɪnɪˈmætɪks, ˌkaɪ-) /
noun
(functioning as singular) the изучение движения тел без привязки к массе или силеСравнить динамику (по умолч. 1)
Производные формы кинематики
кинематический, прилагательноекинематический, наречие
Происхождение слова для кинематики
C19: от греческого движения кинема; см.