Классическая механика и релятивистская механика: Классическая и релятивистская механика

понятия, основные формулы и принципы. Энергия, импульсы и второй закон Ньютона

 

Релятивистская механика

 

Релятивистская механика – это механика, в которую превращается механика Ньютона в случае если тело движется со скоростью, близкой к скорости света. На таких высоких скоростях с вещами начинают происходить ну просто волшебные и совершенно неожиданные вещи, такие как, например, релятивистское сокращение длины или замедление времени.

Но как именно классическая механика становится релятивистской? Обо всем по порядку в нашей новой статье.

Начнем с самого начала…

Принцип относительности Галилея

Принцип относительности Галилея (1564-1642) гласит:

В инерциальных системах отсчета все процессы протекают одинаково, если система неподвижна или движется равномерно и прямолинейно.

В данном случае речь идет исключительно о механических процессах. Что это значит? Это значит, что если мы, например, будем плыть на равномерно и прямолинейно движущемся пароме через туман, мы не сможем определить, движется паром или покоится. Иными словами, если провести эксперимент в двух одинаковых замкнутых лабораториях, одна из которых равномерно и прямолинейно движется относительно другой, результат эксперимента будет одинаковым.

 

Галилео Галилей

 

Преобразования Галилея

Преобразования Галилея в классической механике – это преобразования координат и скорости при переходе от одной инерциальной системы отсчета к другой. Не будем приводить здесь всех вычислений и выводов, а просто запишем формулу для преобразования скорости. Согласно этой формуле скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела в движущейся системе отсчета и скорости движущейся системы отсчета относительно неподвижной.

Приведенный нами выше принцип относительности Галилея является частным случаем принципа относительности Эйнштейна.

Принцип относительности Эйнштейна и постулаты СТО

В начале двадцатого века после более чем двухсотлетнего господства классической механики возник вопрос о распространении принципа относительности на немеханические явления.

Причиной возникновения такого вопроса стало закономерное развитие физики, в частности оптики и электродинамики. Результаты многочисленных экспериментов то подтверждали справедливость формулировки принципа относительности Галилея для всех физических явлений, то в ряде случаев указывали на ошибочность преобразований Галилея.

 

Эйнштейн – человек, создавший специальную теорию относительности

 

Например, проверка формулы сложения скоростей показала ее ошибочность при скоростях, близких к скорости света. Более того, опыт Физо в 1881 году показал, что скорость света не зависит от скорости движения источника и наблюдателя, т.е. в любой системе отсчета остается постоянной. Данный результат эксперимента никак не укладывался в рамки классической механики.

Решение этой и других проблем нашел Альберт Эйнштейн. Для того чтобы теория сошлась с практикой, Эйнштейну пришлось отказаться от нескольких, казалось бы, очевидных истин классической механики. А именно – предположить, что расстояния и промежутки времени в различных системах отсчета не неизменны. Ниже приведем основные постулаты Специальной Теории Относительности (СТО) Эйнштейна:

Первый постулат: во всех инерциальных системах отсчета все физические явления протекают одинаково.  При переходе от одной системы к другой все законы природы и явления, описывающие их,  инвариантны, то есть никакими опытами нельзя отдать предпочтение одной из систем, ибо они инвариантны.

Второй постулат: скорость света в вакууме одинакова во всех направлениях и не зависит от источника и наблюдателя, т.е. не изменяется при переходе от одной инерциальной системы к другой.

Скорость света – предельная скорость. Никакой сигнал или действие не могут распространяться со скоростью, превышающей скорость света.

Преобразования координат и времени при переходе от неподвижной системы отсчета к системе, движущейся со скоростью света, называются преобразованиями Лоренца.

К примеру, пусть одна система покоится, а вторая движется вдоль оси абсцисс.

Здесь

Как видим, время также изменяется наряду с координатами, то есть выступает как бы в роли четвертной координаты. Преобразования Лоренца показывают, что в СТО пространство и время неразделимы в отличие от классической механики.

Помните парадокс двух близнецов, один из которых ждал на земле, а второй летел на космическом корабле с очень большой скоростью? После того как брат-космонавт вернулся на землю, он застал своего брата стариком, хотя сам был практически так же молод, как в момент начала путешествия. Типичный пример того, как изменяется время в зависимости от системы отсчета.

 

Парадокс близнецов

 

При скоростях же много меньших скорости света преобразования Лоренца переходят в преобразования Галилея. Даже при скорости современных реактивных самолетов и ракет отклонения от законов классической механики настолько малы, что их практически невозможно измерить.

Релятивистская механика

Механика, учитывающая преобразования Лоренца,  и называется релятивистской.

В рамках релятивистской механики меняются формулировки некоторых физических величин. Например, импульс тела в релятивистской механике в соответствии с преобразованиями Лоренца может быть записан так:

Соответственно, второй закон Ньютона в релятивистской механике будет иметь вид:

А полная релятивистская энергия тела в релятивистской механике равна

Если тело покоится и скорость равна нулю, данная формула преобразуется в знаменитую

 

Формула энергии покоя тела

 

Данная формула, которую, кажется, знают все, показывает, что масса является мерой полной энергии тела, а также иллюстрирует принципиальную возможность перехода энергии вещества в энергию излучения.

Дорогие друзья, на этой торжественной ноте мы закончим наш сегодняшний обзор релятивистской механики. Мы рассмотрели принцип относительности Галилея и Эйнштейна, а также некоторые основные формулы релятивистской механики. Самым стойким и дочитавшим статью до конца напоминаем – в мире нет «нерешабельных» задач и проблем, которые невозможно решить. Паниковать и переживать из-за незаконченной курсовой нет никакого смысла. Просто вспомните о масштабах Вселенной, вздохните полной грудью и поручите выполнение настоящим профессионалам своего дела – авторам компании Zaochnik.

Классическая и релятивистская 📙 механика

1. Соотношение традиционной и релятивистской механики
2. Кинематика в традиционной и релятивистской механике
3. Различия релятивистской механики от традиционной

Механика является значительной областью в научной деятельности, которая изучает механическое движение физических объектов, а также возникающие в то же время взаимные воздействия между этими объектами.

Областью применимости традиционной механики является движение объектов с большой (по сравнению с атомом) массой, движущихся с малыми (сравнительно со скоростью света) скоростями.

Уравнения релятивистской механики в пределах малых (по сравнению со скоростью света) скоростей переходят в уравнения классической механики. В свою очередь, уравнения квантовой механики в пределах больших (по сравнению с массами атомов) масс переходят в уравнения классической механики.

Перемещение всех макроскопических объектов со скоростями, которые существенно ниже скорости света, исследуется в традиционной механике Исаака Ньютона. Законы материального передвижения физических веществ со скоростями, которые являются приближенными к скорости света, рассматриваются в релятивистской механике.

Непрерывные на протяжении многого десятка лет критические высказывания в сторону обеих гипотез относительности большим количеством знаменитых физиков (в том числе, и лауреатов Нобелевской премии), замечательных математиков и философов вынуждает нынешних исследователей и ученых сегодня поразмышлять над основами данных теорий. Ключевыми материальными телами, передвижение которых во всех случаях исследуется в механике, считаются:

• Материальная точка. Эта точка является рабочим объектом, типоразмерами и внешним видом которого в конкретной ситуации возможно пренебречь.
• Полностью твердый объект. Данным объектом является тело, деформирование которого требуется учесть в обязательном порядке при разрешении непростых заданий.

Сегодня знакома оригинальная с некоторой точки зрения «несимметричность» результатов и итогов с позиции математики: нескончаемое число утверждающих очевидных примеров не в состоянии перевесить даже единого логического, научного разногласия. Вот по какой причине релятивистам требуется поразмыслить на теми бесчисленными возражениями, найденными их оппонентами, а не конкурировать в числе конкретных ситуаций, где конфликтные моменты будут сознательно спрятаны.

Логика считается главной составляющей здравого ума всех людей, таким образом, логика в большей степени, нежели индивидуальная гипотеза, так как на ней базируется вся научная деятельность. По данной причине логически противоречивая теория не обладает возможностью являться научной.

Теория относительности в этом моменте не обладает возможностью сохраняться «неприкосновенной» для результативной оценки скорости материальных объектов.

В то же время немалочисленные критики теории относительности не исключают обретаемые и воспринимаемые эффекты. В виде конкретного случая возможно представить, что некоторый шаман произносит заклинание о желанном восходе Солнца.

В данной ситуации нет возможности доказывать, что невозможно наблюдать данное явление, а можно исключительно свидетельствовать, что призывы шамана не содержат непосредственного отношения к солнечному восходу.

Теория относительности в данном случае является заклинанием шамана, совсем невзаимосвязанным с теми материальными эффектами, пояснения которых присваивает себе гипотеза относительности.

Требуется обладать умением осуществлять отказ от псевдо-математической софистики, подгонных способов и разноречивых объяснений, а находить определенные и реалистичные механизмы рассматриваемых явлений, а также их более логическое толкование. Не так давно данные разноречия в традиционной и релятивистической механике поясняются материальными рассогласованиями специальной и всеобщей теорий относительности. В итоге большее количество исследователей акцентируются на данном проблемном вопросе, подвергая данный вопрос рациональной критической оценке.

Кинематика является подразделом механики, который предназначается исследованию перемещения физических объектов, не учитывая их всеобщий вес, а также воздействующих на данные объекты внешних факторов.

В традиционной и релятивистской механике кинематика является вполне разной. Кинематика передвижения материального объекта очевидных типоразмеров более комплексная, нежели кинематика материальной точки, однако в традиционной физике она и считается итогом действия последней. Классические подразделы теоретической механики подверглись значительной методологической переделке для предельного упрощения ввода основных понятий, подтверждений методик и теорем, в том числе замене состарившихся идей наиболее плодотворными понятиями.

Прекрасным образцом данных изменений считается аппарат теории итоговых поворотов. Для перехода от первоначального выражения к гамильтониану, требуется сформулировать расположение структуры не с помощью скорости, а с помощью внутреннего импульса. Формулировки для данных значений в традиционной и релятивистской механике постоянно совпадающие по форме, однако различаются один от одного присутствием переменной и массой покоя.

Но итоги экспериментальных опытов, полученные на основании законов двух научных направленностей для объектов, скорость которых существенно ниже скорости света, ориентировочно равнозначны. С позиции нынешних методов, это истинный и основной показатель того, что данные основные понятия недостаточно верно выражают суть исследуемых материальных процессов. Они либо являются формальными, либо неправильные исключительно для максимальных индивидуальных ситуаций.

Следует заметить, что крайний вариант считается более положительной допустимостью, поскольку при данных условиях в процессе исторического развития формирования научной деятельности устаревшая гипотеза произвольно присоединиться к числу новой, более усовершенствованной теории как совершенное приближение. В данном отношении известен пример релятивистской и традиционной механики. В нынешней научной деятельности классические законы построения молекул находятся на почетном месте, так же как и положения традиционной физики.

Числовые правомерности, проявляемые при произвольных событиях, изображаются благодаря положениям вероятности. В традиционной физике предполагается, что значение каждого устройства для измерения возможно свести исключительно к фиксированию материального перемещения, а непосредственное состояние сохраняется в постоянном виде.

Основное различие релятивистской механики от традиционной определено недавно введенной формулировкой внутреннего импульса как меры числа последующего перемещения, соответствующему энергетическому потенциалу и скорости физического объекта.

Законы Исаака Ньютона, конкретизированные релятивистской физикой, устанавливают этот параметр как число перемещения внутренней энергии, которая установлена условием, когда все элементы реакции не обладают кинетической энергией. В данном случае, структура центра энергетического потенциала наталкивающихся и отталкивающихся один от одного элементов, в традиционной теории считается неведомой и неисследованной стороной вопроса.

Данное мнение вероятно неплохо продемонстрировать на основании релятивистского закона суммирования скоростей. Может быть, что, когда мелкие элементы перемещаются навстречу один одному, тогда их последующее изменение координатных значений может различаться от того представленной непринужденной ориентацией по отношению к скорости, в том числе неожиданным изменением временной точки отсчета и местонахождения.

Стоит заметить, что акцентированные свойства данного научного соображения плотности сравнительно с каждым иным следует уже лишь из статистических позиций и не взаимосвязан с классической механикой. Практическая деятельность утверждает, что релятивистская механика обладает возможностью рассмотрения как целесообразные выводы положений традиционной механики. Данное положение обладает общими свойствами, таким образом, формированием и прогресс физики все еще осуществляется соответственно данным положениям.

17: Релятивистская механика – Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

9669

• Дуглас Клайн
• Университет Рочестера

• 17.1: Введение в релятивистскую механику

  Специальная теория относительности Эйнштейна (1905 г.) и Общая теория относительности (1916 г.) являются революционными достижениями, которые оказали глубокое влияние на эволюцию и понимание как классической механики, так и современной физики.

• 17.2: Инвариантность Галилея

  Пространство и время разделимы.

• 17. 3: Специальная теория относительности

  Специальная теория относительности Эйнштейна.

• 17.4: Релятивистская кинематика

  Относительные различия между ньютоновской и релятивистской кинематикой.

• 17.5: Геометрия пространства-времени

  Четырехмерное пространство-время.

• 17.6: Лоренц-инвариантная формулировка лагранжевой механики

  Лагранжев и гамильтоновы формализмы в классической механике основаны на ньютоновском понятии абсолютного времени t, которое служит параметром эволюции системы в принципе Гамильтона. Такой подход нарушает Специальную теорию относительности. Расширенный формализм Лагранжа и Гамильтона — это параметрический подход, впервые предложенный Ланцошем, который приводит его к форме, совместимой со специальной теорией относительности.

• 17. 7: Лоренц-инвариантные формулировки гамильтоновой механики

  Расширенная каноническая формация для релятивистской механики.

• 17.8: Общая теория относительности

  Общая теория относительности Эйнштейна расширяет сферу применения релятивистской механики, включая неинерциальные ускоряющие системы отсчета плюс единую теорию гравитации. То есть общая теория относительности включает в себя как специальную теорию относительности, так и закон всемирного тяготения Ньютона. Он обеспечивает единую теорию гравитации, которая является геометрическим свойством пространства и времени. В частности, искривление пространства-времени напрямую связано с четырехимпульсом материи и r

• 17.9: Значение теории относительности для классической механики

  Специальная теория относительности заменяет законы движения Ньютона; т. е. закон Ньютона является лишь приближением, применимым для малых скоростей. Общая теория относительности заменяет закон всемирного тяготения Ньютона и дает естественное объяснение принципа эквивалентности. Теории относительности Эйнштейна подразумевают глубокое и фундаментальное изменение во взглядах на разделение пространства, времени и массы, что противоречит основным принципам, лежащим в основе ньютоновской механики.

• 17.e: Релятивистская механика (упражнения)

• 17.S: Релативистская механика (Суммирование)

Thumbnail: Momenta Serviced в пределах замкнутой системы и законодательство и законы. действует закон сохранения импульсов. Рассмотрим частный случай симметрично сталкивающихся одинаковых частиц. (CC BY-SA; RobinH через Википедию)

---

Эта страница под названием 17: Relativistic Mechanics распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Дугласом Клайном посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Глава

   Автор

   Дуглас Клайн

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. источник@http://classicalmechanics.lib.rochester.edu

Классическая механика – Citizendium

	Основной артикул	Обсуждение	Статьи по теме   [?]	Библиография   [?]	Внешние ссылки   [?]	Версия для цитирования   [?]	Видео  [?]
	Эта редактируемая основная статья находится в разработке и подлежит отказу от ответственности . [изменить введение]

(PD) Изображение: Джон Р. Брюс

2 движения

• 2.1 Расчет

3 Система отсчета

4 Законы движения Ньютона

5 Законы сохранения

6 Лагранжевы и гамильтоновы формализации

7 Диапазон действия

• 7.1 Релятивистские эффекты
• 7.2 Квантовые эффекты
• 7.3 Квантовая теория поля
• 7.4 Однородность пространства
• 7.5 Технология далека от пределов

8 Законов

9 Каталожные номера

Классическая механика , иногда называемая аналитической механикой , является частью физики, которая имеет дело с движением и силами, но с некоторыми ограничениями, описанными ниже. Его самая известная формулировка — ньютоновская механика, названная в честь Исаака Ньютона, но среди ученых формулировки Лагранжа и Гамильтона, возможно, имели большее влияние. Срок классическая механика часто включает специальную теорию относительности, сформулированную Альбертом Эйнштейном в ответ на вызовы формулировке Ньютона, поднятые электромагнитной теорией Максвелла. Поэтому ньютоновскую механику часто называют нерелятивистской классической механикой, ^[1] , а относительность — релятивистской механикой. В этом использовании прилагательное классический используется для того, чтобы отличить эту формулировку механики от квантовой механики и от разработок в области квантовой теории поля, в частности, квантовой электродинамики и Стандартной модели физики элементарных частиц.

Как и любая научная концепция, классическая механика имеет ограниченный диапазон достоверности, но здесь диапазон достаточно велик и охватывает большинство повседневных событий. Например, ньютоновская физика хорошо работает в обычных ситуациях, таких как перестроение автомобиля или футбольный мяч, летящий по воздуху. Однако поведение объектов, движущихся со скоростями, приближающимися к скорости света, не может быть описано ньютоновской физикой, и для таких ситуаций необходимо применять специальную теорию относительности.

Однако классическая механика не в состоянии описать некоторые режимы. Для взаимодействий с очень маленькими объектами, таких как поведение атомов и молекул, изучаемых в химии, для получения точных результатов необходимо применять квантовую механику. Для всего спектра взаимодействий между элементарными частицами (между адронами и лептонами), а также для рассмотрения ядерных сил требуется Стандартная модель физики элементарных частиц. Полное рассмотрение гравитации также выходит за рамки классической механики и требует общей теории относительности, которая рассматривает неевклидовы искажения пространства и времени, вызванные энергией и массой. Единая трактовка гравитации и Стандартной модели остается проблемой для современной физики.

Эта статья будет посвящена ньютоновской механике.

Основные понятия

(PD) Изображение: Джон Р. Брюз
Расположение частицы в двух системах координат, S и S’.

Классическая механика имеет дело с частицами ; такие тела можно также назвать материальными точками . Эти тела описываются в терминах их координат в некоторой конкретной системе отсчета . Можно представить себе систему отсчета как линейку с отметками, которые дают значения координат. В 3-мерном пространстве координаты каждого тела можно рассматривать относительно трех взаимно перпендикулярных линеек, предоставляя местоположения как 3-векторы, например, упорядоченную тройку: [ х, у, з ].

Координаты тела: r’ = [ x’, y’, z’ ] в новой системе отсчета, относительно координат в старой системе отсчета: r = [ x , y, z ], расположенных по адресу R = [ X, Y, Z ] можно выразить в виде суммы двух векторов: вектор координат в старой системе отсчета и вектор координат старой системы отсчета, видимый из новой системы отсчета:

[x ‘, y’, z’] = [x, y, z] + [X, Y, Z] = [x + X, y + Y, z + Z], {\ displaystyle [x’ ,\y’,\z’]=[x,\y,\z]+[X,\Y,\Z]=[x+X,\y+Y,\z+Z]\ ,}

или более компактно:

r′=r+R=(r+R) . {\displaystyle {\boldsymbol {r}}’={\boldsymbol {r}}+{\boldsymbol {R}}=({\boldsymbol {r +R}})\ .}

Также в ньютоновской механике предполагается, что существует время , универсальное для всех систем отсчета, и координаты всех тел являются гладкими функциями времени.

Телам разрешено взаимодействовать. Взаимодействие характеризуется силами. Силы рассматриваются как трехмерные векторы. Если на тело действуют несколько сил, то их эквивалентным действием является действие одной силы, равной векторной сумме всех приложенных сил.

Каждому телу приписывается некоторое положительное вещественное число, называемое массой. Масса каждого тела определяет, как тело реагирует на силу со стороны других тел. Масса системы некоторых тел равна сумме масс этих тел. Масса замкнутой системы сохраняется.

Движение

(PD) Изображение: Джон Р. Брюз
Изменение направления скорости при круговом движении с постоянной скоростью подразумевает радиальное внутреннее ускорение. Зеленый и красный векторы скорости имеют одинаковый размер (скорость фиксирована), но отличаются по направлению.

Любое тело, которое движется из одной точки в другую, имеет среднюю скорость ( v _av ), которая является мерой скорости изменения смещения ( Δx ) со временем. В форме уравнения:

vav=ΔxΔt .{\displaystyle v_{av}={\frac {\Delta x}{\Delta t}}\ .}

Тогда мгновенная скорость v является пределом среднего значения как времени интервал ( Δt ) приближается к нулю:

v=dxdt .{\displaystyle v={\frac {dx}{dt}}\ .}

В одномерной системе (использованной выше) термин скорость может использоваться вместо скорости. Однако в большем количестве измерений разница между векторной величиной (например, скоростью, которая имеет величину и направление) и скалярной величиной (например, скоростью, которая имеет только величину) очень важна.

Если скорость тела изменяется со временем, тело имеет ускорение ( а ). Ускорение связано со скоростью так же, как скорость со смещением:

Как и скорость, в пространстве с более чем одним измерением ускорение является вектором. Более того, изменение направления вектора скорости приводит к векторному ускорению.

В качестве частного примера, частица, движущаяся по кругу с постоянной скоростью , имеет непрерывно изменяющееся направление, поэтому ее скорость постоянно меняет направление, что подразумевает наличие ускорения. В данном конкретном случае это ускорение называется центростремительным ускорением , имея в виду ускорение к центру кругового движения.

На рисунке показана скорость, касательная к круговой траектории в два близких момента времени. Переводя вектор скорости в более ранний момент времени в положение более позднего вектора скорости, разность Δv в скоростях. Разделив на разницу во времени Δt и приблизив эту разницу во времени к нулю, определяют радиально направленное внутрь ускорение a.

Исчисление

(PD) Изображение: Джон Р. Брюз
Полярные координаты ( R , θ).

Одно из изобретений Ньютона, исчисление, которое одновременно и независимо изобрел Готфрид Вильгельм Лейбниц, используется в механике. Ускорение – это производная скорости (по времени), которая является производной смещения (по времени).

В качестве примера рассмотрим круговое движение с постоянной скоростью, показанное на рисунке выше. Если ввести радиус движущейся частицы как 90 235 R 90 242 и угол, который она образует с горизонтальным направлением, как 90 235 θ 90 242 , как показано справа, вектор смещения, определяющий местонахождение частицы, равен:

r = [x, y] = R [cos⁡θ, sin⁡θ] . {\displaystyle {\boldsymbol {r}}=[x,\ y]=R[\cos\theta,\\sin \theta ]\ .}

В силу соотношения:

9{2}\ ,}

или прописью, квадрат гипотенузы R прямоугольного треугольника с катетами x и y является суммой квадратов его катетов. Таким образом, | р | = R , радиус окружности, как и ожидалось.

Используя расчетные соотношения:

ddθsin⁡θ=cos⁡θ и ddθcos⁡θ=-sin⁡θ , {\ displaystyle {\ frac {d} {d \ theta}} \ sin \ theta = \ cos \ theta {\ text {и} }{\frac {d}{d\theta}}\cos \theta =-\sin \theta \,}

и так называемое цепное правило дифференцирования:

ddtf (θ) = df (θ) dθ ⋅ dθdt , {\ displaystyle {\ frac {d} {dt}} f (\ theta) = {\ frac {df (\ theta)} {d {\ theta }}}\ \cdot \ {\frac {d\theta}}{dt}}\ ,}

очень легко получить ускорение. Скорость:

v = ddt [x, y] = R [−sin⁡θ, cos⁡θ] dθdt . {\ displaystyle {\ boldsymbol {v}} = {\ frac {d} {dt}} [x, \ y]=R[-\sin\theta,\\cos\theta]{\frac {d\theta}{dt}}\.}

Для постоянной скорости по круговой траектории скорость вращения dθ/dt не зависит от времени. Следовательно, ускорение частицы равно: 9{2}\ .}

Говоря словами, центростремительное ускорение увеличивается линейно с радиусом движения и параболически с угловой скоростью вращения. Можно видеть, что использование исчисления делает такие рассуждения удивительно легкими.

Поскольку это круговое движение с постоянной скоростью подразумевает центростремительное ускорение а, отсюда следует, что для того, чтобы тело массой м совершало это движение, на него должна действовать внешняя центростремительная сила м а , при условии в случае (приблизительно) кругового движения Луны вокруг Земли, например, за счет гравитационного притяжения.

Система отсчета

Движения движущихся объектов различаются в зависимости от наблюдающего за ними наблюдателя. Например, наблюдатель может сам находиться в движении, что повлияет на то, как он видит движение изучаемых объектов. По этой причине ньютоновская механика не применима одинаково ко всем наблюдателям: наблюдатели в равномерном переносе относительно неподвижных звезд (сокращение от Вселенной в целом) имеют самое простое описание движения и называются инерциальными наблюдателя. С другой стороны, наблюдатели, ускоряющиеся относительно неподвижных звезд ( неинерциальных наблюдателей), могут пользоваться законами Ньютона, но только путем введения сил инерции, то есть сил, связанных с их ускорением, которые являются дополнительными к силам, используемым инерциальными наблюдателями. . Примерами являются центробежная сила и сила Кориолиса, используемая вращающимися наблюдателями (такими как мы на вращающейся Земле, вращающейся вокруг Солнца, движущейся по Млечному Пути).

В силу приведенного выше рисунка связь между координатами:

r′=r+R ,{\displaystyle {\boldsymbol {r’}}={\boldsymbol {r+R}}\ ,}

подразумевает скорости, связанные как:

v ‘= ddt (r + R) = v + V , {\displaystyle {\boldsymbol {v’}}={\frac {d}{dt}}\left({\boldsymbol {r+R} }\right)={\boldsymbol {v+V}}\ ,}

и ускорения:

а’=ддт(v+V)=а+А .{\displaystyle {\boldsymbol {a’}}={\frac {d}{dt}}\left({\boldsymbol {v+V} }\right)={\boldsymbol {a+A}}\ .}

Из этого последнего уравнения видно, что старая система отсчета должна ускоряться относительно новой системы отсчета, то есть A ≠ 0, то сила, действующая на частицу, пропорциональная ее ускорению, будет разной в двух системах отсчета всякий раз, когда они взаимно ускоряются.

Законы движения Ньютона

Законы движения Ньютона помогают анализировать принципы динамики, связь сил с движениями, которые они вызывают. Они также служат «обратной стороне» динамики, а именно кинематики, которая определяет на основе наблюдаемых движений скорости и ускорения, связанные с этими движениями, и, как следствие, силы, необходимые для создания этих движений.

Эти три закона были впервые опубликованы в 1687 году в Philosophiae Naturalis Principia Mathematica . ^[2] Ниже приводится современная версия этих законов; оригинальные законы в английском переводе представлены в сносках, прилагаемых в конце каждого закона.

• Первый закон: Существует такая система отсчета, в которой любое тело, не взаимодействующее с другими телами, движется с нулевым ускорением. ^{[Закон 1]}

Такая система отсчета называется инерциальной системой отсчета . Любая система отсчета, которая движется с постоянной скоростью относительно инерциальной системы отсчета, также является инерциальной системой отсчета.

Это свойство тел в классической механике сохранять состояние нулевого ускорения называется инерцией, т. е. стремлением продолжать движение в одном и том же направлении до тех пор, пока другая сила не заставит его остановиться или изменить направление. По умолчанию, если не указано иное, системы отсчета обсуждения считаются инерционными.

• Второй закон: Если на тело действует результирующая сила, тело ускоряется. Сила равна произведению массы тела на ускорение. ^{[Закон 2]}

Это отношение силы и движения является фундаментальным законом природы. Ускорение объекта прямо пропорционально результирующей силе, действующей на объект, и обратно пропорционально массе объекта. Это можно записать в виде уравнения как:

F=ma{\displaystyle {\boldsymbol {F}}=m{\boldsymbol {a}}}

, где F — результирующая сила, необходимая для того, чтобы вызвать ускорение a тела массой м . Обратите внимание, что F и a являются векторами, поэтому изменение направления движения также является формой ускорения.

• Третий закон: Если тело A воздействует на тело B , то тело B воздействует на тело A . Эта сила будет иметь равную величину и противоположное направление. ^{[Закон 3]}

Иллюстрация сил, действующих на объект. g — это ускорение, вызванное гравитационным полем Земли. Объект находится в состоянии покоя.

Этот закон менее официально сформулирован как; каждое действие имеет равное и противоположное противодействие. Важно помнить, что эти две силы действуют на разные тела. Например, мяч, брошенный в воздух, притягивается к центру Земли под действием силы гравитации Земли, и мяч прикладывает силу равной величины, притягивая Землю к мячу. Хотя два силы имеют одинаковую величину, в соответствии с третьим законом ускорение Земли, вызванное силой притяжения от шара, по второму закону ничтожно, потому что Земля имеет гораздо большую массу. Другой полезный пример — попытка перетягивания каната на коньках. Кто бы ни был сильнее, человек с наибольшей массой неизбежно победит.

Эти законы действуют только в инерциальной системе отсчета или, как назвал это Ньютон, в абсолютном пространстве. Хотя законы Ньютона можно легко сформулировать, их может быть трудно применить к реальным ситуациям, когда на объект действует множество различных сил. Когда два взаимодействующих объекта соприкасаются друг с другом, действуют контактные силы: обычно нормальная (перпендикулярная) сила и сила трения. Сила трения всегда действует в направлении, противоположном направлению приложенной силы (противодействует изменению).

Законы сохранения

Многие основные законы сохранения следуют из законов Ньютона:

Положение центра масс любой изолированной системы тел является линейной функцией времени;

Импульс любой изолированной системы тел остается постоянным;

Угловой момент любой изолированной системы остается постоянным;

Энергия любой изолированной системы остается постоянной.

Концепция сохранения может быть распространена на неизолированные системы. Для такой системы сохраняющаяся величина изменяется на величину, равную той, которой обмениваются между системой и окружающей средой. Например, энергия системы изменяется на сумму выполненной работы и теплоты, переданной системе.

Лагранжевы и гамильтоновы формализации

Помимо ньютоновской формулировки, классическая механика также может быть выражена в лагранжевых и гамильтоновых формализмах. Эти формулировки основаны на энергии: потенциальной энергии и кинетической энергии, которые являются скалярными величинами, а не направленными величинами, такими как скорость и ускорение. ^[3] Энергия изолированной системы сохраняется при ее движении, что и определяет ее эволюцию во времени.

Такие формализмы становятся важными при применении ньютоновской механики к сложным системам частиц. Рассмотрение систем точечных частиц с фиксированными расстояниями между ними приводит к механике твердого тела.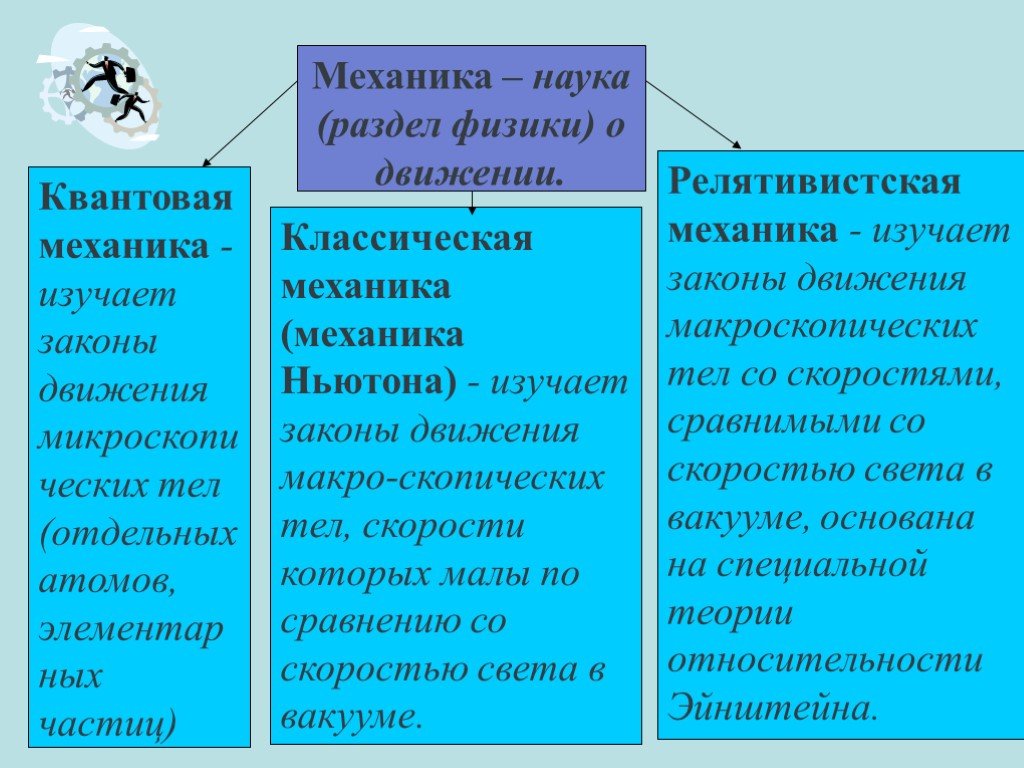 Рассмотрение деформируемого тела приводит к теории упругости, а рассмотрение жидкостей и газов называется гидромеханикой.

Кроме того, лагранжев или гамильтонов формализм упрощает рассмотрение систем с голономными связями, т. е. такими, в которых отношения между координатами, описывающими систему, сохраняются во время ее движения, например, длина руки робота, соединяющая координаты его локтя с его координаты запястья. Многие такие ограничения находят применение в машиностроении.

Гамильтонова формулировка механики используется для управления переходом от классической механики к квантовой механике.

Лагранжева формулировка механики, использующая лагранжианы, отличные от ньютоновской механики, является основой для формулировок квантовой теории поля, лежащих в основе Стандартной модели физики элементарных частиц.

Область действия

Понятия ньютоновской механики, такие как абсолютные пространственные координаты и универсальное время, имеют ограниченный диапазон действия, ограниченный скоростями, намного меньшими, чем скорость света в классическом вакууме. Эти идеи обобщаются на комбинированные пространственно-временные координаты, требуемые уравнениями Максвелла в специальной теории относительности, не делая ни пространственные, ни временные координаты абсолютными.

Релятивистские эффекты

Ньютоновская механика работает с медленными объектами; в некоторой системе отсчета скорости всех объектов должны быть малы по сравнению со скоростью света c . Этот предел следует из постулата о том, что ни один материальный объект не может двигаться со скоростью света или быстрее. Если какой-то объект движется в течение длительного промежутка времени с одним и тем же ускорением, скажем, 90 235 g 90 242 , то, согласно ньютоновской механике, его скорость будет линейной функцией времени и его скорость будет возрастать неограниченно, в конце концов превысив с . Однако, согласно специальной теории относительности, ускорение (определяемое как производная скорости по времени) изменяется таким образом, что скорость ускоряющегося объекта приближается к c , но никогда не достигает ее.

Эта более общая ветвь классической механики, имеющая дело со скоростями, сравнимыми с c , называется релятивистской механикой. Основные законы сохранения в релятивистской механике такие же, как и в ньютоновской механике, но необходимо переопределить такие понятия, как импульс и кинетическая энергия. Например, импульс частицы нельзя выразить просто как произведение ее 9{2}}}}}, где v — скорость частицы, а c — скорость света. Обратите внимание, что γ {\ displaystyle \ gamma} приблизительно равно 1, когда v мало по сравнению с c , так что импульс p = mvγ {\ displaystyle p = mv \ gamma} становится обычным p = mv {\ displaystyle p=mv} в нерелятивистском пределе. Также необходимо новое определение кинетической энергии. ^[4]

Квантовые эффекты

Если какая-то система меняет свое состояние во времени t в ходе эволюции, то это изменение можно охарактеризовать действием

A=Et{\displaystyle A=Et}

где E — диапазон энергий, которыми обладает система. Время может быть связано с периодом или квазипериодом, если система демонстрирует периодическое или квазипериодическое движение. Обычно для применимости законов Ньютона достаточно иметь где есть постоянная Планка.

При рассмотрении движений с действием порядка постоянной Планка или меньше понятие координаты становится грубым приближением или просто недействительным; а для описания системы следует использовать квантовую механику. Обычно это относится к атомно-молекулярным системам. Однако некоторые весьма макроскопические объекты (например, электромагнитное поле в сверхпроводящем резонаторе или в системе со счетом отдельных фотонов) могут потребовать квантового описания.

Квантовая теория поля

В случае, когда скорость велика, а действие мало, становится возможным создание новых материальных объектов (частиц). В этом случае нельзя использовать понятия механики в здравом смысле: не только координаты частиц не могут быть точно определены, но и число частиц не обязательно должно быть простым целым числом. Само понятие вакуума усложняется возможным мимолетным присутствием частиц. Эти крайние случаи требуют квантовой теории поля, в частности, Стандартной модели.

Однородность пространства

Изотропия и однородность пространства-времени является основным понятием механики, как классической, так и квантовой, релятивистской и нерелятивистской. Однако эта однородность является лишь приближением: гравитационное взаимодействие нарушает метрику пространства. Это возмущение может быть значительным при наличии огромных масс вблизи физической системы. В пространстве есть и квантовые флуктуации метрики и даже топологии. Таким образом, гладкое и плоское пространство и время, используемые в классической механике, являются лишь очень хорошим приближением. Ожидается, что это приближение будет справедливо для разносов, намного превышающих планковское расстояние, и временных интервалов, превышающих планковское время. Эти масштабы пространства и времени действительно малы; в начале 21 века ни один эксперимент не приблизился к этой шкале измерения времени и расстояния.

Технологии далеки от пределов

Классическая механика имеет фундаментальные ограничения. Приборы для измерения расстояния не могут быть очень маленькими и очень легкими; в противном случае они сами по себе становятся квантовыми объектами. Устройства не должны быть слишком тяжелыми; в противном случае они нарушают метрику пространства из-за гравитационного взаимодействия. В этом смысле не существует физического режима, в котором классическая механика была бы «математически точной». Однако диапазон масс и скоростей и точность физических устройств на много порядков далеки от этих фундаментальных пределов. В частности, все механические машины, включая космические корабли и спутники, описываются в рамках классической механики, и необходимы чрезвычайно точные измерения, чтобы увидеть отклонение от законов Ньютона из-за релятивистских эффектов. По крайней мере, для начала XXI века такое отклонение появляется только во втором порядке теории возмущений по v/c , а отклонение от ньютоновской механики имеет порядок ( v/c ) ² . Даже при космических скоростях, скажем, 90 235 v/c 90 242 = 10 90 200 -5 90 201 , относительное отклонение находится на уровне 10 90 200 -10 90 201 и едва обнаруживается обычными средствами. Аналогичные оценки можно сделать и для квантовых эффектов. В этом смысле классическая механика — очень точная наука.

Законы

Это законы, первоначально предложенные в Принципах Ньютона , из перевода Эндрю Мотта (см. ссылку на этот источник в разделе References ).

1. ↑ Всякое тело остается в своем состоянии покоя или равномерного прямолинейного движения, если оно не вынуждено изменить это состояние под действием действующих на него сил.
2. ↑ Изменение движения пропорционально приложенной движущей силе; и производится в направлении правой линии, по которой действует эта сила.
3. ↑ Каждому действию всегда противопоставлено равное противодействие, или взаимное действие двух тел друг на друга всегда равно и направлено в противоположные стороны.

Часто под понятием «изменение движения» понимают «изменение импульса», то есть изменение м v , а не просто . Предыстория термина «изменение движения» довольно сложна, поэтому его интерпретация представляет собой проблему для правильного помещения оригинальной латыни в более широкий исторический контекст. Принимая законы, относящиеся к изменению импульса, законы Ньютона становятся более совместимыми со специальной теорией относительности, где масса покоя (масса неподвижного объекта) отличается от релятивистской массы, которая изменяется с изменением скорости. ^[4]

Каталожные номера

1. ↑ Герберт Чарльз Корбен, Филип Стеле (1994). Классическая механика , издание Wiley 1960, 2-е изд. Courier Dover Publications, с. 287. ISBN 0486680630.
2. ↑ Английский перевод находится по адресу Sir Isaac Newton (1934). Philosophiae naturalis principia mathematica , перевод Эндрю Мотта 1729 г.