Минимальное количество баллов
Контакты
Календарь абитуриента
Школьникам
Личный кабинет
Дни
открытых
дверей
2021
Дни
открытых
дверей
2023
Результаты ЕГЭ и вступительных испытаний, проводимых МАИ в 2023 году самостоятельно, подтверждающие успешное прохождение вступительных испытаний по общеобразовательным предметам, входящим в перечень вступительных испытаний, для лиц, поступающих на программы бакалавриата и программы специалитета в МАИ на места, финансируемые за счёт бюджетных ассигнований федерального бюджета.
| # | Общеобразовательный предмет | Минимальный балл |
|---|---|---|
| 1. | Русский язык | 50 |
| 2. | Математика профильного уровня | 46 |
3. | Информатика и информационно-коммуникационные технологии (ИКТ) | 48 |
| 4. | Физика | 44 |
| 5. | Обществознание | 50 |
| 6. | Иностранный язык | 50 |
| 8. | География | 45 |
| 9. | Биология | 40 |
Результаты ЕГЭ и вступительных испытаний, проводимых МАИ в 2023 году самостоятельно, подтверждающие успешное прохождение вступительных испытаний по общеобразовательным предметам, входящим в перечень вступительных испытаний, для лиц, поступающих на программы бакалавриата и программы специалитета в МАИ на места
| # | Общеобразовательный предмет | Минимальный балл |
|---|---|---|
1. | Русский язык | 40 |
| 2. | Математика профильного уровня | 39 |
| 3. | Информатика и информационно-коммуникационные технологии (ИКТ) | 44 |
| 4. | Физика | 39 |
| 5. | Обществознание | 45 |
| 6. | Иностранный язык | 30 |
| 7. | История | 35 |
| 8. | География | 40 |
| 9. | Биология | 39 |
Результаты ЕГЭ и вступительных испытаний, проводимых МАИ в 2023 году самостоятельно, подтверждающие успешное прохождение вступительных испытаний по общеобразовательным предметам, входящим в перечень вступительных испытаний, для лиц, поступающих на программы бакалавриата и программы специалитета на

| # | Общеобразовательный предмет | Минимальный балл |
|---|---|---|
| 1. | Русский язык | 40 |
| 2. | Математика профильного уровня | 39 |
| Информатика и информационно-коммуникационные технологии (ИКТ) | 44 | |
| 4. | Физика | 39 |
| 5. | Обществознание | 45 |
Минимальное количество баллов (бакалавриат и специалитет)
- Главная
| Вступительное испытание |
БЮДЖЕТ |
Минимальное количество баллов для поступающих
на места с оплатой стоимости обучения
КОНТРАКТ |
|
На базе среднего общего и высшего образования |
||
Русский язык |
45 |
40 |
Математика |
45 |
39 |
Физика |
45 |
39 |
Информатика |
50 |
44 |
Обществознание |
55 |
45 |
История |
55 |
35 |
Иностранный язык |
55 |
30 |
Рисунок, живопись и композиция |
50 |
40 |
| На базе среднего профессионального образования | ||
Русский язык |
|
40 |
Математика в профессиональной деятельности |
45 |
39 |
Основы механики и электротехники |
45 |
39 |
Основы алгоритмизации и программирования |
44 |
|
Основы экономики и менеджмента |
55 |
45 |
Основы развития гражданского общества и государства |
55 |
45 |
Россия в мировом сообществе | 55 |
35 |
Рисунок, живопись и композиция |
50 |
40 |
| 1 цифра (S) | 54.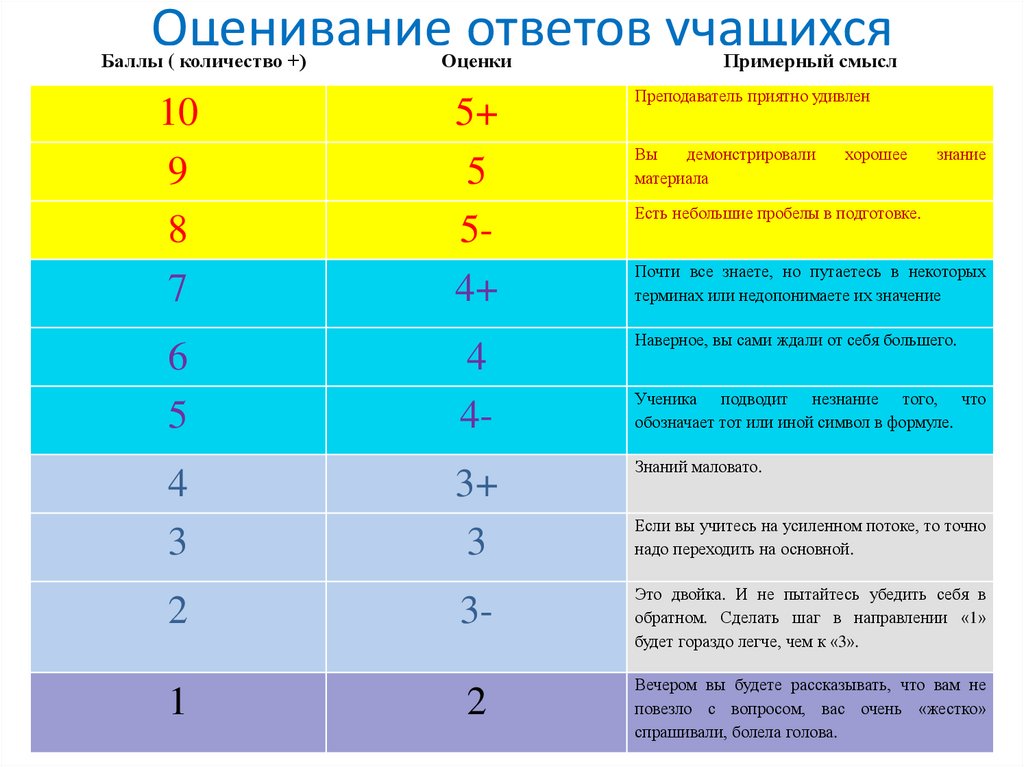 00035 PTS (S) (54) 00035 PTS (S) (54) | |||
| 2 цифр (S) | 108.0007 (S) (108) | |||
| 3 цифра (S) | 162.00105 PTS (S) (162) | |||
| 4 цифр (S) | 216,0014 PTS (S) (216) | |||
| 5 цифр (S) | 270.00175 PTS (S) PTS (S) PTS (S). (270) | |||
| 6 цифр | 324,0021 баллов (324) | |||
| 7 цифр (S) | 378,00245 PTS (S) (378) | |||
| 8 цифр (S) | 432,0028 PTS (S) (432) | |||
| 9 Digit (S) | 486,00315. | |||
| 5 | 486.00315T ) (486) | |||
| 10 цифр (S) | 540,0035 PTS (S) (540) | |||
| 11 Digit (S) | 594,00385 PTS (S) (594) | 12 DIGIT (S) (S) (S) (S) (S) (594) | 14 12 Digit (S) (S) (S) (S) (S) (S) (S) (S) (S) (S) (S) (S) (S) (S). ) | 648,0042 баллов (648) |
| 13 цифр | 702,00455 баллов (702) | |||
| 14 цифр (S) | 756,0049 PTS (S) (756) | |||
| 15 цифр (S) | 810,00525 PTS (S) (810) | |||
| 16 Digit (S) | 9000 864.||||
| 16 Digit (S) | 9 864.005. (S) (864)||||
| 17 цифр (S) | 918.00595 PTS (S) (918) | |||
| 18 Digit (S) | 972.0063 PTS (S) (972) | |||
| 1026,00665 pts (s) (1026) | ||||
| 20 цифр | 1080,007 pts (s) (1080) | |||
| 21 digit(s) | 1134.00735 pts(s) (1134) | |||
| 22 digit(s) | 1188.0077 pts(s) (1188) | |||
| 23 digit(s) | 1242.00805 PTS (S) (1242) | |||
| 4 24 Digit (S) | 1296,0084 PTS (S) (1296) | |||
| 25 цифр (S) | 1350,00875 PTS (S) (1350) | |||
| 1404,0091 балл(ы) (1404) | ||||
| 27 цифра(ы) | 1458.00945 pts(s) (1458) | |||
| 28 digit(s) | 1512.0098 pts(s) (1512) | |||
| 29 digit(s) | 1566.01015 pts(s) (1566) | |||
| 30 цифр (S) | 1620.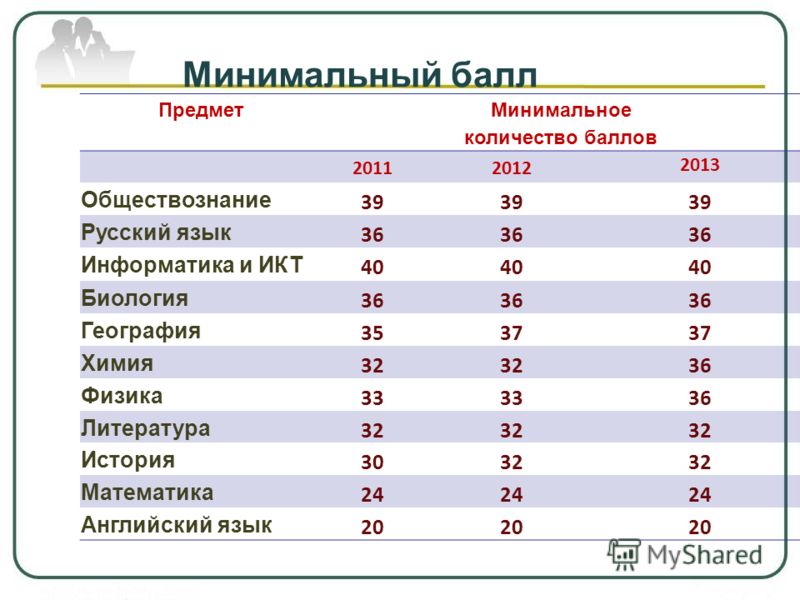 0105 PTS (S) (1620) 0105 PTS (S) (1620) | |||
| 31 цифр (S) | 1674.01085 PTS (S) (1674) | |||
| 32 -цифра (S) | 1728.0112TS (S) | 1728.0112TS (S) | 1728. ) (1728) | |
| 33 цифры | 1782,01155 баллов (1782) | |||
| 34 цифра (S) | 1836.0119 PTS (S) (1836) | |||
| 35 цифр (S) | 1890.01225 PTS (S) (1890) | |||
| 36 DIGIT (S) | 44.012669 20003 | 36 36 DIGIT (S) | ||
| 37 Digit (S) | 1998.01295 PTS (S) (1998) | |||
| 38 Digit (S) | 2052.0133 (S) (S) (S) (S) (S) (S) (S) (2052) | |||
| 3933 DIGIT (S) (2052) | ||||
| 39.0133 (S) (2052) | 9000||||
| 2106,01365 баллов (2106) | ||||
| 40 цифр | 2160,014 баллов (2160) | |||
| 41 digit(s) | 2214.01435 pts(s) (2214) | |||
| 42 digit(s) | 2268. 0147 pts(s) (2268) 0147 pts(s) (2268) | |||
| 43 digit(s) | 2322.01505 PTS (S) (2322) | |||
| 44 цифр (S) | 2376.0154 PTS (S) (2376) | |||
| 45 цифр (S) | 2430.01575 PT цифра(ы) | 2484,0161 баллов (2484) | ||
| 47 цифра(ы) | 2538.01645 pts(s) (2538) | |||
| 48 digit(s) | 2592.0168 pts(s) (2592) | |||
| 49 digit(s) | 2646.01715 pts(s) (2646) | |||
| 50 цифр (S) | 2700.0175 PTS (S) (2700) | |||
| 51 Digit (S) | 2754.01785 PTS (S) (2754) | |||
| 52 DIGIT (S) | 2808.0182. | |||
| . ) (2808) | ||||
| 53 цифры | 2862,01855 баллов (2862) | |||
| 54 digit(s) | 2916.0189 pts(s) (2916) | |||
| 55 digit(s) | 2970.01925 pts(s) (2970) | |||
| 56 digit(s) | 3024.0196 pts( S) (3024) | |||
| 57 Digit (S) | 3078. 01995 PTS (S) (3078) 01995 PTS (S) (3078) | |||
| 58 Digit (S) | 3132.0203 PTS (S) (3132) | |||
| 5959 599 599 5929. s) | 3186,02065 баллов (3186) | |||
| 60 цифр | 3240,021 баллов (3240) | |||
| 61 digit(s) | 3294.02135 pts(s) (3294) | |||
| 62 digit(s) | 3348.0217 pts(s) (3348) | |||
| 63 digit(s) | 3402.02205 PTS (S) (3402) | |||
| 64 цифр (S) | 3456.0224 PTS (S) (3456) | |||
| 65 Digit (S) | 3510.02275 PTS (S) (5510) | |||
| 9 3510.02275. цифра(ы) | 3564,0231 баллов (3564) | |||
| 67 цифра(ы) | 3618.02345 PTS (S) (3618) | |||
| 68 Digit (S) | 3672.0238 PTS (S) (3672) | |||
| 69 Digit (S) | 3726. 02415 PTS (S) (S) 02415 PTS (S) (S) | 3726.02415 PTS (S). | 70 цифр (S) | 3780.0245 PTS (S) (3780) |
| 71 Digit (S) | 3834.02485 PTS (S) (3834) | |||
| 72 DigiT (S) | 388888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888 ) (3888) | |||
| 73 цифры | 3942,02555 баллов (3942) | |||
| 74 digit(s) | 3996.0259 pts(s) (3996) | |||
| 75 digit(s) | 4050.02625 pts(s) (4050) | |||
| 76 digit(s) | 4104.0266 pts( s) (4104) | |||
| 77 digit(s) | 4158.02695 pts(s) (4158) | |||
| 78 digit(s) | 4212.0273 pts(s) (4212) | |||
| 79 digit( s) | 4266,02765 баллов (4266) | |||
| 80 цифр | 4320,028 баллов (4320) | |||
| 81 digit(s) | 4374.02835 pts(s) (4374) | |||
| 82 digit(s) | 4428.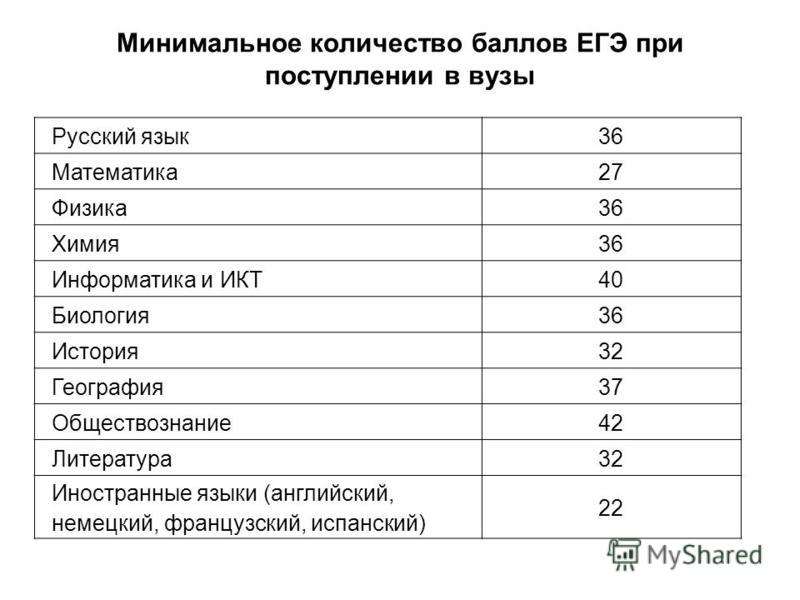 0287 pts(s) (4428) 0287 pts(s) (4428) | |||
| 83 digit(s) | 4482.02905 pts(s) (4482) | |||
| 84 digit(s) | 4536.0294 pts(s) (4536) | |||
| 85 digit(s) | 4590.02975 pts(s) (4590) | |||
| 86 цифра(ы) | 4644,0301 баллов (4644) | |||
| 87 цифра(ы) | 4698.03045 PTS (S) (4698) | |||
| 88 цифр (S) | 4752.0308 PTS (S) (4752) | 89 Digit (S) | 4806.03115 PTS (S) (S) | 4 4806.03115 PTS (S) (S) (S) | 4806.03115 (S) 98068 | 4 4806.03115 (S) 98068 | 4 4806.03115 (S) 98068 | 4 4806.03115. | 90 digit(s) | 4860.0315 pts(s) (4860) |
| 91 digit(s) | 4914.03185 pts(s) (4914) | |||
| 92 digit(s) | 4968.0322 pts(s ) (4968) | |||
| 93 цифры | 5022,03255 баллов (5022) | |||
| 94 digit(s) | 5076.0329 pts(s) (5076) | |||
| 95 digit(s) | 5130.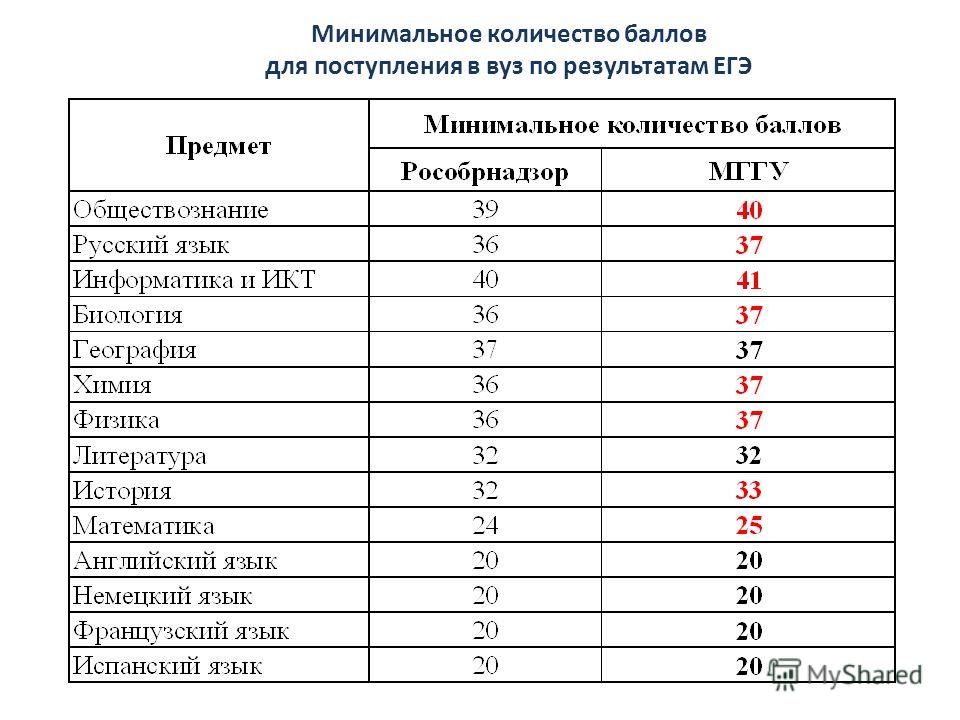 03325 pts(s) (5130) 03325 pts(s) (5130) | |||
| 96 digit(s) | 5184.0336 pts( s) (5184) | |||
| 97 digit(s) | 5238.03395 pts(s) (5238) | |||
| 98 digit(s) | 5292.0343 pts(s) (5292) | |||
| 99 digit( s) | 5346,03465 баллов (5346) | |||
| 100 цифр | 5400,035 баллов (5400) |
3. В бесконечности линии и квадраты имеют одинаковое количество точек
В предыдущих сообщениях мы установили, что два множества имеют одинаковый размер, если существует однозначное соответствие между элементами обоих наборы. Применение этого принципа к теории бесконечности Кантора приводит нас к странному, но верному выводу, что количество точек на отрезке равно количеству точек в квадрате. Чтобы показать, что это так, вот изображение отрезка единичной длины и единичного квадрата.
Выберем точку на отрезке. Скажем, 0,6917381276543… . Он показан большой синей точкой на отрезке слева. Если эта точка соответствует иррациональному числу 90 609, то 90 610 она будет продолжаться вечно, не повторяясь и не показывая различимой закономерности.
Если эта точка соответствует иррациональному числу 90 609, то 90 610 она будет продолжаться вечно, не повторяясь и не показывая различимой закономерности.
Мы собираемся разбить это число на два числа. Первое число – это любая вторая цифра. Под сегментом линии красным цветом показано это число, а именно 0,6131753… . Остальные цифры образуют второе число, показанное зеленым цветом. это 0,978264… .
Таким образом, одно число от нуля до единицы можно разбить на два числа от нуля до единицы. Мы можем взять эти два числа и как координаты x и y на единичном квадрате, показанном справа. Они определяют синюю точку, показанную в квадрате справа. Таким образом, синяя точка на отрезке линии отображается на синюю точку в квадрате.
Для каждой точки на отрезке есть одна и только одна синяя точка в квадрате. Размер множеств бесконечности на отрезке и в квадрате точно такой же. Расширение этого аргумента показывает, что количество точек в кубе такое же, как количество точек на отрезке. Это нелогично и странно.
Это нелогично и странно.
2022) Роберта Дж. Маркса доступно здесь.)
Также возможно обратное преобразование квадрата в сегмент линии. Возьмите две координаты, определяющие синюю точку в квадрате, и перемешайте их вместе, чтобы получить одно число. Два числа от нуля до единицы всегда можно объединить, чтобы получить одно число от единицы до нуля. Это новое число является точкой на отрезке.
Поскольку каждая точка отрезка прямой соответствует каждой точке квадрата, количество точек на отрезке равно количеству точек в квадрате.
Но разве вы не можете нарисовать отрезок и квадрат на листе бумаги и сделать сопоставление? Разве это не иллюстрация бесконечности в реальности? Нет. Предполагается, что каждая точка измеряется с бесконечной точностью. В реальности точность всегда конечна. Таким образом, вывод о том, что бесконечностей в действительности не существует, остается верным.
Этот противоречивый результат, основанный на теории бесконечностей Кантора, странен. Тем не менее, это верное свойство бесконечности.
Тем не менее, это верное свойство бесконечности.
Следующий: 906:10 Мы покажем, что вся Библиотека Конгресса закодирована в цифровом виде почти каждым случайно выбранным числом.
Мы надеемся, что вам понравится эта серия статей об уникальной, бросающей вызов реальности природе математических бесконечностей. Вот все пять частей — и бонус:
Часть 1: Почему бесконечности не существует в реальности. Несколько примеров покажут, к каким абсурдным результатам приводит предположение, что в окружающем нас мире существует бесконечность, как в математике. В серии из пяти постов я объясняю разницу между тем, что означает — и не означает — бесконечность как понятие.
Часть 2. Бесконечность показывает, что у Вселенной есть начало. Логические последствия буквально бесконечного прошлого абсурдны, как покажет простой пример. Абсурдность, которую создало бы бесконечное прошедшее время, хотя и не является окончательным математическим доказательством, является веским доказательством того, что наша Вселенная имела начало.
Часть 3. В бесконечности линии и квадраты имеют одинаковое количество точек Роберт Дж. Маркс: Мы можем продемонстрировать этот факт с помощью простой диаграммы. Этот контринтуитивный результат, основанный на теории бесконечностей Кантора, кажется странным. Тем не менее, это верное свойство бесконечности.
Часть 4. Как практически любые числа можно закодировать Библиотека Конгресса. Роберт Дж. Маркс: Это странное, парадоксальное, но вполне реальное следствие концепции бесконечности в математике. Математика: Почти каждое число между нулем и единицей, случайно выбранное при подбрасывании монеты, в какой-то момент будет содержать двоичную кодировку Библиотеки Конгресса.
и
Часть 5. Некоторые бесконечности больше других, но самой большой из них не существует Георг Кантор придумал гениальное доказательство того, что бесконечности могут различаться по размеру, даже если обе остаются бесконечными. В этой короткой серии из пяти частей мы показываем, что бесконечность — это красивая и доказуемая математическая теория, которая не может существовать в реальности без нелепых последствий.

 005.
005.