По какой формуле можно произвести расчёт удельной теплоёмкости вещества (Cp)
Удельная теплоёмкость — это энергия, которая требуется для увеличения температуры 1 грамма чистого вещества на 1°. Параметр зависит от его химического состава и агрегатного состояния: газообразное, жидкое или твёрдое тело. После его открытия начался новый виток развития термодинамики, науки о переходных процессах энергии, которые касаются теплоты и функционирования системы.
Как правило, удельная теплоёмкость и основы термодинамики используются при изготовлении радиаторов и систем, предназначенных для охлаждения автомобилей, а также в химии, ядерной инженерии и аэродинамике. Если вы хотите узнать, как рассчитывается удельная теплоёмкость, то ознакомьтесь с предложенной статьёй.
Содержание:
- Формула
- Инструкция по расчёту параметра
- Расчёт
- Как рассчитать теплоемкость продуктов питания
- Полезные советы
- Видео
Формула
Перед тем, как приступить к непосредственному расчёту параметра следует ознакомиться с формулой и её компонентами.
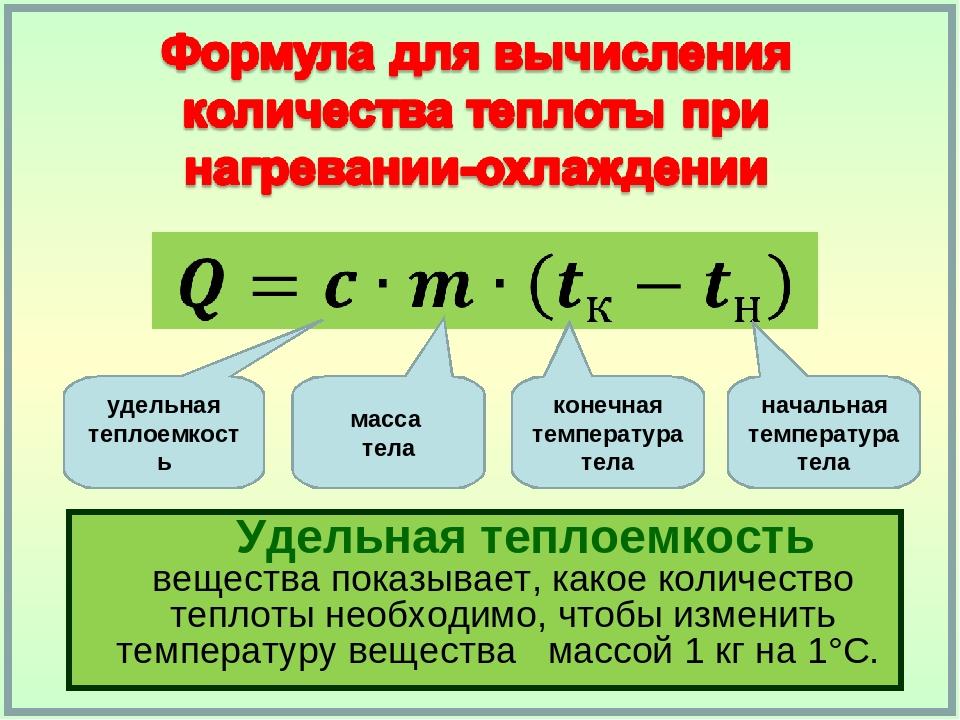
Формула для расчёта удельной теплоёмкости имеет следующий вид:
- с = Q/(m*∆T)
Знание величин и их символических обозначений, использующихся при расчёте, крайне важно. Однако необходимо не только знать их визуальный вид, но и чётко представлять значение каждого из них. Расчёт удельной теплоёмкости вещества представлен следующими компонентами:
ΔT – символ, означающий постепенное изменение температуры вещества. Символ «Δ» произносится как дельта.
ΔT можно рассчитать по формуле:
ΔT = t2–t1, где
- t1 – первичная температура;
- t2 – конечная температура после изменения.
m – масса вещества используемого при нагреве (гр).
Q – количество теплоты (Дж/J)
На основании Цр можно вывести и другие уравнения:
- Q = m*цp*ΔT – количество теплоты ;
- m = Q/цр*(t2 – t1) – массы вещества;
- t1 = t2–(Q/цp*m) – первичной температуры;
- t2 = t1+(Q/цp*m) – конечной температуры.

Инструкция по расчёту параметра
Рассчитать с вещества достаточно просто и чтобы это сделать нужно, выполнить следующие шаги:
- Взять расчётную формулу: Теплоемкость = Q/(m*∆T)
- Выписать исходные данные.
- Подставить их в формулу.
- Провести расчёт и получим результат.
В качестве примера произведём расчёт неизвестного вещества массой 480 грамм обладающего температурой 15ºC, которая в результате нагрева (подвода 35 тыс. Дж) увеличилась до 250º.
Согласно инструкции приведённой выше производим следующие действия:
Выписываем исходные данные:
- Q = 35 тыс. Дж;
- m = 480 г;
- ΔT = t2–t1 =250–15 = 235 ºC.
Берём формулу, подставляем значения и решаем:
с=Q/(m*∆T)=35тыс.Дж/(480 г*235º)=35тыс.Дж/(112800 г*º)=0,31 Дж/г*º.
Расчёт
Выполним расчёт CP воды и олова при следующих условиях:
- m = 500 грамм;
- t1 =24ºC и t2 = 80ºC – для воды;
- t1 =20ºC и t2 =180ºC – для олова;
- Q = 28 тыс.

Для начала определяем ΔT для воды и олова соответственно:
- ΔТв = t2–t1 = 80–24 = 56ºC
- ΔТо = t2–t1 = 180–20 =160ºC
Затем находим удельную теплоёмкость:
- с=Q/(m*ΔТв)= 28 тыс. Дж/(500 г *56ºC) = 28 тыс.Дж/(28 тыс.г*ºC) = 1 Дж/г*ºC.
- с=Q/(m*ΔТо)=28тыс.Дж/(500 гр*160ºC)=28 тыс.Дж/(80 тыс.г*ºC)=0,35 Дж/г*ºC.
Таким образом, удельная теплоемкость воды составила 1 Дж/г *ºC, а олова 0,35 Дж/г*ºC. Отсюда можно сделать вывод о том, что при равном значении подводимого тепла в 28 тыс. Дж олово нагрется быстрее воды, поскольку его теплоёмкость меньше.
Теплоёмкостью обладают не только газы, жидкости и твёрдые тела, но и продукты питания.
Как рассчитать теплоемкость продуктов питания
При расчёте емкости питания уравнение примет следующий вид:
с=(4.180*w)+(1.711*p)+(1.928*f)+(1.547*c)+(0.908 *a), где:
- w – количество воды в продукте;
- p – количество белков в продукте;
- f – процентное содержание жиров;
- c – процентное содержание углеводов;
- a – процентное содержание неорганических компонентов.

Определим теплоемкость плавленого сливочного сыра Viola. Для этого выписываем нужные значения из состава продукта (масса 140 грамм):
- вода – 35 г;
- белки – 12,9 г;
- жиры – 25,8 г;
- углеводы – 6,96 г;
- неорганические компоненты – 21 г.
Затем находим с:
- с=(4.180*w)+(1.711*p)+(1.928*f)+(1.547*c)+(0.908*a)=(4.180*35)+(1.711*12,9)+(1.928*25,8) + (1.547*6,96)+(0.908*21)=146,3+22,1+49,7+10,8+19,1=248 кДж /кг*ºC.
Полезные советы
Всегда помните, что:
- процесс нагревания металла проходит быстрее, чем у воды, так как он обладает CP
- по возможности преобразуйте полученные результаты в более высокий порядок, если позволяют условия;
- в целях проверки результатов можно воспользоваться интернетом и посмотреть с для расчётного вещества;
- при равных экспериментальных условиях более значительные температурные изменения будут наблюдаться у материалов с низкой удельной теплоёмкостью.

Видео
Разобраться в этой теме вам поможет видео урок.
Единицы теплоты
“…- Сколько попугаев в тебе поместится, такой у тебя рост.
– Очень надо! Я не стану глотать столько попугаев!…”
Из м/ф “38 попугаев”
В соответствии с международными правилами СИ (международная система единиц измерения) количество тепловой энергии или количество тепла измеряется в Джоулях [Дж], также существуют кратные единицы килоДжоуль [кДж] = 1000 Дж., МегаДжоуль [МДж] = 1 000 000 Дж, ГигаДжоуль [ГДж] = 1 000 000 000 Дж. и пр. Эта единица измерения тепловой энергии является основной международной единицей и наиболее часто используется при проведении научных и научно-технических расчётов.
Однако, все из нас знают или хотя бы раз слышали и другую единицу измерения количества теплоты (или просто тепла) это калория, а также килокалория, Мегакалория и Гигакалория, что означают приставки кило, Гига и Мега, смотреть пример с Джоулями выше. В нашей стране исторически сложилось так, что при расчёте тарифов за отопление, будь то отопление электроэнергией, газовыми или пеллетными котлами принято считать стоимость именно одной Гигакалории тепловой энергии.
В нашей стране исторически сложилось так, что при расчёте тарифов за отопление, будь то отопление электроэнергией, газовыми или пеллетными котлами принято считать стоимость именно одной Гигакалории тепловой энергии.
Так что же такое Гигакалория, килоВатт, килоВатт*час или килоВатт/час и Джоули и как они связаны между собой?, вы узнаете в этой статье.
Итак, основная единица тепловой энергии это, как уже было сказано, Джоуль. Но прежде чем говорить об единицах измерения необходимо в принципе на бытовом уровне разъяснить что такое тепловая энергия и как и для чего её измерять.
Всем нам с детства известно, чтобы согреться (получить тепловую энергию) нужно что-то поджечь, поэтому все мы жгли костры, традиционное топливо для костра – это дрова. Таким образом, очевидно, при горении топлива (любого: дрова, уголь, пеллеты, природный газ, солярка) выделяется тепловая энергия (тепло). Но, чтобы нагреть, к примеру, различные объёмы воды требуется разное количество дров (или иного топлива). Ясно, что для нагрева двух литров воды достаточно нескольких пален в костре, а чтобы приготовить полведра супа на весь лагерь, нужно запастись несколькими вязанками дров. Чтобы не измерять такие строгие технические величины, как количество теплоты и теплота сгорания топлива вязанками дров и вёдрами с супом, теплотехники решили внести ясность и порядок и договорились выдумать единицу количества теплоты. Чтобы эта единица была везде одинаковая её определили так: для нагрева одного килограмма воды на один градус при нормальных условиях (атмосферном давлении) требуется 4 190 калорий, или 4,19 килокалории, следовательно, чтобы нагреть один грамм воды будет достаточно в тысячу раз меньше теплоты – 4,19 калории.
Ясно, что для нагрева двух литров воды достаточно нескольких пален в костре, а чтобы приготовить полведра супа на весь лагерь, нужно запастись несколькими вязанками дров. Чтобы не измерять такие строгие технические величины, как количество теплоты и теплота сгорания топлива вязанками дров и вёдрами с супом, теплотехники решили внести ясность и порядок и договорились выдумать единицу количества теплоты. Чтобы эта единица была везде одинаковая её определили так: для нагрева одного килограмма воды на один градус при нормальных условиях (атмосферном давлении) требуется 4 190 калорий, или 4,19 килокалории, следовательно, чтобы нагреть один грамм воды будет достаточно в тысячу раз меньше теплоты – 4,19 калории.
Калория связана с международной единицей тепловой энергии – Джоулем следующим соотношением:
1 калория = 4,19 Джоуля.
Таким образом, для нагрева 1 грамма воды на один градус потребуется 4,19 Джоуля тепловой энергии, а для нагрева одного килограмма воды 4 190 Джоулей тепла.
В технике, наряду с единицей измерения тепловой (и всякой другой) энергии существует единица мощности и, в соответствии с международной системой (СИ) это Ватт. Понятие мощности также применимо и к нагревательным приборам. Если нагревательный прибор способен отдать за 1 секунду 1 Джоуль тепловой энергии, то его мощность равна 1 Ватт. Мощность, это способность прибора производить (создавать) определённое количество энергии (в нашем случае тепловой энергии) в единицу времени. Вернёмся к нашему примеру с водой, чтобы нагреть один килограмм (или один литр, в случае с водой килограмм равен литру) воды на один градус Цельсия (или Кельвина, без разницы) нам потребуется мощность 1 килокалория или 4 190 Дж. тепловой энергии. Чтобы нагреть один килограмм воды за 1 секунду времени на 1 грдус нам нужен прибор следующей мощности:
4190 Дж./1 с. = 4 190 Вт. или 4,19 кВт.
Если мы хотим нагреть наш килограмм воды на 25 градусов за ту же секунду, то нам потребуется мощность в двадцать пять раз больше т. е.
е.
4,19*25 =104,75 кВт.
Таким образом, можно сделать вывод, что пеллетный котёл мощностью 104,75 кВт. нагревает 1 литр воды на 25 градусов за одну секунду.
Раз мы добрались до Ватт и килоВатт, следует и о них словечко замолвить. Как уже было сказано Ватт – это единица мощности, в том числе и тепловой мощности котла, но ведь кроме пеллетных котлов и газовых котлов человечеству знакомы и электрокотлы, мощность которых измеряется, разумеется, в тех же килоВаттах и потребляют они не пеллеты и не газ, а электроэнергию, количество которой измеряется в килоВатт часах. Правильное написание единицы энергии килоВатт*час (именно, килоВатт умножить на час, а не разделить), запись кВт/час – является ошибкой!
В электрокотлах электрическая энергия преобразуется в тепловую (так называемое, Джоулево тепло), и , если котёл потребил 1 кВт*час электроэнергии, то сколько же он выработал тепла? Чтобы ответить на это простой вопрос, нужно выполнить простой расчёт.
Преобразуем килоВатты в килоДжоули/секунды (килоДжоуль в секунду), а часы в секунды: в одном часе 3 600 секунд, получим:
1 кВт*час =[ 1 кДж/с]*3600 c. =1 000 Дж *3600 с = 3 600 000 Джоулей или 3,6 МДж.
=1 000 Дж *3600 с = 3 600 000 Джоулей или 3,6 МДж.
Итак,
1 кВт*час = 3,6 МДж.
В свою очередь, 3,6 МДж/4,19 = 0,859 Мкал = 859 ккал = 859 000 кал. Энергии (тепловой).
Теперь перейдём к Гигакалории, цену которой на различных видах топлива любят считать теплотехники.
1 Гкал = 1 000 000 000 кал.
1 000 000 000 кал. = 4,19*1 000 000 000 = 4 190 000 000 Дж.= 4 190 МДж. = 4,19 ГДж.
Или зная, что 1 кВт*час = 3,6 МДж пересчитаем 1 Гигакалорию на килоВатт*часы:
1 Гкал = 4190 МДж/3,6 МДж = 1 163 кВт*часов!
Если прочитав данную статью вы решили, проконсультироваться со специалистом нашей компании по любому вопросу, связанному с теплоснабжением, то вам Сюда!
понятие, расчеты, применение :: SYL.ru
В фокусе внимания нашей статьи – количество теплоты. Мы рассмотрим понятие внутренней энергии, которая трансформируется при изменении этой величины. А также покажем некоторые примеры применения расчетов в человеческой деятельности.
Теплота
С любым словом родного языка у каждого человека есть свои ассоциации. Они определяются личным опытом и иррациональными чувствами. Что обычно представляется при слове «теплота»? Мягкое одеяло, работающая батарея центрального отопления зимой, первый солнечный свет весной, кот. Или взгляд матери, утешительное слово друга, вовремя проявленное внимание.
Физики подразумевают под этим совершенно конкретный термин. И очень важный, особенно в некоторых разделах этой сложной, но увлекательной науки.
Термодинамика
Рассматривать количество теплоты в отрыве от простейших процессов, на которые опирается закон сохранения энергии, не стоит – ничего не будет понятно. Поэтому для начала напомним их читателям.
Термодинамика рассматривает любую вещь или объект как соединение очень большого количества элементарных частей – атомов, ионов, молекул. Ее уравнения описывают любое изменение коллективного состояния системы как целого и как части целого при изменении макропараметров. Под последними понимаются температура (обозначается как Т), давление (Р), концентрация компонентов (как правило, С).
Под последними понимаются температура (обозначается как Т), давление (Р), концентрация компонентов (как правило, С).
Внутренняя энергия
Внутренняя энергия – довольно сложный термин, в смысле которого стоит разобраться прежде, чем говорить о количестве теплоты. Он обозначает ту энергию, которая изменяется при увеличении или уменьшении значения макропараметров объекта и не зависит от системы отсчета. Является частью общей энергии. Совпадает с ней в условиях, когда центр масс исследуемой вещи покоится (то есть отсутствует кинетическая составляющая).
Когда человек чувствует, что некоторый объект (скажем, велосипед) нагрелся или охладился, это показывает, что все молекулы и атомы, составляющие данную систему, испытали изменение внутренней энергии. Однако неизменность температуры не означает сохранение этого показателя.
Работа и теплота
Внутренняя энергия любой термодинамической системы может преобразоваться двумя способами:
- посредством совершения над ней работы;
- при теплообмене с окружающей средой.

Формула этого процесса выглядит так:
dU=Q-А, где U – внутренняя энергия, Q – теплота, А – работа.
Пусть читатель не обольщается простотой выражения. Перестановка показывает, что Q=dU+А, однако введение энтропии (S) приводит формулу к виду dQ=dSxT.
Так как в данном случае уравнение принимает вид дифференциального, то и первое выражение требует того же. Далее, в зависимости от сил, действующих в исследуемом объекте, и параметра, который вычисляется, выводится необходимое соотношение.
Возьмем в качестве примера термодинамической системы металлический шарик. Если на него надавить, подбросить вверх, уронить в глубокий колодец, то это значит совершить над ним работу. Чисто внешне все эти безобидные действия шарику никакого вреда не причинят, но внутренняя энергия его изменится, хоть и очень ненамного.
Второй способ – это теплообмен. Теперь подходим к главной цели данной статьи: описанию того, что такое количество теплоты. Это такое изменение внутренней энергии термодинамической системы, которое происходит при теплообмене (смотрите формулу выше). Оно измеряется в джоулях или калориях. Очевидно, что если шарик подержать над зажигалкой, на солнце, или просто в теплой руке, то он нагреется. А дальше можно по изменению температуры найти количество теплоты, которое ему было при этом сообщено.
Оно измеряется в джоулях или калориях. Очевидно, что если шарик подержать над зажигалкой, на солнце, или просто в теплой руке, то он нагреется. А дальше можно по изменению температуры найти количество теплоты, которое ему было при этом сообщено.
Почему газ – лучший пример изменения внутренней энергии, и почему из-за этого школьники не любят физику
Выше мы описывали изменения термодинамических параметров металлического шарика. Они без специальных приборов не очень заметны, и читателю остается поверить на слово о происходящих с объектом процессах. Другое дело, если система – газ. Надавите на него – это будет видно, нагрейте – поднимется давление, опустите под землю – и это можно с легкостью зафиксировать. Поэтому в учебниках чаще всего в качестве наглядной термодинамической системы берут именно газ.
Но, увы, в современном образовании реальным опытам уделяется не так много внимания. Ученый, который пишет методическое пособие, отлично понимает, о чем идет речь. Ему кажется, что на примере молекул газа все термодинамические параметры будут нужным образом продемонстрированы. Но ученику, который только открывает для себя этот мир, скучно слушать про идеальную колбу с теоретическим поршнем. Если бы в школе существовали настоящие исследовательские лаборатории и на работу в них выделялись часы, все было бы по-другому. Пока, к сожалению, опыты только на бумаге. И, скорее всего, именно это становится причиной того, что люди считают данный раздел физики чем-то чисто теоретическим, далеким от жизни и ненужным.
Но ученику, который только открывает для себя этот мир, скучно слушать про идеальную колбу с теоретическим поршнем. Если бы в школе существовали настоящие исследовательские лаборатории и на работу в них выделялись часы, все было бы по-другому. Пока, к сожалению, опыты только на бумаге. И, скорее всего, именно это становится причиной того, что люди считают данный раздел физики чем-то чисто теоретическим, далеким от жизни и ненужным.
Пример изменения термодинамических параметров
Поэтому мы решили в качестве примера привести уже упоминаемый выше велосипед. Человек давит на педали – совершает над ними работу. Помимо сообщения всему механизму крутящего момента (благодаря которому велосипед и перемещается в пространстве), изменяется внутренняя энергия материалов, из которых сделаны рычаги. Велосипедист нажимает на ручки, чтобы повернуть, – и опять совершает работу.
Внутренняя энергия внешнего покрытия (пластика или металла) увеличивается. Человек выезжает на полянку под яркое солнце – велосипед нагревается, изменяется его количество теплоты. Останавливается отдохнуть в тени старого дуба, и система охлаждается, теряя калории или джоули. Увеличивает скорость – растет обмен энергией. Однако расчет количества теплоты во всех этих случаях покажет очень маленькую, незаметную величину. Поэтому и кажется, что проявлений термодинамической физики в реальной жизни нет.
Останавливается отдохнуть в тени старого дуба, и система охлаждается, теряя калории или джоули. Увеличивает скорость – растет обмен энергией. Однако расчет количества теплоты во всех этих случаях покажет очень маленькую, незаметную величину. Поэтому и кажется, что проявлений термодинамической физики в реальной жизни нет.
Применение расчетов по изменению количества теплоты
Вероятно, читатель скажет, что все это весьма познавательно, но зачем же нас так мучают в школе этими формулами. А сейчас мы приведем примеры, в каких областях человеческой деятельности они нужны непосредственно и как это касается любого в его повседневности.
Для начала посмотрите вокруг себя и посчитайте: сколько предметов из металла вас окружают? Наверняка больше десяти. Но прежде чем стать скрепкой, вагоном, кольцом или флешкой, любой металл проходит выплавку. Каждый комбинат, на котором перерабатывают, допустим, железную руду, должен понимать, сколько требуется топлива, чтобы оптимизировать расходы. А рассчитывая это, необходимо знать теплоемкость металлосодержащего сырья и количество теплоты, которое ему необходимо сообщить, чтобы произошли все технологические процессы. Так как выделяемая единицей топлива энергия рассчитывается в джоулях или калориях, то формулы нужны непосредственно.
А рассчитывая это, необходимо знать теплоемкость металлосодержащего сырья и количество теплоты, которое ему необходимо сообщить, чтобы произошли все технологические процессы. Так как выделяемая единицей топлива энергия рассчитывается в джоулях или калориях, то формулы нужны непосредственно.
Или другой пример: в большинстве супермаркетов есть отдел с замороженными товарами – рыбой, мясом, фруктами. Там, где сырье из мяса животных или морепродуктов превращается в полуфабрикат, должны знать, сколько электричества употребят холодильные и морозильные установки на тонну или единицу готового продукта. Для этого следует рассчитать, какое количество теплоты теряет килограмм клубники или кальмаров при охлаждении на один градус Цельсия. А в итоге это покажет, сколько электричества потратит морозильник определенной мощности.
Самолеты, пароходы, поезда
Выше мы показали примеры относительно неподвижных, статичных предметов, которым сообщают или у которых, наоборот, отнимают определенное количество теплоты. Для объектов, в процессе работы движущихся в условиях постоянно меняющейся температуры, расчеты количества теплоты важны по другой причине.
Для объектов, в процессе работы движущихся в условиях постоянно меняющейся температуры, расчеты количества теплоты важны по другой причине.
Есть такое понятие, как “усталость металла”. Включает оно в себя также и предельно допустимые нагрузки при определенной скорости изменения температуры. Представьте, самолет взлетает из влажных тропиков в замороженные верхние слои атмосферы. Инженерам приходится много работать, чтобы он не развалился из-за трещин в металле, которые появляются при перепаде температуры. Они ищут такой состав сплава, который способен выдержать реальные нагрузки и будет иметь большой запас прочности. А чтобы не искать вслепую, надеясь случайно наткнуться на нужную композицию, приходится делать много расчетов, в том числе и включающих изменения количества теплоты.
Видео с вопросами: Определение правильной формулы для расчета теплоты, передаваемой в калориметрическом эксперименте
Стенограмма видео
Какое из следующих уравнений
можно использовать с результатами калориметрического эксперимента для расчета теплоты
энергия, передаваемая в ходе химической реакции? (A) 𝑞 равно скобкам 𝑐 раз
Δ𝑇 разделить на 𝑚.
Калориметрия – это исследование тепла передаваемые при физико-химических изменениях, где теплота есть поток тепловых энергия из-за разницы температур, где температура является мерой средняя кинетическая энергия вещества в системе. Он также может выражать, насколько жарко или холодно. вещество есть. Итак, теплота и температура другой.
Тепловая энергия обозначена символом 𝑞
и измеряется в джоулях, а температура обозначается заглавной буквой
𝑇 и измеряется в градусах Цельсия или кельвинах. Пример, показывающий разницу
между теплом и температурой находится нагрев воды в кастрюле. Горелка является источником
нагревать. Тепловая энергия передается на
вода в кастрюле. Это приводит к тому, что кинетическая энергия
увеличиваться, что приводит к закипанию воды. Следовательно, происходит увеличение
температура.
Тепловая энергия передается на
вода в кастрюле. Это приводит к тому, что кинетическая энергия
увеличиваться, что приводит к закипанию воды. Следовательно, происходит увеличение
температура.
Температура может быть измерена с помощью термометра. В какой степени температура увеличивается в зависимости от теплоемкости вещества, где теплоемкость отношение количества тепловой энергии, переданной объекту, к полученной повышение его температуры. Теплоемкость, обозначенная символом капитал 𝐶, таким образом, эквивалентен 𝑞, количеству переданной тепловой энергии, деленному на Δ𝑇, изменение температуры. А заглавная Δ означает разницу или изменение в.
Тепловая энергия измеряется в джоулях,
а для изменения температуры можно использовать градусы Цельсия или Кельвина. Величина одного градуса Цельсия и
один градус Кельвина одинаковы. Поэтому изменение температуры в
обе единицы равны. Теплоемкость имеет единицы джоулей
на кельвин или джоуль на градус Цельсия. Итак, мы имеем уравнение для
теплоемкость, но теплоемкость не учитывает массу объекта
нагрелся. Удельная теплоемкость – это
количество энергии в джоулях, необходимое для повышения температуры одного грамма
вещества на один градус Цельсия. Ему присваивается символ нижнего регистра
𝑐, и рассчитывается путем деления теплоёмкости на массу
объект.
Поэтому изменение температуры в
обе единицы равны. Теплоемкость имеет единицы джоулей
на кельвин или джоуль на градус Цельсия. Итак, мы имеем уравнение для
теплоемкость, но теплоемкость не учитывает массу объекта
нагрелся. Удельная теплоемкость – это
количество энергии в джоулях, необходимое для повышения температуры одного грамма
вещества на один градус Цельсия. Ему присваивается символ нижнего регистра
𝑐, и рассчитывается путем деления теплоёмкости на массу
объект.
Освободим немного места и посмотрим
на этом повнимательнее. Как было сказано ранее, единицы
теплоемкость выражается в джоулях на кельвин или джоулях на градус Цельсия. Хотя единицей измерения являются килограммы.
часто используется для обозначения массы, вместо этого часто используются граммы, когда речь идет об удельной теплоемкости. вместимость. Итак, единицы удельной теплоемкости
мощность – джоули на грамм на градус Цельсия.
вместимость. Итак, единицы удельной теплоемкости
мощность – джоули на грамм на градус Цельсия.
Теперь у нас есть два ключевых уравнения что нам нужно решить этот вопрос. Вопрос спрашивает нас, как мы рассчитать тепловую энергию. Итак, нам нужно сделать 𝑞, нагреть энергия, предмет. Мы можем сделать 𝑞 предметом, умножив обе части уравнения на Δ𝑇. Δ𝑇 на правой стороне уравнение отменяется, оставляя нас с 𝑞 равным капиталу 𝐶, теплоемкости, умноженной по Δ𝑇. Затем нам нужно заменить капитал 𝐶, теплоемкость, со строчной 𝑐, удельная теплоемкость и 𝑚, масса.
В первую очередь нам нужно переставить
это уравнение, чтобы сделать капитал 𝐶 предметом. Если мы умножим обе части
уравнения на 𝑚, то 𝑚 в правой части уравнения сократятся, оставив
us с заглавной 𝐶 равно 𝑚 умноженному на строчную 𝑐.
Удельная теплоемкость Объект влияет на количество тепловой энергии, необходимой для его нагрева. Например, вода имеет более высокую удельная теплоемкость больше, чем у песка, поэтому для нагревания требуется больше энергии, чем для земли делает. Вот почему, когда тепло, песок на пляже будет жарко, а морская вода холодная. Поэтому ответ на вопрос «Какое из следующих уравнений можно использовать для расчета теплоты энергия?» равно (C) 𝑞 равно 𝑚, умноженному на 𝑐, умноженному на Δ𝑇.
Удельная теплоемкость | безграничная физика |
Теплоемкость
Теплоемкость измеряет количество тепла, необходимое для повышения температуры объекта или системы на один градус Цельсия.
Цели обучения
Объясните энтальпию в системе с постоянным объемом и давлением
Ключевые выводы
Ключевые моменты
- Теплоемкость – это измеримая физическая величина, характеризующая количество тепла, необходимое для изменения температуры вещества на заданную величину. Измеряется в джоулях на кельвин и дается.
- Теплоемкость — это экстенсивное свойство, которое зависит от размера системы.
- Теплоемкость большинства систем непостоянна (хотя ее часто можно считать таковой). Это зависит от температуры, давления и объема рассматриваемой системы.
Ключевые термины
- теплоемкость : Количество тепловой энергии, необходимое для повышения температуры объекта или единицы материи на один градус Цельсия; в джоулях на кельвин (Дж/К).
- энтальпия : общее количество энергии в системе, включая как внутреннюю энергию, так и энергию, необходимую для вытеснения окружающей среды
Теплоемкость
Теплоемкость (обычно обозначается заглавной С, часто с нижними индексами), или теплоемкость, — измеримая физическая величина, характеризующая количество теплоты, необходимое для изменения температуры вещества на заданную величину. В единицах СИ теплоемкость выражается в джоулях на кельвин (Дж/К).
В единицах СИ теплоемкость выражается в джоулях на кельвин (Дж/К).
Теплоемкость объекта (обозначение C ) определяется как отношение количества тепловой энергии, переданной объекту, к результирующему повышению температуры объекта.
C=QΔT.\displaystyle{\text{C}=\frac{\text{Q}}{ \Delta \text{T}}.} C=ΔTQ.
Теплоемкость является экстенсивным свойством, поэтому она зависит от размера системы. Образец, содержащий в два раза больше вещества, чем другой образец, требует передачи вдвое большего количества тепла (Q) для достижения такого же изменения температуры (ΔT). Например, если для нагревания куска железа требуется 1000 Дж, то потребуется 2000 Дж, чтобы нагреть второй кусок железа, масса которого в два раза больше массы первого.
Измерение теплоемкости
Теплоемкость большинства систем не является постоянной величиной. Скорее, это зависит от переменных состояния изучаемой термодинамической системы. В частности, оно зависит от самой температуры, а также от давления и объема системы, а также от того, как давления и объемы могут изменяться при переходе системы от одной температуры к другой. Причина этого в том, что работа давления-объема, совершаемая системой, повышает ее температуру за счет механизма, отличного от нагревания, в то время как работа давления-объема, совершаемая системой, поглощает тепло, не повышая температуру системы. (Температурная зависимость — вот почему определение калории формально представляет собой энергию, необходимую для нагревания 1 г воды с 14,5 до 15,5 °C, а не обычно на 1 °C.)
Причина этого в том, что работа давления-объема, совершаемая системой, повышает ее температуру за счет механизма, отличного от нагревания, в то время как работа давления-объема, совершаемая системой, поглощает тепло, не повышая температуру системы. (Температурная зависимость — вот почему определение калории формально представляет собой энергию, необходимую для нагревания 1 г воды с 14,5 до 15,5 °C, а не обычно на 1 °C.)
Таким образом, можно проводить различные измерения теплоемкости, чаще всего при постоянном давлении и постоянном объеме. Измеренные таким образом значения обычно подписываются (соответственно буквами p и V), чтобы указать определение. Газы и жидкости обычно также измеряются при постоянном объеме. Измерения при постоянном давлении дают большие значения, чем при постоянном объеме, потому что значения постоянного давления также включают тепловую энергию, которая используется для выполнения работы по расширению вещества против постоянного давления при повышении его температуры. Эта разница особенно заметна для газов, где значения при постоянном давлении обычно на 30-66,7% выше, чем при постоянном объеме.
Эта разница особенно заметна для газов, где значения при постоянном давлении обычно на 30-66,7% выше, чем при постоянном объеме.
Термодинамические соотношения и определение теплоемкости
Внутренняя энергия замкнутой системы изменяется либо за счет добавления теплоты системе, либо за счет совершения системой работы. Вспоминая первый закон термодинамики,
dU=δQ−δW\text{dU}=\delta \text{Q}-\delta \text{W}dU=δQ−δW
.
Для работы в результате увеличения объема системы можно написать
dU=δQ−PdV\text{dU}=\delta \text{Q}-\text{PdV}dU=δQ−PdV
.
Если тепло добавляется при постоянном объеме, то второй член этого соотношения обращается в нуль, и легко получить
(∂U∂T)V=(∂Q∂T)V=CV\displaystyle{\left( \frac{ \partial \text{U}}{\partial \text{T}}\right) _{\text{V}}=\left( \frac{\partial \text{Q}}{\partial \text{T }}\right) _{\text{V}}=\text{C}_{\text{V}}}(∂T∂U)V=(∂T∂Q)V=CV
.
Определяет теплоемкость при постоянном объеме , C В . Еще одно полезное количество — теплоемкость при постоянном давлении , C P . С энтальпией системы, заданной как
H=U+PV\text{H}=\text{U}+\text{PV}H=U+PV
,
наше уравнение для d U меняется на
dH=δQ+VdP\text{dH}=\delta \text{Q}+\text{VdP}dH=δQ+VdP
,
и, следовательно, при постоянном давлении имеем
(∂H∂T) P = (∂Q∂T) P = CP (\ frac {\ partial \ text {H}} {\ partial \ text {T}}) _ {\ text {P}} = (\ frac{\ partial \ text {Q}} {\ partial \ text {T}}) _ {\ text {P}} = \ text {C} _ {\ text {P}} (∂T∂H) P =(∂T∂Q)P=CP
.
Удельная теплоемкость
Удельная теплоемкость — это интенсивное свойство, которое описывает, какое количество теплоты необходимо добавить к конкретному веществу, чтобы повысить его температуру.
Цели обучения
Обобщите количественную взаимосвязь между теплопередачей и изменением температуры
Основные выводы
Ключевые моменты
- В отличие от полной теплоемкости удельная теплоемкость не зависит от массы или объема. Он описывает, какое количество теплоты необходимо добавить к единице массы данного вещества, чтобы повысить его температуру на один градус Цельсия. Единицами удельной теплоемкости являются Дж/(кг·°С) или эквивалентно Дж/(кг·К).
- Теплоемкость и удельная теплоемкость связаны соотношением С=см или с=С/м.
- Масса m, удельная теплоемкость c, изменение температуры ΔT и добавленное (или вычтенное) тепло Q связаны уравнением: Q=mcΔT.
- Значения удельной теплоемкости зависят от свойств и фазы данного вещества. Поскольку их нелегко рассчитать, они измеряются эмпирическим путем и доступны для справки в таблицах.
Ключевые термины
- удельная теплоемкость : Количество теплоты, которое необходимо добавить (или отвести) от единицы массы вещества, чтобы изменить его температуру на один градус Цельсия.
 Это интенсивное свойство.
Это интенсивное свойство.
Удельная теплоемкость
Теплоемкость — это экстенсивное свойство, которое описывает, сколько тепловой энергии требуется для повышения температуры данной системы. Однако было бы довольно неудобно измерять теплоемкость каждой единицы материи. Нам нужно интенсивное свойство, которое зависит только от типа и фазы вещества и может быть применено к системам произвольного размера. Эта величина известна как удельная теплоемкость (или просто удельная теплоемкость), которая представляет собой теплоемкость на единицу массы материала. Эксперименты показывают, что передаваемое тепло зависит от трех факторов: 1) изменения температуры, 2) массы системы и 3) вещества и фазы вещества. Последние два фактора заключены в значении удельной теплоемкости.
Теплопередача и удельная теплоемкость : Теплота Q, передаваемая для изменения температуры, зависит от величины изменения температуры, массы системы, а также вовлеченного вещества и фазы. а) Количество переданного тепла прямо пропорционально изменению температуры. Чтобы удвоить изменение температуры массы m, нужно добавить удвоенное количество теплоты. б) Количество переданного тепла также прямо пропорционально массе. Чтобы вызвать эквивалентное изменение температуры в удвоенной массе, нужно добавить в два раза больше тепла. в) Количество переданного тепла зависит от вещества и его фазы. Если требуется количество Q тепла, чтобы вызвать изменение температуры ΔT в данной массе меди, то потребуется в 10,8 раз больше тепла, чтобы вызвать эквивалентное изменение температуры в той же массе воды, при условии отсутствия фазового перехода ни в одном из веществ.
а) Количество переданного тепла прямо пропорционально изменению температуры. Чтобы удвоить изменение температуры массы m, нужно добавить удвоенное количество теплоты. б) Количество переданного тепла также прямо пропорционально массе. Чтобы вызвать эквивалентное изменение температуры в удвоенной массе, нужно добавить в два раза больше тепла. в) Количество переданного тепла зависит от вещества и его фазы. Если требуется количество Q тепла, чтобы вызвать изменение температуры ΔT в данной массе меди, то потребуется в 10,8 раз больше тепла, чтобы вызвать эквивалентное изменение температуры в той же массе воды, при условии отсутствия фазового перехода ни в одном из веществ.
Удельная теплоемкость : В этом уроке тепло связано с изменением температуры. Мы обсудим, как количество тепла, необходимое для изменения температуры, зависит от массы и вовлеченного вещества, и эта связь представлена удельной теплоемкостью вещества, C.
Зависимость от изменения температуры и массы легко понять. Поскольку (средняя) кинетическая энергия атома или молекулы пропорциональна абсолютной температуре, внутренняя энергия системы пропорциональна абсолютной температуре и количеству атомов или молекул. Поскольку переданное тепло равно изменению внутренней энергии, теплота пропорциональна массе вещества и изменению температуры. Переносимое тепло также зависит от вещества, так что, например, теплота, необходимая для повышения температуры, для спирта меньше, чем для воды. Для одного и того же вещества передаваемая теплота также зависит от фазы (газовая, жидкая или твердая).
Количественная связь между теплопередачей и изменением температуры содержит все три фактора:
Q=mcΔT\text{Q}=\text{mc}\Delta \text{T}Q=mcΔT
,
где Q символ теплопередачи, m — масса вещества, ΔT — изменение температуры. Символ c обозначает удельную теплоемкость и зависит от материала и фазы.
Удельная теплоемкость – это количество теплоты, необходимое для изменения температуры 1,00 кг массы на 1,00ºC. Удельная теплоемкость с является свойством вещества; его единица СИ – Дж / (кг⋅K) или Дж / (кг⋅C). Напомним, что изменение температуры (ΔT) одинаково в единицах кельвина и градусах Цельсия. Обратите внимание, что полная теплоемкость C — это просто произведение удельной теплоемкости c и массы вещества m, т. е.
C=mc\text{C}=\text{mc}C=mc
или
c=Cm=CρV\text{c}=\frac{\text{C}}{\text{m} }=\frac{\text{C}}{\rho \text{V}}c=mC=ρVC
,
где ϱ — плотность вещества, V — его объем.
Значения удельной теплоемкости обычно нужно искать в таблицах, потому что нет простого способа их расчета. Вместо этого они измеряются эмпирически. В общем случае удельная теплоемкость также зависит от температуры. В таблице ниже приведены репрезентативные значения удельной теплоемкости для различных веществ. За исключением газов, зависимость теплоемкости большинства веществ от температуры и объема слабая. Удельная теплоемкость воды в пять раз больше, чем у стекла, и в десять раз больше, чем у железа, а это означает, что требуется в пять раз больше тепла, чтобы поднять температуру воды на ту же величину, что и для стекла, и в десять раз больше тепла, чтобы поднять температуру. воды как для железа. На самом деле вода имеет одну из самых больших удельных теплоемкостей среди всех материалов, что важно для поддержания жизни на Земле.
За исключением газов, зависимость теплоемкости большинства веществ от температуры и объема слабая. Удельная теплоемкость воды в пять раз больше, чем у стекла, и в десять раз больше, чем у железа, а это означает, что требуется в пять раз больше тепла, чтобы поднять температуру воды на ту же величину, что и для стекла, и в десять раз больше тепла, чтобы поднять температуру. воды как для железа. На самом деле вода имеет одну из самых больших удельных теплоемкостей среди всех материалов, что важно для поддержания жизни на Земле.
Удельная теплоемкость : Перечислены удельные теплоемкости различных веществ. Эти значения идентичны в единицах кал/(г⋅С).3. cv при постоянном объеме и при 20,0ºC, если не указано иное, и при среднем давлении 1,00 атм. В скобках указаны cp при постоянном давлении 1,00 атм.
Калориметрия
Калориметрия — это измерение теплоты химических реакций или физических изменений.
Цели обучения
Проанализируйте зависимость между газовой постоянной для выхода идеального газа и объемом
Ключевые выводы
Ключевые моменты
- Калориметр используется для измерения тепла, выделяемого (или поглощаемого) в результате физического изменения или химической реакции.
 Наука измерения этих изменений известна как калориметрия.
Наука измерения этих изменений известна как калориметрия. - Для проведения калориметрии крайне важно знать удельную теплоемкость измеряемых веществ.
- Калориметрию можно проводить при постоянном объеме или постоянном давлении. Тип расчета зависит от условий эксперимента.
Ключевые термины
- калориметр постоянного давления : Прибор, используемый для измерения тепла, выделяемого при изменениях, не связанных с изменениями давления.
- калориметр : Прибор для измерения тепла, выделяемого или поглощаемого в результате химической реакции, фазового перехода или какого-либо другого физического изменения.
- калориметр постоянного объема : Прибор, используемый для измерения тепла, выделяемого при изменениях, не связанных с изменением объема.
Калориметрия
Обзор
Калориметрия — это наука об измерении теплоты химических реакций или физических изменений. Калориметрию проводят с помощью калориметра. Простой калориметр состоит из термометра, прикрепленного к металлическому контейнеру с водой, подвешенному над камерой сгорания. Слово калориметрия происходит от латинского слова калория , что означает тепло. Основателем калориметрии считается шотландский врач и ученый Джозеф Блэк, который первым обнаружил различие между теплом и температурой.
Калориметрию проводят с помощью калориметра. Простой калориметр состоит из термометра, прикрепленного к металлическому контейнеру с водой, подвешенному над камерой сгорания. Слово калориметрия происходит от латинского слова калория , что означает тепло. Основателем калориметрии считается шотландский врач и ученый Джозеф Блэк, который первым обнаружил различие между теплом и температурой.
Калориметрия требует, чтобы нагреваемый материал обладал известными тепловыми свойствами, т. е. удельной теплоемкостью. Классическое правило, признанное Клаузиусом и Кельвином, состоит в том, что давление, оказываемое калориметрическим материалом, полностью и быстро определяется исключительно его температурой и объемом; это правило относится к изменениям, не связанным с фазовым переходом, например к таянию льда. Существует множество материалов, которые не соответствуют этому правилу, и для них требуются более сложные уравнения, чем приведенные ниже.
Ледяной калориметр : Первый в мире ледяной калориметр, использовавшийся зимой 1782-1783 годов Антуаном Лавуазье и Пьером-Симоном Лапласом для определения тепла, выделяющегося при различных химических превращениях; расчеты, основанные на предыдущем открытии Джозефом Блэком скрытой теплоты. Эти эксперименты положили начало термохимии.
Эти эксперименты положили начало термохимии.
Базовая калориметрия при постоянном значении
Калориметрия постоянного объема — это калориметрия, проводимая при постоянном объеме. Это включает использование калориметра постоянного объема (один тип называется калориметром бомбы). Для калориметрии постоянного объема:
δQ=CVΔT=mcVΔT\delta \text{Q}=\text{C}_{\text{V}}\Delta \text{T}=\text{mc}_{\text{V}}\ Delta \text{T}δQ=CVΔT=mcVΔT
где δQ – приращение тепла, полученного образцом, C V – теплоемкость при постоянном объеме, c v – удельная теплоемкость при постоянный объем, а ΔT — изменение температуры.
Измерение изменения энтальпии
Чтобы найти изменение энтальпии на массу (или на моль) вещества А в реакции между двумя веществами А и В, вещества добавляют в калориметр и определяют начальную и конечную температуры (до начала реакции и после ее окончания). отмечены. Умножение изменения температуры на массу и удельную теплоемкость веществ дает значение энергии, выделяемой или поглощаемой в ходе реакции:
отмечены. Умножение изменения температуры на массу и удельную теплоемкость веществ дает значение энергии, выделяемой или поглощаемой в ходе реакции:
δQ=ΔT(mAcA+mBcB)\delta \text{Q}=\Delta \text{T}(\text{m}_{\text{A}}\text{c}_{\text{A }}+\text{m}_{\text{B}}\text{c}_{\text{B}})δQ=ΔT(mAcA+mBcB)
Деление изменения энергии по тому, сколько граммов (или молей) A присутствовало, дает изменение энтальпии реакции. Этот метод используется в основном в академическом обучении, поскольку он описывает теорию калориметрии. Он не учитывает потери тепла через контейнер или теплоемкость термометра и самого контейнера. Кроме того, предмет, помещенный внутрь калориметра, показывает, что предметы передавали свое тепло калориметру и жидкости, а теплота, поглощаемая калориметром и жидкостью, равна теплоте, отдаваемой металлами.
Калориметрия при постоянном давлении
Калориметр постоянного давления измеряет изменение энтальпии реакции, протекающей в растворе, в течение которой атмосферное давление остается постоянным. Примером может служить калориметр кофейной чашки, который состоит из двух вложенных друг в друга чашек из пенополистирола и крышки с двумя отверстиями, позволяющими вставлять термометр и палочку для перемешивания. Внутренняя чаша содержит известное количество растворенного вещества, обычно воды, которое поглощает тепло от реакции. Когда происходит реакция, внешняя чашка обеспечивает изоляцию. Затем
Примером может служить калориметр кофейной чашки, который состоит из двух вложенных друг в друга чашек из пенополистирола и крышки с двумя отверстиями, позволяющими вставлять термометр и палочку для перемешивания. Внутренняя чаша содержит известное количество растворенного вещества, обычно воды, которое поглощает тепло от реакции. Когда происходит реакция, внешняя чашка обеспечивает изоляцию. Затем
CP = WΔHMΔT \ text {C} _ {\ text {P}} = \ frac {\ text {W} \ Delta \ text {H}} {\ text {M} \ Delta \ text {T}} CP =MΔTWΔH
, где C p — удельная теплоемкость при постоянном давлении, ΔH — энтальпия раствора, ΔT — изменение температуры, W — масса растворенного вещества, M — молекулярная масса растворенный. Измерение тепла с помощью простого калориметра, такого как калориметр кофейной чашки, является примером калориметрии постоянного давления, поскольку давление (атмосферное давление) остается постоянным во время процесса. Калориметрия при постоянном давлении используется для определения изменений энтальпии, происходящих в растворе. В этих условиях изменение энтальпии равно теплу (Q=ΔH).
В этих условиях изменение энтальпии равно теплу (Q=ΔH).
Удельная теплоемкость идеального газа при постоянном давлении и объеме
Идеальный газ имеет различную удельную теплоемкость при постоянном объеме или постоянном давлении.
Цели обучения
Объясните, как рассчитать показатель адиабаты
Ключевые выводы
Ключевые моменты
- }}{\partial \text{T}})_{\text{V}}=\text{c}_{\text{v}}(∂T∂U)V=cv .
- Удельная теплоемкость идеального газа при постоянном давлении определяется как _{\text{V}}=\text{c}_{\text{p}}=\text{c}_{\text{v}}+\text{R}(∂T∂H)V =cp=cv+R .
- Коэффициент теплоемкости (или показатель адиабаты) — это отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме.
Ключевые термины
- Фундаментальное термодинамическое соотношение : В термодинамике фундаментальное термодинамическое соотношение выражает бесконечно малое изменение внутренней энергии через бесконечно малые изменения энтропии и объема для замкнутой системы, находящейся в тепловом равновесии, следующим образом: dU =TdS-PdV.
 Здесь U — внутренняя энергия, T — абсолютная температура, S — энтропия, P — давление, V — объем.
Здесь U — внутренняя энергия, T — абсолютная температура, S — энтропия, P — давление, V — объем. - показатель адиабаты : Отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме.
- удельная теплоемкость : Отношение количества теплоты, необходимого для повышения температуры единицы массы вещества на единицу градуса, к количеству теплоты, необходимому для повышения температуры той же массы воды на ту же величину.
Удельная теплоемкость идеального газа при постоянном давлении и объеме
Теплоемкость при постоянном объеме nR = 1 Дж·К −1 любого газа, включая идеальный газ: text{V}}=\text{c}_{\text{v}}(∂T∂U)V=cv
Представляет собой безразмерную теплоемкость при постоянном объеме; обычно это функция температуры из-за межмолекулярных сил. При умеренных температурах константа для одноатомного газа равна c v = 3/2, а для двухатомного газа — c v = 5/2 (см. ). Макроскопические измерения теплоемкости дают информацию о микроскопической структуре молекул.
). Макроскопические измерения теплоемкости дают информацию о микроскопической структуре молекул.
Молекулярные внутренние колебания : При нагревании газа поступательная кинетическая энергия молекул в газе увеличивается. Кроме того, молекулы газа могут улавливать многие характерные внутренние колебания. Потенциальная энергия, запасенная в этих внутренних степенях свободы, вносит свой вклад в удельную теплоемкость газа.
Теплоемкость при постоянном давлении 1 Дж·К −1 идеального газа равна:
(∂H∂T)V=cp=cv+R(\frac{\partial \text{H}}{\partial \ text{T}})_{\text{V}}=\text{c}_{\text{p}}=\text{c}_{\text{v}}+\text{R}(∂ T∂H)V=cp=cv+R
где H=U+pV — энтальпия газа.
Измерение теплоемкости при постоянном объеме может быть чрезвычайно сложным для жидкостей и твердых тел. То есть небольшие изменения температуры обычно требуют больших давлений для поддержания постоянного объема жидкости или твердого тела (это означает, что содержащий сосуд должен быть почти жестким или, по крайней мере, очень прочным). Легче измерить теплоемкость при постоянном давлении (позволяя материалу свободно расширяться или сжиматься) и найти теплоемкость при постоянном объеме, используя математические соотношения, полученные из основных термодинамических законов.
Легче измерить теплоемкость при постоянном давлении (позволяя материалу свободно расширяться или сжиматься) и найти теплоемкость при постоянном объеме, используя математические соотношения, полученные из основных термодинамических законов.
Используя фундаментальное термодинамическое соотношение, мы можем показать:
Cp−CV=T(∂P∂T)V,N(∂V∂T)p,N\text{C}_{\text{p}}- \text{C}_{\text{V}}=\text{T}(\frac{\partial \text{P}}{\partial \text{T}})_{\text{V},\ text{N}}(\frac{\partial \text{V}}{\partial \text{T}})_{\text{p},\text{N}}Cp −CV=T(∂ T∂P)V,N(∂T∂V)p,N
где частные производные взяты при: постоянном объеме и постоянном числе частиц, а также при постоянном давлении и постоянном числе частиц соответственно.
Коэффициент теплоемкости или показатель адиабаты представляет собой отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме. Иногда его также называют коэффициентом изоэнтропического расширения:
γ=CPCV=cpcv\gamma =\frac{\text{C}_{\text{P}}}{\text{C}_{\text{V }}}=\frac{\text{c}_{\text{p}}}{\text{c}_{\text{v}}}γ=CVCP=cvcp
Для идеального газа оценка приведенных выше частных производных в соответствии с уравнением состояния, где R — газовая постоянная для идеального газа, дает: 9{2}}=\text{R}-T(∂V∂P)V(∂T∂V)p2=-TV-PP2R2=R
Это уравнение просто сводится к тому, что известно как отношение Майера:
Юлиус Роберт Майер : Юлиус Роберт фон Майер (25 ноября 1814 г. – 20 марта 1878 г.), немецкий врач и физик, был одним из основателей термодинамики. Он наиболее известен своей формулировкой в 1841 году одного из первоначальных утверждений о сохранении энергии (или того, что сейчас известно как одна из первых версий первого закона термодинамики): «Энергия не может быть ни создана, ни уничтожена». В 1842 году Майер описал жизненно важный химический процесс, который теперь называется окислением, как основной источник энергии для любого живого существа. Его достижения были упущены из виду, и в следующем году заслуга открытия механического эквивалента тепла была приписана Джеймсу Джоулю. фон Майер также предположил, что растения преобразуют свет в химическую энергию.
– 20 марта 1878 г.), немецкий врач и физик, был одним из основателей термодинамики. Он наиболее известен своей формулировкой в 1841 году одного из первоначальных утверждений о сохранении энергии (или того, что сейчас известно как одна из первых версий первого закона термодинамики): «Энергия не может быть ни создана, ни уничтожена». В 1842 году Майер описал жизненно важный химический процесс, который теперь называется окислением, как основной источник энергии для любого живого существа. Его достижения были упущены из виду, и в следующем году заслуга открытия механического эквивалента тепла была приписана Джеймсу Джоулю. фон Майер также предположил, что растения преобразуют свет в химическую энергию.
CP-CV=R\text{C}_{\text{P}}-\text{C}_{\text{V}}=\text{R}CP-CV=R
.
Это простое уравнение, связывающее теплоемкости при постоянной температуре и постоянном давлении.
Решение задач с помощью калориметрии
Калориметрия используется для измерения количества тепла, выделяемого или потребляемого в химической реакции.
Цели обучения
Объясните, что бомбовый калориметр используется для измерения тепла, выделяющегося в реакции горения
Ключевые выводы
Ключевые моменты
- Калориметрия используется для измерения количества тепла, передаваемого веществу или от него.
- Калориметр — это устройство, используемое для измерения количества тепла, вовлеченного в химический или физический процесс.
- Это означает, что количество теплоты, произведенной или израсходованной в реакции, равно количеству теплоты, поглощенной или потерянной раствором.
Ключевые термины
- теплота реакции : изменение энтальпии химической реакции; количество тепла, которое система отдает окружающей среде, чтобы вернуться к своей начальной температуре.
- сжигание : Процесс, при котором два химических вещества объединяются для получения тепла.
Калориметры предназначены для минимизации обмена энергией между изучаемой системой и ее окружением. Они варьируются от простых калориметров для кофейных чашек, используемых студентами-химиками, до сложных калориметров-бомб, используемых для определения содержания энергии в пище.
Они варьируются от простых калориметров для кофейных чашек, используемых студентами-химиками, до сложных калориметров-бомб, используемых для определения содержания энергии в пище.
Калориметрия используется для измерения количества тепла, переданного веществу или от него. Для этого происходит теплообмен с калиброванным объектом (калориметром). Изменение температуры измерительной части калориметра пересчитывается в количество теплоты (поскольку для установления его теплоемкости использовалась предыдущая градуировка). Измерение теплопередачи с использованием этого подхода требует определения системы (вещества или веществ, претерпевающих химические или физические изменения) и ее окружения (других компонентов измерительной аппаратуры, которые служат либо для подачи тепла в систему, либо для поглощения тепла от система). Знание теплоемкости окружающей среды и тщательные измерения массы системы и окружающей среды и их температуры до и после процесса позволяют рассчитать передаваемое тепло, как описано в этом разделе.
Калориметр — это устройство, используемое для измерения количества тепла, выделяемого в химическом или физическом процессе. Например, когда экзотермическая реакция протекает в растворе в калориметре, тепло, выделяемое реакцией, поглощается раствором, что повышает его температуру. Когда происходит эндотермическая реакция, необходимое тепло поглощается из тепловой энергии раствора, что снижает его температуру. Затем изменение температуры вместе с удельной теплоемкостью и массой раствора можно использовать для расчета количества тепла, вовлеченного в любой случай.
Калориметры для кофейных чашек
Студенты, изучающие общую химию, часто используют простые калориметры, изготовленные из чашек из полистирола. Эти простые в использовании калориметры типа «кофейная чашка» обеспечивают больший теплообмен с окружающей средой и, следовательно, дают менее точные значения энергии.
Структура калориметра постоянного объема (или «бомбы»)
Бомбовый калориметр : Это изображение типичной установки бомбового калориметра.
Другой тип калориметра, который работает при постоянном объеме, в просторечии известный как калориметр бомбы, используется для измерения энергии, вырабатываемой реакциями, которые производят большое количество тепла и газообразных продуктов, таких как реакции горения. (Термин «бомба» происходит от наблюдения, что эти реакции могут быть достаточно сильными, чтобы напоминать взрывы, которые могут повредить другие калориметры.) Этот тип калориметра состоит из прочного стального контейнера («бомбы»), который содержит реагенты и сам по себе. погруженный в воду. Образец помещается в бомбу, которая затем заполняется кислородом под высоким давлением. Для воспламенения образца используется небольшая электрическая искра. Энергия, полученная в результате реакции, задерживается в стальной бомбе и окружающей воде. Повышение температуры измеряется и, наряду с известной теплоемкостью калориметра, используется для расчета энергии, выделяемой в результате реакции. Бомбовые калориметры требуют калибровки для определения теплоемкости калориметра и обеспечения точных результатов. Калибровка выполняется с использованием реакции с известным значением q, такой как измеренное количество бензойной кислоты, воспламеняемой искрой от никелевой плавкой проволоки, которая взвешивается до и после реакции. Изменение температуры, вызванное известной реакцией, используется для определения теплоемкости калориметра. Калибровка обычно выполняется каждый раз перед использованием калориметра для сбора данных исследования.
Бомбовые калориметры требуют калибровки для определения теплоемкости калориметра и обеспечения точных результатов. Калибровка выполняется с использованием реакции с известным значением q, такой как измеренное количество бензойной кислоты, воспламеняемой искрой от никелевой плавкой проволоки, которая взвешивается до и после реакции. Изменение температуры, вызванное известной реакцией, используется для определения теплоемкости калориметра. Калибровка обычно выполняется каждый раз перед использованием калориметра для сбора данных исследования.
Пример: идентификация металла по измерению удельной теплоемкости
Кусок металла массой 59,7 г, погруженный в кипящую воду, быстро перенесли в 60,0 мл воды при температуре 22,0°C. Конечная температура составляет 28,5°С. Используйте эти данные для определения удельной теплоемкости металла. Используйте этот результат для идентификации металла.
Раствор
В предположении идеальной теплопередачи тепло, отдаваемое металлом, равно отрицательному значению теплоты, поглощаемой водой, или:
qmetal=-qwater\text{q}_{\text{металл}}=-\text{q}_{\text{вода}}qmetal=-qwater
В развернутом виде это:
cметалл × mметалл × (Tf, металл-Ti, металл) = cвода × mвода × (Tf, вода-Ti, вода) \ text {c} _ {\ text {металл}} \ times \ text {m} _ {\ text{металл}} \times \left( \text{T}_{\text{f,metal}}-\text{T}_{\text{i,metal}} \right) = \text{c} _{\text{вода}} \times \text{m}_{\text{вода}} \times\left( \text{T}_{\text{f,water}}-\text{T}_ {\text{i,water}} \right)cmetal×mmetal×(Tf,metal−Ti,metal)=cwater×mwater×(Tf,water−Ti,water) 9{\text{o}} \text{C}cметалл=(59,7 г)(-71,5°C)−(4,184 Дж/г°C)(60,0 г)(6,5°C)=0,38 Дж/г°C
Наш экспериментальный показатель теплота ближе всего к значению для меди (0,39 Дж/г °C), поэтому мы идентифицируем металл как медь.
Лицензии и авторство
Контент под лицензией CC, совместно используемый ранее
- Курирование и пересмотр. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензионный контент CC, конкретное указание авторства
- Теплоемкость. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- энтальпия. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Тепловая мощность. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Тепловая мощность.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - Удельная теплоемкость. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Удельная теплоемкость. Лицензия : Общественное достояние: Авторские права неизвестны . Условия лицензии : Стандартная лицензия YouTube
- OpenStax College, College Physics. 14 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 14 октября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Калориметрия. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Калориметр.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - калориметр. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Безграничный. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike 9Калориметр постоянного давления 0037. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Удельная теплоемкость. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- OpenStax College, College Physics. 14 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики.
 14 октября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
14 октября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution - Калориметрия. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Copyright
- удельная теплоемкость. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Удельная теплоемкость. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Идеальный газ. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Отношения между тепловыми мощностями. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Юлиус Роберт фон Майер. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- показатель адиабаты.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - Фундаментальное термодинамическое соотношение. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Удельная теплоемкость. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- OpenStax College, College Physics. 14 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 14 октября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Калориметрия. Предоставлено : Википедия. Расположен по адресу : https://en.
 wikipedia.org/wiki/Calorimetry. Лицензия : Общественное достояние: Авторские права неизвестны
wikipedia.org/wiki/Calorimetry. Лицензия : Общественное достояние: Авторские права неизвестны - Юлиус Роберт фон Майер. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторские права
- Термически возбужденная молекула. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Калориметрия. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Химия. 13 октября 2015 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://openstax.org/books/chemistry/pages/1-introduction. Лицензия : CC BY: Атрибуция
- сжигание. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Удельная теплоемкость.
 Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube - OpenStax College, College Physics. 14 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 14 октября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Калориметрия. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Calorimetry. Лицензия : Общественное достояние: Авторские права неизвестны
- Юлиус Роберт фон Майер. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторские права
- Термически возбужденная молекула.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - Бомбовый калориметр. Предоставлено : Wikimedia. Лицензия : CC BY-SA: Attribution-ShareAlike
Расчеты теплоемкости Учебное пособие по химии
Расчеты теплоемкости Учебное пособие по химииКлючевые понятия
- Удельная теплоемкость вещества – это количество тепла, необходимое для повышения температуры 1 грамма вещества на 1°С (или на 1 К). 1
- C г — это символ, используемый для обозначения удельной теплоемкости.
- Единицы СИ 2 удельной теплоемкости:
Дж на градус Цельсия на грамм, Дж °С -1 г -1
или
Дж на Кельвин на грамм, Дж К -1 г -1
- Мы можем выразить зависимость между удельной теплоемкостью (C г ), энергией в джоулях (q), массой в граммах (м) и изменением температуры (ΔT) в виде математического уравнения:
С г = к
м × ΔT= J
г × °C - Это уравнение можно изменить, чтобы найти количество тепловой энергии (q), полученное или потерянное веществом, с учетом его удельной теплоемкости (C г ), массы в граммах (г) и изменения температуры (ΔT)
q = m × C г × ΔT
- Молярная теплоемкость вещества – это количество теплоты, необходимое для повышения температуры 1 моля вещества на 1°С (или на 1 К).

- C n — это символ, используемый для обозначения молярной теплоемкости.
- Единицы молярной теплоемкости:
Дж на градус Цельсия на моль, Дж °С -1 моль -1
или
Дж на Кельвин на моль, Дж К -1 моль -1
- Мы можем выразить зависимость между молярной теплоемкостью (C n ), энергией в джоулях (q), количеством вещества в молях (n) и изменением температуры (ΔT) в виде математического уравнения:
С Н = q
n × ΔT= J
моль × °C - Это уравнение можно преобразовать для расчета количества тепловой энергии, полученной или потерянной веществом, с учетом его молярной теплоемкости (C n ), количества вещества в молях (n) и изменения температуры (ΔT):
q = n × C n × ΔT
- Удельная теплоемкость или молярная теплоемкость могут быть использованы для определения изменения энергии химической реакции в водном растворе (теплота реакции или энтальпия реакции) в школьной лаборатории с использованием простого калориметра, состоящего из полистироловой чашки, снабженной крышкой и термометром.

- Удельная теплоемкость или молярная теплоемкость также могут использоваться для определения изменения энергии реакции горения (см. Теплота сгорания топлива и Теплота сгорания пищи).
Пожалуйста, не блокируйте рекламу на этом сайте.
Нет рекламы = нет денег для нас = нет бесплатных вещей для вас!
Удельная теплоемкость
Если вы осторожно нагреете воду с помощью источника тепла, такого как горелка Бунзена, температура воды увеличится.
Энергия горелки Бунзена заставляет молекулы воды двигаться быстрее, увеличивая их кинетическую энергию.
Мы можем измерить результат увеличения кинетической энергии как повышение температуры.
Количество энергии, поглощаемой молекулами воды для увеличения их кинетической энергии, называется «тепловой энергией». 3
Тепловая энергия частиц воды, q, пропорциональна изменению температуры, ΔT.
ΔT = конечная температура – начальная температура
q ∝ ΔT
Это означает, что если вы используете ту же массу воды, но удваиваете тепловую энергию (q), то изменение температуры (ΔT) также удваивается.
Точно так же, если уменьшить вдвое тепловую энергию (q), то изменение температуры (ΔT) также уменьшится вдвое.
Вы также можете нагреть «холодную» воду, добавив в нее немного «горячей» воды.
Представьте, что у вас есть стакан с водой, содержащий 100 г воды при температуре 25,0°C.
Как изменится температура воды, если добавить 10 г кипятка (100°C)?
Тепло будет переходить от горячей воды к холодной. 4
Кинетическая энергия «горячих» молекул воды будет уменьшаться, а кинетическая энергия «холодных» молекул воды увеличиваться, пока все молекулы воды не будут иметь одинаковую среднюю кинетическую энергию. 5
Поскольку температура является мерой средней кинетической энергии всех молекул воды, мы находим, что температура воды станет постоянной.
В этом примере будет достигнута постоянная температура 6 31,8°C.
Изменение температуры, ΔT составляет
ΔT = конечная температура – начальная температура = 31,8 – 25,0 = 6,8°C
Теперь представьте, что вы повторяете эксперимент, но на этот раз с использованием 20 г кипятка.
Какой будет конечная температура воды?
Снова теплота будет перетекать от горячей воды к холодной, горячая вода охлаждается, а холодная вода нагревается до тех пор, пока во всем объеме воды не будет достигнута постоянная температура.
Но на этот раз температура будет выше, 37,5°C.
Изменение температуры, ΔT составляет
ΔT = конечная температура – начальная температура = 37,5 – 25,0 = 12,5°C
Добавление большей массы горячей воды к той же массе холодной воды приводит к большему повышению температуры.
Это говорит нам о том, что количество тепловой энергии, которое может быть передано от горячего вещества к холодному, зависит от массы используемого вещества.
Тепловая энергия (q) пропорциональна массе используемого вещества (m) и изменению температуры (ΔT):
кв ∝ м × ΔT
Мы могли бы превратить эту зависимость в математическое уравнение, используя константу пропорциональности.
Пусть C – константа пропорциональности, тогда:
q = C × m × ΔT
Давайте посмотрим, что произойдет с этой константой пропорциональности C, когда мы изменим вещество, используемое для нагревания воды.
Что произойдет с температурой 100 г воды, изначально равной 25,0°С, если мы добавим вместо воды 20 г другого вещества, скажем, 20 г металлической меди при 100°С?
Тепло будет перетекать от горячего котла к более холодной воде, медь будет остывать, а вода нагреваться до тех пор, пока не будет достигнута постоянная температура.
Конечная температура воды составляет всего 26,5°C, что ниже температуры при добавлении 20 г воды!
Изменение температуры, ΔT составляет
ΔT = конечная температура – начальная температура = 26,5 – 25,0 = 1,5°C
Для равных масс горячей воды и горячей меди при одинаковой температуре горячая вода может передать холодной воде больше тепловой энергии, чем горячая металлическая медь. 7
То есть значение константы пропорциональности C для воды больше, чем для меди.
Термин, который используется для описания этой способности (или способности) передавать тепловую энергию, называется «теплоемкость».
Когда сравнения производятся с использованием массы в граммах веществ, эта «теплоемкость» называется удельной теплоемкостью .
Итак, удельная теплоемкость воды больше, чем удельная теплоемкость меди.
Удельная теплоемкость была обозначена символом C г (думаем, что «г» означает граммы, то есть массу).
Теперь мы можем заменить константу пропорциональности (C) в нашем математическом уравнении выше удельной теплоемкостью (C g ):
q = C г × m × ΔT
Мы можем изменить это уравнение, разделив обе его части на m × ΔT:
| q м × ΔT | = | C г × |
| q м × ΔT | = | С г |
Теперь, если я хочу сравнить удельные теплоемкости различных веществ, мне нужно будет поддерживать постоянную массу, скажем, 1 грамм, и я буду использовать достаточно тепловой энергии, чтобы произвести изменение температуры на 1°C (или 1K),
Подставив эти значения в уравнение:
| q 1 × 1 | = | С г |
| к | = | С г |
То есть удельная теплоемкость вещества – это энергия (q), необходимая для повышения температуры 1 грамма вещества на 1°C (или 1K)!
Различные вещества имеют разную удельную теплоемкость. Удельная теплоемкость некоторых веществ приведена в таблице ниже: 8
Удельная теплоемкость некоторых веществ приведена в таблице ниже: 8
| Удельная теплоемкость некоторых веществ | |||
|---|---|---|---|
| Элементы | C г (J K -1 г -1 или J °C -1 г 10 -1 -1 -1 -1 -1 -1) 2 | ||
| алюминий | С г = 0,90 | вода (жидкая) | С г = 4,18 |
| углерод | C г = 0,72 | этанол (жидкий) | C г = 2,44 |
| медь | C г = 0,39 | серная кислота (жидкая) | C г = 1,42 |
| свинец | С г = 0,13 | хлорид натрия (твердый) | C г = 0,85 |
| ртуть (жидкая) | C г = 0,14 | гидроксид калия (твердый) | C г = 1,18 |
Из приведенной выше таблицы видно, что удельная теплоемкость меди составляет 0,39 Дж °С -1 г -1 а удельная теплоемкость воды значительно выше, 4,18 Дж °С -1 г -1 .
Для изменения температуры 1 грамма металлической меди на 1°С (или 1 К) требуется 0,39 Дж энергии.
Для изменения температуры 1 грамма жидкой воды на 1°С (или 1 К) требуется 4,18 Дж энергии.
Удельная теплоемкость, C г , как описано выше, полезна, потому что мы можем легко измерить массу многих веществ.
Однако, когда мы смотрим на таблицу значений, некоторые из этих значений кажутся нелогичными.
Почему для повышения температуры 1 г свинца на 1°С требуется 0,13 Дж энергии, а для повышения температуры 1 г алюминия на 1°С требуется почти в 7 раз больше энергии?
И почему углерод имеет более высокую теплоемкость, чем металлическая медь или свинец?
Возможно, сравнение по массе не лучший вариант…..
Молярная теплоемкость
Равные массы различных веществ содержат разное количество «частиц» (атомов, ионов или молекул).
Химики используют «моль» как меру «количества» вещества, потому что моль чистого вещества всегда содержит одинаковое количество частиц (число Авогадро, N A = 6,02 × 10 23 ).
Масса 1 моля чистого вещества равна его относительной молекулярной массе, выраженной в граммах:
масса 1 моля = относительная молекулярная масса в граммах
Напомним, что удельная теплоемкость – это энергия, необходимая для повышения температуры 1 грамма вещества на 1°С (или 1 К).
пример: C г для металлической меди, Cu (s) , is 0,39 Дж °C -1 г -1
Если мы хотим найти теплоемкость 1 моля вещества, нам нужно умножить удельную теплоемкость, C г , на относительную молекулярную массу (M r ) или молярную массу (M) вещества:
теплоемкость 1 моля = M r × C (г)
или
теплоемкость 1 моля = M × C (г)
Величина «M × C г » называется молярной теплоемкостью и обозначается символом C n (n — это символ, используемый для обозначения молей).
Молярная теплоемкость вещества – это энергия, необходимая для повышения температуры 1 моля вещества на 1°C (или 1K).
Например, удельная теплоемкость металлической меди: C г = 0,39 Дж°C -1 г -1
Относительная атомная масса меди из Периодической таблицы: M r = 63,55
Молярная теплоемкость металлической меди = C г × M r = 0,39 × 63,55 = 24,8 Дж °C -1 моль -1
Вы можете самостоятельно выполнить этот расчет для каждого из веществ, перечисленных в таблице удельных теплоемкостей выше.
Вы можете сверить свои расчеты с расчетами, приведенными в таблице молярных теплоемкостей, приведенной ниже:
| Молярная теплоемкость некоторых веществ | |||
|---|---|---|---|
| Элементы | C n (J K -1 моль -1 или J °C -1 моль -1 Соединения | C n | (J K -1 моль -1 или J °C -1 моль -1 2 ) |
| ртуть | С n = 28,1 | серная кислота (жидкая) | C n = 139 |
| свинец | C n = 27,0 | вода | С n = 75 |
| медь | C n = 24,8 | гидроксид калия (твердый) | C n = 66 |
| алюминий | С n = 24,3 | хлорид натрия (твердый) | C n = 50 |
| углерод | C n = 8,6 | этанол (этиловый спирт) | C n = 22 |
Эта таблица позволяет сравнить теплоемкости одного и того же числа частиц, т. е. 1 моля, разных веществ.
е. 1 моля, разных веществ.
Мы находим, что молярная теплоемкость металлов очень похожа, в то время как молярная теплоемкость углерода намного ниже.
Для повышения температуры 1 моля металла на 1 °С (или 1 К) требуется около 25 Дж энергии, но для повышения температуры 1 моля углерода на 1 °С требуется только около 9 Дж энергии ( или 1 К).
Мы могли бы написать новое уравнение для расчета количества тепла, необходимого (q) для повышения температуры (ΔT) количества вещества в молях (n):
q = C n × n × ΔT
Рабочие примеры расчетов теплоемкости
Вопрос 1: Вычислите количество теплоты в джоулях, необходимое для повышения температуры 250 г воды с 20°С до 56°С.
Удельная теплоемкость воды 4,18 Дж°С -1 г -1 .
Решение:
(На основе подхода StoPGoPS к решению проблем.)
- Какой вопрос просит вас сделать?
Рассчитать количество теплоты в джоулях
д = ? Дж - Какие данные (информация) были вам предоставлены в вопросе?
Извлечь данные из вопроса:
м = масса воды = 250 г
T i = начальная температура = 20°C
T f = конечная температура = 56°C
С г = удельная теплоемкость воды = 4,18 Дж°C -1 г -1
- Какая связь между тем, что вы знаете, и тем, что вам нужно узнать?
Напишите уравнение для определения тепловой энергии:
q = m × C г × ΔT
(a) Рассчитайте изменение температуры, ΔT:
ΔT = T f – T i
(b) Подставьте значения для m, C g и ΔT в уравнение и найдите q
- Выполнение расчетов
(a) Рассчитайте изменение температуры, ΔT:
ΔT = T f – T i
ΔT = 56 – 20 = 36°C(b) Подставьте значения для m, C g и ΔT в уравнение и найдите q
q = m × C г × ΔT
q = 250 х 4,18 х 36 = 37 620 Дж - Ваш ответ правдоподобен?
Подумайте, что означает термин «удельная теплоемкость».
 Это энергия, необходимая для повышения температуры 1 г вещества (воды) на 1°С.
Это энергия, необходимая для повышения температуры 1 г вещества (воды) на 1°С.
Следовательно, поскольку у нас 250 г, нам потребуется в 250 раз больше «удельной теплоемкости воды (4.18)»:
то есть нам нужно 250×4,18=1045 Дж
Но мы также повысили температуру на 36°C, а не на 1°C, поэтому нам потребуется в 36 раз больше энергии:
то есть нам нужно 36×1045 = 37 620 ДжПоскольку этот ответ, 37 620 Дж, совпадает с нашим расчетом выше, мы достаточно уверены, что наш ответ правдоподобен.
- Укажите решение задачи “количество теплоты в джоулях”:
q = 37 620 Дж
Вопрос 2: Рассчитайте удельную теплоемкость меди, зная, что 204,75 Дж энергии повышают температуру 15 г меди с 25°С до 60°С.
Решение:
(На основе подхода StoPGoPS к решению проблем.)
- Какой вопрос просит вас сделать?
Рассчитайте удельную теплоемкость меди
C г (Cu) = ? J°C -1 г -1 - Какие данные (информация) были вам предоставлены в вопросе?
Извлечь данные из вопроса:
q = тепловая энергия = 204,75 Дж
м = масса меди = 15 г
T i = начальная температура = 25°C
T f = конечная температура = 60°C
- Какая связь между тем, что вы знаете, и тем, что вам нужно узнать?
Напишите уравнение для определения тепловой энергии:
q = m × C г × ΔT
(a) Рассчитайте изменение температуры, ΔT:
ΔT = T f – T i
(b) Подставьте значения q, m и ΔT в уравнение и найдите C g
- Выполнение расчетов
(a) Рассчитайте изменение температуры, ΔT:
ΔT = T f – T i
ΔT = 60 – 25 = 35°C(b) Подставьте значения q, m и ΔT в уравнение и найдите C g
к = м × C г × ΔT 204,75 = 15 × C г × 35 204,75 = С г × 525 204,75
525= C г × 525
5250,39 = С г - Ваш ответ правдоподобен?
Удельная теплоемкость – это энергия, необходимая для повышения температуры 1 г вещества (меди) на 1°С.

204,75 Дж тепловой энергии было использовано для повышения температуры 15 г меди, поэтому это значение тепловой энергии в 15 раз больше, поэтому нам нужно разделить тепловую энергию на 15:
204,75 Дж ÷ 15 г = 13,65 Дж г -1
Обратите внимание, что повышение температуры составило не 1°С, а 35°С, то есть значение тепловой энергии будет в 35 раз больше, поэтому нам нужно разделить на 35:
13,65 Дж·г -1 ÷ 35°C = 0,39 Дж·г -1 °C -1
То есть 0,39Для повышения температуры 1 г меди на 1°С требуется Дж тепловой энергии.
Тепловая энергия, необходимая для повышения температуры 1 г вещества на 1°С, называется его удельной теплоемкостью.
Следовательно, удельная теплоемкость меди равна 0,39 Дж°C -1 г -1Поскольку этот результат совпадает с тем, который мы рассчитали выше, мы достаточно уверены, что наш ответ правдоподобен.
- Укажите свое решение задачи “Удельная теплоемкость меди”:
C г (Cu) = 0,39 Дж°C -1 г -1
Вопрос 3: Для повышения температуры алюминия с 15°С до 35°С требуется 216 Дж энергии.
Рассчитайте массу алюминия в граммах.
(Удельная теплоемкость алюминия 0,90 Дж°С -1 г -1 ).
Решение:
(На основе подхода StoPGoPS к решению проблем.)
- Какой вопрос просит вас сделать?
Рассчитайте массу алюминия в граммах
м(Al) = ? грамм - Какие данные (информация) были вам предоставлены в вопросе?
Извлечь данные из вопроса:
q = тепловая энергия = 216 Дж
T i = начальная температура = 15°C
T f = конечная температура = 35°C
C г (Al) = 0,90 Дж°C -1 г -1
- Какая связь между тем, что вы знаете, и тем, что вам нужно узнать?
Напишите уравнение для определения тепловой энергии:
д = м × С г × ΔT
(a) Рассчитайте изменение температуры, ΔT:
ΔT = T f – T i
(b) Подставьте значения для q, C g и ΔT в уравнение и найдите m
- Выполнение расчетов
(a) Рассчитайте изменение температуры, ΔT:
ΔT = T f – T i
ΔT = 35 – 15 = 20°C(b) Подставьте значения для q, C g и ΔT в уравнение и найдите m
к = м × C г × ΔT 216 = м × 0,90 × 20 216 = м × 18 216
18= м × 18
1812 = м - Ваш ответ правдоподобен?
Удельная теплоемкость – это энергия, необходимая для повышения температуры 1 г вещества (Al) на 1°С.

Удельная теплоемкость алюминия равна 0,90 Дж°C -1 г -1 .
Изменение температуры составляет не 1°C, а 20°C, поэтому нам нужно умножить удельную теплоемкость на 20, чтобы определить количество энергии, которое потребуется для повышения температуры 1 г Al на 20°C. С:
тепловая энергия = 20°C× 0,90 Дж°C -1г -1 = 18 Дж г -1
были больше 1 г.
Разделите полученную тепловую энергию (216 Дж) на 18 Дж г -1 , чтобы определить массу используемого алюминия:
216Дж÷ 18Джг -1 = 12 гПоскольку этот результат совпадает с тем, который мы рассчитали выше, мы достаточно уверены, что наш ответ правдоподобен.
- Укажите свое решение задачи “масса алюминия в граммах”:
м(Al) = 12 г
Вопрос 4: Начальная температура 150 г этанола составляла 22,0°С.
Какой будет конечная температура этанола в градусах Цельсия, если для повышения температуры этанола потребовалось 3240 Дж?
(Удельная теплоемкость этанола 2,44 Дж°С -1 г -1 )
Решение:
(На основе подхода StoPGoPS к решению проблем.)
- Какой вопрос просит вас сделать?
Рассчитайте конечную температуру этанола
Т ж = ? °С - Какие данные (информация) были вам предоставлены в вопросе?
Извлечь данные из вопроса:
м = масса этанола = 150 г
T i = начальная температура = 22,0°C
q = тепловая энергия, необходимая для повышения температуры = 3240 Дж
C г = теплоемкость этанола = 2,44 Дж°C -1 г -1
- Какая связь между тем, что вы знаете, и тем, что вам нужно узнать?
Напишите уравнение для определения тепловой энергии:
q = m × C г × ΔT
(a) Подставьте значения q, m и C g в уравнение и найдите ΔT
(b) Рассчитайте конечную температуру этанола:
ΔT = T f – T i
T f = ΔT + T i - Выполнить вычисления
(a) Подставьте значения q, m и C g в уравнение и найдите ΔT
к = м × C г × ΔT 3240 = 150 × 2,44 × ΔT 3240 = 366 × ΔT 3240
366= 366× ΔT
3668,85 = ΔТ (b) Рассчитайте конечную температуру этанола:
T f = ΔT + T i
T f = 22,0 + 8,85 = 30,85°C = 30,9°C - Ваш ответ правдоподобен?
Удельная теплоемкость – это энергия, необходимая для повышения температуры 1 г вещества (этанола) на 1°С.

Для повышения температуры 1 г этанола на 1°С необходимо 2,44 Дж тепловой энергии.
Было использовано 150 г этанола, поэтому необходимая тепловая энергия будет в 150 раз больше удельной теплоемкости этанола:
150г× 2,44 Дж°С -1г -1= 366 Дж°С -1
Фактически использованная тепловая энергия была больше 366 Дж, она составила 3240 Дж, т.е. использованная тепловая энергия была в 3240 ÷ 366 = 8,85 раз больше, чем требуется для повышения температуры на 1 °С, следовательно, изменение температуры должно быть 1 × 8,85 = 8,85 °С.
Начальная температура была 22,0°C, поэтому конечная температура должна быть на 8,85°C выше, то есть конечная температура должна быть 22,0 + 8,85 = 30,85 °C. 30,9°С.Поскольку этот результат совпадает с тем, который мы рассчитали выше, мы достаточно уверены, что наш ответ правдоподобен.
- Укажите свое решение задачи “конечная температура этанола”:
T f = 30,9°C
Сноски
1. Поскольку градуировка на шкалах как по шкале Цельсия, так и по шкале Кельвина одинакова, и поскольку нас здесь не интересует ни начальная, ни конечная температура, а только разница между ними, можно видеть, что разница в 1°С равна разнице в 1 К.
Поскольку градуировка на шкалах как по шкале Цельсия, так и по шкале Кельвина одинакова, и поскольку нас здесь не интересует ни начальная, ни конечная температура, а только разница между ними, можно видеть, что разница в 1°С равна разнице в 1 К.
Тщательные эксперименты показывают, что удельная теплоемкость вещества сама по себе является функцией температуры, поэтому в девятнадцатом веке был установлен стандарт, т. е. теплоемкость — это количество теплоты, необходимое для повышения температуры 1 г воды с 14,5°. С до 15,5°С.
2. В 1960 г. Генеральная конференция мер и весов согласовала унифицированную версию метрической системы.
Единицы в этой системе известны как единицы СИ (Systèm International d’Unités).
Семь основных единиц составляют основу системы СИ:
| Physical quantity | Name of Unit | Symbol |
|---|---|---|
| mass | kilogram | kg |
| length | meter | m |
| time | second | s |
| электрический ток | ампер | А |
| температура | кельвин | К |
| сила света | кандела | кд |
| количество вещества | моль | моль |
Производные единицы основаны на вышеуказанных единицах СИ.

Единицей силы является ньютаун (Н), это производная единица, 1 Н = 1 кг м · с -2
Единица энергии также является производной единицей, джоуль (Дж), 1 Дж = 1 Н m = 1 кг m 2 s -2
Электрические измерения обладают большей точностью, чем калориметрические измерения, как описано в этом обсуждении, поэтому джоуль также можно определить как вольт-кулон.
3. Теплота, или тепловая энергия, есть энергия, непосредственно передаваемая от одного объекта к другому.
Тепло — это энергия в пути, вещество, подобное воде при постоянной температуре, не имеет «теплосодержания», но имеет «энергосодержание».
Энергетическое содержание вещества состоит из кинетической энергии (движения) его частиц и потенциальной энергии, такой как запасенная химическая потенциальная энергия в его химических связях.
Температура является мерой средней кинетической энергии частиц.
4. Тепло всегда течет от «горячего» к «холодному».
В 1803 году, через 4 года после его смерти, была опубликована работа Джозефа Блэка по калориметрии (измерению тепловых изменений). В нем он показал, что равенство температур не означает, что в различных веществах существует также «равенство теплоты».
Он исследовал теплоемкость или количество тепла, необходимое для повышения температуры различных тел на заданное число градусов.
Объясняя свои опыты, он рассматривал теплоту как вещество, которое может перетекать от одного тела к другому.
В нем он показал, что равенство температур не означает, что в различных веществах существует также «равенство теплоты».
Он исследовал теплоемкость или количество тепла, необходимое для повышения температуры различных тел на заданное число градусов.
Объясняя свои опыты, он рассматривал теплоту как вещество, которое может перетекать от одного тела к другому.
5. Частицы не будут иметь абсолютно одинаковую кинетическую энергию. Существует распределение кинетических энергий частиц, поэтому мы имеем в виду «среднюю» кинетическую энергию частиц в системе.
6. Это известно как тепловое равновесие.
7. Правильнее сказать, что теплоемкость — это способность вещества передавать теплоту другому веществу, поскольку теплота — это энергия в пути.
То есть теплоемкость – это способность или способность вещества передавать теплоту другому веществу.
Но, поскольку слово «емкость» обычно понимается как «вместимость», например, мерная колба на 250 мл имеет вместимость 250 мл, мы часто думаем о теплоемкости вещества как о его способности удерживать тепловую энергию.
На самом деле мы не можем называть «тепло» накопленным, то есть тепло может поглощаться молекулами для увеличения их кинетической энергии, но оно не «аккумулируется», потому что оно выполнило работу по ускорению частиц.
Тепловая энергия может быть «запасена» как потенциальная энергия в химических связях, если происходит химическая реакция, но в этих примерах это не так.
8. Значения удельных теплоемкостей относятся к условиям постоянного атмосферного давления.
©AUS-e-TUTEwww.ausetute.com.au
Молекулярные формулы и номенклатура
Нижеследующее является содержанием Лекции по общей химии 21. В этой лекции мы рассмотрим определения энергии и процесс калориметрии.
Энергия
К сожалению, чтобы обсудить следующие темы, необходимо сначала обсудить множество определений, так что потерпите меня.
В первую очередь необходимо дать определение этому разделу изучения химии. Термодинамика или, точнее, Термохимия — это изучение поглощения или выделения тепла, которое сопровождает химические реакции.
Энергия определяется как способность выполнять работу, а в химии мы определяем Энергия как сумму выполненной работы (w) и произведенного или потерянного тепла (q).
E = w + q
Энергия также делится на два основных типа:
(1) Кинетическая энергия (E K ) или энергия движения: 1/2 mv 2 , где m — масса, а v — скорость
(2) Потенциальная энергия (E P ): энергия хранится в химических связях, которые высвобождаются при разрыве или образовании связи.
На рисунке ниже, когда вода начинает течь, энергия меняется с потенциальной на кинетическую:
В любом случае измеряемая энергия обычно выражается в одной из двух единиц: Калории (кал) или Джоули (Дж). ) Джоуль определяется как 1 кг . м 2 /с 2 . Калория — это количество тепла, необходимое для нагревания 1 моля воды на 1 градус Цельсия и получения 4,184 Дж = 1 кал.
Закон сохранения энергии
Точно так же, как Закон сохранения массы заложил основу для стехиометрических расчетов, Закон сохранения энергии закладывает основу для термодинамических расчетов.
Закон гласит, что Энергия не может быть ни создана, ни уничтожена, поэтому он известен как Первый Закон Термодинамики. Это означает, что общая Энергия Вселенной постоянна и могут быть измерены только изменения в типе энергии.
В химии это часто означает, что потенциальная энергия химических связей преобразуется в тепловую энергию, которая, в свою очередь, затем преобразуется в кинетическую энергию по мере того, как молекула реагирует на повышение температуры и т. д. Или, как показано ниже, образование связи преобразует химическое энергии в тепловую и световую энергию. Важной особенностью процесса является то, что количество энергии остается постоянным.
Вот еще несколько определений для вас:
1) Температура – в термодинамике это определяется как мера кинетической энергии, полученной из молекулярного движения. Что-то вроде того, что было первым, определение типа «курица или яйцо», поскольку при более высоких температурах молекулы имеют большую кинетическую энергию, но вот она.
Что-то вроде того, что было первым, определение типа «курица или яйцо», поскольку при более высоких температурах молекулы имеют большую кинетическую энергию, но вот она.
2) Тепловая энергия или теплота (q) – определяется как кинетическая энергия, передаваемая от одного объекта к другому в результате разницы температур между ними. Таким образом, мы должны измерить разницу температур между двумя объектами/веществами, чтобы определить тепло.
3) Химическая энергия – как показано выше, это потенциальная энергия химических связей.
Расчеты энергии
На данный момент есть только несколько типов расчетов энергии, которые мы можем сделать из работы и тепла.
Например:
Какова энергия системы, которая совершает 100 Дж работы и поглощает 250 Дж тепла?
Чтобы вычислить это, вам нужно знать правила знаков:
В термодинамике (так же, как и в жизни) выполнение работы имеет отрицательный знак, а выполнение работы над системой положительно. Точно так же потеря тепла имеет отрицательный знак, а поглощение тепла — положительный. Таким образом, для приведенной выше задачи это на самом деле просто процесс интерпретации чтения, поскольку задействованная математика — это просто сложение или вычитание:
Точно так же потеря тепла имеет отрицательный знак, а поглощение тепла — положительный. Таким образом, для приведенной выше задачи это на самом деле просто процесс интерпретации чтения, поскольку задействованная математика — это просто сложение или вычитание:
Система совершает работу, поэтому 100 Дж должно быть отрицательным, и она поглощает тепло, поэтому 250 Дж положительно:
E = -100 Дж + 250 Дж = 150 Дж
и другой тип расчета для кинетической энергии :
E
K = 1/2 mv 2Вот простой пример:
Если полузащитник может пробежать 40 метров за 4,15 секунды и весит 195 фунтов, сколько у него кинетической энергии?
Сначала запомните единицы измерения джоуля: 1 кг . м 2 /с 2
Нам нужно преобразовать фунты в кг: 195 фунтов x 1 кг/2,2 фунта = 88,6 кг
Тогда просто подключи и пей:
9 E
09
09 = ½(88,6 кг)(40 м/4,15 с) 2 = 4,12 кДж
А теперь вернемся к определениям. ..
..
Система и окружение
Как мы узнали ранее, энергия быть эквивалентным для любого процесса, но мы не определили, где мы будем терять или приобретать эту энергию, поэтому мы сделаем это сейчас.
Система – определяется как изучаемый процесс, реакция или объект.
Окружающие s – это все остальное.
Например, в реакции водной кислоты и основания системой будет сама реакция между молекулами кислоты и основания, а окружающей средой будет вода и контейнер, в котором они находятся.
Официально существует три типа систем:
Открытый — может обмениваться теплом и веществом с окружающей средой
Закрытый — может обмениваться теплом, но не имеет значения с окружающей средой
Изолированный — не может обмениваться теплом или веществом с окружающей средой
Здесь я хочу еще раз напомнить вам о Первом Законе Термодинамики: Энергия не создается и не уничтожается. Другой способ заявить об этом состоит в том, что чистое Изменение Энергии между системой и ее окружением должно быть равно нулю. ΔE = E Система + E Окружение =0. Чтобы это было правдой, тогда Энергия системы должна быть эквивалентна энергии окружающей среды, но противоположна по знаку.
Другой способ заявить об этом состоит в том, что чистое Изменение Энергии между системой и ее окружением должно быть равно нулю. ΔE = E Система + E Окружение =0. Чтобы это было правдой, тогда Энергия системы должна быть эквивалентна энергии окружающей среды, но противоположна по знаку.
E Система = -E Окружение или -E Система = E Окружение
И так же, как и раньше, когда система теряет энергию, мы даем отрицательный знак набирает энергию, это положительно.
Тепло
Когда в открытом контейнере происходит химическая реакция, большая часть полученной или потерянной энергии приходится на тепло. Почти никакой работы не делается (т.е. ничего не перемещается). Теплота (q) определяется как передача энергии между системой и ее окружением. Тепло течет между системой и окружающей средой до тех пор, пока они не будут иметь одинаковую температуру. Когда происходит химическая реакция, при которой система поглощает тепло, говорят, что процесс идет эндотермический (на ощупь холодный). Когда происходит химическая реакция, при которой система выделяет тепло, она экзотермическая (она кажется горячей).
Когда происходит химическая реакция, при которой система поглощает тепло, говорят, что процесс идет эндотермический (на ощупь холодный). Когда происходит химическая реакция, при которой система выделяет тепло, она экзотермическая (она кажется горячей).
Определение тепла – калориметрия
Калориметрия – это процесс, посредством которого измеряется изменение температуры системы.
Существует два основных типа калориметрии – постоянное давление и постоянный объем.
Калориметр постоянного давления часто называют калориметром кофейной чашки, потому что он напоминает и часто изготавливается из кофейной чашки в лабораторных экспериментах.
q Sys , показанное здесь, представляет собой общее количество тепла для всего калориметра, который содержит воду и калориметр окружения, как мы определили его ранее, и q Rxn , которое мы определили ранее как систему. Как и выше, где мы заявили, что общая энергия должна быть равна нулю, то же самое и с q Sys .
показано здесь. Это означает, что преобразование приведенного выше уравнения устанавливает q окружения равным по величине, но противоположным по знаку, как и раньше.
Как и выше, где мы заявили, что общая энергия должна быть равна нулю, то же самое и с q Sys .
показано здесь. Это означает, что преобразование приведенного выше уравнения устанавливает q окружения равным по величине, но противоположным по знаку, как и раньше.
Расчет q зависит не только от изменения температуры, но также от его удельной теплоемкости и количества.
Удельная теплоемкость (c)
Удельная теплоемкость (c) вещества – это количество теплоты (q), необходимое для повышения температуры одного грамма вещества на один градус Цельсия.
Это уравнение для теплоты просто означает, что чем больше у вас вещества, тем больше тепла оно может поглотить или выделить, поэтому тепло считается экстенсивным свойством. При этом также учитывается, что разные типы материалов по-разному поглощают/выделяют тепло. Всякий, кто когда-либо готовил в алюминиевой фольге или на чугунной сковороде, понимает эту разницу. К фольге можно прикасаться с минимальной опасностью, так как она становится прохладной почти сразу после снятия с огня, а к железной сковороде еще долго будет опасно прикасаться. Это связано с их разной теплоемкостью (см. таблицу выше).
К фольге можно прикасаться с минимальной опасностью, так как она становится прохладной почти сразу после снятия с огня, а к железной сковороде еще долго будет опасно прикасаться. Это связано с их разной теплоемкостью (см. таблицу выше).
Возвращаясь к калориметрии, другой тип калориметра — это калориметр постоянного объема или «бомба». Часть «бомбы» исходит из того факта, что, поскольку объем постоянен, давление внутри калориметра может быть довольно высоким. Если за этим не следить внимательно, это может привести к плачевным результатам.
Уравнения для расчета тепла практически идентичны уравнениям калориметра постоянного давления. Большая разница между ними заключается в том, что в то время как в калориметре с кофейной чашкой реакция происходит в воде как части водного раствора, реакция в калориметре с бомбой происходит в отдельной камере.
Вот несколько простых примеров калориметрии:
youtube.com/embed/A5rprSe1p10″ frameborder=”0″ gesture=”media” allowfullscreen=””>Проблемы практики калориметрии
Специфический калькулятор тепла + Формула (Уравнение C = Q /(M ΔT)
4444444888888888888888888888888 гг. к
Удельная теплоемкость — это, по сути, мера того, насколько трудно нагреть различных материалов. Чтобы рассчитать удельную теплоемкость (C) любого вещества, вам понадобится формула удельной теплоемкости (уравнение, если хотите).
Далее вы также найдете калькулятор удельной теплоемкости : Вы просто подставляете Q (тепловая энергия) , m (масса) и ΔT (разность температур) , и калькулятор будет динамически рассчитывать удельную теплоемкость для вас. Вот как выглядит калькулятор удельной теплоемкости (скриншот):
Пример расчета: 20 000 Дж тепла нагреют 12 кг вещества на 20°К. Какая удельная теплоемкость? 83,33 Дж/кг×К. Вы можете найти этот калькулятор далее; он будет динамически и автоматически рассчитывать удельную теплоемкость.
Какая удельная теплоемкость? 83,33 Дж/кг×К. Вы можете найти этот калькулятор далее; он будет динамически и автоматически рассчитывать удельную теплоемкость.Сначала рассмотрим формулу удельной теплоемкости. Это довольно простая формула, которую может использовать каждый. В конце приведем также удельные теплоемкости воздуха, воды и некоторых других веществ. Мы также решим несколько простых примеров расчета удельной теплоемкости. Давайте рассмотрим пример, чтобы проиллюстрировать, что на самом деле говорит нам удельная теплоемкость:
Пример: Воздух при комнатной температуре имеет удельную теплоемкость 1012 Дж/кг×К. Вода при комнатной температуре имеет удельную теплоемкость 4181 Дж/кг×К. Это означает, что нам нужно примерно в 4 раза больше тепла, чтобы нагреть килограмм воды, чем килограмм воздуха.
Удельная теплоемкость определяется как количество теплоты, необходимое для повышения температуры 1 кг вещества на 1 К. Чаще всего для этого мы используем единицы СИ (Дж = Джоули, кг = килограммы, К = градусы Кельвина).
Мы можем аккуратно подставить все эти числа в следующую формулу:
Формула удельной теплоемкости
Удельная теплоемкость обозначается C (C для емкости). Вот уравнение для расчета удельной теплоемкости C:
C = Q ÷ (m×ΔT)
Довольно просто, правда?
- Q — это количество тепла, которое мы подводим к веществу. Может быть 1 Дж, 40 Дж или даже 50 000 Дж, любое количество Джоулей.
- м — это масса вещества, которое мы нагреваем. Вы можете нагреть 1 кг вещества, 20 кг или даже 10 г вещества, подходит любой вес.
- ΔT — это разница температур между начальной и конечной температурами, и она всегда измеряется не в градусах Фаренгейта (°F), не в градусах Цельсия (°C), а в кельвинах (K). Пример: если мы нагреем воду с 68°F или 20°C (это 293K) до 158°F или 70°C (это 343K), разница температур составляет 343K – 293K = 50K.
Вот простой пример: допустим, нам нужно 6000 Дж тепла, чтобы нагреть 3 кг вещества на 10К. Вот как мы рассчитываем удельную теплоемкость, используя приведенное выше уравнение;
Вот как мы рассчитываем удельную теплоемкость, используя приведенное выше уравнение;
C = 6000 Дж ÷ (3 кг × 10 К) = 200 Дж/кг × К
Формула удельной теплоемкости говорит нам, что удельная теплоемкость (C) этого вещества составляет 200 Дж/кг × К.
Чтобы еще больше упростить задачу, вы можете использовать этот калькулятор
Калькулятор удельной теплоемкости
По сути, вы просто вводите Q, m и ΔT, и калькулятор автоматически вычисляет удельную теплоемкость. Конечно, вы также можете немного поиграть с цифрами.
С помощью этого калькулятора можно просто определить, какова удельная теплоемкость вещества без необходимости все вычислять самостоятельно.
Давайте посмотрим на удельные теплоемкости некоторых распространенных газов, жидкостей и твердых тел:
Таблица удельной теплоемкости
| Вещество: | Фаза (газ, жидкость, твердое тело): | Удельная теплоемкость (Дж/кг×К) |
| Воздух при комнатной температуре | Газ | 1012 Дж/кг×К |
| Аргон (Ar) | Газ | 520,3 Дж/кг×К |
| Двуокись углерода (CO2) | Газ | 839Дж/кг×К |
| Гелий (Не) | Газ | 5193,2 Дж/кг×К |
| Водород (h3) | Газ | 14 300 Дж/кг×К |
| Сероводород (h3S) | Газ | 1015 Дж/кг×К |
| Метан при 275K (Ch5) | Газ | 2191/кг×K |
| Азот (N2) | Газ | 1040 Дж/кг×К |
| Неон (Ne) | Газ | 1030,1 Дж/кг×К |
| Кислород (O2) | Газ | 918 Дж/кг×К |
| Аммиак (Nh4) | Жидкость | 4700 Дж/кг×К |
| Этанол (Ch4Ch3OH) | Жидкость | 2440 Дж/кг×К |
| Бензин | Жидкость | 2220 Дж/кг×К |
| Меркурий | Жидкость | 139,5 Дж/кг×К |
| Метанол (Ch4OH) | Жидкость | 2140 Дж/кг×К |
| Вода при 25 °C | Жидкость | 4181,3 Дж/кг×К |
| Алюминий (Al) | Твердый | 897 Дж/кг×К |
| Сурьма | Твердый | 207 Дж/кг×К |
| Мышьяк | Твердый | 328 Дж/кг×К |
| Бериллий | Твердый | 1820 Дж/кг×К |
| Кадмий | Твердый | 231 Дж/кг×К |
| Хром | Твердый | 449 Дж/кг×К |
| Медь | Твердый | 385 Дж/кг×К |
| Алмаз | Твердый | 509,1 Дж/кг×К |
| Стекло | Твердый | 840 Дж/кг×К |
| Золото | Твердый | 129 Дж/кг×К |
| Гранит | Твердый | 790 Дж/кг×К |
| Графит | Твердый | 710 Дж/кг×К |
| Железо | Твердый | 412 Дж/кг×К |
| Свинец | Твердый | 129 Дж/кг×К |
| Литий | Твердый | 3580 Дж/кг×К |
| Магний | Твердый | 1020 Дж/кг×К |
| Полиэтилен | Твердый | 2302,7 Дж/кг×К |
| Силикагель | Твердый | 703 Дж/кг×К |
| Серебро | Твердый | 233 Дж/кг×К |
| Натрий | Твердый | 1230 Дж/кг×К |
| Сталь | Твердый | 466 Дж/кг×К |
| Олово | Твердый | 227 Дж/кг×К |
| Титан | Твердый | 528 Дж/кг×К |
| Уран | Твердый | 116 Дж/кг×К |
| Асфальт | Твердый | 920 Дж/кг×К |
| Кирпич | Твердый | 840 Дж/кг×К |
| Бетон | Твердый | 880 Дж/кг×К |
| Гипс | Газ | 1090 Дж/кг×К |
| Песок | Газ | 835 Дж/кг×К |
| Почва | Газ | 800 Дж/кг×К |
Если у вас есть какие-либо вопросы об удельной теплоемкости, вы можете использовать комментарии ниже, и мы постараемся помочь вам, чем сможем.
Содержание
Формула удельной теплоемкости – уравнение, вывод, примеры и часто задаваемые вопросы
При обсуждении термических свойств материалов удельная теплоемкость – это понятие, которое обсуждается и осознается очень немногими. Мы используем понятие удельной теплоемкости, чтобы понять, сколько тепла необходимо подать, чтобы поднять температуру объекта на градус Кельвина или Цельсия. Количество тепла, необходимое для повышения температуры вещества, называется удельной теплоемкостью. Другими словами, удельная теплоемкость — это количество тепла, необходимое для изменения температуры рассматриваемого материала или вещества.
В этой статье мы обсудим, что такое удельная теплоемкость, какова формула удельной теплоемкости вместе с небольшим выводом и решим численные задачи.
Уравнение удельной теплоемкости
В повседневной жизни мы могли бы заметить, что если рассматривать нагревание или кипячение воды в двух сосудах разного объема, то количество теплоты, необходимое для кипячения воды в определенное время, будет полностью зависеть от объем воды. Другими словами, если один сосуд содержит больше воды, чем другой сосуд, то время, которое потребуется сосуду большего объема, будет больше, чем другому сосуду. Это означает, что количество тепла, необходимое для повышения температуры любого данного вещества, различно и зависит от объема вещества. Это конкретное количество тепла, необходимое для изменения температуры, известно как удельная теплоемкость или удельная теплоемкость.
Другими словами, если один сосуд содержит больше воды, чем другой сосуд, то время, которое потребуется сосуду большего объема, будет больше, чем другому сосуду. Это означает, что количество тепла, необходимое для повышения температуры любого данного вещества, различно и зависит от объема вещества. Это конкретное количество тепла, необходимое для изменения температуры, известно как удельная теплоемкость или удельная теплоемкость.
Мы знаем, что термин «удельная теплоемкость» в термодинамике относится к отношению количества тепла, необходимого для повышения температуры вещества на один градус Цельсия, к количеству тепла, необходимому для повышения температуры эквивалентной массы жидкости (скажем, воды). ) на один градус Цельсия. В то же время мы используем термин «удельная теплоемкость» по более традиционной причине, чтобы определить количество тепла в калориях, необходимое для повышения температуры одного грамма материала на один градус Цельсия.
Проще говоря, уравнение удельной теплоемкости или формула удельной теплоемкости представляет собой отношение количества теплоты, необходимого для повышения температуры вещества на один градус Цельсия, к количеству теплоты, необходимому для повышения температуры равного количества воды на один градус Цельсия при комнатной температуре.
Термин «удельная теплоемкость» обычно используется, когда речь идет о чем-то конкретном, например, о повышении температуры определенного вещества. Сейчас обычно все путаются между удельной теплоемкостью и теплоемкостью.
Теплоемкость – это отношение количества тепла, необходимого для изменения температуры на один градус Цельсия, тогда как удельная теплоемкость – это количество тепла, необходимое для повышения температуры вещества, а не только для изменения или изменения температуры вещества. материал. Здесь важно отметить один важный момент: когда мы рассматриваем конкретное количество массы, мы склонны использовать слова «удельная теплоемкость» или «удельная теплоемкость». Удельная теплоемкость большинства термодинамических систем непостоянна и зависит от физических величин, таких как давление, объем и температура.
Вывод
Теперь давайте посмотрим на формулу удельной теплоемкости, которая обозначается буквой С. Согласно определению удельной теплоемкости, мы увидели, что она прямо пропорциональна изменению температуры (в частности повышение температуры). Мы знаем, что количество требуемой теплоты (Q) прямо пропорционально изменению температуры, поэтому мы пишем:
Согласно определению удельной теплоемкости, мы увидели, что она прямо пропорциональна изменению температуры (в частности повышение температуры). Мы знаем, что количество требуемой теплоты (Q) прямо пропорционально изменению температуры, поэтому мы пишем:
⇒ Q ∝ ΔT ……(1)
Где,
ΔT – изменение или повышение температуры
Также мы знаем, что удельная теплоемкость также прямо пропорциональна массе рассматриваемого вещества, таким образом, мы получаем:
⇒ Q ∝ m ……..(2)
Где,
m – масса вещества
Объединяя уравнения (1) и (2), получаем:
⇒ Q ∝ mΔT
⇒ Q = CmΔT
Где,
Кл – удельная теплоемкость
по:
C = \[\frac{Q}{m \Delta t}\]
9{0}\]c ……..(3)
Где
ΔQ — количество полученного или потерянного тепла в джоулях
ΔT — изменение или повышение температуры в градусах Цельсия
m — масса вещества в кг
Уравнение (3) известно как уравнение удельной теплоемкости или формула удельной теплоемкости в физике и используется для решения примеров удельной теплоемкости и для оценки удельной теплоемкости вещества в реальной жизни. Удельная теплоемкость вещества будет варьироваться в зависимости от типа вещества.
Удельная теплоемкость вещества будет варьироваться в зависимости от типа вещества.
Примеры удельной теплоемкости
Теперь давайте рассмотрим несколько конкретных примеров теплоемкости, которые помогут нам лучше понять концепцию удельной теплоемкости и уравнение удельной теплоемкости или формулу удельной теплоемкости.
1) Если для повышения температуры 50 г вещества с 3000°С до 4000°С требуется 968 Дж теплоты. Затем рассчитайте удельную теплоемкость вещества.
Решение:
Дано необходимое количество тепла = Q = 960 Дж
Масса вещества = m = 50 г
Изменение температуры = ΔT = T 2 – T 1 = 40 – 30 = 100°С
Теперь нас просят определить удельную теплоемкость вещество. Мы знаем, что удельная теплоемкость или удельная теплоемкость определяется уравнением:
⇒ C = \[\frac{Q}{m \Delta T}\]
Где,
Q – количество необходимого тепла
ΔT – изменение или повышение температуры
m – масса вещества
Подставляя необходимые значения в приведенное выше уравнение, мы получаем:
⇒ C = \[\frac{Q}{m \Delta T}\] = \[\frac{968}{50 \times 10}\]
= 96850×10
⇒ C = 1,936 Дж/г 0c
Следовательно, удельная теплоемкость вещества составляет 1,94 Дж/г 0c.






 Наука измерения этих изменений известна как калориметрия.
Наука измерения этих изменений известна как калориметрия.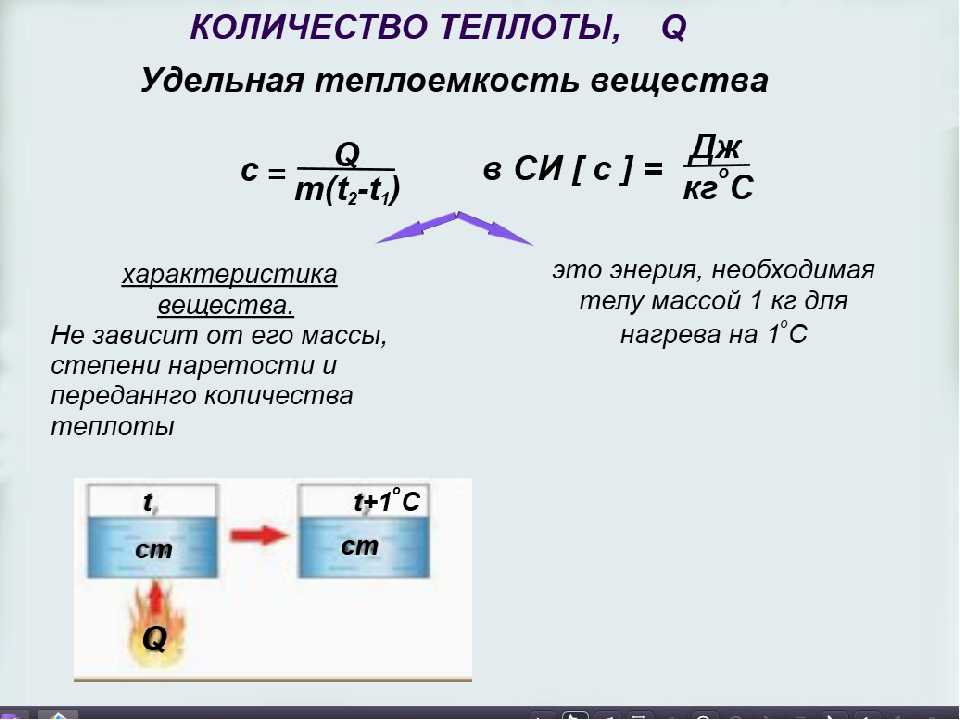 Здесь U — внутренняя энергия, T — абсолютная температура, S — энтропия, P — давление, V — объем.
Здесь U — внутренняя энергия, T — абсолютная температура, S — энтропия, P — давление, V — объем. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike  Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike  14 октября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
14 октября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution  Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike  wikipedia.org/wiki/Calorimetry. Лицензия : Общественное достояние: Авторские права неизвестны
wikipedia.org/wiki/Calorimetry. Лицензия : Общественное достояние: Авторские права неизвестны  Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike