Коммутатор квантовая механика: Недопустимое название | Virtual Laboratory Wiki

5.1.2. Коммутатор операторов

Коммутатором операторов Fˆ и Gˆ называется оператор

ˆ ˆ	ˆ ˆ ˆ ˆ	(5.1.15)
[F,G] ≡ FG −GF .

Порядок операторов в коммутаторе важен: очевидно, что

ˆ ˆ	ˆ ˆ ˆ ˆ	ˆ ˆ	(5.1.16)
[G, F] ≡ GF − FG = −[F,G].

Если операторы коммутируют, FˆGˆ = GˆFˆ , то их коммутатор равен нулевому оператору:

ˆ ˆ	ˆ	(5.1.17)
[F,G] =0.

Вследствие (5.1.13) и (5.1.17)

ˆ ˆ ˆ ˆ	ˆ	(5.1.18)
[F,1] =[1, F] = 0 .

Из (5.1.16), а также из примечания 3 к определению 7 п/п. 5.1.1 очевидно, что для любого оператора

[Fˆ , Fˆ ] = 0ˆ .

282

Вычислим коммутаторы операторов, которые представляют в квантовой механике динамические переменные.

В соответствии с основным свойством оператора координаты (3.3.1), (3.3.11) коммутирующими являются операторы разных координат xˆ, yˆ, zˆ, действующие на волновые функции микрочастицы: например,

xˆyˆψ(t, x, y, z) = xˆ( yˆψ(t, x, y, z)) =

=xˆ( yψ(t, x, y, z)) = yxˆψ(t, x, y, z) = yxψ(t, x, y, z)

ианалогично

yˆxˆψ(t, x, y, z) = xyψ(t, x, y, z) = yxψ(t, x, y, z) ,

т.е.

[xˆ, yˆ] =[ yˆ, xˆ] = 0ˆ .

В общем случае

[x	, x		ˆ	; α, β =1,2,3.	(5.1.19)
		β	] = 0
ˆα	ˆ

283

Легко показать, что коммутируют между собой операторы, являющиеся произвольными функциями координат: в самом деле, поскольку для любой такой функции

f (xˆ, yˆ, zˆ)ψ(x, y, z) = f (x, y, z)ψ(x, y, z),

то

			ˆ	(5. 1.20)
[ f (x, y, z), g(x, y, z)] = 0 .
ˆ ˆ ˆ	ˆ ˆ	ˆ

Точно так же коммутируют между собой и операторы проекций импульса (3.2.39). Например,

p p ψ = −ih	∂		−ih∂ψ = −h3					∂2ψ	;
ˆ x ˆ y	∂x				∂y			∂x∂y
p p ψ = −ih	∂			−ih	∂ψ	= −h3		∂2ψ	= −h3	∂2ψ	,
ˆ y ˆ x								∂y∂x		∂x∂y
	∂y				∂x

т.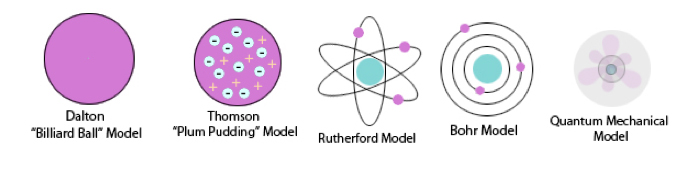

е.

[ pˆ x , pˆ y ] = 0ˆ ,

или в общем случае

[ p	, p		ˆ	; α, β =1,2,3.	(5.1.21)
		β	] = 0
ˆα	ˆ

284

Коммутируют также операторы координаты и проекции импульса, относящиеся к разным степеням свободы микрочастицы: например,

xp ψ = x

−ih

∂ψ

= −ihx

∂ψ

= −ihx

∂ψ

;

ˆˆ y

ˆ

∂y

ˆ

∂y

∂y

p xψ = p

xψ = −ih

∂(xψ)

= −ihx

∂ψ

ˆ y ˆ

ˆ y

∂y

∂y

или

[xˆ, pˆ y ] =[ pˆ y , xˆ] = 0ˆ .

В общем виде

[x	, p		ˆ	; α, β =1,2,3; α ≠ β .	(5.1.22)
		β	] = 0
ˆα	ˆ

Однако операторы «одноимённых» координаты и проекции импульса не коммутируют. Так,

xp ψ = x −ih

∂ψ

= −ihx

∂ψ

= −ihx

∂ψ

;

ˆˆ x

ˆ

ˆ

∂x

∂x

∂x

p xψ = p

xψ = −ih

∂(xψ)

= −ihx

∂ψ

−ihψ ,

ˆ x ˆ

ˆ x

∂x

∂x

и, следовательно,

285

[x, p	ˆ	(5. 1.23)
	] = ih2.
ˆ ˆ x

В общем виде

[x	, p	ˆ	; α =1,2,3.	(5.1.24)
		] = ih2
ˆα	ˆα

Выведем коммутационное соотношение между произвольной

функцией оператора координаты f (x)

[см. п/п. 3.4.3, (3.4.12)] и

ˆ

оператором «одноимённой» проекции импульса p

:

ˆ x

f (x) p ψ =

f (x) −ih

∂ψ

= −ihf

(x)

∂ψ

= −ihf (x)

∂ψ

;

ˆ

ˆ x

ˆ

ˆ

∂x

∂x

∂x

p

f

(x)ψ = p

f (x)ψ = −ih

∂( fψ)

= −ihf (x)

∂ψ

−ih

df

ψ ,

ˆ x

ˆ

ˆ x

∂x

∂x

dx

и, следовательно,

[ f (x), p	] = ih	df	ˆ	(5. 1.25)
			1.
ˆ ˆ x		dx

Задача 5.1.1. Выведите коммутационное соотношение между

ˆ

операторами импульса pˆ x и Гамильтона H (3.4.22)

ˆ	h3 ∂2			ˆ
H =−	2m ∂x2 + Φ(t,x)1
	286

микрочастицы с одной степенью свободы:

ˆ		] = ih	∂Φ	ˆ	(5. 1.26)
[H , p				1.
	ˆ x		∂x

Примечание. При выводе используйте доказанные выше утверждения о коммутации оператора с самим собой и о коммутационном соотношении между операторами импульса и функции координаты. Результат проверьте непосредственным вычислением.

Задача 5.1.2. Выведите	коммутационное	соотношение между
операторами координаты	x и Гамильтона	ˆ	микрочастицы с
		H
	ˆ

одной степенью свободы:

ˆ		ih	p	.	(5.1.27)
[H , x] = −
	ˆ	m	ˆ x

Примечание 1. При выводе используйте доказанные выше утверждения о коммутации любых функций операторов координат.

Примечание 2. Используйте коммутационное соотношение между операторами квадрата проекции импульса и одноимённой координаты:

[ p2	, x] = −2ihp		.	(5.1.28)
ˆ x	ˆ	ˆ x
		287

Квантовая механика, Т.

1 Квантовая механика, Т.1

Мессиа А. Квантовая механика: пер. с фр. Том 1 Книга содержит изложение общего формализма квантовой механики и его приложение к простейшим системам. Изложены история возникновения квантовой теории волновые свойства материи и уравнение Шрёдингера, квантование системы в одном измерении и туннельный эффект. Большое внимание уделено статистической интерпретации дуализма волна – частица, соотношению неопределённости и принципу дополнительности. Разбирается классическое приближение и метод ВКБ для одномерных задач. Подробно излагается математический аппарат и его физическая интерпретация, различные представления, квантовая статистика. Оглавление ПРЕДИСЛОВИЕ К РУССКОМУ ПЕРЕВОДУ ПРЕДИСЛОВИЕ ЧАСТЬ I. ФОРМАЛИЗМ И ЕГО ИНТЕРПРЕТАЦИЯ ГЛАВА I. ИСТОКИ КВАНТОВОЙ ТЕОРИИ Раздел I. КОНЕЦ КЛАССИЧЕСКОГО ПЕРИОДА § 2. Классическая теоретическая физика § 3. Успехи в изучении микроскопических явлений и появление квантов в физике Раздел II. СВЕТОВЫЕ КВАНТЫ, ИЛИ ФОТОНЫ § 5. Эффект Комптона § 6. Световые кванты и явления интерференции § 7. Заключение Раздел III. КВАНТОВАНИЕ В АТОМНЫХ СИСТЕМАХ § 8. Атомная спектроскопия и трудности классической модели Резерфорда § 9. Квантование энергетических уровней атомов § 10. Другие примеры квантования: пространственное квантование Раздел IV. ПРИНЦИП СООТВЕТСТВИЯ И СТАРАЯ КВАНТОВАЯ ТЕОРИЯ § 11. Недостаточность классической корпускулярной теории § 12. Принцип соответствия § 13. Применение принципа соответствия при вычислении постоянной Ридберга § 14. Лагранжева и гамильтонова формы уравнений к лассической механики § 15. Правила квантования Бора — Зоммерфельда § 16. Достижения и ограниченность старой теории квантов § 17. Заключение ГЛАВА II. ВОЛНЫ ВЕЩЕСТВА И УРАВНЕНИЕ ШРЕДИНГЕРА Раздел I. ВОЛНЫ ВЕЩЕСТВА § 3. Свободный волновой пакет. Фазовая и групповая скорости § 4. Волновой пакет в медленно меняющемся поле § 5. Квантование уровней энергии атомов § 6. Дифракция волн вещества § 7. Корпускулярная структура вещества § 8. Универсальный характер дуализма волна — частица Раздел II. УРАВНЕНИЕ ШРЕДИНГЕРА § 9. Закон сохранения числа частиц вещества § 10. Необходимость волнового уравнения и условия, которым оно должно удовлетворять § 11. Понятие оператора § 12. Волновое уравнение для свободной частицы § 13. Частица в области действия скалярного потенциала § 14. Заряженная частица в электромагнитном поле § 15. Общее правило построения уравнения Шредингера по принципу соответствия Раздел III. СТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА § 16. Исследование стационарных состояний § 17. Общие свойства уравнения. Структура энергетического спектра ГЛАВА III. КВАНТОВЫЕ СИСТЕМЫ В ОДНОМ ИЗМЕРЕНИИ Раздел I. ПРЯМОУГОЛЬНЫЕ ПОТЕНЦИАЛЫ § 3. Скачок потенциала. Отражение и прохождение волн § 4. Бесконечно высокий потенциальный барьер § 5. Бесконечно глубокая потенциальная яма. Дискретный спектр § 6. Конечная потенциальная яма. Резонансы § 7. Прохождение прямоугольного потенциального барьера. Туннельный эффект Раздел II. ОБЩИЕ СВОЙСТВА ОДНОМЕРНОГО УРАВНЕНИЯ ШРЕДИНГЕРА § 8. Свойства вронскиана § 9. Асимптотическое поведение решений § 10. Структура спектра собственных значений § 11. Состояния непрерывного спектра: отражение и прохождение волн § 12. Число узлов связанных состояний § 13. Соотношения ортогональности § 14. Замечание по поводу четности ГЛАВА IV. СТАТИСТИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ КОРПУСКУЛЯРНО-ВОЛНОВОГО ДУАЛИЗМА И СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТИ Раздел I. СТАТИСТИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ВОЛНОВЫХ ФУНКЦИИ В ВОЛНОВОЙ МЕХАНИКЕ § 2. Вероятности результатов измерения координаты и импульса частицы § 3. Сохранение нормы во времени § 4. Понятие потока § 5. Средние значения функций от r и от p § 6. Системы многих частиц Раздел II. СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА § 7. Соотношения неопределенности координата-импульс квантовой частицы § 8. Точное выражение соотношений неопределенности координата-импульс § 9. Обобщение: соотношения неопределенности для сопряженных переменных § 10. Соотношение неопределенности время-энергия § 11. Соотношения неопределенности для фотонов Раздел III. СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТИ И МЕХАНИЗМ ИЗМЕРЕНИЯ § 12. Неконтролируемое возмущение в процессе измерения § 13. Измерения положения в пространстве § 14. Измерения импульса Раздел IV. ОПИСАНИЕ ЯВЛЕНИЙ В КВАНТОВОЙ ТЕОРИИ. ДОПОЛНИТЕЛЬНОСТЬ И ПРИЧИННОСТЬ § 16. Описание микроскопических явлений и дополнительность § 17. Дополнительные переменные. Совместные переменные § 18. Корпускулярно-волновой дуализм и дополнительность § 19. Дополнительность и причинность ГЛАВА V. ФОРМАЛИЗМ ВОЛНОВОЙ МЕХАНИКИ И ЕГО ИСТОЛКОВАНИЕ Раздел I. ЭРМИТОВЫ ОПЕРАТОРЫ И ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ § 2. Пространство волновых функций § 3. Определение средних значений § 4. Отсутствие флуктуаций и проблема собственных значений Раздел II. ИССЛЕДОВАНИЕ ДИСКРЕТНОГО СПЕКТРА § 5. Собственные значения и собственные функции эрмитового оператора § 6. Разложение волновой функции в ряд по ортонормированным собственным функциям § 7. Статистическое распределение результатов измерений величины, оператор которой обладает полной системой собственных функций с конечной нормой Раздел III. СТАТИСТИКА ИЗМЕРЕНИЙ В ОБЩЕМ СЛУЧАЕ § 8. Трудности описания непрерывного спектра. Введение дельта-функции Дирака § 9. Разложение по собственным функциям в общем случае. Условие замкнутости § 10. Статистическое распределение результатов измерения в общем случае § 11. Другие методы исследования непрерывного спектра § 12. Комментарии и примеры Раздел IV. ОПРЕДЕЛЕНИЕ ВОЛНОВОЙ ФУНКЦИИ § 13. Операция измерения и редукция волнового пакета. Идеальные измерения § 14. Коммутирующие наблюдаемые и совместные переменные § 15. Полные наборы коммутирующих наблюдаемых § 16. Чистые и смешанные состояния Раздел V. АЛГЕБРА КОММУТАТОРОВ И ЕЕ ПРИЛОЖЕНИЯ § 17. Алгебра коммутаторов и основные свойства коммутаторов § 18. Соотношения коммутации для момента импульса § 19. Изменение статистического распределения во времени. Интегралы движения § 20. Примеры интегралов движения. Энергия. Четность ГЛАВА VI. КЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ И МЕТОД ВКБ Раздел I. КЛАССИЧЕСКИЙ ПРЕДЕЛ ВОЛНОВОЙ МЕХАНИКИ § 2. Теорема Эренфеста § 3. Движение и расплывание волновых пакетов § 4. Классический предел уравнения Шредингера § 5. Кулоновское рассеяние. Формула Резерфорда Раздел II. МЕТОД ВКБ § 7. Решения ВКБ в одном измерении § 8. Условия применимости приближения ВКБ § 9. Граничные точки и формулы согласования § 10. Прохождение потенциального барьера § 11. Уровни энергии в потенциальной яме ГЛАВА VII. ОБЩИЙ ФОРМАЛИЗМ КВАНТОВОЙ ТЕОРИИ А. МАТЕМАТИЧЕСКИЙ АППАРАТ § 1. Принцип суперпозиции и представление динамических состояний векторами Раздел I. ВЕКТОРЫ И ОПЕРАТОРЫ § 2. Векторное пространство. Кет-векторы § 3. Дуальное пространство. Бра-векторы § 4. Скалярное произведение § 5. Линейные операторы § 6. Тензорное произведение двух векторных пространств Раздел II. ЭРМИТОВЫ ОПЕРАТОРЫ, ПРОЕКТОРЫ И НАБЛЮДАЕМЫЕ § 7. Сопряженные операторы и правила сопряжения § 8. Эрмитовы (самосопряженные) операторы, положительна определенные операторы, унитарные операторы § 9. Проблема собственных значений и наблюдаемые § 10. Проекторы (или операторы проектирования) § 11. Алгебра проекторов § 12. Наблюдаемые, обладающие только дискретным спектром § 13. Наблюдаемые в общем случае и обобщенное соотношение замкнутости § 14. Функции наблюдаемых § 15. Операторы, коммутирующие с наблюдаемой. Коммутирующие наблюдаемые Раздел III. ТЕОРИЯ ПРЕДСТАВЛЕНИЙ § 16. Общее понятие о конечных матрицах § 17. Квадратные матрицы § 18. Бесконечные матрицы § 19. Представление векторов и операторов матрицами § 20. Преобразования матриц § 21. Смена представления § 22. Унитарные преобразования операторов и векторов ГЛАВА VIII. ОБЩИЙ ФОРМАЛИЗМ КВАНТОВОЙ ТЕОРИИ Б. ОПИСАНИЕ ФИЗИЧЕСКИХ ЯВЛЕНИЙ Раздел I. ДИНАМИЧЕСКИЕ СОСТОЯНИЯ И ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ § 2. Определение вероятностей. Постулаты измерения § 3. Наблюдаемые квантовой системы и соотношения коммутации § 4. Соотношения неопределенности Гейзенберга § 5. Определение состояний и построение пространства § 6. Квантовая одномерная система, обладающая классическим аналогом § 7. Построение пространства состояний путем тензорного умножения более простых пространств Раздел II. УРАВНЕНИЯ ДВИЖЕНИЯ § 8. Оператор эволюции и уравнение Шредингера § 9. «Представление» Шредингера § 10. «Представление» Гейзенберга § 11. «Представление» Гейзенберга и принцип соответствия § 12. Интегралы движения § 13. Уравнение эволюции средних значений и соотношение неопределенности время-энергия § 14. Промежуточные «представления» Раздел III. РАЗЛИЧНЫЕ ПРЕДСТАВЛЕНИЯ ТЕОРИИ § 16. Волновая механика § 17. Представление {р} § 18. Пример: движение свободного волнового пакета § 19. Другие представления. Представление, в котором диагональна энергия Раздел IV. КВАНТОВАЯ СТАТИСТИКА § 20. Системы с неполной информацией и смешанные состояния § 21. Матрица плотности § 22. Эволюция смешанного состояния во времени § 23. Характеристические свойства матрицы плотности § 24. Чистые состояния § 25. Классическая статистика и квантовая статистика ЧАСТЬ II. ПРОСТЫЕ СИСТЕМЫ ГЛАВА IX. РЕШЕНИЕ УРАВНЕНИЯ ШРЕДИНГЕРА МЕТОДОМ РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. ЦЕНТРАЛЬНО-СИММЕТРИЧНЫЙ ПОТЕНЦИАЛ Раздел I. ЧАСТИЦА В ЦЕНТРАЛЬНО-СИММЕТРИЧНОМ ПОТЕНЦИАЛЬНОМ ПОЛЕ. ОБЩЕЕ РАССМОТРЕНИЕ ПРОБЛЕМЫ § 2. Гамильтониан частицы в сферических координатах § 3. Отделение угловых переменных. Сферические функции § 4. Радиальное уравнение § 5. Собственные решения радиального уравнения. Структура спектра. § 6. Заключение Раздел II. ЦЕНТРАЛЬНО-СИММЕТРИЧНЫЙ ПРЯМОУГОЛЬНЫЙ ПОТЕНЦИАЛ. СВОБОДНАЯ ЧАСТИЦА § 7. Сферические функции Бесселя § 8. Свободная частица. Свободные плоские и сферические волны § 9. Разложение плоской волны по сферическим функциям § 10. Сферическая прямоугольная яма Раздел III. ЗАДАЧА ДВУХ ТЕЛ. ОТДЕЛЕНИЕ ДВИЖЕНИЯ ЦЕНТРА МАСС § 11. Отделение движения центра масс в классической механике § 12. Отделение движения центра масс квантовой системы двух частиц § 13. Система многих частиц ГЛАВА X. ПРОБЛЕМА РАССЕЯНИЯ. ЦЕНТРАЛЬНЫЙ ПОТЕНЦИАЛ И МЕТОД ФАЗОВЫХ СДВИГОВ Раздел I. ЭФФЕКТИВНЫЕ СЕЧЕНИЯ И АМПЛИТУДЫ РАССЕЯНИЯ § 3. Стационарная волна рассеяния § 4. Описание рассеяния при помощи пучка волновых пакетов § 5. Рассеяние волнового пакета на потенциале § 6. Вычисление эффективных сечений § 7. Столкновение двух частиц. Лабораторная система и система центра масс Раздел II. РАССЕЯНИЕ ЦЕНТРАЛЬНЫМ ПОТЕНЦИАЛОМ. ФАЗОВЫЕ СДВИГИ § 8. Разложение по парциальным волнам. Метод фазовых сдвигов § 9. Квазиклассическое представление рассеяния. Прицельный параметр Раздел III. ПОТЕНЦИАЛ ОГРАНИЧЕННОГО РАДИУСА ДЕЙСТВИЯ § 10. Сдвиг фазы и логарифмическая производная § 11. Сдвиги фаз при низких энергиях § 12. Парциальные волны более высокого порядка. Сходимость ряда § 13. Рассеяние на твердой сфере Раздел IV. РЕЗОНАНСНОЕ РАССЕЯНИЕ § 14. Рассеяние глубокой прямоугольной потенциальной ямой § 15. Общий закон резонансного рассеяния. Метастабильные состояния § 16. Наблюдение времени жизни метастабильных состояний Раздел V. РАЗЛИЧНЫЕ ФОРМУЛЫ И СВОЙСТВА § 17. Интегральные представления фазовых сдвигов § 18. Зависимость фазовых сдвигов от формы потенциала § 19. Приближение Борна § 20. Теория эффективного радиуса действия. Формула Бете ГЛАВА XI. КУЛОНОВСКОЕ ВЗАИМОДЕЙСТВИЕ Раздел I. АТОМ ВОДОРОДА § 2. Уравнение Шредингера для атома водорода § 3. Порядок величины энергии связи основного состояния § 4. Решение уравнения Шредингера в сферических координатах § 5. Спектр энергии. Вырождение § 6. Собственные функции связанных состояний Раздел II. КУЛОНОВСКОЕ РАССЕЯНИЕ § 7. Кулоновская функция рассеяния § 8. Формула Резерфорда § 9. Разложение по парциальным волнам § 10. Разложение по сферическим функциям § 11. Модификация кулоновского потенциала короткодействующим взаимодействием ГЛАВА XII. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР Раздел I. СОБСТВЕННЫЕ СОСТОЯНИЯ И СОБСТВЕННЫЕ ВЕКТОРЫ ГАМИЛЬТОНИАНА § 3. Введение операторов § 4. Спектр и базисная система оператора N § 5. Представление [N] § 6. Операторы рождения и уничтожения § 7. Представление {Q}. Полиномы Эрмита Раздел II. ПРИЛОЖЕНИЯ И РАЗЛИЧНЫЕ СВОЙСТВА § 8. Производящая функция собственных функций § 9. Интегрирование уравнений Гейзенберга § 10. Классический и квантовый осцилляторы § 11. Движение минимизирующего волнового пакета и классический предел § 12. Гармонические осцилляторы в термодинамическом равновесии Раздел III. ИЗОТРОПНЫЕ МНОГОМЕРНЫЕ ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ § 13. Общее исследование изотропного осциллятора в р измерениях § 14. Изотропный осциллятор в двух измерениях § 15. Изотропный осциллятор в трех измерениях ДОПОЛНЕНИЕ А ОБОБЩЕННЫЕ ФУНКЦИИ, «ФУНКЦИЯ» ДЕЛЬТА И ПРЕОБРАЗОВАНИЕ ФУРЬЕ § 1. Понятие функционала и строгий подход к проблеме непрерывного спектра § 2. Определение обобщенных функций § 3. Линейная комбинация обобщенных функций § 4. Произведение двух обобщенных функций § 5. Ряды и интегралы обобщенных функций § 6. Дифференцирование обобщенных функций Раздел II. СВОЙСТВА «ФУНКЦИИ» ДЕЛЬТА § 8. Представление в виде предела ядра интегрального оператора § 9. Основные свойства § 10. Производные Раздел III. ПРЕОБРАЗОВАНИЕ ФУРЬЕ § 11. Преобразование Фурье. Определение § 12. Абсолютно интегрируемые функции f(x) § 13. Функции «хи» (основные функции) § 14. Преобразование Фурье обобщенных функций. Определение § 15. Обобщенные функции медленного роста § 16. Квадратично интегрируемые функции § 17. Преобразование свертки ДОПОЛНЕНИЕ Б. СПЕЦИАЛЬНЫЕ ФУНКЦИИ И СВЯЗАННЫЕ С НИМИ ФОРМУЛЫ § 1. Уравнение Лапласа и вырожденная гипергеометрическая функция § 2. Полиномы Лагерра § 3. Собственные функции водородоподобных атомов (теория Шредингера) § 4. Чисто кулоновская волна § 5. Сферические кулоновские функции Раздел II. СФЕРИЧЕСКИЕ ФУНКЦИИ БЕССЕЛЯ § 6. Сферические функции Бесселя Раздел III. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР И ПОЛИНОМЫ ЭРМИТА § 7. Полиномы Эрмита § 8. Собственные функции гармонического осциллятора Раздел IV. ПОЛИНОМЫ И ФУНКЦИИ ЛЕЖАНДРА, СФЕРИЧЕСКИЕ ФУНКЦИИ § 9. Полиномы и функции Лежандра § 10. Сферические функции Раздел V РАЗЛОЖЕНИЯ И РАЗЛИЧНЫЕ ФОРМУЛЫ

коммутаторов в квантовой механике

коммутаторов в квантовой механике
Далее: Линейные векторные пространства в Up: Математический фон Предыдущий: Унитарные операторы Содержимое Коммутатор , определенный в разделе 3. 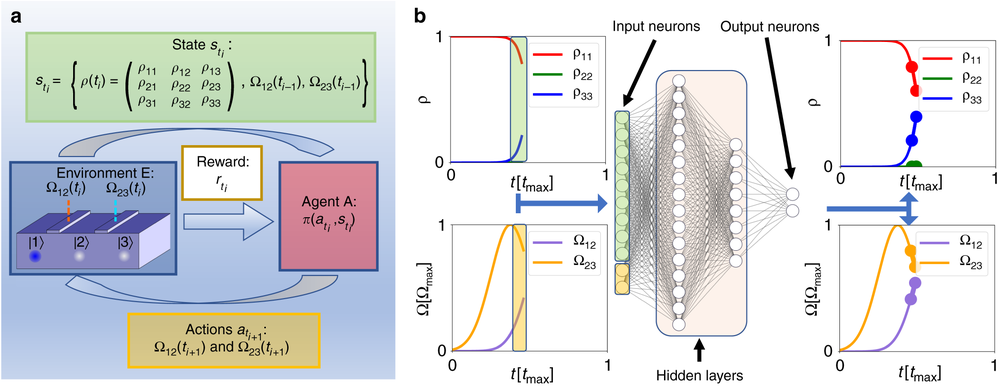1.2, является очень важно в квантовой механике. Поскольку определенное значение наблюдаемая А может быть присвоена системе, только если система находится в собственное состояние , то мы можем одновременно задать определенные значения для двух наблюдаемых A и B, только если система находится в собственное состояние обоих и . Предположим, что в системе есть значение для наблюдаемого A и для наблюдаемого B. Мы требовать

			(64)

Если умножить первое уравнение на, а второе на тогда мы получаем

			(65)

и, используя тот факт, что является собственной функцией и это становится

			(66)

так что, если мы вычтем первое уравнение из второго, мы получим

(67)

Чтобы это выполнялось для общих собственных функций, мы должны иметь , или . 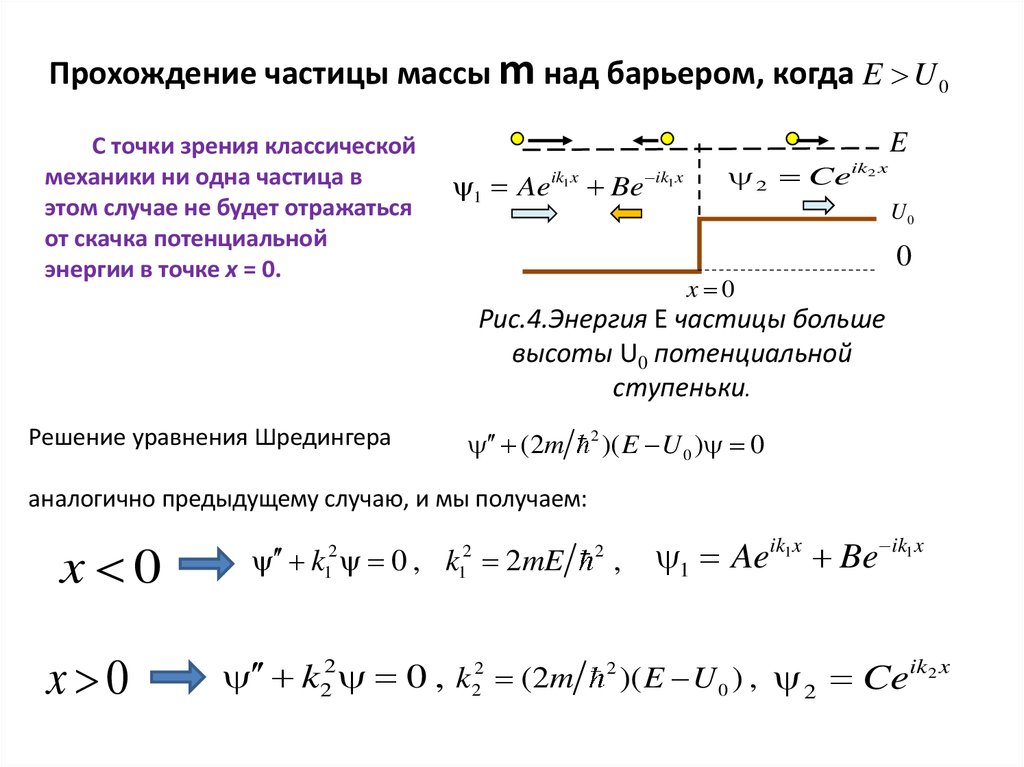То есть на двоих физические величины одновременно наблюдаемы, их оператор представления должны коммутировать.

Раздел 8.8 Мерцбахера [2] содержит некоторые полезные правила оценки коммутаторов. Они кратко изложены ниже.

(68)

(69)

(70)

(71)

(72)

(73)

(74)

Если и два оператора, коммутирующие друг с другом коммутатор, то

(75)

(76)

У нас также есть тождество (полезно для теории связанных кластеров)

(77)

Наконец, если тогда неопределенности в A и B, определяется как , подчиняться отношение ¹

(78)

Это знаменитый принцип неопределенности Гейзенберга. Это легко вывести известное соотношение

(79)

из этого общего правила.

---

Далее: Линейные векторные пространства в Up: Математический фон Предыдущий: Унитарные операторы Содержимое

Дэвид Шерил 2006-08-15

Каков физический смысл коммутаторов в квантовой механике?

спросил 8 лет, 6 месяцев назад

Изменено 5 лет назад

Просмотрено 27 тысяч раз

$\begingroup$

Этот вопрос мне несколько раз задавали студенты, и мне, как правило, трудно сформулировать его так, чтобы они могли его понять. Это естественный вопрос, который обычно не освещается в учебниках, поэтому я хотел бы узнать о различных точках зрения и объяснениях, которые я могу использовать при обучении.

Этот вопрос естественно возникает на втором курсе студентов по квантовой физике/квантовой механике. На этом этапе человек достаточно хорошо знаком с концепцией волновых функций и уравнением Шредингера и имеет ограниченное представление об операторах. Одним из распространенных случаев, например, является объяснение того, что некоторые операторы коммутируют и что это означает, что соответствующие наблюдаемые «совместимы» и что существует взаимный собственный базис; коммутационное отношение обычно выражается как $[A,B]=0$, но об этом объекте больше ничего не говорится.

Это, естественно, вызывает у учащихся недоумение

каково именно физическое значение самого объекта $[A,B]$?

и это не простой вопрос. Я хотел бы, чтобы ответы касались этого напрямую, в идеале на различных уровнях абстракции и необходимого фона. Заметьте также, что меня гораздо больше интересует сам объект $[A,B]$, чем последствия и интерпретации, когда он равен нулю, поскольку это гораздо проще и более подробно изучено в большинстве ресурсов.

---

Одна из причин, по которой этот вопрос является трудным (и что коммутаторы представляют собой такие запутанные объекты для студентов), заключается в том, что они служат множеству целей, и между ними есть только тонкие связующие нити (по крайней мере, если смотреть снизу вверх).

• Коммутационные отношения обычно выражаются в форме $[A,B]=0$, хотя a priori представляется мало мотивации для введения такой терминологии.

• Большое значение придается каноническому коммутационному соотношению $[x,p]=i \hbar$, хотя не всегда понятно, что оно означает.

  (На мой взгляд, фундаментальный принцип, который здесь зашифрован, — это, по существу, соотношение де Бройля $\lambda=h/p$; оно становится строгим благодаря теореме единственности Стоуна — фон Неймана, но это совсем немного, чтобы студент мог понять его. с первого раза.)

• Отсюда естественное расширение принципа неопределенности Гейзенберга, который в своей общей форме включает коммутатор (и, что еще хуже, антикоммутатор). Часто вводятся канонически сопряженные пары наблюдаемых, и этому часто помогают наблюдения над коммутаторами. (С другой стороны, отношения сопряженности энергия-время и угол-угловой импульс не могут быть выражены в терминах коммутаторов, что делает ситуацию еще более нечеткой.)

• Коммутаторы очень часто используются, например, при изучении алгебры углового момента в квантовой механике. Ясно, что они играют большую роль в кодировании симметрии в квантовой механике, но едва ли ясно, как и почему, и особенно почему комбинация $AB-BA$ должна быть важна для рассмотрения симметрии.

  Это становится еще более важным в более строгих трактовках квантовой механики, где специфика гильбертова пространства становится менее важной, а алгебра наблюдаемых операторов занимает центральное место. Коммутатор — это центральная операция этой алгебры, но опять же не очень понятно, почему эта комбинация должна быть особенной.

• Иногда проводят аналогию со скобками Пуассона гамильтоновой механики, но это вряд ли помогает – скобки Пуассона столь же загадочны. Это также связывает коммутатор с эволюцией во времени, как с классической стороны, так и через уравнение движения Гейзенберга.

В данный момент я не могу придумать больше, но это огромное количество противоположных направлений, которые могут сделать все очень запутанным, и редко бывает объединяющая нить. Итак: что такое коммутаторы и почему они так важны?

• квантовая механика
• коммутатор

$\endgroup$

12

$\begingroup$

Самосопряженные операторы входят в КМ, описанную в комплексных гильбертовых пространствах, двумя логически различными путями.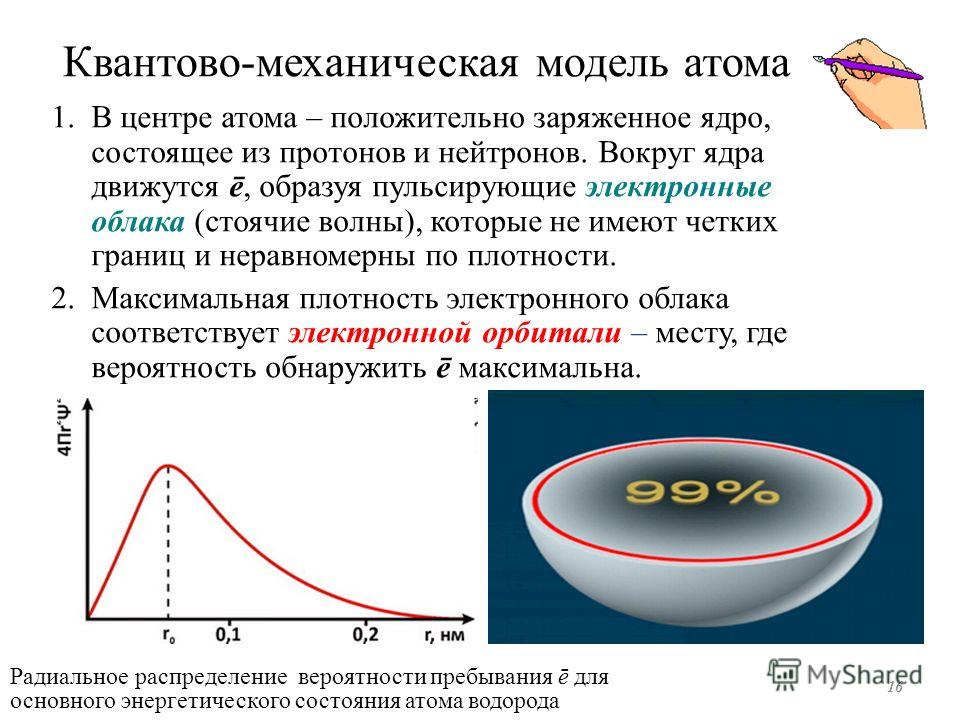 Это приводит к соответствующей паре значений коммутатора.

Первый способ является общим с двумя другими возможными формулировками гильбертова пространства (вещественной и кватернионной): Самосопряженные операторы описывают наблюдаемые .

Две наблюдаемые могут быть совместимыми или несовместимыми в том смысле, что они могут или не могут быть измерены одновременно (соответствующие измерения мешают друг другу при рассмотрении результатов). Вплоть до некоторых математических тонкостей коммутатор представляет собой меру несовместимости с учетом обобщений принципа Гейзенберга, которые вы упоминаете в своем вопросе. Грубо говоря, чем больше коммутатор отличается от $0$, тем более несовместимы между собой наблюдаемые. (Подумайте о таких неравенствах, как $\Delta A_\psi \Delta B_\psi \geq \frac{1}{2} |\langle \psi | [A,B] \psi\rangle|$. Это предотвращает существование общий собственный вектор $\psi$ $A$ и $B$ – наблюдаемые определяются одновременно – поскольку такой собственный вектор подтвердил бы, что $\Delta A_\psi =\Delta B_\psi =0$. {iaA}$ для единственного самосопряженного оператора $A$ и всех вещественных чисел $a$. Такой подход к описанию непрерывных преобразований приводит к квантовой версии теоремы Нётер как раз в силу того (очевидного!) факта, что $A$ 92) \:.$$

Обычно информация, заключенная в коммутационных соотношениях, очень глубока. При работе с группами Ли симметрий это позволяет реконструировать все представление (на эту фундаментальную тему есть замечательная теория Нельсона) при некоторых довольно мягких математических гипотезах. Поэтому коммутаторы играют решающую роль в анализе симметрий.

$\endgroup$

2

$\begingroup$

Я хотел бы немного расширить интерпретацию коммутаторов как меру помех (связанных с несовместимостью, о чем говорилось в других ответах). Моя интерпретация коммутатора заключается в том, что $[A,B]$ определяет степень, в которой действие $B$ изменяет значение динамической переменной $A$, и наоборот.

Предположим, что $A$ — самосопряженный оператор с дискретным невырожденным спектром собственных значений $\{a\}$ с ассоциированными собственными множествами $\lvert a\rangle$. Тогда можно показать, что для любого оператора $B$ существует следующее разложение $$ B = \sum_{\Delta} B(\Delta),$$ такой, что $$[A,B(\Delta)] = \Delta B(\Delta),$$ где $B(\Delta)$ определяется ниже. Рассматривая коммутатор $[A,.]$ как линейный оператор, это имеет вид уравнения на собственные значения. Собственные значения $\Delta$ задаются разностями между парами собственных значений $A$, например $\Дельта = а’-а$. Конкретный вид собственных операторов $B(\Delta)$ таков: $$ B(\Delta) = \sum_{a} \langle a+\Delta\rvert B\lvert a\rangle \;\lvert a+\Delta\rangle\langle a\rvert.$$ Это показывает, что $B(\Delta)$ являются “лестничными операторами”, которые увеличивают значение переменной $A$ на величину $\Delta$. Таким образом, коммутатор индуцирует естественное разложение $B$ на вклады, которые 92. $$ Это сумма (возведенных в квадрат) матричных элементов $B$, которые связывают различные собственные состояния $A$, взвешенных по соответствующему изменению собственных значений (возведенных в квадрат). {i\Delta t} B(\Delta), $$ где здесь $\Delta$ – боровские частоты рассматриваемой системы. Операторы скачка $B(\Delta)$ можно интерпретировать как компоненты Фурье оператор-функции $B(t)$. В контексте теории возмущений мы часто аппроксимируем эффект унитарной эволюции применением эрмитова оператора (возмущающего гамильтониана), и в этом случае интерпретация операторов скачка ясна: они описывают переходы между собственными энергетическими состояниями, вызванные возмущение $B$. Осциллирующая временная зависимость в конечном итоге приводит к сохранению энергии как условию согласования частот. 92,$$ где дельта-символ Кронекера $\delta_{\Delta,\Delta’}$ равен 1, если $\Delta = \Delta’$, и 0 в противном случае.

$\endgroup$

1

$\begingroup$

На базовом уровне:

1) если $[A,B]=0$, и если $A$ и $B$ являются инфинитезимальными генераторами симметрии (а значит, и сохраняющимися величинами), это означает, что оба $A $ инвариантен относительно $B$, а $B$ инвариантен относительно $A$.

Например, $[H,J_z]=0$ означает, что угловой момент сохраняется во время эволюции и что гамильтониан инвариантен при вращении.

Как говорит @Valter Moretti, ненулевой коммутатор $[A,B]$ измеряет отклонение от (обеих) симметрий.

2) Коммутаторы типа $[A, B] = \pm B$, если $A$ ассоциировано с дискретным спектром, означает, что $B$ является повышающим/понижающим оператором с ” $A$-зарядом “$\pm 1$.

Очевидный пример: $[J_z, J_\pm]= \pm J_\pm$

3) Коммутационные соотношения типа $[\hat A, \hat B]= i \lambda$, если $\hat A$ и $\hat B$ — наблюдаемые, соответствующие классическим величинам $a$ и $b$ , можно интерпретировать, рассматривая величины $I = \int a \,db$ или $J = \int b \,da$. Эти классические величины нельзя вывести из квантовых наблюдаемых, потому что неопределенность этих величин всегда около $\lambda$.

Например, $[\hat x,\hat p] = i \hbar$ показывает, что не существует квантовой наблюдаемой, соответствующей действию $S =\int (\vec p\,d \vec x – E\, дт) $. 92 \влево[\шляпа{A}, \шляпа{B} \вправо]} \cdots,$$ где “$\cdots$” содержит члены кубической и более высокой степени в $\hat{A}$ и $\hat{B}$ и может быть выражено как произведение экспонент линейных комбинаций вложенных коммутаторов. Если мы подумаем о $\hat{A}$ и $\hat{B}$ как об эрмитовых операторах (которые почти всегда входят в коммутаторы), соответствующих физическим наблюдаемым, то эта формула конкретно показывает нам, что их некоммутируемость заставляет их «взаимодействуют друг с другом» тонким образом, так что их физические эффекты не могут быть разделены. То есть унитарное преобразование, которое генерирует их сумма (например, оператор перевода времени или симметрии), не является просто комбинированным эффектом каждой отдельной «части» генератора, действующего в одиночку. Из этого простого факта вытекают все странности квантовой механики. Более того, коммутатор является главным отклонением от классического результата.

$\endgroup$

1

$\begingroup$

Начнем с уравнения Шредингера: $$\mathrm i\hbar\frac{\partial}{\partial t}\left|\psi\right> = H\left|\psi\right>$$ Поскольку $H$ является самоприсоединенным, отсюда также следует $$\mathrm -i\hbar\frac{\partial}{\partial t}\left<\psi\right| = \влево<\psi\вправо|H$$ Теперь рассмотрим наиболее общее квантовое состояние, выраженное матрицей плотности $$\rho = \sum_k p_k\left|\psi_k\middle>\middle<\psi_k\right|$$ Мы хотим знать производную по времени от матрицы плотности. Очевидно, что производная по времени является линейной, и мы также можем использовать правило произведения, чтобы получить $$\begin{выровнено}\frac{\partial\rho}{\partial t} &= \sum_k p_k\left(\left(\frac{\partial}{\partial t}\left|\psi\right>\right) \left<\psi\right| + \left|\psi\right> \left(\frac{\partial}{\partial t}\left<\psi\right|\right)\right)\\ &= \sum_k p_k\frac{1}{\mathrm i\hbar}\left(H\left|\psi_k\middle>\middle<\psi_k\right|-\left|\psi_k\middle>\middle<\ psi_k\право|H\право)\\ &= \frac{1}{\mathrm i\hbar}(H\rho - \rho H)\\ &= \frac{1}{\mathrm i\hbar}[H,\rho] \end{выровнено}$$ Итак, вы видите, что здесь вполне естественно появляется коммутатор.

Далее рассмотрим наблюдаемую $A$ и посмотрим на временную зависимость ее ожидаемого значения $\left=\operatorname{tr}(A\rho)$.

Используя линейность и циклическую инвариантность следа, получаем $$\begin{выровнено} \frac{\partial}{\partial t}\left &= \frac{\partial}{\partial t}\operatorname{tr}(A\rho)\\ &= \operatorname{tr}\left(\frac{\partial A}{\partial t}\rho\right) + \operatorname{tr}\left(A\frac{\partial\rho}{\partial t} \верно)\\ &= \left<\frac{\partial A}{\partial t}\right>+\frac{1}{\mathrm i\hbar}\operatorname{tr}(A[H,\rho])\\ &= \left<\frac{\partial A}{\partial t}\right>+\frac{1}{\mathrm i\hbar}\left(\operatorname{tr}(AH\rho) – \operatorname{ tr}(A\rho H)\right)\\ &= \left<\frac{\partial A}{\partial t}\right>+\frac{1}{\mathrm i\hbar}\left(\operatorname{tr}(AH\rho) – \operatorname{ tr}(HA\rho)\right)\\ &= \left<\frac{\partial A}{\partial t}\right>+\frac{1}{\mathrm i\hbar}\operatorname{tr}([A,H]\rho)\\ &= \left<\frac{\partial A}{\partial t}\right> + \frac{1}{\mathrm i\hbar}\left<[A,H]\right> \end{выровнено}$$ Теперь рассмотрим особенно сохраняющуюся величину, которая явно не зависит от времени (то есть $\partial A/\partial t=0$). 2]\right>}_{=0} + \frac{1}{\mathrm i\hbar} \left<[p,V(x)]\right> \stackrel!= \left<-V'(x)\right> \end{выровнено}$$ Нетрудно проверить, что этот результат получается, если $p=-\mathrm i\hbar\partial/\partial x$, что также дает только что полученное коммутационное соотношение.

Насчет связи с симметриями и соотношениями неопределенностей вы уже получили ответы (а сейчас уже совсем поздняя ночь), так что остановлюсь на этом.

$\endgroup$

1

$\begingroup$

Может быть полезно назначить учащимся следующую проблему HW:

Предположим, что $A$ и $B$ — две наблюдаемые

i) При каком необходимом условии $A$ и $B$ могут быть одновременно измеряется в эксперименте без какой-либо неопределенности?

ii) Запишите все многочлены второй степени от $A$ и $B$, которые снова являются наблюдаемыми.

iii) Предположим, что A — гамильтониан**. Время эволюционирует в состояние $|\psi\rangle$ за время $t$ при $A$, и обозначим полученное таким образом состояние как $|\psi(t)\rangle$. Можем ли мы выразить $\displaystyle\frac{d\langle\psi(t)|B|\psi(t)\rangle}{dt}$ как $\langle\psi(t)|\mathcal{O}|\psi(t)\rangle$ для некоторого наблюдаемого $\mathcal{O}$ ? Если да, найдите $\mathcal{O}$.

** В этой задаче мы также можем принять $A$ за какой-то другой генератор симметрии, отличный от гамильтониана.

---

Добавлено позже:

• Когда коммутатор обращается в нуль, две наблюдаемые могут быть одновременно измерены в эксперименте без неопределенности (это следует из аксиом КМ).
• Среднее значение коммутатора $i[H,A]$ (где H — гамильтониан) в состоянии говорит о скорости изменения среднего значения $A$ в этом состоянии во времени. В более общем смысле, математическое ожидание коммутатора $i[B,A]$ в состоянии связано с бесконечно малым изменением математического ожидания $A$ в этом состоянии при однопараметрической симметрии, порожденной $B$.