Концентрация формула физика: Концентрация молекул

Исследование-1. Применение. Определите среднюю кинетическую энергию атомов газа.
Задача. Видимая атмосфера Солнца (фотосфера), можно сказать, состоит из водородного газа. Концентрация атомов в водородном газе фотосферы приблизительно равна n = 1,6 ⋅ 10^-21м^-3, давление же равно p = 1,25 ⋅ 10²Па. Чему будет равна средняя кинетическая энергия поступательного движения атомов водородного газа фотосферы, если принять его за идеальный газ?

• Какова связь между средней кинетической энергией поступательного движения молекул (атомов) идеального газа и его давлением?

Применение в повседневной жизни: Предположим, что окружающий нас воздух состоит из одинаковых молекул. С какой средней квадратичной скоростью эти молекулы, при нормальных условиях, наносят нам удары? При нормальных условиях давление воздуха равно 10⁵Па, а плотность – 1,29 кг/м

ЧТО ВЫ УЗНАЛИ? Запишите в рабочем листке определения для следующих понятий: “идеальный газ”, “микроскопические параметры газа”,“ макроскопические параметры газа”, “основное уравнение МКТ идеального газа”, “концентрация молекул”, “средняя квадратичная скорость молекул”, “давление идеального газа”.

Молекулярно-кинетическая теория газов – примеры, решения

Пример 1:

Каково давление азота, если его плотность равна 1,35 кг/м³, а средняя квадратичная скорость молекул 500 м/с?

Решение от преподавателя:

Запишем для начала уравнение Клапейрона-Менделеева:

Поделим обе части уравнения на объем V, в правой части получившееся отношение m\V заменим на плотность газа ρ:

Среднюю квадратичную скорость молекул υ_кв определяют по такой формуле:

Выразим из выражения температуру газа T:

Это выражение подставим в формулу (1), тогда получим:

Задача решена в общем виде. Все величины, входящие в формулу, даны в единицах системы СИ, поэтому можно сразу посчитать ответ:

Ответ: 0,1 МПа.

Пример 2:

В баллоне находится 20 моль газа. Сколько молекул газа находится в баллоне?

Решение от преподавателя:

Известно, что в 1 моль любого вещества содержится число молекул, равное числу Авогадро N_А. Тогда понятно, что в ν молях вещества содержится в ν раз больше, чем число Авогадро. Запишем сказанное в виде формулы:

Число Авогадро N_А равно 6,022·10²³ 1/моль. Посчитаем численный ответ к задаче:

Поскольку в физике нет единицы измерения “штук”, то так и оставляем полученную величину безразмерной.

Ответ: 1,2·10²⁵.

Пример 3:

Сколько молекул кислорода находится в сосуде объемом 1 л, если температура кислорода 150° C, а давление равно 0,132 нПа?

Решение от преподавателя:

Запишем формулу связи давления идеального газа p с концентрацией его молекул n и абсолютной температурой T:

В этой формуле k – постоянная Больцмана, она равна 1,38·10^-23 Дж/К. Также запишем формулу определения концентрации n (по смыслу это количество молекул в единице объема):

Подставим последнее выражение в первую формулу, получим:

Осталось только выразить количество молекул N:

Переведем объем V в кубические метры, а температуру t – в Кельвины:

Считаем ответ:

Количество молекул в физике – безразмерная величина.

Ответ: 2,26·10⁷.

Пример 4:

Определить массу молекулы кислорода.

Решение от преподавателя:

Рассмотрим ν (произвольное количество) моль кислорода. Напомним, что формула кислорода такая: O₂.

Чтобы найти массу m некоторого количества кислорода, нужно молярную массу кислорода M умножить на число молей ν.

Используя таблицу Менделеева, легко определить, что молярная масса кислорода M равна 32 г/моль или 0,032 кг/моль. В одном моле содержится число Авогадро молекул N_А, а в ν моль – в ν раз больше, то есть:

Чтобы найти массу одной молекулы m₀, нужно всю массу m поделить на число молекул N.

Число Авогадро N_А – это табличная величина, равна 6,022·10²³ моль^-1. Произведем вычисления:

Ответ: 5,3·10^-23 г.

Пример 5:

Определить плотность воздуха при 27° C и давлении 0,1 МПа.

Решение от преподавателя:

Запишем уравнение Клапейрона-Менделеева:

Плотность ρ – это масса единицы объема вещества, её находят как отношение массы вещества m к объему V:

Давайте разделим обе части уравнения Клапейрона-Менделеева на объем V:

Учитывая (1), имеем:

Из полученной формулы выразим плотность ρ:

Молярная масса воздуха M равна 0,029 кг/моль, универсальная газовая постоянная R – 8,31 Дж/(моль·К). Перед тем, как считать ответ, переведем температуру в шкалу абсолютных температур:

Ответ: 1,16 мг/см³.

Пример 6:

Сколько молекул содержится в 5 кг кислорода?

Решение от преподавателя:

Число молекул N находят как произведение количества вещества νν на число Авогадро N_А (равное 6,022·10²³ моль^-1).

Количество вещества νν найдем как отношение массы mm к молярной массе вещества M (у кислорода O₂ она равна 0,032 кг/моль).

В итоге имеем такую окончательную формулу:

Посчитаем численный ответ к задаче:

Помните, что число молекул в физике – это безразмерная величина, не нужно писать никаких “штук”.

Ответ: 9,41·10²⁵.

Пример 7:

Какое давление на стенки сосуда производят молекулы газа, если масса газа 3 г, объем 0,5 л, а средняя квадратичная скорость его молекул 500 м/с?

Решение от преподавателя:

Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:

Концентрацию молекул газа nn находят как отношение числа молекул N к объему газа V:

Тогда имеем:

Интересно, но произведение массы одной молекулы m₀ на количество молекул N по смыслу есть масса газа m, поэтому:

Переведем массу m и объем V газа в систему СИ:

Произведем вычисления:

Ответ: 0,5 МПа.

Пример 8:

При температуре 320 К средняя квадратичная скорость молекулы кислорода 500 м/с. Определить массу молекулы кислорода.

Решение от преподавателя:

Решение:

Как и в механике, среднюю кинетическую энергию молекул кислорода можно определить по формуле:

С другой стороны, есть формула связи средней кинетической энергии с абсолютной температурой:

Приравняем правые части этих двух формул:

Выразим из этого равенства массу одной молекулы m₀:

Напомним, что здесь k – это постоянная Больцмана, равная 1,38·10^-23 Дж/К.

Посчитаем ответ:

Ответ: 5,3·10^-23 г.

Пример 9:

Вычислить среднюю квадратичную скорость молекул углекислого газа при температуре 223 К.

Решение от преподавателя:

Среднюю квадратичную скорость молекул идеального газа υквυкв определяют по такой формуле:

В этой формуле R – универсальная газовая постоянная (R=8,31 Дж/(моль·К)), M – молярная масса газа, у углекислого газа CO₂ равная 0,044 кг/моль. Все величины, входящие в формулу известны, посчитаем ответ:

Ответ: 0,36 км/с.

Пример 10:

Определить давление водорода, если средняя квадратичная скорость его молекул равна 2550 м/с, а концентрация молекул 3,6·10²⁵ м^-3.

Решение от преподавателя:

Воспользуемся основным уравнением молекулярно-кинетической теории (МКТ) идеального газа:

Как вы и сами можете видеть, нам неизвестна только масса одной молекулы m₀, входящее в это уравнение. Её можно найти, поделив молярную массу газа M (а она у водорода равна 0,002 кг/моль) на число Авогадро N_А (оно равно 6,022·10²³ 1/моль).

В итоге получается такая формула:

Произведем расчет ответа:

Ответ: 259 кПа.

Пример 11:

Определить среднеквадратичную скорость молекул газа при давлении 100 кПа и плотности 1,25 кг/м³.

Решение от преподавателя:

Запишем основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:

Вспомним формулу определения концентрации молекул n идеального газа:

Подставим это выражение в формулу (1), получим:

Произведение массы одной молекулы m₀ на количество молекул N равно массе газа m, поэтому:

Отношение массы m к объему V – это физическая величина, называемая плотностью газа ρ, поэтому:

Осталось сделать последнее действие – выразить искомую скорость υ_кв:

Посчитаем численный ответ задачи:

Ответ: 0,49 км/с.

Пример 12:

Какова средняя кинетическая энергия поступательного движения молекул газа, если при концентрации молекул 2,65·10²⁵ м^-3 давление равно 98,8 кПа?

Решение от преподавателя:

Запишем основное уравнение МКТ идеального газа:

Среднюю кинетическую энергию молекул газа можно определить по формуле:

С учетом этой формулы, формула (1) примет такой вид:

Откуда искомая величина E_к равна:

Задача решена в общем виде, теперь посчитаем численный ответ:

В задачнике ответ дан не в Джоулях, а в электрон-Вольтах. Известно, что:

Поэтому:

Ответ: 0,035 эВ.

Пример 13:

В баллоне емкостью 40 л находится 10 кг кислорода под давлением 20 МПа. Найти среднюю квадратичную скорость молекул кислорода.

Решение от преподавателя:

Применим основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:

Распишем концентрацию молекул газа nn как отношение количества молекул N к объему газа V:

Произведение массы одной молекулы m₀ на количество молекул N есть масса газа mm, поэтому:

Выразим искомую среднеквадратичную скорость υ_кв:

Переведем объем баллона в систему СИ и посчитаем ответ:

Ответ: 1763,6 км/ч.

Пример 14:

Определить давление, при котором 1 м³ газа, имеющий температуру 60° C, содержит 2,4·10²⁶ молекул.

Решение от преподавателя:

Запишем формулу связи давления идеального газа с концентрацией молекул и абсолютной температурой:

В этой формуле n – концентрация молекул, которую легко определить по формуле:

Также в условии температура дана в Цельсиях. Чтобы перевести температуру в Кельвины, то есть в абсолютную шкалу, нужно воспользоваться формулой:

учетом всего записанного, формула (1) станет такой:

Здесь k – это постоянная Больцмана, равна 1,38·10^-23 Дж/К. Посчитаем ответ:

Ответ: 1103 кПа.

Пример 15:

Энергия поступательного движения, которой обладают все молекулы газа, находящегося в объеме 0,02 м³ при 17° C, составляет 0,66 Дж. Найти концентрацию молекул этого газа.

Решение от преподавателя:

Кинетическая энергия поступательного движения одной молекулы идеального газа находят по формуле:

Постоянная Больцмана k равна 1,38·10^-23 Дж/К. Умножим обе части этого равенства на число молекул газа N, тогда:

Произведение NE_к по смыслу равна данной в условии энергии поступательного движения всех молекул газа E, поэтому:

Теперь поделим обе части равенства на объем V:

Отношение N\V в правой части есть концентрация молекул n:

Температуру t переведем в шкалу абсолютных температур:

Посчитаем ответ:

Ответ: 5,5·10²¹ м^-3.

Пример 16:

Сколько молекул содержится в 1 л воды?

Решение от преподавателя:

Чтобы определить число молекул N, нужно количество вещества ν (число моль) умножить на число Авогадро N_А:

Число Авогадро N_А – это физическая постоянная, равная 6,022·10²³ 1/моль. Количества вещества ν можно найти, разделив массу m на молярную массу вещества M.

Молярная масса воды (H₂O) равна 0,018 кг/моль. Ну и массу m можно найти как произведение плотности ρ на объем V:

Плотность воды ρ составляет 1000 кг/м³. В итоге Вы должны получить такую формулу:

Обязательно перед подстановкой в формулу переведем объем в единицы системы СИ:

Посчитаем ответ:

Ответ: 3,35·10²⁵.

Пример 17:

Найти концентрацию молекул газа, у которого средняя квадратичная скорость молекул равна 500 м/с при температуре 300 К. Плотность газа 0,27 кг/м³.

Решение от преподавателя:

Запишем основное уравнение молекулярно-кинетической теории идеального газа:

Распишем в этой формуле концентрацию n как отношение числа молекул N к объему газа V:

По смыслу произведение m₀N равно массе газа m, тогда:

Отношение массы газа m к объему газа V – это плотность газа ρ, поэтому:

Также запишем формулу связи давления идеального газа p с концентрацией молекул газа n и абсолютной температурой T:

Приравняем формулы (1) и (2), далее выразим искомую концентрацию n:

Произведем вычисления:

Ответ: 5,43·10²⁴ м^-3.

Пример 18:

Какое значение температуры по шкале Кельвина соответствует температуре 100° C?

Решение от преподавателя:

Чтобы перевести температуру из шкалы Цельсия в шкалу Кельвина (то есть в абсолютную шкалу температур), нужно воспользоваться следующей формулой:

T=t+273

Учитывая это, мы получим такой ответ:

T=100+273=373К

Ответ: 373 К.

Пример 19:

В первом сосуде находится азот, во втором – водород. Чему равно отношение давления p₁ азота к давлению p₂ водорода при одинаковых значениях концентрации молекул и температуре?

Решение от преподавателя:

Применим формулу связи давления газа p с концентрацией молекул n и абсолютной температурой T:

Тогда искомое отношение давлений азота p₁ и водорода p₂ можно найти так:

Поскольку в условии сказано, что концентрация и температура газов равны, то есть

значит:

Ответ: 1.

Пример 20:

Какой объем при нормальных условиях занимают 5 г углекислого газа?

Решение от преподавателя:

Эту задачу проще всего решить, если воспользоваться уравнением Клапейрона-Менделеева:

Выразим из уравнения искомый объем V:

Здесь R – универсальная газовая постоянная, равная 8,31 Дж/(моль·К). Нормальным условиям соответствует давление p, равное 100 кПа, и температура T, равная 0° C или 273 К. Молярная масса углекислого газа (CO₂) равна 0,044 кг/моль. Переведем массу в систему СИ и посчитаем ответ:

Интереса ради представим формулу (1) в следующем виде, где ν – это количество вещества:

Из формулы видно, что равные количества вещества любых газов при нормальных условиях занимают один и тот же объем.

Ответ: 0,0026 м³.

Пример 21:

В сосуде вместимостью 2 м³ находится 2,4 кг газа. Под каким давлением находится газ, если средняя квадратичная скорость его молекул равна 500 м/с?

Решение от преподавателя:

Запишем основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:

Также запишем формулу определения концентрации молекул газа n (это отношение количества молекул N к объему газа V):

Полученное подставим в формулу (1), тогда:

Заметьте, что произведение массы одной молекулы m₀ на число молекул N равно массе газа m:

Посчитаем ответ:

Ответ: 0,1 МПа.

Пример 22:

Чему равна температура газа, если при концентрации 2,65·10²⁵ м^-3 он создает давление 98,8 кПа?

Решение от преподавателя:

Воспользуемся формулой связи давления p с концентрацией молекул n и абсолютной температурой газа T:

В этой формуле k – это постоянная Больцмана, равная 1,38·10^-23 Дж/К. Из этой формулы выразим искомую температуру T:

Посчитаем численный ответ задачи:

Ответ: -3°C.

Пример 23:

Плотность газа в баллоне электрической лампы 0,9 кг/м³, давление при горении 110 кПа. Вычислить среднюю квадратичную скорость молекул газа.

Решение от преподавателя:

Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа записывается так:

Распишем в этой формуле концентрацию nn как отношение количества молекул N к объему газа V:

Произведение массы одной молекулы m₀ на число молекул N дает массу газа m, поэтому:

Отношение массы газа m к объему газа V – это плотность газа ρ, значит:

Выразим искомую среднеквадратичную скорость υ_кв:

Посчитаем численный ответ к задаче:

Ответ: 2180 км/ч.

Пример 24:

Определить число молекул, содержащихся в 1 г воды.

Решение от преподавателя:

В одном моле любого вещества содержится одинаковое число молекул, равное числу Авогадро N_А. Поэтому, чтобы определить число молекул N, нужно количество вещества νν умножить на число Авогадро N_А, т.е. применить такую формулу:

Число Авогадро N_А равно 6,022·10²³ 1/моль (это физическая постоянная). Количество вещества легко определить по формуле:

Здесь M – это молярная масса воды, равная 0,018 кг/моль. Итоговая формула примет вид:

Переведем массу воды mm в систему СИ:

Произведем вычисления:

Ответ: 3,35·10²².

Пример 25:

При какой температуре находится одноатомный газ, если средняя кинетическая энергия его молекулы равна 8·10^-20 Дж?

Решение от преподавателя:

Среднюю кинетическую энергию поступательного движения молекулы одноатомного газа E_к можно определить по такой формуле:

В этой формуле k – постоянная Больцмана, равная 1,38·10^-23 Дж/К. Выразим из формулы искомую температуру T:

Произведем вычисления:

Ответ: 3865 К.

Пример 26:

Определить количество вещества, содержащегося в медной отливке массой 96 кг.

Решение от преподавателя:

Чтобы определить количество вещества ν, нужно найти отношение массы вещества m к молярной массе вещества M.

Молярная масса меди (Cu) равна 0,064 кг/моль. Посчитаем ответ:

Ответ: 1500 моль.

Пример 27:

Под каким давлением находится кислород в баллоне, если при температуре 27° C его плотность 6,44 кг/м³?

Решение от преподавателя:

Запишем уравнение Клапейрона-Менделеева:

Поделим обе части уравнения на объем газа V, получим:

Тогда в правой части имеем отношение массы газа m к его объему V, что равно плотности ρ:

Молярная масса кислорода O₂ M равна 0,032 кг/моль, универсальная газовая постоянная R – 8,31 Дж/(моль·К). Переведем температуру t в Кельвины и посчитаем ответ:

Ответ: 500 кПа.

Пример 28:

В комнате размером 4x5x2,7 м³ испарился кристаллик йода массой 20 мг. Сколько молекул йода оказалось в 1 см³ воздуха комнаты при условии их равномерного распределения? Молярная масса йода равна 127 г/моль.

Решение от преподавателя:

В случае равномерного распределения молекул йода по объему комнаты число его молекул N₀ в объеме V₀ можно определить через концентрацию nn по формуле:

Концентрация молекул nn равна отношению количества всех молекул йода N к объему комнаты V:

Объем комнаты V легко найти как объем прямоугольного параллелепипеда:

V=abc 

Число всех молекул N найдем как произведение количества вещества ν на число Авогадро N_А:

Количество вещества νν равно отношению массу всего йода mm к молярной массе йода M. Учитывая, что молярная масса M молекулярного йода I₂ в два раза больше молярной массы M₀ атомарного йода I, указанной в условии, имеем:

В итоге, если подставить все приведенные формулы в формулу (1), получим:

Число Авогадро равно 6,022·10²³ моль^-1. Переведем некоторые величины в систему СИ:

Посчитаем численный ответ:

Ответ: 8,8·10¹¹.

Пример 29:

Найдите отношение средних скоростей молекул O₂ и H₂ при одинаковой температуре.

Решение от преподавателя:

Вообще, среднюю квадратичную скорость молекул газа можно определить по формуле:

В этой формуле R – универсальная газовая постоянная, T – абсолютная температура газа, M – молярная масса газа. Из формулы видно, что скорость молекул газа тем больше, чем меньше его молярная масса. Тогда отношение скоростей молекул водорода к молекулам кислорода равно:

Так как по условию T₁=T₂, то:

Молярная масса водорода H₂ M₁ равна 0,002 кг/моль, кислорода O₂ M₂ равна 0,032 кг/моль. Посчитаем ответ:

Ответ: 4.

Пример 30:

В лабораторных условиях создан высокий вакуум, то есть очень малое давление, равное 1,33 нПа.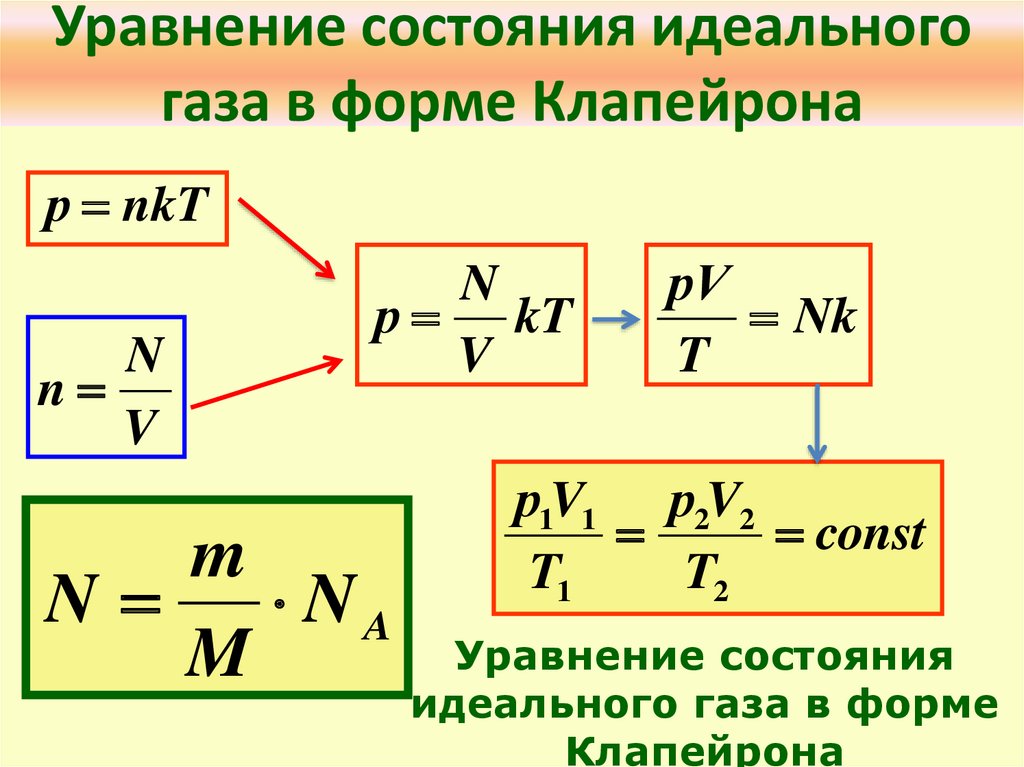 Сколько молекул остается при этом в 1 м³ газа? Температуру принять равной 293 К.

Решение от преподавателя:

Вспомним формулу связи давления идеального газа pp с концентрацией его молекул nn и абсолютной температурой T:

Присутствующая в формуле постоянная Больцмана k равна 1,38·10^-23 Дж/К. Концентрация nn равна отношению количества всех молекул газа N на объем V, который газ занимает:

Тогда формула (1) станет такой:

Откуда искомое число молекул N равно:

Число молекул газа N – это безразмерная величина.

Ответ: 3,3·10¹¹.

Пример 31:

Какова плотность сжатого воздуха при 0° C в камере шины автомобиля “Волга”? Давление 0,17 МПа.

Решение от преподавателя:

Применим уравнение Клапейрона-Менделеева:

Поделим обе части уравнения на объем V, тогда получим:

Отношение массы m к объему V есть плотность газа ρ, заменив в правой части равенства это отношение на плотность, получим:

Теперь выразим искомую величину, в итоге имеем такую формулу:

Молярная масса воздуха MM равна 0,029 кг/моль. Заметьте, что её нельзя определить с помощью таблицы Менделеева, так как воздух – это смесь газов. Переведем температуру tt в шкалу Кельвина:

Посчитаем ответ:

Ответ: 2,17 мг/см³.

Пример 32:

Определить молярную массу газа, если его плотность при нормальных условиях равна 0,09 кг/м³.

Решение от преподавателя:

Запишем уравнение Клапейрона-Менделеева:

Плотность газа ρ, как и любого другого вещества, находят по формуле:

Тогда формула (1) примет следующий вид:

Выразим отсюда искомую молярную массу газа M:

Напомним, что при нормальных условиях давление pp равно 100 кПа, а температура T – 0° C или 273 К. Универсальная газовая постоянная равна 8,31 Дж/(моль·К). Считаем ответ:

По полученной молярной массе легко догадаться, что это водород H₂.

Ответ: 2 г/моль.

Пример 33:

Определить среднюю квадратичную скорость молекул азота при температуре 27° C?

Решение от преподавателя:

Среднюю квадратичную скорость молекул идеального газа υквυкв определяют по такой формуле:

В этой формуле R – универсальная газовая постоянная, равная 8,31 Дж/(моль·К), M – молярная масса газа, равная у азота 0,028 кг/моль. Переведем данную в условии температуру из шкалы Цельсия в шкалу Кельвина:

Посчитаем ответ:

Ответ: 0,5 км/с.

Пример 34:

Найти число молекул в 2 кг углекислого газа.

Решение от преподавателя:

Число молекул N находят по следующей формуле:

В этой формуле ν – количество вещества, а N_А – число Авогадро, равное 6,022·10²³ моль^-1. Количество вещества ν найдем по следующей известной формуле:

Молярная масса M углекислого газа (CO₂) равна 0,044 кг/моль. В итоге Вы должны получить такую формулу:

Посчитаем численный ответ:

Ответ: 2,74·10²⁵.

Пример 35:

Определить плотность воздуха при нормальных условиях. Молярную массу принять равной 29 г/моль.

Решение от преподавателя:

Нормальные условия (н.у) – это:

давление p, равное приближенно атмосферному, т.е. 100 кПа;

температура T, равная 0° C или 273 К.

Запишем уравнение Клапейрона-Менделеева:

В уравнении M – это молярная масса газа, в данном случае воздух. Поделим обе части уравнения на объем газа V:

Отношение m\V в правой части есть плотность газа ρ, поэтому:

Откуда плотность воздуха ρ равна:

Переведем молярную массу газа в систему СИ:

Посчитаем ответ:

Ответ: 1,28 мг/см³.

Пример 36:

Во сколько раз масса молекулы углекислого газа CO₂ больше массы молекулы аммиака NH₃?

Решение от преподавателя:

В общем случае массу одной молекулы m можно найти по такой формуле:

В этой формуле M – молярная масса вещества (т.е. масса 1 моля вещества), а N_А – число Авогадро (количество молекул в 1 моле любого вещества). Тогда отношение масс молекул углекислого газа и аммиака равно:

Молярная масса углекислого газа CO₂ M₁ равно 0,044 кг/моль, а аммиака NH₃ M₂ – 0,017 кг/моль. Таким образом, отношение масс молекул равно:

Ответ: 2,59.

Пример 37:

За 20 суток из стакана полностью испарилась 0,2 кг воды. Сколько в среднем молекул вылетало с поверхности воды за 1 с?

Решение от преподавателя:

Если скорость испарения, то есть количество молекул, вылетающее с поверхности воды за единицу времени, всегда постоянна, тогда справедливо следующее равенство:

Откуда получим:

Общее количество молекул воды N в массе m найдем по формуле:

Здесь N_А – число Авогадро (оно равно 6,022·10²³ моль^-1), а ν – количество вещества, которое определяют по следующему выражению:

В этой формуле M – молярная масса воды, её легко определить по таблице Менделеева, зная химическую формулу вещества. Для воды (H₂O) молярная масса равна 0,018 кг/моль. В итоге мы получим такую формулу:

Переведем время T, данное в сутках, в секунды:

Посчитаем ответ:

Ответ: 3,87·10¹⁸.

Пример 38:

Считая, что диаметр молекул водорода составляет около 0,23 нм, подсчитать, какой длины получилась бы нить, если бы все молекулы, содержащиеся в 1 мг этого газа, были расположены в один ряд вплотную друг к другу.

Решение от преподавателя:

Длину получившейся нити L можно найти, перемножив количество молекул водорода N на диаметр одной молекулы d:

Количество молекул N найдем по такой формуле:

Из последней формулы видно, что нам знать, какое количество вещества ν содержится в массе m. Это можно определить по формуле:

Молярная масса водорода (H₂) M равна 0,002 кг/моль. Подставляя поочерёдно одно выражение в другое, Вы получите такую окончательную формулу:

Переведем массу m в систему СИ и посчитаем ответ:

Ответ: 69,25 Гм.

Пример 39:

В сосуде находится газ под давлением 150 кПа при температуре 23° C. Найти концентрацию молекул.

Решение от преподавателя:

Запишем формулу связи давления pp идеального газа с концентрацией молекул nn и абсолютной температурой T:

В этой формуле k – постоянная Больцмана, равная 1,38·10^-23 Дж/К. Выразим из этой формулы искомую концентрацию n:

Обратите свое внимание, что в формуле фигурирует абсолютная температура, поэтому переведем данную в условии температуру в шкалу Кельвина:

23^∘C=296К

Произведем вычисления:

Ответ: 3,67·1025 м^-3.

Пример 40:

Определить среднюю квадратичную скорость молекул водорода при нормальных условиях.

Решение от преподавателя:

Решение задачи: Кинетическую энергию поступательного движения молекул газа можно определять по двум формулам:

Приравняем эти два выражения и выразим среднюю квадратичную скорость υ_кв:

Массу одной молекулы m0m0 можно узнать, если разделить молярную массу M на число Авогадро N_А:

Молярная масса водорода (H₂) равна 0,002 кг/моль. В таком случае формула (1) примет такой вид: э

Известно, что произведение двух постоянных – постоянной Больцмана k и числа Авогадро N_А – дают в результате универсальную газовую постоянную R, равную 8,31 Дж/(моль·К). Таким образом, получим:

Нормальным условиям соответствует давление p, равное (приближенно) атмосферному, то есть 100 кПа, и температура T, равная 0° C или 273 К. Считаем ответ:

Ответ: 1,8 км/с.

Пример 41:

Под каким давлением находится кислород в баллоне, если при температуре 27° C его плотность 6,24 кг/м³?

Решение от преподавателя:

Применим уравнение Клапейрона-Менделеева:

Молярная масса кислорода (O₂) MM равна 0,032 кг/моль. Разделим обе части уравнения на объем V:

Отношение массы m к объему V равно плотности газа ρ, поэтому:

Переведем температуру в абсолютную шкалу температур и посчитаем ответ:

27^∘C=300К 

Ответ: 0,49 МПа.

Пример 42:

При какой температуре средняя квадратичная скорость молекул кислорода достигнет 600 м/с?

Решение от преподавателя:

Среднюю квадратичную скорость молекул идеального газа υквυкв можно найти по такой формуле:

В этой формуле R – это универсальная газовая постоянная, равная 8,31 Дж/(моль·К), M – молярная масса газа, равная у кислорода 0,032 кг/моль. Выразим из формулы искомую температуру кислорода T:

Численно эта температура равна:

Ответ: 462,1 К.

13.2: Единицы концентрации — Химия LibreTexts

1. Последнее обновление

2. Сохранить как PDF

• Роберт Белфорд
• Университет Арканзаса в Литл-Роке

Введение

Что означает концентрация?

В науке есть два основных значения концентрации; во-первых, насколько вещи близки друг к другу, а во-вторых, состав веществ в смеси. В разделе «Общая химия 1» мы использовали такие понятия, как плотность и молярность, для описания первого понятия, а массовый процент и молярная доля — для описания второго.

• Насколько плотны (упакованы) вещи
  • Плотность (\(d=\frac{масса}{объем}\))
  • Молярность (\(M=\frac{moles}{volume}\)),
    Обратите внимание, вышеприведенное может использоваться для описания чистого вещества или смеси. Молярность была очень полезна для определения количества растворенных частиц в растворе, поскольку вы могли измерить только весь раствор (его массу или объем), но не могли напрямую измерить его компоненты.

• Относительный состав смеси
  • Процент по массе \(\left (Mass\; \%_{A}=100(\frac{Mass_{A}}{Mass_{Total}}) \right )\)
  • Мольная доля \(\left (X_{A}=(\frac{moles_{A}}{moles_{Total}}) \right )\)
    Примечание , приведенное выше можно использовать для описания относительного состав однородных смесей (растворов), но толком не говорят о том, насколько вещи близки друг к другу. Например, мы использовали понятие мольной доли для описания парциального давления газа, где парциальное давление равно мольной доле, умноженной на общее давление, но это ничего не говорит вам о том, насколько близко молекулы расположены друг к другу 9.0036

    Следует также отметить, что «процент» — это просто «доля, умноженная на 100», и, таким образом, это два разных способа выражения одного и того же отношения, и что использование процента для массы и доли для количество молекул, но вы также можете указать «массовую долю» и «молярный процент».

Примечание

Что касается единиц измерения, то здесь тоже есть два принципиально разных способа математического описания концентрации вещей

• От одной части к целому
  • Это единственный тип, с которым мы имели дело, и он описывает такие вещи, как молярность (моль соединения к общему объему) и доли (моль или масса одного соединения к общему количеству молей или массе всех соединений)
• Одна часть к другой части
  • Мы введем несколько новых измерений, которые соответствуют этому, например, моляльность (моль растворенного вещества на кг растворителя) и г растворенного вещества/100 г растворителя. Каждый из них представляет одну сущность (растворенное вещество) другой сущности (растворителю), что отличается от отношения к целому (которое является растворенным веществом и растворителем).

Единицы концентрации

Молярность M:

\[ \text{молярность (M)} =\dfrac{\text{моли растворенного вещества}}{\text{литр раствора}}\]

Молярность полезна, потому что измеряя объем раствора, можно определить количество частиц растворенного вещества (n=MV, где n=моли растворенного вещества). Поскольку многие реакции протекают в фазах растворов, а растворенные вещества часто являются реагентами, мы использовали молярность в стехиометрических расчетах. В следующей главе мы также узнаем, что скорость реакций также зависит от их концентрации, и молярность может выражать это.

ПРИМЕЧАНИЕ. Это тип расчета «Часть к целому», то есть измерение объема (целого: поскольку раствор является растворителем плюс все растворенные вещества, это позволяет определить количество молей вещества (части) , n = MV, где n = моли, M = молярность и V = объем. Например, при приготовлении растворов определенной молярности вы разбавляете растворенное вещество до желаемого объема.

Моляльность m:

\[ \text{моляльность (м)} =\dfrac{\text{моли растворенного вещества}}{\text{килограмм растворителя}}\]

Моляльность – это отношение молей растворенного вещества к массе растворенного вещества в кг. Это часто используется при расчете того, как растворенное вещество влияет на физические свойства растворителя, например на температуру кипения или плавления растворителя. Например, мы могли бы определить, сколько соли требуется, чтобы понизить точку замерзания определенного количества воды на 1 градус.

ПРИМЕЧАНИЕ. Это расчет типа «Часть к части», то есть количество молей растворенного вещества на килограмм растворителя (не раствора). Так, например, при приготовлении растворов желаемой моляльности вы добавляете растворенное вещество к определенному количеству (массе) растворителя 9.{all}Mass\%_n=100\]

Проценты связаны с дробью, это просто дробь, умноженная на 100. Химики обычно используют проценты для описания массовых долей. Обратите внимание, что сумма массовых процентов всех веществ в образце = 100%.

Примечание. Это расчет типа «Часть к целому», т. е. это 100-кратная массовая доля.

Отношение масс

Отношение двух веществ – это количество одного по сравнению с количеством другого. Если одним из них является растворитель, то отношение растворенного вещества к растворителю становится индикатором концентрации растворенного вещества в растворителе. Обычно это не используется, но может помочь вам понять количество растворенных веществ в граммах на 100 г воды (см. ниже).

Примечание. Это расчет типа «Часть к части». Таким образом, массовое отношение растворенного вещества в растворителе будет равно массе растворенного вещества, деленной на массу растворителя (не раствора, а массовой доли)

Грамм растворенного вещества на 100 г H

₂ O (S)

Часто обозначается символом (S) и используется для построения графиков свойств растворителей, например, как концентрация растворенного вещества влияет на точку кипения (температуру) воды. Он говорит вам, насколько концентрировано растворенное вещество в пересчете на г растворенного вещества на 100 г воды. Это просто отношение, умноженное на 100, в единицах г растворенного вещества/100 г растворителя. Примечание: эмпирическое правило: растворимость растворимого вещества превышает 0,1 г/100 г растворителя, а растворимость нерастворимого вещества меньше, но, конечно, все это имеет значение.

\[S=100(масса\; отношение)=\фракция{масса\; раствор {масса\; растворитель}(100)\]

Если вы растворяете раствор Xg в растворителе Yg, S = (X/Y)100 г

Примечание. Это расчет типа «Часть к детали». Проще говоря, это массовое отношение, умноженное на 100.

Части в обозначении

Их часто называют «псевдоединицами», и они представляют собой безразмерные величины, используемые для описания очень разбавленных концентраций растворенных веществ. Значение может быть неоднозначным, но они часто используются в технике. В этом разделе мы рассмотрим водные системы. 96 мкг\; раствор {г} \ справа) = \ гидроразрыва {\ му г \; раствор {L \; Н_2 О}\)

Рабочий лист

Рабочий лист концентрации

Ключ рабочего листа концентрации

Примечание:

Если вы откроете PDF-файл в браузере, вы можете прокомментировать его. Не забудьте пометить его c1403c13 и опубликовать в группе hypothes.is UALRChem1403. Обратитесь к инструктору, если вы не в группе. Вы также можете распечатать рабочий лист, если с ним легче работать.

Проверь себя

Домашние задания

Следующая проблема имеют видео -решения в ответах

Упражнение \ (\ pageindex {4} \)

---

Концентрированный водный аммиак составляет 28%. . Какова молярная доля аммиака в концентрированном аммиаке? Примечание. Ответ содержит видео.

Ответить

X _Аммиак = 0,29, обратите внимание, как это близко к массовым процентам, потому что аммиак и вода имеют одинаковые молярные массы.

Упражнение \(\PageIndex{5}\)

---

Концентрированный водный раствор аммиака содержит 28% по массе NH ₃ и имеет плотность 0,90 г/мл. Какова молярность аммиака в концентрированном аммиаке? Примечание. Ответ содержит видео.

Ответить

М _{Аммиак = 15М.}

Упражнение \(\PageIndex{6}\)

---

Концентрированный водный раствор аммиака содержит 28% по массе NH ₃ и имеет плотность 0,90 г/мл. Какова моляльность аммиака в концентрированном аммиаке? Примечание. Ответ содержит видео.

Ответить

m _{Аммиак = 23 (моль NH 3 /кг H 2 O)}

 

 

Авторы и авторство

• Роберт Э. Белфорд (Университет Арканзаса Литл-Рок; химический факультет). Ответственность за широту, глубину и правдивость этой работы несет Роберт Э. Белфорд, [email protected]. Вы должны связаться с ним, если у вас есть какие-либо опасения. В этом материале есть как оригинальные материалы, так и контент, основанный на предыдущих вкладах сообщества LibreTexts и других ресурсов, включая, помимо прочего:

---

Эта страница под названием 13. 2: Единицы концентрации распространяется в соответствии с лицензией CC BY-NC-SA 4.0, автором, ремиксом и/или куратором которой является Роберт Белфорд.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   Роберт Белфорд

   Встроить Hypothes.is?

   да

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать страницу TOC

   да на странице

2. Теги

   1. концентрация

Единиц концентрации – Химия LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

1624

Растворы представляют собой гомогенные смеси , содержащие одно или несколько растворенных веществ в растворителе . Растворитель, составляющий большую часть раствора, тогда как растворенное вещество — это вещество, растворенное внутри растворителя.

Относительные единицы концентрации

Концентрации часто выражаются в относительных единицах (например, в процентах) с обычно используемыми тремя различными типами процентных концентраций:

1. Массовые проценты : Массовые проценты используются для выражения концентрации раствора, когда даны масса растворенного вещества и масса раствора: \[\text{Массовый процент}=\dfrac{\text{ Масса растворенного вещества}}{\text{Масса растворенного вещества}} \times 100\% \label{1}\]
2. Объемный процент : Объемный процент используется для выражения концентрации раствора, когда объем растворенного вещества и объем раствора заданы: \[\text{Объемный процент}= \dfrac{\text{Объем Раствор}}{\text{Объем раствора}} \times 100\% \label{2}\]
3. Процент массы/объема: Другой вариант процентной концентрации — это процент массы/объема, который измеряет массу или вес растворенного вещества в граммах (например, в граммах) по сравнению с объемом раствора (например, в мл). Примером может служить 0,9% (масса/объем) раствор \(NaCl\) в медицинских солевых растворах, который содержит 0,9 г \(NaCl\) на каждые 100 мл раствора (см. рисунок ниже). Процент массы/объема используется для выражения концентрации раствора, когда дана масса растворенного вещества и объем раствора. Поскольку числитель и знаменатель имеют разные единицы измерения, эта единица концентрации не является истинной относительной единицей (например, процент), однако ее часто используют в качестве простой единицы концентрации, поскольку объемы растворителя и растворов легче измерить, чем веса. Более того, поскольку плотность разбавленных водных растворов близка к 1 г/мл, если объем раствора измеряется в мл (согласно определению), то это хорошо аппроксимирует массу раствора в граммах (составляя истинную относительную единицу измерения). (м/м)).

\[\text{Масса/объем в процентах}= \dfrac{\text{Масса растворенного вещества (г)}}{\text{Объем раствора (мл)}} \times 100\% \label{3}\ ]

Рисунок использован с разрешения Википедии.

Пример \(\PageIndex{1}\): «Крепость» алкоголя как единица концентрации

Например, в Соединенных Штатах содержание алкоголя в спиртных напитках определяется как двойное процентное содержание алкоголя по объему (об./об.). называется доказательством. Какова концентрация алкоголя в спиртных напитках Bacardi 151 , которые продаются с крепостью 151 (отсюда и название)?

Рисунок: Почти пустая бутылка Bacardi 151. из Википедии.

Раствор

Он будет иметь содержание спирта 75,5% (вес/вес) в соответствии с определением «пруф».

При расчете этих процентов единицы измерения растворенного вещества и раствора должны быть эквивалентными единицами (а весовые/объемные проценты (w/v %) определяются в граммах и миллилитрах).

Вы НЕ МОЖЕТЕ подключить…	Вы НЕ МОЖЕТЕ подключить…
(2 г растворенного вещества) / (1 кг раствора)	(2 г растворенного вещества) / (1000 г раствора)
	или (0,002 кг растворенного вещества) / (1 кг раствора)
(5 мл растворенного вещества) / (1 л раствора)	(5 мл растворенного вещества) / (1000 мл раствора)
	или (0,005 л растворенного вещества) / (1 л раствора)
(8 г растворенного вещества) / (1 л раствора)	(8 г растворенного вещества) / (1000 мл раствора)
	или (0,008 кг растворенного вещества) / (1 л раствора)

Единицы концентрации разведения

Иногда, когда растворы слишком разбавлены, их процентная концентрация слишком мала. Таким образом, вместо использования очень низких процентных концентраций, таких как 0,00001% или 0,000000001%, мы выбираем другой способ выражения концентраций. Следующий способ выражения концентраций аналогичен кулинарным рецептам. Например, в рецепте может быть указано, что нужно использовать 1 часть сахара и 10 частей воды. Как вы знаете, это позволяет использовать в уравнении такие количества, как 1 стакан сахара + 10 стаканов воды. Однако вместо того, чтобы использовать количество рецепта «1 часть на десять», химики часто используют частей на миллион , частей на миллиард или частей на триллион для описания разбавленных концентраций.

• Части на миллион : Концентрация раствора, содержащего 1 г растворенного вещества и 1000000 мл раствора (так же, как 1 мг растворенного вещества и 1 л раствора), создаст очень маленькую процентную концентрацию. Поскольку раствор, подобный этому, был бы очень разбавленным, плотность раствора хорошо аппроксимируется плотностью растворителя; для воды это 1 г/мл (но будет отличаться для разных растворителей). Итак, после математических расчетов и преобразования миллилитров раствора в граммы раствора (при условии, что вода является растворителем): \[\dfrac{\text{1 г растворенного вещества}}{\text{1000000 мл раствора}} \times \dfrac {\text{1 мл}}{\text{1 г}} = \dfrac{\text{1 г растворенного вещества}}{\text{1000000 г раствора}}\] Получаем (1 г растворенного вещества)/(1000000 г решение). Поскольку и растворенное вещество, и раствор теперь выражаются в граммах, теперь можно сказать, что концентрация растворенного вещества составляет 1 часть на миллион (ppm). \[\text{1 ppm}= \dfrac{\text{1 мг растворенного вещества}}{\text{1 л раствора}}\] Вместо этого можно использовать единицу ppm в терминах объем/объем (v/v). (см. пример ниже).

• Частей на миллиард : Частей на миллиард (ppb) почти как ppm, за исключением того, что 1 ppb в 1000 раз более разбавлен, чем 1 ppm. \[\text{1 ppb} = \dfrac{1\; \mu \text{g раствор}}{\text{1 л раствора}}\]
• Части на триллион : Как и в случае с ppb, идея частей на триллион (ppt) аналогична концепции ppm. Однако 1 ppt в 1000 раз более разбавлен, чем 1 ppb, и в 1000000 раз более разбавлен, чем 1 ppm. \[\text{1 ppt} = \dfrac{ \text{1 нг растворенного вещества}}{\text{1 л раствора}}\]

Пример \(\PageIndex{2}\): частей на миллион в атмосфере

Вот таблица с объемными процентами различных газов, содержащихся в воздухе. Объемный процент означает, что на 100 л воздуха приходится 78,084 л азота, 20,946 л кислорода, 0,934 л аргона и так далее; Объемный процент массы отличается от состава по массе или состава по количеству молей.

Название элемента	Объемные проценты (об./об.)	частей на миллион (об/об)
Азот	78. 084	780 840
Кислород	20,946	209 460
Водяной пар	4,0%	40 000
Аргон	0,934	9 340
Двуокись углерода	0,0379	379* (но быстро растет)
Неон	0,008	8,0
Гелий	0,000524	5,24
Метан	0,00017	1,7
Криптон	0,000114	1,14
Озон	0,000001	0,1
Моноокись азота	0,00003	0,305

Единицы концентрации, основанные на молях

• Мольная доля : Мольная доля вещества – это доля всех его молекул (или атомов) от общего числа молекул (или атомов). Это также может иногда пригодиться при работе с уравнением \(PV=nRT\). \[\chi_A= \dfrac{\text{количество молей вещества A}}{\text{общее количество молей в растворе}}\] Кроме того, имейте в виду, что сумма мольных долей каждого из веществ в растворе равно 1. \[\chi_A + \chi_B + \chi_C \;+\; … \;=1\]
• Мольные проценты : Мольные проценты (вещества A) выражены \(\chi_A\) в виде процентов. \[\text{Молярный процент (вещества A)}= \chi_A \times 100\%\]
• Молярность : Молярность (M) раствора используется для представления количества молей растворенного вещества на литр раствора. \[M= \dfrac{\text{Моли растворенного вещества}}{\text{Литры раствора}}\]
• Моляльность : Моляльность (m) раствора используется для представления количества молей растворенного вещества на килограмм растворителя. \[m= \dfrac{\text{Моли растворенного вещества}}{\text{Килограммы растворителя}}\]

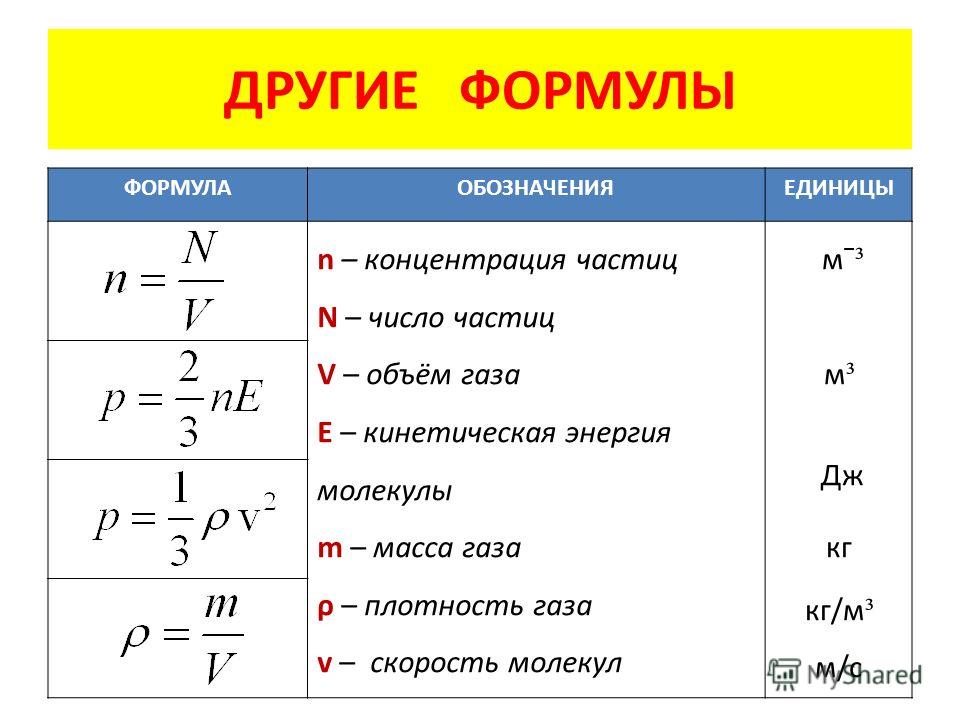Рисунок: Различная молярность жидкостей в лаборатории. 50 мл дистиллированной воды (0 М), раствор гидроксида натрия 0,1 М и раствор соляной кислоты 0,1 М из group4swimmingpool.

Уравнения молярности и моляльности отличаются только своими знаменателями. Однако это огромная разница. Как вы помните, объем зависит от температуры. При более высоких температурах объемы жидкостей увеличиваются, а при более низких температурах объемы жидкостей уменьшаются. Поэтому молярности растворов также различаются при разных температурах. Это создает преимущество использования моляльности над молярностью. Использование моляльностей, а не молярностей для лабораторных экспериментов лучше всего удерживает результаты в более близком диапазоне. Поскольку объем не является частью его уравнения, моляльность не зависит от температуры.

Пример \(\PageIndex{1}\)

В растворе содержится 111,0 мл (110,605 г) растворителя и 5,24 мл (6,0508 г) растворенного вещества. Найдите массовый процент, объемный процент и массовый/объемный процент растворенного вещества.

Раствор

Процент по массе

=(Масса растворенного вещества) / (Масса раствора) x 100%|

=(6,0508г) / (110,605г + 6,0508г) x 100%

=(0,0518688312) x 100%

=5,186883121% 34 Массовый процент = 5,186%

Объемные проценты

= (Объем растворенного вещества) / (Объем раствора) x 100 %

= (5,24 мл) / (111,0 мл + 5,24 мл) x 100 %

= (0,045079 1466) х 100%

= (0,0520) x 100 %

= 5,205 %

Процент массы/объема = 5,2054 %

Пример \(\PageIndex{2}\)

Используя раствор, показанный на рисунке ниже, найдите молярный процент вещества C. (1 моль C / 6,022×10 ²³ молекул C) = 8,30288941×10 ^{– 24} моль C

Всего молей = (24 молекулы) x (1 моль / 6,022×10 ²³ молекулы)= 3,98538691×10 ^{– 23} моль всего

X _C = (8,30288941×10 ^{– 24} моль C) / (3,98538691×10 ^{– 23} моль) = 0,2083333333

Моль-процент C

= Х _С х 100%

= (о. 2083333333) х 100 %

= 20,83333333

Моль Процент C = 20 %

Пример \(\PageIndex{3}\)

г NaCl, растворенного в воде. Найдите его молярность.

Раствор

Моль NaCl = (0,25 г) / (22,99 г + 35,45 г) = 0,004277 моль NaCl

Молярность

= (Моли растворенного вещества) / (Литры раствора)

= (0,004277 моль NaCl) / (1,5 л)

= 0,002851 M

Молярность = 0,0 029M

Пример \(\ PageIndex{4}\)

0,88 г NaCl растворяют в 2,0 л воды. Найдите его моляльность.

Раствор

Моль NaCl= (0,88 г) / (22,99 г + 35,45 г) = 0,01506 моль NaCl

Масса воды = (2,0 л) x (1000 мл / 1 л) x (1 г / 1 мл) x (1 кг / 1000 г) = 2,0 кг воды

Моляльность

= (моль растворенного вещества) / (кг растворителя)

= (0,01506 моль NaCl) / (2,0 кг)

= 0,0075290897m

Моляльность = 0,007 5 м

Каталожные номера

1. Петруччи, Харвуд, Херринг.