Контур электрический – это… Что такое Контур электрический?
- Контур электрический
- контур электрической цепи, любой замкнутый путь, проходящий по нескольким ветвям электрической цепи (См. Электрическая цепь).
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Контур
- Контурная съёмка
Смотреть что такое “Контур электрический” в других словарях:
КОНТУР ЭЛЕКТРИЧЕСКИЙ — (контур электрической цепи) любой замкнутый путь, проходящий по нескольким ветвям электрической цепи. Иногда термин контур электрический используют как синоним термина колебательный контур … Большой Энциклопедический словарь
контур электрический — (контур электрической цепи), любой замкнутый путь, проходящий по нескольким ветвям электрической цепи.

КОНТУР ЭЛЕКТРИЧЕСКИЙ — (контур электрич. цепи), любой замкнутый путь, проходящий по неск. ветвям электрич. цепи. Иногда термин К. э. используют как синоним термина колебательный контур … Естествознание. Энциклопедический словарь
КОНТУР — (фр. contour, от contourner обертывать, очерчивать). Очертание, профиль, очерк. В рисовании: линия, которая определяет внешнюю форму предмета. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. КОНТУР набросок,… … Словарь иностранных слов русского языка
КОНТУР — (1) замкнутая цепь проводников, по которой течёт электрический ток; (2) очертание какого либо предмета, линия, очерчивающая систему точек на плоскости млн. форму конфигурации в пространстве … Большая политехническая энциклопедия
ЭЛЕКТРИЧЕСКИЙ ФИЛЬТР — электрическая цепь, состоящая из конденсаторов и катушек индуктивности (или активных сопротивлений), соединённых определённым образом с целью выделения только полезных сигналов и подавления колебаний др.

Электрический конденсатор — У этого термина существуют и другие значения, см. Конденсатор (значения). См. также: варикап Основа конструкции конденсатора две токопроводящие обкладки, между которыми находится диэлектрик … Википедия
электрический контур — elektrinis kontūras statusas T sritis fizika atitikmenys: angl. electric circuit vok. elektrischer Kreis, m rus. электрический контур, m pranc. circuit électrique, m … Fizikos terminų žodynas
Электрический фильтр — Фильтр в электронике устройство для выделения желательных компонент спектра электрического сигнала и/или подавления нежелательных. Содержание 1 Типы фильтров 2 Принцип работы пассивных аналоговых фильтров … Википедия
Электрический фильтр (электрич. устройство) — Фильтр в электронике устройство для выделения желательных компонент спектра электрического сигнала и/или подавления нежелательных.
 Содержание 1 Типы фильтров 2 Принцип работы пассивных аналоговых фильтров … Википедия
Содержание 1 Типы фильтров 2 Принцип работы пассивных аналоговых фильтров … Википедия
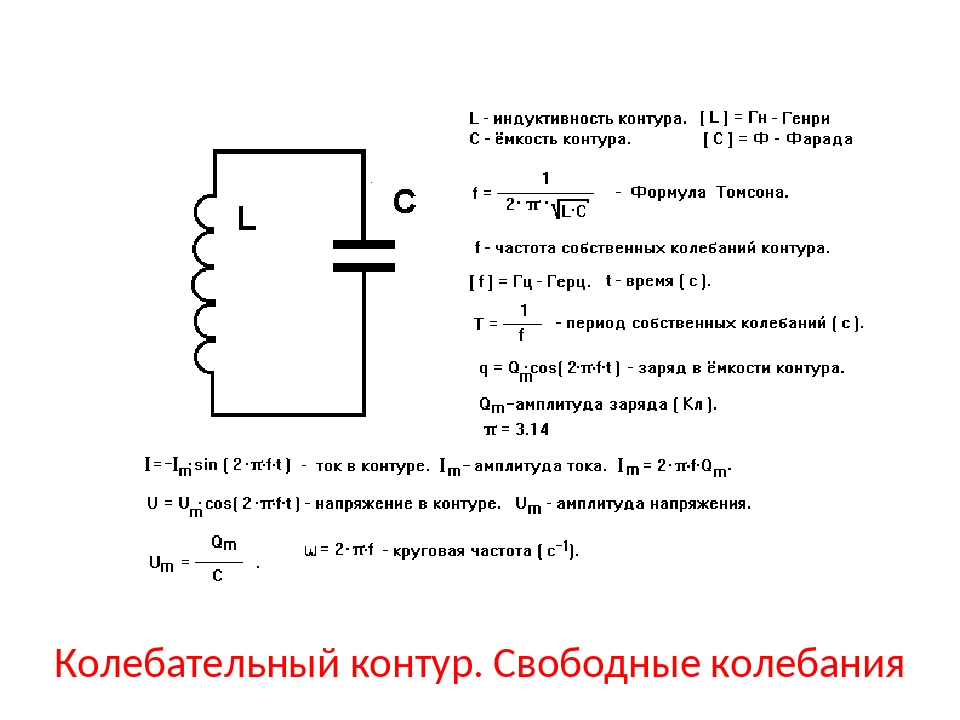
Колебательный контур — урок. Физика, 9 класс.
Колебательный контур — это устройство, в котором могут происходить свободные электромагнитные колебания.
Колебательный контур состоит из конденсатора и катушки индуктивности. Электроёмкость конденсатора — \(C\), индуктивность катушки — \(L\).
Изображение на схемах
Обрати внимание!
В колебательном контуре периодически происходит переход энергии электрического поля в энергию магнитного поля и наоборот.
На некоторое время с помощью переключателя зарядим конденсатор, замкнув его на источник тока (рис. А). Затем наш заряженный конденсатор подсоединим к катушке (рис. Б).
t1=T4. Заряженный конденсатор, подключённый к катушке, начнёт через неё разряжаться. | |
2t1=T2. Так как конденсатор разряжен, то в следующий момент времени ток должен мгновенно исчезнуть, но в результате самоиндукции, которая препятствует убыванию тока, он некоторое время поддерживается в цепи. Индукционный ток сонаправлен с уходящим током цепи и благодаря этому конденсатор заряжается, только заряд на обкладках поменяется на противоположный знак. Энергия магнитного поля перешла в энергию электрического поля. Если рассматривать идеальную модель колебательного контура, который не имеет сопротивления, то энергия в нём не потратится, и конденсатор вновь зарядится до максимального значения. | |
| 3t1=3T4. В третьей четверти периода конденсатор начнёт разряжаться, только теперь ток разряда будет протекать в другом направлении, т. к. полярность напряжения на конденсаторе поменялась. Самоиндукция катушки вновь будет препятствовать быстрому росту тока, который постепенно всё же приобретёт максимальное значение, а конденсатор к тому времени полностью разрядится. Снова энергия электрического поля переходит в энергию магнитного поля. | |
4t1=T. Последняя четверть периода будет похожа на вторую четверть, только ток уже будет протекать в другом направлении. Убыванию тока будет вновь препятствовать самоиндукция, поэтому ток будет убывать постепенно и вновь зарядит конденсатор. И вновь энергия магнитного поля переходит в энергию электрического поля. |
За промежуток времени 4t1 произошло одно полное колебание. Значит, 4t1 \(=T\), где \(T\) — период колебаний.
Период полученных свободных колебаний равен собственному периоду колебательного контура.
Обрати внимание!
Формула для определения периода свободных электромагнитных колебаний: T=2 π ·LC.
Из формулы видно, что период колебательного контура зависит от параметров составляющих его элементов: индуктивности катушки \(L\) и электроёмкости конденсатора \(C\).
Работа колебательного контура представлена на рисунке.
Колебательный контур входит в состав генератора высокочастотных электромагнитных колебаний, который применяется в радиовещании (т. е. передаче звуковой информации на большие расстояния).
Урок 7. свободные и вынужденные электромагнитные колебания. колебательный контур – Физика – 11 класс
Физика, 11 класс
Урок 7. Свободные и вынужденные электромагнитные колебания. Колебательный контур
Свободные и вынужденные электромагнитные колебания. Колебательный контур
Перечень вопросов, рассматриваемых на уроке:
1) электромагнитные колебания, колебательный контур;
2) универсальность основных закономерностей колебательных процессов для колебаний любой физической природы;
3) гармонические колебания;
4) физический смысл характеристик колебаний.
5) графики зависимости электрического заряда, силы тока и напряжения от времени при свободных электромагнитных колебаниях.
6) определение по графику характеристик колебаний;
7) аналогия между механическими и электромагнитными колебаниями.
8) формула Томсона.
Глоссарий по теме
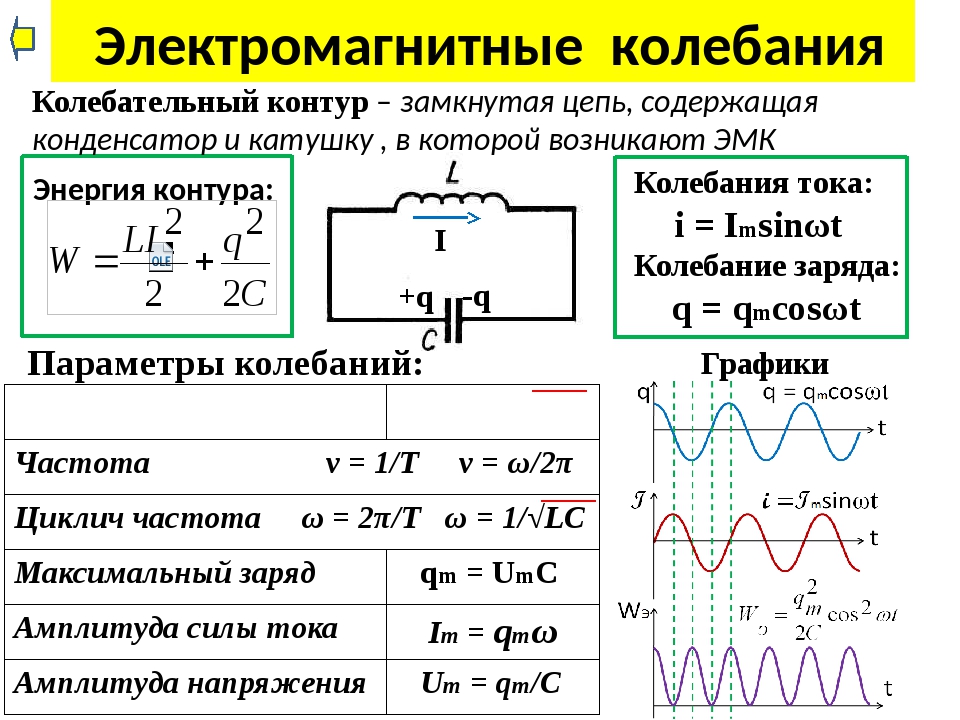
Электромагнитными колебаниями называют периодические изменения со временем заряда, силы тока и напряжения.
Электромагнитные колебания бывают двух видов – свободные и вынужденные.
Свободными колебаниями называют колебания, возникающие в колебательной системе за счет первоначально сообщенной этой системе энергии.
Вынужденные электромагнитные колебания – это периодические изменения заряда, силы тока и напряжения в цепи под действием переменной электродвижущей силы от внешнего источника.
Система, состоящая из конденсатора и катушки индуктивности, присоединенной к его обкладкам, называется колебательным контуром.
Период электромагнитных колебаний
Частота колебаний – число колебаний в единицу времени.
Основная и дополнительная литература по теме урока:
Мякишев Г.Я.,Буховцев Б.Б.,Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций. М.: Просвещение, 2014. – С. 74 – 82.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. -М.: Дрофа, 2009. – С. 126 – 128.
Основное содержание урока
Колебательным контуром называется система, состоящая из конденсатора и катушки, присоединенной к его обкладкам, в которой могут происходить свободные электромагнитные колебания
Электромагнитные колебания в контуре происходят с большой частотой и определять его характеристики без осциллографа невозможно.
Развертка получаемая на экране осциллографа схожа с той, что вычерчивает маятник с песочницей над движущимся листом бумаги при колебаниях математического маятника.
Чтобы в колебательном контуре возникли колебания, необходимо сообщить колебательному контуру энергию, зарядив конденсатор от источника тока.
Энергия, полученная конденсатором заключена в электрическом поле обкладок
где – заряд конденсатора, C – его электроемкость.
Между обкладками конденсатора возникает разность потенциалов .
При разрядке конденсатора энергия электрического поля превращается в энергию магнитного поля, определяемая по формуле
где – индуктивность катушки, – сила переменного тока.
Полная энергия колебательного контура равна
Когда конденсатор разрядится полностью, вся энергия электрического поля превращается в энергию магнитного поля. Когда сила тока и созданное им магнитное поле начинает уменьшаться, возникает ЭДС самоиндукции, стремящийся поддержать ток, и начинается перезарядка конденсатора. При свободных колебаниях через промежутки времени, равные периоду колебаний, состояние системы в точности повторяется. Полная энергия такой системы любой момент времени равно максимальной энергии электрического поля или максимальной энергии магнитного поля.
При свободных колебаниях через промежутки времени, равные периоду колебаний, состояние системы в точности повторяется. Полная энергия такой системы любой момент времени равно максимальной энергии электрического поля или максимальной энергии магнитного поля.
q, u и i – мгновенные значения заряда, напряжения и силы тока. При отсутствии сопротивления в контуре полная энергия электромагнитного поля не изменяется. Колебания затухающие, сопротивление катушки и проводников превращают энергию электромагнитного поля во внутреннюю энергию проводника.
Электромагнитные колебания в контуре имеют сходство со свободными механическими колебаниями. Характер периодического изменения различных величин одинаков. При механических колебаниях периодически изменяются координата тела x и проекция его скорости , а при электромагнитных колебаниях изменяются заряд q конденсатора и сила тока i в цепи.
Индуктивность катушки L аналогична массе тела m, при колебаниях груза на пружине, кинетическая энергия тела , аналогична энергии магнитного поля тока .
Роль потенциальной энергии выполняет энергия заряда конденсатора:
Координата тела аналогична заряду конденсатора.
Полная энергия колебательного контура, в любой момент времени, равна сумме энергий магнитного и электрического полей:
Производная полной энергии по времени равна нулю при R = 0. Следовательно, равна нулю сумма производных по времени от энергий магнитного и электрического полей:
то есть
Знак « – » минус в этом выражении означает, что, когда энергия магнитного поля возрастает, энергия электрического поля убывает и наоборот. Физический смысл этого выражения заключается в том, что скорость изменения энергии магнитного поля равна по модулю и противоположна по направлению скорости изменения электрического поля.
Электрический заряд и сила тока, при свободных колебаниях с течением времени изменяются по закону синуса или косинуса, то есть совершают гармонические колебания.
Циклическая частота для свободных электрических колебаний:
Период свободных колебаний в контуре равен:
Формула Томсона.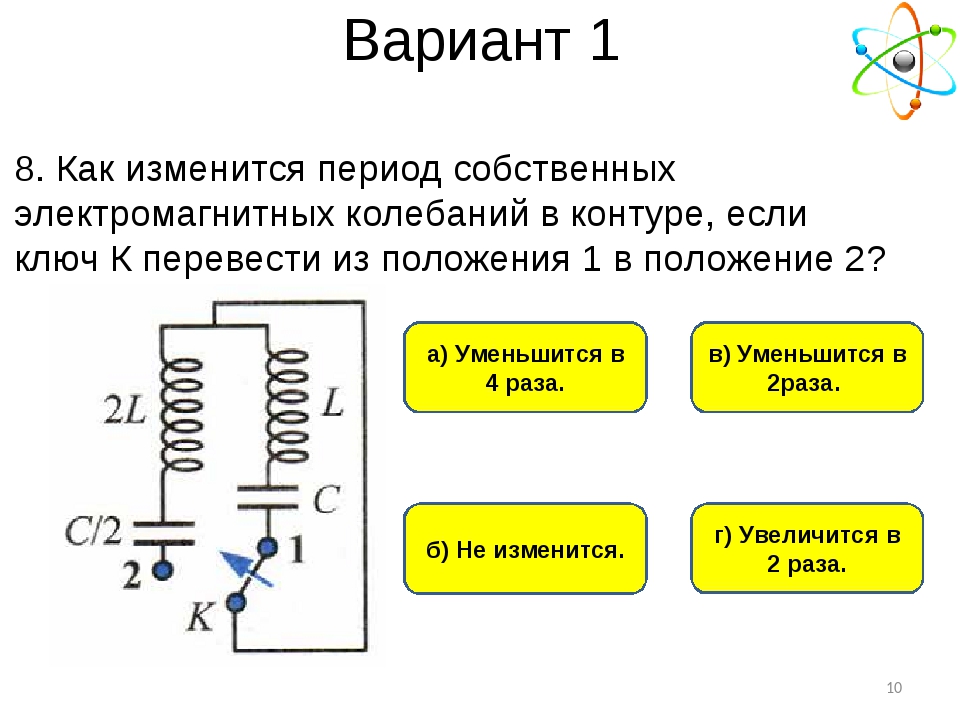
Период свободных электрических колебаний в колебательном контуре зависит от индуктивности катушки и емкости конденсатора.
Период электромагнитных колебаний – промежуток времени, в течение которого ток в колебательном контуре и напряжение на пластинах конденсатора совершает одно полное колебание.
Частотой колебаний называется величина, обратная периоду колебаний:
Частоту свободных колебаний называют собственной частотой колебательной системы.
Заряд конденсатора изменяется по гармоническому закону:
где – амплитуда колебаний заряда. Сила тока также совершает гармонические колебания:
где – амплитуда колебаний силы тока. Колебания силы тока опережают по фазе колебания заряда на .
Разбор типовых тренировочных заданий
Задача 1. Идеальный колебательный контур состоит из конденсатора ёмкостью 2 мкФ и катушки индуктивности. В контуре происходят свободные электромагнитные колебания. В таблице приведена зависимость энергии W, запасённой в конденсаторе идеального колебательного контура, от времени t.
t, нс | 0 | 125 | 250 | 375 | 500 | 625 | 750 | 875 | 1000 |
W, мкДж | 0 | 3,66 | 12,5 | 21,34 | 25,0 | 21,34 | 12,5 | 3,66 | 0,00 |
t, нс | 1125 | 1250 | 1375 | 1500 | 1625 | 1750 | 1875 | 2000 | 2125 |
W, мкДж | 3,66 | 12,5 | 21,34 | 25,0 | 21,34 | 12,50 | 3,66 | 0,00 | 3,66 |
На основании анализа этой таблицы выберите два верных утверждения.
1) Период электромагнитных колебаний в контуре равен 1 мкс.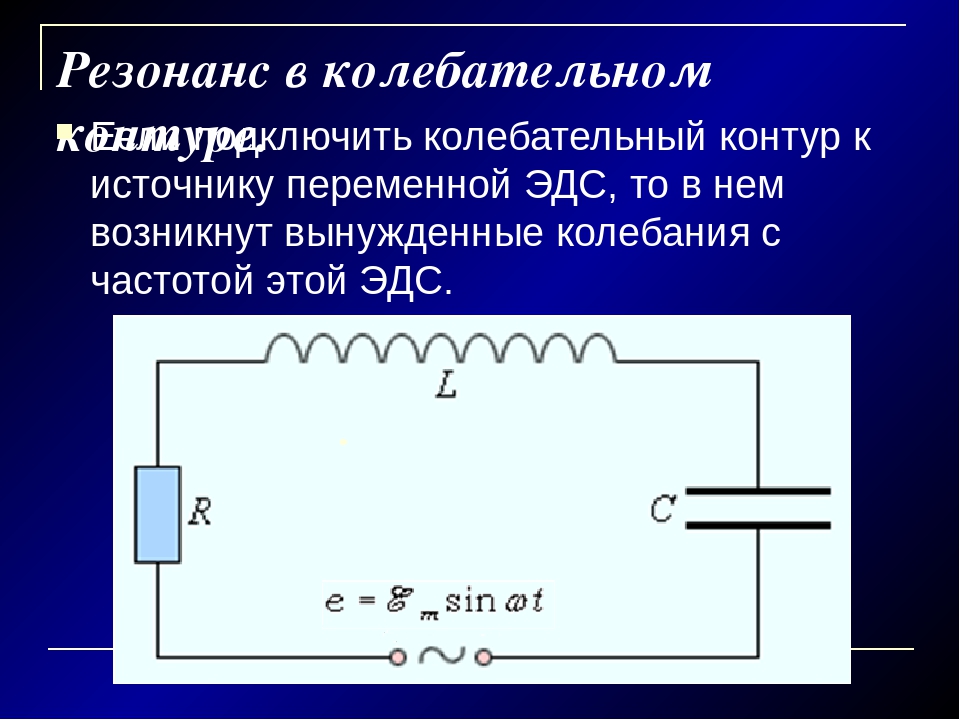
2) Период электромагнитных колебаний в контуре равен 2 мкс.
3) Индуктивность катушки равна примерно 13 нГн.
4) Максимальное напряжение на конденсаторе равно 5 В.
5) Максимальное напряжение на конденсаторе равно 50 кВ.
Решение. При электромагнитных колебаниях в контуре происходит периодическое превращение энергии электрического поля конденсатора в энергию магнитного поля катушки и обратно, при этом максимальная энергия, запасенная в катушке, равна максимальной энергии, запасенной в конденсаторе
Период колебаний конденсатора равен 1000 нс, но период электромагнитных колебаний в контуре в два раза больше и составляет 2000 нс = 2 мкс.
Утверждение 2 — верно, утверждение 1 — неверно.
Воспользуемся формулой Томсона и выразим индуктивность катушки:
Утверждение 3 — неверно.
Максимальное напряжение на конденсаторе равно
Значение находим из таблицы =25 мкДж
Утверждение 4 верно, 5 – неверно
2. Емкость конденсатора колебательного контура С=1мкФ, индуктивность катушки L=0,04 Гн, амплитуда колебаний напряжения Um=100 В.
Емкость конденсатора колебательного контура С=1мкФ, индуктивность катушки L=0,04 Гн, амплитуда колебаний напряжения Um=100 В.
В данный момент времени напряжение на конденсаторе u=80 В. Найти:
1. амплитуду колебаний силы тока Im;
2. полную энергию W;
3. энергию электрического поля Wэл;
4. энергию магнитного поля Wм;
5. мгновенное значение силы тока i.
Дано:
С=1 мкФ=0,000001Ф
L=0,04 Гн
Um=100 В
u=80 В
Найти: Im; W; Wэл; Wм; i.
Решение
Из закона сохранения энергии максимальные энергии конденсатора и катушки индуктивности равны
Откуда
Полная энергия равна
Энергия электрического поля в момент, когда напряжение на конденсаторе
Из закона сохранения энергии выразим :
Мгновенное значение силы тока выразим из формулы:
Колебательный контур в физике – формулы и определения с примерами
Колебательный контур:
Явление возникновения ЭДС индукции при изменении магнитного потока через площадь, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре. Правило Ленца: возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится компенсировать изменение внешнего магнитного потока, вызвавшее данный ток.
Рассмотрим электрическую цепь, содержащую конденсатор электроемкостью С и катушку (соленоид) индуктивностью L (рис. 15). Такая цепь называется идеальным колебательным контуром или LC-контуром.
В отличие от реального колебательного контура, который всегда обладает некоторым электрическим сопротивлением (R
Пусть в начальный момент времени (t = 0) конденсатор С заряжен так, что на его первой обкладке находится заряд +, а на второй —. При этом конденсатор обладает энергией
С течением времени конденсатор начнет разряжаться, и в цепи появится электрический ток, сила l(t) которого будет меняться с течением времени.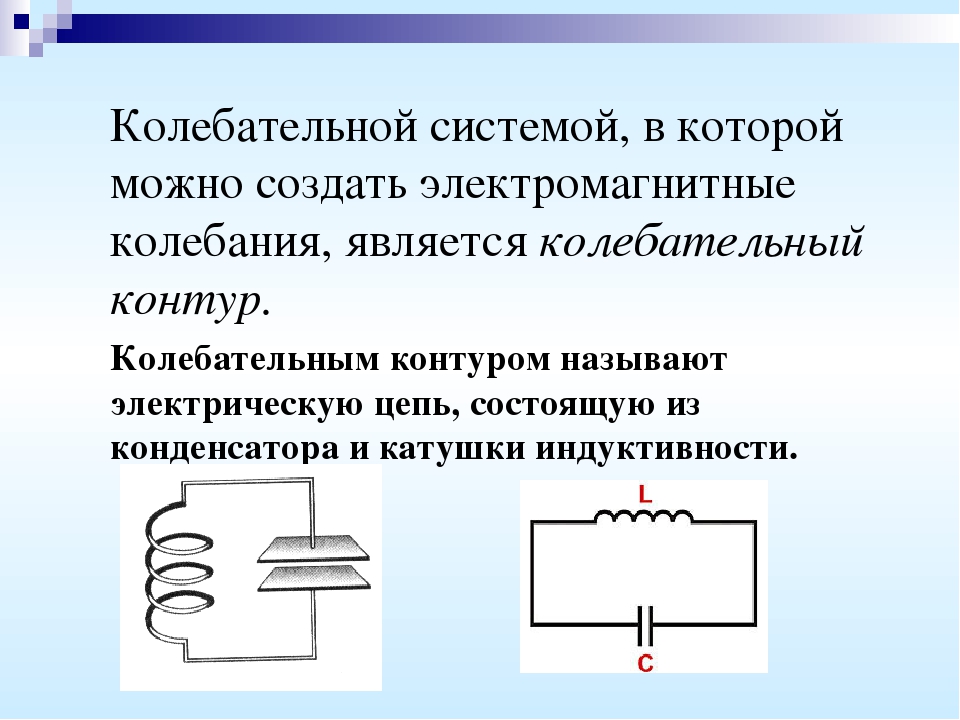 Поскольку при прохождении такого электрического тока в катушке индуктивности возникнет изменяющийся во времени магнитный поток, то это вызовет появление ЭДС самоиндукции, препятствующей изменению силы тока.
Поскольку при прохождении такого электрического тока в катушке индуктивности возникнет изменяющийся во времени магнитный поток, то это вызовет появление ЭДС самоиндукции, препятствующей изменению силы тока.
Вследствие этого сила тока в колебательном контуре будет возрастать от нуля до максимального значения в течение некоторого промежутка времени, определяемого индуктивностью катушки.
В момент полной разрядки конденсатора (q = 0) сила тока в катушке I(t) достигнет своего максимального значения . В соответствии с законом сохранения энергии первоначально запасенная в конденсаторе энергия электростатического поля перейдет в энергию магнитного поля, запасенную в этот момент в катушке:
После разрядки конденсатора сила тока в катушке начнет убывать. Это также произойдет не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создаст индукционный ток. Он будет иметь такое же направление, как и уменьшающийся ток в цепи, и поэтому будет «поддерживать» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезарядит конденсатор до начального напряжения обратной полярности — знак заряда на каждой обкладке окажется противоположным начальному.
Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезарядит конденсатор до начального напряжения обратной полярности — знак заряда на каждой обкладке окажется противоположным начальному.
Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения . При этом его обкладка, первоначально заряженная положительно, будет заряжена отрицательно (см. рис. 15). Далее процесс повторится с той лишь разницей, что электрический ток будет проходить в противоположном направлении.
Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.
Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением в катушке ЭДС самоиндукции, которая «обеспечивает» эту перезарядку. Заметим, что заряд q(t) конденсатора и сила тока I(t) в катушке достигают своих максимальных значений и в различные моменты времени (см. рис. 15).
Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Период свободных электромагнитных колебаний в контуре определяется по формуле Томсона:
Получим эту формулу, используя закон сохранения энергии. Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство
(1)
Поскольку закономерности гармонических колебаний носят универсальный характер, то можно сравнить колебания в LC-контуре с колебаниями пружинного маятника.
Для пружинного маятника полная механическая энергия в любой момент времени 2 ,
(2)
и период его колебаний
Проанализируем соотношения (1) и (2). Сравним выражения для энергии электростатического поля конденсатора и потенциальной энергии упругой деформации пружины энергии магнитного поля катушки и кинетической энергии груза Аналогом координаты x(t) при колебаниях в электрическом контуре является заряд конденсатора q(t), а аналогом проекции скорости груза служит сила тока I(t) в колебательном контуре.
Следуя аналогии, заменим в формуле для периода колебаний пружинного маятника т на L и k на , тогда для периода свободных колебаний в LC-контуре получим формулу Томсона:
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).
Таблица 4
Сопоставление физических величин, характеризующих электромагнитные и механические колебания
Соответственно, зависимость заряда конденсатора от времени будет иметь такой же характер, как и зависимость координаты (смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону (но с другими начальными фазами) будут изменяться сила тока в цепи, напряжение на конденсаторе.
Для определения начальной фазы и амплитуды колебаний заряда необходимо знать заряд конденсатора и силу тока в катушке в начальный момент времени (t = 0).
Полная энергия идеального колебательного контура (R = 0) с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется.
Как уже отмечалось, реальный колебательный контур всегда имеет некоторое сопротивление R, обусловленное сопротивлением катушки, соединительных проводов и т. д. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они «будут происходить» сколь угодно долго.
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без трения, а механическим аналогом реального колебательного контура — пружинный маятник с трением.
Пример №1
При изменении емкости конденсатора идеального LC-контура на = 50 пФ частота свободных электромагнитных колебаний в нем увеличилась с = 100 кГц до = 120 кГц. Определите индуктивность L контура.
Определите индуктивность L контура.
Решение
Частота колебаний в контуре
Поскольку частота колебаний в контуре увеличилась (), то электроемкость должна уменьшится, т. е. .
Из условия задачи получаем систему уравнений
Откуда
Вычитая из первого уравнения второе, получаем
Откуда находим
Ответ: L = 0,015 Гн.
Пример №2
Колебательный контур состоит из конденсатора емкостью С = 400пФ и катушки индуктивностью L=10 мГн. Определите амплитудное значение силы тока в контуре, если амплитудное значение напряжения на конденсаторе = 500 В.
Решение
Максимальная энергия электростатического поля конденсатора
а максимальная энергия магнитного поля катушки
Так как контур идеальный (R = 0), то его полная энергия не меняется с течением времени. Кроме того, в момент, когда заряд конденсатора максимален, сила тока в катушке равна нулю, а в момент, когда заряд конденсатора равен нулю, сила тока в ней максимальна.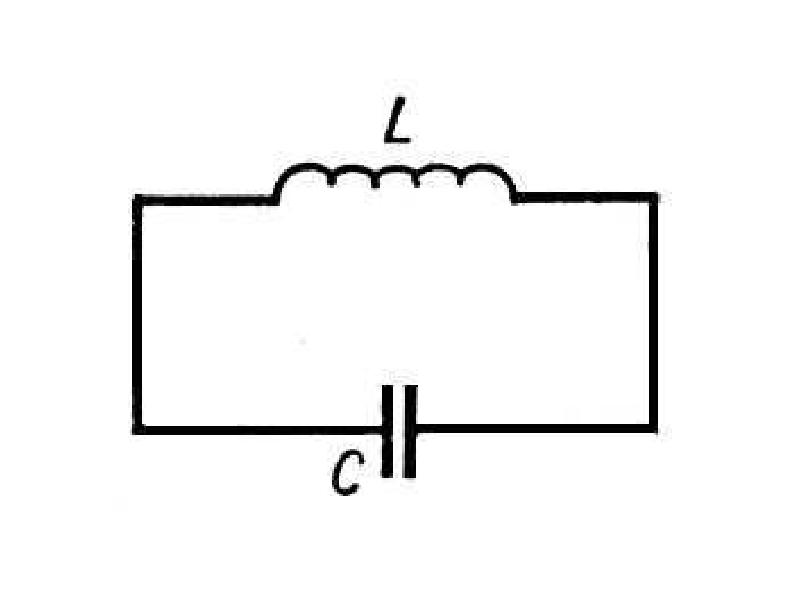 Это позволяет утверждать, что максимальные энергии в конденсаторе и катушке равны: , т. е.
Это позволяет утверждать, что максимальные энергии в конденсаторе и катушке равны: , т. е.
откуда
Ответ: .
Колебательный контур и свободные электромагнитные колебания в контуре
Явление возникновения ЭДС в любом контуре при изменении магнитного потока через поверхность, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в замкнутом проводящем контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре.
Правило Ленца: возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, при котором созданный им магнитный поток через поверхность, ограниченную контуром, стремится компенсировать изменение магнитного потока, вызвавшее данный ток.
Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора электроемкостью и катушки (соленоида) индуктивностью (рис. 29, а), называемую идеальным колебательным контуром или -контуром. Электрическое сопротивление идеального контура считают равным нулю Следовательно, идеальный колебательный контур является упрощенной моделью реального колебательного контура.
Электрическое сопротивление идеального контура считают равным нулю Следовательно, идеальный колебательный контур является упрощенной моделью реального колебательного контура.
Подключив (при помощи ключа источник тока, зарядим конденсатор до напряжения сообщив ему заряд (рис. 29, б). Следовательно, в начальный момент времени конденсатор заряжен так, что на его обкладке 1 находится заряд а на обкладке 2 — заряд При этом электростатическое поле, создаваемое зарядами обкладок конденсатора, обладает энергией
Рассмотрим процесс разрядки конденсатора в колебательном контуре. После соединения заряженного конденсатора с катушкой (при помощи ключа (рис. 30) он начнет разряжаться, так как под действием электрического поля, создаваемого зарядами на обкладках конденсатора, свободные электроны будут перемещаться по цепи от отрицательно заряженной обкладки к положительно заряженной. На рисунке 30 стрелкой показано начальное направление тока в электрической цепи.
Таким образом, в контуре появится нарастающий по модулю электрический ток, сила которого будет изменяться с течением времени (рис. 31, а). Но мгновенная разрядка конденсатора невозможна, так как изменение магнитного поля катушки, создаваемое нарастающим по модулю током, вызывает возникновение вихревого электрического поля. Действительно, в катушке индуктивности возникнет изменяющийся во времени магнитный поток, который вызовет появление ЭДС самоиндукции. Согласно правилу Ленца ЭДС самоиндукции стремится противодействовать вызвавшей ее причине, т. е. увеличению силы тока по модулю.
31, а). Но мгновенная разрядка конденсатора невозможна, так как изменение магнитного поля катушки, создаваемое нарастающим по модулю током, вызывает возникновение вихревого электрического поля. Действительно, в катушке индуктивности возникнет изменяющийся во времени магнитный поток, который вызовет появление ЭДС самоиндукции. Согласно правилу Ленца ЭДС самоиндукции стремится противодействовать вызвавшей ее причине, т. е. увеличению силы тока по модулю.
Вследствие этого модуль силы тока в колебательном контуре будет в течение некоторого промежутка времени плавно возрастать от нуля до максимального значения определяемого индуктивностью катушки и электроемкостью конденсатора (рис. 31, б).
При разрядке конденсатора энергия его электростатического поля превращается в энергию магнитного поля катушки с током. Согласно закону сохранения энергии суммарная энергия идеального колебательного контура остается постоянной с течением времени (уменьшение энергии электростатического поля конденсатора равно увеличению энергии магнитного поля катушки):
где — мгновенное значение заряда конденсатора и — сила тока в катушке в некоторый момент времени после начала разрядки конденсатора.
В момент полной разрядки конденсатора сила тока в катушке достигнет своего максимального по модулю значения (см. рис. 31, б). В соответствии с законом сохранения энергии запасенная в конденсаторе энергия электростатического поля перейдет в энергию магнитного поля, запасенную в этот момент в катушке:
После разрядки конденсатора сила тока в катушке начинает убывать по модулю. Это также происходит не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создает индукционный ток. Он имеет такое же направление, как и уменьшающийся по модулю ток в цепи, и поэтому «поддерживает» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезаряжает конденсатор до начального напряжения но знак заряда на каждой обкладке оказывается противоположным знаку начального заряда. Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения При этом его обкладка, первоначально заряженная положительно, будет заряжена отрицательно. Далее процесс повторится с той лишь разницей, что электрический ток в ко туре будет проходить в противоположном направлении, что отражено на рисунке 31, а.
Далее процесс повторится с той лишь разницей, что электрический ток в ко туре будет проходить в противоположном направлении, что отражено на рисунке 31, а.
Таким образом, в идеальном -контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без пополнения энергии от внешних источников.
Таким образом, существование свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора, вызванной возникновением ЭДС самоиндукции в катушке. Заметим, что заряд конденсатора и сила тока в катушке достигают своих максимальных значений в различные момента времени (см. рис. 31 а, б).
Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальным значениям заряда на каждой из обкладок), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Получим формулу для периода свободных электромагнитных колебаний в контуре, используя закон сохранения энергии. Поскольку полная энергия идеального -контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство:
Процессы, происходящие в колебательном контуре, аналогичны колебаниям пружинного маятника. Для полной механической энергии пружинного маятника в любой момент времени:
где — жесткость пружины, — масса груза, — проекция смещения тела от положения равновесия, — проекция его скорости на ось
Период его колебаний:
Проанализируем соотношения (1) и (2). Видно, что энергия электростатического поля конденсатора является аналогом потенциальной энергии упругой деформации пружины Соответственно, энергия магнитного поля катушки которая обусловлена упорядоченным движением зарядов, является аналогом кинетической энергии груза Следовательно, аналогом координаты пружинного маятника при колебаниях в электрическом контуре является заряд конденсатора Тогда, соответственно, аналогом проекции скорости груза будет сила тока в колебательном контуре, поскольку сила тока характеризует скорость изменения заряда конденсатора с течением времени.
Следуя проведенной аналогии, заменим в формуле для периода колебаний пружинного маятника массу на индуктивность и жесткость тогда для периода свободных колебаний в -контуре получим формулу:
которая называется формулой Томсона.
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).
Для наблюдения и исследования электромагнитных колебаний применяют электронный осциллограф, на экране которого получают временную развертку колебаний (рис. 32).
Зависимость заряда конденсатора от времени имеет такой же вид, как и зависимость координаты (проекции смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону изменяются сила тока (но с другой начальной фазой) в цепи и напряжение на конденсаторе.
Для определения начальной фазы и максимального заряда необходимо знать заряд конденсатора и силу тока в катушке в начальный момент времени
Отметим, что колебательный контур, в котором происходит только обмен энергией между конденсатором и катушкой, называется закрытым.
Полная энергия идеального колебательного контура с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется. Реальный колебательный контур всегда имеет некоторое электрическое сопротивление которое обусловлено сопротивлением катушки и соединительных проводов. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они будут происходить сколь угодно долго.
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без учета трения, а механическим аналогом реального колебательного контура — пружинный маятник с учетом трения.
Пример решения задачи:
Идеальный колебательный контур состоит из конденсатора емкостью пФ и катушки индуктивностью мГн. Определите максимальное значение силы тока в контуре, если максимальное значение напряжения на конденсаторе
Дано:
Решение
Максимальная энергия электростатического поля конденсатора:
а максимальная энергия магнитного поля катушки:
Так как контур идеальный то его полная энергия сохраняется с течением времени. По закону сохранения энергии т. е.
По закону сохранения энергии т. е.
Отсюда
Ответ:
Колебательный контур – Физическая энциклопедия
КОЛЕБАТЕЛЬНЫЙ КОНТУР – электрич. цепь, содержащая индуктивность L, ёмкость С и сопротивление R, в к-рой могут возбуждаться электрич. колебания (рис. 1).
К. к.- электрич. осциллятор,
один из осн. элементов радиотехн. систем. Различают линейные и нелинейные
К. к. В линейном К. к. его параметры L, С и Я не зависят от интенсивности
колебаний и период колебаний не зависит от амплитуды (изохронность колебаний).
При отсутствии потерь (R=0) в линейном К. к. происходят свободные гармонические
колебания с частотой (ф-ла Томпсона). Электрич. энергия колебаний сосредоточивается в ёмкости Wэ=
=,
а магнитная – в катушке индуктивности Wм= =. Периодически с периодом происходит преобразование
электрич. энергии в магнитную, а затем обратно, так что полная энергия системы
энергии в магнитную, а затем обратно, так что полная энергия системы
где t0–
нач. момент зарядки конденсатора, q – заряд на конденсаторе.
В реальных К. к. из-за
наличия потерь при 0<R<
(где
устанавливаются затухающие колебания с частотой
и амплитудой, пропорциональной ,
где
– затухание контура. Качество К. к. характеризуется его добротностью Q =
=. При R> в К. к. колебания отсутствуют и происходит апериодич. процесс разряда конденсатора
через катушку индуктивности.
При включении в линейный
К. к. генератора с переменной эдс
в нём устанавливаются вынужденные колебания с частотой .
Напр., при по-следоват. включении эдс амплитуда колебаний напряжения V на
конденсаторе, определяемая соотношением
зависит не только от амплитуды
внеш.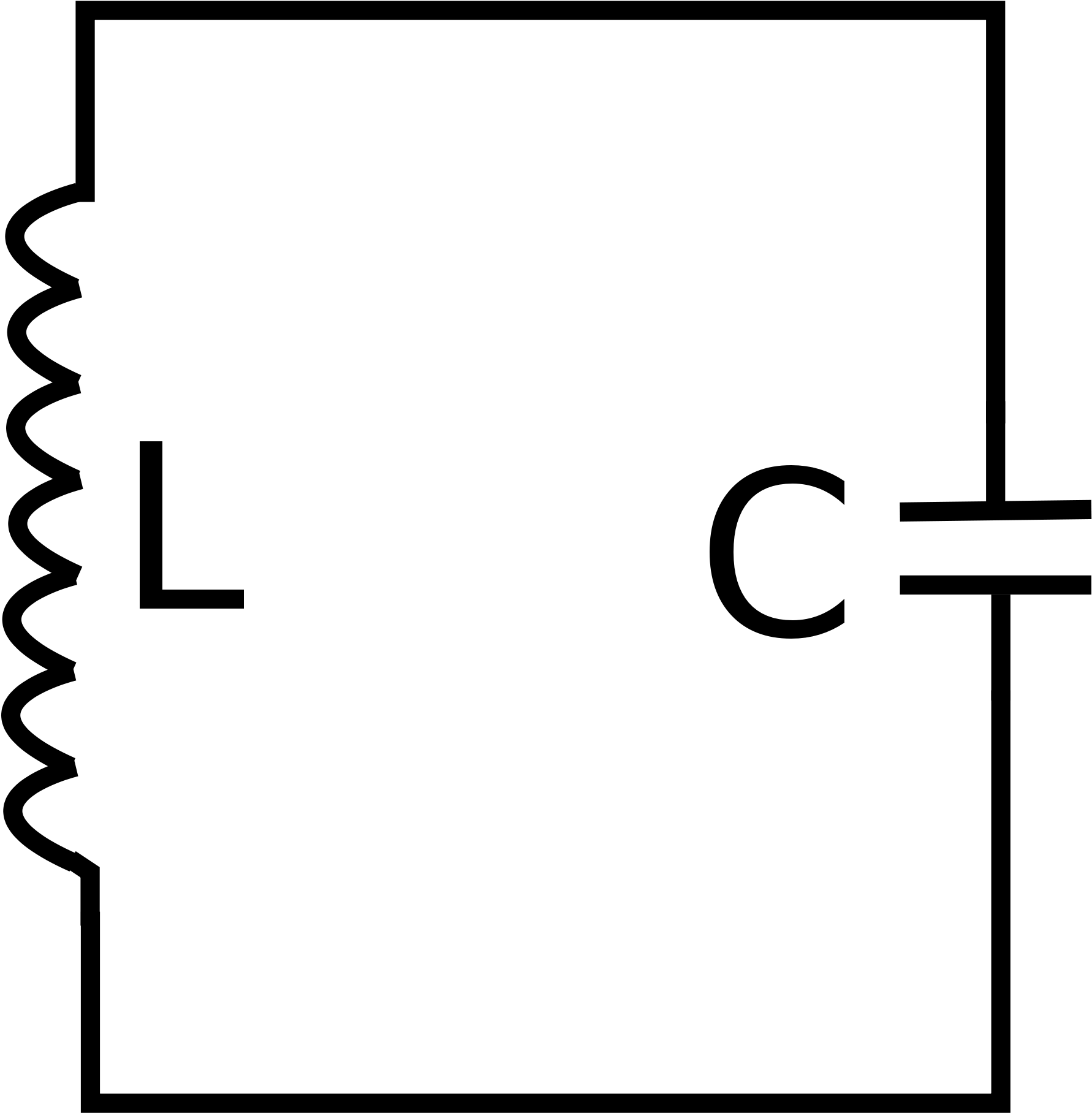 эдс, но и от её частоты .
Зависимость амплитуды колебаний в К. к. от
наз. резонансной характеристикой контура (рис. 2). При
принимает макс. значение, в Q раз превышающее амплитуду внеш. силы Е0. Величину
наз. полосой пропускания К. к. На резонансной характеристике – это область частот
вблизи ,
соответствующая значению амплитуды .
Резонансные свойства К. к. позволяют выделить из множества колебаний те, частоты
которых близки к .
Именно это свойство (избирательность) К. к. используется на практике.
эдс, но и от её частоты .
Зависимость амплитуды колебаний в К. к. от
наз. резонансной характеристикой контура (рис. 2). При
принимает макс. значение, в Q раз превышающее амплитуду внеш. силы Е0. Величину
наз. полосой пропускания К. к. На резонансной характеристике – это область частот
вблизи ,
соответствующая значению амплитуды .
Резонансные свойства К. к. позволяют выделить из множества колебаний те, частоты
которых близки к .
Именно это свойство (избирательность) К. к. используется на практике.
Линейный К. к. описывается
дифференц. ур-нием вида
т. е. является (при Е0=0)системой с одной степенью свободы. Незатухающим колебаниям в К. к. без потерь
(=0, Е0=0) на фазовой плоскости
соответствуют замкнутые интегральные кривые линейного центра (рис. 3) – вложенные
друг в друга эллипсы или, в частном случае, окружности.
В нелинейном К. к., когда
заряд на конденсаторе g – нелинейная ф-ция напряжения или индуктивность
катушки L – нелинейная ф-ция тока (напр., в случае конденсатора с сегнетоэлектриком
и индуктивности с ферромагн. сердечником), колебания будут негармоническими
и незатухающим колебаниям на фазовой плоскости соответствуют замкнутые интегральные
кривые, период обращения по к-рым зависит от энергии, запасённой в К. к.; при
этом частота колебаний становится зависимой от амплитуды колебаний.
к., когда
заряд на конденсаторе g – нелинейная ф-ция напряжения или индуктивность
катушки L – нелинейная ф-ция тока (напр., в случае конденсатора с сегнетоэлектриком
и индуктивности с ферромагн. сердечником), колебания будут негармоническими
и незатухающим колебаниям на фазовой плоскости соответствуют замкнутые интегральные
кривые, период обращения по к-рым зависит от энергии, запасённой в К. к.; при
этом частота колебаний становится зависимой от амплитуды колебаний.
С помощью К. к. часто моделируют
более сложные физ. системы, напр. резонаторы с одной эфф. степенью свободы.
Лит.: Андронов А.
А., Витт А. А., Хайкин С. Э., Теория колебаний, [3 изд.], М., 1981; Основы теории
колебаний, М., 1978; Рабинович М. И., Т р у б е ц-к о в Д. И., Введение в теорию
колебаний и волн, М., 1984.
В. Н. Белых.
Предметный указатель >>
Свободные электромагниные колебания в контуре, катушка, конденсатор, сохранение энергии.
 Курсы по физике
Курсы по физикеТестирование онлайн
Электромагнитные колебания. Основные понятия
Электромагнитные колебания
Свободные электромагнитные колебания
Рассмотрим электрическую цепь, состоящую из катушки индуктивностью L и конденсатора электроемкостью C. Если предварительно зарядить конденсатор (рис. a), то получим колебательный контур (рис. б).
1) В начальный момент времени конденсатор имеет максимальный заряд, обладает максимальной энергией WC.
2) В следующий момент времени конденсатор начинает разряжаться. В цепи появляется ток. По мере разрядки конденсатора ток в цепи и в катушке нарастает. Из-за явления самоиндукции это происходит не мгновенно. Энергия катушки WL становится максимальной.
3) Электрические заряды вновь накапливаются на конденсаторе, но обкладка конденсатора, первоначально заряженная положительно, будет заряжена отрицательно. Энергия конденсатора максимальная.
Энергия конденсатора максимальная.
4) Конденсатор разряжается, но ток протекает уже в обратном направлении.
Этот процесс будет повторяться снова и снова. Возникнут электромагнитные колебания. Если отсутствуют потери (R=0), то сила тока, заряд и напряжение со временем изменяются по гармоническому закону.
Период колебаний. Формула Томсона
Наименьший промежуток времени, в течение которого происходит переход зарядов с одной обкладки конденсатора на другую и обратно, называется периодом свободных электромагнитных колебаний.
Энергия колебательного контура
Если пренебречь потерями (R=0), то полная энергия колебательного контура остается постоянной. Выполняется закон сохранения энергии.
Мгновенное значение силы тока в катушке
Мгновенное значение ЭДС самоиндукции
Краткий конспект подготовки к ЗНО по физике №31 “Электромагнитные колебания (ЭМК). Трансформатор.”
Конспект 31. Электромагнитные колебания (ЭМК). Трансформатор.
Электромагнитные колебания (ЭМК). Трансформатор.
Тема: Электромагнитные колебания и волны
1. Электромагнитные колебания. Колебательный контур
Определение. Электромагнитные колебания (ЭМК):
1) Процесс периодического изменения и взаимопревращения энергий электрического и магнитного полей;
2) Взаимосвязанные колебания вектора напряженности электрического поля и индукции магнитного поля;
3) Периодические изменения напряжения и силы тока в электрической цепи.
Замечание. Наиболее наглядно процесс ЭМК демонстрируется на принципе работы колебательного контура.
Определение. Идеальный колебательный контур – цепь без учета активного сопротивления проводов, состоящая из катушки индуктивности и конденсатора, в которой могут возникнуть свободные ЭМК.
Определение. Свободные электромагнитные колебания в колебательном контуре – это колебания, которые возникают и поддерживаются за счет энергии, которая однократно подается в колебательный контур.
Замечания:
1) Явление самоиндукции в катушке – причина поддержания процесса ЭМК;
2) Во время ЭМК периодически изменяются все электропараметры, которые характеризуют электромагнитное поле в контуре: u,q,i – мгновенные значения напряжения и заряда на конденсаторе и тока на катушке соответственно;
3) Начало свободных ЭМК обычно связано с зарядкой конденсатора, который замыкается на катушку;
4) ЭМК подчиняются тем же гармоническим законам, что и рассмотренные ранее механические колебания.
– формула Томсона (период колебаний в колебательном контуре), с
Превращения энергии в колебательном контуре:
1) t=0: на конденсаторе и ; на катушке и i=0;
2) : на конденсаторе и u=0; на катушке и ;
3) : на конденсаторе и ; на катушке и i=0; полярность зарядки конденсатора обратная;
4) : на конденсаторе и u=0; на катушке и ; направление тока обратное;
5) t=T: на конденсаторе и ; на катушке и i=0.
– закон сохранения полной энергии идеального колебательного контура
– закон сохранения энергии идеального колебательного контура между ее максимальными значениями
Где – максимальное напряжение на конденсаторе, В
– максимальная сила тока в катушке, А
– закон гармонических колебаний напряжения на пластинах конденсатора
– закон гармонических колебаний заряда на пластинах конденсатора
– закон гармонических колебаний силы тока на катушке
Определение. Вынужденные ЭМК – периодические изменения напряжения и силы тока в цепи под действием внешней периодически изменяющейся электродвижущей силы.
Замечание. Как правило, внешними источниками ЭДС в электрических цепях являются генераторы переменного тока.
Определение. Генератор переменного тока – электрическая машина, которая является источником тока с принципом действия, основанным на явлении электромагнитной индукции. В нем происходит преобразование механической энергии в электрическую. В простейшем случае генератор представлен замкнутой катушкой, которая вращается в постоянном магнитном поле (подробнее смотри в конспекте № 28).
В нем происходит преобразование механической энергии в электрическую. В простейшем случае генератор представлен замкнутой катушкой, которая вращается в постоянном магнитном поле (подробнее смотри в конспекте № 28).
Определение. Электрический резонанс – явление резкого увеличения амплитуды колебаний силы тока, при совпадении собственной частоты колебаний контура с частотой внешней периодически изменяющейся ЭДС.
Примеры применения электрического резонанса: настройка радиоприемника на определенную частоту электромагнитной волны, микротоковая медицинская терапия и пр.
Замечание. Средние значения переменного тока называются действующими.
– действующее значение силы переменного тока, А
– действующее значение напряжения переменного тока, В
2. Трансформатор
Определение. Трансформатор – электромагнитное устройство для преобразования значений напряжения и силы тока в цепях переменного тока, обычно представляет собой две катушки (обмотки) одетые на один общий сердечник. Принцип работы основан на явлении электромагнитной индукции.
Принцип работы основан на явлении электромагнитной индукции.
Замечание. Идеальный трансформатор – трансформатор, в котором сопротивлением обмоток можно пренебречь.
– закон трансформации в идеальном трансформаторе
Где k –коэффициент трансформации, ед
– напряжения соответственно в первичной и вторичной обмотках, В
– силы тока соответственно в первичной и вторичной обмотках, А
– количество витков соответственно в первичной и вторичной обмотках, ед
Виды трансформаторов:
1) Понижающий: , ;
2) Повышающий: , 1.
– закон трансформации в реальном трансформаторе
Где – ЭДС соответственно в первичной и вторичной обмотках, В
– КПД реального трансформатора, ед или %
Замечание. КПД идеального трансформатора равно 100 % (или 1).
Основные потери энергии в реальном трансформаторе:
1) Нагрев обмоток;
2) Токи Фуко, которые возникают вследствие явления электромагнитной индукции в сердечниках, усиливающих магнитное поле. {N-1} \ Delta z_n \; е (z_n) \; = \; \ Delta z_1 \, f (z_1) + \ Delta z_2 \, f (z_2) + \ cdots + \ Delta z_ {N-1} \, f (z_ {N-1}).{N-1} \ Delta z_n \; f (z_n). \] Символ \ (\ Gamma \) в нижнем индексе знака интеграла указывает, что интеграл имеет место по контуру \ (\ Gamma \). При определении контурного интеграла всегда необходимо указывать, по какому контуру мы интегрируем. Это аналогично указанию конечных точек интервала, по которому нужно выполнить определенный действительный интеграл. В сложном случае переменная интегрирования \ (z \) лежит в двумерной плоскости (комплексной плоскости), а не на прямой; поэтому мы не можем просто указать две конечные точки, а должны указать весь контур.
{N-1} \ Delta z_n \; е (z_n) \; = \; \ Delta z_1 \, f (z_1) + \ Delta z_2 \, f (z_2) + \ cdots + \ Delta z_ {N-1} \, f (z_ {N-1}).{N-1} \ Delta z_n \; f (z_n). \] Символ \ (\ Gamma \) в нижнем индексе знака интеграла указывает, что интеграл имеет место по контуру \ (\ Gamma \). При определении контурного интеграла всегда необходимо указывать, по какому контуру мы интегрируем. Это аналогично указанию конечных точек интервала, по которому нужно выполнить определенный действительный интеграл. В сложном случае переменная интегрирования \ (z \) лежит в двумерной плоскости (комплексной плоскости), а не на прямой; поэтому мы не можем просто указать две конечные точки, а должны указать весь контур.
Также обратите внимание, что при определении контура \ (\ Gamma \) мы должны указать не только кривую в комплексной плоскости, но также направление, по которому следует пересечь эту кривую. Если интегрировать по той же кривой в противоположном направлении, значение контурного интеграла меняет знак (это похоже на перестановку конечных точек определенного действительного интеграла).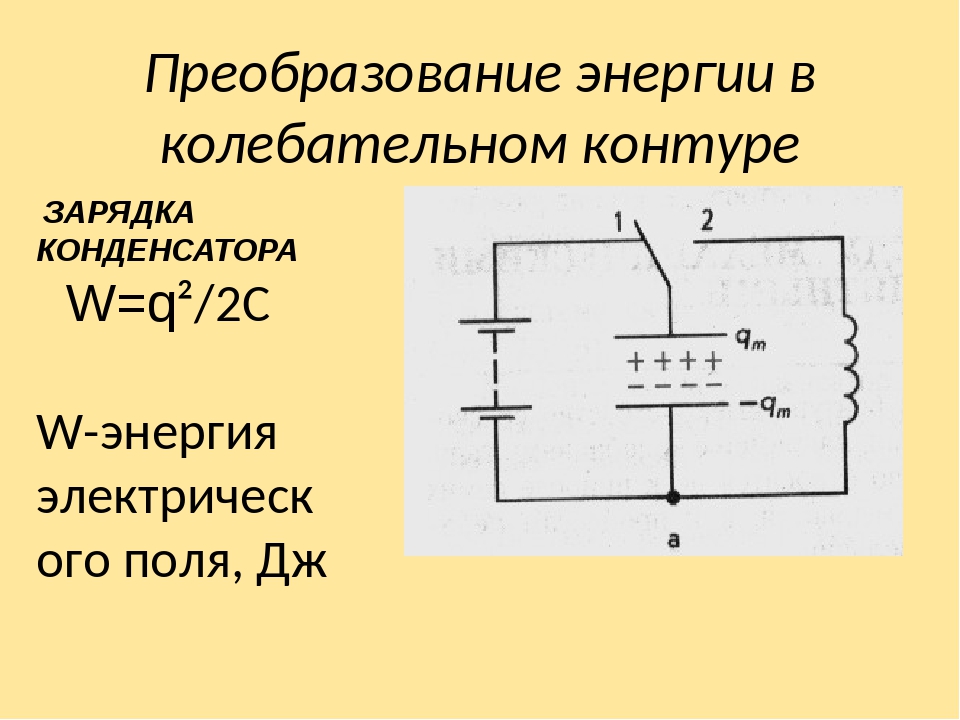
Примечание
Контурный интеграл обычно нельзя интерпретировать как площадь под кривой, в отличие от определенного действительного интеграла.В частности, контур не следует ошибочно интерпретировать как график подынтегрального выражения! Всегда помните, что в контурном интеграле подынтегральное выражение \ (f (z) \) и переменная интегрирования \ (z \) являются комплексными числами.
Более того, понятие неопределенного интеграла не может быть эффективно обобщено на комплексный случай.
Контурный интеграл по параметрической кривой
Простые контурные интегралы могут быть вычислены с помощью параметризации контура . Рассмотрим контурный интеграл \ [\ int_ \ Gamma \, dz \; f (z), \], где \ (f \) – комплексная функция комплексной переменной, а \ (\ Gamma \) – заданный контур.Как обсуждалось в разделе 4.6, мы можем описать траекторию на комплексной плоскости с помощью комплексной функции вещественной переменной , \ (z (t) \): \ [\ Gamma \ Equiv \ Big \ {z (t) \ ; \ Большой | \; t_1
Solutions Physics 122 Промежуточный экзамен № 1
Solutions Physics 122 Промежуточный экзамен № 1Solutions Physics 122 Промежуточный экзамен № 1
Проблема 1
Рисунок Задача 1
Рассмотрим рисунок выше, на котором показано электрическое поле, генерируемое двумя точечными обвинениями.Следующие утверждения могут быть сделаны в соединение с рисунком:
- Направление электрического поля в определенной точке равно
по касательной к силовой линии.
 На букву b указывает электрическое поле.
прямо вверх, а значит, не прямо к Q2.
На букву b указывает электрическое поле.
прямо вверх, а значит, не прямо к Q2. - Величина электрического поля пропорциональна плотность силовых линий. На основе заданной конфигурации поля линий, видно, что плотность силовых линий в точке ‘c’ равна не равно нулю, и, следовательно, электрическое поле в точке с не равно нулю. равняется нулю.
- Плотность силовых линий в точке ‘a’ выше, чем плотность линий поля в точке ‘c’. Таким образом, величина электрического поля в ‘a’ больше, чем величина электрического поля в ‘c’.
- Линейный интеграл электрического поля вдоль пути между ‘e’ и ‘c’ положительны (электрическое поле указывает на одно и то же направление как смещение). Изменение потенциала между ‘e’ и ‘c’ равны противоположности линейного интеграла от электрическое поле и, следовательно, отрицательное.Таким образом, мы заключаем, что потенциал в точке «c» меньше, чем потенциал в точке «e».
- Электрическое поле в точке «d» указывает прямо вниз («юг»).

- Количество силовых линий, выходящих из положительного заряда пропорциональна величине положительного заряда. В количество силовых линий, заканчивающихся отрицательным зарядом, пропорционально величине отрицательного заряда. Есть 18 линий поля выходящий из положительного заряда Q1 и 13 силовых линий, заканчивающихся на отрицательном заряде Q2.Это, | Q1 | > | Q2 | и Q1 + Q2> 0 С.
Проблема 2
Рисунок Задача 2
- Электрическое поле в любой точке направлено перпендикулярно к эквипотенциальным контурам. Электрическое поле в точке ‘e’ будет таким образом, он должен быть направлен перпендикулярно контуру 221,7 В. Электрический поле будет направлено из областей с более высоким потенциалом в области с более низким потенциалом. Таким образом, направление в точке «е» будет от 312.Контур 1 В.
- Заряд, высвобождающийся в состоянии покоя на любом из показанных контуров, будет
почувствуете ненулевую электрическую силу, и в результате начнет
двигаться.
 Для положительного заряда движение будет в направлении области
более низкого потенциала; для отрицательного заряда движение будет
к региону с более высоким потенциалом.
Для положительного заряда движение будет в направлении области
более низкого потенциала; для отрицательного заряда движение будет
к региону с более высоким потенциалом. - Потенциал в точке «a» равен -357,9 В. Потенциал в точке «b» равен 16,3 В и, следовательно, выше, чем потенциал в точке «a».
- Потенциал вблизи положительного заряда будет положительный.Потенциал вблизи отрицательного заряда будет отрицательным. Диаграмма, показанная выше, показывает, что там два положительных заряда и один отрицательный заряд.
- Потенциал в точке «d» равен 118,1 В. Потенциал в точке «c» равен
также 118,1 В. Таким образом, нет разницы потенциалов между ‘d’
и ‘c’, и, как следствие, работа не выполняется, когда вы двигаетесь
заряд от «d» до «c». Примечание: вы также могли заключить
это, наблюдая, что электрическая сила перпендикулярна
траекторию, пока вы двигаетесь по контурной линии, и, таким образом,
работа, совершаемая этой силой, равна 0 Дж.

- Контур 828,9 В вокруг заряда в точке (0,0) находится ближе, чем контурная линия 828,9 В вокруг заряд на (-5,5). Поскольку потенциал зависит от отношения q / r близко к заряду, более высокий заряд будет производить такой же потенциал при большем r. Таким образом, заряд в точке (0,0) больше, чем заряд при (-5,5).
Проблема 3
Рассмотрим бесконечный прямоугольный прямоугольник высотой 2d как гауссовский поверхности, и предположим, что заряд Q расположен в центре этой коробки.Используя закон Гаусса, мы можем заключить, что поток через это поле равно
Из-за симметрии задачи половина потока уйдет через верхнюю бесконечную плоскость коробки, и половина ее будет пройти через нижнюю бесконечную плоскость ящика. Таким образом, поток через каждую плоскость равно
Проблема 4
Рисунок Задача 4
Эту задачу можно решить, используя принцип суперпозиции.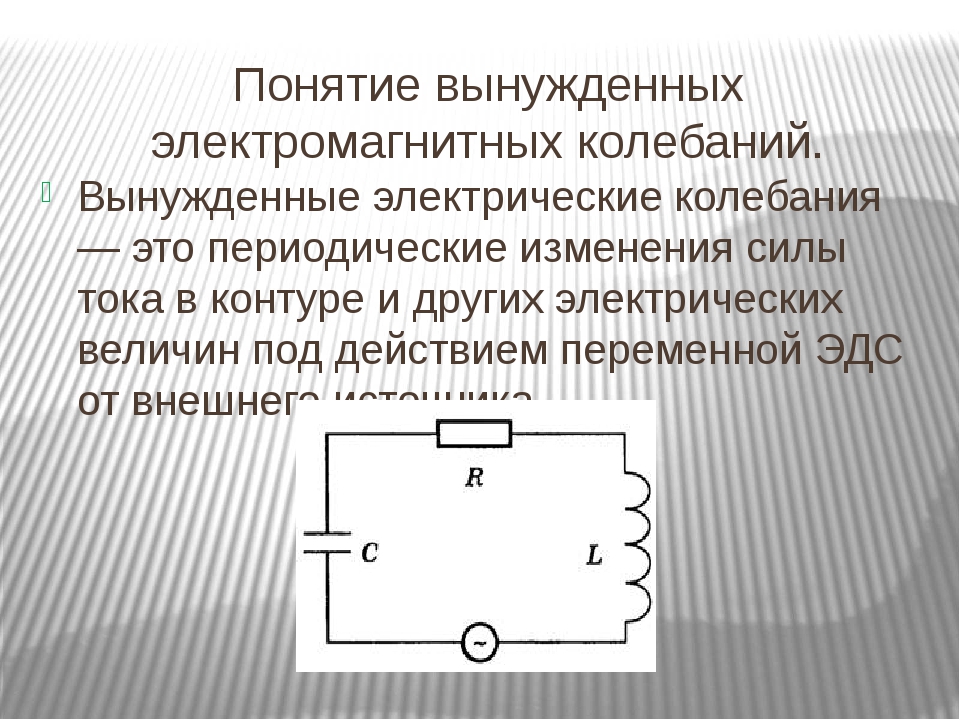 Рассмотрим сначала твердую сферу радиуса R и заряда Q.
поле, создаваемое этим распределением заряда в точке P, равно
к
Рассмотрим сначала твердую сферу радиуса R и заряда Q.
поле, создаваемое этим распределением заряда в точке P, равно
к
Теперь рассмотрим вторую сферу с плотностью заряда, идентичной по величине, но противоположного знака, и диаметром R, расположенным на расстояние R / 2 от центра твердой сферы. Электрический поле, создаваемое этой сферой в точке P, равно
Суперпозиция этих двух зарядовых распределений дает распределение заряда, показанное в этой задаче.Электрическое поле порожденная этим распределением заряда, таким образом, является суперпозицией электрических полей, создаваемых каждым из этих двух распределений заряда раздельно.
Проблема 5
Электрические поля внутри внутренней оболочки и вне внешние оболочки равны нулю N / C. Электрическое поле между это оболочки точечного заряда Q (где Q равно заряд на внутренней гильзе), расположенный в центре гильз:
Соответствующая плотность энергии u (r) равна
Общая энергия, запасенная в системе, может быть получена путем интегрирования плотность энергии по объему между оболочками:
Проблема 6
Рисунок Задача 6
Для генерируемого электрического поля можно сделать следующие выводы: конфигурацией заряда, показанной на рисунке:
- Электрическое поле в точке A из-за заряда + q направлено
вправо.
 Электрическое поле в точке А из-за заряда -q
направлен влево. Однако поскольку величина
электрическое поле спадает как 1 / r2, величина поля
в A из-за заряда + q будет больше, чем величина
поле в A из-за заряда -q. Чистое поле в точке А будет
поэтому быть направленным вправо.
Электрическое поле в точке А из-за заряда -q
направлен влево. Однако поскольку величина
электрическое поле спадает как 1 / r2, величина поля
в A из-за заряда + q будет больше, чем величина
поле в A из-за заряда -q. Чистое поле в точке А будет
поэтому быть направленным вправо. - Электрические поля в источнике, обусловленные каждым из зарядов
направлен влево. В точке A две компоненты направлены
в противоположных направлениях, и, кроме того, компонент из-за
заряд -q значительно меньше (из-за зависимости 1 / r2
электрического поля).Величина чистого электрического поля
при A будет, таким образом, меньше, чем величина электрического
поле в начале координат.
- Направление электрического поля по отрицательной оси Y
направлен влево. В любой точке отрицательной оси Y
величина компонентов из-за зарядов + q и -q
будет равно. Направление этих компонентов таково, что
их вертикальные компоненты сокращаются, и сетевое поле направлено
параллельно оси x влево.

- Электрическое поле в точке (-r, 0) из-за заряда -q направлено
вправо. Электрическое поле в (-r, 0) из-за + q
заряд направлен влево. Однако поскольку величина
электрического поля спадает как 1 / r2, величина
поле в (-r, 0) из-за заряда -q будет больше, чем
величина поля в (-r, 0) из-за заряда + q. Сеть
поле в (-r, 0) поэтому будет направлено вправо.
- Направление электрического поля по положительной оси Y
направлен влево.В любой точке положительной оси Y
величина компонентов из-за зарядов + q и -q
будет равно. Направление этих компонентов таково, что
их вертикальные компоненты сокращаются, и сетевое поле направлено
параллельно оси x влево.
- Электрические поля в источнике, обусловленные каждым из зарядов направлен влево. Чистое электрическое поле в начале координат таким образом, также направлен влево.
Проблема 7
Рисунок Проблема 7
В силу симметрии задачи сразу можно сделать вывод
что чистое электрическое поле на оси кольца направлено
вдоль этой оси (см. рисунок).Рассмотрим небольшой сегмент
кольцо с зарядом dQ. Электрическое поле создается на оси
кольцо этим зарядом dQ равно
рисунок).Рассмотрим небольшой сегмент
кольцо с зарядом dQ. Электрическое поле создается на оси
кольцо этим зарядом dQ равно
Составляющая поля, направленная вдоль оси кольца равно
Таким образом, полное электрическое поле всего кольца равно к
Задача уточняет плотность заряда кольца. С использованием заданной плотности делаем вывод, что
Проблема 8
Мы можем наиболее просто вычислить потенциальную энергию системы. используя следующее уравнение:
Потенциал на z1 из-за двух других зарядов равен
Потенциал на z2 из-за двух других зарядов равен
Потенциал на z3 из-за двух других зарядов равен
Таким образом, полная потенциальная энергия системы равна
.Энергетическая карта Ван-дер-Ваальса, описывающая симметричную упаковку орторомбической углеводородной цепи Pbnm
Энергетическая контурная карта Ван-дер-Ваальса, описывающая симметрию упаковки орторомбической углеводородной цепи
Pbnm rsc.org/schema/rscart38″> Упаковка длинных алифатических цепочек классифицирована расчетами статической энергии решетки.Для ромбической пространственная группа 62 ( Pbnm ), энергия Ван-дер-Ваальса субэлементов с систематически изменяемыми постоянными решетки a SC и b SC был минимизирован путем изменения двугранного угла между плоскостями скелета фрагментов зигзагообразной цепи (–CH 2 –CH 2 -). Рассчитанные энергии относятся к бесконечным алифатическим цепочкам из-за неограниченной периодичности фрагменты в направлении позвоночника C – C.Чтобы облегчить применение критерия энергии в процесс индексации на основе проб и ошибок, результирующий набор из 383 энергетических данных был нанесен на график в виде диаграммы Ван-дер-Ваальса. карта контура энергии, проецируемая на плоскость обратного пространства, которое определяется взаимными интервалами с 110 с . с 020 . Абсолютный и локальный минимум энергии соответствуют разным режимам упаковки орторомбической
подъячейки.Энергетическая гиперповерхность разделена линиями, соответствующими особой геометрии ячеек, на разные области.
Линии локализованы вблизи седловых точек энергетической поверхности. Впервые геометрические и энергетические соотношения между различными режимами упаковки с симметрией Pbnm четко продемонстрированы с помощью расчетов энергии Ван-дер-Ваальса.
На основе этих расчетов предлагается новая номенклатура режимов упаковки цепей.
с 020 . Абсолютный и локальный минимум энергии соответствуют разным режимам упаковки орторомбической
подъячейки.Энергетическая гиперповерхность разделена линиями, соответствующими особой геометрии ячеек, на разные области.
Линии локализованы вблизи седловых точек энергетической поверхности. Впервые геометрические и энергетические соотношения между различными режимами упаковки с симметрией Pbnm четко продемонстрированы с помощью расчетов энергии Ван-дер-Ваальса.
На основе этих расчетов предлагается новая номенклатура режимов упаковки цепей.У вас есть доступ к этой статье
Подождите, пока мы загрузим ваш контент. ..
Что-то пошло не так. Попробуйте снова?
..
Что-то пошло не так. Попробуйте снова?(PDF) Спектр потоков на дискретной паре контуров
Вторая международная конференция по физике, математике и статистике
IOP Conf.Серия: Физический журнал: конф. Series 1324 (2019) 012001
IOP Publishing
doi: 10.1088 / 1742-6596 / 1324/1/012001
7
Если y = 0 или y = 1, то не существует неотрицательного целого числа y, удовлетворяющего уравнение 𝑁𝑦
−
𝑁𝑥
= 𝑁
− 𝑀
. Если 𝑦 = 𝑦
= 2, то число 𝑥 = 𝑥
= 3 удовлетворяет условию, и,
= 10.
Таким образом, имеем g2 = 1, j2 = −1.Условия теоремы 2 выполнены. Следовательно, v1 = 3/5, v2 = 1.
Следовательно, v1 = 3/5, v2 = 1.
Теорема 3. Пусть условие самоорганизации (2) не выполняется и неравенства j1 <0, j2 ≥
0; тогда существует единственный спектральный цикл, и этот цикл содержит состояние (N1 – M1, 0). Период
этого спектрального цикла равен 𝑔 + 𝑀
− 𝑗
. Скорости скоплений равны 𝑣 = 1,
= 𝑔
/ (𝑔 +
𝑀 − 𝑗
).
Мы получим теорему 3 из теоремы 2, если перенумеровать контуры.
Теорема 4. Пусть выполнены неравенства j1 <0, j2 <0. Тогда есть уникальный спектральный цикл. Спектр
содержит состояния (0, N1 – M
1) и (N2 – M2, 0). Период спектрального цикла равен
𝑔 + 𝑔
+ 𝑀
+ 𝑀
− | 𝑗 | – | 𝑗 |. Скорости кластеров равны 𝑣 = 1− (𝑀
− | 𝑗 |) / (𝑔 + 𝑔
+
𝑀 + 𝑀
− | 𝑗 | – | 𝑗 |), 𝑣 = 1− (𝑀
– | 𝑗 |) / (𝑔 + 𝑔
+ 𝑀
+ 𝑀
− | 𝑗 | – | 𝑗 |)
Доказательство. Поскольку условие самоорганизации не выполняется, система не приводит к состоянию
Поскольку условие самоорганизации не выполняется, система не приводит к состоянию
свободного движения. Следовательно, в соответствии с леммой 1 система приводит к состоянию, принадлежащему множеству
A1, в течение конечного времени, и после этого система приводит к состоянию (0, N2 – M2), или система дает
в состоянии, принадлежащем множеству A2, в течение конечного времени, а затем в состоянии (N1 – M
1, 0). В
в соответствии с леммой 5-7 из состояния (0, N2 – M2) в течение конечного времени система переходит в состояние
, принадлежащее A1.В соответствии с леммами 11-13 из состояния (N1 – M
1, 0) в течение конечного времени система
приводит к состоянию, принадлежащему A2. Следовательно, существует уникальный спектральный цикл, и этот спектральный цикл
содержит состояния (0, N2 – M2) и (N1 – M
1, 0). В спектральном цикле система находится в
состояниях, не принадлежащих множеству A (оба кластера движутся в этих состояниях), в течение + 𝑔
единиц времени система
находится в состояниях, принадлежащих множества (в этих состояниях движется только кластер Cl2), в течение M2− | j1 | time
единиц, а система находится в состояниях, принадлежащих множеству A2 (только кластер Cl1 перемещается на
в эти состояния), в течение M1− | j1 | единицы времени. Отсюда следует теорема 4.
Отсюда следует теорема 4.
Пример 2. Предположим, что N1 = 10, M
1 = 4, N2 = 5, M2 = 2. В этом случае = −3, 𝑔
=
3, 𝑗 = – 1, 𝑔
= 6, 𝑣
= 10 11
⁄, 𝑣
= 10 11
⁄. Существует уникальный спектральный цикл. Его период равен
до T = 11.
Теорема 5. Пусть выполнены неравенства j1≥ 0, j2 ≥ 0. Тогда есть два спектральных цикла. Один из
этих циклов содержит состояние (0, N2 – M2).Период этого цикла равен 𝑔 + 𝑁
− 𝑗
. В этом цикле
скоростей скоплений равны 𝑣 = 𝑔
/ (𝑔 + 𝑀
− 𝑗
), 𝑣 = 1. Другой цикл содержит состояние
(N1 – M1, 0). Период этого цикла равен 𝑔 + 𝑀
− 𝑗
. В этом цикле скорости скоплений
равны 𝑣 = 𝑔
𝑔 + 𝑀
− 𝑗
⁄, 𝑣
= 1.
Доказательство.В соответствии с леммой 1, в зависимости от начального состояния, система приводит к состоянию
множества A1, а после этого система приводит к состоянию (0, N2 – M2) или состоянию, принадлежащему установить A2,
в течение конечного времени, а затем в состояние (N1 – M1, 0). В соответствии с леммами 5-7, если система
В соответствии с леммами 5-7, если система
находится в состоянии множества, то, возвращаясь к множеству A, система приводит к состояниям, принадлежащим A2 ∪
(0; 0). В этом случае в течение конечного времени система не будет находиться в принадлежащих состояниях, и система будет
только в состоянии, принадлежащем спектральному циклу, содержащему состояние (0, N2 – M2).В этом случае на спектральном цикле
система находится в состояниях, не принадлежащих набору A, в течение единиц времени, а система
находится в состояниях, принадлежащих набору, в течение M2− j1 единиц времени, и следовательно, = 𝑔
/ (𝑔 + 𝑀
− 𝑗
, 𝑣
=
1. В соответствии с леммами 11-13, если система находится в состоянии установить A1, затем, вернувшись к
, установить A, система будет только в состояниях, принадлежащих A1 ∪ (0; 0).Через некоторое время система не будет находиться в
состояниях, принадлежащих, и система будет только в состояниях, принадлежащих спектральному циклу, содержащему состояние
(N1 – M1, 0). В спектральном цикле система находится в состояниях, не принадлежащих множеству A, в течение
В спектральном цикле система находится в состояниях, не принадлежащих множеству A, в течение
𝑔 единиц времени, а система находится в состояниях, принадлежащих множеству, в течение M1− j2 единиц времени, и, следовательно,
𝑣 = 1, 𝑣
= 𝑔
𝑔 + 𝑀
− 𝑗
⁄.
Пример 3. Предположим, что N1 = 4, M1 = 2, N2 = 6, M2 = 2. В этом случае мы имеем 𝑗 = 0, 𝑔
= 4, 𝑗
=
0, 𝑔 = 6, существует два спектральных цикла. В одном из этих циклов скопления движутся со скоростями
𝑣 =
, 𝑣
= 1 3
⁄. Период этих циклов равен T = 6. В другом спектральном цикле скопления
движутся со скоростями 𝑣 = 1, 𝑣
= 3 7
⁄. Период этих циклов равен T = 8.
Фазоуправляемая когерентная динамика одиночного спина при взаимодействии по замкнутому контуру
Грей, Х. Р., Уитли, Р. М. и Страуд, К. Р. Когерентный захват атомных популяций. Опт. Lett. 3 , 218–220 (1978).
Lett. 3 , 218–220 (1978).
ADS Статья Google ученый
Агапьев Б.Д., Горный М.Б., Матисов Б.Г., Рождественский Ю.В. Когерентный захват населенностей в квантовых системах.Успехи УФН 36 (1993). 763–793.
ADS Статья Google ученый
Флейшхауэр, М., Имамоглу, А. и Марангос, Дж. П. Прозрачность, индуцированная электромагнитным полем: оптика в когерентных средах. Ред. Мод. Phys. 77 , 633–673 (2005).
ADS Статья Google ученый
Косачёв Д.В., Матисов Б.Г., Рождественский Ю. В. Когерентные явления в многоуровневых системах с замкнутым контуром взаимодействия. J. Phys. B 25 , 2473–2488 (1992).
ADS Статья Google ученый
Виндхольц, Л. Когерентный захват населенностей в многоуровневых атомных системах. Phys. Scr. 2001 , 81–91 (2001).
Phys. Scr. 2001 , 81–91 (2001).
Артикул Google ученый
Бакл С., Барнетт С., Найт П., Лаудер М. и Пегг Д. Атомные интерферометры. Опт. Acta 33 , 1129–1140 (1986).
ADS Статья Google ученый
Ямамото К., Ичимура К. и Джемма Н. Повышенное и пониженное поглощение за счет квантовой интерференции: твердая система, управляемая радиочастотным полем. Phys. Ред. A 58 , 2460–2466 (1998).
ADS Статья Google ученый
Корсунский Э. А., Лейнфелльнер Н., Хус А., Балущев С. и Виндхольц Л. Фазозависимая прозрачность, индуцированная электромагнитным полем. Phys. Ред. A 59 , 2302–2305 (1999).
ADS Статья Google ученый
Li, H. et al. Электромагнитно индуцированная прозрачность, управляемая микроволновым полем. Phys. Ред. A 80 , 023820 (2009).
Phys. Ред. A 80 , 023820 (2009).
ADS Статья Google ученый
Preethi, T. M. et al. Фазочувствительный микроволновый оптический двойной резонанс в N-системе. EPL Europhys. Lett. 95 , 34005 (2011).
ADS Статья Google ученый
Roushan, P. et al. Киральные токи основного состояния взаимодействующих фотонов в синтетическом магнитном поле. Нат. Phys. 13 , 146–151 (2017).
Артикул Google ученый
Филлипс Д. Ф., Флейшхауэр А., Майр А., Уолсворт Р. Л. и Лукин М. Д. Хранение света в атомном паре. Phys. Rev. Lett. 86 , 783–786 (2001).
ADS Статья Google ученый
Ванье, Дж. Атомные часы, основанные на когерентном захвате населения: обзор. Заявл. Phys. B 81 , 421–442 (2005).
Заявл. Phys. B 81 , 421–442 (2005).
ADS Статья Google ученый
Чирак, Дж. И., Золлер, П., Кимбл, Х. Дж. И Мабучи, Х. Квантовый перенос состояний и распределение запутанности между удаленными узлами в квантовой сети. Phys. Rev. Lett. 78 , 3221–3224 (1997).
ADS Статья Google ученый
Нортап Т. Э. и Блатт Р. Квантовая передача информации с помощью фотонов. Нат. Фотон. 8 , 356–363 (2014).
Шор, Б. В. Манипулирование квантовыми структурами с помощью лазерных импульсов (Издательство Кембриджского университета, Кембридж, 2011)
Грубер А. и др. Сканирующая конфокальная оптическая микроскопия и магнитный резонанс на единичных дефектных центрах. Наука 276 , 2012–2014 (1997).
Артикул Google ученый

Doherty, M. W. et al. Азотно-вакансионный центр окраски в алмазе. Phys.Отчет 528 , 1–45 (2013).
ADS Статья Google ученый
Барфус, А., Тейсье, Дж., Ной, Э., Нунненкамп, А. и Малетинский, П. Сильное механическое движение спина одного электрона. Нат. Phys. 11 , 820–824 (2015).
Артикул Google ученый
Добровицкий В., Фукс Г., Фальк А., Сантори К.& Awschalom, D. Квантовый контроль над одиночными спинами в алмазе. Annu. Rev. Condens. Matter Phys. 4 , 23–50 (2013).
ADS Статья Google ученый
MacQuarrie, E. R. et al. Когерентное управление ансамблем спинов азот-вакансионных центров с помощью алмазного механического резонатора. Optica 2 , 233–238 (2015).
Артикул Google ученый

Cai, J.-M. и другие. Надежная динамическая развязка с непрерывным непрерывным движением. New J. Phys. 14 , 113023 (2012).
ADS MathSciNet Статья Google ученый
Xu, X. et al. Квантовый вентиль с защитой когерентности за счет непрерывной динамической развязки в алмазе. Phys. Rev. Lett. 109 , 070502 (2012).
ADS Статья Google ученый
Маккуорри, Э. Р., Госави, Т. А., Бхаве, С. А. и Фукс, Г. Д. Непрерывное динамическое разделение спина одиночного азотно-вакансионного центра алмаза с механическим резонатором. Phys. Ред. B 92 , 224419 (2015).
ADS Статья Google ученый
Acosta, V. M. et al. Температурная зависимость азотно-вакансионного магнитного резонанса в алмазе. Phys. Rev. Lett. 104 , 070801 (2010).
ADS Статья Google ученый
Йоас Т., Вэбер А.М., Браунбек Г. и Рейнхард Ф. Квантовое зондирование слабых радиочастотных сигналов с помощью импульсной абсорбционной спектроскопии Моллоу. Нат. Commun. 8 , 964 (2017).
ADS Статья Google ученый
Stark, A. et al. Узкополосное зондирование высокочастотных полей с непрерывной динамической развязкой. Нат. Commun. 8 , 1105 (2017).
ADS Статья Google ученый
Абобей, М. Х., Односекундная когерентность для одного спина электрона, связанного с многокубитовой средой ядерных спинов. Нат. Commun. 9 , 2552 (2018).
Fang, K. et al. Обобщенная невзаимность в оптомеханической схеме через синтетический магнетизм и разработку резервуаров. Нат. Phys. 13 , 465–471 (2017).
Артикул Google ученый
построение двух наборов контуров
Re: построение двух наборов контуров[Предыдущая дата] [Следующая дата] [Предыдущая тема] [Следующая цепочка] [Указатель даты] [Указатель темы]
[email protected] (Энн Уэббер) пишет: > Я пытаюсь нанести два разных набора контуров на одно изображение. В > Наборы контуров сосредоточены вокруг разных точек, поэтому мне нужно > Позиционируйте их отдельно.Я могу перекрыть один набор в нужной точке > но когда дело доходит до второго набора, ключевое слово position не кажется > работать и второй набор перекрывает первый набор. > Нужно ли мне объединить все данные в один файл, т.е. проработать два > графики относительно друг друга, или я могу использовать другое ключевое слово, чтобы > положение второго комплекта? Энн, я думаю, вы неправильно используете CONTOUR. Положение ключевое слово используется для размещения графика в области просмотра в нормализованном или координаты устройства, и никогда в координатах данных.Вы говорите, что контурные графики «сосредоточены в разных точках», но не должно иметь значения. Пока вы устанавливаете координату системы с вашим изображением, тогда вы сможете накладывать контуры используя * координаты контурных изображений *. Главное - установить систему координат с вашим изображением. В одну сторону сделать это с помощью моего ПЛОТИЗАРА или IMDISP Лиама. Или ты можешь это сделать себя (несколько мучительно), загрузив изображение с ТВ, нанесение на карту системы координат, а затем наложение контуров.2 стереть tv, bytscl (zz, min = -1, max = 1, top = 200) +1, 100,100 ;; Нарисуйте изображение ;; Следующий график устанавливает систему координат от 0 до 10, от пикселей. ;; пронумерованы от 100 до 200 сюжет, [0,10], [0,10], / xstyle, / ystyle, / nodata, / noerase, $ позиция = [100,100,200,200], / устройство ;; Наложение данных контура с другого изображения контур, zz2, xx, yy, уровни = [0,2,5,10,20,50,80,100,120,150,180,200], / более Что меня действительно смутило, так это то, что ваша программа-пример была пытаясь очертить вектор, а не изображение > КОНТУР, A (7, *), A (0, *), A (1, *), / нерегулярный, уровни = [6,8,10,15,18,20,25,30,40,50, 60,70,80,90,100,150,200], color = 2, C_LABELS = [1,1,1,1,1,1,1,1,1,0,1,0,1,0,1,0,1] > $ >, position = [515,495,645,625], / device, / noerase, / overplot Подмассив A (7, *) - это одномерный вектор, а не изображение.Я не вижу как это сработает. Удачи, Крейг - -------------------------------------------------- ------------------------ Крейг Б. Маркуардт, доктор философии. ЭЛЕКТРОННАЯ ПОЧТА: [email protected] Астрофизика, IDL, Финансы, Деривативы | Удалите "net" для лучшего ответа -------------------------------------------------- ------------------------
Жан-Пьер Контур (родился 2 июля 1943 г.), консультант по Франции, исследователь физики
Жан-Пьер Контур, французский исследователь физики, консультант.С французской армией, 1970-1972 гг. Член Французского общества физиков, Французского альпийского клуба.Фон
Контур Жан-Пьер родился 2 июля 1943 года в Бур-ла-Рейне, Франция. Сын Пьера и Маргариты (Миллан) Контур.
Образование
Дипломированный инженер, ESCIL, Лион, Франция, 1966 год.Магистр наук, Лионский университет, 1966. Доктор наук, Университет Пьера и Марии Кюри, Париж, 1970.
Карьера
Ответственные исследования, Национальный центр научных исследований, Париж, 1966–1981; директор по исследованиям Национального центра научных исследований, София-Антиполис-Вальбонн, Франция, 1981–1990; директор по исследованиям Национального центра научных исследований, Париж, 1990–1995; директор по исследованиям Национального центра научных исследований, Орсе, Франция, с 1995 года.Консультант Рибер С.А., Рюэй Мальмезон, Франция, 1981–1994 годы, Staib InstrumenteGmbH, Фрайзинг, Германия, 1990–1997 годы.
Членство
С французской армией, 1970-1972 гг. Член Французского общества физиков, Французского альпийского клуба.
Подключения
Женился на Бернадетт Барбо, 6 апреля 1965 года. Дети: Сара, Элоиза.
- Отец:
- Пьер Контур
- Мать:
- Маргарита (Миллан) Контур
- Супруг:
- Бернадетт Барбо
- ребенок:
- Heloïse Contour
- ребенок:
- Сара Контур




 В реальности такого не бывает, потому что часть энергия уйдёт на преодоление сопротивления проводников и превратится в тепловую энергию. В реальном колебательном контуре в этот момент времени конденсатор зарядится уже не полностью.
В реальности такого не бывает, потому что часть энергия уйдёт на преодоление сопротивления проводников и превратится в тепловую энергию. В реальном колебательном контуре в этот момент времени конденсатор зарядится уже не полностью.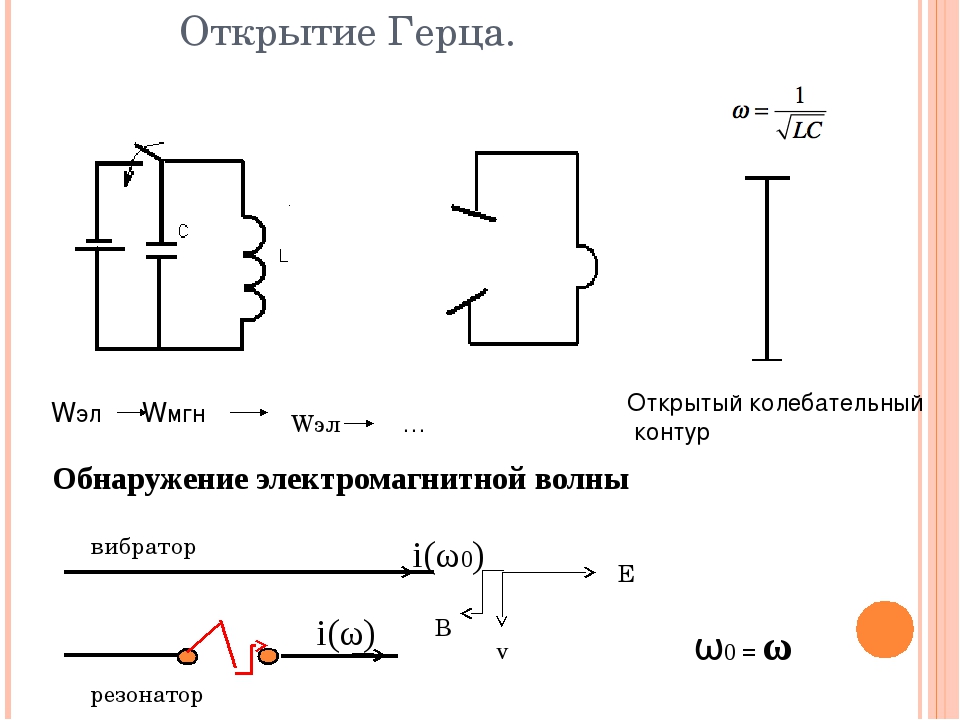 На букву b указывает электрическое поле.
прямо вверх, а значит, не прямо к Q2.
На букву b указывает электрическое поле.
прямо вверх, а значит, не прямо к Q2.
 Для положительного заряда движение будет в направлении области
более низкого потенциала; для отрицательного заряда движение будет
к региону с более высоким потенциалом.
Для положительного заряда движение будет в направлении области
более низкого потенциала; для отрицательного заряда движение будет
к региону с более высоким потенциалом.
 Электрическое поле в точке А из-за заряда -q
направлен влево. Однако поскольку величина
электрическое поле спадает как 1 / r2, величина поля
в A из-за заряда + q будет больше, чем величина
поле в A из-за заряда -q. Чистое поле в точке А будет
поэтому быть направленным вправо.
Электрическое поле в точке А из-за заряда -q
направлен влево. Однако поскольку величина
электрическое поле спадает как 1 / r2, величина поля
в A из-за заряда + q будет больше, чем величина
поле в A из-за заряда -q. Чистое поле в точке А будет
поэтому быть направленным вправо. 