Определение координаты движущегося тела
На прошлом уроке мы с вами говорили о пути и перемещении тела. Давайте вспомним, что путь — это скалярная величина, равная длине траектории, которую описывает тело за некоторый промежуток времени.
А перемещением называется направленный отрезок прямой, соединяющий начальное и конечное положения тела.
Так как перемещение — это векторная величина, то есть имеет модуль и направление, то складывать и вычитать перемещения необходимо по правилам сложения и вычитания векторов. Однако при решении большинства задач, используется понятие не вектора, а проекции вектора на ось координат.
— А что такое проекция вектора и каковы её свойства?
На это вопрос мы с вами и попытаемся сегодня ответить. Начнём с простого — с понятия проекция точки на ось. Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.
На представленном рисунке точка

Теперь разберёмся с проекцией вектора на ось. Согласно определению, проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора на эту ось, взятая со знаком «плюс» или «минус».
Знак «плюс» берут, если угол между вектором и осью острый, а «минус» — если угол тупой.
Обозначать проекцию вектора будем той же буквой, что и вектор, но с индексом внизу (например, ax — это проекция вектора a на ось Ox).
— А если вектор перпендикулярен оси?
Тогда проекция этого вектора равна нулю.
Проекцию вектора можно выразить через его модуль и угол между вектором и осью. Итак, пусть у нас есть вектор a направленный под некоторым острым углом к координатной оси Ox. Укажем проекцию этого вектора на ось.
У
нас с вами получился прямоугольный треугольник, гипотенуза которого равна длине
вектора a,
а катет AB1 — это проекция вектора a на
ось Ox.
Тогда, на основании определения косинуса острого угла, мы можем записать, что проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью
Это правило справедливо при любых значениях угла φ. Например, для углов, больше 90о, косинус угла φ отрицательный. Тогда по формуле получается, что проекция вектора на ось также отрицательна, как и должно быть по определению проекции.
— А можно ли найти модуль и направление вектора по его проекциям на координатные оси?
Чтобы ответить на этот вопрос рассмотрим вектор, лежащий в плоскости xOy. Вектор, лежащий в заданной плоскости, определяется двумя проекциями на оси координат.
Обратим внимание на важное свойство проекций:
Но
вернёмся к нашему прошлому уроку. На нём мы с вами говорили о том, что
положение тела, которое совершило некоторое перемещение, можно найти
графически. Для этого достаточно отложить вектор перемещения от начального
положения этого тела. Однако в большинстве случаев необходимо уметь вычислять
положение тела, то есть уметь определять его координаты. Давайте на примере
решения задачи посмотрим, как можно определить координату движущегося тела,
зная координату его начального положения и вектор перемещения.
Для этого достаточно отложить вектор перемещения от начального
положения этого тела. Однако в большинстве случаев необходимо уметь вычислять
положение тела, то есть уметь определять его координаты. Давайте на примере
решения задачи посмотрим, как можно определить координату движущегося тела,
зная координату его начального положения и вектор перемещения.
Итак, два поезда идут по параллельным путям в противоположных направлениях и встречаются в шестидесяти километрах к востоку от железнодорожного вокзала. Продолжив движение через некоторое время t первый поезд удалился от места встречи на 50 километров в восточном направлении, а второй — на 80 километров в западном. Определите координаты каждого поезда относительно вокзала и расстояние между ними через промежуток времени t.
2. Графики зависимости перемещения и координаты тела от времени при движении с постоянным ускорением
Зависимость проекции перемещения от времени при равноускоренном движении имеет вид:
Δrx=v0xt+axt22.
Учитывая, что проекция перемещения движущегося тела равна:
Δrx=x−x0,
зависимость координаты движущегося тела от времени имеет вид:
x=x0+v0xt+axt22.
Последняя формула выражает кинематический закон равнопеременного движения.
Поскольку при равнопеременном движении зависимости перемещения и координаты тела от времени являются квадратичными функциями, то графиками зависимости данных величин от времени являются участки парабол.
На рисунке \(1\) представлены графики зависимости скорости движения тела при ax=a>0 (прямая \(1\)), при ax=a=0 (прямая \(2\)) и при ax=a<0 (прямая \(3\)).
Рис. 1. Изображение графиков зависимостей V(t)
На рисунке \(2\) представлены графики зависимости проекции перемещения движущегося тела от времени при ax=a>0 (кривая \(1\)), при ax=a=0 (прямая \(2\)) и при ax=a<0 (кривая \(3\)).
Рис. 2. Изображение графиков зависимостей Δrx(t)
2. Изображение графиков зависимостей Δrx(t)
При ax=a>0 проекция перемещения всё время увеличивается (кривая \(1\)).
А при ax=a<0 проекция перемещения увеличивается до момента времени t=tп, а затем уменьшается. Это происходит потому, что в момент времени tn скорость тела становится равной нулю, а направление его движения меняется на противоположное, то есть происходит поворот.
Моменту времени tn на кривой \(3\) рисунка \(2\) соответствует вершина параболы.
График зависимости пути \(s\) от времени при движении, при котором направление скорости не изменяется, совпадает с графиком зависимости проекции перемещения от времени (рис. \(3\), кривые \(1\) (график проекции перемещения) и \(2\) (график пути)).
Рис. 3. Сравнение графиков зависимостей Δrx(t) и \(s(t)\)
Если же направление скорости во время движения изменяется, то есть происходит поворот, то эти графики совпадают только при 0<t<tn (рис. \(3\), кривые \(3\) (график проекции перемещения) и \(4\) (график пути)).
\(3\), кривые \(3\) (график проекции перемещения) и \(4\) (график пути)).
После момента поворота tn проекция перемещения начинает уменьшаться, а путь продолжает увеличиваться. При этом путь увеличивается на столько, на сколько за то же время уменьшается проекция перемещения.
График зависимости координаты от времени (рис. \(4\), кривые \(1\) и \(3\)) получается из графика зависимости перемещения от времени (рис. \(4\), кривая \(2\)) смещением последнего на величину x0 вверх при x0>0 (рис. \(4\), кривая \(1\)) или вниз при x0<0 (рис. \(4\), кривая \(3\)), поскольку x=x0+Δrx (рис. \(4\)).
Рис. 4. Сравнение графиков зависимостей Δrx(t) и \(x(t)\)
Физика в школе 867
Основы
Система отсчета – совокупность тела отсчета, системы координат для определения местоположения этого тела и часов для определения времени.

Перемещение – вектор, соединяющий начальное и конечное положение материальной точки в пространстве.
Траектория – линия, которую описывает в пространстве материальная точка.
Путь – длина траектории.
Обозначения в кинематике
| Обозначение | Измерение | Смысл |
|---|---|---|
| S | м | Перемещение тела |
| v | м/с | |
| t | с | Время |
| x | м | Координата |
| a | м/с2 | Ускорение |
| ω | рад/с | Угловая скорость |
| T | с | Период |
| υ | Гц | Частота |
| R | м | Радиус |
Равномерное прямолинейное движение
Движение тела называется равномерным, если за любые
равные промежутки времени оно проходит равные пути.
Формула перемещения через изменение координаты:
Формула перемещения через скорость и время:
Закон движения тела при равномерном движении:
График равномерного прямолинейного движения тела является линейным, так как движение описывается формулой S = vt, v = const.
Наибольшая скорость у тела 2 – это зависит от наклона прямой – чем она выше, тем больше скорость.
Также скорость можно рассчитать прямо на графике – возьмем одну удобную точку, взглянем на S и t и по формуле S = vt получим значение v.
Для тела 2: тут также только одна удобная точка S = 20 м и t = 5 с. По формуле получим 20 = v*5, v = 4 м/с.
Так как v = const, то есть не зависит от t, то график скорости выглядит таким образом:
Равноускоренное движение
Движение тела называется равноускоренным, если за любые равные
промежутки времени скорость изменяется на одно и то же число.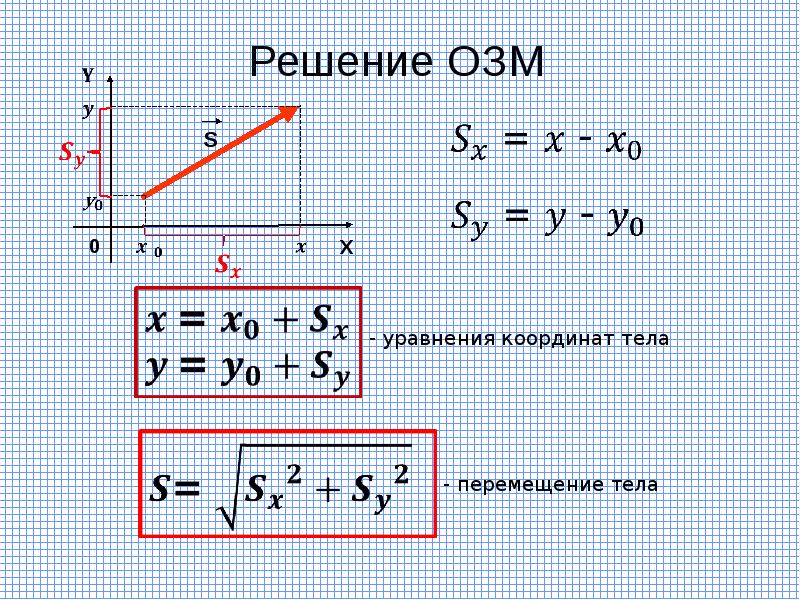
Закон движения тела при равноускоренном движении:
Определение ускорения:
Изменение скорости:
Также полезное соотношение, если неизвестно время:
График движения тела с x0 = 3 м, v0x = 8 м/с и ax = -2 м/с
Так как равноускоренное движение описывается уравнением x = 3 + 8t – 2/2t2 = 3 + 8t – t2, то график является параболой.
График изменения скорости
Так как скорость при равноускоренном движении описывается уравнением v = v0 + at = 8 – 2t, то график является линейной функцией.
По определению равноускоренного движения a = const, потому ускорение не зависит от времени.
Свободное падение
Свободным падением называется движение тела из-за притяжения Земли при отсутствии начальной скорости.
По факту, это такое равноускоренное движение, когда a = g и ускорение направлено вниз. Так что все формулы на равноускоренное движение также работают, остается лишь подставить a = – g и изменить проекцию с Ox на Oy.
Так что все формулы на равноускоренное движение также работают, остается лишь подставить a = – g и изменить проекцию с Ox на Oy.
Высота, с которой упало тело при свободном падении с нулевой начальной скоростью за время t:
Скорость тела, если известна высота, которую пролетело тело:
Уравнение движение тела при свободном падении:
Скорость тела:
Движение горизонтально брошенного тела
График движения тела, брошенного горизонтально, с h0 = 125 м, v0 = 3 м/с. Перемещение по ОХ составило 15 м, само падение – 5 с.
Если пользоваться формулами, которые описывают движение горизонтально брошенного тела, мы получим ту же информацию, что и взглянув на график.
Например, рассчитаем время полета тела, зная изначальную высоту:
Найдя время падения, мы теперь можем рассчитать перемещение по оси OX:
Предположим, требуется рассчитать скорость тела в момент времени t = 2 с:
Не пользуясь графиком, мы можем найти перемещение по обеим осям и вычислить перемещение тела:
Движение тела, брошенного под углом к горизонту
Равномерное движение по окружности
Длина окружности:
Связь периода и частоты вращения:
Линейная скорость:
Угловая скорость:
Связь линейной и угловой скоростей:
Центростремительное ускорение:
| Обозначение | Измерение | Смысл |
|---|---|---|
| L | м | Длина окружности |
| R | м | Радиус окружности |
| l | м | Пройденный путь |
| Δφ | рад | Угловое перемещение |
| v | м/с | Линейная скорость |
| ω | рад/с | Угловая скорость |
| T | с | Период вращение |
| υ | Гц | Частота вращения |
Объяснение на окружности:
Центростремительное ускорение:
Определение координаты движущегося тела интернет урок.
 Движение тела по окружности
Движение тела по окружностиКак определить координаты движущегося тела? Для этого необходимо знать такие понятия, как механическое движение, пройденный путь, скорость, перемещение.
Механическое движение
При механическом движении происходит изменение положения тела в пространстве относительно других тел за промежуток времени. Оно бывает равномерным и неравномерным.
Равномерное движение
При равномерном движении тело за равные промежутки времени проходит одинаковые расстояния (т.е. движется с постоянной скоростью).
Путь, пройденный при равномерном движении равен: Sx=Vxt=x-xо
Следовательно, при равномерном движении координата тела изменяется по следующей зависимости:
Рис. 1. Формула координаты тела при прямолинейном равномерном движении
- Xо – начальная координата тела;
- X – координата в момент времени t;
- Vx – проекция скорости на ось X.
Неравномерное движение
Неравномерное движение – движение, при котором тело за равные промежутки времени проходит неодинаковые расстояния (движется с непостоянной скоростью), то есть движется с ускорением.
Если тело движется неравномерно, то скорость тела в разные моменты отличается не только по величине, но и (или) по направлению. Средняя скорость тела при неравномерном движении определяется по формуле: V (ср)= S (весь)/t (весь)
Ускорение – величина, показывающая, как изменяется скорость за 1 секунду.
Рис. 2. Формула ускорения
Следовательно, скорость в любой момент времени можно найти следующим образом:
V=Vо+at
Если скорость с течением времени увеличивается, то a больше 0, если скорость с течением времени уменьшается, то a меньше 0.
Как найти путь при равноускоренном движении?
Рис. 3. Прямолинейное равноускоренное движение
Пройденный путь численно равен площади под графиком. То есть Sx=(Vox+Vx)t/2
Скорость в любой момент времени равна Vx=Vox+axt, следовательно Sx=Voxt+axt2/2
Так как перемещение тела равно разности конечной и начальной координат (Sx=X-Xo), то координата в любой момент времени вычисляется по формуле X=Xo+Sx, или
X=Xo+Voxt+axt2/2
Движение тела по вертикали
Если тело движется по вертикали, а не по горизонтали, то такое движение всегда является равноускоренным. Когда тело падает вниз, то падает оно всегда с одинаковым ускорением – ускорением свободного падения. Оно всегда одинаковое: g=9,8 м/кв.с.
Когда тело падает вниз, то падает оно всегда с одинаковым ускорением – ускорением свободного падения. Оно всегда одинаковое: g=9,8 м/кв.с.
При движении по вертикали формула скорости приобретает вид: Vy=Voy+gt ,
где Vy и Voy – проекции начальной и конечной скоростей на ось OY.
Движение тела по окружности
При движении по окружности численное значение скорости может и не изменяться, но поскольку обязательно изменяется направление, то движение по окружности – это всегда равноускоренное движение.
Что мы узнали?
Тема «Определение координаты движущего тела», которую изучают в 9 классе, поможет ученикам систематизировать информацию о том, что движение может быть равномерным и неравномерным. Так же для того чтобы знать пройденный путь, нужно выбрать тело отсчета и использовать прибор для отсчета времени.
Оценка доклада
Средняя оценка: 4 . Всего получено оценок: 6.
Тема урока: «Определение координаты движущегося тела»
Цель урока: Ввести понятия векторная и скалярная величина, координата, проекция вектора, модуль вектора. Сформулировать правила определения знака проекции.
Сформулировать правила определения знака проекции.
Тип уроки: Комбинированный урок.
Проверка знаний:
1. Что называется механическим движением?
2. Что входит в понятие «система отсчета»?
3. Почему невозможно описать движение без выбора системы отсчета?
4. Какие точки катящегося вагона движутся и какие находятся в покое относительно дороги?
5. Что такое материальная точка?
6. Какое движение называется поступательным?
7. Что такое траектория?
8. Что такое пройденный путь?
9. Что такое перемещение?
10. ответить на вопросы к §2.
11. ответить на вопросы упр. 2 № 1,2.
Траектории движения двух материальных точек пересекаются. Означает ли это, что тела сталкиваются? Приведите пример, подтверждающий ваш ответ.
Тело, брошенное вертикально вверх, поднялось на высоту 20 м и упало в ту же точку. Чему равен путь, пройденный телом за то время, пока оно двигалось вверх? За время, пока оно двигалось вниз? За все время движения?
При каком условии путь равен модулю перемещения тела? Может ли модуль перемещения быть больше пройденного пути? Приведите примеры таких движений.
Автомобиль проехал 100 км. а) Какие точки колеса совершили максимальное перемещение? Минимальное? б) Какие точки колеса прошли максимальный путь? Минимальный?
Два тела, двигаясь прямолинейно, совершили одинаковые перемещения. Обязательно ли одинаковы пройденные ими пути? Ответ поясните примером.
План изложения нового материала:
Определение координаты движущегося тела.
Векторные и скалярные величины.
Проекция вектора.
Правило определения знака проекции.
Уравнение, с помощью которого можно определить координату тела.
Модуль вектора.
1. Изложение нового материала.
Определение координаты движущегося тела . При решении задач обычно составляют уравнения, связывающие физические величины, а затем решают эти уравнения. Если величины векторные, приходится «следить» не только за модулем каждой такой величины, но и за ее направлением. Решение задач значительно упрощается благодаря тому, что одну векторную величину можно задать с помощью нескольких скалярных величин следующим образом.
Любую векторную величину можно представить в виде суммы трех векторных величин, направленных вдоль осей координат. Эти векторные величины называют ее составляющими. Каждую составляющую векторной величины можно охарактеризовать просто числом: модуль этого числа равен модулю составляющей, а знак числа определяется направлением составляющей. Если она направлена в положительном направлении оси координат, – это число положительное, а если в отрицательном, – отрицательное. Это число называется проекцией данной векторной величины на соответствующую координатную ось.
Проекции векторной величины а на оси координат х, у, z обозначаются а х , а у и а г . Они измеряются в тех же единицах, что и модуль этой величины. Например, проекция перемещения измеряется в метрах, а проекция скорости – в метрах в секунду.
Свяжем проекции перемещения тела с его координатами. Для наглядности ограничимся движением на плоскости.
Для наглядности ограничимся движением на плоскости.
Пусть тело из точки с координатами х 0, у 0 переместилось в точку с координатами х, у. Тогда перемещение s – это вектор, проведенный из точки с координатами х 0, , у 0 в точку с координатами х, у. Следовательно,
s x = х – х 0 , s y =y -y 0. Таким образом,
x = x 0 + s x , y = y Q +s y .
Обращаем внимание: в этих формулах стоит знак «плюс», независимо от того, в каком направлении двигалось тело – в положительном направлении оси или в отрицательном.
2. Отработка знаний и умений.
Решение задачи упр.3 №1
Задание на дом: §3 упр.3 №2.
Есть одна фундаментальная вещь! У меня есть пример, когда студенты до второго курса технического ВУЗа допускали глупые ошибки, потому что недостаточно понимали это.
Положение тела можно задать набором координат. Например, (50, -70, 10), что означает «тело сдвинуто от начала координат на 50 единиц по оси X, на 70 единиц против оси Y, на 10 единиц по Z».
В математике три (или два) числа с указанием координат называются вектором или радиус-вектором . Чтобы представить радиус-вектор в терминах «направленного отрезка-стрелочки», надо вообразить эту стрелку, исходящую из начала координат, и указывающую в интересующую нас точку.
Радиус-вектор точки A.
Зачем вообще нужны эти векторы, ведь, казалось бы, можно обойтись точками?
Но дело в том, что многие уравнения в физике записаны именно векторами (т.к. многие тела движутся в пространстве в каком-либо направлении), и если мы будем воспринимать точки как вектора, то нам будет легче проводить все расчёты.
К тому же есть множество калькуляторов, которые отлично работают с векторами – это позволяет вместо ряда уравнений для скаляров написать всего одно уравнение для векторов. Так что стоит помнить, что вектор – это не только «стрелочка», но и упорядоченный набор чисел.
Так что стоит помнить, что вектор – это не только «стрелочка», но и упорядоченный набор чисел.
Кроме того, векторная запись – это отличный способ не запутаться в знаках. Опыт показывает, что ученики и студенты допускают ощутимо больше ошибок со знаками, когда не пользуются векторной записью.
Смотрите, как можно расписать векторные уравнения очень простым способом.
Векторное уравнение:
В скалярной форме выглядит как система уравнений:
Т.е. чтобы превратить векторное уравнение в скалярное, достаточно расписать проекции этого уравнения на все оси, что значит заменить вектор «» на скаляры «x» и «y», а вектор «» на проекции «v x » и «v y ».
Как определять координаты движущегося тела
Допустим, тётя Люда на Камазе выехала из Москвы и проехала по трассе на север 90 километров. А затем развернулась обратно и проехала 150 километров (утюг, например, забыла выключить в Подмосковье). А дядя Витя на коне за это же время стартовал на 200 км южнее Москвы, и проскакал 120 км на север.
Вопрос: на каком расстоянии друг от друга тётя Люда и дядя Витя?
Примем Москву за начало координат. Введём также одну координатную ось, и направим её на север. Назовём ось X.
Стартовая позиция тёти Люды:
Первое перемещение тёти Люды обозначим как и его проекция на X равна = 90 км (вспоминаем, что она сначала ехала на север).
Второе перемещение тёти Люды и его проекция на X равна = -150 км (минус – потому что вектор направлен против оси X (вниз)).
Тогда последнее местоположение тёти Люды равно
Т.е. начальное положение + 1-е передвижение + 2-е передвижение.
Если переписать в скалярном виде, получается:
x L2 = r L0x + S L1x + S L2x = 0 + 90 – 150 = -60 км
Стартовая позиция дяди Вити на 200 км южнее Москвы, то есть проекция = -200 км. А проекция перемещения дяди Вити равна =120 км.
А радиус-вектор последнего местоположения дяди Вити равен: Т.е. также: стартовая позиция + 1-е перемещение.
Если спроецировать на оси, получится:
x V1 = r V0x + S V1x = -200 + 120 = -80 км.
Расстояние между дядей Витей и тётей Людой равно модулю от разности их радиус-векторов
D LV = |-60 – (-80)| = 20 км
Обратите внимание, что здесь всегда используется модуль, поскольку расстояние между объектами никогда не может быть отрицательным.
Если бы у нас была задача с двумя координатами, мы бы её решали примерно так же, за исключением двух моментов:
- Векторные уравнения мы расписывали бы как системы из двух уравнений с проекциями.
- Модуль вектора мы рассчитывали бы по теореме .
На данном уроке, тема которого: «Определение координаты движущегося тела» мы поговорим о том, как можно определять место нахождения тела, его координату. Поговорим о системах отсчета, рассмотрим для примера задачу, а также вспомним, что такое перемещение
Представьте: вы изо всей силы бросили мяч. Как определить, где он будет находиться через две секунды? Можно подождать две секунды и просто посмотреть, где он. Но, даже не глядя, вы приблизительно можете предсказать, где будет мяч: бросок был сильнее обычного, направлен под большим углом к горизонту, значит, полетит высоко, но недалеко… Используя законы физики, можно будет точно определить положение нашего мяча.
Но, даже не глядя, вы приблизительно можете предсказать, где будет мяч: бросок был сильнее обычного, направлен под большим углом к горизонту, значит, полетит высоко, но недалеко… Используя законы физики, можно будет точно определить положение нашего мяча.
Определить положение движущегося тела в любой момент времени – это и есть основная задача кинематики.
Начнем с того, что у нас есть тело: как определить его положение, как объяснить кому-то, где оно находится? Об автомобиле мы скажем: он на дороге за 150 метров перед светофором или на 100 метров за перекрестком (см. рис. 1).
Рис. 1. Определение местоположения машины
Или на трассе за 30 км к югу от Москвы. О телефоне на столе скажем: он сантиметров на 30 правее клавиатуры или рядом с дальним углом стола (см. рис. 2).
Рис. 2. Положение телефона на столе
Заметьте: мы не сможем определить положение автомобиля, не упомянув другие объекты, не привязавшись к ним: светофор, город, клавиатуру. Мы определяем положение, или координаты, всегда относительно чего-то.
Мы определяем положение, или координаты, всегда относительно чего-то.
Координаты – это набор данных, по которому определяется положение того или иного объекта, его адрес.
Примеры упорядоченных и неупорядоченных имен
Координата тела – это его адрес, по которому мы его можем найти. Он упорядоченный. Например, зная ряд и место, мы точно определяем, где находится наше место в зале кинотеатра (см. рис. 3).
Рис. 3. Зал кинотеатра
Буквой и цифрой, например e2, точно задается положение фигуры на шахматной доске (см. рис. 4).
Рис. 4. Положение фигуры на доске
Зная адрес дома, например улица Солнечная 14, мы будем искать его на этой улице, на четной стороне, между домами 12 и 16 (см. рис. 5).
Рис. 5. Поиск дома
Названия улиц не упорядочены, мы не будем искать Солнечную улицу по алфавиту между улицами Розовой и Тургенева. Также не упорядочены номера телефонов, номерные знаки автомобилей (см. рис. 6).
Рис. 6. Неупорядоченные имена
Эти номера, идущие подряд, – это лишь совпадение, не означающее соседства.
Мы можем задать положение тела в разных системах координат, как нам удобно. Для того же автомобиля, можно задать точные географические координаты (широту и долготу) (см. рис. 7).
Рис. 7. Долгота и широта местности
Рис. 8. Местоположение относительно точки
Причем если мы выберем разные такие точки, то получим разные координаты, хотя они будут задавать положение одного и того же автомобиля.
Итак, положение тела относительно разных тел в разных системах координат будет разным. А что такое движение? Движение – это изменение положения тела со временем. Поэтому описывать движение мы будем в разных системах отсчета по-разному, и нет смысла рассматривать движение тела без системы отсчета.
Например, как движется стакан с чаем на столе в поезде, если сам поезд едет? Смотря относительно чего. Относительно стола или пассажира, сидящего рядом на сидении, стакан покоится (см. рис. 9).
рис. 9).
Рис. 9. Движение стакана относительно пассажира
Относительно дерева около железной дороги стакан движется вместе с поездом (см. рис. 10).
Рис. 10. Движение стакана вместе с поездом относительно дерева
Относительно земной оси стакан и поезд вместе со всеми точками земной поверхности будут еще и двигаться по окружности (см. рис. 11).
Рис. 11. Движение стакана с вращением Земли относительно земной оси
Поэтому нет смысла говорить о движении вообще, движение рассматривается в привязке к системе отсчета.
Всё, что мы знаем о движении тела, можно разделить на наблюдаемое и вычисляемое. Вспомним пример с мячом, который мы бросили. Наблюдаемое – это его положение в выбранной системе координат, когда мы его только бросаем (см. рис. 12).
Рис. 12. Наблюдение
Это момент времени, когда мы его бросили; время, которое прошло после броска. Пусть на мяче нет спидометра, который показал бы скорость мяча, но ее модуль, как и направление, тоже можно узнать, используя, например, замедленную съемку.
С помощью наблюдаемых данных мы можем предсказать, например, что мяч через 5 секунд упадет за 20 м от места броска или через 3 секунды попадет в верхушку дерева. Положение мяча в любой момент времени – это в нашем случае вычисляемые данные.
Что определяет каждое новое положение движущегося тела? Его определяет перемещение, потому что перемещение – это вектор, характеризующий изменение положения. Если начало вектора совместить с начальным положением тела, то конец вектора укажет на новое положение переместившегося тела (см. рис. 13).
Рис. 13. Вектор перемещения
Рассмотрим несколько примеров на определение координаты движущегося тела по его перемещению.
Пусть тело двигалось прямолинейно из точки 1 в точку 2. Построим вектор перемещения и обозначим его (см. рис. 14).
Рис. 14. Перемещение тела
Тело двигалось вдоль одной прямой, значит, нам будет достаточно одной оси координат, направленной вдоль перемещения тела. Допустим, мы наблюдаем за движением со стороны, совместим начало отсчета с наблюдателем.
Перемещение – вектор, удобнее работать с проекциями векторов на оси координат (у нас она одна). – проекция вектора (см. рис. 15).
Рис. 15. Проекция вектора
Как определить координату начальной точки, точки 1? Опускаем перпендикуляр из точки 1 на ось координат. Этот перпендикуляр пересечет ось и отметит на оси координату точки 1. Так же определяем координату точки 2 (см. рис. 16).
Рис. 16. Опускаем перпендикуляры на ось ОХ
Проекция перемещения равна:
При таком направлении оси и перемещения будет по модулю равна самому перемещению .
Зная начальную координату и перемещение, найти конечную координату тела – дело математики:
Уравнение
Уравнение – это равенство, содержащее неизвестный член. В чем его смысл?
Любая задача заключается в том, что что-то нам известно, а что-то – нет, и неизвестное нужно найти. Например, тело из некоторой точки переместилось на 6 м в направлении оси координат и оказалось в точке с координатой 9 (см. рис. 17).
рис. 17).
Рис. 17. Начальное положение точки
Как найти, из какой точки тело начало движение?
У нас есть закономерность: проекция перемещения – это разность конечной и начальной координат:
Смысл уравнения будет в том, что перемещение и конечную координату мы знаем () и можем подставить эти значения, а начальную координату не знаем, она будет неизвестным в этом уравнении:
И уже решая уравнение, мы получим ответ: начальная координата .
Рассмотрим другой случай: перемещение направлено в сторону, противоположную направлению оси координат.
Координаты начальной и конечной точек определяются так же, как и раньше, – опускаются перпендикуляры на ось (см. рис. 18).
Рис. 18. Ось направлена в другую сторону
Проекция перемещения (ничего не меняется) равна:
Обратите внимание, что больше, чем , и проекция перемещения , когда она направлена против оси координат, будет отрицательной.
Конечная координата тела из уравнения для проекции перемещения равна:
Как видим, ничего не меняется: в проекции на ось координат конечное положение равно начальному положению плюс проекция перемещения. В зависимости от того, в какую сторону тело переместилось, проекция перемещения будет положительной или отрицательной в данной системе координат.
В зависимости от того, в какую сторону тело переместилось, проекция перемещения будет положительной или отрицательной в данной системе координат.
Рассмотрим случай, когда перемещение и ось координат направлены под углом друг к другу. Теперь одной оси координат нам недостаточно, нужна вторая ось (см. рис. 19).
Рис. 19. Ось направлена в другую сторону
Теперь перемещение будет иметь ненулевую проекцию на каждую ось координат. Эти проекции перемещения будут определяться, как и раньше:
Заметьте, модуль каждой из проекций в этом случае меньше модуля перемещения. Модуль перемещения можем легко найти, используя теорему Пифагора. Видно, что если построить прямоугольный треугольник (см. рис. 20), то его катеты будут равны и , а гипотенуза равна модулю перемещения или, как часто записывают, просто .
Рис. 20. Треугольник Пифагора
Тогда по теореме Пифагора запишем:
Автомобиль находится в 4 км к востоку от гаража. Воспользуйтесь одной осью координат, направленной на восток, с началом отсчета в гараже. Укажите координату автомобиля в заданной системе через 3 минуты, если автомобиль этим временем ехал со скоростью 0,5 км/мин на запад.
Укажите координату автомобиля в заданной системе через 3 минуты, если автомобиль этим временем ехал со скоростью 0,5 км/мин на запад.
В задаче ничего не сказано о том, что автомобиль поворачивал или изменял скорость, поэтому считаем движение равномерным прямолинейным.
Изобразим систему координат: начало координат у гаража, ось х направлена на восток (см. рис. 21).
Автомобиль изначально был в точке и двигался по условию задачи на запад (см. рис. 22).
Рис. 22. Движение автомобиля на запад
Проекция перемещения, как мы неоднократно писали, равна:
Мы знаем, что автомобиль проезжал по 0,5 км каждую минуту, значит, чтобы найти суммарное перемещение, нужно скорость умножить на количество минут :
На этом физика закончилась, осталось математически выразить искомую координату. Выразим ее из первого уравнения:
Подставим перемещение:
Осталось подставить числа и получить ответ. Не забывайте, что автомобиль двигался на запад против направления оси х, это значит, что проекция скорости отрицательна: .
Задача решена.
Главное, чем мы сегодня пользовались для определения координаты, – выражение для проекции перемещения:
И из него мы уже выражали координату:
При этом сама проекция перемещения может быть задана, может вычисляться как , как в было в задаче о равномерном прямолинейном движении, может вычисляться сложнее, что нам еще предстоит изучить, но в любом случае координату движущегося тела (где тело оказалось) можно определить по начальной координате (где тело было) и по проекции перемещения (куда переместилось).
На этом наш урок окончен, до свидания!
Список литературы
- Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание, передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
- Перышкин А.В., Гутник Е.М. Физика: 9 класс. Учебник для общеобразовательных учреждений. – 14-е изд. – М.: Дрофа, 2009.
- Class-fizika.narod.ru ().
- Av-physics.narod.ru ().

- Class-fizika.narod.ru ().
Домашнее задание
- Что такое перемещение, путь, траектория?
- Как можно определить координаты тела?
- Запишите формулу для определения проекции перемещения.
- Как будет определяться модуль перемещения, если перемещение имеет проекции на две оси координат?
Презентация по теме определение координаты движущегося тела. Определение координаты движущегося тела
Как определить координаты движущегося тела? Для этого необходимо знать такие понятия, как механическое движение, пройденный путь, скорость, перемещение.
Механическое движение
При механическом движении происходит изменение положения тела в пространстве относительно других тел за промежуток времени. Оно бывает равномерным и неравномерным.
Равномерное движение
При равномерном движении тело за равные промежутки времени проходит одинаковые расстояния (т.е. движется с постоянной скоростью).
Путь, пройденный при равномерном движении равен: Sx=Vxt=x-xо
Следовательно, при равномерном движении координата тела изменяется по следующей зависимости:
Рис. 1. Формула координаты тела при прямолинейном равномерном движении
1. Формула координаты тела при прямолинейном равномерном движении
- Xо – начальная координата тела;
- X – координата в момент времени t;
- Vx – проекция скорости на ось X.
Неравномерное движение
Неравномерное движение – движение, при котором тело за равные промежутки времени проходит неодинаковые расстояния (движется с непостоянной скоростью), то есть движется с ускорением.
Если тело движется неравномерно, то скорость тела в разные моменты отличается не только по величине, но и (или) по направлению. Средняя скорость тела при неравномерном движении определяется по формуле: V (ср)= S (весь)/t (весь)
Ускорение – величина, показывающая, как изменяется скорость за 1 секунду.
Рис. 2. Формула ускорения
Следовательно, скорость в любой момент времени можно найти следующим образом:
V=Vо+at
Если скорость с течением времени увеличивается, то a больше 0, если скорость с течением времени уменьшается, то a меньше 0.
Как найти путь при равноускоренном движении?
Рис. 3. Прямолинейное равноускоренное движение
Пройденный путь численно равен площади под графиком. То есть Sx=(Vox+Vx)t/2
Скорость в любой момент времени равна Vx=Vox+axt, следовательно Sx=Voxt+axt2/2
Так как перемещение тела равно разности конечной и начальной координат (Sx=X-Xo), то координата в любой момент времени вычисляется по формуле X=Xo+Sx, или
X=Xo+Voxt+axt2/2
Движение тела по вертикали
Если тело движется по вертикали, а не по горизонтали, то такое движение всегда является равноускоренным. Когда тело падает вниз, то падает оно всегда с одинаковым ускорением – ускорением свободного падения. Оно всегда одинаковое: g=9,8 м/кв.с.
При движении по вертикали формула скорости приобретает вид: Vy=Voy+gt ,
где Vy и Voy – проекции начальной и конечной скоростей на ось OY.
Движение тела по окружности
При движении по окружности численное значение скорости может и не изменяться, но поскольку обязательно изменяется направление, то движение по окружности – это всегда равноускоренное движение.
Что мы узнали?
Тема «Определение координаты движущего тела», которую изучают в 9 классе, поможет ученикам систематизировать информацию о том, что движение может быть равномерным и неравномерным. Так же для того чтобы знать пройденный путь, нужно выбрать тело отсчета и использовать прибор для отсчета времени.
Оценка доклада
Средняя оценка: 4.1 . Всего получено оценок: 8.
https://accounts.google.com
Подписи к слайдам:
Физика Законы взаимодействия и движения тел. Механические колебания и волны. Звук ЭМ-поле. Строение атома и атомного ядра.
Тема 1 «Законы взаимодействия и движения тел» Урок 1. Материальная точка. Система отсчета. Перемещение Юлия Ринатовна Залялиева, учитель физики и математики МБОУ СОШ №8 . 2.09.2015 г
Движение – это неотъемлемое свойство материи Движение
Механическое движение – изменение положения тела в пространстве относительно других тел с течением времени. Механическое движение
Пройденный путь; Скорость; Траектория; Перемещение; Координаты тела. Характеристики движения:
Характеристики движения:
Скорость – это величина, характеризующая быстроту движения Скорость υ (м / с)
Координата тела – положение тела в пространстве в любой момент времени Координата тела
с ловесный табличный г рафический а налитический (формулы) Способы описания движения
Словесное описание Выехав из пункта А, поезд 2 часа ехал со скоростью 100 км/ч, затем час стоял, и в пункт Б прибыл через 3 часа, все это время двигаясь с постоянной скоростью 50 км/ч.
Табличное описание Графическое описание
Аналитическое описание
Способы описания движения
Материальная точка – тело, размерами которого можно пренебречь в условиях данной задачи Материальная точка
Например За материальную точку очень часто рассматривают Землю, если исследуют её движение вокруг Солнца.
Можно ли считать материальными точками тела, описанные в следующих ситуациях? 1.Рассчитывают путь Земли по орбите вокруг Солнца. 3.Для определения объема шарика его опускают в мензурку. 4.Для измерения массы лимона его кладут на весы. 5. Ваши примеры
4.Для измерения массы лимона его кладут на весы. 5. Ваши примеры
Чтобы определить положение тела (материальной точки) в пространстве надо: задать тело отсчета; выбрать систему координат; иметь прибор для отсчёта времени (часы)
Что такое тело отсчета? Тело отсчёта – это тело, относительно которого определяется положение других (движущихся) тел.
Система координат
Система отсчета:
Повторим Что такое механическое движение? Что такое материальная точка? В каких случаях тело можно считать материальной точкой? Какое движение называется поступательным? Что такое система отсчета?
§ 1-2, вопросы после параграфа Упр. 1 (2,4), Упр.2 (1) Знать все определения (!) Домашнее задание:
1 балл № Вид движения Определение Примеры 1 Поступательное 2 Прямолинейное 3 Вращательное 4 Криволинейное 5 Равномерное 6 Неравномерное
Траектория – это линия, вдоль которой движется тело Пройденный путь – это длина траектории Перемещение – вектор, соединяющий начальное положение тело с его последующим положением s (м) s (м)
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts. google.com
google.com
Подписи к слайдам:
Тема урока. ОПРЕДЕЛЕНИЕ КООРДИНАТЫ ДВИЖУЩЕГОСЯ ТЕЛА Урок 2
Скалярные и векторные величины траектория путь перемещение
Траектория – это линия, вдоль которой движется тело Пройденный путь – это длина траектории Перемещение – вектор, соединяющий начальное положение тело с его последующим положением s (м) s (м)
Определение пройденного пути и перемещения
Задача1. Автомобиль переместился из точки с координатой Х 0 =200 м в точку с координатой Х=-200 м. Определите проекцию перемещения автомобиля. Дано: Х 0 =200 м Х=-200 м S х -? Решение Вычисления S х =-200 м-200 м= -400 м Ответ: S х =-400 м
Определите по графику пройденный путь и модуль перемещения материальной точки. S =АВ+ВС+С D=8 м+4 м+8 м=20 м |S| =А D=4 м
Сборник задач по физике А.П. Рымкевич №и 9 №11 № 17
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts. google.com
google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Силы в динамике 19.11.15
Сила тяжести
Сила тяжести
Сила реакции опоры
Сила упругости – сила, возникающая при деформации тела, которая стремится восстановить прежние размеры и форму тела
ЗАКОН ГУКА F = – kx k – коэффициент жесткости (Н/м), зависит от материала пружины и геометрических размеров х – удлинение тела (м) х = ℓ 2 – ℓ 1
СРАВНЕНИЕ СИЛ Сила тяжести Сила упругости Вес тела Природа сил Направление Точка приложения Зависит от Формула
Сила трения – сила сопротивления относительному перемещению контактирующих поверхностей тел. Коэффициент трения μ – величина безразмерная. μ
Домашнее задание Таблица Подготовка к лабораторной работе Тетрадь для лабораторных работ
Подготовка к лабораторной работе
Определение коэффициента трения
***Задание. Груз скатывается с наклонной плоскости. Изобразите все силы действующие на тело.
Груз скатывается с наклонной плоскости. Изобразите все силы действующие на тело.
СРАВНЕНИЕ СИЛ Сила тяжести Сила упругости Вес тела Природа сил Гравитационная Электоро-магнитная Электоро-магнитная Направление К центру Земли Против деформации Различно Точка приложения Центр масс тела Центр масс тела Опора или подвес Зависит от массы тела и высоты над поверхностью коэффициента жесткости пружины и деформации массы тела, ускорения, внешней среды Формула F = mg F = – kx P = m(g±a)
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
13.01.16 Колебательное движение.
Что называют механическими колебаниями? Какие виды колебаний вам известны?
СВОБОДНЫЕ это колебания, происходящие под действием внутренних сил после того, как система была выведена из состояния равновесия. ВЫНУЖДЕННЫЕ это колебания, происходящие под действием внешних сил. Механические колебания – это движения, которые точно или приблизительно повторяются через равные промежутки времени
ВЫНУЖДЕННЫЕ это колебания, происходящие под действием внешних сил. Механические колебания – это движения, которые точно или приблизительно повторяются через равные промежутки времени
Перечислите величины характеризующие колебания
А Амплитуда – это модуль наибольшего значения изменяющейся величины. А [ А ] = м Амплитуда колебаний
Период – это время, за которое совершается одно колебание. [T] = с t T = n X , м t ,с 5 2 4 6 8 10 12 Т Т
Частота – это число колебаний совершаемых за 1 с. v = n t [ v ] = Гц Единица измерения названа так в честь немецкого физика Генриха Герца 1Гц – это одно колебания в секунду. Примерно с такой частотой бьётся человеческое сердце v = 1 T
Д/з §24-26 (Знать определения)
Стр.105 № 1-4 Подготовка к контрольной работе
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Равномерное движение по окружности. § 18-19, упр 18(1)
§ 18-19, упр 18(1)
Механическое движение Прямолинейное (Траектория – прямая) Криволинейное (Траектория – кривая) А О В О А В ДВИЖЕНИЕ
N S Стол (вид сверху) Магнит Наклонный желоб Шарик, скатившийся с желоба
Любую кривую можно всегда представить как совокупность дуг окружностей различных радиусов. ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ МЕНЯЮТСЯ: 1) Координаты 2)Направление движение 3)Направление и модуль скорости и ускорения Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость не меняется.
Мгновенная скорость тела в любой точке траектории направлена по касательной к траектории в этой точке. О А В
Равномерное движение по окружности – это движение по окружности с постоянной по модулю скоростью. А О R R – радиус окружности – начальная скорость В – конечная скорость При равномерном движении по окружности его ускорение во всех точках окружности устремлено к центру – центростремительное ускорение. – центростремительное ускорение В любой точке траектории:
Найдём модуль ускорения А В M N Рассмотрим ∆АОВ и ∆А MN ∆ АОВ – равнобедренный, т. к. ОА=ВО= R ∆ AMN – равнобедренный, т.к. Слайд 9
к. ОА=ВО= R ∆ AMN – равнобедренный, т.к. Слайд 9
По II З.Н. Сила, под действием которой тело движется по окружности с постоянной по модулю скоростью в каждой точке направлена по радиусу к центру окружности – сила центростремительная. Центростремительная сила
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
МУНИЦИПАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ДОМОДЕДОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 2 ФИЗИКА – 9 класс Учитель физики: ШЕКУНОВА Наталья Владимировна
Тема урока: Импульс. Закон сохранения импульса.
Импульсом тела называют векторную величину, равную произведению массы тела на его скорость:
Импульс p – векторная величина. Он всегда совпадает по направлению с вектором скорости тела. Любое тело, которое движется, обладает импульсом.
Понятие импульса
Система тел называется замкнутой, если взаимодействующие между собой тела, не взаимодействуют с другими телами.
В замкнутой системе, векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Закон сохранения импульса.
Проявление импульса
Когда пожарные используют брандс-пойт, они всегда держат его вдвоем или даже втроем. Так необходимо поступать, чтобы противодействовать импульсу бьющей струи.
Закон сохранения импульса на примере столкновения шаров.
Закон сохранения импульса
Дайте ответ: Что называется импульсом тела? Запишите формулу импульса тела. Какова единица измерения импульса тела в СИ? Что такое замкнутая система тел? Приведите примеры проявления закона сохранения импульса. #17. Задача: 1
Задача: На неподвижную тележку массой 100 кг. Прыгает человек массой 50 кг. Со скоростью 6 м / с. С какой скоростью начнет двигаться тележка с человеком?
Подписи к слайдам:
13.11.2015 Законы Ньютона
ВОПРОСЫ Какая СО называется инерциальной? Неинерциальной? Примеры. В каком случае тело движется равномерно? Что называется материальной точкой? Сформулировать первый закон Ньютона? Почему споткнувшийся человек падает вперед, а поскользнувшийся – назад? Почему мяч не остается в покое на наклонной плоскости?
ВОПРОСЫ 1. Что называется силой? 2. Чем характеризуется сила? 3. Как складываются силы, действующие на тело? 4. Как направлено ускорение тела? 5. Сформулируйте второй закон Ньютона? 6. Какую роль в движении играет масса? 7. Как движется тело, если F = 0 ? 8. Как движется тело, если на него действует сила?
Что называется силой? 2. Чем характеризуется сила? 3. Как складываются силы, действующие на тело? 4. Как направлено ускорение тела? 5. Сформулируйте второй закон Ньютона? 6. Какую роль в движении играет масса? 7. Как движется тело, если F = 0 ? 8. Как движется тело, если на него действует сила?
ВОПРОСЫ 1. Сформулировать третий закон Ньютона? 2. В чем заключены особенности этого закона? 3. Привести пример выполнения III закона. 4. Тело брошено под углом к горизонту. Куда направлено ускорение тела, если сопротивление воздуха не учитывать?
Ньютон Первый закон Второй закон Третий закон Границы применимости Макроскопическое тело Система двух тел Модель Материальная точка Система двух материальных точек Описываемое явление Состояние покоя или РПД РУД Взаимодействие тел Суть закона Если F = 0, то V = const F 12 = – F 21
В кинематике решается основная задача механики:
по известным начальным условиям и характеру движения определяется положение тела в любой момент времени.
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ
1. Выбрать удобную систему координат.
2. Схематично показать тела или материальные точки.
3. Показать векторы, начальные координаты, проекции векторов.
4. Записать основные уравнения (в векторной форме или в проекциях).
5. Найти проекции всех известных величин и подставить в уравнения.
6. Решить уравнения
ПРАВИЛА СЛОЖЕНИЯ ВЕКТОРОВ
При решении задач по механике требуется умение работать с векторными величинами.
Как, например, определить равнодействующую силу, если на тело одновременно действует несколько сил?
Как, например, определить направление движения пловца, переплывающего реку, если его сносит течением?
Для этого пригодится одно из правил сложения векторов:
Кинематика – Класс!ная физика
Знаете ли вы?
Наводнения на Марсе
Долгое время каналы на Марсе считали искусственными сооружениями, построенными жителями Марса. Над загадкой происхождения каналов ученые ломают головы и сегодня.
По одной из гипотез, марсианские каналы – результат наводнений, происходивших на планете миллионы лет назад.
Марсианские каналы, судя по фотографиям, очень разные – от небольших, размером со средний земной ручей, до огромных, глубиной в сотни метров и шириной до двух километров.
По мнению ученых, под поверхностью Марса когда-то находились огромные залежи льда. Падения метеоритов или процессы внутри планеты вызывали бурное его таяние. Потоки воды выплескивались на поверхность, образовывали каналы. Потом в холодной разреженной атмосфере Марса лед испарялся и частично возвращался на планету в виде снега.
На данном уроке, тема которого: «Определение координаты движущегося тела» мы поговорим о том, как можно определять место нахождения тела, его координату. Поговорим о системах отсчета, рассмотрим для примера задачу, а также вспомним, что такое перемещение
Представьте: вы изо всей силы бросили мяч. Как определить, где он будет находиться через две секунды? Можно подождать две секунды и просто посмотреть, где он. Но, даже не глядя, вы приблизительно можете предсказать, где будет мяч: бросок был сильнее обычного, направлен под большим углом к горизонту, значит, полетит высоко, но недалеко… Используя законы физики, можно будет точно определить положение нашего мяча.
Но, даже не глядя, вы приблизительно можете предсказать, где будет мяч: бросок был сильнее обычного, направлен под большим углом к горизонту, значит, полетит высоко, но недалеко… Используя законы физики, можно будет точно определить положение нашего мяча.
Определить положение движущегося тела в любой момент времени – это и есть основная задача кинематики.
Начнем с того, что у нас есть тело: как определить его положение, как объяснить кому-то, где оно находится? Об автомобиле мы скажем: он на дороге за 150 метров перед светофором или на 100 метров за перекрестком (см. рис. 1).
Рис. 1. Определение местоположения машины
Или на трассе за 30 км к югу от Москвы. О телефоне на столе скажем: он сантиметров на 30 правее клавиатуры или рядом с дальним углом стола (см. рис. 2).
Рис. 2. Положение телефона на столе
Заметьте: мы не сможем определить положение автомобиля, не упомянув другие объекты, не привязавшись к ним: светофор, город, клавиатуру. Мы определяем положение, или координаты, всегда относительно чего-то.
Мы определяем положение, или координаты, всегда относительно чего-то.
Координаты – это набор данных, по которому определяется положение того или иного объекта, его адрес.
Примеры упорядоченных и неупорядоченных имен
Координата тела – это его адрес, по которому мы его можем найти. Он упорядоченный. Например, зная ряд и место, мы точно определяем, где находится наше место в зале кинотеатра (см. рис. 3).
Рис. 3. Зал кинотеатра
Буквой и цифрой, например e2, точно задается положение фигуры на шахматной доске (см. рис. 4).
Рис. 4. Положение фигуры на доске
Зная адрес дома, например улица Солнечная 14, мы будем искать его на этой улице, на четной стороне, между домами 12 и 16 (см. рис. 5).
Рис. 5. Поиск дома
Названия улиц не упорядочены, мы не будем искать Солнечную улицу по алфавиту между улицами Розовой и Тургенева. Также не упорядочены номера телефонов, номерные знаки автомобилей (см. рис. 6).
Рис. 6. Неупорядоченные имена
Эти номера, идущие подряд, – это лишь совпадение, не означающее соседства.
Мы можем задать положение тела в разных системах координат, как нам удобно. Для того же автомобиля, можно задать точные географические координаты (широту и долготу) (см. рис. 7).
Рис. 7. Долгота и широта местности
Рис. 8. Местоположение относительно точки
Причем если мы выберем разные такие точки, то получим разные координаты, хотя они будут задавать положение одного и того же автомобиля.
Итак, положение тела относительно разных тел в разных системах координат будет разным. А что такое движение? Движение – это изменение положения тела со временем. Поэтому описывать движение мы будем в разных системах отсчета по-разному, и нет смысла рассматривать движение тела без системы отсчета.
Например, как движется стакан с чаем на столе в поезде, если сам поезд едет? Смотря относительно чего. Относительно стола или пассажира, сидящего рядом на сидении, стакан покоится (см. рис. 9).
рис. 9).
Рис. 9. Движение стакана относительно пассажира
Относительно дерева около железной дороги стакан движется вместе с поездом (см. рис. 10).
Рис. 10. Движение стакана вместе с поездом относительно дерева
Относительно земной оси стакан и поезд вместе со всеми точками земной поверхности будут еще и двигаться по окружности (см. рис. 11).
Рис. 11. Движение стакана с вращением Земли относительно земной оси
Поэтому нет смысла говорить о движении вообще, движение рассматривается в привязке к системе отсчета.
Всё, что мы знаем о движении тела, можно разделить на наблюдаемое и вычисляемое. Вспомним пример с мячом, который мы бросили. Наблюдаемое – это его положение в выбранной системе координат, когда мы его только бросаем (см. рис. 12).
Рис. 12. Наблюдение
Это момент времени, когда мы его бросили; время, которое прошло после броска. Пусть на мяче нет спидометра, который показал бы скорость мяча, но ее модуль, как и направление, тоже можно узнать, используя, например, замедленную съемку.
С помощью наблюдаемых данных мы можем предсказать, например, что мяч через 5 секунд упадет за 20 м от места броска или через 3 секунды попадет в верхушку дерева. Положение мяча в любой момент времени – это в нашем случае вычисляемые данные.
Что определяет каждое новое положение движущегося тела? Его определяет перемещение, потому что перемещение – это вектор, характеризующий изменение положения. Если начало вектора совместить с начальным положением тела, то конец вектора укажет на новое положение переместившегося тела (см. рис. 13).
Рис. 13. Вектор перемещения
Рассмотрим несколько примеров на определение координаты движущегося тела по его перемещению.
Пусть тело двигалось прямолинейно из точки 1 в точку 2. Построим вектор перемещения и обозначим его (см. рис. 14).
Рис. 14. Перемещение тела
Тело двигалось вдоль одной прямой, значит, нам будет достаточно одной оси координат, направленной вдоль перемещения тела. Допустим, мы наблюдаем за движением со стороны, совместим начало отсчета с наблюдателем.
Перемещение – вектор, удобнее работать с проекциями векторов на оси координат (у нас она одна). – проекция вектора (см. рис. 15).
Рис. 15. Проекция вектора
Как определить координату начальной точки, точки 1? Опускаем перпендикуляр из точки 1 на ось координат. Этот перпендикуляр пересечет ось и отметит на оси координату точки 1. Так же определяем координату точки 2 (см. рис. 16).
Рис. 16. Опускаем перпендикуляры на ось ОХ
Проекция перемещения равна:
При таком направлении оси и перемещения будет по модулю равна самому перемещению .
Зная начальную координату и перемещение, найти конечную координату тела – дело математики:
Уравнение
Уравнение – это равенство, содержащее неизвестный член. В чем его смысл?
Любая задача заключается в том, что что-то нам известно, а что-то – нет, и неизвестное нужно найти. Например, тело из некоторой точки переместилось на 6 м в направлении оси координат и оказалось в точке с координатой 9 (см. рис. 17).
рис. 17).
Рис. 17. Начальное положение точки
Как найти, из какой точки тело начало движение?
У нас есть закономерность: проекция перемещения – это разность конечной и начальной координат:
Смысл уравнения будет в том, что перемещение и конечную координату мы знаем () и можем подставить эти значения, а начальную координату не знаем, она будет неизвестным в этом уравнении:
И уже решая уравнение, мы получим ответ: начальная координата .
Рассмотрим другой случай: перемещение направлено в сторону, противоположную направлению оси координат.
Координаты начальной и конечной точек определяются так же, как и раньше, – опускаются перпендикуляры на ось (см. рис. 18).
Рис. 18. Ось направлена в другую сторону
Проекция перемещения (ничего не меняется) равна:
Обратите внимание, что больше, чем , и проекция перемещения , когда она направлена против оси координат, будет отрицательной.
Конечная координата тела из уравнения для проекции перемещения равна:
Как видим, ничего не меняется: в проекции на ось координат конечное положение равно начальному положению плюс проекция перемещения. В зависимости от того, в какую сторону тело переместилось, проекция перемещения будет положительной или отрицательной в данной системе координат.
В зависимости от того, в какую сторону тело переместилось, проекция перемещения будет положительной или отрицательной в данной системе координат.
Рассмотрим случай, когда перемещение и ось координат направлены под углом друг к другу. Теперь одной оси координат нам недостаточно, нужна вторая ось (см. рис. 19).
Рис. 19. Ось направлена в другую сторону
Теперь перемещение будет иметь ненулевую проекцию на каждую ось координат. Эти проекции перемещения будут определяться, как и раньше:
Заметьте, модуль каждой из проекций в этом случае меньше модуля перемещения. Модуль перемещения можем легко найти, используя теорему Пифагора. Видно, что если построить прямоугольный треугольник (см. рис. 20), то его катеты будут равны и , а гипотенуза равна модулю перемещения или, как часто записывают, просто .
Рис. 20. Треугольник Пифагора
Тогда по теореме Пифагора запишем:
Автомобиль находится в 4 км к востоку от гаража. Воспользуйтесь одной осью координат, направленной на восток, с началом отсчета в гараже. Укажите координату автомобиля в заданной системе через 3 минуты, если автомобиль этим временем ехал со скоростью 0,5 км/мин на запад.
Укажите координату автомобиля в заданной системе через 3 минуты, если автомобиль этим временем ехал со скоростью 0,5 км/мин на запад.
В задаче ничего не сказано о том, что автомобиль поворачивал или изменял скорость, поэтому считаем движение равномерным прямолинейным.
Изобразим систему координат: начало координат у гаража, ось х направлена на восток (см. рис. 21).
Автомобиль изначально был в точке и двигался по условию задачи на запад (см. рис. 22).
Рис. 22. Движение автомобиля на запад
Проекция перемещения, как мы неоднократно писали, равна:
Мы знаем, что автомобиль проезжал по 0,5 км каждую минуту, значит, чтобы найти суммарное перемещение, нужно скорость умножить на количество минут :
На этом физика закончилась, осталось математически выразить искомую координату. Выразим ее из первого уравнения:
Подставим перемещение:
Осталось подставить числа и получить ответ. Не забывайте, что автомобиль двигался на запад против направления оси х, это значит, что проекция скорости отрицательна: .
Задача решена.
Главное, чем мы сегодня пользовались для определения координаты, – выражение для проекции перемещения:
И из него мы уже выражали координату:
При этом сама проекция перемещения может быть задана, может вычисляться как , как в было в задаче о равномерном прямолинейном движении, может вычисляться сложнее, что нам еще предстоит изучить, но в любом случае координату движущегося тела (где тело оказалось) можно определить по начальной координате (где тело было) и по проекции перемещения (куда переместилось).
На этом наш урок окончен, до свидания!
Список литературы
- Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание, передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
- Перышкин А.В., Гутник Е.М. Физика: 9 класс. Учебник для общеобразовательных учреждений. – 14-е изд. – М.: Дрофа, 2009.
- Class-fizika.narod.ru ().
- Av-physics.narod.ru ().

- Class-fizika.narod.ru ().
Домашнее задание
- Что такое перемещение, путь, траектория?
- Как можно определить координаты тела?
- Запишите формулу для определения проекции перемещения.
- Как будет определяться модуль перемещения, если перемещение имеет проекции на две оси координат?
§1.2 Преобразование координат – Физика 10 класс. Раздел “Механика”
Как следует из рис. 2, координаты точки A в сдвинутой и исходной системах связаны очевидными соотношениями.
Какую из этих систем считать исходной, а какую сдвинутой, безразлично – системы полностью равноправны. Заметьте, что обратные преобразования могут быть получены заменой (x0,y0) на (-x0,-y0) . Последняя пара чисел является координатами начала отсчет исходной системы в сдвинутой.
Эти же
преобразования короче могут быть записаны и в векторной форме (рис. 3)
3)
Аналогичные преобразования при параллельном сдвиге начала отсчета могут быть получены и в трехмерном случае. Более сложный вид имеют формулы преобразования координат при повороте осей (в нашем изложении они нам не понадобятся, поэтому приводить их не будем). Важно, что в любом случае можно найти формулы, позволяющие переходить из одной системы координат в другую. Это обстоятельство, указывает, что произвол в выборе системы координат не вносит существенных трудностей в описание движения тел.
Коротко о главном: |
Как уже было отмечено, координаты точки относительны, они изменяются при переходе в другую систему координат. Во многих случаях, требуется перейти из одной системы координат в другую. Получим формулы таких преобразований для одного частного случая – сдвига начала отсчета на плоскости.
Контрольные вопросы: |
1. Как перенести числа
из одной системы координат в другую?
Как перенести числа
из одной системы координат в другую?
2. Какова векторная формула преобразований из одной системы координат в другую?
Сферические координаты
Запишем вектор положения $ \ vec {r} = r \ cos \ theta \ sin \ phi \, \ hat {\ imath} + r \ sin \ theta \ sin \ phi \, \ hat {\ jmath} + r \ cos \ phi \, \ hat {k} $, а затем используйте определение базисных векторов координат для нахождения ненормированные сферические базисные векторы:
\ [\ begin {выровнено} \ vec {e} _r & = \ frac {\ partial \ vec {r}} {\ partial r} = \ cos \ theta \ sin \ phi \, \ hat {\ imath} + \ sin \ theta \ sin \ phi \, \ hat {\ jmath} + \ cos \ phi \, \ hat {k} \\ \ vec {e} _ \ theta & = \ frac {\ partial \ vec {r}} {\ partial \ theta} = -r \ sin \ theta \ sin \ phi \, \ hat {\ imath} + г \ соз \ тета \ грех \ фи \, \ шляпа {\ jmath} \\ \ vec {e} _ \ phi & = \ frac {\ partial \ vec {r}} {\ partial \ phi} = г \ соз \ тета \ соз \ фи \, \ шляпа {\ imath} + г \ грех \ тета \ соз \ фи \, \ шляпа {\ jmath} – г \ грех \ фи \, \ шляпа {к} \ конец {выровнено} \]
Чтобы нормализовать эти векторы, мы разделим их на длину,
которую мы можем вычислить как $ \ | \ vec {e} _r \ | = 1 $, $ \ |
\ vec {e} _ \ theta \ | = r \ sin \ phi $ и $ \ | \ vec {e} _ \ phi \ |
= г $.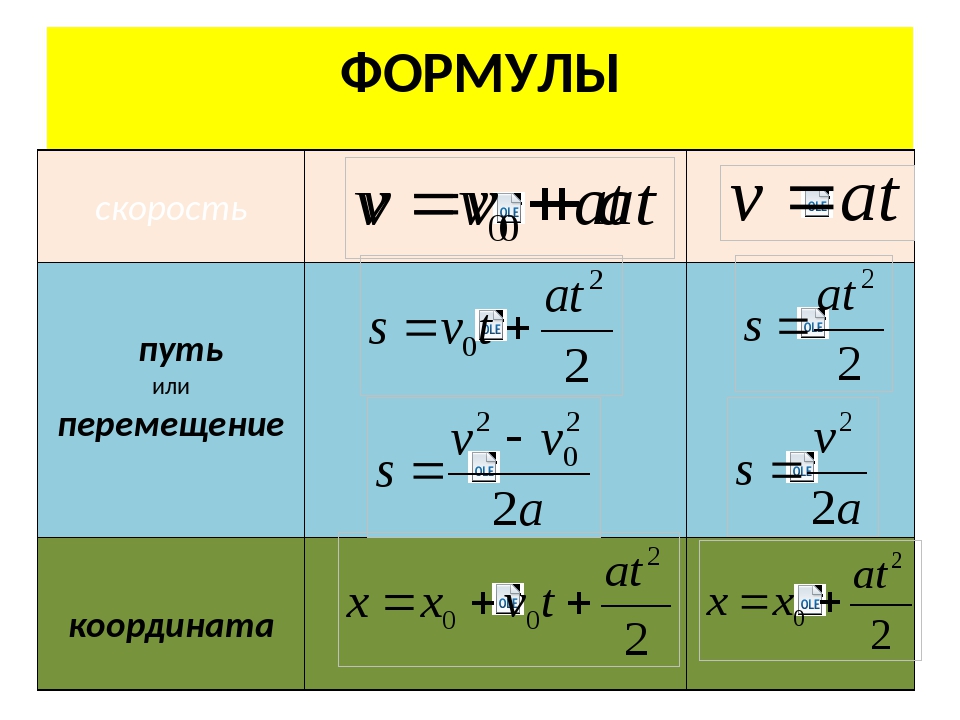 2 \ theta \, \ hat {\ jmath}
= \ шляпа {\ jmath}
\ конец {выровнено} \]
2 \ theta \, \ hat {\ jmath}
= \ шляпа {\ jmath}
\ конец {выровнено} \]
Их перестановка дает приведенные выше выражения декартовых векторов базиса.
Цилиндрические и сферические координаты: определение, уравнения и примеры – видео и стенограмма урока
Полярные системы координат
Идея цилиндрических и сферических координат заключается в использовании углов вместо декартовых координат для задания точек в трех измерениях. Иногда использование углов может упростить математическое представление функций. Полярные координаты представляют точки в координатной плоскости, но не с обычной декартовой упорядоченной парой (x, y) , а с двумя разными координатами (r, phi) , которые функционально связаны с (x, y) .В частности, для данной точки P , r – это абсолютное расстояние от начала координат до P . Угол phi представляет собой угловое положение P с углом, отсчитываемым от положительной оси x .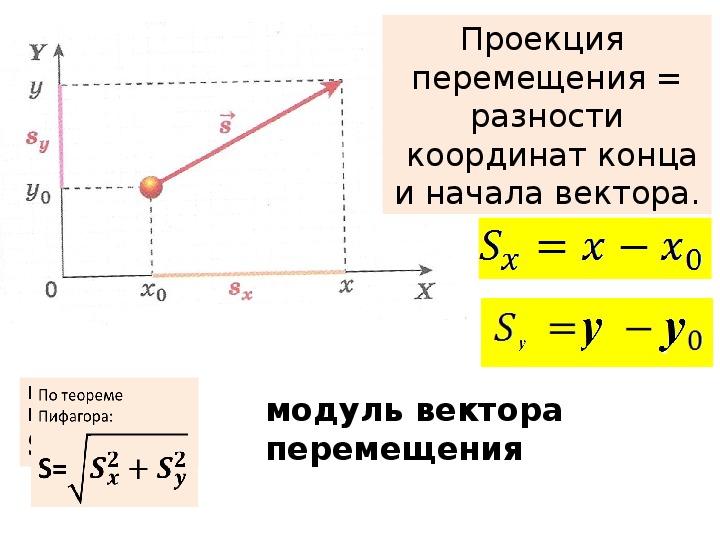 Цилиндрическая и сферическая системы координат являются расширением двумерных полярных координат в трехмерное пространство.
Цилиндрическая и сферическая системы координат являются расширением двумерных полярных координат в трехмерное пространство.
Цилиндрические координаты
Цилиндрические координаты наиболее похожи на двумерные полярные координаты. Давайте рассмотрим точку P , которая имеет координаты (x, y, z) в трехмерной декартовой системе координат.Эта же точка может быть представлена в цилиндрических координатах (r, phi, z) , где r и phi – двумерные полярные координаты изображения P в плоскости xy ( z = 0 ), а z в точности совпадает с декартовой z-координатой P . Вот соотношение между декартовой и цилиндрической координатами точки на графике:
Преобразования координат для перехода от декартовых координат x и y к цилиндрическим координатам r и phi следующие:
Это то же самое, что преобразование в двумерные полярные координаты.
Следует отметить несколько особенностей этого преобразования. Во-первых, координата r при этом преобразовании всегда является положительным числом. r интерпретируется как наименьшее расстояние от P до оси z . Кроме того, phi , выраженное в радианах, всегда будет находиться в диапазоне от -pi до pi .Координата z сохраняет то же значение при преобразовании из одной системы в другую. Обратное преобразование из (r, theta, z) в (x, y, z) также может быть знакомо из двумерных полярных координат.
Рассмотрим следующий вопрос в качестве примера применения преобразования координат: каковы декартовы координаты (x, y, z) точки P, заданной цилиндрическими координатами (2, -pi / 6, 1 ) ?
При переходе от цилиндрических координат к декартовым координата z не изменяется. z обычно является третьим значением в упорядоченном триплете, поэтому z = 1 как в цилиндрических, так и в декартовых координатах. Теперь, чтобы найти x и y , мы должны подставить значения r = 2 и phi = -pi / 6 в уравнения преобразования.
z обычно является третьим значением в упорядоченном триплете, поэтому z = 1 как в цилиндрических, так и в декартовых координатах. Теперь, чтобы найти x и y , мы должны подставить значения r = 2 и phi = -pi / 6 в уравнения преобразования.
Следовательно, декартовы координаты этой точки равны (sqrt (3), -1, 1) .
Сферические координаты
Цилиндрические координаты – не единственный способ указать точку в трехмерном пространстве с помощью угла. Сферические координаты – еще одно обобщение двумерных полярных координат. Однако в этой системе координат есть два угла: theta и phi .
Рассмотрим точку P , заданную координатами (x, y, z) в трехмерной декартовой системе координат. Эта же точка может быть представлена в сферических координатах как (r, theta, phi,) , где r , theta и phi функционально связаны с x , y и z , как мы увидим.
В сферических координатах r – это расстояние от начала координат до точки P вдоль линии, соединяющей их. Первый угол, theta , часто называют полярным углом , потому что он проходит между «полюсами» системы координат, отрицательной и положительной осями z . Theta принимает значение 0 по положительной оси z и pi по отрицательной оси z . Второй угол, phi , называется азимутальным углом , и он идентичен углу phi в цилиндрических координатах.
Преобразования координат переводят точку P в декартовых координатах в соответствующие ей сферические координаты. Следует отметить несколько особенностей этого преобразования. Радиальная координата r при этом преобразовании всегда является положительным числом, которое точно равно евклидову расстоянию от P до начала координат.
Также обратите внимание, что два угла принимают разные диапазоны значений. Полярный угол тета , выраженный в радианах, всегда должен находиться в диапазоне от 0 до пи , но азимутальный угол фи может указывать в любом направлении в плоскости xy , поэтому он принимает значения от -pi до пи .
В зависимости от геометрии обратное преобразование переводит сферические координаты обратно в декартовы координаты.
Рассмотрим пример: каковы сферические координаты (r, theta, phi) точки P, заданные декартовыми координатами (3, -sqrt (3), -2) ?
При переходе от декартовых координат к сферическим следует использовать следующие вычисления:
Приложение: карты звездного неба
Карты звездного неба – это обычное применение сферических координат. По наблюдениям на Земле, звезды кажутся нам внутри сферы с центром вокруг нас. Хотя ранние астрономы и философы считали, что все звезды находятся на одинаковом расстоянии от нас, теперь мы знаем, что точное расстояние до каждой звезды, которую мы видим, разное.
По наблюдениям на Земле, звезды кажутся нам внутри сферы с центром вокруг нас. Хотя ранние астрономы и философы считали, что все звезды находятся на одинаковом расстоянии от нас, теперь мы знаем, что точное расстояние до каждой звезды, которую мы видим, разное.
В сферических координатах относительное положение звезд на небе может быть указано двумя числами (тета, фи) . Фактическое трехмерное расстояние можно включить, задав координату r для каждой звезды.На картах звездного неба для звездочетов обычно используется дополнительный угол к полярному углу theta , который называется высотой , чтобы найти звезду.
Резюме урока
Полярные системы координат используют углы как координаты точек. Цилиндрическая и сферическая системы координат являются обобщением двумерных полярных координат в трех измерениях. Полярные координаты представляют точки на координатной плоскости не с обычной декартовой упорядоченной парой ( x , y ), а с двумя разными координатами ( r , phi ).
Полярные координаты представляют точки на координатной плоскости не с обычной декартовой упорядоченной парой ( x , y ), а с двумя разными координатами ( r , phi ).
Цилиндрические координаты наиболее похожи на двумерные полярные координаты. Они используют ( r , phi , z ), где r и phi – это двумерные полярные координаты изображения P в плоскости x – y и z. в точности совпадает с декартовой координатой P z .
В сферических координатах , другой угол, полярный угол theta , также определяется для задания точки в 3-D. Эти системы координат используются астрономами и инженерами для упрощения математических моделей интересующих систем.
Определение объема внутренней части сферы с использованием сферических координат
Хотя хорошо известный Архимед вывел формулу для внутренней части сферы задолго до нашего рождения, ее вывод, полученный с помощью сферических координат и интеграла по объему, не часто встречается в учебниках для студентов. 3,
3,
\ end {формула}
где $ r $ – радиус.
Обратите внимание на слово «шар» вместо «сфера»; последнее обозначает бесконечно тонкую оболочку или поверхность идеально круглого геометрического объекта в трехмерном пространстве. Поверхность не имеет объема, поэтому мы предпочитаем называть ее шаром.
Это можно рассматривать как должность второго года обучения в университете.
Сферические координаты
Объем кубоида $ \ delta V $ длиной $ a $, шириной $ b $, высотой $ c $ определяется как $ \ delta V = a \ times b \ times c $.
Рисунок 1: Элемент объема шараНа рисунке 1 вы видите эскиз элемента объема шара. Хотя его края изогнуты, для расчета его объема здесь также можно использовать
\ begin {уравнение}
\ delta V \ приблизительно a \ times b \ times c,
\ end {уравнение}
, хотя это только приблизительное значение.
Чтобы использовать сферические координаты, мы можем определить $ a $, $ b $ и $ c $ следующим образом:
\ begin {align}
a & = PQ \ delta \ phi = r \ sin \ theta \, \ delta \ phi, \\
b & = r \ delta \ theta, \\
c & = \ delta r. 2 \ sin \ theta \, dr \, d \ theta \, d \ phi.
2 \ sin \ theta \, dr \, d \ theta \, d \ phi.
\ end {формула *}
Чтобы установить верхнюю и нижнюю границы для наших интегралов, отметим, что шар обладает симметрией вращения относительно оси $ z $ (помимо бесконечного множества других, проходящих через центр).3,
\ end {align}
, что является желаемым результатом, равным уравнению (1).
Положение и перемещение
Положение и перемещениеПоложение и перемещение
Многие предметы, с которыми мы сталкиваемся в повседневной жизни, находятся в движении или состоят из частей.
которые находятся в движении. Движение – это правило, а не исключение. Физические законы, управляющие движением
этих объектов
универсальны, т.е. все объекты движутся по одним и тем же правилам,
и одна из целей этого класса – понять эти правила.
Физические законы, управляющие движением
этих объектов
универсальны, т.е. все объекты движутся по одним и тем же правилам,
и одна из целей этого класса – понять эти правила.
Когда объект движется, его позиция изменяется как функция времени.
Положение объекта
дано относительно некоторой согласованной точки отсчета. Недостаточно просто
укажите расстояние от
ориентир. Также необходимо указать направление . Расстояние – это скаляр количество, это число, указанное в каких-то единицах .Позиция вектор количество. У него тоже есть величина
как направление. Величина векторной величины – это число (в единицах измерения).
сообщая вам, сколько существует количества, и направление сообщает вам, какие
как он указывает. Единичный вектор – это направление
показатель. Это безразмерный вектор с величиной 1, используемый для определения
направление. В тексте векторные величины обычно выделяются жирным шрифтом.
введите или со стрелкой над символом.Таким образом, хотя d = расстояние, д = смещение.
Это безразмерный вектор с величиной 1, используемый для определения
направление. В тексте векторные величины обычно выделяются жирным шрифтом.
введите или со стрелкой над символом.Таким образом, хотя d = расстояние, д = смещение.
Ссылки:
Скаляры и векторы
(Пожалуйста, исследуйте!)
Направление вектора
Позиция
Удобный способ указать позицию
объекта
с помощью системы координат .
Мы выбираем фиксированную точку, которая называется исходной точкой .
и три направленные линии, которые проходят через начало координат и являются
перпендикулярны друг другу.Эти линии называются осями координат .
трехмерной прямоугольной (декартовой) системы координат и помечены
оси x, y и z. Три числа с единицами измерения определяют положение
точка P. Эти числа представляют собой координаты x, y и z точки P.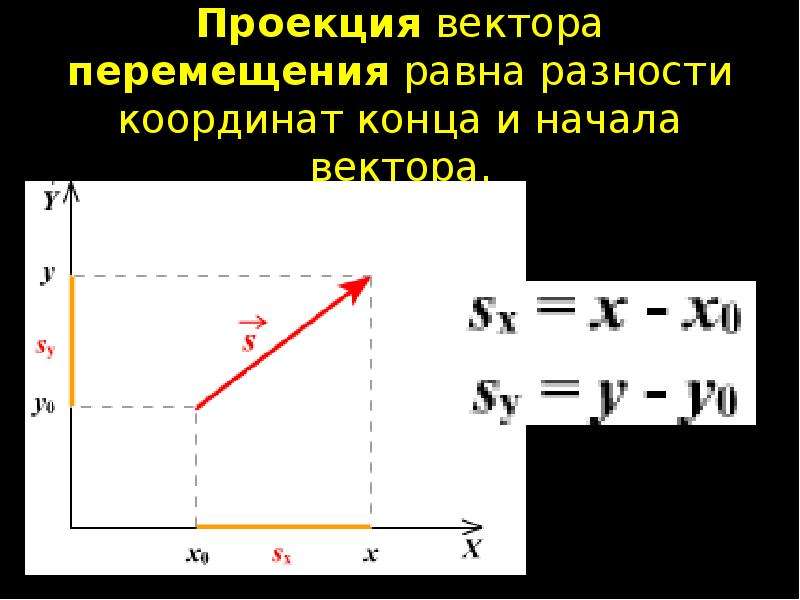 Координаты точки P в
На диаграмме справа находятся (a, b, c).
Координаты точки P в
На диаграмме справа находятся (a, b, c).
Координаты точки P являются компонентами вектора положения.Единичный вектор указание в направлении x имеет x-компоненту 1, а y- и z- компоненты нуль. Обозначается он i . Аналогично единичный вектор указывающий в направлении y, обозначается как j , а единичный вектор в направлении оси z обозначается k . Единичные векторы указатели поворота.
Компоненты любого вектора складываются, чтобы сформировать
вектор.
Вектор положения точки P с координатами (a, b, c)
может быть записано в терминах его компонентов как r = a i + b j +
c к .
| Величина вектора положения равна его длине r. Это
зависит от выбора начала системы координат. Это
расстояние по прямой от точки P до начала координат.
Ниже представлено трехмерное представление вектора положения. r = a i + b j + c k . Пожалуйста, нажмите
на рисунке!
r = a i + b j + c k . Пожалуйста, нажмите
на рисунке!
(Используйте современный браузер. 3D-приложения не работают в Internet Explorer.
или более старые браузеры.)
Чтобы получить наилучший вид, измените область просмотра, перетащив мышь и
увеличивайте или уменьшайте масштаб по мере необходимости.
Нажмите кнопки, чтобы выбрать другой вектор
или другая схема добавления составляющих векторов.
Пример:
Вектор положения здания Nielsen Physics Building на небольшой карте с левым нижним углом в качестве начала координат.
Рабочий объем
Изменение положения называется смещением .На диаграмме ниже показан позиции P 1 и P 2 игрока в два разных момента времени.
Стрелка, указывающая от P 1 к P 2 , – это вектор смещения .
Его величина прямолинейная. расстояние между P 1 и P 2 .
Составляющие вытеснения
вектор из P 1 в
P 2 – это (x 2 – x 1 ) вдоль оси x, (y 2 –
y 1 ) по оси y.
Вектор смещения d от P 1 до P 2 май
можно записать как d = (x 2 – x 1 ) i + (y 2 – y 1 ) j .
Смещение d – это (x 2 – x 1 ) единиц в
Направление x плюс (y 2 – y 1 ) единиц в направлении y.
Величина смещения
равно d = ((x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 ) ½ .Этот
следует из
Пифагорейский
теорема.
Расстояние между двумя точками P 1 с координатами (x 1 ,
y 1 ,
z 1 ) и P 2 с координатами (x 2 , y 2 , z 2 ) составляет
d =
((x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 + (z 2 – z1) 2 ) ½ .
- Расстояние d – это величина вектора смещения d .
- Направление вектора смещения d – это направленный отрезок прямой от точки P 1 к P 2 .
- Мы называем этот направленный отрезок геометрической или графической представление вектора d .
- Нарисуем острие стрелки на P 2 , чтобы указать что отрезок начинается в точке P 1 и заканчивается в точке P 2 .
Тройка действительных чисел d x = (x 2 – x 1 ), d y = (y 2 – y 1 ), d z = (z 2 – z 1 ) называются декартовыми компонентами d .
Ссылка: Расстояние и смещение (пожалуйста, исследуйте!)
Задача:
Футбольный защитник пробежал 15. 0 мес.
прямо по игровому полю (в
положительное направление x) за 2,50 с.
Затем его бьют и толкают на 3,00 м.
прямо назад за 1,75 с. Он
ломает подкат и бежит прямо
вперед еще 21,0 м за 5,20 с.
Рассчитайте его вектор смещения и
общее пройденное расстояние.
0 мес.
прямо по игровому полю (в
положительное направление x) за 2,50 с.
Затем его бьют и толкают на 3,00 м.
прямо назад за 1,75 с. Он
ломает подкат и бежит прямо
вперед еще 21,0 м за 5,20 с.
Рассчитайте его вектор смещения и
общее пройденное расстояние.
Решение:
- Рассуждение:
Выберите систему координат, чтобы вы могли отслеживать игрока. - Детали расчета:
Выберите свою систему координат, чтобы игрок начинает с x = 0. После 2,5 с, он попадает на х = 15 м.
Затем он отступает на 3 м и заканчивает вверх при x = 12 м еще через 1,75 с.
Он продвигается вперед на 21 м в следующем 5,2 с и заканчивается на x = 12 м + 21 м. = 33 м.
Его смещение вектор d = (33 м) i , то есть 33 м вперед.
Его общее пройденное расстояние 15 м. + 3 м + 21 м = 39 м.
Примечание: общее пройденное расстояние НЕ ЯВЛЯЕТСЯ расстоянием по прямой. от начальной до конечной точки, если объект не движется по прямой
линия без изменения направления.
от начальной до конечной точки, если объект не движется по прямой
линия без изменения направления.
Проблема:
Путешествуя по прямой автомагистрали между штатами, вы обратите внимание, что отметка мили показывает 260. Вы путешествуете, пока не достигнете отметки в 150 миль. маркер, а затем вернитесь к маркеру длиной 175 миль.Что величина вашего результирующего смещения от отметки 260 миль?
Решение:
- Рассуждение:
Результирующее смещение – это вектор d , сумма двух векторов д 1 и d 2 , которые указывают в противоположных направлениях. - Детали расчета:
Результирующее смещение – это вектор d , сумма двух векторов д 1 и d 2 , которые указывают в противоположных направлениях.
Проблема:
Острие лопасти вертолета
5,00 м от центра вращения. За один оборот лезвия
вычислить вектор смещения и
общее расстояние, пройденное наконечником
лезвия.
За один оборот лезвия
вычислить вектор смещения и
общее расстояние, пройденное наконечником
лезвия.
Решение:
- Рассуждение:
После одного оборота наконечник возвращается в исходное положение. Его вектор смещения d = 0. - Детали расчета:
Общее пройденное расстояние по кончику равняется окружности окружности радиуса r = 5 м.
Окружность = 2πr = 31,42 м.
Общее расстояние, пройденное наконечник 31,42 м.
Вектор смещения имеет одинаковую величину и направление, независимо от выбор начала координат системы координат. Величина и направление вектор смещения, однако, зависит от системы отсчета , в которой система координат закреплена и находится в состоянии покоя.
Пример:
Автомобиль двинулся вперед
расстояние 6 м, пока ребенок продвинулся с заднего сиденья вперед
сиденье на расстоянии 1 м.
- Использование автомобиля в качестве системы отсчета и привязка системы координат в машине водоизмещение ребенка d (автомобиль) = (1 м) i .
- Использование дороги в качестве системы отсчета и привязка системы координат в дороге перемещение ребенка d (дорога) = (6 м) i + (1 м) i = (7 м) i .
Полярные координаты
Полярные координаты (c) Коалиция Фонда авторского права (С. А. Фуллинг) 1997Класс 6.3 (и 17.M)
Задание по чтению на пятницу, 10 октября
- Stewart 9.4 (Пропустите “Касательные к полярным кривым”, стр. 569-570.)
- Эта веб-страница
- Загляните в главу XII книги Don’t Panic чтобы увидеть, как будут использоваться полярные единичные векторы.
Как и вся эта неделя, сегодня добавлен в стандартную программу
исчисление первого семестра, чтобы предоставить некоторые инструменты, необходимые физике для описания
мир более чем одного измерения. Первая тема, полярные координаты, традиционно рассматривается где-то позже.
в последовательности исчисления.
Вторая тема, полярные единичные векторы, вообще не фигурирует в большинстве расчетов.
учебники. Тем не менее, это логичное место для нас, чтобы представить его.
как на уроках математики, так и на уроках физики.
Мы вернемся к этому в следующем семестре в классе физики и математической лаборатории.
Первая тема, полярные координаты, традиционно рассматривается где-то позже.
в последовательности исчисления.
Вторая тема, полярные единичные векторы, вообще не фигурирует в большинстве расчетов.
учебники. Тем не менее, это логичное место для нас, чтобы представить его.
как на уроках математики, так и на уроках физики.
Мы вернемся к этому в следующем семестре в классе физики и математической лаборатории.
Полярные координаты
Гравитационная сила Земли на спутнике зависит в первую очередь от расстояние спутника от центра Земли.Это пример широкого класса задач, в которых наиболее важные Свойство точки в пространстве – это ее удаленность от некоторой особой точки. Первый разумный шаг – выбрать особую точку в качестве начала отсчета. система координат. Но часто бывает полезно пойти дальше: вместо указания переменной точки по ее координатам x и y относительно некоторого произвольного выбор осей через начало координат, почему бы не обозначить точку наиболее соответствующая величина, ее расстояние от источника, вместе с некоторыми указание его направления от начала координат? В двухмерном пространстве направление может быть указано одним числом, угол между вектором к точке и некоторой осью.
Таким образом, мы приходим к полярной системе координат на плоскости. По определению r – это расстояние нашей переменной точки от начало координат, а ì ì угол между положительной осью x и вектор, представляющий точку.
Примечание. Поскольку Интернет еще не говорит легко по-гречески, мы будем использовать Исландская буква ì для «тета».
Формулы, выражающие декартовы координаты точки через полярные координаты (элементарной тригонометрией)
x = r cos ì , y = r sin ì .(1)
Обратный путь немного сложнее. Найти r легко: возведя в квадрат оба уравнения (1) и сложив и извлечение квадратного корня (или просто вспомнив формулу расстояния между двумя точками) ты ищешь
r = (x 2 + y 2 ) 1/2 . (2)
Но обнаружение ì вызывает некоторые технические вопросы. Разделив второе из уравнений (1) на первое, получим
Разделив второе из уравнений (1) на первое, получим
тангенс Ð = y / x. (3)
Если вы уже знаете о функции арктангенса (Стюарт, раздел 6.6), у вас может возникнуть соблазн написать
Ð = arctan y / x = tan -1 y / x ,
но это не совсем правильно. Узнайте больше о технических тонкостях определения теты. (пока недоступно)
Полярные единичные векторы
Вернемся к проблеме спутника, вращающегося вокруг Земли, и рассмотрим вектор v = x, v y > связанные со спутником, такие как скорость или ускорение спутник.(Напомним, что такой вектор лучше всего изобразить стрелкой с хвостом в положении спутника, который служит источником частная система координат спутника.) Для анализа физики в гравитационном поле Земли наиболее полезны разложение v не на его декартовы компоненты v x и v y , а скорее в ее компонент в направлении (или от) Земли и ее компонент в направлении, перпендикулярном ему. С этой точки зрения физика проста – почти одномерная!
С этой точки зрения физика проста – почти одномерная!Другими словами, мы хотим заменить частную декартову систему на спутнике. систему координат с помощью повернутой системы координат. Это то же самое, что и проблемы с ортогональным базисом, которые мы рассматривали в день 6.1, с дополнительным усложнением, что новый ортогональный базис теперь изменяется от указывать на точку в пространстве. В каждой точке нам нужно найти пару ортогональных единичных векторов, один из которых указывает в радиальном направлении, а другой – в направлении увеличения тета; а затем нам нужно попрактиковаться в разложении произвольного вектора на компоненты вдоль этих двух базисных векторов.
Важно отличать этот расчет от другого, который также
включает полярные координаты.
Для вектора v = x, v y > ,
мы могли бы представить его в полярных координатах, используя такие формулы, как
(1) – (3) выше, но с v x и v y вместо x и y .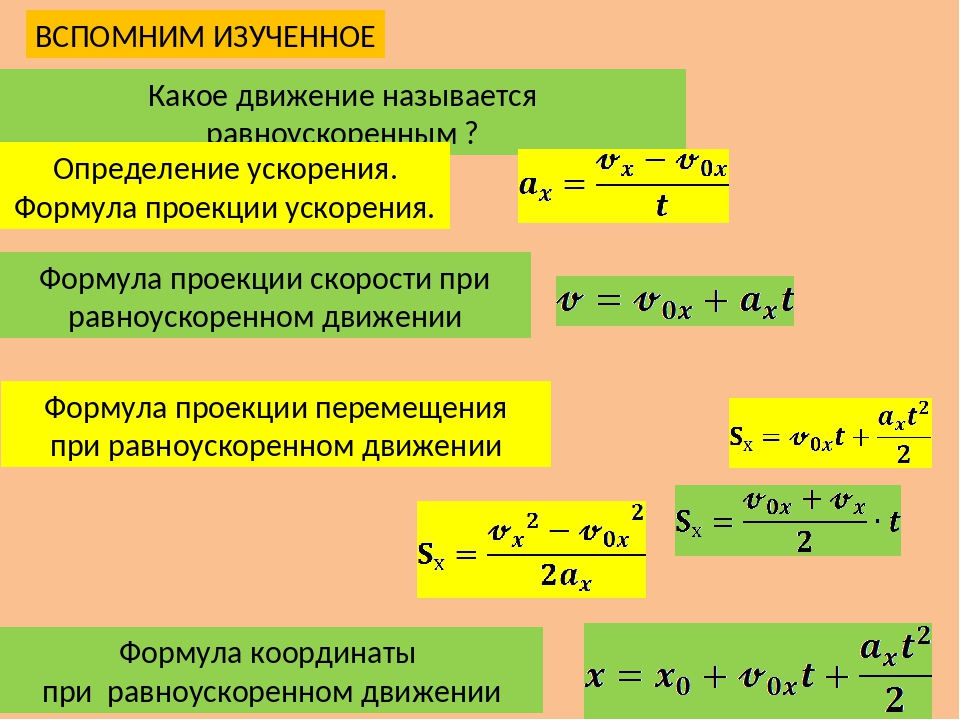 (Тогда аналогом r будет скорость спутника,
если v – скорость.)
Иногда это бывает очень полезно, но это , а не , каковы мы.
говорим о сейчас.
(Тогда аналогом r будет скорость спутника,
если v – скорость.)
Иногда это бывает очень полезно, но это , а не , каковы мы.
говорим о сейчас.
Вот изображение того, о чем мы сейчас говорим, для случая, когда точка r = (x, y) находится в первом квадранте. Формулы, которые мы выведем из него, будут правильными во всех четырех квадрантах, как вы можете проверить.
[вставить чертеж] (пока не имеется)
Пусть точка r имеет полярные координаты (r, Ð) (связано с (x, y) уравнениями (1) – (3)).Мы хотим, чтобы i r было единичным вектором при r указывая в сторону увеличения r , и i ì как единичный вектор при r в сторону увеличения Â .
Мы, как обычно, уточняем эти векторы, перечисляя их обычные декартовы
компоненты; то есть нахождение уравнений вида i r = 1, a 2 >
= a 1 i + a 2 j . Однако компоненты a 1 и a 2 будет функций из r и ì ,
потому что то, что подразумевается под “направлением увеличения r “,
и т. д., варьируется от точки к точке!
Однако компоненты a 1 и a 2 будет функций из r и ì ,
потому что то, что подразумевается под “направлением увеличения r “,
и т. д., варьируется от точки к точке!
Метод 1: Мы можем найти эти полярные единичные векторы с помощью геометрических и тригонометрические рассуждения.
- Мы уже знаем вектор, указывающий в сторону увеличения r , а именно вектор r = сам .Чтобы сформировать единичный вектор, нам нужно только разделить этот вектор на его длину:
i r = r / r = Ð, sin Ð >. (4)
- Чтобы найти вектор, перпендикулярный заданному в размерности 2, вы просто
поменяйте местами компоненты и поменяйте один из знаков.
(Это векторная версия элементарного рецепта,
“Наклон перпендикулярной линии является отрицательной величиной, обратной величине
наклон исходной линии.”)
Таким образом
i ì = Ð, cos Ð > (5)
или отрицательный.
 Из рисунка видно, что (5) – вектор с
правильный общий знак.
Из рисунка видно, что (5) – вектор с
правильный общий знак.
Метод 2: Вот более систематический подход, использующий концепцию касательный вектор.
- Двигаться «в сторону увеличения r »
означает движение по кривой, на которой ì постоянна и r повышается.(Такая кривая – один из лучей, выходящих из начала координат; но мы не
нужно знать, что делать расчет – только чтобы оценить расчет
геометрически.)
На такой кривой r само по себе является параметром, а значит,
дифференцирование параметрических уравнений относительно r дает
касательный вектор к кривой, как объяснялось в день 6.2.
Рассматриваемые параметрические уравнения – это уравнения (1),
- Аналогично двигаться в сторону увеличения ì означает движение по кривой, на которой r постоянный и ì возрастает.
(Это круг с центром в начале координат.)
Параметрические уравнения остаются уравнениями (1), но теперь Â – переменная, а r – постоянная.Таким образом, касательный вектор равен
= r sin ì , r cos ì >.
Это не единичный вектор: он имеет длину r . (Это неудивительно с геометрической точки зрения, если мы подумаем о касательном векторе как скорость, причем время Â . Если r больше 1, то небольшое изменение ì проходит долгий путь; движущаяся точка должна двигаться быстро, чтобы вовремя обойти круг 2 * Пи. Если r меньше единицы, данное изменение в ì производит только небольшое движение точки, уменьшаясь до полного отсутствия движения когда r = 0 .) Деление на длину дает единичный вектор i ì из (5).

x = r cos ì , y = r sin ì ,
, где ì считается константой.Таким образом, касательный вектор равен
= Ð, sin Ð >.
Это уже единичный вектор, так что это желаемый
i r .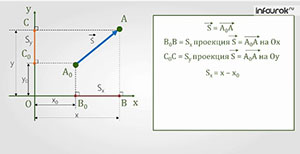 Это воспроизводит результат (4).
Это воспроизводит результат (4).
Задача: Определить координаты u и v от
x = (u 2 – v 2 ) / 2, у = ув.
- Используйте метод 2, чтобы найти формулы для пары перпендикулярных единичных векторов i u и i v эта точка в направлениях увеличивая u и увеличивая v соответственно.
- Нарисуйте эти единичные векторы в точке, где u = 2 и v = 1 . Также нарисуйте кривую через эту точку, вдоль которой v постоянный, и тот, по которому и постоянны. Подсказка: Они называются параболическими координатами .
Теперь, когда у нас есть полярные единичные векторы, мы можем выразить другие векторы в условия их. Рассмотрим постоянный вектор
E = = 3 i – j .
Поскольку i r является единичным вектором, проекция вектора из E на i r есть
( E. i r ) i r = (3 cos ì – sin ì ) i r .
i r ) i r = (3 cos ì – sin ì ) i r .
Аналогично составляющая E вдоль i ì является
– (3 sin ì + cos ì ) i ì .
Поскольку полярные единичные векторы являются ортогональным базисом, сумма этих двух векторов представляет собой разложение E на его компоненты в радиальном и угловые направления (что является целью наших вычислений в этом примере):
E = (3 cos ì – sin Ð ) i r – (3 sin Ð + cos Ð ) i ì .
Подставляя формулы (4) и (5) для полярных единичных векторов в это уравнение и упрощение, вы можете проверить правильность уравнения.
Хотя E – постоянный вектор
(не функция точки r ),
его разложение действительно зависит от координат точки. Фактически, мы замечаем, что это зависит от ì , а не от r .
Вы можете объяснить это геометрически?
Фактически, мы замечаем, что это зависит от ì , а не от r .
Вы можете объяснить это геометрически?
Системы координат – Викиверситет
Этот ресурс посвящен введению, подходящему для вводного курса физики в колледже по электромагнетизму.
Мы описываем три разные системы координат, известные как декартова, цилиндрическая и сферическая.Цилиндрическая система тесно связана с полярными координатами.
См. Также Вывод формул
Декартова координата [править | править источник]
Математическое выражение точки в декартовой координате
- A (x, y)
Полярная координата [править | править источник]
Математическое выражение точки в декартовой координате
- A (г, θ {\ displaystyle \ theta})
Координата преобразования [править | править источник]
- r = x2 + y2 {\ displaystyle r = {\ sqrt {x ^ {2} + y ^ {2}}}}
- θ = загар − yx {\ displaystyle \ theta = Tan ^ {-} {\ frac {y} {x}}}
- Икс (θ) знак равно rCosθ {\ Displaystyle х (\ theta) = rCos \ theta}
- Y (θ) знак равно rSinθ {\ displaystyle y (\ theta) = rSin \ theta}
Слева: иллюстрация декартовой координатной плоскости. Четыре точки отмечены и помечены их координатами: (2,3) зеленым, (−3,1) красным, (−1,5, −2,5) синим и начало координат (0,0) фиолетовым.
Четыре точки отмечены и помечены их координатами: (2,3) зеленым, (−3,1) красным, (−1,5, −2,5) синим и начало координат (0,0) фиолетовым.
Справа: трехмерная декартова система координат с началом O и осевыми линиями X , Y и Z , ориентированными, как показано стрелками. Отметки на осях отстоят друг от друга на одну единицу длины. Черная точка показывает точку с координатами x = 2, y = 3 и z = 4 или (2,3,4).dz {\ displaystyle {\ vec {d}} \ ell = {\ hat {x}} dx + {\ hat {y}} dy + {\ hat {z}} dz}.
известен как линейный элемент .
Линейный интеграл векторного поля в декартовых координатах [править | править источник]
До сих пор мы обсуждали интеграл скалярного поля, f = f (r →) {\ displaystyle f = f ({\ vec {r}})}. Примером скалярного поля является температура как функция положения (в любой момент времени). Скорость ветра как функция положения была бы векторным полем. В декартовых координатах легко проанализировать векторное поле как эквивалентное трем скалярным полям, по одному для каждого направления: Пусть F → (r →) = f (r →) i ^ + g (r →) j ^ + h ( г →) к ^ {\ Displaystyle {\ vec {F}} ({\ vec {r}}) = f ({\ vec {r}}) {\ hat {i}} + g ({\ vec {r }}) {\ hat {j}} + h ({\ vec {r}}) {\ hat {k}} \,} (так что
F x = f,
F y = г,
и F z = h). {\ vec {b}} {\ vec {F}} \ cdot d {\ vec {\ ell}} \ приблизительно \ sum _ {j} {\ vec {F_ {j}}} \ cdot \ Delta {\ vec {\ ell}} \ Equiv \ sum _ {j} F_ {j} \ \ Delta \ ell \ cos \ theta}
{\ vec {b}} {\ vec {F}} \ cdot d {\ vec {\ ell}} \ приблизительно \ sum _ {j} {\ vec {F_ {j}}} \ cdot \ Delta {\ vec {\ ell}} \ Equiv \ sum _ {j} F_ {j} \ \ Delta \ ell \ cos \ theta}
Линейный интеграл однородного поля по прямому пути [править | править источник]
Работа, совершаемая гравитационной силой над объектом, зависит только от его изменения высоты, поскольку гравитационная сила консервативна.Линейные интегралы тривиальны, если векторное поле однородно, что означает, что поле не зависит от положения.{\ vec {b}} {\ vec {F}} \ cdot d {\ vec {\ ell}} = {\ vec {F}} \ cdot ({\ vec {b}} – {\ vec {a}) }) \,} = F | b → −a → | cosθ {\ displaystyle = F \; | {\ vec {b}} – {\ vec {a}} | \ cos \ theta}
Дифференциальный элемент объема в декартовых координатах [править | править источник]
Декартов элемент объема,
- dV = dxdydz, {\ displaystyle dV = dxdydz,}
, который легко допускает интеграл объема по прямоугольной коробке.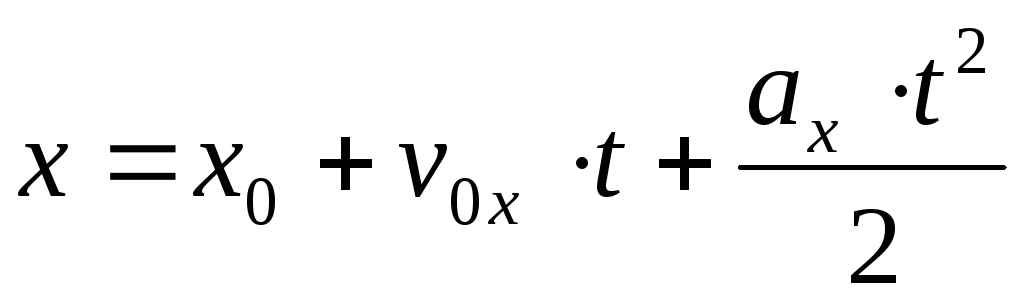 Интеграл функции f = f (x, y, z) по прямоугольнику – это тройной интеграл, который часто неформально записывается с использованием единственного интеграла, знака ∫ {\ displaystyle \ int}.{\ mathrm {function \ of \ x \ only}}}
Интеграл функции f = f (x, y, z) по прямоугольнику – это тройной интеграл, который часто неформально записывается с использованием единственного интеграла, знака ∫ {\ displaystyle \ int}.{\ mathrm {function \ of \ x \ only}}}
Обратите внимание, как переменная интегрирования (x, y или z) будет исчезать каждый раз, когда вычисляется интеграл между конечными точками. Это скалярный интеграл, если функция f = f (x, y, z) {\ displaystyle f = f (x, y, z)}. В общем, пределы могут быть функциями, например (z1, z2) могут быть функциями x и y, а (y1, y2) могут быть функциями x. К счастью, такая сложность не требуется для объемных интегралов, необходимых для понимания электромагнетизма.
Интеграл по объему над прямоугольным прямоугольником [править | править источник]
Если ни один из пределов (z1, z2) и (y1, y2) в приведенном выше интеграле не является функциями, то интеграл находится над прямоугольным прямоугольником.Самый элементарный пример такого интеграла возникает, когда f (x, y, z) = 1 {\ displaystyle f (x, y, z) = 1}:
- ∫1dV = (x2 − x1) × (y2 − y1) × (z2 − z1) ≡∭1dV = объем {\ displaystyle \ int 1dV = (x_ {2} -x_ {1}) \ times (y_ { 2} -y_ {1}) \ times (z_ {2} -z_ {1}) \ Equiv \ iiint 1dV = volume}
Это просто объем коробки.
Дифференциальный элемент поверхности в декартовых координатах [править | править источник]
Поверхностные интегралы также можно рассматривать как предел суммы Римана, но их сложнее построить, чем линейные или объемные интегралы, если только геометрия не очень проста.{+ L / 2} dyF_ {z} (x, y, H)}
В отличие от одномерных интегралов первого года курса математики, пределы не всегда используются для определения области, по которой интегрируется поле. Вместо этого принято указывать интеграл ∫fdA {\ displaystyle \ int f \, dA}, а затем использовать слов для описания площади (например, “, где интеграл вычисляется по квадрату со сторонами длиной L, с центром в начале координат и занимающим плоскость xy ““). Очень просто определенные поверхностные интегралы также могут быть определены с использованием пределов.{1/2}}
- dA = rdrdθ {\ displaystyle dA = rdrd \ theta}
 Точка – это точка с радиальным расстоянием ρ = 4, угловой координатой φ = 130 ° и высотой z = 4.
Точка – это точка с радиальным расстоянием ρ = 4, угловой координатой φ = 130 ° и высотой z = 4.Цилиндрическая система координат определяет положения точек с помощью символов (ρ, φ, z) {\ displaystyle (\ rho, \ varphi, z)}, как показано на рисунке.. {\ displaystyle {\ vec {d}} \ mathbf {\ ell} = \ mathrm {d} \ rho \, {\ boldsymbol {\ hat {\ rho}}} + \ rho \, \ mathrm {d} \ varphi \, {\ boldsymbol {\ hat {\ varphi}}} + \ mathrm {d} z \, \ mathbf {\ hat {z}}.}
Элемент объема
- dV = ρdρdφdz. {\ Displaystyle \ mathrm {d} V = \ rho \, \ mathrm {d} \ rho \, \ mathrm {d} \ varphi \, \ mathrm {d} z.}
элемент поверхности на поверхности постоянного радиуса ρ {\ displaystyle \ rho} (вертикальный цилиндр)
- dSρ = ρdφdz.{\ displaystyle \ mathrm {d} S _ {\ rho} = \ rho \, \ mathrm {d} \ varphi \, \ mathrm {d} z.}
Элемент поверхности на поверхности с постоянным азимутом φ {\ displaystyle \ varphi} (вертикальная полуплоскость)
- dSφ = dρdz.
 ∂f∂z, {\ displaystyle {\ vec {\ nabla}} f = {\ boldsymbol {\ hat {x}} } {\ frac {\ partial f} {\ partial x}} + {\ boldsymbol {\ hat {y}}} {\ frac {\ partial f} {\ partial y}} + \ mathbf {\ hat {z} } {\ frac {\ partial f} {\ partial z}},}
∂f∂z, {\ displaystyle {\ vec {\ nabla}} f = {\ boldsymbol {\ hat {x}} } {\ frac {\ partial f} {\ partial x}} + {\ boldsymbol {\ hat {y}}} {\ frac {\ partial f} {\ partial y}} + \ mathbf {\ hat {z} } {\ frac {\ partial f} {\ partial z}},}
Расхождение векторного поля F → = F → (r →) {\ displaystyle {\ vec {F}} = { \ vec {F}} ({\ vec {r}})} – это
- divF → = ∇ → ⋅F → = ∂Fx∂x + ∂Fy∂y + ∂Fz∂z.∂f∂z, {\ displaystyle {\ vec {\ nabla}} f = {\ boldsymbol {\ hat {\ rho}}} {\ frac {\ partial f} {\ partial \ rho}} + {\ boldsymbol { \ hat {\ varphi}}} {\ frac {1} {\ rho}} {\ frac {\ partial f} {\ partial \ varphi}} + \ mathbf {\ hat {z}} {\ frac {\ partial f} {\ partial z}},}
Расхождение векторного поля F → = F → (r →) {\ displaystyle {\ vec {F}} = {\ vec {F}} ( {\ vec {r}})} – это
- divF → = ∇ → ⋅F → = 1ρ∂∂ρ (ρFρ) + 1ρ∂Fφ∂φ + ∂Fz∂z. {\ Displaystyle \ operatorname {div} \, {\ vec {F}} = {\ vec {\ nabla}} \ cdot {\ vec {F}} = {\ frac {1} {\ rho}} {\ frac {\ partial} {\ partial \ rho}} (\ rho F _ {\ rho}) + {\ frac {1} {\ rho}} {\ frac {\ partial F _ {\ varphi}} {\ partial \ varphi}} + {\ frac {\ partial F_ {z}} {\ partial z}} \ ,.
 {x2} f (x, y_ {0}, z_ {0}) \, dx}
{x2} f (x, y_ {0}, z_ {0}) \, dx}
– линейный интеграл из f (r →) {\ displaystyle f ({\ vec {r}})} из точки (x1, y0, z0) {\ displaystyle (x_ {1}, y_ {0}, z_ {0})} к (x2, y0, z0) {\ displaystyle (x_ {2}, y_ {0}, z_ {0})}.Линия произвольного направления может быть определена параметрически, например:
- r → = r → 0 + β → τ {\ displaystyle {\ vec {r}} = {\ vec {r}} _ {0} + {\ vec {\ beta}} \ tau}
К определить скалярный линейный интеграл, нам нужно преобразовать векторный дифференциал пути в скаляр, взяв величину. Обычно дифференциал в векторе r → {\ displaystyle {\ vec {r}}} обозначается символом dℓ → {\ displaystyle d {\ vec {\ ell}}} вместо dr → {\ displaystyle d { \ vec {r}}}, потому что последний ложно намекает на изменение радиуса, как мы скоро увидим:
- dℓ → ≡dr → = β → dτ⇒dℓ = βdτ, {\ displaystyle d {\ vec {\ ell}} \ Equiv d {\ vec {r}} = {\ vec {\ beta}} d \ tau \ Rightarrow d \ ell = \ beta d \ tau \ ;,}
, где β≡ | β → | {\ displaystyle \ beta \ Equiv | {\ vec {\ beta}} |} – величина вектора. {2}}} \, d \ tau}
{2}}} \, d \ tau}
– линейный интеграл от f (r →) {\ displaystyle f ({\ vec {r}})} от точки (x1, y0, z0) {\ displaystyle (x_ {1}, y_ {0}, z_ {0})} до (x2, y0, z0) {\ displaystyle (x_ { 2}, y_ {0}, z_ {0})}.{1/2} d \ tau}
Приложение: Обучение вектору [edit | править источник]
«Вектор» – нетривиальное понятие, которое возникает даже в римановом исчислении, где определено n-мерное пространство переменных, а понятие метрики используется для генерации векторных и тензорных полей, и все это без того фундаментального смысла «направления», который студенты используют для определения «вектора».
Знакомство студентов с координатами начинается с точек на двумерной плоскости x-y. Есть несколько более или менее эквивалентных способов обозначения этих точек.3 {\ displaystyle z {\ hat {k}} \ rightarrow z {\ hat {z}} \ rightarrow x_ {3} {\ hat {e}} _ {3}}
Можно определить вектор смещения как команду на перемещение на определенное расстояние в определенном направлении. В евклидовом пространстве нет разницы между указанием местоположения (x, y) и инструкцией перейти от начала координат в определенном направлении к точке (x, y).
В евклидовом пространстве нет разницы между указанием местоположения (x, y) и инструкцией перейти от начала координат в определенном направлении к точке (x, y).
Одним из преимуществ векторной нотации является возможность использовать символы для представления вектора и индексы для представления компонентов:
- a = a x i + a y j и b = b x i + b y j
В этом обозначении используется жирный шрифт вместо стрелки и шляпы для различения векторов и скаляров .(Другими словами, a и a → {\ displaystyle {\ vec {a}}} – разные способы выразить одно и то же.) W: скаляр (физика) или w: скаляр (математика) – это просто причудливое слово для “обычного номера”. Например, x и y – это скаляры, которые образуют два компонента вектора a . Известное использование разных символов для представления разных векторов – это F = m a , в котором говорится, что векторное ускорение, a , умноженное на скаляр, m, равно чистой силе, F (последнее является вектор, потому что он имеет величину и направление). {\ displaystyle = (dy _ {\ alpha} dz _ {\ beta} -dz _ {\ alpha} dy _ {\ beta}) {\ hat {x}} + (dz _ {\ alpha} dx _ {\ beta} -dx _ {\ alpha} dz _ {\ beta}) {\ hat {y}} + (dx _ {\ alpha} dy _ {\ beta} -dy _ {\ alpha} dx _ {\ beta}) {\ hat {z}}} Теперь мы можем “заставить” (1) произойти с (3) dzα = 0dzβ <0dxβ = 0 {\ displaystyle dz _ {\ alpha} = 0 \ qquad dz _ {\ beta} <0 \ qquad dx _ {\ beta} = 0} В этом контексте письмо (1) помещает пресловутый круглый колышек в квадратное отверстие.
{\ displaystyle = (dy _ {\ alpha} dz _ {\ beta} -dz _ {\ alpha} dy _ {\ beta}) {\ hat {x}} + (dz _ {\ alpha} dx _ {\ beta} -dx _ {\ alpha} dz _ {\ beta}) {\ hat {y}} + (dx _ {\ alpha} dy _ {\ beta} -dy _ {\ alpha} dx _ {\ beta}) {\ hat {z}}} Теперь мы можем “заставить” (1) произойти с (3) dzα = 0dzβ <0dxβ = 0 {\ displaystyle dz _ {\ alpha} = 0 \ qquad dz _ {\ beta} <0 \ qquad dx _ {\ beta} = 0} В этом контексте письмо (1) помещает пресловутый круглый колышек в квадратное отверстие.
10.4 Уравнения движения в сферических координатах
10.4 Уравнения движения в сферических координатах
Три переменные, используемые в сферических координатах:
- долгота (обозначается λ )
- широта (обозначается φ )
- вертикальное расстояние (обозначается r от центра Земли и z от поверхности Земли, где z = r – a и a – радиус Земли)
Преобразование между сферическими и декартовыми координатами.
Кредит: В. Брун
Обратите внимание, что единичные векторы в сферических координатах меняются с положением. Например, для воздушной посылки на экваторе меридиональный единичный вектор j → параллелен оси вращения Земли, тогда как для воздушной посылки около одного из полюсов j → почти перпендикулярен оси вращения Земли. В сферических координатах вектор скорости и его компоненты имеют вид:
U → = щ → + VJ → + → WK и = rcosφDλDt, v = rDφDt, ш = DzDtMathType @ СПР @ 5 @ 5 + = faaahmart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY = ribbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0 = yr0RYxir = Jbba9q8aq0 = YQ = He9q8qqQ8frFve9Fve9Ff0dc9Gqpi0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaafaWaaeGabaaabaaeeaaaaaaaaigBHn2Aa8qaceWGvbWdayaalaWdbiabg2da9iaadwhaceWGPbWdayaalaWdbiabgUcaRiaadAhaceWGQbWdayaalaWdbiabgUcaRiaadEhaceWGRbWdayaalaaabaWdbiaadwhacqGH9aqpcaWGYbGaci4yaiaac + gacaGGZbGaeqy1dy2aaSaaa8aabaWdbiaadseacqaH7oaBa8aabaWdbiaadseacaWG0baaaiaabYcacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaWG2bGaeyypa0JaamOCamaalaaapaqaa8qacaWGebGaeqy1dygapaqaa8qacaWGebGaamiDaaaacaqGSaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaam4Daiabg2da9maalaaapaqaa8qacaWGebGaamOEaaWdaeaapeGaamiraiaadshaaaaaaaaa @ 6067 @
[10. 17]
17]
, где u , v и w – восточная, северная и восходящая составляющие скорости соответственно. Эти скорости получены из изменений расстояний в восточном, северном и восходящем направлениях, которые задаются по формуле:
dx = rcosϕdλ = изменение расстояния на восток acosϕdλdy = rdϕ = изменение расстояния на север adϕdz = dr = изменение расстояния вверх
Теперь запишем усредненное уравнение сохранения импульса [10.16] в компонентной форме в сферических координатах.Мы просто покажем вам, как выполняется это преобразование, не выполняя на самом деле все этапы. Обратите внимание, что нам нужно взять полные производные единичных векторов, а также скорости:
DU → Dt = DDt (i → u + j → v + k → w) = i → DuDt + uDi → Dt + j → DvDt + vDj → Dt + k → DwDt + wDk → Dt
[10,18]
Термины, содержащие производные единичных векторов, называются «метрическими членами». Они зависят от того, является ли Земля сферой. В декартовых координатах они равны нулю.
Рассмотрим только один из этих метрических терминов:
Dj → Dt = ∂j → ∂t + u∂j → ∂x + v∂j → ∂y + w∂j → ∂z = 0 + u∂j → ∂x + v∂j → ∂y + 0
Так как для любого места, J → постоянна со временем и J → не меняется в зависимости от высоты, что листья J → MathType @ СПР @ 5 @ 5 + = faaagCart1ev2aqaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj = hHeeu0xXdbba9frFj0 = OqFfea0dXdd9vqaq = JfrVkFHe9pgea0dXdar = Jb9hs0dXdbPYxe9vr0 = vr0 = vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaaFiaabaGaamOAaaGaay51Gaaaaa @ 356E @ зависит только от широты и долготы.
Сначала посмотрите на ∂j → ∂y. Установите y = 0 на экваторе и y = a (радиус Земли) возле полюса. Как отмечалось выше, на экваторе j → параллельно оси вращения Земли, но около полюса почти перпендикулярно ей. Таким образом, изменение j → с юга на север (увеличение y ) должно быть направлено вниз к центру Земли, и поэтому j → изменяется на −k → кратное небольшое угловое изменение, в то время как y изменяется на , а в раз такое же небольшое угловое изменение. Чистый результат:
Чистый результат:
Используя тот же подход, мы можем показать, что:
∂j → ∂x = −tanϕ ai →
Суммарные производные всех трех единичных векторов равны:
Di → Dt = uacosϕ (j → sinϕ − k → cosϕ) Dj → Dt = −utanϕai → −vak → Dk → Dt = uai → + vaj →
[10,19]
Собираем все вместе:
DU → Dt = (DuDt − uvtanϕa + uwa) i → + (DvDt + u2tanϕa + uwa) j → + (DwDt − u2 + v2a) k →
[10.20]
Аналогичный анализ можно провести для других членов в уравнении усредненного импульса.
Сила Кориолиса:
-2Ω → × U → = 2Ω (vsinφ-wcosφ) я → – (2Ωusinφ) → J + (2Ωucosφ) K → MathType @ СПР @ 5 @ 5 + = faaahmart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY = ribbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0 = yr0RYxir = Jbba9q8aq0 = YQ = He9q8qqQ8frFve9Fve9Ff0dc9Gqpi0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaqqaaaaaaaaGySf2yRbWdbiabgkHiTiaaikdadaWhcaqaaiabfM6axbGaay51GaGaey41aq7aa8HaaeaacaWGvbaacaGLxdcacqGH9aqpcaaIYaGaeuyQdC1aaeWaa8aabaWdbiaadAhaciGGZbGaaiyAaiaac6gacqaHvpGzcqGHsislcaWG3bGaci4yaiaac + gacaGGZbGaeqy1dygacaGLOaGaayzkaaGabmyAa8aagaWca8qacqGHsisldaqadaqaaiaaikdacqqHPoWvcaWG1bGaci4CaiaacMgacaGGUbGaeqy1dygacaGLOaGaayzkaaGabmOAa8aagaWca8qacqGHRaWkdaqadaqaaiaaikdacqqHPoWvcaWG1bGaci4yaiaac + gacaGGZbGaeqy1dygacaGLOaGaayzkaaGabm4Aa8aagaWcaaaa @ 663A @
[10. 21]
21]
Плотность:
[10,22]
Сила градиента давления (PGF):
−1ρ∇ → p = −1ρ∂p∂xi → −1ρ∂p∂yj → −1ρ∂p∂zk →
[10,23]
Турбулентное трение (только в пограничном слое):
−Cdh | V → | V → = −Cdh | V → | ui → −Cdh | V → | vj →
[10,24]
Суммируя все силы, получаем уравнения усредненного импульса в сферических координатах в зональном, меридиональном и вертикальном направлениях, соответственно:
DuDt − uvtanϕa + uwa = −1ρ∂p∂x + 2Ωv sinϕ − 2Ωw cosϕ − Cdh | V → | uDvDt − u2tanϕa + vwa = −1ρ∂p∂y − 2Ωu sinϕ − Cdh | V → | vDwDt − u2 + v2a = −1ρ∂p∂z − g + 2Ωu cosϕ
.


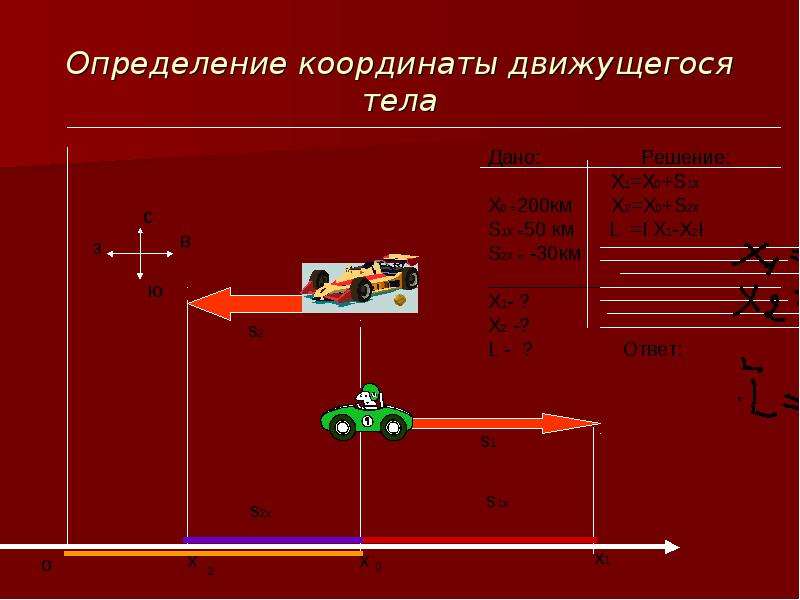
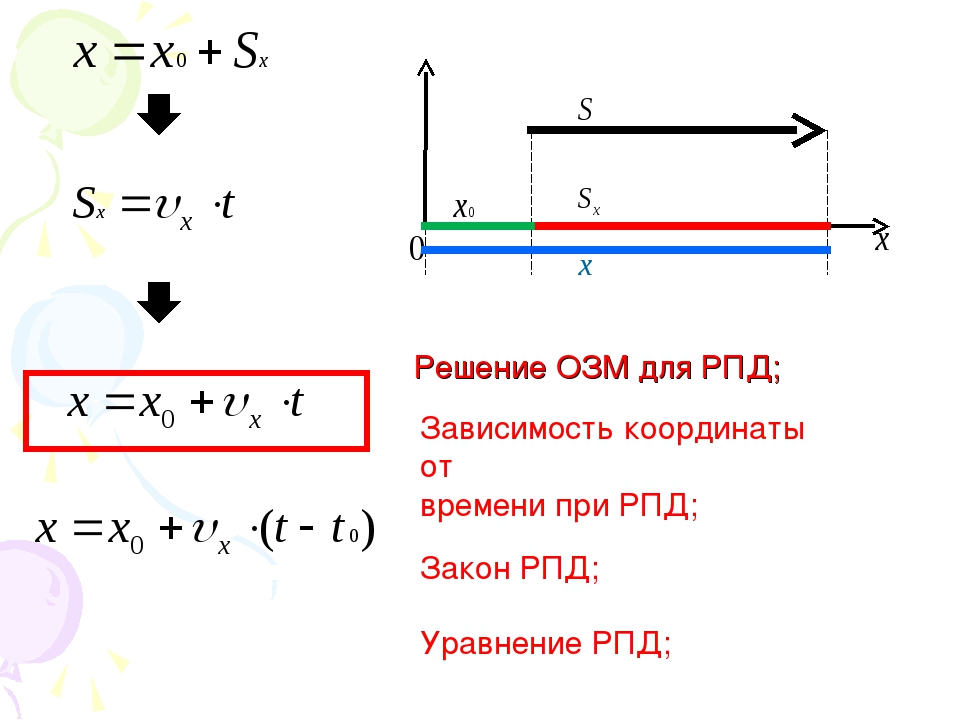 1. Преобразование декартовых координат в цилиндрические.
1. Преобразование декартовых координат в цилиндрические.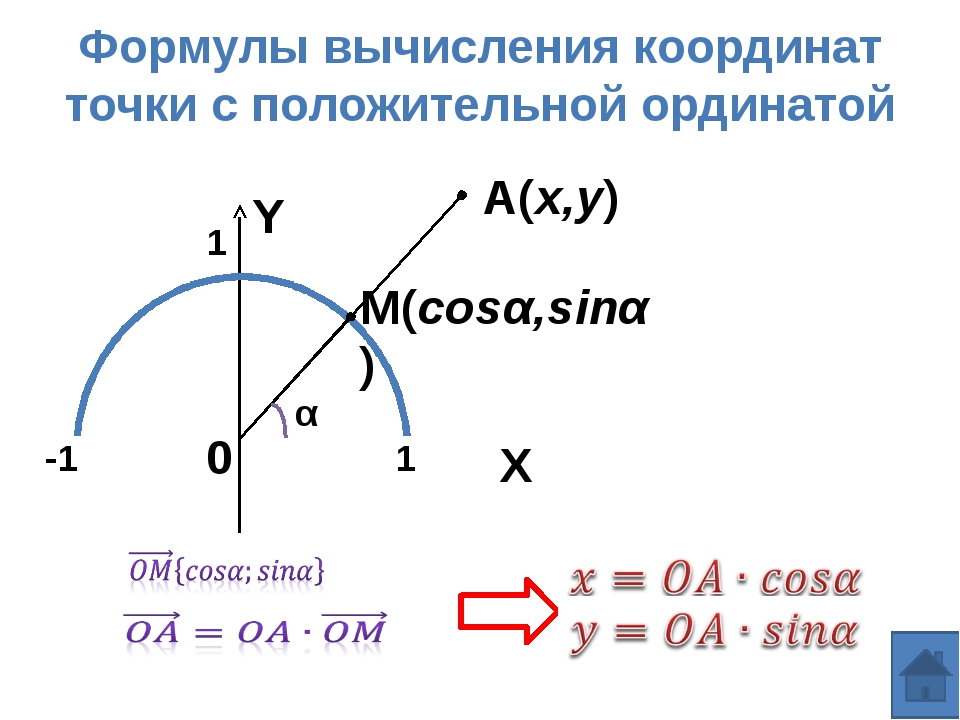 от начальной до конечной точки, если объект не движется по прямой
линия без изменения направления.
от начальной до конечной точки, если объект не движется по прямой
линия без изменения направления. Из рисунка видно, что (5) – вектор с
правильный общий знак.
Из рисунка видно, что (5) – вектор с
правильный общий знак.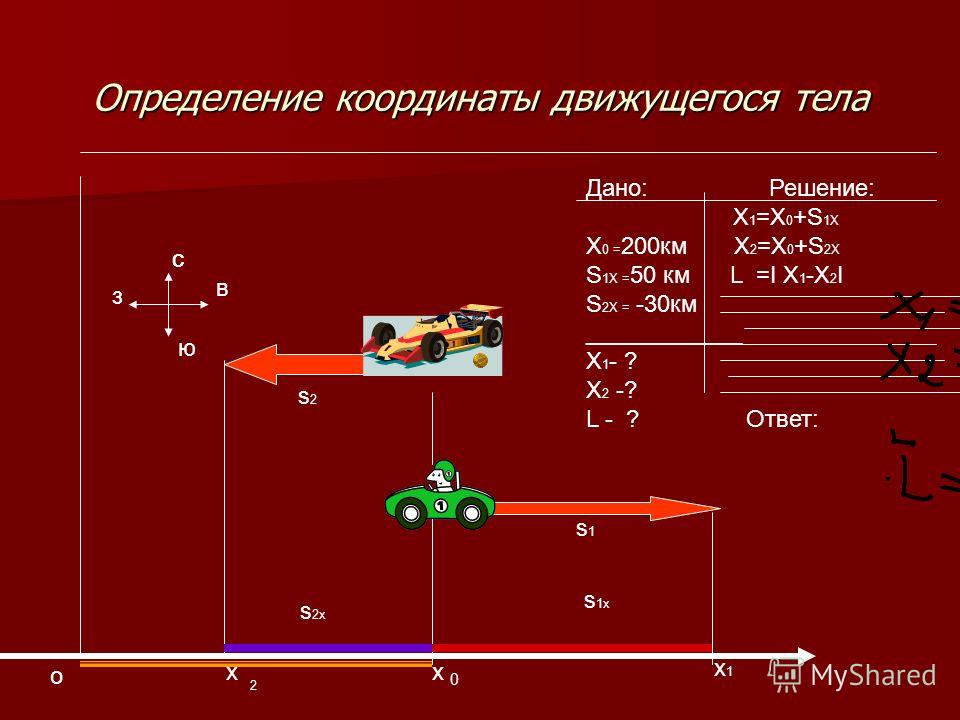
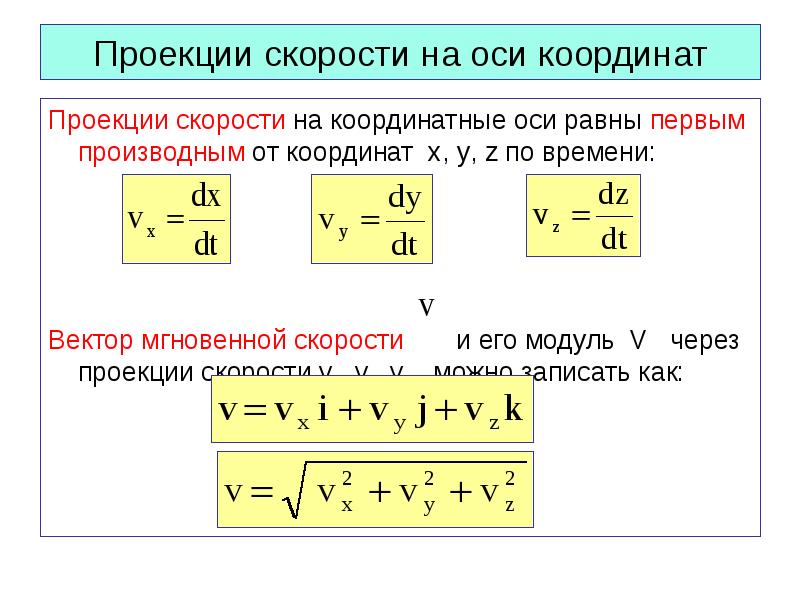 ∂f∂z, {\ displaystyle {\ vec {\ nabla}} f = {\ boldsymbol {\ hat {x}} } {\ frac {\ partial f} {\ partial x}} + {\ boldsymbol {\ hat {y}}} {\ frac {\ partial f} {\ partial y}} + \ mathbf {\ hat {z} } {\ frac {\ partial f} {\ partial z}},}
∂f∂z, {\ displaystyle {\ vec {\ nabla}} f = {\ boldsymbol {\ hat {x}} } {\ frac {\ partial f} {\ partial x}} + {\ boldsymbol {\ hat {y}}} {\ frac {\ partial f} {\ partial y}} + \ mathbf {\ hat {z} } {\ frac {\ partial f} {\ partial z}},} {x2} f (x, y_ {0}, z_ {0}) \, dx}
{x2} f (x, y_ {0}, z_ {0}) \, dx}