Физика. 8 класс
Физика. 8 класс
ОглавлениеГлава 1. Общие сведения о движении§ 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ § 3. ПЕРЕМЕЩЕНИЕ § 4.  § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ) § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ Глава 2. Прямолинейное неравномерное движение § 13. СРЕДНЯЯ СКОРОСТЬ § 14. МГНОВЕННАЯ СКОРОСТЬ § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ Глава 3. Криволинейное движение § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 23.  УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ§ 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА Динамика Глава 4. Законы движения § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ § 31. ИНЕРТНОСТЬ ТЕЛ § 32. МАССА ТЕЛ § 33. МАССА ЛУНЫ § 34. СИЛА § 35. ВТОРОЙ ЗАКОН НЬЮТОНА § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение) § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА Глава 5. Силы природы § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ § 41. СИЛА УПРУГОСТИ § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ § 44. СИЛА ТЯЖЕСТИ § 45. ВЕС ТЕЛ § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ § 47. МАССА ЗЕМЛИ § 48. 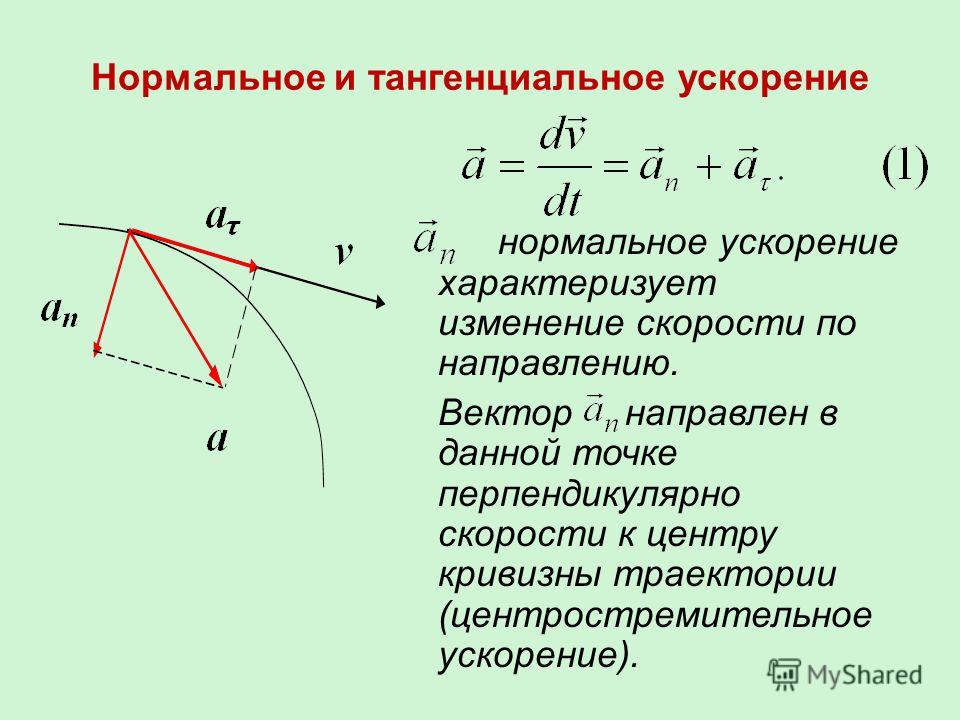 § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ Глава 6. Применение законов движения § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ § 54. НЕВЕСОМОСТЬ § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ § 58. ДВИЖЕНИЕ ПЛАНЕТ § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА Равновесие тел Глава 7.  Элементы статики§ 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ § 67. ПРАВИЛО МОМЕНТОВ § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ Законы сохранения в механике Глава 8. Закон сохранения импульса § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ Глава 9. Механическая работа и мощность § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ § 77. РАБОТА СИЛЫ ТЯЖЕСТИ § 78. РАБОТА СИЛЫ УПРУГОСТИ § 79. РАБОТА СИЛЫ ТРЕНИЯ § 80. МОЩНОСТЬ Глава 10. Закон сохранения энергии § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ 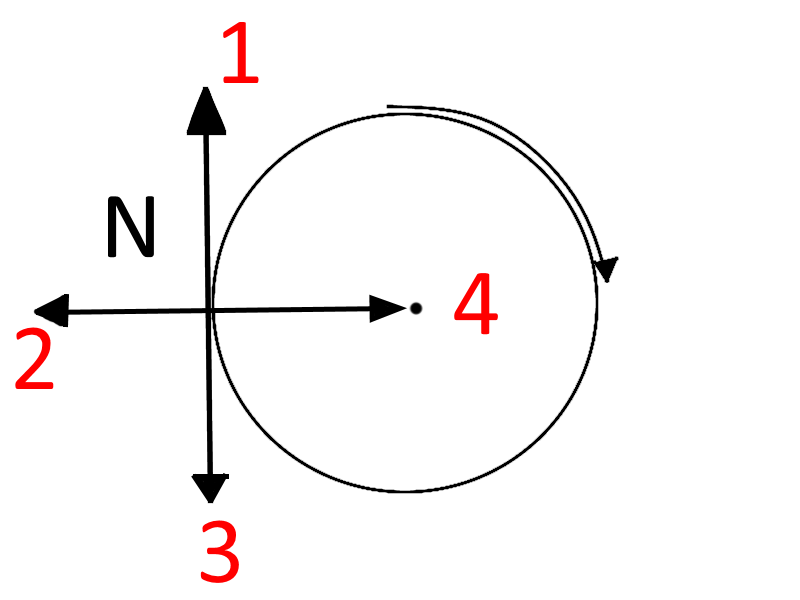 КИНЕТИЧЕСКАЯ ЭНЕРГИЯ§ 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ § 91. СТОЛКНОВЕНИЕ ТЕЛ § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ Заключение Лабораторные работы 1. Определение ускорения тела при равноускоренном движении 2. Определение коэффициента трения скольжения 3. Изучение движения тела по параболе 4. Выяснение условия равновесия рычага 5. Определение центра тяжести плоской пластины |
Векторы ускорения и скорости. Ускорение и сила. Направления тангенциального и нормального ускорений
Как известно, любая физическая величина относится к одному из двух типов, она является либо скалярной, либо векторной. В данной статье рассмотрим такие кинематические характеристики как скорость и ускорение, а также покажем, куда направлены векторы ускорения и скорости.
Что такое скорость и ускорение?
Обе величины, названные в этом пункте, являются важными характеристиками любого вида движения, будь то перемещение тела по прямой линии или по криволинейной траектории.
Скоростью называется быстрота изменения координат во времени. Математически эта величина равна производной по времени пройденного пути, то есть:
v¯ = dl¯/dt.
Здесь вектор l¯ направлен от начальной точки пути к конечной.
В свою очередь ускорение – это скорость, с которой изменяется во времени сама скорость. В виде формулы оно может быть записано так:
a¯ = dv¯/dt.
Очевидно, что взяв вторую производную от вектора перемещения l¯ по времени, мы также получим значение ускорения.
Поскольку скорость измеряется в метрах в секунду, то ускорение, согласно записанному выражению, измеряется в метрах в секунду в квадрате.
Куда направлены векторы ускорения и скорости?
В физике всякое механическое движение тела принято характеризовать определенной траекторией.
Последняя представляет собой некоторую воображаемую кривую, вдоль которой тело перемещается в пространстве. Например, прямая линия или окружность – это яркие примеры распространенных траекторий движения.
Физический смысл ускорения. Угловое ускорение и ускорение…
Ключом к успеху решения задач по физике является четкое понимание смысла величины, которую…
Вектор скорости тела направлен в сторону движения всегда, независимо от того, замедляется или ускоряется тело, движется оно по прямой или по кривой. Если говорить геометрическими терминами, то вектор скорости направлен по касательной к точке траектории, в которой в данный момент находится тело.
Вектор ускорения точки материальной или тела не имеет ничего общего со скоростью. Этот вектор направлен в сторону изменения скорости. Например, для прямолинейного движения величина a¯ может как совпадать по направлению с v¯, так и быть противоположной v¯.
Действующая на тело сила и ускорение
Мы выяснили, что вектор ускорения тела направлен в сторону изменения вектора скорости.
Тем не менее не всегда можно легко определить, как меняется скорость в данной точке траектории. Более того, для определения изменения скорости необходимо выполнить операцию разности векторов. Чтобы избежать этих трудностей в определении направления вектора a¯, существует еще один способ быстро его узнать.
Ниже записан знаменитый и хорошо известный каждому школьнику закон Ньютона:
F¯ = m*a¯.
Формула показывает, что причиной возникновения ускорения у тел является действующая на них сила. Поскольку масса m является скаляром, то вектор силы F¯ и вектор ускорения a¯ направлены одинаково. Этот факт следует запомнить и применять на практике всегда, когда возникает необходимость в определении направления величины a¯.
Физический смысл ускорения. Угловое ускорение и ускорение…
Ключом к успеху решения задач по физике является четкое понимание смысла величины, которую…
Если на тело действуют несколько разных сил, тогда направление вектора ускорения будет равно результирующему вектору всех сил.
Движение по окружности и ускорение
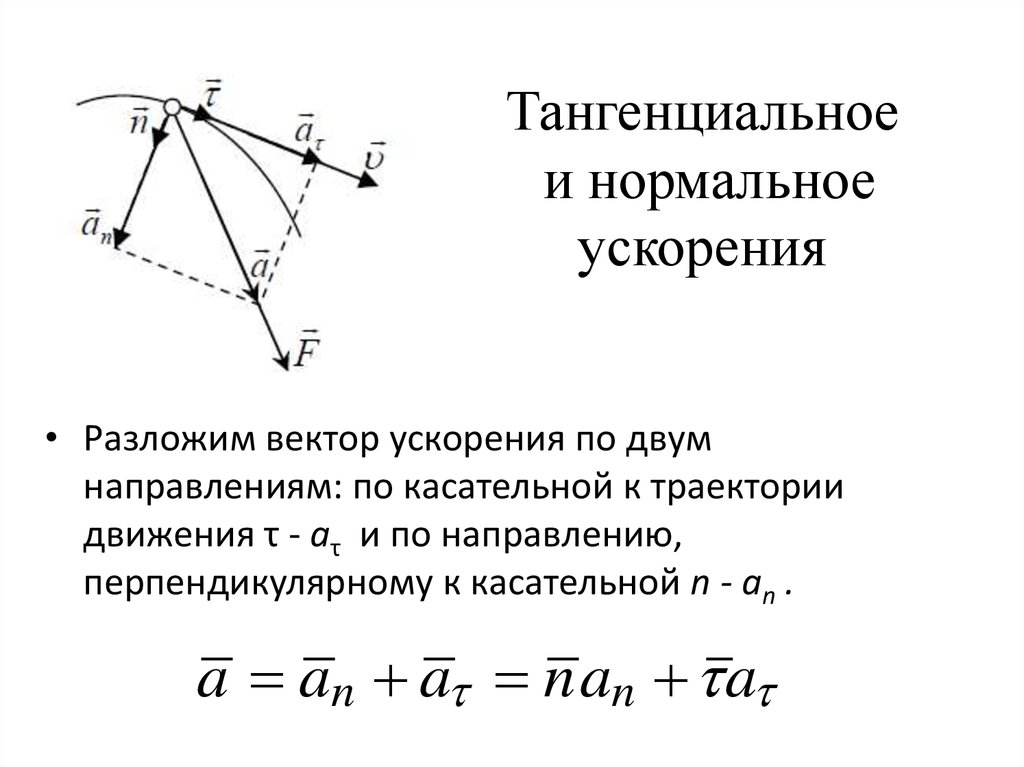
Когда тело перемещается по прямой линии, то ускорение направлено либо вперед, либо назад. В случае же движения по окружности ситуация усложняется тем, что вектор скорости постоянно меняет свое направление. В виду сказанного, полное ускорение определяется двумя его составляющими: тангенциальным и нормальным ускорениями.
Тангенциальное ускорение направлено точно так же, как вектор скорости, или против него. Иными словами, эта компонента ускорения направлена вдоль касательной к траектории. Ускорение тангенциальное описывает изменение модуля самой скорости.
Ускорение нормальное направлено вдоль нормали к данной точке траектории с учетом ее кривизны. В случае движения по окружности вектор этой компоненты указывает на центр, то есть нормальное ускорение направлено вдоль радиуса вращения. Эту компоненту часто называют центростремительной.
Полное ускорение представляет собой сумму названных компонент, поэтому его вектор может быть направлен произвольным образом по отношению к линии окружности.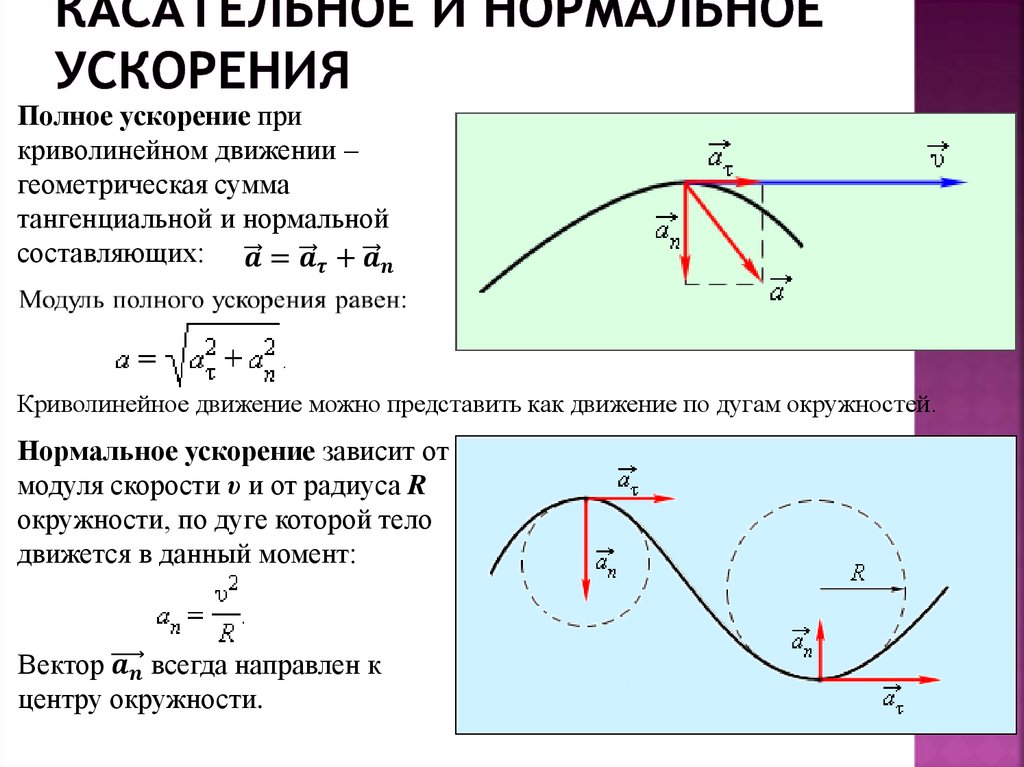
Если тело совершает вращение без изменения линейной скорости, то существует отличная от нуля только нормальная компонента, поэтому вектор полного ускорения направлен к центру окружности. Заметим, что к этому центру также действует сила, удерживающая тело на его траектории. Например, сила гравитации Солнца удерживает нашу Землю и другие планеты на своих орбитах.
векторов – Почему ускорение направлено внутрь, когда объект вращается по окружности?
потому что если вы отпустите мяч, он улетит наружу
Другой человек думает с другой точки зрения, и они расходятся в терминологии.
Когда вы отпускаете мяч, он движется по прямой линии . В этом легко убедиться, взглянув на дисциплину метания молота, которая является почти идеальным практическим экспериментом для нашего теоретического обсуждения.
Но другой человек говорит “наружу”. Это потому, что он думает, что круговой путь (когда он держит мяч) — это нормальный путь, а прямой путь (когда он отпускает мяч) — это 
Но это не объективная рамка. На самом деле все наоборот.
Все объекты, на которые не действуют определенные силы, движутся по прямой. Чтобы объект двигался по-другому, вы должны приложить к нему силу. Итак, давайте вернемся к нашему примеру с броском мяча, но начнем с прямой линии.
Мы хотим, чтобы мяч изгибался влево (и в конечном итоге по круговой траектории). Так в какую сторону мы будем толкать мяч? Слева . И поскольку мы хотим, чтобы траектория была круговой, мы обеспечиваем постоянное левое давление на мяч (где «лево» вращается по мере вращения мяча).
Если вы нарисуете это на диаграмме, вы увидите, что эта «левая сила» указывает на центр.
Черная дорожка показывает траекторию мяча. Красные стрелки указывают направление, в котором движется мяч. Синие стрелки показывают вам силу, которую вы должны приложить, чтобы заставить мяч вращаться, то есть «вращать» красную стрелку.
Синие стрелки указывают внутрь.
На лучше нарисованной диаграмме они указывали бы на центр круга. Это означает, что это сила внутрь .
Интуитивно мы могли бы научиться этому, участвуя в соревнованиях по метанию молота. Подумайте об этом: когда метатель молота вращается, чувствует ли он, что выполняет тянущее или толкающее движение?
Вытягивание . Потому что молот продолжает двигаться по прямой линии (которая в конечном итоге удаляется от метателя). Чтобы этого не произошло, метатель молота тянет на молоток, таким образом прикладывая силу внутрь к молотку.
В качестве отступления, чтобы разрешить конфликт “другой системы отсчета” здесь:
Движение внутрь называется центростремительной силой. Предполагаемое внешнее движение называется центробежной силой. В Интернете вы найдете множество мнений, утверждающих, что центробежной силы не существует. И они в основном правы (хотя я не согласен с тем, что нам не следует об этом вообще говорить).
Центробежная сила на самом деле является стремлением объекта двигаться по прямой линии (что не является силой, это отсутствие силы). Но если вы думает что “нормальная” траектория является круговой (как это делает морской котик в вашем вопросе), тогда эта прямая кажется отклонением от “нормальной” траектории.
Что приводит Морских котиков к выводу, что должна быть сила, вызывающая это отклонение.
Но у него все наоборот. Круговой путь
Центробежная сила представляет собой воспринимаемую силу. Это нереально. Но поскольку объект хочет двигаться по прямой линии и борется, двигаясь по кругу, поставщик внутренней силы чувствует, что объект пытается «оттолкнуться» от него, поэтому он воспринимает его как силу .
Но это не так.
18A: Круговое движение — центростремительное ускорение
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3328
- Джеффри В. Шник
- Колледж Святого Ансельма
Существует тенденция полагать, что если объект движется с постоянной скоростью, то он не имеет ускорения. Это действительно верно в случае объекта, движущегося по прямолинейному пути. С другой стороны, частица, движущаяся по криволинейной траектории, ускоряется независимо от того, меняется ее скорость или нет. Скорость имеет как величину, так и направление. В случае частицы, движущейся по криволинейной траектории, направление скорости постоянно меняется, и, таким образом, частица имеет ускорение.
Обратимся теперь к случаю, когда объект движется по кругу. Мы начнем с простейшего случая кругового движения, случая, когда скорость объекта постоянна, случая, называемого равномерным круговым движением. На данный момент позвольте вам быть объектом. Представьте, что вы находитесь в автомобиле, который едет против часовой стрелки, скажем, со скоростью 40 миль в час, если смотреть сверху, по довольно небольшой круговой дорожке. Вы путешествуете по кругу. Ваша скорость непостоянна. Величина вашей скорости не меняется (постоянная скорость), но направление вашей скорости постоянно меняется, вы продолжаете поворачивать налево! Теперь, если вы постоянно поворачиваете налево, вы должны постоянно приобретать некоторую скорость движения влево. На самом деле, ваше ускорение должно быть точно влево, под прямым углом к вашей скорости, потому что, если ваша скорость не меняется, но ваша скорость постоянно меняется, это означает, что у вас есть некоторое ускорение \(\vec{a}=\dfrac{d \vec{v}}{dt}\), то для каждого бесконечно малого изменения показаний часов \(dt\) изменение скорости \(d\vec{v}\), которое происходит в течение этого бесконечно малого интервала времени, должно быть перпендикулярно к самой скорости.
(Если бы он не был перпендикулярен, то скорость увеличивалась бы или уменьшалась.) Таким образом, независимо от того, где вы находитесь в круге (вокруг которого вы движетесь против часовой стрелки, если смотреть сверху), у вас есть ускорение, направленное точно влево, перпендикулярно направление вашей скорости. Теперь, что всегда находится прямо слева от вас, если вы движетесь против часовой стрелки по кругу? Именно так! Центр круга всегда находится прямо слева от вас. Таким образом, ваше ускорение всегда направлено по центру. Мы называем направленное к центру ускорение, связанное с круговым движением, центростремительным ускорением, потому что слово «центростремительный» означает «направленный к центру». Обратите внимание, что если вы движетесь по кругу по часовой стрелке, если смотреть сверху, вы постоянно поворачиваете направо, и ваше ускорение направлено вправо, прямо к центру круга. Эти соображения применимы к любому объекту — объект, движущийся по кругу, имеет центростремительное (направленное к центру) ускорение.
У нас есть несколько способов описать движение частицы, движущейся по окружности. Во-первых, мы характеризуем его с точки зрения того, как далеко частица прошла по окружности. Если нам нужна переменная положения, мы устанавливаем начальную точку на окружности и положительное направление. Например, для окружности с центром в начале координат плоскости x-y мы можем определить точку, в которой окружность пересекает положительную ось x, как начальную точку, а направление, в котором должна двигаться частица, чтобы двигаться против часовой стрелки вокруг окружности, как начальную точку. положительное направление. Имя, данное этой переменной позиции, — s. Позиция s — это общее расстояние, измеренное по окружности, которое прошла частица. Тогда скорость частицы равна скорости изменения s, \(\dfrac{ds}{dt}\), а направление скорости является касательной к окружности. Сама окружность определяется своим радиусом. Второй способ описания движения частицы состоит в том, чтобы описать его в терминах воображаемого отрезка, идущего от центра окружности к частице.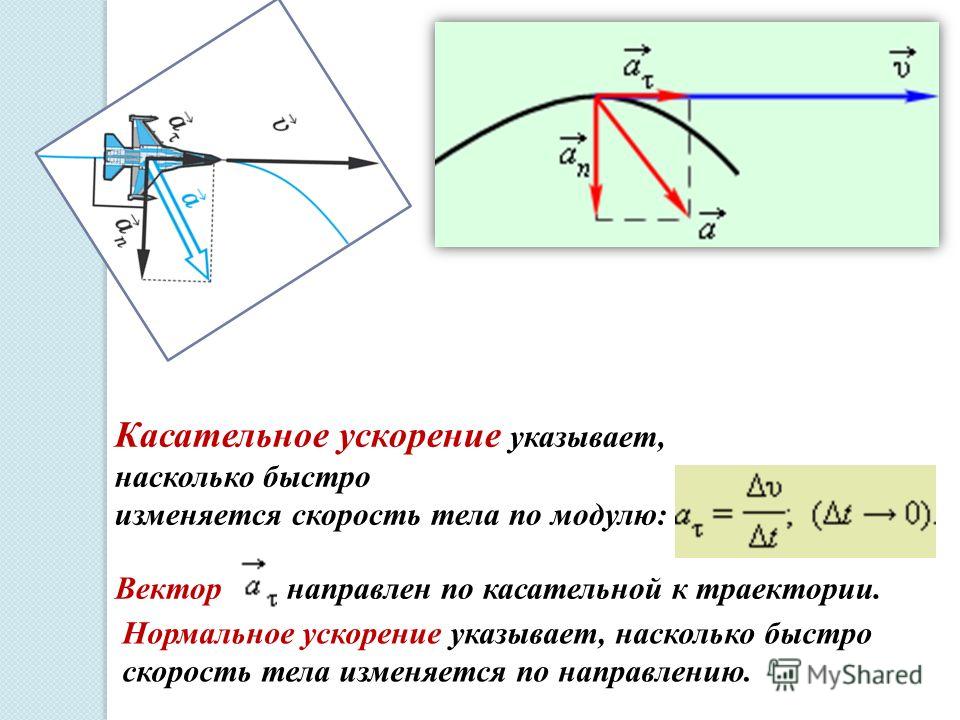
Чтобы использовать этот метод, также необходимо определить отрезок опорной линии — положительная ось x является обычным выбором для случая окружности с центром в начале системы координат x-y. Затем, если вы знаете радиус r окружности, угол \(тета\), который линия к частице образует с опорной линией, полностью определяет местоположение частицы.
В геометрии переменная положения s определяет длину дуги на окружности. Напомним, что по определению угол \(\theta\) в радианах равен отношению длины дуги к радиусу:
\[\theta=\dfrac{s}{r} \номер\]
Решив для s мы имеем:
\[s=r\тета \метка{18-1} \]
, в котором мы интерпретируем s как положение частицы на окружности, а \(\theta\) как угол, который составляет воображаемый отрезок прямой от центра окружности к частице с опорный сегмент линии, такой как положительная ось x. Ясно, что чем быстрее движется частица, тем быстрее изменяется угол тета, и действительно, мы можем получить связь между скоростью частицы и скоростью изменения \(\тета\), просто взяв производную по времени от обоих стороны уравнения \(\ref{18-1}\).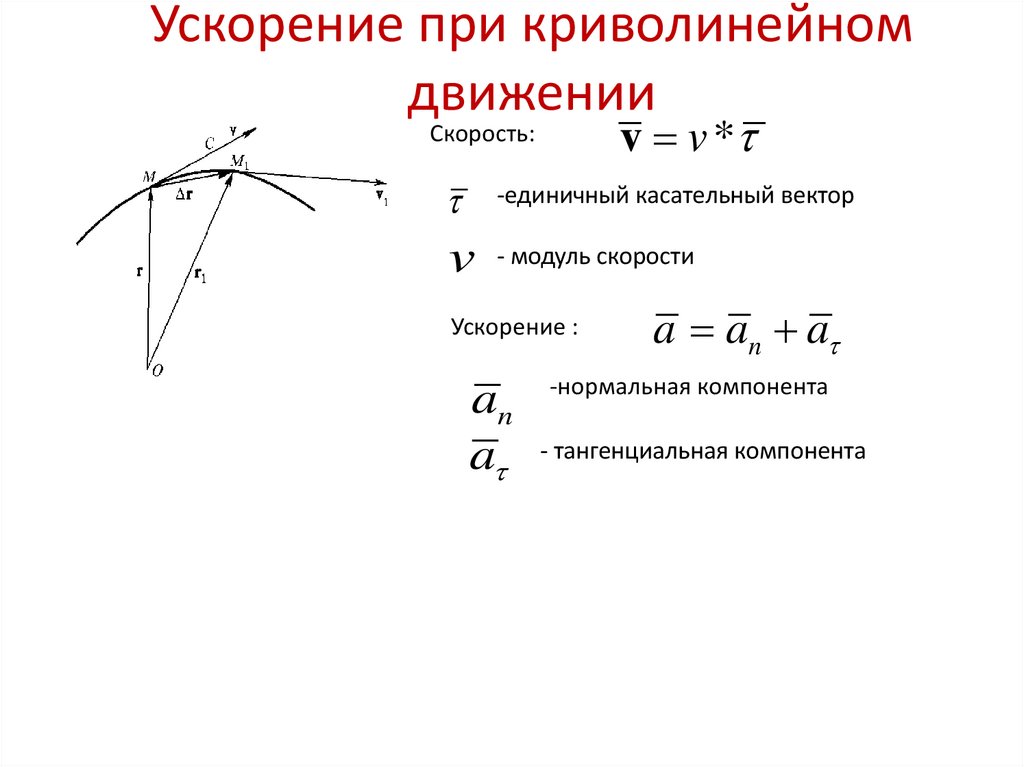
Давайте сделаем это.
Начнем с производной обеих частей уравнения \(\ref{18-1}\) по времени:
\[\dfrac{ds}{dt}=r\dfrac{d\theta}{dt} \nonumber \]
, а затем перепишите результат как:
.\[\dot{s} =r\dot{\theta} \nonnumber \]
просто для того, чтобы читатель привык к идее, что мы представляем производную по времени переменной, то есть скорость изменения этой переменной, записывая символ переменной с точкой над ним. Затем мы перепишем результат как
\[v=r \dot{\theta}\метка{18-2} \]
, чтобы подчеркнуть тот факт, что скорость изменения положения на окружности есть скорость частицы (величина скорости частицы). Наконец, мы определяем переменную \(\omega\) (“omega”) как скорость изменения угла, что означает, что \(\omega\) равно \(\dfrac{d\theta}{dt}\) и \(\omega\) равно \(\dot{\theta}\). Должно быть ясно, что \(\omega\) — это скорость вращения воображаемой линии от центра круга к частице. Мы называем эту скорость вращения величиной угловой скорости сегмента линии.
(Выражение «угловая скорость» \(\omega\) чаще используется для характеристики того, насколько быстро и в какую сторону вращается твердое тело, а не воображаемая линия.) Переписав \(v=r\dot{\theta} \) с заменой \(\dot{\theta}\) на \(\omega\) дает:
\[v=r\omega \label{18-3} \]
Теперь мы можем вывести выражение для направленного к центру (центростремительного) ускорения, о котором мы говорили в начале этой главы. Рассмотрим короткий интервал времени \(\Delta t\). (Мы возьмем предел, когда \(\Delta t\) стремится к нулю до конца этой главы.) В течение этого короткого промежутка времени частица проходит расстояние \(\Delta s\) по окружности и угол, который линия, идущая от центра круга к частице, изменяется с опорной линией на величину \(\Delta \theta\).
Кроме того, за это время \(\Delta t\) скорость частицы изменяется от \(\vec{v}\) до \(\vec{v}’\), изменение \(\ Дельта \vec{v}\), определяемая \(vec{v}’=\vec{v}+\Delta\vec{v}\), изображенная на следующей векторной диаграмме (на которой стрелки представляют векторы \(\ vec{v}\) и \(\vec{v}’\) были скопированы сверху без изменения ориентации или длины).
Обратите внимание, что малый угол \(\Delta \theta\), появляющийся на диаграмме сложения векторов, совпадает с тем \(\Delta \theta\), который появляется на диаграмме выше.
Хотя \(\vec{v}’\) — новый вектор, отличный от \(\vec{v}\), мы оговорили, что скорость частицы является постоянной, поэтому вектор \( \vec{v}’\) имеет ту же величину, что и вектор \(\vec{v}\). То есть \(\vec{v}’=\vec{v}\). Мы перерисовываем диаграмму сложения векторов, помечая оба вектора скорости одним и тем же символом v.
Величина центростремительного ускорения по определению может быть выражена как } \dfrac{\Delta V}{\Delta t} \nonumber \] 9\круг\). Таким образом, в пределе, когда \(\Delta t\) приближается к 0, треугольник является прямоугольным, и в этом пределе мы можем написать:
\[\dfrac{\Delta v}{v}=tan(\Delta \theta ) \nonumber \]
\[\Delta v=v \tan(\Delta \theta) \nonumber \]
Подставив это в наше выражение для \(a_c\), мы получим:
\[a_c=\underset {\Delta t \rightarrow 0}{lim} \dfrac{vtan(\Delta\theta)}{\Delta t} \label{18-4} \]
Теперь мы используем приближение малого угла из математики плоскости геометрия, приближение, которое становится реальным уравнением в пределе, когда \(\Delta\theta\) приближается к нулю.
Приближение малого угла
Для любого угла, который очень мал по сравнению с \(\pi\) радианами (чем меньше угол, тем лучше приближение), тангенс угла приблизительно равен самому углу, выраженному в радианы; а синус угла примерно равен самому углу, выраженному в радианах. Фактически,
\[tan(\Delta \theta) \underset{\Delta \theta \rightarrow 0}{\rightarrow} \Delta\theta \nonumber \]
и
\[sin(\Delta \theta ) \underset{\Delta\theta\rightarrow 0}{\rightarrow} \Delta\theta\nonumber \]
где \(\Delta\theta\) в радианах.
Приближение малых углов позволяет нам записать
\[a_c=\underset{\Delta t\rightarrow 0}{lim} \dfrac{v \Delta \theta}{\Delta t} \nonumber \]
[ где мы заменили \(tan(\Delta\theta)\) в уравнении \(\ref{18-4}\) выше на \(\Delta \theta\) ].
Константа v может быть взята за предел, что даст \(a_c=\underset{\Delta t\rightarrow 0}{lim} \dfrac{\Delta \theta}{\Delta t}\). Но \(\underset{\Delta t\rightarrow 0}{lim} \dfrac{\Delta\theta}{\Delta t}\) – это скорость изменения угла \(\theta\), то есть по определению угловая скорость \(\omega\).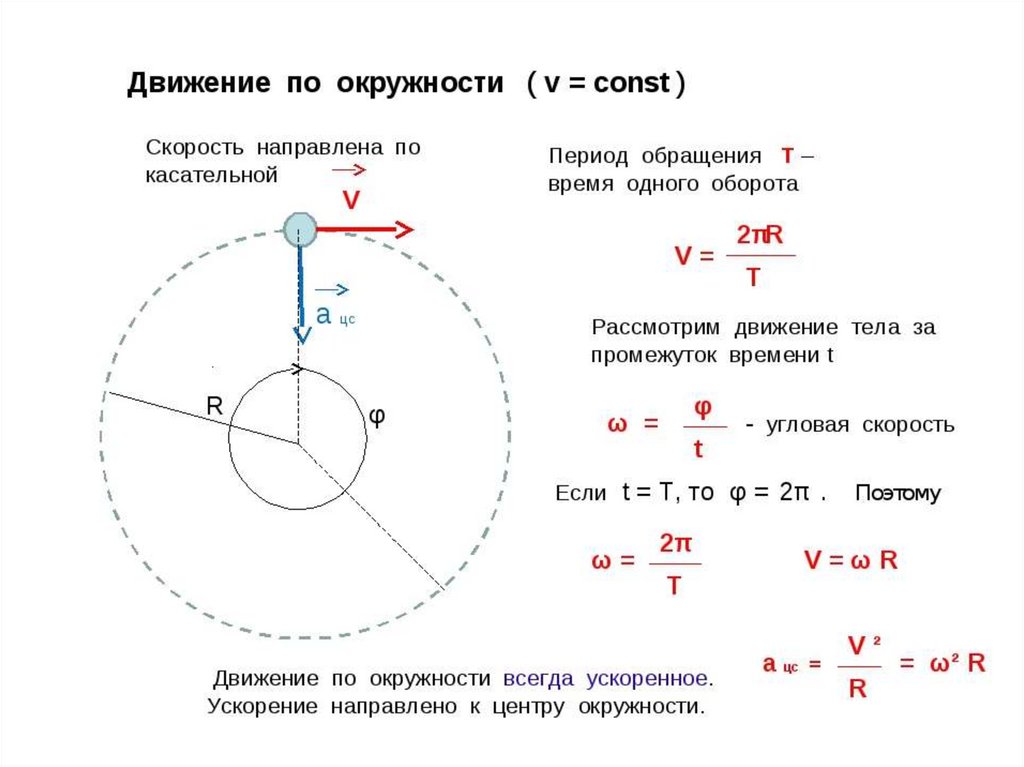
Таким образом 92\label{18-6} \]
Следует отметить, что, несмотря на то, что мы сосредоточили наше внимание на случае, когда частица, движущаяся по окружности, движется с постоянной скоростью, частица имеет центростремительную ускорение независимо от того, меняется скорость или нет. Если скорость частицы изменяется, центростремительное ускорение в любой момент (по-прежнему) определяется уравнением \(\ref{18-5}\), где \(v\) является скоростью частицы в этот момент ( и в дополнение к центростремительному ускорению частица также имеет некоторое ускорение вдоль окружности, известное как тангенциальное ускорение). Случай, который мы исследовали, является, однако, замечательным случаем. Даже если скорость частицы постоянна, частица имеет некоторое ускорение только потому, что направление ее скорости постоянно меняется. Более того, центростремительное ускорение не является постоянным ускорением, потому что его направление постоянно меняется. Визуализируйте это. Если вы едете против часовой стрелки (если смотреть сверху) по круговой трассе, направление, в котором вы видите центр круга, постоянно меняется (и это направление является направлением центростремительного ускорения).
Когда вы находитесь в самой восточной точке круга, центр находится к западу от вас. Когда вы находитесь в самой северной точке круга, центр находится к югу от вас. Когда вы находитесь в самой западной точке круга, центр находится к востоку от вас. А когда вы находитесь в самой южной точке круга, центр находится к северу от вас.
Эта страница под названием 18A: Круговое движение – Центростремительное ускорение распространяется под лицензией CC BY-SA 2.5 и была создана, изменена и/или курирована Джеффри В. Шником посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Джеффри В.
