аспирант ИТМО Дмитрий Царёв ― о работе физика-теоретика и о том, что общего у квантовой физики и спорта высших достижений
Ученые ИТМО совместно с коллегами из Тайваня опубликовали исследование, которое может лечь в основу сверхточных метрологических приборов, которые превзойдут детектор LIGO, сумевший засечь гравитационные волны. В интервью ITMO.NEWS один из авторов работы, аспирант ИТМО Дмитрий Царёв рассказывает о том, как шла работа, и перспективах исследований.
Ваша недавняя работа посвящена квантовой метрологии. Не могли бы вы рассказать для начала, что это за раздел науки?
Перед тем как углубляться в дебри квантовой науки, я приведу простой пример из спорта высших достижений. Я имею в виду прыжки с шестом, которые вполне можно отнести к предельным возможностям человека. Здесь важна не только подготовка спортсмена (предельная по всем параметрам), но и правильно выбранный шест, который сделан из подходящего материала ― он должен быть упругим и не ломаться.
То же самое можно сказать и про квантовую метрологию. Это наука об измерении различных физических величин с такой высокой точностью, какую только допускают фундаментальные ограничения, определяемые квантовыми флуктуациями, которые в принципе неустранимы. Что это значит? В квантовой физике действует принцип неопределенности Гейзенберга, который можно сформулировать так: если у вас есть квантовая частица, то в каждый момент времени вы можете с уверенностью указать, либо где она находится, либо как она движется, но не оба параметра одновременно. То есть координата частицы и ее импульс подчинены принципу неопределенности.
Источник: shutterstock.com
Это фундаментальный закон природы, который мы не можем «отменить» ― мы можем только им правильно пользоваться и управлять.
Управлять в квантовом мире ― это значит использовать такие состояния материальных объектов, которые нам «выгодны» с точки зрения измерения описывающих их величин. Именно на этом и построена квантовая метрология и сенсорика. Понять, почему так устроен мир и что сделать на практике, означает сделать следующий шаг в развитии квантовых технологий и понимании физики вообще.
Теперь, что касается измерений. Например, когда мы хотим измерить скорость объекта, мы используем лидар. Это прибор наподобие радара, только с оптическим излучением вместо радиоволн, который любят использовать инспекторы ДПС. По своей сути лидар является интерферометром. Он излучает два лазерных пучка, один опорный, он остается в приборе, а другой отправляется по воздуху, отражается от объекта и возвращается обратно.
Когда в приборе эти два пучка смешиваются, или, говоря корректнее, интерферируют, то получается картина, позволяющая сделать вывод о скорости объекта. После этого на экране отображается цифра, которую показывают водителю, если он превысил скоростной режим.
Источник: shutterstock.com
А при чем здесь квантовая физика?
Квантовая метрология ― это как спорт высших достижений. Считается, что все технические несоверешенства даже самой совершенной измерительной аппаратуры преодолены; измерения проводят на уровне квантовых шумов. Точность измерения любого интерферометра фундаментально зависит от того, какое квантовое состояние мы будем использовать в качестве исходного.
Классический подход заключается в том, чтобы посветить на вход прибора традиционным (когерентным) лазерным источником света. Это известная процедура, она надежна, но она ограничивает точность наших измерений так называемым стандартным квантовым пределом. Пока мы используем такие «классические» состояния, мы не можем преодолеть этот предел, как бы мы ни улучшали прибор технически.
Это потолок точности. В мире вокруг нас такой точности хватает «почти» всегда, и ничего квантового тут, можно сказать, нет.
Однако за последние десятилетия было неоднократно предсказано теоретически и экспериментально, что можно преодолеть эту отметку и попробовать достичь нового «рекорда» ― так называемого предела Гейзенберга. Но для этого надо использовать неклассические, запутанные (entangled) состояния. Что это такое?
Источник: shutterstock.com
Предположим, у нас есть квантовая частица ― двухатомная молекула с нулевым спином, она распадается на две частицы ― два атома с ненулевым спином каждый, которые начинают отдаляться друг на друга в разные стороны. Так вот, если мы измерим какой-то параметр у одной из них, то мы «автоматически» узнаем этот же параметр у другой частицы, исходя из законов сохранения. По той причине, что они квантовым образом запутаны. Разделенные в пространстве, они остаются единым квантовомеханическим объектом.
Например, ориентация спина атомов может быть любая, и результат его измерения носит вероятностный (случайный) характер.
Однако, если мы измерим ориентацию спина одного атома, то спин второго как бы «подстроится» под этот результат, исходя из того, что суммарный спин был равен нулю. Свойство запутанности важно во всех приложениях квантовых технологий, которые основаны на так называемом квантовом превосходстве устройств, по сравнению с их классическими аналогами: в квантовых вычислениях, квантовых коммуникациях и криптографии. Важен он и для квантовой метрологии.
Дело в том, что, во-первых, любое измерение в квантовой физике имеет разрушающий характер. Частица, которую мы измеряем, прекращает свое существование, поглощается детектором. Однако вторая частица продолжает движение, и теперь мы о ней кое-что знаем за счет измерения первой. Во-вторых, явление запутанности позволяет повышать точность измерений.
Каким образом?
Мы можем эти частицы пустить по каналам (плечам) интерферометра и таким образом за счет квантовой интерференции улучшить видность результирующей интерференционной картинки, которая как раз подчиняется следующему сугубо квантовому ограничению ― пределу Гейзенберга для измерения разности фаз в каналах интерферометра.
Квантовая запутанность. Источник: shutterstock.com
Сложность всего этого в том, что необходимо уникальное запутанное состояние, содержащее сразу много частиц. Запутать две частицы ― не проблема. Можно запутать три, четыре и даже пять частиц. То есть до пяти частиц одновременно как бы находятся и в первом, и во втором канале интерферометра. Понятно, что на самом деле они в каком-то одном из них, но законы квантовой физики обязывают нас к тому, что до самого измерения мы ничего определенного сказать не можем и исходим из того, что они находятся в суперпозиции, то есть в двух каналах сразу.
Такие состояния называют N00N-состояниями, то есть N частиц в одном плече и ноль ― в другом, и наоборот, и это все одновременно! Такое состояние позволяет достичь предел Гейзенберга на любом двухканальном устройстве: лидаре, гироскопе, интерферометре.
Но получить его в эксперименте для большого числа частиц пока не удавалось. Более того, даже в теории прогноз пессимистичен: небольшие потери в интерферометре сводят на нет все магические свойства таких состояний.
И как быть?
Вот, здесь к нам пришла удача! Мы с моим научным руководителем, профессором Александром Алоджанцем некоторое время назад обратили внимание на то, что квантовые солитоны, которые давно хорошо известны и в оптике, и в квантовых коммуникациях, и в науке о материалах, в силу своих нелинейных свойств могут сильно помочь. При определенных условиях их запутанные состояния остаются весьма устойчивыми к потерям, и это мы доказываем в нашей работе, опубликованной в ноябре в журнале New Journal of Physics. Конечно, мы чуть-чуть проигрываем в точности (чудес в природе не бывает), но этот проигрыш не критичен, мы по-прежнему находимся в самой близи предела Гейзенберга.
Иллюстрация из статьи
Уточните, как это все работает, непосредственно в вашей работе, опубликованной в журнале New Journal of Physics?
Мы придумали способ запутывать до тысячи частиц.
Для этого мы используем солитоны конденсата Бозе-Эйнштейна. Тут, наверное, нужны пояснения. Во-первых, Бозе-конденсат ― это особое состояние материи, при котором вещество проявляет квантовые свойства на макроскопическом уровне. Грубо говоря, у нас есть несколько сотен частиц, которые в виде конденсата движутся в пространстве как одна огромная квантовая частица. Такое состояние на сегодня получить стало возможно при очень низких температурах, меньше одного Кельвина. Хотя в 2006 году такое состояние наблюдали в полупроводниковых структурах при температуре в несколько Кельвинов, а в 2013 ― даже и при комнатной температуре в 300 Кельвинов (27 градусов Цельсия).
Теперь о солитоне ― это достаточно устойчивый частице-подобный объект. Запутав два солитона мы можем рассматривать их, условно, как две макрочастицы, получив одновременно запутанность сотен тех частиц, из которых они состоят. Это и есть многочастичное N00N-состояние. Число частиц здесь может доходить до тысячи! Сами посудите, пять и 1000 ― очень большой прогресс.
Иллюстрация из статьи
А были ли проведены какие-то эксперименты?
Нет. Но в работе все расчеты сделаны исходя из сегодняшних экспериментальных возможностей. Мы рассматриваем конденсат лития; это вещество популярно у экспериментаторов. Частицы лития имеют очень важное свойство ― они притягиваются друг к другу, без этого невозможно сформировать солитон. Экспериментаторы умеют получать солитоны конденсатов и умеют их запутывать. Пока никому не приходила в голову идея использовать все это в квантовой метрологии.
А какие горизонты открывает эта фундаментальная работа? Много ли стран занимается таким «спортом высших достижений»?
Да, это фундаментальная работа, но результаты весьма прикладные. Я убежден, что систему, описанную в нашей работе, можно довести до уровня «прибора». Это, во-первых, метрология с холодными атомами, которая есть в России, но требует серьезной экспериментальной доработки. Здесь могут быть существенно улучшены точностные характеристики так называемых «атомных часов», то есть метрологические стандарты частоты и времени.
Но есть и более интересные продолжения. Например, использовать такую технологию в интерферометрах Майкельсона с оптическими полями для увеличения точности регистрации гравитационных волн и исследований галактического пространства. Наше предложение позволит построить детектор с предельной на сегодняшний день точностью измерений. Где будет использоваться такой «прибор»?
Детектор LIGO. Источник: wired.com
В настоящее время в мире есть несколько крупных проектов из разряда mega-science по регистрации гравитационных волн. Я читал об «американском» проекте LIGO, знаю также «японский» ― KAGRA, в котором участвует группа из Тайваня, с которой мы сотрудничаем. Я неспроста использую «кавычки»: на самом деле там идет сотрудничество многих стран, под одним «зонтиком».
А как же Россия?
Это сложный, и, к сожалению, не только научный, вопрос. Нужны как минимум гигантские деньги. Вы же понимаете, что объяснить условному чиновнику, зачем нужен квантовых компьютер, гораздо проще, чем необходимость исследований гравитационных волн, а также космоса в широком смысле этого слова.
Хотя, именно в этом заключается будущее устремление человечества, как мне представляется. Да, кстати, масштабный квантовый компьютер без участия квантовой метрологии тоже не сделать. Но это уже другая история.
Вы не только опубликовали статью, но и представили основанный на ней доклад на Всероссийском научном форуме. Расскажите об этом подробнее.
Форум называется «Наука будущего ― наука молодых». Он проходил в Москве в гибридном формате, москвичи собрались очно, остальные выступали через Zoom. Пришлось пройти большой конкурс проектов и суровый отбор. Я изложил на бумаге то, что рассказал вам сейчас, отправил, рецензенты вслепую, не зная моего имени и аффилиации, выбрали мою работу в числе победителей. Далее в блиц-формате на самом форуме мы выступали по три минуты с нашими докладами. Соответственно тут была задача больше не рассказать о работе, а показать свою мотивированность, понимание предмета, умение доносить сложные мысли простыми словами, ну и некоторый артистизм.
Диплом Дмитрия Царёва с форума «Наука будущего ― наука молодых»
А какую реакцию вызвал доклад?
В каждой секции было 40-45 человек, из них отобрали 10 и через три дня мы выступали уже с полноценными докладами на 10 минут. К сожалению, я растянул речь на все 10 минут, поэтому времени на вопросы не осталось. А вопросы были, и это хороший знак. Да и если судить по лицам, слушателям было интересно. Тема на самом деле очень интересная, но зачастую непонятная человеку со стороны. Поэтому квантовая физика не очень популярный предмет. Но тут аудитория была подготовленная, и всем вроде понравилось. Ну и присуждение мне второго места в секции «Цифровые технологии» говорит само за себя.
Вы сами сказали, что квантовая физика не самый популярный предмет. А почему вы сами ее выбрали?
Все благодаря моему научному руководителю ― на втором курсе бакалавриата, когда я учился во Владимирском государственном университете, Александр Павлович Алоджанц преподавал там квантовую физику.
Он настолько увлек меня своей лекцией, что я тогда принял решение углубиться именно в эту область. Я очень благодарен Александру Павловичу, он помог мне стать тем, кто я есть. Как видите, у нас с тех пор весьма плодотворный коллектив.
Именно Александр Павлович предложил вам поступать в ИТМО после своего переезда в Петербург?
Да. Сначала в магистратуру, а потом в аспирантуру.
Александр Алоджанц
Но все же чем именно вас так привлекла квантовая физика?
Всем нам хочется верить в чудеса, чтобы мир был наполнен магией. Квантовый мир наполнен магией, то, что происходит у нас под носом на микроскопическом уровне, настолько не похоже на привычные нам вещи, что иначе как чудесами это не назвать. Например, нелокальность ― объект может находиться в двух местах одновременно, это как? Это необъятно и это мир в себе. Поэтому я его изучаю.
Вы думаете продолжить научную карьеру?
Да, безусловно
А что можете сказать о самом Университете ИТМО?
ИТМО ― великолепный университет.
Взять, к примеру, лаборатории. Понятно, что для теоретика инструменты ― это бумага и ручка… и мусорная корзина для неудавшихся моделей. Но я видел экспериментальные установки, они потрясающие ― мощные, современные, дорогие. Однако университет ― это, в первую очередь, люди. Профессорско-преподавательский состав ИТМО очень сильный: каждый знает свой предмет, все на своем месте, и они умеют обучать. Меня, во всяком случае, научили здесь очень многому, и я благодарен Университету ИТМО за это.
К началу
КВАНТОВАЯ МЕХАНИКА. ИНОЙ ВЗГЛЯД | Наука и жизнь
Квантово-механическое описание физических
явлений микромира считается единственно верным и наиболее полно отвечающим
реальности. Объекты макромира подчиняются законам другой, классической
механики. Граница между макро- и микромиром размыта, а это вызывает целый
ряд парадоксов и противоречий. Попытки их ликвидировать приводят к появлению
других взглядов на квантовую механику и физику микромира.
Видимо, наилучшим
образом выразить их удалось американскому теоретику Дэвиду Джозефу Бому
(1917-1992).
1. Мысленный эксперимент по измерению компонент спина (собственного количества движения) электрона с помощью некоего устройства – “черного ящика”.
2. Последовательное измерение двух компонент спина. Измеряется “горизонтальный” спин электрона (слева), потом “вертикальный” спин (справа), потом снова “горизонтальный” (внизу).
3А. Электроны с “правым” спином после прохождения через “вертикальный” ящик движутся в двух направлениях: вверх и вниз.
3Б. В том же эксперименте на пути одного из двух пучков поставим некую поглощающую поверхность. Далее в измерениях участвует лишь половина электронов, и на выходе половина их имеет “левый” спин, а половина – “правый”.
4. Состояние любого объекта микромира описывает так называемая волновая функция.
5. Мысленный эксперимент Эрвина Шредингера.
6. Эксперимент, предложенный Д. Бомом и Я. Аароновым в 1959 году, должен был показать, что магнитное поле, недоступное для частицы, влияет на ее состояние.
‹
›
Открыть в полном размере
Чтобы понять, какие трудности испытывает современная квантовая механика, нужно вспомнить, чем она отличается от классической, ньютоновской механики. Ньютон создал общую картину мира, в которой механика выступала как универсальный закон движения материальных точек или частиц – маленьких комочков материи. Из этих частиц можно было построить любые объекты. Казалось, что механика Ньютона способна теоретически объяснить все природные явления. Однако в конце прошлого века выяснилось, что классическая механика неспособна объяснить законы теплового излучения нагретых тел. Этот, казалось бы, частный вопрос привел к необходимости пересмотреть физические теории и потребовал новых идей.
В 1900 году появилась работа немецкого
физика Макса Планка, в которой эти новые идеи и появились. Планк предположил,
что излучение происходит порциями, квантами. Такое представление противоречило
классическим воззрениям, но прекрасно объясняло результаты экспериментов
(в 1918 году эта работа была удостоена Нобелевской премии по физике).
Спустя
пять лет Альберт Эйнштейн показал, что не только излучение, но и поглощение
энергии должно происходить дискретно, порциями, и сумел объяснить особенности
фотоэффекта (Нобелевская премия 1921 года). Световой квант – фотон, по
Эйнштейну, имея волновые свойства, одновременно во многом напоминает частицу
(корпускулу). В отличие от волны, например, он либо поглощается целиком,
либо не поглощается вовсе. Так возник принцип корпускулярно-волнового дуализма
электромагнитного излучения.
В 1924 году французский физик Луи де Бройль выдвинул достаточно “безумную” идею, предположив, что все без исключения частицы – электроны, протоны и целые атомы обладают волновыми свойствами. Год спустя Эйнштейн отозвался об этой работе: “Хотя кажется, что ее писал сумасшедший, написана она солидно”, а в 1929 году де Бройль получил за нее Нобелевскую премию…
На первый взгляд, повседневный опыт гипотезу
де Бройля отвергает: в окружающих нас предметах ничего “волнового” как
будто нет.
Расчеты, однако, показывают, что длина дебройлевской волны электрона,
ускоренно го до энергии 100 электрон-вольт, равна 10-8
сантиметра. Эту волну нетрудно обнаружить экспериментально, пропустив поток
электронов сквозь кристалл. На кристаллической решетке произойдет дифракция
их волн и возникнет характерная полосатая картинка. А у пылинки массой
0,001 грамма при той же скорости длина волны де Бройля будет в 1024
раз меньше, и обнаружить ее никакими средствами нельзя.
Волны де Бройля непохожи на механические
волны – распространяющиеся в пространстве колебания материи. Они характеризуют
вероятность обнаружить частицу в данной точке пространства. Любая частица
оказывается как бы “размазанной” в пространстве, и существует отличная
от нуля вероятность обнаружить ее где угодно. Классическим примером вероятностного
описания объектов микромира служит опыт по дифракции электронов на двух
щелях. Прошедший через щель электрон регистрируется на фотопластинке или
на экране в виде пятнышка.
Каждый электрон может пройти либо через правую
щель, либо через левую совершенно случайным образом. Когда пятнышек становится
очень много, на экране возникает дифракционная картина. Почернение экрана
оказывается пропорциональным вероятности появления электрона в данном месте.
Идеи де Бройля углубил и развил австрийский физик Эрвин Шредингер. В 1926 году он вывел систему уравнений – волновых функций, описывающих поведение квантовых объектов во времени в зависимости от их энергии (Нобелевская премия 1933 года). Из уравнений следует, что любое воздействие на частицу меняет ее состояние. А поскольку процесс измерения параметров частицы неизбежно связан с воздействием, возникает вопрос: что же регистрирует измерительный прибор, вносящий непредсказуемые возмущения в состояние измеряемого объекта?
Таким образом, исследование элементарных
частиц позволило установить, по крайней мере, три чрезвычайно удивительных
факта, касающихся общей физической картины мира.
Во-первых, оказалось, что процессами, происходящими в природе, управляет чистый случай. Во-вторых, далеко не всегда существует принципиальная возможность указать точное положение материального объекта в пространстве. И, в-третьих, что, пожалуй, наиболее странно, поведение таких физических объектов, как “измерительный прибор”, или “наблюдатель”, не описывается фундаментальными законами, справедливыми для прочих физических систем.
Впервые к таким выводам пришли сами основоположники квантовой теории – Нильс Бор, Вернер Гейзенберг, Вольфганг Паули. Позднее данная точка зрения, получившая название Копенгагенской интерпретации квантовой механики, была принята в теоретической физике в качестве официальной, что и нашло свое отражение во всех стандартных учебниках.
Вполне возможно, однако, что подобные заключения
были сделаны слишком поспешно. В 1952 году американский физик-теоретик
Дэвид Д.
Бом создал глубоко проработанную квантовую теорию, отличную от
общепринятой, которая так же хорошо объясняет все известные ныне особенности
поведения субатомных частиц. Она представляет собой единый набор физических
законов, позволяющий избежать какой-либо случайности в описании поведения
физических объектов, а также неопределенности их положения в пространстве.
Несмотря на это, бомовская теория до самого последнего времени почти полностью
игнорировалась.
Чтобы лучше представить себе всю сложность
описания квантовых явлений, проведем несколько мысленных экспериментов
по измерению спина (собственного момента количества движения) электрона.
Мысленных потому, что создать измерительный прибор, позволяющий точно измерять
обе компоненты спина, пока что не удалось никому. Столь же безуспешными
оказываются попытки предсказать, какие
именно электроны поменяют свой спин в ходе описанного эксперимента, а какие
нет.
Эти эксперименты включают в себя измерение двух компонент спина, которые условно будем называть “вертикальным” и “горизонтальным” спинами. Каждая из компонент в свою очередь может принимать одно из значений, которые мы также условно назовем “верхним” и “нижним”, “правым” и “левым” спинами соответственно. Измерение основано на пространственном разделении частиц с разными спинами. Приборы, осуществляющие разделение, можно представить себе как некие “черные ящики” двух типов – “горизонтальный” и “вертикальный” (рис. 1). Известно, что разные компоненты спина свободной частицы совершенно независимы (физики говорят – не коррелируют между собой). Однако в ходе измерения одной компоненты значение другой может измениться, причем совершенно неконтролируемым образом (2).
Пытаясь объяснить полученные результаты, традиционная квантовая теория пришла к выводу, что необходимо полностью отказаться от детерминистского, то есть полностью определяющего состояние
объекта, описания явлений микромира.
Поведение электронов подчиняется принципу
неопределенности, согласно которому компоненты спина не могут быть точно
измерены одновременно.
Продолжим наши мысленные эксперименты. Будем теперь не только расщеплять пучки электронов, но и заставим их отражаться от неких поверхностей, пересекаться и снова соединяться в один пучок в специальном “черном ящике” (3).
Результаты этих экспериментов противоречат
обычной логике. Действительно, рассмотрим поведение какого-либо электрона
в случае, когда поглощающая стенка отсутствует (3 А). Куда он будет двигаться?
Допустим, что вниз. Тогда, если первоначально электрон имел “правый” спин,
он так и останется правым до конца эксперимента. Однако, применив к этому
электрону результаты другого эксперимента (3 Б), мы увидим, что его “горизонтальный”
спин на выходе должен быть в половине случаев “правым”, а в половине -
“левым”. Явное противоречие. Мог ли электрон пойти вверх? Нет, по той же
самой причине.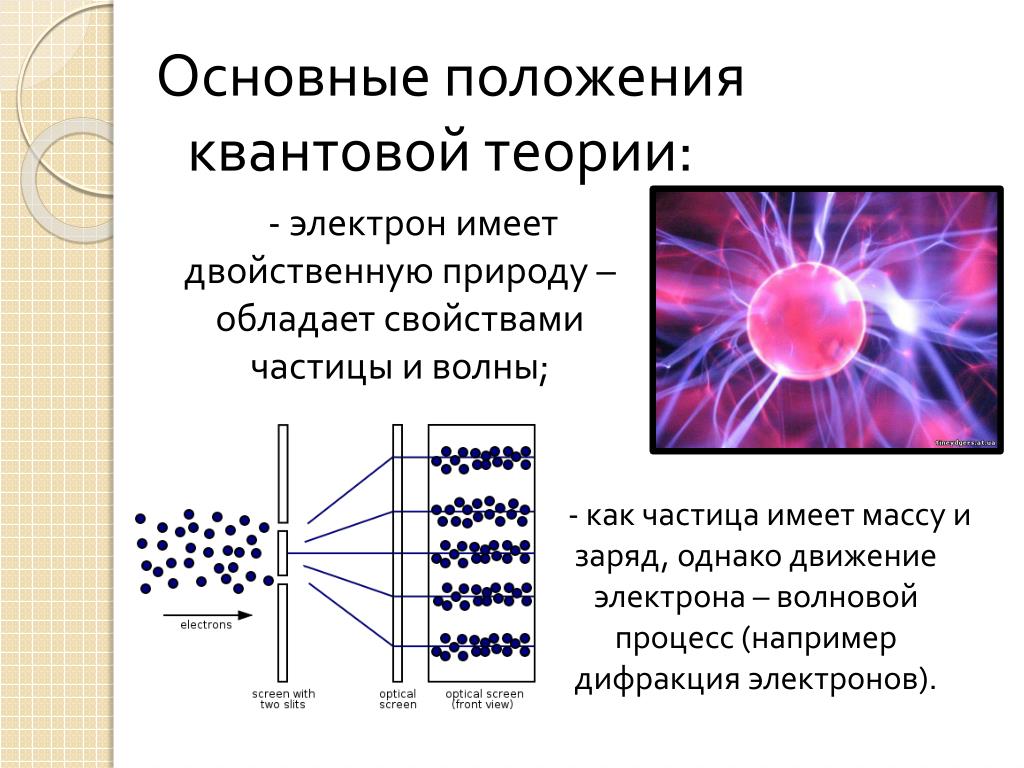
Быть может, он двигался не вниз, не вверх, а как-то по-другому?
Но, перекрыв верхний и нижний маршруты поглощающими стенками, мы на выходе
не получим вообще ничего. Остается предположить, что электрон может двигаться
сразу по двум направлениям. Тогда, имея возможность фиксировать его положение
в разные моменты времени, в половине случаев мы находили бы его на пути
вверх, а в половине – на пути вниз. Ситуация достаточно парадоксальная:
материальная частица не может ни раздваиваться, ни “прыгать” с одной траектории
на другую.
Что говорит в данном случае традиционная
квантовая теория? Она просто объявляет все рассмотренные ситуации невозможными,
а саму постановку вопроса об определенном направлении движения электрона
(и соответственно о направлении его спина) – некорректной. Проявление квантовой
природы электрона в том и заключается, что ответа на данный вопрос в принципе
не существует. Состояние электрона представляет собой суперпозицию, то
есть сумму двух состояний, каждое из которых имеет определенное значение
“вертикального” спина.
Понятие о суперпозиции – один из основополагающих
принципов квантовой механики, с помощью которого вот уже более семидесяти
лет удается успешно объяснять и предсказывать поведение всех известных
квантовых систем.
Для математического описания состояний
квантовых объектов используется волновая функция, которая в случае одной
частицы просто определяет ее координаты. Квадрат волновой функции равен
вероятности обнаружить частицу в данной точке пространства. Таким образом,
если частица находится в некой области А, ее волновая функция равна нулю
всюду, за исключением этой области. Аналогично частица, локализованная
в области Б, имеет волновую функцию, отличную от нуля только в Б. Если
же состояние частицы оказывается суперпозицией пребывания ее в А и Б, то
волновая функция, описывающая такое состояние, отлична от нуля в обеих
областях пространства и равна нулю всюду вне их. Однако, если мы поставим
эксперимент по определению положения такой частицы, каждое измерение будет
давать нам только одно значение: в половине случаев мы обнаружим частицу
в области А, а в половине – в Б ( 4).
Это означает, что при взаимодействии
частицы с окружением, когда фиксируется только одно из состояний частицы,
ее волновая функция как бы коллапсирует, “схлопывается” в точку.
Одно из основных утверждений квантовой механики заключается в том, что физические объекты полностью описываются их волновыми функциями. Таким образом, весь смысл законов физики сводится к предсказанию изменений волновых функций во времени. Эти законы делятся на две категории в зависимости от того, предоставлена ли система самой себе или же она находится под непосредственным наблюдением и в ней производятся измерения.
В первом случае мы имеем дело с линейными
дифференциальными “уравнениями движения”, уравнениями детерминистскими,
которые полностью описывают состояние микрочастиц. Следовательно, зная
волновую функцию частицы в какой-то момент времени, можно точно предсказать
поведение частицы в любой последующий момент.
Однако при попытке предсказать результаты измерений каких-либо свойств
той же частицы нам придется иметь дело уже с совершенно другими законами
– чисто вероятностными.
Возникает естественный вопрос: как отличить
условия применимости той или другой группы законов? Создатели квантовой
механики указывают на необходимость четкого разделения всех физических
процессов на “измерения” и “собственно физические процессы”, то есть на
“наблюдателей” и “наблюдаемых”, или, по философской терминологии, на субъект
и объект. Однако отличие между этими категориями носит не принципиальный,
а чисто относительный характер. Тем самым, по мнению многих физиков и философов,
квантовая теория в такой интерпретации становится неоднозначной, теряет
свою объективность и фундаментальность. “Проблема измерения” стала основным
камнем преткновения в квантовой механике. Ситуация несколько напоминает
знаменитую апорию Зенона “Куча”. Одно зерно – явно не куча, а тысяча (или,
если угодно, миллион) – куча. Два зерна – тоже не куча, а 999
(или 999999) – куча. Эта цепочка рассуждений приводит к некоему количеству
зерен, при котором понятия “куча – не куча” станут неопределенными.
Они
будут зависеть от субъективной оценки наблюдателя, то есть от способа измерений,
хотя бы и на глаз.
Все окружающие нас макроскопические тела предполагаются точечными (или протяженными) объектами с фиксированными координатами, которые подчиняются законам классической механики. Но это означает, что классическое описание можно продолжить вплоть до самых малых частиц. С другой стороны, идя со стороны микромира, следует включать в волновое описание объекты все большего размера вплоть до Вселенной в целом. Граница между макро- и микромиром не определена, и попытки ее обозначить приводят к парадоксу. Наиболее четко указывает на него так называемая “задача о кошке Шредингера” – мысленный эксперимент, предложенный Эрвином Шредингером в 1935 году (5).
В закрытом ящике сидит кошка. Там же находятся
флакон с ядом, источник излучения и счетчик заряженных частиц, подсоединенный
к устройству, разбивающему флакон в момент регистрации частицы.
Если яд
разольется, кошка погибнет. Зарегистрировал счетчик частицу или нет, мы
не можем знать в принципе: законы квантовой механики подчиняются законам
вероятности. И с этой точки зрения, пока
счетчик не произвел измерения, он находится в суперпозиции двух состояний
– “регистрация – нерегистрация”. Но тогда в этот момент и кошка оказывается
в суперпозиции состояний жизни и смерти.
В действительности, конечно, реального парадокса здесь быть не может. Регистрация частицы – процесс необратимый. Он сопровождается коллапсом волновой функции, вслед за чем срабатывает механизм, разбивающий флакон. Однако ортодоксальная квантовая механика не рассматривает необратимых явлений. Парадокс, возникающий в полном согласии с ее законами, наглядно показывает, что между квантовым микромиром и классическим макромиром имеется некая промежуточная область, в которой квантовая механика не работает.
Итак, несмотря на несомненные успехи квантовой
механики в объяснении экспериментальных фактов, в настоящий момент она
едва ли может претендовать на полноту и универсальность описания физических
явлений.
Одной из наиболее смелых альтернатив квантовой механики и стала
теория, предложенная Дэвидом Бомом.
Задавшись целью построить теорию, свободную
от принципа неопределенности, Бом предложил считать микрочастицу материальной
точкой, способной занимать точное положение в пространстве. Ее волновая
функция получает статус не характеристики вероятности, а вполне реального
физического объекта, некоего квантовомеханического поля, оказывающего мгновенное
силовое воздействие. В свете этой интерпретации, например, “парадокс Эйнштейна-Подольского-Розена”
(см. “Наука и жизнь” № 5, 1998 г.) перестает быть парадоксом. Все законы,
управляющие физическими процессами, становятся строго детерминистскими
и имеют вид линейных дифференциальных уравнений. Одна группа уравнений
описывает изменение волновых функций во времени, другая – их воздействие
на соответствующие частицы. Законы
применимы ко всем физическим объектам без исключения – и к “наблюдателям”,
и к “наблюдаемым”.
Таким образом, если в какой-то момент известны
положение всех частиц во Вселенной и полная волновая функция каждой, то
в принципе можно точно рассчитать положение частиц и их волновые функции
в любой последующий момент времени. Следовательно, ни о какой случайности
в физических процессах не может быть и речи. Другое дело, что мы никогда
не сможем обладать всей информацией, необходимой для точных вычислений,
да и сами расчеты оказываются непреодолимо сложными. Принципиальное незнание
многих параметров системы приводит к тому, что на практике мы всегда оперируем
некими усредненными величинами. Именно это “незнание”, по мнению Бома,
заставляет нас прибегать к вероятностным законам при описании явлений в
микромире (подобная ситуация возникает и в классической статистической
механике, например в термодинамике, которая имеет дело с огромным количеством
молекул). Теория Бома предусматривает определенные
правила усреднения неизвестных параметров и вычисления вероятностей.
Вернемся к экспериментам с электронами,
изображенным на рис. 3 А и Б. Теория Бома дает им следующее объяснение.
Направление движения электрона на выходе из “вертикального ящика” полностью
определяется исходными условиями – начальным положением электрона и его
волновой функцией. В то время как электрон движется либо вверх, либо вниз,
его волновая функция, как это следует из дифференциальных уравнений движения,
расщепится и станет распространяться сразу в двух направлениях. Таким образом,
одна часть волновой функции окажется “пустой”, то есть будет распространяться
отдельно от электрона. Отразившись от стенок, обе части волновой функции
воссоединятся в “черном ящике”, и при этом электрон получит информацию
о том участке пути, где его не было. Содержание этой информации, например
о препятствии на пути “пустой” волновой функции, может оказать существенное
воздействие на свойства электрона. Это и снимает логическое противоречие
между результатами экспериментов, изображенных на рисунке.
Необходимо отметить
одно любопытное свойство “пустых” волновых функций: будучи реальными, они
тем не менее никак не влияют на посторонние объекты и не могут быть зарегистрированы
измерительными приборами. А на “свой” электрон “пустая” волновая функция
оказывает силовое воздействие независимо от расстояния, причем воздействие
это передается мгновенно.
Попытки “исправить” квантовую механику
или объяснить возникающие в ней противоречия предпринимали многие исследователи.
Построить детерминистскую теорию микромира, например, пытался де Бройль,
который был согласен с Эйнштейном, что “Бог не играет в кости”. А видный
отечественный теоретик Д. И. Блохинцев считал, что особенности квантовой
механики проистекают из-за невозможности изолировать частицу от окружающего
мира. При любой температуре выше абсолютного нуля тела излучают и поглощают
электромаг нитные волны. С позиций квантовой механики это означает, что
их положение непрерывно “измеряется”, вызывая коллапс волновых функций.
“С этой точки зрения никаких изолированных, предоставленных самим себе
“свободных” частиц не существует, – писал Блохинцев. – Возможно, что в
этой связи частиц и cреды и скрывается природа той невозможности изолировать
частицу, которая проявляется в аппарате
квантовой механики”.
И все-таки – почему же интепретация квантовой механики, предложенная Бомом, до сих пор не получила должного признания в научном мире? И как объяснить почти повсеместное господство традиционной теории, несмотря на все ее парадоксы и “темные места”?
Долгое время новую теорию не хотели рассматривать
всерьез на основании того, что в предсказании исхода конкретных экспериментов
она полностью совпадает с квантовой механикой, не приводя к существен но
новым результатам. Вернер Гейзенберг, например, считал, что “для любого
опыта его (Бома) результаты совпадают с копенгагенской интерпретацией.
Отсюда первое следствие: интерпретацию Бома нельзя опровергнуть экспериментом. ..”
Некоторые считают теорию ошибочной, так как в ней преимущественная роль
отводится положению частицы в пространстве. По их мнению, это противоречит
физической реальности, ибо явления в квантовом мире принципиально не могут
быть описаны детерминистскими законами. Существует немало и других, не
менее спорных аргументов против теории Бома, которые сами требуют серьезных
доказательств. Во всяком случае, ее пока что действительно никому не удалось
полностью опровергнуть. Более того – работу над ее совершенствованием продолжают
многие, в том числе отечественные, исследователи.
Объединяя загадочные миры квантовой физики и музыки
Квантовая физика странна и нелогична. По этой причине слово «квант» стало сокращением для всего мощного или мистического, независимо от того, имеет ли оно какое-либо отношение к квантовой механике. Как квантовый физик, у меня выработалось рефлекторное закатывание глаз, когда я услышал, что это слово применяется ко всему, что не связано с физикой. Он используется для описания гомеопатии, моющих средств для посудомоечных машин и дезодорантов.
Если бы я впервые не услышал о квантовой музыке от уважаемого физика, я бы так же насмехался над другими нелепыми употреблениями этого слова. Но в исполнении Клауса Мёльмера это было интригующе. В проекте Quantum Music физики и музыканты работали вместе, чтобы впервые объединить «таинственные миры квантовой физики и музыки». Они разработали устройство, которое прикрепляется к каждой клавише фортепиано, так что, когда пианист играет, информация передается на компьютер и синтезатор, который воспроизводит «квантовые» тона в дополнение к знакомым реверберациям фортепиано.
Среди используемых тонов есть те, которые представляют очень квантовый объект: конденсат Бозе-Эйнштейна (БЭК). Это облако атомов, охлажденных чуть выше абсолютного нуля. При такой низкой температуре микроскопические квантовые свойства отдельных частиц можно рассматривать вместе как единую макроскопическую квантовую сущность. Изучение БЭК — это способ изучения следствий квантовой механики в большем масштабе, чем это обычно возможно.
Одним из аспектов, который можно изучать с помощью БЭК, является квантовая акустика — поведение колебаний и вибраций в облаке. Эти же типы вибраций в воздухе производят звуки, которые мы слышим. Квантовые свойства атомов, например то, как они взаимодействуют друг с другом, определяют частоты звуковых волн, которые могут распространяться в БЭК.
Проект Quantum Music объединил фортепиано с этими квантовыми звуками для создания странной, но красивой музыки, не похожей ни на что, что я слышал раньше. Я думал, что это был очень хороший просветительский проект. Но, видимо, Мёльмер надеялся на большее. В рекламном ролике 2016 года он выразил надежду, что музыканты смогут дать ему представление о квантовой механике:
Если вы возьмете людей с сильной интуицией, например, в волнах и волновом поведении, таких как музыканты, будут ли они в состоянии принести дополнительное понимание? Могут ли их профессиональные знания о волнах — знания, которые есть у музыканта, — быть использованы в квантовых исследованиях?
Мои глаза, может, и не закатились, но скептически сузились. Я не мог представить, чтобы кто-то, у кого не было физического образования, привнесет какую-либо полезную интуицию в квантовую механику. Это настолько противоречило нашему повседневному опыту, что я думал, что единственный способ понять квантовый мир — это изучить и разобраться с математикой, которая его описывает. Вдобавок казалось, что цели музыканта и физика совершенно разные — возможно, даже конкурирующие. В то время как композитор работает в рамках теории музыки, чтобы создать что-то красивое и интересное, физик заинтересован только в том, чтобы найти истину о том, как устроен мир, независимо от того, красива эта истина или нет.
Но опять же, квантовая механика в основном связана с волнами. А что такое музыка, как не сочетание волн? Хотя, безусловно, существуют явления квантовой механики, которые слишком странны, чтобы их можно было уловить с помощью классических звуковых волн, используемых в музыке, многие аспекты квантовой механики вытекают из одного факта: все, от света до частиц, даже до человека, имеет частицеподобную природу и волнообразный характер. Для чего-то такого большого, как человек, длина этой волны — так называемая «длина волны де Бройля» — настолько мала, что ею можно пренебречь, поэтому нам не нужно беспокоиться о наложении или запутывании людей. Но чем меньше и холоднее вы становитесь, тем длиннее становится длина волны де Бройля, и тем большую роль играет волнообразная природа частицы. (Это чрезмерное упрощение проблемы, но ради этой статьи я остановлюсь на этом. Эссе Филипа Болла об Эоне «Квантовый здравый смысл» прекрасно объясняет, как наш классический опыт возникает из квантовых правил.)
Возможно, опыт объединения звуковых волн в музыкальные композиции дает людям глубокое интуитивное понимание физики других явлений, связанных с волнами, включая квантовую механику. Возможно, есть связь между музыкой и физикой вообще. Возможно, это не совпадение, что многие из самых успешных физиков прошлого были также музыкантами.
Как оказалось, я опоздал на вечеринку. Мол, опоздал более чем на 2000 лет. Около 500 г. до н. э. Пифагор уже комбинировал музыку и физику, пытаясь понять мир. Хотя, возможно, он наиболее известен своим одноименным геометрическим уравнением (хотя несколько культур независимо знали об этом соотношении за сотни лет до него), Пифагор также применил свои математические рассуждения для определения взаимосвязи между длиной струны инструмента и нотой, которую она издает при нажатии. . Заметив, что одни сочетания нот звучат приятно (или согласно на музыкальном языке), а другие — безобразно (диссонансно), он разработал систему настройки, связывающую музыкальные ноты по соотношению их частот. Например, интервал согласных от C до F, известный как чистая кварта, был определен таким образом, что частота F была ровно в 4/3 раза больше частоты C. Точно так же была определена G, которая является чистой квинтой выше C. быть ровно 3/2 частоты базовой ноты до. Высокая до на октаву вверх была ровно в два раза выше частоты основной ноты до. Пифагор видел в этих совершенных соотношениях один из аспектов мистического мира, где числа раскрывали высшие истины, записанные Богом.
Возможно, тогда эти божественные пропорции проявились в других аспектах природы. Понимая математику, лежащую в основе музыкальных гармоний, Пифагор взглянул на небо. Что, если Вселенная была гигантской лирой, на которой Бог играл свою космическую музыку? Пифагор видел планеты, вращающиеся вокруг Земли (это было задолго до революции Коперника, когда ученые поняли, что планеты вращаются вокруг Солнца), как струны инструмента, с математической зависимостью между скоростью, с которой они движутся по небу, и высотой звука неслышимого звука. , таинственный тон, который они издают, причем каждый тон способствует тому, что Пифагор назвал «Гармонией сфер».
Это была прекрасная идея. Каждая планета вращается вокруг Земли по идеальному кругу, издавая идеальную ноту, и все это способствует идеальной гармонии: тайному языку Вселенной. Но, как известно, планеты вращаются не вокруг Земли, а вокруг Солнца, они движутся не по кругу, а по эллипсу, и уж точно не издают никаких космических тонов, слышимых или неслышимых. По словам Аристотеля, «какой бы мелодичной и поэтичной ни была эта теория, она не может быть верным изложением фактов». Это породило вариации этой идеи от таких идей, как Птолемей и Иоганн Кеплер. Даже Моцарт написал оперу, вдохновленную этой идеей.
Люди имеют привычку цепляться за объяснения мира, которые «кажутся» правильными. Мы чувствуем, что во Вселенной должен быть какой-то основополагающий порядок, поэтому вместо того, чтобы сохранять непредвзятость и пытаться раскрыть этот порядок (или, возможно, беспорядок — кто знает?), мы навязываем Вселенной наше собственное ощущение порядка, даже перед лицом противоречивые доказательства.
Чтобы утверждать, что красоте нет места в науке, нужно сначала выяснить, что вообще такое красота
В ее книге Lost in Math (2018) немецкий физик Сабина Хоссенфельдер утверждает, что эта догма о том, что правильная теория должна быть красивой, тормозит прогресс в физике. Представления о красоте и симметрии позволили теориям струн и суперсимметрии выжить на протяжении десятилетий без каких-либо доказательств их истинности просто потому, что они слишком красивы , а не , чтобы быть правдой.
Хоссенфельдер утверждает, что теоретики используют очень жесткое определение красоты в качестве критерия для своих теорий: элегантность и естественность. В этом я согласен с ней, что глупо накладывать это ограничение на теорию. Самонадеянно предполагать априори, что теория всего должна быть прекрасной в ровно так, как мы думаем, что это должно быть.
Но я не хочу сбрасывать со счетов роль красоты. Я думаю, что это немного сложнее. Для начала, чтобы утверждать, что красоте нет места в науке, нужно сначала выяснить, что вообще такое красота. Некий божественный, неизменный идеал симметрии и элегантности? Или наши культурные идеалы красоты развиваются, возможно, в ответ на наши постоянно развивающиеся знания о том, как устроен мир?
Чтобы исследовать это понятие красоты, давайте вернемся к музыке. Пифагор разработал систему настройки, основанную на идеальных соотношениях частот: 4:3, 3:2 и 2:1. Но есть проблема с этой системой. Математически невозможно, чтобы все 12 нот одновременно удовлетворяли этим соотношениям. 12*440 Гц, что составляет четверть пути к A# вместо A. Чтобы избежать этой проблемы, пифагорейские тюнеры изменили частоту одной из нижних нот так, чтобы она не была связана с другие ноты в идеальном соотношении 3/2 и 4/3. Но в результате некоторые интервалы звучали очень диссонансно.
Веками музыкантов это, казалось, не беспокоило. Музыка Средневековья и раннего Возрождения была достаточно простой, чтобы можно было просто не играть диссонансные интервалы. А изящность дробей, используемых в пифагорейской системе, казалась слишком совершенной, чтобы быть случайной, — она казалась предначертанной Богом. На самом деле католическая церковь твердо стояла на стороне сохранения пифагорейской системы настройки.
Винченцо Галилей не был. В конце 1500-х годов он был одним из первых и самых ярых сторонников другой системы настройки, называемой «равномерной темперацией». Галилей утверждал, что вместо того, чтобы иметь одну очень диссонирующую ноту, они должны равномерно распределить этот диссонанс между всеми нотами, чтобы ни одна из них не звучала так совершенно, как в пифагорейской системе, но, по крайней мере, все клавиши можно было бы играть без необходимость перенастройки инструмента.
Так кто же в данном случае следовал принципам красоты? Пифагор, искавший идеальные, простые отношения частот, или Галилей, допустивший некоторую сложность и путаницу в теории, что привело к более эстетически приятному набору нот? Я думаю, что последнее. Борьба Галилея за ровный темперамент позволила музыкантам экспериментировать с изменениями тональности и более сложными гармониями в своей музыке, создавая шедевры, которые никогда не были бы возможны при скучных идеалах простоты и элегантности Пифагора.
Галилей также внес свой вклад в развитие теории музыки, трактуя диссонанс в композициях. Он считал, что для диссонанса есть место, если его «разрешить» игрой согласного аккорда после того, как он был использован. Использование «уродливых» диссонансных интервалов было основополагающим для некоторых из самых красивых композиций в истории. Без диссонанса у нас не было бы многого из самой известной классической музыки, включая произведения Баха и Моцарта.
Возможно, не случайно, что в то время как Галилей боролся со статус-кво и католической церковью, продвигая вперед эволюцию музыки, его сын Галилео Галилей боролся с теми же силами в сфере науки. Он стал сторонником гелиоцентрической модели Солнечной системы, бросив вызов другой пифагорейской догме Церкви: космическому совершенству небес, в центре которого находится Земля. Его настойчивость в том, что все планеты, включая Землю, вращаются вокруг Солнца, а не вокруг Земли, вызвала гнев Церкви. Он умер, находясь под домашним арестом.
Кеплер, современник Галилея, также стремился понять движение планет в этой модели, ориентированной на Солнце. Он также был большим любителем музыки и, как до него Пифагор, пытался соединить музыку с астрономией. После индивидуальной публикации своих трех законов движения планет в 1619 году он опубликовал Harmonices Mundi или Гармонию Мира , явную отсылку к Пифагоровой Гармонии Сфер. Однако
Harmonices Mundi был не только о планетах. В одной из глав Кеплер обсуждал турецкий стиль музыки, который он слышал ранее в своей жизни в Праге. Ему явно не нравилась музыка, он называл ее «раздражающей» и «отвратительной». Он сказал: «Кажется, что никто не мог бы с должным руководством природы и добровольно по собственному желанию когда-либо регулярно созерцать что-либо подобное». , плавное скольжение от одной ноты к другой — вспомните начало девятки Джорджа Гершвина.0033 Rhapsody in Blue (1924) или медленно меняющийся тон сирены скорой помощи. В то время как это распространено в более современной музыке, во времена Кеплера глиссандо вообще не использовалось в западной музыке.
Эйнштейн часто делал перерывы в работе над научной теорией, чтобы играть на фортепиано
В Harmonices Mundi Кеплер попытался перевести движения планет в музыку, которая уловила все нюансы, которые он открыл в течение трех законы:
- Планеты вращаются вокруг Солнца по эллипсам, причем Солнце находится в одном из фокусов.
- Скорость планеты зависит от расстояния планеты от Солнца.
- Период обращения планеты пропорционален ее среднему расстоянию от Солнца.
В частности, его первый и второй законы подразумевают, что, поскольку скорость планеты изменяется по мере ее обращения вокруг Солнца, ее нельзя записать как одну музыкальную ноту. Есть какие-нибудь предположения о том, как он транскрибировал изменение скорости орбиты планеты в музыку? Ага. Глиссандо. Немного иронично, что тот же человек, который утверждал, что турки не черпали вдохновение в красоте природы в своей музыке, позже черпал вдохновение в турецкой музыке для описания природы.
Кеплер по-прежнему ненавидел глиссандо и усердно работал над тем, чтобы его музыкальное кодирование движения планет звучало для него приятно. Он не мог. Он думал, что не имеет смысла, что Бог создал эту систему планетарного движения, не будучи красивой. И я думаю, что он был прав. Через четыреста лет после того, как Harmonices Mundi были опубликованы, Карл Саган выбрал навязчивую интерпретацию движения планет, первоначально записанного Кеплером — глиссандо и все такое — для включения в «золотой рекорд» на борту 9.0033 Вояджер . Сейчас он находится на обоих Voyager , плывущих в межзвездном пространстве на расстоянии более 10 миллиардов миль от Земли.
Трудно дать определение красоте, но если мы воспользуемся определением, данным физиком Джаном Франческо Джудиче из ЦЕРНа в Женеве, которое цитируется в книге Хоссенфельдера — «чувство» или «физическая интуиция», — то я думаю, что оно имеет место быть. в физике. Альберт Эйнштейн, пожалуй, самый известный пример силы физической интуиции, полагающийся на мысленные эксперименты для развития своих теорий. Он также был любителем музыки и опытным скрипачом. Однажды он сказал, что если бы он не был физиком, он был бы музыкантом. Но эти два великих его начинания — музыка и физика — не были несовместимы. По словам его жены, Эйнштейн часто делал перерывы в работе над научной теорией, чтобы поиграть на фортепиано, и часто, когда он сидел за клавиатурой, у него происходил научный прорыв.
Это не случайно. О своей теории относительности Эйнштейн сказал: «Это пришло ко мне интуитивно, и музыка была движущей силой этой интуиции. Мое открытие было результатом музыкального восприятия». Он утверждал, что ни один ученый не мыслит уравнениями. Эйнштейн говорил, что иногда он мыслил образами, иногда — музыкальными построениями.
Более современный физик Стефон Александр из Университета Брауна в Род-Айленде также черпал вдохновение в музыке, особенно в джазе. Черпая вдохновение у таких джазовых гениев, как Джон Колтрейн (который, в свою очередь, вдохновлялся Эйнштейном, особенно в его 19-летнем возрасте).67 работа Межзвездное пространство ) , Александр придумал теорию циклической космологии, которая, по его словам, напоминает джазовые импровизации. В своей книге The Jazz of Physics (2017) он описывает себя как интуитивного мыслителя, склонного полагаться на свои инстинкты, а не на математические формализмы. Я считаю, что именно его музыкальное образование повлияло на то, как он видит мир.
Вот где я думаю, что музыка может сыграть самую большую роль в физике: в развитии интуиции. Интуиция не дарована только гениям или ей доверяют лишь немногие избранные Эйнштейны мира. Большая часть исследований в области физического образования основана именно на этом: помощь учащимся в построении концептуальной и интуитивно понятной основы для решения физических задач. Исследователи физического образования обнаружили, что предоставление учащимся времени для «бездельничания» или самостоятельного изучения физической системы — будь то в лаборатории, с помощью компьютерного моделирования или, возможно, даже с помощью музыки — помогает учащимся сформировать интуитивное понимание физики. что демонстрируется их улучшением в ответах на вопросы концептуальной физики.
Как музыка может помочь развить интуицию в физике? Это другой способ осмысления математики, языка физики. Хотя некоторые музыкальные особенности, безусловно, культурно специфичны (например, глиссандо, как обсуждалось ранее), многие аспекты музыки обладают удивительной универсальностью. Например, определенный лад, называемый пентатонической гаммой в западной музыке, снова и снова появляется во многих культурах по всему миру. Музыка, как и математика, подчиняется одним и тем же законам, где бы вы ни находились. Но, также как и математика, это настолько широкая область, что она позволяет творчески изобретать новые подмножества математических правил, что приводит к новым стилям и жанрам музыки и, возможно, вдохновляет на новые направления исследований в физике.
Если мы относимся к музыке как к испытательному полигону волновых явлений и других физических явлений, то внутреннее чувство прекрасного, которое человек приобретает, «играя» с музыкой, может быть полезным проводником к новым идеям в физике. Не единственное руководство — очевидно, теории должны быть проверены экспериментом. Но тем не менее полезный.
Допустив путаницу в музыке и научных теориях, мы открыли Вселенную, которая стала богаче
Проект «Квантовая музыка» предоставил мне возможность проверить эту идею. Они сделали доступной загрузку пакета «квантовый осциллятор» на своем веб-сайте. Это библиотека звуков, основанная на квантовой акустической физике БЭК.
Как объяснялось выше, в традиционных музыкальных нотах каждая новая октава создается путем удвоения частоты нот в октаве ниже нее, поэтому шкала соответствует экспоненциальному соотношению. В БЭК все совсем по-другому: частоты колебаний не подчиняются этому экспоненциальному закону, поэтому некоторые комбинации нот звучали очень странно, когда я впервые их услышал. Этот факт также приводит к появлению интересных волновых явлений в этих квантовых тонах, о которых никогда не приходится беспокоиться в неквантовой музыке.
Играя с этим программным обеспечением для создания различных волновых форм на основе квантовой механики, я по-новому оценил некоторые из этих явлений. С каждым новым гармоническим тоном, который я добавлял к форме волны, я пытался визуализировать добавление нового гармонического режима движения в это облако БЭК в моей голове. Я не думаю, что у меня был бы такой же опыт, если бы я не изучил BEC заранее, но сочетание глубокого, интуитивного развития интуиции через музыку, руководствуясь знаниями, полученными из уравнений, разработанных моими предшественниками, дало мне более глубокое понимание того, что я использую в лаборатории каждый день.
Я думаю, что конфликт между интуитивным чувством красоты и правдой о том, как устроена Вселенная, возникает, когда мы думаем, что интуиция и красота являются фиксированными качествами. Интуиция развивается с опытом, а эстетические вкусы развиваются и становятся более тонкими по мере взросления художника или музыканта. Проблема не в поиске красоты в физике. Эйнштейн, Галилей и Кеплер показали, что вдохновение в красоте музыки может привести к плодотворным открытиям. Где мы сталкиваемся с проблемами, так это в том, что мы жестко прописываем свое определение красоты, не позволяя ей расти и развиваться так, как это делают наша музыка и наши знания о Вселенной. Допустив некоторую путаницу и сложность в музыке и научных теориях, мы открыли Вселенную, которая богаче, интереснее и да, красивее, чем мы могли себе представить.
Это эссе стало возможным благодаря поддержке гранта Aeon от Фонда Джона Темплтона. Мнения, выраженные в данной публикации, принадлежат автору и не обязательно отражают точку зрения Фонда. Спонсоры Aeon Magazine не участвуют в принятии редакционных решений.
5 вещей, которые вы должны знать, чтобы стать квантовым физиком | CU Boulder Today
Заглавное изображение: член палаты представителей США Джо Негус (справа) осматривает лабораторию физика Джун Йе в JILA в декабре 2021 года. Фото Гленна Асакавы / CU Boulder.
Посмотреть видео
12 апреля JILA собрала исследователей и лидеров бизнеса со всего Колорадо, чтобы обсудить проблемы и возможности, с которыми сталкиваются женщины, работающие в квантовом мире.
CU Боулдер долгое время был лидером в области квантовых исследований. Четыре из пяти Нобелевских премий университета были присуждены исследователям, изучающим квантовую сферу в JILA, совместном исследовательском институте с Национальным институтом стандартов и технологий (NIST). В последние годы университет также запустил ряд инициатив в области квантовых исследований, в том числе CUbit Quantum Initiative, Quantum Systems through Entangled Science and Engineering (Q-SEnSE) и Quantum Engineering Initiative.
В ознаменование Всемирного дня квантовых вычислений 14 апреля, организованного учеными со всего мира для повышения осведомленности об этой области, CU Boulder Today побеседовал с тремя аспирантами, занимающимися квантовыми исследованиями: Джейкобом Бекки, который работает в JILA над разработкой квантовых компьютеров для будущее; Грегори Крупер, изучающий физику оптического волокна на факультете электротехники, вычислительной техники и энергетики; и Джоанна Лис, которая улавливает атомы и манипулирует ими с помощью лазеров в JILA.
Они говорили о том, что ждет квантовую физику в будущем и как квантовые открытия уже подпитывают современную цифровую эпоху.
Прежде всего, что такое квантовая физика?
Беки: Квантовая физика — это модель Вселенной, которая с невероятной точностью описывает поведение крошечных частиц, таких как электроны и протоны. Понимание квантовой области позволило ученым описать химические процессы, функционирование важных устройств во многих электронных устройствах, называемых полу- и сверхпроводниками, взаимодействие света и материи и многое, многое другое.
Lis: По мере того, как объекты становятся все меньше и меньше, а температура становится все ниже и ниже, физика начинает отклоняться от нашего обычного повседневного опыта. Например, атом поглощает и испускает строго определенные количества или «кванты» света.
Еще одним квантовым свойством является запутанность, корреляция между атомами или другими системами, в которой измерение одного атома влияет на результат измерения других. Наконец, в квантовой физике акт измерения также сильно отличается. В классической физике я могу одновременно измерить положение и скорость объекта. В квантовой физике, когда я очень точно знаю положение, у меня нет возможности узнать, как быстро движутся объекты.
Как квантовые открытия могут изменить жизнь обычных людей?
Беки: Квантовая теория лежит в основе некоторых наиболее важных инноваций прошлого века, включая лучевую терапию, МРТ и лазеры. Если бы не глубокое понимание квантовой механики, транзистор не был бы изобретен. Так что, в некотором смысле, мы должны благодарить квантовую теорию за современную цифровую эпоху.
Lis: Квантовая технология уже начала заменять классическую технологию в области безопасной связи. Квантовая криптография опирается на законы квантовой физики для безопасного кодирования или декодирования сообщения. Обычный человек однажды может использовать квантовую связь при совершении транзакции по кредитной карте.
Почему вы решили работать в этой области?
Lis: Во время учебы в бакалавриате я посетил два занятия по квантовой теории и квантовой информации, которые читали два замечательных лектора, и обнаружил, что хочу узнать больше. Мне очень нравилось работать в лаборатории, решать проблемы, поэтому я решил, что экспериментальная атомная физика лучше всего сочетает в себе два моих интереса. Кроме того, на протяжении всего моего обучения в бакалавриате у меня были замечательные женщины-профессора в качестве образцов для подражания, которые действительно поощряли и вдохновляли меня оставаться в академических кругах.
Krueper: Будучи студентом, у меня было несколько проектов, направленных на разработку датчиков для измерения некоторых величин — например, концентрации химических веществ в образце. Вскоре после переезда в Боулдер я узнал, что мы можем использовать квантовую физику для улучшения измерений в этих датчиках, особенно в оптике. В тот момент квантовая физика стала для меня чем-то, что нужно не просто изучать и прорабатывать, а использовать и разрабатывать в наших интересах.
Не могли бы вы немного рассказать мне о ваших исследованиях?
Krueper: Мои исследования сосредоточены на измерении определенных свойств волоконно-оптических проводов, которые обычно используются в телекоммуникациях и дистанционном зондировании. Я изучаю, как квантовые состояния света могут повысить точность измерений в оптоволоконном датчике. Эти датчики могут, например, измерять вибрации и температуру глубоко под землей.
Бекки: Мои исследования до сих пор находились на стыке квантового восприятия и квантовых вычислений.