Диаграмма – ламерей – Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
| Диаграмма Ламерея логистического уравнения для Х 0 5. [1] |
Диаграмма Ламерея показывает, что х ], – 0 – притягивающая точка, х – I – отталкивающая. [2]
Из полученной таким образом диаграммы Ламерея непосредственно видно, что точечное отображение Т рассматриваемой модели часов обладает единственной глобально устойчивой неподвижной точкой. [3]
Функция доследования по-прежнему определяется соотношениями (4.51), а диаграмма Ламерея имеет вид, показанный на рис. 4.39. Таким образом, в случае 3 О точечное отображение (4.51) имеет единственную неподвижную точку, которая является устойчивой. [4]
| Перестройка диаграмм Ламерея. [5] |
В зависимости от вида возмущений / и g диаграмма Ламерея
 [6]
[6]На рис. 8 – 8 построены функция исследования и диаграммы Ламерея. [7]
На рис, 8 – 3 для примера приведены различные функции после-лованяя и диаграммы Ламерея. [8]
Следовательно, график функций последования для Г2 имеет вид, показанный на рис. 4.30. Нанесем теперь найденные кривые для точечных отображений 7 и Г2 на одной диаграмме, тогда получим диаграмму Ламерея, показанную на рис. 4.31. Проведенное исследование показывает, что в рассматриваемом случае ( 0 / ti х, 0 / г2 1) существует единственная неподвижная точка отображения Т Ti – T2, которая является глобально устойчивой. [9]
| Лестница Ламерея. [10] |
Он называется диаграммой Ламерея. [11]
Таким образом, без построения пол ш фазовых траекторий ( фазового портрета), что руднптелыю для систем высоких порядков, с помощью треобразований и построения диаграмм Ламерея могут т елены устойчивость ч л и неустойчивость рассматривае-ейной колебательной системы, наличие или отсутствие ний ъ заданном ( исследуемом) диапазоне – изменения условий, определен характер, а также найдены пара-колебаний по любой переменной состояния, ление устойчивости, наличия автоколебаний в системе ix циклов), движение которых описывается нелиней-ференпиалышмк уравнениями выше второго порядка, низводиться на основании точечного преобразования ча, осуществляемого ня одной фазовой плоскости с по-оекции пространственной фазовой траектории на эту юскость, принимаемую за основную.
Ламерея, построенная на этих кривых, может содержать самое большее две ступеньки. Соответствующее разбиение фазовой плоскости ху на траектории для рассматриваемого случая 0 с Р 1 показано на рис. 4.38. Рассмотрение случая р 0 проводится аналогично. Функция последования по-прежнему определяется соотношениями (4.51), а
Страницы: 1
Математические модели хаоса
Введение
На Habr уже обсуждалась теория хаоса в статьях [1,2,3]. В этих статьях рассмотрены следующие аспекты теории хаоса: обобщённая схема генератора Чуа; моделирование динамики системы Лоренца; программируемые логическими интегральными схемами аттракторы Лоренца, Ресслера, Рикитаке и Нозе-Гувера.
Однако, техники теории хаоса используются и для моделирования биологических систем, которые, бесспорно, являются одними из наиболее хаотических систем из всех, что можно себе представить.
В действительности, почти любая хаотическая система может быть смоделирована — рынок ценных бумаг порождает кривые, которые можно легко анализировать при помощи странных аттракторов, процесс падения капель из протекающего водопроводного крана кажется случайным при анализе невооруженным ухом, но, если его изобразить как странный аттрактор, открывается сверхъестественный порядок, которого нельзя было бы ожидать от традиционных средств.
Целью настоящей статьи является рассмотрение теории хаоса на примере роста численности биологических популяций и удвоения цикла в механических системах с графической визуализацией математических моделей основанной на простых интуитивно понятных программах, написанных на Python.
Статья написана с целью обучения, но позволит, даже не имеющему опыта программирования читателю, используя приведенные программы, самостоятельно решить большинство новых учебных задач по теме моделирования явлений хаоса.
Удвоение периода циклов и хаос на примере роста численности биологических популяций
Начнём с рассмотрения логистического дифференциального уравнения, которое моделирует ограниченный, а не экспоненциальный рост численности биологических популяций:
Именно это уравнение может предсказать экзотические и неожиданные модели поведения некоторых популяций. Действительно, согласно (1) при численность популяции приближается к граничной равной a/b.
Для численного решения логистического дифференциального решения можно использовать самый простой алгоритм, с численным значением шага времени, приняв , тогда решение (1) можно получить путём многократного применения следующего соотношения:
(2)
Представим уравнение (2) в виде логистического уравнения в конечных разностях:
. (3),
где: r=1+ah и s=bh.
Подстановкой в (3) , получим итерационную формулу:
, (4)
Рассчитывая значения, заданные соотношением (3), можно сгенерировать последовательность
максимальных значений численности популяций, которые будет поддерживать среда в заданные моменты времени .
Предполагаем, что существует предельное значение дробей, выражающих часть численности популяций:
, (5).
Будем исследовать, как зависит от параметра роста r в уравнении (4). Для этого на Python напишем программу, которая, начиная с , вычисляет результаты при нескольких сотен итераций (
Код программы
# -*- coding: utf8 -*-
from numpy import *
print(" n r=1,5 r=2,0 r=2,5 ")
M=zeros([201,3])
a=[1.5,2.0,2.5]
for j in arange(0,3,1):
M[0,j]=0.5
for j in arange(0,3,1):
for i in arange(1,201,1):
M[i,j]=a[j]*M[i-1,j]*(1-M[i-1,j])
for i in arange(0,201,1):
if 0<=i<=2:
print(" {0: 7.0f} {1: 7.4f} {2: 7.4f} {3: 7.4f} "
. format(i,M[i,0],M[i,1],M[i,2]))
elif 2<i<=5:
print(".")
elif 197<=i<=200:
print(" {0: 7.0f} {1: 7.4f} {2: 7.4f} {3: 7.
4f} "
. format(i,M[i,0],M[i,1],M[i,2]))
Результат работы программы (для сокращения вывода результатов приведены первые три и последние четыре значения):
n r=1,5 r=2,0 r=2,5
0 0.5000 0.5000 0.5000
1 0.3750 0.5000 0.6250
2 0.3516 0.5000 0.5859
.
.
.
197 0.3333 0.5000 0.6000
198 0.3333 0.5000 0.6000
199 0.3333 0.5000 0.6000
200 0.3333 0.5000 0.6000
Анализ дискретной модели показывает, что для r=1,5;2,0;2,5 с ростом количества итераций значение стабилизируется и становится практически равным предельному , которое определяется соотношением (5). Причём для приведенных значений
Увеличим r=3,1;3,25;3,5 и число итераций n=1008, для этого внесём следующие изменения в программу:
Код программы
# -*- coding: utf8 -*-
from numpy import *
print(" n r=3,1 r=3,25 r=3,5 ")
M=zeros([1008,3])
a= [3. 1,3.25,3.5]
for j in arange(0,3,1):
M[0,j]=0.5
for j in arange(0,3,1):
for i in arange(1,1008,1):
M[i,j]=a[j]*M[i-1,j]*(1-M[i-1,j])
for i in arange(0,1008,1):
if 0<=i<=3:
print(" {0: 7.0f} {1: 7.4f} {2: 7.4f} {3: 7.4f} "
. format(i,M[i,0],M[i,1],M[i,2]))
elif 4<i<=7:
print(".")
elif 1000<=i<=1007:
print(" {0: 7.0f} {1: 7.4f} {2: 7.4f} {3: 7.4f} "
. format(i,M[i,0],M[i,1],M[i,2]))
1,3.25,3.5]
for j in arange(0,3,1):
M[0,j]=0.5
for j in arange(0,3,1):
for i in arange(1,1008,1):
M[i,j]=a[j]*M[i-1,j]*(1-M[i-1,j])
for i in arange(0,1008,1):
if 0<=i<=3:
print(" {0: 7.0f} {1: 7.4f} {2: 7.4f} {3: 7.4f} "
. format(i,M[i,0],M[i,1],M[i,2]))
elif 4<i<=7:
print(".")
elif 1000<=i<=1007:
print(" {0: 7.0f} {1: 7.4f} {2: 7.4f} {3: 7.4f} "
. format(i,M[i,0],M[i,1],M[i,2]))
Результат работы программы (для сокращения вывода результатов приведены первые четыре и последние восемь значений):
n r=3,1 r=3,25 r=3,5
0 0.5000 0.5000 0.5000
1 0.7750 0.8125 0.8750
2 0.5406 0.4951 0.3828
3 0.7699 0.8124 0.8269
.
.
.
1000 0.5580 0.4953 0.5009
1001 0.7646 0.8124 0.8750
1002 0.5580 0.4953 0.3828
1003 0.7646 0.8124 0.8269
1004 0.5580 0.4953 0.5009
1005 0.
7646 0.8124 0.8750
1006 0.5580 0.4953 0.3828
1007 0.7646 0.8124 0.8269
Как следует из приведенных данных, вместо того, чтобы стабилизироваться возле единственной предельной численности популяции, дробная часть численности популяции колеблется между двумя дробями по мере изменения времени. По сравнению с r=3,1, период цикла для r=3,25 увеличивается вдвое, а для r=3,5 в четыре раза.
Программа для графического отображения циклов роста популяции
# -*- coding: utf8 -*-
import matplotlib.pyplot as plt
from numpy import *
M=zeros([1008,3])
a= [3.1,3.25,3.5]
for j in arange(0,3,1):
M[0,j]=0.5
for j in arange(0,3,1):
for i in arange(1,1008,1):
M[i,j]=a[j]*M[i-1,j]*(1-M[i-1,j])
x=arange(987,999,1)
y=M[987:999,0]
y1=M[987:999,1]
y2=M[987:999,2]
plt.title('Удвоение цикла роста популяции для r=3,1;3,25;3,5')
plt.plot(x,y, label="T=1,ymax=%s,ymin=%s"%(round(max(y),3),round(min(y),3)))
plt. plot(x,y1, label="T=2,ymax=%s,ymin=%s"%(round(max(y1),3),round(min(y1),3)))
plt.plot(x,y2, label="T=4,ymax=%s,ymin=%s"%(round(max(y2),3),round(min(y2),3)))
plt.grid()
plt.legend(loc="best")
plt.ylabel("x(n)")
plt.xlabel("n")
plt.show()
plot(x,y1, label="T=2,ymax=%s,ymin=%s"%(round(max(y1),3),round(min(y1),3)))
plt.plot(x,y2, label="T=4,ymax=%s,ymin=%s"%(round(max(y2),3),round(min(y2),3)))
plt.grid()
plt.legend(loc="best")
plt.ylabel("x(n)")
plt.xlabel("n")
plt.show()
Результат выполнения программы:
Благодаря удвоению периода итерация, стала широко известной. Когда значение скорости роста превосходит r=3,56, удвоение периода ускоряется и уже в точке r=3,57 возникает чрезвычайный хаос. Для отображения наступления хаоса воспользуемся следующей программой:
Код программы
# -*- coding: utf8 -*-
import matplotlib.pyplot as plt
from numpy import *
print(" n r=3,57 ")
M=zeros([1041,1])
a= [3.57]
for j in arange(0,1,1):
M[0,j]=0.5
for j in arange(0,1,1):
for i in arange(1,1041,1):
M[i,j]=a[j]*M[i-1,j]*(1-M[i-1,j])
for i in arange(0,1041,1):
if 1000<=i<=1015:
print(" {0: 7. 0f} {1: 7.4f}"
. format(i,M[i,0]))
x=arange(999,1040,1)
y=M[999:1040,0]
plt.title(' Не детерминированный хаос для r=3,57')
plt.plot(x,y)
plt.grid()
plt.ylabel("x(n)")
plt.xlabel("n")
plt.show()
0f} {1: 7.4f}"
. format(i,M[i,0]))
x=arange(999,1040,1)
y=M[999:1040,0]
plt.title(' Не детерминированный хаос для r=3,57')
plt.plot(x,y)
plt.grid()
plt.ylabel("x(n)")
plt.xlabel("n")
plt.show()
Результат выполнения программы:
n r=3,57 1000 0.4751 1001 0.8903 1002 0.3487 1003 0.8108 1004 0.5477 1005 0.8844 1006 0.3650 1007 0.8275 1008 0.5096 1009 0.8922 1010 0.3434 1011 0.8050 1012 0.5604 1013 0.8795 1014 0.3784 1015 0.8397
Напишем программу для визуализации зависимости поведения итераций от параметра роста r. Для каждого значения r в интервале выполняется 1000 итераций для достижения устойчивости. Затем, каждые 250 значений, полученных в результате итераций, наносятся на график по вертикальной оси, образуя точки (r,x):
Код программы
# -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(2.8,4.0,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-y[n-1]),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.title("Диаграмма ветвления при 2,8<= r<=4,0,0<=x<=1") plt.xlabel("r") plt.ylabel("y") plt.axvline(x=3.01,color='black',linestyle='--') plt.axvline(x=3.45, color='black',linestyle='--') plt.axvline(x=3.6,color='black',linestyle='--') plt.axvline(x=3.7,color='black',linestyle='--') plt.axvline(x=3.8,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.show()
Результат в виде диаграммы:
Полученный график называется “диаграммой ветвления”, которая позволяет определить, чему соответствует данное значение r — циклу или хаосу. Единственное значение численности популяции определяется до значения , затем цикл с периодом 2 до , затем цикл с периодом 4, затем цикл с периодом 8 и далее с быстрым приближением к хаосу.
Следует отметить, что вертикальные области незаполненного пространства на графике- это области r=3,6 и r=3,7, между r=3,7 и r=3,8, между r=3,8 и r=3,9, куда возвращается циклический порядок из предыдущего хаоса.
Для рассмотрения появления цикла с периодом кратным 3 в области внесём изменения в предыдущую программу:
Код программы
# -*- coding: utf8 -*-
import matplotlib.pyplot as plt
from numpy import*
N=1000
y=[]
y.append(0.5)
for r in arange(3.8,3.9,0.0001):
for n in arange(1,N,1):
y.append(round(r*y[n-1]*(1-y[n-1]),4))
y=y[N-250:N]
x=[r ]*250
plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1)
plt.title("Диаграмма ветвления при 3,8<= r<=3,9,0<=x<=1")
plt.xlabel("r")
plt.ylabel("y")
plt.axvline(x=3.83,color='black',linestyle='--')
plt.show()
Результат выполнения программы:
Цикл периода 3 появляется в окрестности точки r=3,83, а затем разбивается последовательно на циклы 6,12,24. Существование цикла с периодом 3 подразумевает наличие циклов любого другого конечного периода, а так же хаотических циклов вообще без периода.
Существование цикла с периодом 3 подразумевает наличие циклов любого другого конечного периода, а так же хаотических циклов вообще без периода.
Диаграмма ветвления позволяет проследить за развитием системы при плавном изменении параметра. При фиксированном значении параметра за орбитами точек позволяет проследить паутинная диаграмма (диаграмма Ламерея).
Построение паутинной диаграммы позволяет выявить различные эффекты, незаметные на диаграмме ветвления. Напишем программу:
Код программы
# -*- coding: utf8 -*-
import matplotlib.pyplot as plt
from numpy import *
a=2.7
x1=0.62
def ff(x):
return a*x*(1-x)
b=a*x1*(1-x1)/x1
def fl(x):
return b*x
x=0.1
y=0
Y=[]
X=[]
for i in arange(1,30,1):
X.append(x)
Y.append(y)
y=ff(x)
X.append(x)
Y.append(y)
x=y/b
plt.title('Паутинная диаграмма логистической n функции λx(1-x) при λ = 2.7')
plt.plot(X,Y,'r')
x1=arange(0,1,0.001)
y1=[ff(x) for x in x1]
y2=[fl(x) for x in x1]
plt. plot(x1,y1,'b')
plt.plot(x1,y2,'g')
plt.grid(True)
plt.show()
plot(x1,y1,'b')
plt.plot(x1,y2,'g')
plt.grid(True)
plt.show()
Диаграмма Ламерея:
Удвоение периода в механических системах
Рассмотрим дифференциальное уравнение, которое моделирует свободные затухающие колебания материальной точки заданной массы на нелинейной пружине, при которых затухание определяется скоростью.
(6)
В уравнении (6) член kx представляет силу линейной пружины, приложенной к материальной точке заданной массы, а член представляет фактическую нелинейность пружины.
Если на систему свободных колебаний (6) действует сила, то перемещение материальной точки массы, к которой приложена эта сила, описывается дифференциальным уравнением Дуффинга для вынужденных колебаний:
(7)
Уравнение (7) для большинства входящих в него параметров решается численным методом. Механическая система для математической модели по уравнению (7) приведена на рисунке:
Особенностью приведенной системы является то, что вместо пружины используется гибкая металлическая нить, которая колеблется в вертикальной плоскости, для которой константа Гука k отрицательна. В этой схеме точки устойчивого равновесия (а) и (с), а точка неустойчивого равновесия (b).
В этой схеме точки устойчивого равновесия (а) и (с), а точка неустойчивого равновесия (b).
При смещении материальной точки из положения (b), действующая на неё сила является отталкивающей. Если периодическая сила, например, созданная осциллирующим магнитным полем частично гасится сопротивлением воздуха. Тогда, уравнение (7) является приемлемой математической моделью для горизонтального перемещения x(t) материальной точки при следующих областях параметров .
Для исследования поведения такой нелинейной системы примем , тогда дифференциальное уравнение (7) принимает вид:
, (8)
Напишем программу численного интегрирования уравнения (8) при начальных условиях в области и для каждого из следующих значений амплитуды , причем в каждом случае вывести на график решения для плоскостей и :
Код программы
# -*- coding: utf8 -*- from numpy import * from scipy. integrate import odeint import matplotlib.pyplot as plt for F in [0.6,0.7,0.75,0.8]: def f(y,t): y1,y2=y return [y2,-y2-y1**3+y1+F*cos(t)] t=arange(100,200,0.001) y0=[1.0,0.0] [y1,y2]=odeint(f, y0, t, full_output=False,rtol=1e-12).T if F==0.6: plt.subplot(221) plt.title('Фазовая плоскость F=0.6,T=2'r'$pi$') plt.plot(y1,y2, color='black', linestyle=' ', marker='.', markersize=0.1) plt.grid(True) plt.subplot(222) plt.title('Решение x(t): F=0.6,T=2'r'$pi$') plt.plot(t,y1, color='black', linestyle=' ', marker='.', markersize=0.1) plt.grid(True) elif F==0.7: plt.subplot(223) plt.plot(y1,y2, color='black', linestyle=' ', marker='.', markersize=0.1, label='Фазовая плоскость n F=0.7,T=4'r'$pi$') plt.legend(loc='upper left') plt.
grid(True) plt.subplot(224) plt.plot(t,y1, color='black', linestyle=' ', marker='.', markersize=0.1, label='Решение x(t): F=0.7,T=4'r'$pi$') plt.legend(loc='upper left') plt.grid(True) plt.show() if F==0.75: plt.subplot(221) plt.title('Фазовая плоскость F=0.75,T=8'r'$pi$') plt.plot(y1,y2, color='black', linestyle=' ', marker='.', markersize=0.1) plt.grid(True) plt.subplot(222) plt.title('Решение x(t): F=0/75,T=8'r'$pi$') plt.plot(t,y1, color='black', linestyle=' ', marker='.', markersize=0.1) plt.grid(True) elif F==0.8: plt.subplot(223) plt.plot(y1,y2, color='black', linestyle=' ', marker='.', markersize=0.1, label='Фазовая плоскостьn F=80,Хаос') plt.
legend(loc='upper left') plt.grid(True) plt.subplot(224) plt.plot(t,y1, color='black', linestyle=' ', marker='.', markersize=0.1, label='Решение x(t): F=80,Хаос') plt.legend(loc='upper left') plt.grid(True) plt.show()
Графики как результат работы программы
Этот переход от удвоения периода к хаосу показывает общий характер поведения нелинейной механической системы в ответ на изменение соответствующего физического параметра, например: . Такие явления не происходят в линейных механических системах.
Аттрактор Лоренца
Подстановка в уравнение Дуффинга для вынужденных колебаний (7) приводят к двумерной нелинейной системе дифференциальных уравнений, что и было приведено в предыдущем листинге. Трёхмерную нелинейную систему дифференциальных уравнений применительно к задачам метеорологии рассматривал Э.Н. Лоренц:
(9)
Решение системы (9) лучше рассматривать в проекции на одну из трёх плоскостей. Напишем программу численного интегрирования при значениях параметров b=frac{8}{3},s=10,r=28 и начальных условиях x(0)=-8, y(0)=8, z(0)=27:
Напишем программу численного интегрирования при значениях параметров b=frac{8}{3},s=10,r=28 и начальных условиях x(0)=-8, y(0)=8, z(0)=27:
Код программы
# -*- coding: utf8 -*-
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
s,r,b=10,28,8/3
def f(y, t):
y1, y2, y3 = y
return [s*(y2-y1),
-y2+(r-y3)*y1,
-b*y3+y1*y2]
t = np.linspace(0,20,2001)
y0 = [-8, 8, 27]
[y1,y2,y3]=odeint(f, y0, t, full_output=False).T
plt.plot(y1,y3, color='black', linestyle=' ', marker='.',
markersize=2)
plt.xlabel('x')
plt.ylabel('z')
plt.grid(True)
plt.title("Проекция траектории Лоренца на плоскость xz")
plt.show()
Результат работы программы:
Рассматривая изображение на графике во времени, можно предположить, что точка P(x(t), y{t), z(t)) совершает случайное число колебаний то справа, то с слева. Для метеорологического приложения системы Лоренца, после случайного числа ясных дней, следует случайное число дождливых дней.
Рассмотрим программу для отображения аттрактора Лоренца в плоскости xyz для мало различающихся начальных условий:
Код программы
# -*- coding: utf8 -*-
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#Создаем функцию правой части системы уравнений.
s,r,b=10,25,3
def f(y, t):
y1, y2, y3 = y
return [s*(y2-y1),
-y2+(r-y3)*y1,
-b*y3+y1*y2]
#Решаем систему ОДУ и строим ее фазовую траекторию
t = np.linspace(0,20,2001)
y0 = [1, -1, 10]
[y1,y2,y3]=odeint(f, y0, t, full_output=False).T
fig = plt.figure(facecolor='white')
ax=Axes3D(fig)
ax.plot(y1,y2,y3,linewidth=2)
plt.xlabel('y1')
plt.ylabel('y2')
plt.title("Начальные условия: y0 = [1, -1, 10]")
y0 = [1.0001, -1, 10]
[y1,y2,y3]=odeint(f, y0, t, full_output=False).T
fig = plt.figure(facecolor='white')
ax=Axes3D(fig)
ax.plot(y1,y2,y3,linewidth=2)
plt.xlabel('y1')
plt.ylabel('y2')
plt.title("Начальные условия: y0 = [1. 0001, -1, 10]")
plt.show()
0001, -1, 10]")
plt.show()
Результаты работы программы показаны на следующих графиках:
Из приведенных графиков следует, что изменение начального условия для с 1,0 до 1,0001 резко меняет характер изменения аттрактора Лоренца.
Система Росслера
Это очень интенсивно изучаемая нелинейная трехмерная система:
(10)
Напишем программу для численного интегрирования системы (10) для следующих параметров a=0,39, b=2, c=4 при начальных условиях x(0)=0, y(0)=0, z(0)=0:
Код программы
# -*- coding: utf8 -*-
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
a,b,c=0.398,2.0,4.0
def f(y, t):
y1, y2, y3 = y
return [(-y2-y3),
y1+a*y2,
b+y3*(y1-c)]
t = np.linspace(0,50,5001)
y0 = [0,0, 0]
[y1,y2,y3]=odeint(f, y0, t, full_output=False).T
plt.plot(y1,y2, color='black', linestyle=' ', marker='.',
markersize=2)
plt.xlabel('x')
plt.ylabel('y')
plt. grid(True)
plt.title("Проекция ленты Ройсслера на плоскость xy")
plt.show()
grid(True)
plt.title("Проекция ленты Ройсслера на плоскость xy")
plt.show()
Результат работы программы:
В плоскости лента Росслера выглядит как петля, но в пространстве она оказывается перекручена подобно ленте Мебиуса.
Выводы
Для демонстрации явлений хаоса приведены простые и интуитивно понятные программы на высокоуровневом языке программирования Python, которые легко модернизировать под новые проекты по данной теме. Статья имеет учебно-методическую направленность и может быть использована в процессе обучения.
Ссылки
- Немного о хаосе и о том, как его сотворить
- Критический взгляд на аттрактор Лоренца
- Генераторы хаоса на ПЛИС
- Дифференциальные уравнения и краевые задачи: моделирование и вычисление с помощью Mathematica, Maple и MATLAB. 3-е издание.: Пер. с англ. — М.: ООО «И.Д. Вильяме», 2008. — 1104 с.: ил. — Парал. тит. англ.
Автор: Юрий Тараненко
Источник
Aproches de Almeria (Морская карта: ES_ES400459)
Войти
- Морские карты Испании
- Aproches de Almeria (Морская карта: ES_ES400459)
Морская карта Aproches de Almeria включена в сборник морских карт Испании. Он доступен как часть приложения iBoating: Spain Marine & Fishing (теперь поддерживается на нескольких платформах, включая Android, iPhone/iPad, MacBook и Windows (планшет и телефон)/картплоттер на базе ПК).
Он доступен как часть приложения iBoating: Spain Marine & Fishing (теперь поддерживается на нескольких платформах, включая Android, iPhone/iPad, MacBook и Windows (планшет и телефон)/картплоттер на базе ПК).
Когда вы покупаете наше приложение Nautical Charts, вы получаете все замечательные функции приложения морских карт, такие как места для рыбалки, а также морскую карту Aproches de Almeria. Приложение морской навигации предоставляет расширенные функции морского картплоттера, включая регулировку смещения уровня воды и индивидуальное затенение глубины. Слои мест для рыбалки и контуров глубины доступны на большинстве карт озера. Морские навигационные функции включают расширенные инструменты для определения направления скорости ветра, температуры воды, глубины воды и точного GPS с приемниками AIS (с использованием NMEA через TCP/UDP). Поддержка автопилота может быть включена во время «Goto WayPoint» и «Route Assistance». Теперь для вод, отображенных на этой карте, доступна автоматическая маршрутизация скольжения к слипу на основе осадки лодки (осадки).
Есть еще вопросы о приложении Nautical Chart? Спроси нас.
| Апрош-де-Альмерия | |
| Масштаб | 1:45000 |
| Мин. Долгота | -2,58 |
| Мин. Широта | 36,51 |
| Макс. Долгота | -2,13 |
| Max Latitude | 36,85 |
| Этикетка издания 1 | |
| Этикетка издания 2 | |
| Идентификатор | ES_ES400459 |
| Страна | Испания |
| Проекция | Меркатор |
| * некоторые характеристики могут включать близлежащие/соединяющиеся водоемы | |
|
Almeria Ежедневные графики погоды — LocalConditions.com
Сегодня вечером Преимущественно ясно, возможен небольшой дождь
вечером грозы, затем переменная облачность, возможна
ливни и грозы после полуночи. Минимум около 50.
Ветер юго-восточный со скоростью около 10 м/с. Вероятность осадков
30 процентов.
Вс Небольшая облачность. Небольшая вероятность ливней и
утром грозы, затем возможны дожди и
грозы во второй половине дня. Максимум середины 70-х. К северо-востоку
ветер 10-15 м/с. Вероятность осадков 40 процентов.
ПРИМЕЧАНИЕ. Наведите указатель мыши на точки, чтобы просмотреть дополнительные данные, или нажмите, если используется сенсорный экран.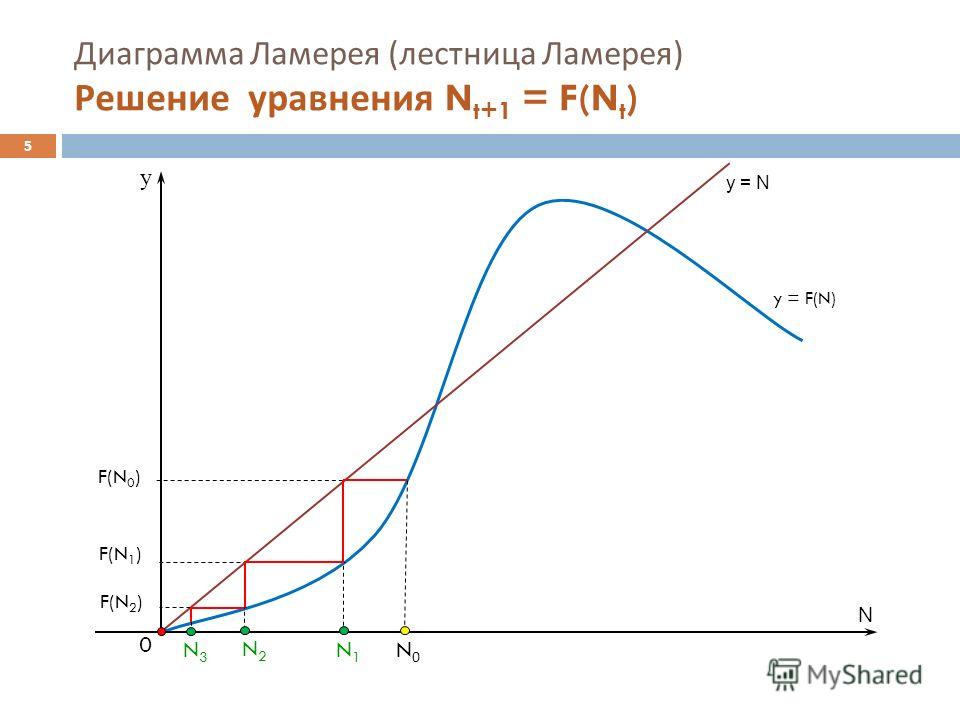
Температура в Альмерии на сегодня с 00:00 до 03:04 Вс, 7 мая 2023 г.
На следующем графике показана почасовая температура в Альмерии сегодня (вс, 7 мая 2023 г.). Самая низкая температура была 57,2 градуса по Фаренгейту в 00:00, а самая высокая температура — 64,4 градуса по Фаренгейту в 00:55.
Альмерия влажность сегодня с 00:00 вс, 7 мая 2023 г. до 03:04.
На следующем графике показана почасовая влажность в Альмерии сегодня (воскресенье, 7 мая 2023 г.). Самый низкий показатель влажности составил 63,64 процента в 00:55, а самый высокий зарегистрированный уровень влажности — 87,75 процента в 00:00.
Атмосферное давление в Альмерии сегодня с 00:00 воскресенья, 7 мая 2023 г., до 03:04.
На следующем графике показано почасовое атмосферное давление в Альмерии сегодня (воскресенье, 7 мая 2023 г.). Самое низкое показание барометрического давления было 29,82 дюйма ртутного столба в 00:00, а самое высокое зарегистрированное барометрическое давление — 29. 0,89 дюйма ртутного столба в 2:50.
0,89 дюйма ртутного столба в 2:50.
Скорость ветра в Альмерии сегодня с 00:00 вс, 7 мая 2023 г., до 03:04.
На следующем графике показана почасовая скорость ветра в Альмерии сегодня (вс, 7 мая 2023 г.). Самая низкая скорость ветра была 3 мили в час в 00:30, а самая высокая наблюдаемая скорость ветра — 14 миль в час в 2:35.
Порывы ветра в Альмерии сегодня с 00:00 в воскресенье, 7 мая 2023 г., до 03:04.
На следующей диаграмме представлены ежечасные порывы ветра в Альмерии сегодня (воскресенье, 7 мая 2023 г.). Самый низкий показатель порыва ветра был 18 миль в час в 00:53, а самый высокий наблюдаемый порыв ветра – 22 мили в час в 2:45.
Количество осадков в Альмерии сегодня с 00:00 воскресенья, 7 мая 2023 г., до 03:04.
На следующем графике показаны почасовые осадки в Альмерии сегодня (вс, 7 мая 2023 г.). Осадков пока не зафиксировано.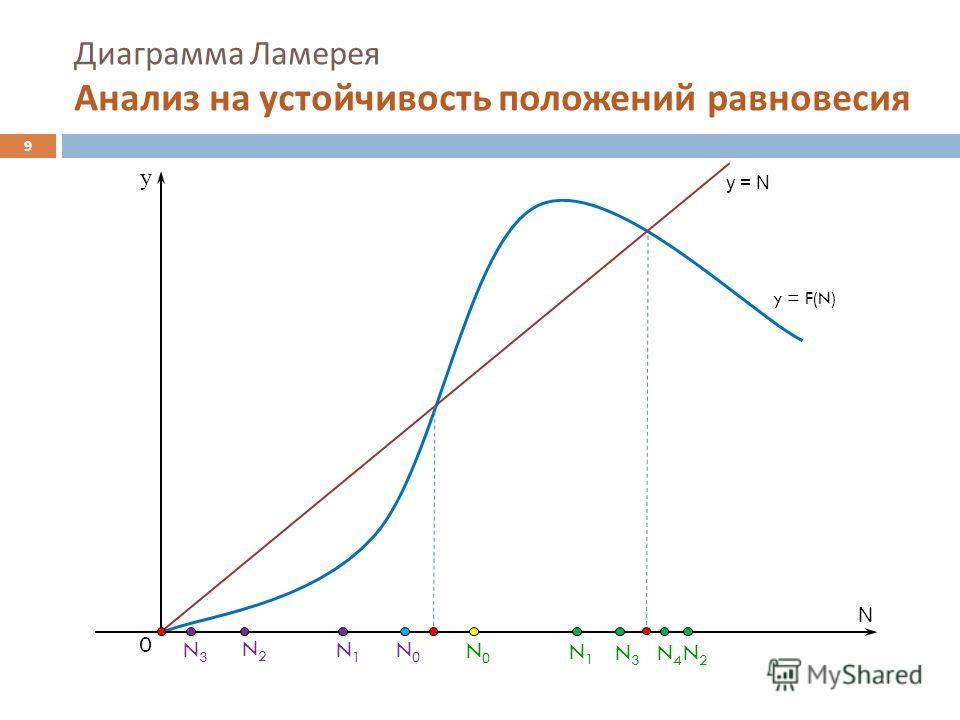
Точка росы Альмерия сегодня с 00:00 вс, 7 мая 2023 до 03:04.
На следующем графике показаны почасовые точки росы Альмерии сегодня (вс, 7 мая 2023 г.). Самая низкая точка росы была 51,8 градуса по Фаренгейту в 2:35, а самая высокая точка росы — 53,6 градуса по Фаренгейту в 1:05.
Отказ от ответственности в отношении диаграммы
Данная информация о погоде в прошлом предоставляется КАК ЕСТЬ и исключительно в развлекательных, образовательных и информационных целях; мы отказываемся от любой ответственности, включая, помимо прочего, ответственность за качество, производительность, товарность и пригодность для конкретной цели, возникающие в результате использования или невозможности использования данных. Информация может быть неточной или неполной в зависимости от того, насколько успешно или неудачно соответствующая метеостанция сообщила или записала ее с помощью инструментов, которые измеряли погоду в то время; включая промежутки между часами или даже днями. В частности, LocalConditions.com и эти данные в том виде, в каком они представлены, не могут и не должны использоваться в качестве справочных материалов по каким-либо причинам, связанным с судебными разбирательствами, страховыми случаями, возмещением, предотвращением убытков, прогнозированием или критическими решениями. Наконец, метеостанция может находиться в нескольких милях от интересующей вас области. Эти данные не могут быть похищены или опубликованы повторно.
В частности, LocalConditions.com и эти данные в том виде, в каком они представлены, не могут и не должны использоваться в качестве справочных материалов по каким-либо причинам, связанным с судебными разбирательствами, страховыми случаями, возмещением, предотвращением убытков, прогнозированием или критическими решениями. Наконец, метеостанция может находиться в нескольких милях от интересующей вас области. Эти данные не могут быть похищены или опубликованы повторно.
“Приблизительное количество осадков/дождя” рассчитывается в целом на основе последнего измерения за каждый отчетный час, которое накапливается и сбрасывается в начале каждого часа – в идеале. Однако некоторые станции сбрасываются в неподходящее время, например, через несколько минут после окончания часа. Мы попытались учесть эту проблему. Большинство датчиков сообщают несколько раз в час. Например, количество осадков в 8:15 утра может составлять 0,04 дюйма водяного столба, а в 8:30 — 0,06 дюйма, а в 8:56 — 0,08 дюйма.

 1,3.25,3.5]
for j in arange(0,3,1):
M[0,j]=0.5
for j in arange(0,3,1):
for i in arange(1,1008,1):
M[i,j]=a[j]*M[i-1,j]*(1-M[i-1,j])
for i in arange(0,1008,1):
if 0<=i<=3:
print(" {0: 7.0f} {1: 7.4f} {2: 7.4f} {3: 7.4f} "
. format(i,M[i,0],M[i,1],M[i,2]))
elif 4<i<=7:
print(".")
elif 1000<=i<=1007:
print(" {0: 7.0f} {1: 7.4f} {2: 7.4f} {3: 7.4f} "
. format(i,M[i,0],M[i,1],M[i,2]))
1,3.25,3.5]
for j in arange(0,3,1):
M[0,j]=0.5
for j in arange(0,3,1):
for i in arange(1,1008,1):
M[i,j]=a[j]*M[i-1,j]*(1-M[i-1,j])
for i in arange(0,1008,1):
if 0<=i<=3:
print(" {0: 7.0f} {1: 7.4f} {2: 7.4f} {3: 7.4f} "
. format(i,M[i,0],M[i,1],M[i,2]))
elif 4<i<=7:
print(".")
elif 1000<=i<=1007:
print(" {0: 7.0f} {1: 7.4f} {2: 7.4f} {3: 7.4f} "
. format(i,M[i,0],M[i,1],M[i,2]))

 plot(x,y1, label="T=2,ymax=%s,ymin=%s"%(round(max(y1),3),round(min(y1),3)))
plt.plot(x,y2, label="T=4,ymax=%s,ymin=%s"%(round(max(y2),3),round(min(y2),3)))
plt.grid()
plt.legend(loc="best")
plt.ylabel("x(n)")
plt.xlabel("n")
plt.show()
plot(x,y1, label="T=2,ymax=%s,ymin=%s"%(round(max(y1),3),round(min(y1),3)))
plt.plot(x,y2, label="T=4,ymax=%s,ymin=%s"%(round(max(y2),3),round(min(y2),3)))
plt.grid()
plt.legend(loc="best")
plt.ylabel("x(n)")
plt.xlabel("n")
plt.show()
 0f} {1: 7.4f}"
. format(i,M[i,0]))
x=arange(999,1040,1)
y=M[999:1040,0]
plt.title(' Не детерминированный хаос для r=3,57')
plt.plot(x,y)
plt.grid()
plt.ylabel("x(n)")
plt.xlabel("n")
plt.show()
0f} {1: 7.4f}"
. format(i,M[i,0]))
x=arange(999,1040,1)
y=M[999:1040,0]
plt.title(' Не детерминированный хаос для r=3,57')
plt.plot(x,y)
plt.grid()
plt.ylabel("x(n)")
plt.xlabel("n")
plt.show()
 append(0.5)
for r in arange(2.8,4.0,0.0001):
for n in arange(1,N,1):
y.append(round(r*y[n-1]*(1-y[n-1]),4))
y=y[N-250:N]
x=[r ]*250
plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1)
plt.title("Диаграмма ветвления при 2,8<= r<=4,0,0<=x<=1")
plt.xlabel("r")
plt.ylabel("y")
plt.axvline(x=3.01,color='black',linestyle='--')
plt.axvline(x=3.45, color='black',linestyle='--')
plt.axvline(x=3.6,color='black',linestyle='--')
plt.axvline(x=3.7,color='black',linestyle='--')
plt.axvline(x=3.8,color='black',linestyle='--')
plt.axvline(x=3.9,color='black',linestyle='--')
plt.show()
append(0.5)
for r in arange(2.8,4.0,0.0001):
for n in arange(1,N,1):
y.append(round(r*y[n-1]*(1-y[n-1]),4))
y=y[N-250:N]
x=[r ]*250
plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1)
plt.title("Диаграмма ветвления при 2,8<= r<=4,0,0<=x<=1")
plt.xlabel("r")
plt.ylabel("y")
plt.axvline(x=3.01,color='black',linestyle='--')
plt.axvline(x=3.45, color='black',linestyle='--')
plt.axvline(x=3.6,color='black',linestyle='--')
plt.axvline(x=3.7,color='black',linestyle='--')
plt.axvline(x=3.8,color='black',linestyle='--')
plt.axvline(x=3.9,color='black',linestyle='--')
plt.show()
 plot(x1,y1,'b')
plt.plot(x1,y2,'g')
plt.grid(True)
plt.show()
plot(x1,y1,'b')
plt.plot(x1,y2,'g')
plt.grid(True)
plt.show()
 6,0.7,0.75,0.8]:
def f(y,t):
y1,y2=y
return [y2,-y2-y1**3+y1+F*cos(t)]
t=arange(100,200,0.001)
y0=[1.0,0.0]
[y1,y2]=odeint(f, y0, t, full_output=False,rtol=1e-12).T
if F==0.6:
plt.subplot(221)
plt.title('Фазовая плоскость F=0.6,T=2'r'$pi$')
plt.plot(y1,y2, color='black', linestyle=' ', marker='.',
markersize=0.1)
plt.grid(True)
plt.subplot(222)
plt.title('Решение x(t): F=0.6,T=2'r'$pi$')
plt.plot(t,y1, color='black', linestyle=' ', marker='.',
markersize=0.1)
plt.grid(True)
elif F==0.7:
plt.subplot(223)
plt.plot(y1,y2, color='black', linestyle=' ', marker='.',
markersize=0.1, label='Фазовая плоскость n F=0.7,T=4'r'$pi$')
plt.legend(loc='upper left')
plt.
6,0.7,0.75,0.8]:
def f(y,t):
y1,y2=y
return [y2,-y2-y1**3+y1+F*cos(t)]
t=arange(100,200,0.001)
y0=[1.0,0.0]
[y1,y2]=odeint(f, y0, t, full_output=False,rtol=1e-12).T
if F==0.6:
plt.subplot(221)
plt.title('Фазовая плоскость F=0.6,T=2'r'$pi$')
plt.plot(y1,y2, color='black', linestyle=' ', marker='.',
markersize=0.1)
plt.grid(True)
plt.subplot(222)
plt.title('Решение x(t): F=0.6,T=2'r'$pi$')
plt.plot(t,y1, color='black', linestyle=' ', marker='.',
markersize=0.1)
plt.grid(True)
elif F==0.7:
plt.subplot(223)
plt.plot(y1,y2, color='black', linestyle=' ', marker='.',
markersize=0.1, label='Фазовая плоскость n F=0.7,T=4'r'$pi$')
plt.legend(loc='upper left')
plt.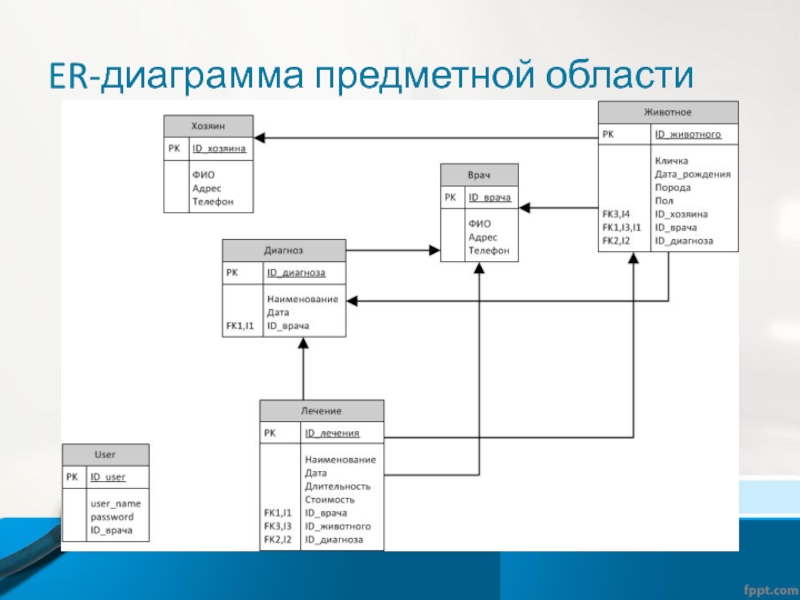 grid(True)
plt.subplot(224)
plt.plot(t,y1, color='black', linestyle=' ', marker='.',
markersize=0.1, label='Решение x(t): F=0.7,T=4'r'$pi$')
plt.legend(loc='upper left')
plt.grid(True)
plt.show()
if F==0.75:
plt.subplot(221)
plt.title('Фазовая плоскость F=0.75,T=8'r'$pi$')
plt.plot(y1,y2, color='black', linestyle=' ', marker='.',
markersize=0.1)
plt.grid(True)
plt.subplot(222)
plt.title('Решение x(t): F=0/75,T=8'r'$pi$')
plt.plot(t,y1, color='black', linestyle=' ', marker='.',
markersize=0.1)
plt.grid(True)
elif F==0.8:
plt.subplot(223)
plt.plot(y1,y2, color='black', linestyle=' ', marker='.',
markersize=0.1, label='Фазовая плоскостьn F=80,Хаос')
plt.
grid(True)
plt.subplot(224)
plt.plot(t,y1, color='black', linestyle=' ', marker='.',
markersize=0.1, label='Решение x(t): F=0.7,T=4'r'$pi$')
plt.legend(loc='upper left')
plt.grid(True)
plt.show()
if F==0.75:
plt.subplot(221)
plt.title('Фазовая плоскость F=0.75,T=8'r'$pi$')
plt.plot(y1,y2, color='black', linestyle=' ', marker='.',
markersize=0.1)
plt.grid(True)
plt.subplot(222)
plt.title('Решение x(t): F=0/75,T=8'r'$pi$')
plt.plot(t,y1, color='black', linestyle=' ', marker='.',
markersize=0.1)
plt.grid(True)
elif F==0.8:
plt.subplot(223)
plt.plot(y1,y2, color='black', linestyle=' ', marker='.',
markersize=0.1, label='Фазовая плоскостьn F=80,Хаос')
plt. legend(loc='upper left')
plt.grid(True)
plt.subplot(224)
plt.plot(t,y1, color='black', linestyle=' ', marker='.',
markersize=0.1, label='Решение x(t): F=80,Хаос')
plt.legend(loc='upper left')
plt.grid(True)
plt.show()
legend(loc='upper left')
plt.grid(True)
plt.subplot(224)
plt.plot(t,y1, color='black', linestyle=' ', marker='.',
markersize=0.1, label='Решение x(t): F=80,Хаос')
plt.legend(loc='upper left')
plt.grid(True)
plt.show()
 0001, -1, 10]")
plt.show()
0001, -1, 10]")
plt.show()
 grid(True)
plt.title("Проекция ленты Ройсслера на плоскость xy")
plt.show()
grid(True)
plt.title("Проекция ленты Ройсслера на плоскость xy")
plt.show()
 05 Вс 03:00
05 Вс 03:00 05 Пн 21:00
05 Пн 21:00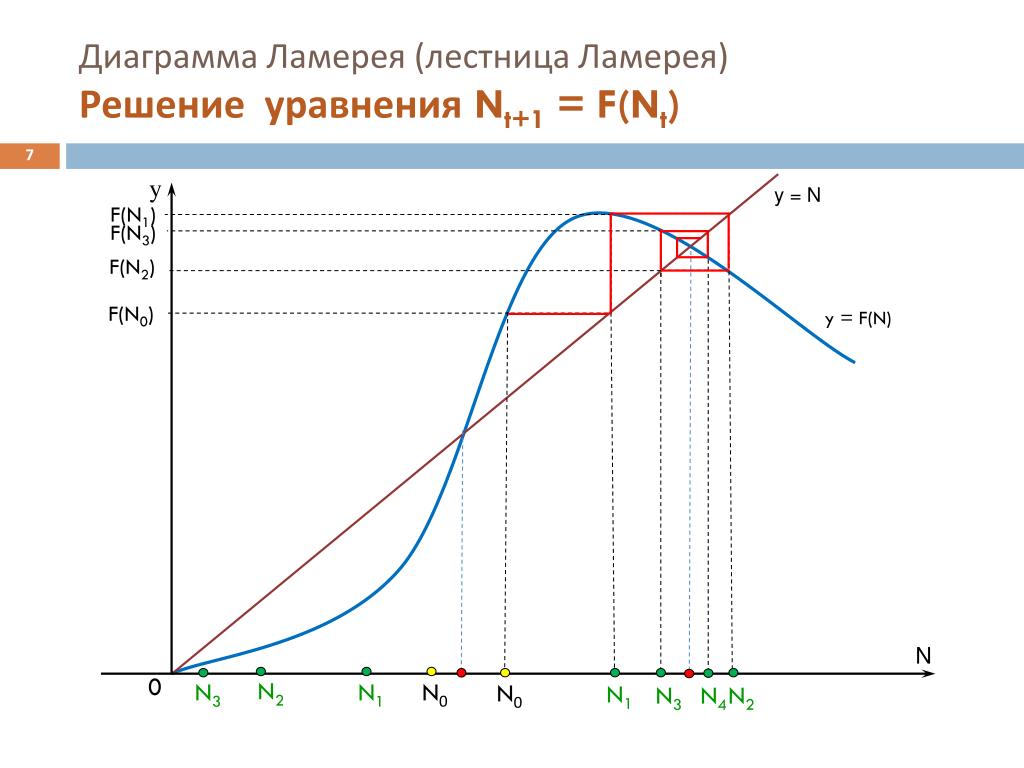 02
02