Lim 0 бесконечность: Lim x стремится к 0 примеры. Предел функции – определения, теоремы и свойства

«Деление на ноль. Бесконечность или запрещённое действие?» — Яндекс Кью

Математика и математики

Популярное

Сообщества

Совершенно запутался.
В школе учили что на ноль делить нельзя. Потому как ответа не существует.
Когда перешли к пределам, оказывается решение деления конечного числа на ноль существует, это будет бесконечно большая величина. Доказывалось(решалось) это методом приближения к нулю.
Так все таки, разделить число на ноль можно или нельзя?

МатематикаДелениеНоль

Крехта Виталий

Математика и математики

3 декабря 2021  ·

41,3 K

ОтветитьУточнить

Владимир Горбацевич

Математика

1,7 K

математика нестандартный психоанализ  · 4 дек 2021

В школе на нуль делить запрещено.

Там еще много другого запрещено 🙂

Делить на нуль нельзя, но если очень хочется, то можно! Только уметь надо… На нуль запрещено делить только тем, кто не умеет это делать.

Достаточно добавить к обычным числам еще одно число ∞ , именуемое бесконечностью. Тогда, например, 7/0=∞. Вот только делить 0 на 0 нельзя, так как здесь нет разумных вариантов ответа (в математике это называют неопределенностью).

С пределами все примерно аналогично Например 1/x при x->0 в пределе дает ту же ∞.

Прямую линию (на которой располагаются обычные вещественные числа) можно пополнить одной точкой ∞ и получить “расширенную числовую ось. И еще много интересного можно с помощью ∞ сделать…

1 эксперт согласен

Andrei Novikov

подтверждает

7 августа

Необоснованные минусы этому ответу создают желание дать ответу эаспертное подтверждение. Вообще принцип, что да… Читать дальше

Комментировать ответ…Комментировать…

Maxim Vyalkov

Математика

1,3 K

Интересующие темы: история математики, история христианства, библеистика.   · 4 дек 2021

Вы делаете логическую ошибку. У функции может быть “выколот” ноль, но могут существовать пределы 0+ и 0- (то есть, существует предел 0, т.к. есть и 0+ и 0- и они совпадают). Видите, предел стремления к 0 , 0+ и 0- — абсолютно не то же самое, что и, собственно 0. На 0 как число делить _нельзя_ — конец истории. И арифметически нельзя и алгебраически нельзя. При… Читать далее

Виктор Семенов

29 октября

Действительно интересует вопрос: существует ли число сопряжённое нолю?

Комментировать ответ…Комментировать…

Достоверно

Вадим Романский

Физика

6,8 K

младший научный сотрудник ФТИ им. Иоффе  · 4 дек 2021  ·

astropolytech

Вот это – “Когда перешли к пределам, оказывается решение деления конечного числа на ноль существует, это будет бесконечно большая величина. Доказывалось(решалось) это методом приближения к нулю.” – абсолютная неправда.

Делить на ноль – нельзя. Вычисление предела при стремлении знаменателя к нулю – это совершенно другая операция, а не деление на ноль

астрофизическое образование

Перейти на vk.com/astropolytech

2 эксперта согласны

19,4 K

Andrei Novikov

7 августа

Ну, как нельзя…. см. Алгебраическую структуру “колесо” https://ru.m.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BB%D0%B5%… Читать дальше

Комментировать ответ…Комментировать…

Дмитрий Иванов

Астрономия

938

По образованию физик и математик (МФТИ). Любитель астрономии .Кроме родного русского…  · 3 дек 2021

Проблема в делении на ноль не в бесконечности , а в неопределённости. Если разрешить такое деление, то можно доказать, любое число равно чему угодно.

Вот смотрите , очевидное тождество x *0= y *0, где x, y -любые числа. Сокращаем на 0 и получаем x=y.

А Вы путаете 0 c бесконечно малыми числами. Они хоть и бесконечно малы, но вовсе не равны нулю.

Владимир Горбацевич

12 августа

Бесконечно малые числа? Это Вы так выразились про “бесконечно малые функции” или Вы знакомы с нестандартным математ… Читать дальше

Комментировать ответ…Комментировать…

Анонимный ответ

Математика и математики12 декабря

Математика нужна не просто так по фану, а чтобы ее использовать в прикладных задачах. А в прикладных задачах нуля не бывает, как не бывает и бесконечности. Бывает только “очень маленькое число, которое можно считать почти нулем” или “очень большое число, которое можно считать бесконечностью”. Так, например, в инженерных задачах, если считают массу вагона поезда, то. .. Читать далее

1 эксперт не согласен

Maxim Vyalkov

возражает

13 декабря

Катющиковщина

Комментировать ответ…Комментировать…

Прохор Никифоров

19

вероисповедание – симпатия к православному язычеству хобби: программирование/ассемблер/fas…  · 5 дек 2021

Без обид. Или Вы бедовый студент, который не тем местом слушал, или учителя Ваши недоинститута…. Деление на ноль запрещеное дествие. ЭТО БЫЛО, ЕСТЬ И БУДЕТ. При изучении пределов это никак не меняется!!!! График операции деления (параметр а/х) помните? график представлен строго в 1 и 3 четвертях координатной плоскости. Асимптотами такого графика являются оси… Читать далее

Вадим Романский

6 декабря 2021

эмм… ответ тоже так себе, уровня “недоинститута”

Комментировать ответ…Комментировать…

Достоверно

Леонид Коганов

181

Член ММО – Московского математического Общества.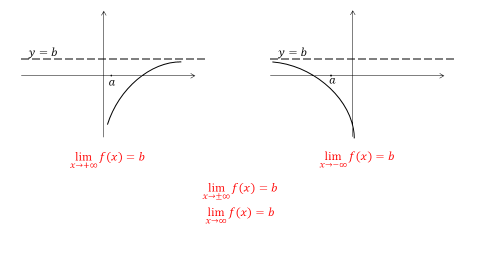 Кстати, старейшего в мире. Л.М. Коганов.  · 25 окт

Деление на  нуль есть решение двучленного уравнения, первоначально с неопределённой искомой буквой – значением х, когда у нас: ах = b, (*)  причём в нашем случае в простейшем уравнении (*) именно а = 0 по условию (на букву а, точнее на её числовое значение мы пытаемся поделить с сохранением всех свойств, допустим рационального поля = поля действительных рациональных… Читать далее

2 эксперта согласны

Комментировать ответ…Комментировать…

Достоверно

Сергей Перовский

Топ-автор

5,1 K

Научные заметки о жизни. https://zen.yandex.ru/id/5c43498395753900ac66852d  · 6 дек 2021

Все упирается в множество, на котором мы работаем. На множестве положительных чисел нельзя вычесть из меньшего большее. На множестве целых чисел “не работает” во многих случаях деление. Точно такой же смысл а в запрете деления на ноль: на множестве действительных (и комплексных) чисел нет элемента для результата операции.

Есть проективная математика, в которой… Читать далее

2 эксперта согласны

Александр

подтверждает

11 декабря 2021

Первая часть ответа правильна: Операция деления ноль (существование обратного элемента по умножению, для нуля) на… Читать дальше

Комментировать ответ…Комментировать…

Борис Зубов

1,4 K

Лучший ИТ-журналист РФ по версии Минцифры. Окончил физфак. Linux admin/coder. Китайский…  · 3 дек 2021

В обычной арифметике (с вещественными числами) a/0 не имеет смысла, так как: при а ≠ 0 не существует числа, которое при умножении на 0 даёт а, поэтому ни одно число не может быть принято за частное а⁄0; при а = 0 деление на ноль также не определено, поскольку любое число при умножении на 0 даёт 0 и может быть принято за частное 0⁄0. Исторически одна из первых ссылок на м… Читать далее

1 эксперт согласен

Комментировать ответ…Комментировать…

Dims

2,5 K

demystifier  · 6 дек 2021

Разделить на ноль так и осталось нельзя. Предел — это способ, которым можно приблизиться к делению на ноль, но не реализовать его. Бывают случаи, когда пределы различаются при стремлении к нулю справа или слева, так же, когда они не существуют. Предел функции 1/x при x стремящемся к 0 равен бесконечности.

1 эксперт согласен

Andrei Novikov

7 августа

См. Алгебраическую структуру “колесо”. https://ru.m.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BB%D0%B5%D1%81%D0%BE_(%D0%B0… Читать дальше

Комментировать ответ…Комментировать…

О сообществе

Математика и математики

Сообщество практикующих математиков разного уровня. Оригинальные решения, нетворкинг и общение. Не отвечаем на школьные задачки!

23. Предел функции, свойства Раскрытие неопределённостей вида (бесконечность/бесконечность). Свойства предела функции

1.       Для того, чтобы число А было пределомf(x) приx->a, необходимо и достаточно, чтобы эта функция была представима в видеf(x)=A+альфа(х), где альфа(х) – бесконечно малая. x,x->б = бесконечности, еслиc>1 и 0, если 0<c<1.

Неопределенность вида бесконечность на бесконечность

 

Разделить все на х в наивысшей степени, учитывая уменьшение степени в корне.

Lim(x->0) sin 5x/sin3x = [0/0]=lim(x->0) x sin5x/x sin3x = lim(x->0) sin5x/x*lim(x->0) x/sin3x=lim(x->0) 5sin5x/5x*lim 3sin3x/3x)=5/3

Lim(x-unl) (1+1/x)^x=e;

1/x=a=>x=1/a, a->0

Lim(a-0) (1+a)^1/2=e

Lim(x-0) (log_a(1+x))/x = lim(x-0) 1/x*log_a(1+x)=lim(x-0) log_a(1+x)^1/x=log_alim(x-0)(1+x)^1/x=log_ae

Lim(x-0) ln(1+x)/x=ln e=1

Lim(x-0) a^x-1/x=|a^x-1=t;a^x=t+1;ln a^x=ln(t+1)

Сравнение бесконечно малых функций

Пусть a(x,b(x) – бесконечно малые ф-ции при х->a

Тогда

1.       Lim(x->a)a(x)/b(x)=0 =>a(x) – бесконечно малая более высокого порядка, чемb(x)

2.        Lim(x->a)a(x)/b(x) =c<>0=>aиb– бесконечно малые функции одного порядка

3.       Lim(x->a)a(x)/b(x) = 1 =>aub– эквивалентные бесконечно малые функции

4.       Lim(x->a)d(x)/bⁿ(x) =c<>0 =>a– бесконечно малая функция н-ного порядка относительноb(x)

Cos2x=1-2sin²x

Теорема: если б.м. а(х) эквивалентна а₁(х) иb(x) ~b₁(x) иlim(x->a)a(x)/b(x) =>lim(x->a)a₁(x)/b₁(x)

1.       Sinkx~kx

2.       Tgkx~kx

3.       Arcsinkx~kx

4.       Arctgkx~kx

5.       E^kx-1 ~ kx

6.       A^kx~kx ln a

7.       Ln |1+kx|~kx

8.       1-cos kx ~kx²/2

23. Предел функции, теоремы о пределах. Неопределённость вида 0/0.  Бесконечно большие и бесконечно малые.

Функция f(x) стремится к бесконечности при x стремящимся к a, если для любого M > 0 можно указать такое значение  > 0, что для всех x удовлетворяющих неравенству xa <  имеет место неравенство f(x) > M.

lim_xa=

 Функция ограниченная при x a.

 Функция ограниченная при x .

 Теорема. Если lim_xaf(x)=b, то функция f(x) ограниченная при x a.

 Бесконечно малые и их свойства. lim_xa (x)=0

Теорема. 1. Если f(x)=b+, где  – б.м. при x a, то lim_xaf(x)=b и обратно, если lim_xaf(x)=b, то можно записать f(x)=b+(x).

Теорема. 2. Если lim_xa (x)=0 и (x)  0, то 1/ .

Теорема. 3. Сумма конечного числа б. м. есть б.м.

Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м.

 Теоремы о пределах.

Теорема. 1. Предел суммы есть сумма пределов.

Теорема. 2. Предел произведения есть произведение пределов.

Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).

Теорема. 4. Если u(x)  z(x)  v(x), и lim_xau(x)=lim_xav(x)=b, то lim_xaz(x)=b. (“Теорема о двух милиционерах”).

 Первый замечательный предел.

0.5sin(x) < 0.5x < 0.5tg(x)

lim x 0  sin(x) x =1.

 Второй замечательный предел.

Переменная величина

  1+ 1 n   n

при nимеет предел, заключенный между 2 и 3. В данной работе мы рассмотрим неопределенность видадля функции. Для нахождения предела функции мы применяем метод преобразования, метод замены и определение бесконечно малых величин.

Пусть требуется найти предел дроби

(1)

где P(x) и Q(x) функции определенные в окрестности предельного аргумента a, но в самом предельном значении обращаются в ноль.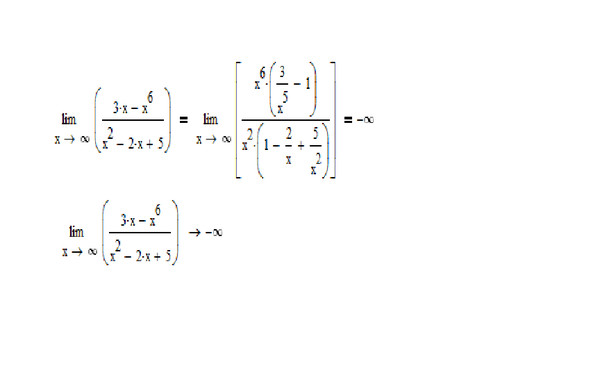

Теорема 1. Пусть число a для многочлена n-й степени P(x) = P_n(x) является k кратным решением, а для многочлена m-й степени Q(x) = Q_n(x) является r кратным решением, тогда

(2)

где P_n-k(a) и Q_m-r(a) значения соответствующих многочленов P_n-k(x) и Q_m-r(x) в точке x = a.

Доказательство. Так как, число a является решением многочленов P_n(x) и Q_m(x), то их в любое время можно представить в виде:

Тогда

(3)

Биномы (x – a)^kи (x – a)^rв окрестности точки x = a бесконечно малы, а их основания эквивалентные бесконечно малые. Отсюда

Полагаясь на последнее равенство, можно из (3) предела получить формулу (2). 25. 1-ый Замечательный предел.

 Первый замечательный предел:

y$ сходится к 0 при $|c|<1$, расходится к бесконечности при $c>1$, колеблется без сходимости при $c \leq -1$ и неопределенно при $c=1$.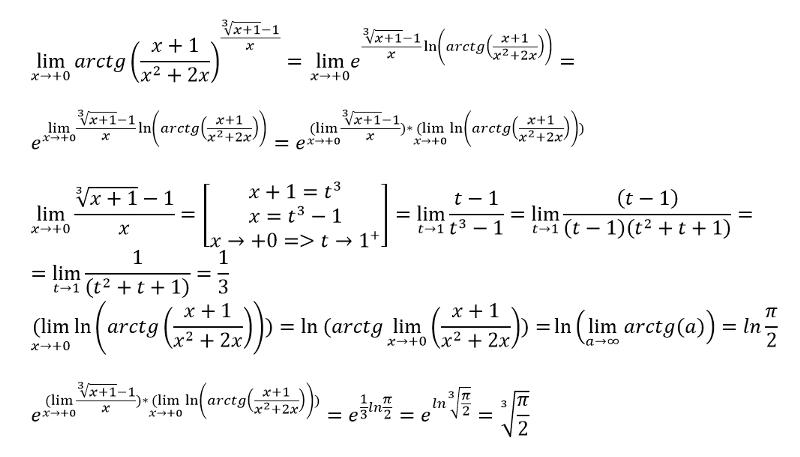 +$. 9речь идет о \infty$, которые абсолютно неопределенны.

$\endgroup$

8

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

предел 0 раз бесконечность, перепишите, чтобы найти предел

спросил 9 лет, 2 месяца назад

Изменено 9 лет, 2 месяца назад

Просмотрено 15 тысяч раз

$\begingroup$ 94}$.