Предел (lim), предел последовательности
Мы уже знаем, что арифметическая и геометрическая прогрессии – это последовательность чисел. Давайте возьмем последовательность an = 1/n, если k
и m натуральные числа, тогда для каждого k верно ak > am, поэтому, чем больше становится
n тем меньше становится an и это число всегда позитивно, но никогда не становится равным нулю. В этом случае, мы говорим, что 0 есть
пределом lim an->∞ если n->∞, или, если записать по-другому: limn->∞ an = 0.
Определение предела
Число a называется пределом последовательности, если для каждого ε > 0 может быть найдено число nε, то для всех членов последовательности an with index n > nε верно, что a – ε n .
Основное правило
Если limn->∞ an = a, an -> a an – a -> 0 |an – a| -> 0
Последовательность не всегда имеет предел, а иногда имеет предел бесконечности ( -∞ or +∞ ).
Если обе последовательности an and bn имеют действительные пределы, тогда последовательности
an + bn,
an – bn, an.bn и an / bn также имеют действительный предел и:
limn -> ∞(an + bn) = limn -> ∞an + limn -> ∞bn
limn -> ∞(an – bn) = limn -> ∞a
limn -> ∞(an . bn) = limn -> ∞an . limn -> ∞bn
limn -> ∞(an/ bn) = limn -> ∞an / limn -> ∞bn
если bn ≠ 0 and limn->∞bn ≠ 0
Если ann для каждого натурального n
и limn->∞an = a,
limn->∞bn = b
тогда a ≤ b
Если an ≤ bn ≤ cn или каждое действительное
n и если limn->∞an = limn->∞cn = A
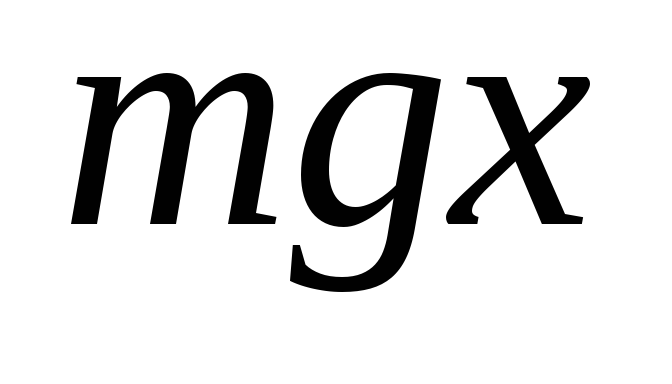
Если an ≥ 0 и limn->∞an = a, тогда последовательность bn = √an также имеет предел и limn->∞√an = √an.
Если an = 1/nk и k ≥ 1 тогда limn->∞an = 0.
Если -1 n->∞qn = 0.
limn->∞(1 – 1/n)n = limn->∞(1 + 1/n)n+1 = e
(1+1/n)nn-1
e is the number of Neper.
Если последовательность a
Если последовательности an иbn имеют бесконечные пределы и limn->∞an=+∞, limn->∞bn=+∞ тогда:
limn->∞(an + bn) = +∞
limn->∞(an . bn) = +∞
bn) = +∞
limn->∞ank = +∞ если k > 0
limn->∞an
Упражнения с пределами
Упражнение 1:
Если an = 5.4n, limn->0an = ?
Ответ:
limn->0an = limn->05 . limn->04n = 5 . 40 = 5.1 = 5
Упражнение 2:
| Если an = | then limn->∞an = ? |
Ответ:
| limn->∞ | = limn->∞ | . | = limn->∞ | = -3 |
Упражнение 3:
Ответ:
| liman->1 = | = | liman->∞ | = |
Больше о пределах на страницах математического форума
Для участия в математическом форуме регистрация не требуется!
Победами в олимпиадах я обязан учителю — Datification
В коллекции юного физика Владимира Лима есть медали из южноафриканского государства Ботсвана и арабского Катара, передаёт корреспондент pavlodarnews. kz.
kz.
Девятиклассник школы-лицея № 8 для одаренных детей Павлодара считает своего педагога Николая Билиду одним из главных людей в своей жизни.
— В физико-математическом классе, где я учусь, физика появилась в пятом классе, и вначале я вообще ничего не понимал на уроках, — рассказал Владимир Лим на пресс-конференции в Региональной службе коммуникаций. — С первого урока давали углубленные знания, было тяжело. Уже в шестом классе стал проникаться предметом. Анатолий Николаевич вначале нам все объяснял, показывал, а мы набивали руку. Теперь можем сами качественно самостоятельно готовиться к участию в олимпиадах.
Девятиклассник считает, что не достиг бы сегодняшних высот, если бы не Анатолий Билида.
— Анатолий Николаевич — один из главных людей в моей жизни, — уверен школьник. — Он все правильно объясняет, дает хорошие знания, при этом достаточно справедлив и строг, что мне в нем очень нравится. Еще я очень благодарен своим родителям, не без их помощи я стал победителем нескольких олимпиад.
Отметим, что, не считая побед на областных и республиканских предметных олимпиадах, Владимир Лим — призер двух международных.
В XV международной юниорской естественнонаучной олимпиаде, которая прошла в декабре 2018 года в южноафриканском государстве Ботсвана, он завоевал бронзу.
Через год на XVI международной естественнонаучной юниорской олимпиаде в столице арабского государства Катар — Дохе стал обладателем бронзы.
— В Ботсване прошла первая моя международная олимпиада, я сильно волновался, — вспоминает Владимир Лим. – Уровень знаний был невысоким, боялся, что мне его не хватит. За год добавил знаний, появилась уверенность в более высоком результате, и я его улучшил, выиграв серебряную медаль.
Свое будущее олимпиец планирует связать с прикладной физикой, ему очень нравится что-то создавать.
Кроме физики, Владимир Лим увлекается выпечкой тортов, однако сейчас на выполнение заказов у школьника нет времени, он готовится к участию в республиканской предметной олимпиаде.
Кроме того, в мае его ждет ежегодное состязание по физике среди школьников стран Азиатско-Тихоокеанского региона. Планируется, что она пройдет в Тайване.
Это вторая по значимости олимпиада для школьников по физике после Всемирной олимпиады, в ней участвуют только азиатские страны.
— Мне нравится процесс решения задач, и чем они сложнее, тем интереснее, — говорит школьник. — Погружаясь в их решение, остановиться я уже не могу, настолько это захватывающе и увлекательно. Особых секретов в моих успехах нет, чем больше работаешь, тем выше результат, надо много готовиться. У меня учеба отнимает по 12 часов в день. Уверен, при желании любой человек может добиться больших высот.
Напомним, что в 2019 году на ежегодной августовской педагогической конференции в Нур-Султане Анатолий Билида из рук Президента Казахстана Касым-Жомарта Токаева получил орден «Құрмет» как один из лучших учителей республики.
По словам руководителя регионального управления образования Дінислама Болатханұлы, в области накоплен богатый опыт по интеллектуальному развитию школьников, обобщённый в республике как наиболее результативный.
— Ежегодно с целью стимулирования учебно-познавательной деятельности учащихся, выявления и поддержки одаренных детей, популяризации среди школьников интеллектуальных игр, конкурсов, соревнований, повышения интереса к основам наук среди учащихся проводится более 70 мероприятий областного, республиканского и международного уровней, — сообщил глава ведомства. — В них принимает участие около 50% школьников области.
Роза Мустафина
Фото РСК
Теория пределов, формулы и примеры решений
Дальнейшее свое активное применение теория пределов получила при создании дифференциального и интегрального исчислений в 17 в., прежде всего в работах английского физика, математика, механика и астронома Исаака Ньютона (1642-1727). Впервые определение понятия предела было введено в работе английского математика Джона Валлиса (1616-1703) «Арифметика бесконечных величин». Хотя все же исторически понятие предела не лежало в основе дифференциального и интегрального исчислений.
Предел последовательности
Свойства предела последовательности
1. Если предел последовательности существует, то он единственный.
2.
3. (если оба предела в правой части существуют).
4. .
5. (если оба предела в правой части существуют).
6. (если оба предела в правой части существуют и предел знаменателя не равен нулю).
7. Теорема про двухстороннее ограничение (Теорема про двух милиционеров): если , то и
Предел функции
Замечание. Для пределов функций справедливы аналогичные свойства, как и для пределов последовательностей, которые приведены выше.
| Понравился сайт? Расскажи друзьям! | |||
Школьные предметы в России и Британии
В России в школах учат алгебру и физику, а в Британии – богословие и бухучет. А еще там много платят за учебу!
Как вы думаете, где легче учиться: в российской или британской школе? К слову,в Британии дети идут в школу на год раньше (c 5, а иногда даже с 4 лет!), чем в России, и заканчивают ее на год позже. Зато в российских школах изучают больше предметов. Кстати, помните ли вы все школьные предметы на английском?
Давайте взглянем на два интересных аспекта двух систем образования, – и вы сможете определиться, какая из них лично вам нравится больше. Начнем с самого важного – уроков и предметов.
Начнем с самого важного – уроков и предметов.
«Чему бы ты ни учился, ты учишься для себя.»
Арбитр Петроний (автор древнеримского романа «Сатирикон»)
Школьные дисциплины в России
Знаете, что общего между российскими и британскими школами? Это классно-урочная форма обучения. Практически все остальные аспекты обучения имеют существенные отличия. Итак, список школьных предметов.Большинство из них типичны и для российских, и для британских школ. Особенности дисциплин в Британии будут рассмотрены под таблицей.
|
Начальные классы |
||
|
Reading |
[ˈriːdɪŋ] |
Чтение |
|
Writing |
[ˈraɪtɪŋ] |
Письмо |
|
Music |
[ˈmjuːzɪk] |
Музыка |
|
Natural History |
[ˈnæʧrəl ˈhɪstərɪ] |
Природоведение |
|
Foreign Language |
[ˈfɔrɪnˈlæŋgwɪʤ] |
Иностранный язык |
|
Mother Language |
[ˈmʌðə ˈlæŋgwɪʤ] |
Родной язык |
|
Drawing |
[ˈdrɔːɪŋ] |
Рисование |
|
Technology |
[tekˈnɒləʤɪ] |
Труды |
|
Physical Education (PE) |
[ˈfɪzɪkəledjʊˈkeɪʃn] |
Физкультура |
|
Средние и старшие классы |
||
|
Russian (The Russian language) |
[rʌʃn ˈlæŋgwɪʤ] |
Русский язык |
|
Russian Literature |
[rʌʃn ˈlɪt(ə)rəʧə] |
Русская литература |
|
History |
[ˈhɪstərɪ] |
История |
|
Geography |
[ʤɪˈɒgrəfɪ] |
География |
|
Social Science |
[ˈsəʊʃəlˈsaɪəns] |
Обществознание |
|
English(The Englishlanguage) |
[ˈɪŋglɪʃ ˈlæŋgwɪʤ] |
Английский язык |
|
German(The Germanlanguage) |
[ˈʤɜːmən ˈlæŋgwɪʤ] |
Немецкий язык |
|
Maths (Mathematics) |
[mæθ] ([mæθɪˈmætɪks]) |
Математика |
|
Algebra |
[ˈælʤɪbrə] |
Алгебра |
|
Geometry |
[ʤɪˈɒmɪtrɪ] |
Геометрия |
|
Chemistry |
[ˈkemɪstrɪ] |
Химия |
|
Physics |
[ˈfɪɪzɪks] |
Физика |
|
Computer Science (ComputerStudies) |
[kəmˈpjuːtə ˈsaɪəns] ([kəmˈpjuːtəˈstʌdɪz] |
Информатика |
|
Astronomy |
[əsˈtrɒnəmɪ] |
Астрономия |
|
Life Safety |
[laɪf ˈseɪftɪ]] |
ОБЖ (Основы безопасности жизнедеятельности) |
|
Technology and Design |
[tekˈnɒləʤɪænddɪˈzaɪn] |
Труд |
|
Physical Education (PE) |
[ˈfɪzɪkəledjʊˈkeɪʃn] |
Физкультура |
|
Art |
[ɑːt] |
Рисование |
|
Technical Drawing |
[ˈteknɪkəl ˈdrɔːɪŋ] |
Черчение |
Лайфхак!
Самый действенный способ быстро запомнить названия школьных предметов на английском – перевести свое школьное расписание.Параллельное чтение расписаний на русском и английском ускорят запоминание в несколько раз. Ваша задача – один раз написать и просто просматривать записи каждый день, а остальное за вас сделает зрительная память. Распечатайте готовый шаблон расписания и впишите туда свои занятия на английском
Что изучают в Британии?
Как звучат типичные для британских школ школьные предметы на английском языке, написано чуть ниже. Там учащиеся, в принципе, изучают немного другой перечень предметов.
- В начальной и средней школе (с 1 по 8 классы) все ученики учат одинаковые базовые предметы.
Большинство предметов на этом этапе схожи с типичными для российских школ. Что интересно, там нет отдельных уроков по химии, биологии и физике. Британские дети изучают Science (научный блок), который и включает все вышеназванные дисциплины. Также нет разделения математики на алгебру и геометрию (учат просто Mathematics). Свой родной язык и литературу британцы тоже изучают как один предмет – English. Есть и такие предметы, которых нет у нас. Например, Citizenship (основы правовой ответственности) и «Religious Education» (религиозное воспитание).
Есть и такие предметы, которых нет у нас. Например, Citizenship (основы правовой ответственности) и «Religious Education» (религиозное воспитание). - Старшие школьники выбирают 5-10 профильных предметов для более тщательной подготовки к экзаменам.
Те, кто их успешно сдает, продолжают учиться в старшей школе и могут поступать в высшие учебные заведения. Остальные получают профессиональное образование. С 9 класса можно выбирать дисциплины, которые соответствуют профилю будущего обучения в вузе. К таким предметам относятся следующие (приводим лишь некоторые, наиболее популярные, школьные предметы на английском языке с переводом):
|
Accounting |
[əˈkaʊntɪŋ] |
Бухгалтерский учет |
|
Applied Information and Communication Technology |
[əˈplaɪd ɪnfəˈmeɪʃn ænd kəmjuːnɪˈkeɪʃn tekˈnɒləʤɪ] |
Прикладные информационные и коммуникативные технологии |
|
ArtandDesign |
[ɑːtænddɪˈzaɪn] |
Искусство и дизайн |
|
Business |
[ˈbɪznɪs] |
Бизнес |
|
TravelandTourism |
[trævlændˈtʊərɪzəm] |
Путешествия и туризм |
|
Divinity |
[dɪˈvɪnɪtɪ] |
Богословие |
|
EnvironmentalManagement |
[ɪnvaɪərənˈmentl [ˈmænɪʤmənt]] |
Управление окружающей средой |
|
FoodStudies |
[fuːd ˈstʌdɪz] |
Производство продуктов питания |
|
Law |
[lɔː] |
Право (законодательство, закон) |
|
MarineScience |
[məˈriːn ˈsaɪəns] |
Наука о море |
|
Media Studies |
[ˈmiːdɪə ˈstʌdɪz] |
Изучение средств массовой информации |
|
Psychology |
[saɪˈkɒləʤɪ] |
Психология |
|
Sociology |
[səʊsɪˈɒləʤɪ] |
Социология |
|
ForeignLanguages |
[ˈfɒrɪn ˈlæŋɡwɪʤɪz] |
Иностранные языки |
Как рассказать о своих любимых уроках по-английски?
«I like Physics because it’s cognitive and useful. »- Мне нравится физика, потому она познавательная и полезная.
»- Мне нравится физика, потому она познавательная и полезная.
«My favorite subject is History because it’s catching and interesting.» – Мой любимый предмет – история, потому что она увлекательная и интересная.
«I really like Computer Science. For me this subject is breathtaking! Besides, it’s in great demand today.» – Мне очень нравится информатика. Для меня этот предмет, просто захватывающий дух. Кроме того, он сегодня очень востребован.
«What I love at school is Art. It’s not even a subject, it’s just my hobby. When I draw I can relax and dream. It’s really cool!» – Что я просто обожаю в школе, так это рисование. Это даже не предмет, а мое хобби. Когда я рисую, я могу отдохнуть и помечтать. Это круто!
А сейчас пора перейти ко второму аспекту, в котором мы нашли различия между системами образования Великобритании и России.
Почему английские школы признаются одними из лучших в мире?
Эффективность английского образования во многом объясняется тем, что в стране очень много частных школ. Обучение в них обходится родителям, в среднем, от 15 до 30 тысяч долларов США в год. Наряду с частными, в Великобритании есть и государственные, бесплатные школы.Заметьте, в России школьное образование преимущественно бесплатное.
Обучение в них обходится родителям, в среднем, от 15 до 30 тысяч долларов США в год. Наряду с частными, в Великобритании есть и государственные, бесплатные школы.Заметьте, в России школьное образование преимущественно бесплатное.
Если вы хотите поехать учиться в Англию
Одна из особенностей британского образования заключается в том, что здесь могут учиться дети из любой страны мира. Единственное, что необходимо – это своевременная оплата учебы (за каждый триместр). Кроме оплаты самой учебы, придется платить еще и за время, которые дети из других стран проводят в опекунских семьях на выходных и во время каникул. В некоторых школах опекунство бесплатное, в других это стоит примерно 2-5 тысяч долларов в год.
В чем преимущества образования в России
То, что школьное образование в России бесплатное, не делает его некачественным. Это делает его доступным – и в этом его главное преимущество перед зарубежным. К тому же, у нас обучение строится на объяснении, растолковывании и закреплении материала, а за рубежом учителя просто предъявляют ученикам информацию.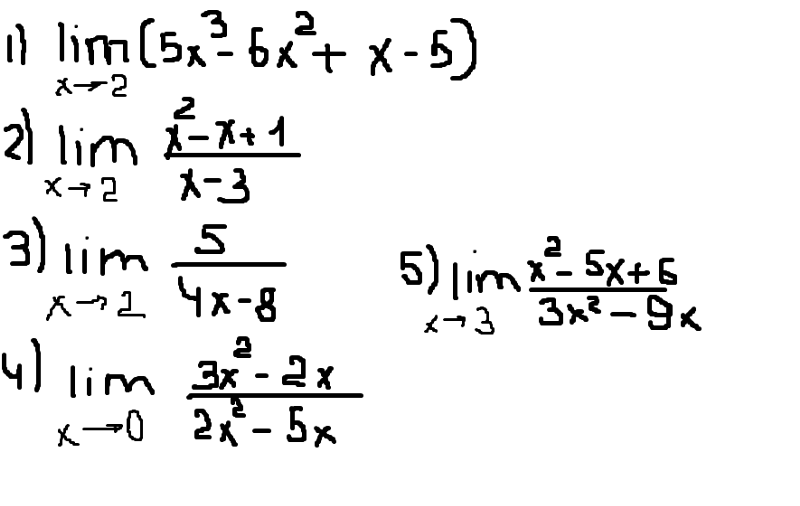 Там, конечно, меньше домашнего задания, но поэтому и образование более поверхностное.
Там, конечно, меньше домашнего задания, но поэтому и образование более поверхностное.
В зарубежных школах нет классного руководства и никто не дежурит по школе. Отсюда огромная проблема хулиганства – bullying. Это по сути издевательства одноклассниками над отдельными детьми. У нас такого нет, или практически нет.
Цени то, что можешь учиться, потому что каждый урок – это твои новые возможности. Чем больше ты знаешь, тем больше можешь!
Правление
Марина Медведева родилась в Москве в 1971 году. Вошла в состав правления ООО «СИБУР» в 2016 году, в этом качестве курирует вопросы корпоративного управления, развития процессного управления и общекорпоративных сервисов.
Выпускница колледжа МИД, с 1992 года начала работу в компаниях нефтяной отрасли. В 2000 году с отличием окончила Московскую Академию экономики и права по специальности юрист. Еще в процессе обучения принимала участие в структурировании проектов на условиях соглашения о разделе продукции.
С 2003 года Медведева занимала руководящие позиции в международных и российских нефтяных компаниях, включая Quest Petroleum (UK), ARCO Overseas Petroleum Inc. и «ТНК-ВР Менеджмент», где занималась, в том числе, сопровождением сделок слияния и, позднее, развитием корпоративного управления. Этот период позволил развить экспертизу с точки зрения предметного понимания отрасли, стрессоустойчивость, получить опыт создания проектных команд, считает Марина Владимировна. «Но хотелось дальнейшего развития, драйва от новых задач, другой культуры», – говорит Медведева.
В 2008 году, к тому моменту окончив МГИМО по направлению «Международный нефтегазовый бизнес» и, параллельно, несколько программ Международной школы бизнеса INSEAD, Медведева возглавила блок общекорпоративных сервисов и органов управления ООО «СИБУР». Позднее стала управляющим директором компании. С момента прихода в СИБУР в 2008 году периметр задач расширялся и включал разнонаправленные, диверсифицированные блоки обеспечения бизнеса.
С приходом в СИБУР Марина Медведева стала инициатором реструктуризации и переосмысления подходов к организации работы блока общекорпоративных сервисов и органов управления. «Основным вызовом стала необходимость в организации административных процессов прийти к динамичной, гибкой культуре, основанной на коллаборации. Ключевая идея: все внутренние сервисы должны быть удобны и прозрачны для заказчиков – сотрудников организации», – отмечает Медведева.
Под ее управлением был оптимизирован документооборот, процессы протокольных служб, решена задача централизации общих (не классических для ЦОБ) сервисов на платформе ОЦО СИБУР, выстроены функциональные вертикали вверенных блоков во всех географиях компании, начат процесс трансформации и развития процессного управления. По блоку работы Корпоративное управление в 2012 году Медведева стала лауреатомVII Национальной премии «Директор года» в номинации «Директор по корпоративному управлению/ Корпоративный секретарь» Российского союза промышленников и предпринимателей при партнерстве с PwС, а в 2013 году – победителем этой премии. Но однажды зафиксированный прогресс – не повод останавливаться в поисках еще более эффективных решений, убеждена Марина Медведева.
Но однажды зафиксированный прогресс – не повод останавливаться в поисках еще более эффективных решений, убеждена Марина Медведева.
С течением времени одной из важных составляющих деятельности Медведевой стало участие в независимых сообществах и форумах, что позволяет делиться наработанным опытом с профессиональным сообществом. «Сегодня СИБУР – один из признанных лидеров не только в отраслевом, нефтегазохимическом смысле. Но и с точки зрения внедрения лучших практик в организацию своей работы», – говорит Медведева. Она представляет компанию в Ассоциации независимых директоров, входит в состав общероссийской общественной организации «Национальное объединение корпоративных секретарей», является Сертифицированным независимым директором Института директоров Великобритании (Cet.IoD)
Вне работы Марина стремится находить возможность как для занятий спортом (большой теннис, горные лыжи), так и на отдых культурологического плана. В детстве серьезно занималась синхронным плаванием: «уникальный вид спорта, который дисциплинирует, учит одновременно и самостоятельной, и командной работе, а также тому, как «переключаться» с одного режима на другой». Но на первое место Марина ставит возможность провести время с семьей.
Но на первое место Марина ставит возможность провести время с семьей.
PushkinOnline — Article
Проблема миграции существовала и существует как в Америке, Европе так и в Российской Федерации. Многие граждане других государств приезжают на работу в Россию на долгосрочный период, мигранты не только устраиваются на работу, но часто перевозят свои семьи с детьми разных возрастов. Конечно, этих детей необходимо обучать русскому языку, чтобы они успешно ассимилировались в российском обществе. При этом важно, чтобы они не только изучали русский язык, но и овладевали, хотя бы на начальном уровне, языком научного стиля, получали знания по физике, географии, химии, биологии и т.д. Тем более что дети по окончании 9 класса должны сдавать ГИА, а в 11 классе – ЕГЭ не только по русскому языку, но и по другим предметам. Таким образом, создание пособий по научному стилю для разных предметов необходимо, причем эти учебные пособия должны быть пропедевтического характера, т. е. предложены на начальном этапе изучения предмета. Дальнейшее освоение дисциплины должно осуществляться в рамках классно-урочной системы по предложенным программам общеобразовательной школы.
е. предложены на начальном этапе изучения предмета. Дальнейшее освоение дисциплины должно осуществляться в рамках классно-урочной системы по предложенным программам общеобразовательной школы.
В 2013 году по всей России стали образовываться центры по тестированию мигрантов, одной из таких площадок стал Российский государственный университет имени И.М. Губкина, поэтому кафедра русского языка с миграционными проблемами хорошо знакома.
Разработка пособий по научному стилю определенного школьного предмета пропедевтического характера требует многоаспектной подготовки преподавателей и тесного сотрудничества между школой и вузом. С одной стороны, вузовские преподаватели должны владеть методикой преподавания РКИ и РКН, знать специфику научного стиля, особенности преподавания предметов технического и естественно-научного профиля. Такую профессиональную подготовку имеют, как правило, преподаватели РКИ в технических вузах, в частности, на кафедре русского языка РГУ нефти и газа имени И. М. Губкина. С другой стороны, для создания пропедевтических курсов необходимо знание особенностей преподавания школьных дисциплин, в частности физики, химии, географии и т.д., что находится в профессиональной компетенции школьных учителей-предметников. Тесное сотрудничество между школой и вузом в контексте данной работы необходимо, иначе невозможно достичь положительного результата. Согласование планирования пропедевтического курса и школьного учебника, отбор материала, апробирование пособия, обратная связь – условия продуктивного сотрудничества. Школа – вуз – современный тренд, только такой симбиоз позволит соединить теорию с практикой, поможет понять общие проблемы и выработать стратегию и тактику совместных действий.
М. Губкина. С другой стороны, для создания пропедевтических курсов необходимо знание особенностей преподавания школьных дисциплин, в частности физики, химии, географии и т.д., что находится в профессиональной компетенции школьных учителей-предметников. Тесное сотрудничество между школой и вузом в контексте данной работы необходимо, иначе невозможно достичь положительного результата. Согласование планирования пропедевтического курса и школьного учебника, отбор материала, апробирование пособия, обратная связь – условия продуктивного сотрудничества. Школа – вуз – современный тренд, только такой симбиоз позволит соединить теорию с практикой, поможет понять общие проблемы и выработать стратегию и тактику совместных действий.
Кафедра русского языка РГУ нефти и газа имени И.М. Губкина стоит у истоков нового направления «Мигранты – школа – вуз»: на кафедре открыта площадка по работе с мигрантами, на кафедре обучают русскому языку иностранных студентов, будущих специалистов технического профиля, преподаватели кафедры тесно сотрудничают со школами.
Преподавателями кафедры русского языка РГУ нефти и газа имени И.М. Губкина Гусевой Е.Ю., Дворкиной Е.А., Поляковой Ю.Д. создан первое учебное пособие по физике «Научный стиль. Физика 7», которое предназначено для детей мигрантов РКИ, РКН и является пропедевтическим курсом.
В соответствии с поурочным планированием в пособие входит 29 уроков, из них 4 контрольные работы. Каждый урок пособия охватывает один или несколько параграфов учебника. Например, параграф 1 “Наблюдения и опыты” включает в себя с первого по шестой параграфы учебника. Такое, на первый взгляд крупное, объединение объясняется повторяющимися грамматическими конструкциями, общей лексикой, небольшими по объему текстами вводных уроков. Параграф 24 пособия “Механическая работа” включает в себя только один урок учебника. Сложный лексико-грамматический материал, физические формулы, определения не позволяют объединить данный урок с другими уроками.
Каждый урок имеет от десяти до пятнадцати заданий, которые можно разделить на предтекстовые и послетекстовые. Центральное место каждого урока занимает научно-популярный текст, сокращенный и адаптированный для чтения учащихся, для которых русский не является родным языком.
Центральное место каждого урока занимает научно-популярный текст, сокращенный и адаптированный для чтения учащихся, для которых русский не является родным языком.
Предтекстовые задания направлены, в первую очередь, на лексическую работу. Работа с научным стилем речи, чтение научно-популярных текстов предполагает работу со словарем, поэтому словарная работа представлена в каждом уроке пособия. В первых уроках учащимся предлагается посмотреть незнакомое слово в словаре и записать его значение, в дальнейшем задание усложняется: учащимся дается толкование значения слова на русском языке, в последних уроках лексическим единицам дается толкование на русском языке, но учащимся необходимо самим выбрать, какой лексической единице соответствует то или иное объяснение. Подобная словарная работа развивает память, языковую интуицию, расширяет словарный запас, учит работать со словарем. Большой блок заданий дается на словообразовательную работу. В русском языке богато представлены однокоренные слова. От одного корня, как правило, можно образовать и существительное, и прилагательное, и глагол и глагольные формы, и наречие. Понимая значения корня, учащийся может догадаться, понять значение однокоренной лексической единицы. Это имеет важное значение при работе с научно-популярными текстами. В некоторых уроках нужно задать вопросы к каждой лексической единице, распределить однокоренные слова по частям речи.
От одного корня, как правило, можно образовать и существительное, и прилагательное, и глагол и глагольные формы, и наречие. Понимая значения корня, учащийся может догадаться, понять значение однокоренной лексической единицы. Это имеет важное значение при работе с научно-популярными текстами. В некоторых уроках нужно задать вопросы к каждой лексической единице, распределить однокоренные слова по частям речи.
Также перед текстом мы обращаем внимание на грамматические конструкции, характерные для научного стиля речи, к каждой грамматической конструкции даны примеры, которые затем учащийся встретит в тексте. Затем, в ходе чтения текста учащимся предлагается найти эти конструкции в тексте и привести свои примеры их употребления.
Практическая направленность пособия предполагает обучение владению русским языком в четырех видах речевой деятельности, которая подразделяется на рецептивную (аудирование и чтение) и продуктивную (говорение и письмо). Обучение аудированию, формирование слухопроизносительных навыков – важная задача при обучении школьников, для которых русский язык неродной, им нужно слышать и понимать, что учитель говорит на уроке, что отвечают одноклассники. Поэтому небольшая работа над этим аспектом тоже включена в предтекстовые задания.
Поэтому небольшая работа над этим аспектом тоже включена в предтекстовые задания.
Когда все лексико-грамматические трудности сняты, предлагается прочитать текст. Перед прочтением каждого текста стоит вопрос, направленный на понимание общего смысла текста, его темы, проблемы.
Выполнение послетекстовых заданий направлены на контроль усвоения лексики и грамматики урока и понимание предметного содержания предложенной в уроке темы. В заданиях “вставить пропущенные слова, предлоги, глаголы”, как правило, используются те лексические единицы, которые встречались в предтекстовых заданиях. Необходимость употребить правильную грамматическую форму вставляемых слов контролирует усвоение грамматических конструкций, усвоение предложно-падежной системы русского языка и глагольного управления. Также, на наш взгляд, полезными являются задания определить основу предложения, объяснить, чем выражены подлежащее, сказуемое, дополнение (это особенно важно в предложениях, где формы именительного и винительного падежей существительного совпадают, и учащимся трудно понять смысл предложения).
Мы обращаем внимание учащихся на определенные правила функционирования научного стиля, например, на употребление формы первого лица множественного числа глаголов, которые используются при описании опытов (поставим, рассмотрим, установим, поместим и т.д.)
Трудность представляют задание на определение верной или неверной информации, наличие в прочитанном тексте данной информации. Также трудным бывает задание, требующее правильного выбора лексической единицы из ряда паронимов. Но следует отметить, что эти задания формируют навыки работы с текстом, внимание, память, логическое мышление. Эти навыки необходимы не только для работы с научно-популярным текстом, но и для успешной учебы и жизни.
Также после текста предлагаются задания, направленные на понимание русской синтаксической системы, формирующие умения и навыки выражения условных, уступительных, временных, причинно-следственных отношений в простых и сложных предложениях.
Итоговые задания направлены на продуктивную речевую деятельность в устной и письменной форме.
Апробация учебного пособия была проведена в 7 классах в СОШ № 282 г. Москвы (директор И. Г. Егорова). Результаты апробации показали, что ученики отработали следующие навыки и умения: самостоятельное чтение, анализ и запись условия задачи; понимание формулировки вопроса и ответы на вопросы; работа со словарем под руководством учителя, а впоследствии самостоятельная словарная работа; понимание определений терминов, встречаемых в курсе физики 7-го класса; использование различных грамматических конструкций для выражения условия совершения действия, цели действия, пропорционального изменения признака, сравнения понятий и пр. соединение или замена близких по значению понятий.
Апробация учебного пособия доказала, что ученики, для которых русский язык является иностранным или неродным, повысили свой уровень владения языком, закрепили знания учебного материала по физике.
Апробация проводилась в группе учащихся из Вьетнама и Таджикистана. При анкетировании ученики отметили, что уроки по научному стилю речи помогают им лучше понимать учебный материал на уроках физики, а также писать контрольные работы по физике.
В пособии использован методический принцип концентрического повторения лингвистического материала. По мере усложнения изучаемого материала по предмету (физике) усложняются и расширяются ранее изученные на более простом языковом материале грамматические темы, с каждым уроком вводится новая лексика и повторяется лексика, изученная на первых уроках. Таким образом, обеспечивается повторение и закрепление всего пройденного языкового материала.
В учебное пособие включены 4 контрольные работы по темам: «Взаимодействие тел», «Давление твердых тел, жидкостей и газов», «Архимедова сила. Плавание тел», «Работа. Мощность. Энергия». Контрольные работы предусматривают проверку языковых знаний по научному стилю речи, именно поэтому обобщающие задания идентичны тем, которые выполнялись в процессе обучения. Четыре предложенных контрольных работы основаны на языковом материале дополнительного чтения учебника А.В. Пёрышкина «Физика 7 класс», то есть прежде учениками не читались и, по сути, представляют собой фрагменты новой информации по предмету, одновременно являясь новыми текстами для грамматического контроля.
Например, при изучении темы «Измерение атмосферного давления. Опыт Торричелли» (44) описывается опыт, проведенный итальянским ученым, и дается его объяснение. В разделе «Это любопытно…» учебника А.В. Пёрышкина подробно описывается история открытия атмосферного давления. Именно этот текст взят за языковую основу контрольной работы № 2 «Давление твердых тел, жидкостей и газов». Такой выбор текста не случаен: во-первых, это новый в предметном отношении материал, который не был бы прочитан учениками в рамках уроков физики; во-вторых, это просто интересный в историко-культурном плане материал; в-третьих, это новый материал в языковом смысле, который дает возможность проверить достигнутый уровень языковой компетенции.
Анализ проведенных контрольных работ показал, что учащиеся добились определенного прогресса в усвоении предложно-падежной системы, причем, прогресс этот наиболее заметен у учеников из Вьетнама. При выполнении заданий, связанных с усвоением материала по предмету (физике) разница в достигнутых результатах между учениками из Вьетнама и Таджикистана не так заметна: количество ошибок и правильных ответов примерно одинаково в обеих национальных группах.
Так как в СОШ № 282 апробацию учебного пособия по научному стилю речи проводил учитель – предметник, коллективом авторов пособия были созданы методические рекомендации для учителя. По сути это подробным образом разработанные ответы на все вопросы и задания пособия. Таким образом, работать в классе могут не только преподаватели филологи, но и преподаватели не филологи.
Как показали результаты экспериментального обучения, предложенная системы заданий эффективна, так как учитывает и принципы сознательного усвоения материала и бессознательного, происходящего во время многократного повторения лексико-грамматических конструкций и информации текста урока.
Гусева Елена Юрьевна,
Дворкина Екатерина Александровна,
Полякова Юлия Давидовна
Российский государственный университет имени И.М. Губкина
Диссертация (Экстремальные задачи в теории относительного роста выпуклых и целых функций) – PDF, страница 12
Нижняя дискретная усредненная плотность ∆ и нижeняя усредненная плотность ∆∗ произвольной бесконечно большой последовательности Λ ⊂ C совпадают:∗∆=∆ . e69Доказательство. Очевидно, чтоN (|λn |)N (x)= ∆∗ .∆ = limρ > limρx→+∞ xe n→∞ |λn |Чтобы получить неравенство противоположного смысла, рассмотрим функN (x)цию Φ(x) =, для изучения которой при k ∈ N положимxρΦk (t) =N (|λnk |) + nk ln t,tρt > 0.Поскольку на промежутках Ik = [|λnk |, |λnk +1|) имеем nΛ (t) ≡ nk , тоN (|λnk |) + nk ln |λxn |1xk=Φk,x ∈ Ik .Φ(x) =xρ|λnk |ρ|λnk |Согласно пункту III леммы 1.1 функция Φ(x) либо монотонна на Ik , либоимеет на этом промежутке единственный максимум. В любом случае имеемk ∈ N.inf {Φ(x)} = min Φ(|λnk |), Φ(|λnk+1 |) ,x∈IkПоэтому∆∗ = lim inf Φ(x) = lim min Φ(|λnk |), Φ(|λnk+1 |) >k→∞ x∈Ikk→∞> lim inf Φ(|λm|) = lim Φ(|λm |) = ∆, т. е. ∆∗ > ∆ .m→∞k→∞ m>kee∗Сопоставляя с предыдущим, получаем ∆ = ∆ , что и требовалось.eТеорема 1.20.
e69Доказательство. Очевидно, чтоN (|λn |)N (x)= ∆∗ .∆ = limρ > limρx→+∞ xe n→∞ |λn |Чтобы получить неравенство противоположного смысла, рассмотрим функN (x)цию Φ(x) =, для изучения которой при k ∈ N положимxρΦk (t) =N (|λnk |) + nk ln t,tρt > 0.Поскольку на промежутках Ik = [|λnk |, |λnk +1|) имеем nΛ (t) ≡ nk , тоN (|λnk |) + nk ln |λxn |1xk=Φk,x ∈ Ik .Φ(x) =xρ|λnk |ρ|λnk |Согласно пункту III леммы 1.1 функция Φ(x) либо монотонна на Ik , либоимеет на этом промежутке единственный максимум. В любом случае имеемk ∈ N.inf {Φ(x)} = min Φ(|λnk |), Φ(|λnk+1 |) ,x∈IkПоэтому∆∗ = lim inf Φ(x) = lim min Φ(|λnk |), Φ(|λnk+1 |) >k→∞ x∈Ikk→∞> lim inf Φ(|λm|) = lim Φ(|λm |) = ∆, т. е. ∆∗ > ∆ .m→∞k→∞ m>kee∗Сопоставляя с предыдущим, получаем ∆ = ∆ , что и требовалось.eТеорема 1.20.
Для произвольной бесконечно большой последовательно∗∗сти Λ ⊂ C с усредненной верхней ρ -плотностью ∆ρ (Λ) = ∆ ∈ (0, +∞)выполняются неравенства()eρ∆∆∗exp−1 ,(1.105)∆ 6ρ∆)(e∆ρ∆∗∆ 6−1 .(1.106)expρ∆Доказательство. Из определений усредненной дискретной верхней плотности, верхней и нижней плотности последовательности получаем, что для любого ε > 0 и достаточно больших k выполняются неравенстваN (|λnk |)e< (1 + ε)∆,|λnk |ρ70nk< (1 + ε)∆,|λnk |ρ∆nk>.|λnk+1 |ρ(1 + ε)Сохраняя обозначения теоремы 1.19 и применяя утверждение части III леммы 1.1, для x ∈ Ik имеемΦ(x) =N (|λnk |) + nk ln |λxnkxρ|<()e + ∆ ln x∆eρ∆∆|λn |ρ k 6 (1 + ε) exp−1 ,< (1 + ε)xρ∆|λnk |и такжеΦ(x) =e+(1 + ε) ∆<∆1+εx|λnk+1 |N (|λnk+1 |) + nk ln |λnxk+1xρln |λnxρk+1|6 (1 + ε)∗k→∞ x∈Ik∗∆ = lim sup Φ(x) 6 (1 + ε)k→∞ x∈Ik<∆exp {dε − 1} .ρeρ∆. Отсюда получаемЗдесь dε =∆(1 + ε)2∆ = lim sup Φ(x) 6 (1 + ε)|∆expρ()eρ∆−1 ,∆∆∆6 (1 + ε) exp {dε − 1} ,ρρчто при ε → 0 приводит к (1.105) и (1.106).eОтметим тот факт, что в силу ρ ∆/ ∆ − 1 6 0 неравенство (1.105)∗местоуточняет классическое соотношение ∆ 6 ∆/ρ .
Из определений усредненной дискретной верхней плотности, верхней и нижней плотности последовательности получаем, что для любого ε > 0 и достаточно больших k выполняются неравенстваN (|λnk |)e< (1 + ε)∆,|λnk |ρ70nk< (1 + ε)∆,|λnk |ρ∆nk>.|λnk+1 |ρ(1 + ε)Сохраняя обозначения теоремы 1.19 и применяя утверждение части III леммы 1.1, для x ∈ Ik имеемΦ(x) =N (|λnk |) + nk ln |λxnkxρ|<()e + ∆ ln x∆eρ∆∆|λn |ρ k 6 (1 + ε) exp−1 ,< (1 + ε)xρ∆|λnk |и такжеΦ(x) =e+(1 + ε) ∆<∆1+εx|λnk+1 |N (|λnk+1 |) + nk ln |λnxk+1xρln |λnxρk+1|6 (1 + ε)∗k→∞ x∈Ik∗∆ = lim sup Φ(x) 6 (1 + ε)k→∞ x∈Ik<∆exp {dε − 1} .ρeρ∆. Отсюда получаемЗдесь dε =∆(1 + ε)2∆ = lim sup Φ(x) 6 (1 + ε)|∆expρ()eρ∆−1 ,∆∆∆6 (1 + ε) exp {dε − 1} ,ρρчто при ε → 0 приводит к (1.105) и (1.106).eОтметим тот факт, что в силу ρ ∆/ ∆ − 1 6 0 неравенство (1.105)∗местоуточняет классическое соотношение ∆ 6 ∆/ρ .
Если жездесь имеет∗e ∆ − 1 > 0,знак равенства, т. е. ∆ = ∆/ρ, то из (1.105) вытекает ρ ∆/∗e > ∆/ρ, и ∆ ∗ = ∆. e Таким образом, если ∆ ∗ принимает своеоткуда ∆ > ∆наибольшее возможное значение, равное ∆/ρ, то это значение достигаетсяна некоторой части последовательности Λ (в общем случае не на всей).Заметим, что формулировке теоремы 1.20 можно придать более компактный вид ∆∆∗∆ 6 min h,h,ρρ71)e∆−1 .где h(x) = x expxВ формулировке следующего результата используем стандартное обозначение a+ = max {a, 0} .(Теорема 1.21. Для произвольной бесконечно большой последовательно∗∗сти Λ ⊂ C с усредненной верхней ρ -плотностью ∆ρ (Λ) = ∆ ∈ (0, +∞)выполняются неравенства∗ee∆ 6∆ee∆ 6∆∗ρ ν−1ρν(1.107),ρ ν−1(1.108),ρνlρ∗e∆ 6∆,ln lρ + 1l−ρ∗e∆ 6∆.(ln l−ρ + 1)+(1.109)(1.110)Доказательство.
e Таким образом, если ∆ ∗ принимает своеоткуда ∆ > ∆наибольшее возможное значение, равное ∆/ρ, то это значение достигаетсяна некоторой части последовательности Λ (в общем случае не на всей).Заметим, что формулировке теоремы 1.20 можно придать более компактный вид ∆∆∗∆ 6 min h,h,ρρ71)e∆−1 .где h(x) = x expxВ формулировке следующего результата используем стандартное обозначение a+ = max {a, 0} .(Теорема 1.21. Для произвольной бесконечно большой последовательно∗∗сти Λ ⊂ C с усредненной верхней ρ -плотностью ∆ρ (Λ) = ∆ ∈ (0, +∞)выполняются неравенства∗ee∆ 6∆ee∆ 6∆∗ρ ν−1ρν(1.107),ρ ν−1(1.108),ρνlρ∗e∆ 6∆,ln lρ + 1l−ρ∗e∆ 6∆.(ln l−ρ + 1)+(1.109)(1.110)Доказательство.
Отметим сразу, что неравенство (1.109) уточняет неравенство (1.90) в случае l > 1. Теперь приступим непосредственно к доказательству.e = ∆ ∗, то неравенства (1.107)–(1.110) выполняются очевиднымЕсли ∆e в правых частяхобразом, поскольку каждый из сомножителей величины ∆этих неравенств не меньше единицы.e < ∆ ∗ . Выберем положительное число ε < ∆ ∗ − ∆e иПусть теперь ∆используя определение верхней усредненной плотности, найдем последовательности индексов K и точек xk так, чтобы выполнялись соотношения:∗∆ = lim sup Φ(x) = lim sup Φ(x),k→∞ x∈Ikk∈K x∈Ike + ε,Φ(xk ) = sup Φ(x) > ∆x∈Ikk ∈ K. При достаточно больших номерах k функция Φ(x) принимает на концахпромежутков Ik значенияe + ε < Φ(xk ).Φ(|λnk |) < ∆Поэтому (отбрасывая при необходимости конечное число индексов из K ) можем считать, что для каждого k ∈ K точка xk лежит строго внутри Ik ,т.
При достаточно больших номерах k функция Φ(x) принимает на концахпромежутков Ik значенияe + ε < Φ(xk ).Φ(|λnk |) < ∆Поэтому (отбрасывая при необходимости конечное число индексов из K ) можем считать, что для каждого k ∈ K точка xk лежит строго внутри Ik ,т.
е.|λnk | < xk < |λnk+1 |,k ∈ K.72|λnk+1 |N (|λnk |)и νk =. Применяя пункт III леммы 1.1|λnk |nkк функции Φk (t) , с учетом равенства1xΦ(x) =Φk,x ∈ Ik ,|λnk |ρ|λnk |получаем1xk(1.111)1<= e ρ −νk < ck ,|λnk |Обозначим ck =N (|λnk |) e ρ νk −1e ρ νk −1nkρ νk −1e== Φ(|λnk |).Φ(xk ) =|λnk |ρ|λnk |ρρ νkρ νkЛогарифмирование (1.111) приводит к неравенству1 − ln cρk < ρ νk < 1.(1.112)(1.113)Теперь после проведенной подготовительной работы оценка (1.107) легкодоказывается предельным переходом в равенстве (1.112). Именно,e ρ νk −1e ρ νk −1e ρ ν−1∗e∆ = lim Φ(xk ) = lim Φ(|λnk |).6 lim Φ(|λnk |) lim6∆k∈Kk∈Kk→∞k→∞ ρ νkρ νkρνex−1Здесь мы учли, что функция q2(x) =убывает на интервале (0, 1) ,xсогласно пункту II леммы 1. 1.Неравенство (1.108) доказывается аналогичным образом.
1.Неравенство (1.108) доказывается аналогичным образом.
ЗапишемN (|λnk+1 |) + nk ln |λnx |1xk+1Φ(x) ==Φk,x ∈ Ik .xρ|λnk+1 |ρ|λnk+1 |1N (|λnk+1 |)′1x, получим<= e ρ −νk < 1, или, послеnkck|λnk+1 |логарифмирования,1 < ρ νk′ < 1 + ln cρk .(1.114)Обозначив νk′ =Следующее соотношение выводится так же, как и формула (25), и на этотраз приобретает видΦ(xk ) =nk|λnk+1 |ρ′ρ νk′ −1e′N (|λnk+1 |) eρ νk −1eρ νk −1= Φ(|λnk+1 |).=|λnk+1 |ρ ρ νk′ρ νk′(1.115)Снова используя пункт II леммы 1.1 (но теперь на промежутке (1, +∞) ,где функция ex−1 /x возрастает), предельным переходом из (1.112) получаемнеравенство (1.108):′e ρ νk −1e ρ ν−1e.∆ = lim Φ(xk ) 6 lim Φ(|λnk+1 |) lim6∆k∈Kk→∞k→∞ ρ νk′ρν∗73Для доказательства неравенства (1.109) воспользуемся определением индексалакунарности, согласно которому при любом ε > 0 и всех k > k0(ε) выполняется ck < l + ε .
Это позволяет для достаточно больших k ∈ K сначалаиз (1.113) вывести, что 1 < ρ νk′ < 1 + ln(l + ǫ)ρ, а затем из (1. 115) и пункта IIлеммы 1.1 получитьρρeln(l+ε)e + ε) (l + ε)Φ(xk ) < Φ(|λnk+1 |)< (∆.ln(l + ε) + 1ln(l + ε) + 1Последовательный переход к пределу при k → ∞, k ∈ K, и ε → 0 приводитк нужной оценке (1.109) .Неравенство (1.110) доказывается с использованием аналогичных соображений.
115) и пункта IIлеммы 1.1 получитьρρeln(l+ε)e + ε) (l + ε)Φ(xk ) < Φ(|λnk+1 |)< (∆.ln(l + ε) + 1ln(l + ε) + 1Последовательный переход к пределу при k → ∞, k ∈ K, и ε → 0 приводитк нужной оценке (1.109) .Неравенство (1.110) доказывается с использованием аналогичных соображений.
Действительно, из (1.113) следуют неравенства1 − ln(l + ǫ)ρ < 1 − ln ck < ρ νk < 1,ρ νk > 0,откуда ρ νk > (1 + ln(l + ǫ)−ρ )+ . Дальнейшее ясно. Доказательство теоремы 1.21 завершено.Следующий доказываемый ниже результат можно извлечь из нашей монографии [19].Теорема 1.22. Пусть Λ — бесконечно большая последовательностькомплексных чисел с ρ -плотностями ∆ρ (Λ) = ∆ ∈ (0, +∞), ∆ρ (Λ) = ∆,∗∗e ρ (Λ) = ∆.e Тогда выполняются неравенства∆ρ (Λ) = ∆ , ∆ρ∗(Λ) = ∆ ∗, ∆∗∗∗ρ a1 ∆ 6 ∆ 6 ρ ea1 ∆ ,Здесь a1 , a2 — корни уравненияa ln∗ρea2 ∆ 6 ∆ 6 ρ a2 ∆ .e∗= ∆∗ / ∆ ,a(1.116)(1.117)а ea1 , ea2 — корни подобного же уравнения с „подправленной“ правой частью:a lnee ∆∗ .= ∆/a(1.118)Корни уравнений связаны неравенствами 0 6 a1 6 ea1 6 1 6 ea2 6 a2 6 e. Если Λ — дискретно измеримая последовательность, то верны равенства∗∗∆ = ρ a2 ∆ .(1.119)∆ = ρ a1 ∆ ,74Доказательство.
Если Λ — дискретно измеримая последовательность, то верны равенства∗∗∆ = ρ a2 ∆ .(1.119)∆ = ρ a1 ∆ ,74Доказательство.
Обозначим N1(x) = N (ex ) и n1 (x) = n(ex ) . Тогда будутвыполняться равенстваn1 (x),x→+∞ eρxn1 (x),ρxx→+∞ e∆ = lim∆ = limN1 (x)N1(x)∗=lim,∆.ρxx→+∞ eρxx→+∞ eК выпуклым функциям f (x) = N1(x) = N (ex ) и g(x) = eρx применимeтеорему 1.7. Учитывая, что ϕg (a) = a ln , получаем согласно этой теоремеaкрайние неравенства в (1.116):∗∆ = lim∗∗ρ a1 ∆ 6 ∆,∆ 6 ρ a2 ∆ .Теперь воспользуемся неравенствами теоремы 1.20. Так, неравенство (1.105)перепишем в видеρ 1−(ρ∆e )/ ∆1e6 ∗,∆∆илиe 1− ρ∆e / ∆eρ∆e∆e )/ ∆1−(ρ∆()e=eln6 ∗.e∆∆e1−(ρ∆)/ ∆eeПоскольку e1−(ρ∆)/ ∆ > 1 , а функция ϕ(a) = a ln убывает на отрезке [1, e] ,ae )/ ∆1−(ρ∆>ea2 . Логарифмируя, последовательно получаемто e1−eρ∆> ln ea2 ,∆lneρ∆e>,ea2∆ae2 ∆eρ∆e>,ea2∆∆ > ae2 ρ∆ .eeρ∆,6ea1∆ee∆eρ∆,=ln6ae1 ∆ ∗ea1∆∆ 6 ae1 ρ∆ .e∆∗= lnАналогично преобразуем и неравенство (1.106):∗ee 1− ρ∆e / ∆e∆ρ∆ee ( ) = e1−(ρ∆)/ ∆ ln6∗. e )/ ∆1−(ρ∆∆∆eeeНо теперь e1−(ρ∆)/ ∆ 6 1 , и функция ϕ(a) = a ln (ϕ(0) = 0) возрастает наae )/ ∆1−(ρ∆отрезке [0, 1] , поэтому e6ea1 .
e )/ ∆1−(ρ∆∆∆eeeНо теперь e1−(ρ∆)/ ∆ 6 1 , и функция ϕ(a) = a ln (ϕ(0) = 0) возрастает наae )/ ∆1−(ρ∆отрезке [0, 1] , поэтому e6ea1 .
Отсюда, как и выше, последовательно получаем1ρ 1−(ρ∆e )/ ∆e6 ∗,∆∆1−eρ∆6 ln ea1 ,∆ln∗Оба центральных неравенства в (1.116) проверены. Утверждение о корняхeуравнений вытекает из того, что функция ϕ(a) = a ln (ϕ(0) = 0) возрасaтает на [0, 1] и убывает на [1, e]. Последнее утверждение теоремы следуетиз (1.116), поскольку для дискретно измеримых последовательностей выполe = ∆∗ . Теорема полностью доказана.няется условие ∆75Дополним теперь неравенство (1.107) оценкой снизу через нижние усредненную и относительную плотности.Предложение 1.17.
Шуанг Фанг Лим | Кафедра физики
Био
После получения докторской степени. в Кембриджском университете, Великобритания, 2004 г., Шуанг Фанг Лим работал на постдокторской исследовательской должности в Принстонском университете с 2004 по 2008 гг. Ее работа там была сосредоточена на преобразовании наночастиц (UCNP), а также на синтезе, фотофизике и биологических применениях наночастиц. После этого назначения она затем в течение одного года занимала постдокторскую должность в Государственном университете Северной Каролины, а затем в течение трех лет занимала должность доцента-исследователя, прежде чем принять назначение на должность доцента, которое начнется осенью 2012 года.
После этого назначения она затем в течение одного года занимала постдокторскую должность в Государственном университете Северной Каролины, а затем в течение трех лет занимала должность доцента-исследователя, прежде чем принять назначение на должность доцента, которое начнется осенью 2012 года.
Специализированная область
Лим сосредоточен на синтезе, описании, фотофизике, биоконъюгации и применении UCNP. Эти UCNP разработаны для применения в качестве биосенсоров в микрочипах и в качестве биотерапевтических средств в фотодинамической и фототермической терапии. UCNP возбуждаются в ближней инфракрасной области (NIR) и излучают флуоресценцию в видимой области спектра, обладают превосходной фотостабильностью и высоким отношением сигнал / шум для визуализации биологических образцов благодаря нулевой автофлуоресценции тканей.Эти свойства делают UCNP идеальными для трехмерной визуализации и мониторинга биологических процессов в течение длительного времени. Механизм повышающего преобразования в UCNP основан либо на последовательном возбуждении одного и того же излучающего центра в однократно легированных редкоземельных преобразователях с повышением частоты, называемом APTE (добавление de photon par transferts d’energie), либо на возбуждении двух центров и последующей передаче энергии в совместно легированных редкоземельных элементах. преобразователи с повышением частоты, известные как эффект ETU (преобразование с повышением частоты передачи энергии). Переход флуоресценции из более высокого возбужденного состояния в основное состояние приводит к флуоресценции, которая наблюдается как антистоксова эмиссия, в результате чего испускаемый фотон имеет более высокую энергию, чем энергия возбуждения.Большая глубина проникновения БИК-возбуждения и низкий фон многофотонной флуоресценции, а также активное нацеливание делают эти наноматериалы идеальными 3D-диагностическими зондами. UCNP использовались в диагностике в месте оказания медицинской помощи (POC), например, в анализах латерального потока, анализах массивов в лунках и анализах микроматриц.
Механизм повышающего преобразования в UCNP основан либо на последовательном возбуждении одного и того же излучающего центра в однократно легированных редкоземельных преобразователях с повышением частоты, называемом APTE (добавление de photon par transferts d’energie), либо на возбуждении двух центров и последующей передаче энергии в совместно легированных редкоземельных элементах. преобразователи с повышением частоты, известные как эффект ETU (преобразование с повышением частоты передачи энергии). Переход флуоресценции из более высокого возбужденного состояния в основное состояние приводит к флуоресценции, которая наблюдается как антистоксова эмиссия, в результате чего испускаемый фотон имеет более высокую энергию, чем энергия возбуждения.Большая глубина проникновения БИК-возбуждения и низкий фон многофотонной флуоресценции, а также активное нацеливание делают эти наноматериалы идеальными 3D-диагностическими зондами. UCNP использовались в диагностике в месте оказания медицинской помощи (POC), например, в анализах латерального потока, анализах массивов в лунках и анализах микроматриц.
Она также работает над эпигенетическим картированием отдельных молекул ДНК и хроматина. В ядрах эукариотических клеток геномная ДНК упакована в виде хроматина. Фундаментальной повторяющейся единицей хроматина является нуклеосома, представляющая собой комплекс, образующийся, когда двухцепочечная ДНК оборачивается вокруг октамера гистона, состоящего из центрального тетрамера h4 / h5.Каждый из этих 4 типов корового гистона (h3A, h3B, h4, h5) имеет гибкий аминокислотный хвост из 25-40 остатков, известный как гистоновый хвост. Общие ковалентные модификации гистонового хвоста, такие как ацетилирование, моно-, ди- и три-метилирование, фосфорилирование и убиквитинирование, выполняют функцию модуляции структуры хроматина более высокого порядка. Некоторые модификации могут быть унаследованы между поколениями клеток и, таким образом, являются эпигенетическими метками, такими как состояние метилирования некоторых генов, которые можно использовать в качестве биомаркера онкогенеза.Ее усилия сосредоточены на методах идентификации специфических маркеров метилирования и ацетилирования при разрешении генома.
Группы
Чтобы связаться со мной : Сай-Пэн Lim Калифорния Государственный университет Нортриджа Отделение физики и астрономии 18111 Nordhoff Street, CA 91330-8268 Электронная почта: сказать[email protected] Телефон: (818) 677-5612 Факс: (818) 677-3234 Кабинет: Дуб живой 1128 | | Справочная информация: Я профессор кафедры физики и астрономии Калифорнийского университета. Государственный университет Нортриджа.Я обучаюсь в сжатой форме дело с упором на электронную структуру. Я был родился в Малайзии и после окончания там средней школы переехал в Соединенные Штаты для моего послесреднего образования. Я получил степень бакалавра степень по физике (1982) в Swarthmore Колледж и доктор философии. Кандидат физико-математических наук (1988 г.) в университете Висконсин – Мэдисон.Моим научным руководителем был профессор Дэвид Л. Хубер. После получения докторской степени я несколько лет работал в докторантуре. научный сотрудник Университета Западной Вирджинии под руководством профессора Бернарда Р. Купера до того, как я Текущее положение. Курсов: Весна 2015 PHYS 220A: Механика |
Профессор Юджин Лим
Профессор Юджин ЛимБраузер не поддерживает скрипт.
Браузер не поддерживает скрипт.
Профессор теоретической физики
Направления исследований
Контактные данные
Биография
Юджин получил докторскую степень в области астрономии и астрофизики в 2004 году в Чикагском университете.Он был докторантом в Йельском университете (2004–2007) и Колумбийском университете (2007–2010), а также был приглашенным профессором в Университете Фондвы на Гаити. В 2010 году он стал преподавателем кафедры прикладной математики и теоретической физики Кембриджского университета. В 2012 году Юджин поступил в Королевский колледж Лондона в качестве преподавателя на факультете физики.
В 2012 году Юджин поступил в Королевский колледж Лондона в качестве преподавателя на факультете физики.
Область научных интересов
Космология ранней вселенной в широком смысле. Текущие интересы:
1.Числовая теория относительности в космологии (сайт: http://grchombo.github.io/)
2. Высокогамма-столкновения солитонов и дефектов. Эффективная теория
Солитонное рассеяние
3. Проверка сильной гравитации в космологии и физике черных дыр
4. Модифицированная гравитация
5. Приложения квантовой теории информации в космологии
Космология Multimessenger: корреляция космического микроволнового фона и измерений фона стохастической гравитационной волны
Адсхед, П., Афшорди, Н., Димастрогиованни, Э., Фасиелло, М. , Лим, Э.А. и Тасинато, Г., 26 января 2021 г., В: Physical Review D. 103, 2, 023532. Результат исследования: Материалы для журнала – Статья – экспертная оценка. DOI: https://doi.org/10.1103/PhysRevD.103.023532
, Лим, Э.А. и Тасинато, Г., 26 января 2021 г., В: Physical Review D. 103, 2, 023532. Результат исследования: Материалы для журнала – Статья – экспертная оценка. DOI: https://doi.org/10.1103/PhysRevD.103.023532Когерентные формы гравитационных волн и память из петель космических струн
Ауррекоэчеа, Дж. К., Хелфер, Т. и Лим, Э. А., 22 октября 2020 г., В: Классическая и квантовая гравитация. 37, 20, aba28b. Результат исследования: Вклад в журнал – статья – рецензирование.DOI: https://doi.org/10.1088/1361-6382/aba28bВлияние потенциальной формы на неоднородную инфляцию
Aurrekoetxea, J.C., Clough, K., Flauger, R. & Lim, E.A., май 2020 г., В: Journal of Cosmology and Astroparticle Physics. 2020, 5, 030. Результат исследования: Материалы для журнала – статья – рецензирование. DOI: https://doi.org/10.1088/1475-7516/2020/05/030Образование черной дыры при столкновениях релятивистских осциллатонов
Widdicombec, J. Y., Helfer, T.И Лим Э.А., 10 января 2020 г., В: Журнал космологии и физики астрономических частиц. 2020, 1, 027. Результат исследования: Материалы для журнала – статья – рецензирование. DOI: https://doi.org/10.1088/1475-7516/2020/01/027
Y., Helfer, T.И Лим Э.А., 10 января 2020 г., В: Журнал космологии и физики астрономических частиц. 2020, 1, 027. Результат исследования: Материалы для журнала – статья – рецензирование. DOI: https://doi.org/10.1088/1475-7516/2020/01/027Эванесцентные гравитационные волны
Голат С., Лим Э. и Родригес Фортуно Ф., 22 апреля 2020 г., В: Physical Review D. 101, 8, 084046. Результат исследования: Материалы для журнала – статья – рецензирование. DOI: https://doi.org/10.1103/PhysRevD.101.084046Коллапс петли космической струны в полной общей теории относительности
Хелфер, Т., Aurrekoetxea, J. C. & Lim, E. A., 15 мая 2019 г., In: Physical Review D. 99, 10, 104028. Результат исследования: Вклад в журнал – статья – рецензирование. DOI: https://doi.org/10.1103/PhysRevD.99.104028Излучение гравитационных волн при столкновениях компактных скалярных солитонов
Хелфер, Т., Лим, Э.А. , Гарсия, М.А.Г. и Амин, М.А., 26 февраля 2019 г., В: Physical Review D (Частицы, поля, гравитация и космология). 99, 4, с. 1-8 044046. Результат исследования: Материалы для журнала – статья – рецензирование.DOI: https://doi.org/10.1103/PhysRevD.99.044046
, Гарсия, М.А.Г. и Амин, М.А., 26 февраля 2019 г., В: Physical Review D (Частицы, поля, гравитация и космология). 99, 4, с. 1-8 044046. Результат исследования: Материалы для журнала – статья – рецензирование.DOI: https://doi.org/10.1103/PhysRevD.99.044046Образование релятивистских аксионных звезд
Виддикомб Дж. Й., Хелфер Т., Марш Д. Дж. Э. и Лим Э. А., 3 октября 2018 г., В: Journal of Cosmology and Astroparticle Physics. 2018, 10, 005. Результат исследования: Материалы для журнала – статья – рецензирование. DOI: https://doi.org/10.1088/1475-7516/2018/10/005Устойчивость инфляции к большим тензорным возмущениям
Лим, Э., Клаф, К. и Флогер, Р., 29 мая 2018 г., В: Журнал космологии и физики астрономических частиц. 2018, май Результат исследования: Материалы для журнала – статья – рецензирование. DOI: https://doi.org/10.1088/1475-7516/2018/05/065Образование черной дыры из аксионных звезд
Хелфер, Т. , Марш, Д. Дж. Э., Клаф, К. А., Фэйрберн, М., Лим, Э. и Бесеррил, Р., 29 марта 2017 г., В: Journal of Cosmology and Astroparticle Physics. 2017, 3, 55. Результат исследования: Материалы для журнала – статья – рецензирование. DOI: https: // doi.org / 10.1088 / 1475-7516 / 2017/03/055
, Марш, Д. Дж. Э., Клаф, К. А., Фэйрберн, М., Лим, Э. и Бесеррил, Р., 29 марта 2017 г., В: Journal of Cosmology and Astroparticle Physics. 2017, 3, 55. Результат исследования: Материалы для журнала – статья – рецензирование. DOI: https: // doi.org / 10.1088 / 1475-7516 / 2017/03/055
Браузер не поддерживает скрипт.
Браузер не поддерживает скрипт.
Браузер не поддерживает скрипт.
Браузер не поддерживает скрипт.
Браузер не поддерживает скрипт.
Браузер не поддерживает скрипт.
Тек-Ках Лим (родился 1 декабря 1942 г.), американский преподаватель физики, исследователь
Тек-Ках Лим, американский преподаватель физики, исследователь. Стипендиат Humboldt Stiftung, Федеративная Республика Германия, 1980 год; Коломбо Плановый ученый, правительство Австралии, 1961–1968 годы. Основная китайская школа Main Line, Уэйн, Пенсильвания, 1980; Президент Водного Клуба Лоуэр Мерион (Пенсильвания), 1988.Член Американского физического общества; член Академии наук в Филадельфии (основатель) тематической группы по немногим системам тела (секретарь, казначей 1985–1993).
Стипендиат Humboldt Stiftung, Федеративная Республика Германия, 1980 год; Коломбо Плановый ученый, правительство Австралии, 1961–1968 годы. Основная китайская школа Main Line, Уэйн, Пенсильвания, 1980; Президент Водного Клуба Лоуэр Мерион (Пенсильвания), 1988.Член Американского физического общества; член Академии наук в Филадельфии (основатель) тематической группы по немногим системам тела (секретарь, казначей 1985–1993).Фон
Лим Тек-Ках родился 1 декабря 1942 года в Малакке, Малайзия. Сын Чин-То и Сью-Ленг Лим. приехал в США в 1968 году.
Образование
Бакалавр наук с отличием, У.Аделаида, Южная Австралия, 1965 год; Доктор философии, Университет Аделаиды, Южная Австралия, 1968.
Карьера
Лектор, Университет Малайи, Куала-Лумпур, Малайзия, 1968 г .;
научный сотрудник, Государственный университет Флориды, Таллахасси, 1968-1970 годы;
доцент, Дрексель У., Филадельфия, 1970–1975 годы;
доцент, Дрексель У. , Филадельфия, 1975–1982 годы;
профессор, Drexel U., Филадельфия, с 1982 г.Программа развития консультантов ООН, Нью-Йорк, 1985. Научный советник Министерства образования, Гуанси, Китайская Народная Республика, с 1985 года.
, Филадельфия, 1975–1982 годы;
профессор, Drexel U., Филадельфия, с 1982 г.Программа развития консультантов ООН, Нью-Йорк, 1985. Научный советник Министерства образования, Гуанси, Китайская Народная Республика, с 1985 года.
Членство
Основная китайская школа Main Line, Уэйн, Пенсильвания, 1980. Президент Водного клуба Нижнего Мериона (Пенсильвания), 1988. Член Американского физического общества.
Член Академии наук в Филадельфии (основатель), тематическая группа по немногим системам тела (секретарь, казначей 1985–1993).
Подключения
Женился на Ньок-Кхенг Лью, 28 января 1966 г. Дети: Киан-Тат, Ай-Ли.
- Отец:
- Чин-То Лим
- Мать:
- Сью-Ленг Лим
- Супруг:
- Nyok-Kheng Liew
- ребенок:
- Ай-Ли Лим
- ребенок:
- Киан-Тат Лим
Dr Lim Kok Geng | Саутгемптонский университет Малайзия
Название: Феноменологические исследования сегнетоэлектрических сверхрешеток с градиентным составом (открыто для подачи заявки на докторскую степень)
Главный исследователь: Доктор Кок-Генг Лим
Введение:
Сегнетоэлектрик с градиентным составом на основе бессвинцовой системы твердых растворов, такой как BaxSr1-xTiO3, может проявлять большие градиенты поляризации и желаемую термостабильную восприимчивость. Этот новый твердый раствор не только соответствует будущей тенденции к бессвинцовой технологии, но также отвечает требованиям большого пьезоэлектрического отклика сегнетоэлектриков для современных электронных приложений.
Этот новый твердый раствор не только соответствует будущей тенденции к бессвинцовой технологии, но также отвечает требованиям большого пьезоэлектрического отклика сегнетоэлектриков для современных электронных приложений.
Аннотация:
Сегнетоэлектрик с градиентным составом на основе бессвинцовой системы твердых растворов, такой как BaxSr1-xTiO3, может проявлять большие градиенты поляризации и желаемую термостабильную восприимчивость. Этот новый твердый раствор не только соответствует будущей тенденции к бессвинцовой технологии, но также отвечает требованиям большого пьезоэлектрического отклика сегнетоэлектриков для современных электронных приложений.Настраивая их состав на атомном уровне, мы можем управлять физическими свойствами и функциональными возможностями сегнетоэлектрика с градиентным составом. Следовательно, данное исследование направлено на разработку термодинамической модели, основанной на теории Ландау-Гинзбурга, для изучения фундаментальных физических свойств сегнетоэлектрических сверхрешеток с градиентным составом с учетом межфазного эффекта. Теоретическое исследование фундаментальных физических свойств очень важно при изготовлении сегнетоэлектрических сверхрешеток с градиентным составом для технологических применений, например: преобразователи, диэлектрики с высокой диэлектрической проницаемостью, пироэлектрические датчики, пьезоэлектрические устройства, перестраиваемый сегнетоэлектрический конденсатор и др.
Теоретическое исследование фундаментальных физических свойств очень важно при изготовлении сегнетоэлектрических сверхрешеток с градиентным составом для технологических применений, например: преобразователи, диэлектрики с высокой диэлектрической проницаемостью, пироэлектрические датчики, пьезоэлектрические устройства, перестраиваемый сегнетоэлектрический конденсатор и др.
Название: Дионическая червоточина в теории Эйнштейна-Янга-Миллса-Хиггса (открыто для подачи заявки на соискание ученой степени доктора философии)
Главный исследователь: Доктор Кок-Генг Лим
Введение:
Червоточины – это гипотетические компактные объекты, которые соединяют две далекие области Вселенной, что позволяет путешествовать во времени или межзвездном пространстве. Например, проходимая червоточина, изображенная в научно-фантастическом фильме Кристофера Нолана «Интерстеллар».Первая постулируемая червоточина в общей теории относительности (ОТО) – это мост Эйнштейна-Розена (ER), возникающий, когда структура пространства-времени искривляется и сильно искривляется под действием силы тяжести.
Аннотация:
Червоточины – это гипотетические компактные объекты, которые соединяют две далекие области Вселенной, что позволяет путешествовать во времени или межзвездном пространстве. Например, проходимая червоточина, изображенная в научно-фантастическом фильме Кристофера Нолана «Интерстеллар». Первая постулируемая червоточина в общей теории относительности (ОТО) – это мост Эйнштейна-Розена (ER), возникающий, когда структура пространства-времени искривляется и сильно искривляется под действием силы тяжести.Недавно мы обнаружили неабелевы решения кротовых нор, поддерживаемые фантомным полем в теории Эйнштейна-Янга-Миллса-Хиггса (EYMH), которые обладают волосами YMH в присутствии гравитации [Phys. Ред. D 102, 124068 (2020)]. В плоском космосе дион – это частица, которая обладает как магнитным, так и электрическим зарядом. В искривленном пространстве-времени теория EYMH также обладает гравитирующими дионами и растворами дионных черных дыр. Следовательно, поучительно изучить дионную кротовую нору в теории EYMH.
Домашняя страница Woei Chet Lim
Домашняя страница Woei Chet LimОфис: Г.3,05
Телефон: (+64) 7 858 5148
Электронная почта: [email protected]
Обучение
MATh411-12A Расширенное исчислениеMATh359-12B Математическое моделирование
MATH542-12B Уравнения в частных производных 2
MATh411-13A Расширенный расчет
MATh355-13B / ENGG284-13B Дифференциальные уравнения
MATh433-13Y / MATH565-13B Общая теория относительности
MATh411-14A Расширенный расчет
MATh355-14B / ENGG284-14B Дифференциальные уравнения
MATH543-14B Нелинейная динамика и хаос
(В учебном отпуске в течение семестра 15А)
MATh355-15B / ENGG284-15B Дифференциальные уравнения
MATh433-15Y / MATH565-15B Общая теория относительности
MATH541-15B Классические дифференциальные уравнения с частными производными
MATh411-16A Расширенный расчет
MATH541-16A Классические дифференциальные уравнения с частными производными
MATh355-16B / ENGG284-16B Дифференциальные уравнения
MATh351-17A / ENGG285-17A Многопараметрическое исчисление
MATh355-17B / ENGG284-17B Дифференциальные уравнения
MATh433-17Y / MATH565-17B Общая теория относительности
ENGG285-17T Многопараметрическое исчисление
(В учебном отпуске в течение семестра 18А)
ENGEN201-18B Инженерная математика 2
MATHS201-18B Непрерывное исчисление (первые 8 недель)
MATHS203-18B Дифференциальные уравнения и моделирование (последние 4 недели)
MATH541-18B Классические дифференциальные уравнения с частными производными
ENGEN201-19S Инженерная математика 2 (первая половина)
MATHS101-19A Введение в исчисление
MATHS565-19A Общая теория относительности
ENGEN201-19B Инженерная математика 2
MATHS201-19B Непрерывное исчисление (первые 8 недель)
MATHS203-19B Дифференциальные уравнения и моделирование (последние 4 недели)
MATHS101-20A Введение в исчисление
MATHS543-20A Нелинейная динамика и хаос
ENGEN201-20B Инженерная математика 2
MATHS201-20B Продолжающийся исчисление (первые 8 недель)
ENGEN201-20C (NET) Инженерная математика 2
ENGEN201-21A Инженерная математика 2
MATHS201-21A Продолжающееся исчисление (первые 8 недель)
MATHS565-21A Общая теория относительности
(В учебном отпуске в течение триместра 21B)
Исследования
Моя область исследований – математическая и вычислительная космология. Мои исследования включают моделирование Вселенной в целом с использованием системы
уравнения в частных производных (PDE). Поскольку PDE редко допускают точное
решения,
Я использую динамические системы и асимптотический анализ в более простых режимах
модели и проводить численное моделирование в общих режимах.
Мои исследования включают моделирование Вселенной в целом с использованием системы
уравнения в частных производных (PDE). Поскольку PDE редко допускают точное
решения,
Я использую динамические системы и асимптотический анализ в более простых режимах
модели и проводить численное моделирование в общих режимах. Мои текущие исследования были сосредоточены на
так называемое неоднородное поведение Миксмастера вблизи гравитационного
необычность. Этой теме посвящена большая часть моей докторской диссертации.
Шоковый числовой код CLAWPACK, а также два конечных
разностные коды, разработанные мной, использовались для моделирования неоднородных
Поведение Mixmaster и результаты показывают, что в типичной модели
эффект неоднородности незначителен вдоль большинства мировых линий, за исключением
для особых мировых линий, где эффект становится важным время от времени
время и приводит к повторяющемуся образованию шипов.В 2007 году я обнаружил явное решение спайков OT G_2.
Затем были разработаны более совершенные числовые коды. Численное моделирование моделей G_2 подтверждает повторяемость всплесков в разные эпохи Гауди,
и что явное решение для пиков описывает пики.
В 2015 году я обнаружил явное решение спайков не-OT G_2, которое обобщает решение спайков OT G_2.
Численное моделирование моделей G_2 подтверждает повторяемость всплесков в разные эпохи Гауди,
и что явное решение для пиков описывает пики.
В 2015 году я обнаружил явное решение спайков не-OT G_2, которое обобщает решение спайков OT G_2.
Мои другие текущие проекты включают:
- Динамика пространственно однородных (Бьянки) моделей
- Вывод и применение формулы наддува
- Вывод асимптотических разложений для космологических моделей
- Анализ особенностей точных решений
Текущие активные проекты:
- Различные аспекты шипов.
Предыдущие должности:
- Докторант (Отделение геометрического анализа и гравитации)
Институт гравитационной физики Макса Планка (Институт Альберта Эйнштейна). Сентябрь 2008 г. – декабрь 2011 г.
Сентябрь 2008 г. – декабрь 2011 г. - Постдокторант (с Франсом Преториусом)
Физический факультет, Университет Альберты, Канада.Сентябрь 2006 г. – январь 2007 г.
Физический факультет, Принстонский университет, США. Февраль 2007 г. – август 2008 г. - Постдокторант (с Аланом Коли)
Математико-статистический факультет, Университет Далхаузи, Канада. Сентябрь 2004 г. – август 2006 г.
Образование:
- Доктор философии по прикладной математике, Университет Ватерлоо, Канада (2004 г.)
Диссертация: «Динамика неоднородных космологий».Супервайзер: Джон Уэйнрайт - Прикладная математика MMath, Университет Ватерлоо, Канада (2000)
Диссертация: «Анизотропия космического микроволнового фона. температура во вселенных Бьянки ». Супервайзер: Джон Уэйнрайт - BMath награждает совместную прикладную математику и информатику, Университет Ватерлоо, Канада (1998 г.)
Премия:
- Премия С.
 Чандрасекара
за лучшую постдокторскую презентацию на всех занятиях по общей математической теории относительности
(A1 Точные решения и их интерпретация,
A2 Математическая теория относительности и другие достижения классической гравитации,
A3 Modified Gravity Theories) на 19-й Международной конференции по общей теории относительности
и гравитация в Мехико, 5-9 июля 2010 г.
Чандрасекара
за лучшую постдокторскую презентацию на всех занятиях по общей математической теории относительности
(A1 Точные решения и их интерпретация,
A2 Математическая теория относительности и другие достижения классической гравитации,
A3 Modified Gravity Theories) на 19-й Международной конференции по общей теории относительности
и гравитация в Мехико, 5-9 июля 2010 г.
Ссылка на страницу ResearcherID
Ссылка на страницу Google Scholar
Журнальные статьи:
- «Цилиндрические шипы»
М.З.А. Moughal, W.C. Lim Классическая и квантовая гравитация , 38 , 075029 (22pp) (2021); arXiv: 2102.12028.
Примечание. Это сокращенная версия диссертации Могала, arXiv: 2102.09776. - «Жесткие жидкие шипованные растворы из семенных растворов Bianchi типа V»
Д.Грегорис, W.C. Лим, А.А. Coley Классическая и квантовая гравитация , 34 , 235013 (21pp) (2017); arXiv: 1705. 02747.
02747.
Errata: Ссылка [4] должна быть Lim et al 2009, PRD 79, 123526, а не 103526. - «О первом решении пика жесткой жидкости G_1 в общей теории относительности»
А.А. Коли, Д. Грегорис, W.C. Lim Классическая и квантовая гравитация , 33 , 215010 (11pp) (2016); arXiv: 1606.07177.
Errata: Ссылка [17] должна быть Lim et al 2009, PRD 79, 123526, а не 103526. - «Пики и неоднородности вещества в безмассовых скалярных моделях поля»
А.А. Коли, W.C. Lim Классическая и квантовая гравитация , 33 , 015009 (20pp) (2016); arXiv: 1511.07095.
Ошибка: в (39) член n_30 должен читать n_30 exp (- (w + 1) tau). Ссылка [6] должна быть Lim et al 2009, PRD 79, 123526, а не 103526. - “Неортогонально транзитивное решение спайков G_2”
W.C. Lim Классическая и квантовая гравитация , 32 , 162001 (8pp) (2015); arXiv: 1507.2. Игнорируйте уравнения (53) – (54). Последнее предложение в абзаце перед (49) должно относиться к n_10 и n_30.
Ссылка [15] должна быть Lim et al 2009, PRD 79, 123526, а не 103526.
Последнее предложение в абзаце перед (49) должно относиться к n_10 и n_30.
Ссылка [15] должна быть Lim et al 2009, PRD 79, 123526, а не 103526. - «Демонстрация феномена спайка с использованием моделей LTB»
А.А. Коли, W.C. Lim Классическая и квантовая гравитация , 31 , 115012 (15pp) (2014); arXiv: 1405,5252.
Errata: Ссылка [4] должна быть Lim et al 2009, PRD 79, 123526, а не 103526. - «Общерелятивистские возмущения плотности»
W.C. Лим, А.А. Коли, Классическая и квантовая гравитация , 31 , 015020 (13pp) (2014); arXiv: 1311.1857.
Errata: Ссылка [4] должна быть Lim et al 2009, PRD 79, 123526, а не 103526. - «Сферически-симметричные космологические пространства-времени с пылью и излучением – численная реализация»
W.C. Лим, М. Регис, К. Кларксон, Журнал космологии и физики астрономических частиц , 10 , 010 (17pp) (2013); arXiv: 1308. 2 член должен иметь обратный знак. Ссылку [15] следует называть Lim et al, PRD 79, 123526 (2009).
2 член должен иметь обратный знак. Ссылку [15] следует называть Lim et al, PRD 79, 123526 (2009). - «Решения электромагнитных пиков»
E. Nungesser, W.C. Лим, Классическая и квантовая гравитация , 30 , 235020 (11pp) (2013); arXiv: 1304.2964. - «Спайковые колебания»
J.M. Heinzle, C. Uggla, W.C. Лим, Physical Review D , 86 , 104049 (26pp) (2012); arXiv: 1206.0932.
Ошибка: (2b) неверно.См. [51]. - «Создание неоднородностей материи в общей теории относительности»
А.А. Коли, W.C. Лим, Physical Review Letters , 108 , 191101 (5 стр.) (2012); более длинная версия в arXiv: 1205.2142. - “Будущая асимптотика наклонных космологий Бианки типа II”
S. Hervik, W.C. Лим, П. Сандин, К. Уггла, Классическая и квантовая гравитация , 27 , 185006 (18pp) (2010); arXiv: 1004. 3661.
3661. - «Свойства кинематических особенностей»
А.А. Coley, S. Hervik, W.C. Лим, М.А.Х. МакКаллум, Классическая и квантовая гравитация , 26 , 215008 (8pp) (2009); arXiv: 0907.1620. - «Пики в режиме Mixmaster космологий G_2»
W.C. Лим, Л. Андерссон, Д. Гарфинкль, Ф. Преториус, Physical Review D , 79 , 123526 (15 стр.) (2009); arXiv: 0904.1546.
Исправление: В (A2) показатель степени должен иметь обратный знак: – (tau-tau_0).В последней строке (B2) w должно иметь знак абсолютного значения. - “Эволюция к гладкой вселенной в фазе экпиротического сжатия с w>
1 ”
D. Garfinkle, W.C. Лим, Ф. Преториус, П. Дж. Стейнхардт, Physical Review D , 78 , 083537 (8pp) (2008); arXiv: 0808.0542. - “Новое явное решение спайков – нелокальная составляющая обобщенного
Аттрактор Mixmaster ”
W.C. Лим, Классическая и квантовая гравитация , 25 , 045014 (17pp) (2008); arXiv: 0710. 0628.
0628.
Исправление: третий знак минус в (28) должен быть плюсом. Фактор 4 в (34) не должно быть.
Информационный документ CQG 2007/2008. - «Позднее поведение наклонного типа Бьянки VI-1/9.
модели ”
С. Хервик, Р.Дж. ван ден Хооген, W.C. Лим, А.А. Коли, Классическая и квантовая гравитация , 25 , 015002 (15pp) (2008); arXiv: 0706.3184. - «Позднее поведение наклонных моделей VIh типа Бьянки»
С.Hervik, R.J. ван ден Хооген, W.C. Лим, А.А. Коли, Классическая и квантовая гравитация , 24 , 3859-3895 (2007); гр-qc / 0703038. - “Космический микроволновый фон ограничивает пространственно однородную
космологические модели с космологической постоянной »,
А.А. Коли, W.C. Лим, Классическая и квантовая гравитация , 24 , 889-895 (2007); astro-ph / 0610498. - «Кинематические и вейлевские особенности»,
Вт. К. Лим, С. Хервик, А.А. Коли, Классическая и квантовая гравитация , 24 , 595-604 (2007);
гр-qc / 0608134.
К. Лим, С. Хервик, А.А. Коли, Классическая и квантовая гравитация , 24 , 595-604 (2007);
гр-qc / 0608134. - “Жидкие наблюдатели и космология наклона”,
А.А. Coley, S. Hervik, W.C. Лим, Классическая и квантовая гравитация , 23 , 3573-3591 (2006), гр-qc / 0605128. - “Наклонные космологии Бьянки VII_0 – бифуркация излучения”,
W.C. Лим, Р.Дж. Дили, Дж. Уэйнрайт, Классическая и квантовая гравитация , 23 , 3215-3234 (2006); гр-qc / 0601040. - «Наклон и фантомная космология»,
А.А. Coley, S. Hervik, W.C. Лим, Physics Letters B , 638 , 310-313 (2006); gr-qc / 0512085. - «Позднее поведение вихревых Вселенных Бьянки типа VIII»,
S. Hervik, W.C. Лим, Классическая и квантовая гравитация , 23 , 3017-3035 (2006); гр-qc / 0512070.
Информационный документ CQG 2005/2006.
- «Асимптотические особенности, нарушающие молчание»,
Вт.К. Лим, К. Уггла, Дж. Уэйнрайт, Классическая и квантовая гравитация , 23 , 2607-2630 (2006); gr-qc / 0511139. - “Будущее космологий типа VII0 Бьянки с завихренностью”,
С. Хервик, Р.Дж. ван ден Хооген, W.C. Лим, А.А. Коли, Классическая и квантовая гравитация , 23 , 845–866 (2006); гр-qc / 0509032. - «Асимптотический анализ пространственно неоднородных жестких и сверхжестких
космологии »,
А.А. Коли, W.C. Лим, Классическая и квантовая гравитация , 22 , 3073–3082 (2005); гр-qc / 0506097. - «Асимптотическое молчание типичных космологических особенностей»,
Л. Андерссон, Х. ван Эльст, W.C. Лим, К. Уггла, Physical Review Letters , 94 , 051101 (4 стр.) (2005); gr-qc / 0402051;
Популярная статья «Тихо в конце» Давиде Кастельвекки в Physical Review Focus , 15 , рассказ 8 (2005).
- “Изотропная сингулярность в неоднородных космологических моделях браны”,
А.А. Coley, Y. He, W.C. Лим, Классическая и квантовая гравитация , 21 , 1311–1342 (2004); gr-qc / 0312075. - «Асимптотическая изотропизация в неоднородной космологии»,
W.C. Лим, Х. ван Эльст, К. Уггла, Дж. Уэйнрайт, Physical Review D , 69, , 103507 (22 стр.) (2004); гр-qc / 0306118. - «Анизотропные вселенные с изотропным космическим микроволновым фоном.
радиация »,
Вт.К. Лим, США Нильссон, Дж. Уэйнрайт, Классическая и квантовая гравитация , 18 , 5583-5590 (2001); гр-qc / 9912001. - “Почти изотропная космическая микроволновая температура не означает почти
изотропная вселенная “,
U.S. Nilsson, C. Uggla, J. Wainwright, W.C. Лим, Астрофизический журнал , 522 , L1 – L3 (1999); astro-ph / 92.
Материалы конференции:
- «Общий релятивистский наклон и темная энергия»,
А. А. Коли, С. Хервик, W.C. Лим, AIP Conf. Proc. , 1083 ,
65-73 (2008).
А. Коли, С. Хервик, W.C. Лим, AIP Conf. Proc. , 1083 ,
65-73 (2008). - «Космологические модели с точки зрения динамических систем»,
Дж. Уэйнрайт, W.C. Лим, Журнал гиперболических дифференциальных уравнений , 2 , 437-470 (2005); гр-qc / 0409082.
Конкурс сочинений:
- “Космология: взгляд с высоты птичьего полета”, почетное упоминание в Gravity Research.
Фонд конкурса сочинений, 2006 г.
А.А. Коли, С. Хервик, W.C. Лим, Международный журнал современной физики D , 15 , 2187-2190 (2006), гр-qc / 0605089.
Презентации на конференциях и семинарах:
- «Монотонные функции в моделях Бианки со скалярным полем»,
представлен на
- Конференция по случаю 60-летия Йорга Фрауэндинера, Университет Отаго, 29 августа 2018 г.
- Коллоквиум NZMS в Университете Отаго, 4-6 декабря 2018 г.
- 10-я Австралазийская конференция по общей теории относительности и гравитации в Университете Виктории, Веллингтон, 10-12 декабря 2019 г.

- «Динамика спайка вблизи пространственноподобных особенностей», представлены в KTH, Стокгольм, 26 апреля 2018 г., и на 2-м семинаре «Особенности общей теории относительности и их квантовая судьба», Банахский математический центр, Варшава, 21-25 мая 2018 г.
- “Точные решения спайков G_1 в общей теории относительности”,
представлен на
- 9-я Австралийская конференция по общей теории относительности и гравитации в Центре гравитационных открытий, Гингин, 27-30 ноября 2017 г.
- Коллоквиум NZMS в Оклендском университете, 5-7 декабря 2017 г.
- 6-я встреча ANZAMP, Такапуна, 30 января – 1 февраля 2018 г.
- «Резкая релятивистская динамика вблизи пространственноподобных особенностей», представлена на коллоквиуме NZMS в Университете Виктории, Веллингтон, 5-7 декабря 2016 г.
- “Спайковое решение без OT G_2”,
представлен на
- 8-я Австралазийская конференция по общей теории относительности и гравитации в Университете Монаша, Мельбурн, 2-4 декабря 2015 г.

- 16-я Канадская конференция по общей теории относительности и релятивистской астрофизике в Ванкувере, 6-8 июля 2016 г.
- 21-я Международная конференция по общей теории относительности и гравитации в Колумбийском университете в Нью-Йорке, 10-15 июля 2016 г.
- 8-я Австралазийская конференция по общей теории относительности и гравитации в Университете Монаша, Мельбурн, 2-4 декабря 2015 г.
- «Демонстрация феномена спайка с использованием моделей LTB»,
представлен на
- Конференция Centennial GRG в Государственном университете Пенсильвании в Государственном колледже, штат Пенсильвания, 8–12 июня 2015 г.
- коллоквиум NZMS в Университете Мэсси, Палмерстон-Норт, 3-5 декабря 2019 г.
- «Остроконечные неоднородные точные решения в общей теории относительности», представлен на Конгрессе Австралийского института физики в ANU, Канберра, 8 декабря 2014 г.
- «Наклон, всплески и образование сверхплотности материи»,
представлен на 7-й Австралазийской конференции по общей теории относительности и гравитации на острове Гамильтон, 10 декабря 2013 г.

- «БКЛ сингулярность, пики и неоднородная космология», представлена в программе ИИГС «Общая математическая теория относительности» 26 ноября 2013 г.
- «Генерация неоднородностей материи в общей теории относительности», представлена на 13-й встрече Марселя Гроссмана в Стокгольме 1-6 июля 2012 г. Более новая версия представлена на 20-й Международной конференции по общей теории относительности и гравитация в Варшаве, 7-13 июля 2013 г.
- «Динамика вблизи пространственноподобных особенностей более неоднородна, чем предполагал БКЛ»,
представлен на
- Семинар SFB в AEI, 25 октября 2010 г.
- Шведская встреча GR в Карлстаде, 3-4 декабря 2010 г.
- Семинар по космологии Кейптаунского университета, 22 февраля 2011 г.
- Практикум “Динамика общей теории относительности: аналитический и численный подходы”, в Институте математической физики Эрвина Шредингера, Вена, 20 июля 2011 г.
- 6-я Австралазийская конференция по общей теории относительности и гравитации в Квинстауне, 11 февраля 2012 г.

- «Спайковые пересечения в пространстве-времени с одним векторным полем Киллинга», представлен на 19-й Международной конференции по общей теории относительности и гравитация в Мехико, 5-9 июля 2010 г.Получил награду С. Чандрасекара за лучшую постдокторскую презентацию на всех сессиях общей математической теории относительности. (A1 Точные решения и их интерпретация, A2 Математическая теория относительности и другие достижения классической гравитации, A3 Модифицированные теории гравитации).
- «Колючая динамика Mixmaster», представленная на 13-й канадской
Конференция по общим
Теория относительности и релятивистская астрофизика в Калгари, 16-18 мая 2009 г.
Также представлен на мини-конференции по Атлантической теории относительности в
Фредериктон, 25 апреля 2009 г .;
на 12-й встрече Марселя Гроссмана в Париже 13-18 июля 2009 г .;
и на конференции “Новые разработки в лоренцевой геометрии” в Берлинском техническом университете 18-20 ноября 2009 г.

- «Шипы – нелокальная составляющая обобщенного аттрактора Миксмастера», представлены на семинаре по геометрическому анализу и гравитации в АЕИ 29 сентября 2008 г. Также представлены на семинаре по геометрии, анализу и общей теории относительности, в Институте Миттаг-Леффлера, Стокгольм, ноябрь 2008 г. Также представлен на семинаре по нелинейному анализу Свободного университета, Берлин, 15 июля 2010 г.
- «Пики в режиме Mixmaster космологий G_2», представлен на 11-м Восточном собрании по гравитации в Государственном колледже, штат Пенсильвания, 12-13 мая 2008 г.
- «Неоднородный миксмастер и шипы», представленный на открытии IGC конференция в Государственном университете Пенсильвании в Государственном колледже, Пенсильвания, 9-11 августа, 2007 г.
- «Кинематика и особенности Вейля», представленная на 12-й канадской
Конференция по общей теории относительности и релятивистской астрофизике в г.
Фредериктон, 17-19 мая 2007 г.
Также представлен на 18-й Международной конференции по общей теории относительности.
 и гравитация в Сиднее, Австралия, 8-13 июля 2007 г.
и гравитация в Сиднее, Австралия, 8-13 июля 2007 г. - “Жидкие наблюдатели и космология наклона”, представленная на Мини-конференция по атлантической теории относительности во Фредериктоне, 6 мая 2006 г.Также представлен на 2-м Международном совещании по гравитации и Космология в Санта-Кларе, Куба, 29 мая – 1 июня 2006 г., и в Встреча APCTP-TPI в Университете Альберты, 18-23 декабря 2006 г.
- «Динамический системный подход к неоднородной космологии», представленный на семинар по динамическим системам для глобальных задач математики Теория относительности, 12-25 сентября 2005 г., Институт Исаака Ньютона. Математические науки, Кембриджский университет.
- «Колючие пространственные неоднородности», представленная на 11-й канадской
Конференция по общим
Теория относительности и релятивистская астрофизика в Ванкувере, 19-21 мая 2005 г.Также был представлен на мини-конференции по Атлантической теории относительности во Фредериктоне,
30 апреля 2005 г.

- «Асимптотическая изотропизация в неоднородной космологии», представленная на 10-я Канадская конференция по всеобщему Теория относительности и релятивистская астрофизика в Гвельфе, 28-31 мая 2003 г.
- «Возмущения моделей Фридмана-Леметра: ограничения и ловушки », представленный на 9-й Канадской конференции по общим вопросам Теория относительности и релятивистская астрофизика в Эдмонтоне, 24-26 мая 2001 г.
Поддерживает Вой Чет Лим. Последнее обновление 5 августа 2021 г.
| 2021 | ||
| 10. | Элиза Риветт, Лим Хео, Майкл Фейг, Эрик Хегг: Биосинтез и торговля гема o и гема a: новые структурные идеи и их значение для механизмов реакции и переноса пренилированного гема Критические обзоры в биохимии и молекулярной биологии (2021) хх , 1957668 Абстрактный PDF | |
9. | Лим Хео, Джакомо Янсон, Майкл Фейг: Уточнение структуры белков на основе физики в эпоху искусственного интеллекта Белки (2021) в печати , Абстрактный PDF | |
| 8. | Лим Хео, Коллин Ф. Арбор, Джакомо Янсон, Майкл Фейг: Улучшенные стратегии отбора проб для уточнения модели белка на основе моделирования молекулярной динамики Журнал химической теории и вычислений (2021) 17 , 1931-1943 Абстрактный PDF | |
| 2020 | ||
| 7. | Лим Хео, Майкл Фейг: Моделирование белков тяжелого острого респираторного синдрома Коронавируса 2 (SARS-CoV-2) с помощью машинного обучения и уточнения на основе физики bioRxiv (2020) 2020.03.25.008904 , Абстрактный PDF | |
| 6. | Лим Хео, Майкл Фейг: Высокоточные белковые структуры за счет объединения машинного обучения с уточнением на основе физики Белки (2020) 88 , 637-642 Абстрактный PDF | |
| 2019 | ||
5. | Лим Хео, Коллин Ф. Арбор, Майкл Фейг: Доведено до почти экспериментальной точности путем уточнения с помощью моделирования молекулярной динамики Белки (2019) 87 , 1263-1275 Абстрактный PDF | |
| 2018 | ||
| 4. | Лим Хео, Майкл Фейг: Экспериментальная точность уточнения структуры белка с помощью моделирования молекулярной динамики Труды Национальной академии наук, США (2018) 115 , 13276-13281 Абстрактный PDF | |
| 3. | Берсем Дутагачи, Лим Хео, Майкл Фейг: Уточнение структуры мембранных белков с помощью моделирования молекулярной динамики Белки (2018) 86 , 738-750 Абстрактный PDF | |
| 2. | Лим Хео, Майкл Фейг: PREFMD: веб-сервер для уточнения структуры белка с помощью моделирования молекулярной динамики Bioinformatics (2018) 34 , 1063-1065 Абстрактный PDF | |
1. |

 Параллельное чтение расписаний на русском и английском ускорят запоминание в несколько раз. Ваша задача – один раз написать и просто просматривать записи каждый день, а остальное за вас сделает зрительная память. Распечатайте готовый шаблон расписания и впишите туда свои занятия на английском
Параллельное чтение расписаний на русском и английском ускорят запоминание в несколько раз. Ваша задача – один раз написать и просто просматривать записи каждый день, а остальное за вас сделает зрительная память. Распечатайте готовый шаблон расписания и впишите туда свои занятия на английском Есть и такие предметы, которых нет у нас. Например, Citizenship (основы правовой ответственности) и «Religious Education» (религиозное воспитание).
Есть и такие предметы, которых нет у нас. Например, Citizenship (основы правовой ответственности) и «Religious Education» (религиозное воспитание).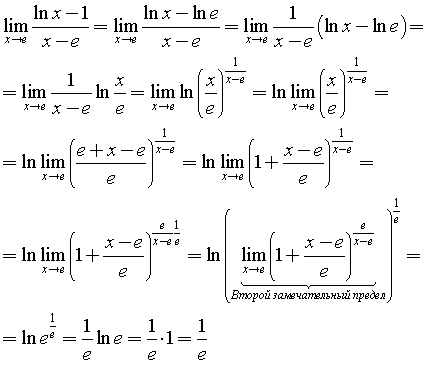 Я также являюсь заведующим кафедрой.
Я также являюсь заведующим кафедрой. , Лим, Э.А. и Тасинато, Г., 26 января 2021 г., В: Physical Review D. 103, 2, 023532. Результат исследования: Материалы для журнала – Статья – экспертная оценка. DOI: https://doi.org/10.1103/PhysRevD.103.023532
, Лим, Э.А. и Тасинато, Г., 26 января 2021 г., В: Physical Review D. 103, 2, 023532. Результат исследования: Материалы для журнала – Статья – экспертная оценка. DOI: https://doi.org/10.1103/PhysRevD.103.023532 Y., Helfer, T.И Лим Э.А., 10 января 2020 г., В: Журнал космологии и физики астрономических частиц. 2020, 1, 027. Результат исследования: Материалы для журнала – статья – рецензирование. DOI: https://doi.org/10.1088/1475-7516/2020/01/027
Y., Helfer, T.И Лим Э.А., 10 января 2020 г., В: Журнал космологии и физики астрономических частиц. 2020, 1, 027. Результат исследования: Материалы для журнала – статья – рецензирование. DOI: https://doi.org/10.1088/1475-7516/2020/01/027 , Гарсия, М.А.Г. и Амин, М.А., 26 февраля 2019 г., В: Physical Review D (Частицы, поля, гравитация и космология). 99, 4, с. 1-8 044046. Результат исследования: Материалы для журнала – статья – рецензирование.DOI: https://doi.org/10.1103/PhysRevD.99.044046
, Гарсия, М.А.Г. и Амин, М.А., 26 февраля 2019 г., В: Physical Review D (Частицы, поля, гравитация и космология). 99, 4, с. 1-8 044046. Результат исследования: Материалы для журнала – статья – рецензирование.DOI: https://doi.org/10.1103/PhysRevD.99.044046 , Марш, Д. Дж. Э., Клаф, К. А., Фэйрберн, М., Лим, Э. и Бесеррил, Р., 29 марта 2017 г., В: Journal of Cosmology and Astroparticle Physics. 2017, 3, 55. Результат исследования: Материалы для журнала – статья – рецензирование. DOI: https: // doi.org / 10.1088 / 1475-7516 / 2017/03/055
, Марш, Д. Дж. Э., Клаф, К. А., Фэйрберн, М., Лим, Э. и Бесеррил, Р., 29 марта 2017 г., В: Journal of Cosmology and Astroparticle Physics. 2017, 3, 55. Результат исследования: Материалы для журнала – статья – рецензирование. DOI: https: // doi.org / 10.1088 / 1475-7516 / 2017/03/055 Сентябрь 2008 г. – декабрь 2011 г.
Сентябрь 2008 г. – декабрь 2011 г. Чандрасекара
за лучшую постдокторскую презентацию на всех занятиях по общей математической теории относительности
(A1 Точные решения и их интерпретация,
A2 Математическая теория относительности и другие достижения классической гравитации,
A3 Modified Gravity Theories) на 19-й Международной конференции по общей теории относительности
и гравитация в Мехико, 5-9 июля 2010 г.
Чандрасекара
за лучшую постдокторскую презентацию на всех занятиях по общей математической теории относительности
(A1 Точные решения и их интерпретация,
A2 Математическая теория относительности и другие достижения классической гравитации,
A3 Modified Gravity Theories) на 19-й Международной конференции по общей теории относительности
и гравитация в Мехико, 5-9 июля 2010 г. 02747.
02747.  Последнее предложение в абзаце перед (49) должно относиться к n_10 и n_30.
Ссылка [15] должна быть Lim et al 2009, PRD 79, 123526, а не 103526.
Последнее предложение в абзаце перед (49) должно относиться к n_10 и n_30.
Ссылка [15] должна быть Lim et al 2009, PRD 79, 123526, а не 103526. 2 член должен иметь обратный знак. Ссылку [15] следует называть Lim et al, PRD 79, 123526 (2009).
2 член должен иметь обратный знак. Ссылку [15] следует называть Lim et al, PRD 79, 123526 (2009). 3661.
3661. 0628.
0628.  К. Лим, С. Хервик, А.А. Коли, Классическая и квантовая гравитация , 24 , 595-604 (2007);
гр-qc / 0608134.
К. Лим, С. Хервик, А.А. Коли, Классическая и квантовая гравитация , 24 , 595-604 (2007);
гр-qc / 0608134.

 А. Коли, С. Хервик, W.C. Лим, AIP Conf. Proc. , 1083 ,
65-73 (2008).
А. Коли, С. Хервик, W.C. Лим, AIP Conf. Proc. , 1083 ,
65-73 (2008).




 и гравитация в Сиднее, Австралия, 8-13 июля 2007 г.
и гравитация в Сиднее, Австралия, 8-13 июля 2007 г.