Лим что такое в математике: «Что такое lim в математике?» — Яндекс Кью

Предел функции. Лекция 5 – презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Ащеулова Алена Сергеевна,
кандидат физико-математических наук
Пусть функция f, принимающая действительные значения,
определена в некоторой окрестности точки x0, кроме, быть может,
самой точки x0.
Функция f имеет предел в точке x0, если для любой
последовательности точек xn, n = 1, 2,…, xn ≠ x0, стремящейся к
точке x0, последовательность значений функции f (xn) сходится к

одному и тому же числу А, которое и называется пределом
функции f в точке x0, (или при x → x0) при этом пишется
у
lim f ( x) A.
А
О
x x0
х0
х
Число А называется пределом функции f в точке x0, если для любого
числа ε > 0 существует такое число δ > 0, что для всех
точек х ≠ x0, удовлетворяющих условию |х — x0| < δ,
x ≠ x0, выполняется неравенство |f (x) — A| < ε
lim f ( x) A.
x x0
у
А+ε
А
А-ε
О
х0
х0-δ
х0+δ
х
Все основные элементарные функции: постоянные, степенная функция (хα),
показательная
функция
(ax),
тригонометрические
функции
(sinx, cosx, tgx и ctgx) и обратные тригонометрические функции

(arcsinx, arccosx, arctgx и arcctgx) во всех внутренних точках своих областей
определения имеют пределы, совпадающие с их значениями в этих точках.
у= x2
lim y 4
x 2
Предел
функции
при
x→2
(при x→2 значения функции → 4).
y=x
равен
4
Предел функций
равен 0.
при x → 0
Если функции f (x) и g (x) имеют конечные пределы в точке a, причем
lim f ( x) A
x a
То
lim g ( x) B
x a
lim f ( x) g ( x) A B
x a
lim f ( x) g ( x) A B
x a
f ( x) A
lim
x a g ( x)
B
если B ≠ 0 и если g (x) ≠ 0 в δ-окрестности точки a.
lim x 2 5 x 8
x 5 x 8 x 3
3 5 3 8 9 15 8 2
lim 2
2
0, 2
2
x 3 x x 4
3 3 4
9 3 4 10
lim x x 4
2
x 3
lim sin x
x
2
lim cos 2 x
x
2
x 0,5 x
lim
2
При нахождении предела иногда сталкиваются с неопределенностями
вида
0
0
0
,
,
,
1
,
0
,
0
,
.
0
Отыскание предела
неопределенности.
в
таких
случаях
называется
Для того, чтобы раскрыть неопределенность
числитель и знаменатель на х в старшей степени.
необходимо разделить
2 x 2 3x 5
2
2 x 2 3 x 5 разделим
x
lim
lim
lim
2
2
x 1 x 3 x 2
x
x
1 x 3x
на x
0
0
x2
3 5
2 2
x x 2
lim
x 1
1
3
3
x2 x
0
0
раскрытием
2 x 2 3x 5
2 2
2
x
x
x
1
x 3x 2
2 2
2
x
x
x
7 x 3 15 x 2 9 x 5
lim
4
2
x
5x 7 x 5
3x 2 6 x 5
lim
x
x 5
x 4 6 x 2 12
lim 4
x 4 x 4 х 3
x 4 6 x 2 12
lim 4
x 4 x 4 х 3
3 x 2 12 x 9
lim
2
x 4 x х 4

English     Русский Правила

Производные и лимы(lim), выполненное решение задач по высшей математике на Автор24

выполнено на сервисе Автор24

Студенческая работа на тему:

Производные и лимы(lim)

Как заказчик описал требования к работе:

Задание: сделать решение задач по высшей математике за 2 дня, красиво оформить. Сколько стоит решение задач пишите точно.

Стоимость
работы

20 ₽

Заказчик не использовал рассрочку

Гарантия сервиса
Автор24

20 дней

Заказчик принял работу без использования гарантии

Производные и лимы(lim).jpg

Общая оценка

5

Положительно

Выполнено очень качественно, с приложенной теорией и пояснением, в срок. Очень доволен!

Хочешь такую же работу?
Зарегистрироваться

Тебя также могут заинтересовать

по этому предмету по этому типу и предмету

ЭКЗАМЕН по Выш. Мат. по рядам и диф.уравнениям

Контрольная работа

Высшая математика

Стоимость:

300 ₽

математика на базе 10-11 классов

Другое

Высшая математика

Стоимость:

300 ₽

Экспериментально-статистические методы математического описания

Реферат

Высшая математика

Стоимость:

300 ₽

Общее решение математической модели волнового движения. Метод Фурье

Курсовая работа

Высшая математика

Стоимость:

700 ₽

Выполнить работу по математике на фото (16 вариант)

Контрольная работа

Высшая математика

Стоимость:

300 ₽

Функции нескольких переменных в экономике

Реферат

Высшая математика

Стоимость:

300 ₽

Расчётная работа по мат. анализу.

Решение задач

Высшая математика

Стоимость:

150 ₽

Контрольная работа по математике. 1-ый курс.

Контрольная работа

Высшая математика

Стоимость:

300 ₽

Дискретная математика. Синтез комбинационных схем

Курсовая работа

Высшая математика

Стоимость:

700 ₽

Решение математических задач

Решение задач

Высшая математика

Стоимость:

150 ₽

Задачи по Рябушко

Решение задач

Высшая математика

Стоимость:

150 ₽

математика ( 1768)

Контрольная работа

Высшая математика

Стоимость:

300 ₽

Дискретная математика

Решение задач

Высшая математика

Стоимость:

150 ₽

Область сходимости функциональных рядов

Решение задач

Высшая математика

Стоимость:

150 ₽

Решение задач математика

Решение задач

Высшая математика

Стоимость:

150 ₽

математика 19в

Решение задач

Высшая математика

Стоимость:

150 ₽

Поставить краевую задачу, применив принцип максимума Понтрягина

Решение задач

Высшая математика

Стоимость:

150 ₽

t критерий стьюдента

Решение задач

Высшая математика

Стоимость:

150 ₽

матрицы алгебра

Решение задач

Высшая математика

Стоимость:

150 ₽

работа с функциями

Решение задач

Высшая математика

Стоимость:

150 ₽

обчислити площу фiгури, обмежену графiком функцiї y = (x + 1)3 + 1, пр

Решение задач

Высшая математика

Стоимость:

150 ₽

зачет по математике 1 курс колледжа

Решение задач

Высшая математика

Стоимость:

150 ₽

𝑥1 + 2𝑥2 + 3𝑥3 = 6; 4𝑥1 − 2𝑥2 − 2𝑥3 = 0; 3𝑥1 + 𝑥2 − 3𝑥3

Решение задач

Высшая математика

Стоимость:

150 ₽

Дискретная математмка

Решение задач

Высшая математика

Стоимость:

150 ₽

Читай полезные статьи в нашем

Предел

Предел функции как один из важнейших разделов математического анализа определяет предельное значение функции, т. е. такое значение, после достижения которого функция уже не существует.
Разберем обозначение «предела»:
Среди данных обозначений х является числовой переменной, которая изменяется на области Х (координатной плоскости оХ и оY). Рассмотрим график простейшей функции на рис.1. Оси графика обра…

подробнее

Сложение и вычитание дробей

С алгебраическими дробями можно проводить любые математические операции, такие как сравнение, сложение, вычитание, умножение, деление и возведение в степень.
Алгебраические дроби с одинаковыми знаменателями складывают по тому же правилу, что и обыкновенные дроби:
т.е. при сложении алгебраических дробей с одинаковыми знаменателями необходимо сложить числители исходных дробей, а знаменатель оставить п…

подробнее

Признаки параллельности прямых

Рассмотрим две прямые

a

и

b

и секущую прямую

сс

.

При их пересечении возникают углы, которые обозначим цифрами от 1 до 8.
У каждого из этих углов есть название, которое часто приходиться употреблять в математике:
Из рассмотренных признаков вытекает параллельность прямых.

подробнее

Простые и составные числа, свойства простых чисел

Значит, для того, чтобы найти делители числа надо найти все натуральные числа, на которые данное делится без остатка. Нетрудно заметить, что число

1

будет являться делителем любого натурального числа.
Чтобы найти наибольший общий делитель двух чисел, необходимо:
Действительно, простое число

17

можно представить в виде произведения множителей только так:

17=1\cdot 17

, а составное число $18=1\cd…

подробнее

Предел

Предел функции как один из важнейших разделов математического анализа определяет предельное значение функции, т. е. такое значение, после достижения которого функция уже не существует.
Разберем обозначение «предела»:
Среди данных обозначений х является числовой переменной, которая изменяется на области Х (координатной плоскости оХ и оY). Рассмотрим график простейшей функции на рис.1. Оси графика обра…

подробнее

Сложение и вычитание дробей

С алгебраическими дробями можно проводить любые математические операции, такие как сравнение, сложение, вычитание, умножение, деление и возведение в степень.
Алгебраические дроби с одинаковыми знаменателями складывают по тому же правилу, что и обыкновенные дроби:
т.е. при сложении алгебраических дробей с одинаковыми знаменателями необходимо сложить числители исходных дробей, а знаменатель оставить п…

подробнее

Признаки параллельности прямых

Рассмотрим две прямые

a

и

b

и секущую прямую

сс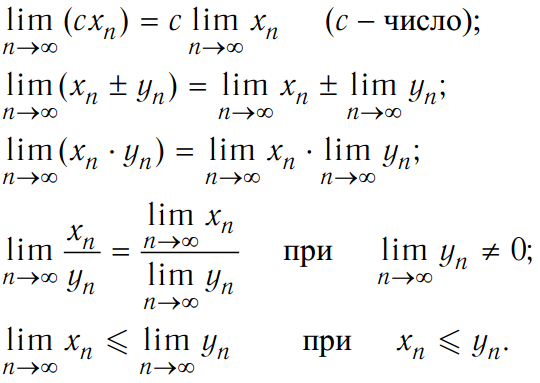

.

При их пересечении возникают углы, которые обозначим цифрами от 1 до 8.
У каждого из этих углов есть название, которое часто приходиться употреблять в математике:
Из рассмотренных признаков вытекает параллельность прямых.

подробнее

Простые и составные числа, свойства простых чисел

Значит, для того, чтобы найти делители числа надо найти все натуральные числа, на которые данное делится без остатка. Нетрудно заметить, что число

1

будет являться делителем любого натурального числа.
Чтобы найти наибольший общий делитель двух чисел, необходимо:
Действительно, простое число

17

можно представить в виде произведения множителей только так:

17=1\cdot 17

, а составное число $18=1\cd…

подробнее

Lim, предел последовательности

Мы уже знаем, что такое арифметическая и геометрическая прогрессия. последовательности значений. Возьмем последовательность a _n = 1/n, если k и м есть натуральные числа, то для каждого k k > a _m , так как чем больше становится, тем меньше становится _n и он всегда положителен, но никогда не достигает нуля. В этом случае мы говорим, что 0 равно
lim a _n->∞ если n->∞, или другой способ записать это lim _n->∞ a _n = 0.

Определение предела

Число а называется пределом последовательности, если для каждого ε > 0 можно найти число п _е , так что для всех членов последовательности a _n с индексом n > n _ε верно, что a – ε n

Основное правило

Если lim _n->∞ a _n = a, a _n -> a a _n – a -> 0 |a _n – a| -> 0

Последовательность не всегда имеет предел, а иногда имеет нереальный предел (-∞ или +∞). Пределы +∞ и -∞ называются нереальными пределами.

Если последовательности a _n и b _n имеют действительные пределы, то последовательности
a _n + b _n , a _n – b _n , a _n .b _n и a _n / b _n также имеют реальный предел и:

Lim _{N -> ∞} (A _N + B _N ) = LIM _{N -> ∞} A _N + LIM _{N -> ∞} B _N
Lim _{N -> ∞} (а _№ -B _N ) = LIM _{N -> ∞} A _N -LIM _{N -> ∞} B _N
LIM _{N -> ∞} (A _N . B _N ) = lim _{n -> ∞} a _n . LIM _{N -> ∞} B _N
LIM _{N -> ∞} (A _N / B _N ) = LIM _{N -> ∞} A _N / LIM _{N -> ∞} b _n
, если b _n ≠ 0 и lim _n->∞ b _n ≠ 0

Если _n n для каждого натурального n и lim _n->∞ a _n = a,
lim _n->∞ b _n = b тогда а ≤ б

Если a _n ≤ b _n ≤ c _n или каждый вещественный n и если lim _n->∞ a _n = lim _n->∞ c _n = A
, то lim _n->∞ b _n = A.

Если a _n ≥ 0 и lim _n->∞ a _n = а, тогда последовательность b _n = √a _n также имеет предел и lim _n->∞ √a _n = √a _n .

Если a _n = ¹ / _{n k} и k ≥ 1, тогда lim _n->∞ a _n = 0.

Если -1 n->∞q ⁿ = 0.

lim _n->∞ (1 – 1/n) ⁿ = lim _{n->∞(1 + 1/n) ⁿ⁺¹} = e
(1+1/n) ⁿ н-1

e – число Непера.

Если последовательность a _n имеет нереальный предел (-∞ или +∞ ) то последовательность 1/a _n имеет предел и lim _n->∞ ¹ / _{a n} = 0

Если последовательности a _n и b _n имеют нереальные пределы и lim _n->∞ a _n =+∞, lim _n->∞ b _n =+∞ тогда:

lim _n->∞ (a _n + b _n ) = +∞
LIM _{N-> ∞} (A _N . B _N ) = +∞
LIM _{N-> ∞} A _N ^K = +∞, если K> 0
LIM _{N-> ∞} a _n ^k = 0; если к lim _n->∞ -a _n = -∞

Лим проблемы

Упражнение 1:
Если a ⁿ = 5,4 ⁿ , lim _n->0 a _n = ?

Ответ:
lim _n->0 a _n = lim _n->0 5 . lim _n->0 4 ⁿ = 5 . 4 ⁰ = 5,1 = 5

Упражнение 2:

Если n =

3n 2 + 1 2n – n 2

затем lim n->∞a n = ?

Ответ:

lim n->∞

3n 2 + 1 2n – n 2

= lim n->∞

.

3 + 1/н 2 2/н – 1

= lim n->∞

3 + 0 0 – 1

= -3

Упражнение 3:

Если lim a n ->1 =

2а н 2 – а н – 1 а н – 1 1 = ? Ответ: lim a n ->1 = 2а н 2 – а н – 1 а п – 1 = lim a n ->∞ (a n – 1)(2a n + 1) a n – 1 = = lim a n -> 1 (2a n + 1) = 3 Плоттер предельных графиков Подробнее о lim на математическом форуме Регистрация на форуме Невозможность смежных нечетных чисел ни в одном цикле Коллатца? Восстановление надлежащего баланса углеродного цикла Земли Развитие физики ДОКАЗАТЕЛЬСТВО ГИПОТЕЗЫ БИЛА Эффективное использование бюджета Какие есть хорошие учебники по математике для студентов, изучающих математику? Ошибка в программе итеративного углубления поиска в глубину Как проверить, не имеет ли задача поиска решения в глубине limi Pycharm продолжает падать Может ли массовая гибернация помочь спасти человечество? limit – Как произносится обозначение $\lim\limits_{x \to \infty \\ y \to \infty} F(x, y) = 1$ Задавать вопрос спросил 4 года, 6 месяцев назад Изменено 2 года, 10 месяцев назад Просмотрено 582 раза $\begingroup$ Как следующие обозначения читаются на простом английском языке: $$\lim\limits_{x \to \infty \\ y \to \infty} F(x, y) = 1$$ Насколько я можно прочитать: Если $x$ и $y$ приближаются к $\infty$, значение функции $F(x, y)$ приближается к $1$. т.е. Значение функции $F(x, y)$ равно $1$ где-то рядом, но до $(x, y) = (\infty, \infty)$. $Предел$ функции $F(x, y)$ равен $1$ при $(x, y) = (\infty, \infty)$. пределы обозначения произношение $\endgroup$ 4 $\begingroup$ (1) правильно. (2) и (3) нет. То, что вы пишете как “$(\infty, \infty)$”, не имеет смысла. Бесконечность — это не число, и места с такими координатами нет, поэтому нет смысла спрашивать там значение $F$. 92 + 1} . $$ Правка. На самом деле существует некоторая двусмысленность в отношении того, рассматриваем ли мы две переменные $x$ и $y$ как независимо большие и положительные, или же ОП намеревается спросить о том, что происходит, когда $||(x,y)|| $ большой. В любом случае (2) и (3) не имеют смысла. Оставить комментарий Отменить ответ Для отправки комментария вам необходимо авторизоваться. Меню Поиск: