Сучков Николай Михайлович | Институт математики и фундаментальной информатики СФУ
доктор физико-математических наук, профессор
тел.: (391) 206-20-76, 206-28-27
e-mail:
адрес: пр. Свободный, 79, ауд. 34-17
год рождения: 1950
Место работы и должность
Образование
- Красноярский государственный университет — Математика, квалификация “Математик”, 1972 г., тема дипломной работы: «О свободной группе ранга 2 многообразия, порожденным группой Судзуки»
Стаж работы (полных лет)
- Общий: 45
По специальности: 45
Научные направления, профессиональные интересы
Диссертации
- Кандидатская диссертация
- Автоморфно факторизуемые группы — 1979 г.
- Докторская диссертация
- Бесконечные дважды транзитивные группы и группы с инволюциями — 2003 г.
Преподаваемые дисциплины
- Алгебра
- Высшая математика
Награды
- Министерская грамота
Членство в научных, профессиональных, общественных организациях
- Член диссертационного совета Д 212.

Публикации
Последние публикации:
- О ПОДГРУППАХ ГРУППЫ Lim(N) : научное издание [статья из журнала]
2020, Сибирские электронные математические известия
- ON SUBGROUPS OF GROUP LIM(N) : научное издание [статья из журнала]
2020, SIBERIAN ELECTRONIC MATHEMATICAL REPORTS-SIBIRSKIE ELEKTRONNYE MATEMATICHESKIE IZVESTIYA
- NORMAL CLOSURES OF ELEMENTS IN GROUP LIM(N) : научное издание [статья из журнала]
2019, SIBERIAN ELECTRONIC MATHEMATICAL REPORTS-SIBIRSKIE ELEKTRONNYE MATEMATICHESKIE IZVESTIYA
- Locally Finite Suzuki-Higman 2-Groups : сборник научных трудов [статья из журнала]
2018, ALGEBRA AND LOGIC
- Локально конечные 2-группы Сузуки-Хигмана : научное издание [статья из журнала]
2017, Алгебра и логика
- О ЛОКАЛЬНО КОНЕЧНОМ РАДИКАЛЕ ГРУППЫ ОГРАНИЧЕННЫХ ПОДСТАНОВОК [статья из журнала]
2016, Труды института математики и механики УрО РАН
- О НОРМАЛЬНЫХ ПОДГРУППАХ ГРУПП ОГРАНИЧЕННЫХ ПОДСТАНОВОК [статья из журнала]
2015, Сибирские электронные математические известия
- О ПОРОЖДАЮЩИХ ГРУПП ПОДСТАНОВОК С КОНЕЧНЫМИ ПАРАМЕТРАМИ РАССЕИВАНИЯ [статья из журнала]
2014, Сибирские электронные математические известия
- On uniform permutations with finite dispersion parameters [статья из журнала]
- О РАВНОМЕРНЫХ ПОДСТАНОВКАХ С КОНЕЧНЫМИ ПАРАМЕТРАМИ РАССЕИВАНИЯ [статья из журнала]
2013, Труды института математики и механики УрО РАН
- Аналитическая геометрия : методическое пособие [методическое пособие]
2012
- Группы подстановок с конечными параметрами рассеивания [статья из журнала]
2012, Журнал Сибирского федерального университета.
 Серия: Математика и физика
Серия: Математика и физика - Бесконечные группы с инволюциями [монография]
2011
- О группах ограниченных подстановок [статья из журнала]
2010, Журнал Сибирского федерального университета. Серия: Математика и физика
- Влияние потоков прямого ино странного инвестирования на динамику развития экономики России : научное издание [статья из журнала]
2007, Вестник Красноярского государственного аграрного университета
- On classes of infinite groups with involutions [статья из журнала]
2005, ACTA APPLICANDAE MATHEMATICAE
- Бесконечные дважды транзитивные группы подстановок и группы с инволюциями : автореферат диссертации на соискание ученой степени доктора физико-математических наук [автореферат диссертации]
2003
- О периодических группах с абелевыми централизаторами инволюций [статья из журнала]
2002, Математический сборник
- On periodic groups with Abelian centralizers of involutions [статья из журнала]
2002, SBORNIK MATHEMATICS
- О НЕКОТОРЫХ БЕСКОНЕЧНЫХ РАСЩЕПИМЫХ (B, N)-ПАРАХ РАНГА 1 : научное издание [статья из журнала]
2001, Доклады Академии наук
- On the number of generating pairs for the groups L2(2m) and Sz(22k+1) : научное издание [статья из журнала]
2001, Siberian Mathematical Journal
- Finiteness of Some Sharply Doubly Transitive Groups [статья из журнала]
2001, Algebra and Logic
- On some infinite split (B, N)-pairs of rank 1 [статья из журнала]
2001, DOKLADY MATHEMATICS
- О бесконечных группах с заданной сильно изолированной 2-подгруппой [статья из журнала]
- On infinite groups with a given strongly isolated 2-subgroup [статья из журнала]
2000, MATHEMATICAL NOTES
- Структурные и характеризационные проблемы теории групп лиевых типов и ее приложений : отчет о НИР [отчёт о НИР]
1996
Список публикаций сформирован в автоматическом режиме. Сообщите, если заметили неточности.
Сообщите, если заметили неточности.
Наиболее значимые публикации:
- Сучков Н.М. Пример смешанной группы, факторизуемой двумя периодическими подгруппами. Алгебра и логика. 1984, т. 23, №5, с. 573-577.
- Сучков Н.М. О периодических группах с абелевыми централизаторами инволюций. Математический сборник. 2002, т. 193, №2, с. 153-160.
- Созутов А.И., Сучков Н.М., Сучкова Н.Г., Бесконечные группы с инволюциями, Красноярск, Сибирский федеральный университет, 2011, 149 с..(монография)
Всего публикаций: 80.
Ссылка на профиль в Scopus
Ссылка на профиль в Академии Google
Урок 8. предел функции на бесконечности – Алгебра и начала математического анализа – 11 класс
Урок Конспект Дополнительные материалыПредел функции на бесконечности
Найдите предел функции:
ПодсказкаПрименить свойство нахождения предела от произведения
$$ \lim_{x\to\infty} ((\frac {1}{x} -1)\cdot( \frac{5}{x^2} -4 )) = $$ -4 4 1 5
Предел функции на бесконечности
Найдите предел функции:
$\lim_{x\to \infty} \frac{5x^{3}-3}{x^{3}-2}$
ПодсказкаПрименить свойство нахождения предела от частного
Предел функции на бесконечности
Поставьте в соответствие пределу его решение:
ПодсказкаПрименить свойство нахождения предела от произведения
Предел функции на бесконечности
Найдите предел функции:
ПодсказкаПрименить свойство нахождения предела от суммы
Предел функции на бесконечности
Найдите предел заданной функции
ПодсказкаПрименить свойство нахождения предела от частного
$$\lim_{x\to\infty} \frac {-7x^3+3}{x^3 -2}$$
$$\lim_{x\to\infty} \frac {9x^3+4}{3x^2 -2}$$
$$\lim_{x\to\infty} \frac {x^5-3}{2x^5 -2}$$
Предел функции на бесконечности
Подчеркните верный ответ.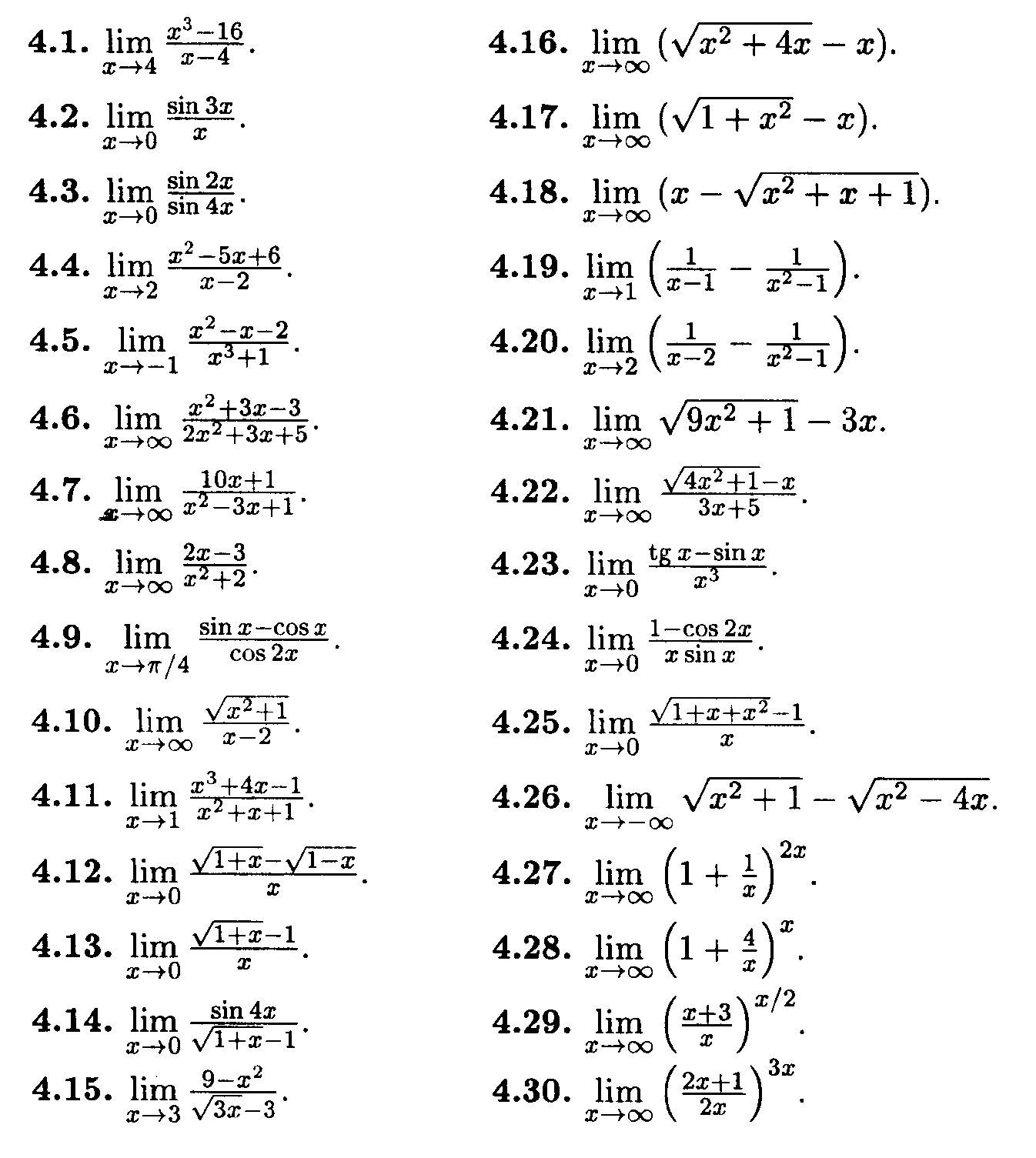
Для функции $ y = \frac {6-x}{x-3} $ найдите вертикальную асимптоту:
Подсказкаобратите внимание на знаменатель
Предел функции на бесконечности
Найдите асимптоты по чертежу:
ПодсказкаВспомнить, что такое горизонтальная и вертикальная асимптоты
Предел функции на бесконечности
Вычислите предел функции $$ \lim_{x\to\infty} \frac {7x^2-3x+10}{8x^3+5} $$
ПодсказкаРазделите числитель и знаменатель дроби на $х^3$ и воспользуйтесь основным свойством нахождения предела от частного
Предел функции на бесконечности
Вычислите предел функции $ \lim_{x\to \infty} \frac{x^{4}-3x^{2}+11}{5x^{4}-9}$
Подсказка Разделите числитель и знаменатель дроби на $х^4$ и воспользуйтесь основным свойством нахождения предела от частного.
Предел функции на бесконечности
Поставьте в соответствие пределу- ответ:
ПодсказкаВ каждом примере разделите числитель и знаменатель на $x$ в самой большой степени
Предел функции на бесконечности
Поставьте в соответствие пределу- ответ:
ПодсказкаВ каждом примере разделите числитель и знаменатель на $х$ в самой большой степени
Формулы и уравнения математического анализа
Формулы и уравнения математического анализа- Предел последовательности
- Арифметическая прогрессия { an } – числовая последовательность a1, a2, … , an, n ∈ N такая, что
∀n > 1, an = an-1 + d (d – разность).
(n > 1). - Геометрическая прогрессия { bn } – числовая последовательность b1, b2, … , bn, n ∈ N такая, что
b1 ≠ 0 и ∀n > 1, bn = bn-1 × q (q – знаменатель).
(n > 1)
, q ≠ 1.
, если 0 < |q| < 1. - Основные определения
{xn} – последовательность xn.
xn = f(n) — формула общего члена последовательности.
— предел последовательности {xn}; если a ∈ R, последовательность {xn} называется сходящейся.
{xn} бесконечно малая последовательность, если .
{xn} бесконечно большая последовательность, если
∀M > 0 ∃N = N(M): ∀n > N(M) ⇒ |xn| > M. - Свойства сходящихся последовательностей
если yn ≠ 0, b ≠ 0; - Если для любого n xn ≤ b, то ≤ b.

Если для любого n xn ≥ b, то ≥ b.
Если для любого n xn ≤ yn ≤ zx и то
где {an} – бесконечно малая последовательность. - Свойства бесконечно малых и бесконечно больших последовательностей (б.м.п. и б.б.п.)
1. Б.м.п. ограничена.
2. Сумма, разность и произведение двух б.м.п. есть также б.м.п.
3. Произведение ограниченной последовательности на б.м.п. есть также б.м.п.
4. Если элементы б.м.п. {xn} не равны нулю, то
последовательность – б.б.п.
5. Если {xn} – б.б.п. и xn ≠ 0, то
последовательность – б.м.п. - Важные соотношения:
n!=1∙2∙3∙…∙n, формула Стирлинга: при n → ∞ n!≈
Неравенство Бернулли: (1+α)n ≥ 1 + nα, α > -1, n ∈ N.
Формула бинома Ньютона:
- Свойства функций, имеющих предел
- , если пределы f и ϕ существуют.

- , если пределы f и ϕ существуют.
- .
- , если пределы f и ϕ существуют и ≠0.
- f(x) ≤ ϕ(x) ≤
- f(x) ≤ ϕ(x) ≤ g(x), (теорема о пределе промежуточной функции).
- Замечательные пределы
- Первый замечательный предел :
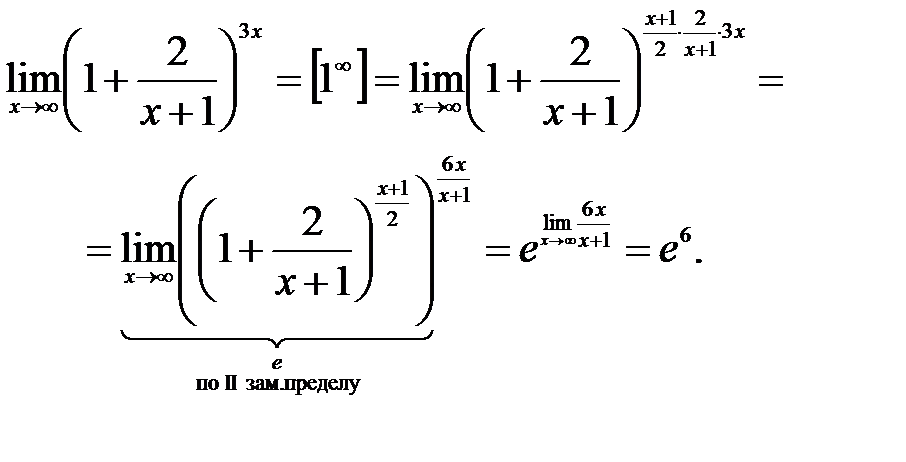
- Второй замечательный предел :
- Таблица производных (с учетом u = ϕ(x))
- .
- (a > 0, a ≠ 1) .
- (a > 0, a ≠ 1) .
- .
- .
- .
- .
- .
- .
- .
- .
- . Гиперболический синус .
- . Гиперболический косинус .
- . Гиперболический тангенс .
- . Гиперболический котангенс .
- Правила вычисления производной n-го порядка
- Производная суммы:
[f(x)+g(x)](n)=f(n)(x)+g(n)(x). x$$
x$$Определение. Пусть — произвольная числовая последовательность. Пусть задана строго возрастающая последовательность натуральных чисел Рассмотрим последовательность Эта последовательность называется подпоследовательностью последовательности .
Упражнения.
1. Пусть последовательность имеет предел . Докажите, что тогда и любая ее подпоследовательность имеет тот же предел .
2. Пусть последовательность разбита на две подпоследовательности и . Докажите, что если и , то и сходится к .
В частности, если последовательности и сходятся к , то и последовательность .
Мы определяли число как предел последовательности
Теперь докажем более общий результат:
По упражнению, имеет место и равенство
если — произвольная последовательность натуральных чисел, растущих вместе с номером до бесконечности.
Пусть теперь пробегает какую-нибудь последовательность значений, стремящихся к ; можно считать также, что все .
 Положим , так что
Положим , так чтоТак как при этом
то
Два крайних выражения могут быть преобразованы так:
причем, в силу того, что
в то время как, очевидно,
таким образом, оба выражения стремятся к общему пределу , а тогда и заключенное между ними выражение также стремится к (по теореме о сжатой последовательности). Это и доказывает наше утверждение.
Для доказательства же утверждения
предположим теперь, что последовательность имеет пределом (причем можно считать все ). Если положить , тогда (и все ). Очевидно,
Так как, по доказанному, первый множитель последнего выражения стремится к , второй же, очевидно, имеет пределом , то и выражение слева стремится к . Формула доказана.
Заменим теперь в выражении переменную на ; если придать последовательность положительных или отрицательных значений, стремящихся к нулю (но не равных нулю), то будет стремиться к .
 10+x+7),-inf)
ans =
0
10+x+7),-inf)
ans =
0 Мы не только можем ввести бесконечность в MATLAB, но и MATLAB может также сказать нам, что результатом ограничения является бесконечность. Например, мы проверяем:
>> syms x; >> limit(1/abs(x)) ans = InfЕсли есть точка разрыва, то предел функции в этой точке не существует. Чтобы иметь дело со случаем, когда функция не является непрерывной при x = a, мы определяем символы для левого и правого пределов функции.
Используйте «left» и «right» в MATLAB, чтобы найти левый и правый пределы.
Если левый предел равен правому пределу, значит, предел функции в этой точке существует.
Например: укажите
Лимита не существует.>> syms x; >> f = (x-3)/abs(x-3); >> a = limit(f,x,3,'left') a = -1 >> b = limit(f,x,3,'right') b = 1Результаты не равны, поэтому ограничения на данный момент не существует.
Следует отметить, что мы также переходим, чтобы ограничить переменную x, используемую для вычисления предела.

Затем мы можем нарисовать изображение функции, чтобы показать прерывность функции, мы устанавливаем домен:
>> ezplot(f,[-1 5])Математика. Строительство – презентация онлайн
4. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ
ФУНКЦИЙ
4.1 Функция. Основные понятия и свойства
4.2 Предел функции
4.3 Непрерывность функции
ФУНКЦИЙ
4.2 Предел функции
4.2.1. Предел функции в точке
4.2.2. Односторонние пределы
4.2.3. Конечный предел функции при бесконечно больших значениях
аргумента
4.2.4. Бесконечный предел функции в точке
4.2.5. Основные теоремы о пределах
4.2.6. Бесконечно малые функции и их свойства
4.2.7. Бесконечно большие функции и их свойства
4.2.8. Теорема о единственности предела
4.2.9. Теорема о пределе сложной функции
4.2.10. Вычисление пределов
4.2.11. Эквивалентные бесконечно малые функции
4.2.6. БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ СВОЙСТВА
Функция y = f(x) называется бесконечно малой функцией (б.
при x a , если
lim f ( x) 0
x a
Замечание.
Никакое, даже очень маленькое, отличное от нуля постоянное
число не может быть б.м.ф.
Свойства бесконечно малых функций.
Функция y = f(x) имеет в точке x a конечный предел А
тогда и только тогда, когда эта функция равна сумме числа А и
б.м.ф. (x) при x a :
lim f ( x) A f ( x) A ( x)
x a
4.2.6. БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ СВОЙСТВА
Далее все б.м.ф. рассматриваются при
x a.
Сумма (разность) конечного числа б.м.ф. есть снова б.м.ф.
Произведение б.м.ф. на ограниченную функцию в окрестности
точки x a есть б.м.ф.
Произведение двух б.м.ф. есть снова б.м.ф.
Частное от деления б.м.ф. на функцию, имеющую отличный от
нуля предел, есть б.м.ф.
4.2.7. БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ И ИХ СВОЙСТВА
Функция y = f(x) называется бесконечно большой функцией
(б.б.ф.) при x a , если
lim f ( x)
x a
Замечание.
Никакое, даже очень большое, постоянное число не может быть
б.б.ф.
Свойства бесконечно больших функций.
Далее все б.б.ф. рассматриваются при
x a.
Произведение двух б.б.ф. есть снова б.б.ф.
Произведение б.б.ф. на функцию, имеющую отличный от нуля
Сумма б.б.ф. и ограниченной функции в окрестности точки
есть б.б.ф.
x a
СВЯЗЬ МЕЖДУ Б.М.Ф. И Б.Б.Ф.
Если f(x) – б.б.ф. при
x a , тогда
Если (x) – б.м.ф. при
x a , тогда
1
f ( x)
1
( x)
– б.м.ф. при
x a .
– б.б.ф. при
x a .
Примеры
1
0;
x x
1) lim x lim
x
1
2) lim x 0 lim .
x 0
x 0 x
НЕОПРЕДЕЛЁННОСТИ
0
0
0
1
0
0
0
4.2.8. ТЕОРЕМА О ЕДИНСТВЕННОСТИ ПРЕДЕЛА
Если предел функции y = f(x) при
единственный.
x a существует, то он
Доказательство:
Самостоятельно, от противного, используйте теорему о
связи функции, её предела и б. м.ф.
м.ф.
4.2.9. ПРЕДЕЛ СЛОЖНОЙ ФУНКЦИИ
lim f ( x) b
Если
x a
и если
lim g ( y) c
y b
, причём
f ( x) b
,
(b и c – конечные),
lim g ( f ( x)) c .
тогда
x a
Замечание.
Это свойство позволяет использовать замену переменной при
вычислении пределов сложных функций.
Пример
0
1
1
2x
y
x
y
2
1
y
y
2
lim
lim
0
lim
lim 3
x
2
x
y y y 3 1 y y y y
1
x
8
3
y
8
0
x
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Вычисление предела:
lim f ( x) A
x x0
начинают с подстановки предельного значения x0 в функцию f(x).
Если при этом получается конечное число, то предел равен этому
числу.
Пример
3 x 1 3 1 1
lim 2
2
2
x 1
x
1
Способы раскрытия неопределённостей
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Правило 1.
Pn x
lim
x Q x
m
Разделить числитель и знаменатель дроби на х в наивысшей
степени.
Примеры
3x 2 1
1) lim
;
x 13 2 x x 2
3×3 x 1
2) lim 2
;
x x 4 x 3
2 x2 7
3) lim
;
x 4 2 x 4 x 2
n 3 ! 2n 1 !
4) lim
.
n 2n ! n 1 !
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Примеры
1 0
3x 2 1
3 2
2
2
3
3x 2 1
x
x
x
lim
lim
3
1) lim
2
x
x
13
2
x 13 2 x x 2
13 2 x x
1
1
x2 x
x2 x2 x2
0 0
3×3 x 1
2) lim 2
x x 4 x 3
3×3 x 1
1 0 1 0
3 3
3 2 3
3
3
x
x
x
x
x
lim
lim 2
x
x
1
4
3
x 4x 3
0
x x 2 x3
x3 x3 x3
0 0 0
2 0 7 0
2×2 7
4
4
2
4
0
2×2 7
x
x
x
x
lim
lim
0
3) lim
4
2
4
2
x
x
4
1
x 4 2 x x
4 2x
x
2
2
4 4
4
x4
x2
x
x
x
0
0
4. 2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Примеры
4)
n 3 ! 2n 1 !
n 3 ! 2n ! 2n 1
lim
lim
n 2n ! n 1 !
n 2n ! n 3 ! n 2 n 1
2n 1
2n 1
lim
lim 2
n n 2 n 1
n n 3n 2
2n 1
2 01 0
2
2
2
0
n
lim 2 n
lim n n 0
n n
n
3 2 1
3n 2
1
2
2 2
2
n 0n 0
n n n
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Правило 2.
Pn x
0
lim
x a Q x
0
m
1 способ: разделить числитель и знаменатель дроби на ( х – ).
2 способ: разложить числитель и знаменатель дроби на множители.
Примеры
3x 2 5 x 2
1) lim1
;
3x 1
x
3
x3 4 x 5
2) lim 3
.
2
x 1 x 2 x x 2
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Примеры
3x 2 5 x 2
0
1) lim1
3x 1
0
x
3
3 x 1 x 2
lim
x
1
3
3x 1
lim1 x 2
x
3
1
1
2 2
3
3
3x 2 5 x 2 0
D 52 4 3 2 49
x1
5 49 2 1
2 3
6 3
5 49 12
2
2 3
6
1
3 x 2 5 x 2 3 x x 2 3 x 1 x 2
3
x2
4. 2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Примеры
x3 0 x 2 4 x 5
x3 x 2
x3 4 x 5
0
2) lim 3
x 1 x 2 x 2 x 2
0
x x 5 x 1
lim
x 2x x 2
2
3
x 1
x
lim
x 1
x 5 x 1
2
x 1
x 1 x 1 x 2
x2 x
5x 5
5x 5
2
2
x 1
x2 4x 5
0
x x 5 x 1
lim
x x 2 x 2
x 1 x 2
x x 5 x 1
x x 5
1
lim
lim
2
x2 x 5
2
2
2
x 1
x 1 x 2
1 5
7
1 1 1 2 6
2
x 1
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Правило 3.
f x
0
lim
x a g x
0
или
lim f x g x
x
(функции f(x) и g(x) содержат корни)
Умножить числитель и знаменатель дроби на сопряжённое
выражение и использовать формулы:
2
2
a
b
a
b
a
b
;
2
2
3
3
a
b
a
ab
b
a
b
.
Примеры
x 1 1
1) lim
;
x 0
3x
2) lim
x
x3 4 x3 2 .
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Примеры
x 1 1
1) lim
x 0
3x
lim
x 0
x 0
3
x 1 1
1
x 1 1
3x
x 1 1
x 1 1
2
x 1 12
3x
lim
0
lim
x 0
0
x 1 1
x 1 1
lim
x 0
3
3x
1
x 1 1
0 1 1
1
6
lim
x 0
3x
x
x 1 1
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Примеры
2) lim
x
lim
x
lim
x
x3 4 x3 2
x3 4 x3 2
x3 4 x3 2
x3 4 x3 2
x3 4 x3 2
x3 4 x3 2
lim
x
lim x 4 x 2
3
x
6
x3 4 x3 2
3
x3 4 x3 2
6
0
ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
sin x
lim
1
x 0
x
Следствия:
x
lim
1
x 0 sin x
lim
x a
sin x
x
sin kx
lim
1
x 0
kx
1, где x б.м.ф. при x a
ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
x
1
lim 1 e
x
x
1
x
lim 1 x e
x 0
Следствия:
1
lim 1
x a
f x
lim 1 x
x a
f x
1
x
e, где f x б. б.ф. при x a
б.ф. при x a
e, где x б.м.ф. при x a
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Правило 4.
f x
0
lim
x a g x
0
(функции f(x) и g(x) содержат
тригонометрические функции)
Применить первый замечательный предел.
Примеры
sin 3 x
1) lim
;
x 0 sin 2 x
tg x 5
2) lim 2
.
x 5 x 25
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Примеры
1)
0
sin 3 x
sin 3 x 3 x
sin 3 x
3x
lim
lim
lim
lim
x 0 sin 2 x
x
0
x
0
x
0
0
sin 2 x 3 x
3x
sin 2 x
3x
2 3x
2x
3
3
1 lim
lim
lim
lim 1 1,5
x 0 sin 2 x
x 0 2 sin 2 x
x 0 sin 2 x x 0 2
2
sin x 5
tg x 5
0
lim
2) lim 2
x
5
x 5 x 25
cos x 5 x 5 x 5
0
sin x 5
1
lim
lim
x 5
x
5
cos x 5 x 5
x 5
1
1
1
1
cos 5 5 5 5 cos 0 10 10
4. 2.11. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ
2.11. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ
(x) и (x) называются эквивалентными бесконечно малыми
функциями при
x a , если
Обозначение:
x x при x a
( x)
lim
1
x a ( x)
Таблица основных эквивалентностей (при
1) sin x
x
2) tg x
x
3) arcsin x
4) arctg x
x2
2
5) 1 cos x
x
x
6) e 1
x
7) a 1
x
x
x ln a
x 0)
8) ln 1 x
x
9) log a 1 x
10)
1 x
k
1
x
ln a
kx
4.2.11. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ
Свойства эквивалентных б.м.ф.
Если (x) ~ (x) и (x) ~ (x) при
то (x) ~ (x) при
x a,
x a.
Предел отношения двух б.м.ф. не изменится, если одну из них
(или обе сразу) заменить эквивалентными б.м.ф., т.е.
если (x) ~ (x) и (x) ~ (x) при
x a , то
( x)
( x)
lim
lim
.
x a ( x )
x a ( x )
Примеры
tg11x
1) lim 7 x ;
x 0 e
1
2) lim
x 0
ln 1 sin 4 x
arcsin x 8 x
2
.
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Примеры
tg11x 11x 11x 0
tg11x
0
1) lim 7 x
7x
x 0 e
1
0
e 1 7 x 7 x 0
11x
11 11
lim
lim
x 0 7 x
x 0 7
7
ln 1 sin 4 x
0
2) lim
2
x 0 arcsin x 8 x
0
ln 1 sin 4 x sin 4 x 4 x 4 x 0
2
2
2
arcsin
x
8
x
x
8
x
x
8x 0
4x
4
4
lim
lim
0,5
x 0 x x 8
x 0 x 8
0 8
0
4x
lim
x 0 x 2 8 x
0
ПРОДОЛЖЕНИЕ СЛЕДУЕТ…Артур Лим | Люди | Кафедра математики
Профессор практики
Образование
Магистр наук, Национальный университет Сингапура, 1994 г.
Доктор философии, Университет Юты, 2001 г.Исследовательская группа
Алгебра и алгебраическая геометрия
Зона исследований
Алгебра и теория представлений
Био
“Вот курсы, которые я разрабатываю и преподаю: ”
— веб-ссылки следуют —
Математика 10350 – Исчисление А
Математика 10360 – Исчисление B
Математика 20480 – Введение в динамические системы для ученых
Научные интересыЯ одинаково увлечен математическими исследованиями и педагогикой.
 Мои математические исследования связаны с комбинаторным матричным анализом и его приложениями. В настоящее время я исследую связь между разностными уравнениями и представлением алгебр Ли с помощью комбинаторных методов.
Мои математические исследования связаны с комбинаторным матричным анализом и его приложениями. В настоящее время я исследую связь между разностными уравнениями и представлением алгебр Ли с помощью комбинаторных методов.Математическая педагогика для меня – это искусство общения. Мне нравится объяснять технические аспекты математики в контексте ее истории и развития. Другой аспект моего педагогического интереса заключается в разработке математических упражнений, которые способствуют более глубокому мышлению и обучению.
Избранные публикации- Межрыночная интеграция и саботаж, с участием Го, Цзяна и Вахариа в «Управлении производством и операциями», 2019 г.
- Кластеры розничной торговли в развивающихся странах, с Чжао, Го, Дин и Сонг, Управление производством и обслуживанием, 2018 г.
- Влияние конкуренции между интернет-провайдерами и поставщиками контента на дебаты о сетевом нейтралитете, с Гуо, Бандйопадхьяем, Янгом и Ченгом, MIS Quarterly Vol.
 41 № 2, стр. 353-370/июнь 2017 г.
41 № 2, стр. 353-370/июнь 2017 г. - О произведении матриц-компаньонов , с Цзялин Дай, Приложение линейной алгебры. ~ 435 (2011), вып. 11, 2921-2935.
- Аппроксимативное преобразование Фурье орбитального интеграла , К.К. Артур Лим, J. Math. Анальный. заявл. ~ 296 (2004), 594-602.
- Мультиразрешение на компактных группах , с Чен-Бо Чжу, приложение линейной алгебры. ~ 293 (1999), вып. 1-3, 15-38.
Lim, предел последовательности
Мы уже знаем, что такое арифметическая и геометрическая прогрессия. последовательности значений.Возьмем последовательность a n = 1/n, если k и м есть натуральных чисел, тогда для каждого k верно a k > a m , так что чем больше становится, тем меньше становится n и он всегда положителен, но никогда не достигает нуля. В этом случае мы говорим, что 0 равно
lim a n->∞ если n->∞, или другой способ записать это lim n->∞ a n = 0.
Определение предела
Число а называется пределом последовательности, если для каждого ε > 0 можно найти число п е , так что для всех членов последовательности a n с индексом n > n ε верно, что a – ε n .
Основное правило
Если lim n->∞ a n = a, a n -> a a n – a -> 0 |a n – a| -> 0
Последовательность не всегда имеет предел, а иногда имеет нереальный предел (-∞ или +∞). Пределы +∞ и -∞ называются нереальными пределами.
Если последовательности a n и b n имеют действительные пределы, то последовательности
a n + b n , а н – б н , а н .b n и a n / b n также имеют реальный лимит и:LIM N -> ∞ (A N + B N ) = LIM N -> ∞ A N + LIM N -> ∞ B N
LIM N -> ∞ (A N – B N – B N ) = Lim N -> ∞ A N – Lim N -> ∞ B N
LIM N -> ∞ (A N . B n ) = lim n -> ∞ a n .lim n -> ∞ b n
B n ) = lim n -> ∞ a n .lim n -> ∞ b n
lim n -> ∞ (A N / B N ) = LIM N -> ∞ A N / LIM N -> ∞ b n
, если b n ≠ 0 и lim n->∞ b n ≠ 0Если n n для каждого натурального n и lim n->∞ a n = a,
lim n->∞ b n = b тогда а ≤ бЕсли a n ≤ b n ≤ c n или каждое вещественное n и если lim n->∞ a n = lim n->∞ c n = A
, то lim n->∞ b n = A.Если a n ≥ 0 и lim n->∞ a n = a, тогда последовательность b n = √a n также имеет предел и lim n->∞ √a n = √a n .
Если a n = 1 / n k и k ≥ 1, тогда lim n->∞ a n = 0.

Если -1 n->∞q n = 0.
lim n->∞ (1 – 1/n) n = lim n->∞(1 + 1/n) n+1 = e
(1+1/n) n п-1e – число Непера.
Если последовательность a n имеет нереальный предел (-∞ или +∞ ) то последовательность 1/a n имеет предел и lim n->∞ 1 / a n = 0
Если последовательности a n и b n имеют нереальные пределы и lim n->∞ a n =+∞, lim n->∞ b n =+∞ тогда:
lim n->∞ (a n + b n ) = +∞
lim n->∞ (a n .b n ) = +∞
lim n->∞ a n k = +∞ if k > 0
lim n->∞ a n 900 если к lim n->∞ -a n = -∞Лим проблемы
Упражнение 1:
Если a n = 5,4 n , lim n->0 a n = ?Ответ:
lim n->0 a n = lim n->0 5 . lim n->0 4 n = 5 . 4 0 = 5,1 = 5
lim n->0 4 n = 5 . 4 0 = 5,1 = 5Упражнение 2:
Если n = затем lim n->∞a n = ? Ответ:
lim n->∞ = lim n->∞ . = lim n->∞ = -3 Упражнение 3:
Ответ:
= lim a n -> 1 (2a n + 1) = 3lim a n ->1 = = lim a n ->∞ = Плоттер предельных графиков
Подробнее о лиме на математическом форуме
Регистрация на форуме
Лим, Мэн Фай-华中师范大学数学学院中文站
Личное знакомство
2015-: доцент Центрально-китайского педагогического университета.
 2010-2014: Постдокторский научный сотрудник, Университет Торонто, Торонто, Канада (постдокторский советник: В.Кумар Мурти)
2010-2014: Постдокторский научный сотрудник, Университет Торонто, Торонто, Канада (постдокторский советник: В.Кумар Мурти)Образование
2010: к.т.н. по математике, Университет Макмастера, Гамильтон, Канада. (Доктор философии: Ромьяр Т. Шарифи) 2005: Магистр наук. по математике, Национальный университет Сингапура, Сингапур. (Советник магистра наук: А. Джон Беррик) 2003: бакалавр наук. по математике, Национальный университет Сингапура, Сингапур.
Поле исследований
Алгебраическая теория чисел, теория Ивасавы
Публикация
Суман Ахмед и Менг Фай Лим, О подписанных группах Сельмера конгруэнтных эллиптических кривых с полустабильной редукцией по всем простым числам выше p, представлены.Пин-Чи Хунг и Мэн Фай Лим, О росте рангов Морделла-Вейля в p-адических расширениях Ли, представлено, arXiv: 1902.01068 [math.
 NT]. Мэн Фай Лим, О делимости числа классов и дискриминанта мнимых квадратичных полей, arXiv:1601.05180v2[math.NT]. Суман Ахмед и Менг Фай Лим, Об эйлеровых характеристиках знаковых групп Зельмера, принятых к публикации в Бюллетене Австралийского математического общества. Мэн Фай Лим и Рамдорай Суджата, О структуре тонких групп Зельмера и групп Зельмера эллиптических кривых СМ, принятых к публикации в серии лекций Математического общества Рамануджана.r\rtimes Z_p-extensions, Acta Arithmetica 189 (2019), вып. 2, 191-208.
[16] Мэн Фай Лим и Рамдорай Суджата, Файн Зельмер группы конгруэнтных представлений Галуа. Журнал теории чисел 187 (2018) 66-91.
[15] Менг Фай Лим, M_H(G)-свойство и конгруэнтность представлений Галуа. Журнал Математического общества Рамануджана 33 (2018) № 1, 37-74.
[14] Мэн Фай Лим, Сравнение π-примарных подмодулей дуальных групп Зельмера. Азиатский математический журнал, Vol. 21 (2017) Нет.6, 1153-1182.
[13] Мэн Фай Лим, О полной точности p-свободных фактор-модулей дуальных групп Зельмера.
NT]. Мэн Фай Лим, О делимости числа классов и дискриминанта мнимых квадратичных полей, arXiv:1601.05180v2[math.NT]. Суман Ахмед и Менг Фай Лим, Об эйлеровых характеристиках знаковых групп Зельмера, принятых к публикации в Бюллетене Австралийского математического общества. Мэн Фай Лим и Рамдорай Суджата, О структуре тонких групп Зельмера и групп Зельмера эллиптических кривых СМ, принятых к публикации в серии лекций Математического общества Рамануджана.r\rtimes Z_p-extensions, Acta Arithmetica 189 (2019), вып. 2, 191-208.
[16] Мэн Фай Лим и Рамдорай Суджата, Файн Зельмер группы конгруэнтных представлений Галуа. Журнал теории чисел 187 (2018) 66-91.
[15] Менг Фай Лим, M_H(G)-свойство и конгруэнтность представлений Галуа. Журнал Математического общества Рамануджана 33 (2018) № 1, 37-74.
[14] Мэн Фай Лим, Сравнение π-примарных подмодулей дуальных групп Зельмера. Азиатский математический журнал, Vol. 21 (2017) Нет.6, 1153-1182.
[13] Мэн Фай Лим, О полной точности p-свободных фактор-модулей дуальных групп Зельмера. Журнал Математического общества Рамануджана 32 (2017), № 3, 299–326.
[12] Мэн Фай Лим, Заметки о тонких группах Зельмера. Азиатский журнал математики 21 (2017) № 2, 337-362.
[11] Мэн Фай Лим, ряд Акаши, характеристические элементы и конгруэнтность представлений Галуа. Международный журнал теории чисел 12 (2016), № 3, 593-613.
[10] Мэн Фай Лим и В.Кумар Мурти, Рост тонких групп Зельмера. Журнал Математического общества Рамануджана 31 (2016), № 1, 79-94.
[9] Мэн Фай Лим, О псевдонулевости двойственных тонких групп Зельмера. Международный журнал теории чисел 11 (2015), № 7, 2055–2063.
[8] Мэн Фай Лим и В. Кумар Мурти, Рост групп Зельмера абелевых многообразий CM. Канадский журнал математики 67 (2015) № 3, 654-666.
[7] Мэн Фай Лим, О полностью точных группах Зельмера эллиптических кривых и деформациях Хида.Журнал алгебры 432 (2015) 72-90.
[6] Мэн Фай Лим, О гомологиях групп когомологий Ивасавы. Журнал Математического общества Рамануджана 30 (2015) № 1, 51-65.
[5] Мэн Фай Лим, Замечание о M_H(G)-гипотезе и серии Акаши.
Журнал Математического общества Рамануджана 32 (2017), № 3, 299–326.
[12] Мэн Фай Лим, Заметки о тонких группах Зельмера. Азиатский журнал математики 21 (2017) № 2, 337-362.
[11] Мэн Фай Лим, ряд Акаши, характеристические элементы и конгруэнтность представлений Галуа. Международный журнал теории чисел 12 (2016), № 3, 593-613.
[10] Мэн Фай Лим и В.Кумар Мурти, Рост тонких групп Зельмера. Журнал Математического общества Рамануджана 31 (2016), № 1, 79-94.
[9] Мэн Фай Лим, О псевдонулевости двойственных тонких групп Зельмера. Международный журнал теории чисел 11 (2015), № 7, 2055–2063.
[8] Мэн Фай Лим и В. Кумар Мурти, Рост групп Зельмера абелевых многообразий CM. Канадский журнал математики 67 (2015) № 3, 654-666.
[7] Мэн Фай Лим, О полностью точных группах Зельмера эллиптических кривых и деформациях Хида.Журнал алгебры 432 (2015) 72-90.
[6] Мэн Фай Лим, О гомологиях групп когомологий Ивасавы. Журнал Математического общества Рамануджана 30 (2015) № 1, 51-65.
[5] Мэн Фай Лим, Замечание о M_H(G)-гипотезе и серии Акаши. Международный журнал теории чисел 11 (2015) № 1, 269-297.
[4] Мэн Фай Лим и В. Кумар Мурти, Рост группы Зельмера эллиптической кривой с расщепленной мультипликативной редукцией. Международный журнал теории чисел 10 (2014) №.3, 675-687.
[3] Менг Фай Лим и Ромьяр Шарифи, Двойственность Нековара над p-адическими расширениями Ли глобальных полей. Документа Математика 18 (2013) 621-678.
[2] Мэн Фай Лим, Двойственность Пуату-Тейта над расширениями глобальных полей. Журнал теории чисел 132 (2012) 2636-2672.
[1] Джон Беррик и Мэн Фай Лим, Матрицы переплетения для числовых полей: дополнение к «Переплетениям и K-теории коммутативных колец». Дж. Рейн Ангью. Мат. 601 (2006) 159-162.
Международный журнал теории чисел 11 (2015) № 1, 269-297.
[4] Мэн Фай Лим и В. Кумар Мурти, Рост группы Зельмера эллиптической кривой с расщепленной мультипликативной редукцией. Международный журнал теории чисел 10 (2014) №.3, 675-687.
[3] Менг Фай Лим и Ромьяр Шарифи, Двойственность Нековара над p-адическими расширениями Ли глобальных полей. Документа Математика 18 (2013) 621-678.
[2] Мэн Фай Лим, Двойственность Пуату-Тейта над расширениями глобальных полей. Журнал теории чисел 132 (2012) 2636-2672.
[1] Джон Беррик и Мэн Фай Лим, Матрицы переплетения для числовых полей: дополнение к «Переплетениям и K-теории коммутативных колец». Дж. Рейн Ангью. Мат. 601 (2006) 159-162.Дэвид Бенджамин Лим
С начала тотальной блокировки в Малайзии 06.01.2021, меня все больше интересует попытка понять распространение COVID-19 в Малайзии.
Неудача FMCO 2021
Я утверждаю, что неспособность предотвратить создание кластеров на рабочих местах была причиной провала FMCO 2021 года в долина Кланг, Джохор, Пулау-Пинанг и Негери-Сембилан.
 Пожалуйста, посмотрите этот pdf
здесь. Кроме того, пожалуйста, ознакомьтесь с этим заявлением для прессы
(совместно с IDEAS и Bait Al-Amanah), призывая федеральное правительство решить эту проблему как можно скорее.
Пожалуйста, посмотрите этот pdf
здесь. Кроме того, пожалуйста, ознакомьтесь с этим заявлением для прессы
(совместно с IDEAS и Bait Al-Amanah), призывая федеральное правительство решить эту проблему как можно скорее.Критерий повторного открытия Пенанга
Критерий открытия Пенанга (а также других штатов Малайзии) на уровне района , исходя из базового репродуктивного числа и ежедневных новых случаев на 100 000 Население.
На приведенном выше рисунке показано изменение во времени ($R_0$, ежедневных новых случаев/100 000) для каждый из 5 районов Пенанга, т.е.е. Тимур Лаут, Барат Дайя, Себеранг Перай Утара, Себеранг Пераи Тенга и Себеранг Пераи Селатан.
 Они были сокращены соответственно
как TL, BD, SPU, SPT, SPS.
Они были сокращены соответственно
как TL, BD, SPU, SPT, SPS.
Критерий повторного открытия, который мы предлагаем, зависит от определения пороговых значений. заштрихованы зеленым, желтым и красным на рисунке выше. Теоретически эти пороги функция состояния системы здравоохранения, e.г. Наполняемость отделений интенсивной терапии и уровень вакцинации. Однако, поскольку у меня нет доступа к данным о заполняемости отделений интенсивной терапии в Пенанге, Я заштриховал пороговые значения, определенные эмпирически на основе прошлых данных: вернитесь назад во времени и запишите дату, которая составляет две недели или около того от до до система здравоохранения перегружена. Запишите ($R_0$, ежедневные новые случаи/100 000) примерно в это же время и установите это будет вашим порогом.
Код для расчета $R_0$ для каждого района (любого штата!) в Малайзии. доступен на моем GitHub здесь. Базовое число репродукции рассчитывали по методу обычных наименьших квадратов. применяется к ежедневным новым номерам случаев в течение короткого периода времени.
Сбор пожертвований Баян Бару 2021
Цель состоит в том, чтобы поднять 50 000 ринггитов (ок.12 000 долларов США) для выплаты наличными Семьи B40 в районе Баян-Бару, Пенанг, Малайзия, во время FMCO 2021 года (Приказ о полном контроле за передвижением). GIVE.азия страница для пожертвований находится здесь. Этот проект является совместным с депутатом для Баян Бару, YB Sim Tze Tzin.

Сонхи Лим
Факультет математических наук
Сеульский национальный университетстройная@сну.ак.кр
Преподавание Исследования Препринты- Размерность для дважды плохо аппроксимируемых аффинных форм (совместно с Уён Кимом) отправлена. (апрель 2019 г.) arXiv.
- Локальная предельная теорема об отрицательной кривизне (совместно с Франсуа Ледрапье), Duke Mathematical Journal (опубликовано в Интернете в январе 2021 г.) arXiv, онлайн.
- Анализ топологических данных коронарных бляшек демонстрирует естественное течение коронарного атеросклероза (совместно с Doyeon Hwang, Haneol Kim, Seung-Pyo Lee, et al.) JACC Cardiovasc Imaging (принято в январе 2021 г.) онлайн.
- Граница Мартина броуновского движения на гиперболических метрических графах Громова (совместно с Сунки Хонгом), DCDS-A (опубликовано в сети в январе 2021 г.
 ) arXiv, онлайн.
) arXiv, онлайн. - Заметки о значениях объемной энтропии графов (совместно с Уён Ким), DCDS-A, Vol 40, no. 9, №2. (сентябрь 2020 г.) arXiv, онлайн.
- Задержка созревания и асимметричный информационный поток связей мозга в SHR-модели СДВГ, выявленные топологическим анализом метаболических сетей (Seunggyun Ha, Hyekyoung Lee, Yoori Choi, Hyejin Kang, Se Jin Jeon, Jong Hoon Ryu, Hee Jin Kim, Jae Hoon Cheong, Seonhee Lim, Bungnyun Kim и Dong Soo Lee), принятые в Scientific Reports (январь 2020 г.).
- Предельное распределение геодезических в геометрически конечных частных обычных деревьев (с Санхуном Квоном), которые появятся в группах, геометрии и динамике. (ожидается, что он будет опубликован в сети весной 2020 г.) arXiv.
- Размерность Хаусдорфа в неоднородном диофантовом приближении (совместно с Яном Бюжо, Донг Хан Кимом и Михал Рамс), IMRN (опубликовано в Интернете 4 апреля 2019 г.
 ).АрХив онлайн.
).АрХив онлайн. - Размерность для плохо аппроксимируемых сеток (с Николя де Саксе и Ури Шапира), IMRN. (опубликовано в сети в январе 2018 г.) arXiv, онлайн.
- Равнораспределение с частотой ошибок и диофантовой аппроксимацией над функциональными полями (с Санхуном Квоном), Дискретные и непрерывные динамические системы – A, 38 (опубликовано в Интернете в сентябре 2017 г.) arXiv, онлайн.
- Асимптотическое распределение значений изотропных квадратичных форм в S-целых точках (совместно с Кейваном Маллахи-Караи и Джиён Ханом), Journal of Modern Dynamics.об. 11, 501–550 (опубликовано в Интернете в октябре 2017 г.) arXiv, онлайн.
- Распределение точек целочисленной решетки на эллипсоиде с диофантовым центром (совместно с Jiyoung Han, Hyunsuk Kang, Yong-Cheol Kim) J. Теория чисел, том. 157 (декабрь 2015 г.), 468-506.arxiv, онлайн
- Карта Фарея, диофантово приближение и дерево Брюа-Титса (с Донг Ханом Кимом, Хитоши Накада, Рие Нацуи), приложение Finite Fields.
 Том. 30 (ноябрь 2014 г.), стр. 14-32, архив, онлайн
Том. 30 (ноябрь 2014 г.), стр. 14-32, архив, онлайн - О распределении орбит геометрически конечных гиперболических групп на границе (с Хи О), Эргод.Т. & Динам. систем, том 32 (2011), 173-189. онлайн, архив
- Доказательство эргодической теоремы L1/2 (совместная работа с Ф. Ледрапье), препринт. pdf (2006)
- Объемная энтропия для гиперболических зданий (совместная работа с Ф. Ледрапье), Журнал современной динамики, том 4, № 1 (2010), стр. 139-165. arxiv, онлайн (улучшено, чтобы включить все обычные здания)
- Минимальная объемная энтропия для графов, Пер. амер. Мат. соц. 360 (2008), 5089-5100. архив
- Квази-штурмовские раскраски на деревьях (совместно с Донг Хан Ким, Сыльби Ли, Деоквон Шим), Эргод.Т. & Динам. Сис. (опубликовано онлайн 09 августа 2019 г.). АрХив онлайн.
- Алгоритм непрерывной дроби для Штурмовых раскрасок деревьев (с Донг Хан Кимом), Ergod.
 Т. & Динам. Сис. (опубликовано онлайн 12 декабря 2017 г.) arXiv, онлайн.
Т. & Динам. Сис. (опубликовано онлайн 12 декабря 2017 г.) arXiv, онлайн. - Раскраски деревьев с линейной, промежуточной и экспоненциальной сложностью подслов (совместно с Сылби Ли), J. Korean Math. соц. Том. 52, № 6, 1123-1137 (ноябрь 2015 г.) онлайн.
- Сложность подслов и Штурмовы раскраски деревьев (совместно с Донг Хан Кимом), Эргод.Т. & Динам. Сис. Том 35, вып. 2 (апрель 2015 г.) 461-481. arxiv, онлайн.
- Гиперболическая мозаика и раскраска деревьев (совместно с Донг Хан Ким), Абстрактный и прикладной анализ, том. 2013 г., ID 706496 (2013 г.) онлайн
Геометрическая теория групп
- On Commensurizer Growth (совместная работа с Ниром Авни и Эраном Нево), Israel J. Math 188. (2012) 259-279 arxiv, онлайн
- Теория покрытия для комплексов групп (совместная работа с А. Томасом), J. Pure Appl.Алгебра 212 (2008) 1632-1663. архив
- Подсчет надрешеток для многогранных комплексов (совместная работа с А.
 Томасом), Сборник топологических исследований, том 36 (2010 г.), стр. 229–247. pdf, онлайн
Томасом), Сборник топологических исследований, том 36 (2010 г.), стр. 229–247. pdf, онлайн - Подсчет надрешеток в группах автоморфизмов деревьев, Геом. Посвященный, Vol. 118 (2006), вып. 1, стр. 1-21. архив
- Объемная энтропия для моделирования потока информации на графе мозга (совместно с Heykyoung Lee, Eunkyung Kim, Youngmin Huh, Youngjo Lee и Dong Soo Lee), Scientific Reports.(опубликовано онлайн 22 января 2019 г.) arXiv. онлайн
- Интегрированный мультимодальный сетевой подход к ПЭТ и МРТ, основанный на многомерной стойкой гомологии (совместно с Hyekyong Lee, Dong Soo Lee et al.), Human Brain Mapping (ноябрь 2016 г.), arxiv, онлайн.
Последние статьи
Эргодическая теория и теория чисел (диофантово приближение, гипотеза Оппенгейма и др.)
Эргодическая теория и объемная энтропия
Раскраски деревьев
Прикладная математика
Сонхи Лим
Сонхи ЛимСонхи Лим
Сейчас я в Сеульском национальном университете. Для моего текущего веб-сайта, пожалуйста, нажмите здесьХ.К. Ван Доцент
Математический факультет,
593 Малотт Холл, Корнельский университет
Итака, Нью-Йорк, 14853-4201
Рабочий телефон: (607) 255-7113, факс: (607) 255-7149
Электронная почта: slim@math.
 cornell.edu
cornell.eduОбучение
Весна 2009: Математика 7520, Семинар Бернштейна по топологии и геометрической теории групп
Весна 2009 г.: Математика 4320, Введение в алгебру
Осень 2008: Математика 618, Эргодическая теория
Исследования
Научные интересы: геометрическая теория групп и динамика
- Динамика групповых воздействий на деревья и здания, в более общем случае метрические пространства неположительной кривизны
- Решетки групп Ли и группы автоморфизмов деревьев и полиэдральные комплексы, подгруппы-соизмерители и т.д.
- Энтропийная жесткость
Статьи
- Рост соразмерителя (совместная работа с Нир Авни и Эраном Нево), в подготовке.
- Объемная энтропия для зданий (совместная работа с Ф. Ледрапье), препринт. Аннотация пдф ps (2008.10, переработано (улучшено, чтобы включить все обычные здания) 2009.7)
- Доказательство эргодической теоремы L1/2 (совместная работа с Ф.
 Ледрапье).
pdf, пс (2006.12)
Ледрапье).
pdf, пс (2006.12) - Счетные надрешетки для многогранных комплексов (совместная работа с А.Томас), представленный для публикации. Аннотация пдф PS (пересмотрено в 2007.11)
- Теория покрытия для комплексов групп (совместная работа с А. Томасом), J. Pure Appl. Алгебра 212 (2008) 1632–1663. Аннотация, архив
- Минимальная объемная энтропия для графов, Пер. амер. Мат. соц. 360 (2008), 5089-5100. реферат, pdf, ps
- Счетные надрешетки в группах автоморфизмов деревьев, Геом. Посвященный, Vol. 118 (2006), вып. 1, стр. 1-21. Аннотация, pdf, ps
Организованные предстоящие и недавние конференции
Предстоящие и недавние выступления
- Примеры групп, Университет штата Огайо, Колумбус, Огайо (11–14 мая 2009 г.).
- Корнельский фестиваль топологии, Итака, Нью-Йорк (4 мая 2009 г.).
- Семинар по жесткости, часть Корнельского фестиваля топологии, Итака, Нью-Йорк (1 мая 2009 г.).
- Совместное собрание по математике, Специальная сессия AMS по групповым действиям в однородных пространствах и приложениях, Вашингтон, округ Колумбия (5 января 2009 г.
 )
) - Коллоквиум, Корейский передовой институт науки и технологий, Тэджон, Южная Корея (10 декабря 2008 г.)
- Семинар по динамике групповых действий, Йельский университет (10 ноября 2008 г.)
- Летняя школа по квазиконформному анализу и границам гиперболических групп, Блумингтон, Индиана (14 августа 2008 г.) (по результату Бурдона и Пажо о жесткости квазиизометрии, конспекты лекций)
- Семинар по геометрии, Афинский университет, Афины, Греция (4 августа 2008 г.)
- Семинар по анализу и геометрии в группах, University Paris 7, Париж, Франция (23 июля 2008 г.)
- Семинар по геометрии, ETH, Цюрих, Швейцария (9 июля 2008 г.)
- Миникурс графов групп и комплексов групп, унив.Невшатель, Швейцария (2, 9, 16, 23 июня 2008 г.)
- Семинар по геометрии и динамике, Ecole Normale Superieure de Lyon, Франция (18 июня 2008 г.)
- Конференция по анализу, геометрии и динамике групп, Невшатель, Швейцария (13 июня 2008 г.)
- Конференция по дискретным группам и геометрическим структурам с приложениями, Кортрейк, Бельгия (29 мая 2008 г.
 )
) - Семинар по динамике, Северо-Западный университет (13 мая 2008 г.)
- Весеннее восточное секционное собрание AMS, специальная сессия по геометрической топологии, Институт Куранта (март.15-16, 2008)
- Семинар по топологии и геометрической теории групп, Корнельский университет (26 февраля 2008 г.)
- Семинар по геометрии и топологии, SUNY Buffalo (22 февраля 2008 г.)
- Семинар по геометрии и топологии, Бингемтонский университет (21 февраля 2008 г.)
- еще
Ссылки
Доктор Джейсон Лим – Учебный центр математических наук
Бакалавр наук. (с отличием), доктор философии, NUS, Сингапур
Эксперт-экзаменатор и маркер для различных местных и международных экзаменационных комиссий
Д-р Лим — старший преподаватель Учебного центра математических наук в Сингапуре.Он имеет степень бакалавра наук и степень доктора философии Национального университета Сингапура. Доктор Лим по профессии преподаватель-тренер и имеет более чем 20-летний опыт преподавания как в местных школах, так и в частных практиках.
 Он работал классным руководителем, адъюнкт-профессором и тренером по подготовке к олимпиадам по математике и естественным наукам. В настоящее время он продолжает выступать на конференциях, преподавать математику и естественные науки, а также вносить свой вклад в образовательное сообщество математических наук.
Он работал классным руководителем, адъюнкт-профессором и тренером по подготовке к олимпиадам по математике и естественным наукам. В настоящее время он продолжает выступать на конференциях, преподавать математику и естественные науки, а также вносить свой вклад в образовательное сообщество математических наук.Д-р Лим является членом различных международных математических обществ по всему миру. Разнообразные математические общества позволяют ему быть в курсе современных тенденций и практики в области математического и естественнонаучного образования. Кроме того, он является членом Всемирного совета по делам одаренных и талантливых детей. Всемирный совет для одаренных и талантливых детей, Inc. (WCGTC) — всемирная некоммерческая организация, основной целью которой является защита и поддержка одаренных детей.Он специализируется на преподавании как интегрированной программы (IP), так и программы обучения для одаренных (GEP).
Активно занимается исследованиями в области математических наук в области образования, его также часто приглашают проводить семинары для родителей и учителей как на местном уровне, так и в соседних странах, а также представлять результаты исследований на международных конференциях.

Международное обозначение математики
- Член Чартерного педагогического колледжа, Лондон, Соединенное Королевство.
- Международный сотрудник Австралийской ассоциации учителей математики, Inc., Австралия.
- Член Ассоциации преподавателей математики, Сингапур.
- Член Национального совета учителей математики, Америка.
- Член Ассоциации учителей математики, Соединенное Королевство.
- Член Сингапурского математического общества, Сингапур.
- Член Американского математического общества, Америка.
- Член Европейского математического общества, Финляндия.
Международное обозначение науки
- Член Национальной ассоциации преподавателей естественных наук, Америка.
- Член Ассоциации научного образования, Соединенное Королевство.
- Член Общества преподавателей естественных наук в колледжах, Америка.
- Член Ассоциации преподавателей естественнонаучного образования, Великобритания.



 Серия: Математика и физика
Серия: Математика и физика


 x$$
x$$ Положим , так что
Положим , так что 10+x+7),-inf)
ans =
0
10+x+7),-inf)
ans =
0 


 м.ф.
м.ф.
 2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ 2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
 б.ф. при x a
б.ф. при x a 2.11. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ
2.11. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ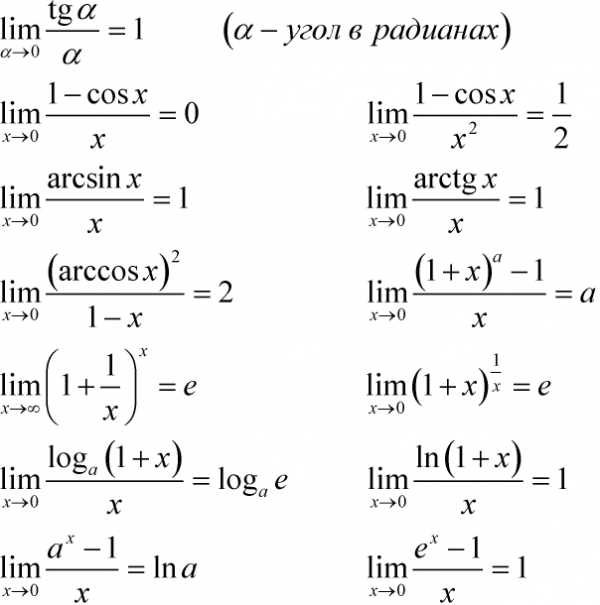
 Мои математические исследования связаны с комбинаторным матричным анализом и его приложениями. В настоящее время я исследую связь между разностными уравнениями и представлением алгебр Ли с помощью комбинаторных методов.
Мои математические исследования связаны с комбинаторным матричным анализом и его приложениями. В настоящее время я исследую связь между разностными уравнениями и представлением алгебр Ли с помощью комбинаторных методов. 41 № 2, стр. 353-370/июнь 2017 г.
41 № 2, стр. 353-370/июнь 2017 г.
 B n ) = lim n -> ∞ a n .lim n -> ∞ b n
B n ) = lim n -> ∞ a n .lim n -> ∞ b n 
 lim n->0 4 n = 5 . 4 0 = 5,1 = 5
lim n->0 4 n = 5 . 4 0 = 5,1 = 5 2010-2014: Постдокторский научный сотрудник, Университет Торонто, Торонто, Канада (постдокторский советник: В.Кумар Мурти)
2010-2014: Постдокторский научный сотрудник, Университет Торонто, Торонто, Канада (постдокторский советник: В.Кумар Мурти) NT]. Мэн Фай Лим, О делимости числа классов и дискриминанта мнимых квадратичных полей, arXiv:1601.05180v2[math.NT]. Суман Ахмед и Менг Фай Лим, Об эйлеровых характеристиках знаковых групп Зельмера, принятых к публикации в Бюллетене Австралийского математического общества. Мэн Фай Лим и Рамдорай Суджата, О структуре тонких групп Зельмера и групп Зельмера эллиптических кривых СМ, принятых к публикации в серии лекций Математического общества Рамануджана.r\rtimes Z_p-extensions, Acta Arithmetica 189 (2019), вып. 2, 191-208.
[16] Мэн Фай Лим и Рамдорай Суджата, Файн Зельмер группы конгруэнтных представлений Галуа. Журнал теории чисел 187 (2018) 66-91.
[15] Менг Фай Лим, M_H(G)-свойство и конгруэнтность представлений Галуа. Журнал Математического общества Рамануджана 33 (2018) № 1, 37-74.
[14] Мэн Фай Лим, Сравнение π-примарных подмодулей дуальных групп Зельмера. Азиатский математический журнал, Vol. 21 (2017) Нет.6, 1153-1182.
[13] Мэн Фай Лим, О полной точности p-свободных фактор-модулей дуальных групп Зельмера.
NT]. Мэн Фай Лим, О делимости числа классов и дискриминанта мнимых квадратичных полей, arXiv:1601.05180v2[math.NT]. Суман Ахмед и Менг Фай Лим, Об эйлеровых характеристиках знаковых групп Зельмера, принятых к публикации в Бюллетене Австралийского математического общества. Мэн Фай Лим и Рамдорай Суджата, О структуре тонких групп Зельмера и групп Зельмера эллиптических кривых СМ, принятых к публикации в серии лекций Математического общества Рамануджана.r\rtimes Z_p-extensions, Acta Arithmetica 189 (2019), вып. 2, 191-208.
[16] Мэн Фай Лим и Рамдорай Суджата, Файн Зельмер группы конгруэнтных представлений Галуа. Журнал теории чисел 187 (2018) 66-91.
[15] Менг Фай Лим, M_H(G)-свойство и конгруэнтность представлений Галуа. Журнал Математического общества Рамануджана 33 (2018) № 1, 37-74.
[14] Мэн Фай Лим, Сравнение π-примарных подмодулей дуальных групп Зельмера. Азиатский математический журнал, Vol. 21 (2017) Нет.6, 1153-1182.
[13] Мэн Фай Лим, О полной точности p-свободных фактор-модулей дуальных групп Зельмера. Журнал Математического общества Рамануджана 32 (2017), № 3, 299–326.
[12] Мэн Фай Лим, Заметки о тонких группах Зельмера. Азиатский журнал математики 21 (2017) № 2, 337-362.
[11] Мэн Фай Лим, ряд Акаши, характеристические элементы и конгруэнтность представлений Галуа. Международный журнал теории чисел 12 (2016), № 3, 593-613.
[10] Мэн Фай Лим и В.Кумар Мурти, Рост тонких групп Зельмера. Журнал Математического общества Рамануджана 31 (2016), № 1, 79-94.
[9] Мэн Фай Лим, О псевдонулевости двойственных тонких групп Зельмера. Международный журнал теории чисел 11 (2015), № 7, 2055–2063.
[8] Мэн Фай Лим и В. Кумар Мурти, Рост групп Зельмера абелевых многообразий CM. Канадский журнал математики 67 (2015) № 3, 654-666.
[7] Мэн Фай Лим, О полностью точных группах Зельмера эллиптических кривых и деформациях Хида.Журнал алгебры 432 (2015) 72-90.
[6] Мэн Фай Лим, О гомологиях групп когомологий Ивасавы. Журнал Математического общества Рамануджана 30 (2015) № 1, 51-65.
[5] Мэн Фай Лим, Замечание о M_H(G)-гипотезе и серии Акаши.
Журнал Математического общества Рамануджана 32 (2017), № 3, 299–326.
[12] Мэн Фай Лим, Заметки о тонких группах Зельмера. Азиатский журнал математики 21 (2017) № 2, 337-362.
[11] Мэн Фай Лим, ряд Акаши, характеристические элементы и конгруэнтность представлений Галуа. Международный журнал теории чисел 12 (2016), № 3, 593-613.
[10] Мэн Фай Лим и В.Кумар Мурти, Рост тонких групп Зельмера. Журнал Математического общества Рамануджана 31 (2016), № 1, 79-94.
[9] Мэн Фай Лим, О псевдонулевости двойственных тонких групп Зельмера. Международный журнал теории чисел 11 (2015), № 7, 2055–2063.
[8] Мэн Фай Лим и В. Кумар Мурти, Рост групп Зельмера абелевых многообразий CM. Канадский журнал математики 67 (2015) № 3, 654-666.
[7] Мэн Фай Лим, О полностью точных группах Зельмера эллиптических кривых и деформациях Хида.Журнал алгебры 432 (2015) 72-90.
[6] Мэн Фай Лим, О гомологиях групп когомологий Ивасавы. Журнал Математического общества Рамануджана 30 (2015) № 1, 51-65.
[5] Мэн Фай Лим, Замечание о M_H(G)-гипотезе и серии Акаши. Международный журнал теории чисел 11 (2015) № 1, 269-297.
[4] Мэн Фай Лим и В. Кумар Мурти, Рост группы Зельмера эллиптической кривой с расщепленной мультипликативной редукцией. Международный журнал теории чисел 10 (2014) №.3, 675-687.
[3] Менг Фай Лим и Ромьяр Шарифи, Двойственность Нековара над p-адическими расширениями Ли глобальных полей. Документа Математика 18 (2013) 621-678.
[2] Мэн Фай Лим, Двойственность Пуату-Тейта над расширениями глобальных полей. Журнал теории чисел 132 (2012) 2636-2672.
[1] Джон Беррик и Мэн Фай Лим, Матрицы переплетения для числовых полей: дополнение к «Переплетениям и K-теории коммутативных колец». Дж. Рейн Ангью. Мат. 601 (2006) 159-162.
Международный журнал теории чисел 11 (2015) № 1, 269-297.
[4] Мэн Фай Лим и В. Кумар Мурти, Рост группы Зельмера эллиптической кривой с расщепленной мультипликативной редукцией. Международный журнал теории чисел 10 (2014) №.3, 675-687.
[3] Менг Фай Лим и Ромьяр Шарифи, Двойственность Нековара над p-адическими расширениями Ли глобальных полей. Документа Математика 18 (2013) 621-678.
[2] Мэн Фай Лим, Двойственность Пуату-Тейта над расширениями глобальных полей. Журнал теории чисел 132 (2012) 2636-2672.
[1] Джон Беррик и Мэн Фай Лим, Матрицы переплетения для числовых полей: дополнение к «Переплетениям и K-теории коммутативных колец». Дж. Рейн Ангью. Мат. 601 (2006) 159-162. Пожалуйста, посмотрите этот pdf
здесь. Кроме того, пожалуйста, ознакомьтесь с этим заявлением для прессы
(совместно с IDEAS и Bait Al-Amanah), призывая федеральное правительство решить эту проблему как можно скорее.
Пожалуйста, посмотрите этот pdf
здесь. Кроме того, пожалуйста, ознакомьтесь с этим заявлением для прессы
(совместно с IDEAS и Bait Al-Amanah), призывая федеральное правительство решить эту проблему как можно скорее. Они были сокращены соответственно
как TL, BD, SPU, SPT, SPS.
Они были сокращены соответственно
как TL, BD, SPU, SPT, SPS.

 ) arXiv, онлайн.
) arXiv, онлайн. ).АрХив онлайн.
).АрХив онлайн. Том. 30 (ноябрь 2014 г.), стр. 14-32, архив, онлайн
Том. 30 (ноябрь 2014 г.), стр. 14-32, архив, онлайн Т. & Динам. Сис. (опубликовано онлайн 12 декабря 2017 г.) arXiv, онлайн.
Т. & Динам. Сис. (опубликовано онлайн 12 декабря 2017 г.) arXiv, онлайн. Томасом), Сборник топологических исследований, том 36 (2010 г.), стр. 229–247. pdf, онлайн
Томасом), Сборник топологических исследований, том 36 (2010 г.), стр. 229–247. pdf, онлайн cornell.edu
cornell.edu Ледрапье).
pdf, пс (2006.12)
Ледрапье).
pdf, пс (2006.12) )
) )
) Он работал классным руководителем, адъюнкт-профессором и тренером по подготовке к олимпиадам по математике и естественным наукам. В настоящее время он продолжает выступать на конференциях, преподавать математику и естественные науки, а также вносить свой вклад в образовательное сообщество математических наук.
Он работал классным руководителем, адъюнкт-профессором и тренером по подготовке к олимпиадам по математике и естественным наукам. В настоящее время он продолжает выступать на конференциях, преподавать математику и естественные науки, а также вносить свой вклад в образовательное сообщество математических наук.