Лучший ответ по мнению автора
| |||||||||||||||||
11.18Другие ответы
| ||||||||||||
2. Ответ: бесконечность.
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Коля, Дима и Саша собрали.
(2/3)+n… -reshimne.ru
Новые вопросы
Ответы
Похожие вопросы
sinx/3*cosп/5-cosx/3*sinп/5=√2/2…
Помогите пожалуйста, очень прошу…
У=-5х+4 решить и построить график, пожалуйста…
На какое общее число делятся 63 95 105…
Решите пожалуйста уравнения в развернутом виде ; 19(39-2х)=703 ; 7(3х-х)=42 ; 2(2х+3х)=20….
Помогите решить, пожалуйста!.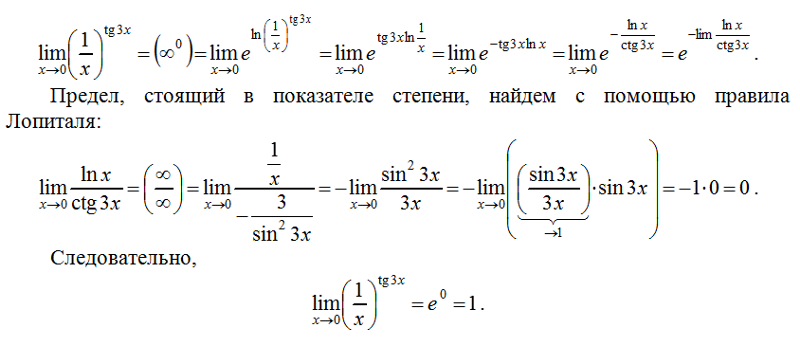
..
Математика
Литература
Алгебра
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Limits at Infinity Проблемы и решения – Matheno.
comОбновление: По состоянию на сентябрь 2022 года у нас есть гораздо дополнительных интерактивных способов узнать об основополагающей концепции Limits at Infinity, активно используя графические калькуляторы Desmos . Пожалуйста, посетите наш Введение в Пределы в Бесконечности, чтобы начать действительно получить этот материал для себя. Все это бесплатно и предназначено для того, чтобы помочь вам преуспеть в вашем курсе.
Если вам сейчас просто нужно попрактиковаться в решении проблем с ограничениями, предыдущие ученики сочли нижеприведенную информацию очень полезной. А если у вас есть вопросы, задавайте их на нашем форуме!
Пределы в бесконечности: проблемы и решения
Вы работаете над решением задач о $\displaystyle{\lim_{x \to \infty}}$ и $\displaystyle{\lim_{x \to\, -\infty }}$? Давайте рассмотрим общий предел в бесконечных задачах и решениях, чтобы вы могли научиться решать их регулярно.
РЕЗЮМЕ ПО ВЫЧИСЛЕНИЮ: Пределы в бесконечности
Вот краткое изложение нашего подробного рассмотрения Пределов в бесконечности. Вы можете бесплатно получить доступ к этому материалу, включая специально разработанные графические калькуляторы Desmos, которые иллюстрируют основные моменты, в разделе нашего сайта, посвященном ограничениям в бесконечности.
Сводка закрытия/открытия
Эта сводка представляет собой изображение, поэтому вы можете легко сохранить его, если хотите.
[свернуть]
Чтобы получить доступ к другим проблемам и решениям, включая вопросы с несколькими вариантами ответов в стиле AP, бесплатно войдите в свою учетную запись Google, Apple или Facebook или создайте специальный Matheno за 60 секунд. Вы также сможете отмечать задачи , которые вы хотите обязательно просмотреть перед экзаменами. Просто используйте область входа в систему в нижней части этого экрана.
92} \\[8px]
&= \frac{5}{3} \quad \cmark
\end{align*} \]
Теоретически числитель и знаменатель растут с одинаковой скоростью, поскольку изменены только коэффициенты этих наибольших членов.
Кстати, на графике видно, что линия $y = \dfrac{5}{3}$ является горизонтальной асимптотой для этой функции: кривая функции сколь угодно близко подходит к этой линии при $x \to \infty $.
Открыт для более тщательной разработки ответа
4} \\[8px]
&= 0 \quad \cmark
\end{align*} \]
, потому что наибольшая степень в знаменателе больше, чем наибольшая степень в числителе. (Именно так; рассуждения так просты.)
Концептуально рост знаменателя «выигрывает» над ростом числителя, что означает, что знаменатель растет быстрее, чем числитель, и поэтому дробь стремится к нулю по мере роста x и растет и растет в положительном направлении.
2} \\[8px]
&= \lim_{x \to \infty}\frac{x}{3} \\[8px]
&= \infty \quad \cmark
\end{align*} \]
Вторая строка решения показывает, что функция приближается к $\dfrac{x}{3}$ по мере увеличения размера x , что соответствует графику. Предел на бесконечности равен (положительному) $\infty$, потому что функция всегда растет в положительном направлении y по мере того, как x становится больше и больше в положительном направлении.
[свернуть]
Задача № 5: sin & cos
(a) Найдите $\displaystyle{\lim_{x \to \infty} \sin(x)}$.
(b) Найдите $\displaystyle{\lim_{x \to -\infty} \cos(x)}$.
Нажмите, чтобы просмотреть решение исчисления
Решение (a)Решение (b)
$\displaystyle{\lim_{x \to \infty} \sin(x)}$ не существует (DNE)$\ quad \cmark$
Предел на бесконечности не существует, потому что функция постоянно колеблется между -1 и 1 навсегда как x растет и растет.
Если бы вы шли вдоль функции, идущей вправо, вы бы продолжали идти вверх по холмам и вниз по долинам вечно, никогда не приближаясь ни к одному значению. Следовательно, предела на бесконечности не существует.
$\displaystyle{\lim_{x \to -\infty} \cos(x)}$ не существует (DNE)$\quad \cmark$
Предел на бесконечности не существует для одного и того же причина $\displaystyle{\lim_{x \to \infty} \sin(x)}$ не существует: если бы вы всегда шли по функции, идущей налево, вы бы продолжали подниматься по холмам и спускаться по долины между $y = 1$ и $-1,$ никогда не приближаются к одному значению. Следовательно, предела не существует.
[свернуть]
Предел в бесконечности Задачи с квадратными корнями
У нас есть отдельная страница, чтобы помочь вам конкретно с Предел в бесконечности Задачи с квадратными корнями.
Хотите получить доступ к всем нашим задачам и решениям исчисления? Войдите бесплатно с помощью своей учетной записи Google, Facebook или Apple или с помощью специальной учетной записи Matheno (которую вы можете создать за 60 секунд). Затем посетите наш главный экран исчисления.
И если у вас есть вопрос о проблеме ограничения на бесконечности, с которой вам может понадобиться помощь, или о ограничениях в целом, пожалуйста, зайдите на наш форум и напишите. Будем рады помочь!
По состоянию на сентябрь 2022 года мы используем наш форум для комментариев и обсуждения этой темы, а также для любых математических вопросов. Будем рады вас видеть и помочь! Нажмите, чтобы посетить наш форум: community.matheno.com.
Войти
Вы можете бесплатно войти в систему, чтобы получить доступ ко всем нашим материалам, с помощью своей учетной записи Facebook, Google или Apple ИЛИ с помощью специальной учетной записи Matheno.