Lim n стремится к бесконечности: Mathway | Популярные задачи

2

Вокруг бесконечных пределов

На прошлой лекции мы обсуждали, как пределы взаимодействуют с арифметическими операциями, и выяснили, что взаимодействуют «хорошо». Однако, это только до тех пор, пока пределы существуют (как обычные вещественные числа). Тот факт, что предел последовательности, входящей в арифметическое выражение, может оказаться равен бесконечности (а также плюс бесконечности и минус бесконечности), сильно расширяет пространство возможностей. Иногда предел такого арифметического выражения удаётся найти однозначно, иногда же он может оказаться равен любому числу или бесконечности. Важно уметь различать эти случаи.

7.1Арифметика пределов и бесконечности

7.1.1Ошибочное и верное применение арифметики пределов

Для начала я приведу пример неверного применения арифметики пределов. Пример 1. Пусть мы хотим вычислить предел

limn→∞n2+2n2n2+3.

Следующая цепочка равенств содержит ошибку. Попробуйте найти её, не заглядывая ниже.

limn→∞n2+2n2n2+3=limn→∞(n2+2n)limn→∞(2n2+3)=∞∞=1.

Собственно, неверны все равенства. В первом равенстве, применяя теорему о пределе частного, мы предполагаем, что пределы числителя и знаменателя существуют. Однако, как мы выясняем в дальнейшем, они оба равны бесконечности, то есть не существуют. Это означает, что первый переход сделать нельзя. Второй и третий переходы просто не имеют смысла, поскольку ∞∞ — не является нормальным арифметическим выражением, и обычные правила арифметики здесь не работают — нельзя дробь «сократить на бесконечность».

Как следовало решать этот номер? Нужно было преобразовать дробь таким образом, чтобы пределы числителя и знаменателя существовали. Это можно сделать, разделив числитель и знаменатель на n2 (значение дроби от этого не поменяется, и n2 никогда не равно нулю, так что можно смело делить). Имеем:

limn→∞n2+2n2n2+3=limn→∞n2+2nn22n2+3n2=limn→∞1+2n2+3n2.

И вот теперь можно применить к этой дроби теорему о пределе частного:

limn→∞1+2n2+3n2=limn→∞(1+2n)limn→∞(2+3n3).

К пределам в числителе и знаменателе можно применить теорему о пределе суммы: первое слагаемое является константой и сходится само к себе, второе (в обоих случаях) стремится к нулю, как мы уже доказывали на семинарах. Значит числитель сходится к 1, знаменатель — к 2.

Теперь можно проследить, что каждое из правил арифметики пределов применено обоснованно. Теорема о пределе суммы к числителю и знаменателю была применена обоснованно, потому что предел каждого из слагаемых существует. Теперь мы видим, что теорема о пределе произведения ко всей дроби тоже была применена обоснованно: мы нашли предел числителя и знаменателя, они оказались конечными числами, предел знаменателя не равен нулю. Имеем:

limn→∞n2+2n2n2+3=12.

7.1.2Неопределенности

Допустим, мы хотели бы сформулировать какую-нибудь теорему вида «если an→∞ и bn→∞, то an/bn стремится туда-то». Покажем, что никакую теорему такого типа сформулировать нельзя: предел an/bn может быть любым. А именно:

• Он может быть любым вещественным ненулевым числом. Можно выбрать последовательности an=n и bn=An, где A — это число.
• Он может быть равен нулю. Предыдущий пример не работает (почему?), но работает такой: an=n, bn=n2.
• Он может равняться бесконечности и плюс бесконечности: положим an=n2 и bn=n.
• Минус бесконечности тоже может быть равен (придумайте пример самостоятельно).
• Может не иметь ни конечного, ни бесконечного предела (придумайте пример самостоятельно).

Краткое выражение этой мысли звучит так: «∞∞ является неопределенностью». Здесь под ∞∞ подразумевается не арифметическое выражение, а символическая запись, которая означает предел последовательности вида {an/bn}, где пределы числителя и знаменателя равны бесконечностям.

Приведём пример ещё одной неопределенности: (∞)+(∞). (Я взял каждую из бесконечностей в скобки, чтобы подчеркнуть, что это «бесконечности без знака».) Действительно, пусть мы знаем, что an→∞ и bn→∞. Что можно сказать про limn→∞(an+bn)? Он может равняться чему угодно:

• Любому вещественному числу A: возьмём an=n, bn=−n+A. (Напомним, что мы требуем, чтобы оба слагаемых стремились к бесконечности без знака, и значит {−n+A} подходит: по модулю эта последовательность становится сколь угодно большой.)
• Плюс бесконечности: возьмём an=n, bn=n.
• Минус бесконечности: возьмём an=−n, bn=−n.
• Не иметь ни конечного, ни бесконечного предела: возьмём an=n, bn=(−1)n⋅n.
• Бесконечности без знака, которая не является ни плюс, ни минус бесконечностью (придумайте пример).

Есть и другие примеры неопределенностей: 0/0, 0⋅∞, 1∞ и др.

Упражнение 1. Докажите, что 0/0 и 0⋅∞ тоже неопределенности, то есть могут принимать любые вещественные значения, а также стремиться к бесконечности.

С 1∞ мы разберёмся позже, когда обсудим логарифмы.

7.2«Арифметика бесконечностей»

Не все арифметические выражения с последовательностями, стремящимися к бесконечностям (или иначе нарушающими правила арифметики пределов), обязательно являются неопределенностями.

7.2.1Сумма плюс бесконечностей

Утверждение 1. Пусть an→+∞ и bn→+∞. Тогда (an+bn)→+∞. Неформально это утверждение можно записать так: (+∞)+(+∞)=+∞.

Доказательство. Как обычно в таких доказательствах, начнём с формализации:

Нам дано. ∀C1 ∃N=N1(C1) ∀n>N: an>C1;∀C2 ∃N=N2(C2) ∀n>N: bn>C2.(7.1)(7.2)

Хотим получить.

∀C ∃N=N(C) ∀n>N:an+bn>C.

Возьмём C1=C2=C/2. Тогда гарантированно C1+C2=C. Пусть N=max(N1(C/2),N2(C/2)). Тогда для всех n>N выполняются неравенства в конце (7.1) и (7.2). Их можно сложить и получить:

an+bn>C1+C2=C.

Что и требовалось.∎

Конечно, можно было догадаться до ответа, и не записывая всё это рассуждение. Можно было думать так: нам сказано, что an и bn с течением времени становятся о-о-очень большими, причём не по модулю большими, а на самом деле большими (положительными и большими). Значит, их сумма тоже будет очень большой.

Заметим, что это рассуждение не работает в том случае, когда an или bn стремятся не к плюс бесконечности, а к бесконечности без знака: если два числа велики по модулю, мы не можем сказать, что их сумма большая по модулю: они могут оказаться разных знаков и «сократить» друг друга.

7.2.2Деление на ноль и на бесконечность

Рассмотрим ещё пару примеров, связанных с делением.Утверждение 2. Пусть an→∞. Тогда 1an→0. Неформально можно записать так: 1∞=0. Доказательство. Ну, как обычно.

Имеем.

∀C ∃N=N1(C) ∀n>N:|an|>C.

Хотим доказать.

∀ε>0 ∃N=N(ε) ∀n>N:|1/an|<ε.

Теперь можно доказывать. Для всякого ε>0 положим C:=1/ε. Возьмём N:=N1(1/ε). Тогда для всех n>N:

|an|>C=1ε.

Умножим на ε и разделим на |an| (поскольку |an|>C>0, на него можно делить):

∣∣∣1n∣∣∣=1|an|<ε.

Что и требовалось.∎

Утверждение 3. Пусть an→0 и для всех n, an≠0. Тогда 1/an→∞. Неформально можно записать так: 1/0=∞. (Ура! Нам разрешили делить на ноль! Хоть и только неформально.)

Доказательство. Нужно повторить предыдущее доказательство «наоборот».

Имеем.

∀ε>0 ∃N=N1(ε) ∀n>N:|an|<ε.

Хотим доказать.

∀C ∃N=N(C) ∀n>N:∣∣∣1an∣∣∣>C.

Докажем. Если C≤0, то подойдёт любое N, потому что |an|≥0 всегда. Пусть теперь C>0. Положим ε=1/C (это можно сделать, потому что C>0 и тогда обязательно получится ε>0) и возмём N:=N1(1/C). Тогда для всех n>N:

|an|<ε.

Поделим всё на |an|ε (имеем право, потому что an≠0 и значит |an|ε>0). Тогда для всех n>N:

∣∣∣1an∣∣∣=1|an|>1ε=C.

Что и требовалось.∎

7.3Заключение

Мир последовательностей за пределами «арифметики пределов» выглядит непривычно: например, похожие выражения могут приводить к очень разным результатам (сравните (∞)+(∞) и (+∞)+(+∞)). Нам нужно приобрести интуицию, чтобы научиться делать выводы о последовательностях, анализируя формулы для их общего члена, не занимаясь каждый раз утомительным доказательством через определения. В каких-то случаях мы сможем свести всё к конечным пределам и воспользоваться арифметикой пределов. В каких-то нам придётся разбираться с бесконечностями. Иногда нас будет интересовать не предел, а более грубые свойства последовательности — например, ограниченность. Невозможно запастись теоремами на все случаи жизни — именно поэтому мы изучаем, как они доказываются, чтобы при необходимости уметь доказывать похожие утверждения — ровно те, которые нам нужны для конкретного случая.

Как обычно, ключ к успеху — самостоятельное решение задач.

---

← Предыдущая глава Следующая глава →

0 lim

Вы искали 0 lim? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 1 0 lim, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «0 lim».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 0 lim,1 0 lim,1 lim,1 x предел,cosx x предел,lim,lim 0,lim 0 1,lim 0 x,lim 0 бесконечность,lim 1,lim 1 0,lim 1 x 1,lim 1 равен,lim a x,lim a x a lim x,lim f x бесконечность,lim n,lim n стремится к бесконечности,lim n стремится к бесконечности n,lim n стремится к бесконечности как решать,lim sin,lim sinx,lim tgx,lim x,lim x 0,lim x 0 1 x 0,lim x 0 x 1 x,lim x 0 x sinx,lim x 1,lim x 2 a 2 x a,lim x a 1 x 1,lim x n 1 x 1,lim x бесконечность,lim x стремится,lim x стремится к,lim x стремится к 0,lim x стремится к 0 sinx x,lim x стремится к 0 x tgx,lim x стремится к 0 как решать,lim x стремится к 1,lim x стремится к бесконечности,lim x стремится к бесконечности x,lim x стремится к бесконечности как решать,lim алгебра,lim в математике,lim в математике что это,lim в математике это,lim как решить,lim математика,lim пределы,lim решение,lim стремится к 0,lim стремится к бесконечности,lim формулы,lim функции,lim что значит,lim что такое,lim что это,lim что это в математике,lim что это в физике,lim это,lim это в математике,lim это что,x lim,x lim 0,алгебра lim,виды пределов,вычисление лимитов,вычисление предела,вычисление предела функции,вычисление пределов,вычисление пределов с подробным решением,вычисление пределов функции,вычисление пределов функций,вычисления пределов,вычислите предел,вычислите предел функции,вычислите пределы,вычислить предел,вычислить предел функции,вычислить предел функции lim,вычислить пределы,вычислить пределы функции,вычислить пределы функций,вычислить функции пределы,если предел равен 0,если предел стремится к бесконечности,как вычислить предел,как вычислить предел функции,как вычислить пределы,как вычислять пределы,как вычислять пределы функции,как искать пределы,как найти предел,как найти предел функции,как найти предел функции примеры решения,как найти пределы,как находить предел,как находить пределы,как находить пределы функций,как понять пределы,как посчитать предел,как решать lim,как решать предел функции,как решать пределы функции,как решить lim,как решить предел,как решить пределы,как считать предел,как считать пределы,как считать пределы функций,лим в математике,лим математика,лим что такое в математике,лимит алгебра,лимит найти,лимит функции,лимиты и пределы,лимиты математика,математика lim,математика лим,математика пределы функций объяснение с нуля,математика решение пределов,найдите предел,найдите предел функции lim,найдите пределы,найти предел,найти предел lim x стремится к бесконечности,найти предел функции,найти пределы,найти пределы как,найти пределы функции,найти пределы функций,найти указанные пределы,нахождение предела,нахождение предела функции,нахождение пределов,нахождение пределов функции,понятие предела,предел,предел 0 1,предел 1,предел 1 0 равен,предел 1 x,предел 1 x 1,предел 1 равен 0,предел x 1 x,предел в алгебре,предел как найти,предел как находить,предел как посчитать,предел как решать,предел как считать,предел посчитать,предел при x стремящемся к 0,предел при х стремящемся к бесконечности,предел равен 0 когда,предел решение,предел стремится к бесконечности,предел стремится к нулю,предел стремящийся к бесконечности,предел функции,предел функции в математике это,предел функции в точке примеры решения,предел функции вычисление предела функции,предел функции как найти,предел функции как решать,предел функции примеры,предел функции решение,предел функции формулы,предел функции это в математике,предел функций,предел х в степени х,предел х при х стремящемся к бесконечности,предел х стремится к 0,предел х стремится к бесконечности,предел х стремится к бесконечности х,предел что такое,предел что это,предел это,предел это что такое,предела,предела значение,предела решение,пределе,пределов функции решение,пределы,пределы lim,пределы и лимиты,пределы как вычислить,пределы как искать,пределы как найти,пределы как понять,пределы при х стремится к бесконечности,пределы решать,пределы решение,пределы решить,пределы стремящиеся к бесконечности,пределы функции,пределы функции как решать,пределы функции примеры,пределы функции решение,пределы функций,пределы функций примеры,пределы что такое,пределы что это,пределы это,пределы это что,придел это,примеры предел функции,примеры пределы функции,расчет пределов,решать пределы,решение lim,решение лимитов,решение предел,решение предел функции,решение предела,решение пределов,решение пределов функции,решение пределов функций,решение пределы,решение функции пределов,решение функций пределов,решения пределов,решения пределы,решить предел,решить пределы,стремится к бесконечности,стремится к нулю предел,формулы lim,функции lim,функции пределы как решать,функции пределы примеры,что такое lim,что такое lim в алгебре,что такое lim в математике,что такое в математике lim,что такое в физике lim,что такое предел. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 0 lim. Просто введите задачу в окошко и нажмите «решить» здесь (например, 1 lim).

Где можно решить любую задачу по математике, а так же 0 lim Онлайн?

Решить задачу 0 lim вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Вопрос 5!

Сходящиеся последовательности и их свойства

Рассмотрим числовые последовательности.

Последовательность (x_n) действительных чисел называетсясходящейся, если существует действительное числоaи для произвольногоε> 0 существует натуральное числоmтакое, что для всехn>mсправедливо неравенство |x_n–a| <ε.

При этом число aназываютпределом последовательности(x_n), что символически записываютилиx_n→aприn→ ∞.

С помощью логических символов определение запишется следующим образом: числовая последовательность (x_n) называетсясходящейся, если

Вопрос 6! Бесконечно большие и бесконечно малые последовательности

   Определение. Последовательность { х_n} называется бесконечно большой, если для как угодно большого любого положительного числа А существует номер N, зависящий от этого числа А, такой, что для всех последующих номеров n > N выполняется неравенство | x_n | > A:

   Замечание. Очевидно, что любая бесконечно большая последовательность является неограниченной. Однако неограниченная последовательность может и не быть бесконечно большой. Например, неограниченная последовательность 1, 2, 1, 3, …, 1, n + 1, … не является бесконечно большой, поскольку при A > 1 неравенство | x_n| > A выполняется не для всех элементов x_n с нечетными номерами.    Определение. Последовательность {α_n} называется бесконечно малой, если для любого как угодно малого положительного числа ε > 0 существует номер N, зависящий от этого ε, такой, что для любых n > N выполняется неравенство |α_n| < ε:

Связь между бесконечно малыми и бесконечно большими последовательностями

   Теорема 1. Если { х_n} — бесконечно большая последовательность и все ее члены отличны от нуля, то последовательность

бесконечно малая, и, обратно, если {α_n} — бесконечно малая последовательность и все её члены отличны от нуля {α_n} ≠ 0, то последовательность { 1 / α_n } – бесконечно большая.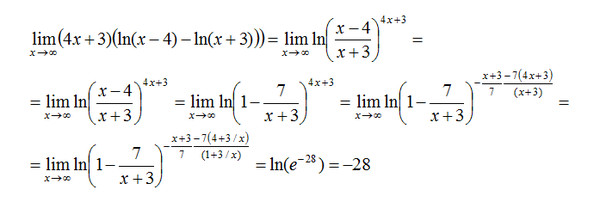   Доказательство. Пусть { х_n} — бесконечно большая последовательность. Возьмем любое как угодно малое положительное число ε > 0 и положим

Согласно определению для этого существует такой номер N , что при n > N будет | x_n | > A. Отсюда получаем, что

для всех n > N. А это значит, что последовательность

бесконечно малая.

Вопрос 7!!! Теорема об ограниченности сходящейся последовательности

  Если последовательность имеет конечный предел, то последовательность ограничена. Определение. Числовая последовательность {x_n} ограничена, если существует такое конечное числоК, что для всех n выполнено

d(x_n,a) <K.

  Доказательство. Пусть

Тогда

N: n > N: d (x_n, a) < 1.

 Внутри окрестности радиусаR= 1 бесконечное число точек, а вне этой окрестности конечное число точек, допустим, что это точкиx₁,x₂, …x_N. Выберем число

,

тогда уже для всех nбудет выполнено

d(x_n,a) <K.

Вопрос 8!!

“Единственность предела числовой последовательности”

Определение: Если последовательность an имеет предел, то этот предел единственный.Используются 3 основных стиля:

Доказательство(от противного): Допустим, что этот предел не единственный, т.е. существует 2-а предела последовательности, отличных друг от друга : lim(при n -> к бесконечности) an = в1 ; lim(при n -> к бесконечности) an = в2 ; в1 = в2Рассмотрим число А = (в1 + в2)/2 (рисунок на прямой со стрелочкой взят отрезок в1в2 и А – середина отрезка) В1 < A, тогда найдётся номер №1 ; A(наоб-т)n > №1 : an < A (по свойству если дана последовательность an lim (n стремится к бесконечности) an = в, в>@, то начиная с некоторого номера все члены будут меньше @). в2>A, тогда найдётся номер №2, такой что для любого n > №2 выполняется неравенство : an > A.Пусть № = max {№1 ; №2}, и для любого n > №, выполянются оба неравенства одновременно, следовательно, для любого члена любого члена последовательности выполняется неравенство: A < an < A -а это противоречие.

Свойство №1: Пусть дана последовательность an lim (n стремится к бесконечности) an = в, в>@, то начиная с некоторого номера все члены последовательности будут меньше @). Следствие: Если в > B, то начиная с некоторого номера, все члены последовательности будут больше B. Если @ < в < B, то начиная с некоторого номера все члены последовательности будут удовлетворять неравенству : @ < an < B

Свойство №2:“Ограниченность последовательности имеющей предел”: Если lim(n стремящаяся к бесконечности) an = в, то последовательность является ограниченной и для всех её членов выполянется неравенство @ < an < B.

Теоремы о пределах: пусть имеются 2-е последовательности {an}, {вn} => lim(n стремится к бесконечности)an = a ; lim(n стремится к бесконечности) вn = в

–lim(n стремится к бесконечности) (an + вn) = lim(n стремится к бесконечности) an + lim(n стремится к бесконечности) вn = a + в –lim(n стремится к бесконечности) (an + вn) = lim(n стремится к бесконечности) an + lim(n стремится к бесконечности) вn = a – в –lim(n стремится к бесконечности) (an * вn) = lim(n стремится к бесконечности) an * lim(n стремится к бесконечности) вn = a * в –lim(n стремится к бесконечности) (an / вn) = lim(n стремится к бесконечности) an / lim(n стремится к

Поведение функции от n когда n стремится к бесконечности

Содержание:

Поведение функции от n когда n стремится к бесконечности

• Поведение функции n%, когда n имеет тенденцию быть бесконечным. Здесь, основываясь на замечаниях, сделанных в предыдущем абзаце, мы рассмотрим некоторые предложения, которые всегда встречаются в высшей математике. рассматривать Например, следующие два утверждения: (a) -small for large Значение n, (b) 1 -… приблизительно равно 1 для больших значений n. Несмотря на то, что они могут показаться очень очевидными, они содержат много достойного внимания читателя.

Сначала рассмотрим (а) несколько простое предложение. Это, как мы видели, неравенство <ГГ0,001 / Конкретное определенное значение, в данном случае более 1000. Следующее утверждение также сохраняется: * ~ Менее 0,0001 Если значение pi \ большое, если n> 10000, оно на самом деле равно 0,0001. Вы можете использовать 0,00001 или 0,000001, или любое положительное число вместо 0,001 или 0,0001.

Если круговая стоимость велика, мы уже рассматриваем заявления ниже 0,001. Людмила Фирмаль

Очевидно, что полезно следующее короткое выражение: Тип заявления Если значение l «большое, оно будет больше 0,001.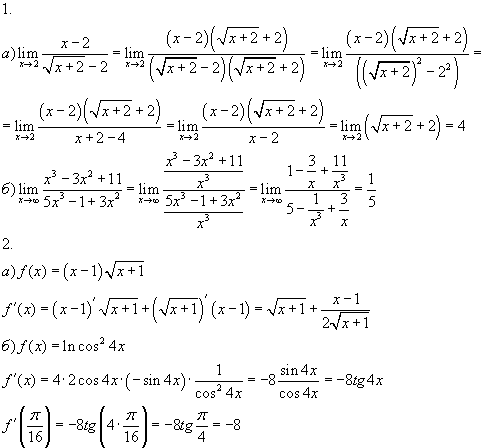 мало.

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

• Как приятно Следовательно, (b) на самом деле <p (/ 2) = 1- Во-вторых, утверждение 1 — cp (/ r) <8 сохраняется для достаточно больших значений η, независимо от положительного значения, назначенного b (например, 0,001 или 0,0001). Какое утверждение (б) 1 — Очевидно, учитывая тот факт, что cp (x) = -. Существует другой способ выражения фактов, содержащихся в утверждениях (а) и (b) и предложенных в пункте 55. Если значение r велико, говорят, что «когда n становится со (или когда n становится со), оно стремится стать 0». Аналогично, «1 — стремится к 1 для n». Эти утверждения следует считать строго эквивалентными утверждениям (а) и (б).

Эквивалентно более формальным предложениям, которые эквивалентны друг другу: «Если b — любое небольшое положительное число, Для достаточно больших значений l, Или даже более формальные предложения: «Если 5 — небольшое положительное число, Вы можете найти число nf) i такое, что k больше / rn для всех значений n.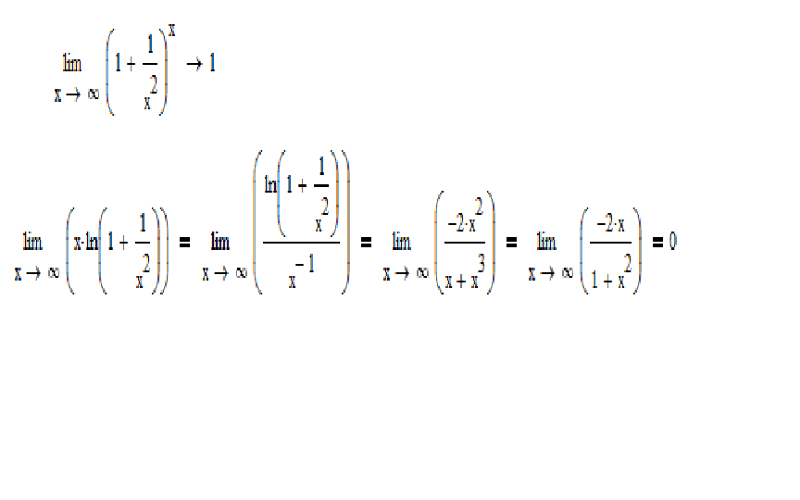 — <0,0000001, как только я> 10 000 000 и т. Д. здесь В простом случае ясно, что читатель выигрывает конфликт. Далее я представлю другой способ выражения Свойства функции. «Предел-I, N Если co (или n имеет тенденцию быть co), оно равно 0. Это утверждение *) lim i = 0, Я с п Или просто lim- = 0. 1 р 0 для -n -oo, Это можно прочитать следующим образом: Если n имеет тенденцию быть соевым, это имеет тенденцию быть 0. Или просто «как, мы пишем lim (l-M = l, lim (l- = 1, „-. Итак \ n) \ n, 1 Или 1 — V 1. N

Далее рассмотрим другой пример: 9 (h) = riK Если n большое, n2 большое. Это утверждение эквивалентно следующему более формальному утверждению: Если D — любое большое положительное число, для достаточно больших значений n * y / 2r> D Вы можете найти число 00 ()), которое будет я3]> для всех n больше, чем «0 ()). В этом случае «n2 имеет тенденцию быть oo, и n имеет тенденцию быть co», или пn становится г с oq, « п2-> оо.

Наконец, рассмотрим функцию <p (η) = -Λ2.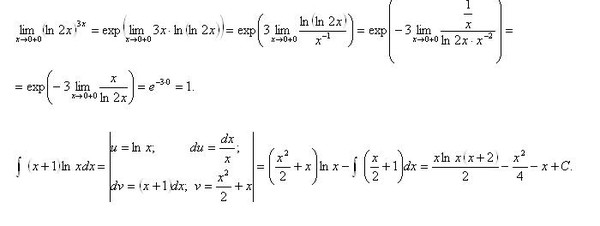 В этом случае 9 (i) велико, но если n велико, оно отрицательно, и описывается «-l * становится -co, а n имеет тенденцию быть со». -г г-с. В этом смысле использование символа -co может потребовать некоторых удобных обозначений. Вместо π — * — оо. В общем Может быть удобно использовать символ -j-oo вместо co для объединения обозначений. Однако во всех этих утверждениях символы oo, -j-oo и -so не означают ничего отдельно, они приобретают конкретное значение только тогда, когда они определены в определенном контексте, и их значение определено Приведенное выше объяснение следует подчеркнуть еще раз.

Как считать пределы

В учебниках по математическому анализу значительное внимание уделяется приемам вычисления пределов функций и последовательностей. Существуют готовые правила и методы, применяя которые, можно с легкостью решать даже относительно сложные задачи на пределы.

В математическом анализе существуют понятия пределов последовательностей и функций. Когда требуется найти предел последовательности, это записывают следующим образом: lim xn=a. 2 стремится к нулю.

Обычно переменная величина x стремится к конечному пределу a, причем, x постоянно приближается к a, авеличина a постоянна. Это записывают следующим образом: limx =a, при этом, n также может стремиться как к нулю, так и к бесконечности. Существуют бесконечные функции, для них предел стремится к бесконечности. В других случаях, когда, например, функцией описывается замедление хода поезда, можно говорить о пределе, стремящемся к нулю.
У пределов имеется ряд свойств. Как правило, любая функция имеет только один предел. Это главное свойство предела. Другие их свойства перечислены ниже:
* Предел суммы равен сумме пределов:
lim(x+y)=lim x+lim y
* Предел произведения равен произведению пределов:
lim(xy)=lim x*lim y
* Предел частного равен частному от пределов:
lim(x/y)=lim x/lim y
* Постоянный множитель выносят за знак предела:
lim(Cx)=C lim x
Если дана функция 1 /x, в которой x →∞, ее предел равен нулю. Если же x→0, предел такой функции равен ∞.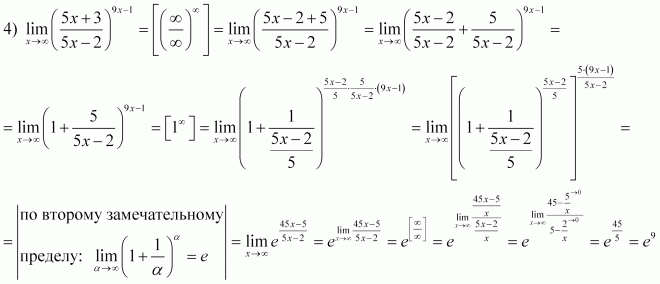
Для тригонометрических функций имеются исключения из этих правил. Так как функция sin x всегда стремится к единице, когда приближается к нулю, для нее справедливо тождество:
lim sin x/x=1

x→0

В ряде задач встречаются функции, при вычислении пределов которых возникает неопределенность – ситуация, при которой предел невозможно вычислить. Единственным выходом из такой ситуации становится применение правила Лопиталя. Существует два вида неопределенностей:
* неопределенность вида 0/0
* неопределенность вида ∞/∞
К примеру, дан предел следующего вида: lim f(x)/l(x), причем, f(x0)=l(x0)=0. В таком случае, возникает неопределенность вида 0/0. Для решения такой задачи обе функции подвергают дифференцированию, после чего находят предел результата. Для неопределенностей вида 0/0 предел равен:
lim f(x)/l(x)=lim f'(x)/l'(x) (при x→0)
Это же правило справедливо и для неопределенностей типа ∞/∞. Но в этом случае справедливо следующее равенство: f(x)=l(x)=∞
С помощью правила Лопиталя можно находить значения любых пределов, в которых фигурируют неопределенности. (n-1)

Решение пределов с дробями из многочленов

Здесь мы рассмотрим примеры и методы решения пределов функций, составленных из отношений многочленов. Это дроби из многочленов и разности дробей. Обзор и обоснование методов решения пределов изложены на странице «Методы вычисления пределов функций и раскрытия неопределенностей».

Методы решения пределов дробей из многочленов

1. Рассмотрим предел функции, которая является отношением многочленов:
, где
(1)   ,
и – многочлены степеней m и n, соответственно:
;
.

1.1. Пусть есть бесконечность:
.
Тогда возникает неопределенность вида . Для ее раскрытия, нужно числитель и знаменатель дроби разделить на x^s, где s – наибольшее из чисел m и n.   Примеры ⇓

1.2. Пусть есть конечное число. Найдем значение знаменателя дроби, подставив :
.
1.2.1. Если , то неопределенности нет. Функция определена и непрерывна при . Значение предела равно значению функции в точке :
.   Пример ⇓

1.2.2. Если знаменатель равен нулю, а числитель нет: ,
то неопределенность также отсутствует. Предел равен бесконечности:
.   Пример ⇓

1.2.3. Пусть теперь и числитель, и знаменатель равны нулю:
.
В этом случае у нас возникает неопределенность вида 0/0. Для ее раскрытия, делим числитель и знаменатель на . Деление можно выполнять либо уголком, либо в уме, приравнивая коэффициенты при одинаковых степенях переменной x.   Примеры ⇓

2. Теперь рассмотрим пределы от суммы или разности отношений многочленов. В этом случае, может возникнуть неопределенность вида бесконечность плюс-минус бесконечность: . Для ее раскрытия, нужно привести дроби к общему знаменателю. В результате получим предел от функции вида (1), методы решения которого мы уже рассмотрели.   Пример ⇓

Примеры решений

Все примеры Далее мы приводим подробные решения пределов дробей из многочленов.
⇓   ⇓   ⇓   ⇓   ⇓   ⇓   ⇓   ⇓   ⇓   ⇓

Пределы при x стремящемся к бесконечности

Пример 1

Все примеры ⇑ Найти предел отношения многочленов при x стремящемся к бесконечности:
.

Решение

Разделим числитель и знаменатель дроби на . При имеем:
.
На основании свойств степенной функции,   при  . Применяя арифметические свойства предела функции, находим:
.

Ответ

.

Пример 2

Все примеры ⇑ Найти предел функции, которая является отношением многочленов:
.

Решение

Разделим числитель и знаменатель дроби на . При имеем:
.
Применяя арифметические свойства предела функции, находим:
.

Ответ

.

Пример 3

Все примеры ⇑ Найти предел:
.

Решение

Разделим числитель и знаменатель дроби на . При имеем:
.
Применим арифметические свойства предела функции к числителю и знаменателю:
;
.
Применим свойства бесконечно малых и бесконечно больших функций:
.

Мы получили правильную величину предела: . Но бесконечно удаленная точка может включать в себя два частных случая: и . Как , так и являются . Если и, для достаточно больших |x|, , то .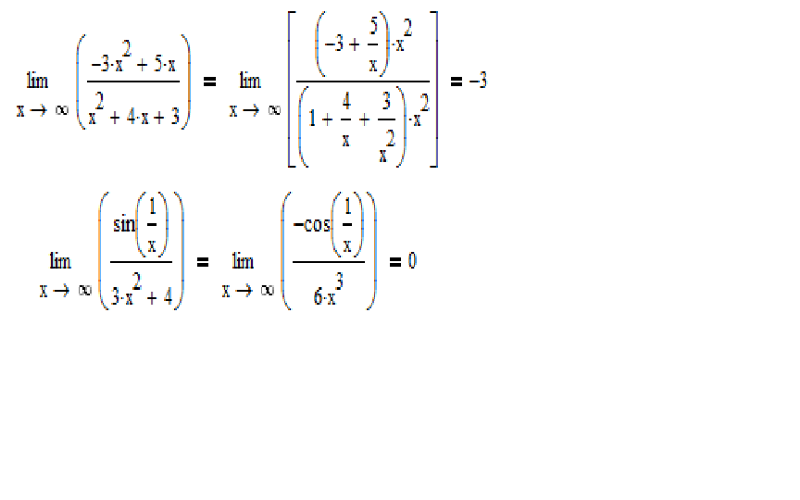 Если, для достаточно больших |x|, то .

Выясним, имеет ли наш предел определенный знак? Для этого преобразуем знаменатель и переведем бесконечно большую часть в числитель:
;
.
Поскольку , то . Тогда

.

Ответ

.

Пределы в конечной точке

Пример 4. Непрерывные функции

Все примеры ⇑ Найти пределы функции

a) при ;   б) при .

Решение

а) Найдем значение знаменателя в точке :
.
Поскольку знаменатель не обращается в нуль, то функция непрерывна в точке . Поэтому предел функции равен ее значению при :
.

б) Найдем значение знаменателя в точке :
.
Здесь также знаменатель не обращается в нуль. Функция непрерывна. Ее предел при равен значению при :
.

Ответ

а) ;   б) .

Пример 5. Бесконечно большие функции

Все примеры ⇑ Задана функция в виде отношения многочленов:
.
Найти односторонние пределы:
а) ;   б) .

Решение

Найдем значение знаменателя дроби в точке :
.
Знаменатель равен нулю. Поэтому функция не является непрерывной при . Выясним, есть ли неопределенность вида 0/0? Для этого найдем значение числителя в этой точке:
.
Числитель не равен нулю. Поэтому неопределенности вида 0/0 нет. Предел при равен бесконечности:
.

Но нам нужно найти односторонние пределы. Для этого выделим из многочлена в знаменателе множитель . То есть представим знаменатель в следующем виде:
.
Раскрываем скобки:

.
Сравнивая левую и правую части, находим:
.
Отсюда ,
;
.

Функция непрерывна в точке , поскольку знаменатель дроби не обращается в нуль. При , имеем:
.
Тогда
;
  при  .
а) Подставим :
.
б) Подставим :
.

Ответ

а) ,   б) .

Если бы знаменатель дроби не равнялся нулю при , то функция была бы непрерывной в точке . В этом случае, пределы слева и справа были бы равны:
.

Неопределенность вида 0/0

Пример 6

Все примеры ⇑ Найти предел
.

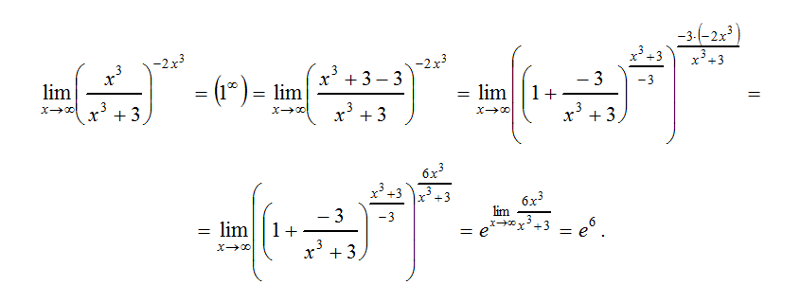
Решение

Найдем значение знаменателя дроби при :

.
Знаменатель дроби равен нулю. Поэтому функция не определена и, следовательно, не является непрерывной в точке .

Найдем значение числителя при :
.
Числитель дроби также равен нулю. Мы имеем неопределенность вида 0/0. Для ее раскрытия, выделим в многочленах множитель .

Ищем разложение знаменателя в виде:
.
Раскрываем скобки и группируем члены с одинаковыми степенями x:

.
Сравнивая левую и правую части, находим:
.
Отсюда ,
.

На практике, нет необходимости выписывать неопределенные коэффициенты разложения, а затем решать систему уравнений. Подобные вычисления легко проводить в уме. Для числителя имеем:
.

Находим предел:

.

Ответ

.

Пример 7

Все примеры ⇑ Найти предел отношения многочленов:
.

Решение

Найдем значение знаменателя при :
.
Знаменатель равен нулю. Поэтому функция не является непрерывной в точке .

Найдем значение числителя дроби при :
.
Числитель дроби также равен нулю. У нас неопределенность вида 0/0. Для ее раскрытия, выделим в многочленах множитель .

Вычисления делаем в уме:
,
.
Делим числитель и знаменатель на . Тогда при имеем:
.

Снова находим значения числителя и знаменателя при : ;
.
Опять неопределенность 0/0. Снова выделяем множитель :
;
.

При имеем:
.
Функция непрерывна в точке , поскольку знаменатель дроби не равен нулю при . Поскольку функции и отличаются только в одной точке ( определена и непрерывна при , а не определена), то их пределы в любой точке равны (см. «Влияние значений функции в конечном числе точек на величину предела»). Находим искомый предел:
.

Ответ

.

Пример 8. Неопределенность вида ∞

&pm;∞

Все примеры ⇑ Найти предел разности дробей из многочленов:
.

Решение

При имеем:
;
;
;
.
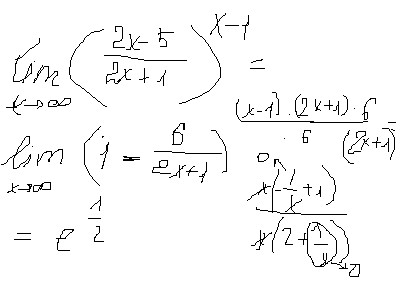
Поскольку знаменатель каждой из дробей равен нулю, а числители отличны от нуля, то при , каждая из дробей стремится к бесконечности:
  при  .
То есть мы имеем неопределенность вида “бесконечность минус бесконечность”.

Для раскрытия неопределенности, приводим дроби к общему знаменателю. Чтобы упростить выкладки, предварительно выделим в знаменателях дробей множитель .
;
;


;
.

Таким образом, задача свелась к вычислению предела от дроби многочленов:
.
Применяем описанные выше методы.

Находим значения числителя и знаменателя при :
;
.
Поскольку числитель и знаменатель равны нулю, то это неопределенность вида 0/0. В знаменателе множитель уже выделен. Выделим этот множитель в числителе:
.
Находим предел:

.

Ответ

.

Автор: Олег Одинцов.     Опубликовано: 23-01-2019

Mathway | Популярные задачи

1	Найдите производную – d / dx	натуральное журнал x
2	Оцените интеграл	интеграл натурального логарифма x относительно x
3	Найдите производную – d / dx	е ^ х
4	Оцените интеграл	интеграл от e ^ (2x) относительно x
5	Найдите производную – d / dx	1 / х
6	Найдите производную – d / dx	х ^ 2
7	Найдите производную – d / dx	1 / (х ^ 2)
8	Найдите производную – d / dx	грех (х) ^ 2
9	Найдите производную – d / dx	сек (x)
10	Оцените интеграл	интеграл e ^ x относительно x
11	Оцените интеграл	интеграл x ^ 2 относительно x
12	Оцените интеграл	интеграл квадратного корня x относительно x
13	Найдите производную – d / dx	соз (х) ^ 2
14	Оцените интеграл	интеграл от 1 / x по отношению к x
15	Оцените интеграл	интеграл sin (x) ^ 2 относительно x
16	Найдите производную – d / dx	х ^ 3
17	Найдите производную – d / dx	сек (x) ^ 2
18	Оцените интеграл	интеграл cos (x) ^ 2 относительно x
19	Оцените интеграл	интеграл от sec (x) ^ 2 относительно x
20	Найдите производную – d / dx	е ^ (х ^ 2)
21	Оцените интеграл	интеграл от 0 до 1 кубического корня из 1 + 7x относительно x
22	Найдите производную – d / dx	грех (2x)
23	Найдите производную – d / dx	загар (x) ^ 2
24	Оцените интеграл	интеграл 1 / (x ^ 2) относительно x
25	Найдите производную – d / dx	2 ^ х
26	График	натуральное бревно из
27	Найдите производную – d / dx	cos (2x)
28	Найдите производную – d / dx	хе ^ х
29	Оцените интеграл	интеграл от 2x относительно x
30	Найдите производную – d / dx	(натуральный логарифм x) ^ 2
31	Найдите производную – d / dx	натуральный логарифм (x) ^ 2
32	Найдите производную – d / dx	3x ^ 2
33	Оцените интеграл	интеграл xe ^ (2x) относительно x
34	Найдите производную – d / dx	2e ^ x
35	Найдите производную – d / dx	натуральное бревно 2x
36	Найдите производную – d / dx	-sin (х)
37	Найдите производную – d / dx	4x ^ 2-x + 5
38	Найдите производную – d / dx	y = 16 корень четвертой степени из 4x ^ 4 + 4
39	Найдите производную – d / dx	2x ^ 2
40	Оцените интеграл	интеграл от e ^ (3x) относительно x
41	Оцените интеграл	интеграл от cos (2x) относительно x
42	Найдите производную – d / dx	1 / (квадратный корень из x)
43	Оцените интеграл	интеграл e ^ (x ^ 2) относительно x
44	Оценить	e ^ бесконечность
45	Найдите производную – d / dx	х / 2
46	Найдите производную – d / dx	-cos (x)
47	Найдите производную – d / dx	грех (3x)
48	Найдите производную – d / dx	1 / (х ^ 3)
49	Оцените интеграл	интеграл tan (x) ^ 2 относительно x
50	Оцените интеграл	интеграл 1 по x
51	Найдите производную – d / dx	х ^ х
52	Найдите производную – d / dx	x натуральное бревно x
53	Найдите производную – d / dx	х ^ 4
54	Оценить предел	предел, когда x приближается к 3 из (3x-5) / (x-3)
55	Оцените интеграл	интеграл x ^ 2 натуральный логарифм x относительно x
56	Найдите производную – d / dx	f (x) = квадратный корень из x
57	Найдите производную – d / dx	х ^ 2sin (х)
58	Оцените интеграл	интеграл sin (2x) относительно x
59	Найдите производную – d / dx	3e ^ x
60	Оцените интеграл	интеграл xe ^ x относительно x
61	Найдите производную – d / dx	у = х ^ 2
62	Найдите производную – d / dx	квадратный корень из x ^ 2 + 1
63	Найдите производную – d / dx	грех (x ^ 2)
64	Оцените интеграл	интеграл от e ^ (- 2x) относительно x
65	Оцените интеграл	интеграл натурального логарифма квадратного корня x относительно x
66	Найдите производную – d / dx	е ^ 2
67	Найдите производную – d / dx	х ^ 2 + 1
68	Оцените интеграл	интеграл sin (x) относительно x
69	Найдите производную – d / dx	арксин (х)
70	Оценить предел	предел, когда x приближается к 0 of (sin (x)) / x
71	Оцените интеграл	интеграл e ^ (- x) относительно x
72	Найдите производную – d / dx	х ^ 5
73	Найдите производную – d / dx	2 / х
74	Найдите производную – d / dx	натуральное бревно из 3х
75	Найдите производную – d / dx	х ^ (1/2)
76	Найдите производную – d / d @ VAR	f (x) = квадратный корень из x
77	Найдите производную – d / dx	соз (х ^ 2)
78	Найдите производную – d / dx	1 / (х ^ 5)
79	Найдите производную – d / dx	кубический корень из x ^ 2
80	Оцените интеграл	интеграл cos (x) относительно x
81	Оцените интеграл	интеграл e ^ (- x ^ 2) относительно x
82	Найдите производную – d / d @ VAR	е (х) = х ^ 3
83	Оцените интеграл	интеграл от 0 до 10 из 4x ^ 2 + 7 по x
84	Оцените интеграл	интеграл (натуральный логарифм x) ^ 2 относительно x
85	Найдите производную – d / dx	журнал x
86	Найдите производную – d / dx	арктан (x)
87	Найдите производную – d / dx	натуральное бревно 5x
88	Найдите производную – d / dx	5e ^ x
89	Найдите производную – d / dx	cos (3x)
90	Оцените интеграл	интеграл x ^ 3 относительно x
91	Оцените интеграл	интеграл x ^ 2e ^ x относительно x
92	Найдите производную – d / dx	16 корень четвертой степени из 4x ^ 4 + 4
93	Найдите производную – d / dx	х / (е ^ х)
94	Оценить предел	предел, когда x приближается к 3 от arctan (e ^ x)
95	Оцените интеграл	интеграл от (e ^ x-e ^ (- x)) / (e ^ x + e ^ (- x)) относительно x
96	Найдите производную – d / dx	3 ^ х
97	Оцените интеграл	интеграл xe ^ (x ^ 2) относительно x
98	Найдите производную – d / dx	2sin (x)
99	Оценить	сек (0) ^ 2
100	Найдите производную – d / dx	натуральный логарифм x ^ 2

Экспоненциальный предел (1 + 1 / n) ^ n = e | eMathZone

В этом руководстве мы обсудим очень важную формулу пределов, \ [\ mathop {\ lim} \ limits_ {x \ to \ infty} {\ left ({1 + \ frac {1} {x}} \ right) ^ x} = e \]

Рассмотрим отношение
\ [{\ left ({1 + \ frac {1} {x}} \ right) ^ x} \]

Мы докажем эту формулу с помощью разложения в биномиальный ряд. x} = e \]

Исчисление I – Пределы в бесконечности, часть I

Показать общее уведомление Показать мобильное уведомление Показать все заметки Скрыть все заметки

Это немного заранее, но я хотел сообщить всем, что мои серверы будут проходить техническое обслуживание 17 и 18 мая с 8:00 AM CST до 14:00 PM CST.Будем надеяться, что единственное неудобство будет заключаться в периодическом «потерянном / разорванном» соединении, которое следует исправить, просто перезагрузив страницу. В остальном обслуживание (скрестив пальцы) должно быть «невидимым» для всех.

Пол
6 мая 2021 г.

Похоже, вы используете устройство с “узкой” шириной экрана (, т.е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 2-7: Пределы в бесконечности, Часть I

В предыдущем разделе мы видели пределы, которые были бесконечностью, и теперь пора взглянуть на пределы в бесконечности.Под предельными значениями на бесконечности мы понимаем один из следующих двух пределов.

\ [\ mathop {\ lim} \ limits_ {x \ to \ infty} f \ left (x \ right) \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ mathop {\ lim} \ limit_ {x \ to – \ infty} f \ left (x \ right) \]

Другими словами, мы собираемся посмотреть, что произойдет с функцией, если мы позволим \ (x \) стать очень большим в положительном или отрицательном смысле. r}}} = 0 \]

Если задуматься, первая часть этого факта должна иметь смысл.{r} \) определяется для отрицательного \ (x \). Это условие здесь, чтобы избежать таких случаев, как \ (r = \ frac {1} {2} \). Если бы это \ (r \) было разрешено, мы извлекали бы квадратный корень из отрицательных чисел, которые были бы комплексными, и мы хотим избежать этого на этом уровне.

Обратите внимание, что знак \ (c \) не повлияет на ответ. Независимо от знака \ (c \) у нас все равно будет постоянная, деленная на очень большое число, что приведет к очень маленькому числу, и чем больше \ (x \), тем меньше становится дробь.Знак \ (c \) будет влиять на то, в каком направлении дробь приближается к нулю (, т.е. с положительной или отрицательной стороны), но она все равно приближается к нулю.

Если задуматься, это действительно частный случай последнего факта из фактов в предыдущем разделе. Однако, чтобы увидеть прямое доказательство этого факта, см. Раздел «Доказательство различных предельных свойств» в главе «Дополнительные возможности».

Давайте начнем с примеров, которые приведут нас к хорошей идее, которую мы будем регулярно использовать, относительно пределов на бесконечности для многочленов.2} – 8x} \ right) \) Показать решение

Наша первая мысль здесь, вероятно, состоит в том, чтобы просто «вставить» бесконечность в полином и «оценить» каждый член, чтобы определить значение предела. Довольно просто увидеть, что будет делать каждый член в пределе, и поэтому это кажется очевидным шагом, особенно с учетом того, что мы делали это для других ограничений в предыдущих разделах.

Итак, давайте посмотрим, что мы получим, если это сделаем. Когда \ (x \) приближается к бесконечности, тогда \ (x \) в степени может только увеличиваться, а коэффициент при каждом члене (первом и третьем) только сделает член еще больше.2} – 8x} \ right) = \ infty – \ infty – \ infty \]

Итак, у нас есть небольшая, но легко решаемая проблема. Мы, вероятно, испытываем искушение сказать, что ответ равен нулю (потому что у нас есть бесконечность минус бесконечность) или, возможно, \ (- \ infty \) (потому что мы вычитаем две бесконечности из одной бесконечности). Однако в обоих случаях мы ошибаемся. Это одна из тех неопределенных форм , которые мы впервые начали видеть в предыдущем разделе.

Бесконечности не всегда ведут себя так, как действительные числа, когда дело доходит до арифметики.5} \) в этом случае.

Теперь все, что нам нужно сделать, это взять предел в два члена. В первом случае не забывайте, что, поскольку мы идем в сторону \ (- \ infty \) и повышаем \ (t \) до степени 5 ^th , предел будет отрицательным (отрицательное число возведено в нечетная мощность по-прежнему отрицательна). Во втором члене мы снова будем активно использовать вышеизложенный факт, чтобы увидеть, что это конечное число.

Следовательно, используя модификацию Фактов из предыдущего раздела, значение лимита составляет

\ [\ mathop {\ lim} \ limits_ {t \ to – \ infty} \ left ({{\ textstyle {1 \ over 3}} {t ^ 5} + 2 {t ^ 3} – {t ^ 2}) + 8} \ right) = – \ infty \]

Хорошо, теперь, когда мы увидели, как работает пара многочленов, мы можем привести простой факт о многочленах в целом. n} \]

Этот факт на самом деле говорит о том, что когда мы берем предел на бесконечность для многочлена, все, что нам действительно нужно сделать, это посмотреть на член с наибольшей степенью и спросить, что этот член делает в пределе, поскольку многочлен будет иметь такое же поведение.

Вы можете увидеть доказательство в разделе «Доказательство различных предельных свойств» в главе «Дополнительно».

Давайте теперь перейдем к более сложным ограничениям.

Пример 2 Оцените оба следующих предела.4} + 7}} \] Показать решение

Во-первых, единственное различие между этими двумя состоит в том, что один стремится к положительной бесконечности, а другой – к отрицательной бесконечности. Иногда эта небольшая разница влияет на значение лимита, а иногда – нет.

Давайте начнем с первого предела, и, как и в случае с нашим первым набором примеров, может возникнуть соблазн просто «подключить» бесконечность. Поскольку числитель и знаменатель являются многочленами, мы можем использовать вышеуказанный факт для определения поведения каждого из них. 4} + 7}} = \ frac {\ infty} {{- \ infty}} \]

Это еще одна неопределенная форма . В этом случае у нас может возникнуть соблазн сказать, что предел – это бесконечность (из-за бесконечности в числителе), ноль (из-за бесконечности в знаменателе) или -1 (потому что что-то, что делится само по себе, равно единице). Здесь работают три отдельных арифметических «правила», и без работы невозможно узнать, какое «правило» будет правильным, и, что еще хуже, возможно, что ни одно из них не может сработать, и мы можем получить совершенно другой ответ, скажем, \ (- \ frac {2} {5} \), чтобы выбрать число наугад.4}}}}} \\ & = \ frac {{2 + 0 + 0}} {{- 5 + 0}} \\ & = – \ frac {2} {5} \ end {align *} \]

В этом случае неопределенная форма не была ни одним из «очевидных» вариантов выбора бесконечности, нуля или -1, поэтому будьте осторожны с такими предположениями с такими неопределенными формами.

Второй предел выполняется аналогичным образом. 2}}}}}} {{\ frac {5} {x} – 2}} = \ frac {{\ sqrt {3 + 0}}} {{0 – 2}} = – \ frac { {\ sqrt 3}} {2} \ end {align *} \]

Давайте теперь посмотрим на второй предел (с отрицательной бесконечностью).2}}}}}} {{\ frac {5} {x} – 2}} \\ & = \ frac {{\ sqrt 3}} {2} \ end {align *} \]

Итак, как мы видели в последних двух примерах, иногда бесконечность в пределе влияет на ответ, а иногда – нет. Также обратите внимание, что он не всегда просто меняет знак числа. Иногда это может полностью изменить значение. Мы увидим один или два примера в следующем разделе.

Прежде чем перейти к еще парочкам примеров, давайте вернемся к идее асимптот, которую мы впервые увидели в предыдущем разделе.Так же, как мы можем иметь вертикальные асимптоты, определенные в терминах пределов, мы также можем иметь горизонтальные асимптоты, определенные в терминах пределов.

Определение

Функция \ (f (x) \) будет иметь горизонтальную асимптоту в точке \ (y = L \), если выполняется одно из следующих утверждений.

\ [\ mathop {\ lim} \ limits_ {x \ to \ infty} f \ left (x \ right) = L \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ mathop {\ lim } \ limits_ {x \ to – \ infty} f \ left (x \ right) = L \]

Мы не собираемся здесь много делать с асимптотами, но это несложный факт, и мы можем использовать предыдущий пример, чтобы проиллюстрировать все идеи асимптот, которые мы видели как в этом, так и в предыдущем разделах.4}}}}} {{2 + \ frac {3} {t}}} \\ & = \ frac {0} {2} \\ & = 0 \ end {align *} \]

В этом случае, используя Факт 1, мы можем видеть, что числитель равен нулю, и, поскольку знаменатель также не равен нулю, дробь и, следовательно, предел будут равны нулю.

В этом разделе мы сосредоточились на пределах бесконечности с функциями, которые включают только многочлены и / или рациональные выражения, содержащие многочлены. Есть еще много типов функций, которые мы могли бы использовать здесь.\ infty f_n (x) \, dx $ с использованием четных целых чисел в качестве точек деления. Для корректной последовательности функций эта разница должна стремиться к нулю.

Итак, проблема имеет мало общего с биномиальными коэффициентами как таковыми.

Предел «бесконечности» – подход к исчислению

4

Определение «становится бесконечным»

Пределы рациональных функций

Изменение переменной

БЕСКОНЕЧНОСТЬ вместе со своим символом ∞ не является числом и не местом.Когда мы говорим в математике, что что-то «бесконечно», мы просто имеем в виду, что у его значений нет предела.

Пусть, например, f ( x ) будет. Затем, когда значения x становятся все меньше и меньше, значения f ( x ) становятся все больше и больше. Независимо от того, какое большое число мы назовем, можно будет назвать значение x таким образом, чтобы значение f ( x ) было больше, чем это число, которое мы назвали.

Затем мы говорим, что значения f ( x ) становятся бесконечными или стремятся к бесконечности. Мы говорим, что, когда x приближается к 0, предел f ( x ) равен бесконечности.

Теперь предел – это число – граница. Поэтому, когда мы говорим, что предел бесконечности, мы имеем в виду, что не существует , которое мы можем назвать.

Студент должен знать, что слово бесконечный в том виде, в котором оно используется и исторически использовалось в исчислении, не имеет того же значения, что и в теории бесконечных множеств.См. Это из Википедии, особенно взгляды Карла Фридриха Гаусса в разделе «Прием аргументов».

ОПРЕДЕЛЕНИЕ 4. становится бесконечным. Мы говорим, что переменная «становится бесконечной» или «стремится к бесконечности», если, начиная с определенного члена в последовательности его значений, абсолютное значение этого термина и любого последующего термина, который мы называем, больше любого положительного числа, которое мы называем. , каким бы большим он ни был.

Когда переменная имеет размер x и принимает только положительные значения, тогда x становится положительно бесконечным. Мы пишем

Если x принимает только отрицательные значения, оно становится отрицательно бесконечным, и в этом случае мы пишем

В обоих случаях мы имеем в виду: какое бы большое число M мы ни называли, мы добираемся до точки в последовательности значений x , в которой их абсолютные значения становятся больше, чем M.

Когда переменная является функцией f ( x ), и она становится положительно или отрицательно бесконечной, когда x приближается к значению c , тогда мы пишем

Хотя мы пишем символ «lim» для обозначения предела, эти алгебраические утверждения означают: Предел f ( x ), поскольку x приближается к c , не существует.Опять же, предел – это число. (Определение 2.1.)

Определение 4 – это определение «становится бесконечным»; это не определение предела.

Что касается символа ∞, мы используем его в алгебраических утверждениях, чтобы обозначить, что определение становится бесконечным. Сам по себе этот символ не имеет значения.

В качестве примера приведем график функции

y

=

1 x

:

Давайте посмотрим, что происходит со значениями y , когда x приближается к 0 справа:

Поскольку последовательность значений x становится очень маленькими числами, тогда последовательность значений y , обратных величин, становится очень большими числами.Значения y станут и останутся больше, например, чем 10 ^100000000 . y становится бесконечным.

Пишем:

Если x приближается к 0 слева, то значения становятся большими отрицательными числами. В этом случае мы пишем

Когда функция становится бесконечной, когда x приближается к значению c , тогда функция является прерывистой при x = c , и прямая линия x = c является вертикальной асимптотой графика. (Тема 18 Precalculus.) Таким образом, график y = является разрывным при x = 0, а прямая линия x = c является вертикальной асимптотой.

Далее, давайте рассмотрим случай, когда x становится бесконечным, то есть когда его значения становятся большими положительными числами в крайнем правом углу от 0.

В этом случае число становится очень маленьким, а именно 0. Мы пишем

.

Мы должны читать, что как «предел x становится бесконечным», а не как « x приближается к бесконечности», потому что снова бесконечность не является ни числом, ни местом.С другой стороны, мы могли бы прочитать это, как бы нам ни хотелось («предел x становится головокружительным»), если любое используемое нами выражение относится к условию из определения 4.

См. Первые принципы элементов Евклида, комментарий к определениям. Обратите особое внимание на то, что определение номинальное ; он утверждает только то, как слово или имя будут использоваться; и мы должны согласиться с этим.

Наконец, когда x становится бесконечно отрицательным, то есть когда принимает значения, лежащие в крайнем левом углу от 0 (-∞), тогда снова p приближается к 0.Пишем

Другими словами, всякий раз, когда x становится бесконечным положительно или отрицательно, значения y = приближаются к горизонтальной линии y = 0. Эта линия называется горизонтальной асимптотой графика.

Проблема 1. Оценить

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!

At, tan x не существует. (Тема 15 и тема 18 тригонометрии.)

По мере приближения x слева, загар x становится больше любого числа, которое мы могли бы назвать. (Определение 4.)

Пределы рациональных функций

Рациональная функция – это частное от многочленов (Тема 6 Precalculus). Он будет иметь следующий вид:

, где f и g – многочлены ( g 0).

Помимо постоянного члена, каждый член полинома будет иметь множитель x ⁿ ( n ≥ 1). Поэтому давайте исследуем следующие ограничения.

c может быть любой положительной константой. Студент должен заполнить каждую правую часть.

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала сделай сам!

1)		=	0
2a)		=	∞
	n чет.
2b)		=	∞
	n нечет.
2c)		=	−∞
	n нечет.

Сравнить y =

1 x

выше, где n = 1.

3)		=	∞
4)		=	∞

Пример. Доказательство:

Раствор . Разделите числитель и знаменатель на наибольшую степень x .В этом случае разделите их на x ² :

Согласно пункту 1), предел каждого члена, который содержит x , равен 0. Следовательно, согласно теоремам темы 2, у нас есть требуемый ответ.

В аналогичных случаях первый шаг: Разделите числитель и знаменатель на степень x , которая появляется в главном члене любого из них.

Проблема 2.

=

4

Результат следует при делении числителя и знаменателя на x .

Проблема 3.

=

Другими словами: Когда числитель и знаменатель равны,
, тогда предел, когда x становится бесконечным, равен частному ведущих коэффициентов.

Задача 4.

В дальнейшем рациональная функция обратна предыдущей:

=

=

∞

Эта проблема иллюстрирует:

Когда степень знаменателя больше степени числителя, то есть когда знаменатель преобладает, тогда предел, когда x становится бесконечным, равен 0.Но когда числитель доминирует – когда степень числителя больше – тогда предел, когда x становится бесконечным, равен .

Изменение переменной

Рассмотрим этот предел:

Вместо того, чтобы использовать переменную, приближающуюся к 0, мы иногда предпочитаем, чтобы она стала бесконечной. В этом случае мы меняем переменную. Ставим x = или, неважно. Для x приближение к 0 эквивалентно z , становящемуся бесконечным.Тогда

При замене x на, мы позволяем z стать бесконечным. Предел остается 1.

Где это появится? В том пределе, из которого мы вычисляем число e:

(Урок 15.)

Проблема 5. В приведенном выше пределе измените переменную на n и позвольте ей стать бесконечным.

Следующий урок: производная

Содержание | Дом

---

Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.

---

Авторские права © 2021 Лоуренс Спектор

Вопросы или комментарии?

Эл. Почта: [email protected]

Пример: {rn} | Модуль бесконечной серии

Предыдущая статья: Пример теоремы сжатия

Следующая статья: Видео о бесконечных последовательностях

Пример

Определите значения r так, чтобы последовательность

сходится.

Полное решение

Мы можем решить эту проблему, рассмотрев случаи для значения r .

Корпус 1

Если r > 1, то r ⁿ стремится к бесконечности, как n стремится к бесконечности. В данном случае последовательность расходящихся .

Корпус 2

Если r = 1, то

, поэтому последовательность сходится для этого случая.

Корпус 3

Если, то

, так что последовательность сходится для этого случая.

Корпус 4

Если, то

не существует, поэтому последовательность расходится для этого случая.

Корпус 5

Если, то стремится к отрицательной бесконечности, поскольку не стремится к единственному конечному числу. В данном случае последовательность расходящихся .

Сводка

Следовательно, последовательность сходится, когда.

Объяснение каждого шага

Корпус 1

Рассмотрим случай, когда. Тогда наша последовательность становится

которая стремится к бесконечности.

Корпус 2

Здесь мы используем фундаментальное свойство пределов, что предел константы равен этой константе:

для любой постоянной и.

Корпус 3

Рассмотрим случай, когда. Тогда наша последовательность становится

который стремится к нулю.

Аналогично, если. Тогда наша последовательность становится

который также стремится к нулю.

Корпус 4

В данном случае имеем последовательность

По мере приближения к бесконечности последовательность не приближается к уникальному значению, поэтому предел не существует.

Корпус 5

Этот случай аналогичен случаю 1. Рассмотрим случай, когда. Тогда наша последовательность становится

Термины чередуются между положительными и отрицательными числами и не стремятся к единственному конечному числу.

Области возможных проблем

Соединение результатов с определением сходимости

В каждом из случаев мы использовали предел, чтобы определить, сходится ли последовательность. Согласно нашему определению сходимости последовательности, пока существуют наши соответствующие пределы, последовательность сходится.

Предыдущая статья: Пример теоремы сжатия

Следующая статья: Видео о бесконечных последовательностях

Бесконечные последовательности II | SpringerLink

• Миклош Лачкович
• Вера Т.Сос

Часть Тексты для бакалавриата по математике серия книг (UTM)

Аннотация

Нахождение предела последовательности, как правило, является сложной задачей. Иногда сложно просто определить, есть ли у последовательности предел. Рассмотрим последовательность (18) в примере 4.1, то есть пусть a _n будет n -й цифрой в десятичном разложении \ (\ sqrt {2} \). Мы знаем, что ( a _n ) не имеет ограничения.Но есть ли у последовательности \ (c_ {n} = \ root {n} \ of {a_ {n}}} \) предел? Прежде всего, отметим, что a _n ≥ 1, и, следовательно, c _n ≥ 1 для бесконечного множества n . Теперь, если среди членов бесконечно много нулей a _n , то c _n = 0 также выполняется для бесконечного числа n , поэтому последовательность ( c _n ) расходится.Однако если среди членов только конечное число нулей a _n , то есть a _n ≠ 0 для всех n > n ₀ , то 1 ≤ a _n ≤ 9, поэтому \ (1 \ leq c_ {n} \ leq \ root {n} \ of {9} \) также выполняется, если n > n ₀ . По теореме 4.17 \ (\ root {n} \ of {9} \ rightarrow 1 \). Таким образом, для данного ɛ > 0 существует n ₁ такой, что \ (\ root {n} \ of {9} <1+ \ varepsilon \) для всех n > n ₁ .Итак, если \ (n> \ max (n_ {0}, n_ {1}) \), то \ (1 \ leq c_ {n} <1+ \ varepsilon \), и, следовательно, c _n → 1.

Ключевые слова

Десятичное разложение Отрицательное бесконечное частное Последовательность Теорема сжатия Известная открытая проблема

Эти ключевые слова были добавлены машиной, а не авторами. Это экспериментальный процесс, и ключевые слова могут обновляться по мере улучшения алгоритма обучения.

Это предварительный просмотр содержимого подписки,

войдите в

, чтобы проверить доступ.

Информация об авторских правах

© Springer New York 2015

Авторы и аффилированные лица

• Миклош Лацкович