Пределы, пределы функций
Задача с касательнойДана функция f(x) и точка P(x0, y0) на графике этой функции. Найдите уравнение прямой, касательной к графику функции в точке P
Задача с площадью
Дана функция f, найдите площадь между графиком f и отрезеом [a,b] на x-axis
Прямая называется касательной к окружности, если она касается окружности только в одной точке.
Но это определение не является удовлетворительным для другого вида кривых, таких как
Прямая, являющаяся касательной, касается кривой более чем один раз.
Прямую, которая занимает эту позицию, мы рассматриваем как касательную в точке P.
Площади некоторых плоских фигур могут быть вычислены путем разделения их на конечное число прямоугольников или треугольников, а затем сложением площадей этих фигур.
Для многих площадей нужен более общий подход.
Аппроксимируем площадь этого области, вписывая прямоугольники одинаковой ширины под кривую и складывая площади этих прямоугольников.
Наша аппроксимация будет приближаться к точной площади под кривой как “предельное значение”.
Давайте возьмем
f(x) = sin(x)/x
Где x – в радианах.
Предел справа
limx → 0+ sin(x)/x “Пределы функции f(x) когда x стремится к 0 справа”
Предел слева
limx → 0+ sin(x)/x
“Пределы функции f(x) когда x стремится к 0 слева.”
Переключив калькулятор в режим “радианы”, мы получим
|
|
89670Когда x стремится к 0 слева или справа, f(x) стремится 1.
В таблице приведено несколько примеров пределов функций.
| ЗАПИСЬ | КАК ЧИТАТЬ ЗАПИСЬ |
| limx→ x0+ = L1 | Предел f(x) когда x стремится x0 справа, равен L1 |
| limx→ x0- = L2 | Предел f(x) когда x стремится x0 слева, равен L2 |
| limx→ x0 = L | Предел f(x) когда x стремится x0 равен L |
Числовые ловушки
f(x) = sin(φ/x)
limx → 0 sin(φ/x) = limx → 0+ sin(φ/x) = limx → 0- sin(φ/x)
Таблица 2.
4.4 | x | f(x) | x | f(x) |
| 1 | 0 | 0 | |
| 0.1 | 0 | -0.1 | 0 |
| 0.01 | 0 | -0.01 | 0 |
| 0.001 | 0 | -0.001 | 0 |
| 0.0001 | 0 | -0.0001 | 0 |
Существование пределов
limx→ x0- f(x) = limx→ x0+ f(x) = limx→ x0 f(x) = +∞
x стремится к
limx→ x0- f(x) = limx→ x0+ f(x) = limx→ x0 f(x) = -∞
x стремится к x0 справа
Пример
limx→ x0- f(x) = -∞ limx→ x0+ f(x) = +∞
Предел функции не существует в X0
Пример
Here
limx→ –∞ f(x) = -1 limx → +∞ f(x) = 4
So, limit of function does not exist.
Example
Здесь
as x → -∞, f(x) → +∞
as x → +∞, f(x) → -2
Поэтому, предела функции не существует.
Пример
Здесь
as x → -∞, f(x) → -∞
as x → +∞, f(x) → oscillates
Поэтому, предела функции не существует.
Пределы
0) Постоянная величина (число) сама себе служит пределом: .
1а) Величина, обратная бесконечно большой, есть бесконечно малая величина, т.е. если х → ∞, то .
1b) Величина, обратная бесконечно малой, есть бесконечно большая величина, т.е. если х → 0, то .
2a) Если две переменные стремятся к одному и тому же пределу, а третья переменная заключена между ними, то и она стремится к этому же пределу. Если
2b) Если две функции F(x) и Ф(х) стремятся к одному и тому же пределу A при х → p, а значения функции f(x) заключены между значениями F(x) и Ф(х), то f(x)
Если F(x) ≤ f(x) ≤ Ф(х) и
, то .
3) Предел суммы (разности) конечного числа слагаемых равен сумме (разности) пределов этих слагаемых:
lim (u ± v ± … ± t) = lim u ± lim v ± … ± lim t.
4) Предел произведения конечного числа множителей равен произведению пределов этих множителей:
lim (u · v · … · t) = lim u ·lim v · … · lim t.
Постоянный множитель можно выносить за знак предела lim c·u = с · lim u.
5) Предел частного равен частному пределов, если только предел делителя (знаменателя) не равен нулю: , если lim v ≠ 0.
6) Если предел числителя не равен
нулю, а предел знаменателя равен нулю,
то предел дроби является бесконечно
большой величиной (см.
Если lim u ≠ 0, а lim v = 0, то . Если же lim u =0 и lim v =0, то для нахождения предела необходимы дополнительные исследования.
0) Постоянная величина (число) сама себе служит пределом: .
1а) Величина, обратная бесконечно большой, есть бесконечно малая величина, т.е. если х → ∞, то .
1b) Величина, обратная бесконечно малой, есть бесконечно большая величина, т.е. если х → 0, то .
2a) Если две переменные стремятся к одному и тому же пределу, а третья переменная заключена между ними, то и она стремится к этому же пределу. Если
2b) Если две функции F(x) и Ф(х) стремятся к одному и тому же пределу A при х → p, а значения функции f(x) заключены между значениями F(x) и Ф(х), то f(x) стремится к этому же пределу A
при х → p .
, то .
3) Предел суммы (разности) конечного числа слагаемых равен сумме (разности) пределов этих слагаемых:
lim (u ± v ± … ± t) = lim u ± lim v ± … ± lim t.
4) Предел произведения конечного числа множителей равен произведению пределов этих множителей:
lim (u · v · … · t) = lim u ·lim v · … · lim t.
Постоянный множитель можно выносить за знак предела
lim c·u = с · lim u.
5) Предел частного равен частному пределов, если только предел делителя (знаменателя) не равен нулю: , если lim v ≠ 0.
6) Если предел числителя не равен нулю, а предел знаменателя равен нулю, то предел дроби является бесконечно большой величиной (см. п.1b): Если lim u ≠ 0, а lim v = 0, то . Если же lim u =0 и lim v =0, то для нахождения предела необходимы дополнительные исследования.
Раскрытие некоторых типов неопределённостей.
7) Чтобы раскрыть неопределенность
вида
,
заданную отношением двух многочленов,
надо и числитель и знаменатель разделить
на самую высокую входящую в них степень х.
8) Чтобы раскрыть неопределенность вида , заданную в форме: , надо и в числителе и в знаменателе выделить критический множитель (х – а) и сократить на него дробь.
9) Чтобы раскрыть неопределенность вида , в которой числитель или знаменатель иррациональны, следует надлежащим образом избавиться от иррациональности.
Первый замечательный предел:
Второй замечательный предел:
Другие замечательные пределы
Понижение степени
Раскрытие некоторых типов неопределённостей.
7) Чтобы раскрыть неопределенность вида , заданную отношением двух многочленов, надо и числитель и знаменатель разделить на самую высокую входящую в них степень х.
8) Чтобы раскрыть неопределенность
вида
,
заданную в форме:
,
надо и в числителе и в знаменателе
выделить критический множитель (х –
а) и сократить на него дробь.
9) Чтобы раскрыть неопределенность вида , в которой числитель или знаменатель иррациональны, следует надлежащим образом избавиться от иррациональности.
Первый замечательный предел:
Второй замечательный предел:
Другие замечательные пределы
Понижение степени
Понимание концепции пределов – MathsTips.com
Мы знаем, что в математике деление на ноль невозможно. Если мы рассмотрим определение функции как
, значение f(x) при x=1 неопределенно.
Проще говоря, значение функции f(x) не существует при x=1. Итак, вместо x=1 мы рассматриваем значения x, достаточно близкие к 1, т. е. максимально близкие к 1.
| х | ф(х) |
|---|---|
| 0,5 | 1,50000 |
| 0,9 | 1. |
| 0,99 | 1,99000 |
| 0,999 | 1,99900 |
| 0,9999 | 1,99990 |
| 0,99999 | 1,99999 |
| … | … |
Из приведенной выше таблицы видно, что по мере того, как значения x приближаются к 1, значение функции f(x) приближается к 2. В таблице мы остановились на 0,9.9999, но если мы возьмем значения x еще ближе к 1, соответствующие значения f(x) будут еще ближе к 2. Здесь, когда значения x увеличиваются к 1, значения f(x) увеличиваются к 2. Это символически записывается так:
Это читается как «предел x стремится к 1 плюс f(x) равно 2». Следует отметить, что знак «+» означает значения x больше 1, а не «положительные» значения x.
Теперь посмотрим на следующую таблицу
| x | ф(х) |
|---|---|
| 1,5 | 2,50000 |
| 1.1 | 2. 10000 |
| 1.01 | 2.01000 |
| 1,001 | 2.00100 |
| 1.0001 | 2.00010 |
| 1.00001 | 2.00001 |
| … | … |
Снова из приведенной выше таблицы мы видим, что по мере того, как значения x все ближе и ближе к 1, соответствующие значения f(x) все ближе и ближе к 2. Другими словами, по мере того, как значения x приближаются к 1 соответствующие значения f(x) приближаются к 2. Единственное отличие состоит в том, что здесь значения x уменьшаются в сторону 1, а значения f(x) уменьшаются в сторону 2. Это символически записывается как:
Он гласит: «предел x стремится к 1 минус f(x) равно 2». Следует отметить, что знак «-» означает значения x меньше 1, а не «отрицательные» значения x.
На практике числовая разница между значением x=1 и значением x, достаточно близким к 1 (например, x=1,0000001 или x=0,9999999) может быть сделана сколь угодно малой и, следовательно, ею можно пренебречь.
Точно так же числовая разница между значением f(x)=2 и значением f(x), очень близким к 2, может быть сделана сколь угодно малой и, следовательно, ею можно пренебречь, если значение x достаточно близко к 1.
В общем, когда значение f(x) не может быть определено для конкретного значения x, скажем, x=a, тогда может существовать определенное конечное число b, такое, что значение f(x) постепенно стремится к это конечное число b, когда x стремится к a. Однако мы не можем сказать, всегда ли будет существовать это конечное число b или нет. Из этого наблюдения математики разработали понятие предела.
Предел переменной
Рассмотрим реальную переменную x. Пусть а постоянная. Тогда под «х стремится к а» мы подразумеваем, что х последовательно принимает значения, большие или меньшие, чем а, и числовая разница между предполагаемым значением х, т. е. |x-a| становится все меньше и меньше. В этом случае x становится очень близким к a (но x≠a), и мы говорим «x приближается к a».
Если x приближается к a при значениях, превышающих a, то мы говорим «x стремится к a с правой стороны» и обозначаем это через .
Если х приближается к а при значениях, меньших а, то мы говорим «х стремится к а с левой стороны» и обозначаем это через .
Предельное значение функции
Мы предполагаем, что x — действительная переменная, a — действительная константа, а f(x) — однозначная функция x.
Если x постепенно приближается к a при предполагаемых значениях, превышающих a, и если соответствующие значения f(x) существуют и эти значения постепенно приближаются к конечной константе , то $latexl_1$ называется правым предельным значением f(x) или правый предел f(x) и обозначается
Опять же, если x постепенно приближается к a, принимая значения, меньшие a, и если соответствующие значения f(x) существуют и эти значения постепенно приближаются к конечной константе $latexl_2$, то $latexl_2$ называется левой рукой. предельное значение f(x) или левый предел f(x) и обозначается как
значение x, и если эти значения f(x) постепенно приближаются к конечной константе l, то l называется предельным значением f(x).
Обозначается
Предел функции существует, только если оба (правый предел) и (левый предел) существуют и , т. е. если
l не существует, если
- неопределенно ИЛИ
- неопределенно ИЛИ
- .
Что мы подразумеваем под и ?
Если реальная переменная x принимает положительные значения и неограниченно возрастает, принимая значения, большие, чем любое большое число, которое можно себе представить, то мы говорим, что переменная x стремится к бесконечности в положительном направлении, и обозначаем ее через .
Если действительная переменная x принимает отрицательные значения и численно возрастает неограниченно, принимая значения, численно большие, чем любое большое число, которое можно себе представить, то мы говорим, что переменная x стремится к бесконечности в отрицательном направлении, и обозначаем ее через .
Некоторые важные ограничения
1. Если n — рациональное число, то
2.
Если n — рациональное число, то
3.
4.
5.
30 90 90 0 0 2 0 9 0Следует помнить
- не означает, что x принимает положительные значения. Это означает, что x приближается к 0 при значениях больше 0.
- не означает, что x принимает отрицательные значения. Это означает, что x приближается к 0 при значениях меньше 0. 90 165 называется правым пределом f(x) при x=a и называется левым пределом f(x) при x=a.
- существует, если и оба существуют, и
- Предел функции может отсутствовать, если указанные выше условия не выполняются. Если нет, то предел функции в этой точке не существует.
Вопросы и ответы
Вопрос 1: Существует ли? Если да, то найдите его значение?
Решение: Пусть
| x | ф(х) |
|---|---|
| 1,9 | 3,9 |
| 1,99 | 3,99 |
| 1,999 | 3,999 |
| 1,9999 | 3,9999 |
| … | … |
2. 1 | 4.1 |
| 2.01 | .401 |
| 2,001 | 4.001 |
| … | … |
Из приведенной выше таблицы видно, что по мере приближения x к конечному значению 2 (при условии, что значения больше или меньше 2 и достаточно близки к 2), значения f(x) постепенно приближаются к 4, а разница между значения f(x) и 4 можно сделать сколь угодно малыми. Следовательно, как , но x≠2, потому что f(x) не определена при x=2.
- Левый предел =
- Правый предел =
Ясно, что и правый предел, и левый предел существуют и равны.
Следовательно, существует и
Вопрос 2: Оценить
Решение: Пусть
| x | ф(х) |
|---|---|
| 0,9 | |
| 0,99 | |
| 0,999 | |
| … | … |
1. 1 | |
| 1.01 | |
| 1,001 | |
| … | … |
Из приведенной выше таблицы видно, что по мере того, как x постепенно приближается к конечному значению 1 слева, принимая значения меньше 1, значение f(x) продолжает увеличиваться и приближается к большому числу, настолько большому, насколько мы можем представить.
Левый предел =
Кроме того, мы можем видеть, что по мере того, как x постепенно приближается к конечному значению 1 справа, принимая значения больше 1, значение f(x) продолжает увеличиваться и приближается к большому числу, настолько большому, насколько мы можем себе представить.
Правый предел =
Таким образом, левый предел равен правому пределу.
Следовательно,
ПРИМЕЧАНИЕ: Здесь x≠1, потому что x=1, что не определено.
Вопрос 3: Оценить
Решение: Пусть
| х | ф(х) |
|---|---|
| -0,1 | -10 |
| -0,01 | -100 |
| -0,001 | -1000 |
| … | … |
| 0,1 | 10 |
| 0,01 | 100 |
| 0,001 | 1000 |
| 0,0001 | 10000 |
| … | … |
Из вышеприведенной таблицы видно, что и
Ясно, т.
е. левосторонний предел и правосторонний предел существуют, но они не равны.
Следовательно, не существует.
Вопрос 4: Оценка .
Решение: Пусть .
| х | ф(х) |
|---|---|
| -10 | -1,02 |
| -100 | -1.0002 |
| -1000 | -1.000002 |
| -10000 | 1.00000002 |
| … | … |
Из таблицы видно, что при неограниченном численном увеличении x, принимая отрицательные значения, числовая разница между f(x) и конечным значением 1 может быть сделана сколь угодно малой. Следовательно, как .
Поэтому .
Вопрос 5: Оценка
Решения:
а.
=
=
=
= 7
б. Пусть
Теперь
Следовательно,
=
= 3 + 3 = 6
Упражнение
1.
Покажите, что
2. Оцените . (Подсказка: разложите числитель и знаменатель на множители)
3. Оцените .
4. Покажите, что .
5. Оценить . [Подсказка: умножьте и числитель, и знаменатель на . и рационализировать]
6. Функция f(x), определяемая следующим образом:
Проверить, существует или нет.
7. Вычислить (Подсказка: умножить числитель и знаменатель на sin x. Положить sin x = z)
8. Вычислить [Подсказка: положить ]
9. Вычислить [Подсказка: положить ]
10. Вычислить
| 1 | Найдите производную – d/dx | натуральное бревно х | |
| 2 92) | |||
| 21 | Оценка интеграла | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найдите производную – d/dx | грех(2x) | |
| 23 | Найдите производную – d/dx | 9(3x) по отношению к x||
| 41 | Оценка интеграла | интеграл от cos(2x) по x | |
| 42 | Найдите производную – d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найдите производную – d/dx | х/2 | |
| 46 | Найдите производную – d/dx | -cos(x) | |
| 47 | Найдите производную – d/dx | грех(3x) | 92+1|
| 68 | Оценка интеграла | интеграл от sin(x) по x | |
| 69 | Найдите производную – d/dx | угловой синус(х) | |
| 70 | Оценить предел | предел, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найдите производную – d/dx | лог х | |
| 86 | Найдите производную – d/dx | арктан(х) | |
| 87 | Найдите производную – d/dx | натуральное бревно 5х92 |
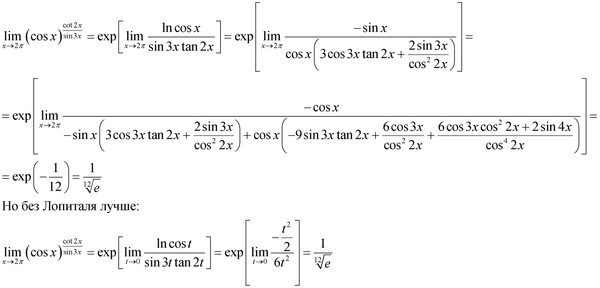
Вычисление lim x → 0 sin5x-sin3x/x по предельным правилам
- Математические сомнения
- Проблемы
- Ограничения
- Тригонометрические функции
Используйте метод прямой подстанции для нахождения предела синуса угла, умноженного на $x$, умноженного на пять, минус синус угла, умноженного на $x$, умноженного на $x$, деленного на $x$, поскольку значение $x$ ближе к нулю.
$\displaystyle \large \lim_{x\,\to\,0}{\normalsize \dfrac{\sin{5x}-\sin{3x}}{x}}$ $\,=\,$ $ \dfrac{0}{0}$
В соответствии с прямым методом подстанции оценивается, что предел частного вычитания трехкратного $x$ синуса угла из пятикратного $x$ синуса угла на $x$ как значение $x $ приближается к нулю неопределенно. Он выражает, что метод прямой подстановки бесполезен для нахождения предела данной рациональной функции. Так что лучше подумать об альтернативном математическом подходе.
Распространить операцию Лимит на Условия
Рациональную функцию можно разделить как разность двух членов, распределив выражение в знаменателе на оба члена в числителе.
$=\,\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \Big(\dfrac{\sin{5x}}{x}-\dfrac{ \sin{3x}}{x}\Big)}$
Предельная операция может быть распределена на разность дробей для нахождения предела разности функций путем вычисления разности их пределов по правилу разности пределов.
$=\,\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \dfrac{\sin{5x}}{x}}$ $-$ $\ displaystyle \large \lim_{x\,\to\,0}{\normalsize \dfrac{\sin{3x}}{x}}$
Преобразование функций в известное правило предела
Посмотрите на рациональную функцию в каждом член математического выражения.
Выражение в каждом члене точно соответствует правилу тригонометрического предела в синусоидальной функции. Углы внутри синусоидальных функций в первом и втором членах равны $5x$ и $3x$ соответственно. Следовательно, знаменатели в обоих терминах должны быть соответственно $5x$ и $3x$.
Внесем некоторые приемлемые изменения для приведения рациональных функций к нужному виду.
$=\,\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \Big(1 \times \dfrac{\sin{5x}}{x}\ Большой)}$ $-$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \Big(1 \times \dfrac{\sin{3x}}{x}\Big)}$
$=\,\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \Big(\dfrac{5}{5} \times \dfrac{\sin{ 5x}}{x}\Big)}$ $-$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \Big(\dfrac{3}{3} \times \dfrac{ \sin{3x}}{x}\Big)}$
$=\,\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \Big(5 \times \dfrac{\sin{5x}}{5 \times x}\Big)}$ $-$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \Big(3 \times \dfrac{\sin{3x}}{3 \times x }\Big)}$
$=\,\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \Big(5 \times \dfrac{\sin{5x }}{5x}\Big)}$ $-$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \Big(3 \times \dfrac{\sin{3x}}{3x }\Big)}$
Числа $5$ и $3$ являются коэффициентами рациональных функций и являются константами.
Следовательно, их можно отделить от предельных операций в соответствии с правилом постоянного кратного предела.
$=\,\,\,$ $\displaystyle 5 \times \large \lim_{x\,\to\,0}{\normalsize \dfrac{\sin{5x}}{5x}}$ $- $ $\displaystyle 3 \times \large \lim_{x\,\to\,0}{\normalsize \dfrac{\sin{3x}}{3x}}$
Вычислить предел каждой функции
В первый член, угол внутри синусоидальной функции равен $5x$, и такой же угол $5x$ есть и в знаменателе. Во втором слагаемом угол внутри синуса равен $3x$, и такой же угол $3x$ есть и в знаменателе. Две рациональные функции аналогичны правилу тригонометрического предела в синусоидальной функции.
Однако тригонометрическое предельное правило не может быть применено к обоим терминам, потому что ввод предельной операции также должен быть равен либо углу внутри синусоидальной функции, либо функции в знаменателе. Поэтому давайте попробуем внести некоторые коррективы, чтобы применить его к каждому термину.
Если $x \,\to\, 0$, то $5 \times x \,\to\, 5 \times 0$.