Заранее спасибо ! 🙂
предел
задан 19 Ноя ’13 12:40
Майленко
7●2●2●4
изменен 20 Ноя ’13 1:18
Deleted
1●2●6
старыеновыеценные
|
3) Докажем из определения, что $$\lim\limits_{x\to\infty}\frac{2x-1}{x+3}=2. ссылка отвечен 19 Ноя ’13 15:46  org/Person”>falcao286k●9●38●51 |
Ваш ответ
Если вы не нашли ответ, задайте вопрос.
Здравствуйте
Математика – это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Присоединяйтесь!
регистрация »
отмечен:
предел
×172
задан 
19, 2013, 12:40 п.п.”>19 Ноя ’13 12:40
показан
55352 раза
обновлен
20 Ноя ’13 17:30
Связанные вопросы
Отслеживать вопрос
по почте:
Зарегистрировавшись, вы сможете подписаться на любые обновления
по RSS:
Ответы
Ответы и Комментарии
Как решать пределы? — Финансовая жизнь
В курсе матанализа большой временной отрезок выделяется на изучение приемов того, как решать пределы, как для функций, так и для последовательностей. Сейчас существует некое количество уже правил и готовых методов, каковые при верном применении смогут оказать помощь решить достаточно тяжёлые задания с пределами.
В матанализ были введены понятия того, как решать пределы функций, и пределы последовательностей.
В случае если нужно вычислить предел последовательности, то запись этого примера выглядит так: lim xn=a. Из данной последовательности видно, что xn пытается к а. Со своей стороны n напротив пытается к бесконечности. Значительно чаще последовательности представляются в виде последовательностей, таких как, к примеру, р1, р2, р3. рm. рn.
Все последовательности принято разделять на две группы: убывающие последовательности, и возрастающие последовательности.
Как решать пределы: формулы
Значительно чаще величина, которая есть переменной, к примеру, х стремиться к конечному пределу, коим есть величина а. Наряду с этим величина х всегда приближается к величине а, в кто время как величина а остается постоянной. Запись этого сложного определения весьма несложная: limx =a. В этом случае n может стремиться к бесконечности, и к нулю.
Существуют особенные функции, каковые именуются нескончаемыми. В них предел кроме этого пытается к бесконечности. В случае если же рассматривается вторая функция, которая обрисовывает замедление хода чего-либо, то тут имеется суть сказать и о пределе, что будет стремиться к нулю.
Все приделы имеют собственный определенный последовательность особенностей. Значительно чаще у одной функции возможно только один предел. Это и имеется самоё важное и самое основное свойство пределов.
Все остальные свойства пределов связаны с их решением и определением задач. Кроме этого студентам стоит обратить внимание на тему о том, как решать пределы с корнями.
- Предел суммы равен сумме
всех пределов: lim(x+y)=lim x+lim y.
- Предел частного равен частному от всех пределов: lim(x/y)=lim x/lim y.
- Предел произведения равен произведению от всех пределов: lim(xy)=lim x*lim y.
- Постоянный множитель возможно вынесен за символ предела без утраты целостности задачи: lim(Cx)=C lim x.
В случае если в задании предоставлена функция 1/х, для которой х пытается к бесконечности, то предел данной функции будет равен нуля. В случае если же х будет стремиться к нулю, то соответственно и предел данной функции будет равен бесконечности.
Существуют особые исключения их этих правил для тригонометрических функций. Функция синуса х постоянно стремится к единице. В то время, когда эта функция приближается к нулю, для нее делается честным данное тождество: lim sin x/x=1.
Существуют кроме этого и для того чтобы рода задачи, где в ходе вычисления пределов появляется некая обстановка, именуемая неопределенностью. Неопределенность – это та обстановка, в которой вычисление предела нереально. Единственный способ ответа таких задач – это применение правил Лопиталя.
Все неопределенности принято дробить на две категории: неопределенность вида ноль дробить на ноль, и неопределенность вида бесконечность дробить на бесконечность. В случае если разглядывать предел lim f(x)/l(x), в то время, когда f(x0)=l(x0)=0, то в этом случае отмечается явное происхождение неопределенности вида ноль дробить на ноль. Чтобы верно решить эту задачу, обе функции должны быть подвергнуты сперва дифференцированию, а после этого вычислению предела результата.
В случае если разглядывать неопределенность вида ноль дробить на ноль, то предел функции будет равен: lim f(x)/l(x)=lim f'(x)/l'(x) (при x стремящемуся к нулю).
Существуют особые сервисы, где возможно решить предел онлайн любой сложности. К примеру, сайт Вычислить предел онлайн предлагает обычный подсчет предела функций при помощи особого калькулятора. В случае если же нужно подсчитать предел последовательности, то лучше обратиться к онлайн-калькулятору пределов на сайте Ответ пределов онлайн .
Источник: elhow.ru
Математика Без Ху%!ни. Пределы. Часть 2.
Интересные записи
- Как подключить автоплатеж мтс
- Можно ли выехать за границу с долгами
- Как зарегистрироваться в букмекерской конторе
Похожие статьи, которые вам, наверника будут интересны:
Консорциум r3, digital assets holding и swift — кому решать судьбу блокчейна?
Стандарты — сердце финансовой системы и блокчейна.
Надежда косарева: «административные решения об изменениях границ города не решают проблемы этого города»
Будут ли арендодатели платить налоги? В то время, когда у нас покажутся прибыльные дома и малоэтажное строительство? Как идет опыт по созданию «новой…
Облачная платформа берется решать банковские проблемы с psd2
Новая платежная облачная платформа Token обещает уменьшить банкам жизнь в области комплаенс в соответствии со Второй платежной директивой (PSD2). Эта…
Как решать задачи на проценты 7 класс
Карточка 4. Скорость легковой машины 96 км/ч, что образовывает 12% скорости самолета. Какова скорость самолета? На решение дается 5 – 7 мин., по…
При кредитовании решающим станет человеческий фактор
Пять главных трендов на рынке кредитования МСБ. Кредитная пауза закончилась Два года рынок жил в вынужденной кредитной паузе.
Часть предпринимателей,…Как решать задачи на проценты
Урок 1 Тема урока: Проценты. Как решать задачи на проценты. Тему Проценты начинают изучать в 5 классе, тут же и начинают решать задачи на проценты….
Часть предпринимателей,…Предел в бесконечности Задачи с квадратными корнями – Matheno.com
Обновление: По состоянию на сентябрь 2022 года у нас есть гораздо дополнительных интерактивных способов узнать об основополагающей концепции пределов в бесконечности, широко используя графики Desmos калькуляторы. Пожалуйста, посетите наш Введение в Пределы в Бесконечности, чтобы начать действительно получить этот материал для себя. Все это бесплатно и предназначено для того, чтобы помочь вам преуспеть в вашем курсе.
Если вам сейчас просто нужно попрактиковаться в решении проблем с ограничениями, предыдущие ученики сочли нижеприведенную информацию очень полезной. А если у вас есть вопросы, задавайте их на нашем форуме! 92}$ в любой задаче, где $x \to\, -\infty$, поскольку тогда вы автоматически просматриваете отрицательные значения x .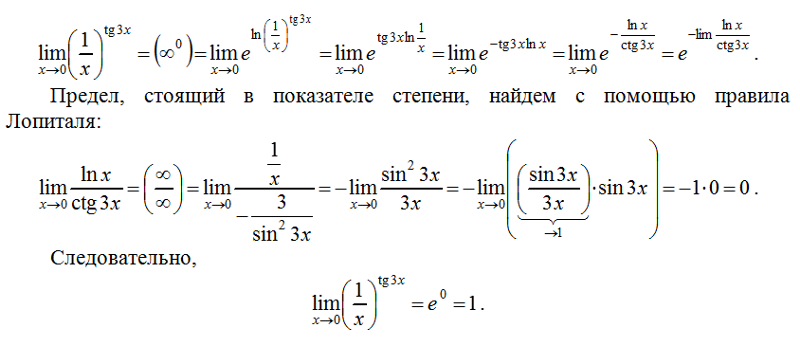
Для более полного обсуждения этого важного вопроса, пожалуйста, посетите экран «Предел в бесконечности с квадратными корнями» в нашей главе «Пределы», посвященной этой теме. У нас также есть специально разработанные интерактивные графические калькуляторы Desmos, которые помогут вам понять, что вы делаете, когда вычисляете эти пределы.
Приведенные ниже задачи иллюстрируют, начиная с части (b) первой. 92}}}{1} \\[8px]
&= \lim_{x \to \infty} \sqrt{5 + \dfrac{2}{x}} \\[8px]
&= \sqrt{\lim_{x \to \infty} 5 + \cancelto{0}{\lim_{x \to \infty}\left( \dfrac{2}{x}\right)}} \\[ 8px]
&= \sqrt{5} \quad \cmark
\end{align*} \]
Обратите внимание, что на последнем шаге мы использовали тот факт, что $\displaystyle{\lim_{x \to \infty}\frac{ 2}{х} = 0}$.
Мы можем проверить результат, взглянув на график функции. Обратите внимание, что горизонтальная линия $y = \sqrt{5}$ является горизонтальной асимптотой для этого графика.
92\left( 5 + \frac{2}{x} \right)}}{x}$, числитель всегда будет положительным из-за квадратного корня. Знаменатель, с другой стороны, всегда будет отрицательным, потому что мы рассматриваем постоянно увеличивающиеся отрицательные значения для x . Следовательно, поскольку $x \to\, -\infty$, дробь всегда будет иметь отрицательное значение , и поэтому, если мы найдем число в качестве предела, мы ожидаем, что оно будет отрицательным. Это быстрое начальное рассуждение является хорошей проверкой нашего окончательного результата.
Чтобы получить этот результат, мы снова используем наш обычный «трюк» деления числителя и знаменателя на 92}}}{1} \\[8px]
&= \lim_{x \to\, -\infty} -\sqrt{5 + \dfrac{2}{x}} \\[8px]
&= -\sqrt{5} \quad \cmark
\end{align*} \]
Обратите внимание, что на последнем шаге мы использовали тот факт, что $\displaystyle{\lim_{x \to\, -\infty}\frac {2}{x} = 0}$.
Обратите внимание, что в качестве ответа мы получили отрицательное число, что соответствует нашим быстрым первоначальным рассуждениям выше.
Мы можем проверить результат, взглянув на график функции. Обратите внимание, что горизонтальная линия $y = -\sqrt{5}$ является горизонтальной асимптотой для этого графика. 92 + x} – x \\[8px]
f(10) &= \sqrt{100 + 10} – 10 \приблизительно 10,488 – 10 = 0,488 \\[8px]
f(20) &= \sqrt{400 + 20} – 20 \приблизительно 20,494 – 20 = 0,494 \\[8px]
f(100) &= \sqrt{10,000 + 100} – 100 \приблизительно 100,499 -100 = 0,499
\end{align*} \]
[свернуть]
Практическая задача №3
Эта задача предоставлена по запросу учащегося. У него есть другой (тот же самый) классный, удивительный результат.
Найти $\displaystyle{\lim_{x \to \infty}\left(\sqrt{x + \sqrt{x}} – \sqrt{x} \right)}$.
Нажмите, чтобы просмотреть решение исчисления
По мере роста $x$, как $\sqrt{x + \sqrt{x}}$, так и $\sqrt{x}$ растут и растут.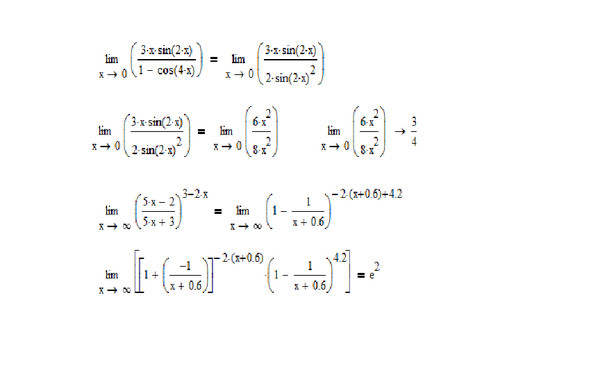
Таким образом, мы не сразу знаем, в чем разница между двумя терминами. $(“\infty – \infty”$ может быть чем угодно — это «неопределенное выражение», означающее, что у нас есть еще работа.)
Чтобы продолжить, мы будем использовать тот же подход, который мы использовали ранее при оценке пределов, которые имели в них квадратные корни: мы рационализируем выражение, умножив его на сопряженное $\sqrt{x + \sqrt{x}} + \sqrt{x}$, деленное само на себя: 92}{\sqrt{x + \sqrt{x}} + \sqrt{x}} \\[8px]
&= \lim_{x \to \infty} \frac{\left(x + \sqrt{x } \right) – x}{\sqrt{x + \sqrt{x}} + \sqrt{x}} \\[8px]
&= \lim_{x \to \infty}\frac{\sqrt{x }}{\sqrt{x + \sqrt{x}} + \sqrt{x}} \\[8px]
\end{align*} \]
Теперь воспользуемся нашим обычным приемом деления числителя и знаменателя на самая большая степень в знаменателе . Эта мощность равна $\sqrt{x}.$
\[ \begin{align*}
&= \lim_{x \to \infty}\frac{\dfrac{\sqrt{x}}{\sqrt{x} }}{\dfrac{\sqrt{x + \sqrt{x}}+ \sqrt{x}}{\sqrt{x}}} \\[8px]
&= \lim_{x \to \infty}\frac{1}{\dfrac{\sqrt{x + \sqrt{x}}}{\sqrt{x}}+ \dfrac{\sqrt{x}} {\sqrt{x}}} \\[8px]
&= \lim_{x \to \infty}\frac{1}{\sqrt{\dfrac{x + \sqrt{x}}{x}}+ 1} \\[8px]
&= \lim_{x \to \infty}\frac{1}{\sqrt{1 + \dfrac{1}{\sqrt{x}}}+ 1} \\[8px ]
&= \frac{1}{\sqrt{1 + \cancelto{0}{\dfrac{1}{\sqrt{x}}}}+ 1} \\[8px]
&= \frac{1 }{\sqrt{1}+ 1} \\[8px]
&= \dfrac{1}{2} \quad \cmark
\end{align*} \]
Обратите внимание, что ближе к концу мы использовали тот факт, что $\displaystyle{\lim_{x \to\, \infty}\frac{1}{\sqrt{x}} = 0}$.
Этот предел неожиданный, по крайней мере для нас! Но вы можете проверить несколько чисел, чтобы увидеть, как это работает:
\[ \begin{align*}
f(x) &= \sqrt{x + \sqrt{x}} – \sqrt{x} \\[8px ]
f(100) &= \sqrt{100 + \sqrt{100}} – \sqrt{100} \приблизительно 10,48 – 10 = 0,48 \\[8px]
f(10000) &= \sqrt{10000 + 100 } – 100 \приблизительно 100,499 – 100 = 0,499 \\[8px]
\end{align*} \]
[свернуть]
Практическая задача № 4
Это обобщенная версия задачи № 2 выше . 92 + ax} \right) }$, где $a$ — константа.
Нажмите, чтобы просмотреть решение исчисления
При $x \to \, -\infty$ член $x$ становится все больше и больше в отрицательном направлении, а член квадратного корня становится все больше и больше в положительном направлении направление.
2 + ax}$, деленное само на себя: 92}}}\\[8px]
&= \lim_{x \to\, -\infty}\frac{-a}{1 + \sqrt{1 + \frac{a}{x}}} \\ [8px]
&= \frac{-a}{1 + \sqrt{1}} \\[8px]
&= \frac{-a}{2} \quad \cmark
\end{align*} \ ]
Обратите внимание, что в предпоследней строке мы использовали тот факт, что $\displaystyle{\lim_{x \to\, -\infty} \frac{a}{x} = 0 }.$
[ свернуть]
Практическая задача #7
Учащийся разместил этот вопрос в комментариях ниже.
Найти $\displaystyle{\lim_{x \to \infty}\big[\sqrt{x}\sqrt{x}\sqrt{x} – \sqrt{x} \big]}.$ 93}} = \infty$ и $ \displaystyle{\lim_{x \to \infty}\sqrt{x}} = \infty,$ имеем $”\infty – \infty”$, что неопределенно: мы не Мы не знаем, каков на самом деле предел, но у нас есть еще много работы.
Как это часто бывает, разложение на множители обеспечивает путь вперед: обратите внимание, что мы можем извлечь $\sqrt{x}$ из обоих членов:
\begin{align*}
\sqrt{x}\sqrt{ x}\sqrt{x} – \sqrt{x} &= \sqrt{x} \big( \sqrt{x}\sqrt{x} – 1 \big) \\[8px]
&= \sqrt{x }(х – 1)
\end{выравнивание*}
Как только мы это сделали, предел становится ясным:
\begin{align*}
\lim_{x \to \infty}\big[\sqrt{x}\sqrt{x}\sqrt{x} – \ sqrt{x} \big] &= \lim_{x \to \infty}\big[\sqrt{x}(x – 1)\big] \\[8px]
&= \big[\lim_{x \ к \infty}\sqrt{x} \big] \cdot \big[\lim_{x \to \infty}(x – 1)\big] \\[8px]
&= \infty \cdot \infty \\ [8px]
&= \infty \quad \cmark
\end{align*}
[свернуть]
Практическая задача №8
Учащийся разместил этот вопрос в комментариях ниже.
Найти $\displaystyle{ \lim_{x \to \infty}\sqrt{x + \sqrt{x + \sqrt{x}}} – \sqrt{x} }$.
Нажмите, чтобы просмотреть решение исчисления
Есть два основных шага, чтобы найти этот предел.
Шаг 1 : Как и в предыдущих задачах, мы умножаем выражение на его сопряженное деление на себя:
\begin{align*}
\lim_{x \to \infty}\left( \sqrt{x + \sqrt{x + \sqrt{x}}} – \sqrt{x}\right) &= \lim_{x \to \infty}\left(\sqrt{x + \sqrt{x + \sqrt{x) }}} – \sqrt{x} \right)\cdot \frac{\sqrt{x + \sqrt{x + \sqrt{x}}} + \sqrt{x}}{\sqrt{x + \sqrt{ х + \sqrt{x}}} + \sqrt{x}} \\[8px]
&= \lim_{x \to \infty} \frac{\left(\sqrt{x + \sqrt{x + \sqrt{x}}}\right)\left(\sqrt{x + \sqrt{x) + \sqrt{x}}} \right) + \cancel{\left(\sqrt{x + \sqrt{x + \sqrt{x}}} – \sqrt{x} \right)\left(\sqrt{ x} \right)} – \cancel{\left(\sqrt{x}\right)\left(\sqrt{x + \sqrt{x + \sqrt{x}}} – \sqrt{x} \right) } + \left( -\sqrt{x}\right)\left(\sqrt{x} \right) }{\sqrt{x + \sqrt{x + \sqrt{x}}} + \sqrt{x} }\\[8px]
&=\lim_{x \to \infty} \frac{\left(x + \sqrt{x + \sqrt{x}} \right) -x}{\sqrt{x + \ sqrt{x + \sqrt{x}}} + \sqrt{x}} \\[8px]
&= \lim_{x \to \infty}\frac{\sqrt{x + \sqrt{x}}}{\sqrt{x + \sqrt{x + \sqrt{x}}} + \sqrt{x }}
\end{align*}
С этим переписанным выражением вы можете посмотреть на него и увидеть, что в числителе преобладает (первый) член $\sqrt{x}$, в то время как числитель преобладает в равной степени на два множителя $\sqrt{x}$, поэтому предел будет $\dfrac{1}{2}.
$
Но если вы этого не видите (поскольку вы еще не сделали 10 000 такие типы задач), или вам нужно это доказать, мы переходим к нашему обычному подходу Шаг 2 : Разделите числитель и знаменатель на наибольший множитель в знаменателе, который равен $\sqrt{x}.$ Итак, давайте умножим и числитель, и знаменатель на $\dfrac{1}{\sqrt{x} } $:
\begin{align*}
\lim_{x \to \infty}\frac{\sqrt{x + \sqrt{x}}}{\sqrt{x + \sqrt{x + \sqrt{x }}} + \sqrt{x}}
&= \lim_{x \to \infty}\frac{\frac{1}{\sqrt{x}}\sqrt{x + \sqrt{x}}}{ \frac{1}{\sqrt{x}}\left( \sqrt{x + \sqrt{x + \sqrt{x}}} + \sqrt{x}\right)} \\[8px]
&= \ lim_ {x \ to \ infty} \ frac {\ sqrt {\ frac {x + \ sqrt {x}} {x}}} {\ sqrt {\ frac {x + \ sqrt {x + \ sqrt {x} }}{x}} + \frac{\sqrt{x}}{\sqrt{x}}}\\[8px]
&= \lim_{x \to \infty}\frac{\sqrt{1 + \frac{1}{\sqrt{x}}}}{\sqrt{1 + \frac{\sqrt{x + \sqrt {x}}}{x}}+1} \\[8px]
&= \frac{\sqrt{1 + \cancelto{0}{\left( \lim_{x \to \infty}\frac{1 }{\sqrt{x}}\right)}}}{\sqrt{1 + \cancelto{0}{\left( \lim_{x \to \infty}\frac{\sqrt{x + \sqrt{x }}}{x}\right)}}+1} \\[8px]
&= \frac{\sqrt{1}}{\sqrt{1} + 1} \\[8px]
&= \frac {1}{2} \quad \cmark
\end{align*}
Ого! : )
[свернуть]
Хотите доступ к все наших проблем исчисления и решения? Войдите бесплатно с помощью своей учетной записи Google, Facebook или Apple или с помощью специальной учетной записи Matheno (которую вы можете создать за 60 секунд).