Lim в математике это: «Что такое lim в математике?» — Яндекс Кью

Предел (в математике). Большая российская энциклопедия

Преде́л, одно из основных понятий математики, означающее, что некоторая переменная в рассматриваемом процессе её изменения неограниченно приближается к какому-то постоянному значению. Точный смысл термин «предел» имеет лишь при наличии корректного понятия близости между элементами (точками) множества, в котором указанная переменная принимает значения. Основные понятия математического анализа – непрерывность, производная, интеграл – определяются с помощью предела. Наиболее простыми являются понятия предела функции (в частности, предела последовательности) и понятие предела интегральных сумм.

Предел числовой последовательности

Число aaa называют пределом последовательности{xn} \{x_n\}{xn​}, n=1,2,…n=1, 2, \ldotsn=1,2,…, если для любого числа ε>0ε>0ε>0 существует (зависящее от него) натуральное число NNN такое, что при всех n>Nn>Nn>N выполняется неравенство

∣xn−a∣<ε.(1)\left |x_n-a \right |\lt ε. n\}{(–1)n}, n=1,2,…,n=1, 2, \ldots,n=1,2,…, не стремится ни к какому пределу, её элементы попеременно равны –1–1–1 и +1+1+1 и не могут одновременно попасть в интервал (a−ε,a+ε)(a-ε, a+ε)(a−ε,a+ε) при 0<ε<10\lt ε\lt 10<ε<1 ни при каком a.a.a. Последовательность, не имеющая предела, называется расходящейся.

Последовательность может иметь лишь единственный предел. Если последовательность сходится, то она ограничена, т. е. её элементы лежат на некотором ограниченном отрезке действительной оси. Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность (теорема Больцано – Вейерштрасса). Если последовательности {xn}\{x_n\}{xn​} и {yn}\{y_n\}{yn​} сходятся, то справедливы равенства: для любых чисел λλλ и μμμ

lim⁡n→∞(λxn+μyn)=λlim⁡n→∞xn+μlim⁡n→∞yn,lim⁡n→∞(xnyn)=(lim⁡n→∞xn)(lim⁡n→∞yn),\begin{aligned}\lim_{n→∞}(λx_n+μy_n) &=λ\lim_{n→∞}x_n +μ\lim_{n→∞}y_n, \\ \lim_{n→∞}(x_ny_n) &=(\lim_{n→∞}x_n)(\lim_{n→∞}y_n), \end{aligned}n→∞lim​(λxn​+μyn​)n→∞lim​(xn​yn​)​=λn→∞lim​xn​+μn→∞lim​yn​,=(n→∞lim​xn​)(n→∞lim​yn​),​если yn≠0y_n≠0yn​=0 и lim⁡n→∞yn≠0\lim\limits_{n→∞}y_n\neq 0n→∞lim​yn​=0, то

lim⁡n→∞xnyn=lim⁡n→∞xnlim⁡n→∞yn.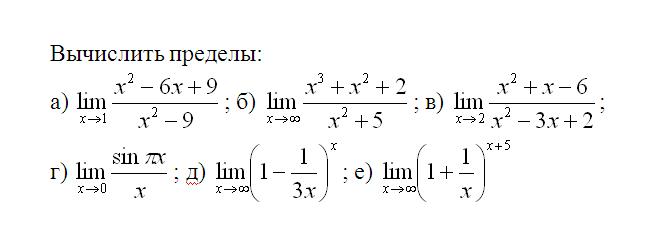 \lim_{n→∞}\frac{x_n}{y_n}=\frac{\lim_{n→∞}x_n}{\lim_{n→∞}y_n}.n→∞lim​yn​xn​​=limn→∞​yn​limn→∞​xn​​.Числовая последовательность сходится к конечному пределу тогда и только тогда, когда она удовлетворяет условию Коши: для любого числа ε>0ε>0ε>0 существует натуральное число NNN (зависящее от εεε) такое, что для всех n>Nn>Nn>N и любого натурального mmm расстояние между элементами последовательности xnx_nxn​ и xn+mx_{n+m}xn+m​ меньше εεε, т. е. ∣xn−xn+m∣<ε\left | x_n-x_{n+m}\right |\lt ε∣xn​−xn+m​∣<ε (критерий Коши). Такие последовательности называются фундаментальными. Т. о., сходящимися являются фундаментальные последовательности и только они.

Всякая ограниченная и монотонная последовательность является сходящейся. В частности, если последовательность не убывает (не возрастает) и ограничена сверху (снизу), то она имеет предел и этот предел есть точная верхняя (нижняя) грань множества значений элементов последовательности. Примером возрастающей и ограниченной сверху последовательности является последовательность периметров правильных nnn-угольников, n⩾3n⩾3n⩾3, вписанных в некоторую окружность. \alpha}=0, \quad a\gt 0,\,a\neq1,\,\alpha\gt 0. n→∞lim​na​=1,a>0;n→∞lim​nn​=1;n→∞lim​naqn=0,a>0,∣q∣<1;n→∞lim​nn​!1​=0;n→∞lim​(1+na​)n=ea,−∞<a<∞;n→∞lim​(1+1!1​+2!1​+…+n!1​)=e;n→∞lim​nαloga​n​=0,a>0,a=1,α>0.Стремящаяся к нулю последовательность называется бесконечно малой. Бесконечно малые последовательности играют особую роль в теории пределов последовательностей, т. к. общее определение предела последовательности может быть дано в терминах бесконечно малых: предел последовательности {xn}\{x_n\}{xn​}, n=1,2,…n=1, 2, \ldotsn=1,2,…, равен aaa тогда и только тогда, когда последовательность {xn−a}\{x_n-a\}{xn​−a}, n=1,2,…n=1, 2, \ldotsn=1,2,…, есть бесконечно малая. В период формирования основных понятий математического анализа он назывался анализом бесконечно малых.

Иногда рассматриваются бесконечные пределы последовательностей. Бесконечный предел последовательности вводится как свойство последовательности {xn}\{x_n\}{xn​}, n=1,2,…n=1, 2, \ldotsn=1,2,…, быть бесконечно большой: для любого положительного числа KKK существует такое натуральное число NNN, что при всех n>Nn>Nn>N справедливо неравенство ∣xn∣>K|x_n|>K∣xn​∣>K. n→∞2n→∞, n!→∞n!→∞n!→∞. Если последовательность {xn}\{x_n\}{xn​}, n=1,2,…n= 1, 2, \ldotsn=1,2,…, бесконечно большая и, начиная с некоторого nnn, принимает только положительные (отрицательные) значения, то lim⁡n→∞xn=+∞\lim\limits_{n→∞}x_n=+\inftyn→∞lim​xn​=+∞ (соответственно, lim⁡n→∞xn=−∞\lim\limits_{n→∞}x_n=-\inftyn→∞lim​xn​=−∞).

Если множества точек xxx, удовлетворяющие условиям x>1εx\gt\frac{1}{ε}x>ε1​, x<−1εx\lt-\frac{1}{ε}x<−ε1​ и ∣x∣>1ε|x|\gt\frac{1}{ε}∣x∣>ε1​, ε>0ε\gt 0ε>0, назвать εεε-окрестностями +∞+∞+∞, –∞–∞–∞ и ∞∞∞ соответственно, то определения как конечного, так и бесконечного пределов формулируются одинаково: предел последовательности {xn}\{x_n\}{xn​}, n=1,2,…n=1, 2, \ldotsn=1,2,…, равен aaa (где aaa – число или один из символов +∞+∞+∞, –∞–∞–∞, ∞∞∞), если для любого числа ε>0ε>0ε>0 существует такое натуральное NNN, что все элементы последовательности с номерами n>Nn>Nn>N лежат в εεε-окрестности aaa.

Некоторые свойства предела последовательности одинаковы в случае конечного и бесконечного пределов. Например, если последовательности{xn} \{x_n\}{xn​}, n=1,2,…,n=1, 2, \ldots,n=1,2,…, и {yn}\{y_n\}{yn​}, n=1,2,…n=1, 2,\ldotsn=1,2,…, имеют пределы (конечные или бесконечные) и, начиная с некоторого nnn, справедливы неравенства xn⩽ynx_n⩽y_nxn​⩽yn​, то и lim⁡n→∞xn⩽lim⁡n→∞yn\lim\limits_{n\rightarrow\infty} x_n⩽\lim\limits_{n\rightarrow\infty} y_nn→∞lim​xn​⩽n→∞lim​yn​, т. е. при предельном переходе нестрогие неравенства сохраняются.

Если последовательность имеет предел (конечный или определённого знака бесконечный), то любая её подпоследовательность имеет тот же предел. Конечный или бесконечный пределы подпоследовательности данной последовательности называют её частичным пределом. Наибольший (наименьший) из частичных пределов числовой последовательности всегда существует и называется верхним (нижним) пределом этой последовательности. Совпадение верхнего и нижнего пределов последовательности равносильно тому, что она имеет (конечный или определённого знака бесконечный) предел.

Для последовательности комплексных чисел определение предела аналогично: число a=α+iβa=α+iβa=α+iβ называется пределом последовательности {zn}\{z_n\}{zn​}, zn=xn+iynz_n=x_n+iy_nzn​=xn​+iyn​, n=1,2,…n=1, 2, \ldotsn=1,2,…, если для любого числа ε>0ε>0ε>0 существует натуральное число NNN такое, что при всех n>Nn>Nn>N имеет место неравенство ∣zn−a∣<ε|z_n-a|<ε∣zn​−a∣<ε. Этот предел сводится к пределу последовательностей действительных чисел, т. к. lim⁡n→∞zn=a\lim\limits_{n→\infty} z_n=an→∞lim​zn​=a тогда и только тогда, когда lim⁡n→∞xn=α\lim\limits_{n→\infty} x_n=\alphan→∞lim​xn​=α и lim⁡n→∞yn=β\lim\limits_{n→\infty}y_n=\betan→∞lim​yn​=β. Кроме того, по определению,lim⁡n→∞zn=∞\lim\limits_{n→\infty} z_n=\inftyn→∞lim​zn​=∞ если lim⁡n→∞∣zn∣=∞\lim\limits_{n→\infty} |z_n|=\inftyn→∞lim​∣zn​∣=∞.

С помощью понятия предела числовой последовательности определяются многие понятия пределов последовательностей, состоящих из элементов более сложной природы. Например, пусть на множестве MMM задана последовательность функций {fn}\{f_n\}{fn​}, n=1,2,…n=1, 2,\ldotsn=1,2,…, и функция fff. Говорят, что эта последовательность сходится к fff поточечно, если для любого x∈Mx∈Mx∈M числовая последовательность {fn(x)}\{f_n(x)\}{fn​(x)}, n=1,2,…n=1, 2, \ldotsn=1,2,…, сходится к числу f(x)f(x)f(x). Говорят, что эта последовательность функций сходится к fff равномерно на MMM, если числовая последовательность точных верхних граней {sup⁡x∈M∣fn(x)−f(x)∣}\{\sup\limits_{x∈M}\left|f_n(x)-f(x)\right|\}{x∈Msup​∣fn​(x)−f(x)∣}, n=1,2,…n=1, 2, \ldotsn=1,2,…, сходится к нулю.

Предел функции

Говорят, что функция fff, принимающая действительные значения, имеет в конечной или бесконечно удалённой точке x0x_0x0​ конечный или бесконечный предел aaa, если для любой последовательности

{xn},n=1,2,…,(2)\{x_n\},\quad n=1, 2, \ldots,\tag2{xn​},n=1,2,…,(2)стремящейся к точке x0x_0x0​, числовая последовательность {f(xn)}\{f(x_n)\}{f(xn​)}, n=1,2,…n=1, 2, \ldotsn=1,2,…, стремится к aaa. В этом случае пишут:

lim⁡x→x0f(x)=a  или  f(x)→a  при  x→x0.(3)\lim\limits_{x→x_0}f(x)=a\,\,или\,\,f(x)→a\,\,при\,\,x→x_0.\tag3x→x0​lim​f(x)=aилиf(x)→aприx→x0​.(3)Здесь предполагается, что все элементы последовательности (2) принадлежат области определения функции fff. Если это множество лежит на действительной оси, то x0x_0x0​ может быть либо действительным числом, либо одной из бесконечностей +∞+∞+∞, –∞–∞–∞, ∞∞∞. Если область определения функции fff лежит в плоскости, в пространстве, вообще говоря, mmm-мерном, m>1m>1m>1, то x0x_0x0​ может быть либо точкой этой плоскости, соответственно пространства, либо бесконечно удалённой точкой.

Предел функции может быть либо числом, либо одной из бесконечностей +∞+∞+∞, –∞–∞–∞, ∞∞∞.

Точка x0x_0x0​, в которой рассматривается предел функции, может принадлежать или не принадлежать области определения этой функции. Например, lim⁡x→0sin⁡x=0\lim\limits_{x→0}\sin x=0x→0lim​sinx=0 и lim⁡x→0sin⁡xx=1.\lim\limits_{x→0}\frac{\sin x}{x}=1.x→0lim​xsinx​=1. В первом случае функция sin x определена для всех действительных значений xxx, а во втором – для всех, кроме x=0x=0x=0. Если точка x0x_0x0​ принадлежит области определения функции fff, существует предел (3) и он равен f(x0)f(x_0)f(x0​), т. е.

lim⁡x→x0f(x)=f(x0),\lim_{x→x_0} f(x)=f(x_0),x→x0​lim​f(x)=f(x0​),то функция fff называется непрерывной в точке x0x_0x0​.

Иногда при определении предела (3) на функции накладывается дополнительное ограничение

xn≠x0,n=1,2,…(4)x_n≠x_0,\quad n=1, 2, \ldots\tag4xn​=x0​,n=1,2,…(4)Так, определённое понятие «предела» является частным случаем введённого выше, а именно, соответствующим случаю, когда точка x0x_0x0​ не принадлежит множеству, на котором рассматривается функция fff.

{\it m}X⊂Rm, m⩾1m⩾1m⩾1, имеет в точке x0x_0x0​ (конечной или бесконечно удалённой) конечный предел, если для любого ε>0ε>0ε>0 существует такая окрестность UUU точки x0x_0x0​, что как только x∈X∩Ux∈X∩Ux∈X∩U, x′∈X∩Ux’∈X∩Ux′∈X∩U, то выполняется неравенство ∣f(x)−f(x′)∣<ε|f(x)-f(x’)|\lt ε∣f(x)−f(x′)∣<ε.

Функция, имеющая конечный предел в точке x0x_0x0​, локально ограничена, т. е. существует окрестность точки x0x_0x0​, на пересечении которой с областью определения функции эта функция ограничена.

В случае существования предела в неравенствах для функций можно переходить к пределу: если функции fff, ggg, hhh заданы на множестве XXX, существуют конечные или определённого знака бесконечные пределы

lim⁡x→x0f(x)=lim⁡x→x0g(x)=a,\lim_{x→x_0} f(x)=\lim_{x→x_0} g(x)=a,x→x0​lim​f(x)=x→x0​lim​g(x)=a,и для всех x∈Xx∈Xx∈X выполняются неравенства f(x)⩽h(x)⩽g(x)f(x)⩽h(x)⩽g(x)f(x)⩽h(x)⩽g(x), то существует

lim⁡x→x0h(x)=a.\lim_{x→x_0} h(x)=a.x→x0​lim​h(x)=a.Если существуют конечные пределы

lim⁡x→x0f(x)иlim⁡x→x0g(x),\lim_{x→x_0} f(x)\quadи\quad\lim_{x→x_0} g(x),x→x0​lim​f(x)иx→x0​lim​g(x),то справедливы равенства, аналогичные тем, что справедливы для пределов числовых последовательностей: для любых чисел λλλ и μμμ

lim⁡x→x0(λf(x)+μg(x))=λlim⁡x→x0f(x)+μlim⁡x→x0g(x),lim⁡x→x0(xnyn)=(lim⁡x→x0f(x))(lim⁡x→x0g(x)),если  g(x)≠0иlim⁡x→x0g(x)≠0,тоlim⁡x→x0xnyn=lim⁡x→x0f(x)lim⁡x→x0g(x).

\alpha-1}{x}=\alpha. x→∞lim​(1+x1​)x=x→0lim​(1+x)1/x=e;x→0lim​xax−1​=lna,x→+∞lim​xαloga​x​=0,a>0,a=0,α>0;x→0lim​xln(1+x)​=1;x→0lim​xsinx​=1;x→+∞lim​arctgx=2π​;x→0lim​x(1+x)α−1​=α.Предел композиции функций: если определена сложная функция F(f(x))F(f(x))F(f(x)) и существуют конечные или бесконечные пределы

lim⁡x→x0f(x)=aиlim⁡y→aF(y)=b,\lim\limits_{x→x_0} f(x)=a\quad и\quad\lim\limits_{y→a} F(y)=b,x→x0​lim​f(x)=aиy→alim​F(y)=b,то существует предел

lim⁡x→x0F(f(x))=lim⁡y→aF(y)=b.\lim\limits_{x→x_0} F(f(x))=\lim\limits_{y→a} F(y)=b.x→x0​lim​F(f(x))=y→alim​F(y)=b.Определение предела (3) для функций, принимающих действительные значения, переносится на комплекснозначные функции.

Основным общим методом вычисления пределов функций является выделение главных частей функций в окрестности данной точки, что делается обычно с помощью формулы Тейлора.

Понятие предела функции обобщается и на более широкие классы функций: если функция fff задана на множестве XfX_fXf​, являющемся подмножеством топологического пространства XXX, а множество её значений принадлежит топологическому пространству YYY (в этом случае вместо термина «функция» обычно употребляют термин «отображение»), то точка a∈Ya∈Ya∈Y называется пределом функции fff при x→x0∈Xx→x_0∈Xx→x0​∈X, если для любой окрестности VVV точки aaa в пространстве YYY существует такая окрестность UUU точки x0x_0x0​ в пространстве XXX, что f(X∩U)⊂Vf(X∩U)⊂Vf(X∩U)⊂V.

n_j=0{xj​}jn​=0 отрезка [a,b][a, b][a,b], для которого max⁡l⩽j⩽nΔxj<δ\max\limits_{l⩽j⩽n}\Delta x_j\lt δl⩽j⩽nmax​Δxj​<δ, и каковы бы ни были точки ξjξ_jξj​, xj−1⩽ξj⩽xjx_{j-1}⩽ξ_j⩽x_jxj−1​⩽ξj​⩽xj​, j=1,2,…,nj=1, 2, \ldots, nj=1,2,…,n, выполняется неравенство

∣f(ξ1)Δx1+f(ξ2)Δx2+…+f(ξn)Δxn−A∣<ε.\left| f(ξ_1)\Delta x_1+f(ξ_2)\Delta x_2+ \ldots+f(ξ_n)\Delta x_n-A\right |\lt ε.∣f(ξ1​)Δx1​+f(ξ2​)Δx2​+…+f(ξn​)Δxn​−A∣<ε.Понятие предела интегральных сумм может быть введено и с помощью предела последовательности.

Обобщения понятия предела

Ввиду разнообразия употребляемых в математике специальных видов понятия предела естественно возникло стремление включить их как частные случаи в более широкое понятие предела. Можно ввести понятие предела, обобщающее как предел числовой функции, так и понятие предела интегральных сумм. Система SSS непустых подмножеств некоторого множества XXX называется направлением, если для каждых двух подмножеств AAA и BBB этой системы выполняется одно из включений A⊂BA⊂BA⊂B или B⊂AB⊂AB⊂A. b f(x)dx.∫ab​f(x)dx.

Понятие предела обобщается на более широкие классы функций, например на функции, заданные на частично упорядоченных множествах, или на функции, являющиеся отображениями одного пространства (метрического или, более общо, топологического) в другое. Наиболее полно задача определения предела решается в топологии и означает в общем случае, что некоторый объект, обозначенный f(x)f(x)f(x), меняющийся при изменении другого объекта, обозначенного xxx, при достаточно близком приближении объекта xxx к объекту x0x_0x0​ сколь угодно близко приближается к объекту aaa, который и называется пределом f(x)f(x)f(x) при xxx, стремящемся к x0x_0x0​. Основным в такого рода понятиях предела являются понятия близости объектов xxx и x0x_0x0​, f(x)f(x)f(x) и aaa, которые нуждаются в строгих определениях. Только после того как это сделано, высказанному определению предела можно придать чёткий смысл и оно станет содержательным. Различные понятия близости и изучаются, в частности, в топологии.

Встречаются, однако, понятия предела и другой природы, не связанные с топологией, например понятие предела последовательности множеств. Последовательность множеств {An}\{A_n\}{An​}, n=1,2,…n=1, 2, \ldotsn=1,2,…, называется сходящейся, если существует множество AAA, называемое её пределом, такое, что каждая его точка принадлежит всем множествам AnA_nAn​, начиная с некоторого номера nnn, и каждая точка из объединения всех множеств AnA_nAn​, не принадлежащая AAA, принадлежит лишь конечному числу множеств AnA_nAn​.

Историческая справка

К понятию предела вплотную подошли ещё древнегреческие учёные при вычислении площадей и объёмов некоторых фигур и тел с помощью метода исчерпывания. Так, Архимед, рассматривая последовательности вписанных и описанных ступенчатых фигур (тел) с помощью метода исчерпывания, доказывал, что разность между их площадями (объёмами) может быть сделана меньше любой наперёд заданной положительной величины. Включая в себя, по существу, представление о бесконечно малых, метод исчерпывания являлся зародышем теории пределов. Однако в явном виде в древнегреческой математике понятие предела не было сформулировано, не было создано и каких-либо основ общей теории.

Новый этап в развитии понятия предела наступил в эпоху создания дифференциального и интегрального исчисления. Г. Галилей, И. Кеплер, Б. Кавальери, Б. Паскаль и др. при вычислении площадей и объёмов широко использовали метод «неделимых», метод актуально бесконечно малых, т. е. таких бесконечно малых, которые, по их представлениям, являются неизменными величинами, не равными нулю и вместе с тем меньшими по абсолютной величине любых конечных положительных величин. В этот период продолжает применяться и развиваться метод исчерпывания (швейцарский математик П. Гульдин, Х. Гюйгенс и др.). На основе интуитивного понятия предела появляются попытки создать общую теорию пределов. Так, И. Ньютон первый отдел первой книги («О движении тел») своего труда «Математические начала натуральной философии» посвятил своеобразной теории пределов под названием «Метод первых и последних отношений», которую он положил в основу своего метода флюксий. В этой теории Ньютон взамен актуально бесконечно малых предложил концепцию «потенциально» бесконечно малой, которая лишь в процессе своего изменения становится по абсолютной величине меньше любой положительной конечной величины. Точка зрения Ньютона была существенным шагом вперёд в развитии представления о пределе. Понятие о пределе, наметившееся у математиков 17 в., в следующем 18 в. постепенно анализировалось и уточнялось (Л. Эйлер, Ж. Д’Аламбер, Н. Л. С. Карно, Я. Бернулли и И. Бернулли и др.). В этот период оно служило лишь для попыток объяснить правильность дифференциального и интегрального исчисления и ещё не являлось основой разработки проблем математического анализа.

Современная теория пределов начала формироваться в начале 19 в. в связи с изучением свойств различных классов функций, прежде всего непрерывных, а также в связи с попытками доказательства существования ряда основных объектов математического анализа (интегралов, сумм рядов, корней алгебраических и более общих уравнений и т. п.). В работах О. Коши понятие предела впервые стало основой построения математического анализа. Им были установлены основные свойства существования предела, основные теоремы о пределе и, что очень важно, получен внутренний критерий сходимости последовательности, носящий ныне его имя. Наконец, он определил интеграл как предел интегральных сумм и изучил его свойства. Окончательно понятие предела последовательности и функции оформилось на базе теории функций действительного переменного в работах Б. Больцано и К. Вейерштрасса.

Редакция математических наук. По материалам статей Л. Д. Кудрявцева и Т. С. Пиголкиной из Математического энциклопедического словаря

Дата публикации:  21 мая 2022 г. в 09:59 (GMT+3)

Предел и непрерывность функции / Математика для школы

 

Предел функции y = f(x) при х → ∞

Вычисление пределов функции при х → ∞

Непрерывные функции

Теоремы про непрерывность функции

Замечательные пределы

Вычисление пределов функции в точке

  

Предел функции

y = f(x) при х → ∞

Определение.

Число b называется пределом функции y = f(x) при х→+∞, если для любого числа ε > 0 найдётся такое число М > 0, что для всех х > М выполняется неравенство |f(x) – b|< ε.

Записывают так:

lim _х→+∞f(x) = b.

Геометрически это означает, что график функции y = f(x) при выборе достаточно больших значений х безгранично приближается к прямой у = b. Это означает, что расстояние от точки графика до прямой у = b по мере удаления точки в бесконечность может быть сделано меньше любого числа ε > 0. Прямая  называется в этом случае горизонтальной асимптотой графика функции y = f(x).  

Например: lim _х→+∞ 1/х = 0 и функция y = 1/х имеет горизонтальную асимптоту у = 0.

 

Определение.

Число b называется пределом функции y = f(x) при х→–∞, если для любого числа ε > 0 найдётся такое число М > 0, что для всех х < –М выполняется неравенство |f(x) – b|< ε.

Записывают так:

lim _х→–∞f(x) = b.

В этом случае прямая y = b также является горизонтальной асимптотой функции  y = f(x), график которой бесконечно близко приближается к ней при достаточно больших по модулю, но отрицательных значениях х.

Например: lim _х→–∞ (3 + 2^х) = 3 и функция y = (3 + 2^х) имеет горизонтальную асимптоту у = 3.

 

Наконец, прямая у = b  может быть горизонтальной асимптотой графика функции  и при х→+∞, и при х→–∞. Пишут так: х→∞.

Определение.

Число b называется пределом функции y = f(x) при х → ∞, если для любого числа ε > 0 найдётся такое число М > 0, что для всех x таких, что |х| > М, выполняется неравенство |f(x) – b|< ε.

Записывают так:

lim _х→∞f(x) = b.

Например: lim _х→∞х²/(х²+1) = 1 и функция y = х²/(х²+1) имеет горизонтальную асимптоту у = 1.

 

Вычисление пределов функции при

х → ∞

Для вычисления пределов функций при х→∞ используются следующие теоремы об операциях над пределами:

 

Теорема о вынесении постоянного множителя за знак предела:

Если lim _х→∞f(x) = a, то lim _х→∞k · f(x) = k · а.

 

Теорема о пределе суммы:

Если lim _х→∞ f(x) = a, lim _х→∞ g(x) = b, то lim _х→∞ (f(x) + g(x)) = а + b.

 

Теорема о пределе произведения:

Если lim _х→∞ f(x) = a, lim _х→∞ g(x) = b, то lim _х→∞ f(x) · g(x) = а · b.

 

Теорема о пределе частного:

Если lim _х→∞ f(x) = a, lim _х→∞ g(x) = b и b ≠ 0, то lim _х→∞ f(x) / g(x) = а / b.

  

Непрерывные функции 

Определение.

Функция y = f(x) называется непрерывной в точке х = а, если существует предел функции в этой точке, т.е.

lim _х→а f(x) = f(a).

Функция y = f(x) будет непрерывной в точке х = а тогда и только тогда, когда выполняются условия:

• функция y = f(x) определена в точке х = а, т. е. существует f(a);
• существует предел lim _х→а f(x) функции в точке х = а;
• предел функции в точке х = а равен значению функции в этой точке, т.е.

lim _х→а f(x) = f(a). 

Другими словами верно и такое

Определение.

Функция y = f(x) непрерывна в точке х = а, если для любого числа ε > 0 существует такое число δ > 0, что для всех х, удовлетворяющих условию |x – a| < δ, выполняется неравенство |f(x) – f(a)| < ε.

Определение.

Если функция y = f(

x) непрерывна в каждой точке некоторого промежутка, то её называют непрерывной на данном промежутке.

 

Теоремы про непрерывность функции

Теорема 1:

Если функции f(x) и g(x) непрерывны в точке х = а, то в этой точке непрерывны и функции  f(x) + g(x), f(x) – g(x), f(x) · g(x).

 

Теорема 2:

Если функции f(x) и g(x) непрерывны в точке х = а и g(а) ≠ 0, то в точке х = а  будет непрерывной также функция f(x) / g(x)

.

 

Исходя из двух последних теорем можно утверждать:

• многочлен y = a₀ + a₁x + . . . + a_nxⁿ – непрерывная функция в любой точке а ∈ R;
• дробно-рациональная функция

y =	a0 + a1x + a2x2 + . . . + anxn
	b0 + b1x + b2x2 + . . . + bmxm

        непрерывна во всех точках числовой оси, кроме нулей знаменателя;

• функции у = sin x, y = cos x, y = tg x, y = ctg x, y = a^x, y = log_ax, y = ⁿ√х, y = |x|, у = arcsin x, y = arccos x, y = arctg x, y = arcctg x также непрерывны во всех точках области определения.

 

Замечательные пределы

Замечательные пределы – термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:

 

Первый замечательный предел:

lim х→ 0	sin x	= 1.
	x

Следствия из первого замечательного предела: 

lim х→ 0	tg x	= 1,
	x

lim х→ 0	arcsin x	= 1,
	x

lim х→ 0	arctg x	= 1,
	x

lim х→ 0	2 · (1 – cos x)	= 1.
	x2

 

Второй замечательный предел:

lim _х→∞ (1 + 1/x)^x = e  или  lim _х→0 (1 + x)^1/x = e.

 

Следствия из второго замечательного предела:

lim х→ 0

(1 + u)1/u = e,

lim х→ ∞

(1 + k/x)x = ek,

lim х→ 0	ln(1 + x)	= 1,
	x

lim х→ 0	ex – 1	= 1,
	x

lim х→ 0	ax – 1	= 1,
	x · ln a

lim х→ 0	(1 + x)α – 1	= 1.
	αx

 

Вычисление пределов функции в точке 

Если y = f(x) непрерывна в точке х = а, то lim _х→а f(x) = f(a).

Если в результате подстановки х = а при вычислении предела получаем выражение типа 0 / 0, то имеет смысл попытаться воспользоваться одним из следующих приёмов:

• попробовать разложить числитель и знаменатель дроби на множители, выполнить сокращение, а затем найти предел;
• избавиться от иррациональности в знаменателе, а затем находить предел:
• преобразовать функцию так, чтобы можно было воспользоваться первым замечательным пределом или его следствием.

 

     Смотрите также:

Таблицы чисел 

Алгебраические тождества

Степени

Арифметический корень n-й степени

Логарифмы 

Графики элементарных функций

Построение графиков функций геометрическими методами

Тригонометрия

Таблицы значений тригонометрических функций

Треугольники

Четырёхугольники

Многоугольники

Окружность 

Площади геометрических фигур

Прямые и плоскости

Многогранники 

Тела вращения 

 

Сонхи Лим

Сонхи Лим

---

Сейчас я в Сеульском национальном университете. Для моего текущего веб-сайта, пожалуйста, нажмите здесь

Х.К. Ван Доцент

Математический факультет,

593 Малотт Холл, Корнельский университет

Итака, Нью-Йорк, 14853-4201

Рабочий телефон: (607) 255-7113, факс: (607) 255-7149

Электронная почта: [email protected]

---

Обучение

Spring 2009: Math 7520, Семинар Бернштейна по топологии и геометрической теории групп

Весна 2009 г.: Математика 4320, Введение в алгебру

Осень 2008: Математика 618, Эргодическая теория

---

Исследования

Научные интересы: геометрическая теория групп и динамика

• Динамика групповых воздействий на деревья и здания, в более общем случае метрические пространства неположительной кривизны
• Решетки групп Ли и группы автоморфизмов деревьев и полиэдральные комплексы, подгруппы-соизмерители и т.д.
• Энтропийная жесткость

Документы

• Рост компенсатора (совместная работа с Нир Авни и Эран Нево), в подготовке.
• Объемная энтропия для зданий (совместная работа с Ф. Ледрапье), препринт. абстрактный пдф ps (2008.10, переработано (улучшено, чтобы включить все обычные здания) 2009.7)
• Доказательство эргодической теоремы L1/2 (совместная работа с Ф. Ледрапье). pdf, пс (2006.12)
• Счетные надрешетки для многогранных комплексов (совместная работа с А. Томасом), представлено к публикации. абстрактный пдф пс (пересмотрено в 2007.11)
• Теория покрытия для комплексов групп (совместная работа с А. Томасом), J. Pure Appl. Алгебра 212 (2008) 1632–1663. абстрактный, архив
• Минимальная объемная энтропия для графов, Пер. амер. Мат. соц. 360 (2008), 5089-5100. реферат, pdf, ps
• Счетные надрешетки в группах автоморфизмов деревьев, Геом. Посвященный, Vol. 118 (2006), вып. 1, стр. 1-21. абстрактный, pdf, ps

Организованы предстоящие и недавние конференции

• Первая совместная международная встреча AMS и Корейского математического общества, Сеул (16-20 декабря 2009 г. ).
Будет проведено специальное занятие по геометрической теории групп и низкоразмерной топологии (и группам Ли). Пожалуйста, напишите мне по электронной почте для получения дополнительной информации, если вы заинтересованы.
• Семинар AIM: Жесткость объемной энтропии, Цюрих (июнь 2009 г.).
• Заседание Западной секции AMS, специальная сессия, посвященная последним достижениям в области геометрической теории групп, Сан-Франциско (апрель 2009 г.) (Заседание связано с приглашенным выступлением К. Фогтмана).

Предстоящие и недавние выступления

• Примеры групп, Университет штата Огайо, Колумбус, Огайо (11–14 мая 2009 г.)).
• Корнельский фестиваль топологии, Итака, Нью-Йорк (4 мая 2009 г.).
• Семинар по жесткости, часть Корнельского фестиваля топологии, Итака, Нью-Йорк (1 мая 2009 г.).
• Совместное собрание по математике, Специальная сессия AMS по групповым действиям в однородных пространствах и приложениях, Вашингтон, округ Колумбия (5 января 2009 г. )
• Коллоквиум, Корейский передовой институт науки и технологий, Тэджон, Южная Корея (10 декабря 2008 г.)
• Семинар по динамике групповых действий, Йельский университет (10 ноября 2008 г.)
• Летняя школа по квазиконформному анализу и границам гиперболических групп, Блумингтон, Индиана (14 августа 2008 г.) (по результату Бурдона и Пажо о жесткости квазиизометрии, конспекты лекций)
• Семинар по геометрии, Афинский университет, Афины, Греция (4 августа 2008 г.)
• Семинар по анализу и геометрии в группах, University Paris 7, Париж, Франция (23 июля 2008 г.)
• Семинар по геометрии, ETH, Цюрих, Швейцария (9 июля 2008 г.)
• Миникурс графов групп и комплексов групп, унив. Невшатель, Швейцария (2, 9 июня, 16, 23, 2008)
• Семинар по геометрии и динамике, Ecole Normale Superieure de Lyon, Франция (18 июня 2008 г.)
• Конференция по анализу, геометрии и динамике групп, Невшатель, Швейцария (13 июня 2008 г.)
• Конференция по дискретным группам и геометрическим структурам с приложениями, Кортрейк, Бельгия (29 мая 2008 г. )
• Семинар по динамике, Северо-Западный университет (13 мая 2008 г.)
• Весеннее восточное секционное собрание AMS, специальная сессия по геометрической топологии, Институт Куранта (15-16 марта 2008 г.)
• Семинар по топологии и геометрической теории групп, Корнельский университет (26 февраля 2008 г.)
• Семинар по геометрии и топологии, SUNY Buffalo (22 февраля 2008 г.)
• Семинар по геометрии и топологии, Бингемтонский университет (21 февраля 2008 г.)
• еще

---

Ссылки

• Список конференций по геометрической теории групп
• Список конференций в динамических системах
• Задачи по геометрической теории групп

резюме

Добро пожаловать на домашнюю страницу Тонгсока Лима!

Тонгсок Лим — доцент кафедры количественных методов в Школе бизнеса им. Митчелла Э. Дэниэлса-младшего Университета Пердью.

Тонгсок Лим интересуется различными областями, и его исследования включают (i) (Мартингейл-) Оптимальный транспорт в многомерном пространстве и его приложения к экономике, финансам и статистике, (ii) Анализ вариационных задач, возникающих в физике, геометрии и данных Наука и (iii) теория Ходжа на графах и ее связь со стохастическим исчислением и теорией игр.

Дополнительную информацию о Тонгсоке Лиме см. в резюме и Google Scholar.

⁍ Новости (март 2022 г.): Статья Лима «Геометрия векторных мартингальных оптимальных транспортировок и двойственность» будет опубликована в серии A «Математическое программирование». мотивированы надежными математическими финансами.

⁍ Новости (февраль 2023 г.): Статья Лима, анонсированная в марте 2022 г., была полностью переписана с новыми результатами и новым названием: Распределение Ходжа для кооперативных вознаграждений: обобщение теории распределения кооперативной стоимости Шепли через теорию Ходжа на графах.

⁍ Новости (декабрь 2022 г.): Статья Лима, анонсированная в июле 2022 г., значительно расширена по сравнению с предыдущей версией и носит новое название: Максимальная монотонность и циклическая инволютивность мультисопряженных выпуклых функций.

⁍ Новости (ноябрь 2022 г.): Статья Лима «Классификация состояний с минимальной энергией для взаимодействующих частиц: регулярные симплексы» будет опубликована в «Communications in Mathematical Physics». Это совместная работа с Робертом Дж. Макканном и его учеником Кэмероном Дэвисом.

⁍ Новости (июль 2022 г.): Появилась новая статья Лима «Полнота и максимальная монотонность мультисопряженных выпуклых функций на прямой». В работе вводится понятие обобщенной инволюции нескольких выпуклых функций, которое мы называем полнотой выпуклого сопряжения, и изучается его справедливость и связь с максимальной монотонностью, индуцируемой мультисопряженными выпуклыми функциями.

⁍ Новости (май 2022 г.): Статья Лима «Классификация состояний с минимальной энергией для взаимодействующих частиц: сферические оболочки» будет опубликована в SIAM Journal on Applied Mathematics. Это совместная работа с Робертом Дж. Макканном и его учеником Кэмероном Дэвисом. 9d, подчиняющийся слегка тупому углу, будет опубликован в SIAM Journal on Discrete Mathematics. Это совместная работа с Робертом Дж. Макканном.

⁍ Новости (январь 2022 г.): Статья Лима «Максимизация ожидаемых степеней угла между парами точек в проективном пространстве» опубликована в Интернете в журнале Probability Theory and Related Fields. Это совместная работа с Робертом Дж. Макканном.

⁍ Новости (сентябрь 2021 г.): Появились новые статьи Лима «Классификация состояний с минимальной энергией для взаимодействующих частиц: сферические оболочки» и «Классификация состояний с минимальной энергией для взаимодействующих частиц: регулярные симплексы». Это совместная работа с Робертом Дж. Макканном и его учеником Кэмероном Дэвисом. В работах исследуется задача минимизации энергии взаимодействия, в которой энергия определяется степенным законом, граничным слабоотталкивающим потенциалом. Мы предоставляем полную характеристику минимизаторов для этого критического режима и выше.

⁍ Новости (июль 2021 г.): Появились новые статьи Лима «Теоретическое расширение аксиом Шепли по Ходжу» и «Распределение вознаграждения по теории Ходжа для обобщенных кооперативных игр на графах». В статье предлагается новое расширение знаменитых аксиом Шепли для кооперативных игр в свете разложения Ходжа и их реализация с помощью интригующего стохастического интеграла по путям, управляемого канонической обратимой во времени цепью Маркова.