пределы / Посчитать предел $%\lim xctgπx$% при $%x→0$% / Математика
|
$$\lim xctgπx$$ $$x→0$$ пределы задан 24 Апр ’14 23:27 АляТФ изменен 26 Апр ’14 14:52 Angry Bird |
старыеновыеценные
Если я правильно поняла задание, то тут надо воспользоваться следствием из первого замечательного предела: $$\lim_{x\rightarrow 0} x*ctg ( \pi x)= \lim_{x\rightarrow 0} \frac {x}{tg ( \pi x)}=\frac {1}{ \pi } \lim_{x\rightarrow 0} \frac { \pi x}{tg ( \pi x)}=\frac {1}{ \pi }$$ P. ссылка отвечен 25 Апр ’14 0:24 Leila изменен 25 Апр ’14 0:28 |
|
$$\lim_{x\rightarrow0}x\textrm{ctg}~\pi x=\lim_{x\rightarrow0}\frac{x\cos \pi x}{\sin\pi x}=\lim_{x\rightarrow0}\frac{\pi x\cos \pi x}{\pi \sin\pi x}=\lim_{x\rightarrow0}\frac{\cos \pi x}{\pi}=\frac{1}{\pi},$$
поскольку имеет место первый замечательный предел: $$\lim_{x\rightarrow0}\frac{\sin x}{ x}=0. Последние вопросы
Все предметы Выберите язык и регион English United States Polski Polska Português Brasil English India Türkiye English Philippines Español España Bahasa Indonesia Indonesia Русский Россия How much to ban the user? 1 hour 1 day 100 years 2+.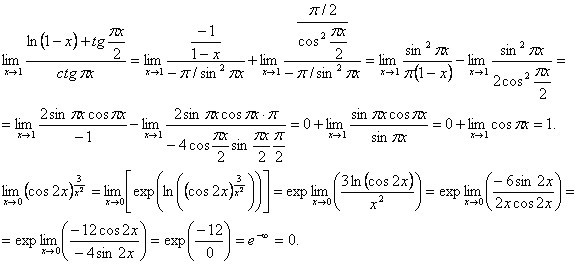 |

 следствие из 1-го замечательного предела: $$ \lim_{x\rightarrow 0} \frac { tg x} {x}=1$$
следствие из 1-го замечательного предела: $$ \lim_{x\rightarrow 0} \frac { tg x} {x}=1$$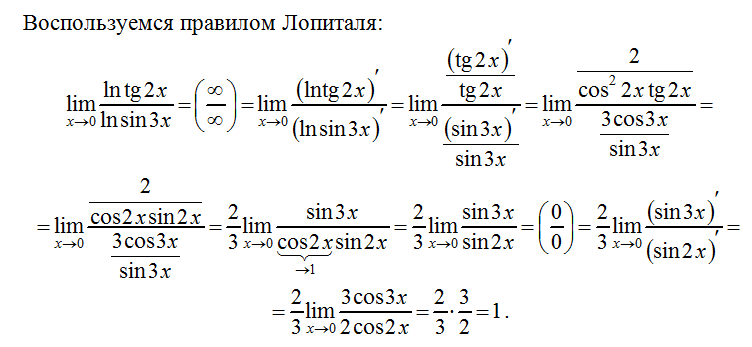
 Игорь 36 лет)
Игорь 36 лет)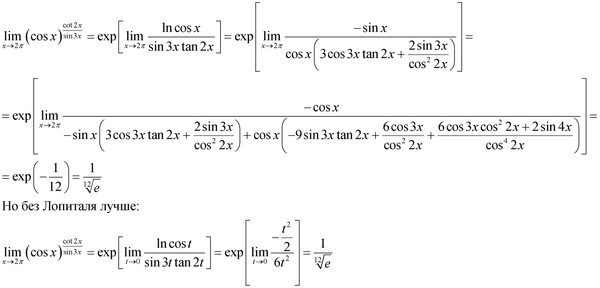 Цiна желе 15,6 грн. Скільки таких желе можна придбати на 170 грн? Скільки грошей залишиться? огодні. Скільки гривень мож 13. 3H ПР
Цiна желе 15,6 грн. Скільки таких желе можна придбати на 170 грн? Скільки грошей залишиться? огодні. Скільки гривень мож 13. 3H ПР