Внеклассный урок – Предел функции
Предел функции
Предел функции в заданной точке, предельной для области определения функции, – это такая величина, к которой стремится функция при стремлении ее аргумента к данной точке.
Предел функции – это обобщение понятия предела последовательности.
Любой предел функции состоит из трех частей: – значка предела lim; – записи под lim предельной точки, к которой стремится х; – самой функции. |
Пример 1: Возьмем выражение lim (x + 5)
x→1
Читается оно так: предел функции х + 5 при стремлении х к единице.
Что значит «стремление х к единице»?
Это значит, что х последовательно принимает значения, которые бесконечно приближаются к единице, но не совпадают с ней.
Вопрос: чему равен предел такой функции?
Решение:
Чтобы найти предел функции в нашем примере, надо просто подставить 1 в функцию (так как x→1):
lim (x + 5) = 1 + 5 = 6.
x→1
Ответ: пределом функции x + 5 при стремлении х к единице является 6:
lim (x + 5) = 6.
x→1
Пример 2 (с бесконечностью):
Возьмем наш первый пример, но при стремлении х к бесконечности:
lim (x + 5).
x→∞
x→∞ – это случай, когда х не стремится к какому-то числу, а неограниченно возрастает.
К примеру, сначала х = 10, потом х = 20, потом х = 30 и т.д. до бесконечности.
В этом случае функция тоже неограниченно возрастает, стремясь к бесконечности:
10 + 5 = 15
20 + 5 = 25
30 + 5 = 35 и т.д.
Таким образом, получаем ответ:
lim (x + 5) = ∞
x→∞
Пример 3 (с минус бесконечностью):
Найдем предел функции 5 – х:
lim (5 – х) = ?
x→∞
Решение:
Допустим, х имеет следующие значения: 2, 4, 6, 8, 10, 12 и т. д. до бесконечности.
д. до бесконечности.
Тогда наша функция будет иметь следующие значения: 3, 1, –1, –3, –5, –7 и так до минус бесконечности.
Мы видим, что функция неограниченно убывает, стремясь к минус бесконечности.
Ответ: lim (5 – х) = –∞
x→∞
Пример 4 (с дробью):
Не всегда при x→∞функция неограниченно возрастает.
Возьмем функцию с дробью и найдем ее предел при стремлении х к бесконечности:
lim 3/х = ?
x→∞
Решение:
Допустим, х имеет следующие значения: 1, 2, 3, 4, 5 и т.д. до бесконечности.
Тогда мы получим следующие значения функции: 3, 3/2, 1, 3/4, 3/5 и т.д.
Если мы продолжим этот ряд до бесконечности, то увидим, что каждое последующее значение функции меньше предыдущего, но ни одно из них не опускается ниже нуля. То есть функция стремится к нулю, но не пересекает его. А говоря иначе, ноль является пределом нашей функции.
Таким образом:
lim 3/х = 0.
x→∞
Предел функции – rajak.rs
Предел функции в бесконечности
Число $A$ называется пределом функции $y = f\left( x \right)$ при $x$ стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного $\varepsilon $, найдется такое число $M$ (зависящее от $\varepsilon $), что для всех $x$ таких, что $\left| x \right| > M$,выполнено неравенство: \[\left| {f\left( x \right) – A} \right| < \varepsilon .\]
На языке кванторов определение предела функции в бесконечности запишется следующим образом:
$A = \mathop {\lim }\limits_{x \to \infty } f\left( x \right),$ если $\forall \varepsilon > 0\exists M:\forall \left| x \right| > M\left| {f\left( x \right) – A} \right| < \varepsilon $
Предел функции в точке
Число $A$ называется пределом функции $y = f\left( x \right)$ при $x$ стремящемся к определенному значению $a$ если для любого, даже сколь угодно малого положительного $\varepsilon $, найдется такое число $\delta > 0$ (зависящее от $\varepsilon $), что для всех $x$ из $\delta$-окрестности точки $a$, выполнено неравенство: \[\left| {f\left( x \right) – A} \right| < \varepsilon .
Запишем на языке кванторов определение предела функции в точке:
$A = \mathop {\lim }\limits_{x \to \ a } f\left( x \right)$, если $\forall \delta \left( \varepsilon \right) > 0:\left| {x – a} \right| < \delta \Rightarrow \left| {f\left( x \right) – A} \right| < \varepsilon $
Критерий Коши существования предела функции
Будем говорить, что функция $f$ удовлетворяет в точке ${x_0}$ условию Коши, если для любого положительного числа $\varepsilon > 0$, найдётся отвечающее ему положительное число $\delta$ такое, что для любых двух значений аргумента ${x_1}$ и ${x_2}$, удовлетворяющих условиям
$\left| {{x_1} – {x_0}} \right| < \delta $ и $\left| {{x_2} – {x_0}} \right| < \delta $,
справедливо неравенство
$\left| {f\left( {{x_1}} \right) – f\left( {{x_2}} \right)} \right| < \varepsilon$.
Для того чтобы функция $f$ имела в точке ${x_0}$ конечный предел, необходимо и достаточно, чтобы функция $f$ удовлетворяла в точке ${x_0}$ условию Коши.
Односторонние пределы
Кроме определения обычного предела функции в точке возможно также дать определение понятия
Пределом функции $f$ в точке ${x_0}$ слева называется предел, вычисляемый в предположении, что $x \to {x_0}$, оставаясь всё время меньше значения ${x_0}$.
Аналогично, пределом справа называется предел функции $f$ при $x \to {x_0}$, при том, что $x > {x_0}$. Односторонние пределы обозначаются так:
$\mathop {\lim }\limits_{x \to {x_0} + 0} f\left( x \right) = L$, $\left( {\mathop {\lim }\limits_{x \to {x_0} – 0} f\left( x \right) = L} \right)$
Функция $f$ имеет предел в точке ${x_0}$ тогда т только тогда, когда она имеет в этой точке правый и левый предел и они равны.
Пределы на бесконечности
Пусть числовая функция $f$ задана на множестве $Х$, в котором отыщется сколь угодно большой элемент, то есть для всякого положительного $\delta $ в нём найдётся элемент, лежащий за границами отрезка $\left[ { – \delta , + \delta } \right]$. В этом случае число $L$ называется пределом функции $f$ на бесконечности, если для произвольного положительного числа $\varepsilon > 0$ отыщется отвечающее ему положительное число $\delta $ такое, что для всех точек, превышающих $\delta $ по абсолютному значению, справедливо неравенство $|f\left( x \right) – L| < \varepsilon $.
В этом случае число $L$ называется пределом функции $f$ на бесконечности, если для произвольного положительного числа $\varepsilon > 0$ отыщется отвечающее ему положительное число $\delta $ такое, что для всех точек, превышающих $\delta $ по абсолютному значению, справедливо неравенство $|f\left( x \right) – L| < \varepsilon $.
Обозначается: $\mathop {\lim }\limits_{x \to \infty } f(x) = L$
Пусть числовая функция $f$ задана на множестве $Х$, в котором для любого числа $\delta $ найдётся элемент, лежащий правее него. В этом случае число $L$ называется пределом функции $f$ на плюс бесконечности, если для произвольного положительного числа $\varepsilon > 0$ отыщется отвечающее ему положительное число $\delta $ такое, что для всех точек, лежащих правее $\delta $, справедливо неравенство $|f\left( x \right) – L| < \varepsilon $.
Обозначается: $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L$
Пусть числовая функция $f$ задана на множестве $Х$, в котором для любого числа $\delta $ найдётся элемент, лежащий правее него.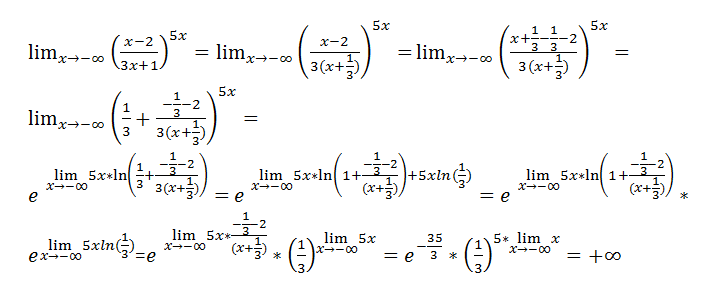
Обозначается: $\mathop {\lim }\limits_{x \to – \infty } f\left( x \right) = L$
Основные теоремы о пределе
Если для случаев
$x \to {x_0}$, $x \to {x_0} \pm 0$, $x \to {x_0} \pm 0$,
существуют пределы
$\lim f\left( x \right) = a$ и $\lim g\left( x \right) = b$,
тогда
- $\lim \left( {f\left( x \right) \pm g\left( x \right)} \right) = a \pm b$,
- $\lim \left( {C \cdot f\left( x \right)} \right) = Ca,{\text{ }}S \in \mathbb{R}$,
- $\lim \left( {f\left( x \right) \cdot g\left( x \right)} \right) = ab$ ,
- $\lim \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{a}{b}$, ако је $b \ne 0$,
- Если $\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = a$ и $\mathop {\lim }\limits_{x \to a} g\left( x \right) = b$, тогда
$\mathop {\lim }\limits_{x \to {x_0}} \left( {g \circ f} \right)\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} g\left( {f\left( x \right)} \right) = b$.

Пределы
0) Постоянная величина (число) сама себе служит пределом: .
1а) Величина, обратная бесконечно большой, есть бесконечно малая величина, т.е. если х → ∞, то .
1b) Величина, обратная бесконечно малой, есть бесконечно большая величина, т.е. если х → 0, то .
2a) Если две переменные стремятся к одному и тому же пределу, а третья переменная заключена между ними, то и она стремится к этому же пределу. Если
2b) Если две функции F(x) и Ф(х) стремятся к одному и тому же пределу A при х → p, а значения функции f(x) заключены между значениями F(x) и Ф(х), то f(x) стремится к этому
же пределу A при х → p .
Если F(x) ≤ f(x)
, то .
3) Предел суммы (разности) конечного числа слагаемых равен сумме (разности) пределов этих слагаемых:
lim (u ± v ± … ± t) = lim u ± lim v ± … ± lim t.
4) Предел произведения конечного числа множителей равен произведению пределов этих множителей:
lim (u · v · … · t) = lim u ·lim v · … · lim t.
Постоянный множитель можно выносить за знак предела lim c·u = с · lim u.
5) Предел частного равен частному пределов, если только предел делителя (знаменателя) не равен нулю: , если lim v ≠ 0.
6) Если предел числителя не равен нулю, а предел знаменателя равен нулю, то предел дроби является бесконечно большой величиной (см. п.1b):
Если lim u ≠ 0, а lim v = 0, то . Если же lim u =0 и lim v =0, то для нахождения предела необходимы дополнительные исследования.
0) Постоянная величина (число) сама
себе служит пределом:
.
1а) Величина, обратная бесконечно большой, есть бесконечно малая величина, т.е. если х → ∞, то .
1b) Величина, обратная бесконечно малой, есть бесконечно большая величина, т.е. если х → 0, то .
2a) Если две переменные стремятся к одному и тому же пределу, а третья переменная заключена между ними, то и она стремится к этому же пределу. Если
2b) Если две функции F(x) и Ф(х) стремятся к одному и тому же пределу A при х → p, а значения функции f(x) заключены между значениями F(x) и Ф(х), то f(x) стремится к этому же пределу A
при х → p . Если F(x) ≤ f(x) ≤ Ф(х) и
,
то
.
3)
lim (u ± v ± … ± t) = lim u ± lim v ± … ± lim t.
4) Предел произведения конечного числа множителей равен произведению пределов этих множителей:
lim (u · v · … · t) = lim u ·lim v · … · lim t.
Постоянный множитель можно выносить за знак предела
lim c·u = с · lim u.
5) Предел частного равен частному пределов, если только предел делителя (знаменателя) не равен нулю: , если lim v ≠ 0.
6) Если предел числителя не равен нулю, а предел знаменателя равен нулю, то предел дроби является бесконечно большой величиной (см. п.1b): Если lim u ≠ 0, а lim v = 0, то . Если же lim u =0 и lim v =0, то для нахождения предела необходимы дополнительные исследования.
Раскрытие некоторых типов неопределённостей.
7) Чтобы раскрыть неопределенность
вида
,
заданную отношением двух многочленов,
надо и числитель и знаменатель разделить
на самую высокую входящую в них степень х.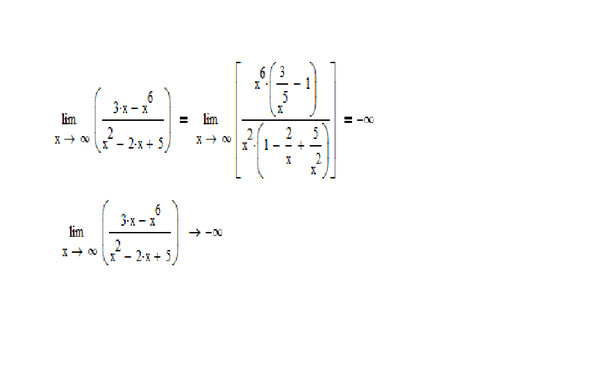
8) Чтобы раскрыть неопределенность вида , заданную в форме: , надо и в числителе и в знаменателе выделить критический множитель (х – а) и сократить на него дробь.
9) Чтобы раскрыть неопределенность вида , в которой числитель или знаменатель иррациональны, следует надлежащим образом избавиться от иррациональности.
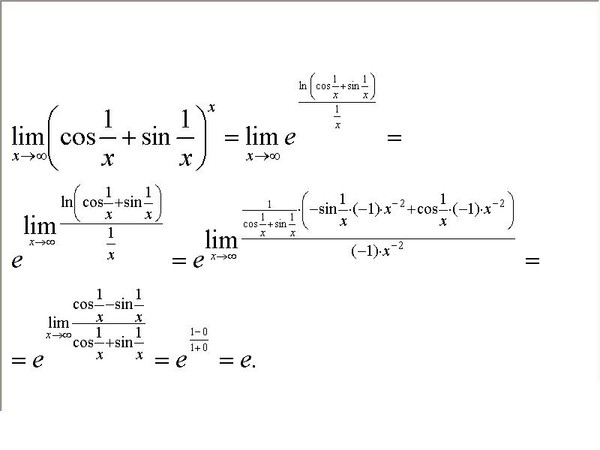
Первый замечательный предел:
Второй замечательный предел:
Другие замечательные пределы
Понижение степени
Раскрытие некоторых типов неопределённостей.
7) Чтобы раскрыть неопределенность вида , заданную отношением двух многочленов, надо и числитель и знаменатель разделить на самую высокую входящую в них степень х.
8) Чтобы раскрыть неопределенность
вида
,
заданную в форме:
,
надо и в числителе и в знаменателе
выделить критический множитель (х –
а) и сократить на него дробь.
9) Чтобы раскрыть неопределенность вида , в которой числитель или знаменатель иррациональны, следует надлежащим образом избавиться от иррациональности.
Первый замечательный предел:
Второй замечательный предел:
Другие замечательные пределы
Понижение степени
Бесконечность стремится к нулю
1
Бесконечность равна нулю…
Что скрывается под этой фразой, что она означает, откуда в конце концов взялась? Спонтанна или обдумана она, имеет ли какую-то перспективу, способна ли изменить у человека представление о мире как о универсуме?
Почему она равна нулю, откуда такой смелый вывод, и стоить поверить сказавшему эту фразу? Глупа ли она по своей сути или же, наоборот, несёт в себе ничтожную частицу истинного и высокого, за выведение которого ученые годами, десятками, сотнями лет жертвовали жизнь и время науке, осознанно ставя перед собой вопросы, ответив на который, они поднимут несколько новых, оставив их без ответа?
2
Только противоборство радикальных теорий, идей, концепций и так далее способно действительно двигать общественную мысль и науку вперед. Взгляды, с помощью которых кто-то хотел бы вслепую найти экватор, затерянный между двумя полюсами, заранее обречены на провал. «Минус один» плюс «плюс один» равно нулю, как экватору. Экватор как таковой не существует, география говорит о нём лишь как об условной линии, хотя современные технологии скоро, возможно, позволят с мельчайшей погрешностью в точности провести через океаны и континенты каменную стену огромной высоты. Вопрос-то в другом: какой ущерб мы нанесем своей планете, материализовав абстрактное? Соответственно, что будет с нами, если материализуется ноль? С помощью человека, естественно. Так что не стоит пытаться воплотить божественное в жизнь, достаточно просто в совершенстве его изучить.
Взгляды, с помощью которых кто-то хотел бы вслепую найти экватор, затерянный между двумя полюсами, заранее обречены на провал. «Минус один» плюс «плюс один» равно нулю, как экватору. Экватор как таковой не существует, география говорит о нём лишь как об условной линии, хотя современные технологии скоро, возможно, позволят с мельчайшей погрешностью в точности провести через океаны и континенты каменную стену огромной высоты. Вопрос-то в другом: какой ущерб мы нанесем своей планете, материализовав абстрактное? Соответственно, что будет с нами, если материализуется ноль? С помощью человека, естественно. Так что не стоит пытаться воплотить божественное в жизнь, достаточно просто в совершенстве его изучить.
Можно взять что угодно, глобально-абстрактного характера: религию, государство, время, жизнь, смерть, войну – к каждому из перечисленного отношение (как преимущественно позитивное, так и преимущественно негативное) окажется весьма сложным и необъяснимым в двух словах. О таких вещах никогда не может быть сказано всё, и это «всё» по сути будет в определенном плане истиной. А истина недостижима человеку до конца, поэтому лучше много раз понемногу, чем сразу и один раз. Кстати, один из законов логики утверждает: не может одно утверждение быть одновременно истинным и ложным. Это правда. Но будет однобоким лишь в голове того, кто его услышал. Даже если его услышало несколько человек в одном месте и в одно время, все равно истинным или ложным оно будет только в отдельности для каждого из них. Человечество никогда не сможет договориться о чем-либо всем своим составом, оно не продукт конвейера, программа которого не допускает какую-либо вариацию в произведенной им продукции. Утопичны продукты человеческого разума, но не человеческая природа.
А истина недостижима человеку до конца, поэтому лучше много раз понемногу, чем сразу и один раз. Кстати, один из законов логики утверждает: не может одно утверждение быть одновременно истинным и ложным. Это правда. Но будет однобоким лишь в голове того, кто его услышал. Даже если его услышало несколько человек в одном месте и в одно время, все равно истинным или ложным оно будет только в отдельности для каждого из них. Человечество никогда не сможет договориться о чем-либо всем своим составом, оно не продукт конвейера, программа которого не допускает какую-либо вариацию в произведенной им продукции. Утопичны продукты человеческого разума, но не человеческая природа.
3
Давайте вспомним математику. Все в школе находили с помощью числовой прямой знак какого-либо значения переменной «х» на всем промежутке. И зажаты все числа между «минус бесконечностью» и «плюс бесконечностью». Теперь давайте в уме представим, что выпрямленная нитка, лежащая на столе – это материализованное графическое изображение числовой прямой. Соединим ее концы – получится фигура, очень похожая на ноль. Теперь складываем противоположные по знаку бесконечности, заменив значок лежащей восьмерки на любое число, пусть это будет та же восьмерка! И что мы получаем? «Минус восемь» плюс «плюс восемь» равно нулю. В итоге наблюдаем вот что: ноль мы получили и материально, и умственно. Ноль в абстракции равен нулю в реальности. Вот он, смысл: ноль существует в природе (так ли это? – на деле нет, но закончу фразу), и этот ноль есть сумма разных по знаку бесконечностей, этот ноль – ничтожная частица вечности, ощущаемая человеком, которую он называет жизнью. Стоп, а разве существует ли фактически отрицательная бесконечность? Конечно же, нет. Значит, что-то не складывается.
Соединим ее концы – получится фигура, очень похожая на ноль. Теперь складываем противоположные по знаку бесконечности, заменив значок лежащей восьмерки на любое число, пусть это будет та же восьмерка! И что мы получаем? «Минус восемь» плюс «плюс восемь» равно нулю. В итоге наблюдаем вот что: ноль мы получили и материально, и умственно. Ноль в абстракции равен нулю в реальности. Вот он, смысл: ноль существует в природе (так ли это? – на деле нет, но закончу фразу), и этот ноль есть сумма разных по знаку бесконечностей, этот ноль – ничтожная частица вечности, ощущаемая человеком, которую он называет жизнью. Стоп, а разве существует ли фактически отрицательная бесконечность? Конечно же, нет. Значит, что-то не складывается.
Однако невозможно рассуждать о бесконечности, равной нулю, руководствуясь лишь двумя составляющими данного равенства. Необходима и конкретика, то есть факты из жизни, подтверждающие верность мысли.
4
Человек рождается и умирает. В материальном смысле от него что-то, возможно, и остается. Но не от всех, конечно. А в вычислительном? Представим рождение знаком «плюс» и смерть знаком «минус». Снова возьмем любую цифру, хотя бы священную единицу. «Минус один» плюс «плюс один» равно нулю. Вот и всё, что остается от человека как от существа – ничего, ноль!
Но не от всех, конечно. А в вычислительном? Представим рождение знаком «плюс» и смерть знаком «минус». Снова возьмем любую цифру, хотя бы священную единицу. «Минус один» плюс «плюс один» равно нулю. Вот и всё, что остается от человека как от существа – ничего, ноль!
Да вот только мне думается, что я сам себе противоречу. От человека много что остается, пусть мы порой можем этого не заметить. От него остаются дети, недвижимость, следы на песке, объекты искусства, воспоминания у других… Самого же человека как биологического существа на планете после смерти не остается, хотя сохраняются его останки, то есть кости, иногда несущие функцию святых мощей. Так что остается от человека далеко не ноль, но и далеко не единица. А значит, что? А значит, что-то среднее между ними.
С самого «появления» (кавычки, потому что неизвестно, появлялся ли он когда-нибудь вообще или всегда существовал не эволюционируя)себя на планете человек осознал, что он ничтожество по сравнению с этим огромным миром. Он как капля в море, если не атом молекулы воды или, того гляди, что-то меньшее, еще не известное ученому. Полный ноль, как говорится. В одиночку он беззащитен: вокруг хищные звери, еду на блюдечке никто не поднесет, морозы скажут свое слово. Потому и начал он придумывать для себя панацею, дабы избавиться от комплекса мизерности и склонности самоунижать свое эго, ведь человек сам по себе изначально существо эгоистичное. Начал человек строить социальную дифференциацию, придумал государство, научно-технический прогресс, произошло и происходит одомашнивание животных и освоение природных богатств, начали шить теплую одежду, появился антропоцентризм. Отсюда, определенно, следует некий вывод: развитие человека происходит из-за страха перед природой и в полной мере не подчиненным ему. Не было бы страха – сидел бы и не дергался. Но долго не просидел бы… И вымер.
Он как капля в море, если не атом молекулы воды или, того гляди, что-то меньшее, еще не известное ученому. Полный ноль, как говорится. В одиночку он беззащитен: вокруг хищные звери, еду на блюдечке никто не поднесет, морозы скажут свое слово. Потому и начал он придумывать для себя панацею, дабы избавиться от комплекса мизерности и склонности самоунижать свое эго, ведь человек сам по себе изначально существо эгоистичное. Начал человек строить социальную дифференциацию, придумал государство, научно-технический прогресс, произошло и происходит одомашнивание животных и освоение природных богатств, начали шить теплую одежду, появился антропоцентризм. Отсюда, определенно, следует некий вывод: развитие человека происходит из-за страха перед природой и в полной мере не подчиненным ему. Не было бы страха – сидел бы и не дергался. Но долго не просидел бы… И вымер.
5
Но давайте посмотрим на ситуацию более позитивно. А раз позитивно, то по смыслу здесь ближе знак «плюс», о сакральности которого нельзя не упомянуть. Как мной уже заявлялось, рождение можно принять за прибавление человека к остальной общей массе, за «плюс». После смерти почти каждого человека всегда остается что-то, хоть капельку изменившее материю. Это следы на песке, это философские трактаты, это потомство, идеология… много можно говорить об этом, но я в силу сохранения эстетики формы этой статьи не стану уходить в сторону. Когда человек уходит в мир иной, можно характеризовать такое явление знаком «минус» (употребление в данном случае слова «процесс» вместо «явление» было бы циничным, жестоким и не в достаточной мере взвешенным). Но здесь догадываешься: за знаки «плюс» и «минус» мы приняли только стадии некого пребывания, если можно так выразиться, человека в материальном мире. Самое главное – мы оставили за бортом деятельность человека… А она будет явно положительного знака в своей основе – думаю, объяснять это подробно и с уходом в сторону не нужно. Как бы не был знаменит и хорош либо плох какой-нибудь отдельно взятый человек, какой бы масштаб ни приобрела его деятельность, но для мира все сделанное им подобно капле в море, которым мир, собственно и является.
Как мной уже заявлялось, рождение можно принять за прибавление человека к остальной общей массе, за «плюс». После смерти почти каждого человека всегда остается что-то, хоть капельку изменившее материю. Это следы на песке, это философские трактаты, это потомство, идеология… много можно говорить об этом, но я в силу сохранения эстетики формы этой статьи не стану уходить в сторону. Когда человек уходит в мир иной, можно характеризовать такое явление знаком «минус» (употребление в данном случае слова «процесс» вместо «явление» было бы циничным, жестоким и не в достаточной мере взвешенным). Но здесь догадываешься: за знаки «плюс» и «минус» мы приняли только стадии некого пребывания, если можно так выразиться, человека в материальном мире. Самое главное – мы оставили за бортом деятельность человека… А она будет явно положительного знака в своей основе – думаю, объяснять это подробно и с уходом в сторону не нужно. Как бы не был знаменит и хорош либо плох какой-нибудь отдельно взятый человек, какой бы масштаб ни приобрела его деятельность, но для мира все сделанное им подобно капле в море, которым мир, собственно и является. Не думаю, что возможно вычислить долю одной капли или хотя бы молекулы воды в масштабах мировых запасов воды как питьевой, так и не питьевой – такую десятичную дробь, во-первых, физически не вычислить, а во-вторых, не записать цифрами. Поэтому я бы обозначил ее, деятельность, как 0,(0)1. Потому я считаю следующее: бесконечность стремится к нулю. Я не математик или физик, чтобы выводить какую-то формулу, но методом примитивного мыслепостроения я вывожу следующее:
Не думаю, что возможно вычислить долю одной капли или хотя бы молекулы воды в масштабах мировых запасов воды как питьевой, так и не питьевой – такую десятичную дробь, во-первых, физически не вычислить, а во-вторых, не записать цифрами. Поэтому я бы обозначил ее, деятельность, как 0,(0)1. Потому я считаю следующее: бесконечность стремится к нулю. Я не математик или физик, чтобы выводить какую-то формулу, но методом примитивного мыслепостроения я вывожу следующее:
Бесконечность -> Коэффициент жизни – Коэффициент смерти = 0,(0)1. -> 0
Что я подразумеваю под коэффициентом жизни? На мой взгляд, это сумма рождения человека и его деятельности в течение жизни. Коэффициент жизни равен 1,(0)1, то есть «Рождение + Деятельность». Коэффициент смерти равен одному (равно как и рождение, смерть бывает только одна и одномоментна). Значит, из жизни вычесть смерть – останется деятельность? Именно так.
Из полученного значения следует, что деятельность влечет за собой ничтожно малое материальное изменение мира. Итог: бесконечность стремится к нулю и является деятельностью. Здесь может возникнуть некоторое понимание следующего: как это бесконечность стремится к чему-либо, ведь она статична. Да, она статична, но не забывайте, что абсолютно все, что находится вокруг нас – камни, трава, здания, животные, люди – и даже мы сами были кем-то когда созданы (то есть кто-то когда-то нас «сделал», то есть осуществил деятельность), а лучше считайте так и ни при каких условиях никогда не сомневайтесь в этом – зачем усложнять себе жизнь ненужным рассуждательским барахлом?
Итог: бесконечность стремится к нулю и является деятельностью. Здесь может возникнуть некоторое понимание следующего: как это бесконечность стремится к чему-либо, ведь она статична. Да, она статична, но не забывайте, что абсолютно все, что находится вокруг нас – камни, трава, здания, животные, люди – и даже мы сами были кем-то когда созданы (то есть кто-то когда-то нас «сделал», то есть осуществил деятельность), а лучше считайте так и ни при каких условиях никогда не сомневайтесь в этом – зачем усложнять себе жизнь ненужным рассуждательским барахлом?
6
Ноль, как и бесконечность, являются одними из величайших тайн мира. Великая тайна – откуда взялась единица. Но еще больше великая и неразрешимая – откуда взялся ноль? Откуда взялось ничего, из чего это ничего появилось? Что было началом, когда начало началось? Всё это вопросы философского порядка, ответы на которые окончательно найти не удастся никогда. Выводы из этой главы, я боюсь, можно сделать неутешительные.
А есть ли ноль Бог? А есть ли ноль любая деятельность? А есть ли Бог деятельность. С туманом в глазах и огоньками, мерцающими в душе, мы каждый раз начинаем новый миг, ожидая пришествия того, чего хотим добиться. Кто-то хочет семью, кто-то деньги, кто-то славу, кто-то всеобщую любовь, ну, а кто-то постичь истину. Желательно, конечно, получить не один из приведенных пунктов, а несколько их вкупе, и в том числе те, которые в этом коротком списке не были найдены их искателем.
С туманом в глазах и огоньками, мерцающими в душе, мы каждый раз начинаем новый миг, ожидая пришествия того, чего хотим добиться. Кто-то хочет семью, кто-то деньги, кто-то славу, кто-то всеобщую любовь, ну, а кто-то постичь истину. Желательно, конечно, получить не один из приведенных пунктов, а несколько их вкупе, и в том числе те, которые в этом коротком списке не были найдены их искателем.
Кому истина, кому правда жизни – а кому-то бесконечность…
Некоторая интерпретация тезиса «бесконечность стремится к нулю» содержится во главе «Аксиома коэффициентарности бытия».
http://vk.com/club37892037 милости прошу)) ))))))))))) прЭлестно! Ощущение, что занять мозги больше было нечем)) Приходите в мою группу, я уже несколько лет пытаюсь через поэзию донести смысл этой фразы людям)
Портал Проза.ру предоставляет авторам возможность свободной публикации своих литературных произведений в сети Интернет на основании пользовательского договора. Все авторские права на произведения принадлежат авторам и охраняются законом. Перепечатка произведений возможна только с согласия его автора, к которому вы можете обратиться на его авторской странице. Ответственность за тексты произведений авторы несут самостоятельно на основании правил публикации и законодательства Российской Федерации. Вы также можете посмотреть более подробную информацию о портале и связаться с администрацией.
Перепечатка произведений возможна только с согласия его автора, к которому вы можете обратиться на его авторской странице. Ответственность за тексты произведений авторы несут самостоятельно на основании правил публикации и законодательства Российской Федерации. Вы также можете посмотреть более подробную информацию о портале и связаться с администрацией.
Ежедневная аудитория портала Проза.ру – порядка 100 тысяч посетителей, которые в общей сумме просматривают более полумиллиона страниц по данным счетчика посещаемости, который расположен справа от этого текста. В каждой графе указано по две цифры: количество просмотров и количество посетителей.
© Все права принадлежат авторам, 2000-2019. Портал работает под эгидой Российского союза писателей. 18+
Давным давно, я решаю загадку бесконечности и нуля. Эту божественную загадку в решение которой, нет смысла, но одновременно смысл везде. Что же такое ноль? Это пустота, это ничего, но как не прискорбно признавать, это утверждение верно только на половину.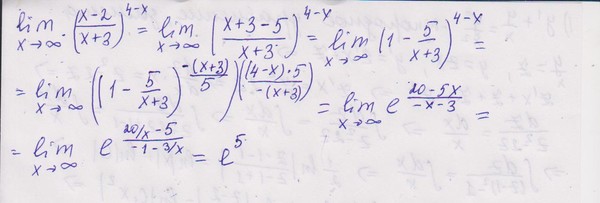 Ноль это не только пустота, ноль это бесконечность.
Ноль это не только пустота, ноль это бесконечность.
Почему я решил поставить между нулем и бесконечностью знак равенства? Попробую объяснить, при деление любого числа на ноль n/0 (n-произвольное число) обычно люди говорят два ответа. Либо “на ноль дель нельзя”, либо “Бесконечность” . С первым ответом все понятно, но что делать со вторым? Почему при деление на ноль получается бесконечность?
Если рассмотреть картинку поста, то можно заметить функцию и её график (у)=1/x. Мы видим как меняется значение (у), если (х) стремится к +∞(∞-бесконечность), то (у) стремится к 0 и наоборот чем меньше (х) тем больше (у), то есть если (х) стремится к 0, то (у) стремится к +∞. Но мы забываем про отрицательные числа и отрицательную бесконечность -∞. на отрицательной стороне координат мы видим такую же ситуацию правда направленную в противоположную сторону, при(х) стремящимся к -∞ (у) стремится к 0, при (у) стремящемся к -∞ (х) стремится к 0, но здесь и появляется парадокс деления на 0. То есть
Но у нас два ответа, какой же нам выбрать? В такой ситуации можно найти среднею арифметическую, то есть
Под ∞ я беру всю прямую от -∞ до +∞.
P.S. В следующем посте попытаюсь объяснить, почему 0=n (n-произвольное число).
Дубликаты не найдены
Во-первых, если вы под нулем понимаете число (самое обыкновенное, знакомое со второго класса), то ответ тут один – неопределенность, а потому делить нельзя. Все, кто говорят иное, не понимают основ.
Во-вторых, если вам так хочется получить бесконечность, то надо под нулем понимать класс эквивалентности, вмещающий в себя все последовательности x_n/ функции f(x), стремящиеся к нулю (бесконечно малые) при n->∞ / x->x0.
При X = 0 у нас неопределенность, как уже было сказано. Можно рассматривать предел, при X->0. Первокурсникам говорят, что предела нет. Ибо предел, если существует, то единственен. Но есть односторонние пределы (если в терминах последовательностей, можно говорить о пределах частичных). К концу первого курса обычно говорят, что если пределы по всем направлениям – какая-то знаковая бесконечность, то можно сказать, что предел – просто бесконечность, без знака.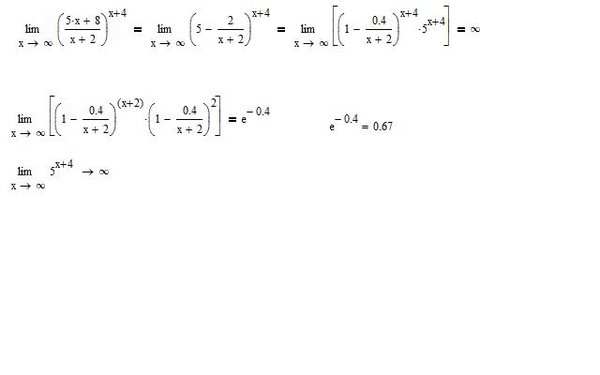 2. f(x) + g(x) = x -> +∞, при x->+∞
2. f(x) + g(x) = x -> +∞, при x->+∞
Еще дальше. Забудем о всех этих ужасных ошибках, которые вы допускаете с бесконечностями. Вы пишите, что можно взять два результата и обобщить их с помощью среднего арифметического. Когда кто-то пользуется средним арифметическим как “лекарством от всего”, в мире рыдают все нормальные статистики. Обязательно нужно пояснять адекватность выбора метода усреднения, иначе получаем средний доход человека в 100К в доме с одним миллионером и девятью безработными.
>
Шикарно! Давайте вообще все числа будем обозначать одним и тем же знаком, это же так здорово! Сразу решаются все проблемы мирозданья.
Таким образом, я делаю вывод, что весь этот пост очередной бред из серии “Школьник доказал существование жизни после смерти с помощью матанализа.”
Рассмотрим основные типы неопределенностей пределов на бесконечности с примерами решений:
- $ [frac<0><0>] $
- $ [infty – infty] $
- $[frac<infty><infty>]^ <[infty]>и [1 ^ infty] $
| Пример 1 |
| Вычислить предел функции, стремящейся к бесконечности $ lim _limits frac$ |
| Решение |
Первым делом подставляем $ x o infty $ в предел, чтобы попытаться его вычислить. x = e qquad (1) $$
x = e qquad (1) $$
Из выражения, стоящего под знаком предела вычитаем единицу, чтобы его подстроить под формулу (1).
Перепишем предел из условия задачи в новом виде и подставим в него $x o infty$.
Пользуясь формулой (1) проведем вычисление лимита. В скобках перевернем дробь.
По условиями формулы второго замечательного предела (1) в скобках знаменатель дроби должен быть равен степени за скобкой. Выполним преобразование степени. Для этого умножим и разделим на $frac<3x+2><-6>$.
Остаётся сократить степень экспоненты и найти её предел.
Предел дроби равен отношению коэффициентов при старшей степени $x$.
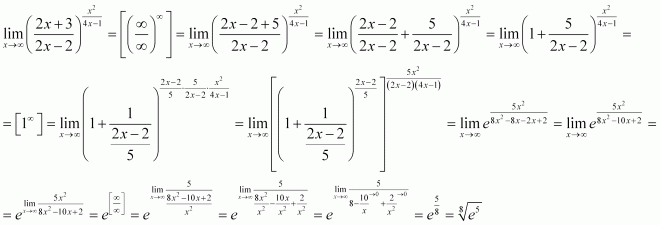
Предел функции на бесконечности
Продолжаем разбирать готовые ответы по теории пределов и сегодня остановимся только на случае, когда переменная в функции или номер в последовательности стремится к бесконечности. Инструкция по вычислению предела при переменной стремящейся к бесконечности приведена ранее, здесь только остановимся на отдельных случаях, которые не являются всем очевидными и простыми. n, на него и упрощаем
n, на него и упрощаем
Далее оцениваем вклад каждого слагаемого
Слагаемые 3/8 стремятся к нулю при переменной направляюейся к бесконечности, поскольку 3/8<1 (свойство степенно-показательной функции).
Пример 37.Предел последовательности с факториалами раскрывается розписанням факториала к наибольшему общему множителю для числителя и знаменателя.
Далее на него сокращаем и оцениваем лимит по значению показателей номера в числителе и знаменателе.
В нашем примере знаменатель быстрее растет, поэтому предел равен нулю.
Здесь использована следующее
свойство факториала.
Пример 38.Не применяя правила Лопиталя сравниваем максимальные показатели переменной в числителе и знаменателе дроби.
Так как знаменатель содержит старший показатель переменной 4>2 то и растет он быстрее.
Отсюда делаем вывод, что предел функции стремится к нулю.
Пример 39.Раскрываем особенность вида бесконечность разделить на бесконечность методом вынесения x^4 с числителя и знаменателя дроби.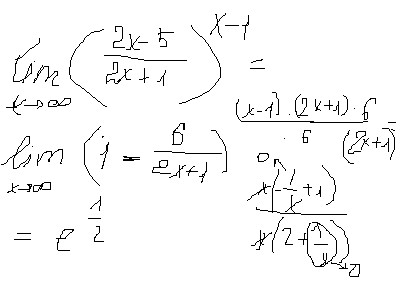 3 и выполним предельный переход
3 и выполним предельный переход
Пример 41.Имеем особенность типа единица в степени бесконечность.
А это значит, что выражение в скобках и сам показатель надо свести под вторую важную границу.
Распишем числитель, чтобы выделить в нем выражение идентичное знаменателе.
Далее переходим к выражению, содержащем единицу плюс слагаемое.
В степени нужно выделить множителем 1/(слагаемое).
Таким образом получим экспоненту в степени предела дробной функции.
Для раскрития особенности использовали второй предел:
Пример 42.Имеем особенность типа единица в степени бесконечность.
Для ее раскрытия следует свести функцию под второй замечатеьный предел.
Как это сделать подробно показано в приведенной далее формуле
Подобных задач Вы можете найти очень много. Их суть в том, чтобы в показателе получить нужный степень, а он равен обратному значению слагаемого в скобках при единицы.
Таким методом получаем экспоненту. Дальнейшее вычисление сводится к вичислению предела степени экспоненты.
Дальнейшее вычисление сводится к вичислению предела степени экспоненты.
Здесь экспоненциальная функция стремится к бесконечности , поскольку значение больше единицы e=2.72>1.
Пример 43 В знаменателе дроби имеем неопределенность типа бесконечность минус бесконечность, фактически равное делению на ноль.
Чтобы избавиться корня домножим на сопряженное выражение, а дальше по формуле разности квадратов перепишем знаменатель.
Получим неопределенность бесконечность разделить на бесконечность, поэтому выносим переменную в наибольшей степени и сокращаем на нее.
Далее оцениваем вклад каждого слагаемого и находим предел функции на бесконечности
Пример 44.Найти повторные границы
Решение: Вычисляем предел функции двух переменных сначала по y, а дальше – x)
a)
б)
Пример 45. Вычислить повторные границы
Решение: Методика вычисления повторных границ не сложна:
сначала находим границу по одной переменной, считая вторую переменную постоянной.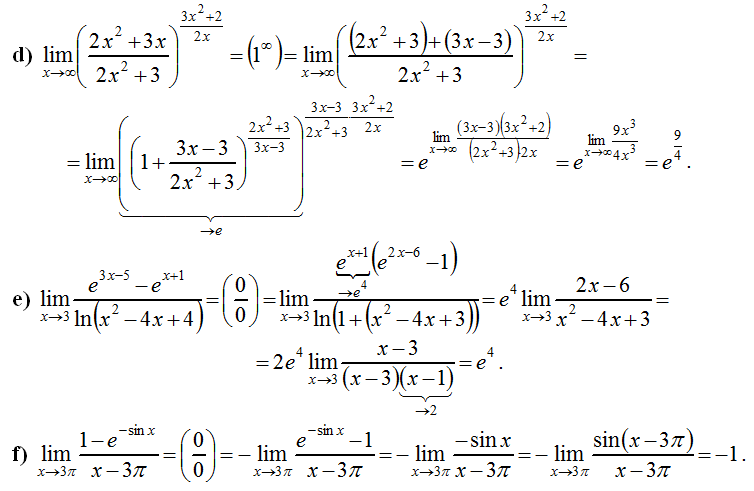
Далее остается функция от одной переменной, а таких пределов мы разобрали очень много.
а)
б)
В этом задании предел по первой переменной равен нулю, поэтому повторные записываем только для формальности.
Предел в данном случае от порядка нахождения не зависит.
Однако, если взглянуть ответ из предыдущего примера то такое утверждение не всегда выполняется.
Ищите эффективные схемы вычисления пределов на страницах сайта, если возникают проблемы с пределами на экзаменах и модулях – обращайтесь за помощью!
x # принимает любое ненулевое комплексное значение бесконечно много раз в любой сколь угодно малой окрестности # oo #. Это называется существенной сингулярностью на бесконечности .| 1 | Найдите производную – d / dx | натуральное бревно х | |
| 2 | Оцените интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найдите производную – d / dx | e ^ x | |
| 4 | Оцените интеграл | интеграл от e ^ (2x) относительно x | |
| 5 | Найдите производную – d / dx | 1 / х | |
| 6 | Найдите производную – d / dx | х ^ 2 | |
| 7 | Найдите производную – d / dx | 1 / (х ^ 2) | |
| 8 | Найдите производную – d / dx | грех (х) ^ 2 | |
| 9 | Найдите производную – d / dx | сек (x) | |
| 10 | Оцените интеграл | интеграл e ^ x относительно x | |
| 11 | Оцените интеграл | интеграл x ^ 2 относительно x | |
| 12 | Оцените интеграл | интеграл квадратного корня x относительно x | |
| 13 | Найдите производную – d / dx | соз (х) ^ 2 | |
| 14 | Оцените интеграл | интеграл 1 / x относительно x | |
| 15 | Оцените интеграл | интеграл sin (x) ^ 2 относительно x | |
| 16 | Найдите производную – d / dx | х ^ 3 | |
| 17 | Найдите производную – d / dx | сек (x) ^ 2 | |
| 18 | Оцените интеграл | интеграл cos (x) ^ 2 относительно x | |
| 19 | Оцените интеграл | интеграл от sec (x) ^ 2 относительно x | |
| 20 | Найдите производную – d / dx | е ^ (х ^ 2) | |
| 21 | Оцените интеграл | интеграл от 0 до 1 кубического корня из 1 + 7x относительно x | |
| 22 | Найдите производную – d / dx | грех (2x) | |
| 23 | Найдите производную – d / dx | загар (x) ^ 2 | |
| 24 | Оцените интеграл | интеграл от 1 / (x ^ 2) относительно x | |
| 25 | Найдите производную – d / dx | 2 ^ х | |
| 26 | График | натуральное бревно из | |
| 27 | Найдите производную – d / dx | cos (2x) | |
| 28 | Найдите производную – d / dx | хе ^ х | |
| 29 | Оцените интеграл | интеграл 2x по отношению к x | |
| 30 | Найдите производную – d / dx | (натуральный логарифм x) ^ 2 | |
| 31 | Найдите производную – d / dx | натуральный логарифм (x) ^ 2 | |
| 32 | Найдите производную – d / dx | 3x ^ 2 | |
| 33 | Оцените интеграл | интеграл xe ^ (2x) относительно x | |
| 34 | Найдите производную – d / dx | 2e ^ x | |
| 35 | Найдите производную – d / dx | натуральное бревно 2х | |
| 36 | Найдите производную – d / dx | -син (х) | |
| 37 | Найдите производную – d / dx | 4x ^ 2-x + 5 | |
| 38 | Найдите производную – d / dx | y = 16 корень четвертой степени из 4x ^ 4 + 4 | |
| 39 | Найдите производную – d / dx | 2x ^ 2 | |
| 40 | Оцените интеграл | интеграл e ^ (3x) относительно x | |
| 41 | Оцените интеграл | интеграл от cos (2x) относительно x | |
| 42 | Найдите производную – d / dx | 1 / (квадратный корень из x) | |
| 43 | Оцените интеграл | интеграл e ^ (x ^ 2) относительно x | |
| 44 | Оценить | e ^ бесконечность | |
| 45 | Найдите производную – d / dx | х / 2 | |
| 46 | Найдите производную – d / dx | -cos (x) | |
| 47 | Найдите производную – d / dx | грех (3x) | |
| 48 | Найдите производную – d / dx | 1 / (х ^ 3) | |
| 49 | Оцените интеграл | интеграл tan (x) ^ 2 относительно x | |
| 50 | Оцените интеграл | интеграл 1 относительно x | |
| 51 | Найдите производную – d / dx | х ^ х | |
| 52 | Найдите производную – d / dx | х натуральное бревно х | |
| 53 | Найдите производную – d / dx | х ^ 4 | |
| 54 | Оценить предел | предел, когда x приближается к 3 из (3x-5) / (x-3) | |
| 55 | Оцените интеграл | интеграл от x ^ 2 натурального логарифма x относительно x | |
| 56 | Найдите производную – d / dx | f (x) = квадратный корень из x | |
| 57 | Найдите производную – d / dx | х ^ 2sin (х) | |
| 58 | Оцените интеграл | интеграл sin (2x) относительно x | |
| 59 | Найдите производную – d / dx | 3e ^ x | |
| 60 | Оцените интеграл | интеграл xe ^ x относительно x | |
| 61 | Найдите производную – d / dx | г = х ^ 2 | |
| 62 | Найдите производную – d / dx | квадратный корень из x ^ 2 + 1 | |
| 63 | Найдите производную – d / dx | грех (x ^ 2) | |
| 64 | Оцените интеграл | интеграл от e ^ (- 2x) относительно x | |
| 65 | Оцените интеграл | интеграл натурального логарифма квадратного корня x относительно x | |
| 66 | Найдите производную – d / dx | e ^ 2 | |
| 67 | Найдите производную – d / dx | х ^ 2 + 1 | |
| 68 | Оцените интеграл | интеграл sin (x) относительно x | |
| 69 | Найдите производную – d / dx | арксин (х) | |
| 70 | Оценить предел | Предел, когда x приближается к 0 of (sin (x)) / x | |
| 71 | Оцените интеграл | интеграл e ^ (- x) относительно x | |
| 72 | Найдите производную – d / dx | х ^ 5 | |
| 73 | Найдите производную – d / dx | 2 / х | |
| 74 | Найдите производную – d / dx | натуральное бревно 3х | |
| 75 | Найдите производную – d / dx | х ^ (1/2) | |
| 76 | Найдите производную – d / d @ VAR | f (x) = квадратный корень из x | |
| 77 | Найдите производную – d / dx | соз (х ^ 2) | |
| 78 | Найдите производную – d / dx | 1 / (х ^ 5) | |
| 79 | Найдите производную – d / dx | кубический корень из x ^ 2 | |
| 80 | Оцените интеграл | интеграл cos (x) относительно x | |
| 81 | Оцените интеграл | интеграл e ^ (- x ^ 2) относительно x | |
| 82 | Найдите производную – d / d @ VAR | е (х) = х ^ 3 | |
| 83 | Оцените интеграл | интеграл от 0 до 10 из 4x ^ 2 + 7 относительно x | |
| 84 | Оцените интеграл | интеграл (натуральный логарифм x) ^ 2 относительно x | |
| 85 | Найдите производную – d / dx | журнал x | |
| 86 | Найдите производную – d / dx | арктан (x) | |
| 87 | Найдите производную – d / dx | натуральное бревно 5х | |
| 88 | Найдите производную – d / dx | 5e ^ x | |
| 89 | Найдите производную – d / dx | cos (3x) | |
| 90 | Оцените интеграл | интеграл x ^ 3 относительно x | |
| 91 | Оцените интеграл | интеграл x ^ 2e ^ x относительно x | |
| 92 | Найдите производную – d / dx | 16 корень четвертой степени из 4x ^ 4 + 4 | |
| 93 | Найдите производную – d / dx | х / (е ^ х) | |
| 94 | Оценить предел | Предел, когда x приближается к 3 от arctan (e ^ x) | |
| 95 | Оцените интеграл | интеграл от (e ^ x-e ^ (- x)) / (e ^ x + e ^ (- x)) относительно x | |
| 96 | Найдите производную – d / dx | 3 ^ х | |
| 97 | Оцените интеграл | интеграл xe ^ (x ^ 2) относительно x | |
| 98 | Найдите производную – d / dx | 2sin (x) | |
| 99 | Оценить | сек (0) ^ 2 | |
| 100 | Найдите производную – d / dx | натуральный логарифм x ^ 2 |
Формальное определение лимита
Формальное определение лимита К концу этой лекции вы сможете формально определить, что такое предел, используя точный математический язык, и использовать этот язык для объяснения расчетов пределов и графиков, которые мы выполнили в предыдущих разделах.
До сих пор мы работали с неформальным определением лимита:
Предел (неофициальное определение)Если f (x) в конечном итоге становится все ближе и ближе к определенному значению L, поскольку x приближается к выбранному значению c из справа , то мы говорим, что предел f (x) как x подходит к c справа – это L .
Если f (x) в конечном итоге становится все ближе и ближе к определенному значению L, поскольку x приближается к выбранному значению c из левого , тогда мы говорим, что предел f (x) x подходит к c слева – это L .
Если предел f (x) при приближении x к c одинаков как справа, так и слева, то мы говорим, что предел f (x) при приближении x к c равен L .
Если f (x) никогда не приближается к определенному конечному значению, поскольку x приближается к c , то мы говорим, что предел не существует . Если f (x) имеет разные правый и левый пределы, то двусторонний предел ( lim x → c f (x) ) не существует .
Если f (x) имеет разные правый и левый пределы, то двусторонний предел ( lim x → c f (x) ) не существует .
Обозначение:
Конкретно пишем:
lim x → c- f (x) = L для обозначения «предела f (x), когда x приближается к c слева, это L »
lim x → c + f (x) = L для обозначения «предела » f (x) при приближении x к c слева составляет L »
lim x → c f (x) = L для обозначения «предела » f (x), когда x приближается к c is L “
Однако это определение неформальное , потому что мы официально не определили, что мы подразумеваем под «подходами» или «в конечном итоге становится все ближе и ближе к». Чтобы прийти к формальному определению, нам нужно будет уточнить, когда именно мы можем сказать, что x или f (x) приближаются к определенному значению. Мы делаем это сейчас, давая формальное математическое определение:
Чтобы прийти к формальному определению, нам нужно будет уточнить, когда именно мы можем сказать, что x или f (x) приближаются к определенному значению. Мы делаем это сейчас, давая формальное математическое определение:
Конечные ограничения:
Если f (x) – это функция, которая определена на открытом интервале около x = c , а L – действительное число, то
lim x → c f (x) = L
означает, что:
Для любого числа ε> 0, которое мы выберем, можно найти другое число δ> 0, так что:
для всех x между c-δ и c + δ (за исключением, возможно, c точно ), f (x) будет находиться между L-ε и L + ε.
Другими словами, если мы выберем интервал на оси y вокруг L, мы всегда сможем найти интервал на оси x- вокруг c , который заставит f (x) остаться с выбрал диапазон y -значения (за исключением, пожалуй, f (c) ). Вероятно, лучше всего это понять, посмотрев на график:
Вероятно, лучше всего это понять, посмотрев на график:
Если нам нужно формальное определение того, что означает неограниченное увеличение или уменьшение лимита, мы также можем адаптировать этот подход к этому случаю:
Бесконечные лимиты:
Если f (x) – функция, которая определена на открытом интервале около x = c , то
lim x → c f (x) = + ∞
означает, что:
Для любого числа M> 0, которое мы выберем, можно найти другое число δ> 0, так что:
для всех x между c-δ и c + δ (за исключением, возможно, c точно ), f (x) будет больше, чем M.
Другими словами, если мы выберем значение на оси y вокруг, мы всегда сможем найти интервал на оси x- вокруг c , который заставит f (x) оставаться выше этого значения. (кроме, возможно, f (c) ). Вероятно, лучше всего это понять, посмотрев на график:
(кроме, возможно, f (c) ). Вероятно, лучше всего это понять, посмотрев на график:
Мы также можем использовать ту же идею для определения пределов на бесконечности:
Пределы на бесконечности:
Если f (x) – функция, а L – действительное число, то
lim x → ∞ f (x) = L
означает, что:
Для любого числа ε> 0, которое мы выберем, можно найти другое число M> 0, так что:
для всех x больше M, f (x) будет находиться между L-ε и L + ε.
Другими словами, если мы выберем интервал на оси y вокруг L, мы всегда сможем найти значение отсечки на оси x- , которое заставит f (x) оставаться в выбранном диапазоне и -значны, когда они проходят через это место отсечки. Это также, вероятно, лучше всего понять, посмотрев на график:
Итак, если существует ограничение, должна быть возможность ограничить область около c , что заставит f (x) оставаться в пределах любого выбранного конкретного расстояния L . Давайте посмотрим, как это определение можно применить к примерным расчетам пределов, которые мы сделали в предыдущих лекциях. В случаях, когда предел не существует, мы должны суметь понять, почему δ не существует для всех возможных ε: другими словами, мы должны быть в состоянии найти ε в этих случаях, для которых невозможно найти возможное δ. что заставит f (x) оставаться на расстоянии ε от L.
Давайте посмотрим, как это определение можно применить к примерным расчетам пределов, которые мы сделали в предыдущих лекциях. В случаях, когда предел не существует, мы должны суметь понять, почему δ не существует для всех возможных ε: другими словами, мы должны быть в состоянии найти ε в этих случаях, для которых невозможно найти возможное δ. что заставит f (x) оставаться на расстоянии ε от L.
Пределы специальных функций
Для каждого из следующих примеров мы рассмотрим, как формальное определение предела позволяет нам доказать, что предел существует или что он не существует.Мы делаем это как с помощью графиков, чтобы увидеть, можем ли мы аппроксимировать подходящие значения для δ или M, так и путем проверки, можем ли мы вычислить эти значения точно, подойдя к уравнению алгебраически.
Простой пример, где
lim x → c f (x) = f (c) :Для этой функции нас интересует предел, поскольку x приближается к 1:
.
Мы уже вычислили этот предел графически и алгебраически и определили, что он равен 2.Но теперь мы хотели бы использовать формальное определение лимита, чтобы лучше понять, почему он существует. Для этого мы собираемся найти значение (я) δ, которое будет соответствовать требованиям определения предела для ε = 0,05.
Чтобы сделать это графически, мы можем переместить ползунок ε на интерактивной анимации ниже, пока он не достигнет 0,05. Затем мы можем перемещать ползунок δ до тех пор, пока не появятся пунктирные зеленые линии, которые представляют часть графика, где все точки находятся в пределах δ-расстояния или меньше от x = 1.Как только эти зеленые пунктирные вертикальные линии будут достаточно близко друг к другу, чтобы гарантировать, что все f (x) между ними остаются внутри красной заштрихованной части графика, мы нашли δ, которое будет удерживать f (x) на расстоянии. от ε предела 2.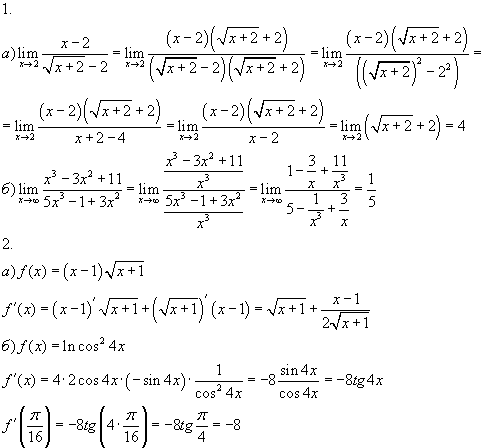 При приблизительно каком значении δ вертикальные зеленые пунктирные линии удерживают график f (x) внутри красной части графика?
При приблизительно каком значении δ вертикальные зеленые пунктирные линии удерживают график f (x) внутри красной части графика?
ε
δ
Взаимодействуя с анимацией, вы должны были обнаружить, что δ = 0.0248, или что-то близкое к нему, кажется достаточно малым, чтобы гарантировать, что f (x) остается на расстоянии 0,05 от предела 2.
Теперь, чтобы сделать это алгебраически, мы начнем с ограничения f (x) с помощью L-ε слева и L + ε справа, а затем решим это неравенство для x . Это позволяет нам определить, какие значения x позволят нам удерживать f (x) на расстоянии ε от предела 2:
.Итак, если x остается в пределах 0.025 расстояние от c = 1, f (x) останется в пределах 0,05 расстояния от L = 2. (Конечно, любое значение δ меньше 0,025 также будет работать!)
Пример с отверстием
x = c: Нас снова интересует предел, поскольку x приближается к -2, и мы помним из последних нескольких лекций, что предел в этом случае равен -4.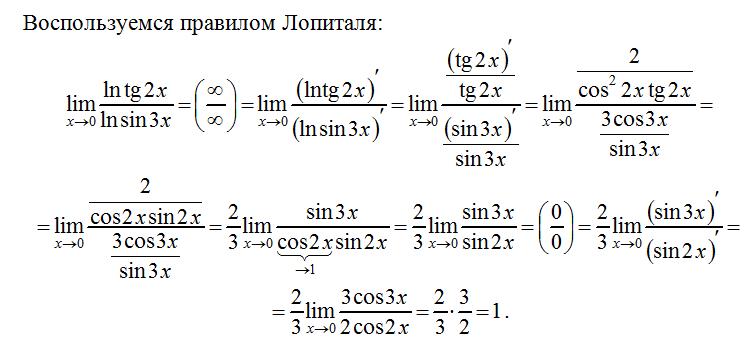 В этой задаче давайте поищем δ, которое будет работать при ε = 0,02.
В этой задаче давайте поищем δ, которое будет работать при ε = 0,02.
Для начала мы попытаемся найти δ графически, взаимодействуя с приведенной ниже анимацией, которая даст нам приблизительное значение:
ε
δ
Взаимодействуя с анимацией, я получил значение около 0.0206 для δ. Что ты получил?
Теперь решаем алгебраически относительно δ, чтобы получить точное значение:
Пример с функцией, имеющей разрыв скачка при
x = c , состоящий из одной точки :Нас снова интересует предел, поскольку x приближается к -2, и мы помним из последних нескольких лекций, что предел в этом случае равен -4. В этом примере мы снова ищем δ, которое работает при ε = 0.02.
Сначала мы стремимся оценить δ графически, используя анимацию ниже:
ε
δ
Мы замечаем, что эта проблема на самом деле ничем не отличается от предыдущей: единственная разница здесь заключается в том, что в то время как на предыдущем графике была дыра размером x = 2, тогда как на этом графике, помимо этой дыры, есть изолированная точка в (-2,1). Но это не влияет на предел, потому что предел не касается того, что происходит при x = c , а только того, что происходит вокруг x = c .Таким образом, в этом случае наше предыдущее значение δ = 0,02 все еще будет работать, даже если точка (-2,1) находится за пределами 0,02 от -4. Мы должны точно исключить этот момент, глядя на предел по определению.
Но это не влияет на предел, потому что предел не касается того, что происходит при x = c , а только того, что происходит вокруг x = c .Таким образом, в этом случае наше предыдущее значение δ = 0,02 все еще будет работать, даже если точка (-2,1) находится за пределами 0,02 от -4. Мы должны точно исключить этот момент, глядя на предел по определению.
В следующем примере мы будем использовать формальное определение предела для оценки односторонних пределов, и прежде чем мы это сделаем, мы хотим кратко представить часть обозначений, которые мы будем использовать:
Замечание: L L и L R Мы будем использовать обозначение L R для обозначения предела, рассчитанного как x , приближающегося к c справа, и мы будем использовать обозначение L L для обозначения предела, рассчитанного как x , приближающегося к c слева.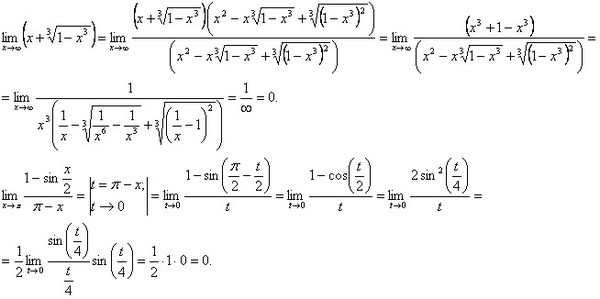
Пример с функцией, имеющей разрыв скачка при
x = c и разные пределы справа и слева:Здесь нас интересует предел x → 1, и мы будем стремиться найти δ, удовлетворяющее формальному определению предела для ε = 0,1. Поскольку это кусочная функция с разрывом скачка при x = 1, сначала рассмотрим предел отдельно справа и слева:
Сначала мы рассматриваем предел справа, который мы уже вычислили в предыдущей лекции, как 2.Сначала мы оценим его графически, используя интерактивную анимацию ниже, а затем вычислим его алгебраически.
ε
δ
Используя ползунки для установки ε на 0,1, а затем перемещая ползунок для δ, пока зеленая пунктирная линия справа не удержит график f (x) слева от x = 1 внутри красной заштрихованной области , Я получил аппроксимацию δ из графика, которая составила 0,0777. Что ты получил?
Что ты получил?
Теперь вычисляем δ алгебраически для правого предела:
Теперь мы считаем предел слева, который мы уже вычислили в предыдущей лекции, как -2.Мы снова начнем с графической оценки, используя приведенную ниже анимацию, а затем вычислим ее алгебраически.
ε
δ
Используя ползунки для установки ε на 0,1, а затем перемещая ползунок для δ, пока зеленая пунктирная линия слева не удержит график f (x) слева от x = 1 в пределах красной заштрихованной области , Я получил аппроксимацию δ из графика, которая составила 0,037. Что ты получил?
Перейдем к алгебраическому вычислению значения δ для левого предела:
Теперь рассмотрим двусторонний предел.Если мы попытаемся использовать формальное определение предела со значением ε = 0,1, мы столкнемся с проблемой: мы не можем выбрать любое δ, которое всегда будет удерживать f (x) на расстоянии ε от левого предела. -2 слева, потому что независимо от того, насколько маленьким мы сделаем наше δ, всегда будет небольшой участок графика справа от x = 1, где f (x) выпадает далеко за пределы области, которая расстояние ε или меньше от левого предела. Точно так же мы не можем выбрать любое δ, которое всегда будет удерживать f (x) на расстоянии ε от правостороннего предела 2, потому что независимо от того, насколько маленьким мы сделаем наше δ, всегда будет кусочек графика просто для того, чтобы слева от x = 1, где f (x) находится далеко за пределами области, которая находится на расстоянии ε или меньше от правого предела.
-2 слева, потому что независимо от того, насколько маленьким мы сделаем наше δ, всегда будет небольшой участок графика справа от x = 1, где f (x) выпадает далеко за пределы области, которая расстояние ε или меньше от левого предела. Точно так же мы не можем выбрать любое δ, которое всегда будет удерживать f (x) на расстоянии ε от правостороннего предела 2, потому что независимо от того, насколько маленьким мы сделаем наше δ, всегда будет кусочек графика просто для того, чтобы слева от x = 1, где f (x) находится далеко за пределами области, которая находится на расстоянии ε или меньше от правого предела.
Фактически, нам нужно иметь ε равное 4 или больше, чтобы заставить все значения f (x) в окрестности x = 1 находиться в пределах расстояния ε как слева, так и от правильные предельные значения. Но формальное определение гласит, что мы должны быть в состоянии найти δ для ВСЕХ возможных ненулевых вариантов для ε. Итак, если мы можем найти даже , одно ненулевое значение для ε, для которого невозможно δ, мы показали, что предел не существует.
Итак, если мы можем найти даже , одно ненулевое значение для ε, для которого невозможно δ, мы показали, что предел не существует.
Пример с функцией, которая имеет бесконечный разрыв (или вертикальную асимптоту) при
x = c :Для этой функции нас интересует предел, поскольку x приближается к 0.Мы можем видеть здесь, что мы не сможем найти δ для любого ε в этом случае, которое будет работать для конечного предела, потому что f (x) здесь неограниченно возрастает, поскольку x приближается к 0 с любой стороны. Поэтому в этом случае мы будем использовать формальное определение бесконечных пределов, чтобы найти значение для δ, когда M = 100.
Начнем с аппроксимации δ графически: с помощью ползунков на интерактивной анимации ниже.
M
δ
Я получил приблизительное значение 0. 095. Что ты получил?
095. Что ты получил?
Теперь решаем относительно δ алгебраически:
Пример с функцией, которая имеет бесконечный разрыв (или вертикальную асимптоту) при
x = c, с различным поведением предела слева и справа:Для этой функции нас интересует предел, поскольку x приближается к 1. Давайте теперь посмотрим, сможем ли мы найти подходящее значение δ для M = 40 с правой стороны и соответствующее значение δ для M = -40 с левой стороны. , сначала используя график для аппроксимации значения:
M
δ
M
δ
И для левого, и для правого я получил значение δ = 0.026, используя ползунки на интерактивной анимации выше. Что ты получил?
Теперь вычислим δ точно алгебраически. Сначала мы начнем с определения того, какое значение δ сохранит f (x) выше M (в правой части).
Теперь мы вычисляем, какое значение δ сохранит f (x) ниже -40 (слева).
Мы снова можем видеть, почему двусторонний предел не существует в этом случае, потому что не существует возможного δ, которое мы могли бы выбрать, которое удерживало бы все значения f (x) выше 40 (потому что всегда было бы какое-то значения слева от x = 1 включены, и все они отрицательны), независимо от того, насколько мало δ.Мы столкнулись бы с аналогичной проблемой с положительными значениями f (x) справа от 1, если бы попытались найти δ, которое работает для двустороннего предела, когда M = 40 (потому что всегда будут некоторые значения справа от x = 1 включено, и все они положительные).
Пример с функцией, имеющей предел нуля на бесконечности:
Для этой функции нас интересует предел, когда x приближается к -∞, и предел, когда x приближается к + ∞. Мы будем искать значения M, которые удовлетворяют формальному определению предела, когда ε равно 0,45. Из-за относительной сложности этого конкретного уравнения мы будем оценивать значения M только графически, а не проверять их алгебраически в этом случае. Используйте ползунки в интерактивной анимации ниже, чтобы найти M для ε = 0,45 для обоих пределов:
Мы будем искать значения M, которые удовлетворяют формальному определению предела, когда ε равно 0,45. Из-за относительной сложности этого конкретного уравнения мы будем оценивать значения M только графически, а не проверять их алгебраически в этом случае. Используйте ползунки в интерактивной анимации ниже, чтобы найти M для ε = 0,45 для обоих пределов:
ε
M
Рассматривая предел, когда x приближается к -∞, мы получаем значение M, равное примерно 4.4, и глядя на предел, когда x приближается к + ∞, мы получаем значение M, которое составляет приблизительно 4,35.
Пример с функцией, предел которой не существует на бесконечности:
Мы рассматриваем предел этой функции, когда x приближается к + ∞, и мы рассматриваем, можем ли мы найти M для ε = 0,5. Опять же, для этой проблемы, поскольку уравнение относительно сложное, мы используем анимацию для аппроксимации значений M, а не пытаемся найти M алгебраически. Попробуйте поэкспериментировать с ползунками ниже, чтобы увидеть, сможете ли вы найти значение M, которое сохранит значения f (x) в красной заштрихованной области для всех x > M.
Попробуйте поэкспериментировать с ползунками ниже, чтобы увидеть, сможете ли вы найти значение M, которое сохранит значения f (x) в красной заштрихованной области для всех x > M.
ε
M
Мы видим, что в этом примере никогда не удастся найти такое M, потому что по мере неограниченного увеличения x f (x) также неограниченно увеличивается. Независимо от того, какое значение мы выберем для M, мы никогда не сможем удержать график f (x) в пределах красной заштрихованной области.
Пример функции с колеблющимся разрывом:
Мы рассматриваем предел этой функции, поскольку x приближается к 1, и мы стремимся найти δ, которое удовлетворяет формальному определению предела для ε = 0,5. Это еще одна проблема, когда мы просто будем смотреть на график, чтобы попытаться найти δ, а не пытаться найти δ алгебраически. Глядя на анимацию ниже, потратьте некоторое время, чтобы поэкспериментировать с ползунками, чтобы увидеть, сможете ли вы найти δ для ε = 0.5 для одностороннего или двустороннего ограничения при x = 1.
Глядя на анимацию ниже, потратьте некоторое время, чтобы поэкспериментировать с ползунками, чтобы увидеть, сможете ли вы найти δ для ε = 0.5 для одностороннего или двустороннего ограничения при x = 1.
ε
δ
ε
M
Вы, возможно, заметили, что невозможно найти такое δ, потому что независимо от того, насколько маленькое δ вы выберете, всегда будет какая-то часть графика внутри пунктирных зеленых линий, которая колеблется от 1 до -1. . Таким образом, не существует такого значения, которое удерживало бы график f (x) внутри красной заштрихованной области, и мы можем видеть, как формальное определение предела показывает нам, что этого предела не существует.
Правило госпиталя
Правило госпиталя (c) Коалиция Фонда авторского права (С. А. Фуллинг) 1998Класс 19.T
Задание по чтению на вторник, 10 февраля
- Стюарт 6,8
- Эта веб-страница
Это не полное изложение правила Л’Опиталя,
это просто набор дополнительных замечаний. На самом деле предполагается, что вы сначала прочитали раздел учебника!
На самом деле предполагается, что вы сначала прочитали раздел учебника!
Напомним вкратце то, что нам сообщает l’Hôpital: Предположим, мы хотим вычислить предел f (x) / g (x) как x . приближается к некоторому значению a ( a может быть бесконечным), и предположим, что и f (x) и g (x) приближаются к нулю в этом пределе, или оба приближаются бесконечность.Тогда предел такой же, как предел f ‘(x) / g’ (x) – что может быть легче вычислить.
Предупреждение: (версия .dvi) (версия .pdf) Когда НЕ использовать правило Л’Опиталя Самое важное, что нужно знать о правиле Л’Опиталя когда его не следует использовать:
- Когда пределы двух частей не равны 0 или обе бесконечны.
В этом случае правило, скорее всего, даст неправильный ответ! Пример:
lim x -> 0 + (cos x ) / x
положительная бесконечность, потому что числитель стремится к 1, а знаменатель приближается к 0.
 Если мы неправильно применяем правило l’Hôpital, мы
получать
Если мы неправильно применяем правило l’Hôpital, мы
получатьlim x -> 0 + (- sin x ) / 1 = 0.
- Когда это усугубляет проблему. Пример: (версия .dvi)
(версия .pdf)
Когда есть лучший способ получить ответ.
Пример 1: Бесконечный предел
(x 2 – 1) / (2x 2 + 1)
можно правильно оценить двумя последовательными применениями Правило Л’Опиталя; но его также можно найти по правилу, которое мы узнали ранее: Разделите числитель и знаменатель на наибольшую степень. ( x 2 ) и сразу возьмем предел, получив 1/2 очень быстро.
Пример 2: Рассмотрим предел на 0 из
(cos x – 1) / x .
Так как верх и низ оба приближаются к 0, допустимо использовать правило и получить
lim x -> 0 (- sin x ) / 1 = 0.
Однако менее загадочно и поучительно вспомнить (из раздел о дифференциалах), что косинус-функция имеет квадратичную приближение
cos x ÷ 1 – x 2 /2
и, следовательно, числитель ведет себя около 0 как – x 2 /2.
 Очевидно, это исчезает быстрее, чем знаменатель, x ,
так что предел равен нулю.
Очевидно, это исчезает быстрее, чем знаменатель, x ,
так что предел равен нулю.
Очевидно, что первые два пункта в этом списке являются абсолютными запретами, а
последний – просто дружеский совет.
Многие студенты злоупотребляют правилом Л’Опиталя, полагаясь на него как на «черный ящик».
когда они узнают гораздо больше (и решат проблемы одинаково быстро)
просто внимательно рассмотрев и сравнив,
поведение числителя и знаменателя как x -> a .В частности, вы должны сначала спросить себя, знаете ли вы линейный или
квадратичная аппроксимация числителя или знаменателя около x =
а .
Если так, то, вероятно, станет ясно, что дробь равна
приблизительно равно постоянной, умноженной на некоторую степень (x – a) ,
и предел бесконечен, конечен или равен нулю в зависимости от того,
отрицательное, нулевое или положительное значение (см. Пример 2 выше).
Точно так же, когда предел берется на бесконечность, спросите, числитель или
знаменатель “ведет себя как” определенная степень x , поскольку x становится
большой; соотношение двух степеней приближается к очевидному пределу на бесконечности,
в зависимости от двух показателей (как в Примере 1).
Когда СЛЕДУЕТ использовать правило Л’Опиталя?
Безусловно, наиболее важная ситуация для использования правила – это когда числитель или знаменатель не имеет очевидное властное поведение, поскольку x приближается к a . Так обстоит дело с функцией логарифма, поскольку x приближается к либо 0, либо бесконечность, а для экспоненциальной функции как x приближается либо к положительной, либо к отрицательной бесконечности. (Вот почему раздел о правиле Л’Опиталя находится в эта глава!)В качестве домашнего задания у вас есть ряд ограничений отношений экспонент, логарифмы и обычные степени, которые вам следует оценить на практике.Однако через некоторое время результаты таких расчетов стали очень предсказуемо. Их можно свести к списку общих выводов:
- По мере приближения x к положительной бесконечности e x увеличивается быстрее любой мощности, x n .
- По мере приближения x к положительной бесконечности e -x убывает быстрее любой отрицательной мощности, x -n .

- По мере приближения x к положительной бесконечности ln x , хоть и уходит в бесконечность, увеличивается медленнее, чем любая положительная сила, x a (даже дробная степень, например a = 1/200).
- Как x -> 0 + , – ln x уходит в бесконечность, но медленнее, чем любая отрицательная сила, x -a (даже дробное).
Показательные неопределенные формы, и 0
0 спор Предел (поскольку x приближается к a ) f (x) g (x) не всегда можно найти, просто взяв пределы f и g по отдельности – точно так же, как предел f (x) / g (x) не является частным от индивидуальных пределов, если те
пределы равны 0 или бесконечности.Чтобы узнать, когда и почему возникла проблема, обратите внимание, что логарифм f (x) g (x) is g (x) ln f (x) ,
и считайте предел , что . Если g приближается к 0, а логарифм приближается к положительному или отрицательному
бесконечность, или если g стремится к бесконечности, а логарифм стремится к 0,
тогда у нас есть неопределенная форма типа «0 умножить на бесконечность».
(Что нам тогда делать?)
Эти три случая соответствуют в исходной функции
Если g приближается к 0, а логарифм приближается к положительному или отрицательному
бесконечность, или если g стремится к бесконечности, а логарифм стремится к 0,
тогда у нас есть неопределенная форма типа «0 умножить на бесконечность».
(Что нам тогда делать?)
Эти три случая соответствуют в исходной функции
- g -> 0, f -> бесконечность;
- г -> 0, f -> 0;
- г -> бесконечность, f -> 1.
Остальная часть этой страницы – просто интересное замечание, не важное к курсу.
Вы можете быть удивлены, увидев второй элемент в списке, так как
0 0 на первый взгляд выглядит довольно ручным объектом.
На самом деле, однако, если вы в любой день заглянете в Интернет,
группу новостей, посвященную обсуждению математики, вы, вероятно, найдете
ведутся оживленные дискуссии о том, равно ли 0 0 1 или
неопределенный.
(Иногда эти аргументы исходят от «чудака», который обвиняет
профессия математика прикрывает неловкий скандал, связанный с
со значением 0 0 . )
)
Чтобы понять, почему возникла проблема, сначала обратите внимание, что
- x 0 = 1 для всех ненулевых x ;
- 0 y = 0 для всех положительных значений y ;
- 0 y не определено (или бесконечно) для негатива y .
Аргумент в пользу определения 0 0 как 1: Есть много полезных формул, включающих выражения вида x y , которые остаются значимыми и истинными, когда x и y равно 0, если 0 0 интерпретируется как 1. Самый простой пример – биномиальная формула
Самый простой пример – биномиальная формула
(а + б) 2 = а 2 б 0 + 2a 1 b 1 + a 0 b 2 .
Связанный пример: Теорема Тейлора, который включает степени (x – a) .
Аргумент в пользу выхода 0 0 undefined: Если f (a) = 0 = g (a) , и обе функции непрерывны, тогда мы могли бы прийти к выводу, что
lim x -> a f (x) g (x) = 1,
забывая, что 0 0 действительно является неопределенной формой.Во избежание путаницы мы объявили 0 0 вне закона.
Более подробную информацию по теме можно найти в Список часто задаваемых вопросов sci.math
Есть над чем подумать: Почему бы нам не определить 0/0 как 1 вместо того, чтобы настаивать на том, что 0/0 не определено? (ответ)
Предел функции при x стремится к бесконечности
Предел функции
x стремится к бесконечностиВ этом модуле мы объясняем, что это означает, когда предел функции стремится к бесконечности, по крайней мере, к бесконечности или к истинной связи, в то время как x стремится к бесконечности или бесконечности.
 Мы также объясняем, что означает, что функция стремится быть действительной, а x стремится к определенному действительному числу.
Мы также объясняем, что означает, что функция стремится быть действительной, а x стремится к определенному действительному числу. В любом случае мы приводим пример функции, которая не достигает предела. Чтобы освоить описанные здесь техники, важно, чтобы вы выполняли много упражнений, чтобы это стало второй натурой.
В этом примере мы используем программирование на Python, чтобы проверить предел, когда x стремится к бесконечности. Предел – это значение, к которому функция «приближается», потому что вход приближается к некоторому значению. Пределы являются неотъемлемой частью исчисления и определяются с помощью непрерывности, производных и интегралов.
В этой статье использовались различные библиотеки Python. Теперь давайте посмотрим, как найти предел для данной функции, когда x стремится к бесконечности в коде Python.
1. Обсудите предел следующей функции, когда x → ∞
импортировать numpy как np из sympy import * x = символы ('x') init_printing (use_unicode = True) print (предел (sin (1 / x), x, oo, '+')) сюжет (sin (1 / x)) Выход: 0
| Предел функции, когда x стремится к бесконечности |
2.
 Обсудите предел следующей функции, когда x → ∞
Обсудите предел следующей функции, когда x → ∞ импортировать numpy как np
из sympy import *
x = символы ('x')
init_printing (use_unicode = True)
print (предел (exp (1) / x, x, oo, '+'))
сюжет (exp (1) / x)
Выход: 0
| Предел функции, когда x стремится к бесконечности |
3. Обсудите пределы следующей функции, когда x → ∞
импортировать numpy как np
из sympy import *
x = символы ('x')
init_printing (use_unicode = True)
print (предел (exp (-1) / x, x, oo))
сюжет (exp (-1) / x)
Выход: 0 | Предел функции, когда x стремится к бесконечности |
4.Обсудите предел следующей функции, когда x → ∞
импортировать numpy как np из sympy import * x = символы ('x') init_printing (use_unicode = True) print (предел (exp (x) / x, x, oo)) сюжет (exp (x) / x) Выход: oo
| Предел функции, когда x стремится к бесконечности |
5. Обсудите предел следующей функции, когда x → ∞
импортировать numpy как np из sympy import * x = символы ('x') init_printing (use_unicode = True) print (предел (exp (-x) / x, x, oo)) сюжет (exp (-x) / x))
| Предел функции, когда x стремится к бесконечности |
6.Обсудите предел следующей функции, когда x → ∞
импортировать numpy как np из sympy import * x = символы ('x') init_printing (use_unicode = True) print (предел (x ** 2 * sin (1 / x), x, oo, '+')) сюжет (x ** 2 * sin (1 / x)) Выход: oo
Предел функции, когда x стремится к бесконечности 7. Обсудите предел следующей функции, когда x → ∞
импортировать numpy как np из sympy import * x = символы ('x') init_printing (use_unicode = True) print (предел (x / (1 + x), x, oo, '+')) участок (x / (1 + x)) Выход: 1
Предел функции, когда x стремится к бесконечности
Нахождение пределов при приближении X к бесконечности
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. – относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Пределы на бесконечности — Корни и абсолютные значения
Краткий обзор
- Во-первых, если есть квадратный корень, вычтите за скобки наибольшую степень $$ x $$, которая находится под корнем.
 2} = | a | $$
2} = | a | $$ - $$ | a | = a $$, если $$ a $$ положительно, но $$ | a | = -a $$, если значение $$ 4a $$ отрицательное.
Примеры
Пример 1
Вычислить $$ \ displaystyle \ lim_ {x \ to \ infty} \, \ frac {| x | +2} {4x + 3} $$
Шаг 1Упростите абсолютное значение.
Поскольку предел учитывает положительные значения $$ x $$, мы знаем, что $$ | x | = x $$.Таким образом, мы можем переписать предел как
$$ \ displaystyle \ lim_ {x \ to \ infty} \, \ frac {\ blue {| x |} +2} {4x + 3} % = \ displaystyle \ lim_ {x \ to \ infty} \, \ frac {\ blue x + 2} {4x + 3}. $$
Шаг 2 Выносим за скобки числитель и знаменатель $$ x $$. Затем разделите общий множитель.
Затем разделите общий множитель.
$$ \ begin {align *}% \ lim_ {x \ to \ infty} \, \ frac {\ blue x + 2} {4 \ blue x + 3} % & = \ lim_ {x \ to \ infty} \, \ frac {% \ синий x \ left (% 1 + \ frac 2 {\ blue x} \верно) } {% \ синий x \ left (% 4 + \ frac 3 {\ blue x} \верно) } \\ [6pt] % & = \ lim_ {x \ to \ infty} \, \ frac {% 1 + \ гидроразрыва 2 х } {% 4 + \ гидроразрыва 3 х } \ end {выровнять *} $$
Шаг 3 Оцените предел.
$$ \ Displaystyle \ lim_ {х \ к \ infty} \, \ гидроразрыва {% 1 + \ синий {\ frac 2 x} } {% 4 + \ красный {\ frac 3 x} } % = \ frac {1 + \ blue 0} {4 + \ red 0} % = \ frac 1 4 $$
Отвечать$$ \ displaystyle \ lim_ {x \ to \ infty} \, \ frac {| x | + 2} {4x + 3} = \ frac 1 4 $$
Пример 2
Вычислить $$ \ displaystyle \ lim_ {x \ to- \ infty} \, \ frac {| x | +2} {4x + 3} $$
Обратите внимание, что это та же функция, что и в примере 1, но на этот раз $$ x $$ становится отрицательным.
Упростите абсолютное значение.
Поскольку этот предел рассматривает отрицательные значения $$ x $$, мы знаем, что $$ | x | = -x $$. Это означает, что мы можем переписать предел как
$$ \\ \ displaystyle \ lim_ {x \ to- \ infty} \, \ frac {\ blue {| x |} + 2} {4x + 3} % = \ lim_ {x \ to- \ infty} \, \ frac {\ blue {-x} + 2} {4x + 3} \\ $$
Шаг 2Выдавите за скобки числитель и знаменатель наибольшую степень $$ x $$.Затем разделите общий множитель.
$$ \ begin {align *}% \ lim_ {x \ to- \ infty} \, \ frac {- \ blue x + 2} {4 \ blue x + 3} % & = \ lim_ {x \ to- \ infty} \, \ frac {% \ синий x \ left (% -1 + \ frac 2 {\ blue x} \верно) } {% \ синий x \ left (% 4+ \ frac 3 {\ blue x} \верно) } \\ [6pt] % & = \ lim_ {x \ to- \ infty} \, \ frac {-1 + \ frac 2 x} {4+ \ frac 3 x} \ end {выровнять *} $$
Шаг 3 Оцените предел.


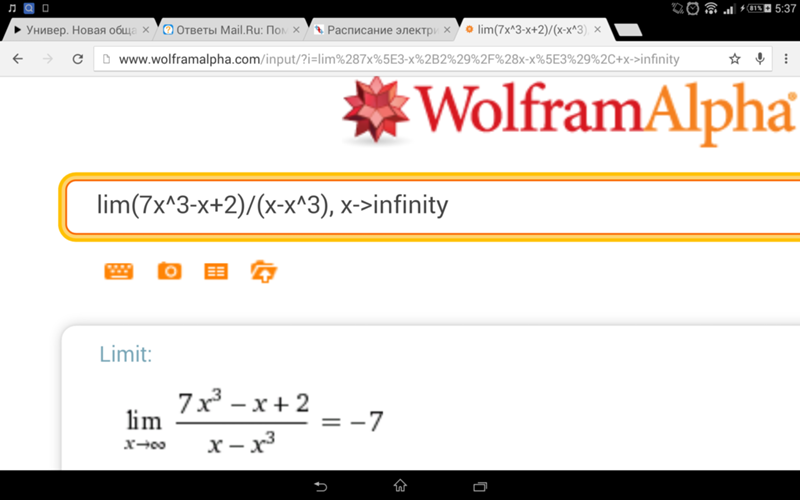 Если мы неправильно применяем правило l’Hôpital, мы
получать
Если мы неправильно применяем правило l’Hôpital, мы
получать Очевидно, это исчезает быстрее, чем знаменатель, x ,
так что предел равен нулю.
Очевидно, это исчезает быстрее, чем знаменатель, x ,
так что предел равен нулю.
 Обсудите предел следующей функции, когда x → ∞
Обсудите предел следующей функции, когда x → ∞
 Обсудите предел следующей функции, когда x → ∞
Обсудите предел следующей функции, когда x → ∞
 2} = | a | $$
2} = | a | $$