Аналитическая геометрия для «чайников»
Настоящая книга позволит вам в сжатые сроки (2-3 недели) освоить основы аналитической геометрии и научиться решать наиболее распространённые задачи по теме. Материал предназначен для студентов-заочников и других читателей, которые хотят быстро освоить минимум теории и максимум практики
Сначала немного о предмете…. Наверняка вам сейчас вспомнился курс школьной геометрии с многочисленными теоремами, их доказательствами, чертежами и т.д. Что скрывать, нелюбимый и часто малопонятный предмет для значительной доли учеников. Аналитическая геометрия, как ни странно, может показаться более интересной и доступной. Что означает «аналитическая»? На ум сразу приходят два «штампованных» математических оборота: графический метод решения и аналитический метод решения.
Графический метод связан с построением графиков, чертежей. Аналитический же метод предполагает решение задач  В этой связи алгоритм решения многих задач аналитической геометрии прост и прозрачен, зачастую достаточно аккуратно применить нужные формулы – и ответ готов! Нет, конечно, совсем без чертежей тут не обойдется, к тому же для лучшего понимания материала я постараюсь приводить их сверх необходимости.
В этой связи алгоритм решения многих задач аналитической геометрии прост и прозрачен, зачастую достаточно аккуратно применить нужные формулы – и ответ готов! Нет, конечно, совсем без чертежей тут не обойдется, к тому же для лучшего понимания материала я постараюсь приводить их сверх необходимости.
1. Векторы
1.1. Что такое вектор?
1.2. Коллинеарность векторов
1.3. Основные действия с векторами
1.4. Координаты вектора на плоскости и в пространстве
1.5. Простейшие задачи с векторами
1.5.1. Как найти вектор по двум точкам?
1.5.2. Как найти длину отрезка?
1.5.3. Как найти длину вектора?
1.5.5. Как найти единичный вектор
1.5.6. Деление отрезка в данном отношении
1.5.7. Формулы координат середины отрезка
1.6. Скалярное произведение векторов
1.6.1. Определение скалярного произведения
1.6.2. Угол между векторами и знак скалярного произведения
1.
 6.3. Скалярный квадрат вектора
6.3. Скалярный квадрат вектора1.6.4. Свойства скалярного произведения
1.6.5. Как найти угол между векторами?
1.6.6. Скалярное произведение векторов в координатах
1.6.7. Как проверить векторы на ортогональность?
1.6.8. Если векторы заданы суммами векторов с известными координатами
1.7. Ортогональные проекции векторов
1.7.1. Как найти проекцию вектора на вектор?
1.7.2. Проекции вектора на координатные оси. Направляющие косинусы
1.8. Линейная зависимость и линейная независимость векторов.
Базис векторов. Аффинная система координат.
1.8.1. «Плоский» случай
1.8.2. Как определить коллинеарность векторов плоскости?
1.8.3. Как определить коллинеарность векторов пространства?
1.8.4. Базис и система координат пространства
1.9. Векторное произведение векторов
1.9.1. Определение векторного произведения
1.
 9.3. Векторное произведение в координатах
9.3. Векторное произведение в координатах1.10. Смешанное произведение векторов
1.10.1. Определение смешанного произведения
1.10.2. Как вычислить смешанное произведение?
1.10.3. Как вычислить объём треугольной пирамиды?
2. Прямая на плоскости
2.1. Уравнение прямой с угловым коэффициентом
2.2. Общее уравнение прямой
2.2.1. Общее уравнение и направляющий вектор прямой
2.2.2. Как составить уравнение прямой по точке и направляющему вектору?
2.2.4. Как составить уравнение прямой по двум точкам?
2.2.5. Нормальный вектор прямой
2.2.6. Как составить уравнение прямой по точке и вектору нормали?
2.3. Уравнение прямой в отрезках
2.4. Параметрические уравнениЯ прямой
2.5. Простейшие задачи с прямой на плоскости
2.5.1. Взаимное расположение двух прямых
2.5.2. Как найти прямую, параллельную данной?
2.5.
 3. Как найти точку пересечения прямых?
3. Как найти точку пересечения прямых?2.5.4. Как найти прямую, перпендикулярную данной?
2.5.5. Как вычислить расстояние от точки до прямой.
2.5.6. Как найти расстояние между параллельными прямыми?
2.5.7. Как найти угол между прямыми?
2.5.8. Как найти проекцию вектора на прямую?
2.6. Линейные неравенства
2.7. Системы линейных неравенств
2.8. Как научиться решать задачи по геометрии?
2.9. Типовая задача с треугольником
3. Линии второго порядка
3.1. Алгебраическая линия и её порядок
3.2. Классификация линий второго порядка
3.3. Эллипс
3.3.1. Каноническое уравнение эллипса. Как построить эллипс?
3.3.2. Определение эллипса. Фокусы эллипса
3.3.3. Эксцентриситет эллипса и его геометрический смысл
3.3.4. Поворот и параллельный перенос эллипса
3.4.1. Каноническое уравнение и построение гиперболы
3.
 4.2. Определение гиперболы
4.2. Определение гиперболы3.4.3. Фокусы и эксцентриситет гиперболы
3.4.4. Равносторонняя гипербола
3.4.5. Поворот и параллельный перенос гиперболы
3.5. Парабола
3.5.1. Построение, уравнение, определение, фокусы, директриса, эксцентриситет
3.5.2. Поворот и параллельный перенос параболы
3.6. Неравенства с линиями второго порядка
3.7. Задачи с линиями второго порядка
3.7.1. Директрисы эллипса
3.7.2. Директрисы гиперболы
3.8. Приведение уравнения к каноническому виду
3.8.2. Приведение уравнения нецентральной линии
3.8.3. Универсальный метод приведения
4. Полярная система координат
4.1. Что такое полярные координаты?
4.2. Порядок и техника построения точек в полярных координатах
4.3. Взаимосвязь прямоугольной и полярной системы координат
4.4. Уравнение линии в полярных координатах
4.5. Полярная роза
4.6. Как построить линию в полярных координатах?
5.
 Плоскость и прямая в пространстве
Плоскость и прямая в пространстве
5.1. Плоскость и её уравнение
5.1.1. Понятие плоскости
5.1.2. Общее уравнение плоскости
5.1.3. Линейные неравенства в пространстве
5.1.5. Уравнение плоскости в отрезках
5.2. Как составить уравнение плоскости?
5.2.1. Уравнение плоскости по точке и двум неколлинеарным векторам
5.2.2. Как составить уравнение плоскости по трём точкам?
5.2.3. Вектор нормали плоскости (нормальный вектор)
5.2.4. Как составить уравнение плоскости по точке и вектору нормали?
5.3. Простейшие задачи с плоскостью
5.3.1. Как найти плоскость, параллельную данной?
5.3.2. Как найти расстояние от точки до плоскости?
5.3.3. Как найти расстояние между плоскостями?
5.3.4. Взаимное расположение двух плоскостей
5.3.5. Как найти угол между плоскостями?
5.3.7. Взаимное расположение трёх плоскостей
5.
 4. УравнениЯ прямой в пространстве
4. УравнениЯ прямой в пространстве5.4.1. Канонические уравнения прямой
5.4.2. Как составить уравнения прямой по двум точкам?
5.4.3. Параметрические уравнения прямой
5.4.4. Прямая, заданная пересечением двух плоскостей
5.5. Задачи с прямой в пространстве
5.5.1. Взаимное расположение прямых
5.5.2. Скрещивающиеся прямые
5.5.3. Как найти прямую, содержащую общий перпендикуляр?
5.5.4. Как найти расстояние между скрещивающимися прямыми?
5.5.5. Пересекающиеся прямые в пространстве
5.5.6. Как найти прямую, перпендикулярную данной?
5.5.8. Как найти точку, симметричную относительно прямой?
5.5.9. Как найти угол между прямыми?
5.5.10. Параллельные прямые в пространстве
5.6. Основные задачи с прямой и плоскостью
5.6.1. Взаимное расположение прямой и плоскости
5.6.2. Как найти точку пересечения прямой и плоскости?
5.6.3. Как найти проекцию прямой на плоскость?
5.
 6.4. Как найти угол между прямой и плоскостью?
6.4. Как найти угол между прямой и плоскостью?5.6.5. Прямая перпендикулярна плоскости
5.6.6. Прямая параллельна плоскости
5.6.7. Добро пожаловать в «реальные боевые условия»!
6. Поверхности второго порядка
6.1. Понятие алгебраической поверхности
6.2. Цилиндрические поверхности
6.3. Эллипсоид
6.4. Коническая поверхность
6.5. Параболоиды
6.6. Гиперболоиды
6.7. Альтернативные системы координат
6.7.1. Цилиндрическая система координат
6.7.2. Сферическая система координат
7. Решения и ответы, а также Приложения доступны в полной версии.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
Автор: Aлeксaндр Eмeлин
Математика для программиста: советы, разделы, литература
Наверняка вы задумывались над вопросом: нужна ли математика программисту? И если нужна, то как “приручить” эту самую математику?
Если у вас есть проблемы с математикой, вы решились на освоение предмета и не знаете, с чего начать, эта статья станет хорошим фундаментом для дальнейшего обучения. В ней собраны полезные советы, названы главные разделы математики для программиста и литература для самостоятельного обучения.
В ней собраны полезные советы, названы главные разделы математики для программиста и литература для самостоятельного обучения.
Человек, которому никогда прежде не приходилось сталкиваться с математическими рассуждениями, может испытывать некоторые трудности с решением задач, восприятием фактов. Ему трудно отличить истинные утверждения от ложных, понять, какие следствия вытекают из того или иного утверждения.
“Незнание математики грозит кашей в голове.”
– А. Савватеев, доктор физико-математических наук, эксперт отдела теоретических и прикладных разработок компании Яндекс, научный руководитель Лаборатории социального анализа при Университете Дмитрия Пожарского.
Статья разделена на несколько частей:
- советы;
- основные разделы математики для программиста;
- список полезной литературы.
- Осознайте и примите тот факт, что хорошим математиком по одному желанию и щелчку пальцев стать невозможно. Все люди, добившиеся успехов в этом предмете, потратили на него часы упорного и напряжённого труда.
 Если вы встречаете человека, который решает математические задачи гораздо лучше вас, не стоит упрекать себя в отсутствии способностей к предмету или в отсутствии знаний.
Если вы встречаете человека, который решает математические задачи гораздо лучше вас, не стоит упрекать себя в отсутствии способностей к предмету или в отсутствии знаний. - Занимайтесь там, где вас ничто не может отвлекать; отключите телефон, выйдите из соц. сетей и проявите силу воли.
- Занимайтесь ежедневно. Занимайтесь всегда и везде, где только возможно. Уберите из своих привычек бесцельный просмотр соцсетей, телевизора, увлечение видеоиграми и т. п. Вы сразу же ощутите, сколько свободного времени у вас появится. Используйте его с толком.
- Не занимайтесь слишком долго. Делайте перерывы. Не засиживайтесь над одной задачей часами напролёт, это может привести к стрессу. Иногда полезно менять деятельность на день-два, чтобы отдохнуть, но не слишком часто.
- Изучение нового в математике построено на уже приобретенных знаниях, поэтому все время повторяйте пройденное и упражняйтесь в решении задач. Если у вас есть пробелы в математике по программе пятого класса (да, бывает и такое), начните изучение с программы пятого класса.
 В этом нет ничего постыдного.
В этом нет ничего постыдного. - Обязательно заведите две тетради: одну для теории, другую для практики. Пронумеруйте каждый лист. На заднем листе тетради с теорией составьте оглавление (тема – страница). В будущем это вам очень пригодится.
- Если в задаче у вас выходит неверный ответ, решите её ещё раз. Не надо придумывать себе оправдания и откладывать повторное решение. В таких ситуациях важно не просто найти правильный ответ, но и понять, почему в прошлый раз вы решили задачу неверно. Помните, что задача стоит потраченного времени.
- Не стесняйтесь просить помощи у человека, разбирающегося в предмете. Идеальным вариантом будут платные занятия с высококвалифицированным репетитором, если у вас есть такая возможность.
- Логика и дискретная математика.Тут же основы теории множеств, теории чисел, теории графов. Базовые вещи начинают изучать ещё в школе.
- Математический анализ. С одной стороны, он демонстрирует всю красоту и мощь математики, а с другой – агонию математического образования.
 Раздел сложен в плане понимания, так что тут без посторонней помощи не обойтись. Необходим людям, собирающимся в Computer Science.
Раздел сложен в плане понимания, так что тут без посторонней помощи не обойтись. Необходим людям, собирающимся в Computer Science. - Линейная алгебра. Необходимость освоения раздела зависит от будущих целей. Если вы хотите пойти в GameDev, VR, графику и проч. – линейная алгебра обязательна. Развивает абстрактное мышление, что важно в программировании в целом. Представлять себе многомерные структуры и их взаимосвязь: это очень круто.
- Статистика и комбинаторика. Базовый раздел, который начинают изучать ещё в школе. Темы из этого курса в работе программиста встречаются практически ежедневно.
- Теория алгоритмов. В русском языке принято такое название, однако оно не очень удачное. В оригинале это звучит как “Theory of Computation”. Для изучения потребуется основной мат. аппарат, поэтому начинать с этого раздела не рекомендуется. Зато после изучения вы понимаете, почему алгоритмы выполняются, и компьютеры на самом деле работают всегда.

Как отдельный пункт, стоит вынести криптографию. Она не изучается в школе и даже в некоторых технических вузах. К ней стоит приступать только с хорошей мат. подготовкой (разбираться во всех темах, описанных выше). Однако её необходимо знать, т.к. криптография используется повсеместно: от сообщений в мессенджерах до криптовалют.
Школьная программа:
- Сборник задач по алгебре. 8 – 9 класс. М.Л. Галицкий, А.М. Гольдман. Создан для учащихся в классах физико-математического профиля.
- Алгебра и начала математического анализа. 10 класс. В 2 ч. Ч.1. Учебник (профильный уровень) Мордкович А.Г., Семенов П.В. (2009, 424с.)
- Алгебра и начала математического анализа. 10 класс. В 2 ч. Ч.2. Задачник (профильный уровень). Мордкович А.Г. и др. (2009, 343с.
- Алгебра и начала математического анализа. 11 класс. Учебник. (базовый и углублённый уровни). Мордкович А.Г., Семенов П.В. (2014, 311с.)
- Алгебра и начала математического анализа. 11 класс.
 Задачник. (базовый и углублённый уровни). Мордкович А.Г. и др. (2014, 264с.)
Задачник. (базовый и углублённый уровни). Мордкович А.Г. и др. (2014, 264с.)
Вузовская математика:
Наша статья с подборкой материалов по вузовской математике.
- Задачник Смирнов Ю.М. Сборник задач по аналитической геометрии и линейной алгебре: учеб. пособие для студентов ун-тов, обучающихся по специальностям ”Математика” и ”Приклад. математика”
- Основы высшей алгебры – Сушкевич А. К. (1937 г.)
- Путь в современную математику – Сойер У. У. (1972 г.)
- Курс математического анализа. – Кудрявцев Л.Д.
Комбинаторика:
- Популярная комбинаторика – Н. Я. Виленкин (1975 г.)
- Статистика. Вероятность. Комбинаторика – Я. С. Бродский
- Комбинаторика для программистов – В. Липский
- Комбинаторика – М. Холл (1970 г.)
- Введение в комбинаторный анализ – Дж. Риордан (1963 г.)
Дискретная математика:
- Введение в дискретную математику – С. В. Яблонский
- Графы и их применение – Л.
 Ю. Березина
Ю. Березина - Дискретная математика – Горбатов В.А., Горбатов А.В., Горбатова М.В. (2006 г.)
Видеокурс “Основы линейной алгебры”
Видеокурс по алгоритмам
Mobile Meetup
29 сентября Онлайн Бесплатно
QIWI Server Party SOFT EDITION
22 сентября Онлайн Бесплатно
Yandex Scale 23.09
23 сентября Онлайн Бесплатно
Аутстаффинг от А до Я
24 сентября Онлайн Бесплатно
Junior Python Developer
Москва, от 80000 RUB до 100000 RUB
GoLang-разработчик
Москва, по итогам собеседования
JAVA developer
Новосибирск, от 50000 RUB
+ Показать еще Опубликовать вакансиюМатематика для программистов: 7 крутых YouTube-каналов
Математика для программистов: «Насколько важна?», «Какие разделы?», «Как ее учить?» и другие злободневные вопросы, на которые ответит наша подборка.
13 ресурсов, чтобы выучить математику
Среди разработчиков часто возникают споры о том, необходимо ли изучать математику. Если вас мучает ее незнание, то скорее читайте нашу статью.
4 книги, которые разбудят в вас математика
Программисту без математики никуда, даже если вы еще сомневаетесь в этом. Однако понять ее, не имея необходимых знаний и желания, достаточно сложно.
Основные правила математики с примерами. 7 класс Алгебра.
Основные правила математики с примерами. 7 класс Алгебра.
Содержание
- Уравнения. Равносильные уравнения. Свойства
- Линейное уравнение
- Одночлены и многочлены
- Формулы сокращенного умножения
- Степень. Свойства степени с целым показателем
- Функция. Область определения и область значений функции
- Линейная функция, её график и свойства
- Системы линейных уравнений с двумя переменными
- Графический метод решения системы двух линейных уравнений с двумя переменными
- Решение системы двух линейных уравнений с двумя переменными методом подстановки
- Решение систем линейных уравнений методом сложения
Уравнения.
 Равносильные уравнения. Свойства
Равносильные уравнения. СвойстваКорень уравнения
- Корнем уравнения называют значение переменной, при котором уравнение обращается в верное числовое равенство.
- Решить уравнение означает найти все его корни или убедиться, что их вообще нет. Также можно сказать, что решить уравнение — это значит найти множество его корней.
2 x + 6 =36x = 15 —корень уравнения, поскольку2 · 15 + 6 =3636 = 36 —верное равенство.5x — 5x = 100 —не имеет корней, посколькуx(5 — 5)∥0 = 100 0 = 100 — неверно.
Равносильные уравнения
Два уравнения называют равносильными, если они имеют одно и тоже множество корней.
2x — 5 = 5 ≡равносильно 4x — 10 =10,поскольку x = 5 корень и для 1—го, и для 2—го уравнения.
Свойства уравнений
- Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, равносильное данному.
2x — 5 = 7 +52x — 5 + 5 = 7 + 52x = 12x = 12 : 2x = 6
- Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.

2x — 5 =+5→ 72x = 7 + 52x =12x = 12 : 2x =6
- Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, равносильное данному
12x = 24 : 1212x :12 = 24 : 12x = 2.×5 = 3 · 5×5 · 5 = 3 · 5x = 15
Линейное уравнение
Уравнение вида , где — переменная, и некоторые числа, называют линейным уравнением с одной переменной.
| Значения и | |||
|---|---|---|---|
| Корни уравнения | -любое число | корней нет |
2x = 0, 5y —3 = 12 — линейные уравненияx2 —4 = 0, 5x = 8 —нелинейные уравнения
Одночлены и многочлены
Одночлены
- Выражения, являющиеся произведениями чисел, переменных и их степеней, называют одночленами.
2x, 356x2y, 0,2a20, b, 15 — одночлены.
- Одночлен, содержащий только один отличный от нуля числовой множитель, стоящий на первом месте, а все остальные множители которого — степени с разными основаниями, называют одночленом стандартного вида.
 К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени.
К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени.
2x, 356x2y, 0,2a20 — одночлены стандартного вида.
- Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
2x, 356x2y, 0,2a20.2, 356, 0,2 —коэффициенты.
- Одночлены, имеющие одинаковые буквенные части, называют подобными. Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него. Степень одночлена, являющегося числом, отличным от нуля, считают равной нулю.
2x2y3z , —15x2y3z, 0,5x2y3z —подобные.2x2y3z и 2x2y3 — не подобные.
- Нуль-одночлен степени не имеет.
Многочлены
- Выражение, являющееся суммой нескольких одночленов, называют многочленом.
2x + 3x2y
- Одночлены, из которых состоит многочлен, называют членами многочлена.
2x + 3x2y —многочлен;2x и 3x2y — его одночлены
- Одночлен является частным случаем многочлена.
 Считают, что такой многочлен состоит из одного члена.
Считают, что такой многочлен состоит из одного члена.
Умножение одночлена на многочлен
Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и полученные произведения сложить.
Умножение многочлена на многочлен
Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.
Формулы сокращенного умножения
Разность квадратов двух выражений
Разность квадратов двух выражений равна произведению разности этих выражений и их суммы:
Произведение разности и суммы двух выражений
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:
Квадрат суммы и квадрат разности двух выражений
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения:
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражении:
Преобразование многочлена в квадрат суммы или разности двух выражений
Формулы
позволяют «свернуть» трёхчлен в квадрат двучлена.
Трёхчлен, который можно представить в виде квадрата двучлена, называют полным квадратом.
Сумма и разность кубов двух выражений
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности:
Многочлен называют неполным квадратом суммы.
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:
Многочлен называют неполным квадратом разности.
Степень. Свойства степени с целым показателем
Свойства степени с целым показателем
Для любого и любых целых выполняются равенства:
Для любых , и любого целого выполняются равенства:
Функция. Область определения и область значений функции
Функция
Правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной, называют функцией, а соответствующую зависимость одной пeременной от другой — функциональной.
Обычно независимую переменную обозначают , зависимую обозначают , функцию(правило) — .
Независимую переменную называют аргументом функции. Значение зависимой переменной называют значением функции.
Тогда функциональную зависимость обозначают .
Значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.
Способы задания функции
Описательный, табличный, с помощью формулы, графический.
График функции
Графиком функции называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Линейная функция, её график и свойства
- Функцию, которую можно задать формулой вида , где и — некоторые числа, — независимая переменная, называют линейной.
- Графиком линейной функции является прямая.
- Линейную функцию, заданную формулой , где , называют прямой пропорциональностью.

Системы линейных уравнений с двумя переменными
Уравнение с двумя переменными
Пару значений переменных, обращающую уравнение с двумя переменными в верное равенство, называют решением уравнения с двумя переменными.
Решить уравнение с двумя переменными — значит найти все его решения или показать, что оно не имеет решений.
Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.
Если некоторая фигура является графиком уравнения, то выполняются два условия:
- все решения уравнения являются координатами точек, принадлежащих графику;
- координаты любой точки, принадлежащей графику, — это пара чисел, являющаяся решением данного уравнения.
Графический метод решения системы двух линейных уравнений с двумя переменными
Графический метод решения системы уравнений заключается в следующем:
- построить в одной координатной плоскости графики уравнений, входящих в систему;
- найти координаты всех точек пересечения построенных графиков;
- полученные пары чисел и будут искомыми решениями.

Если графиками уравнений, входящих в систему линейных уравнении, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:
- если прямые пересекаются, то система имеет единственное решение.
- если прямые совпадают, то система имеет бесконечно много решении.
- если прямые параллельны, то система решений не имеет.
Решение системы двух линейных уравнений с двумя переменными методом подстановки
Чтобы решить систему линейных уравнений методом подстановки, следует:
- выразить из любого уравнения системы одну переменную через другую;
- подставить в уравнение системы вместо этой переменной выражение, полученное на первом шаге;
- решить уравнение с одной переменной, полученное на втором шаге;
- подставить найденное значение переменной в выражение, полученное на первом шаге;
- вычислить значение второй переменной;
- записать ответ.
Решение систем линейных уравнений методом сложения
Чтобы решить систему линейных уравнений методом сложения, следует:
- подобрать такие множители для уравнений, чтобы после преобразований коэффициенты при одной из переменной стали противоположными числами
- сложить почленно левые и правые части уравнений, полученных на первом шаге
- решить уравнение с одной переменной, полученной на втором шаге
- подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;
- вычислить значение второй переменной;
- записать ответ.

Данная информация взята из УМК А.Г.Мерзляк, В.Б.Полонский, М.С. Якир
Data Science с нуля: подробный гайд для начинающих
Можно ли погрузиться в мир данных, самостоятельно освоив Data Science с нуля? Спойлер: да. В этом материале мы вместе с Факультетом Искусственного интеллекта GeekUniversity расскажем о навыках и дисциплинах, которые необходимо освоить на пути к карьере Data Scientist.
Чем отличаются Artificial Intelligence, Machine Learning, Deep Learning и Data Science?
Искусственный интеллект фокусируется на создании технологий, которые действуют и реагируют, как человеческий разум. В большинстве областей ИИ всё ещё не может полностью заменить человека.
Машинное обучение — техника, позволяющая смоделировать определённое поведение, основываясь на данных (например обучение нейронной сети, чтобы та могла отличать кошек от собак по фотографиям).
Глубокое обучение нейронных сетей — это создание многослойных нейронных сетей в областях, где требуется более продвинутый анализ, и традиционное машинное обучение с ним не справляется.
Наука о данных — сбор, визуализация и обработка данных, а также принятие решений на их основе.
Чем занимается Data Scientist?
В Data Science обучении стоит отталкиваться от задач, поставленных перед специалистом. При этом задачи Data Scientist могут отличаться в зависимости от сферы деятельности компании. Вот несколько примеров:
- обнаружение аномалий — например нестандартных действий с банковской картой, мошенничества;
- анализ и прогнозирование — показатели эффективности, качество рекламных кампаний;
- системы баллов и оценок — обработка больших объёмов данных для принятия решения, например, о выдаче кредита;
- базовое взаимодействие с клиентом — автоматические ответы в чатах, голосовые помощники, сортировка писем по папкам.
Но для любой из вышеперечисленных задач всегда нужно выполнять примерно одни и те же шаги:
- Сбор данных — поиск источников и способов получения информации, а также сам процесс сбора.

- Проверка — валидация, удаление аномалий.
- Анализ — изучение данных, построение предположений, выводов.
- Визуализация — приведение данных в вид, понятный для человека (графики и диаграммы).
- Результат — принятие решений на основе анализируемых данных, например об изменении маркетинговой стратегии или увеличении бюджета на какую-либо деятельность компании.
Что нужно знать?
Несмотря на то, что знать нужно довольно много, сейчас есть огромное число онлайн-курсов и книг, которые помогут получить нужные навыки гораздо быстрее.
Статистика, математика, линейная алгебра
Вам понадобится изучить фундаментальный курс по теории вероятностей, математический анализ, линейную алгебру и математическую статистику. Математические знания важны, чтобы уметь анализировать результаты применения алгоритмов обработки данных.
Книги по теме:
- «Практическая статистика для специалистов Data Science», П. Брюс, Э. Брюс — подойдёт тем, кто уже имеет начальные знания в статистике;
- «Наука о данных с нуля», Дж.
 Грас — книга для быстрого погружения в профессию, охватывающая большинство необходимых дисциплин;
Грас — книга для быстрого погружения в профессию, охватывающая большинство необходимых дисциплин; - «Нейронные сети. Полный курс», С. Хайкин — материал, раскрывающий математическую составляющую нейросетей.
Машинное обучение
Машинное обучение позволяет научить компьютеры самостоятельно принимать решения, чтобы автоматизировать выполнение определённых задач. По этой причине МО применяется во многих областях, среди которых есть и наука о данных.
Чтобы освоить Data Science с нуля, первым делом нужно изучить три основных раздела машинного обучения:
- Обучение с учителем (Supervised Learning)
Позволяет спрогнозировать результат по заранее размеченным данным. Если нужно предсказать несколько значений (например отличить фотографии машин от самолётов и поездов), то это задача классификации, если одно (скажем, предположить цену квартиры в зависимости от её характеристик) — задача регрессии. - Обучение без учителя (Unsupervised learning)
Здесь входные данные не размечены, то есть ни результат, ни способ обработки данных не известны заранее. В пример можно привести поиск аномалий — необычных транзакций по кредитной карте, ошибочных показаний датчиков и тому подобное.
В пример можно привести поиск аномалий — необычных транзакций по кредитной карте, ошибочных показаний датчиков и тому подобное. - Обучение с подкреплением (Reinforcement learning)
Исходные данные тоже не размечены, но при каждом действии нейросеть получает стимул — положительный или отрицательный. По такому принципу ИИ учат играть в компьютерные игры, например в Dota 2 и Starcraft II.
Книги по теме
- «Машинное обучение. Наука и искусство построения алгоритмов, которые извлекают знания из данных» П. Флах — книга о методах построения моделей и алгоритмах МО.
- «Вероятностное программирование на Python: байесовский вывод и алгоритмы», К. Дэвидсон-Пайлон — рассказывает об алгоритмах обработки данных и развивает аналитические навыки.
- «Введение в машинное обучение с помощью Python», А. Мюллер, С. Гвидо — книга для оттачивания практических навыков машинного обучения.
Что нужно уметь?
Программировать на Python
Большим преимуществом будет знание основ программирования. Но это довольно обширная и сложная область, и чтобы немного упростить её изучение, можно сосредоточиться на одном языке. Python идеально подходит начинающим — у него относительно простой синтаксис, он многофункциональный и часто используется для обработки данных.
Но это довольно обширная и сложная область, и чтобы немного упростить её изучение, можно сосредоточиться на одном языке. Python идеально подходит начинающим — у него относительно простой синтаксис, он многофункциональный и часто используется для обработки данных.
Книги по теме:
- «Python для сложных задач. Наука о данных и машинное обучение», Дж. Вандер Плас — руководство по статистическим и аналитическим методам обработки данных;
- «Python и анализ данных», Уэс Маккинни — пособие по применению Python в науке о данных;
- «Автоматизация рутинных задач с помощью Python», Эл Свейгарт — книга даёт хорошие практические основы для начинающих.
- «Изучаем Python», М. Лутц — учебник с практическим подходом, который подойдёт как новичкам, так и разработчикам с опытом.
После того, как вы изучите основы Python, можете ознакомиться с библиотеками для Дата Сайнс.
Основные библиотеки:
- Numpy
- Scipy
- Pandas
Визуализация:
- Matplotlib
- Seaborn
Машинное обучение и глубокое обучение:
- SciKit-Learn
- TensorFlow
- Theano
- Keras
Обработка естественного языка:
- NLTK
Веб-скрейпинг:
- BeautifulSoup 4
Собирать данные
Data Mining — важный аналитический процесс, предназначенный для исследования данных. Он позволяет находить скрытые паттерны, чтобы получить ранее неизвестную полезную информацию, необходимую для принятия каких-либо решений. Сюда же входит визуализация данных — представление информации в понятном графическом виде.
Он позволяет находить скрытые паттерны, чтобы получить ранее неизвестную полезную информацию, необходимую для принятия каких-либо решений. Сюда же входит визуализация данных — представление информации в понятном графическом виде.
Книги по теме:
- «Технологии анализа данных: Data Mining, Visual Mining, Text Mining, OLAP» В.В. Степаненко, И.И. Холод — описание методов обработки данных с примерами;
- «Data mining. Извлечение информации из Twitter, LinkedIn, GitHub», М. Рассел. М. Классен — книга, которая учит практическим приёмам анализа данных на примере популярных соцсетей.
Хорошая стратегия — получить базу по Data Science в онлайн-университете, а потом решать более сложные практические задачи на стажировке в компании.
Что дальше?
После того, как вы изучите основы и пройдёте всевозможные Data Science курсы, попробуйте свои силы в открытых проектах или соревнованиях, а затем начинайте искать работу.
Как вы уже поняли, изучение Data Science с нуля — это не только теория. Для практического опыта хорошо подойдёт Kaggle — веб-сайт, где постоянно проводятся соревнования по анализу данных, в которых принимают участие все желающие. Также есть много открытых наборов данных — можете анализировать их и публиковать свои результаты. Также изучайте на Kaggle работы других участников и учитесь на чужом опыте.
Чтобы подтвердить свою квалификацию, зарабатывайте баллы за участие в соревнованиях Kaggle и публикуйте свои проекты на GitHub. Главное — не прекращать обучение и получать удовольствие от того, что вы делаете.
Адаптированный перевод статьи «A Beginner’s Guide To Data Science»
Линейная функция | ЮКлэва
Зависимость одной величины от другой математики называют функций одной величины от другой.
Количество денег — это функция вашей зарплаты (иногда говорят «от зарплаты»).
Вес — это функция от съеденных круассанов. Чем меньше съел, тем меньше весишь.
Расстояние — это функция времени. Чем дольше ты будешь идти, тем больше пройдешь.
Ну а теперь перейдем к одному из видов функций – линейной функции.
Линейная функция
Но сначала официальное определение «Функции» – теперь ты его поймешь. Держи в уме: деньги – зарплата, вес – круассаны, расстояние – время.
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция \( y=f\left( x \right)\), это значит что каждому допустимому значению переменной \( x\) (которую называют «аргументом») соответствует одно значение переменной \( y\) (называемой «функцией»).
Что значит «допустимому»?
Все дело в понятии «область определения»: для некоторых функций не все аргументы «одинаково полезны» — не все можно подставить в зависимость.
Например, для функции \( y=\sqrt{x}\) отрицательные значения аргумента \( x\) – недопустимы.
Ну и вернемся, наконец, к теме данной статьи.
Линейной называется функция вида \( y=kx+b\), где \( k\) и \( b\) – любые числа (они называются коэффициентами).
Другими словами, линейная функция – это такая зависимость, что функция прямо пропорциональна аргументу.
Как думаешь, почему она называется линейной?
Все просто: потому что графиком этой функции является прямая линия. Но об этом чуть позже.
Как уже говорилось в теме «Функции», важнейшими понятиями, связанными с любой функцией, являются ее область определения \( D\left( y \right)\) и область значений \( E\left( y \right)\).
Область значений линейной функции
Тут тоже все просто: поскольку функция прямо пропорциональна аргументу, то чем больше аргумент \( x\), тем больше значение функции \( y\).
Значит, \( y\) так же как и \( x\) может принимать все возможные значения, то есть \( E\left( y \right)=\mathbb{R}\), верно?
Верно, да не всегда. Есть такие линейные функции, которые не могут принимать любые значения. Как думаешь, в каком случае возникают ограничения?
Вспомним формулу: \( y=kx+b\). Какие нужно выбрать коэффициенты \( k\) и \( b\), чтобы значение функции y не зависело от аргумента \( x\)?
А вот какие: \( b\) – любое, но \( k=0\). И правда, каким бы ни был аргумент \( x\), при умножении на \( k=0\) получится \( 0\)!
Тогда функция станет равна \( y=0\cdot x+b=b\), то есть она принимает одно и то же значение при всех \( x\):
\( y = kx + b:{\rm{ }}\left[ \begin{array}{l}E\left( y \right) = \mathbb{R}{\rm{ при }}k \ne 0\\E\left( y \right) = \left\{ b \right\}{\rm{ при }}k = 0.\end{array} \right.\)
Теперь рассмотрим несколько задач на линейную функцию.
График линейной функции
Как я уже упоминал ранее, график такой функции – прямая линия.
Как известно из геометрии, прямую можно провести через две точки (то есть, если известны две точки, принадлежащие прямой, этого достаточно, чтобы ее начертить).
Предположим, у нас есть функция линейная функция \( y=2x+1\). Чтобы построить ее график, нужно вычислить координаты любых двух точек.
То есть нужно взять любые два значения аргумента \( x\) и вычислить соответствующие два значения функции.
Затем для каждой пары \( \left( x;y \right)\) найдем точку в системе координат, и проведем прямую через эти две точки.
Проще всего найти функцию, если аргумент \( x=0:y\left( 0 \right)=2\cdot 0+1=1\).
Итак, первая точка имеет координаты \( \left( 0;1 \right)\).
Теперь возьмем любое другое число в качестве \( x\), например, \( x=1:y\left( 1 \right)=2\cdot 1+1=3\).
Вторая точка имеет координаты \( \left( 1;3 \right)\).
Ставим эти две точки на координатной плоскости:
Теперь прикладываем линейку, и проводим прямую через эти две точки:
Вот и все, график построен!
Давай теперь на этом же рисунке построим еще два графика: \( y={x} -1\) и \( y=-x+2\).
Построй их самостоятельно так же: посчитай значение y для любых двух значений \( x\), отметь эти точки на рисунке и проведи через них прямую.
Должно получиться так:
Коэффициенты линейной функции
Для начала выясним, что делает коэффициент \( \displaystyle b\). Рассмотрим функцию \( \displaystyle y=x+b\), то есть \( \displaystyle k=1\).
Меняя \( \displaystyle b\) будем следить, что происходит с графиком.
Итак, начертим графики для разных значений \( \displaystyle b:b=-2,\text{ -}1,\text{ }0,\text{ }1,\text{ }2\):
Что ты можешь сказать о них? Чем отличаются графики?
Это сразу видно: чем больше \( \displaystyle b\), тем выше располагается прямая.
Более того, заметь такую вещь: график пересекает ось \( \displaystyle \mathbf{y}\) в точке с координатой, равной \( \displaystyle \mathbf{b}\)!
И правда. Как найти точку пересечения графика с осью \( \displaystyle y\)? Чему равен \( \displaystyle x\) в такой точке?
В любой точке оси ординат (это название оси \( \displaystyle y\), если ты забыл) \( \displaystyle x=0\).
Значит достаточно подставить \( \displaystyle x=0\) в функцию, и получим ординату пересечения графика с осью \( \displaystyle y\):
\( \displaystyle y=k\cdot 0+b=b\)
Теперь по поводу \( \displaystyle k\). Рассмотрим функцию \( \displaystyle \left( b=0 \right).\) Будем менять \( \displaystyle k\) и смотреть, что происходит с графиком.
Построим графики для \( \displaystyle k=-3,\text{ -}1,\text{ }0,\text{ }1,\text{ }2:\)
Так, теперь ясно: \( \displaystyle k\) влияет на наклон графика.
Чем больше \( \displaystyle k\) по модулю (то есть несмотря на знак), тем «круче» (под большим углом к оси абсцисс – \( \displaystyle Ox\)) расположена прямая.
Если \( \displaystyle k>0\), график наклонен «вправо», при \( \displaystyle k<0\) – «влево». А когда \( \displaystyle k=0\), прямая располагается вдоль оси абсциссс.
Давай разбираться. Начертим новый график \( \displaystyle y=kx+b\):
Выберем на графике две точки \( \displaystyle A\) и \( \displaystyle B\). Для простоты выберем точку \( \displaystyle A\) на пересечении графика с осью ординат. Точка \( \displaystyle B\) – в произвольном месте прямой, пусть ее координаты равны \( \displaystyle \left( x;y \right)\).
Для простоты выберем точку \( \displaystyle A\) на пересечении графика с осью ординат. Точка \( \displaystyle B\) – в произвольном месте прямой, пусть ее координаты равны \( \displaystyle \left( x;y \right)\).
Рассмотрим прямоугольный треугольник \( \displaystyle ABC\), построенный на отрезке \( \displaystyle AB\) как на гипотенузе.
Из рисунка видно, что \( \displaystyle AC=x\), \( \displaystyle BC=y-b\).
Подставим \( \displaystyle y=kx+b\) в \( \displaystyle BC:BC=y-b=kx+b-b=kx\).
Получается, что \( BC = k \cdot AC{\rm{ }} \Rightarrow {\rm{ }}k = \frac{{BC}}{{AC}} = {\mathop{\rm tg}\nolimits} \alpha \).
Итак, коэффициент \( \displaystyle k\) равен тангенсу угла наклона графика, то есть угла между графиком и осью абсциссс.
Именно поэтому его (коэффициент \( \displaystyle k\)) обычно называют угловым коэффициентом.
В случае, когда \( k < 0,{\mathop{\rm tg}\nolimits} \alpha < 0,\) что соответствует тупому углу:
Если же \( \displaystyle k=0\), тогда и \( {\mathop{\rm tg}\nolimits} \alpha = 0,\) следовательно \( \displaystyle \alpha =0\), то есть прямая параллельна оси абсцисс.
Понимать геометрическое значение коэффициентов очень важно, оно часто используется в различных задачах на линейную функцию.
Решение задачи №3
И снова в первую очередь смотрим на \( \displaystyle b:b=3\). Значит, есть смысл рассматривать только функции a), b) и d).
Теперь посмотрим, каким должен быть угловой коэффициент?
Во-первых, он должен быть отрицательным, значит, выбрасываем ответ b). Остается a) и d).
Чтобы выбрать из них, придется найти тангенс угла наклона графика:
\( \begin{array}{l}k = {\mathop{\rm tg}\nolimits} \alpha = — {\mathop{\rm tg}\nolimits} \beta ;\\tg\beta = \frac{{AC}}{{BC}} = 2{\rm{ }} \Rightarrow {\rm{ }}k = — 2\end{array}\)
Отлично, значит уравнение этой прямой выглядит так:
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
Элементарные функции и их графики (ЕГЭ 18.
 Задача с параметром)
Задача с параметром)Задачи с параметром из ЕГЭ зачастую предполагают исследование функций или хотя бы знание их свойств.
Чтобы научиться исследовать функции, для начала лучше всего научиться строить их графики.
На этом уроке мы рассмотрим основные элементарные функции, научимся строить их графики и узнаем, как на них влияют разные параметры (коэффициенты в функциях).
Мы рассмотрим:
- степенную функцию (линейную, квадратичную, обратную зависимость, корни),
- тригонометрические и обратные тригонометрические,
- показательную и
- логарифмическую функции.
Преобразования графиков функций. ЕГЭ 18. Задачи с параметром.
Научились строить график какой-то функции? А что, если я теперь поменяю один из коэффициентов? Или «заключу» часть функции в модуль?
Можно ли не строить для этого новый график, а просто передвинуть/растянуть старый?
Можно! И на этом уроке мы научимся производить такие трансформации.
Благодаря таким трансформациям мы станем понимать, как выглядят графики функций при всех значениях параметра и научимся решать задачи из ЕГЭ на эту тему.
Линейные уравнения
Сегодня мы познакомимся с линейными уравнениями. Узнаем, как их решать. Разберём и простые примеры, и довольно хитрые. Это один из важнейших уроков в курсе алгебры 7 класса.
Содержание
- Краткая вводная по уравнениям
- Что такое линейное уравнение
- Решение простых уравнений
- Более сложные задачи
- Практика: 3 дополнительных уравнения
1. Краткая вводная по уравнениям
Уравнение — это любое равенство, в котором присутствует хотя бы одна переменная.
Примеры равенств и уравнений.
- Равенство $5-3=2$ — это не уравнение. Да, оно верное, но в нём нет переменной.
- Равенство $5+3=2$ — тоже не уравнение. Оно ещё и само по себе неверное.
- А вот равенство $5-x=2$ или $5+3x=2$ — это уравнения. В них есть переменная $x$.
Мы знаем, что равенства могут быть верными, а могут быть и неверными. Чтобы проверить это, достаточно вычислить выражение, стоящее с каждой стороны от знака «равно» и сравнить полученные значения: если числа слева и справа одинаковые, то равенство верно. А если числа получились разные — равенство неверное.
С уравнениями всё сложнее. Их нельзя просто взять и вычислить, потому что мы не знаем, какое значение принимает переменная. Но если вместо переменной подставить какое-либо число, то уравнение превращается в обычное равенство — и дальше всё легко.
Пример 1. Рассмотрим уравнение: $x+5=8$.
Если подставить $x=10$, получим равенство $10+5=8$, которое, очевидно, не верно.
Но если $x=3$, то получится $3+5=8$ — это верное равенство.
Итак, есть значения переменных, при которых уравнение обращается в верное числовое равенство. А есть значения, при которых равенство получается неверным. Это позволяет ввести понятие корня уравнения.
А есть значения, при которых равенство получается неверным. Это позволяет ввести понятие корня уравнения.
Определение. Корень уравнения — это такое значение переменной, при подстановке которого это уравнение обращается в верное числовое равенство.
Решить уравнение — значит найти все его корни, либо доказать, что таких корней нет.
Существует бесчисленное множество разных уравнений. Одни решаются легко, другие вообще не решаются.
Умение решать такие уравнения — это сложный и очень ценный навык. И сегодня мы начнём осваивать этот навык. Для этого рассмотрим самый простой вид уравнений — линейные.
2. Что такое линейное уравнение
Определение. Линейным уравнением называется уравнение вида $ax+b=0$, где $a$ и $b$ — числа, $x$ — переменная.
Также линейными называют все уравнения, которые сводятся к виду $ax+b=0$ путём элементарных преобразований. {2}} &=0 \\ \frac{5}{x} &=1 \\ \left| x \right| &=64 \end{align}\]
{2}} &=0 \\ \frac{5}{x} &=1 \\ \left| x \right| &=64 \end{align}\]
Ещё раз: линейные уравнения могут выглядеть очень по-разному. Но все они сводятся к виду $ax+b=0$ с помощью элементарных преобразований. По таким преобразованиям у нас будет отдельный урок, а сейчас просто вспомним, что это такое.
2.1. Элементарные преобразования уравнений
Существует ровно три вида преобразований, которые называются элементарными:
- 1.Прибавить к обеим частям уравнения одно и то же выражение.
- 2.Умножить обе части уравнения на одно и то же выражение, отличное от нуля.
- 3.Поменять местами выражения, стоящие слева и справа от знака равенства.
Замечательное свойство всех этих преобразований состоит в том, что они не меняют корни уравнения. Но при этом зачастую позволяют получить уравнение, разрешённое относительно переменной, т.е. уравнение вида $x=a$, где $a$ — некоторое числовое выражение, которое уже не содержит переменную $x$.
Пример 3. Решите уравнение: $x+5=18$.
Вычтем из обеих частей пятёрку:
\[\begin{align}x+5-5 &=18-5 \\ x &=13 \end{align}\]
Получили $x=13$ — это и есть корень.
Иногда переход от уравнения $x+5=18$ к уравнению $x=18-5$ называют «переносом слагаемого их левой части в правую». Мы тоже будем так говорить. Но помните: во «взрослой» алгебре (а именно такой мы будем заниматься с 7 по 11 класс) никаких «переносов» нет. Есть только прибавление слагаемых (пускай и противоположных к исходным).
3. Решение простых уравнений
Итак, у нас есть уравнение $ax+b=0$. Первое, что хочется сделать — это перенести слагаемое $b$ вправо, а затем разделить всё на $a$:
\[\begin{align}ax+b &=0 \\ ax &=-b \\ x &=-\frac{b}{a} \end{align}\]
С первым шагом проблем возникнуть не должно: мы вправе прибавлять к обеим частям уравнения любое выражение, в т.ч. $-b$:
\[\begin{align}ax+b-b &=0-b \\ ax &=-b\end{align}\]
А вот дальше начинаются проблемы. Если коэффициент $a\ne 0$, то снова никаких проблем: мы вправе поделить обе части уравнения на любое ненулевое выражение, в т.ч. на это самое $a\ne 0$:
Если коэффициент $a\ne 0$, то снова никаких проблем: мы вправе поделить обе части уравнения на любое ненулевое выражение, в т.ч. на это самое $a\ne 0$:
\[\begin{align}ax &=-b \\ \frac{ax}{a} &=-\frac{b}{a} \\ x &=-\frac{b}{a} \end{align}\]
Большинство уравнений действительно так и решаются. Взгляните на примеры:
Пример 4. Решите уравнение: $5x=10$.
Просто делим обе части уравнения на 5:
\[\begin{align}5x &=10 \\ x &=2 \end{align}\]
Получили $x=2$ — это и есть искомый корень.
Пример 5. Решите уравнение: $-8x=48$.
Всё то же самое, просто делим на отрицательное число:
\[\begin{align}\frac{-8x}{-8} &=\frac{48}{-8} \\ x &=-6 \end{align}\]
Корень уравнения: $x=-6$. То, что он отрицательный, нисколько не должно нас смущать.
Но что делать вот с такими уравнениями?
\[0\cdot x=10;\quad 0\cdot x=0\]
В первом случае корней вообще нет. Потому что при любом значении $x$ мы умножаем это значение на ноль и получаем ноль, который никак не может равняться 10.
Потому что при любом значении $x$ мы умножаем это значение на ноль и получаем ноль, который никак не может равняться 10.
Во втором уравнении корнем наоборот будут все числа. Потому что опять же любое число при умножении на ноль даст ноль — и именно этот ноль от нас и требуется.
3.1. Основной алгоритм
Итого мы получаем три варианта развития событий. Пусть дано уравнение $ax+b=0$. Тогда:
- 1.Если $a\ne 0$, то уравнение имеет один корень: $x=-{b}/{a}\;$.
- 2.Если $a=0$, но $b\ne 0$, то корней нет.
- 3.Если же $a=0$ и $b=0$, то корни — все числа.
Вот так всё просто. Однако я не хочу, чтобы вы просто зазубрили эти три пункта и бездумно применяли их, когда видите линейное уравнение. Пожалуйста, помните, как и почему возникают эти правила, что такое элементарные преобразования и какие ограничения в них присутствуют (на самом деле ограничение лишь одно: нельзя умножать и делить на ноль).
Пример 6. Решите уравнение: $7x-2=6+3x$.
Вычитаем из обеих частей $3x$ и добавляем 2:
\[\begin{align}7x-2 &=6+3x|-3x+2 \\ 4x &=8 \end{align}\]
Делим обе части уравнения на 4:
\[\begin{align}4x &=8|:4 \\ x &=2 \end{align}\]
Получили корень уравнения $x=2$.
Пример 7. Решите уравнение: $x-11=x+5$.
Вычитаем из обеих частей $x$ и добавляем 11:
\[\begin{align}x-11 &=x+5|-x+11 \\ 0 &=16 \end{align}\]
Последнее равенство уже не является уравнением. Точнее, является, но это будет уравнение вида $0\cdot x=16$. Коэффициент $a=0$, коэффициент $b=16\ne 0$. Следовательно, корней нет.
При решении настоящих уравнений вовсе не обязательно детально комментировать каждый шаг. Достаточно поставить вертикальную черту справа от уравнения и арифметическими знаками пояснить, что именно вы собираетесь делать.
А в будущем и этих пояснений от вас уже не потребуется.
4. Более сложные соображения
В начале урока мы обнаружили, что далеко не все уравнения сводятся к линейным с помощью элементарных преобразований. Существует множество способов преобразовать уравнение, но нам пока доступны лишь три элементарных преобразования и ещё вот такая хитрость:
Существует множество способов преобразовать уравнение, но нам пока доступны лишь три элементарных преобразования и ещё вот такая хитрость:
Теорема. Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю.
Другими словами, если $a\cdot b=0$, то обязательно либо $a=0$, либо $b=0$.
А это уже интересный приём, который значительно расширяет наши возможности!
Пример 8. Решите уравнение: $\left( 2x-6 \right)\left( x+1 \right)=0$.
Произведение равно нулю, поэтому либо $2x-6=0$, либо $x+1=0$. Получили два линейных уравнения. Решим первое из них:
\[\begin{align}2x-6 &=0 \\ 2x &=6 \\ x &=3 \end{align}\]
Теперь решим второе. Тут вообще всё просто:
\[\begin{align}x+1 &=0 \\ x &=-1 \end{align}\]
Итого уравнение имеет два различных корня: $x=3$ и $x=-1$.
Пример 9. Решите уравнение: $x\left( 5x+15 \right)=0$.
Всё то же самое: произведение равно нулю, поэтому либо $x=0$, либо $5x+15=0$.
Первое уравнение уже решено, а второе решается по стандартному алгоритму:
\[\begin{align}5x+15 &=0 \\ 5x &=-15 \\ x &=-3 \end{align}\]
Итого вновь два корня: $x=0$ и $x=-3$.
Разумеется, множителей может быть не два, а три и более. Алгоритм решения от этого никак не меняется: приравнять каждый множитель к нулю и решить каждое полученное уравнение отдельно.
5. Практика
Задача 1
Решите уравнение:
\[6x+72=0\]
Решение. Это линейное уравнение решается через элементарные преобразования:
\[\begin{align}6x+72 &=0 \\ 6x &=-72 \\ x &=-\frac{72}{6} \\ x &=-12 \end{align}\]
Ответ: $x=-12$. Уравнение имеет один корень.
Задача 2
Решите уравнение:
\[5\left( x+9 \right)=5x+45\]
Решение. Сначала раскроем скобки.
Это действие не является элементарным преобразованием уравнений. Оно вообще не относится к уравнениям — оно относился к выражениям с переменной (точнее, как мы позже узнаем, к многочленам):
\[5x+45=5x+45\]
Теперь собираем все слагаемые с переменной $x$ слева, а все числовые слагаемые — справа:
\[\begin{align}5x+45 &=5x+45 \\ 5x-5x &=45-45 \\ 0\cdot x &=0 \end{align}\]
Ответ: все числа. Это уравнение имеет бесконечное множество корней.
Это уравнение имеет бесконечное множество корней.
Задача 3
Решите уравнение:
\[\left( 6-x \right)+\left( 12+x \right)-\left( 3-2x \right)=15\]
Решение. Вновь сначала раскроем все скобки и упростим полученное выражение:
\[\begin{align}\left( 6-x \right)+\left( 12+x \right)-\left( 3-2x \right) &=15 \\ 6-x+12+x-3+2x &=15 \\ 2x+15 &=15 \end{align}\]
Дальше остаётся лишь выполнить элементарные преобразования:
\[\begin{align}2x &=15-15 \\ 2x &=0 \\ x &=0 \end{align}\]
Ответ: $x=0$. Уравнение имеет единственный корень.
Важное замечание
Линейное уравнение вида $ax+b=0$ требует особого внимания при $a=0$. Потому что делить на ноль нельзя.
Однако если $a\ne 0$, но зато $b=0$, то ничего страшного и «нестандартного» не происходит. Получается уравнение $ax=0$, корнем которого является $x=0$.
Смотрите также:
- Иррациональное уравнение: учимся решать методом уединения корня
- Что такое дискриминант? И зачем он нужен для решения квадратных уравнений.

- Тест на тему «Значащая часть числа»
- Иррациональные неравенства. Часть 1
- Процент: налоги и зарплата. Считаем с помощью коэффициентов
- Более сложные задачи на производительность
Линейная алгебра для читфэт-шпаргалки
BY: Мэри Джейн Стерлинг и
Обновлен: 03-14-2022
Из книги: Linear Algebra для Dummies. Купить на Amazon.
Часто используемые значения выбранных триггерных функций
При выполнении преобразований в триггерных функциях, таких как вращения, необходимо использовать числовые значения этих функций. Вот некоторые из наиболее часто используемых углов.
Как выполнить требования к векторному пространству
В линейной алгебре набор элементов называется векторным пространством , когда выполняются определенные требования. Например, пусть набор состоит из векторов u , v и в . Также пусть k и l — действительные числа, и рассмотрим определенные операции ⊕ и ⊗. Множество является векторным пространством, если при выполнении операции ⊕ оно удовлетворяет следующим требованиям:
Например, пусть набор состоит из векторов u , v и в . Также пусть k и l — действительные числа, и рассмотрим определенные операции ⊕ и ⊗. Множество является векторным пространством, если при выполнении операции ⊕ оно удовлетворяет следующим требованиям:
Закрытие. u ⊕ v в наборе.
Коммутативность. и ⊕ v = v ⊕ и.
Ассоциативность. и ⊕ ( v ⊕ w ) = ( u ⊕ v ) ⊕ w.
Элемент идентичности 0. u ⊕ 0 = 0 ⊕ u = u для любого элемента u.
Обратный элемент −u. и ⊕ – и = – и ⊕ и = 0
При операции ⊗ множество является векторным пространством, если оно удовлетворяет следующим требованиям:
Закрытие.
 k ⊗ u в наборе.
k ⊗ u в наборе.Распределение по векторной сумме. к ⊗ ( и ⊕ v ) = к ⊗ и ⊕ к ⊗ v .
Распределение по скалярной сумме. ( k + l ) ⊗ u = k ⊗ u ⊕ l ⊗ u.
Ассоциативность скалярного произведения. к ⊗ ( л ⊗ у ) = ( кл ) ⊗ у.
Умножение на скалярное тождество. 1 ⊗ ед. = ед.
Алгебраические свойства, которые вы должны знать
При работе с линейными алгебраическими выражениями вы можете использовать ряд свойств, включая коммутативные, ассоциативные и дистрибутивные свойства сложения и умножения, а также тождества и обратные значения сложения и умножения:
Команды калькулятора для линейной алгебры
Графические калькуляторы — прекрасные инструменты, помогающие решать процессы линейной алгебры; они позволяют вам истощать заряд батареи, а не мощность мозга. Поскольку существует множество графических калькуляторов, ниже приведены общие инструкции по линейной алгебре, применимые к большинству графических калькуляторов:
Поскольку существует множество графических калькуляторов, ниже приведены общие инструкции по линейной алгебре, применимые к большинству графических калькуляторов:
Для решения систем уравнений графически:
1. Запишите каждое уравнение в у = м х + б форма.
2. Вставьте формулы в меню и .
3. Нарисуйте линии.
4. Используйте инструмент Пересечение, чтобы получить ответ.
Для добавления или вычитания матриц:
1. Вставьте элементы в матрицы A и B.
2. На новом экране нажмите [A] + [B] или [A] – [B] и нажмите Enter.
Чтобы умножить на скаляр:
1. Вставить элементы в матрицу А.
2. На новом экране нажмите скаляр и умножьте: k * [A], и нажмите Enter.
Чтобы перемножить две матрицы:
1.
 Вставьте элементы в матрицы A и B.
Вставьте элементы в матрицы A и B.2. На новом экране нажмите [A] * [B] и нажмите Enter.
Для переключения строк:
1. Вставьте элементы в матрицу.
2. Используйте замену строк : rowSwap ([имя матрицы], первая строка, вторая строка) и нажмите Enter.
Чтобы сложить две строки вместе:
1. Вставьте элементы в матрицу.
2. Используйте добавление строки : « строка +», ([имя матрицы], строка для добавления к целевой строке, целевая строка) и нажмите Enter.
Чтобы прибавить кратность одной строки к другой:
1. Вставьте элементы в матрицу.
2. Используйте строку , сумму – из – , кратную : «* строка +», (множитель, [имя матрицы], умножаемая строка, целевая строка, к которой добавлено несколько), и нажмите Enter.

Чтобы умножить строку на скаляр:
1. Вставьте элементы в матрицу.
2. Используйте строку несколько : «*строка» (множитель, [имя матрицы], строка) и нажмите Enter.
Для создания формы эшелона:
1. Вставьте элементы в матрицу.
2. Используйте ряд – эшелон форма : ref ([имя матрицы]) или сокращенную форму строки-эшелона: rref ([имя матрицы]) и нажмите Enter.
Чтобы возвести матрицу в степень: 9
p и нажмите Enter.Чтобы найти инверсию:
1. Вставьте элементы в матрицу.
2. Используйте обратную операцию x −1 : [имя матрицы] −1 и нажмите Enter.
Для решения систем линейных уравнений:
(Это работает только тогда, когда система имеет единственное решение; оно не работает, когда матрица A вырождена. )
)
1. Запишите каждое уравнение с переменными в том же порядке и константой с другой стороны знака уравнения.
2. Создайте матрицу A, элементами которой являются коэффициенты переменных.
3. Создайте матрицу B, элементами которой являются константы.
4. Нажмите A −1 * B и нажмите Enter.
Результирующий вектор содержит значения переменных по порядку.
Об этой статье
Эта статья из книги:
- Линейная алгебра для чайников,
Об авторе книги:
Мэри Джейн Стерлинг является автором многочисленных книг For Dummies . Она преподает в Университете Брэдли в Пеории, штат Иллинойс, где в течение почти 30 лет читает курсы по алгебре, исчислению и другим математическим дисциплинам.
Эту статью можно найти в категории:
- Алгебра,
Книга по линейной алгебре для чайников
Обзор
Учитесь:
- Решение линейных уравнений алгебры несколькими способами
- Поместите данные в порядок с матрицей
- Определите значения с Detrinants
- Работайте с EIGNELES . практические приложения линейной алгебры
Линейная алгебра заставляет вас чувствовать себя потерянным? Не беспокойтесь — это простое в использовании руководство объясняет, как и почему решать задачи линейной алгебры на простом английском языке. От матриц до векторных пространств и линейных преобразований — вы поймете ключевые понятия и увидите, как они связаны со всем, от генетики до питания и вымирания пятнистых сов.
- Выстроить основы — открыть для себя несколько различных подходов к организации чисел и уравнений и решать системы уравнений алгебраически или с помощью матриц
- Связать векторы и линейные преобразования — связать векторы и матрицы с линейными комбинациями и найти решения однородные системы
- Вычисление определителей — посмотрите, как выполнять функцию определителя на матрицах разных размеров и воспользоваться правилом Крамера
- Оттачивайте свои навыки работы с векторными пространствами — определяйте свойства векторных пространств и их подпространств и наблюдайте за линейным преобразованием в действии
- Работайте с собственными значениями и собственными векторами — определяйте и находите собственные значения и собственные векторы и понимайте, как они взаимодействуют с определенными матрицами
Откройте книгу и найдите:
- Теоретические и практические способы решения задач линейной алгебры
- Определения терминов повсюду и в глоссарии
- Новые взгляды на операции
- Как линейная алгебра связывает вместе векторы, матрицы, определители и линейные преобразования
- Применение матриц и определителей в реальных условиях
Изучите:
- Решите уравнения линейной алгебры несколькими способами
- Поместите данные по порядку с матрицами
- Определить значения с детерминантами
- Работа с eigenvalues и eigenvectors Work EighenValues и EigenVectors .
 линейной алгебры
линейной алгебры Линейная алгебра заставляет вас чувствовать себя потерянным? Не беспокойтесь — это простое в использовании руководство объясняет, как и почему решать задачи линейной алгебры на простом английском языке. От матриц до векторных пространств и линейных преобразований — вы поймете ключевые понятия и увидите, как они связаны со всем, от генетики до питания и вымирания пятнистых сов.
- Выстроить основы — открыть для себя несколько различных подходов к организации чисел и уравнений и решать системы уравнений алгебраически или с помощью матриц
- Связать векторы и линейные преобразования — связать векторы и матрицы с линейными комбинациями и найти решения
однородных систем
- Вычислить определители — посмотреть, как выполнить функцию определителя на матрицах разных размеров и воспользоваться правилом Крамера
- Оттачивайте свои навыки работы с векторными пространствами — определяйте свойства векторных пространств и их подпространств и наблюдайте за линейным преобразованием в действии
- Работайте с собственными значениями и собственными векторами — определяйте и находите собственные значения и собственные векторы и понимайте, как они взаимодействуют с определенными матрицами
- Теоретические и практические способы решения задач линейной алгебры
- Определения терминов в словаре
- Новые взгляды на операции
- Как линейная алгебра связывает вместе векторы, матрицы, определители и линейные преобразования
- Реальные приложения матриц и определителей
Закрытие. u ⊕ v в наборе.
Коммутативность. и ⊕ v = v ⊕ и.
Ассоциативность. и ⊕ ( v ⊕ w ) = ( и ⊕ v ) ⊕ w.
Элемент идентичности 0. u ⊕ 0 = 0 ⊕ u = u для любого элемента u.
Обратный элемент −u. и ⊕ – и = – и ⊕ и = 0
Закрытие.
 k ⊗ u в наборе.
k ⊗ u в наборе.Распределение по векторной сумме. к ⊗ ( и ⊕ v ) = к ⊗ и ⊕ к ⊗ v .
Распределение по скалярной сумме. ( k + l ) ⊗ u = k ⊗ u ⊕ l ⊗ u.
Ассоциативность скалярного произведения. к ⊗ ( л ⊗ у ) = ( кл ) ⊗ у.
Умножение на скалярное тождество. 1 ⊗ ед. = ед.
- Назовите курс Линейная алгебра , но сосредоточьтесь на вещах, называемых матрицами и векторами
- Обучайте таким понятиям, как порядок строк/столбцов, с помощью мнемоники вместо объяснения рассуждений
- Отдайте предпочтение абстрактным примерам (2D-векторы! 3D-векторы!) и избегайте реальных тем до последней недели
- Если 3 фута вперед имеют подъем на 1 фут, то прохождение в 10 раз должно дать 10-кратный подъем (30 футов вперед — это подъем на 10 футов)
- Если 3 фута вперед имеют подъем на 1 фут, а 6 футов имеют подъем на 2 фута, то (3 + 6) футов должны иметь подъем на (1 + 2) фута
- У нас есть куча входных данных для отслеживания
- Нам нужно выполнить предсказуемые линейные операции (наша «мини-арифметика»)
- Генерируем результат, возможно снова преобразуем
Откройте книгу и найдите:
Шпаргалка по линейной алгебре для чайников
Чтобы успешно изучать и решать уравнения линейной алгебры, вам необходимо знать общие числовые значения триггерных функций, какие элементы определяют векторное пространство, основные алгебраические свойства и общие команды с использованием графических калькуляторов для решения задач линейной алгебры.

Статьи из книги
4 результата
Статьи по алгебре
Алгебраические свойства, которые следует знать
При работе с линейными алгебраическими выражениями можно использовать ряд свойств, включая коммутативные, ассоциативные и распределительные свойства сложения и умножения. , а также тождества и обратные при сложении и умножении:
Статьи по алгебре
Часто используемые значения выбранных триггерных функций
При выполнении преобразований в триггерных функциях, таких как вращения, необходимо использовать числовые значения этих функций. Вот некоторые из наиболее часто используемых углов.
Статьи по алгебре
Как выполнить требования к векторному пространству
В линейной алгебре набор элементов называется векторным пространством , когда выполняются определенные требования.
 Например, пусть набор состоит из векторов u , v и w . Также пусть k и l — действительные числа, и рассмотрим определенные операции ⊕ и ⊗. Множество является векторным пространством, если при выполнении операции ⊕ оно удовлетворяет следующим требованиям:
Например, пусть набор состоит из векторов u , v и w . Также пусть k и l — действительные числа, и рассмотрим определенные операции ⊕ и ⊗. Множество является векторным пространством, если при выполнении операции ⊕ оно удовлетворяет следующим требованиям:При операции ⊗ множество является векторным пространством, если оно удовлетворяет следующим требованиям:
Интуитивное руководство по линейной алгебре – BetterExplained
Несмотря на два занятия по линейной алгебре, мои знания состояли из «Матрицы, определители, собственное что-то что-то».

Почему? Что ж, давайте попробуем этот формат курса:
Выжившие – физики, программисты графики и прочие мазохисты. Мы упустили ключевую мысль:
Линейная алгебра дает вам мини-таблицы для ваших математических уравнений. 92$.
«Линейная алгебра» означает, грубо говоря, «линейные отношения». Давайте немного уточним.
Прямые линии предсказуемы. Представьте себе крышу: продвиньтесь вперед на 3 фута по горизонтали (относительно земли) и вы можете подняться на 1 фут по высоте (Уклон! Подъем/бег = 1/3). Продвиньтесь вперед на 6 футов, и вы ожидаете подъема на 2 фута. Сравните это с восхождением на купол: каждый горизонтальный фут вперед поднимает вас на разную величину.

Линии красивые и предсказуемые:
В математических терминах операция F является линейной, если масштабирование входных данных масштабирует выходные данные, а добавление входных данных добавляет выходные данные:
В нашем примере $F(x)$ вычисляет подъем при движении вперед на x футов, свойства: 92 доллара — это 400. Мы удвоили ввод, но в четыре раза увеличили вывод.
Удивительно, но регулярное сложение тоже не является линейным. Рассмотрим функцию «добавить три» $F(x) = x + 3$:
Мы удвоили ввод и не удвоили вывод. (Да, $F(x) = x + 3$ оказывается уравнением для линии со смещением , но оно все еще не «линейно», потому что $F(10) \neq 10 \cdot F(1)$.
 2$. Ограничение себя линейными операциями имеет свои преимущества.
2$. Ограничение себя линейными операциями имеет свои преимущества.Организация ввода и операций
Большинство курсов поразят вас деталями матрицы. «Хорошо, дети, давайте учиться говорить. Выберите подлежащее, глагол и дополнение. Далее спрягайте глагол. Затем добавьте предлоги…»
Нет! Грамматика не в центре внимания. Какова ключевая идея?
Хорошо. Во-первых, как мы должны отслеживать набор входных данных? Как насчет списка:
x у г
Неплохо. Мы могли бы написать и это (x, y, z) — цепляйтесь за эту мысль.
Далее, как мы должны отслеживать наши операции? Помните, у нас есть только «мини-арифметика»: умножение на константу с окончательным сложением. Если наша операция $F$ ведет себя так:
Мы могли бы сократить всю функцию до (3, 4, 5).
 Мы знаем, что нужно умножать первый вход на первое значение, второй вход на второе значение, третий вход на третье значение и складывать результаты.
Мы знаем, что нужно умножать первый вход на первое значение, второй вход на второе значение, третий вход на третье значение и складывать результаты.Нужен только первый ввод?
Давайте оживим: как мы должны обрабатывать несколько наборов входных данных? Допустим, мы хотим запустить операцию F как для (a, b, c), так и для (x, y, z). Мы могли бы попробовать это:
Но это не сработает: F ожидает 3 входа, а не 6. Мы должны разделить входы на группы:
1-й вход 2-й вход -------------------- х по с я
Гораздо аккуратнее.
А как мы можем прогнать один и тот же ввод через несколько операций? Имейте строку для каждой операции:
Ф: 3 4 5 Г: 3 0 0
Аккуратный. Мы организуемся: вводы в вертикальных столбцах, операции в горизонтальных рядах.
Визуализация Матрицы
Слов недостаточно. Вот как я визуализирую входы, операции и выходы:
Представьте себе «заливку» каждого входа через каждую операцию:
Когда вход проходит операцию, он создает элемент вывода.
 В нашем примере ввод (a, b, c) идет против операции F и выводит 3a + 4b + 5c. Это противоречит операции G и дает 3a + 0 + 0,9.0005
В нашем примере ввод (a, b, c) идет против операции F и выводит 3a + 4b + 5c. Это противоречит операции G и дает 3a + 0 + 0,9.0005Время для красной таблетки. Матрица — это сокращение для наших диаграмм:
Матрица — это одна переменная, представляющая электронную таблицу входных данных или операций.
Хитрость № 1: Порядок чтения
Вместо потока ввода => матрицы => вывода мы используем функциональную запись, например y = f(x) или f(x) = y. Обычно мы пишем матрицу с заглавной буквы (F), а один входной столбец — со строчной буквы (x). Поскольку у нас есть несколько входов (A) и выходов (B), они тоже считаются матрицами:
Хитрость № 2: Нумерация
Размер матрицы измеряется как RxC: количество строк, затем количество столбцов и сокращение «m x n» (я слышал, «r x c» было бы легче запомнить). Элементы в матрице обозначаются одинаково: a ij — это i-я строка и j-й столбец (я слышал, «i» и «j» легко перепутать на доске).
 Мнемоники в порядке с контекстом , и вот что я использую:
Мнемоники в порядке с контекстом , и вот что я использую:- RC, например Roman Centurion или RC Cola
- Используйте L-образную форму. Отсчитайте L, затем через
Почему имеет смысл заказывать RC? Наша операционная матрица 2×3, а наша входная матрица 3×2. Запись их вместе:
[Матрица операций] [Матрица ввода] [количество операций x размер операции] [размер входных данных x количество входных данных] [м х п] [п х д] = [м х д] [2 х 3] [3 х 2] = [2 х 2]
Обратите внимание, что матрицы касаются «размера операции» и «размера ввода» (n = p). Они должны совпадать! Если наши входы имеют 3 компонента, наши операции должны ожидать 3 элемента. На самом деле мы можем только умножают матрицы, когда n = p.
Выходная матрица содержит m строк операций для каждого входа и q входов, что дает матрицу «m x q».
Fancier Operations
Давайте освоимся с операциями. Предполагая 3 входа, мы можем составить несколько матриц с 1 операцией:
- Сумматор: [1 1 1]
- Усреднитель: [1/3 1/3 1/3]
«Сумма» — это просто a + b + c.
 «Усреднение» аналогично: (a + b + c)/3 = a/3 + b/3 + c/3.
«Усреднение» аналогично: (a + b + c)/3 = a/3 + b/3 + c/3.Попробуйте эти однострочные:
- Только первый ввод: [1 0 0]
- Только второй ввод: [0 1 0]
- Только третий ввод: [0 0 1]
А если объединить их в единую матрицу:
[1 0 0] [0 1 0] [0 0 1]
Вау — это «матрица идентичности», которая копирует 3 входа в 3 выхода без изменений. Как насчет этого парня?
[1 0 0] [0 0 1] [0 1 0]
Он переупорядочивает входные данные: (x, y, z) становится (x, z, y).
А этот?
[2 0 0] [0 2 0] [0 0 2]
Он удвоитель ввода. Мы могли бы переписать его в
2*I(тождественная матрица), если бы захотели.И да, когда мы решим рассматривать входные данные как векторные координаты, матрица операций преобразует наши векторы. Вот несколько примеров:
- Масштаб: сделать все входные данные больше/меньше
- Перекос: сделать некоторые входные данные больше/меньше
- Перевернуть: сделать входы отрицательными
- Повернуть: создать новые координаты на основе старых (восток становится севером, север становится западом и т.
 д.)
д.)
Это геометрические интерпретации умножения и способы деформации векторного пространства. Просто помните, что векторы — это примеров данных для изменения.
Невекторный пример: портфели фондового рынка
Давайте попрактикуемся в линейной алгебре в реальном мире:
- Входные данные: портфели акций с долларами в акциях Apple, Google и Microsoft
- Операции: изменение стоимости компании после новостного события
- Вывод: обновленные портфели
И бонусный вывод: давайте сделаем новый портфель со списком чистой прибыли/убытка от события.
Обычно мы отслеживаем это в электронной таблице. Давайте научимся думать с помощью линейной алгебры:
Входной вектор может быть (\$Apple, \$Google, \$Microsoft), показывающим стоимость каждой акции в долларах. (О! Эти значения в долларах могут быть получены из другой матрицы , которая умножает количество акций на их цену. Представьте себе!)
Должны быть 4 операции вывода: Обновить значение Apple, Обновить значение Google, Обновить значение Microsoft, Вычислить прибыль
Визуализируйте проблему.
 Представьте, что вы выполняете каждую операцию:
Представьте, что вы выполняете каждую операцию:Ключ в понимании , почему мы настраиваем матрицу именно так, а не вслепую перемалываем числа.
Понял? Давайте представим сценарий.
Предположим, запущен секретный iDevice: Apple подскочила на 20%, Google упала на 5%, а Microsoft осталась прежней. Мы хотим скорректировать стоимость каждой акции, используя что-то похожее на матрицу идентичности:
New Apple [1.2 0 0] Новый Гугл [0 0,95 0] Новая Майкрософт [0 0 1]
Новое значение Apple является исходным, увеличенным на 20% (Google = уменьшение на 5%, Microsoft = без изменений).
Ой, подождите! Нам нужна общая прибыль:
Общее изменение = (0,20 * Apple) + (-,05 * Google) + (0 * Microsoft)
Наша конечная операционная матрица:
New Apple [1,2 0 0] Новый Google [0 0,95 0] Новая Майкрософт [0 0 1] Общая прибыль [0,20 - 0,05 0]
Имеет смысл? Три входа входят, четыре выхода выходят. Первые три операции представляют собой «модифицированную копию», а последняя объединяет изменения.

Теперь давайте добавим портфели для Алисы \$1000, \$1000, \$1000) и Боба \$500, \$2000, \$500). Мы можем обработать числа вручную или использовать Wolfram Alpha (расчет):
(Примечание: вводимые данные должны быть в столбцах, но проще вводить строки. Операция транспонирования, обозначенная t (тау), преобразует строки в столбцы.)
Окончательные цифры: Алиса имеет 1200 долларов в AAPL, 950 долларов в GOOG, 1000 долларов в MSFT, с чистой прибылью в 150 долларов. У Боба 600 долларов в AAPL, 1900 долларов в GOOG и 500 долларов в MSFT с чистой прибылью в 0 долларов.
Что происходит? Мы занимаемся математикой в собственной электронной таблице. Линейная алгебра появилась в 1800-х годах, а электронные таблицы были изобретены в 1980-х. Я виню в пробеле плохое образование в области линейной алгебры.
Исторические заметки: решение одновременных уравнений
В начале таблицы чисел (еще не «матрица») использовались для учета линейных систем:
становится
вычитание строк в матрице и вывод вместо перезаписи полных уравнений.
 По мере того, как матрица превращается в единичную матрицу, значения x, y и z раскрываются на выходе.
По мере того, как матрица превращается в единичную матрицу, значения x, y и z раскрываются на выходе.Этот процесс, называемый методом исключения Гаусса-Жордана, экономит время. Однако линейная алгебра в основном касается матричных преобразований, а не решения больших наборов уравнений (это все равно, что использовать Excel для списка покупок).
Терминология, детерминанты и собственные элементы
Слова имеют технические категории для описания их использования (существительные, глаголы, прилагательные). Аналогичным образом можно разделить матрицы.
Такие описания, как «верхнетреугольная», «симметричная», «диагональная» являются формой матрицы и влияют на их преобразования.
Определитель — это «размер» выходного преобразования. Если вход был единичным вектором (представляющим площадь или объем равным 1), определителем является размер преобразованной площади или объема. Определитель 0 означает, что матрица «деструктивна» и не может быть обращена (аналогично умножению на ноль: информация была потеряна).

Собственный вектор и собственное значение представляют «оси» преобразования.
Представьте себе вращение земного шара: каждое место смотрит в новом направлении, кроме полюсов.
«Собственный вектор» — это вход, который не меняет направление при прохождении через матрицу (он указывает «вдоль оси»). И хотя направление не меняется, размер может измениться. Собственное значение — это величина, на которую собственный вектор увеличивается или уменьшается при прохождении через матрицу.
(Моя интуиция здесь слаба, и я хотел бы изучить больше. Вот хорошая диаграмма и видео.)
Матрицы как входы
Странная мысль: мы можем рассматривать операционную матрицу как входы!
Думайте о рецепте как о списке команд ( Добавить 2 стакана сахара, 3 стакана муки… ).
Что делать, если нам нужна метрическая версия? Возьмите инструкции, обработайте их как текст и преобразуйте единицы измерения. Рецепт «вводится» для модификации.
 Когда мы закончим, мы можем снова следовать инструкциям.
Когда мы закончим, мы можем снова следовать инструкциям.Матрица операций похожа: команды для изменения. Применение одной матрицы операций к другой дает новую матрицу операций, которая применяет и преобразований по порядку. 93$.
Можем ли мы использовать обычное дополнение, пожалуйста?
Да, потому что вы вежливо попросили. Наша «мини-арифметика» кажется ограничивающей: умножения, но без сложения? Время расширить наши мозги.
Представьте, что к нашему вводу добавляется фиктивная запись 1: (x, y, z) становится (x, y, z, 1).
Теперь наша операционная матрица имеет дополнительное известное значение для игры! Если нам нужно
x + 1, мы можем написать:[1 0 0 1]
И
x + y - 3будет:[1 1 0 -3]
Ура!
Хотите интересное объяснение? Мы притворяемся, что наш ввод существует в измерении на 1 выше, и ставим «1» в этом измерении. Мы искажаем то высшее измерение, которое выглядит как слайд в текущем.
 Например: возьмите ввод (x, y, z, 1) и выполните его:
Например: возьмите ввод (x, y, z, 1) и выполните его:[1 0 0 1] [0 1 0 1] [0 0 1 1] [0 0 0 1]
Результат (x + 1, y + 1, z + 1, 1). Игнорируя 4-е измерение, каждый ввод получил +1. Мы сохраняем фиктивную запись и можем сделать больше слайдов позже.
В конце концов, мини-арифметика не так уж ограничена.
Далее
Я упустил из виду некоторые тонкости линейной алгебры, и меня это не слишком беспокоит. Почему?
Эти метафоры помогают мне думать с помощью матриц больше, чем классы, которые я «сдал». Наконец-то я могу ответить на вопрос «Почему линейная алгебра полезна?» с «Почему электронные таблицы полезны?»
Нет, если только вам не нужен инструмент для решения почти всех реальных проблем. Спросите бизнесмена, что лучше: он пожертвует почку или будет навсегда забанен в Excel. Это влияние линейной алгебры, которое мы упустили из виду: эффективная запись для включения электронных таблиц в наши математические уравнения.
Счастливая математика.

Другие сообщения из этой серии
- Наглядное интуитивное руководство по воображаемым числам
- Интуитивная арифметика с комплексными числами
- Понимание того, почему сложное умножение работает
- Интуитивное руководство по углам, градусам и радианам
- Интуитивное понимание формулы Эйлера
- Интерактивное руководство по преобразованию Фурье
- Интуитивное руководство по свертке
- Интуитивное понимание синусоидальных волн
- Интуитивное руководство по линейной алгебре
- Интуиция программиста для умножения матриц
- Мнимое умножение против мнимых показателей
- Интуитивное руководство по гиперболическим функциям
Линейные уравнения
линейное уравнение является уравнением прямой линии
Все линейные уравнения:
у = 2х + 1, 5х = 6 + 3у у/2 = 3 – х Рассмотрим более подробно один пример:
Пример:
y = 2x + 1 представляет собой линейное уравнение:График y = 2x+1 представляет собой прямую линию
- Когда x увеличивается, y увеличивается в два раза быстрее , поэтому нам нужно 2x
- Когда x равен 0, y уже равен 1.
 Так что +1 тоже нужен
Так что +1 тоже нужен- Итак: у = 2х + 1
Вот несколько примеров значений:
| x | у = 2х + 1 |
|---|---|
| -1 | у = 2 × (-1) + 1 = -1 |
| 0 | у = 2 × 0 + 1 = 1 |
| 1 | у = 2 × 1 + 1 = 3 |
| 2 | у = 2 × 2 + 1 = 5 |
Убедитесь сами, что эти точки являются частью линии выше!
Различные формы
Существует множество способов записи линейных уравнений, но обычно они содержат константы (например, “2” или “с”) и должны иметь простые переменные (например, “х” или “у”).
Примеры: Это линейные уравнения:
| у = 3х – 6 | ||
| у – 2 = 3(х + 1) | ||
| у + 2х – 2 = 0 | ||
| 5х = 6 | ||
| г/2 = 3 |
Но переменные (такие как “x” или “y”) в линейных уравнениях имеют НЕ :
- Экспоненты (например, 2 дюйма x 2 )
- Квадратные корни, кубические корни и т.
 д.
д.
Примеры: Это
НЕ линейные уравнения:| г 2 – 2 = 0 | ||
| 3√х – у = 6 | ||
| х 3 /2 = 16 |
Форма пересечения уклонов
Наиболее распространенной формой является уравнение пересечения наклона прямой линии:
| Наклон (или градиент) | Д Перехват |
Пример: y = 2x + 1
- Уклон: м = 2
- Пересечение: б = 1
Играй с этим!Вы можете увидеть влияние различных значений m и b в разделе Исследование прямолинейного графика |
Форма «точка-наклон»
Другой распространенной является форма «точка-наклон» уравнения прямой линии:
у – у 1 = м(х – х 1 ) |
Пример: y − 3 = (¼)(x − 2)
Оно имеет форму y – y 1 = m(x – x 1 ) где:
- y 1 = 3
- м = ¼
- х 1 = 2
Общая форма
А также есть Общая форма уравнения прямой:
Топор + В + С = 0 |
| (A и B не могут быть одновременно равны 0) |
Пример: 3x + 2y − 4 = 0
Оно имеет форму Ax + By + C = 0 где:
- A = 3
- Б = 2
- С = -4
Существуют и другие, менее распространенные формы.
В виде функции
Иногда линейное уравнение записывается в виде функции с f(x) вместо y:
| y = 2x − 3 |
| f(x) = 2x − 3 |
| Это одно и то же! |
И функции не всегда пишутся с использованием f(x):
| у = 2х – 3 |
| w(u) = 2u − 3 |
| h(z) = 2z − 3 |
| Это тоже самое! |
Функция тождества
Существует специальная линейная функция, называемая «функция тождества»:
f(x) = x
А вот ее график:
1)
Это называется “Идентификация”, потому что получается идентичен тому, что входит:
| В | Выход |
|---|---|
| 0 | 0 |
| 5 | 5 |
| −2 | −2 |
. ..и т. д. ..и т. д. | …и т. д. |
Постоянные функции
Еще один особый тип линейной функции — постоянная функция… это горизонтальная линия:
f(x) = C
Независимо от того, какое значение “x”, f(x) всегда равно некоторому постоянному значению.
Использование линейных уравнений
Вы можете прочитать о том, что можно делать с линиями:
- Нахождение середины отрезка линии
- Поиск параллельных и перпендикулярных линий
- Нахождение уравнения прямой по 2 точкам
Нежное введение в линейную алгебру
Джейсон Браунли on 26 января 2018 г. в линейной алгебре
Последнее обновление: 9 августа 2019 г.
Что такое линейная алгебра?
Линейная алгебра — это область математики, которая, по общему мнению, является необходимым условием для более глубокого понимания машинного обучения.
Несмотря на то, что линейная алгебра — обширная область со множеством эзотерических теорий и открытий, базовые инструменты и обозначения, взятые из этой области, полезны для специалистов-практиков в области машинного обучения. Имея прочную основу того, что такое линейная алгебра, можно сосредоточиться только на хороших или важных частях.
В этом руководстве вы узнаете, что такое линейная алгебра с точки зрения машинного обучения.
После прохождения этого урока вы будете знать:
- Линейная алгебра — это математика данных.
- Линейная алгебра оказала заметное влияние на область статистики.
- Линейная алгебра лежит в основе многих практических математических инструментов, таких как ряды Фурье и компьютерная графика.
Начните свой проект с моей новой книги «Линейная алгебра для машинного обучения», включающей пошаговые руководства и файлы исходного кода Python для всех примеров.
Начнем.
Нежное введение в линейную алгебру
Фотография Стива Кори, некоторые права защищены.
Обзор учебника
Этот туториал разделен на 4 части; они:
- Линейная алгебра
- Числовая линейная алгебра
- Линейная алгебра и статистика
- Приложения линейной алгебры
Нужна помощь с линейной алгеброй для машинного обучения?
Пройдите мой бесплатный 7-дневный экспресс-курс по электронной почте прямо сейчас (с образцом кода).
Нажмите, чтобы зарегистрироваться, а также получить бесплатную электронную версию курса в формате PDF.
Линейная алгебра
Линейная алгебра — это раздел математики, но правда в том, что линейная алгебра — это математика данных. Матрицы и векторы — это язык данных.
Линейная алгебра касается линейных комбинаций. То есть, используя арифметику для столбцов чисел, называемых векторами, и массивов чисел, называемых матрицами, для создания новых столбцов и массивов чисел. Линейная алгебра — это изучение прямых и плоскостей, векторных пространств и отображений, необходимых для линейных преобразований.
Линейная алгебра — это изучение прямых и плоскостей, векторных пространств и отображений, необходимых для линейных преобразований.
Это относительно молодая область исследований, которая первоначально была формализована в 1800-х годах для поиска неизвестных в системах линейных уравнений. Линейное уравнение — это просто набор терминов и математических операций, где некоторые термины неизвестны; например:
у = 4 * х + 1
у = 4 * х + 1 |
Подобные уравнения являются линейными в том смысле, что они описывают линию на двумерном графике. Линия возникает из-за подстановки различных значений в неизвестный x, чтобы выяснить, что уравнение или модель делает со значением y.
Мы можем составить систему уравнений одинаковой формы с двумя или более неизвестными; например:
у = 0,1 * х1 + 0,4 * х2 у = 0,3 * х1 + 0,9 * х2 у = 0,2 * х1 + 0,3 * х2 …
y = 0,1 * x1 + 0,4 * x2 y = 0,3 * x1 + 0,9 * x2 y = 0,2 * x1 + 0,3 * x2 . |
Столбец значений y может быть взят как вектор-столбец выходных данных уравнения. Два столбца значений с плавающей запятой являются столбцами данных, скажем, a1 и a2, и могут быть взяты как матрица A. Два неизвестных значения x1 и x2 могут быть взяты как коэффициенты уравнения и вместе образуют вектор неизвестных б решить. Мы можем записать это компактно, используя обозначения линейной алгебры, как:
у = А . б
у = А . б |
Задачи этой формы обычно сложны для решения, потому что неизвестных больше (здесь у нас 2), чем уравнений для решения (здесь у нас 3). Кроме того, часто не существует единой линии, которая безошибочно удовлетворяла бы всем уравнениям. Системы, описывающие часто интересующие нас проблемы (например, линейная регрессия), могут иметь бесконечное количество решений.
Это дает небольшое представление о самой сути линейной алгебры, которая интересует нас как специалистов по машинному обучению. Большая часть остальных операций направлена на облегчение понимания и решения этой и подобных проблем.
Большая часть остальных операций направлена на облегчение понимания и решения этой и подобных проблем.
Числовая линейная алгебра
Применение линейной алгебры в компьютерах часто называют числовой линейной алгеброй.
«Числовая» линейная алгебра — это действительно прикладная линейная алгебра.
– Страница ix, Численная линейная алгебра, 1997.
Это больше, чем просто реализация операций линейной алгебры в библиотеках кода; это также включает в себя тщательное решение проблем прикладной математики, таких как работа с ограниченной точностью цифровых компьютеров с плавающей запятой.
Компьютеры хорошо выполняют вычисления линейной алгебры, и большая часть зависимости от графических процессоров (GPU) современных методов машинного обучения, таких как глубокое обучение, связана с их способностью быстро выполнять операции линейной алгебры.
Эффективные реализации векторных и матричных операций были первоначально реализованы на языке программирования FORTRAN в 1970-х и 1980-х годах, и большое количество кода или кода, перенесенного из этих реализаций, лежит в основе большей части линейной алгебры, выполняемой с использованием современных языков программирования, таких как Python.
Три популярные библиотеки числовой линейной алгебры с открытым исходным кодом, которые реализуют эти функции:
- Пакет линейной алгебры или LAPACK.
- Подпрограммы базовой линейной алгебры, или BLAS (стандарт для библиотек линейной алгебры).
- Программное обеспечение для автоматической настройки линейной алгебры или ATLAS.
Часто, когда вы вычисляете операции линейной алгебры прямо или косвенно с помощью алгоритмов более высокого порядка, ваш код, скорее всего, использует одну из этих или подобных библиотек линейной алгебры. Название одной или нескольких из этих базовых библиотек может быть вам знакомо, если вы установили или скомпилировали любую из числовых библиотек Python, таких как SciPy и NumPy.
Линейная алгебра и статистика
Линейная алгебра является ценным инструментом в других разделах математики, особенно в статистике.
Обычно ожидается, что студенты, изучающие статистику, хотя бы один семестр изучали линейную алгебру (или прикладную алгебру) на уровне бакалавриата.
– Страница xv, Линейная алгебра и матричный анализ для статистики, 2014.
Важно учитывать влияние линейной алгебры, учитывая фундаментальную связь обеих областей с областью прикладного машинного обучения.
Некоторые четкие отпечатки линейной алгебры в статистике и статистических методах включают:
- Использование векторной и матричной записи, особенно с многомерной статистикой.
- Решения метода наименьших квадратов и взвешенного метода наименьших квадратов, например, для линейной регрессии.
- Оценки среднего и дисперсии матриц данных.
- Ковариационная матрица, играющая ключевую роль в полиномиальных распределениях Гаусса.
- Анализ главных компонентов для сокращения данных, объединяющий многие из этих элементов.
Как видите, современная статистика и анализ данных, по крайней мере, в том, что касается интересов специалиста по машинному обучению, зависят от понимания и инструментов линейной алгебры.
Приложения линейной алгебры
Поскольку линейная алгебра — это математика данных, инструменты линейной алгебры используются во многих областях.
В своей классической книге на тему «Введение в линейную алгебру» Гилберт Стрэнг предлагает главу, посвященную приложениям линейной алгебры. В нем он демонстрирует конкретные математические инструменты, основанные на линейной алгебре. Кратко:
- Матрицы в машиностроении, такие как ряд пружин.
- Графики и сети, такие как анализ сетей.
- Марковские матрицы, население и экономика, такие как рост населения.
- Линейное программирование, метод симплексной оптимизации.
- Ряд Фурье: линейная алгебра для функций, широко используемых в обработке сигналов.
- Линейная алгебра для статистики и вероятности, например метод наименьших квадратов для регрессии.
- Компьютерная графика, например различные переводы, масштабирование и поворот изображений.
Еще одним интересным применением линейной алгебры является то, что это тип математики, используемый Альбертом Эйнштейном в некоторых частях его теории относительности. В частности, тензоры и тензорное исчисление. Он также ввел в физику новый тип нотации линейной алгебры, названный нотацией Эйнштейна или соглашением о суммировании Эйнштейна.
В частности, тензоры и тензорное исчисление. Он также ввел в физику новый тип нотации линейной алгебры, названный нотацией Эйнштейна или соглашением о суммировании Эйнштейна.
Учебники по линейной алгебре
Если вам нужна помощь, чтобы начать работу с линейной алгеброй, взгляните на некоторые из этих руководств:
- Линейная алгебра для машинного обучения (7-дневный мини-курс)
- Шпаргалка по линейной алгебре для машинного обучения
- Основы математической записи для машинного обучения
Удлинители
В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.
- Найдите в книгах и Интернете 5 цитат, определяющих область линейной алгебры.
- Найдите и перечислите еще 5 приложений или применений линейной алгебры в области вероятностей и статистики.
- Перечислите и напишите краткие определения для 10 терминов, используемых при описании линейной алгебры.

Если вы изучите какое-либо из этих расширений, я хотел бы знать.
Дополнительное чтение
В этом разделе содержится больше ресурсов по теме, если вы хотите углубиться.
Книги
- Введение в линейную алгебру, 2016.
- Численная линейная алгебра, 1997.
- Линейная алгебра и матричный анализ для статистики, 2014.
Артикул
- Линейная алгебра в Википедии
- Категория линейной алгебры в Википедии
- Линейная алгебра Список тем в Википедии
- ЛАПАК в Википедии
- Основные подпрограммы линейной алгебры в Википедии
- Автоматически настраиваемое программное обеспечение для линейной алгебры в Википедии
- Обозначение Эйнштейна в Википедии
- Математика общей теории относительности в Википедии
Похожие сообщения
- Линейная алгебра для машинного обучения
Резюме
В этом уроке вы нашли небольшое введение в линейную алгебру с точки зрения машинного обучения.
В частности, вы узнали:
- Линейная алгебра — это математика данных.
- Линейная алгебра оказала заметное влияние на область статистики.
- Линейная алгебра лежит в основе многих практических математических инструментов, таких как ряды Фурье и компьютерная графика.
Есть вопросы?
Задавайте свои вопросы в комментариях ниже, и я постараюсь ответить.
Освойте линейную алгебру для машинного обучения!
Развивайте практическое понимание линейной алгебры
…путем написания строк кода на Python
Узнайте, как это сделать, в моей новой электронной книге:
Линейная алгебра для машинного обучения
В ней содержится учебных пособий для самостоятельного изучения по таким темам, как:
Векторные нормы, умножение матриц, тензоры, собственное разложение, SVD, PCA и многое другое…
Наконец-то поймите математику данных
Пропустите академические дисциплины. Просто Результаты.
Просто Результаты.
Посмотреть, что внутри
О Джейсоне Браунли
Джейсон Браунли, доктор философии, специалист по машинному обучению, который обучает разработчиков тому, как получать результаты с помощью современных методов машинного обучения с помощью практических руководств.
Просмотреть все сообщения Джейсона Браунли →
Почему алгоритмы машинного обучения работают с новыми данными?
5 причин изучать линейную алгебру для машинного обучения
Линейные уравнения — определение, формула, график, примеры
Линейное уравнение — это уравнение, в котором наивысшая степень переменной всегда равна 1. Оно также известно как уравнение одной степени. Стандартная форма линейного уравнения с одной переменной имеет вид Ax + B = 0. Здесь x — переменная, A — коэффициент, B — постоянная. Стандартная форма линейного уравнения с двумя переменными имеет вид Ax + By = C. Здесь x и y — переменные, A и B — коэффициенты, а C — константа.
| 1. | Что такое линейное уравнение? |
| 2. | Формула линейного уравнения |
| 3. | График линейных уравнений |
| 4. | Часто задаваемые вопросы о линейных уравнениях |
Что такое линейное уравнение?
Уравнение, имеющее наивысшую степень 1, называется линейным уравнением. Это означает, что ни одна переменная в линейном уравнении не имеет показатель степени больше 1. График линейного уравнения всегда образует прямую линию.
Линейное уравнение Определение: Линейное уравнение — это алгебраическое уравнение, где каждый член имеет показатель степени 1, и когда это уравнение изображается на графике, оно всегда приводит к прямой линии. Вот почему оно называется «линейным уравнением».
Существуют линейные уравнения с одной переменной и линейные уравнения с двумя переменными. Давайте научимся определять линейные уравнения и нелинейные уравнения с помощью следующих примеров.
Давайте научимся определять линейные уравнения и нелинейные уравнения с помощью следующих примеров.
| Уравнения | Линейный или нелинейный |
|---|---|
| у = 8х – 9 | Линейный |
| у = х 2 – 7 | Нелинейный, степень переменной x равна 2 |
| √у + х = 6 | Нелинейный, степень переменной y равна 1/2 |
| у + 3х – 1 = 0 | Линейный |
| у 2 – х = 9 | Нелинейный, степень переменной y равна 2 |
Формула линейного уравнения
Формула линейного уравнения — это способ выражения линейного уравнения. Это можно сделать разными способами. Например, линейное уравнение может быть выражено в стандартной форме, в форме точки пересечения или в форме точка-наклон. Теперь, если мы возьмем стандартную форму линейного уравнения, давайте узнаем, как оно выражается. Мы видим, что оно варьируется от случая к случаю в зависимости от количества переменных, и следует помнить, что наивысшая (и единственная) степень всех переменных в уравнении должна быть 1.
Мы видим, что оно варьируется от случая к случаю в зависимости от количества переменных, и следует помнить, что наивысшая (и единственная) степень всех переменных в уравнении должна быть 1.
Линейные уравнения в стандартной форме
Стандартная форма или общая форма линейных уравнений с одной переменной записывается как Ax + B = 0; , где A и B — действительные числа, а x — единственная переменная. Стандартная форма линейных уравнений с двумя переменными выражается как Ax + By = C; , где A, B и C — любые действительные числа, а x и y — переменные.
График линейных уравнений
График линейного уравнения с одной переменной x образует вертикальную линию, параллельную оси y, и наоборот, тогда как график линейного уравнения с двумя переменными x и y образует прямую линию. Построим график линейного уравнения с двумя переменными с помощью следующего примера.
Пример: Постройте график линейного уравнения с двумя переменными, x – 2y = 2.
Построим график линейного уравнения, выполнив следующие шаги.
- Шаг 1: Данное линейное уравнение имеет вид x – 2y = 2.
- Шаг 2: Преобразуйте уравнение в виде y = mx + b. Это даст: y = x/2 – 1.
- Шаг 3: Теперь мы можем заменить значение x на другие числа и получить результирующее значение y для создания координат.
- Шаг 4: Когда мы подставляем x = 0 в уравнение, мы получаем y = 0/2 – 1, то есть y = -1. Точно так же, если мы подставим значение x вместо 2 в уравнение y = x/2 – 1, мы получим y = 0, .
- Шаг 5: Если мы заменим значение x на 4, мы получим y = 1. Значение x = -2 дает значение y = -2. Теперь эти пары значений (x, y) удовлетворяют заданному линейному уравнению y = x/2 – 1. Поэтому мы перечисляем координаты, как показано в следующей таблице.
| х | 0 | 2 | 4 | -2 |
|---|---|---|---|---|
| и | -1 | 0 | 1 | -2 |
- Шаг 6: Наконец, мы наносим эти точки (4,1), (2,0), (0,-1) и (-2,-2) на график и соединяем точки в получить прямую линию.
 Так линейное уравнение изображается на графике.
Так линейное уравнение изображается на графике.
Линейные уравнения с одной переменной
Линейное уравнение с одной переменной — это уравнение, в котором присутствует только одна переменная. Оно имеет форму Ax + B = 0, где A и B — любые два действительных числа, а x — неизвестная переменная, имеющая только одно решение. Это самый простой способ представить математическое утверждение. Это уравнение имеет степень, которая всегда равна 1. Линейное уравнение с одной переменной решается очень просто. Переменные разделяются и подводятся к одной стороне уравнения, а константы объединяются и подводятся к другой стороне уравнения, чтобы получить значение неизвестной переменной.
Пример: Решить линейное уравнение с одной переменной: 3x + 6 = 18.
Чтобы решить данное уравнение, подносим числа в правую часть уравнения и сохраняем переменную в левая сторона. Это означает, что 3x = 18 – 6. Затем, когда мы решим для x, мы получим 3x = 12. Наконец, значение x = 12/3 = 4.
Наконец, значение x = 12/3 = 4.
Линейные уравнения с двумя переменными
Линейное уравнение в Две переменные имеют вид Ax + By + C = 0, где A, B, C — действительные числа, а x и y — две переменные, каждая из которых имеет степень 1. Если мы рассмотрим два таких линейных уравнения, они называются одновременными линейными уравнениями. Например, 6х + 2у + 9= 0 — линейное уравнение с двумя переменными. Существуют различные способы решения линейных уравнений с двумя переменными, такие как графический метод, метод подстановки, метод перекрестного умножения, метод исключения и метод определителя.
Как решать линейные уравнения?
Уравнение похоже на весы с одинаковыми весами с обеих сторон. Если мы прибавим или вычтем одно и то же число из обеих частей уравнения, оно останется верным. Точно так же, если мы умножаем или делим одно и то же число в обеих частях уравнения, это правильно. Мы подносим переменные к одной стороне уравнения, а константу к другой стороне, а затем находим значение неизвестной переменной. Это способ решения линейного уравнения с одной переменной. Давайте разберемся в этом с помощью примера.
Это способ решения линейного уравнения с одной переменной. Давайте разберемся в этом с помощью примера.
Пример: Решите уравнение, 3x – 2 = 4.
Выполняем математические операции с левой (левой) и правой (правой) частями так, чтобы баланс не нарушался. Итак, давайте добавим 2 с обеих сторон, чтобы уменьшить LHS до 3x. Это не нарушит баланс. Новая левая сторона равна 3x – 2 + 2 = 3x, а новая правая сторона равна 4 + 2 = 6. Теперь давайте разделим обе части на 3, чтобы уменьшить левую часть до x. Таким образом, мы имеем х = 2 . Это один из способов решения линейных уравнений с одной переменной.
Советы по линейным уравнениям:
- Значение переменной, которая делает линейное уравнение верным, называется решением или корнем линейного уравнения.
- На решение линейного уравнения не влияет сложение, вычитание, умножение или деление одного и того же числа на обе части уравнения.
- График линейного уравнения с одной или двумя переменными всегда образует прямую линию.

☛ Статьи по теме:
- Решения линейного уравнения
- Введение в графику
- Линейный полином
- Калькулятор решения линейных уравнений
Примеры линейных уравнений
Пример 1: Сумма двух чисел равна 44. Если одно число на 10 больше другого, найдите числа, составив линейное уравнение.
Решение:
Пусть число равно x, значит, другое число равно x + 10. Мы знаем, что сумма обоих чисел равна 44. Следовательно, линейное уравнение можно представить в виде x + x + 10. = 44. В результате получается 2x + 10 = 44. Теперь давайте решим уравнение, изолируя переменную с одной стороны и вводя константы с другой стороны. Это означает, что 2x = 44 – 10. Упрощая RHS, мы получаем 2x = 34, поэтому значение x равно 17. Это означает, что одно число равно 17, а другое число равно 17 + 10 = 27,
Ответ: Таким образом, эти два числа равны 17 и 27.

Пример 2: Число, умноженное на шесть, равно 48. Составьте линейное уравнение и найдите неизвестное число.
Решение: Пусть неизвестное число равно x. Шесть раз это число равно 48, значит 6x = 48. Итак, это линейное уравнение можно решить, чтобы найти значение x, которое является неизвестным числом. 6x = 48 означает, что x = 48/6 = 8.
Ответ: Следовательно, неизвестное число равно 8.
Пример 3: Решите заданное линейное уравнение: 5x – 95 = 75.
Решение: Данное уравнение составляет 5x – 95 = 75.
⇒ 5x = 75 + 95
. = 170
⇒ x = 34
Ответ: Следовательно, значение x равно 34.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими экспертами Cuemath
Узнайте, почему стоит математика, с нашими экспертами Cuemath
Запишитесь на бесплатный пробный урок
Практические вопросы по линейным уравнениям
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о линейном уравнении
Что такое линейное уравнение? Объясните на примере.
Линейное уравнение — это уравнение, в котором наивысшая степень переменной всегда равна 1. Оно также известно как уравнение одной степени. Когда это уравнение изображается на графике, оно всегда приводит к прямой линии. По этой причине его называют «линейным уравнением». Существуют линейные уравнения с одной переменной, с двумя переменными, с тремя переменными и так далее. Стандартная форма линейного уравнения с одной переменной имеет вид Ax + B = 0. Уравнение вида Ax + By = C называется линейным уравнением с двумя переменными. Вот несколько примеров линейных уравнений: 5x + 6 = 1, 42x + 32y = 60, 7x = 84 и т. д.
Какая формула линейного уравнения?
Формула линейного уравнения — это способ выражения линейного уравнения. Это может быть выражено в стандартной форме, в форме пересечения наклона или в форме точка-наклон. Стандартная форма линейного уравнения с одной переменной имеет вид Ax + B = 0. Здесь x — переменная, A — коэффициент при x, а B — константа. Стандартная форма линейного уравнения с двумя переменными имеет вид Ax + By = C. Здесь x и y — переменные, а A, B и C — любые действительные числа.
Это может быть выражено в стандартной форме, в форме пересечения наклона или в форме точка-наклон. Стандартная форма линейного уравнения с одной переменной имеет вид Ax + B = 0. Здесь x — переменная, A — коэффициент при x, а B — константа. Стандартная форма линейного уравнения с двумя переменными имеет вид Ax + By = C. Здесь x и y — переменные, а A, B и C — любые действительные числа.
Почему линейное уравнение называют линейным?
Линейное уравнение называется линейным, потому что когда мы пытаемся построить график данной линейной функции, получается прямая линия.
Как вы решаете линейные уравнения?
Мы можем решить линейное уравнение с одной переменной, переместив переменные в одну часть уравнения, а числовую часть — в другую. Например, x – 1 = 5 – 2x можно решить, переместив числовые части в правую часть уравнения, оставив переменные в левой части. Следовательно, мы получаем x + 2x = 5 + 1. Таким образом, 3x = 6. Это дает x = 2,
Могут ли линейные уравнения содержать дроби?
Да, линейные уравнения могут иметь дроби только до тех пор, пока знаменатель в дробной части является постоянной величиной. Переменные не могут быть частью знаменателя любой дроби в линейном уравнении.
Переменные не могут быть частью знаменателя любой дроби в линейном уравнении.
Что такое линейные уравнения с одной переменной?
Линейное уравнение с одной переменной — это уравнение, в котором присутствует только одна переменная. Оно имеет форму Ax + B = 0, где A и B — любые два действительных числа, а x — неизвестная переменная, имеющая только одно решение. Например, 9x + 78 = 18 — линейное уравнение с одной переменной.
Что такое линейные уравнения с двумя переменными?
Линейное уравнение с двумя переменными имеет форму Ax + By + C = 0, где A и B — коэффициенты, C — постоянный член, а x и y — две переменные, каждая со степенью 1 Например, 7x + 9y + 4 = 0 — это линейное уравнение с двумя переменными. Если мы рассмотрим два таких линейных уравнения, они называются одновременными линейными уравнениями.
Чем квадратные уравнения отличаются от линейных уравнений?
Линейные уравнения не имеют степени, отличной от 1, в любом члене. Общая форма линейного уравнения выражается как Ax + By + C = 0, где A, B и C — любые действительные числа, а x и y — переменные. Принимая во внимание, что квадратные уравнения имеют по крайней мере один член, содержащий переменную, которая возведена во вторую степень. Общая форма квадратного уравнения выражается как ax 2 + bx + c = 0. Другое различие между двумя типами уравнений заключается в том, что линейное уравнение образует прямую линию, тогда как квадратное уравнение образует на графике параболу.
Принимая во внимание, что квадратные уравнения имеют по крайней мере один член, содержащий переменную, которая возведена во вторую степень. Общая форма квадратного уравнения выражается как ax 2 + bx + c = 0. Другое различие между двумя типами уравнений заключается в том, что линейное уравнение образует прямую линию, тогда как квадратное уравнение образует на графике параболу.
Как строить графики линейных уравнений?
Когда мы рисуем линейные уравнения, они образуют прямую линию. Чтобы построить график уравнения формы Ax + By = C, мы получаем два решения, которые соответствуют точкам пересечения x и y. Преобразуем уравнение к форме y = mx + b. Затем мы заменяем значение x другими числами и получаем значение y, которое создает набор координат (x, y). Эти координаты можно нанести на график, а затем соединить линией.
Как решать линейные уравнения с дробями?
Линейные уравнения с дробями решаются так же, как мы решаем обычные уравнения. Нам нужно ввести переменную с одной стороны и константы с другой стороны и найти переменную.

 Если вы встречаете человека, который решает математические задачи гораздо лучше вас, не стоит упрекать себя в отсутствии способностей к предмету или в отсутствии знаний.
Если вы встречаете человека, который решает математические задачи гораздо лучше вас, не стоит упрекать себя в отсутствии способностей к предмету или в отсутствии знаний. В этом нет ничего постыдного.
В этом нет ничего постыдного. Раздел сложен в плане понимания, так что тут без посторонней помощи не обойтись. Необходим людям, собирающимся в Computer Science.
Раздел сложен в плане понимания, так что тут без посторонней помощи не обойтись. Необходим людям, собирающимся в Computer Science.
 Задачник. (базовый и углублённый уровни). Мордкович А.Г. и др. (2014, 264с.)
Задачник. (базовый и углублённый уровни). Мордкович А.Г. и др. (2014, 264с.) Ю. Березина
Ю. Березина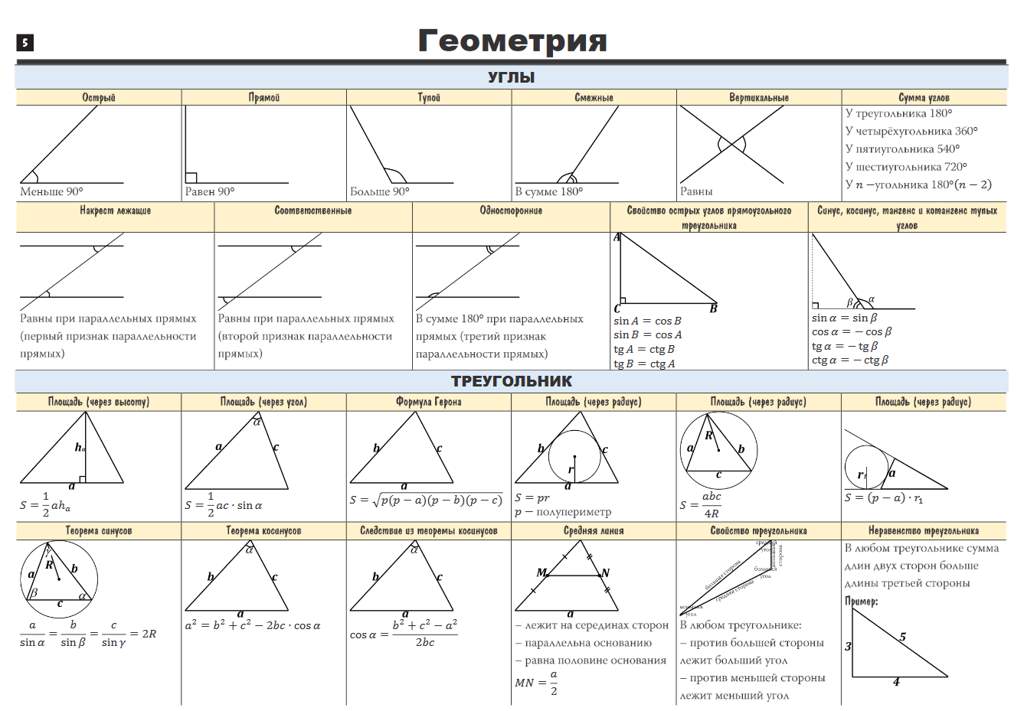
 К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени.
К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени. Считают, что такой многочлен состоит из одного члена.
Считают, что такой многочлен состоит из одного члена.



 Грас — книга для быстрого погружения в профессию, охватывающая большинство необходимых дисциплин;
Грас — книга для быстрого погружения в профессию, охватывающая большинство необходимых дисциплин;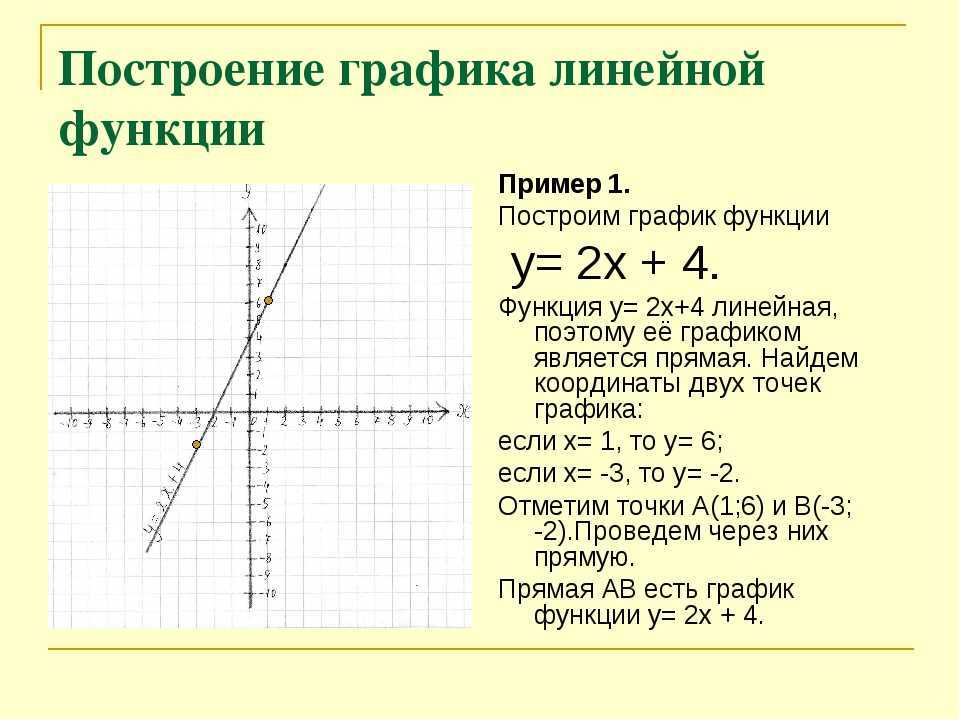 В пример можно привести поиск аномалий — необычных транзакций по кредитной карте, ошибочных показаний датчиков и тому подобное.
В пример можно привести поиск аномалий — необычных транзакций по кредитной карте, ошибочных показаний датчиков и тому подобное.

 Первое уравнение уже решено, а второе решается по стандартному алгоритму:
Первое уравнение уже решено, а второе решается по стандартному алгоритму:
 k ⊗ u в наборе.
k ⊗ u в наборе. Вставьте элементы в матрицы A и B.
Вставьте элементы в матрицы A и B.
 линейной алгебры
линейной алгебры 
 Например, пусть набор состоит из векторов u , v и w . Также пусть k и l — действительные числа, и рассмотрим определенные операции ⊕ и ⊗. Множество является векторным пространством, если при выполнении операции ⊕ оно удовлетворяет следующим требованиям:
Например, пусть набор состоит из векторов u , v и w . Также пусть k и l — действительные числа, и рассмотрим определенные операции ⊕ и ⊗. Множество является векторным пространством, если при выполнении операции ⊕ оно удовлетворяет следующим требованиям: k ⊗ u в наборе.
k ⊗ u в наборе.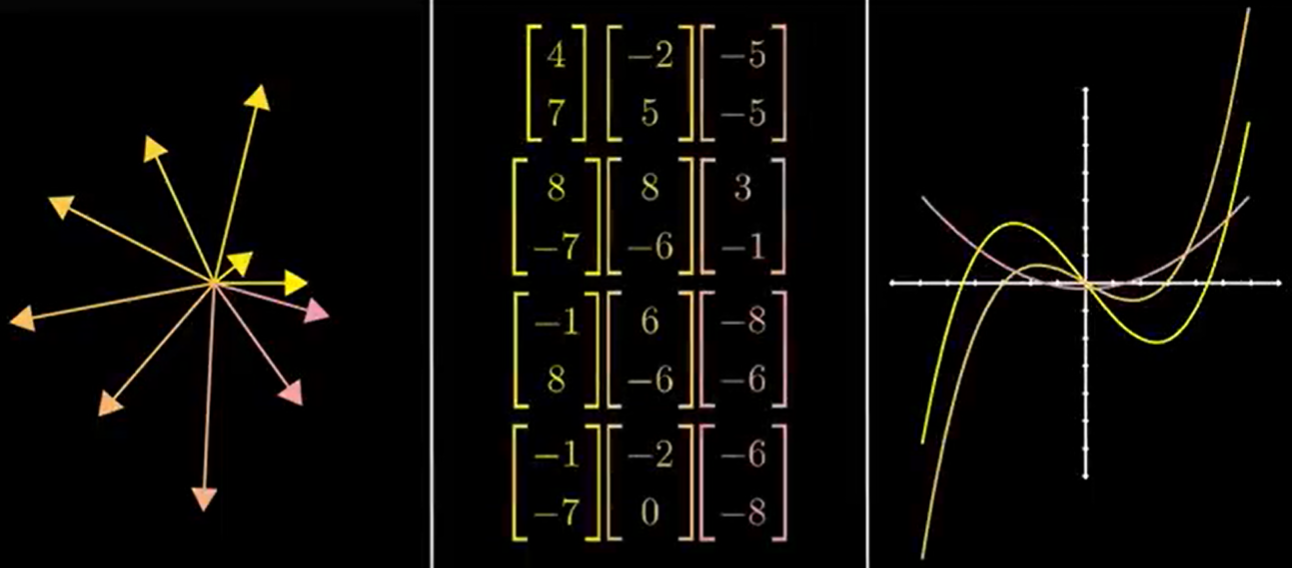

 2$. Ограничение себя линейными операциями имеет свои преимущества.
2$. Ограничение себя линейными операциями имеет свои преимущества. Мы знаем, что нужно умножать первый вход на первое значение, второй вход на второе значение, третий вход на третье значение и складывать результаты.
Мы знаем, что нужно умножать первый вход на первое значение, второй вход на второе значение, третий вход на третье значение и складывать результаты. В нашем примере ввод (a, b, c) идет против операции F и выводит 3a + 4b + 5c. Это противоречит операции G и дает 3a + 0 + 0,9.0005
В нашем примере ввод (a, b, c) идет против операции F и выводит 3a + 4b + 5c. Это противоречит операции G и дает 3a + 0 + 0,9.0005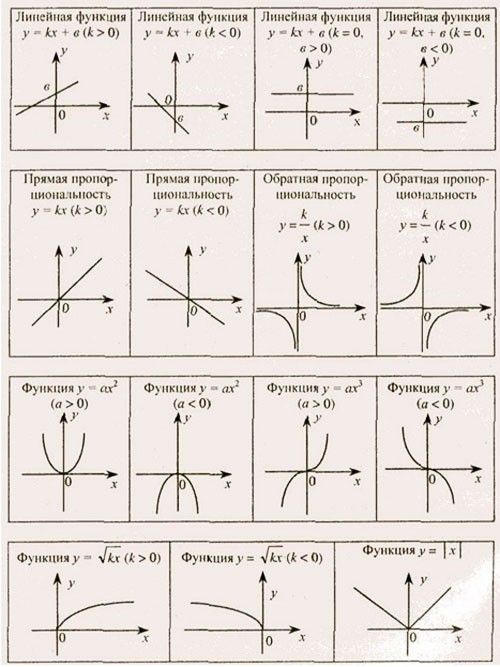 Мнемоники в порядке с контекстом , и вот что я использую:
Мнемоники в порядке с контекстом , и вот что я использую: «Усреднение» аналогично: (a + b + c)/3 = a/3 + b/3 + c/3.
«Усреднение» аналогично: (a + b + c)/3 = a/3 + b/3 + c/3. д.)
д.) Представьте, что вы выполняете каждую операцию:
Представьте, что вы выполняете каждую операцию:
 По мере того, как матрица превращается в единичную матрицу, значения x, y и z раскрываются на выходе.
По мере того, как матрица превращается в единичную матрицу, значения x, y и z раскрываются на выходе.
 Когда мы закончим, мы можем снова следовать инструкциям.
Когда мы закончим, мы можем снова следовать инструкциям. Например: возьмите ввод (x, y, z, 1) и выполните его:
Например: возьмите ввод (x, y, z, 1) и выполните его:
 Так что +1 тоже нужен
Так что +1 тоже нужен д.
д. ..
..

 Так линейное уравнение изображается на графике.
Так линейное уравнение изображается на графике.
