Лекция № 4. Метод Гаусса. Решение систем линейных уравнений методом Гаусса.
Рассмотрим систему m–линейных уравнений c n-неизвестными
(1)
Теорема: Если какое-либо уравнение системы умножить на произвольное число и прибавить это произведение к другому уравнению системы, оставив при этом неизменными все остальные уравнения системы, включая то, которое умножалось на число, то получим систему, равносильную исходной.
Составим расширенную матрицу системы (1) .
Строки матрицы соответствуют уравнениям системы. Умножение уравнения на число и сложение этого произведения с другим, эквивалентно умножению строки матрицы на это число и почленному сложению произведения с другой строкой матрицы. Таким образом, работа с уравнениями заменяется работой со строками матрицы.
Этапы решения:
I Этап: прямой ход заключается в том, что система (1) приводится к ступенчатому виду: , (2)
в частности, к
треугольному виду: . (3)
(3)
Следует запомнить.
Другими словами, если данная система уравнений (1) после выполнения ряда элементарных преобразований приводится к треугольному виду, то это означает, что система (1) является совместной и определенной.
Замечание.
Если в процессе приведения системы (1) к ступенчатому виду появляется уравнение вида , то система несовместна.
II этап: обратный ход заключается в решении ступенчатой (треугольной) системы.
Двигаясь снизу вверх по уравнениям системы (3) находим ; затем, подставляя значение в предыдущее уравнение, находим и т. д..
Если система (1) после элементарных преобразований приводится к ступенчатой системе (2), то, перенеся члены с неизвестными , в правую часть, получим систему вида (4).
. (4)
Придаем неизвестным
,
произвольные значения и получаем треугольную систему.
(5)
Если система (1) после элементарных преобразований приводится к ступенчатой системе (2), то, перенеся члены с неизвестными , в правую часть, получим систему вида (4).
Замечание.
– свободные неизвестные.
– базисные неизвестные.
Из системы (5), поднимаясь снизу вверх, найдем последовательно все остальные неизвестные .
Замечание.
Так как числа могут иметь различные значения, то исходная система (1) имеет бесчисленное множество решений.
Однородная система m линейных уравнений с n – неизвестными.
– однородная СЛАУ. (6)
Однородная система всегда совместна, т. к. , , …, образуют решение системы. Это решение называется нулевым.
Нулевое решение
будет единственным решением системы
(6). Либо помимо нулевого решения должно
существовать бесчисленное множество
ненулевых решений.
Либо помимо нулевого решения должно
существовать бесчисленное множество
ненулевых решений.
Задачи
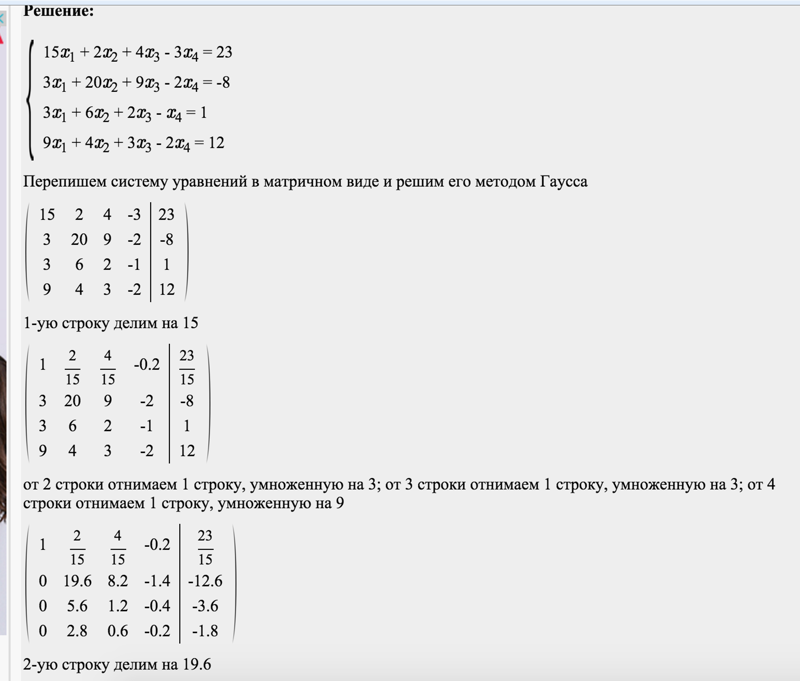
Пример 1. Решить систему уравнений
Решение
Составляем расширенную матрицу системы и приводим ее к ступенчатому виду.
~ ~ ~
Система несовместна.
Пример 2. Решить систему уравнений
Составляем расширенную матрицу системы и приводим ее к ступенчатому виду.
~ ~ ~ ~
Система совместна и определена. Двигаясь снизу вверх по уравнениям системы , находим , ; , .
Таким образом, получаем единственное решение системы .
Пример 3. Решить систему уравнений .
Решение
Составляем
расширенную матрицу системы и приводим
ее к ступенчатому виду.
~ ~ ~
Так как после преобразований число уравнений меньше числа неизвестных, то система неопределена.
Для решения необходимо определить базисные и свободные неизвестные.
Таким образом, и – базисные неизвестные, а и – свободные неизвестные системы.
.
. Отсюда .
Общее решение системы . Положив, например, , , получаем одно из частных решений: , , , .
Придавая свободным неизвестным произвольные значения, найдем различные решения системы.
MathOnWeb.com – Исключение Гаусса
- Что такое система линейных уравнений?
- Некоторые уроки, которые можно извлечь из построения графика двух уравнений с двумя неизвестными
- Расширенная матрица
- Элементарные операции со строками
- Исключение Гаусса
- Резервный корпус
- Противоречивый случай
Что такое система линейных уравнений?
Линейное уравнение на n неизвестных x 1 , x 2 , …, x N – это уравнение формы:
A 1 x 1 + A 2 X 2 + + + … + a n x n = b
где a 1 , a 6 62 ,
… , a n и 
Название линейный происходит от того факта, что такое уравнение с двумя неизвестными или переменными представляет собой прямую линию. Набор таких уравнений называется системой . Пример системы трех линейных уравнений с тремя неизвестными х , у и z это:
Некоторые уроки, которые можно извлечь из построения графика 2 уравнений с 2 неизвестными
Графический метод не очень полезен в качестве вычислительного инструмента, но полезен для визуализации такие понятия, как уникальность решения или значение противоречивых или избыточных систем. Рассмотрим следующую систему двух линейных уравнений с двумя неизвестными:
В этом методе мы просто рисуем графики уравнений, как мы делали справа.
Обратите внимание, что график каждого уравнения представляет собой прямую линию. (Это отличительная черта линейной системы.
Здесь нет кривых, только прямые линии.)
(Это отличительная черта линейной системы.
Здесь нет кривых, только прямые линии.)
Любая точка на одной прямой является решением одного уравнения, а любая точка на другой прямой является решением другого уравнения. Точка пересечения линий {
Система линейных уравнений с единственным решением является «нормальной» ситуацией. Однако это можно иметь систему уравнений без решения. Такая система уравнений называется противоречивый . Часто это результат неточного или неправильного анализа физического состояния. система описывается системой уравнений.
Рассмотрим следующую систему двух линейных уравнений с двумя неизвестными:
Эта система уравнений несовместима, так как x + y никак не могут равняться
2 и 4 одновременно. На рисунке справа показано, что граф этой системы состоит
двух параллельных прямых, которые никогда не пересекаются. Таким образом, решения нет.
На рисунке справа показано, что граф этой системы состоит
двух параллельных прямых, которые никогда не пересекаются. Таким образом, решения нет.
Также возможна система уравнений с бесконечным числом решений. Такая система уравнений называется избыточной . Часто это результат неполного анализ физической системы.
Рассмотрим следующую систему уравнений:
Эта система является избыточной, поскольку второе уравнение эквивалентно первому. График состоит из двух линий, лежащих одна над другой. Они «пересекаются» в бесконечном числе точек, поэтому существует бесконечное количество решений.
Подводя итог, линейная система с двумя неизвестными должна иметь как минимум два уравнения, чтобы получить единственное решение.
Иметь 1 уравнение недостаточно, потому что 1 уравнение с 2 неизвестными представлено целой строкой.
Достаточно двух уравнений, если они не избыточны и не противоречат друг другу. Наличие 3 (или более) уравнений — это слишком много. Третье уравнение должно быть либо избыточным, либо противоречивым.
Наличие 3 (или более) уравнений — это слишком много. Третье уравнение должно быть либо избыточным, либо противоречивым.
Эти идеи можно обобщить на линейные системы уравнений с большим количеством неизвестных:
Линейное уравнение в n переменных представляет собой «гиперплоскость» в пространстве n измерений.
Линейная система уравнений с n неизвестными должна иметь по крайней мере n уравнений, чтобы получить
уникальное решение. Иметь меньшее количество недостаточно; решение не будет единственным.
Достаточно иметь n уравнений, если они не являются избыточными или противоречивыми.
Имея более n уравнений слишком много; система будет либо избыточной, либо непоследовательной.
Расширенная матрица
Мы представим систему уравнений прямоугольным массивом чисел, называемым дополненная матрица . Вот расширенная матрица для приведенного выше примера:
Немного терминологии:
- Элементы расширенной матрицы называются элементами .

- Строки проходят через всю матрицу.
- Столбцы идут вниз по матрице.
- Диагональ матрицы представляет собой набор элементов, который начинается в верхнем, левом углу и идет по диагонали вниз и вправо. Диагональ вышеуказанной матрицы состоит из чисел 4, 1 и 2.
- Любые элементы в позиции a считаются лежащими на выше диагонали , а любой в позиции B на ниже диагонального :
Имейте в виду следующее:
- I -THTH -ряд -ТИТ.
- j -й столбец (слева от вертикальной черты) представляет собой (коэффициенты) j -я переменная или неизвестная
- вертикальная линия представляет знаки равенства
Элементарные операции с строками
Напомним, что такое уравнение, как:
7( x −4)=14,
можно решить для разрешения x , применив следующие операции:
- Разделив обе части уравнения на одно и то же значение, а именно на 7, получим x -4=2,
- , затем прибавив одинаковое количество к обеим сторонам, а именно 4, чтобы получить х = 6.

Решение x = 6, в чем можно убедиться, подставив его обратно в исходное значение. уравнение и нахождение тождества 14=14.
Аналогично, решением системы уравнений является любой набор значений всех
переменных, удовлетворяющих всем уравнениям одновременно. Например, система:
имеет решение:
{ x = 7, y = 5, z = 3}.
Это можно проверить, подставив эти значения во все три уравнения и создание трех тождеств.
Система уравнений может быть решена путем обобщения двух операций, описанных выше, и заметив, что решение системы уравнений не меняется при:
- делении обеих частей уравнения на константу, или
- вычитание кратного одного уравнения из другого уравнения.
Эти же операции можно применить к строкам расширенной матрицы, поскольку каждая строка просто
представляет уравнение. Затем они называются Elementary Row Operations .
Затем они называются Elementary Row Operations .
Элементарные операции со строками (E.R.O.):
- E.R.O.#1: Выберите строку расширенной матрицы и разделите (каждый элемент) строку константой.
Пример:
Обозначение означает разделить первую строку расширенной матрицы на 2, чтобы получить новую расширенную матрицу.
- E.R.O.#2: Выберите любую строку расширенной матрицы и вычтите кратное любой другую строку из него (поэлементно).
Пример:
Обозначение означает взять строку 2 и вычесть из нее 3 раза строку 1, чтобы получить новую расширенную матрицу.
Мы будем применять E.R.O. в определенной последовательности (метод исключения Гаусса, описанный ниже)
преобразовать расширенную матрицу в треугольную эшелонированную форму . В этой форме
расширенная матрица имеет 1 по диагонали, 0 по диагонали и любые числа по диагонали.
Например, расширенная матрица:
В этой форме
расширенная матрица имеет 1 по диагонали, 0 по диагонали и любые числа по диагонали.
Например, расширенная матрица:
в виде треугольного эшелона:
Эта новая расширенная матрица представляет собой систему уравнений:
Она решается обратной подстановкой. Подставляя z = 3 из третьего уравнения в второе уравнение дает y = 5, а подстановка z = 3 и y = 5 в первое уравнение дает x = 7 . Таким образом, полное решение:
{ x = 7, y = 5, z = 3}.
Исключение по Гауссу
В методе исключения по Гауссу элементарные операции со строками (E.R.O.) применяются в определенном
чтобы максимально эффективно преобразовать расширенную матрицу в треугольную эшелонированную форму.
В этом суть метода: Дана система m уравнений в n переменных или неизвестных, выберите первое уравнение и вычтите подходящие множители его из оставшиеся м -1 уравнения. В каждом случае выберите кратное так, чтобы вычитание отменяет или исключает ту же самую переменную, скажем, x 1 . В результате оставшиеся m -1 уравнения содержат только n -1 неизвестных ( x 1 больше не появляется).
Теперь отложите первое уравнение и повторите вышеуказанный процесс с оставшимися м -1 уравнения в n -1 неизвестных.
Продолжайте повторять процесс. Каждый цикл уменьшает количество переменных и количество уравнений. Процесс останавливается, когда:
- Остается одно уравнение с одной переменной. В этом случае существует единственное решение
а обратная замена используется для поиска значений других переменных.

- Остались переменные, но нет уравнений. В этом случае нет единственного решения.
- Остались уравнения, но нет переменных (т. е. самые нижние строки расширенной матрицы содержат только нули слева от вертикальной линии). Это свидетельствует о том, что либо система уравнения противоречивы или избыточны. В случае несоответствия информации, содержащейся в уравнениях противоречиво. В случае избыточности все еще может быть уникальное решение и обратная замена может использоваться для поиска значений других переменных.
Примеры всех этих возможностей приведены ниже.
Алгоритм исключения Гаусса:
Преобразование столбцов расширенной матрицы по одному в треугольную ступенчатую форму.
Столбец, который в настоящее время преобразуется, называется сводным столбцом .
Продолжайте слева направо, пусть основной столбец будет первым столбцом, затем вторым столбцом,
и т. д. и, наконец, последний столбец перед вертикальной чертой. Для каждого сводного столбца выполните
следующие два шага, прежде чем перейти к следующему сводному столбцу:
д. и, наконец, последний столбец перед вертикальной чертой. Для каждого сводного столбца выполните
следующие два шага, прежде чем перейти к следующему сводному столбцу:
- Найдите диагональный элемент в опорном столбце. Этот элемент называется стержнем . Строка, содержащая сводную строку, называется сводной строкой . Разделите каждый элемент в своде ряд по оси (т. е. используйте E.R.O. #1), чтобы получить новую строку оси с 1 в позиции оси.
- Получите 0 в каждой позиции ниже точки поворота, вычитая подходящее кратное значение точки поворота. строку из каждой из строк под ней (т. е. с помощью E.R.O. #2).
По завершении этой процедуры расширенная матрица будет иметь форму треугольного эшелона и можно решить обратной заменой.
Пример: Используйте исключение Гаусса для решения системы уравнений:
Решение: Выполните эту последовательность E. R.O. на расширенной матрице.
Установите сводной столбец в столбец 1. Получите 1 в диагональной позиции (подчеркнуто):
R.O. на расширенной матрице.
Установите сводной столбец в столбец 1. Получите 1 в диагональной позиции (подчеркнуто):
Затем установите 0 под опорной точкой (подчеркнуто):
Теперь пусть опорная колонка = вторая колонка. Сначала получите 1 в диагональной позиции:
Затем получите 0 в позиции ниже опорной:
Теперь пусть опорная колонка = третья колонка. Получите 1 в диагональной позиции:
Эта матрица, которая теперь имеет форму треугольного эшелона, представляет:
Она решается обратной подстановкой. Замена z = 3 из третьего уравнения в второе уравнение дает y = 5, а подстановка z = 3 и y = 5 в первое уравнение дает x = 7 . Таким образом, полное решение:
{ x = 7, y = 5, z = 3}.
Пример применения исключения Гаусса к избыточной системе линейных уравнений решите, если возможно:
Решение: Выполните эту последовательность E.R.O. на расширенной матрице. Установить сводную колонку в столбец 1. 1 уже находится в опорной позиции, поэтому продолжайте получать 0 под опорной точкой:
Теперь установите опорную колонку на вторую колонку. Сначала получите 1 в диагональной позиции:
Затем получите 0 в позиции ниже опорной:
Теперь установите опорную колонку в третью колонку. Первое, что нужно сделать, это получить 1 в диагональное положение, но нет возможности сделать это. На самом деле эта матрица уже в виде треугольного эшелона и представляет собой:
Эта система уравнений не может быть решена обратной подстановкой, потому что у нас нет значения для z .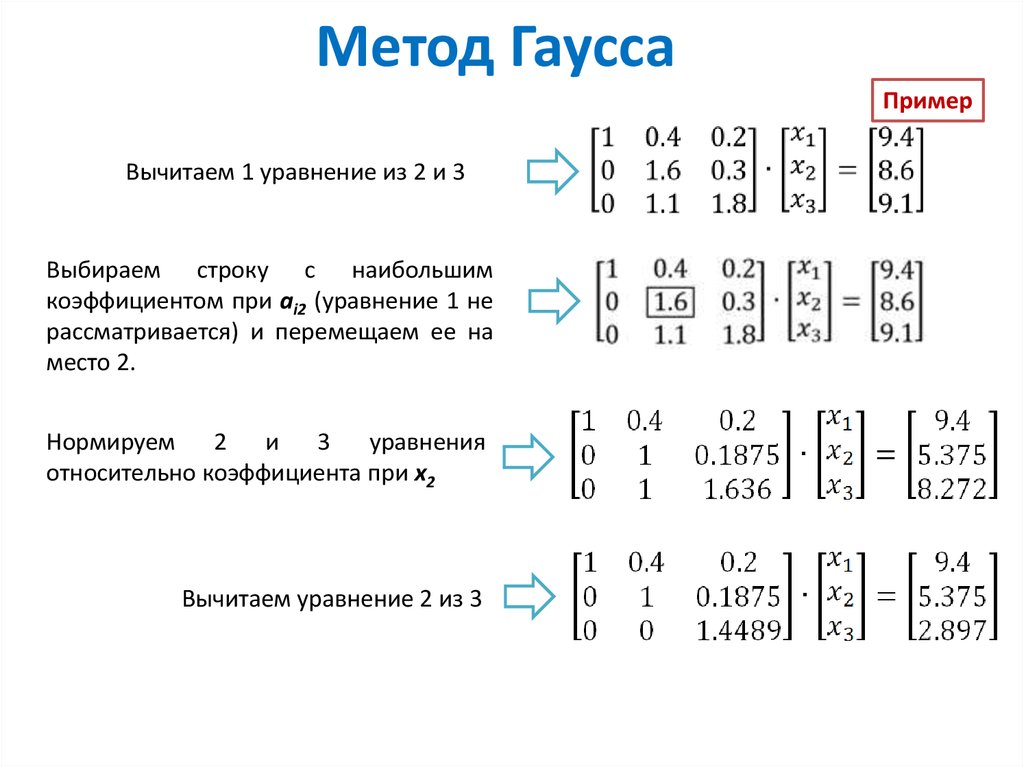 Последнее уравнение просто утверждает, что 0=0. Единого решения не существует, потому что z могут принимать
на любом значении.
Последнее уравнение просто утверждает, что 0=0. Единого решения не существует, потому что z могут принимать
на любом значении.
Обычно одна или несколько строк нулей внизу расширенной матрицы, которая была помещена в треугольную эшелонированную форму указывает на избыточную систему уравнений.
Пример применения исключения Гаусса к противоречивой системе линейных уравнений
Используйте исключение Гаусса, чтобы привести эту систему уравнений к решите, если возможно:
Решение: Выполните эту последовательность E.R.O. на расширенной матрице. Установить точку опоры от столбца к столбцу 1. В опорной позиции уже есть 1, поэтому продолжайте получать 0 ниже опорной точки:
Теперь установите опорный столбец на второй столбец. В позиции поворота уже есть 1, поэтому продолжайте, чтобы получить 0 ниже опорной:
Теперь установите опорную колонку на третью колонку. Первое, что нужно сделать, это получить 1 в
диагональное положение, но нет возможности сделать это. На самом деле эта матрица уже находится в
имеет форму треугольного эшелона и представляет собой:
Первое, что нужно сделать, это получить 1 в
диагональное положение, но нет возможности сделать это. На самом деле эта матрица уже находится в
имеет форму треугольного эшелона и представляет собой:
Эта система уравнений противоречива и не имеет решения. Последнее уравнение утверждает противоречие, а именно 0 = −50.
В общем, расширенная матрица, которая представлена в виде треугольного эшелона и которая содержит одну или несколько нижних строк, состоящих из всех нулей слева от вертикальной линии и ненулевое число справа указывает на противоречивую систему уравнений, не имеющую решения.
Как вы решаете, используя исключение Гаусса или исключение Гаусса Жордана, x-2y-z=2 ,2x – y + z = 4, -x + y -2z = -4 ?
Ответ
Verified
197.7k+ views
Подсказка: Решая систему линейных уравнений методом исключения Гаусса, мы записываем все коэффициенты и константы уравнений в матричной форме, а затем, выполняя операции со строками, пытаемся сделать коэффициент любой строки 0, кроме одного коэффициента, а затем решить для неизвестных.
Полное пошаговое решение:
Уравнения, данные в вопросе: x-2y-z=2 ,2x – y + z = 4, -x + y -2z = -4 , если мы запишем в матричной форме получить
$\слева| \begin{matrix}
1 & -2 & -1 & 2 \\
2 & -1 & 1 & 4 \\
-1 & 1 & -2 & -4 \\
\end{matrix} \right| $
Теперь мы можем выполнить операцию со строками, давайте запишем ${{R}_{3}}$ как сумму ${{R}_{1}}$ и ${{R}_{3}}$ и $ {{R}_{2}}$ как ${{R}_{2}}-2{{R}_{1}}$
$\left| \begin{matrix}
1 & -2 & -1 & 2 \\
0 & 3 & 3 & 0 \\
0 & -1 & -3 & -2 \\
\end{matrix} \right|$
Теперь запишите ${{R}_{3}}$ как $\dfrac{1}{3}{{R}_{2}}+{{R}_{3}}$
$\left| \begin{matrix}
1 & -2 & -1 & 2 \\
0 & 3 & 3 & 0 \\
0 & 0 & -2 & -2 \\
\end{matrix} \right|$
Из строки 3 мы получаем, что -2z равно -2, поэтому z равно 1
. Из строки 2 мы получаем 3y + 3z = 0, поэтому, если мы положим z = 1, y получится -1.
Из строки 1 мы получаем x – 2y – z = 2, если мы положим z = 1 и y = -1, мы получим x равным 1.