НОУ ИНТУИТ | Лекция | Компьютерное моделирование и решение линейных и нелинейных многомерных систем
< Лекция 8 || Лекция 9: 123 || Лекция 10 >
Аннотация: Лекция рассматривает метод и алгоритм решения систем линейных уравнений методом Гаусса
Ключевые слова: оптимальный план, транспортная, гипотеза, математическая модель, системы линейных уравнений, система линейных уравнений, коэффициенты, свободными членами, матричная форма, метод Гаусса, метод прогонки, коэффициентами системы
При моделировании экономических задач, таких как задачи управления и планирования производства, определения оптимального размещения оборудования, оптимального плана производства, оптимального плана перевозок грузов (транспортная задача), распределения кадров и др., может быть положена гипотеза линейного представления реального мира.
Математические модели таких задач представляются линейными уравнениями. Если задача многомерна, то ее математическая модель представляется системой линейных уравнений.
Если задача многомерна, то ее математическая модель представляется системой линейных уравнений.
Линейные математические модели также используются в нелинейных системах при условии, если эта нелинейная система условно линеаризирована.
В общем виде система линейных уравнений имеет вид:
где
bi – свободные члены,
xj – неизвестные системы,
– номер строки,
– номер столбца,
n – порядок системы.
В матричной форме система линейных уравнений имеет вид:
intuit.ru/2010/edi”>где- точные или прямые методы,
- приближенные методы.
Приближенные методы реализуют на ЭВМ нахождение корней с заданной точностью и являются итерационными методами.
Точные методы позволяют получить решение системы за конечное число итераций. К точным методам относятся:
- правило Крамера,
- метод прогонки.
Решение систем линейных уравнений методом Гаусса
Метод Гаусса является точным методом. Он позволяет получить решение системы за конечное число арифметических действий. В основе метода лежит идея последовательного исключения неизвестных. Метод состоит из двух этапов. На первом этапе (прямой ход) система при помощи последовательного исключения неизвестных приводится к треугольному виду. На втором этапе (обратный ход) из системы треугольного вида последовательно, в обратном порядке, начиная c n-го уравнения, находятся неизвестные системы.
В основе метода лежит идея последовательного исключения неизвестных. Метод состоит из двух этапов. На первом этапе (прямой ход) система при помощи последовательного исключения неизвестных приводится к треугольному виду. На втором этапе (обратный ход) из системы треугольного вида последовательно, в обратном порядке, начиная c n-го уравнения, находятся неизвестные системы.
В качестве примера возьмем систему 4 порядка.
| ( 9.1) |
Прямой ход. На первом шаге прямого хода (к=1) находим x1 из первого уравнения системы (9.1).
– ведущий элемент первой строки.
(
9. 2) 2) |
Обозначим:
| ( 9.3) |
Подставляя (9.3) в (9.2), получим
| ( 9.4) |
где
Подставляем (9.4) во 2, 3 и 4 уравнение системы (9.1), получим:
Обозначив коэффициенты при неизвестных полученной системы через , а свободные члены через перепишем полученную систему:
(
9. |
где
Таким образом, в результате выполнения первого шага прямого хода исходная система (9.1) n-го порядка преобразована к совокупности уравнения (9.4) и системы линейных уравнений (9.5), порядок которой равен n-1.
На втором шаге прямого хода (к=2) из первого уравнения системы (9.5) находим x2.
Если , то из первого уравнения системы (9.5) имеем:
| ( 9.6) |
где
intuit.ru/2010/edi”>Подставив выражение (9.6) во второе и третье уравнения системы (9.5), получим новую систему линейных уравнений, порядок которой равен n-2.| ( 9.7) |
где
Таким образом, в результате выполнения второго шага прямого хода исходная система (9.1) преобразована к совокупности уравнений (9.4), (9.6) и системы линейных уравнений (9.7),порядок которой равен n-2.
Дальше >>
< Лекция 8 || Лекция 9: 123 || Лекция 10 >
Элементы высшей математики: Решение систем линейных уравнений
7.
Решение систем линейных уравнений
7.1.
Системы линейных алгебраических уравнений
Сегодня вы изучите вопросы
-
Методы решения систем линейных алгебраических уравнений (СЛАУ)
-
Метод обратной матрицы
-
Метод Крамера
-
Метод Гаусса
-
Условия разрешимости данных систем
-
Критерий совместности
Изучив тему занятия, вы сможете
-
решать СЛАУ методом обратной матрицы, по формулам Крамера, методом Гаусса;
-
решать произвольные системы линейных уравнений и системы однородных уравнений.

Основные понятия
7.1.1.
Системы линейных алгебраических уравнений
Системой линейных алгебраических уравнений (СЛАУ) называется система вида
(4.1)
Решением системы (4.1) называется такая совокупность n чисел
, при подстановке которых каждое уравнение системы обращается в верное равенство.
Решить систему означает найти все ее решения или доказать, что ни одного решения нет.
СЛАУ называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.
Если совместная система имеет только одно решение, то она называется определенной, и неопределенной, если она имеет более чем одно решение.
Например, система уравнений совместная и определенная, так как имеет единственное решение ; система
несовместная, а система совместная и неопределенная, так как имеет более одного решения .
Две системы уравнений называются равносильными или эквивалентными, если они имеют одно и то же множество решений. В частности, две несовместные системы считаются эквивалентными.
В частности, две несовместные системы считаются эквивалентными.
Основной матрицей СЛАУ (4.1) называется матрица А размера , элементами которой являются коэффициенты при неизвестных данной системы, то есть
.
Матрицей неизвестных СЛАУ (4.1) называется матрица-столбец Х, элементами которой являются неизвестные системы (4.1):
.
Матрицей свободных членов СЛАУ (4.1) называется матрица-столбец В, элементами которой являются свободные члены данной СЛАУ:
.
С учетом введенных понятий СЛАУ (4.1) можно записать в матричном виде или
. (4.2)
7.1.2.
Решение систем линейных уравнений. Метод обратной матрицы
Перейдем к изучению СЛАУ (4.1), которой соответствует матричное уравнение (4.2). Сначала рассмотрим частный случай, когда число неизвестных равно числу уравнений данной системы () и , то есть основная матрица системы A невырождена. В этом случае, согласно предыдущему пункту, для матрицы существует единственная обратная матрица A-1. Ясно, что она согласована с матрицами и . Покажем это. Для этого умножим слева обе части матричного уравнения (4.2) на матрицу :
Ясно, что она согласована с матрицами и . Покажем это. Для этого умножим слева обе части матричного уравнения (4.2) на матрицу :
Следовательно, с учетом свойств умножения матриц получаем
Так как , а , тогда
. (4.3)
Убедимся, что найденное значение является решением исходной системы. Подставив (4.3) в уравнение (4.2), получим , откуда имеем .
Покажем, что это решение единственное. Пусть матричное уравнение (4.2) имеет другое решение , которое удовлетворяет равенству
.
Покажем, что матрица равна матрице
С этой целью умножим предыдущее равенство слева на матрицу A-1.
В результате получим
Такое решение системы уравнений с неизвестными называется решением системы (4.1) методом обратной матрицы.
Пример. Найти решение системы
.
Выпишем матрицу системы:
,
Для этой матрицы ранее мы уже нашли обратную:
или
Здесь мы вынесли общий множитель , так как нам в дальнейшем нужно будет произведение .
Ищем решение по формуле: .
Найденные значения переменных подставляем в уравнения системы и убеждаемся, что они являются ее решением.
Упражнение. Проверку этого факта сделайте самостоятельно.
7.1.3.
Правило и формулы Крамера
Рассмотрим систему линейных уравнений с неизвестными
От матричной формы (4.3) перейдем к более удобным и в ряде случаев более простым при решении прикладных задач формулам для нахождения решений системы линейных алгебраических уравнений.
Учитывая равенство , или в развернутом виде
.
Таким образом, после перемножения матриц получаем:
или
.
Заметим, что сумма есть разложение определителя
по элементам первого столбца, который получается из определителя путем замены первого столбца коэффициентов столбцом из свободных членов.
Таким образом, можно сделать вывод, что
Аналогично: , где получен из путем замены второго столбца коэффициентов столбцом из свободных членов, .
Следовательно, нами найдено решение заданной системы по равенствам
, , ,
известным и как формулы Крамера.
Для нахождения решения СЛАУ, последние равенства можно записать в общем виде следующим образом:
. (4.4)
Согласно этим формулам, имеем правило Крамера для решения СЛАУ:
-
по матрице системы вычисляется определитель системы ;
-
если , то в матрице системы каждый столбец последовательно заменяется столбцом свободных членов и вычисляются определители получаемых при этом матриц;
-
решение системы находится по формулам Крамера (4.4).
Пример. С помощью формул Крамера решить систему уравнений
Решение. Определитель данной системы
.
Так как , то формулы Крамера имеют смысл, то есть система имеет единственное решение. Находим определители:
, , .
Следовательно, по формулам (4.4) получаем:
, , .
Найденные значения переменных подставляем в уравнения системы и убеждаемся, что они являются ее решением.
Упражнение. Проверку этого факта сделайте самостоятельно.
Критерий совместности СЛАУ (теорема Кронекера-Капелли)
Расширенной матрицей системы (4.1) называется матрица, получаемая добавлением к основной матрице А справа столбца свободных членов с отделением его вертикальной чертой, то есть матрица
.
Заметим, что при появлении у матрицы новых столбцов ранг может увеличиться, следовательно . Расширенная матрица играет очень важную роль в вопросе совместности (разрешимости) системы уравнений. Исчерпывающий ответ на этот вопрос дает теорема Кронекера-Капелли.
Сформулируем теорему Кронекера-Капелли (без доказательства).
Система линейных алгебраических уравнений (4.1) совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы . Если — число неизвестных системы, то система имеет единственное решение, а если , то система имеет бесчисленное множество решений.
Опираясь на теорему Кронекера-Капелли, сформулируем алгоритм решения произвольной системы линейных уравнений.
-
Вычисляют ранги основной и расширенной матриц СЛАУ. Если , то система не имеет решений (несовместна).
-
Если , система совместна. В этом случае берут любой отличный от нуля минор основной матрицы порядка и рассматривают уравнений, коэффициенты которых входят в этот базисный минор, а остальные уравнения отбрасывают. Неизвестные коэффициенты, которые входят в этот базисный минор, объявляют главными или базисными, а остальные свободными (неосновными). Новую систему переписывают, оставляя в левых частях уравнений только члены, содержащие базисных неизвестных, а все остальные члены уравнений, содержащих неизвестных, переносят в правые части уравнений.
-
Находят выражения базисных неизвестных через свободные. Полученные решения новой системы с базисными неизвестными называются общим решением СЛАУ (4.
 1).
1). -
Придавая свободным неизвестным некоторые числовые значения, находят так называемые частные решения.
Проиллюстрируем применение теоремы Кронекера-Капелли и вышеприведенного алгоритма на конкретных примерах.
Пример. Определить совместность системы уравнений
Решение. Запишем матрицу системы и определим ее ранг.
Имеем:
Так как матрица имеет порядок , то наивысший порядок миноров равен 3. Число различных миноров третьего порядка Нетрудно убедиться, что все они равны нулю (проверьте самостоятельно). Значит, . Ранг основной матрицы равен двум, так как существует отличный от нуля минор второго порядка этой матрицы, например,
Ранг расширенной матрицы этой системы равен трем, так как существует отличный минор третьего порядка этой матрицы, например,
Таким образом, согласно критерию Кронекера-Капелли, система несовместна, то есть не имеет решений.
Пример. Исследовать совместность системы уравнений
Исследовать совместность системы уравнений
Решение. Ранг основной матрицы этой системы равен двум, так как, например, минор второго порядка равен
а все миноры третьего порядка основной матрицы равны нулю. Ранг расширенной матрицы также равен двум, например,
а все миноры третьего порядка расширенной матрицы равны нулю (убедиться самостоятельно). Следовательно, система совместна.
Возьмем за базисный минор, например . В этот базисный минор не входят элементы третьего уравнения, поэтому ее отбрасываем.
Неизвестные и объявляем базисными, так как их коэффициенты входят в базисный минор, неизвестную объявляем свободной.
В первых двух уравнениях члены, содержащие переменную , перенесем в правые части. Тогда получим систему
Решаем эту систему с помощью формул Крамера.
,
.
Таким образом, общим решением исходной системы является бесконечное множество наборов вида ,
где — любое действительное число.
Частным решением данного уравнения будет, например, набор , получающийся при .
7.1.4.
Решение систем линейных алгебраических уравнений методом Гаусса
Одним из наиболее эффективных и универсальных методов решений СЛАУ является метод Гаусса. Метод Гаусса состоит из однотипных циклов, позволяющих последовательно исключать неизвестные СЛАУ. Первый цикл направлен на то, чтобы во всех уравнениях, начиная со второго, обнулить все коэффициенты при . Опишем первый цикл. Полагая, что в системе коэффициент (если это не так, то следует на первое место поставить уравнение с отличным от нуля коэффициентом при x1 и переобозначить коэффициенты), преобразуем систему (4.1) следующим образом: первое уравнение оставляем без изменения, а из всех остальных уравнений исключаем неизвестную x1 с помощью элементарных преобразований. Для этого умножим обе части первого уравнения на и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на и сложим с третьим уравнением системы. Продолжая этот процесс, на последнем шаге цикла умножим обе части первого уравнения на и сложим с последним уравнением системы. Первый цикл завершен, в результате получим эквивалентную систему
Первый цикл завершен, в результате получим эквивалентную систему
(4.5)
Замечание. Для удобства записи обычно используют расширенную матрицу системы. После первого цикла данная матрица принимает следующий вид:
(4.6)
Второй цикл является повторением первого цикла. Предположим, что коэффициент . Если это не так, то перестановкой уравнений местами добьемся того, что . Первое и второе уравнение системы (4.5) перепишем в новую систему (в дальнейшем будем оперировать только расширенной матрицей).
Умножим второе уравнение (4.5) или вторую строку матрицы (4.6) на , сложим с третьим уравнением системы (4.5) или третьей строкой матрицы (4.6). Аналогично поступаем с остальными уравнениями системы. В результате получим эквивалентную систему:
(4.7)
Продолжая процесс последовательного исключения неизвестных, после k — 1-го шага, получим расширенную матрицу
(4.8)
Последние m — k уравнений для совместной системы (4.1) являются тождествами . Если хотя бы одно из чисел не равно нулю, то соответствующее равенство противоречиво, следовательно, система (4. 1) несовместна. В совместной системе при ее решении последние m — k уравнений можно не рассматривать. Тогда полученная эквивалентная система (4.9) и соответствующая расширенная матрица (4.10) имеют вид
1) несовместна. В совместной системе при ее решении последние m — k уравнений можно не рассматривать. Тогда полученная эквивалентная система (4.9) и соответствующая расширенная матрица (4.10) имеют вид
(4.9)
(4.10)
После отбрасывания уравнений, являющихся тождествами, число оставшихся уравнений может быть либо равно числу переменных , либо быть меньше числа переменных. В первом случае матрица имеет треугольный вид, а во втором — ступенчатый. Переход от системы (4.1) к равносильной ей системе (4.9) называется прямым ходом метода Гаусса, а нахождение неизвестных из системы (4.9) — обратным ходом.
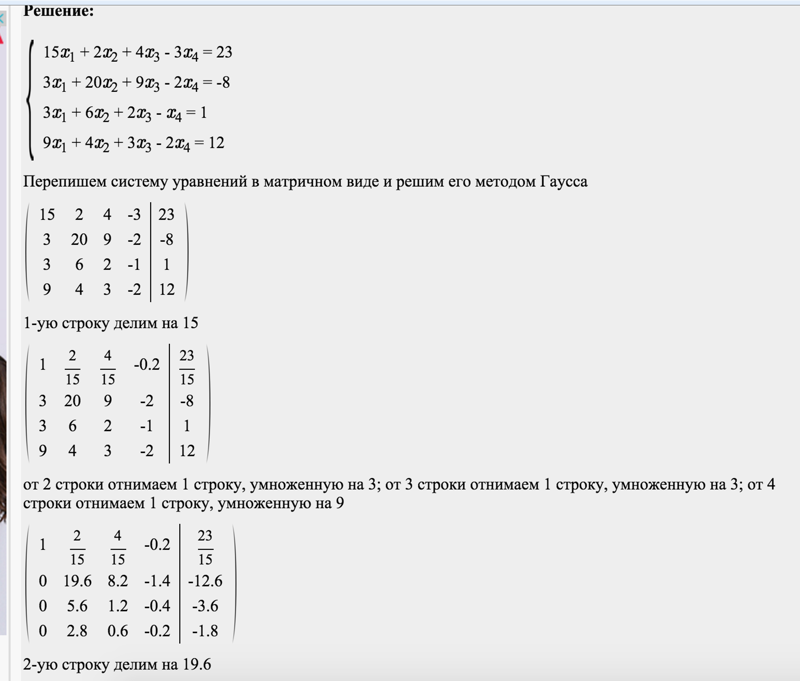
Пример. Решить систему методом Гаусса:
.
Решение. Расширенная матрица этой системы имеет вид
.
Проведем следующие преобразования расширенной матрицы системы: умножим первую строку на и сложим со второй строкой, а также умножим первую строку на и сложим с третьей строкой. Результатом будет расширенная матрица первого цикла (в дальнейшем все преобразования будем изображать в виде схемы)
.
Полученная расширенная матрица соответствует системе уравнений
которая эквивалентна исходной системе. Далее последовательно находим:
, , .
Пример. Решить систему методом Гаусса:
.
Преобразуем расширенную матрицу системы по методу Гаусса:
Последняя строка последней матрицы соответствует не имеющему решения уравнению .
Следовательно, исходная система несовместна.
Системы однородных уравнений
Система линейных алгебраических уравнений называется однородной, если она тождественными преобразованиями приводится к виду:
(4.11)
Ясно, что однородная система всегда совместна, хотя бы потому, что она всегда имеет тривиальное решение x1 = x2 = … = xn = 0.
Сплошь нулевое решение часто называют тривиальным решением системы.
Содержательным вопросом, очевидно, является следующий: при каких условиях однородная система имеет и ненулевые решения? Ответом служит следующая теорема.
Теорема. Для того чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, .
Необходимость.
Так как ранг не может превосходить размера матрицы, то, очевидно, . Пусть . Тогда один из миноров размера отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение:
. Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то .
Достаточность.
Пусть r < n. Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т.е. имеет и ненулевые решения.
В заключении выделим частный случай последней теоремы.
Пусть дана однородная система n линейных уравнений с n неизвестными (4.11).
Теорема. Для того чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель ∆ был равен нулю, т. е. ∆ = 0.
е. ∆ = 0.
Если система имеет ненулевые решения, то ∆ = 0, так как при ∆ ≠ 0 система имеет единственное, нулевое решение. Если же ∆ = 0, то ранг r основной матрицы системы меньше числа неизвестных, то есть r < n. Это означает, что система имеет бесконечное множество ненулевых решений.
Пример. Решить систему
Решение.
Так как r < n, то система имеет бесчисленное множество решений. Найдем их.
Стало быть, — общее решение.
Положив х3 = 0, получаем одно частное решение: х1 = 0, х2 = 0, х3 = 0. Положив х3 = 1, получаем второе частное решение: х1 = 2, х2 = 3, х3 = 1, и т.д.
Контрольные вопросы
-
Что понимается под системой линейных алгебраических уравнений?
-
Запишите в общем виде СЛАУ. Каков смысл величин, входящих в уравнения системы?
-
Дайте определение решения системы, определения совместной, несовместной системы.

-
При каких условиях СЛАУ имеет единственное решение?
-
К какой СЛАУ применим метод обратной матрицы?
-
К какой СЛАУ применимо правило Крамера?
-
Сформулируйте теорему Кронекера-Капелли.
-
Сформулируйте алгоритм решения произвольной системы линейных уравнений.
-
Какая система линейных алгебраических уравнений называется однородной?
-
При каких условиях система однородных уравнений имеет ненулевое решение?
Задания для самостоятельной работы
Задание 1. Примеры для самоподготовки
(решение систем линейных уравнений)
-
Решить следующие системы уравнений по формулам Крамера
1.1.
Ответ.

1.2.
Ответ. Нет решений.
1.3.
Ответ. x = α, y = 3,5 —0,5α, где α — произвольное действительное число.
1.4.
Ответ. .
-
Решить систему уравнений с применением теории матриц:
2.1.
Ответ. x = 2; y = 0; z = 3.
2.2.
Ответ. x1 = 2; x2 = -1; x3 = 0; x4 = -2.
2.3.
Ответ. x1 = -17α + 29β + 5; x2 = 10α — 17β — 2; x3 = α; x4 = β
Задание 2. Примеры для самопроверки
(отметьте правильный вариант ответа)
-
Решить следующую систему уравнений
1) ;
2) ;
3) ;
4) ;
5) .
-
Решить следующую систему уравнений
1) ;
2) ;
3) нет решений;
4) ;
5) .

-
Решить следующую систему уравнений
1) ;
2) ;
3) ;
4) ;
5) .
-
Решить следующую систему уравнений
1) ;
2) ;
3) ;
4) ;
5) .
-
Решить следующую систему уравнений
1) ;
2) ;
3) ;
4) ;
5) .
-
Решить следующую систему уравнений
1) ;
2) ;
3) ;
4) ;
5) .
Система линейных уравнений с использованием алгоритма исключения Гаусса | Программа инженерного образования (EngEd)
Система линейных уравнений представляет собой набор одного или нескольких линейных уравнений, включающих один и тот же набор переменных. Линейные системы встречаются при построении регрессионных моделей в машинном обучении.
Линейные системы встречаются при построении регрессионных моделей в машинном обучении.
Существуют различные способы решения этой проблемы. Некоторые методы сложны, другие просты для понимания и реализации. Метод исключения Гаусса является одним из лучших решений для этих систем.
В этой статье мы рассмотрим интуицию, лежащую в основе метода исключения Гаусса, проведем удобное вычисление и, наконец, проиллюстрируем, как мы можем реализовать этот метод в R.
Предварительные условия
Читатель должен иметь: понимание элементарной линейной алгебры.
Понимание алгоритма исключения Гаусса
Эти шаги необходимы для решения системы линейных уравнений с использованием алгоритма исключения Гаусса.
Предположим, нам дана система линейных уравнений, показанная ниже.
Шаг 1:
Представить приведенную выше систему линейных уравнений в матричной форме, т. е.
е.
Присвоить A, X и b матрице коэффициентов, вектору переменных и вектору решений соответственно.
То есть:
Шаг 2:
Используя матрицы A и b, мы создаем расширенную матрицу, т.е. присоединяем b к матрице A как последний столбец.
Теперь, чтобы привести приведенную выше матрицу ${C}$ к форме, которую можно легко решить для неизвестных, нам нужно выполнить некоторые операции. Эти операции не должны изменять решения линейной системы.
Некоторые из разрешенных операций:
- Изменение порядка строк.
- Увеличение строки, т. е. умножение на константу.
- Чтобы исключить определенные значения, вы можете умножить одну строку на константу и добавить вывод в другую строку. 9{rd}$ описанной выше операции, мы делаем все значения ниже опорного значения нулями. Это показано в матрице ниже.
Шаг 4:
Мы сохраняем первое значение после нуля во второй строке во второй итерации.
 Затем, как и в первой итерации, сделайте все значения ниже этого значения нулями.
Затем, как и в первой итерации, сделайте все значения ниже этого значения нулями.Это показано ниже:
Шаг 5:
Повторяйте описанные выше операции, пока не получите верхнюю треугольную матрицу. Матрица, которую мы получили на предыдущем шаге, уже имеет верхнетреугольную форму.
Следующим шагом будет поиск решения нашей исходной системы с использованием этой уменьшенной матрицы. Из нашей сокращенной матрицы мы можем записать следующую систему линейных уравнений.
Эту новую систему уравнений решить намного проще, чем исходную. Чтобы найти решение нашей исходной системы, мы решим эти уравнения, которые мы только что вывели из верхней треугольной матрицы. Это очень просто и быстро по сравнению с вычислительным решением исходной системы.
Теперь в приведенной выше системе все, что нам нужно сделать, это выполнить обратную замену. Обратная замена выполняется в порядке, указанном ниже:
Обратите внимание: сначала мы нашли последнюю переменную $(x_3)$, а затем включили ее решение в решение предыдущей переменной, пока не получили $x_1$.
 Как мы все знаем, системы линейных уравнений в реальных данных могут состоять из миллионов уравнений. Решать эти системы вручную нецелесообразно. Это требует от нас использования вычислительного программного обеспечения. В последнем разделе этой статьи мы увидим, как мы можем реализовать этот метод.
Как мы все знаем, системы линейных уравнений в реальных данных могут состоять из миллионов уравнений. Решать эти системы вручную нецелесообразно. Это требует от нас использования вычислительного программного обеспечения. В последнем разделе этой статьи мы увидим, как мы можем реализовать этот метод.R Реализация алгоритма исключения Гаусса
Здесь нам нужно создать матрицу, ту, которую мы использовали для объяснения этой концепции, которую мы затем напишем, чтобы преобразовать ее в верхнюю треугольную матрицу. Ниже приведен процесс реализации этого метода.
# создать матрицу A <- матрица (c (-3,2,-1,6,-6,7,3,-4,4),byrow = T,nrow=3,ncol=3) A # напечатать матрицу b <- матрица (c (-1,-7,-6),nrow=3,ncol=1) b # матрица печати b # размерность матрицы A nrow <- nrow(A) сейчас # соедините матрицу A и вектор b Ugmt.mtx <- cbind(A,b) Ugmt.mtx Ugmt.mtx[1,] <- Ugmt.mtx[1,]/Ugmt.mtx[1,1] for (i in 2:nrow){ # цикл по строкам for (j in i:nrow) { # цикл по столбцам Ugmt. mtx[j, ] <- Ugmt.mtx[j, ] - Ugmt.mtx[i-1, ] * Ugmt.mtx[j, i-1] # заменить значения строки в j-й позиции левыми вычислениями
}
Ugmt.mtx[i,] <- Ugmt.mtx[i,]/Ugmt.mtx[i,i]
}
# вывод на печать
Ugmt.mtx
mtx[j, ] <- Ugmt.mtx[j, ] - Ugmt.mtx[i-1, ] * Ugmt.mtx[j, i-1] # заменить значения строки в j-й позиции левыми вычислениями
}
Ugmt.mtx[i,] <- Ugmt.mtx[i,]/Ugmt.mtx[i,i]
}
# вывод на печать
Ugmt.mtx
Выполнив код получаем:
[1] [2] [3] [4] [1,] 1 -0,6666667 0,3333333 0,3333333 [2,] 0 1,0000000 -2,5000000 4,5000000 [3,] 0 0,0000000 1,0000000 -1,0000000
Примечание, чтобы найти значения наших переменных; нам нужно выполнить обратную замену, используя этот вывод. Однако для дальнейшего упрощения мы можем взять приведенную выше матрицу и сделать элементы в верхнем треугольнике равными нулям. Это гарантирует, что нам не нужно выполнять обратную замену в конечном выводе, что может потребовать значительных вычислительных ресурсов. Вместо создания матрицы идентичности по отношению к выходным переменным.
Этот метод уменьшения матрицы называется методом исключения Гаусса-Жордана. Чтобы лучше понять, как работает этот метод, я рекомендую посетить этот блог.

Этот метод реализован в R следующим образом:
A <- matrix(c(-3,2,-1,6,-6,7,3,-4,4),byrow = T,nrow=3 ,nкол=3) А b <- матрица (c (-1,-7,-6),nrow=3,ncol=1) б # размерность матрицы A nrow <- nrow(A) сейчас # соедините матрицу A и вектор b Ugmt.mtx <- cbind(A,b) Ugmt.mtx Ugmt.mtx[1,] <- Ugmt.mtx[1,]/Ugmt.mtx[1,1] для (я в 2: nrow) { для (j в i:nrow) { Ugmt.mtx[j, ] <- Ugmt.mtx[j, ] - Ugmt.mtx[i-1, ] * Ugmt.mtx[j, i-1] } Ugmt.mtx[i,] <- Ugmt.mtx[i,]/Ugmt.mtx[i,i] } для (я в р: 2) { для (j в i: 2-1) { Ugmt.mtx[j, ] <- Ugmt.mtx[j, ] - Ugmt.mtx[i, ] * Ugmt.mtx[j, i] } } Ugmt.mtxЭтот код возвращается.
[1] [2] [3] [4] [1,] 1 0 0 2 [2,] 0 1 0 2 [3,] 0 0 1 -1
Как мы видим, возвращаемый результат содержит точные значения переменных, которые мы решаем.
Заключение
В данной статье введена концепция решения систем линейных уравнений методом исключения Гаусса. Используя редуцированную матрицу, мы определили решение для наших переменных, используя концепцию обратной подстановки.
 Наконец, мы реализовали этот процесс в R.9.0003
Наконец, мы реализовали этот процесс в R.9.0003Поскольку окончательный результат по-прежнему требовал от нас поиска неизвестных, мы пошли еще дальше, используя обратную замену, и продемонстрировали обновленную версию нашего предыдущего подхода, метода исключения Джордана-Гаусса. Мы продемонстрировали, как реализовать этот метод, когда он возвращает точные значения неизвестных переменных.
Автор: Стейси Джелагат
Рецензирование: Пол Одиамбо
Решение систем уравнений методом исключения Гаусса
В этом посте вы узнаете, что такое метод исключения Гаусса и как решить систему уравнений методом исключения Гаусса.
Содержание
Что такое метод исключения Гаусса?
Метод исключения Гаусса , также называемый методом редукции строк , представляет собой алгоритм, используемый для решения системы линейных уравнений с матрицей. Метод исключения Гаусса состоит из выражения линейной системы в матричной форме и применения к матрице элементарных операций со строками, чтобы найти значение неизвестных.

Однако, чтобы понять, как работает исключение Гаусса, мы должны сначала узнать, как выразить систему линейных уравнений в матричной форме и какие операции над строками можно вычислить. Итак, сначала мы объясним эти две вещи, а затем увидим, как применять метод исключения Гаусса.
Дополненная матрица системы линейных уравнений
В линейной алгебре система уравнений может быть выражена в матричной форме: коэффициенты при неизвестном x соответствуют первому столбцу матрицы, коэффициенты при неизвестном y — первому столбцу матрицы. второй столбец, коэффициенты неизвестного z в третий столбец и константы в четвертый столбец.
Например:
Матрица, представляющая систему уравнений, называется расширенной матрицей .
Цель метода Гаусса состоит в том, чтобы преобразовать исходную систему уравнений в ступенчатую систему, то есть систему, в которой каждое уравнение имеет на одно меньше неизвестных, чем предыдущее:
Другими словами, мы должны преобразовать расширенную матрицу в матрицу в эшелонированном виде строк :
Для этого нужно применить элементарные операции над строками матрицы.
 Итак, давайте посмотрим, какие операции можно сделать в методе исключения Гаусса.
Итак, давайте посмотрим, какие операции можно сделать в методе исключения Гаусса.Элементарные операции со строками
Чтобы преобразовать расширенную матрицу в матрицу в виде эшелона строк, можно выполнить любую из следующих элементарных операций:
- Поменять местами две строки матрицы.
Например, мы можем поменять местами 2 и 3 строки матрицы:
- Умножить или разделить все члены в строке на ненулевое число.
Например, первую строку мы можем умножить на 4, а третью строку разделить на 2:
- Добавить к строке еще одну строку , умноженную на скаляр.
Например, в следующей матрице мы добавляем строку 3, умноженную на 1, к строке 2:
Как выполнить исключение Гаусса
Теперь мы увидим на решенном примере , как решить систему линейных уравнений с помощью метода исключения Гаусса:
Прежде всего находим расширенную матрицу системы уравнений:
Как мы увидим позже, лучше, если первое число первой строки равно 1.
 Поэтому мы собираемся изменить порядок строк 1 и 2:
Поэтому мы собираемся изменить порядок строк 1 и 2:Цель метода исключения Гаусса состоит в том, чтобы числа под главной диагональю сделать равными 0. Итак, мы должны преобразовать красные числа в 0:
Чтобы исключить эти числа, мы должны выполнить соответствующие операции с элементарными строками.
Например, число -1, являющееся первым элементом второй строки, является отрицательным числом 1, первого элемента первой строки. Итак, если мы добавим первую строку ко второй строке, -1 будет устранено:
Складывая строки, мы получаем следующую матрицу:
Таким образом, мы преобразовали -1 в 0.
Теперь мы собираемся обнулить число 2. Для этого прибавляем первую строку, умноженную на -2, к третьей строке:
И получается следующая матрица:
Теперь нам нужно преобразовать -8 в 0. Для этого умножаем третью строку на 3 и добавить вторую строку, умноженную на 8:
Таким образом, мы получаем следующую матрицу:
Как видите, со всеми этими преобразованиями мы сделали все числа ниже главной диагонали 0.



 1).
1).


 Затем, как и в первой итерации, сделайте все значения ниже этого значения нулями.
Затем, как и в первой итерации, сделайте все значения ниже этого значения нулями. Как мы все знаем, системы линейных уравнений в реальных данных могут состоять из миллионов уравнений. Решать эти системы вручную нецелесообразно. Это требует от нас использования вычислительного программного обеспечения. В последнем разделе этой статьи мы увидим, как мы можем реализовать этот метод.
Как мы все знаем, системы линейных уравнений в реальных данных могут состоять из миллионов уравнений. Решать эти системы вручную нецелесообразно. Это требует от нас использования вычислительного программного обеспечения. В последнем разделе этой статьи мы увидим, как мы можем реализовать этот метод. mtx[j, ] <- Ugmt.mtx[j, ] - Ugmt.mtx[i-1, ] * Ugmt.mtx[j, i-1] # заменить значения строки в j-й позиции левыми вычислениями
}
Ugmt.mtx[i,] <- Ugmt.mtx[i,]/Ugmt.mtx[i,i]
}
# вывод на печать
Ugmt.mtx
mtx[j, ] <- Ugmt.mtx[j, ] - Ugmt.mtx[i-1, ] * Ugmt.mtx[j, i-1] # заменить значения строки в j-й позиции левыми вычислениями
}
Ugmt.mtx[i,] <- Ugmt.mtx[i,]/Ugmt.mtx[i,i]
}
# вывод на печать
Ugmt.mtx

 Наконец, мы реализовали этот процесс в R.9.0003
Наконец, мы реализовали этот процесс в R.9.0003
 Итак, давайте посмотрим, какие операции можно сделать в методе исключения Гаусса.
Итак, давайте посмотрим, какие операции можно сделать в методе исключения Гаусса.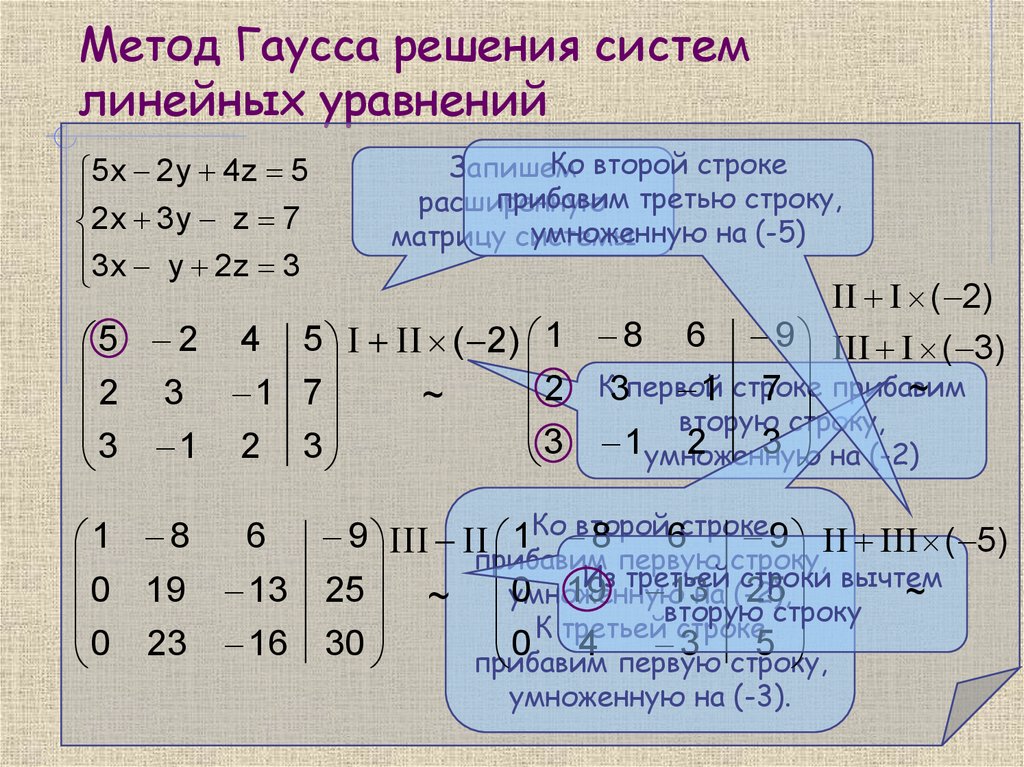 Поэтому мы собираемся изменить порядок строк 1 и 2:
Поэтому мы собираемся изменить порядок строк 1 и 2: