M физика формула: Формула массы тела

формулы для расчета, пояснения, примеры / Справочник :: Бингоскул

Все замечали, что разные вещества, занимающие один объем, весят по-разному. Ведёрко воды весит меньше, чем песка или камней. Вес тела зависит от его плотности – концентрации вещества в единице объема. Рассмотрим связь между этими величинами, способы, как найти массу воды в физике, зная её объём.

Что такое плотность

Плотностью называется скалярная величина, определяющаяся как отношение массы вещества к занимаемому им объёму. Плотность – величина не постоянная, поэтому для многих веществ берётся усреднённое значение, измеренное в нормальных условиях. Так, например, плотность многих встречаемых в повседневной жизни тел зависит от внешних условий. Если говорить о зерне, древесине, грунте, песке, их единица объёма весит тем больше, чем вещество влажнее – в нём больше влаги.

На плотность жидкостей заметное влияние оказывает температура: при охлаждении концентрация в единице объёма увеличивается, при нагревании вещество становится менее плотным.

Здесь есть исключения – вода. Её вес, вязкость достигают пика при температуре 4 °C, при охлаждении и нагревании они снижаются. Лёд получается легче, чем вода, поэтому он образовывается на поверхности водоёмов, на дно не опускается.

При измерении плотности пористых, сыпучих материалов указывается его:

• Насыпное значение – реальное, измеряемое без учёта пустот. Например, сыпучие крупы, щебень, известняк.


• Истинное – от занимаемого объёма отнимаются пустоты. Они определяются практическим путём, например, погружением тела в воду, или через ранее вычисленные коэффициенты.

Плотность при переходе вещества между фазовыми состояниями обычно изменяется скачкообразно, наибольшая разница наблюдается при испарении твёрдых веществ – сублимации.

Формула массы жидкости

Плотность в физике обозначается буквой греческого алфавита , измеряется в кг/м3. Зависит от массы тела и объёма, который занимает:

ρ= m : V, где:

• m – масса тела;
• V – объём.

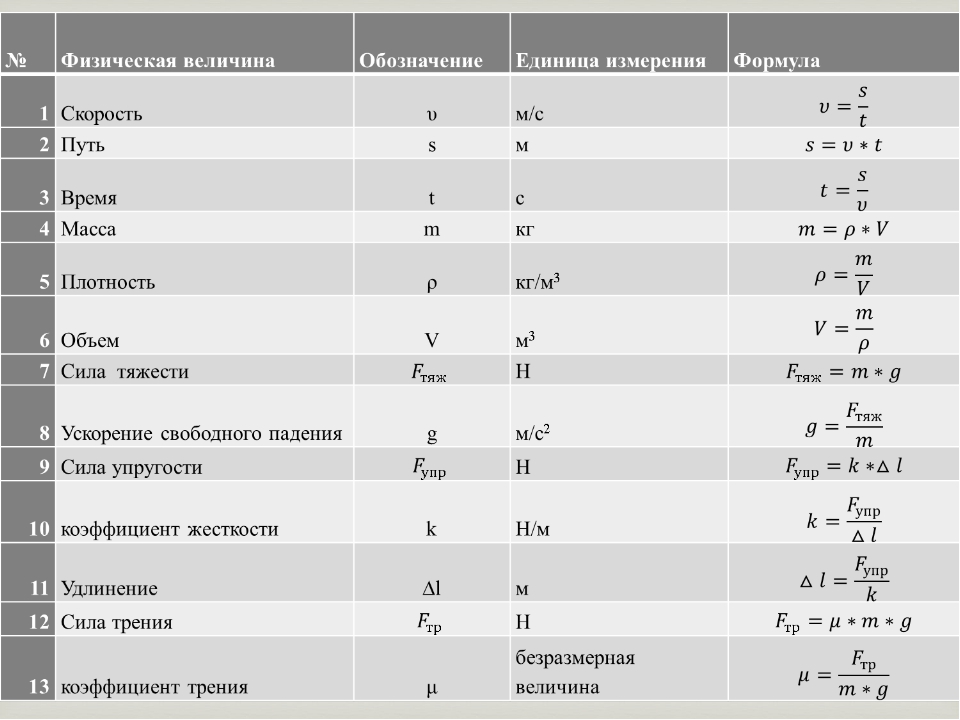
Все ли знают, как найти массу газа через давление и занимаемый им объем? Для этого пользуются формулой Клапейрона-Менделеева:

pV = (m : M) * RT, где:

• p – давление газа;


• M и T– его молярная масса и температура;


• R – постоянная, равняется 8,314 Дж/(моль⋅К).

Для вычисления массы необходимо провести ряд математических операций: разделим обе части уравнения на ρV, затем – умножим на m, получим:

m = pVM : RT.

Рассмотрим, как найти объем детали, погруженной в жидкость, используя приведённую формулу.

Задачи

В ведро цилиндрической формы налили 5 л воды. Её уровень составил 0,4 м. После погружения в ведро тела уровень жидкости поднялся до 0,55 м. Определите его объём.

Дан объём воды: 5 л или 5000 см³, остальные величины переведём в сантиметры для простоты вычислений: 40 см, 55 см.

Объём цилиндра вычисляется по формуле: V = S_осн * H. Найдём площадь основания:

S_осн = V : H = 5000 : 40 = 125 см².

Далее вычисляем занимаемый водой и деталью объём:

V = S_осн * H = 125 * 55 = 6875 см³.

Высчитываем разницу: 6875 – 5000 = 1875 см³.

Далее рассмотрим, как найти массу жидкости, зная её вес, объём.

Вычислим вес 5-литровой бутыли подсолнечного масла.

Объём известен – 0,005 м³, плотность подсолнечного масла принимают за 920 кг/м³.

Подставим значения в формулу:

m = V * ρ = 0,005 * 920 = 4,6 кг.

формулы по физике

4

Площади

l – длинна

b – высота, ширина.

Площадь круга:

Кинематика.

Равномерное движение:

a = 0

V = S/t

Ускоренное движение:

a > 0

a = (V – V₀ )/ t

S = S₀ + V₀t  (at² )/2

a = (V² – V₀² )/ 2S

Последовательный ряд нечетных чисел:

– ую:

просто:

Движение под углом к горизонту.

Скорость по оси ОХ:

Скорость по оси ОУ:

Максимальное время подъема:

t_полн = 2t

Расстояние :

S = V_xt_полн.

Максимальная высота:

Движение тела, брошенного горизонтально:

;

Динамика.

F = ma

P = mg

F_тр. = -N

F = -F

Момент сил.

M=Fl

M1+M2+…+Mn = 0

Пружина.

x – удлинение.

k – кооф. растяжения.

l = l – l₀

l – абсолют. удлинение пружины.

ε -относит. удлинение.

l₀ – начальная длинна

Работа и энергия.

;

;

Движение по окр-ти.

;

w – угловая скорость.[рад/с]

v -линейная скорость.

n – частота обращения. [об./мин.]

T – период обращения. [время]

Угловая скорость. Период обращения.

; ;

; ;

Для случаев, когда n = [обороты]

;

– частота [1/с = 1 Гц]

– угол.

l – длинна дуги.

Импульс.

;

Не упругое вз-вие.

до: после:

в проекции на ось х:

Упругое соударение.

до вз-я: после:

в проекции на ось х:

Реактивное движение:

в проекции на ось х: (вверх)

║

0 изначально.

– импульс газов

Импульс силы.

Механика жидкостей и газов.

Давление. Закон Паскаля.

-//- жидкости на дно сосуда.

; F – сила давления

S – поверхность[1Па = 1Н/1]

h – высота уровня жидкости.

Сообщающиеся сосуды.

;

Архимедова сила. Атм. давление

;

;

/

вытесненной жидкости цилиндром.

Закон Гука. Растягив. сила.

l –первоначальная длинна стержня

Δl –абсолютное удлинение

S –площадь поперечного сеч.

E –кооф. пропорцион., модуль Юнга, модуль упругости.

– напряженность

-закон Гука

КПД машин.

; [1дж/1с = 1 Вт]

Колебания и волны. Звук.

F – возвращающая сила

k – постоянная возвращающ.

x – смещение

Маятник.

;l – длинна маятника

Математический маятник – точка, подвешенная на невесомой и нерастяжимой нити.

Пружинный маятник:

;

– циклическая частота колебаний

Фаза колебаний.

– угловая скорость

– угол поворота

Скорость распространения волн

;

Электромагнитные колебания.

;

– собственна частота колебаний в контуре

;

;

– фаза колебаний

– амплитуда тока

С – скорость в ваакуме

n – абс. показатель преломления среды

Молекулярно-кинетическая

теория

;

– масса молекулы

– молярная масса

; N – число молекул.

Теплоемкость тела.

с – теплоемкость тела

U – внутренняя энергия

А – работа

q – теплота сгорания

!!! Бывает наоборот!

Линейное расширение твердых тел. -23 Дж/К

– среднеквадратичная ск-ть

– средняя кинетич. энергия движ. мол-лы.

КПД тепловой машины.

– кол-во теплоты, получ. рабочим телом от нагрев.

– t холод.

– нагреват.

Электричество и магнетизм.

[В/м] ;

Эквипотенциальные пов-ти.

;

l – расстояние

– поверхностная плотность заряда

Закон Кулона

; [Н]

Ф/м

\ эл. постоянная

Электроемкость. Конденсаторы.

[Дж]

W – Энергия

Электроемкость плоского:

Шара:

Параллельное подключение конденсаторов:

Последовательное подключение:

Постоянный электрический ток. -1]

постоянная:

Последовательное и парал-ное соединение проводников.

Последовательное:

Параллельное:

Закон Ома для полной цепи:

Последоват. соед. батарей:

;

n – кол-во батарей

Параллельное соед. батарей:

;

Работа при перемещении эл. заряда в эл. поле. Потенциал.

;

– потенциал эл. поля

– потенциальная энергия заряда в поле.

Работа и мощность эл. тока:

Напряжение.

Магнитное поле

;

При расположении проводника с током под углом альфа к вектору В.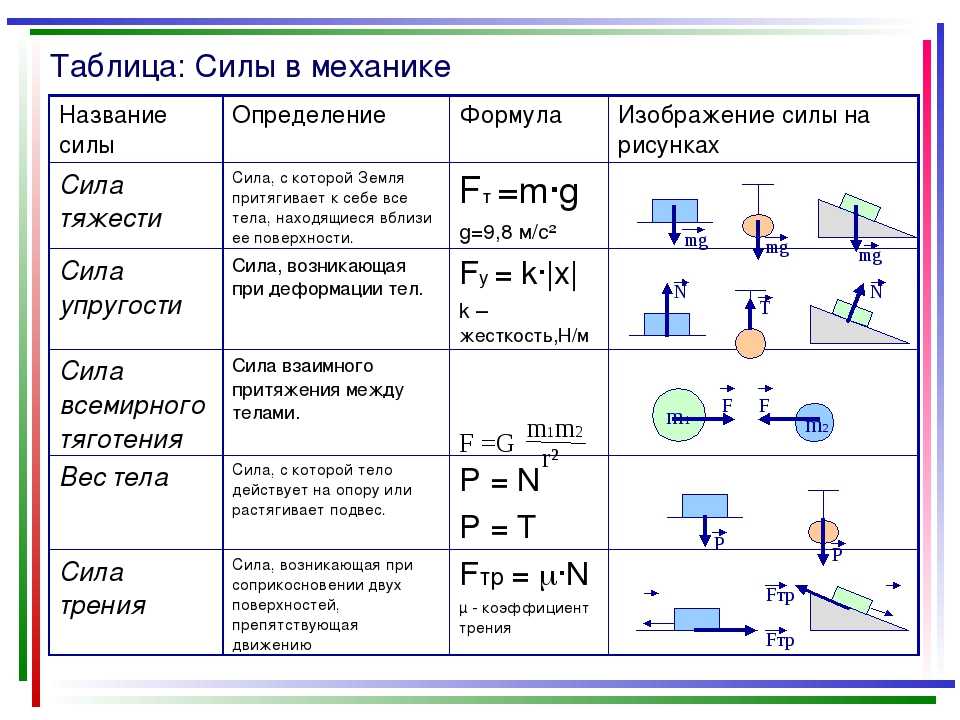

B – магнитная индукция

I – сила тока

l – длинна проводника

M – макс. момент сил

S – площадь рамки

Сила Лоуренца

;

n – концентр. свободных частиц

v –скорость упор. движ.

S –площадь поперечного сечения проводника

Магнитная прониуаемость.

;

– магнитная прониц. среды

H- напряженность магнитного поля.

Электромагнитная индукция

[Вб]

;

Ф – магнитный поток

;

Самоиндукция.

; [Гн]

;

; W – энергия

Магнитная рамка.

b,a – стороны рамки

S – площадь рамки

Электроны.

;

Электролиты

Оптика

Закон преломления

; – ваакум

; ; ;

– относит. показатель преломления.

– скорости света во 2-й и первой средах.

Линзы

d –расстояние предмета от линзы

f –расстояние от изображения до предмета

F – фокус

D –Оптическая сила линзы [диоптрии]

k – увеличение линзы

Квантовая физика

; ;

;

– длинна волны излучения

– импульс фотона

– частота излучения

В магнитно-преломляющих средах:

В однородно прозрачной среде:

– относит. диэликтрич. проницаемость среды

– относит. магнитная проницаемость среды.

n – постоянная

Уравнение Эйнштейна.

;

А – работа выхода электрона из в-ва

Фотоэффект.

Для того, чтобы фотоэффект имел место, необходимо что бы энергия кванта света была больше работы выхода. Предльное значение частоты, при которой еще наблюдается фотоэффект, наз. красной границей фотоэффекта.

Каковы наиболее распространенные физические уравнения?

Есть несколько физических уравнений, которые используются физиками для описания явлений мира и движения. Эти уравнения можно реорганизовать для решения с различными неизвестными переменными. Поэтому то, что может выглядеть как два отдельных уравнения, часто является переработанным одним и тем же уравнением. Некоторые из наиболее распространенных физических уравнений используются для описания энергии, силы и скорости.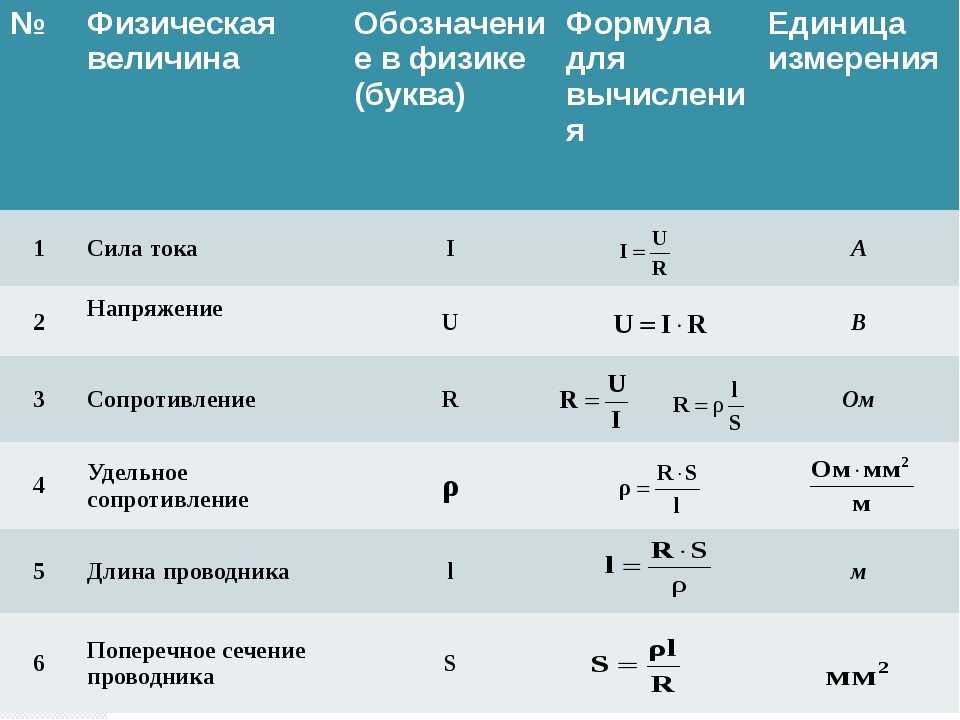 Эти уравнения могут помочь ученым выяснить, как объекты будут реагировать в определенных обстоятельствах, без необходимости непосредственно экспериментировать с объектами.

Возможно, самые известные физические уравнения связаны с энергией: E=mc2. В этом уравнении E обозначает энергию, m — массу, а c — скорость света в вакууме (около 186 000 миль в секунду или 3×108 метров в секунду. Это уравнение было разработано ученым Альбертом Эйнштейном. Он определил, что масса объекта и его энергия – это два типа одного и того же. Другими словами, масса объекта может быть преобразована в энергию и наоборот

Другие физические уравнения, имеющие отношение к энергии, это те, которые описывают кинетическую и потенциальную энергию Кинетическая энергия (K или иногда KE) описывается уравнением K=½mv2, где m равно массе объекта, а v равно скорости U=mgy — это физическое уравнение, описывающее потенциальную гравитационную энергию, где U означает потенциал энергии, m для массы, y для расстояния объекта над землей и g для ускорения силы тяжести на земле (примерно 32,174 фута/с2 или 90,81 м/с2). Это значение может незначительно меняться в зависимости от высоты и широты и технически является отрицательным числом, поскольку объект движется вниз, однако отрицательное значение часто игнорируется. Использование заглавной буквы в переменной «g» важно, поскольку «g» известно как ускорение свободного падения, а «G» — гравитационная постоянная.

Конечно, когда имеешь дело с гравитацией, чаще всего знаешь силу, с которой гравитация воздействует на объект. Это описывается физическим уравнением F=Gm1m2/r2. В этом случае G — обратите внимание на заглавные буквы — это универсальная гравитационная постоянная (примерно 6,67×10-11 Н.м2/кг2), m1 и m2 — две массы объектов, а r — расстояние между двумя объектами. Другое физическое уравнение, имеющее отношение к силе, описывает второй закон движения Ньютона. Это описывается выражением F=ma, где F — сила, m — масса, а — ускорение.

Физические уравнения, имеющие отношение к скорости: d=vt, описывающие расстояние, которое проходит объект за определенное время, и d=½at2+v0t, описывающие расстояние, пройденное при ускорении. В обоих уравнениях d обозначает расстояние, v — скорость, t — время. В первом уравнении t — это время, которое прошел объект, а во втором уравнении t обозначает время ускорения. Переменная а во втором уравнении обозначает ускорение объекта. Некоторые используют переменную vi для описания начальной скорости, а не v0.

Вам нужен репетитор по математике, чтобы заниматься с вами один на один? Свяжитесь с нашим академическим консультантом сегодня, чтобы подобрать онлайн-репетитора по математике!

Гармоническое движение

Гармоническое движение

Говорят, что объект, движущийся вдоль оси X, демонстрирует простое гармоническое движение , если его положение как функция времени изменяется как

x(t) = x ₀ + A cos(ωt + φ).

Объект колеблется вокруг положения равновесия x ₀ . Если мы выберем начало нашей системы координат так, что x ₀ = 0, тогда смещение x от положения равновесия в зависимости от времени равно

x(t) = A cos(ωt + φ).

А – амплитуда колебаний, т. е. максимальное смещение объекта из положения равновесия либо в положительное или отрицательное направление x. Простое гармоническое движение повторяется. период T — время, за которое объект совершить одно колебание и вернуться в исходное положение. угловая частота ω определяется как ω = 2π/T. Угловая частота измеряется в радианах в секунду. Обратная сторона период частота f = 1/T. частота f = 1/T = ω/2π движения дает число полных колебаний в единицу времени. Измеряется в герцах (1 Гц = 1/с).

Скорость объекта как функция времени определяется как

v(t) = dx(t)/dt = -ω A sin(ωt + φ),

а ускорение дается

a(t) = dv(t)/dt = -ω ² A cos(ωt + φ) = -ω ² x.

Величина φ называется фазовой постоянной . Он определяется начальными условиями движения. Если при t = 0 объект имеет максимальное смещение в положительном направлении x, тогда φ = 0, если он имеет максимальное смещение в отрицательном направлении x, тогда φ = π. Я толстый t = 0 частица движется через положение равновесия с максимальным скорость в отрицательном направлении x, тогда φ = π/2. Величина ωt + φ равна называется фаза .

На рисунке ниже положение и скорость представлены как функция времени. для колебательного движения с периодом 5 с. Амплитуда и максимальная скорость имеют условные единицы. Положение и скорость вне фазы . Скорость равна нулю при максимальном смещении, и смещение равно нулю на максимальной скорости.

Для простого гармонического движения ускорение a = -ω ² x равно пропорционально смещению, но в обратном направлении. Простой гармоническое движение – ускоренное движение . Если объект демонстрирует простое гармоническое движение, на него должна действовать сила. объект. Сила

F = ma = -mω ² х.

Он подчиняется закону Гука , F = -kx, при k = mω ² .

Ссылка: простая гармоническое движение (Youtube)

---

F = ma = md ² x/dt ² с F = -kx приводит к второго порядка дифференциальное уравнение

d ² х/dt ² = -(к/м)х.

Теперь мы знаем, как решить это уравнение. Решение

x(t) = Acos(ωt + φ), где ω ² = k/m.

Решение дифференциального уравнения второго порядка включает две константы интеграция. Здесь этими константами являются A и φ. Они определяются начальными условиями задачи.

Одни и те же уравнения имеют одни и те же решения. Всякий раз, когда вы сталкиваетесь с дифференциальное уравнение вида d ² x/dt ² = -b ² x, знаете ли что решение x(t) = Acos(ωt + φ), при ω = b.

---

Сила пружины подчиняется закону Гука. Предположим, что объект прикреплен к пружине, которая растягивается или сжимается. Тогда пружина давит сила на объект. Эта сила пропорциональна смещению х тела. пружинит из положения равновесия и движется в направлении, противоположном смещение.

Ф = -кх

Предположим, что пружина растянута на расстояние A от положения равновесия, а затем отпущена. Объект прикрепленный к пружине, ускоряется, возвращаясь к положению равновесия.

a = -(к/м)х

Он набирает скорость по мере продвижения к положению равновесия, потому что его ускорение направлено в сторону его скорости. Когда он находится в равновесии положение, ускорение равно нулю, но объект имеет максимальная скорость. Он выходит за пределы положения равновесия и начинает замедляться. вниз, потому что ускорение теперь в направлении, противоположном направлению от его скорости. Пренебрегая трением, он останавливается, когда пружина сжимается на расстояние А, а затем ускоряется обратно к равновесию должность. Он снова промахивается и останавливается в исходном положении, когда пружина растягивается на расстояние A. Движение повторяется. Объект колеблется взад и вперед. Он выполняет простое гармоническое движение. Угловой частота движения

ω = √(к/м),

период

Т = 2π√(м/к),

и частота

f = (1/(2π))√(к/м).

Резюме: Если единственная сила, действующая на тело массой m, является силой закона Гука, F = -kx тогда движение объекта представляет собой простое гармоническое движение. Если x — смещение от равновесия, мы имеем . х(t) = Acos(ωt + φ), v(t) = -ωAsin(ωt + φ), a(t) = -ω2Acos(ωt + φ) = -ω2x. ω = (к/м) ½ = 2πf = 2π/T. А = амплитуда ω = угловая частота f = частота Т = период φ = фазовая постоянная

Проблема:

Частица совершает простые гармонические колебания, так что ее перемещение изменяется согласно выражению x = (5 cm)cos(2t + π/6) где x в сантиметрах, t в секундах. При t = 0 найти
(а) смещение частицы,
(б) его скорость и
(c) его ускорение.
(г) Найдите период и амплитуду движения.

Решение:

• Обоснование:
  Анализ простого гармонического движения.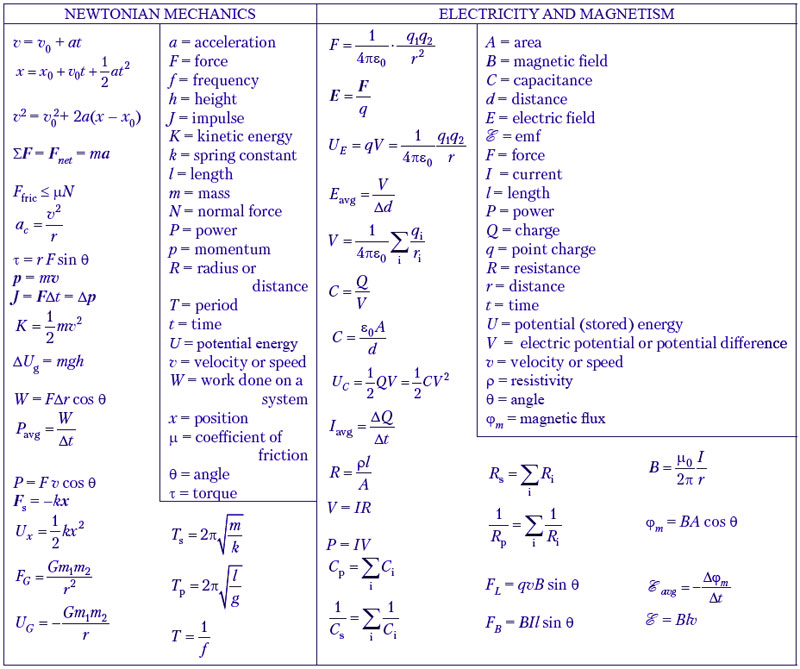
  x(t) = A cos(ωt + φ). A = амплитуда, ω = угловая частота, φ = фазовая постоянная.
  v(t) = -ω A sin(ωt + φ), a(t) = -ω ² A cos(ωt + φ) = -ω ² x.
• Детали расчета:
  (a) Смещение как функция времени: x(t) = Acos(ωt + ф). Здесь ω = 2/s, φ = π/6, A = 5 см.
  Перемещение при t = 0 равно x(0) = (5 см)cos(π/6) = 4,33 см.
  (b) Скорость при t = 0 равна v(0) = -ω(5 см)sin(π/6) = -5 см/с.
  (c) Ускорение при t = 0 равно a(0) = -ω ² (5 см)cos(π/6) = -17,3 см/с ² .
  (d) Период движения T = 2π/ω = π с, а амплитуда равна 5 см.

Проблема:

Частица массой 20 г движется в простом гармоническом движении с частотой 3 колебаний в секунду и амплитудой 5 см.
(а) Какое общее расстояние проходит частица за один цикл его движение?
(b)  Какова его максимальная скорость? Где это происходит?
(с) Найдите максимальное ускорение частицы. Где в движении делает происходит максимальное ускорение?

Решение:

• Рассуждение:
  Проанализируйте простое гармоническое движение, x(t) = A cos(ωt + φ).
• Детали расчета:
  (a) Общее расстояние d, которое проходит частица за один цикл, равно от x = -A до x = +A и обратно к x = -A, поэтому d = 4A = 20 см.
  (b) Максимальная скорость частицы
  v _макс. = ωA = 2πfA = 2π 15 см/с = 0,94 м/с.
  Частица имеет максимальную скорость при прохождении через положение равновесия.
  (c) Максимальное ускорение частицы равно
  до _макс. = ω ² А = (2πf) ² А = 17,8 м/с ² .
  Частица имеет максимальное ускорение в точках поворота, где имеет максимальное водоизмещение.

Проблема:

Груз массой 1 кг, прикрепленный к пружине с постоянной силой 25 Н/м, совершает колебания на горизонтальная дорожка без трения. При t = 0 масса выходит из состояния покоя при x = -3 см, то есть пружина сжата на 3 см. Пренебречь массой весны. Найти
(а) период его движения,
(б) максимальное значение его скорости и ускорения и
(в) перемещение, скорость и ускорение как функция времени.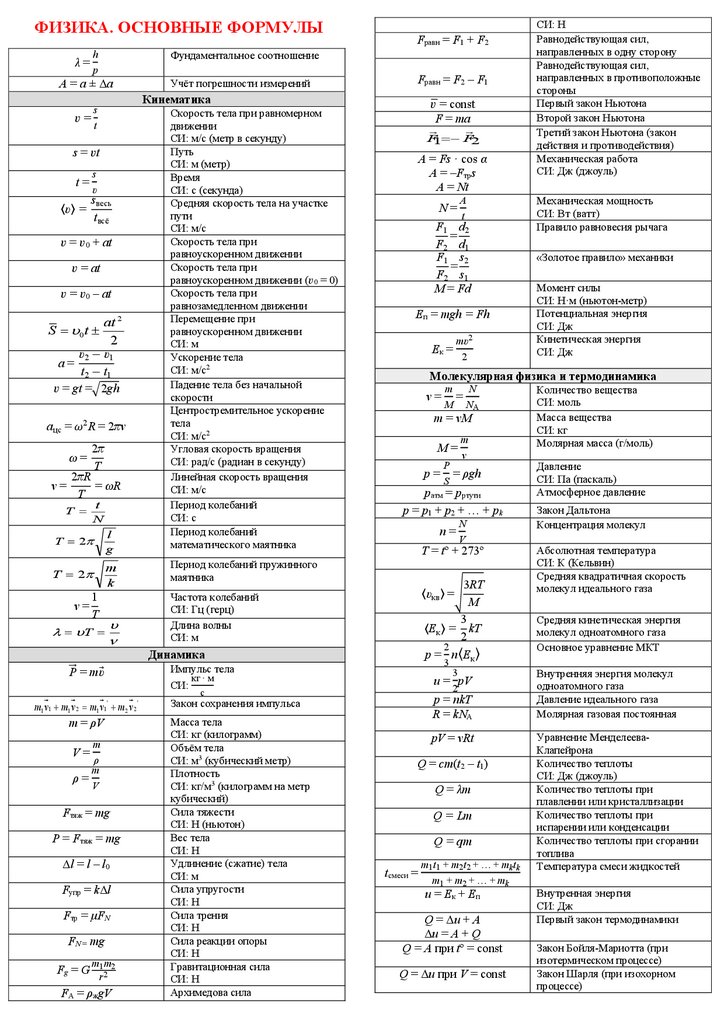

Решение:

• Обоснование:
  Для простого гармонического движения
  x(t) = Acos(ωt + φ),
  v(t) = -ωAsin(ωt + φ),
  a(t) = -ω2Acos(ωt + φ) = -ω2x.
  ω = (к/м) ^½ = 2πf = 2π/T.
• Детали расчета:
  (a) Период равен T = 2π(m/k) ^½ = 2π(1 с ² /25) ^½ = 1,26 с.
  (b)  Угловая скорость ω = (к/м) ^½ = 5/с.
  Максимальная скорость v _max = ωА = 15 см/с.
  Максимальное ускорение частицы составляет _макс. = ω ² А = 0,75 м/с ² .
  (в) x(t) = Acos(ωt + φ) = (3 см)cos((5/с)t + π) = -(3 см)cos((5/с)t),
  v(t) = -ωAsin(ωt + φ) = (15 см/с)sin((5/с)t),
  a(t) = -ω ² Acos(ωt + φ) = (0,75 м/с ² )cos((5/с)t).

Предположим, что масса подвешена к вертикальной пружине с жесткостью k. В равновесия пружина растянута на расстояние x ₀ = mg/k. Если масса смещается из положения равновесия вниз, а пружина растягивается дополнительное расстояние x, то полная сила, действующая на массу, равна mg – k(x ₀ + x) = -kx, направленный в сторону положения равновесия. Если масса смещен вверх на расстояние x, то полная сила, действующая на массу, равна mg – k(x ₀ – х) = кх, направленный к положению равновесия. Масса будет выполнять простые гармонические движения. Угловая частота ω = (к/м) ^½ то же для массы, колеблющейся на пружине в вертикальном или горизонтальном положении. Но равновесная длина пружины, вокруг которой она колеблется, различна для вертикальное положение и горизонтальное положение.

---

Предположим, что объект, прикрепленный к пружине, совершает простое гармоническое движение. Позволять один конец пружины прикрепите к стене и дайте предмету двигаться горизонтально на столе без трения.

Какова полная энергия объекта?

Кинетическая энергия объекта

K = ½mv ² = ½mω ² A ² sin ² (ωt + ф).

Его потенциальная энергия является упругой потенциальной энергией. Упругий потенциал энергия, накопленная в пружине, смещенной на расстояние x от положения равновесия U = ½kx ² . Таким образом, потенциальная энергия объекта равна

.

U = ½kx ² = ½mω ² x ² = ½mω ² A ² cos ² (ωt + φ).

Полная механическая энергия объекта

E = K + U = ½mω ² A ² (sin ² (ωt + φ) + cos ² (ωt + φ)) = ½mω ² A ² .

Энергия E в системе пропорциональна квадрату амплитуды .

E = ½ кА ² .

Это постоянно меняющаяся смесь кинетической и потенциальной энергии.

Для любого объекта, совершающего простое гармоническое движение с угловой частотой ω, восстанавливающая сила F = -mω ² x подчиняется закону Гука и, следовательно, является консервативная сила . Мы можем определить потенциальную энергию U = ½mω ² x ² , а полная энергия объекта определяется выражением E = ½mω ² А ² .

Проблема:

Частица, подвешенная на пружине, совершает колебания с угловой частотой 2 рад/с. Пружина подвешена к потолку кабины лифта и висит неподвижно (относительно автомобиля) по мере снижения автомобиля с постоянной скоростью 1,5 РС. Затем машина внезапно останавливается. Массой пружины пренебречь.
С какой амплитудой колеблется частица?

Решение:

• Рассуждение:
  При движении в лифте с постоянной скоростью общая сила, действующая на масса равна нулю. Сила, действующая на пружину, по величине равна силе силы тяжести, действующей на массу, пружина имеет равновесную длину вертикальная пружина. Когда лифт внезапно останавливается, конец пружины крепятся к потолочным упорам. Однако масса имеет импульс, p = mv, и поэтому начинает растягивать пружину. Он движется через положение равновесия вертикальной пружины с ее максимальной скоростью v _макс. = 1,5 м/с.
  Его скорость как функция времени равна v(t) = -ωAsin(ωt + φ).