ТЕХНОЛОГИЯ МАГНИТНОЙ ОБРАБОТКИ ВОДЫ ПРОТИВ СОЛЕОТЛОЖЕНИЯ: ТЕОРИЯ И ПРАКТИКА
Актуальность исследования определяется широким применением водных георесурсов в качестве рабочих тел в гидро- и теплоэнергетике, в системах теплоснабжения и охлаждения. При этом часто требуется произвести технологическую водоподготовку перед выполнением основного производственного цикла. В частности,воду требуется очищать от коллоидных, накипеобразующих и газообразных примесей. Наибольшую сложность представляет очистка воды от солей жесткости, то есть ее умягчение. Соли кальция и магния обычно выпадают на поверхностях теплообмена с образованием накипи, что приводит к резкому снижению эффективности работы теплообменного оборудования, перерасходу топлива и частым остановкам для чистки. Удаляют накипь обычно путем кислотных промывок внутренних поверхностей теплообмена или механическим способом. Все эти методы связаны с применением большого количества химических реагентов и сильно загрязняют сточные воды.
 Описаны электрохимические процессы, происходящие на этапе магнитной обработки и на последующем этапе нагревания омагниченной воды. Показано, что в присутствии магнитного поля ионы разных знаков дрейфуют во взаимно противоположных направлениях. По этой причине образование гидрокарбонатов кальция и магния на поверхности нагревателя затруднено.Как следствие, не происходит и отложения карбонатов на нагреваемых поверхностях.Определена наиболее эффективная конструкция магнитной установки, ее оптимальные параметры. Приведены сведения об эксплуатации установок «Магнуст» на нескольких бытовых и производственных объектах.
Описаны электрохимические процессы, происходящие на этапе магнитной обработки и на последующем этапе нагревания омагниченной воды. Показано, что в присутствии магнитного поля ионы разных знаков дрейфуют во взаимно противоположных направлениях. По этой причине образование гидрокарбонатов кальция и магния на поверхности нагревателя затруднено.Как следствие, не происходит и отложения карбонатов на нагреваемых поверхностях.Определена наиболее эффективная конструкция магнитной установки, ее оптимальные параметры. Приведены сведения об эксплуатации установок «Магнуст» на нескольких бытовых и производственных объектах.Урок 3. магнитная индукция. действие магнитного поля на проводник с током и движущуюся заряженную частицу – Физика – 11 класс
Физика, 11 класс
Урок 3. Магнитная индукция. Действие магнитного поля на проводник и движущуюся заряжённую частицу
Перечень вопросов, рассматриваемых на уроке:
1) магнитное поле;
2) вектор магнитной индукции, линии магнитной индукции;
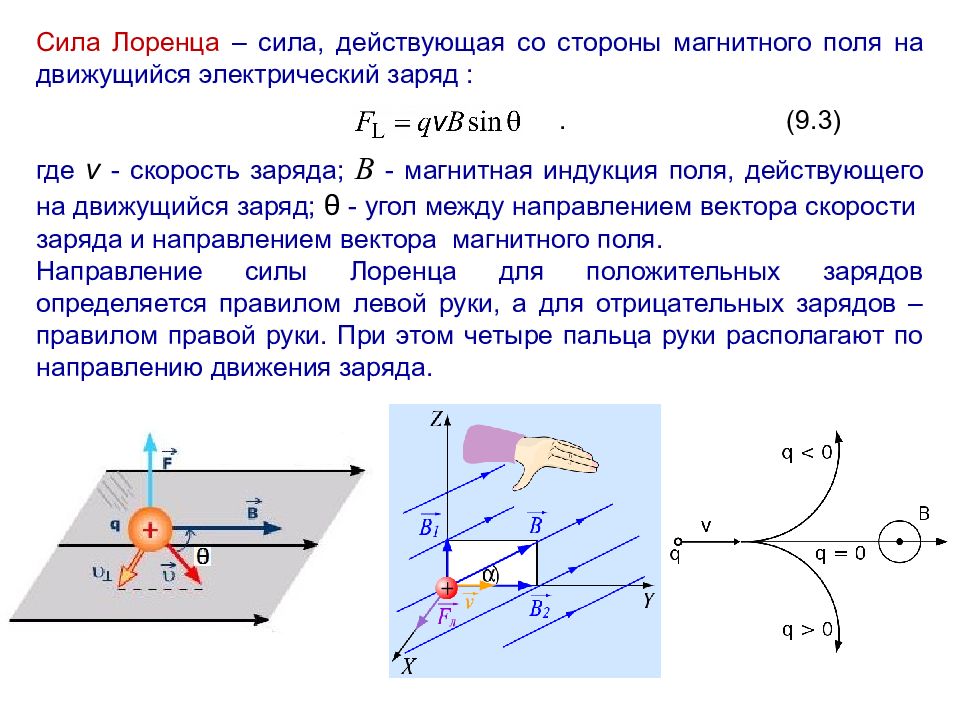
3) сила Ампера, сила Лоренца;
4) правило буравчика, правило левой руки.
Глоссарий по теме
Магнитная индукция – векторная величина, характеризующая величину и направление магнитного поля.
Сила Ампера – сила, действующая со стороны магнитного поля на проводник с током.
Сила Лоренца – сила, действующая со стороны магнитного поля на движущую частицу с зарядом.
Правило «буравчика» – правило для определения направления магнитного поля проводника с током.
Правило левой руки – правило для определения направления силы Ампера и силы Лоренца.
Соленоид – проволочная катушка.
Рамка с током – небольшой длины катушка с двумя выводами из скрученного гибкого проводника с током, способная поворачиваться вокруг оси, проходящей через диаметр катушки.
Основная и дополнительная литература по теме урока
Мякишев Г.Я., Буховцев Б.Б.,. Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций. М.: Просвещение, 2014. – С. 3 – 20
2. А.П. Рымкевич. Сборник задач по физике. 10-11 классы. – М: Дрофа, 2009. – С.109 – 112
– С.109 – 112
Основное содержание урока
Магнитное поле – особый вид материи, которая создаётся электрическим током или постоянными магнитами. Для демонстрации действия и доказательства существования магнитного поля служат магнитная стрелка, способная вращаться на оси, или небольшая рамка (или катушка) с током, подвешенная на тонких скрученных гибких проводах.
Рамка с током и магнитная стрелка под действием магнитного поля поворачиваются так, что северный полюс (синяя часть) стрелки и положительная нормаль рамки указывают направление магнитного поля.
Магнитное поле, созданное постоянным магнитом или проводником с током, занимает всё пространство в окрестности этих тел. Магнитное поле принято (удобно) изображать в виде линий, которые называются линиями магнитного поля. Магнитные линии имеют вихревой характер, т.е. линии не имеют ни начала, ни конца, т.е. замкнуты. Направление касательной в каждой точке линии совпадает с направлением вектора магнитной индукции.
Магнитное поле характеризуется векторной величиной, называемой магнитной индукцией. Магнитная индукция характеризует «силу» и направление магнитного поля – это количественная характеристика магнитного поля.
Она обозначается символом За направление вектора магнитной индукции принимают направление от южного полюса к северному магнитной стрелки, свободно установившейся в магнитном поле.
Направление магнитного поля устанавливают с помощью вектора магнитной индукции.
Направление вектора магнитной индукции прямого провода с током определяют по правилу буравчика (или правого винта).
Правило буравчика звучит следующим образом:
если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока.
Направление магнитного поля внутри соленоида определяют по правилу правой руки.
Определим модуль вектора магнитной индукции.
Наблюдения показывают, что максимальное значение силы, действующей на проводник, прямо пропорционально силе тока, длине проводника, находящегося в магнитном поле.
F_max ~ I; F ~ Δl.
Тогда, зависимость силы от этих двух величин выглядит следующим образом
Отношение зависит только от магнитного поля и может быть принята за характеристику магнитного поля в данной точке.
Величина, численно равная отношению максимальной силы, действующей на проводник с током, на произведение силы тока и длины проводника, называется модулем вектора магнитной индукции:
Единицей измерения магнитной индукции является 1 тесла (Тл).
1Тл = 1Н/(1А∙1м).
Закон Ампера:
Сила, действующая на проводник с током в магнитном поле, равна произведению модуля магнитной индукции, силы тока, длины проводника и синуса угла между вектором магнитной индукции и направлением тока:
где α – угол между вектором B и направлением тока.
Направление силы Ампера определяется правилом левой руки:
Если ладонь левой руки развернуть так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90
Сила Ампера – сила, действующая на проводник с током со стороны магнитного поля.
Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля. Её численное значение равно произведению заряда частицы на модули скорости и магнитной индукции и синус угла меду векторами скорости и магнитной индукции:
– заряд частицы;
– скорость частицы;
B – модуль магнитной индукции;
– угол между векторами скорости частицы и магнитной индукции.
Направление силы Лоренца также определяют по правилу левой руки:
Если четыре вытянутых пальца левой руки направлены вдоль вектора скорости заряженной частицы, а вектор магнитной индукции направлен в ладонь, то отведённый на 90 Если частица имеет заряд отрицательного знака, то направление силы Лоренца противоположно тому направлению, которое имела бы положительная частица.
Если частица имеет заряд отрицательного знака, то направление силы Лоренца противоположно тому направлению, которое имела бы положительная частица.
Получим формулы для радиуса окружности и периода вращения частицы, которая влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции, применяя формулы второго закона Ньютона и центростремительного ускорения.
Согласно 2-му закону Ньютона
Отсюда
Время, за которое частица делает полный оборот (период обращения), равно:
Многим юным бывает досадно, что они не родились в старые времена, когда делались открытия. Им кажется, что теперь всё известно и никаких открытий на их долю не осталось.
Одной из нераскрытых тайн является механизм земного магнитного поля. Как же и чем вызывается магнитное поле Земли? Подумайте и может быть…
Одна из возможных гипотез.
Как известно, ядро Земли имеет высокую температуру
и высокую плотность. Судя по исследованиям, в самом центре содержится твёрдое ядро. При вращении Земли вокруг своей оси центр тяжести не совпадает с геометрическим центром из-за притяжения Солнца. В результате сместившееся из центра ядро вращаясь относительно оболочки Земли вызывает такое же движение жидкой расплавленной массы мантии, как чайная ложка, перемешивающая воду в стакане. Получается не что иное, как направленное движение зарядов. Есть электрический ток, а он, в свою очередь, создаёт магнитное поле.
Судя по исследованиям, в самом центре содержится твёрдое ядро. При вращении Земли вокруг своей оси центр тяжести не совпадает с геометрическим центром из-за притяжения Солнца. В результате сместившееся из центра ядро вращаясь относительно оболочки Земли вызывает такое же движение жидкой расплавленной массы мантии, как чайная ложка, перемешивающая воду в стакане. Получается не что иное, как направленное движение зарядов. Есть электрический ток, а он, в свою очередь, создаёт магнитное поле.
Разбор тренировочных заданий
1. На рисунке изображён проводник с током, помещённый в магнитное поле. Стрелка указывает направление тока в проводнике. Вектор магнитной индукции направлен перпендикулярно плоскости рисунка к нам. Как направлена сила, действующая на проводник с током?
Варианты ответов:
1. вправо →;
2. влево ←;
3. вниз ↓;
4. вверх ↑.
– точка означает, что магнитная индукция направлена на нас из глубины плоскости рисунка.
Используя правило левой руки, определяем направление силы Ампера:
Левую руку располагаем так, чтобы линии магнитной индукции входили в ладонь, 4 пальца направим вниз по направлению тока, тогда отогнутый на 900 большой палец покажет направление силы Ампера, т. е. она направлена влево.
е. она направлена влево.
Правильный вариант:
2. влево ←.
2. По проводнику длиной 40 см протекает ток силой 10 А. Чему равна индукция магнитного поля, в которое помещён проводник, если на проводник действует сила 8 мН?
(Ответ выразите в мТл).
3. Определите модуль силы, действующей на проводник длиной 50 см при силе тока 10 А в магнитном поле с индукцией 0,15 Тл. (Ответ выразите в мН).
4. Протон в магнитном поле с индукцией 0,01 Тл описал окружность радиусом 10 см. Найдите скорость протона. (Ответ выразите в км/с, округлив до десятков)
5. С какой скоростью влетает электрон в однородное магнитное поле (индукция 1,8 Тл) перпендикулярно к линиям индукции, если магнитное поле действует на него с силой 3,6∙10–¹² Н? Ответ выразите в км/с.
6. Электрон движется в однородном магнитном поле с индукцией 3,14мТл. Чему равен период обращения электрона? (Ответ выразите в наносекундах, округлив до целых)
2. Дано:
l = 40cм = 0,4 м,
I = 10 A,
F =8 мН = 0,008 Н.
Найти: B
Решение:
Запишем формулу модуля магнитной индукции:
Делаем расчёт:
B = 0,008 Н / ( 0,4м·10 A) = 0,002 Tл = 2 мTл.
Ответ: 2 мTл.
3. Дано:
l = 50 cм = 0,5 м,
I = 10 A,
B = 0,l5 Tл.
Найти: F
Решение:
Запишем формулу силы Ампера:
Делаем расчёт:
F = 0,l5 Tл· 10 A· 0,5 м = 0,75 Н = 750 мН
Ответ: 750 мН.
4. Дано:
B = 0,0l Tл,
r = l0 cм = 0,l м.
Найти: v
Решение:
Заряд протона равен: q₀ = l,6·l0⁻ˡ⁹ Кл,
масса протона: m = l,67·l0⁻²⁷ кг.
Согласно 2-му закону Ньютона:
Отсюда следует:
Делаем расчёт:
v = ( l,6·l0⁻ˡ⁹ Кл·0,l м·0,0l Tл) / l,67·l0⁻²⁷ кг ≈ 0,00096·l0⁸ м/с ≈ l00 км/с.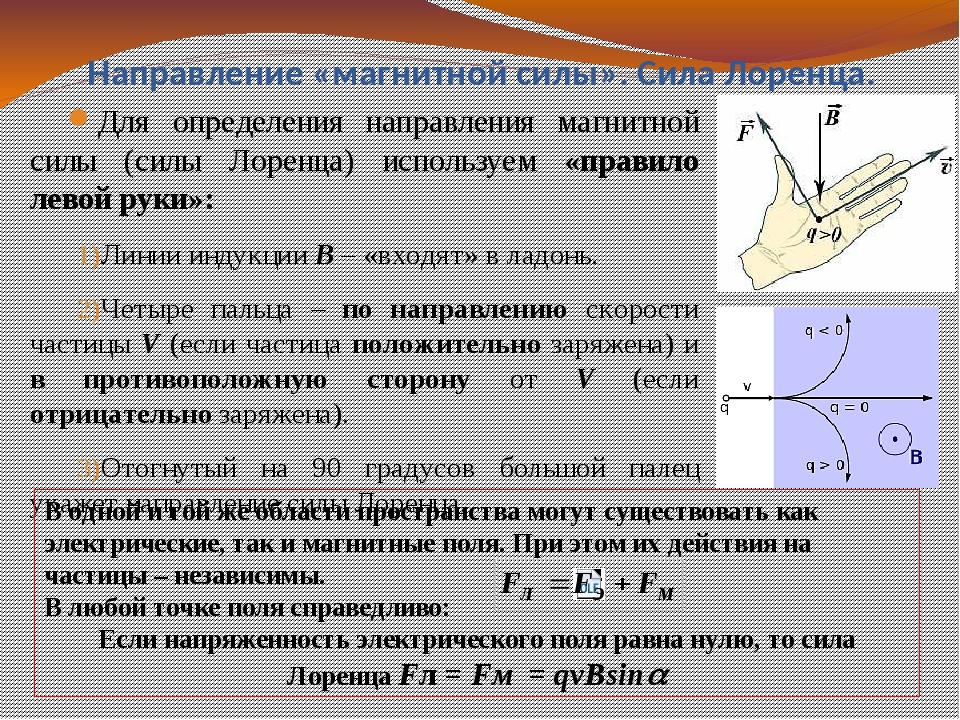
Ответ: v ≈ l00 км/с.
5. Дано:
B = l,8 Tл,
F = 3,6·l0⁻¹² Н,
α = 90°.
Найти:
Решение:
Заряд электрона равен: q₀ = l,6·l0⁻ˡ⁹ Кл.
Используем формулу силы Лоренца:
.
Выразим из формулы силы скорость, учитывая, что sin90°=l,
Делаем расчёт:
v = 3,6·l0⁻¹² Н / (l,6·l0⁻ˡ⁹ Кл· l,8 Tл) = l,25·l0⁷м/с = l2500 км/с.
Ответ: v = l2500 км/с.
6. Дано:
B = 3,l4 мТл = 3,l4·l0⁻³ Tл,
q₀ = l,6·l0⁻ˡ⁹ Кл,
Найти: Т
Решение:
Масса электрона равна: m = 9,l·l0⁻³¹ кг.
Время, за которое частица делает полный оборот (период обращения), равно:
Делаем расчёт:
T = 2·3,l4·9,l·l0⁻³¹ кг/( l,6·l0⁻ˡ⁹ Кл·3,l4·l0⁻³ Tл) = ll,375·l0⁻⁹ с ≈ ll нс.
Ответ: T ≈ ll нс.
Сила магнита: от чего она зависит?
Всем известно, что магнит обладает мощным магнитным полем. Это природный материал, который можно встретить в виде камня магнетита. Этот камень обладает особым свойством – он способен притягивать не только подобные камни, но и металлические предметы. На языках многих народов слово «магнит» означает «любящий». Это связано с его «желанием» притягиваться к другим предметам.
Существую искусственные магниты, которые создают из порошка: кобальт, железо и др.
Магнитная сила
Рассматривая магниты, можно заметить, что сила притягивания, например, к одному и тому же предмету у разных магнитов разная. Именно этот момент и называется магнитной силой. Так от чего же она зависит?
Чтобы понять различие, необходимо взять несколько магнитов разной формы и размера – диск, брусок, магнит в виде подковы. Также для сравнения нужны любые железные предметы: гайки, скрепки, саморезы, которые горкой высыпаем в 3 разные тарелки.
А дальше всё просто: магниты по очереди подносятся к каждой тарелки, и считается количество примагниченных предметов одного типа.
Результат будет в том, сколько одинаковых предметов поднимает каждый из магнитов.
Итог:
Сила магнита напрямую зависит от формы и размера магнита. Так, магнит-подкова мощнее прямоугольника, а диск слабее прямоугольника. Если взять магниты одной формы, но с разным размером, то сильнее окажется самый большой.
Магнитная сила и вода
Чтобы проверить, работает ли магнитная сила через воду, необходимо взять следующие предметы:
- Стакан с водой
- Скрепка
- Магнит
Опускаем скрепку в стакан с водой. Прислоняем магнит к стенке стакана и скрепка начинает приближаться к нему. Если двигать магнитом вдоль стакана, скрепка также будет двигаться за ним. Таким способом можно достать скрепу, не намочив руки.
Итог:
Вода никаким образом не мешает действию магнитной силы. Более того, будь стакан железным, опыт проходил бы ровно также, только с меньшей силой. Это связано с тем, что металл поглощает магнитную силу.
Моделирование электродинамических подшипников в среде COMSOL Multiphysics®
Электродинамические или магнитные подшипники используются во многих отраслях промышленности, включая производство электроэнергии, переработку нефти, в турбинных механизмах, насосах и инерциальных системах накопления энергии. В отличие от механических подшипников, такие подшипники позволяют подвижные нагрузки без физического контакта за счет магнитной левитации. Магнитные подшипники ценятся за отсутствие трения и возможность работы без смазки и, благодаря низким эксплуатационным расходам, являются альтернативой механическим подшипникам, при этом имея более долгий срок службы. Давайте ознакомимся с техниками вычисления параметров конструкции, таких как магнитные силы, вращающий момент и магнитная жесткость, с использованием пакета COMSOL Multiphysics®.
Виды магнитных подшипников
По принципу действия магнитные подшипники могут быть классифицированы на: активные магнитные подшипники (АМП) и пассивные магнитные подшипники (ПМП). АМП функционируют за счет притяжения между ферромагнитным материалом и электромагнитами (катушка и сердечник). В ПМП используется отталкивающая сила между постоянными магнитами (ПМ) и/или проводящей поверхностью и ПМ.
Активные магнитные подшипники
Активные магнитные подшипники состоят из неподвижной части — статора, который содержит электромагниты и датчики положения, и вращающейся части — ротора, который двигается вместе с валом. При нормальных условиях работы, ротор идеально центрируется, образуя эквидистантный зазор вокруг статора. Однако, при возмущениях положение ротора контролируется с помощью замкнутой системы с обратной связью. Изменение положения ротора измеряется датчиком, а данные затем передаются цифровому контроллеру. После обработки данных, контроллер посылает сигнал усилителю мощности. Усилитель перенастраивает токи в электромагнитах для того, чтобы вернуть ротор в исходное положение. Чтобы подрегулировать ротор, для конструкторов важно знать магнитную силу при различных положениях ротора, а также соответствующие токи.
Усилитель перенастраивает токи в электромагнитах для того, чтобы вернуть ротор в исходное положение. Чтобы подрегулировать ротор, для конструкторов важно знать магнитную силу при различных положениях ротора, а также соответствующие токи.
Схематическое изображение компонентов АМП. Изображение из Wikimedia Commons.
Преимущество АМП заключается в активном контроле положения ротора, но это означает более высокую стоимость создания их электронной схемы, а также больших эксплуатационных расходов. Эксплуатационные расходы конечно могут быть уменьшены, путем оптимизацией дизайна электромагнитов для уменьшения энергии, требуемой на их питание. COMSOL Multiphysics является полезным инструментом в данном процессе оптимизации.
Наиболее удобный способ в COMSOL для проектирования АМП, включая статор и ротор, заключается в использовании интерфейса Вращающиеся Механизмы, Магнетизм (Rotating Machinery, Magnetic) в модуле AC/DC. При этом процесс моделирования очень похож на такой же для электрического генератора или двигателя, который уже был продемонстрирован в нашей обучающей модели Generator in 2D tutorial. Общие рекомендации вы можете прочитать в нашей предыдущей записи “Каким образом моделировать вращающиеся механизмы в 3D-пространстве”.
Общие рекомендации вы можете прочитать в нашей предыдущей записи “Каким образом моделировать вращающиеся механизмы в 3D-пространстве”.
С использованием интерфейса Магнитные Поля (Magnetic Fields), вы можете моделировать постоянные магниты, а также проводящие катушки (в том числе в приближении однородной многовитковой катушки). Однако, вы не сможете учесть индуцированный ток вызванный вращением. Если индуцированными токами можно пренебречь, вы можете настроить стационарное решение или решение в частотной области, а затем добавить параметрическое исследование для различных положений ротора для вычисления магнитной силы или крутящего момента.
Пассивные магнитные подшипники
Пассивные магнитные подшипники используют постоянные магниты и не требуют датчика, управляющих схем или питания. Постоянный воздушный зазор сохраняется магнитной силой отталкивания между противоположными полюсами ПМ, как продемонстрировано здесь, или электродинамической подвеской между ПМ и вращающимся диском или валом, как показано здесь. Геометрия и результаты моделирования пассивного магнитного подшипника с использованием ПМ, показаны ниже.
Геометрия и результаты моделирования пассивного магнитного подшипника с использованием ПМ, показаны ниже.
Слева: Геометрия осевого магнитного подшипника с постоянными магнитами. Направление намагничивания постоянных магнитов изображено чёрными стрелками. Справа: График, демонстрирующий магнитную индукцию (стрелочная диаграмма) и норму магнитной индукции (поверхностный график).
Электродинамические подшипники
При вращении в магнитном поле, созданном постоянным магнитом, электропроводящий ротор вызывает вихревые токи на проводящем роторе. Эти вихревые токи, в свою очередь, генерируют магнитное поле, которое противонаправлено магнитным полям ПМ и вызывает силы отталкивания между вращающимся проводником и стационарным ПМ. Смещение ротора всегда компенсируется этой отталкивающей магнитной силой. Таким образом, ротор продолжает вращаться в центре с равномерным зазором.
Электродинамические подшипники могут быть далее классифицированы как радиальные электродинамические и осевые электродинамические подшипники.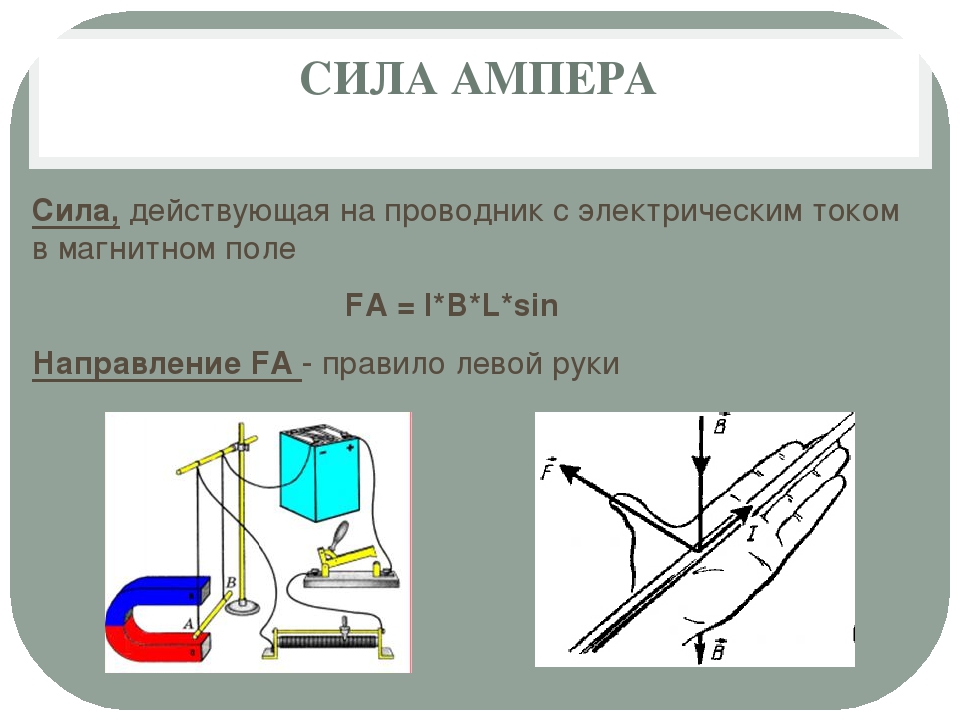 Это разделение основано на том, параллелен ли магнитный поток оси ротора, либо, соответственно, перпендикулярен.
Это разделение основано на том, параллелен ли магнитный поток оси ротора, либо, соответственно, перпендикулярен.
Электродинамическая радиальный подшипник
Радиальный электродинамический подшипник состоит из проводящего цилиндра, прикрепленного к вращающемуся валу. Компоненты ПМ помещены между железными кольцами в стек так, что радиально внутренний или наружный магнитный поток — относительно оси вала — создаётся в воздушном зазоре между статором и ротором. Учебная модель Электродинамический подшипник, доступная в нашей Галереи приложений, использует для решения интерфейс Магнитные и Электрические Поля (Magnetic and Electric Fields). При этом магнитные силы рассчитываются для различных положений смещения.
Слева: 3D-геометрия радиального электродинамического подшипника. Справа: Радиальный электродинамический подшипник и изображение магнитной индукции в статоре (магнитопровод и магниты) и вихревые токи (в оттенках серого) в проводящем роторе при смещении вдоль оси x на 1. 5 мм.
5 мм.
Осевой электродинамический подшипник
Ниже показано поперечное сечение конфигурации осевого электродинамического подшипника. Проводящий диск прикреплен к ротору и магнитный материал (железный “хомут”) используется для отведения магнитных полей от ПМ так, чтобы линии магнитной индукции стали параллельны оси ротора. Именно по этому и появился термин осевой электродинамический подшипник.
В этой конструкции, путь магнитного потока является очень эффективным при относительно небольшом воздушном зазоре. Полная учебная модель доступна для скачивания из нашей Галереи Приложений.
Слева: Поперечный срез осевого электродинамического подшипника. Справа: Осевой электродинамический подшипник, с изображением магнитной индукции в статоре и вихревых токов в проводящем роторе. Стрелочная диаграмма для магнитной индукции в статоре и вихревых токов в роторе.
Оба примера электродинамических подшипников, рассмотренных выше, смоделированы в среде COMSOL Multiphysics с использованием интерфейса Магнитные и Электрические Поля. В обоих случаях, функция Скорость (фактор Лоренца) используется, чтобы задать скорость вращения. С помощью такого подхода, вам не нужно будет использовать интерфейс Двигающаяся сетка (Moving Mesh) для учета вращения ротора.
В обоих случаях, функция Скорость (фактор Лоренца) используется, чтобы задать скорость вращения. С помощью такого подхода, вам не нужно будет использовать интерфейс Двигающаяся сетка (Moving Mesh) для учета вращения ротора.
Обратите внимание на то, что функция Velocity Lorentz Term может быть использована только в случае, когда движущаяся область не содержит магнитных источников, таких как токи или намагничивание (фиксированное или индуцированное), которые двигаются вместе с материалом, и двигающиеся области являются инвариантными в направлении перемещения. В частности, функция Velocity Lorentz Term может использоваться для моделирования проводящего (не магнитный) однородного вращающегося диска. Другие примеры включают применения в моделях магнитных тормозов, электродинамического подшипника, униполярного электрического генератора, магнитов над движущейся бесконечной однородной плоскостью (в частности магнита,падающего внутри медной трубы, или поезда на магнитной подушке), потока однородной проводящей жидкости через магнита (в частности насосов для жидких металлов или датчиков Холла, а также электрогидравлических преобразователей).
Примечание: Область, на которую применяется функция Velocity Lorentz Term, не может содержать токи или постоянные магниты. Кроме того, вращающаяся область не может представлять собой проницаемый или насыщаемый материал (например железо), так как они будут содержать индуцированную намагниченность. Движущиеся магнитные источники, индуцированные в магнитном материале, в свою очередь вызвали бы электрическое поле в окружающих участках, которое не может быть смоделировано данной функцией.
Магнитная сила/крутящий момент
В среде COMSOL Multiphysics доступны два метода для вычисления электромагнитных сил и крутящих моментов. Наиболее общим методом является метод тензора натяжений Максвелла (Maxwell stress tensor), который используется функцией Вычисление Силы (Force Calculation) в интерфейсах Магнитные поля; Магнитные Поля, без токов; Магнитные и Электрические Поля Вращающиеся Механизмы, Магнетизм.
Таким образом, при добавлении этой функции, для постобработки становятся доступны пространственный компоненты магнитных сил (mf.Forcex_0, mf.Forcey_0, mf.Forcez_0) и осевой крутящий момент ( mf.Tax_0) в интерфейсе Магнитные поля. Функция Вычисление Силы (Force Calculation) просто интегрирует натяжение Максвелла, вычисляемое непосредственно вне выбранной области (или областей) и по всей внешней границе выборки области, которая должна быть группой движущихся вместе областей (т.е. единым механическим элементов). Поскольку, этот метод основан на интегрировании по поверхности, вычисляемая сила является чувствительной к размеру сетки. Поэтому при использовании этого метода всегда важно выполнять исследование качества сетки (mesh refinement study), чтобы правильно вычислять силу или крутящий момент.
Расчет силы не будет верным, если область, в которой применяется функция Вычисление Силы (Force Calculation), косается внешней границы, периодической границы и тождественной пары.
Кроме того, чтобы вычислить силу на прикрепленном к ферромагнитной поверхности магните, контактные границы должны иметь тонкий зазор с малой диэлектрической проницаемостью (тонкий зазор с малой диэлектрической проницаемостью для электростатического эквивалента), поскольку натяжения Максвелла должны быть рассчитаны скорее в воздухе, чем в ферромагнитном (диэлектрическом) материале.
Второй метод — метод Силы Лоренца (Lorentz force) — работает только в особых случаях для вычисления магнитной силы на немагнитных, токопроводящих областях. Сила Лоренца определяется как F = J × B, где J — плотность тока и B — магнитная индукция. Сила Лоренца предпочтительна (и является очень точным методом) для вычислений силы в электропроводящих областях, поскольку вычисление проводится по объёму, а не по границе. Поэтому в тех случаях, когда это возможно, желательно использовать метод силы Лоренца, а не метод тензора натяжения Максвелла.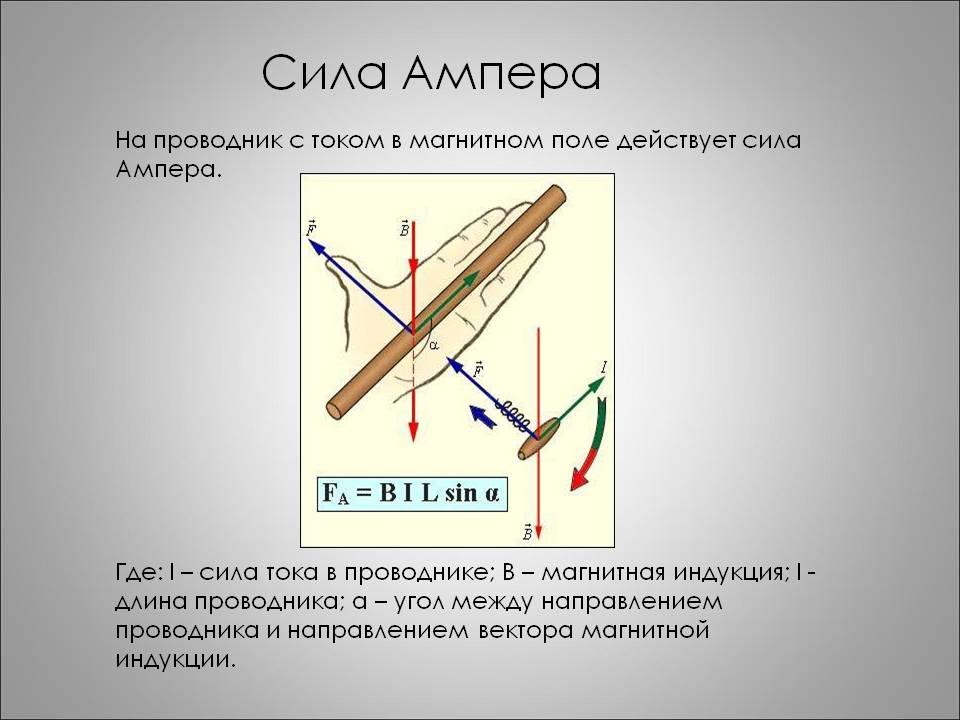
Помимо этих встроенных методов, указанных выше, магнитная сила и крутящий момент также могут быть вычислены с использованием метода виртуальной работы или принципа виртуального смещения. В этой технике, сила рассчитывается путем изучения влияния малого смещения на электромагнитную энергию. Метод виртуальной работы может быть внедрён с помощью функций деформированной сетки и анализа чувствительности в среде COMSOL Multiphysics. Пример его реализации представлен по ссылке.
Магнитная жесткость
В механике твердого тела, жесткость — это т.н. твердость объекта — степень, до которой объект сопротивляется деформации в ответ на приложенную силу. Аналогичным образом, применительно к магнитным подшипникам, такой параметр определяется как магнитная жесткость и означает взятую с отрицательным знаком производную полной магнитной силы по пространственной координате. Если магнитная сила определена как Fz, магнитная жесткость относительно положения z, вычисляется по формуле:
k_{zz} = – \frac{dF_z}{ dz}
Учебная модель, иллюстрирующая этот метод для вычисления магнитной жесткости в осевом магнитном подшипнике, доступна по следующей ссылке. Этот пример, однако, ограничивается случаем осевой симметрии. Т.е., магнитная жесткость не может быть оценена в x– и y– направлениях. Чтобы рассчитать магнитную жесткость во всех направлениях, вам необходимо смоделировать проблему в 3D-постановке. В рамках данного блога мы создадим 3D-версию осевого магнитного подшипника, описанного выше, и определим жесткость kx. Вы можете скачать такую учебную модель из нашей Галлереи Приложений.
Этот пример, однако, ограничивается случаем осевой симметрии. Т.е., магнитная жесткость не может быть оценена в x– и y– направлениях. Чтобы рассчитать магнитную жесткость во всех направлениях, вам необходимо смоделировать проблему в 3D-постановке. В рамках данного блога мы создадим 3D-версию осевого магнитного подшипника, описанного выше, и определим жесткость kx. Вы можете скачать такую учебную модель из нашей Галлереи Приложений.
Такой подход в первую очередь предполагает использование интерфейсов Магнитные поля, Деформированная геометрия и Чувствительность (Sensitivity). Как и в 2D-модели, используется интерфейс Магнитные поля. Магниты моделируются с помощью функции закон Ампера, в котором материальная модель определена как “Остаточная магнитная индукция” с величиной 1 [Тл]. Функция Вычисление Силы добавлена только к внутренним магнитам, при этом геометрия параметризована таким образом, что позиция внутренних магнитов параметром X0 (сдвиг по оси x).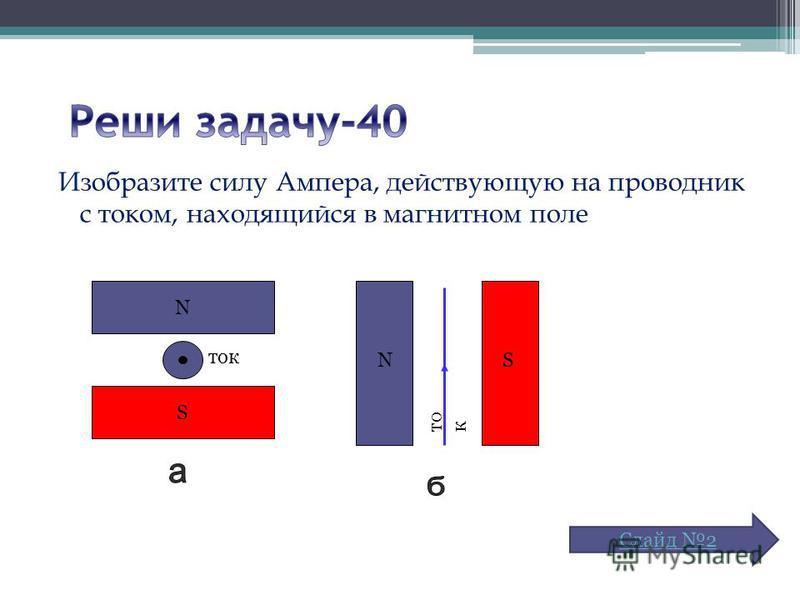 Этот параметр будет использоваться в дальнейшем для параметрического исследования, а также для определения предустановленного смещения сетки
Этот параметр будет использоваться в дальнейшем для параметрического исследования, а также для определения предустановленного смещения сетки dX в интерфейсе Деформируемая Геометрия. Будем использовать только четверть геометрии для вычисления магнитной жесткости в x-направлении.
Обратите внимание, что в такой конфигурации будет правильно рассчитана только сила вдоль оси х0. В сили симметрии сила в y- и z-направлениях должна быть равна нулю. Однако, из-за того, что только четверть геометрии смоделирована, вычисленная сила будет достаточно большой. Жесткость в y-направлении может быть вычислена аналогичным образом при анализе четверти модели, симметричной в yz– и xy-плоскостях.
Слева: 3D-модель четверти осевого магнитного подшипника для вычисления жесткости. Справа: Норма магнитной индукции и диаграмма направления магнитной индукции в половине модели. Результаты визуализированы с помощью набора данных 3D-Зеркало в xy-плоскости.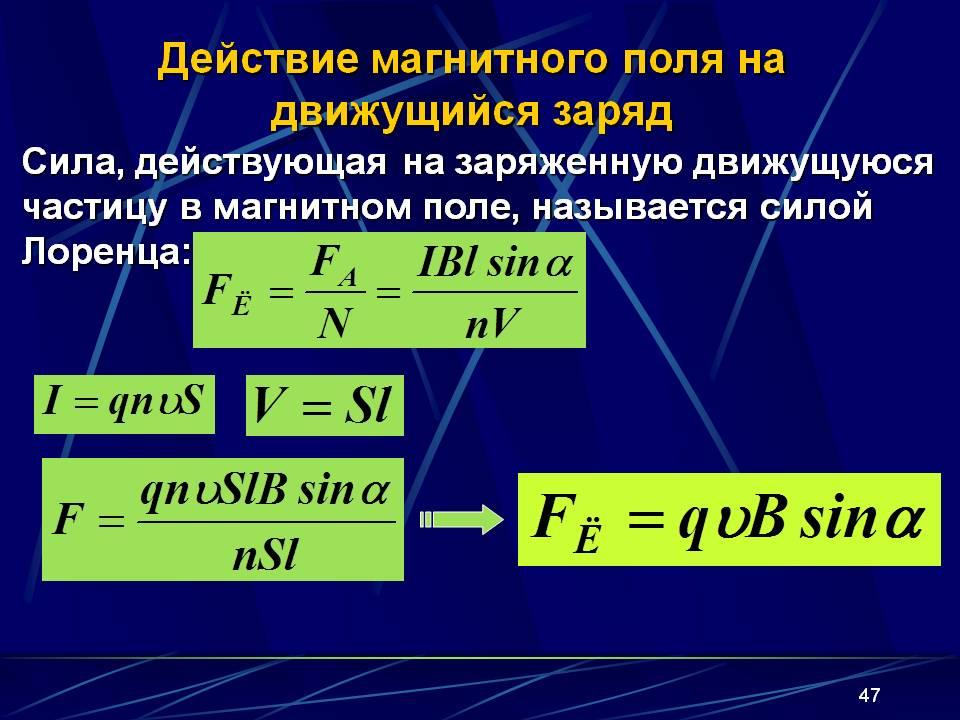
Решение уравнений интерфейса Деформируемая Геометрия проводится везде за исключением области с бесконечными элементами (infinite element domain). Чтобы найти решение для этого участка, для начала нужно добавить узел Свободная деформация (Free Deformation) для воздушного участка вокруг магнитов. Кроме того, вы можете добавить предустановленную деформацию dX к области внутренних магнитов вдоль оси x. Наконец, добавьте два узла Предустановленного смещения сетки (Prescribed Mesh Displacement) для внутренних магнитных границ и границы симметрии, как показано ниже.
Параметры для предустановленной деформации на областях внутренних магнитов.
Параметры для предустановленного смещения сетки на границах внутренних магнитов.
Параметры для предустановленного смещения сетки на границе симметрии.
В интерфейсе Чувствительность (Sensitivity), добавьте функцию Глобальный целевой параметр (Global Objective) и укажите полную силу в x-направлении (например 4*mf.) в выражении для целевого параметра в настройках интерфейса. Здесь,  Forcex_0
Forcex_0mf.Forcex_0 x-компонент силы тензора натяжения Максвелла, который вычисляется с помощью функции Вычисление силы в интерфейсе Магнитные поля. Точно так же добавьте глобальную контрольную переменную (global control variable) dX.
Настройки для Глобального целевого параметра (global objective) — слева — и глобальных контрольных переменных (global control variables) — справа.
Поскольку исследование чувствительности (и Оптимизация) не может быть совмещено с исследованием узла Параметрическое исследование, модель должна быть разрешена с использованием двух отдельных исследований. Первое исследование будет включать решатель для чувствительности (Sensitivity) и стационарный решатель. Второе исследование тогда будет включать в себя Параметрическое исследование , но будет использовать Исследование 1 (Study 1) в качестве референсного. Выполните параметрический свип по параметру X0, использовав следующий интервал значений (0,1. 5/20,1.5), с настройками, изображенными ниже.
5/20,1.5), с настройками, изображенными ниже.
Слева: Параметры и настройки стационарного исследования для анализа чувствительности (sensitivity analysis). Справа: Настройки для параметрического исследования (Parametric Sweep), использующего Решение 1 (Study 1) в качестве референсного.
Магнитная сила в оси-x и магнитная жесткость в x-направлении построены как глобальные 1D-графики.
Параметры графиков для магнитной силы (слева) и магнитной жесткости (справа).
Слева: x-компонента электромагнитной силы как функция смещения по x- оси. Справа: Магнитная жесткость kxx как функция смещения по оси x.
Резюме
Сегодня мы обсудили несколько типов магнитных подшипников, которые могут быть смоделированы в среде COMSOL Multiphysics с использованием доступных интерфейсов модуля AC/DC. Моделирование обеспечивает упрощенный подход для определения конструктивных параметров этих типов подшипников, помогая оптимизировать их работу, а также срок их службы.
В следующей записи в этой серии нашего блога, мы сфокусируемся на том, как может использоваться COMSOL Multiphysics для моделирования магнитных редукторов. Оставайтесь с нами!
Примечание редактора: этот пост был обновлен 09/05/2017.
автомобильные держатели, которые удержат даже через чехол
Магнитная сила: автомобильные держатели, которые удержат даже через чехол
Представьте, что Ваше устройство, будь то телефон или навигатор, просто можно прислонить к держателю и, о чудо, он держится! Не падает даже в чехле! Без креплений, которые нужно для начала сдвинуть в стороны и, иногда с большим усилием, попытаться поместить туда свой телефон. Да и представлять не нужно, вот он – держатель с неодимовым магнитом, невероятно мощным, но, в тоже время, безопасным!
Такой магнит обладает высокой стойкостью, всего 1% силы теряется за 10 лет работы! Способен удерживать даже тяжелые предметы: планшет или электронную сигарету.
Сама конструкция держателя может поворачиваться под удобным углом, чтобы можно было расположить устройство так, как удобно Вам или повернуть к пассажирам. Ножка также регулируется: ее можно настроить при помощи фиксирующих кнопочек на корпусе.
В комплекте две металлические пластинки разного диаметра для любых девайсов. Крепится держатель на силиконовую присоску со специальным рычажком для плотной фиксации на стекле или приборной панели автомобиля.
Бытует мнение, что магнит в таком аксессуаре может навредить мобильному телефону или навигатору. На самом же деле этот факт тщательно изучен со всех сторон.Факт №1: магнитный держатель безопасен для мобильных устройств.
Современные мобильные устройства не восприимчивы к магнитным помехам и не содержат магнитных полей в своей конструкции. Поэтому внешний магнит держателя никак не может повлиять на работу устройства.
Факт №2: магнит не влияет на память устройства.

Магнит не может оказать негативного влияния на память гаджета, поскольку хранение информации происходит при помощи флэш-накопителя, а, как известно, такой вид хранения абсолютно не содержат каких-либо магнитных свойств.
Факт №3: магнит не повлияет на GPS.
Магнитный держатель не может навредить встроенной системе GPS, потому что Ваш телефон для определения местоположения использует спутниковый сигнал, который не может быть подвержен действию магнита.
Факт №4: динамики не пострадают.
Ваши динамики, также останутся невредимыми, так как при производстве современных мобильных устройств используются специальные экранирующие материалы, для защиты от негативного воздействия внешних магнитных полей.
Пользуйтесь с удовольствием!
Большой выбор держателей с креплением на дефлектор, с основанием-липучкой или на присоске. С длинной или короткой ножкой. В комплекте две металлические пластинки разного диаметра для любых Ваших устройств.
Протестируйте магнитные держатели телефона торговой марки SKYWAY!
Предлагаем вам бесплатно получить один из магнитных держателей и провести его испытания!Подробная информация в нашей группе ВКонтакте.
Электрические и магнитные силы
Физика > Электрические и магнитные силы
Как электрическая и магнитная сила влияют на траекторию движения заряженной частицы в поле: сила Лоренца, линии магнитного поля, уравнения, правило правой руки.
Траектория заряженной частички подчиняется электрической и магнитной силам, но проявляют они себя по-разному.
Задача обучения
- Сравнить влияние обеих сил на заряженную частичку.
Основные пункты
- Сила на заряженной частичке, созданная электрическим полем, направляется параллельно его вектору при положительном знаке и антипараллельно при отрицательном. Она не основывается на скорости частички.
- Магнитная сила выступает ортогональной вектору магнитного поля и основывается на скорости частички.
 Для определения направленности используют правило правой руки.
Для определения направленности используют правило правой руки. - Над заряженной частичкой может функционировать электрическое поле, но не магнитное.
- Сила Лоренца – комбинация обеих сил.
- На положительных зарядах электрические линии создаются, а заканчиваются на отрицательных. Линии изолированного заряда располагаются радиально наружу, касаясь электрического поля.
- Линии магнитного поля создаются на северном полюсе и заканчиваются на южном. Магнитные полюса не пребывают в изоляции и касаются магнитного поля.
Термин
- Ортогональные – расположены перпендикулярно друг другу.
Электрические и магнитные силы
Зараженные частички испытывают на себе влияние электрических и магнитных сил. Но результирующее изменение траектории будет отличаться, если рассматривать каждую по отдельности.
Электростатическая и магнитная силы на заряженной частичке
В статическом стабильном электрическом поле сила:
F = qE (F – вектор силы, q – заряд, E – вектор электрического поля). В положительном заряде направленность F идентична E, а в отрицательном будет противоположной. Электрическое поле можно установить большим зарядом Q, влияющим на меньший q на дистанции r:
В положительном заряде направленность F идентична E, а в отрицательном будет противоположной. Электрическое поле можно установить большим зарядом Q, влияющим на меньший q на дистанции r:
Не забывайте, что электрическая сила располагается параллельно электрическому полю. Ее коррекция приравнивается к нулю:
▽ × Е = 0
Получается, что электрическое поле способно функционировать, а заряд последует за касательной линией.
А вот магнитная сила на заряженной частичке будет ортогональна к магнитному полю, поэтому:
F = qv × B = qvBsinθ (В – вектор магнитного поля, v – скорость частицы, а θ – угол между магнитным полем и скоростью частиц). Правило правой руки поможет вычислить направленность F.
Перемещающиеся заряды ощущают влияние магнитного поля. Это одна из наиболее распространенных сил. Ее направленность выступает перпендикулярной плоскости и соответствует правилу правой руки. Величина пропорциональна q, v, B и синусу угла между v и B
Если скорость частички выровняется параллельно по отношению к магнитному полю или приравняется к нулю, то и магнитная сила достигнет 0. И в этом отличие от электрического варианта, где скорость частички никак не влияет на величину или направленность электрической силы.
И в этом отличие от электрического варианта, где скорость частички никак не влияет на величину или направленность электрической силы.
Зависимость от угла также приводит к тому, что заряженные частички перемещаются перпендикулярно по отношению к линиям магнитного поля, выполняя круговые/спиральные движения. Стоит отметить, что магнитное поле не функционирует при круговой траектории, так как частичка возвращается на исходную точку:
W = ∮B ⋅ dr = 0
Сила Лоренца
Передает сложенные электрические и магнитные силы на заряженной частичке. Сила высчитывается уравнением:
F = q [Е + vBsinθ]
Электрические и магнитные линии
Линии электрического поля из положительно изолированного заряда выглядят как последовательность радиально направленных линий, установленных наружу от заряда. Если же заряд несет отрицательный знак, то направленность поля меняется на противоположную. Завиток электрической линии приравнивается к 0.
Электрическое поле сосредоточено вокруг трех разных точечных зарядов: (а) – положительный, (b) – отрицательный с равной величиной, (с) – больший отрицательный заряд
Если активировано несколько зарядов, то линии поля создаются на положительных и заканчиваются в отрицательных. В магнитах они возникают на северном полюсе (+) и завершаются на южном (-). Но они путешествуют парами, поэтому завиток магнитного поля не всегда приравнивается к нулю. Если у частичек есть ненулевой компонент скорости, то они будут вращаться вокруг линий.
В магнитах они возникают на северном полюсе (+) и завершаются на южном (-). Но они путешествуют парами, поэтому завиток магнитного поля не всегда приравнивается к нулю. Если у частичек есть ненулевой компонент скорости, то они будут вращаться вокруг линий.
На этой модели видны два противоположных полюса: северный (+) и южный (-). Они разделены дистанцией (d) и формируют линии
Можно создать магнитное поле током с линиями поля. На схеме отобразится в виде концентрических окружностей вокруг проводящего ток провода. В любой точке магнитную силу можно будет вычислить по правилу правой руки.
Магнитная система StampTec | Солан-Д
StampTec – магнитная система для быстрого крепления штампов на штамповочных прессах. StampTec состоит из двух магнитных модулей, удобна в установке и интегрировании в существующий станок и его управление.
Преимущества
- Легко адаптируется к любым процессам. Модульный принцип позволяет приспосабливать систему согласно любым требованиям. Не требует никаких модификаций пресса. Уменьшенная толщина модулей позволяет сохранить межплитовое расстояние.
- Не требует модификации штампов. StampTec подходит для штампов любой формы и размера без их модификации. Стандартизация не обязательна, что сокращает временные и денежные затраты. Рабочая поверхность и часть штампа не намагничиваются, позволяя удалять отходы производства без помех.
- Удобство в использовании. Один оператор при помощи инструментов может легко осуществлять всю процедуру крепления штампа в условиях полной безопасности, находясь вне пресса.
- Компактный и простой в установке пульт управления.
- Равномерное крепление. Равномерность крепления штампа обеспечивает повторяемость и сохранение устойчивости процесса штамповки.
Технические характеристики:
| Модель StampTec | EASY | ST |
| Магнитная сила | до 16 кг/см² | до 16 кг/см² |
| Сила действия магнитного поля в области контакта со штампом | до 90 тонн/см² | до 90 тонн/см² |
|
Толщина верхнего магнитного модуля |
47 мм | 47 мм |
| Толщина нижнего магнитного модуля | 47 мм | 47 мм |
| U-образное расположение роликов на нижнем модуле | стандартно | стандартно |
| Центральное отверстие для сброса отходов штамповки | стандартно | стандартно |
| Отверстия для механического крепления | стандартно | стандартно |
| Тип пульта управления | ST 110P | ST 400 |
| Система контроля тока UCS | стандартно | стандартно |
| Напряжение | 230 В/50-60 | 200-480 В/50-60 |
| Система обнаружения магнитного потока FCS |
|
стандартно |
| Цифровой кнопочный пульт для циклов MAG/DEMAG | встроенный | удаленный |
| Активация станка | стандартно | стандартно |
| Сенсорный экран управления – IPC | по запросу | |
| Дополнительный ключ активации DCM (режим смены заготовки) | стандартно | стандартно |
| Модули соединения с пультом управления, интерфейс и кабели питания | стандартно | стандартно |
| Датчики наличия пресс-формы | стандартно | стандартно |
| Набор болтов крепления | стандартно | стандартно |
| Руководство по эксплуатации и сертификации CE | стандартно | стандартно |
Перейти на сайт Tecnomagnete
Стресс | физика | Britannica
Stress , в физических науках и технике, сила на единицу площади в материалах, возникающая в результате приложенных извне сил, неравномерного нагрева или остаточной деформации и позволяющая точно описать и спрогнозировать поведение упругости, пластичности и текучести. Напряжение выражается как отношение силы к площади.
Подробнее по этой теме
порода: напряжение и деформация
Когда к материалу, например горной породе, прикладывается напряжение σ (сила на единицу площади), материал претерпевает изменения в размере, объеме или…
Есть много видов стресса. Нормальное напряжение возникает из-за сил, перпендикулярных площади поперечного сечения материала, тогда как напряжение сдвига возникает из-за сил, параллельных плоскости поперечного сечения и лежащих в ней. Если стержень, имеющий площадь поперечного сечения 4 квадратных дюйма (26 квадратных см), тянут в продольном направлении силой 40000 фунтов (180000 ньютонов) на каждом конце, нормальное напряжение внутри стержня равно 40000 фунтов, разделенных на 4 квадрата дюймов, или 10 000 фунтов на квадратный дюйм (psi; 7 000 ньютонов на квадратный см).Это специфическое нормальное напряжение, возникающее в результате растяжения, называется растягивающим напряжением. Если две силы меняются местами, чтобы сжимать стержень по его длине, нормальное напряжение называется напряжением сжатия. Если силы повсюду перпендикулярны всем поверхностям материала, как в случае объекта, погруженного в жидкость, которая сама может сжиматься, нормальное напряжение называется гидростатическим давлением или просто давлением. Напряжение под поверхностью Земли, которое сжимает горные породы до большой плотности, называется литостатическим давлением.
Напряжение сдвига в твердых телах возникает в результате таких действий, как скручивание металлического стержня вокруг продольной оси, как при затягивании винта. Напряжение сдвига в жидкостях возникает в результате таких воздействий, как поток жидкостей и газов по трубам, скольжение металлической поверхности по жидкой смазке и прохождение самолета через воздух. Напряжения сдвига, какими бы небольшими они ни были, приложенные к истинным жидкостям, вызывают непрерывную деформацию или течение, поскольку слои жидкости перемещаются друг над другом с разной скоростью, как отдельные карты в разложенной колоде карт.Для напряжения сдвига см. Также модуль сдвига.
Реакция на напряжения в упругих твердых телах заставляет их возвращаться к своей исходной форме после снятия приложенных сил. Предел текучести, обозначающий переход от упругого к пластическому поведению, представляет собой минимальное напряжение, при котором твердое тело будет подвергаться постоянной деформации или пластическому течению без значительного увеличения нагрузки или внешней силы. Земля демонстрирует упругую реакцию на напряжения, вызванные землетрясениями, так как она распространяет сейсмические волны, в то время как она подвергается пластической деформации под поверхностью под большим литостатическим давлением.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчасОдежда | физика | Britannica
Wear , удаление материала с твердой поверхности в результате механического воздействия другого твердого тела. Износ в основном возникает как прогрессирующая потеря материала в результате механического взаимодействия двух поверхностей скольжения под нагрузкой. Износ – это настолько универсальное явление, что два твердых тела редко скользят друг по другу или даже касаются друг друга без измеримого переноса материала или потери материала.Таким образом, монеты изнашиваются в результате постоянного контакта с тканями и пальцами человека; карандаши изнашиваются после скольжения по бумаге; рельсы изнашиваются в результате продолжающегося катания по ним колес поезда. Только живые существа (например, костные суставы) в некотором смысле невосприимчивы к необратимым повреждениям, вызванным износом, поскольку они обладают свойством возобновления роста и заживления.
Британская викторина
Викторина “Все о физике”
Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какая единица измерения для циклов в секунду? Проверьте свою физическую хватку с помощью этой викторины.
Существует четыре основных типа износа: адгезионный, абразивный, коррозионный и усталостный.
Самый распространенный тип, адгезионный износ, возникает из-за сильных адгезионных сил, возникающих на границе раздела двух твердых материалов. Когда твердые поверхности прижимаются друг к другу, происходит тесный контакт через множество небольших участков или стыков. Во время скольжения эти стыки продолжают образовываться и разрушаться, и, если стык не разрывается вдоль исходной границы раздела, образуется частица износа.Эти частицы в конечном итоге отрываются. Адгезионный износ нежелателен по двум причинам: во-первых, потеря материала в конечном итоге приведет к ухудшению работы механизма; и, во-вторых, образование крупных частиц износа в плотно прилегающих элементах скольжения может вызвать заклинивание механизма на ранней стадии его срока службы. Адгезионный износ металлических поверхностей без смазки во много раз больше, чем для эффективно смазываемых.
Абразивный износ возникает, когда твердая шероховатая поверхность скользит по более мягкой, образуя на ней бороздки.Это также может быть вызвано незакрепленными абразивными частицами, катящимися между двумя мягкими поверхностями скольжения, или частицами, застрявшими в одной из противоположных поверхностей. Абразивные фрагменты, переносимые потоком жидкости или газа, могут изнашивать поверхность, если они ударяются о поверхность с высокой скоростью. Поскольку абразивный износ имеет место, когда абразивный материал является шероховатым и тверже, чем поверхность, подлежащая шлифованию, его можно предотвратить либо путем устранения твердой, шероховатой составляющей, либо путем еще большего усиления защиты поверхности.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчасКоррозионный износ возникает всякий раз, когда газ или жидкость химически атакуют поверхность, оставшуюся открытой в результате процесса скольжения. Обычно, когда поверхность корродирует, продукты коррозии (например, патина) имеют тенденцию оставаться на поверхности, тем самым замедляя дальнейшую коррозию. Но если имеет место непрерывное скольжение, действие скольжения удаляет поверхностные отложения, которые в противном случае защищали бы от дальнейшей коррозии, которая, таким образом, происходит быстрее.Поверхность, подвергшаяся коррозийному износу, обычно имеет матовый, относительно гладкий вид.
Поверхностный усталостный износ возникает в результате повторяющихся высоких напряжений, возникающих при качении, например, металлических колес на гусеницах или качения шариковых подшипников в машине. Напряжение вызывает образование подповерхностных трещин либо в движущемся, либо в неподвижном элементе. По мере роста этих трещин крупные частицы отделяются от поверхности, и возникает точечная коррозия. Поверхностный усталостный износ является наиболее распространенной формой износа таких элементов качения, как подшипники или шестерни.Для поверхностей скольжения адгезионный износ обычно протекает достаточно быстро, чтобы не успеть возникнуть усталостный износ поверхности.
Хотя процесс износа обычно считается вредным, и в большинстве практических ситуаций так и есть, он также имеет практическое применение. Например, многие методы изготовления поверхности на изготовленном объекте зависят от абразивного износа, в том числе опиливание, шлифование, притирка и полировка. Многие пишущие инструменты, в основном карандаш, мелок и мел, зависят от адгезионного износа.Другое применение – износ резцов у грызунов. Эти зубы имеют твердое эмалевое покрытие вдоль внешней изогнутой поверхности, но только мягкий дентин на внутренней поверхности. Следовательно, абразивный и адгезивный износ, который происходит быстрее на более мягкой стороне, способствует сохранению острой режущей кромки на зубах.
Одна из четырех фундаментальных сил, слабое взаимодействие, включает обмен промежуточными векторными бозонами, W и Z.Поскольку масса этих частиц равна порядка 80 ГэВ принцип неопределенности определяет диапазон примерно 10 -18 метров, что составляет около 0,1% диаметра протона. Слабое взаимодействие меняет один аромат кварка на другой. Например, при распаде нейтрона, изображенном диаграммой Фейнмана слева вверху, один нижний кварк заменяется верхним кварком, превращая нейтрон в протон. Примитивные вершины диаграмм Фейнмана для слабого взаимодействия бывают двух типов: заряженные и нейтральные.Для лептонов они имеют вид Электрон используется в качестве примера на этих диаграммах, но любой лептон может быть заменен на входящей стороне. Сторона выхода (вверху) будет такой же для нейтральной вершины, но определяется зарядом W в заряженной вершине. Помимо сохранения заряда, вершина должна сохранять лептонное число, поэтому процесс с электроном может производить электронное нейтрино, но не мюонное нейтрино.
Заряженные вершины в слабом взаимодействии с кварками принимают вид Итак, видно, что кварк меняет свой аромат при взаимодействии через W – или W + . Как показано на рисунке, это взаимодействие невозможно наблюдать, поскольку оно подразумевает изоляцию ап-кварка. Из-за удержания кварков изолированные кварки не наблюдаются.Но вращение диаграммы Фейнмана дает альтернативное взаимодействие, показанное ниже как для электронных, так и для мюонных продуктов. Это указывает на механизм слабого взаимодействия для распада пиона, который наблюдается по мюонному пути. Слабое взаимодействие в электронной форме слева вверху отвечает за распад нейтрона и за бета-распад в целом. | Index Основные концепции сил Ссылка Griffiths |
Что такое магнетизм? | Магнитные поля и магнитная сила
Магнетизм – это один из аспектов комбинированной электромагнитной силы. Это относится к физическим явлениям, возникающим из-за силы, вызванной магнитами, объектами, которые создают поля, которые притягивают или отталкивают другие объекты.
Согласно веб-сайту HyperPhysics Университета штата Джорджия, магнитное поле воздействует на частицы в поле за счет силы Лоренца. Движение электрически заряженных частиц порождает магнетизм.Сила, действующая на электрически заряженную частицу в магнитном поле, зависит от величины заряда, скорости частицы и силы магнитного поля.
Все материалы обладают магнетизмом, некоторые сильнее, чем другие. Постоянные магниты, сделанные из таких материалов, как железо, испытывают сильнейшее воздействие, известное как ферромагнетизм. За редким исключением, это единственная форма магнетизма, достаточно сильная, чтобы ее могли почувствовать люди.
Противоположности притягиваются
Магнитные поля генерируются вращающимися электрическими зарядами, согласно HyperPhysics.Все электроны обладают свойством углового момента или спина. Большинство электронов имеют тенденцию образовывать пары, в которых один из них имеет «спин вверх», а другой – «спин вниз», в соответствии с принципом исключения Паули, который гласит, что два электрона не могут находиться в одном и том же энергетическом состоянии одновременно. В этом случае их магнитные поля направлены в противоположные стороны, поэтому они компенсируют друг друга. Однако некоторые атомы содержат один или несколько неспаренных электронов, спин которых может создавать направленное магнитное поле. По данным Ресурсного центра неразрушающего контроля (NDT), направление их вращения определяет направление магнитного поля.Когда значительное большинство неспаренных электронов выровнены своими спинами в одном направлении, они объединяются, чтобы создать магнитное поле, достаточно сильное, чтобы его можно было почувствовать в макроскопическом масштабе.
Источники магнитного поля биполярные, с северным и южным магнитными полюсами. По словам Джозефа Беккера из Университета Сан-Хосе, противоположные полюса (северный и южный) притягиваются, а подобные полюса (северный и северный, или южный и южный) отталкиваются. Это создает тороидальное поле или поле в форме пончика, поскольку направление поля распространяется наружу от северного полюса и входит через южный полюс.
Земля сама по себе является гигантским магнитом. Согласно HyperPhysics, планета получает свое магнитное поле от циркулирующих электрических токов внутри расплавленного металлического ядра. Компас указывает на север, потому что маленькая магнитная стрелка в нем подвешена, так что он может свободно вращаться внутри своего корпуса, выравниваясь с магнитным полем планеты. Как ни парадоксально, то, что мы называем Северным магнитным полюсом, на самом деле является южным магнитным полюсом, потому что он притягивает северные магнитные полюса стрелок компаса.
Ферромагнетизм
Если выравнивание неспаренных электронов продолжается без приложения внешнего магнитного поля или электрического тока, образуется постоянный магнит. Постоянные магниты – результат ферромагнетизма. Приставка «ферро» относится к железу, потому что постоянный магнетизм впервые наблюдался в форме естественной железной руды, называемой магнетитом, Fe 3 O 4 . Кусочки магнетита можно найти разбросанными на поверхности земли или вблизи нее, и иногда они намагничиваются.Эти встречающиеся в природе магниты называются магнитными камнями. «Мы до сих пор не уверены в их происхождении, но большинство ученых считают, что магнитный камень – это магнетит, пораженный молнией», – говорится в сообщении Университета Аризоны.
Вскоре люди узнали, что можно намагнитить железную иглу, поглаживая ее магнитом, в результате чего большинство неспаренных электронов в игле выстраиваются в одном направлении. По данным НАСА, примерно в 1000 году нашей эры китайцы обнаружили, что магнит, плавающий в чаше с водой, всегда выстраивается в направлении север-юг.Таким образом, магнитный компас стал огромным помощником в навигации, особенно днем и ночью, когда звезды были скрыты облаками.
Было обнаружено, что другие металлы, помимо железа, обладают ферромагнитными свойствами. К ним относятся никель, кобальт и некоторые редкоземельные металлы, такие как самарий или неодим, которые используются для создания сверхпрочных постоянных магнитов.
Другие формы магнетизма
Магнетизм принимает множество других форм, но, за исключением ферромагнетизма, они обычно слишком слабы, чтобы их можно было наблюдать за исключением чувствительных лабораторных приборов или при очень низких температурах.Диамагнетизм был впервые открыт в 1778 году Антоном Бругнамсом, который использовал постоянные магниты в поисках материалов, содержащих железо. По словам Джеральда Кюстлера, широко публикуемого независимого немецкого исследователя и изобретателя, в его статье «Диамагнитная левитация – исторические вехи», опубликованной в Румынском журнале технических наук, Бругнамс заметил: «Только темный и почти фиолетовый висмут проявлял конкретное явление в исследовании; когда я положил его кусок на круглый лист бумаги, плавающий на воде, он оттолкнулся обоими полюсами магнита.
Было установлено, что висмут обладает самым сильным диамагнетизмом из всех элементов, но, как обнаружил Майкл Фарадей в 1845 году, это свойство всей материи отталкиваться магнитным полем.
Диамагнетизм вызван орбитальным движением электронов, создающих крошечные токовые петли, которые создают слабые магнитные поля, согласно HyperPhysics. Когда к материалу прикладывается внешнее магнитное поле, эти токовые петли имеют тенденцию выравниваться таким образом, чтобы противостоять приложенному полю.Это заставляет все материалы отталкиваться постоянным магнитом; однако результирующая сила обычно слишком мала, чтобы быть заметной. Однако есть некоторые заметные исключения.
Пиролитический углерод, вещество, похожее на графит, демонстрирует даже более сильный диамагнетизм, чем висмут, хотя и только вдоль одной оси, и фактически может подниматься над сверхсильным редкоземельным магнитом. Некоторые сверхпроводящие материалы демонстрируют даже более сильный диамагнетизм ниже своей критической температуры, поэтому над ними можно левитировать редкоземельные магниты.(Теоретически из-за их взаимного отталкивания один может левитировать над другим.)
Парамагнетизм возникает, когда материал временно становится магнитным при помещении в магнитное поле и возвращается в немагнитное состояние, как только внешнее поле удаляется. При приложении магнитного поля некоторые из неспаренных электронных спинов выравниваются с полем и преодолевают противоположную силу, создаваемую диамагнетизмом. Однако, по словам Дэниела Марша, профессора физики Южного государственного университета Миссури, эффект заметен только при очень низких температурах.
Другие, более сложные формы включают антиферромагнетизм, при котором магнитные поля атомов или молекул выстраиваются рядом друг с другом; и поведение спинового стекла, которое включает как ферромагнитные, так и антиферромагнитные взаимодействия. Кроме того, ферримагнетизм можно рассматривать как комбинацию ферромагнетизма и антиферромагнетизма из-за множества общих черт между ними, но, по данным Калифорнийского университета в Дэвисе, он все же имеет свою уникальность.
Электромагнетизм
Когда провод перемещается в магнитном поле, поле индуцирует ток в проводе.И наоборот, магнитное поле создается движущимся электрическим зарядом. Это соответствует закону индукции Фарадея, который лежит в основе электромагнитов, электродвигателей и генераторов. Заряд, движущийся по прямой линии, как по прямому проводу, создает магнитное поле, которое вращается вокруг провода по спирали. Когда этот провод превращается в петлю, поле приобретает форму пончика или тора. Согласно Руководству по магнитной записи (Springer, 1998) Marvin Cameras, это магнитное поле можно значительно усилить, поместив ферромагнитный металлический сердечник внутрь катушки.
В некоторых приложениях постоянный ток используется для создания постоянного поля в одном направлении, которое можно включать и выключать вместе с током. Это поле может затем отклонить подвижный железный рычаг, вызывая слышимый щелчок. Это основа телеграфа, изобретенного в 1830-х годах Сэмюэлем Ф. Б. Морзе, который позволял осуществлять связь на большие расстояния по проводам с использованием двоичного кода, основанного на импульсах большой и малой длительности. Импульсы посылались опытными операторами, которые быстро включали и выключали ток с помощью подпружиненного переключателя с мгновенным контактом или ключа.Другой оператор на принимающей стороне затем переводил слышимые щелчки обратно в буквы и слова.
Катушка вокруг магнита также может двигаться по шаблону с изменяющейся частотой и амплитудой, чтобы индуцировать ток в катушке. Это основа для ряда устройств, в первую очередь для микрофона. Звук заставляет диафрагму двигаться внутрь и наружу с волнами переменного давления. Если диафрагма соединена с подвижной магнитной катушкой вокруг магнитопровода, она будет производить переменный ток, аналогичный падающим звуковым волнам.Затем этот электрический сигнал может быть усилен, записан или передан по желанию. Крошечные сверхсильные магниты из редкоземельных элементов в настоящее время используются для изготовления миниатюрных микрофонов для сотовых телефонов, сообщил Марш Live Science.
Когда этот модулированный электрический сигнал подается на катушку, он создает колеблющееся магнитное поле, которое заставляет катушку двигаться внутрь и наружу по магнитному сердечнику по той же схеме. Затем катушка прикрепляется к подвижному диффузору динамика, чтобы он мог воспроизводить слышимые звуковые волны в воздухе.Первым практическим применением микрофона и динамика был телефон, запатентованный Александром Грэмом Беллом в 1876 году. Хотя эта технология была улучшена и усовершенствована, она все еще является основой для записи и воспроизведения звука.
Применение электромагнитов практически бесчисленное множество. Закон индукции Фарадея составляет основу многих аспектов нашего современного общества, включая не только электродвигатели и генераторы, но и электромагниты всех размеров. Тот же принцип, который используется гигантским краном для подъема старых автомобилей на свалку металлолома, также используется для выравнивания микроскопических магнитных частиц на жестком диске компьютера для хранения двоичных данных, и каждый день разрабатываются новые приложения.
Штатный писатель Таня Льюис внесла свой вклад в этот отчет.
Дополнительные ресурсы
Сила на движущийся заряд в магнитном поле – College Physics
Каков механизм, с помощью которого один магнит действует на другой? Ответ связан с тем фактом, что весь магнетизм вызван током, потоком заряда. Магнитные поля действуют на движущиеся заряды , и поэтому они действуют на другие магниты, у всех из которых есть движущиеся заряды.
Правило правой руки 1
Магнитная сила, действующая на движущийся заряд, – одна из самых фундаментальных известных. Магнитная сила так же важна, как электростатическая или кулоновская сила. И все же магнитная сила более сложна как по количеству влияющих на нее факторов, так и по ее направлению, чем относительно простая кулоновская сила. Величина магнитной силы, действующей на заряд, движущийся со скоростью в напряженном магнитном поле, равна
.где – угол между направлениями и Эту силу часто называют силой Лоренца.Фактически, именно так мы определяем напряженность магнитного поля – в терминах силы, действующей на заряженную частицу, движущуюся в магнитном поле. Единица СИ для напряженности магнитного поля называется тесла (Тл) в честь эксцентричного, но блестящего изобретателя Николы Тесла (1856–1943). Чтобы определить, как тесла соотносится с другими единицами СИ, мы решаем для.
Поскольку без единицы измерения, тесла составляет
(обратите внимание, что C / s = A).
Еще одна меньшая единица измерения, называемая гауссом (G), где иногда используется.Самые сильные постоянные магниты имеют поля около 2 Тл; сверхпроводящие электромагниты могут достигать 10 Тл или более. Магнитное поле Земли на ее поверхности составляет всего около 0,5 Гс.
Направление магнитной силы перпендикулярно плоскости, образованной и, как определено правилом правой руки 1 (или RHR-1), которое проиллюстрировано на (Рисунок). RHR-1 утверждает, что для определения направления магнитной силы на положительный движущийся заряд вы указываете большим пальцем правой руки в направлении, пальцы в направлении, а перпендикуляр к ладони указывает в направлении из .Один из способов запомнить это – это одна скорость, и поэтому большой палец представляет ее. Есть много линий поля, поэтому пальцы представляют их. Сила направлена в том направлении, в котором вы толкаете ладонью. Сила, действующая на отрицательный заряд, прямо противоположна силе, действующей на положительный заряд.
Установление соединений: заряды и магниты
На статические заряды не действует магнитная сила. Однако на движущиеся заряды действует магнитная сила. Когда заряды неподвижны, их электрические поля не влияют на магниты.Но когда заряды движутся, они создают магнитные поля, которые действуют на другие магниты. Когда есть относительное движение, возникает связь между электрическим и магнитным полями – одно влияет на другое.
Расчет магнитной силы: магнитное поле Земли на заряженном стеклянном стержне
За исключением компасов, вы редко видите или лично испытываете силы из-за небольшого магнитного поля Земли. Чтобы проиллюстрировать это, предположим, что в физической лаборатории вы натираете стеклянный стержень шелком, помещая на него положительный заряд 20 нКл.Вычислите силу, действующую на стержень из-за магнитного поля Земли, если вы бросите его с горизонтальной скоростью 10 м / с на запад в место, где поле Земли направлено на север параллельно земле. (Направление силы определяется правилом правой руки 1, как показано на (Рисунок).)
Положительно заряженный объект, движущийся строго на запад в области, где магнитное поле Земли направлено на север, испытывает силу, направленную прямо вниз, как показано. Отрицательный заряд, движущийся в том же направлении, почувствовал бы силу, направленную прямо вверх.
Стратегия
Нам дан заряд, его скорость, сила и направление магнитного поля. Таким образом, мы можем использовать уравнение, чтобы найти силу.
Решение
Магнитная сила
Мы видим это, поскольку угол между скоростью и направлением поля равен. Ввод других заданных количеств дает
Обсуждение
Эта сила совершенно незначительна для любого макроскопического объекта, что согласуется с опытом.(Он рассчитывается только с точностью до одной цифры, поскольку поле Земли меняется в зависимости от местоположения и выражается только в одной цифре.) Магнитное поле Земли, однако, оказывает очень важное влияние, особенно на субмикроскопические частицы. Некоторые из них рассматриваются в книге «Сила движущегося заряда в магнитном поле: примеры и приложения».
Магнитные силы обеспечивают контролируемую доставку лекарств путем разрушения эндотелиальных межклеточных соединений.
Комарова Ю. и Малик А. Б. Регулирование проницаемости эндотелия через параклеточные и трансцеллюлярные пути транспорта. Annu. Rev. Physiol. 72 , 463–493 (2010).
CAS Статья Google Scholar
Кармелиет П. и Джейн Р. К. Молекулярные механизмы и клиническое применение ангиогенеза. Nature 473 , 298–307 (2011).
CAS ОБЪЯВЛЕНИЯ Статья Google Scholar
Фанг, Дж., Накамура, Х. и Маэда, Х.Эффект ЭПР: уникальные особенности кровеносных сосудов опухоли для доставки лекарств, задействованные факторы, а также ограничения и усиление эффекта. Adv. Препарат Делив. Ред. 63 , 136–151 (2011).
CAS Статья Google Scholar
Джейн Р. К. и Стилианопулос Т. Доставка наномедицины к солидным опухолям. Nat. Преподобный Clin. Онкол. 7 , 653–664 (2010).
CAS Статья Google Scholar
О, П.и другие. Живая динамическая визуализация кавеол, быстро перекачивающих целевые антитела через эндотелий в легких. Nat. Biotechnol. 25 , 327–337 (2007).
CAS Статья Google Scholar
Proescholdt, M.A. et al. Фактор роста эндотелия сосудов (VEGF) модулирует проницаемость сосудов и воспаление в головном мозге крыс. J. Neuropathol. Exp. Neurol. 58 , 613–627 (1999).
CAS Статья Google Scholar
Monsky, W. L. et al. Увеличение трансваскулярного транспорта макромолекул и наночастиц в опухолях с использованием фактора роста эндотелия сосудов. Cancer Res. 59 , 4129–4135 (1999).
CAS PubMed PubMed Central Google Scholar
Бейтс, Д. О. Факторы роста эндотелия сосудов и проницаемость сосудов. Cardiovasc. Res. 87 , 262–271 (2010).
CAS Статья Google Scholar
Rapoport, S. I. Успехи в осмотическом открытии гематоэнцефалического барьера для усиления химиотерапии ЦНС. Мнение эксперта. Расследование. Наркотики 10 , 1809–1818 (2001).
CAS Статья Google Scholar
Тимби, К. Ф., Мид, Б.П. и Прайс, Р. Дж. Доставка лекарств и генов через гематоэнцефалический барьер с помощью сфокусированного ультразвука. J. Control. Выпуск 219 , 61–75 (2015).
CAS Статья Google Scholar
Хернот, С. и Клибанов, А. Л. Микропузырьки в инициируемой ультразвуком доставке лекарств и генов. Adv. Препарат Делив. Ред. 60 , 1153–1166 (2008).
CAS Статья Google Scholar
Гарг, С., Thomas, A. & Borden, M.A. Влияние жесткости липидного монослоя в плоскости на устойчивость циркуляции микропузырьков in vivo . Биоматериалы 34 , 6862–6870 (2013).
CAS Статья Google Scholar
Бао, Г., Митраготри, С. и Тонг, С. Многофункциональные наночастицы для доставки лекарств и молекулярной визуализации. Annu. Преподобный Биомед. Англ. 15 , 253–282 (2013).
CAS Статья Google Scholar
Dames, P. et al. Адресная доставка капель магнитного аэрозоля в легкие. Nat. Nanotechnol. 2 , 495–499 (2007).
Артикул Google Scholar
Namiki, Y. et al. Новая магнитная липидная наноструктура кристаллов для магнитно-управляемой доставки гена in vivo . Nat.Nanotechnol. 4 , 598–606 (2009).
CAS ОБЪЯВЛЕНИЯ Статья Google Scholar
Альсберг, Э., Файнштейн, Э., Джой, М. П., Прентисс, М. и Ингбер, Д. Э. Самосборка фибриновых матриц с упорядоченной наноразмерной структурой для тканевой инженерии под магнитным контролем. Tissue Eng. 12 , 3247–3256 (2006).
CAS Статья Google Scholar
Эль-Хадж, А.J. et al. Модель in vitro нацеливания на мезенхимальные стволовые клетки с использованием мечения магнитных частиц. J. Tissue Eng. Regen. Med. 9 , 724–733 (2015).
CAS Статья Google Scholar
Ламковски М.С., Гепперт М., Шмидт М.М. и Дринген Р. Ускорение накопления магнитных наночастиц оксида железа культивированными астроцитами мозга под действием магнитного поля. Дж.Биомед. Матер. Res. А 100 , 323–334 (2012).
Артикул Google Scholar
Гарсия-Химено, С., Эскрибано, Э., Керальт, Дж. И Эстельрих, Дж. Селективное биораспределение магнитолипосом, индуцированное внешним магнитным полем, у мышей. Nanoscale Res. Lett. 10 , 452 (2012).
ADS Статья Google Scholar
Ландазури, Н.и другие. Магнитное нацеливание мезенхимальных стволовых клеток человека с помощью интернализованных суперпарамагнитных наночастиц оксида железа. Малый 9 , 4017–4026 (2013).
CAS Статья Google Scholar
Шен, Х., Тонг, С., Бао, Г. и Ван, Б. Структурные реакции клеток на внутриклеточную магнитную силу, индуцированную суперпарамагнитными наночастицами оксида железа. Phys. Chem. Chem. Phys. 16 , 1914–1920 (2014).
CAS Статья Google Scholar
Mannix, R.J. et al. Наномагнитное срабатывание рецепторной передачи сигнала. Nat. Nanotechnol. 3 , 36–40 (2008).
CAS ОБЪЯВЛЕНИЯ Статья Google Scholar
Hoffmann, C. et al. Пространственно-временной контроль зарождения и сборки микротрубочек с помощью магнитных наночастиц. Nat. Nanotechnol. 8 , 199–205 (2013).
CAS ОБЪЯВЛЕНИЯ Статья Google Scholar
Картмелл, С. Х., Добсон, Дж., Вершуерен, С. Б. и Эль Хадж, А. Дж. Разработка методов магнитных частиц для длительного культивирования костных клеток с периодической механической активацией. IEEE Trans. Нанобиология 1 , 92–97 (2002).
Артикул Google Scholar
Ху, Б., Добсон, Дж. И Эль-Хадж, А. Дж. Контроль повышения регуляции альфа-актина (SMA) гладких мышц в HBMSC с помощью дистанционной механоактивации магнитными частицами. Наномедицина 10 , 45–55 (2014).
CAS Статья Google Scholar
Millan, J. et al. Адгезивные соединения соединяют стрессовые волокна между соседними эндотелиальными клетками. BMC Biol. 8 , 11 (2010).
Артикул Google Scholar
Дежана, Э.Соединения эндотелиальных клеток с клетками: счастливы вместе. Nat. Rev. Mol. Cell Biol. 5 , 261–270 (2004).
CAS Статья Google Scholar
Bazzoni, G. & Dejana, E. Поры в сите и каналы в стенке: контроль парацеллюлярной проницаемости с помощью соединительных белков в эндотелиальных клетках. Микроциркуляция 8 , 143–152 (2001).
CAS Статья Google Scholar
Вашке, Дж., Карри, Ф. Э., Адамсон, Р. Х. и Дренкхан, Д. Регулирование динамики актина имеет решающее значение для функций эндотелиального барьера. Am. J. Physiol. Heart Circ. Physiol. 288 , h2296 – h2305 (2005 г.).
CAS Статья Google Scholar
Sun, S. et al. Монодисперсные наночастицы MFe2O4 (M = Fe, Co, Mn). J. Am. Chem. Soc. 126 , 273–279 (2004).
CAS Статья Google Scholar
Ян Х.Т., Огава, Т., Хасегава, Д., Такахаши, М. Синтез и магнитные свойства монодисперсных нанокубов магнетита. J. Appl. Phys. 103 , 07D526 (2008).
Артикул Google Scholar
Тонг, С., Хоу, С., Рен, Б., Чжэн, З. и Бао, Г. Самосборка покрытия фосфолипид-ПЭГ на наночастицах посредством двойной замены растворителя. Nano Lett. 11 , 3720–3726 (2011).
CAS ОБЪЯВЛЕНИЯ Статья Google Scholar
Липовски, Х.H. Поток-зависимая регуляция функции сосудов (ред. Беван, Дж. И Кейли, Г.) (Oxford Univ. Press, 1985).
Гэлбрейт, К. Г., Скалак, Р. и Чиен, С. Напряжение сдвига вызывает пространственную реорганизацию цитоскелета эндотелиальных клеток. Cell Motil. Цитоскелет 40 , 317–330 (1998).
CAS Статья Google Scholar
Чиен, С. Механотрансдукция и гомеостаз эндотелиальных клеток: мудрость клетки. Am. J. Physiol. Heart Circ. Physiol. 292 , h2209 – h2224 (2007).
CAS Статья Google Scholar
Myers, D. R. et al. Эндотелиализированная микрофлюидика для изучения микрососудистых взаимодействий при гематологических заболеваниях. J. Vis. Exp. 64 , e3958 (2012).
Google Scholar
Tsai, M. et al. In vitro моделирование окклюзии микрососудов и тромбозов, возникающих при гематологических заболеваниях, с использованием микрожидкостной технологии. J. Clin. Вкладывать деньги. 122 , 408–418 (2012).
CAS Статья Google Scholar
van Geemen, D. et al. Фокальные спайки, заякоренные F-актином, различают эндотелиальные фенотипы артерий и вен человека. Артериосклер. Тромб. Васк. Биол. 34 , 2059–2067 (2014).
CAS Статья Google Scholar
Севик-Мурака, Э.М. Перевод технологий ближней инфракрасной флуоресцентной визуализации: новые клинические применения. Annu. Rev. Med. 63 , 217–231 (2012).
CAS Статья Google Scholar
Ng, C.P. & Pun, S.H. Перфузионная трехмерная камера для культивирования ткани с клеточным матриксом для in situ оценки проникновения и транспорта наночастиц. Biotechnol. Bioeng. 99 , 1490–1501 (2008).
CAS Статья Google Scholar
Gleich, B. & Weizenecker, R. Создание томографических изображений с использованием нелинейного отклика магнитных частиц. Nature 435 , 1214–1217 (2005).
CAS ОБЪЯВЛЕНИЯ Статья Google Scholar
Goodwill, P. W. et al. X-space MPI: магнитные наночастицы для безопасной медицинской визуализации. Adv.Матер. 24 , 3870–3877 (2012).
CAS Статья Google Scholar
Riegler, J. et al. Направленная магнитная доставка и отслеживание клеток с помощью системы магнитно-резонансной томографии. Биоматериалы 31 , 5366–5371 (2010).
CAS Статья Google Scholar
Muthana, M. et al. Направление клеточной терапии на анатомические участки-мишени in vivo с нацеливанием на магнитный резонанс. Nat. Commun. 6 , 8009 (2015).
CAS Статья Google Scholar
Каннингем К. С. и Готлиб А. И. Роль напряжения сдвига в патогенезе атеросклероза. Lab. Вкладывать деньги. 85 , 9–23 (2005).
CAS Статья Google Scholar
Дэвис П. Ф. и Трипати С. Механизмы механических напряжений и клетки.Эндотелиальная парадигма. Circ. Res. 72 , 239–245 (1993).
CAS Статья Google Scholar
Тарбелл, Дж. М. Массовый транспорт в артериях и локализация атеросклероза. Annu. Преподобный Биомед. Англ. 5 , 79–118 (2003).
CAS Статья Google Scholar
Сарагоса, К., Маркес, С. и Саура, М.Эндотелиальные механосенсоры напряжения сдвига как регуляторы атерогенеза. Curr. Opin. Липидол. 23 , 446–452 (2012).
CAS Статья Google Scholar
Шай, Дж. Я. и Чиен, С. Роль интегринов в эндотелиальном механочувствлении напряжения сдвига. Circ. Res. 91 , 769–775 (2002).
CAS Статья Google Scholar
Тонтон, Дж.и другие. Актин-зависимое продвижение эндосом и лизосом за счет привлечения N-WASP. J. Cell Biol. 148 , 519–530 (2000).
CAS Статья Google Scholar
Тонг, С., Рен, Б., Чжэн, З., Шен, Х. и Бао, Г. Крошечные зерна дают огромные преимущества: усиление сигнала на основе нанокристаллов для обнаружения биомолекул. ACS Nano 7 , 5142–5150 (2013).
CAS Статья Google Scholar
Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследовать
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О Массачусетском технологическом институте
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О Массачусетском технологическом институте
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
.
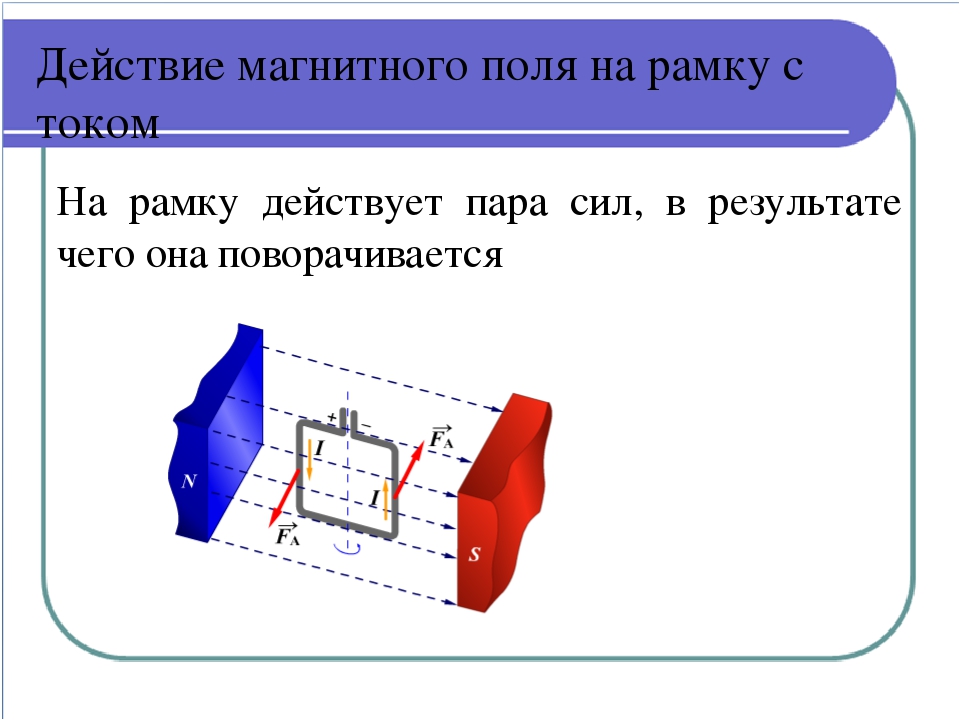 Кроме того, чтобы вычислить силу на прикрепленном к ферромагнитной поверхности магните, контактные границы должны иметь тонкий зазор с малой диэлектрической проницаемостью (тонкий зазор с малой диэлектрической проницаемостью для электростатического эквивалента), поскольку натяжения Максвелла должны быть рассчитаны скорее в воздухе, чем в ферромагнитном (диэлектрическом) материале.
Кроме того, чтобы вычислить силу на прикрепленном к ферромагнитной поверхности магните, контактные границы должны иметь тонкий зазор с малой диэлектрической проницаемостью (тонкий зазор с малой диэлектрической проницаемостью для электростатического эквивалента), поскольку натяжения Максвелла должны быть рассчитаны скорее в воздухе, чем в ферромагнитном (диэлектрическом) материале. Для определения направленности используют правило правой руки.
Для определения направленности используют правило правой руки.