Магнитное поле как определить: Направление тока и направление линий его магнитного поля — урок. Физика, 8 класс. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Физика Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки

Материалы к уроку

Конспект урока

Вспомним, как можно обнаружить магнитное поле, ведь оно невидимо и наши органы чувств его не воспринимают? Магнитное поле можно обнаружить только по его действию на другие тела, например, на магнитную стрелку. Поле действует на стрелку с какой-то силой, заставляющей ее изменить первоначальную ориентацию. Магнитное поле создается при движении зарядов вдоль проводника в цепи или за счет одинаковой ориентации кольцевых токов в постоянных магнитах. Открытие Эрстеда, о взаимосвязи между электричеством и магнетизмом побудила ученых проводить различные опыты, с помощью которых были установлены новые закономерности. Мы уже знаем, что вокруг проводника с током создается магнитное поле. А как будет вести себя проводник с током, если его поместить в другое магнитное поле?
Проведем опыт.
Соберем установку, состоящую из подвижной рамки из меди, закрепленной на изолирующей штанге, источника тока, реостата и ключа. Включи цепь. Рамка останется неподвижной. Мы уже знаем, что вокруг проводника есть магнитное поле, но обнаружить мы его не можем. Разомкнем цепь. Расположим дугообразный магнит вблизи рамки так, чтобы горизонтальная часть рамки располагалась между его полюсами (т.к. вблизи полюсов магнитное поле наиболее сильное). Вокруг дугового магнита так же есть магнитное поле, но пока в рамке не течет ток, обнаружить его мы так же не можем. Замкнем цепь. Рамка пришла в движение и отклонилась влево. Некоторая сила, направленная в сторону магнита привела рамку в движение и отклонила ее на некоторый угол. Магнитное поле вокруг проводника создается электрическим током. Обнаружить магнитное поле можно по его действию электрический ток. На рисунке отмечено направление движения тока в проводнике.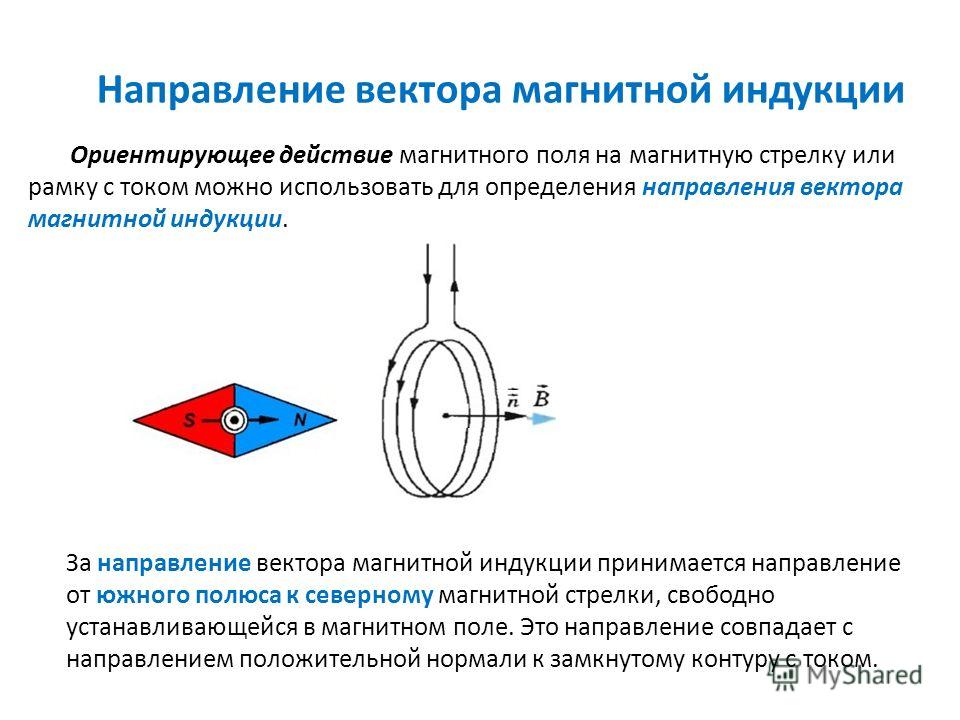

За направление тока выбрано движение от положительного полюса источника тока к отрицательному полюсу. Изменим направление тока, поменяв полярность. Замыкаем цепь и опять обнаруживаем магнитное поле по действию на рамку – она отклонилась на некоторый угол в противоположную от магнита сторону. Если в последнем опыте поменять расположение полюсов магнита на противоположное, рамка втянется в дуговой магнит. Направление силы, под действием которой проводник движется в конкретном направлении, можно определить по правилу левой руки. Это мнемоническое правило, с помощью которого легко определить, куда будет направлена сила, обозначим ее на рисунке буквой F. Если левую руку расположить так, чтобы линии магнитного поля входили перпендикулярно в ладонь, четыре пальца показывали направление тока, тогда отставленный на 900 большой палец покажет направление действующей на проводник силы. Запомните, что за направление тока выбрано движение от плюса к минусу. Так в проводящей среде движутся положительные заряды, создающие ток.

Значит, по правилу правой руки так же можно определить направление силы для положительно заряженной частицы. А когда мы хотим определить направление силы, действующей на отрицательную частицу, четыре пальца должны располагаться против движения отрицательно заряженной частицы.
Определите, как расположены полюса магнита, направление силы тока и силы, действующей со стороны магнитного поля на проводник с током. Воспользуемся правилом левой руки. Четыре пальца левой руки показывают направление тока. Проводник расположен перпендикулярно плоскости, а так как мы видим оперение стрелы (крест), следовательно, ток движется от нас. Направление силы, действующей со стороны магнитного поля, показывает отставленный на 900 большой палец. Ладонь левой руки смотрит вверх, следовательно, в нее будут входить линии магнитного поля, то есть северный полюс магнита должен располагаться сверху. Если направление тока в проводнике или скорость частицы совпадают с линией магнитной индукции или параллельны ей, то сила действия магнитного поля или движущуюся заряженную частицу равна нулю.

Остались вопросы по теме? Наши репетиторы готовы помочь!

Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитораОставить заявку на подбор

Нейросеть помогла определить магнитное поле на дальней стороне Солнца

Ученые использовали нейросеть для определения пространственной структуры магнитного поля Солнца. Программа успешно справилась с получением карт распределения поля как на видимой, так и на обратной стороне светила. Результаты опубликованы в журнале Nature Astronomy.

Стандартным методом представления структуры магнитного поля Солнца являются магнитограммы, которые в графическом виде отображают его пространственные вариации, а одним из распространенных методов определения магнитного поля является картирование Зеемана—Доплера. Этот способ заключается в способности магнитного поля поляризовать излучение — по разности доплеровских скоростей, определенных в различных каналах поляризации, можно определить проекцию магнитного поля на луч зрения. Тем не менее, этот метод работает только на непосредственно наблюдаемой стороне звезды. В случае обратной стороны можно воспользоваться методами гелиосейсмологии, для которых необходимы только данные о видимой стороне, однако в таком случае качестве полученных данных значительно уступает прямым наблюдениям.

Сегодня за Солнцем наблюдает сразу несколько космических телескопов, в том числе американские Обсерватория солнечной динамики (SDO) и STEREO. Особенность второй миссии заключается в том, что она состоит из двух одинаковых аппаратов, которые независимо движутся по орбитам, близким к земной. В результате один из них постепенно все больше отстает от планеты, а второй — обгоняет. Это позволяет наблюдать светило с различных сторон и даже получать трехмерные изображения, используя стереоскопический эффект. Однако после череды проблем с электроникой и последовавшей потерей контроля над ориентацией данные со STEREO-B доступны только до 1 октября 2014 года.

Тэен Ким (Taeyoung Kim) из Университета Кенхи в Южной Корее и его коллеги натренировали алгоритм глубокого обучения создавать магнитограммы. Исходными для первой части работы были данные SDO: ультрафиолетовые снимки прибора Atmospheric Imaging Assembly (AIA) и измерения магнитного поля на луче зрения, проведенные инструментом Helioseismic and Magnetic Imager (HMI). Данные собирались каждые 12 часов в течение 2011–2017 годов. В результате получилось 4972 пар изображений и магнитограмм, из которых 4147 (все данные, кроме полученных в сентябре и октябре каждого года) использовались в качестве обучающей выборки, а оставшиеся 825 — в качестве тестовой.

В исследовании применялась генеративно-состязательная сеть, то есть комбинация двух нейросетей, одна из которых (генератор) создает образцы, а вторая (дискриминатор) пытается выбрать из них наиболее похожие на представленные в обучающей выборке. Авторы сравнили результаты работы алгоритма, то есть магнитограммы за сентябрь и октябрь, с данными прибора HMI. Оказалось, что программа качественно воссоздала структуру поля. В частности, результат ее работы соответствовал эмпирическому закону Хейла, который гласит, что в северном полушарии одна полярность всегда предшествует другой, а в южном полушарии наблюдается обратная ситуация. Полярность солнечного магнитного поля меняется на противоположную от цикла к циклу, но вся обучающая выборка была получена в течение 24 солнечного цикла, поэтому нейросеть в текущем виде эффективна при работе с четными циклами, а точность ее предсказаний при нечетных циклах необходимо отдельно проверять.

Тем не менее, созданные программой магнитограммы не во всем соответствовали измерениям. Например, угол между парами солнечных пятен разной полярности не всегда оказывался правильным. Авторы связывают эти расхождения с тем фактом, что излучение в ультрафиолетовом диапазоне рождается в переходной зоне между хромосферой и короной, в то время как магнитограмма строится по данным о фотосфере, расположенной значительно ближе к поверхности звезды.

Вторая часть работы была посвящена данным STEREO, которые можно использовать для генерации распределения магнитного поля на дальней стороне Солнца. Для проверки авторы взяли данные со спутника STEREO-B, который 4 июня 2013 года находился на -164 градуса гелиографической долготы, то есть получал изображения преимущественно обратной стороны. Прибор Extreme UltraViolet Imager (EUVI) на борту этого аппарата собирает данные в том же диапазоне, что и AIA на борту SDO, что позволило использовать обученную ранее сеть. Ученые отследили движение активной области 12087, которая в период с 4 по 13 июня 2014 года перешла с обратной стороны звезды на видимую с Земли. Астрономы заключают, что программа в целом правильно воспроизвела структуру магнитного поля, что позволяет получать данные о временной эволюции магнитной активности Солнца на любом участке, где есть данные ультрафиолетового диапазона.

Ученые заключают, что им удалось показать удачный пример непосредственного преобразования изображений с помощью нейросетевой модели. Они отмечают, что в области астрономии и геофизики часто имеется большое количество данных различных диапазонов, что потенциально позволяет применять подобные модели во множестве ситуаций. Непосредственно в случае наблюдения Солнца, такая модель позволяет лучше понимать временную эволюцию активных областей, которые являются источниками вспышек, определяющих космическую погоду.

Магнитное поле Солнца значительно сложнее земного, подвержено намного более сильным изменениям как во времени, так и в пространстве. Подробно об исследованиях изменения земного поля мы писали в материале «Мой компас земной».

Тимур Кешелава

Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.

5.4 Сила, действующая на движущийся заряд в магнитном поле: примеры и приложения

Цели обучения

К концу этого раздела вы сможете делать следующее:

Описать воздействие магнитного поля на движущийся заряд
Рассчитать радиус кривизны пути заряда, движущегося в магнитном поле

Информация, представленная в этом разделе, поддерживает следующие цели обучения и научные практики AP®:

3.C.3.1 Учащийся может использовать правила правой руки для анализа ситуации, включающей проводник с током и движущийся электрически заряженный объект, чтобы определить направление магнитной силы, действующей на заряженный объект из-за магнитное поле, создаваемое проводником с током. (СП 1.4)

Магнитная сила может заставить заряженную частицу двигаться по круговой или спиральной траектории. Космические лучи — это энергичные заряженные частицы в космическом пространстве, некоторые из которых приближаются к Земле. Магнитное поле Земли может заставить их двигаться по спирали. Протоны в гигантских ускорителях удерживаются на круговой траектории благодаря магнитной силе. Фотография пузырьковой камеры на рис. 5.11 показывает заряженные частицы, движущиеся по таким изогнутым траекториям. Искривленные траектории заряженных частиц в магнитных полях лежат в основе ряда явлений и даже могут использоваться аналитически, например, в масс-спектрометре.

Рис. 5.11. Следы пузырьков образуются заряженными частицами высокой энергии, движущимися через перегретый жидкий водород в этом художественном исполнении пузырьковой камеры. Существует сильное магнитное поле, перпендикулярное странице, что приводит к искривлению траекторий частиц.

Радиус пути можно использовать для определения массы, заряда и энергии частицы.

Значит, магнитная сила вызывает круговое движение? Магнитная сила всегда перпендикулярна скорости, поэтому на заряженную частицу она не действует. Таким образом, кинетическая энергия и скорость частицы остаются постоянными. Направление движения влияет, но не скорость. Это характерно для равномерного кругового движения. Простейший случай имеет место, когда заряженная частица движется перпендикулярно однородному полю размером 12{B} {} B-B, как показано на рис. 5.12. (Если это происходит в вакууме, магнитное поле является доминирующим фактором, определяющим движение.) Здесь магнитная сила создает центростремительную силу Fc=mv2/r.Fc=mv2/r.size 12{F rSub { size 8 {c} } = ital “mv” rSup { size 8{2} } /r} {} Заметив, что sinθ=1,sinθ=1,size 12{“sin”θ=1} {} мы видим, что F=qvB .F=qvB.size 12{F= ital “qvB”} {}

Рис. 5.12. Отрицательно заряженная частица движется в плоскости страницы в области, где магнитное поле перпендикулярно странице (представлено маленькими кружками с крестиком — как хвосты стрелок).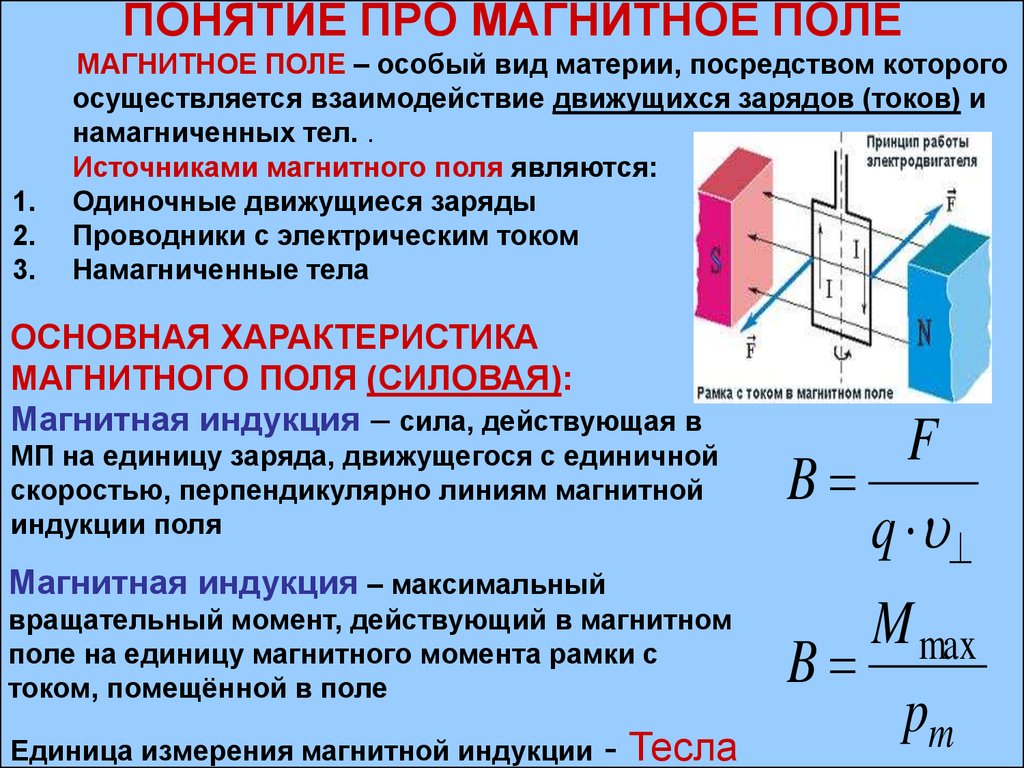 Магнитная сила перпендикулярна скорости, поэтому скорость изменяется по направлению, но не по величине. Результат равномерного кругового движения.

Поскольку магнитная сила FF размера 12{F} {} обеспечивает центростремительную силу Fc,Fc,размер 12{F rSub { размер 8{c} } } {}, мы имеем

5.6 qvB=mv2r.qvB=mv2r. size 12{ ital “qvB”= { { ital “mv” rSup { size 8{2} } } over {r} } “.” } {}

Решение для размера rr 12{r} {} дает

5,7 r=mvqB.r=mvqB. size 12{r= { { ital “mv”} over { ital “qB”} } “.” } {}

Здесь rr размер 12{r} {} — радиус кривизны пути заряженной частицы с массой mm размером 12{m} {} и зарядом q,q,размером 12{q} {} движущегося со скоростью vv размером 12{v} {} перпендикулярно магнитному полю напряженностью B.B.size 12{B} {} Если скорость не перпендикулярна магнитному полю, то vv размером 12{v} {} является составляющей скорости перпендикулярно полю. Составляющая скорости, параллельная полю, не изменяется, потому что магнитная сила равна нулю для движения, параллельного полю.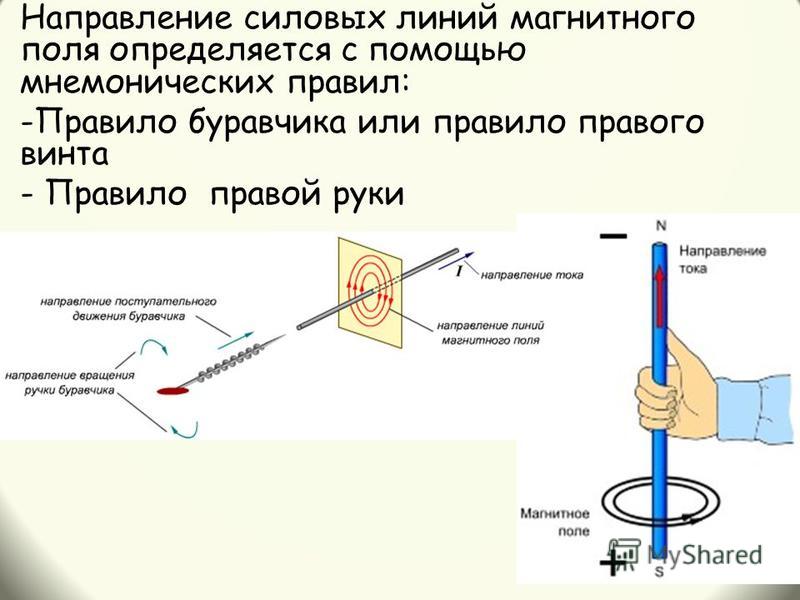

Это создает спиральное движение, а не круговое.

Пример 5.2 Расчет кривизны пути электрона, движущегося в магнитном поле: магнит на экране телевизора ЖК-экранов) сильно искажает его изображение, изменяя путь электронов, которые заставляют его люминофоры светиться.

(Не пытайтесь повторить это дома, так как это приведет к необратимому намагничиванию и повреждению телевизора.) Чтобы проиллюстрировать это, рассчитайте радиус кривизны пути электрона, имеющего скорость 6,00×107 м/с6,00 ×107 м/с размер 12{6 “.” «00» умножить на «10» rSup { размер 8{7} } `”м/с”} {} (соответствует ускоряющему напряжению около 10,0 кВ, используемому в некоторых телевизорах) перпендикулярно магнитному полю напряженностью B=0,500 ТБ =0,500 T размер 12{B=0 “.” “500” T} {} (доступно с постоянными магнитами).

Рисунок 5.13 Вид сбоку, показывающий, что происходит, когда магнит входит в контакт с монитором компьютера или экраном телевизора. Электроны движутся к экрану по спирали вокруг силовых линий магнитного поля, сохраняя составляющую своей скорости, параллельную силовым линиям. Это искажает изображение на экране.

Стратегия

Радиус кривизны rr можно найти непосредственно из уравнения r=mvqB,r=mvqB, так как все остальные величины в нем заданы или известны.

Решение

Использование известных значений массы и заряда электрона вместе с заданными значениями размера vv 12{v} {} и размера BB 12{B} {} дает нам

5,8 r=mvqB=9,11 ×10−31кг6,00×107м/с1,60×10−19C0,500T=6,83×10−4mr=mvqB=9,11×10−31кг6,00×107м/с1,60×10−19C0,500T=6,83×10 −4malignl { stack { size 12 {r = { { ital “mv”} over { ital “qB”} } = { { left (9 “.” “11” умножить на “10” rSup { size 8{ – “31” } } `”кг” вправо ) влево (6 “.” “00” раз “10” rSup { размер 8{7} } `”м/с” вправо )} над { влево (1 “.” “60” раз “10” rSup {размер 8{-“19”} } `C справа ) слева (0 “.” “500”`T справа )} } } {} # =6 “.” “83” умножить на “10” rSup { size 8{ – 4} } `m { } } } {}

или

5,9 r=0,683 мм.r=0,683 мм Размер 12{r=0 “.” “683”” мм”} {}

Обсуждение

Малый радиус означает

На рис. 5.14 показано, как электроны, движущиеся не перпендикулярно линиям магнитного поля, следуют за силовыми линиями. скорость, параллельная линиям, не изменяется, и поэтому заряды закручиваются вдоль силовых линий. Если напряженность поля увеличивается в направлении движения, поле будет оказывать силу, замедляющую заряды, образуя своего рода магнитное зеркало, как показано ниже.

Рис. 5.14 Когда заряженная частица движется вдоль силовой линии магнитного поля в область, где поле становится сильнее, на частицу действует сила, уменьшающая составляющую скорости, параллельную полю. Эта сила замедляет движение вдоль силовой линии и здесь меняет его направление, образуя магнитное зеркало .

Свойства заряженных частиц в магнитных полях связаны с такими разными вещами, как Aurora Australis или Aurora Borealis и ускорителями частиц. Заряженные частицы, приближающиеся к силовым линиям магнитного поля, могут попасть в ловушку на спиральных орбитах вокруг линий, а не пересекать их , как показано выше. Некоторые космические лучи, например, следуют линиям магнитного поля Земли, проникая в атмосферу вблизи магнитных полюсов и вызывая южное или северное сияние за счет ионизации молекул в атмосфере. Это свечение возбужденных атомов и молекул видно на рис. 5.1. Те частицы, которые приближаются к средним широтам, должны пересекать силовые линии магнитного поля, и многие из них не могут проникнуть в атмосферу. Космические лучи являются компонентом фонового излучения; следовательно, они дают более высокую дозу радиации на полюсах, чем на экваторе.

Рис. 5.15 Энергичные электроны и протоны, составляющие космические лучи, исходящие от Солнца и глубокого космоса, часто следуют за силовыми линиями магнитного поля Земли, а не пересекают их. (Напомним, что северный магнитный полюс Земли на самом деле является южным полюсом с точки зрения стержневого магнита.)

Некоторые прилетающие заряженные частицы захватываются магнитным полем Земли, образуя два пояса над атмосферой, известные как радиационные пояса Ван Аллена в честь первооткрывателя Джеймса. А. Ван Аллен, американский астрофизик. (См. рис. 5.16.) Частицы, попавшие в эти пояса, образуют радиационные поля (подобные ядерному излучению) настолько интенсивные, что пилотируемые космические полеты избегают их, а спутники с чувствительной электроникой не попадают в них. За несколько минут, которые потребовались лунным миссиям для пересечения радиационных поясов Ван Аллена, астронавты получили дозы радиации, более чем в два раза превышающие допустимую годовую дозу радиационных работников. Подобные пояса есть и у других планет, особенно у тех, у которых сильные магнитные поля, таких как Юпитер.

Рис. 5.16 Радиационные пояса Ван Аллена представляют собой две области, в которых энергичные заряженные частицы захватываются магнитным полем Земли. Один пояс лежит на высоте около 300 км над поверхностью Земли, другой — на высоте около 16 000 км. Заряженные частицы в этих поясах мигрируют вдоль силовых линий магнитного поля и частично отражаются от полюсов более сильными там полями. Заряженные частицы, попадающие в атмосферу, восполняются солнцем и источниками в глубоком космосе.

На Земле у нас есть устройства, использующие магнитные поля для удержания заряженных частиц. Среди них гигантские ускорители частиц, которые использовались для изучения субструктуры материи. (См. рис. 5.17.) Магнитные поля не только контролируют направление заряженных частиц, они также используются для фокусировки частиц в пучки и преодоления отталкивания одноименных зарядов в этих пучках.

Рис. 5.17 В лаборатории Фермилаб в Иллинойсе есть большой ускоритель частиц (самый мощный в мире до 2008 г.), который использует магнитные поля (магниты здесь выделены оранжевым цветом) для сдерживания и направления луча. Этот и другие ускорители используются уже несколько десятилетий и позволили нам открыть некоторые законы, лежащие в основе всей материи. (ammcrim, Flickr)

Термоядерный синтез (подобный происходящему на Солнце) — это надежда на будущий источник чистой энергии. Одним из самых перспективных устройств является 9Токамак 0044 , который использует магнитные поля для удержания (или захвата) и направления реактивных заряженных частиц. (См. рис. 5.18.) Менее экзотические, но более практичные усилители в микроволновых печах используют магнитное поле для сдерживания колеблющихся электронов. Эти колеблющиеся электроны генерируют микроволны, направляемые в духовку.

Рис. 5.18 Токамаки, подобные показанному на рисунке, изучаются с целью экономичного производства энергии путем ядерного синтеза. Магнитные поля в устройстве в форме пончика удерживают и направляют реактивные заряженные частицы. (кредит: Дэвид Меллис, Flickr)

Масс-спектрометры имеют различные конструкции, и многие из них используют магнитные поля для измерения массы. Кривизна пути заряженной частицы в поле связана с ее массой и измеряется для получения информации о массе. (См. Дополнительные применения магнетизма.) Исторически такие методы использовались при первых прямых наблюдениях за зарядом и массой электрона. Сегодня масс-спектрометры (иногда в сочетании с газовыми хроматографами) используются для определения состава и последовательности крупных биологических молекул.

электромагнетизм – Можем ли мы рассчитать магнитное поле постоянного магнита?

спросил 3 года, 8 месяцев назад

Изменено 3 года, 7 месяцев назад

Просмотрено 2к раз

$\begingroup$

Знакомство с магнитами всегда происходит благодаря картинкам, изображающим параллелепипедный магнит, подковообразный магнит и т. д.
Так или иначе, первый раз, когда мы вычисляем магнитное поле, мы делаем это для электромагнитов.
Действительно, я редко видел объяснение или расчет магнитного поля постоянного магнита.
Я знаю формулы для магнитного поля движущегося заряда вокруг проводящего провода внутри соленоида, но понятия не имею, как рассчитать поле простого постоянного магнита.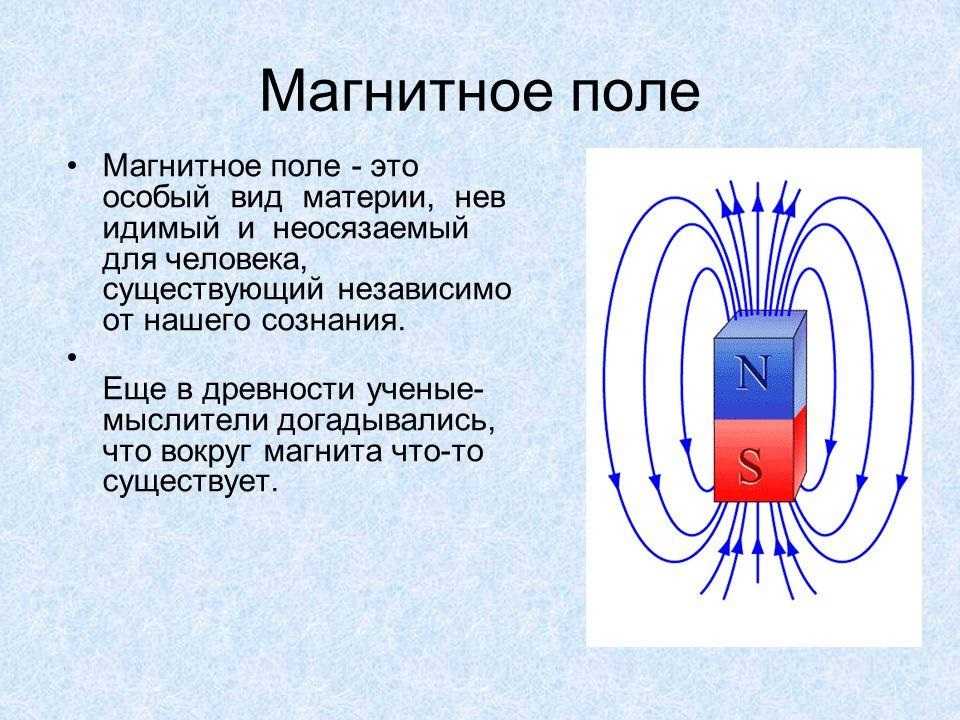
Это так без помощи электричества я застрял.
Я предполагаю, что это сильно зависит от магнитного материала, его формы и среды, в которую он помещается.
Я надеюсь, что кто-нибудь подскажет мне, почему такие формулы никогда не вводился в большинство курсов физики и содержит несколько примеров расчета поля постоянного магнита.

электромагнетизм
магнитные поля

$\endgroup$