Магнитный поток это физическая величина равная: Тест с ответами Магнитный поток (Физическая величина, равная произведению …)

Тест с ответами Магнитный поток (Физическая величина, равная произведению …)

Рубрика: Физика

(правильные ответы отмечены плюсом)

1. Физическая величина, равная произведению модуля вектора магнитной индукции на площадь S и косинус угла α между векторами и нормалью:

а) магнитный поток +
б) магнитный ток
в) магнетизм

2. Магнитный поток зависит от:
а) нагрузки
б) модуля вектора магнитной индукции +
в) напряжения

3. Магнитный поток зависит от:
а) напряжения
б) нагрузки
в) площади контура +

4. Магнитный поток зависит от:
а) ориентации контура по отношению к линиям индукции магнитного поля +
б) напряжения
в) нагрузки

5. Как должна располагаться плоскость витка по отношению к линиям магнитной индукции, чтобы магнитный поток был равен нулю:
а) перпендикулярно линиям
б) под некоторым углом к линиям
в) параллельно линиям +

 

6. Как должна располагаться плоскость витка по отношению к линиям магнитной индукции, чтобы магнитный поток был максимальным:
а) параллельно линиям
б) перпендикулярно линиям +
в) под некоторым углом к линиям

7. Замкнутый контур расположен под некоторым углом к линиям магнитной индукции. Как изменится магнитный поток, если модуль вектора магнитной индукции увеличится в 3 раза:

а) уменьшится в 3 раза
б) увеличится в 6 раз
в) увеличится в 3 раза +

8. Замкнутый контур расположен под некоторым углом к линиям магнитной индукции. Как изменится магнитный поток, если площадь контура уменьшится в 2 раза:
а) уменьшится в 2 раза +
б) увеличится в 2 раза
в) уменьшится в 4 раза

9. Замкнутый контур расположен под некоторым углом к линиям магнитной индукции. Как изменится магнитный поток, если площадь контура уменьшится в 2 раза, а модуль вектора магнитной индукции увеличится 4 раза:
а) уменьшится в 2 раза
б) уменьшится в 4 раза
в) увеличится в 2 раза +

10. Замкнутый контур расположен под некоторым углом к линиям магнитной индукции. Как изменится магнитный поток, если площадь контура уменьшится в 3 раза, а модуль вектора магнитной индукции увеличится в 3 раза:

а) уменьшится в 3 раза
б) не изменится +
в) увеличится в 3 раза

11. Линии магнитной индукции лежат в плоскости замкнутого контура. Как изменится магнитный поток, если модуль вектора магнитной индукции увеличится в 3 раза:
а) не изменится +
б) уменьшится в 3 раза
в) увеличится в 3 раза

12. Кто открыл явление электромагнитной индукции:
а) Вольта
б) Фарадей +
в) Кулон

13. Как называется единица измерения магнитного потока:
а) Вебер +

б) Фарад
в) Тесла

14. Выводы катушки из медного провода присоединены к чувствительному гальванометру. В каком из перечисленных опытов гальванометр обнаружит возникновение ЭДС электромагнитной индукции в катушке:
1. В катушку вставляется постоянный магнит
2. Из катушки вынимается постоянный магнит
3. Постоянный магнит вращается вокруг своей продольной оси внутри катушки
а) в случаях 1 и 3
б) в случаях 3 и 2
в) в случаях 1 и 2 +

15. Прямолинейный проводник длиной l с током I помещен в однородное магнитное поле так, что направление вектора магнитной индукции B перпендикулярно проводнику.

Если силу тока уменьшить в 2 раза, а индукцию магнитного поля увеличить в 4 раза, то действующая на проводник сила Ампера:
а) увеличится в 2 раза +
б) уменьшится в 4 раз
в) уменьшится в 2 раза

16. Плоский контур из проводника подключен к гальванометру и помещен в постоянное однородное магнитное поле. Стрелка гальванометра отклонится если:
а) контур неподвижен
б) контур вращается +
в) если контур движется поступательно

17. В каком из представленных ниже технических объектов используется явление движения проводника с током под действием магнитного поля:
а) в электрогенераторе
б) в электромагните

в) в электродвигателе +

18. 2 катушки вставлены одна в другую и подключены, первая через ключ к источнику тока, а вторая к гальванометру. Стрелка гальванометра отклоняется:
а) все время протекания тока по первой катушке
б) в момент замыкания и размыкания ключа +
в) только в момент замыкания ключа

19. Прямолинейный проводник длиной L с током I помещен в однородное магнитное поле так, что направление вектора магнитной индукции B перпендикулярно проводнику.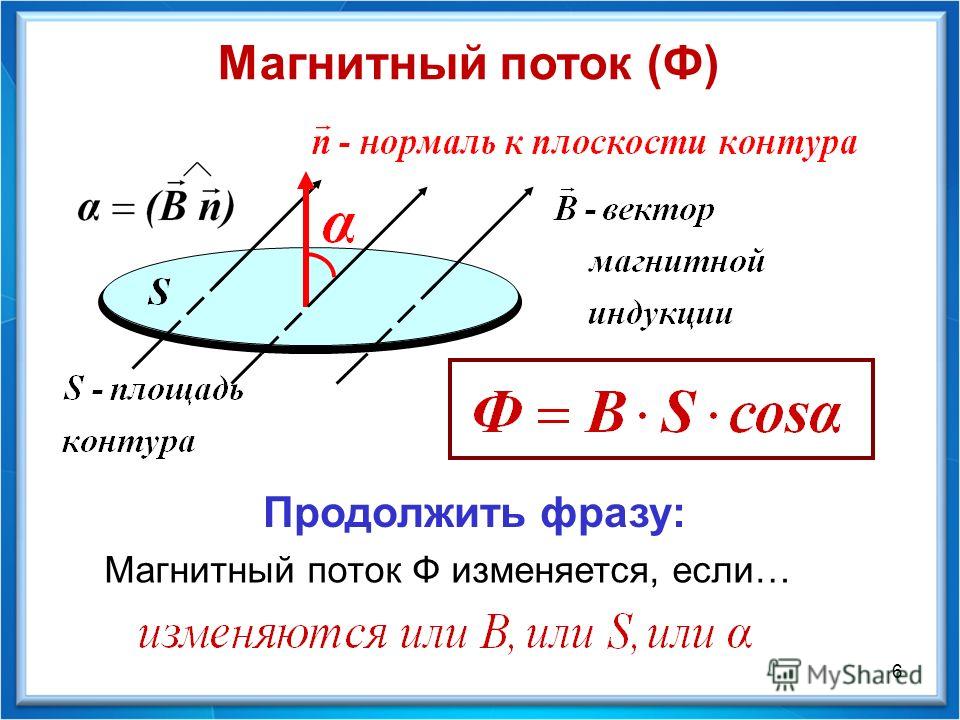 Если силу тока увеличить в 2 раза, а индукцию магнитного поля уменьшить в 4 раза, то действующая на проводник сила Ампера:
а) увеличится в 2 раза
б) увеличится в 4 раза

в) уменьшится в 2 раза +

20. Прямолинейный проводник длиной 0,2 м находится в однородном магнитном поле с индукцией 4 Тл и расположен под углом 30° к вектору индукции. Чему равен модуль силы, действующей на проводник со стороны магнитного поля при силе тока в нем 2 А:
а) 0,2 Н
б) 0,8 Н +
в) 0,4 Н

21. Квадратная рамка вращается в однородном магнитном поле вокруг одной из своих сторон. Первый раз ось вращения совпадает с направлением вектора магнитной индукции, второй раз перпендикулярна ему. Ток в рамке:
а) возникает только во втором случае +
б) возникает в обоих случаях
в) возникает только в первом случае

22. В каком из представленных ниже технических устройств используется явление возникновения тока при движении проводника в магнитном поле:

а) электродвигатель
б) электрогенератор +
в) электромагнит

23. Для наблюдения явления электромагнитной индукции собирается электрическая схема, включающая в себя подвижную проволочную катушку, подсоединенную к амперметру и неподвижный магнит. Индукционный ток в катушке возникнет:
а) только если катушка надевается на магнит
б) только если катушка снимается с магнита
в) если катушка надевается на магнит или снимается с магнита +

24. В момент замыкания электрической цепи, содержащей катушку:

а) индукционный ток не появится
б) появится индукционный ток, препятствующий установлению тока +
в) появится постоянный индукционный ток

25. Как измениться энергия магнитного поля катушки, если силу тока увеличить в 2 раза, а количество витков в обмотке увеличить в 3 раза:
а) увеличиться в 12 раз
б) увеличиться в 6 раз
в) увеличиться в 36 раз +

26. В качестве одного из основных источников электромагнитного поля можно выделить:
а) гальванический элемент
б) линии электропередач +
в) батарейку

27. В качестве одного из основных источников электромагнитного поля можно выделить:

а) персональные компьютеры +
б) гальванический элемент
в) батарейку

28. В каком году М. Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного поля возникает так называемый индукционный ток:
а) 1841 г.
б) 1851 г.
в) 1831 г. +

29. Что является одним из источников магнитного поля:
а) движущаяся заряженная частица +
б) любое движущееся тело
в) покоящаяся заряженная частица

30. Сила, с которой магнитное поле действует на проводник с током, называется:
а) силой тока
б) силой Ампера +
в) магнитная индукция

 

 

 

• Тест с ответами Магнетизм (Прямолинейный проводник длиной …)
• Тест с ответами Физические поля, Электрическое, магнитное и электромагнитное поле ( Поле – это форма материи …)
• Тест по физике с ответами Магнитное поле (Что такое магнит …)
• Тест с ответами Магнитное поле (Как взаимодействуют два параллельных проводника …)
• Тест с ответами Индукция (В однородное магнитное поле перпендикулярно линиям …)

 

5.

Магнитный поток. Работа перемещения витка с током в магнитном поле.

4. Магнитный поток. Теорема о магнитном потоке через замкнутую поверхность. Вихревой характер магнитного поля. Магнитным потоком сквозь некоторую поверхность называют физическую величину, равную полному числу линий магнитной индукции, пронизывающих эту поверхность.

Или: магнитным потоком Ф через некоторую поверхность S называется скалярная величина, равная произведению модуля вектора магнитной индукции на площадь этой поверхности и косинус угла между нормалью n к ней и направлением вектора магнитной индукции B:Ф=|B|Scosa.

Рассмотрим однородное магнитное поле (такое поле существует внутри длинного соленоида с током вдали от его краев). Условимся рисовать линии магнитной индукции столь густо, что через единицу площади поверхности, перпендикулярную этим линиям, будет пронизываться количество линий, равное модулю магнитной индукции.

Рассмотрим плоскую прямоугольную площадку , перпендикулярную линиям магнитной индукции.

Тогда магнитный поток Ф, пронизывающий эту поверхность, будет равен . Рассмотрим наклонную площадку S такую, что сквозь нее проходит тот же магнитный поток, что и через . Из рисунка видно, что . Подставим :

(*)

Полученная формула может использоваться для расчета магнитного потока, пронизывающего наклонную плоскую площадку, расположенную в однородном магнитном поле с индукцией B. Проведем к поверхности S нормаль . Эта нормаль образует с также угол (по свойству углов со взаимно перпендикулярными сторонами). Значит в формуле (*) – угол между и .

Единица измерения магнитного потока – 1 Вебер. 1 Вб – это магнитный поток, пронизывающий плоскую поверхность, расположенную перпендикулярно линиям магнитной индукции в однородном магнитном поле, индукция которого равна 1 Тл.

В общем случае магнитное поле неоднородно, а поверхность, сквозь которую пронизываются линии магнитной индукции не является плоскостью. В этом случае мы делим всю поверхность на столь малые участки, что в пределах каждого магнитное поле можно буде считать однородным. Находим элементарные магнитные потоки, а затем их складываем.

Магнитный поток, как и поток вектора напряженности электрического поля, можно считать равным числу магнитных силовых линий, пересекающих рассматриваемую поверхность. Магнитное поле является вихревым, то есть его линии магнитной индукции замкнуты. Поэтому замкнутая поверхность, помещенная в магнитное поле, пронизывается линиями магнитной индукции так, что любая линия, входящая в эту поверхность, выходит из нее. Следовательно, полный магнитный поток через произвольную замкнутую поверхность равен нулю. Это утверждение носит название теоремы Гаусса для магнитных полей. Равенство нулю магнитного потока через замкнутую поверхность является следствием того, что в природе нет магнитных зарядов, и магнитные поля образуются только электрическими зарядами.

Линии магнитной индукции непрерывны: они не имеют ни начала, ни конца. Это имеет место для любого магнитного поля, вызванного какими угодно контурами с током.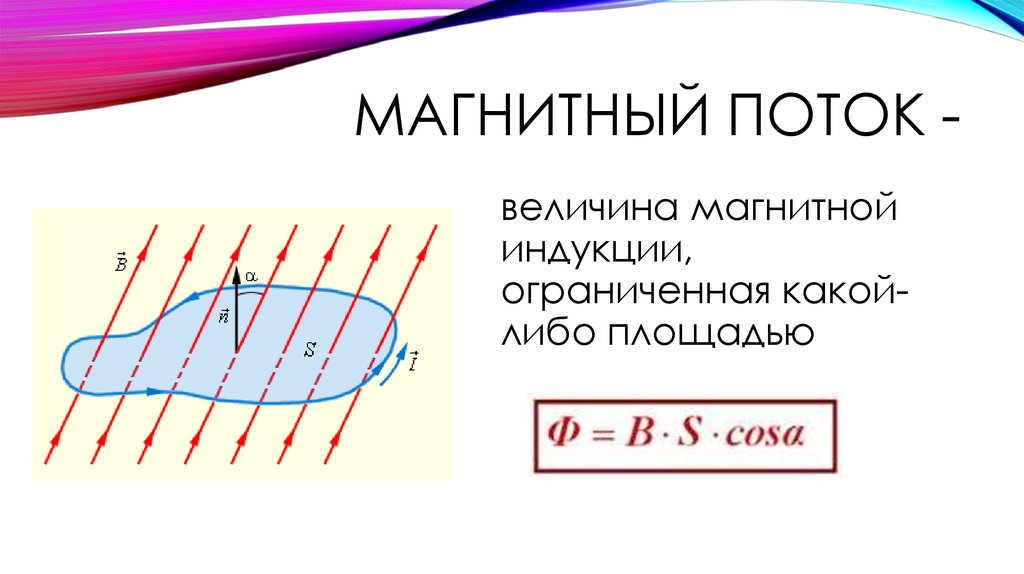 Векторные поля, обладающие непрерывными линиями, получили название вихревых полей. Мы видим, что магнитное поле есть вихревое поле. В этом заключается существенное отличие магнитного поля от электростатического.

Замкнутость линий магнитной индукции – фундаментальное свойство магнитного поля, вызванное тем, что изолированных магнитных зарядов, подобных электрическим, не существует. Любое магнитное поле, возникающее при движении электрических зарядов, всегда содержит N и S-полюса, и сколько бы мы ни дробили постоянный магнит, каждая его песчинка всегда будет содержать разноимённые магнитные полюса.

Магнитным потоком сквозь некоторую поверхность называют физическую величину, равную полному числу линий магнитной индукции, пронизывающих эту поверхность.

Или: магнитным потоком Ф через некоторую поверхность S называется скалярная величина, равная произведению модуля вектора магнитной индукции на площадь этой поверхности и косинус угла между нормалью n к ней и направлением вектора магнитной индукции B:Ф=|B|Scosa.

Рассмотрим однородное магнитное поле (такое поле существует внутри длинного соленоида с током вдали от его краев). Условимся рисовать линии магнитной индукции столь густо, что через единицу площади поверхности, перпендикулярную этим линиям, будет пронизываться количество линий, равное модулю магнитной индукции.

Рассмотрим плоскую прямоугольную площадку , перпендикулярную линиям магнитной индукции. Тогда магнитный поток Ф, пронизывающий эту поверхность, будет равен . Рассмотрим наклонную площадку S такую, что сквозь нее проходит тот же магнитный поток, что и через . Из рисунка видно, что . Подставим :

(*)

Полученная формула может использоваться для расчета магнитного потока, пронизывающего наклонную плоскую площадку, расположенную в однородном магнитном поле с индукцией B. Проведем к поверхности S нормаль . Эта нормаль образует с также угол (по свойству углов со взаимно перпендикулярными сторонами). Значит в формуле (*) – угол между и .

Единица измерения магнитного потока – 1 Вебер. 1 Вб – это магнитный поток, пронизывающий плоскую поверхность, расположенную перпендикулярно линиям магнитной индукции в однородном магнитном поле, индукция которого равна 1 Тл.

В общем случае магнитное поле неоднородно, а поверхность, сквозь которую пронизываются линии магнитной индукции не является плоскостью. В этом случае мы делим всю поверхность на столь малые участки, что в пределах каждого магнитное поле можно буде считать однородным. Находим элементарные магнитные потоки, а затем их складываем.

Работа перемещения витка с током в магнитном поле

Рассмотрим сначала частный случай. Пусть параллельные провода AB и CD (рис. 168) помещены в однородное постоянное поле, перпендикулярное к плоскости рисунка и направленное к читателю. Слева находится источник тока, не показанный на рисунке. По проводам может свободно перемещаться проводящий мостик KL, замыкающий ток

т екущий по проводам левее мостика. Если l- длина мостика, то на него магнитное поле действует с силой

При перемещении мостика на dx эта сила совершает работу:

Где, S- площадь прямоугольника AKLC. Величина BS есть магнитный поток через тот же прямоугольник. Обозначив его через Ф, получим для элементарной работы

а для конечной работы

Таким образом, работа, совершаемая магнитным полем над током, равна приращению магнитного потока, умноженному на . При выводе предполагалось, что ток при перемещении мостика KL поддерживался постоянным.

Результат справедлив и в том случае, когда магнитное поле направлено произвольно. Чтобы убедиться в этом, разложим вектор B на три составляющие . Составляющая вдоль мостика параллельна току в нём, а потому не оказывает на мостик силового воздействия. Составляющая вдоль перемещения даёт силу, перпендикулярную к перемещению, и работы не производит. Работа производится лишь составляющей , перпендикулярной к плоскости рисунка, в которой перемещается мостик KL. Эта работа представляется выражениями (62.1) и (62.2).

Докажем наконец, что формулы (62.1) и (62.2) справедливы для любого витка с током при произвольном перемещении его в постоянном неоднородном магнитном поле.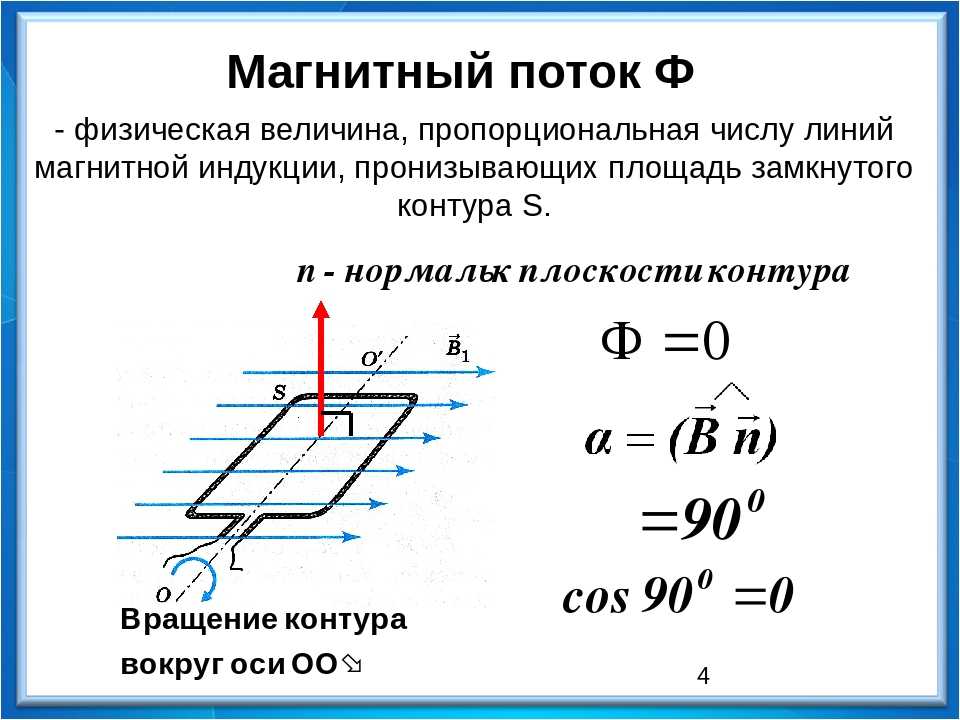 Виток может не только перемещаться как целое, но и произвольно деформироваться. Для доказательства достаточно мысленно разбить виток на бесконечно малые элементы тока и рассмотреть бесконечно малые их перемещения. При бесконечно малом перемещении элемента тока магнитное поле, в котором он перемещается, может считаться однородным. К такому перемещению применимо выражение (62.1) для элементарной работы. Сложением таких элементарных работ для всех элементов тока, на которые разбит виток, снова получается (62.1), в котором dФ означает приращение магнитного потока через весь виток. После этого переход от формулы (62.1) к формуле (62.2) совершается простым интегрированием. Подчеркнём ещё раз, что при перемещении витка сила тока в нём должна поддерживаться постоянной. Это достигается путём увеличения электродвижущей силы источника.

Разница между магнитным потоком и плотностью магнитного потока

26 апреля 2016 г.

by Kuma

Чтение через 4 мин.

Основное отличие — магнитный поток и плотность магнитного потока

В магнетизме несколько физических величин, таких как магнитный поток, плотность магнитного потока и напряженность магнитного поля, используются для объяснения поведения или влияния магнитных полей. Некоторые люди используют эти термины взаимозаменяемо. Но они имеют разные и особые значения. Основное различие между магнитным потоком и плотностью магнитного потока заключается в том, что магнитный поток является скалярной величиной, тогда как плотность магнитного потока является векторной величиной. Магнитный поток представляет собой скалярное произведение плотности магнитного потока и вектора площади. В этой статье делается попытка дать четкое объяснение магнитному потоку и плотности магнитного потока.

Что такое магнитный поток

Магнитный поток является важной скалярной величиной в магнетизме. Обычно магнитные поля визуализируют с помощью силовых линий магнитного поля. Величина поля представлена ​​плотностью силовых линий. Стрелки силовых линий обозначают направление магнитного поля. С точки зрения силовых линий магнитного поля магнитный поток через данную поверхность прямо пропорционален общему числу силовых линий, проходящих через нее. Однако силовые линии не являются реальными линиями в пространстве. Это всего лишь воображаемые линии, используемые в качестве простой модели для объяснения магнитных влияний движущихся заряженных частиц и магнитных материалов.

Магнитный поток в постоянном магнитном поле может быть выражен математически как ɸ = B.S.

ɸ — магнитный поток через векторную поверхность, B — плотность магнитного потока, S — площадь поверхности. Другими словами, магнитный поток через заданную площадь поверхности равен скалярному произведению (точечному произведению) плотности магнитного потока и вектора площади.

В более общем смысле магнитный поток можно выразить как ɸ = ∫∫ B.dS.

Легко показать, что магнитный поток через любую замкнутую поверхность равен нулю. Но магнитный поток через открытую поверхность может быть как нулевым, так и ненулевым. Электродвижущая сила создается изменяющимся магнитным потоком, проходящим через проводящую петлю. Это явление является основным принципом работы генераторов. Согласно Закон индукции Фарадея , величина электродвижущей силы, индуцируемой в проводящей петле изменяющимся магнитным потоком, равна скорости изменения магнитного потока, связанного с петлей.

Что такое плотность магнитного потока

Магнитный поток, также известный как « магнитная индукция », является еще одной важной величиной в магнетизме. Плотность магнитного потока определяется как количество магнитного потока через единицу площади, расположенной перпендикулярно направлению магнитного поля. Это векторная величина, обычно обозначаемая B.

Единицей плотности магнитного потока в системе СИ является Тесла (Тл) . Gauss (G) — единица плотности магнитного потока в СГС; он также широко используется, особенно при работе со слабой плотностью магнитного потока, поскольку один тесла равен 10000 Гс. – уравнение Савара. Его можно выразить как

Здесь I — ток, δl ^→ — вектор с бесконечно малой величиной, а rˆ — единичный вектор r.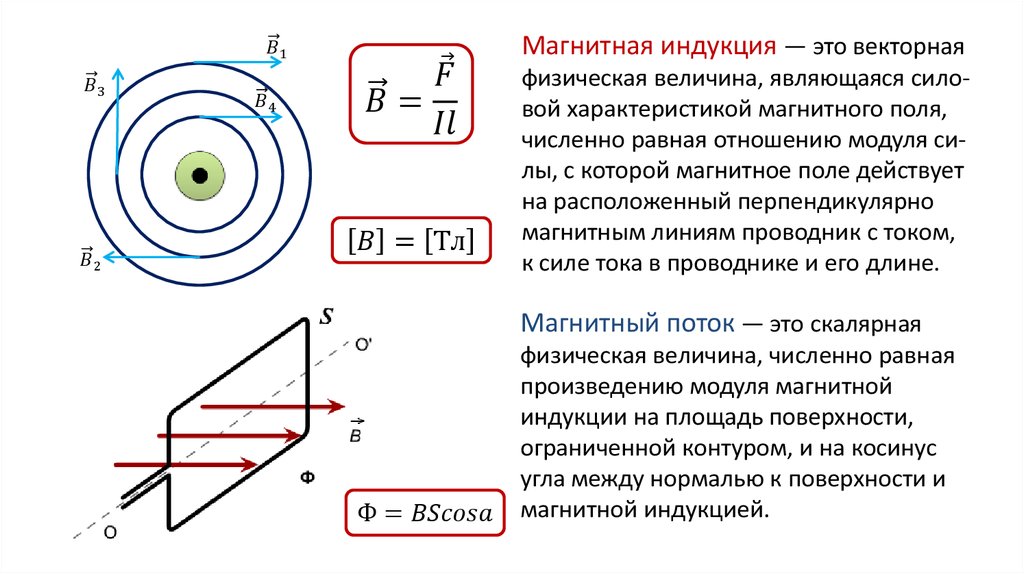 Это очень важное уравнение при работе с магнитными полями, создаваемыми проводами или цепями с током. Плотность магнитного потока, создаваемая проводом с током, зависит от нескольких факторов, таких как геометрия провода, величина и направление тока и положение точки, в которой должна быть найдена плотность магнитного потока. Закон Био-Савара представляет собой комбинацию всех этих факторов. Таким образом, его можно использовать для расчета результирующей плотности магнитного потока B в любой заданной точке от провода с током.

Плотность магнитного потока (B) внутри материальной среды равна магнитной проницаемости этой среды (µ), умноженной на напряженность магнитного поля (H). Его можно выразить как B=µH. Магнитная проницаемость ферромагнитных материалов увеличивается до определенного значения при увеличении напряженности приложенного магнитного поля. Затем она уменьшается по мере дальнейшего увеличения напряженности поля. Таким образом, плотность магнитного потока также приближается к уровню насыщения, а затем уменьшается при дальнейшем увеличении напряженности магнитного поля в соответствии с уравнением B=µH. Это явление известно как магнитное насыщение .

Разница между магнитным потоком и плотностью магнитного потока

Плотность магнитного потока:  Плотность магнитного потока обозначается буквой B.

Единицы СИ:

Магнитный поток: Единицей СИ является Вебер (Вб).

Плотность магнитного потока: единиц СИ:   Вбм ^-2 , Тесла (Т).

Характер количества:

Магнитный поток: Магнитный поток является скаляром.

Плотность магнитного потока: Плотность магнитного потока представляет собой вектор.

Об авторе: Кума

Просмотреть все сообщения

Вам также могут понравиться эти

Какая физическая величина представлена ​​поверхностным интегралом магнитного поля?

спросил 2 года 10 месяцев назад

Изменено 2 года, 10 месяцев назад

Просмотрено 1к раз

$\begingroup$

Ответ дается как магнитный поток в одном месте и закон Гаусса в другом. Так какой из них правильный и почему?

• магнитные поля

$\endgroup$

1

$\begingroup$

Магнитное поле всегда циркулирует (в ситуациях постоянного тока) следующим образом

Итак, если вы возьмете любой замкнутый объем , содержащий магнитное поле, вы обнаружите, что линии поля входят с одной стороны и выходят с другой стороны, поэтому , для любого замкнутого объема $$ \oint_A \mathbf{B} \cdot d\mathbf{A} = 0$$ По теореме о расходимости $$ \oint_V (\nabla \cdot \mathbf{B}) dV = \oint_A \mathbf{B} \cdot d\mathbf{A} $$ Следовательно, мы можем написать $$ \oint_V (\nabla \cdot \mathbf{B}) dV = 0$$ и так как это верно для любого объема, то $$ \nabla \cdot \mathbf{B} =0~~~~~~ ~(1)$$

Уравнение (1) называется Законом магнетизма Гаусса . Однако, если мы возьмем любую замкнутую поверхность (пожалуйста, поймите, что замкнутая поверхность отличается от замкнутого объема, круг — это замкнутая поверхность, а сфера — это замкнутый объем), то мы возьмем поверхностный интеграл вокруг любой замкнутой поверхности, т.