Магнитный поток закон электромагнитной индукции: 1.20. Электромагнитная индукция. Правило Ленца

Явление электромагнитной индукции. Магнитный поток. Закон электромагнитной индукции

Самая большая ошибка в том,

что мы быстро сдаёмся.

Иногда, чтобы получить желаемое,

надо просто попробовать ещё один раз.

Томас Эдисон

Современный мир не может обойтись без таких, казалось бы, уже повседневных приборов, как микрофоны и громкоговорители, трансформаторы и генераторы, планшеты и мобильные телефоны, и многое-многое другое.

Что лежит в основе работы данных приборов? Без явления, которое было открыто Майклам Фарадеем чуть более 180 лет назад, эти приборы создать было бы не возможно и по сей день.

В прошлых уроках мы говорилось о том, что магнитное поле в каждой точке пространства полностью характеризуется вектором магнитной индукции.

Возникает вопрос: можно ли ввести такую величину, которая характеризовала магнитное поле не только в данной точке поля, а во всех точках поверхности, ограниченной замкнутым контуром?

Для ответа на этот вопрос, рассмотрим плоский замкнутый контур, который помещен в однородное магнитное поле, и ограничивающий поверхность площадью S. Пусть нормаль (вектор, длина которого равна единице, и который всегда перпендикулярен контуру) составляет с вектором магнитной индукции некий угол a.

Рассмотрим, что будет происходить с контуром и с линиями магнитной индукции при изменении некоторых величин.

Первое изменим магнитное поле, например, усилив его с помощью еще одного магнита. Как можем заметить, при усилении магнитного поля количество силовых линий возрастает

, следовательно, возрастает и их количество, которое будет пронизывать наш контур.

Если уменьшить площадь контура при неизменной индукции магнитного поля, то это приведет к уменьшению числа линий, пронизывающих контур.

Поворот контура также приводит к изменению числа линий, пронизывающих замкнутый контур.

Если же плоскость контура расположить параллельно линиям магнитной индукции, то ни одна из этих линий не будет пронизывать контур.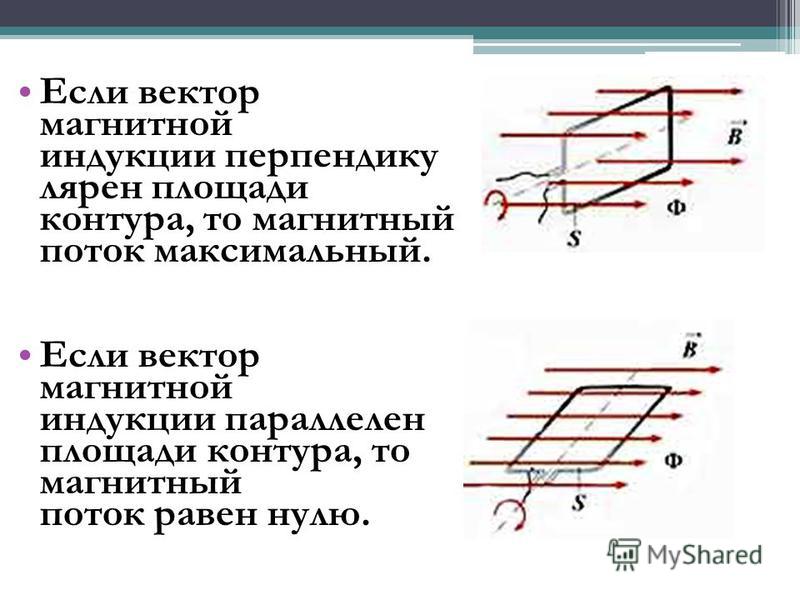

Требовалось ввести величину, которая характеризовала бы все эти закономерности магнитного поля. И физики нашли выход. По аналогии с потоком воздуха, который меняется в зависимости от силы ветра или области пространства, в котором он ограничен, или потока воды в реке, в зависимости от ее ширины или проливных дождей, эту величину назвали

магнитным потоком или потоком вектора магнитной индукции.

В настоящее время под магнитным потоком через плоскую поверхность понимают скалярную физическую величину, численно равную произведению модуля магнитной индукции на площадь поверхности, ограниченную контуром, и на косинус угла между нормалью к поверхности и магнитной индукцией.

Произведение модуля магнитной индукции на косинус угла альфа представляет собой проекцию вектора магнитной индукции на нормаль к плоскости контура.

Анализируя формулу, легко заметить, что магнитный поток тем больше, чем больше линий магнитной индукции пронизывает контур и чем больше площадь этого контура.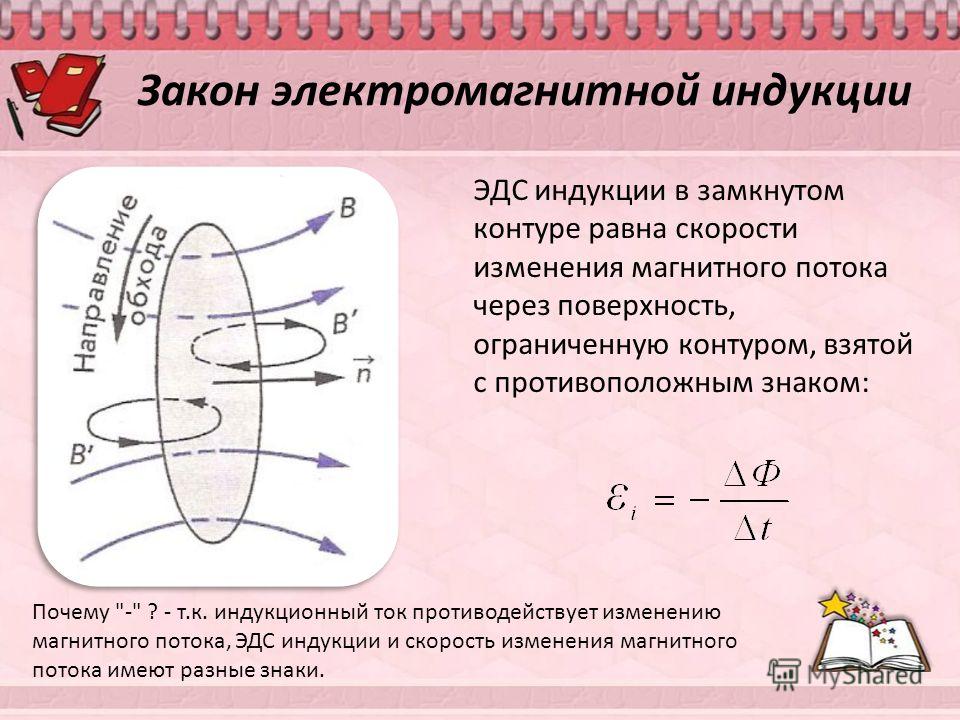

Обозначается магнитный поток большой греческой буквой F

Единицей магнитного потока в СИ является Вб (вебер).

[F] = [Вб]

1 вебер — это магнитный поток однородного магнитного поля с индукцией 1 Тл через перпендикулярную ему поверхность площадью 1 м

2.

Введенная физическая величина, является одной из главных в описании важнейшего физического явления современного мира: речь идет о явлении электромагнитной индукции.

Что это за явление?

Как известно, в 1820 году Ханс Кристиан Эрстед с помощью серии опытов показал, что вокруг любого проводника с током существует магнитное поле. Значит, имея электрический ток, можно получить магнитное поле.

Однако вставал тогда и другой вопрос: нельзя ли наоборот, имея магнитное поле, получить электрический ток? А если можно, то, что для этого нужно сделать?

Такую задачу в начале XIX в. попытались решить многие ученые.

Среди них швейцарский физик Жан-Даниэль Колладон и английский физик Майкл Фарадей, которые практически одновременно начали заниматься решением этой проблемы. Записав в своем дневнике фразу «Превратить магнетизм в электричество!», Фарадей 10 лет потратил на упорные эксперименты, для решения поставленной задачи.

Майкл Фарадей был уверен в том, что электрические и магнитные явления — это явления одной природы. Благодаря своему упорству и вере в неделимость электрических и магнитных явлений, он сделал открытие, которое вошло в основу устройства генераторов всех электростанций мира, превращающих механическую энергию в энергию электрического тока.

Открытие было сделано 17 октября 1831 года.

Вот полное описание первого успешного опыта: «Двести три фута медной проволоки в одном куске были намотаны на большой деревянный барабан; другие двести три фута такой же проволоки были проложены в виде спирали между витками первой обмотки, причем металлический контакт был везде устранен посредством шнурка. Одна из этих спиралей была соединена с гальванометром, а другая — с хорошо заряженной батареей из ста пар пластин в четыре квадратных дюйма с двойными медными пластинками. При замыкании контакта наблюдалось внезапное, но очень слабое действие на гальванометр, и подобное же слабое действие имело место при размыкании контакта с батареей».

Таков был первый опыт, давший положительный результат после десятилетних поисков. Фарадей устанавливает, что при замыкании и размыкании  возникают индукционные токи противоположных направлений.

Далее он переходит к изучению влияния железа на индукцию. «Из круглого брускового, мягкого железа было сварено кольцо; толщина металла была равна семи-восьми дюймам, а наружный диаметр кольца — шести дюймам. На одну часть этого кольца было намотано три спирали, каждая из которых содержала около двадцати четырех футов медной проволоки толщиной в одну двадцатую дюйма. Спирали были изолированы от железа и друг от друга и наложены одна на другую.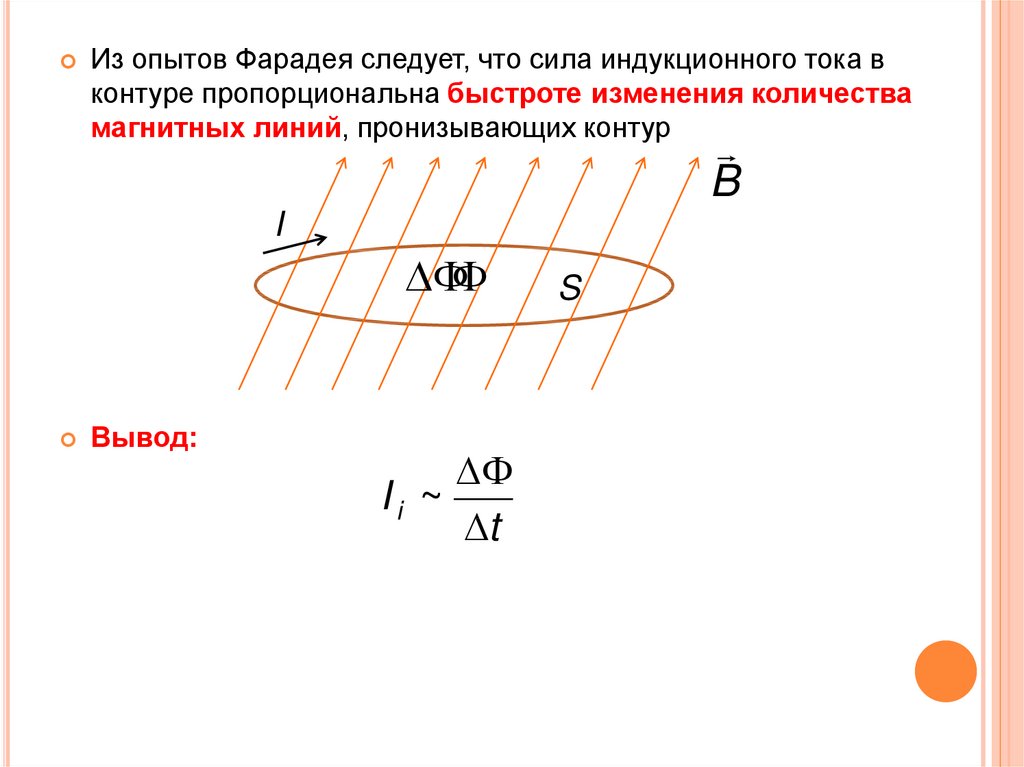

.. Ими можно было пользоваться по отдельности и в соединении; эта группа обозначена буквой А. На другую часть кольца было намотано таким же способом около шестидесяти футов такой же медной проволоки в двух кусках, образовавших спираль B, которая имела одинаковое направление со спиралями А, но была отделена от них на каждом конце на протяжении примерно полу дюйма голым железом.

Спираль B соединялась медными проводами с гальванометром, помещенным на расстоянии трех футов от кольца. Отдельные спирали А соединялись конец с концом так, что образовали общую спираль, концы которой были соединены с батареей из десяти пар пластин в четыре квадратных дюйма. Гальванометр реагировал немедленно, притом значительно сильнее, чем это наблюдалось выше, при пользовании в десять раз более мощной спиралью без железа».

Таким образом, задача, поставленная Фарадеем в 1820 году, была решена: магнетизм был превращен в электричество

.

Какого рода случайности могли помешать открытию, показывает следующий факт. Как говорилось в начале, одновременно с Фарадеем получить ток в катушке с помощью магнита пытался и швейцарский физик Колладон. Он пользовался в своей работе гальванометром, легкая магнитная стрелка которого помещалась внутри катушки прибора. Что бы магнит непосредственно не оказывал никакого влияния на магнитную стрелку, концы катушки были выведены в отдельную комнату и там присоединены к гальванометру.

Вставив магнит в катушку, Колладон шел в соседнюю комнату и разочарованный убеждался, что гальванометр не показывал наличие тока в цепи.

Действительно, ведь покоящийся относительно катушки магнит не может вызвать в ней тока. Стоило бы ему, например, наблюдать за гальванометром, а ассистента попросить заняться магнитом, и проблема была бы решена.

О вопросах надобности и ненадобности открытия данного явления долго спорил научный, и не только, мир.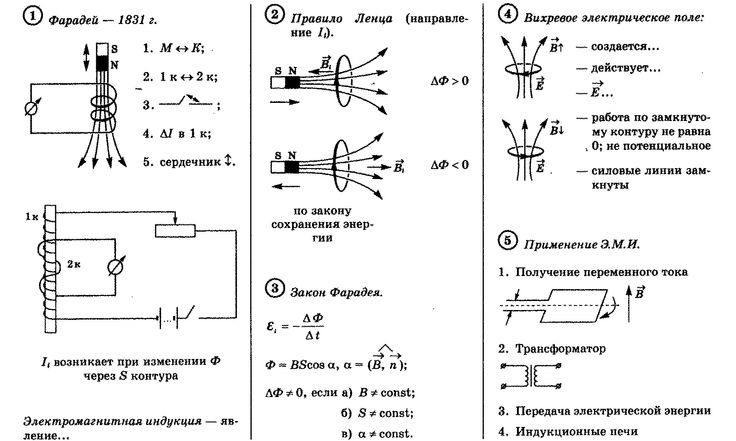 В архивах сохранилась следующая примечательная запись: «Однажды после лекции Фарадея в Королевском обществе, где он демонстрировал свои опыты, к нему подошел богатый коммерсант, оказывавший обществу материальную поддержку, и надменным голосом спросил:

- Всё, что вы нам здесь показывали, господин Фарадей, действительно красиво. Но теперь скажите мне, для чего годится эта магнитная индукция!?

- А для чего годится только что родившийся ребёнок? — ответил рассердившийся Фарадей.»

На вопрос коммерсанта в последующие годы ответили многие учёные и изобретатели, и прежде всего, Вернер фон Сименс, изобретший в 1866 г. динамо-машину, положившую основу для промышленного производства электроэнергии.

Впоследствии опыт Фарадея видоизменили и теперь в школах он представлен в следующем виде.

Берется катушка с намотанной на нее проволокой, концы которой присоединены к гальванометру. Если постоянный магнит, например полосовой, вдвигать внутрь катушки, то в цепи возникает электрический ток. Если же магнит выдвигать из катушки, то гальванометр также регистрировал ток в цепи, но уже противоположного направления. Электрический ток возникает и в том случае, если магнит оставить неподвижным, а двигать относительно него катушку.

Однако не при всяком движении магнита (или катушки) в цепи возникает электрический ток. Например, если вращать магнит внутри катушки, то гальванометр не зафиксирует наличие тока в цепи.

Аналогичный опыт можно проделать, используя вместо постоянного магнита, другую катушку, но уже с током. Не трудно заметить, что ток в катушке возникает всякий раз, когда изменяется магнитный поток, пронизывающий катушку.

Таким образом, явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, пронизывающего контур, называется явлением электромагнитной индукции. Полученный таким образом ток, называется индукционным током.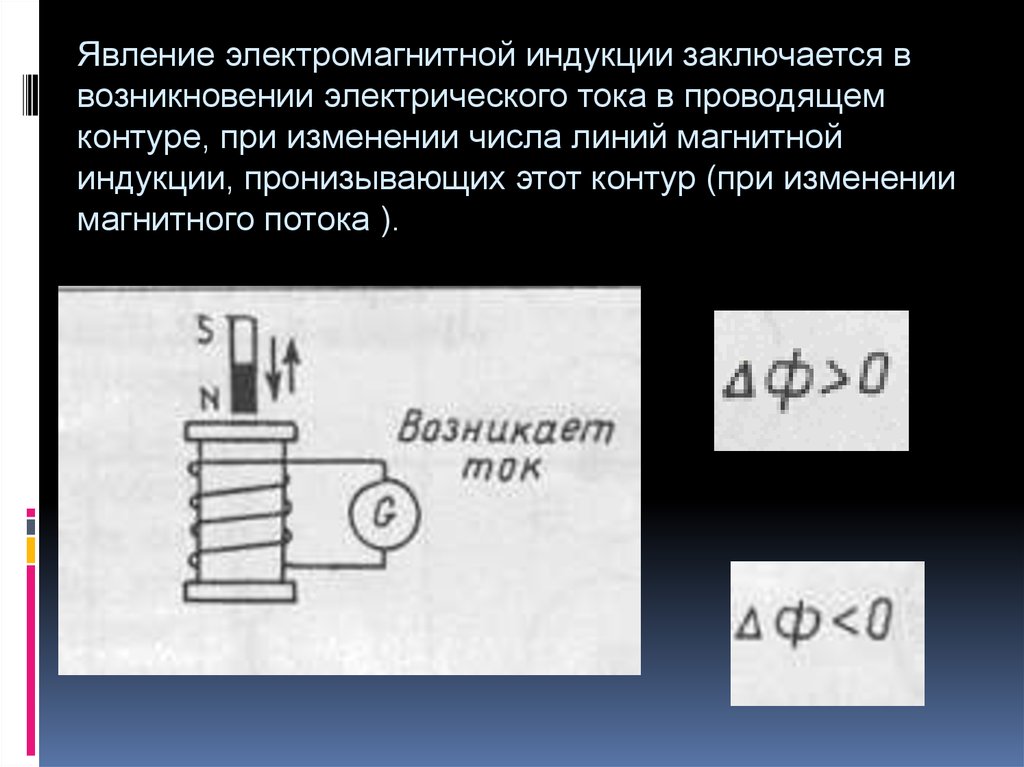

Как известно, ток в проводнике возникает лишь в том случае, если на свободные заряды проводника будут действовать сторонние силы. Работу этих сил при перемещении единичного заряда вдоль замкнутого проводника называют электродвижущей силой (сокращенно ЭДС).

Следовательно, при изменении магнитного потока через поверхность, ограниченную контуром (т.е. при изменении количества линий магнитной индукции, пронизывающих поверхность), в нем появляются сторонние силы, действие которых характеризуется ЭДС, называемой ЭДС индукции.

Обозначают ее греческой буквой x_i (кси), а измеряется она в В (вольт).

Как показывают опыты, значение индукционного тока, а, следовательно, и ЭДС индукции, не зависит от причин изменения магнитного потока (меняется ли площадь, ограниченная контуром, или его ориентация в пространстве, или за счет изменения среды и т.д.). Самое главное и существенное значение имеет лишь скорость изменения магнитного потока (так, стрелка гальванометра будет отклоняться сильнее, чем быстрее мы будем вдвигать и выдвигать магнит).

Поэтому мы можем сказать, что сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром.

Сформулируем непосредственно сам закон электромагнитной индукции: среднее значение ЭДС индукции в проводящем контуре пропорционально скорости изменения магнитного потока через поверхность, ограниченную контуром.

где Dt – промежуток времени, в течении которого произошло изменение магнитного потока.

Стоит обратить внимание, что закон электромагнитной индукции формулируется именно для ЭДС, а не для силы индукционного тока, т.к. сила тока зависит и от свойств проводника, а ЭДС определяется только изменением магнитного потока.

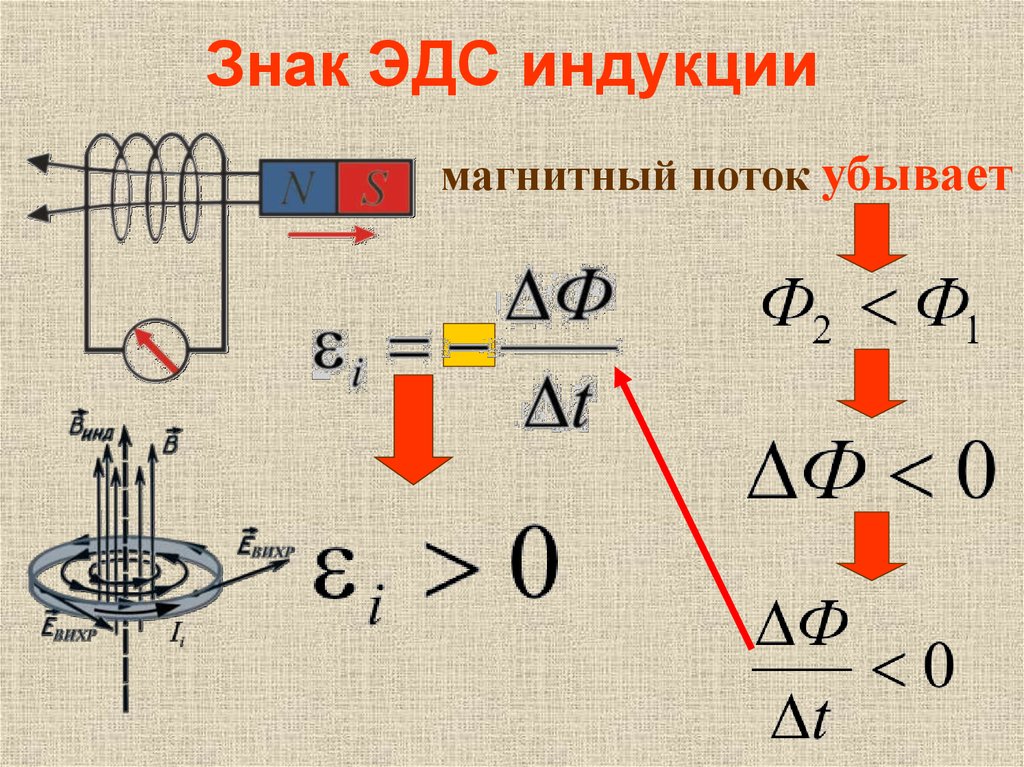
Почему в законе электромагнитной индукции стоит знак «минус»? Какого его назначение? Индукционный ток противодействует изменению магнитного потока. Поэтому ЭДС индукции и скорость изменения магнитного потока имеют разные знаки.

Упражнения.

Задача. Из провода длиной 2 м сделан квадрат, который расположен горизонтально. Какой заряд пройдет по проводу, если его потянуть за две диагонально противоположные вершины так, чтобы он сложился? Сопротивление провода 0,1 Ом, а вертикальная составляющая индукции магнитного поля Земли 50 мкТл.

Основные выводы:

– Магнитный поток через плоскую поверхность — это скалярная физическая величина, численно равная произведению модуля магнитной индукции на площадь поверхности, ограниченную контуром, и на косинус угла между нормалью к поверхности и магнитной индукцией.

– Единицей магнитного потока в системе СИ является Вб (вебер).

– Явление возникновения ЭДС в проводящем контуре (или тока, если контур замкнут) при изменении магнитного потока, пронизывающего контур, называется явлением электромагнитной индукции.

– Полученный таким способом ток называется индукционным током.

Закон электромагнитной индукции: среднее значение ЭДС индукции в проводящем контуре пропорционально скорости изменения магнитного потока через поверхность, ограниченную контуром.

Явление электромагнитной индукции. Магнитный поток. Закон электромагнитной индукции

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

1. Тема урока

Явление электромагнитной индукции.
Магнитный поток.
Закон электромагнитной индукции.
Учитель ГБОУ СОШ №1877 «Люблино» Л. Н. Молочко

2. План изложения нового материала

1. История открытия явления
электромагнитной индукции
2. Опыты Фарадея
3. Явление электромагнитной индукции
4. Магнитный поток. Единицы измерения
магнитного потока.
5. Закон электромагнитной индукции

3. В1820 г.Эрстед обнаружил действие электрического тока на магнитную стрелку

М. Фарадей с 1821 по 1831 год проводил опыты и
получил электрический ток с помощью магнитного поля.
Ему удалось « Превратить магнетизм в электричество».
Основоположник учения об
электромагнитном поле; ввел
понятия «электрическое» и
«магнитное поле»;
высказал идею существования
электромагнитных волн.

4. Опыты М. Фарадея

«На деревянную катушку была
29 августа
1831
намотана медная
проволока,
между
года
ее витками была намотана
проволока изолированная от
первой хлопчатобумажной нитью.
Одна из этих спиралей была
соединена с гальванометром,
другая – с батареей.
При замыкании цепи стрелка
гальванометра отклонялась, при
размыкании цепи то же самое.
При непрерывном же прохождении
тока через одну из спиралей не
удалось обнаружить отклонения
стрелки гальванометра…»
Вывод:
электрический
ток возникал
тогда,
когда
проводник
оказывался
в области
действия
переменного
магнитного
Электромагнитная индукция – физическое
явление, заключающееся в возникновении
электрического тока в замкнутом проводящем
контуре при изменении числа линий магнитной
индукции , пронизывающих поверхность,
ограниченную этим контуром.
Возникающий при этом ток называют
индукционным.

7. Поток магнитной индукции

• Потоком магнитной индукции
(магнитным потоком) через
поверхность площадью S называют
величину, равную произведению
модуля вектора магнитной индукции В
на площадь S и косинус угла между
векторами В и n.

8. Математическая формула потока магнитной индукции

• Магнитный поток пропорционален числу
линий магнитной индукции,
пронизывающих поверхность площадью S.
• Магнитный поток характеризует
распределение магнитного поля по
поверхности , ограниченной контуром.

9. Единица магнитного потока

Единицей магнитного потока является
вебер (1 Вб)
1 Вб – магнитный поток, созданный
однородным магнитным полем с
индукцией 1Тл через поверхность
площадью 1м2, расположенную
перпендикулярно вектору магнитной
индукции.
1 Вб=1Тл*1 м2,

10. Явление электромагнитной индукции

• Индукционный ток в замкнутом контуре
возникает при изменении магшнитного
потока через площадь ,ограниченную
контуром

11. Закон электромагнитной индукции – ЭДС индукции прямо пропорциональна скорости изменения магнитного потока

Закон электромагнитной индукции ЭДС индукции прямо пропорциональна
скорости изменения магнитного потока
1. При всяком изменении магнитного
потока через проводящий контур в
этом контуре возникает электрический
ток.
2. ЭДС индукции в замкнутом
контуре равна скорости изменения
магнитного потока через площадь,
ограниченную этим контуром.
3. Ток в контуре имеет положительное
направление при убывании внешнего
магнитного потока.

12. Математическая формула закона электромагнитной индукции

• ε=-ΔΦ/Δt
• ΔΦ/Δt- скорость изменения магнитного
потока ( единицы измерения Вб/с)

13. ЭДС электромагнитной индукции в замкнутом контуре численно равна и противоположна по знаку скорости изменения магнитного потока

через
поверхность, ограниченную этим контуром.
( зависит только от характера изменения
магнитного поля).
ЭДС электромагнитной индукции не
зависит от
материала проводника;
рода носителей тока;
сопротивления проводника;
температуры проводника.

14. Закрепление нового:

1. Какая величина характеризует магнитное
поле в каждой его точке?
2. От чего зависит магнитный поток,
пронизывающий площадь плоского контура,
помещенного в однородное магнитное поле?
3. При какой ориентации контура по
отношению к линиям магнитной индукции
магнитный поток, пронизывающий
площадь этого контура максимален? равен
нулю?
4. В каком случае магнитный поток равен 1 Вб?
5. Как формулируется закон
электромагнитной индукции?
6. Почему в законе электромагнитной
индукции стоит знак «минус»?

15. Задача №1

Магнитный поток через квадратную
проволочную рамку со стороной
5 см, плоскость которой перпендикулярна
линиям индукции однородного магнитного
поля, равен 0,1м Вб.
Каков модуль вектора магнитной индукции
поля? ( Ответ:40 мТл)

16. Задача №2

Какова величина магнитного потока,
пронизывающего плоскую поверхность
площадью 50 см2 при индукции поля
0,4 Тл, если эта поверхность: а)
перпендикулярна вектору индукции
поля; б) расположена под углом 450 к
вектору индукции; в) расположена под
углом 300 к вектору индукции? (Ответ:
2 мВб, 1,4 мВб; 1 мВб)

17. Задача №3

Металлический стержень длиной 0,5 м
равномерно вращается вокруг одного из его
концов в однородном магнитном поле в
плоскости, перпендикулярной к линиям
поля. Какова ЭДС индукции поля, если
магнитная индукция поля 0,2 Тл, а угловая
скорость вращения стержня 50 рад/с?
(Ответ: 1,25 В)

18. Домашнее задание:

§8,9,11,
№№921, 922,928 (Сборник Рымкевича )

English     Русский Правила

Магнитный поток и закон Фарадея

Лоуренс Чиу, Дейл Грей, Июль Томас, и

способствовал

Содержимое

• Магнитный поток
• Закон Фарадея
• Дифференциальная форма
• использованная литература

Простейшим примером наведенного электрического поля является поле, создаваемое внутри небольшой круглой проводящей петли из-за изменяющегося магнитного поля и ответственное за последующий ток. Вообще говоря, индуцированное электрическое поле зависит не только от того, как магнитное поле B \mathbf{B}B изменяется со временем, но и от того, как может измениться геометрическое соотношение между контуром и магнитным полем. Например, даже в однородном и постоянном магнитном поле изменение формы проводящей петли или ее ориентации относительно силовых линий магнитного поля будет создавать электрическое поле и, следовательно, ток. Соответствующая комбинация геометрии и магнитного поля, необходимая для описания индуцированного электрического поля, когда они изменяются, называется магнитным потоком. Самое основное определение – это магнитный поток через плоскую фигуру из-за однородного магнитного поля. Рассмотрим плоскую область площадью AAA и выберите единичный вектор n \mathbf{n}n, перпендикулярный поверхности. Для удобства вектор площади A \mathbf{A}A определяется как A \mathbf{A}A === AAAn \mathbf{n}n. В общем случае A \mathbf{A}A будет наклонен под некоторым углом θ \theta θ с силовыми линиями магнитного поля, т. е. θ \theta θ будет меньшим углом между A \mathbf{A}A и B \mathbf{B } Б. (См. рисунок ниже.)

Вектор, помеченный как «нормальный», является нашим единичным вектором n \mathbf{n}n, а магнитный поток через плоскую область AAA определяется как

Φ=B⋅A. \Phi = \mathbf{B} \cdot \mathbf{A}. Ф=В⋅А.

По сути, скалярное произведение проецирует нашу исходную площадь AAA на плоскость, перпендикулярную B \mathbf{B}B.

Магнитный поток через поверхность, склеенную вместе с небольшими плоскостями (подумайте о чем-то вроде геодезического купола), представляет собой просто сумму магнитного потока через каждый «участок». Участку поверхности назначается вектор ai \mathbf{a}_i ai​, который указывает нормаль (перпендикуляр) к поверхности. Кроме того, величина каждого ai \mathbf{a}_i ai​ определяется как площадь соответствующего участка.

Магнитный поток Φi \Phi_{i} Φi​, проходящий через участок, определяется скалярным произведением, которое вычисляет компонент Bi \mathbf{B}_i Bi​, параллельный ai \mathbf{a}_i ai​ :

Φi=Bi⋅ai \Phi_{i} = \mathbf{B}_i \cdot \mathbf{a}_i Φi​=Bi​⋅ai​

Следовательно, полный магнитный поток через поверхность, состоящую из многих небольшие участки, ai \mathbf{a}_i ai​, представляет собой сумму по всем участкам:

Φ=∑iBi⋅ai. \Phi = \sum_i \mathbf{B}_i \cdot \mathbf{a}_i .Φ=i∑​Bi​⋅ai​.

Поскольку ai \mathbf{a}_i ai​ становится исчезающе малым, как и в случае гладкой поверхности, сумма заменяется на поверхностный интеграл :

Φ=∫SB⋅da. \Phi = \int_S \mathbf{B} \cdot d\mathbf{a}. Φ=∫S​B⋅да.

К счастью, магнитный поток часто можно вычислить, не прибегая к явному вычислению интеграла. Как правило, расчет магнитного потока довольно прост, поскольку в основном рассматриваются плоские петли. Однако после обсуждения следующей темы, закона Фарадея, необходимо будет допустить, что SSS гладкой поверхности может быть произвольным, чтобы определить дифференциальную форму закона Фарадея в следующем разделе.

Небольшая плоская проволочная петля площадью A A A ориентирована перпендикулярно однородному магнитному полю внутри цилиндрического соленоида с числом витков на единицу длины n n n и током I I I. Каков поток через петлю?

---

В этом случае B⋅da \mathbf{B} \cdot d\mathbf{a} B⋅da постоянна, поэтому поток равен просто Φ=BA=µ0nIA \Phi = BA = \mu_0 n I A Φ=BA =μ0​nIA.

Фарадей обнаружил, что индуцированная ЭДС E \mathcal{E} E (электродвижущая сила) через токовую петлю равна

E=−dΦdt, \mathcal{E} = – \frac{d \Phi}{d t}, E=−dtdΦ​,

где Φ \Phi Φ — магнитный поток через контур (напомним, что точки ЭДС в направлении, противоположном напряжению). Обычно определяют Φ \Phi Φ как функцию t t t, что позволяет рассчитать E \mathcal{E} E.

В закон Фарадея включено направление индуцированного тока в контуре. Как и в случае закона Био-Савара и закона Ампера, ориентация петли определяется таким образом, что обход петли против часовой стрелки (относительно a \mathbf{a} a) положителен. Таким образом, отрицательный знак dΦ/dt d \Phi/dt dΦ/dt указывает на то, что увеличение потока через петлю приводит к по часовой стрелке протекание тока в петле. Точно так же уменьшение потока через петлю (положительное увеличение относительно противоположной стороны петли) приводит к течению тока против часовой стрелки .

Это соглашение о знаках легко запомнить, используя так называемое правило правой руки . Если большой палец указывает в направлении увеличения магнитного потока , то ток течет в направлении, противоположном скручиванию пальцев (противоположное из-за отрицательного знака в законе Фарадея).

Обратите внимание, что сама петля создает магнитное поле. Можно убедиться, что магнитное поле всегда создается в направлении убывания потока (опять же из-за отрицательного знака). В некотором смысле можно думать об индуцированном магнитном поле как о «противодействующем» изменению внешнего магнитного поля, результат, который часто называют законом Ленца.

Небольшая плоская проволочная петля площадью A A A и сопротивлением R R R ориентирована перпендикулярно однородному направленному вверх магнитному полю внутри цилиндрического соленоида с числом витков на единицу длины n n n и током I(t)=I0+Bt I(t) = I_0 + Bt I(t)=I0​+Bt, где I0 I_0 I0​ и B B B — константы. Каковы размер и направление текущей Iloop(t) I_\text{loop}(t) Iloop​(t), индуцированной в петле, в зависимости от t t t?

---

Как и в предыдущем примере, для заданного t t t B⋅da \mathbf{B} \cdot d\mathbf{a} B⋅da постоянна, поэтому поток через контур составляет всего

Φ(t)=BA=µ0n(I0+Bt)A. \Phi(t) = BA = \mu_0 n (I_0 + Bt) A. Φ(t)=BA=µ0​n(I0​+Bt)A.

Следовательно, закон Фарадея дает

E=-dΦdt=-μ0nAB. \mathcal{E} = – \frac{d\Phi}{dt} = -\mu_0 n A B. E=−dtdΦ​=−µ0​nAB.

Отсюда следует, что ток, индуцируемый в контуре, имеет величину μ0nAB/R \mu_0 n A B / R μ0​nAB/R и направлен по часовой стрелке (из-за отрицательного знака), что также можно проверить с помощью правила правой руки.

Небольшой плоский виток из проволоки площадью A A A первоначально ориентирован параллельно однородному магнитному полю величиной B B B. Если виток вращается с угловой скоростью ω \omega ω, какова величина ЭДС индукции E \mathcal{E } E в цикле?

---

Хотя площадь петли остается постоянной, угол петли по отношению к полю постоянно меняется. Угол по отношению к полю определяется выражением cos⁡ωt \cos{\omega t} cosωt, поэтому

Φ=BAcos⁡ωt \Phi = BA \cos{\omega t} Φ=BAcosωt

E=−dΦdt=ωABsin⁡ωt. \mathcal{E} = – \frac{d \Phi}{dt} = \omega A B \sin{\omega t}. E=−dtdΦ​=ωABsinωt.

По сути, можно генерировать электричество путем механического вращения проволочной петли в магнитном поле.

Напомним, что ЭДС E \mathcal{E} E вокруг любого замкнутого пути CCC определяется в направлении, противоположном напряжению, а именно

E=∮CE⋅ds. \mathcal{E} = \oint_\text{C} \mathbf{E} \cdot d\mathbf{s}. E=∮C​E⋅ds.

Пусть CCC — граничная кривая произвольной гладкой незамкнутой поверхности SSS. Из закона Фарадея следует, что магнитный поток через ССС,

Φ=∫SB⋅da, \Phi = \int_S \mathbf{B} \cdot d\mathbf{a}, Φ=∫S​B⋅da ,

и ЭДС вокруг ССС связаны соотношением

∮CE⋅ds=−ddt∫SB⋅da. \oint_\text{C} \mathbf{E} \cdot d\mathbf{s} = – \frac{d}{dt} \int_S \mathbf{B} \cdot d\mathbf{a}. ∮C​E⋅ds=−dtd​∫S​B⋅da.

Как и в случае с законом Ампера, можно применить теорему Стокса в левой части, чтобы приравнять два подынтегральных выражения:

∫S∇×E⋅da=−ddt∫SB⋅da. \int_S \nabla \times \mathbf{E} \cdot d\mathbf{a} = – \frac{d}{dt} \int_S \mathbf{B} \cdot d\mathbf{a}. ∫S​∇×E⋅da=−dtd​∫S​B⋅da.

Опять же, можно утверждать, что, поскольку соотношение должно выполняться для любой произвольной поверхности S S S, должно быть так, что два подынтегральных выражения равны, и, следовательно,

∇×E=−∂B∂t. \nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}. ∇×E=−∂t∂B​.

Это так называемая дифференциальная форма закона Фарадея. В то время как в электростатике электрическое поле консервативно и ∇×E=0 \nabla \times \mathbf{E} = 0 ∇×E=0, в мире электродинамики электрическое поле не является безвихревым.

[1] Гриффитс, Д.Дж. Введение в электродинамику . Четвертое издание. Pearson, 2014.

[2] Purcell, EM Electricity and Magnetism . Третье издание. Издательство Кембриджского университета, 2013.

Цитировать как: Магнитный поток и закон Фарадея. Brilliant.org . Полученное из https://brilliant.org/wiki/magnet-flux-and-faradays-law-quantitative/

Закон электромагнитной индукции Фарадея

Магнитный поток через любую поверхность, помещенную в магнитное поле, определяется как количество магнитных линий сила пересекает поверхность нормально. Он обозначается «ⲫ», а его единицей измерения является вебер (Вб). Электромагнитная индукция – это явление производства ЭДС индукции из-за изменения магнитного потока (количества силовых линий магнитного поля), подключенного к замкнутой цепи, называется электромагнитной индукцией.

Эксперименты Фарадея

Эксперимент 1: Для проведения этого эксперимента Фарадей взял круглую катушку и соединил ее с гальванометром и сильным стержневым магнитом. При перемещении северного полюса стержневого магнита в сторону катушки гальванометр показал отклонение вправо от нулевой отметки гальванометра. Когда магнит снова отдалили от катушки, он показал отклонение, но в противоположном направлении. Точно так же эксперимент проводится с южным полюсом стержневого магнита, снова наблюдается отклонение, но противоположное направлению, указанному северным полюсом стержневого магнита. Когда магнит удерживается неподвижно около катушки, в гальванометре не наблюдается никакого отклонения.

Вывод: По мере приближения магнита к катушке магнитный поток увеличивается, следовательно, в катушке возникает индукционный ток в одном направлении. Когда магнит удаляется от катушки, магнитный поток уменьшается, следовательно, в катушке возникает индуцированный ток в противоположном направлении. Когда магнит неподвижен внутри катушки, магнитный поток перестает изменяться, следовательно, индуктируемый ток в катушке становится равным нулю.

Эксперимент 2: В этом эксперименте стержневой магнит остается неподвижным, а катушка перемещается. Наблюдается тот же результат, что и в опыте 1. При быстром относительном движении магнита и катушки отклонение в гальванометре больше, и наоборот.

Эксперимент 3: Как видно из рисунка ниже. Две катушки первичная (p) и вторичная (s) намотаны на цилиндрическую опору. Первичная катушка соединена с ключом, реостатом и аккумулятором. Вторичка связана с гальванометром. При нажатии клавиши в первичной обмотке гальванометр показывает отклонение в одну сторону. Когда ключ отпускается, он снова показывает отклонение, но в противоположном направлении. При удерживании клавиши в нажатом состоянии через первичные катушки течет постоянный ток, гальванометр не показывает никакого отклонения. Когда ток в первичной обмотке увеличивается с помощью реостата, индуцированный ток течет во вторичной обмотке в том же направлении, что и в первичной обмотке.

Закон электромагнитной индукции Фарадея

Первый закон: Он гласит, что всякий раз, когда магнитный поток связан с изменением в замкнутом контуре, в нем индуцируется ЭДС, которая существует только до тех пор, пока происходит изменение потока. место. Если цепь замкнута, то внутри цепи также индуцируется ток, который называется «Индуцированный ток».

Магнитные поля можно изменить:

• Перемещение стержневого магнита к катушке или от нее.
• Перемещение катушки в магнитное поле или вне магнитного поля.
• Вращение катушки относительно магнита.
• Изменение площади катушки, помещенной в магнитное поле.

Второй закон: Он гласит, что величина ЭДС индукции равна скорости изменения магнитного потока, связанного с замкнутой цепью.

|∈| = dⲫ/dt

E = -N dⲫ/dt

E = -N (ⲫ ₂ -ⲫ ₁ )/t ⇢ («t» – время)

Закон Ленца

Ленц утверждает, что направление индукционного тока в цепи таково, что оно препятствует изменению магнитного потока. Закон Ленца назван в честь немецкого физика Эмиля Ленца, который сформулировал его в 1834 году. Это научный закон, определяющий направление индуцированного тока, но ничего не говорящий о его величине.

E = -N(d∅/dt) ⇢ (отрицательный знак означает, что направление ЭДС индукции таково, что она препятствует изменению магнитного потока)

Применение закона Фарадея

• Индукционные двигатели
• Трансформеры
• Электрические генераторы
• Эффект Холла
• Текущие зажимы
• Индукционная кулинария
• Индийская шваделя
• 110
• 1010101010101010101010101010101010101010110110 гг.

Примеры задач

Вопрос 1: Магнитный поток, связанный с катушкой, изменяется с 2Вб до 0,2Вб за 0,5 секунды. Вычислите ЭДС индукции.

Ответ:

Δ ⲫ = 0,2-2 = 1,8 Вт

ΔT = 0,5 с

E = -(Δ/ΔT)

E = -1,8/0,5 Volts

E).

Следовательно, ЭДС индукции будет -3,6 вольта.

Вопрос 2: В катушке сопротивлением 200 индуцируется ток за счет изменения магнитного потока через нее, как показано на рисунке. Рассчитайте величину изменения потока через катушку.

Решение:

dq = – (N/R) dt

i= (1/R). (dq/dt)

Δⲫ = R.Δq

Δⲫ = 200 × (Площадь кругового графика)

Δⲫ = 200 × (1/2×20×0,5)

Δⲫ0 = 200 × 3 9008 1000 Вб

Следовательно, величина изменения потока равна 1000 Вб.

Вопрос 3: Рассчитайте ЭДС индукции в проводе. Когда небольшой кусок металлической проволоки протащили через зазор между полюсными наконечниками магнита за 0,6 сек. Известно, что магнитный поток между полюсами равен 9×10 ^-4 Вб.

Solution:

dt=0.5 s

dⲫ = 9×10 ^-4 -0 = 9×10 ^-4 Wb

E = (dⲫ)/dt

E= ( 9×10 ^-4 )/0,6

E= 0,0036 В

Следовательно, ЭДС индукции 0,0036 В

Вопрос 4: Цилиндрический стержневой магнит удерживается вдоль оси круглого стержневого магнита.