| Уравнения МаксвеллаMaxwell’s equations Уравнения Максвелла − уравнения классической электродинамики, описывающие динамику электромагнитного
поля и его связь с зарядами и токами.
где E − напряжённость электрического поля, H − напряжённость магнитного
поля, D − электрическая индукция, B − магнитная индукция, ρ − плотность
электрического заряда, j − плотность электрического тока. D = εE, ε − диэлектрическая проницаемость среды, μ − магнитная проницаемость
среды, σ – электропроводность среды.
Эта система дифференциальных уравнений имеет решение
– гармоническую плоскую волну. c = (μ0ε0)-1/2. c − скорость света в вакууме, c = 2.99792458·108 м/с,
|
Боттомоний
Чармоний
Уравнения Максвелла явились теоретическим
обобщением экспериментальных законов: Кулона, Ампера, законов электромагнитной
индукции и других.
Векторы электрического и магнитного полей
перпендикулярны направлению распространения волны и друг другу и находятся
в фазе. Волна распространяется со скоростьюСтраница не найдена
Поиск по сайту Авторизация
|
|
Семинары Дек 16, 2022 Семинар “Прикладная гидродинамика” Дек 14, 2022 Научный семинар “Механика макро- и нано-структур” 19.12.2022. Тема: «Влияние снежного покрова на эффективность разрушения ледяного покрова амфибийными судами на воздушной подушке резонансным методом» Оценка результативности ИГиЛ СО РАН 2013-2015 гг Программа развития ИГиЛ СО РАН Заключение РАН по Программе развития | ||||||||||||||||
..Уравнения Максвелла
Щелкните здесь, чтобы перейти на нашу страницу, посвященную методу конечного интегрирования (новинка февраля 2015 г.!) 13 сентября 2009 года в Гленэр-Хаусе, семейном доме Максвелл в Кирккадбрайтшире, Шотландия.
Доктор Раутио является основателем Sonnet Software и потратил много личного времени и денег на честь Максвелла и восстановление дома Максвелла (а не кофе, который раньше производился в Хобокене).
Читайте о докторе Раутио здесь. Ниже представлена серия видеороликов, в которых он рассказывает об истории Максвелла, но она неполная. Будем надеяться, что когда-нибудь MTT-S заплатит несколько долларов и сделает профессиональное видео этой потрясающей лекции. Как насчет того, чтобы снять его на IMS 2015 в Финиксе?
Максвелл1
Максвелл2
Максвелл3
Максвелл4 Волынки и тигры!
Maxwell5
Maxwell6 Bullies and vampires
Maxwell7
Maxwell8
Maxwell9
Maxwell10
Maxwell11
Maxwell12
Maxwell13 death of Maxwell
Below, Dr. James Rautio explains Maxwell’s equations (new for October 2014) .
Если вы знакомы с техническим описанием уравнений Максвелла и знакомы с векторным исчислением, посетите http://en.wikipedia.org/wiki/Maxwell%27s_equations. Вместо того, чтобы пытаться грубо воспроизвести это первоклассное и подробное описание, здесь мы представляем гораздо более физическое и интуитивное понимание.
Хорошо, если вы понимаете, что интеграл есть сумма чего-либо, каким-то образом, но и это на самом деле не требуется.
Во-первых, вот уравнения. Не позволяйте им напугать вас. По мере продвижения каждый член каждого уравнения начнет ощущаться как друг. Затем, когда и если вы изучите векторное исчисление, вы будете знать общую картину заранее. Вы будете знать, куда все идет. Вы поймете .
1)
2)
3)
4)
В конце 1800-х годов в физике начался переход от игры с магнитами к теории относительности Эйнштейна. Это было вызвано тем, что мы сейчас называем «уравнениями Максвелла». Максвелл (1831-1879 гг.)) — самый известный физик 19 -го -го века. Четыре уравнения Максвелла, показанные здесь в одной из их современных форм, на самом деле были открыты несколькими физиками. Максвелл понял, что все уравнения работают вместе, и добавил один термин, что-то под названием «ток смещения». Набор уравнений теперь называется «уравнениями Максвелла» в основном потому, что он показал, как все четыре работают вместе, чтобы полностью определить поле «электромагнетизма».
Хотя сегодня это может показаться простым, с учетом того, что было известно в то время, это был настоящий гениальный ход.
Мы называем уравнения Максвелла «первыми принципами», потому что они не были выведены из других уравнений или теорий. Вернее, в 19 -м -м веке физики проводили эксперименты с магнитами, батареями и тому подобным. Затем путем проб и ошибок они разработали математические уравнения, которые дают тот же ответ, что и их эксперименты.
Четыре уравнения Максвелла описывают поведение магнитных и электрических полей. Например, если вы обернете проволоку вокруг гвоздя и подключите батарейку, вы получите магнит. Первое уравнение Максвелла, закон Ампера, говорит нам, как магнит будет толкать или притягивать другие магниты. Согласно второму уравнению, закону Фарадея, вы можете взять магнит и вращать его, чтобы получился электрический генератор. Вот откуда берется электричество для работы вашего компьютера. Третье уравнение — закон Гаусса. Это говорит о том, что статическое электричество (электрический заряд) генерирует напряжение.
Вы можете убедиться в этом в любой сухой день, шаркая ногами по ковру и дотрагиваясь до дверной ручки. Четвертое уравнение говорит о том, что магнитного заряда не существует — великая загадка, которую физики все еще пытаются понять.
«Ток смещения» Максвелла — это последний член первого уравнения. Это связано с тем, что происходит с электрическими полями, когда они изменяются, например, когда статическое электричество от вашего пальца падает на дверную ручку. Электрическое поле вокруг вашего пальца внезапно падает до нуля. Это внезапное изменение электрического поля порождает магнитное поле. Второе уравнение говорит, что верно обратное. Если вы изменяете магнитное поле (скажем, включая и выключая электромагнит), вы создаете электрическое поле. На самом деле электрические и магнитные поля могут продолжать работать вместе, сами по себе, постоянно меняясь, иногда в течение миллионов лет. В результате получается то, что мы знаем как свет, или радиоволны, или гамма-лучи, или вообще «электромагнитное излучение».
Если вы хотите увидеть электромагнитное излучение возрастом в несколько миллионов лет, просто посмотрите на небо какой-нибудь звездной ночью.
В конце 19 -го -го века молодой швейцарский патентный клерк Альберт Эйнштейн узнал об уравнениях Максвелла и задался вопросом, что произойдет, если источник электромагнитного излучения (например, лампочка) будет двигаться, а он стоит на месте. Тогда, что случилось бы, если бы он двигался, а источник оставался бы неподвижным. Если скорость движения приближается к скорости света, происходят действительно странные вещи. Но, что более важно, он обнаружил, что может развивать свою теорию, предполагая, что все зависит только от относительного движения. Кто из них двигался, а кто стоял на месте, абсолютно не имело значения. Так родилась теория относительности Эйнштейна.
Даже сегодня физики могут потратить всю свою жизнь на поиск новых решений уравнений Максвелла. Но мы иногда упускаем из виду тот факт, что уравнения Максвелла не объясняют, почему, например, два магнита могут притягиваться или отталкиваться.
Они лишь позволяют рассчитать, насколько сильно и в каком направлении притянуты магниты. Вопрос «Почему?» еще предстоит ответить.
Начнем с классического эксперимента с электромагнитом:
Сначала намотайте провод на гвоздь и подключите батарейку. У нас есть магнит. Однако, когда мы подключаем батарею (при условии, что это не очень большая батарея и все это сгорает в дыму!), Ничего не меняется. Мы ничего не видим, ничего не чувствуем. Он выглядит точно так же, как и до того, как мы подключили аккумулятор.
Но мы знаем, что вокруг магнита существует магнитное поле. Мы знаем, что магнитное поле может притягивать или отталкивать другие магниты. Мы знаем, что магнитное поле сильнее вблизи полюсов магнита и что более сильное магнитное поле означает, что другие магниты толкаются или притягиваются сильнее. Мы знаем, что будет ли магнит толкаться или тянуться, зависит от того, куда мы поместим магниты и в каком направлении мы держим магнит. Если мы повернем магнит встык, мы сможем превратить толчок в притяжение.
Все это вызвано магнитным полем вокруг магнита. Так как же выглядит магнитное поле? Давайте воспользуемся старым трюком с железной опилкой:
Возьмите лист бумаги с железными опилками. Положите бумагу на магнит и встряхните его. Железные опилки образуют линии. Мы называем это «магнитными силовыми линиями». Глядя на силовые линии, мы можем видеть, где магнитное поле сильнее. Он сильнее, когда линии расположены ближе друг к другу. Вы также можете увидеть направление магнитного поля. Магнитное поле имеет то же направление, что и силовые линии. Если вы поместите кусок железа в магнитное поле, он попытается двигаться вдоль силовых линий туда, где магнитное поле наиболее сильное. Вот почему важны как направление, так и сила магнитного поля.
Магнитные поля используются при изготовлении устаревших (ЭЛТ, электронно-лучевых трубок) телевизоров. В задней части кинескопа начинается пучок электронов. Электромагниты по бокам кинескопа направляют луч к передней части тубуса, где создается изображение.
Луч следует за силовыми линиями, созданными магнитами. Дизайнер телевизора управляет электромагнитами с помощью высокоскоростной электроники, так что луч скользит вперед и назад по передней части кинескопа, рисуя изображение по ходу движения.
Математический символ магнитного поля — «H». На самом деле вы можете получить счетчики, которые измеряют магнитное поле. Если метр показывает более сильное поле, тогда будет больше магнитного притяжения или отталкивания. С помощью простого компаса можно определить направление магнитного поля. Магнитное поле Земли направлено с юга на север.
А теперь сюрприз. Несмотря на то, что вы можете видеть силовые линии прямо в этих железных опилках, они не настоящие. Причина, по которой вы можете видеть «силовые линии» в железных опилках, заключается в том, что каждая маленькая железная опилка стала магнитом. Так одна маленькая частичка железного магнита притягивает вторую. Это делает магнит сильнее. Этот более сильный магнит притягивает другую железную опилку.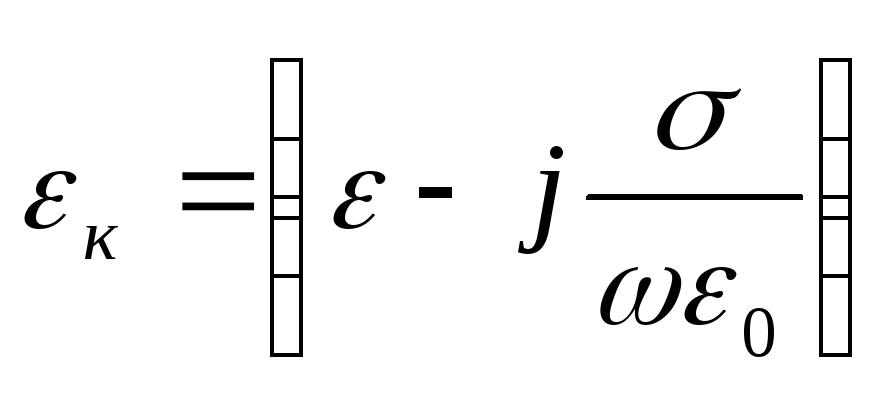
И так до тех пор, пока все железные опилки не сформируются в линии. Линии железных опилок просто формируются в зависимости от магнитного поля.
Фарадей ввел понятие силовых линий. Он нашел их полезными для получения практического понимания того, что происходит. Таким образом, несмотря на то, что силовые линии не реальны, они все же полезны для той же цели, которую задумал Фарадей. Не стесняйтесь представлять их себе, когда пытаетесь понять, что происходит, когда вы делаете магнит или собираете телевизор.
В нашем обсуждении магнитного поля мы отмечаем, что поле имеет две важные величины в каждой точке: направление и напряженность. То же самое справедливо и для электрического поля. Кроме того, как и в случае с магнитным полем, легко визуализировать электрические силовые линии, которые помогают нам увидеть, на что похоже электрическое поле.
Начнем с другого классического эксперимента. Найдите генератор Ван де Граффа и человека с длинными тонкими волосами, который очень доверчив.
Генератор Ван де Граффа производит статическое электричество. Запустите генератор и попросите человека положить одну руку на генератор. Волосы у человека встают дыбом (лучше работает в сухие дни, иначе статическое электричество уходит в воздух).
Посмеявшись над действительно странным зрелищем, взгляните на волосы. При прикосновении к генератору статическое электричество стекает с генератора на голову человека. Голова человека теперь полна статического электричества. Статическое электричество создает вокруг себя электрическое поле. Электрическое поле — это то, что заставляет волосы человека светиться во всех направлениях.
Посмотрите внимательно на волосы человека. Понятно, что электрическое поле сильнее всего ближе к голове человека, где сосредоточено все статическое электричество. Это также место, где волосы человека находятся ближе всего друг к другу. Силовые линии (волосы), расположенные близко друг к другу, означают сильные поля.
Волосы также показывают направление электрического поля.
Все волосы исходят прямо из головы человека. Как и силовые линии. Если вы поместите что-то в электрическое поле, например, волосы, они попытаются двигаться вдоль силовых линий. Насколько его толкают или тянут, зависит от силы электрического поля.
Вы можете получить счетчики, измеряющие электрическое поле. Однако будьте осторожны. Если чтение станет слишком сильным, будут дуги и искры! Вот что происходит, когда вас ударяет молния, когда вы касаетесь дверной ручки.
Также, как и магнитные силовые линии, электрические силовые линии не реальны. Но представление силовых линий очень полезно, когда вам нужно точно представить, как выглядит электрическое поле, особенно в плохой день или если вы попали в грозу.
Первое из четырех уравнений Максвелла называется законом Ампера. Это связано с электрическим током, создающим магнитное поле. Любой, кто намотал проволоку на гвоздь и подключил батарейку, испытал на себе действие закона Ампера. На самом деле электрический ток сегодня измеряется в «Амперах» или «Амперах» для краткости.
Ампер разработал это уравнение, экспериментируя с магнитами. Если вы пропускаете электрический ток через провод, возможно, намотанный на железный сердечник (например, гвоздь), вы создаете магнитное поле.
Ампер обнаружил, что иногда один магнит притягивает другой магнит, а иногда отталкивается. Затем он обнаружил, что притяжение или отталкивание зависит от направления тока, протекающего по проводу, и от того, в какой ориентации вы держите магниты. Пробуя разные эксперименты и разные уравнения, он постепенно обнаружил, что это уравнение (без последнего члена) можно использовать для расчета результатов его экспериментов.
Это уравнение связано с магнитным полем, “ H », а текущий — « I ». Чтобы использовать это уравнение, вы должны сначала выбрать замкнутую кривую. Это может быть любая кривая, где угодно. Единственным важным ограничением является то, что он должен быть закрытым. Хорошим примером является круг (обратите внимание на маленький кружок в самом первом символе).
Левая часть уравнения требует сначала рассчитать магнитное поле по всей длине выбранной вами кривой. Далее необходимо просуммировать все магнитные поля, параллельные кривой. Магнитное поле, перпендикулярное кривой, исключается.
Правая часть уравнения (игнорируя сложно выглядящий последний член) представляет собой полный ток, протекающий по той же кривой, которую мы использовали для левой части.
Это уравнение говорит о том, что если мы увеличим ток, протекающий по замкнутой кривой, общее магнитное поле вокруг этой кривой также увеличится. Если вы хотите на самом деле вычислить числа, вы можете сложить магнитное поле вокруг кривой и точно сказать, какой ток протекает через кривую (игнорируя этот надоедливый последний член). На самом деле есть счетчики, которые зажимают провод и суммируют магнитное поле. Затем измеритель считывает, какой ток протекает в проводе.
Что удивительно, так это то, что мы можем выбрать любую кривую, которую захотим, в любом месте, любой формы и в любое время.
Пока это замкнутая кривая, это уравнение работает идеально. Довольно прикольно!
На практике этот закон гласит, что если вам нужен более сильный магнит, поместите еще одну батарею на этот виток провода. Только не ставьте на него слишком много батареек, иначе он сгорит и магнитное поле исчезнет. Но даже если это произойдет, закон Ампера по-прежнему работает в любое время, в любом месте и с любой замкнутой кривой.
Прежде чем мы перейдем к самому последнему сложному на вид члену, мы изучим остальные уравнения Максвелла.
Закон Фарадея, второе из четырех уравнений Максвелла, описывает, как изменяющееся магнитное поле создает электрическое поле. Это почти точное зеркальное отображение закона Ампера. Здесь « E » представляет электрическое поле, а « H » представляет магнитное поле. Фарадей сначала описал этот закон в практических терминах, затем его хороший друг Максвелл перевел эту идею в это уравнение.
Левая часть этого уравнения аналогична левой части закона Ампера, только с электрическим полем вместо магнитного поля.
Как и в случае с законом Ампера, мы можем выбрать любую замкнутую кривую (обратите внимание на тот же маленький кружок в самом первом символе) и просуммировать электрическое поле, параллельное этой кривой, по всей длине кривой. Как и прежде, все поля, перпендикулярные кривой, игнорируются.
Правая сторона выглядит сложной, но идея проста. Он говорит нам сначала рассчитать полное магнитное поле, «текущее» по той же кривой, которую мы использовали для левой стороны. Это уравнение работает для любой замкнутой кривой, в любое время и в любом месте. Вам просто нужно использовать одну и ту же кривую в обеих частях уравнения.
Далее посмотрите на д/дт . Это похоже на дробь, но это не так. Это называется «производной по времени». Это говорит о том, что нас не интересует фактическое значение полного магнитного поля, которое «прыгает через обруч». Скорее, нас интересует, как быстро она меняется. У нас может быть огромное магнитное поле, но если оно не меняется, нас это ничуть не волнует.
Если бы мы действительно вычислили число для этого члена, то чем быстрее меняется магнитное поле, тем больше результат.
Это уравнение говорит, что когда у вас есть изменяющееся магнитное поле (правая часть), оно генерирует электрическое поле (левая часть). Кроме того, чем быстрее меняется магнитное поле, тем больше электрическое поле. Так работает электрический генератор. Быстро меняющееся магнитное поле создается вращением магнита вокруг и вокруг. Это изменяющееся магнитное поле генерирует электрическое поле или напряжение. Если вам нужно большее напряжение, просто вращайте магнит быстрее. Именно так сегодня вырабатывается почти вся электроэнергия в мире.
Обратите внимание, что в правой части также есть греческая буква « µ » (пишется «мю» и произносится как «мью»). Это связано с такими вещами, как железо. Железо легко подвергается воздействию магнитного поля и имеет большое µ . Большой µ усиливает эффект изменяющегося магнитного поля (правая часть закона Фарадея).
Вот почему железо часто используется в магнитах. Если вы используете железо с µ , которое в 80 раз прочнее воздуха, то ваш магнит в 80 раз сильнее, а ваш генератор в 80 раз мощнее.
Вы также можете делать вещи в обратном порядке. Вы можете использовать напряжение, чтобы создать изменяющееся магнитное поле. Просто возьмите электрический генератор и подайте на него напряжение. Магнит внутри начнет вращаться. Именно так работает двигатель. (Предупреждение: если вы делаете это на самом деле, лучше всего использовать генератор, который также предназначен для использования в качестве двигателя.) Закон Фарадея гласит, что если вы хотите, чтобы двигатель вращался быстрее, просто увеличьте напряжение. Конечно, это перестает работать, когда плавится провод в двигателе. Но даже в этом случае закон Фарадея по-прежнему работает везде и всегда для любой замкнутой кривой. Просто удивительно.
Третье уравнение Максвелла, закон Гаусса говорит, что электрический заряд, q v , (т.
е. статическое электричество) генерирует электрическое поле, E , (напряжение).
По сути, это уравнение говорит, что если вы хотите больше электрического поля, просто получите больше заряда. Вы можете получить больше заряда, используя такие вещи, как генератор Ван де Граффа, или просто шаркая ногами по ковру в сухой день.
Но будьте осторожны, если вы получаете слишком большой заряд, то закон Гаусса говорит, что вы получаете слишком большое электрическое поле. Если у вас слишком сильное электрическое поле, вы получите слишком большое напряжение. Если у вас слишком большое напряжение, вы получите дуги и искры! Перетасуйте ковер, а затем коснитесь дверной ручки, вы знаете, что произойдет. Итак, в следующий раз, когда вы почувствуете удар статического электричества, вы можете воскликнуть: «Черт! Опять по закону Гаусса!
Левая часть этого уравнения требует суммирования всего электрического поля, проходящего через замкнутую поверхность, например сферу (обратите внимание на маленький кружок на двух символах интегрирования).
Или пончик. (Хммм, я проголодался!) Или любую закрытую поверхность. Поверхность, подобная диску или чаше, не является замкнутой поверхностью. Закон Гаусса работает только с замкнутой поверхностью, такой как сфера.
Правая часть с тремя символами интегрирования предлагает сложить весь заряд или статическое электричество внутри той же сферы или замкнутой поверхности, которую мы использовали для левой части уравнения. Если у вас больше заряда внутри сферы, у вас больше электрического поля (или напряжения), пересекающего поверхность сферы.
Самый первый символ в законе Гаусса — это греческая буква « ε », которая пишется и произносится как «эпсилон». Это также называется «диэлектрической проницаемостью». Хорошие изоляторы, такие как керамика и стекло, могут иметь большую диэлектрическую проницаемость. Поскольку диэлектрическая проницаемость умножает левую часть, эффект большой диэлектрической проницаемости заключается в уменьшении электрического поля и, следовательно, напряжения, необходимого для данного количества заряда.
Электронные компоненты, называемые конденсаторами, накапливают заряд. Если вы хотите сохранить больше заряда для данного напряжения, закон Гаусса говорит нам просто добавить что-то вроде стекла или керамики с высокой диэлектрической проницаемостью.
Четвертое уравнение Максвелла похоже на зеркальное отражение третьего уравнения, закона Гаусса. Закон Гаусса касается электрического заряда, то есть статического электричества, генерирующего напряжение (электрическое поле). Закон Гаусса гласит, что сумма электрического поля, пересекающего поверхность любого шара, равна общему электрическому заряду внутри шара. Это уравнение говорит о том, что сумма магнитных полей, пересекающих поверхность любой сферы, всегда должна быть равна нулю.
Другими словами, это уравнение говорит о том, что не существует известной частицы, которая генерирует магнитное поле так же, как электрон генерирует электрическое поле. Не то чтобы физики его не искали. Они провели всевозможные эксперименты, чтобы найти его, и, возможно, когда-нибудь им это удастся.
В ожидании у них уже есть название для него «магнитный монополь». Но пока абсолютно ничего не нашли.
Это одна из величайших загадок физики и космологии. Почему при сотворении Вселенной мы получили триллионы и триллионы электронов, но, по крайней мере, насколько нам известно, ни единого магнитного монополя?
Если когда-либо будут найдены магнитные монополи, мы изменим этот закон, включив в него магнитный заряд. Нам также придется модифицировать закон Фарадея, включив в него магнитный ток (течение магнитных монополей), точно так же, как закон Ампера включает электрический ток (течение электронов). До тех пор четвертое уравнение остается без названия и (за исключением случайных математических удобств) без правой части.
Чтобы увидеть пример этого закона, представьте себе сферу с магнитом внутри. Этот закон гласит, что для каждого бита магнитного поля, выходящего из сферы, должно быть равное количество магнитного поля, возвращающегося в сферу. Это то же самое, что сказать, что каждый магнит должен иметь как северный, так и южный полюс.
Если бы вы могли разрезать магнит пополам и получить только северный полюс, вы бы только что нашли самый первый магнитный монополь!
Ток смещения
Ток смещения — это сложно выглядящий последний член закона Ампера, первого уравнения Максвелла. Именно этот член Максвелл добавил в уравнения Максвелла. Именно благодаря этому термину происходит все волшебство.
Вспомните, что левая часть говорит нам суммировать все магнитное поле, H , которое параллельно замкнутой кривой, любой кривой, которую мы выберем. Первый член правой части представляет собой полный электрический ток, протекающий по той же кривой.
Последний член такой же, как последний член закона Фарадея, только он связан с электрическим полем, а не с магнитным полем. Два знака интеграла (в форме буквы «S») говорят нам суммировать все электрическое поле, E , протекающее по замкнутой кривой, точно такой же кривой, которую мы использовали для левой части уравнения.
Еще раз, как и в случае с аналогичным термином в законе Фарадея, нас не интересует фактическое значение полного электрического поля, которое «прыгает через петлю». Скорее, « d/dt » говорит нам, что мы должны рассчитать, как быстро меняется общее электрическое поле. Это может быть очень сильное электрическое поле (включите генератор Ван де Граффа на полную мощность!), но если оно все время остается одним и тем же, это не имеет ни малейшего значения. В этом термине нас интересуют только изменяющиеся электрические поля, и чем быстрее они изменяются, тем важнее они.
Обратите внимание, что изменение электрического поля влияет на это уравнение точно так же, как ток I . Ток нуждается в проводнике, таком как медь, чтобы течь. Напротив, изменяющееся электрическое поле без проблем «течет» через идеальные изоляторы. Поэтому его называют «током смещения». Если вы знаете об электронных компонентах, называемых конденсаторами, ток смещения — это то, что «течет» через диэлектрик между двумя пластинами.
Максвелл заметил, что закон Фарадея и закон Ампера поразительно похожи, за исключением того, что в первоначальном законе Ампера не было этого последнего члена. Поэтому Максвелл сделал обоснованное предположение и добавил этот термин в закон Ампера. Теперь два закона были бы почти точным зеркальным отображением друг друга. Хотя это было эмоционально удовлетворительно, значило ли это что-нибудь на самом деле? Поэтому он играл с уравнениями, чтобы увидеть, что произойдет. И то, что произошло, было волшебством.
Термин тока смещения говорит о том, что изменяющееся электрическое поле (правая часть закона Ампера выше) создает магнитное поле (левая часть закона Ампера). Закон Фарадея гласит, что изменяющееся магнитное поле создает электрическое поле (видите симметрию?). Итак, Максвелл задался вопросом, почему электрические поля и магнитные поля, если они правильно настроены, не могут просто продолжать изменяться и создавать друг друга, и продолжать существовать… вечно? Каждый меняется, создавая другой, сам по себе, абсолютно ничем не помогая им.
Именно это они и делают. В результате возникает то, что мы называем электромагнитным излучением. Различные виды электромагнитного излучения включают видимый свет (который вы используете, чтобы прочитать это), радиоволны (используемые вашим мобильным телефоном), рентгеновские лучи (используемые в медицине) и так далее.
Максвелл математически предсказал, что радиоволны на самом деле являются электромагнитным излучением. Однако судьба распорядилась так, что только в 1887 году, через восемь лет после смерти Максвелла, Генрих Герц на самом деле доказал это экспериментально.
Решения уравнений Максвелла.
Уравнения Максвелла верны всегда и везде. Однако уравнения Максвелла не говорят нам, что такое поля. Мы знаем только, что любое правильное решение должно одновременно и точно удовлетворять всем четырем уравнениям. Даже сегодня основным способом поиска решений является угадывание. Если догадка не удовлетворяет всем четырем уравнениям, мы пробуем другую догадку.
К счастью, мы часто можем угадывать решения для целых групп проблем. Затем мы используем компьютер, чтобы получить решение любой конкретной проблемы в этой группе.
Одной из проблем являются прямоугольные коробки, как внутри микроволновой печи. Духовка использует электромагнитное излучение, колеблющееся туда-сюда, чтобы приготовить наш обед. Используя решение для прямоугольных коробок, мы можем выяснить, каковы электрические и магнитные поля печи. Теперь мы можем выяснить, как приготовить наш обед более равномерно, или узнать, сколько энергии микроволн уходит из коробки, если дверца повреждена.
В вашем мобильном телефоне используются электромагнитные волны, называемые радиоволнами. Решение уравнений Максвелла дает представление о том, как спроектировать антенну, чтобы получить наилучший возможный сигнал.
Скорость компьютеров с тактовой частотой в несколько ГГц означает, что электрические и магнитные поля внутри переключаются туда-сюда как сумасшедшие, пока мы играем в последнюю видеоигру.
Уравнения Максвелла говорят нам, что чем быстрее изменяются поля, тем больше поля они генерируют. Все эти изменяющиеся поля прокладывают свой путь через наши компьютеры. Компьютерный дизайнер удерживает этот невероятный беспорядок от уничтожения следующего байта данных, находя решения уравнений Максвелла.
Решения уравнений Максвелла часто близки к точным. Это единственная область техники, где распространены такие точные решения. Например, постройте мост и спросите у инженера, какой вес он может выдержать, прежде чем рухнет в реку: «10, может быть, 15 тонн». Постройте самолет и спросите у инженера, насколько хорошо он будет летать в сложной ситуации. Из-за турбулентности, которую можно рассматривать только приблизительно, вы получаете только приблизительный ответ. Но спросите инженера, с какой скоростью луч света пройдет 1 миллион километров, и вы получите ответ вроде 3,3356409.5 секунд.
Несмотря на эту точность, мы должны помнить, что даже уравнения Максвелла могут быть нарушены.
На самом деле они разрушаются очень слабыми радиоволнами, очень тусклым светом и т. д. Свет и все электромагнитное излучение состоят из небольших пакетов энергии, называемых фотонами. Когда свет настолько тусклый, что вы можете начать считать фотоны (например, с помощью фотоумножителя), в дело вступает новая теория под названием «Квантовая электродинамика» или КЭД.
Теперь небольшой секрет. Мы говорим об электрических полях и магнитных полях так, как будто они реальны. Конечно, вы видели, как движутся железные опилки, но никто никогда не видел и не прикасался к полю. Как и силовые линии, поля — это просто математическое удобство, позволяющее нам предсказать, что произойдет, когда мы проведем эксперимент. КЭД говорит, что электромагнитные поля на самом деле представляют собой триллионы и триллионы фотонов, которые вместе ведут себя как поля.
Если вы когда-нибудь изучите КЭД, вы откроете для себя еще более глубокую тайну. Физики описывают фотоны в терминах «волновых функций», которые тесно связаны с функциями вероятности.
(Одним из примеров функции вероятности является «гауссовая кривая», используемая для корректировки тестовых результатов.) Эта модель фотона работает невероятно хорошо для предсказания действительно странных результатов многих экспериментов. Но физики первыми признают, что их модель — это чисто абстрактная математика. Они до сих пор не имеют ни малейшего представления о том, что такое фотон на самом деле.
Итак, что на самом деле происходит, когда магнит притягивает кусок железа или солнечный свет падает на ваше лицо? Это самый большой секрет из всех: даже со всеми знаниями, теориями и уравнениями, собранными воедино за более чем столетие интенсивных исследований, никто еще не знает окончательного ответа.
Уравнения Максвелла. Нежное введение | by Panda the Red
Прежде чем мы начнем, имейте в виду, что любой осмысленный разговор об электромагнетизме означает разговор о векторном исчислении. Пожалуйста, не пугайтесь, даже если вы понятия не имеете, что означают какие-либо символы или термины.
Векторное исчисление сложное, но его основные идеи интуитивно понятны, и я объясню все по ходу дела.
Известные уравнения Максвелла для электрических и магнитных полей в единицах СИ: электрическое поле E и магнитное поле B при наличии функции заряда ρ («ро») и электрического тока Дж . Величины ε₀ («эпсилон-ноль») и μ₀ («мю-ноль») являются физическими константами, называемыми диэлектрической проницаемостью и магнитной проницаемостью вакуума. скорость света c подчиняется важному соотношению c² = 1/ ε₀μ₀. При задании граничных условий для полей эти уравнения полностью и однозначно определяют поля.
Обычно не пытаются решать эти уравнения напрямую для данной конфигурации граничных условий, зарядов и токов. Вместо этого было изобретено множество математических уловок для упрощения самых разных задач. Тем не менее, по-прежнему важно понимать физику, стоящую за этими уравнениями.
Электрическое и магнитное поля
Заряд q с вектором скорости v и скоростью намного меньшей, чем c в присутствии электрического поля E и магнитного поля B подчиняется закону Лоренца сила:
Интересно, что это все еще верно в релятивистском случае, когда сила F предназначена для обозначения скорости изменения во времени релятивистского импульса вместо классического импульса. В силе Лоренца есть два члена. Первый q E , называемая электростатической силой. Эта сила вызвана электрическим полем E , которое создается стационарными зарядами. Вторая сила равна q v ⨯ B и называется магнитной силой. Символ ⨯ называется вектором или векторным произведением и обозначает вектор, перпендикулярный v и B , и с величиной | против || Б | sin(θ) где θ — угол между v и B .
Магнитное поле B создается током и взаимодействует с движущимся зарядом, создавая силу. Ток — это заряд, умноженный на скорость, поэтому q v — элемент тока, и отсюда следует, что между токами действуют магнитные силы.
Для упрощения предположим, что токи и заряды — это отдельные объекты, существующие независимо друг от друга. Очевидно, что это не так, потому что ток по определению является движущимся зарядом, но когда мы начинаем говорить о движущихся зарядах, мы должны ввести специальную теорию относительности. Однако без теории относительности можно очень далеко продвинуться, как это сделали Джеймс Максвелл и его современники. Оказывается, уравнения Максвелла уже релятивистские, хотя 19физики 19-го века не могли этого знать. Продолжение этой статьи будет посвящено этому, если есть достаточный интерес.
Таким образом, для наших целей неподвижные заряды воздействуют на другие неподвижные заряды посредством электрической силы, а токи воздействуют на движущиеся заряды посредством магнитной силы.
Пример силы Лоренца можно увидеть в случае циклотронного движения. Предположим, что на эту страницу направлено магнитное поле и вектор скорости электрона полностью лежит в плоскости этой страницы.
Символы x обозначают однородное магнитное поле, направленное на страницу. Вектор силы, выделенный красным, представляет собой перекрестное произведение v и B , поэтому по правилу правой руки вектор силы указывает на центр окружности. Если заряду в однородном магнитном поле придать некоторую начальную скорость с направлением, перпендикулярным B , то заряд будет двигаться по окружности с постоянной скоростью. Это называется циклотронным движением.
Источник Трубка Телтрона (на фото выше) представляет собой устройство, демонстрирующее циклотронное движение. Свободные электроны образуются при нагревании небольшой нити накала и придают начальную скорость за счет создания электрического поля в небольшой области вокруг устройства.
Поле в трубке, создаваемое двумя катушками, приблизительно однородно, поэтому оно затягивает движение электронов в кольцо. Электроны излучают свет, когда сталкиваются с атомами газа с очень низким давлением.
Векторные поля, силовые линии и потоки
Электрические и магнитные поля являются векторными полями. Векторное поле — это функция, которая связывает векторы с точками в пространстве, как показано на следующем рисунке, на котором показаны векторы электрического поля электрического диполя, состоящего из положительного заряда в точке (+1,0) и отрицательного заряда в точке (-1, 0). Обратите внимание, что для ясности векторы показывают только направление, а не величину.
Вы можете видеть, что векторы электрического поля направлены от положительных зарядов (источники) к отрицательным зарядам (стоки). Поскольку сила положительного пробного заряда q равна F =q E , это соответствует тому, что заряды противоположного знака притягиваются, а заряды одного знака отталкиваются.
Мы почти всегда предполагаем, что источники полей, будь то заряды или токи, не движутся.
Линии поля не менее важны, чем векторы векторного поля. Для электрического диполя силовые линии, вероятно, многим из вас знакомы:
Чтобы получить более четкое представление о том, о чем говорят нам силовые линии, давайте выберем несколько из них и покажем их вместе с векторами поля:
На этой диаграмме показаны некоторые важные свойства силовых линий.
- Линии поля — это не просто кривые в пространстве, они также имеют направление. Линия поля начинается в источнике и заканчивается в стоке. Он также может начинаться или заканчиваться в бесконечности. Кажется, что они ломаются на картинках из-за ограничений программного обеспечения, которое я использовал для их рисования.
- Линии поля касаются векторов поля в каждой точке.
- Линии поля никогда не пересекаются друг с другом, иначе вектор в точке пересечения указывал бы сразу в двух направлениях, что невозможно.
- Линии поля постоянно меняют свое направление.
Давайте теперь ненадолго переключим внимание с электромагнетизма на гидродинамику. Предположим, что скорость воды с однородной плотностью (кг/м², поскольку мы рассматриваем двумерную задачу) ρ вокруг источника задана в каждой точке вектор-функцией v (r, θ), где r – радиальное расстояние от источника, а θ – угол между вектором положения r и горизонталью.
Предположим, что источник расположен в синей точке, а граница S представляет собой окружность радиуса R. Сколько воды проходит мимо этой границы в секунду?
Пространственный анализ — всегда отличное место для начала такой задачи. Нас спрашивают что-то в единицах кг/с, и нам дают плотность площади в единицах кг/м² и скорость в единицах м/с. Мы можем объединить их, чтобы получить импульс на единицу площади, который измеряется в кг/м⋅с. Если мы сможем исключить единицы измерения 1/м из этого количества, то получим что-то с правильными единицами измерения.
Это должно навести нас на мысль об интегрировании величины ρ v по длине l вдоль кривой C , но ρ v является векторной величиной и нас просят скалярную величину, поэтому нам нужно где-то ввести скалярное произведение. Поскольку вода течет по S, естественно предположить, что кривая C должна быть окружностью S, а вектор должен быть единичным вектором, направленным из окружности. Оказывается, это правильный подход, и ответом на задачу является величина
Это называется потоком векторного поля v над границей S. Поток трехмерного векторного поля через поверхность или двумерного векторного поля через кривую можно интерпретировать как указание на то, насколько это векторное поле «течет» по поверхности или кривой. Если v — любое векторное поле, а S — граница (поверхность или кривая), охватывающая область (объем или площадь) V, то мы также имеем критически важную теорему о расходимости, которую мы приводим здесь без доказательства:
Таким образом, сумма поток на границе объема равен интегралу от ∇⋅ v внутри объема, поэтому мы можем думать о ∇⋅ v как о потоке, выходящем из каждой точки внутри V.
Величина ∇⋅ v называется дивергенцией v и является предметом первых двух уравнений Максвелла.
Закон Гаусса
Это дифференциальная форма закона Гаусса. Сначала рассмотрим интегральную форму. Предположим, что S является замкнутой поверхностью и что общий заряд в области, заключенной в S, равен Q. Тогда:
Итак, закон Гаусса говорит нам, что поток электрического поля через S равен общему заряду, заключенному в S, деленному на диэлектрическую проницаемость . Одной из замечательных особенностей этого закона является то, что S может быть равно 9.0009 любая поверхность , которая полностью охватывает распределение заряда, и поток через поверхность будет одинаковым.
Дифференциальная форма получается с помощью теоремы о расходимости:
Обратите внимание, что в общем случае ρ является функцией положения. Мы не будем рассматривать случай, когда она также является функцией времени, поскольку для этого потребовалась бы специальная теория относительности, хотя в продолжении этой статьи это возможно.
Дифференциальную форму можно рассматривать как интегральную форму, применимую к бесконечно малым сферам, охватывающим каждую точку пространства.
Закон Гаусса говорит нам несколько полезных вещей:
- Если ρ(x,y,z) положительно, то точка выхода потока (x,y,z) положительна, а если ρ(x,y,z) равно отрицательно, то поток, выходящий из точки (x, y, z), отрицателен, что эквивалентно утверждению, что положительный поток входит в точку (x, y, z). Это формализует наше более раннее утверждение о том, что линии поля начинаются с положительных зарядов и заканчиваются с отрицательными зарядами.
- Если в области пространства нет заряда, то любая линия поля, входящая в эту область, должна выйти из этой области.
Давайте выведем закон Кулона как демонстрацию теоремы Гаусса. Предположим, что точечный заряд Q расположен в начале координат, а пробный заряд q расположен на расстоянии r от начала координат. Поскольку F = q E , эту проблему можно решить, найдя E благодаря Q.
Пусть гауссова поверхность S будет сферой радиуса r с центром в начале координат. Начнем с записи закона Гаусса:
Единичный вектор направлен в радиальном направлении, а дифференциальный элемент площади dS для поверхности сферы радиуса r равен r²sin(θ)dθdφ, где φ и θ такие, как на диаграмме:
Примечание. Некоторые авторы меняют местами φ и θ. ИсточникСледовательно:
По симметрии мы видим, что электрическое поле зависит только от расстояния от начала координат, поэтому мы можем вытащить его и r из интеграла:
E должно быть радиальным, потому что электрические силы действуют на линии между два заряда:
Тогда мы получаем Закон Кулона с F =q E :
Закон Гаусса для магнетизма
Этот закон говорит нам, что все магнитные поля безрасходимы. Используя идеи, которые мы развили в предыдущем разделе, это означает, что:
- Чистый поток, входящий или выходящий из любой области в присутствии магнитного поля, точно равен нулю. Любая линия поля, входящая в какую-либо область, должна выходить из этой области.
- Все линии поля образуют замкнутые петли.
- Нет источников или стоков для силовых линий магнитного поля. Эквивалентно, мы можем сказать, что магнитные заряды, или монополи, не существуют в классической электродинамике (до сих пор не решено, существуют ли они в квантовой электродинамике).
Любая линия поля, входящая в какую-либо область, должна выходить из этой области.Наиболее важным применением закона Гаусса для магнетизма является определение векторного потенциала. Это выведет нас за рамки этой статьи, поэтому мы просто продолжим.
Interlude: Conservative fields
Из основ физики мы знаем, что работа, совершаемая над частицей, когда эта частица перемещается на расстояние ∆x под действием постоянной силы F, равна W=F∆x. Если вместо этого F непрерывно меняется и частицу заставляют двигаться по прямой линии от a к b, то работа равна
Что, если вместо этого частица движется по кривой произвольной формы в трехмерном силовом поле? Предположим, что F — силовое поле и что частица движется по кривой C , которые могут образовывать или не образовывать замкнутый цикл.
В любой точке кривой мы можем сказать, что F является вектором с тремя компонентами: одна вдоль êₙ, перпендикулярная кривой, одна вдоль êₜ, касательная к кривой, и компонента вдоль êₙ⨯êₜ, перпендикулярная êₙ и êₜ. Работает только компонент F в направлении пути, поэтому мы берем его скалярное произведение с êₜ и интегрируем по d l , дифференциальный элемент длины пути:
Существует особый класс силовых полей, называемых консервативными полями, которые можно записать как отрицательный градиент функции потенциальной энергии: F =-∇U. Если это так, то основная теорема исчисления для линейных интегралов говорит нам, что: а не на избранном пути. На самом деле это обычно дается как определение консервативного силового поля, но определение консервативного поля как векторного поля, возникающего из градиента потенциала, точно эквивалентно: силовое поле F является консервативным тогда и только тогда, когда мы можем сказать, что F = -∇У.
Из этого уравнения также видно, что если частица движется по любой замкнутой кривой C , то выполненная работа равна 0. Запишем это как:
Кружок в знаке интеграла показывает, что путь интегрирования представляет собой замкнутый цикл.
В дополнение к теореме о дивергенции есть еще одна теорема, которую вы должны знать, чтобы чего-то добиться в изучении электромагнетизма, — это теорема Стокса, которую мы приводим без доказательства. Для любая -поверхность S, для которой C является границей:
Отсюда сразу видно и другое эквивалентное определение консервативного поля: так как если F консервативно, то оно есть градиент функции, а так как ∇⨯(∇A)=0 для любой функции A, мы видим, что ∇⨯ F =0 тогда и только тогда, когда F является консервативным. Мы можем думать о ∇⨯ F как о тенденции поля вызывать вращательное движение вокруг точки. Эта величина известна как завиток F и является предметом следующих двух уравнений Максвелла.
Уравнение Максвелла-Фарадея
Это одно из первых двух уравнений, связывающих E и B . Это говорит нам о том, что E является консервативным полем в отсутствие магнитного поля или если магнитное поле постоянно во времени. Чтобы объяснить это, давайте начнем с того, что мы знаем о потенциальной и кинетической энергии.
Физические системы будут развиваться с течением времени таким образом, что позволят им свести к минимуму накопленную потенциальную энергию. Они делают это, преобразуя потенциальную энергию в кинетическую энергию, совершая работу. В консервативном силовом поле частица не работает, двигаясь по замкнутому контуру, и поэтому консервативное силовое поле никак не может заставить частицу, изначально находящуюся в состоянии покоя, двигаться по контуру. Замкнутые орбиты могут возникать в зависимости от начальной скорости, как в случае движения планет.
Предположим, что мы хотим, чтобы заряженная частица, изначально находившаяся в состоянии покоя, двигалась по замкнутому контуру.
Это означает, что мы должны сделать электрическое поле неконсервативным, поэтому мы должны придать ему ненулевой ротор. Мы обращаемся к размерному анализу, чтобы руководствоваться нашей интуицией. Поскольку E имеет единицы N/C, ∇⨯ E имеет единицы N/C⋅m. Мы знаем, что B имеет единицы Тесла, а 1T = N⋅s/C⋅m. Следовательно, ∇⨯ E имеет единицы Тл/с. Поскольку ∇⨯ E является векторным полем, это означает, что мы должны подвергнуть заряженную частицу воздействию векторного поля с единицами T/s, если мы хотим, чтобы она двигалась по замкнутому контуру.
Поскольку величина -∂ B/ ∂t является векторным полем с единицами Тл/с, вполне возможно, что это именно та величина, которую мы ищем, и Максвелл определил, что это действительно так, что ∇⨯ E =-∂ B/ ∂t при интерпретации экспериментальных данных Фарадея.
Мы можем использовать это уравнение для вывода закона индукции Фарадея, который утверждает, что:
Величина ℰ (буква E) называется электродвижущей силой в проволочной петле и измеряется в вольтах, а 𝛷 представляет собой поток магнитное поле через область, ограниченную петлей.
ЭДС — это работа, совершаемая единичным зарядом при однократном движении по петле, поэтому:
Итак, по теореме Стокса:
Тогда по уравнению Максвелла-Фарадея:
Частная производная по времени вытягивается из интеграла и превращается в обычную производную, потому что интеграл не зависит от положения. По определению, этот интеграл представляет собой поток B через область, окруженную петлей провода C , так что это завершает доказательство того, что
Это объясняет, почему изменяющееся магнитное поле вблизи цепи индуцирует ток в этой цепи.
Круговой закон Ампера
И, наконец, мы подошли к закону Ампера. Закон Ампера позволяет завершить процесс построения полной единой теории электромагнетизма и электромагнитных волн.
Начнем с исходной формы этого закона, ∇⨯ B = μ₀ j, , которая выполняется, когда нет зависимости от времени. Это говорит нам о том, что циркуляция магнитного поля вокруг точки пропорциональна току в этой точке.
Интегральная форма этого уравнения:
Это говорит о том, что интеграл B вокруг замкнутого контура пропорционален общему току, проходящему через область, окруженную контуром. В качестве демонстрации мы можем использовать это, чтобы найти магнитное поле вокруг провода. В этом случае касательный вектор находится в направлении полярного угла, поэтому, если мы поместим проволоку в центр воображаемой петли радиуса r, то dl = rdθ. Тогда:
Это формализует правило правой руки для магнитного поля вокруг провода:
Источник В случае, не зависящем от времени, E всегда консервативен, потому что его локон равен нулю. Но мы только что видели, что даже в независимом от времени случае B является консервативным только в области, где нет токов, а самые интересные проблемы касаются областей, близких к токам. Кроме того, магнитная сила F = q v ⨯ B никогда не бывает консервативной, поскольку она зависит от скорости.
Таким образом, мы не можем относиться к B как к консервативному полю вообще, а те редкие случаи, когда мы можем, для нас сейчас не важны.
Теперь давайте поговорим о втором члене в правой части закона Ампера, называемом током смещения. Название происходит от другого поля, называемого электрическим смещением D = ε₀ E , которое полезно в задачах, связанных с полями в материалах, а не в пустом пространстве. Первоначально закон Ампера не включал этот термин, и Максвелл обнаружил, что он необходим. До этого неполнота закона Ампера вызывала некоторые проблемы. Самое главное, это означало бы, что электромагнитные волны не могут существовать.
В физике волновое уравнение представляет собой дифференциальное уравнение вида:
Оператор ∇² называется лапласианом и определяется по формуле:
И k — это скорость, с которой волна распространяется в пространстве. Если функция f является векторным полем, то каждая компонента вектора удовлетворяет уравнению.
Попробуем получить волновые уравнения в свободном пространстве (без зарядов и токов), делая вид, что ничего не знаем о токе смещения. Тогда уравнения Максвелла будут такими:
Начнем с тождества векторного исчисления ∇⨯(∇⨯ A )=∇(∇⋅ A )-∇² A , где ∇² A означает, что оператор функции Лапласа применяется к каждой компоненте А . Поскольку ∇⋅ E =∇⋅ B =0, это означает, что ∇⨯(∇⨯ E )=-∇² E для электрического поля и ∇⨯(∇⨯ B4 ) –
∇² B для магнитного поля. Если ∇⨯ B =0 в свободном пространстве, то обратите внимание, что мы не можем получить правильные волновые уравнения. Для E получаем:
А для B получаем:
Чтобы исправить это, мы должны добавить ток смещения. Конечно, мы не можем просто включить ток смещения, потому что он даст нам нужные нам уравнения, нам нужно их обосновать.
Для этого предположим, что проблема заключается в уравнении ∇⨯ B =μ₀ j . Возьмем расхождение обеих сторон: ∇⋅(∇⨯ B )=μ₀∇⋅ j . Поскольку расходимость завитка всегда равна нулю, это означает, что ∇⋅ j =0 всегда. Но это не так. Электрические токи подчиняются уравнению непрерывности:
Это уравнение говорит, что скорость изменения заряда в области является отрицательной величиной чистого тока, вытекающего из области. Если ∇⋅ j положительно, так что есть чистый отток заряда, то заряд в области должен уменьшиться, и наоборот, если он отрицателен.
Это означает, что вместо этого мы должны иметь:
Это означает, что ρ является дивергенцией некоторого векторного поля. К счастью, закон Гаусса говорит нам, что существует векторное поле, дивергенция которого равна ρ, то есть ε₀ E , объем. Если мы подставим ε₀∇⋅ E вместо ρ и сократим дивергенцию с обеих сторон, то получим правильное уравнение:
Это дает нам правильные уравнения Максвелла для свободного пространства:
Теперь мы можем получить правильные волновые уравнения :
Для E .
Тогда для B :
Вот почему эти уравнения названы в честь Максвелла, хотя он и не открывал законы, которые они описывают. Именно его гениальная идея ввести ток смещения в закон Ампера позволила окончательно унифицировать теорию классического электромагнетизма.
Заключение
Если вам удалось дойти до конца, то вы должны собой гордиться. Это довольно сложная вещь, и мы только что поцарапали поверхность. Если будет достаточный интерес, то в следующей статье будут раскрыты некоторые моменты теории относительности, на которые я ссылался в этой статье. Дайте мне знать в комментариях, если вы думаете, что я должен написать это. Я закончу эту статью небольшим тизером о том, что это повлечет за собой.
Стингер: Ковариация
Принцип ковариации гласит, что законы физики должны казаться одинаковыми для всех наблюдателей во Вселенной, в том смысле, что форма уравнений, описывающих эти законы, должна быть одинаковой во всех отсчетах. кадры.
Предположим, что начала двух систем координат S и S’ находятся в относительном движении с постоянной скоростью V вдоль оси x.
Координаты со штрихом связаны с координатами без штриха преобразованием Галилея:
Давайте рассмотрим только одномерное волновое уравнение для x-компоненты E . Принцип ковариации говорит нам, что если кто-то в системе S наблюдает электромагнитную волну и определяет, что волновое уравнение имеет вид
, то наблюдатель в S’, измеряющий ту же волну, должен наблюдать уравнение в терминах своих координат как
.0005
Можем ли мы добиться этого, выполнив преобразование Галилея по координатам? Используя преобразования и цепное правило, частные производные преобразуются как:
Таким образом, нештрихованное волновое уравнение преобразуется в:
Это означает, что есть проблема, и это либо волновое уравнение, либо преобразование. Это не может быть волновое уравнение, потому что уравнения Максвелла проверяются экспериментально, поэтому проблема заключается в преобразовании. Чтобы решить эту проблему, мы должны отказаться от некоторых из наших самых фундаментальных представлений о мире и ввести специальную теорию относительности.