Математическая запись второго закона ньютона: Второй закон Ньютона — урок. Физика, 10 класс.

Физические основы механики

ЦЕЛЬ РАБОТЫ

Изучение равнопеременного и равномерного прямолинейных движений в поле земного тяготения. Определение ускорения свободного падения.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

Основные законы динамики материальных точек – это законы Ньютона. В частности, второй закон Ньютона, математическая запись которого, как известно, имеет вид:

(1)

называют основным уравнением динамики.

Эскиз машины Атвуда показан на рис. 1.

Рис. 1. Эскиз машины Атвуда

Два одинаковых груза с массами М соединены нитью, перекинутой через неподвижный блок. Если на один из грузов положить перегрузок  массой m (в виде шайбы), то система приходит в ускоренное движение.

Каждый из грузов натягивает участок нити, который, стараясь сократиться, действует на соответствующий груз с силой натяжения Т₁ или Т₂, а на блок – с силами Т’₁ и Т’₂. Тогда на каждый груз действует сила тяжести и сила натяжения нити.

Основное уравнение динамики для груза с перегрузком имеет вид:

(2)

а для другого груза (без перегрузка):

(3)

Основное уравнение динамики вращательного движения неподвижного блока имеет вид:

(4)

где SM_k – алгебраическая сумма моментов сил, действующих на блок, относительно оси вращения; I – момент инерции блока относительно оси вращения; e – его угловое ускорение.

Если вращение по часовой стрелке считать положительным, то, согласно рис. 1, получим

(4а)

где: R – радиус блока; М_тр – момент силы трения.

Будет считать, что нить невесомая, нерастяжимая и не скользит по блоку. Из условия невесомости нити следует:

(5)

Из условия нерастяжимости нити следуют равенства модулей перемещений, скоростей и ускорений грузов и нити:

(6)

Наконец, в отсутствие скольжения нити по блоку, ускорение грузов и нити а равно модулю тангенциального ускорения точек обода блока:

или

(7)

Проецируя уравнения (2) и (3) на ось

у, направленную вертикально вверх, получим с учетом формул (5), (6) и (7) систему уравнений, к которой присоединим уравнение (4а):

(8)

Умножая первое из уравнений (8) на (-1), и складывая все уравнения (8), получим

(9)

В данной лабораторной установке момент сил трения настолько мал, что выполняется неравенство

(10)

Кроме того, в лабораторной установке величина момента инерции I блока такова, что справедливо другое неравенство:

(11)

Пренебрегая малыми величинами, из уравнения (9) получим формулу для расчёта ускорения а системы грузов под действием перегрузка массой m:

(12)

а модули сил натяжения нити Т₁ и Т₂ по обе стороны блока равны:

(13)

Можно сказать, что равенство (13) выполняется при двух предположениях (10) и (11).

Равноускоренное движение системы грузов вдоль оси у описывается уравнениями движения произвольной точки системы:

где у₁,

v₁ – начальные параметры.

Исключая из этих уравнений время t, при условии v₁=0, получим

(14)

Система грузов перемещается на величину s_y=L₁, двигаясь равноускоренно под действием перегрузка массой m с ускорением, которое определяется формулой (12).

В точке с координатой у₂ и скоростью v₂ перегрузок подхватывается столиком, и система грузов движется равномерно, перемещаясь на величину

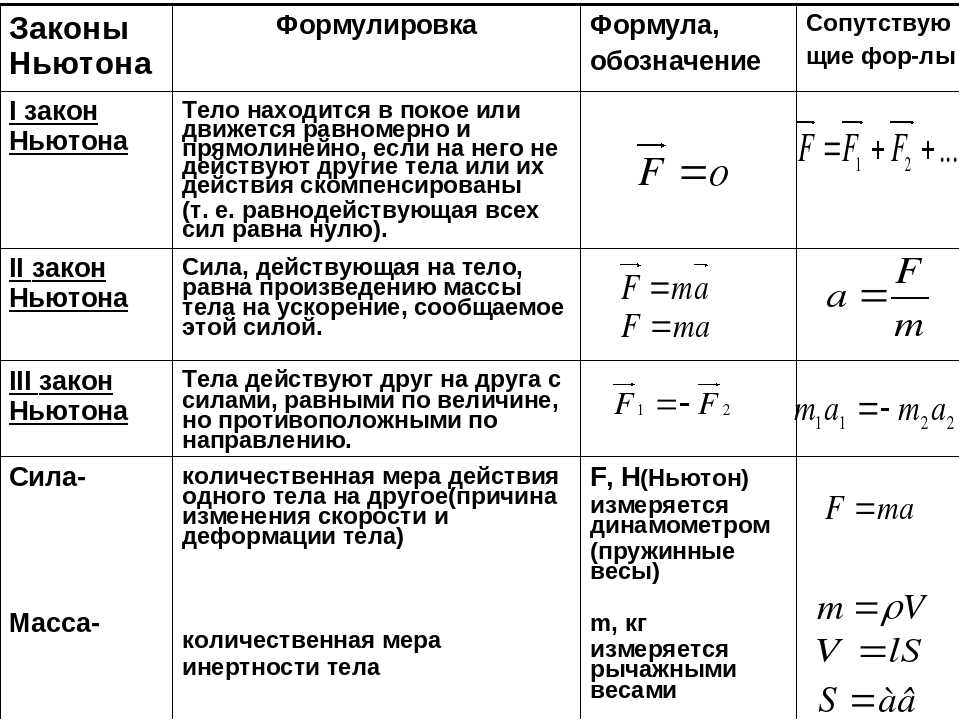L₂ за время t, измеряемое миллисекундомером экспериментальной установки. Подставляя в равенство (14) формулу

получим

(15)

При изменении L₂ меняется время t, измеряемое секундомером, но ускорение

а должно оставаться неизменным.

С помощью формулы (15) найдём расчётную формулу для величины ускорения  а грузов с перегрузком:

(16)

ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

К основанию 1 экспериментальной установки (см. рис. 2), которая стоит на ножках 2, прикреплена вертикальная стойка

3. К стойке крепится кронштейн 4, который может перемещаться вдоль стойки. На кронштейне находится столик для снятия перегрузка.

Рис. 2. Схема экспериментальной установки

На верхнем конце стойки находится неподвижный блок 5. Для наблюдения ускоренного движения грузов на правый груз 6 помещают перегрузок 7 и поднимают их в верхнее положение путем нажатия кнопок «+» или «-». Значение массы перегрузка показывается в окне «масса После нажатия кнопки «ПУСК» начинается ускоренное движение грузов и перегрузка до того момента, когда столик 4 подхватит перегрузок. Одновременно включается миллисекундомер, измеряющий время равномерного движения грузов до остановки. Итак, во время равноускоренного движения грузы проходят расстояние L₁ (см. рис. 1) и приобретают скорость v₂, с которой, двигаясь равномерно, проходят расстояние L₂ за время t, измеренное миллисекундомером в секундах и показанное в окне «время».

Для подготовки прибора к следующему измерению нажимают кнопку «СБРОС».

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Упражнение 1. ИЗМЕРЕНИЕ УСКОРЕНИЯ ГРУЗОВ

1. Измерьте расстояние L с помощью линейки и занесите результат в таблицу измерений 1. Цена деления линейки 1 см.

Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.

Таблица 1

 

m=… кг		L=… м	L2=… м
№ наблюдения	Время ti, с
1
2
3
4
5

2. Выберите значение массы перегрузка m и занесите ее значение в таблицу 1. Выбор производится мышкой с помощью нажатия ей на кнопки со значками «+» или «-». Значение массы перегрузка показывается в окне «масса». Оптимальным для выбора является значение массы от 5 до 10 г. Учтите, что масса в данной работе определена при взвешивании тел на весах с точностью, равной половине цены деления весов. Приборная погрешность весов составляла 0.1 г.

Обратите внимание на необходимость записывать данные в системе СИ, то есть, в килограммах.

3. Установите, взяв мышкой, кронштейн со столиком на некотором расстоянии L₂ от нижнего фиксатора расстояний. Возможные пределы варьирования расстояния от 12 до 25 см. Измерьте установленное расстояние L₂ по линейке, взяв отсчёт по красной черте. Результаты измерения запишите в таблицу 1 результатов измерений 1. Цена деления линейки 1 см.

Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.

4. Нажмите кнопку «ПУСК».

5. После остановки грузов запишите в таблицу 1 время t равномерного движения грузов, измеренное миллисекундомером и показанное на табло «время». Время необходимо записывать в системе СИ, то есть в секундах. Погрешность миллисекундомера составляет 0.001 с.

6. Нажмите кнопку «СБРОС».

7. Повторите пункты 3 – 5 ещё четыре раза, не меняя расстояние L₂.

8. Вычислите среднее значение времени <t>. Результат занесите в таблицу расчетов 2.

Таблица 2

№ наблюдения	ti	ti-<t>	(ti-<t>)2
1
2
3
4
5
Суммы	Sti=…		S(ti-<t>)2
	<t>=…		s=…
	E=

9. Найдите отклонения каждого из пяти измерений t_i от среднего значения времени <t>.

10. Возведите в квадрат каждое отклонение и просуммируйте квадраты отклонений.

11. Рассчитайте среднее квадратичное отклонение s, применив для его расчёта формулу для выборочной  оценки S(<t>) стандартного отклонения результата измерения по формуле из теории погрешностей

 

12. Умножив это значение среднего квадратичного отклонения на коэффициент Стьюдента, найдём полуширину доверительного интервала в определении времени

где t_P(n) – коэффициент Стьюдента, соответствующий вероятности Р и числу степеней свободы n=n-1.

Для n=5 измерений при рекомендуемой доверительной вероятности P=0.9 имеем из таблицы коэффициентов Стьюдента t_0.9(5-1)=2.13.

13. Приборная погрешность в определении времени в нашем случае значительно меньше случайной, поэтому приборная погрешность в определении времени в данном случае не учитывается.

Тогда результат измерения времени t запишем в виде

14. Произведите расчет относительной погрешности в определении времени E_t (в процентах) по формуле:

15. Приборная погрешность в определении расстояний уже не может быть отброшена, так как случайной погрешности здесь нет, Тогда для расстояний L и L₂ имеем приборные погрешности, равные половине цены деления линейки

 

16. Ускорение грузов а рассчитывается по формуле (16), в которую подставляется среднее значение времени <t> и измеренные линейкой значения расстояний L и L₂.

 

17. Относительная погрешность в определении ускорения  найдётся по формуле:

18. Результат измерения ускорения а запишется в виде

Упражнение 2. ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ

19. Определите величину ускорения свободного падения g по формуле

При этом значение массы грузов принять равным M=90 г.

20. Полуширину доверительного интервала Dg найдите с помощью формулы

Значения погрешностей в определении масс в данной работе принять равными приборной погрешности при их взвешивании:

21. Оформите отчёт по работе.

ВЫПОЛНЕНИЕ ЛАБОРАТОРНОЙ РАБОТЫ

На рис.3 представлена реальная лабораторная установка, используемая для выполнения данной работы.

   Рис.3. Лабораторная установка “Машина Атвуда”

После ознакомления с принципом работы установки необходимо проделать работу на виртуальной лабораторной установке, представленной в правом окне. В процессе выполнения измерений можно свернуть-развернуть окно с описанием лабораторной работы либо свернуть-развернуть окно с лабораторной установкой.

После окончания измерений следует сохранить результаты работы.  Для этого необходимо нажать на клавишу   или. После этого будет предложено сохранить результаты в файле, имя которого – название лабораторной работы (имя файла изменять не рекомендуется), месторасположение – рабочий стол (можно изменить место сохранения файла). Так как результаты сохраняются в формате html, в дальнейшем вы можете просмотреть результаты, открыв сохраненный файл, а также можете отправить файл на проверку правильности выполнения лабораторной работы преподавателю.

РЕКОМЕНДАЦИИ

по оформлению отчета по лабораторным работам (физика)

1. Отчет оформляют в электронном виде в редакторе Word

2. Объем отчета составляет 2-3 страницы.

3. В отчете необходимо указать:

3.1 Фамилию, имя, отчество студента;

3.2 Номер группы;

3.3 Дисциплину;

3.4 Фамилию, имя, отчество преподавателя;

4. Рекомендуемая структура отчета:

          4.1 Название работы;

          4.2 Цель работы;

          4.3 Таблицы измерений и таблицы расчетов, сохраненные в виде отдельного файла.

          4.5 Формулы и законы, используемые для расчетов;

          4.6 Результаты расчетов, не вошедшие в таблицу расчётов;

          4.7 Выводы, которые можно сделать из работы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется системой отсчета?

2. Дайте определение материальной точки.

3. Сравните понятия пути и перемещения.

4. Дайте определения средней и мгновенной скоростей.

5. Дайте определения среднего и мгновенного ускорений.

6. Укажите формулы, связывающие кинематические величины при равноускоренном прямолинейном движении.

7. Дайте определение силы.

8. Что характеризует масса тела?

9. Сформулируйте основные законы динамики – законы Ньютона.

10. Какая система тел называется изолированной?

11. Сформулируйте законы сохранения импульса и полной механической энергии системы.

12. Какое движение тела называется свободным падением?

13. Как изменится ускорение свободного падения при подъеме с уровня моря на высоту h=10 км? Радиус Земли R₃=6 370 км.

14. При каком условии ускорения тел, используемых в машине Атвуда, одинаковы по модулю?

Первый, Второй и третий законы Ньютона

I закон Ньютона

Первый постулат состоит в следующем. Если на тело не действуют никакие внешние силы, то оно либо находится в покое, либо движется равномерно и прямолинейно. Это означает, что для начала движения или изменения скорости необходимо применение к объекту внешнего воздействия.

В современной физической теории это утверждение называют законом инерции. Под термином инерция понимают способность материальной точки двигаться с постоянной скоростью и в неизменном направлении, если нет действия сторонних сил. В то же время, это свойство сопротивления внешнему влиянию на скорость. Таким образом, для изменения скорости объекта требуется применения силы извне.

Инертность у каждого физического тела разная. Количественно она определяется массой. Отсюда система отсчета, в которой работает Первый закон Ньютона, сегодня называется инерциальной. В жизни это подтверждается тем, что воздушный шарик легко сдвинуть с места, а тяжелый большой камень гораздо сложнее. Чем меньше масса, тем меньшую силу необходимо применить для придания телу ускорения.

В качестве источника внешнего воздействия законом рассматривается стороннее тело. Любое действие со стороны является противовесом внутренних сил материальной точки. Т.е. покоящийся предмет может находиться под скомпенсированным воздействием сил. Тогда Первый постулат есть закон сохранения движущегося состояния.

Представим все действующие силы в виде одной результирующей ƩF.

Если ƩF = 0, то ускорение будет тоже равно 0. При нулевом ускорении тело либо стоит на месте, либо не двигается без ускорения, т.е. скорость неизменна.

Задачи на I закон

Закон инерции не имеет графического выражения, поэтому решение задач на данную тему сводится к логическим рассуждениям и нахождению компенсирующей (результирующей) силы.

Классическим примером является задача про лифт, движущийся в шахте на тросе.

II закон Ньютона

Этот постулат показывает связь силы, массы объекта и ускорения его движения. Ускорение находится в прямой пропорциональной зависимости от действующей силы и в обратной – с его массой.

Формулировка: Действующая на тело сила есть произведение его массы на ускорение.

Математически зависимость выглядит так:

где

      m – масса объекта, кг;

      a – вектор ускорения м/с².

Формула F = m∙a составляет основу раздела «динамика».

Направление вектора ускорения совпадает с направлением вектора силы.

В реальных условиях на тело одновременно действуют различные силы. Для решения задач прежде всего необходимо найти суммарную силу.

Движение лыжника с горы – характерный пример комплексного воздействия.

 

Как показано на рисунке, результирующая сила складывается из силы тяжести ->Ft , давления ->Fn и силы ->F , которая дает ускорение:

Отсюда видно, что в отсутствии ускорения ->F=0, что означает покой либо равномерное движение. Первый закон есть частный случай Второго.

Динамика оперирует также понятием импульса. Импульс является количественной мерой движения и находится как произведение вектора скорости на массу:

Тогда для инерциальной системы отсчета результирующая сила равна производной импульса тела по времени t:

Примеры задач

В большинстве задач понятия ускорения и сил представляются в виде проекций векторов a_x, F_x. В примерах по умолчанию будем подразумевать именно проекции.

Простейшие задачи на применение второго закона сводятся к подстановке значений величин в формулу.

1. Найдите ускорение тела массой 600 г под действием внешней силы, равной 0,3Н.

Решение.

Зная, что a_x = , подставим значения массы в килограммах и силы в ньютонах.

Получаем: a_x =  = 0,5 м/с².

2. Сила тяги двигателя машины составляет 1200 Н. Масса автомобиля 700 кг. За какое время автомобиль разгонится из состояния покоя до 72 км/ч?

Решение.

Для использования формулы Второго закона необходимо представить ускорение в виде отношения скорости ко времени. Машина была в покое, т.е. имела начальную скорость v₀, равную 0 м/с; конечная скорость v₁72 км/ч или 20 м/с.

Тогда:

F = m∙a = m∙(v₁ – v₀)/t, откуда время разгона t = m∙( v₁ – v₀)/F.

Подставив числовые значения, получим: t = 700∙(20 – 0)/1200 ≈ 11,7 с.

Т.е. для разгона автомобиля массой 700 кг до 72 км/ч при тяге двигателя 1,2 кН необходимо 11,7 секунды.

Исаак Ньютон в труде «Математические начала натуральной философии» дал формулировки трех законов, положивших основу классической теории механики. Первый закон детерминирует понятие движения. Во втором постулате обозначена взаимосвязь силы, массы и ускорения. Третий закон Ньютона касается взаимодействия двух тел между собой.

Формулировка

Если тело №1 воздействует с некоторой силой на тело №2, то тело №2 воздействует на тело №1 с силой, равной по модулю и противоположной по направлению.

При взаимодействии материальных точек силы всегда имеют общее происхождение и должны компенсировать друг друга, но этого не происходит, поскольку объекты их приложения разные.

Математическая запись постулата такова:

Принимая во внимание Второй закон Ньютона, получим выражение:

Т.е. массы взаимодействующих объектов обратно пропорциональны их ускорениям.

В физике Третий закон Ньютона называют также законом действия и противодействия.

Современные ученые трактуют закон следующим образом. Две материальные точки взаимодействуют между собой с силами, которые равны по модулю, направлены противоположно и действуют по прямой, проходящей через эти точки.

Третий закон в реальных условиях

1. По дороге едет автомобиль. Дорожное покрытие подталкивает колёса вперед, сами колеса при этом толкают дорогу назад. Это приводит в движение всю машину.
2. При взлете вертолет толкает воздух вниз, тогда как воздушная масса толкает вертолет наверх, заставляя подниматься.
3. В бассейне пловец под водой ускоряется от борта, совершая ногами толчок назад, но движение пловца направлено вперед.

Пример задачи на Третий закон

Кабина лифта имеет ускорение a = 3 м/с². На полу лежит груз, имеющий массу 15 кг. Найти силу, с которой груз действует на пол при движении лифта вверх.

Решение.

Милы, действующие на груз:

• реакция опоры ->N;
• сила тяжести ->Ft

По условию вектор ускорения направлен вертикально. Тогда:

m∙a = F_т∙+ N;

m∙a = m∙g + N;

N = m∙ (a +g) = 15∙(3+9,8) = 192 Н.

Согласно III закону, сила реакции опоры по модулю равна силе, действующей на пол со стороны груза, а значит, равна также 192 Н.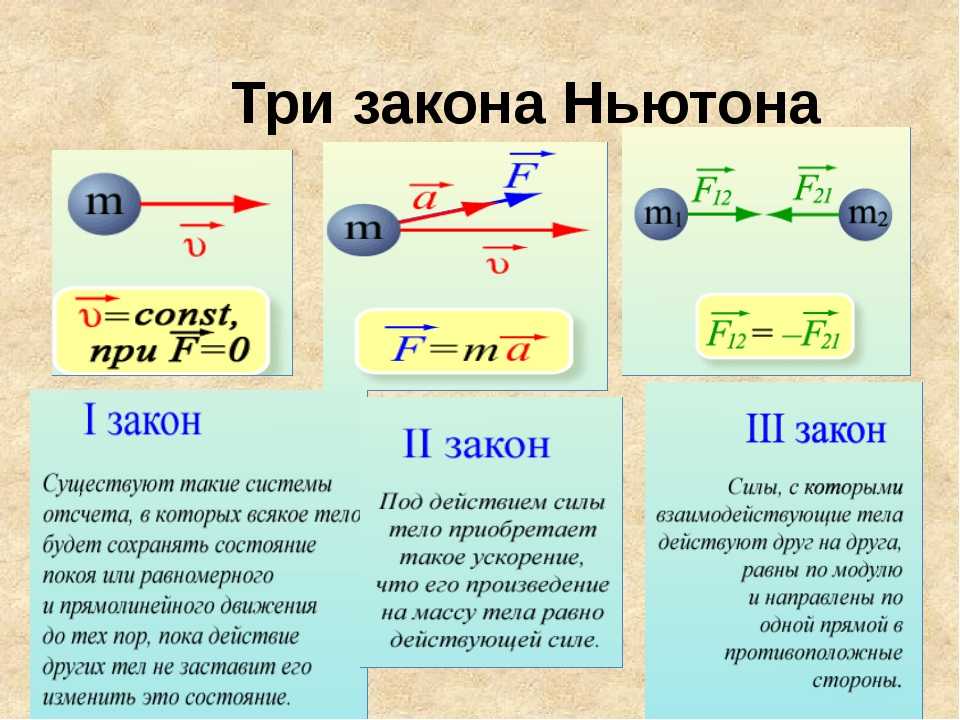

Второй закон движения Ньютона

Чтобы по-настоящему оценить законы Ньютона, иногда полезно увидеть, как они строятся друг на друге.

• Первый закон описывает, что произойдет, если не будет силы .
• Второй закон описывает, что произойдет, если будет силой .

«Когда на объект действует внешняя неуравновешенная сила,
объект будет ускоряться в том же направлении, что и сила. Ускорение изменяется прямо пропорционально силе, и обратно как масса».

«Когда внешняя неуравновешенная сила…»
Мы все еще говорим об этих внешних силах, но теперь мы добавили понятие «неуравновешенная».

• Неуравновешенность просто означает, что никто (или что-либо) не сопротивляется силе достаточно сильно, чтобы нейтрализовать ее.

«…ускоряется в том же направлении, что и сила…»
Некоторые думают, что это означает, что объект будет двигаться в том же направлении, что и сила… не обязательно!

• Возможно, объект движется вправо, а сила толкает влево.
• Это означает, что объект замедлится.
• Его ускорение направлено в сторону действия силы (влево), но он все еще движется вправо.

«Ускорение изменяется прямо пропорционально силе…»
Это просто означает, что если сила увеличивается, ускорение увеличивается. Если сила уменьшается, ускорение уменьшается.

• В этом есть смысл… нажми на что-нибудь посильнее, и оно ускорится сильнее! Они напрямую зависят друг от друга.

«…и обратно пропорционально массе».
Это означает, что чем больше масса, тем меньше ускорение. Чем меньше масса, тем больше ускорение.

• В этом тоже есть смысл… если что-то имеет меньшую массу, его легче заставить двигаться быстрее! Они обратно пропорциональны друг другу.

Математически это будет записано как…

• Символ маленькой плавающей рыбки (α) — это греческая буква «альфа», которая в математике означает «изменяется как».
• не означает, что они равны друг другу, но показывает, что они каким-то образом связаны друг с другом.

Если объединить эти два соотношения, получится одна из самых основных и важных формул, когда-либо открытых в физике.

F = ma

F = сила (Ньютоны)

m = масса (кг)

a = ускорение (м/с ² )

Единица силы называется Ньютон (006 равен 90 кг м/с ² ).

• Назван в честь выдающейся работы Ньютона в области физики.
• По определению масса в один килограмм будет ускорена со скоростью 1 м/с ² , если к ней приложена сила в 1 Ньютон.

Пример 1: Определить силу, действующую на объект массой 5,46 кг, если он движется со скоростью 17 м/с ² .

F = ma
= (5,46 кг)(17 м/с ² )
F = 93N

Пример 2: Определите ускорение автомобиля массой 1000 кг, если на него действует сила 2,5e3 Н?

Вращательная форма второго закона Ньютона

Содержание

• Вращательная форма второго закона Ньютона для точечной массы
• Вращательная форма второго закона Ньютона для твердого тела

Сначала рассмотрим случай, когда вся масса находится в одном месте.

Световой стержень, на конце которого закреплен небольшой предмет, вращающийся вокруг оси, перпендикулярной его длине и проходящий через другой его конец

Предположим, что точечный объект массы \(m\), прикрепленный к легкому жесткому стержню длиной \(l\), вращается вокруг оси, перпендикулярной стержню и проходящей через его конец. На частицу действует сила, увеличивающая угловую скорость вращения. Разбейте силу на составляющие. Один компонент направлен к оси и называется радиальным компонентом силы \({F_r}\), а другой компонент находится в тангенциальном направлении \({F_t}\).

Крутящий момент радиальной составляющей относительно оси равен нулю, так как линия действия силы проходит через саму ось. Крутящий момент тангенциальной составляющей попытается увеличить угловую скорость объекта и создать угловое ускорение.

Чистый крутящий момент силы вдоль оси равен \[\начать{выравнивать} \overrightarrow \tau
&= \overrightarrow r \times \overrightarrow F \\ & = \ overrightarrow r \ times \ Big ({\ overrightarrow F _r} + {\ overrightarrow F _t} \ Big) \\ &= \overrightarrow r \times {\overrightarrow F _t} &\qquad \Big(\text{since} r \times {\overrightarrow F _r} = 0 \text{с } r \text{параллельно} {F_r} \Большой)\\ &= л{F_t}. \qquad (1) \конец{выравнивание}\] 92},\) имеем

\[\тау = I\альфа. \ _\квадрат\]

Если относительное расстояние между любыми двумя частицами на теле остается одним и тем же на протяжении всего движения, то тело называется жестким . Такое тело сохраняет свою форму и размеры независимо от действующих на него сил.

Твердое тело, вращающееся вокруг неподвижной оси под действием нескольких сил и моментов

Если твердое тело вращается вокруг неподвижной оси и на него действуют многочисленные силы, изменяющие его угловую скорость, то можно считать, что тело состоит из множества небольших точечных масс, прикрепленных к концам безмассовых стержней и вращающихся вокруг та самая ось. Поскольку тело твердое, все частицы совершают круговое движение вместе, и угловое ускорение для всех частиц одинаково.
Применение вращательной формы второго закона Ньютона для отдельных частиц,

\[{\tau _1} = {I_1}\alpha ,\,{\tau _2} = {I_2}\alpha ,\ldots, {\tau _n} = {I_n}\alpha. \]

Добавление все эти уравнения,

\[\begin{align} {\ tau _1} + {\ tau _2} + \ cdots + {\ tau _n} &= ({I_1} + {I_2} +\ cdots + {I_n}) \ alpha \\\\ {\tau _\text{net}} &= {I_\text{твердое тело}}\alpha. \end{выравнивание}\]

Что быстрее катится с горы, полый цилиндр или сплошной цилиндр? Считайте, что они имеют одинаковую массу и радиус.

---

Если два объекта имеют одинаковый размер и массу, то внешние крутящие моменты будут одинаковыми. Полый объект имеет больший момент инерции, поскольку масса рассеивается от оси. Так как \(\tau = I\alpha\), то при заданном крутящем моменте его угловое ускорение будет меньше. Это остается верным, даже если объекты имеют разные массы. Это связано с тем, что масса исключается из уравнения: крутящий момент из-за силы тяжести пропорционален массе, как и момент инерции.

Стержень массой

M и длиной L , шарнирно закрепленный на одном конце без трения и удерживаемый горизонтально, внезапно высвобождается под действием силы тяжести. Найдите угловое ускорение стержня сразу после отпускания.

Стержень, шарнирно закрепленный на левом конце, освобождается под действием силы тяжести.

---

Чтобы проанализировать движение стержня сразу после его отпускания, сначала нарисуйте диаграмму его свободного тела. На диаграмме свободного тела на стержень действуют две силы:

\(\quad \text{1) } Mg\), гравитационная сила, действующая в центре тяжести стержня
\(\quad \text{2) } {F_\text{шарнир}}\), сила к шарниру на стержне.

В точке шарнира чистый крутящий момент \({\tau _\text{net}}\) равен векторной сумме крутящего момента из-за силы шарнира и силы тяжести.

Крутящий момент из-за усилия шарнира относительно шарнира равен нулю, так как усилие шарнира проходит через шарнир. Крутящий момент из-за силы тяжести вокруг шарнира равен \(\overrightarrow \tau = \overrightarrow r \times \overrightarrow F \): \[{\tau _{Mg/o}} = Mg\frac{L}{2}.