Методическая разработка по учебной дисциплине «Математика». ” Дифференциальное исчисление. Функции. Предел функции”. | Методическая разработка на тему:
ОБЛАСТНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
НИЖНЕУДИНСКОЕ МЕДИЦИНСКОЕ УЧИЛИЩЕ
Цикловая методическая комиссия
гуманитарных, социально-экономических и общих естественнонаучных дисциплин
Специальность 060101.52 Лечебное дело
Методическая разработка
по учебной дисциплине
«Математика»
Тема 1.1.1. Дифференциальное исчисление. Функции. Предел функции.
для преподавателя
Составила: Быкова Н.Г.
Нижнеудинск, 2013 г.
Рассмотрено и одобрено на заседании ЦМК ГСЭОЕНД Протокол № ____ от «____» __________ 2013 г. Председатель __________ /Быкова Н.Г./ | Составлена в соответствии с ФГОС ОПОП СПО углубленной подготовки по специальности 060101. Заместитель директора по УВР: ___________ Заремба Е.В. |
Содержание методической разработки:
стр | ||
1 | Актуальность темы | 4 |
2 | Выписка из приказа об утверждении и введении в действие федерального государственного образовательного стандарта среднего профессионального образования по специальности 060101.52 Лечебное дело. Требования к результатам освоения основной профессиональной образовательной программы «математика» | 5 |
3 | Требования к результатам освоения темы «Дифференциальное исчисление. | 7 |
4 | Методическая разработка теоретического занятия № 1 (для преподавателя) | 8 |
5 | Конспект лекционного занятия «Дифференциальное исчисление. Функции. Предел функции». | 10 |
Актуальность темы
Дифференциальное исчисление это раздел математики, в котором изучаются производные и дифференциалы функций и их применения к исследованию функций. Дифференциальное исчисление в самостоятельную математическую дисциплину связано с именами И.Ньютона и Г. Лейбница (вторая половина 17 в.). Они сформулировали основные положения дифференциальное исчисление и чётко указали на взаимно обратный характер операций дифференцирования и интегрирования. С этого времени дифференциальное исчисление развивается в тесной связи с интегральным исчислением, вместе с которым оно составляет основную часть математического анализа (или анализа бесконечно малых). Создание дифференциального и интегрального исчислений открыло новую эпоху в развитии математики. Оно повлекло за собой появление ряда математических дисциплин: теории рядов, теории дифференциальных уравнений, дифференциальной геометрии и вариационного исчисления. Методы математического анализа нашли применение во всех разделах математики. Неизмеримо расширилась область приложений математики к вопросам естествознания и техники. «Лишь дифференциальное исчисление дает естествознанию возможность изображать математически не только состояния, но и процессы, а именно движение» (Энгельс Ф.)
Создание дифференциального и интегрального исчислений открыло новую эпоху в развитии математики. Оно повлекло за собой появление ряда математических дисциплин: теории рядов, теории дифференциальных уравнений, дифференциальной геометрии и вариационного исчисления. Методы математического анализа нашли применение во всех разделах математики. Неизмеримо расширилась область приложений математики к вопросам естествознания и техники. «Лишь дифференциальное исчисление дает естествознанию возможность изображать математически не только состояния, но и процессы, а именно движение» (Энгельс Ф.)
Дифференциальное исчисление даёт аппарат для исследования функций, поведение которых в достаточно малой окрестности каждой точки близко к поведению линейной функции или многочлена.
В области медицины исчисление можно применить для нахождения оптимального угла ветвления кровеносных сосудов, максимизирующего поток. Зная закон затухания применительно к выводу какого-либо препарата из тела, исчисление используется для оценки уровня дозирования этих препаратов. Методической целью создания данной методической разработки является оказание помощи преподавателю в повышении эффективности проведения занятия.
Методической целью создания данной методической разработки является оказание помощи преподавателю в повышении эффективности проведения занятия.
Выписка из приказа № 472
от «12» ноября 2009 г.
ОБ УТВЕРЖДЕНИИ И ВВЕДЕНИИ В ДЕЙСТВИЕ
ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО СТАНДАРТА
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ПО СПЕЦИАЛЬНОСТИ 060101 ЛЕЧЕБНОЕ ДЕЛО
ТРЕБОВАНИЯ К РЕЗУЛЬТАТАМ ОСВОЕНИЯ ОСНОВНОЙ
ПРОФЕССИОНАЛЬНОЙ ОБРАЗОВАТЕЛЬНОЙ ПРОГРАММЫ Математика
Общие компетенции
5.1. Фельдшер должен обладать общими компетенциями, включающими в себя способность (по углубленной подготовке):
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения возложенных на него профессиональных задач, а также для своего профессионального и личностного развития.
ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.
ОК 12. Организовывать рабочее место с соблюдением требований охраны труда, производственной санитарии, инфекционной и противопожарной безопасности.
ОК 14. Исполнять воинскую обязанность, в том числе с применением полученных профессиональных знаний (для юношей).
Профессиональные компетенции, соответствующие основным видам профессиональной деятельности (по углубленной подготовке):
5.2.1. Диагностическая деятельность.
ПК 1.1. Планировать обследование пациентов различных возрастных групп.
ПК 1.2. Проводить диагностические исследования.
ПК 1.3. Проводить диагностику острых и хронических заболеваний.
ПК 1.4. Проводить диагностику беременности.
ПК 1. 5. Проводить диагностику комплексного состояния здоровья ребёнка.
5. Проводить диагностику комплексного состояния здоровья ребёнка.
ПК 1.7. Оформлять медицинскую документацию.
5.2.2. Лечебная деятельность.
ПК 2.1. Определять программу лечения пациентов различных возрастных групп.
ПК 2.2. Определять тактику ведения пациента.
ПК 2.3. Выполнять лечебные вмешательства.
ПК 2.4. Проводить контроль эффективности лечения.
ПК 2.5. Осуществлять контроль состояния пациента.
ПК 2.8. Оформлять медицинскую документацию.
5.2.3. Неотложная медицинская помощь на догоспитальном этапе.
ПК 3.1. Проводить диагностику неотложных состояний.
ПК 3.2. Определять тактику ведения пациента.
ПК 3.3. Выполнять лечебные вмешательства по оказанию медицинской помощи на догоспитальном этапе.
ПК 3.4. Проводить контроль эффективности проводимых мероприятий.
ПК 3.5. Осуществлять контроль состояния пациента.
ПК 3.7. Оформлять медицинскую документацию.
5.2.4. Профилактическая деятельность.
ПК 4.1. Организовывать диспансеризацию населения и участвовать в ее проведении.
ПК 4.2. Проводить санитарно-противоэпидемические мероприятия на закрепленном участке.
ПК 4.3. Проводить санитарно-гигиеническое просвещение населения.
ПК 4.4. Проводить диагностику групп здоровья.
ПК 4.5. Проводить иммунопрофилактику.
ПК 4.6. Проводить мероприятия по сохранению и укреплению здоровья различных возрастных групп населения.
ПК 4.9. Оформлять медицинскую документацию.
5.2.6. Организационно-аналитическая деятельность.
ПК 6.1. Рационально организовывать деятельность персонала с соблюдением психологических и этических аспектов работы в команде.
ПК 6.2. Планировать свою деятельность на ФАПе, в здравпункте промышленных предприятий, детских дошкольных учреждениях, центрах, общей врачебной (семейной) практики и анализировать ее эффективность.
ПК 6.3. Вести медицинскую документацию.
ПК 6.4. Организовывать и контролировать выполнение требований противопожарной безопасности, техники безопасности и охраны труда на ФАПе, в здравпункте промышленных предприятий, детских дошкольных учреждениях, центрах офисе общей врачебной (семейной) практики.
В результате изучения обязательной части цикла обучающийся должен:
уметь:
решать прикладные задачи в области профессиональной деятельности;
знать:
значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы;
основные математические методы решения прикладных задач в области профессиональной деятельности;
основные понятия и методы теории вероятностей и математической статистики;
основы интегрального и дифференциального исчисления
Требования к результатам освоения темы «Дифференциальное исчисление. Функции. Предел функции»
В результате изучения темы «Дифференциальное исчисление. Функции. Предел функции»
Обучающийся должен уметь:
− вычислять предел функции;
− исследовать функцию на непрерывность.
.
Обучающийся должен знать:
− определение функции, аргумента, графика функции, области определения функции, области изменения функции, сложной функции;
− определение предела функции;
− определение непрерывности функции, точки разрыва функции
Содержание:
Предел функции. Непрерывность функции. Точки разрыва функции.
Непрерывность функции. Точки разрыва функции.
Методическая разработка теоретического занятия № 1
«Дифференциальное исчисление. Функции. Предел функции»
УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА ЗАНЯТИЯ
ПРЕДМЕТ: математика
ТЕМА ЗАНЯТИЯ: «Дифференциальное исчисление. Функции. Предел функции»
ВРЕМЯ: 90 минут
ВИД ЗАНЯТИЯ: теоретическое занятие. Урок первичного предъявления новых знаний
ЦЕЛИ ЗАНЯТИЯ:
Образовательная: Формирование представлений о функции, аргумента, графика функции, области определения функции, области изменения функции, сложной функции; Формирование представлений о пределе функции, непрерывности функции, точках разрыва функции; научить вычислять пределы функций, исследовать функцию на непрерывность.
Воспитательная: способствовать воспитанию поведения, трудолюбия, товарищества, взаимопомощи, воспитывать адаптивность к современным условиям обучения
Развивающая: Развивать математические способности, логическое мышление, сообразительность, наглядно-образной памяти, математической речи обучащихся.
ОБЕСПЕЧЕНИЕ ЗАНЯТИЯ:
РАЗДАТОЧНЫЙ МАТЕРИАЛ: опорный конспект лекции
УЧЕБНЫЕ МЕСТА: аудитория медицинского училища
ЛИТЕРАТУРА:
1.Филимонова Е.В. Математика: Учебное пособие для средних специальных учебных заведений. / Е.В. Филимонова. – 2-е изд., доп. и перераб. – Ростов-на- Дону.: Феникс, 2008.
2. Михеев В.С., Стяжкина О.В., Шведова О.М. Математика: Учебное пособие для среднего профессионального образования. / В.С.Михеев. – Ростов-на-Дону.: Феникс, 2009.
3. Омельченко В.П., Демидова АА. Математика: компьютерные технологии в медицине. – Ростов-на-Дону,»Феникс», 2010. – 588с
Дополнительные источники:
1. Богомолов Н. В. Практические занятия по математике: Учебное пособие для средних учебных заведений. / Н.В. Богомолов. – 7-е изд. М.: Высшая школа, 2004.- 495 с.
Ход занятия:
№ | Основные этапы занятия | Методические указания | Время |
1 | Организационная часть | Отметка отсутствующих. | 2 минуты |
2 | Мотивация учебной деятельности | Сообщение темы, целей данного занятия. Преподаватель мотивирует обучающихся для изучения темы. Говорит о роли Математики и дифференциального исчисления в профессиональной деятельности. Далее обучающиеся фиксируют план занятия. | 5минут |
3 | Изучение нового материала. При изложении нового материала используются словесные методы в сочетании с использованием классной доски, плакатов, где зафиксированы основные понятия темы и на которые преподаватель время от времени акцентирует внимание обучающихся. | Преподаватель излагает новый материал, руководствуясь планом: План лекции: План: 1. 1.1. Понятие функции. Способы задания функции. 1.2. Специальные классы функций. 2. Теория пределов. 2.1. Понятие предела в данной точке. 2.2. Понятие бесконечно малой величины. 2.3. Основные теоремы о пределах. 2.4. Некоторые приемы вычисления пределов функций. 3. Непрерывность функции. Точки разрыва функции. План из опорных конспектов записывается обучающимися в тетрадь. Изучение нового материала проводится в сочетании словесных и наглядных методов. Каждый вопрос плана сопровождается выводом. Обучающиеся по ходу рассказа преподавателя конспектируют основные моменты (конспект лекционного занятия прилагается). Весь материал излагается по заданному плану, конспектируют основные моменты темы, используется опорный конспект лекции. Обеспечивая вовлеченность обучающихся в изучение темы, преподаватель по ходу изложения материала предлагает выполнять задания по нахождению производной, дифференциала функции, производить приближенные вычисления. | 72 минуты |
4 | Закрепление материала. | Закрепление материала проводится в форме опроса | 7 минут |
6 | Домашнее задание | К следующему занятию необходимо выполнить задания, приведенные в конце лекции. | 2 минуты |
5 | Подведение итогов. | Преподаватель совместно со обучающийся формулирует вывод. | 2 минуты |
Конспект лекции «Дифференциальное исчисление. Функции. Предел функции».
План лекции:
1. Понятие функции.
1.1. Понятие функции. Способы задания функции.
Способы задания функции.
1.2. Специальные классы функций.
2. Теория пределов.
2.1. Понятие предела в данной точке.
2.2. Понятие бесконечно малой величины.
2.3. Основные теоремы о пределах.
2.4. Некоторые приемы вычисления пределов функций.
3. Непрерывность функции. Точки разрыва функции.
1. Понятие функции.
1.1. Понятие функции. Способы задания функции.
Человеку, изучающему различные явления и процессы, приходится иметь дело с разнообразными величинами (длина, скорость, вес, температура…). Для каждой величины выбрана своя единица измерения, в результате сравнения некоторой величины с ее числовой мерой мы получаем число или числовое значение данной величины. В результате измерения физических величин (время, площадь, объем, масса, скорость и т.д.) определяются их числовые значения. Математика занимается величинами, отвлекаясь от их конкретного содержания. В дальнейшем, говоря о величинах, мы будем иметь в виду их числовые значения. В различных явлениях некоторые величины изменяются, а другие сохраняют свое числовое значение. Например, при равномерном движении точки время и расстояние меняются, а скорость остается постоянной.
В различных явлениях некоторые величины изменяются, а другие сохраняют свое числовое значение. Например, при равномерном движении точки время и расстояние меняются, а скорость остается постоянной.
Например. – скорость, t – время, т – масса, S – расстояние.
Величины делятся на постоянные и переменные.
Определение 1. Величины, значения которых с течением изучаемого процесса не изменяются, называются постоянными величинами.
Определение 2. Величины, значения которых с течением изучаемого процесса изменяются, называются переменными величинами.
Например. 1) При движении масса некоторого тела остается постоянной, а расстояние, пройденное телом, будет переменной величиной; 2) При вычислении длины окружности значение числа – переменная величина, а величины l и R –переменные.
Определение 3. Множество значений, которое может принимать переменная величина, называется областью изменения величины (областью определения).
Все явления или процессы в окружающем мире находятся в постоянном изменении и развитии. При этом изменения различных величин протекают в определенной зависимости.
При этом изменения различных величин протекают в определенной зависимости.
Если две величины связаны собой так, что каждому значению одной из них ставится в соответствие значение другой, то говорят, что величины находятся в функциональной зависимости.
Согласно теоретико-множественному подходу к трактовке понятия «функция», под функцией у = f (х) на множестве D понимают правило (закон) соответствия f, относящего каждому действительному числу (х) из некоторого множества D, единственное действительное число (у) из некоторого множества Е. При этом х называется независимой переменной или аргументом, а у –зависимой переменной или функцией.
Определение 4. Множество значений аргумента х называется областью определения функции (Df).
Определение 5. Множество значений функции называется областью значений функции (Еf)
Способы задания функции. Существуют 4 способа задания функции:
- аналитический (формулой)
- Графический (графиком функции y = f (x), заданной в некоторой области Х, называется множество точек х и у, координаты которых связаны соответствием y = f (x), при этом х может принимать любые значения их области Х)
- таблица (чаще используется при экспериментах)
- словесный или описание.

1.2. Специальные классы функций.
Специальные классы функций:
1. Обратная функция.
Функцией, обратной функции у = f (х) называется такое соответствие g между элементами множеств Е и D, которое каждому элементу у из множества Е ставит в соответствие именно тот элемент х из множества D, для которого f(х )= у.
Аргументом для обратной функции служит переменная у, а функцией – х, поэтому саму функцию принято обозначать х = g(у).
Область определения обратной функции – это область значения прямой функции.
Чтобы найти обратную функцию, нужно решить уравнение у = f(х) относительно . Если оно имеет более чем один корень, то функции обратной к не существует.
Пример. Найти для функций у = 2х +3, у = х3, у = 3 – х3 обратную функцию.
Решение:
Нахождение обратной функции:
2х +3 = у у = х3 у = 3 – х2
х = х = х = обратной функции не существует
2. Монотонная функция.
Монотонная функция.
3. Ограниченная функция.
Если для всех х найдется такое М > 0, при котором выполняется ≤ М, то функция называется ограниченной.
Если для всех х найдется такое М > 0, при котором выполняется ≥ М, то функция называется неограниченной.
4. Четная и нечетная функция.
Функция называется четной, если выполняется следующее равенство:
f (– x) = f(x).
Функция называется нечетной, если выполняется следующее равенство:
f (– x) = – f(x).
5. Периодическая функция.
Функция называется периодической в области определения, если справедливо равенство: f ( x±Т) = f(x), если Т > 0.
2. Теория пределов.
2.1. Понятие предела в данной точке.
Понятие предела позволяет определить характер поведения функции y = f (x) при заданном изменении аргумента.
Пусть функция y = f (x) определена в некоторой окрестности точки х = х0, за исключением быть может самой точки х0.
Определение 1. Число А называется пределом функции f (x) в точке х0, если для любого числа ε >0 найдется такое положительное число δ, что для любого х ≠ х0, удовлетворяющего неравенству , выполняется соотношение .
Обозначение: .
Геометрический смысл. (устно)
Существование данного предела означает, что каково бы ни было ε>0, найдется такое число δ, что для всех х, заключенных между х0 + δ и х0 – δ (кроме, быть может, самой точки х0), график функции y = f (x) лежит в полосе, ограниченной прямыми у = А + ε и у = А – ε.
Таким образом, ПРЕДЕЛ – это число, к которому стремится функция, когда значения аргумента стремятся к х0.
2.2. Понятие бесконечно малой величины.
В природе существует много переменных величин, значения которых в процессе своего изменения неограниченно приближаются к нулю. Такие величины называются бесконечно малыми.
Переменная величина х0 называется бесконечно малой, если она в процессе своего изменения становится и затем остается по абсолютной величине меньше любого, наперед заданного, сколько угодно малого положительного числа, т. е. х0
е. х0
Примеры бесконечно малых величин: масса тающей в воде льдины, скорость перемещающегося человека в движущемся автобусе и т.д.
2.3. Основные теоремы о пределах.
Рассмотрим некоторые теоремы о пределах, которые используются для нахождения пределов функций:
Теорема 1. Предел постоянной равен самой постоянной.
Теорема 2. Предел алгебраической суммы конечного числа функций равен сумме пределов этих функций.
Теорема 3. Предел произведения конечного числа функций равен произведению пределов этих функций.
Следствие 1. Если функция имеет предел при х →х0, то
, где п – натуральное число
Следствие 2. Постоянный множитель можно выносить за знак предела
Теорема 4. Предел частного функций равен частному пределов этих функций.
Теорема 5. Функция не может иметь двух пределов.
2.4. Некоторые приемы вычисления пределов. Функций.
2.4.1. Вычисление пределов функций с помощью теорем о пределах.
Например: а)= =
Самостоятельно: = – 9
б)
Самостоятельно: = –1
2.4.2. Раскрытие неопределенности .
Чтобы раскрыть неопределенность , нужно разложить числитель или знаменатель (или оба) на множители, сократить полученную дробь и найти значение полученного предела.
Например:
Самостоятельно: = –22
2.4.3. Раскрытие неопределенности .
Чтобы раскрыть неопределенность , нужно разделить числитель и знаменатель на наивысшую степень числителя и знаменателя и найти значение полученного предела.
Например:
Самостоятельно:=
3. Непрерывность функции
Представление о непрерывности функции интуитивно связано у нас с тем, что ее графиком является плавная, нигде не прерывающаяся линия. При рассмотрении графика такой функции мы видим, что близким значениям аргумента соответствуют близкие значения функции. Если независимая переменная приближается к точке , то значение функции неограниченно приближается к значению функции в точке .
Дадим строгое определение непрерывности функции.
Определение. Функция называется непрерывной в точке , если:
1) эта функция определена в некоторой окрестности точки ;
2) существует предел ; 3) этот предел равен значению функции в точке , т.е. .
Если функция непрерывна в каждой точке некоторой области (интервала, сегмента и т. п.), то она называется непрерывной в этой области. Часто приходится рассматривать непрерывность функции в точке справа и слева. Пусть функция определена в точке . Если , то говорят, что функция непрерывна в точке справа. Если , то функция непрерывна в точке слева.
Введем теперь понятие точки разрыва.
Определение. Точка называется точкой разрыва функции , если она принадлежит области определения функции или ее границе и не является точкой непрерывности.
В этом случае говорят, что при функция разрывная. Это может произойти, если в точке функция не определена, или не существует предел функции при , или, наконец, если предел функции существует, но не равен значению функции в точке : .
Точки разрыва бывают двух типов.
Определение. Точка разрыва функции называется точкой разрыва I рода, если существуют оба односторонних предела и .
Определение. Точка разрыва функции называется точкой разрыва II рода, если хотя бы один из двух пределов или стремится к бесконечности.
Пример. Рассмотрим функцию:
Даная функция имеет в точке разрыв первого рода, поскольку для нее существуют пределы при и справа и слева:
Пример. Рассмотрим следующую функцию: Данная функция имеет в точке разрыв второго рода, поскольку для нее не существуют конечные пределы при ни слева, ни справа:
На рисунке представлены графики двух функций, которые были рассмотрены в примерах и .
Домашнее задание:
- Лекционный материал
- Вычислить пределы функций:
а) Отв. 7,5
б) Отв.1
в) Отв.
- Исследовать функции на непрерывность и построить график:
- Отв. терпит разрыв 2-го рода
Решение
Найдём область определения данной функции. . Итак, имеем две точки разрыва: и . Теперь определим, каков характер разрыва функции в каждой из этих точек.
Точка является точкой бесконечного разрыва (второго рода), так как: .
Точка является точкой устранимого разрыва, так как:
.
Окончательный ответ: функция непрерывна при ; точка является точкой бесконечного разрыва; точка является точкой устранимого разрыва и .
Что такое предел? Объяснение математических понятий
Давайте поговорим о понятии, которое может сбить с толку, когда вы только начинаете изучать исчисление: ограничивает . Когда вы впервые знакомитесь с ограничениями, вы часто слышите, как ваш профессор говорит что-то вроде:
Когда вы впервые знакомитесь с ограничениями, вы часто слышите, как ваш профессор говорит что-то вроде:
” Каков предел f(x) = при приближении x к 5? »
В такой формулировке ограничения кажутся не очень естественными или интуитивными, но в сегодняшней статье я собираюсь убедить вас, что ограничения — это очень естественный способ смотреть на мир. Я также приведу несколько примеров пределов, которые мы можем решить, вообще не занимаясь «математикой»!
Начнем с примера. Представьте, что вы наблюдаете, как ваша подруга едет на своем велосипеде по гладкой поверхности , и рисуете график зависимости положения ее велосипеда от времени.
График может выглядеть примерно так:
Теперь предположим, что, продолжая рисовать график, вы на мгновение отводите взгляд от своей подруги, так что вы пропустите, где она находится через 4 секунды. Итак, на вашем графике теперь есть «дыра» в тот момент, когда вы отвели взгляд.
Даже если вы не знаете наверняка, где была ваша подруга в 4 секунды, можете ли вы угадать, где она была? Конечно, можете — она была, вероятно, на высоте 10 футов . Откуда вы знаете? Потому что прямо на до 4 секунд она была всего на футов меньше, а прямо на через секунд она была всего на после 10 футов. Если только она не была волшебным образом перенесена в тот самый момент, когда вы отвели взгляд, она должна была пройти 10 футов, чтобы график имел смысл.
Ограничения — это просто очень очевидная идея — вы можете «угадать», какие значения функция принимает в точке, основываясь на том, какое значение она принимает в соседних точках.
Когда вы видите выражение вроде:
, вы должны подумать про себя: хм, какое значение я бы предположил, что функция f(x) должна принимать, когда x примерно равно h, основываясь ТОЛЬКО на значениях, которые функция принимает БЛИЗКО к час? (стрелка в выражении просто означает «приближается»).
Если f(x) это позиция вашего друга в момент времени x, то
Я хочу отметить, что функция не обязательно должна быть линейной, чтобы вы могли устанавливать пределы. Давайте рассмотрим другой пример, когда ваша подруга снова едет на своем велосипеде, но теперь замедляет скорость, когда доезжает до знака «стоп».
График ее положения может выглядеть примерно так (это определенно не линейная функция!):
На этом графике ваш друг начинает движение очень быстро, но резко замедляется, начиная примерно с полминуты. второй. Опять же, хотя мы «отвели взгляд» на x=4 , поэтому функция f(x) не определена в этой точке, мы все еще можем оценить предел. В данном случае
Итак, мы уже видели, что пределы позволяют нам «угадывать» поведение функций в тех точках, где мы по какой-либо причине не знаем точного значения функции.
Часто нам интересно знать, какое значение примет функция при бесконечности . Мы не можем изобразить функцию до бесконечности, и мы не можем «вставить» бесконечность в формулу, чтобы напрямую оценить ответ.
Мы не можем изобразить функцию до бесконечности, и мы не можем «вставить» бесконечность в формулу, чтобы напрямую оценить ответ.
Оказывается, это еще один случай, когда нас могут выручить ограничения. Помните, что пределы — это наша лучшая «догадка» о том, как будет вести себя функция, основываясь на известных нам точках. Так, например, если мы снова посмотрим на этот последний график (воспроизведенный ниже) — когда ваш друг приближается к знаку остановки — мы можем спросить: «Если он продолжит свою текущую траекторию, где он окажется через бесконечное количество времени? ”
В этом случае было бы разумно сказать, что есть асимптота на высоте 10 футов . Идея здесь в том, что ваш друг замедляется, замедляется и, в конце концов, остановится прямо у знака остановки, расположенного примерно в 10 футах. Если функция не изменится (другими словами, она снова не начнет ездить на велосипеде), то ее положение через бесконечное количество времени будет 10 футов.
На математическом языке мы запишем это как:
Пределы бесконечности немного отличаются от пределов в конечной точке — вместо того, чтобы смотреть на соседние значения, мы вместо этого смотрим на общий тренд функции, f(x) , и попытайтесь угадать, где закончится функция по мере того, как она становится все больше и больше.
Иногда предел функции на бесконечности может быть положительной или отрицательной бесконечностью! Можете ли вы выяснить, каков предел первого (самого верхнего) графа, как ?
Также бывают случаи, когда лимит не существует (или вы можете услышать, что лимит равен undefined ). Вот пример такого случая:
Что бы вы назвали пределом, когда ? Это смотря куда смотреть! Если вы посмотрите на время меньше 4 секунд, может показаться, что она будет на высоте 8 футов, но если вы посмотрите на время больше 4 секунд, покажется, что она будет на высоте 11 футов! Когда у вас есть противоречивые предположения, вы можете сказать, что предела просто не существует.
Конечно, в большинстве реальных ситуаций этого не происходит! Чтобы предела не существовало, ваш друг должен волшебным образом переместиться с 8 футов на 11 футов именно в тот момент, когда вы не смотрели! Сила пределов в том, что они точно описывают большинство реальных функций, которые являются непрерывными и гладкими.
Да, это все, что касается концепции предела. На самом деле вам обычно не будут давать графики для оценки пределов. Вместо этого вам будут даны математические функции, из которых вы должны будете определить, какие соседние значения находятся рядом с интересующей вас точкой. Будут случаи, когда соседние значения принимают противоречивые значения, а предел не установлен. определенный. В других случаях вам придется учитывать, существуют ли в задаче асимптоты, поскольку вы решаете, к каким значениям приближаются функции в положительной или отрицательной бесконечности.
Надеюсь, теперь, когда у вас есть конкретная картина, вы сможете уверенно решать эти проблемы!
Абу — один из наших замечательных преподавателей математики в Кембридже. Если вы заинтересованы в работе с ним в Кембридже или онлайн, свяжитесь с нами сегодня!
Если вы заинтересованы в работе с ним в Кембридже или онлайн, свяжитесь с нами сегодня!
Вы ищете больше материалов по математике? Ознакомьтесь с некоторыми из наших предыдущих сообщений в блоге ниже!
Математические парадоксы демонстрируют пределы возможностей ИИ — ScienceDaily
Обычно люди довольно хорошо распознают ошибки, а системы искусственного интеллекта — нет. Согласно новому исследованию, ИИ обычно страдает от присущих ему ограничений из-за векового математического парадокса.
Как и некоторые люди, системы ИИ часто обладают степенью уверенности, намного превышающей их реальные возможности. И как самоуверенный человек, многие системы ИИ не знают, когда делают ошибки. Иногда системе ИИ даже сложнее понять, когда она совершает ошибку, чем дать правильный результат.
Исследователи из Кембриджского университета и Университета Осло говорят, что нестабильность является ахиллесовой пятой современного ИИ и что математический парадокс показывает ограничения ИИ.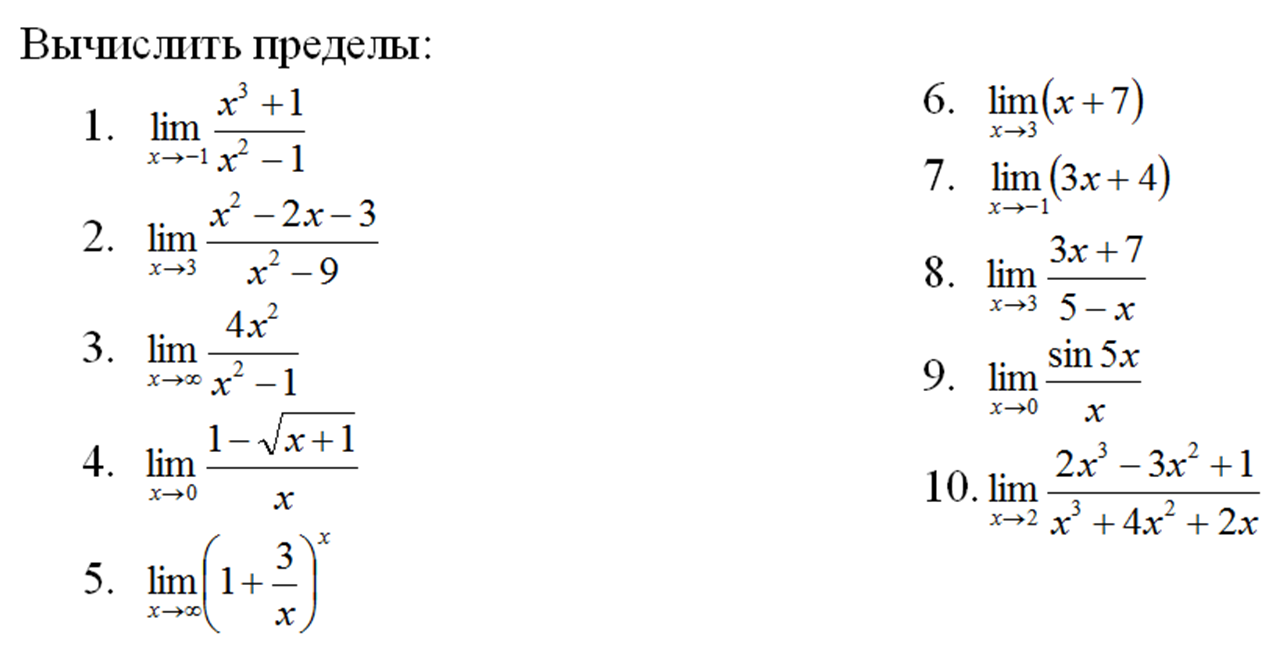 Нейронные сети, современный инструмент ИИ, примерно имитируют связи между нейронами в мозгу. Исследователи показывают, что существуют проблемы, когда существуют стабильные и точные нейронные сети, но ни один алгоритм не может создать такую сеть. Только в определенных случаях алгоритмы могут рассчитывать стабильные и точные нейронные сети.
Нейронные сети, современный инструмент ИИ, примерно имитируют связи между нейронами в мозгу. Исследователи показывают, что существуют проблемы, когда существуют стабильные и точные нейронные сети, но ни один алгоритм не может создать такую сеть. Только в определенных случаях алгоритмы могут рассчитывать стабильные и точные нейронные сети.
Исследователи предлагают классификационную теорию, описывающую, когда нейронные сети можно обучить для создания надежной системы искусственного интеллекта при определенных условиях. Их результаты представлены в Proceedings of the National Academy of Sciences .
Глубокое обучение, ведущая технология искусственного интеллекта для распознавания образов, было предметом многочисленных заголовков. Примеры включают более точную диагностику заболеваний, чем врачи, или предотвращение дорожно-транспортных происшествий с помощью автономного вождения. Однако многие системы глубокого обучения ненадежны и их легко обмануть.
«Многие системы ИИ нестабильны, и это становится серьезной проблемой, особенно потому, что они все чаще используются в областях с высоким риском, таких как диагностика заболеваний или автономные транспортные средства», — сказал соавтор профессор Андерс Хансен из Кембриджского отделения прикладной математики и науки. Теоретическая физика. «Если системы искусственного интеллекта используются в областях, где они могут нанести реальный вред, если что-то пойдет не так, доверие к этим системам должно быть главным приоритетом».
Теоретическая физика. «Если системы искусственного интеллекта используются в областях, где они могут нанести реальный вред, если что-то пойдет не так, доверие к этим системам должно быть главным приоритетом».
Парадокс, обнаруженный исследователями, восходит к двум математическим гигантам 20-го века: Алану Тьюрингу и Курту Гёделю. В начале 20 века математики пытались оправдать математику как окончательный непротиворечивый язык науки. Однако Тьюринг и Гёдель выявили парадокс, лежащий в основе математики: невозможно доказать, истинны или ложны определенные математические утверждения, а некоторые вычислительные задачи нельзя решить с помощью алгоритмов. И всякий раз, когда математическая система достаточно богата, чтобы описать арифметику, которую мы изучаем в школе, она не может доказать свою непротиворечивость.
Десятилетия спустя математик Стив Смейл предложил список из 18 нерешенных математических задач для 21 ст века. Проблема 18 th касалась пределов интеллекта как людей, так и машин.
«Парадокс, впервые обнаруженный Тьюрингом и Гёделем, теперь был перенесен в мир ИИ Смейлом и другими», — сказал соавтор доктор Мэтью Колбрук из Департамента прикладной математики и теоретической физики. «Существуют фундаментальные ограничения, присущие математике, и точно так же алгоритмы ИИ не могут существовать для определенных задач».
Исследователи говорят, что из-за этого парадокса есть случаи, когда хорошие нейронные сети могут существовать, но нельзя построить заслуживающую доверия по своей сути. «Независимо от того, насколько точны ваши данные, вы никогда не сможете получить идеальную информацию для построения необходимой нейронной сети», — сказал соавтор доктор Вегард Антун из Университета Осло.
Невозможность вычисления хорошей существующей нейронной сети также верна независимо от количества обучающих данных. Независимо от того, к какому количеству данных может получить доступ алгоритм, он не создаст желаемую сеть. «Это похоже на аргумент Тьюринга: есть вычислительные проблемы, которые невозможно решить независимо от вычислительной мощности и времени выполнения», — сказал Хансен.
Исследователи говорят, что не весь ИИ изначально ошибочен, но он надежен только в определенных областях, используя определенные методы. «Проблема связана с областями, где вам нужна гарантия, потому что многие системы ИИ — это черный ящик», — сказал Колбрук. «В некоторых ситуациях для ИИ совершенно нормально совершать ошибки, но он должен быть честным в этом. И это не то, что мы наблюдаем для многих систем — нет никакого способа узнать, когда они более или менее уверены в себе. о решении».
«В настоящее время системам ИИ иногда приходится строить догадки, — сказал Хансен. надоело не получать желаемое,и попробуете другой метод.Важно понимать ограничения разных подходов.Мы находимся на этапе,когда практические успехи ИИ намного опережают теорию и понимание.Программа на понимание для преодоления этого разрыва необходимы основы вычислений ИИ».
«Когда математики 20-го века определили различные парадоксы, они не прекратили изучение математики. Им просто нужно было найти новые пути, потому что они понимали ограничения», — сказал Колбрук.

 52 «Лечебное дело» базовый уровень подготовки
52 «Лечебное дело» базовый уровень подготовки Функции. Предел функции»
Функции. Предел функции»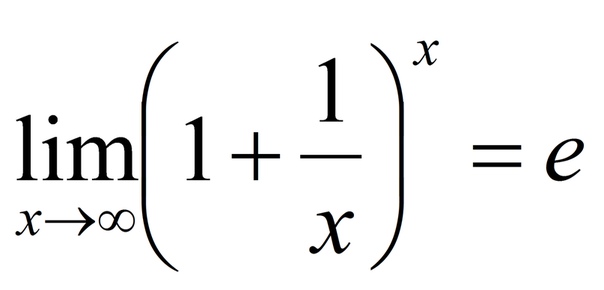 Проверка подготовленности аудитории и обучающихся к занятию.
Проверка подготовленности аудитории и обучающихся к занятию.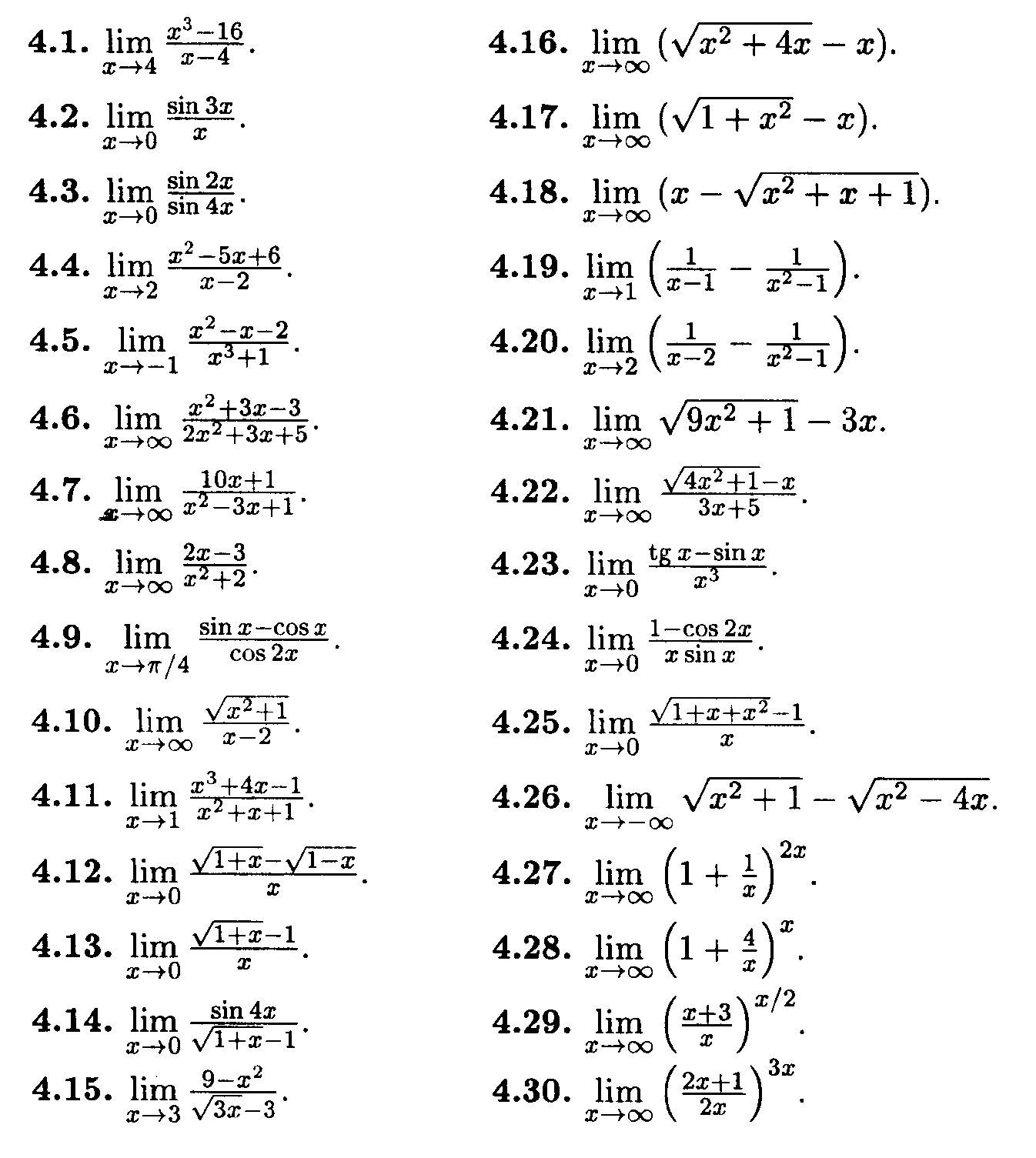 Понятие функции.
Понятие функции.
