ГДЗ по математике 3 класс учебник Моро, Волкова 1 часть
- Тип: ГДЗ, Решебник.
- Автор: Моро М. И., Волкова С. И., Бантова М. А.
- Год: 2020.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
❤️️Ответ к странице 89. Математика 3 класс учебник 1 часть. Автор: М.И. Моро.
Решебник – страница 89Готовое домашнее задание
Номер 4.
Начерти в тетради такие фигуры. Проведи в каждой фигуре один отрезок так, чтобы стало видно, что все три фигуры имеют одинаковые площади.
Ответ:
Номер 5.
Поставь в кружки знаки арифметических действий так, чтобы равенства стали верными.Если надо, используй скобки.
Ответ:
8 ∙ 4 + 2 = 34 8 : 4 : 2 = 1 8 + 4 − 2 = 10 8 ∙ 4 − 2 = 30 8 : 4 + 2 = 4 8 ∙ (4 + 2) = 48 8 + 4 + 2 = 14 8 ∙ (4 ∙ 2) = 64
Номер 6.
Вычислительная машина работает так, как показано на рисунке.
1) Какое число будет получаться на выходе из машины, если в нее ввести число: 3, 8, 2, 11, 14?
2) Какое число ввели в машину, если на выходе из машины получили число 3?
Ответ:
1) (3 + 5) ∙ 2 = 16
(8 – 5) ∙ 3 = 9
(2 + 5) ∙ 2 = 14
(11 – 5) ∙ 3 = 18
(14 − 5 ) ∙ 3 = 27
2) 3 : 3 = 1 + 5 = 6
6 > 5 – да
6 − 5 ∙ 3 = 3
Рейтинг
Выберите другую страницу
| Учебник Моро | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
2 часть
| 4 | 5 | 6 | 7 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
Стр.
89 – Математика 1 класс Учебник Моро Часть 2- Главная
- ГДЗ
- 1 класс
- Математика
- Моро учебник
- Табличное вычитание
- Страница 89. Часть 2
Вернуться к содержанию учебника
Табличное вычитание
Вопрос
1.
Реши с устным объяснением.
| 7 + 6 | 11 – 5 | 12 – 3 + 6 | 12 – 8 + 7 |
| 8 + 6 | 12 – 5 | 17 – 8 + 7 | 15 – 9 + 4 |
| 9 + 6 | 13 – 5 | 11 – 7 + 8 | 14 – 7 + 2 |
Ответ
Вопрос
2.
Ответ
Вопрос
3. Андрей и Сергей решили испытать себя в качестве вратарей. Каждый из них пробил 10 мячей в ворота противника. Андрей отбил 6 мячей, а Сергей — 8. Сколько голов забил в ворота каждый мальчик? Кто из них забил больше голов и на сколько?
Ответ
Вопрос
4.
| 18 20 | 9 11 – 2 | 1 дм 9 см |
| 16 14 | 9 10 – 0 | 1 дм 10 см |
Ответ
Вопрос
5. Сначала назови те числа, которые меньше, чем число 7, а потом — те, которые расположены в ряду между числами 10 и 6.
Ответ
Вопрос
6. Начерти ломаную из трёх звеньев: длина первого – 1 дм, второго – 6 см, а третьего – 4 см. Узнай, на сколько сантиметров первое звено длиннее второго, а второе – длиннее третьего.
Ответ
Вопрос
Найди лишнюю фигуру:
Ответ
Вопрос
«Проверочные работы», с.
50, 51.
Ответ
На нашем сайте есть решение варианта 1 проверочной работы № 2 на странице 50.
На нашем сайте есть решение варианта 2 проверочной работы № 2 на странице 51.
Вернуться к содержанию учебника
Бесконечные возможности. Как Кен Оно, AB’89, нашел жизнь и… | Журнал Чикагского университета | Журнал Чикагского университета
Кен Оно. (Фотография Брайана Мельца, предоставлена Университетом Эмори)Автор: Хелен Грегг, AB’09
У него были идеи, которые изменят математику, но никто не мог их прочитать. Итак, в 1911 году Шриниваса Рамануджан, дважды бросивший колледж, работавший клерком на юге Индии, начал отправлять свои работы в местные математические журналы и, когда они оставались незамеченными, писать письма математикам за границу. Он приложил страницы своих новаторских теорем и закономерностей, которые он нашел в числах; никаких доказательств, только всплески математической проницательности.
В 1913 году он наконец получил ответ от кембриджского математика Г. Х. Харди. Известный английский теоретик чисел увидел великолепие работы Рамануджана и стал его наставником и защитником, представив Рамануджана в Кембридже, а его работу — широкой аудитории.
Шриниваса Рамануджан (в центре) с коллегами, включая Годфри Гарольда Харди (крайний справа), в Тринити-колледже Кембриджского университета. (Общественное достояние)«Я не изобрел его — как и другие великие люди, он изобрел себя, — позже сказал Харди о Рамануджане, — но я был первым действительно компетентным человеком, у которого была возможность увидеть некоторые из его работ, и… сразу понял, какое сокровище я нашел».
Сегодня математик Кен Оно, AB’89, профессор математики Асы Григгс Кэндлер в Университете Эмори и сам известный теоретик чисел, охотится за теми, кто обладает подобным нераскрытым потенциалом. Его инициатива Spirit of Ramanujan Math Talent — это глобальный поиск одаренных молодых математиков из скромных слоев общества, который объединяет их с наставниками и академическими возможностями.
В лице Рамануджана «у нас есть человек, которого математика легко могла бы потерять, и человек, который действительно изменил то, как мы занимаемся математикой», — говорит Оно. С поиском талантов «мы хотим быть выносливыми».
Оно давно чувствует связь и родство с Рамануджаном. Будучи специалистом в области алгебраической теории чисел, Оно, как и Рамануджан, ищет новые закономерности и истины в целых числах. Он опирался на работу индийского математика в своей докторской диссертации и заложил основы своей математики отчасти благодаря подтверждению некоторых идей Рамануджана о статистических суммах.
Совсем недавно Оно с двумя сотрудниками нашел то, что он назвал «материнской жилой» математических тождеств — уравнений, которые верны для любого значения своих переменных, — используя два тождества, которые были среди тех, которые Рамануджан отправил Харди в 1919 году.13. А его доказательство 2014 года гипотезы о сумрачном самогоне, которая имеет приложения в областях от теории чисел до квантовой физики, основано на работе, которую Рамануджан яростно писал, умирая от туберкулеза в 1920 году.
Оно даже помогло воплотить в жизнь историю Рамануджана. в качестве консультанта по математике и ассоциированного продюсера биографического фильма 2015 года «Человек, который знал бесконечность ». Его энтузиазм по поводу Рамануджана на съемочной площадке был заразителен, и в прошлом году кинокомпании стали партнерами Оно, чтобы запустить инициативу Spirit of Ramanujan Math Talent Initiative.
Письмо 1984 года от вдовы Рамануджана, Джанаки Аммаль. (Изображение предоставлено Кеном Оно)В угловом офисе Оно в Эмори на стенах плакат с наградами в рамке. Но одна рама посередине, прямо над столом Оно, содержит что-то другое. Это письмо, которое вдова Рамануджана написала отцу Оно в 1984 году, свидетельствует о глубоком влиянии индийского вундеркинда не только на творчество Оно, но и на саму его личность.
Когда Оно рос, его родители часто рассказывали ему, как всего в три года он открыл бесконечность — когда он впервые пришел к выводу, что не может быть самого большого числа, поскольку всегда есть возможность прибавить единицу.
Математика была частью жизни Оно, сколько он себя помнит; некоторые из его любимых ранних воспоминаний связаны с тем, как он сидел за детским столом в домашнем офисе семьи и решал наборы задач, в то время как его отец, математик Такаси Оно, вместе с ним работал над своим следующим открытием.
Менее приятны воспоминания Оно о том, что произошло за кухонным столом, где после неудовлетворительного результата теста или другой предполагаемой неудачи он столкнулся с шквалом резкой критики со стороны Такаши и его матери Сатико: он был неряшлив, он был несовершенным, он позорил свою семью.
Оно с раннего возраста считался математическим вундеркиндом. Он был включен в известное исследование психолога Джулиана Стэнли о не по годам развитой математике, и его родители решили, что он будет математиком, как и его отец. Все его время должно было быть потрачено на учебу. Внеклассные занятия, спорт, телевидение и друзья были запрещены. Он не помнит, как его обнимали или как он слышал «Я люблю тебя».
Два старших брата Оно воспитывались так же: Момаро, одаренный музыкант, и Санта Оно, AB’84. (Санта, который в детстве не считался вундеркиндом, как его братья, столкнулся с теми же родительскими требованиями, но без ожиданий успеха — ирония судьбы, — говорит Оно, поскольку он считает Санту, ныне президента Университета Британской Колумбии, самым успешным в профессиональном плане из три.)
Оно училось в старшей школе, когда давление стало невыносимым. В качестве отдушины и вопреки желанию своих родителей он присоединился к конкурентоспособной команде по велоспорту, но этого было недостаточно. Он понял, что ему нужно выбраться из дома, и начал многомесячную кампанию, чтобы убедить родителей позволить ему бросить школу.
Его окончательный успех зависел от письма, которое прибыло весной 1984 года в конверте из рисовой бумаги из Индии. Джанаки Аммаль, пожилая вдова Рамануджана, написала письмо отцу Оно, чтобы поблагодарить его за помощь в создании статуи ее покойного мужа. Это было короткое письмо, но Оно никогда не видел, чтобы его мужественный отец был так взволнован.
Стоя в своем домашнем офисе с письмом в руке, Такаши впервые рассказал Оно о Рамануджане, чья история вдохновила Такаши как борющегося математика в послевоенной Японии. У Такаши даже был свой Харди — Андре Вейл, математик из Чикагского университета, который заметил талант Такаши на математической конференции в Токио и обеспечил ему место в Институте перспективных исследований в Принстоне, штат Нью-Джерси, в 1955 году.
Итак, во время одной из их многочисленных ссор из-за ухода из школы Оно напомнило отцу, что Рамануджан, его кумир, дважды бросал учебу в колледже. Его родители уступили, и Оно сам бросил учебу. Вскоре он сел на поезд Amtrak в Монреаль, чтобы жить с Сантой, тогда еще студентом докторантуры Университета Макгилла. Санта предоставил кушетку для сна, подработку в лаборатории кампуса и столь необходимое сочувствие. Меньше чем через год, почувствовав, что снова может дышать, Оно начал подавать документы в колледжи.
В Университете Чикаго Оно сразу же обрел свободу.
Он присоединился к Psi Upsilon и проводил больше времени на диджейских вечеринках, игре в настольный футбол и поедании жареного цыпленка Гарольда, чем на учебе. Он также снова начал участвовать в соревнованиях по велоспорту, так он познакомился со своей женой Эрикой (Андерсон) Оно, AB’90; будучи студенткой, работающей в столовой Пирса, она начала каждое субботнее утро откладывать бананы в качестве топлива для ребенка, который пришел рано на своем гоночном велосипеде.
Но в конце третьего года обучения приглашенный профессор математики, знакомый Такаши, сказал Оно, что его работа некачественная и что он никогда не станет профессиональным математиком. Уязвленный и отказывающийся признать правоту своих родителей, Оно с новой силой взялся за математику.
На последнем курсе Оно привлекла внимание профессора математики и «математического пирата» Пола Салли-младшего, который был известен тем, что наставлял студентов в Гайд-парке и за его пределами.
Они начали встречаться несколько раз в неделю, чтобы поговорить о математике или просто поговорить. Их сблизил нетрадиционный путь — Салли несколько лет водил такси и преподавал в средней школе в Бостоне, прежде чем решил, что хочет заниматься математикой, — и Салли помог Оно получить место в программе докторантуры по математике в Калифорнийском университете в Лос-Анджелесе.
В Калифорнийском университете в Лос-Анджелесе Оно все еще слышал голоса своих родителей, говорящих ему, что он недостаточно хорош, что он потерпит неудачу. Он чуть не провалил свою первую попытку на квалификационном экзамене в выбранной им области, абстрактной алгебре, и дрейфовал, пока не пошел на занятия к Бэзилу Гордону. Впечатленный, когда Оно предложил альтернативное доказательство в классе, Гордон пригласил его поговорить в рабочее время и вскоре взял Оно в качестве своего последнего аспиранта.
Для своей диссертации Гордон предложил Оно использовать модульные формы, класс функций, основанный на тождествах Рамануджана.
Это был первый раз, когда Оно понял, что работа Рамануджана имеет современное значение. В 1991, когда Оно работал над докторской диссертацией, биограф Роберт Канигель опубликовал книгу «Человек, познавший бесконечность: жизнь гения Рамануджана » (Сыновья Чарльза Скрибнера). Оно быстро купило книгу и прочитало ее от корки до корки.
Оно и Гордон по субботам проводили долгие и напряженные рабочие сессии, делая перерывы, чтобы прогуляться по пляжу или поговорить о литературе. Гордон мог цитировать длинные отрывки по памяти; Оно живо помнит, как он декламировал начало Моби Дика . «Я был загипнотизирован его способностью делать математику красивой, проводя аналогии с классическим искусством, литературой и музыкой», — написал Оно после смерти Гордона в 2012 году. Гордон рассматривал математику как форму искусства, способ понять и принять мир. вокруг него. От него Оно впервые научилось по-настоящему, как он сам говорит, «заниматься математикой».
Кен Оно, AB’89, и Эрика (Андерсон) Оно, AB’90.
(Фото предоставлено Кеном Оно) Приближаясь к докторской диссертации, Оно поехал в родной город Эрики, Миссула, штат Монтана, чтобы выступить на математической конференции. Его доклад касался представлений Галуа, части современной теории чисел, связанной с модулярными формами. Но Оно, желая произвести впечатление на свою аудиторию, совершил ошибку, подготовив лекции, которые были слишком техническими. Аудитория не смогла уследить, и один профессор впоследствии отругал его за трату времени. Взаимные обвинения его родителей вернулись. Оно чувствовал, что потерпел неудачу в абстрактной теории чисел, области, в которой, по его мнению, он добился реальных успехов, перед математиками, которыми он глубоко восхищался, и в городе, где молва могла дойти до семьи его новой жены. В последний день конференции Оно ехал по дождливому шоссе Монтаны, опустошенный и одинокий, если не считать критических голосов, звучащих в его голове. В поле зрения попал встречный грузовик, и, увидев выход, он дернул руль и вывел машину за осевую линию.
Оно не помнит, как нашел другую сторону дороги и остановил машину, только то, что сидел, трясясь от ужаса. «Я не мог поверить в то, что почти сделал», — писал он позже. «У меня никогда раньше не было суицидальных мыслей. … Это был импульсивный поступок, который я никогда полностью не пойму».
Почти 20 лет он никому не рассказывал, что произошло на этой трассе, но на следующей неделе ему пришлось рассказать Гордону, как прошла конференция. Ответ воодушевил его. Гордон сказал Оно, что не потерпел неудачу и не разочаровал его. Математика, напомнил он Оно, заключается в том, чтобы рисковать, путешествовать в неизвестное и иногда перебарщивать. Слишком глубокое погружение в свою тему было признаком превращения в математика. Это было именно то, что Оно должно было услышать.
В 1997 году на математической конференции, посвященной 65-летию Гордона, банкетная речь Оно началась просто и без преувеличений: «Я благодарю Бэзила Гордона за спасение моей жизни».
Оно успешно защитил диссертацию о представлениях Галуа в 1993 году.
Он получил должности в Университете Джорджии, а затем в Университете Иллинойса в Урбана-Шампейн и стал соавтором того, что он называет «полуважной статьей по теории представлений». Несмотря на эти успехи, в его голове все еще звучали голоса неодобрения. Теперь он называет это синдромом самозванца — стойкой убежденностью в том, что успех был незаслуженным, что это только вопрос времени, когда кто-то будет разоблачен как мошенник. «Когда я только начинал, я был благодарен, что кто-нибудь придет послушать мою лекцию», — говорит он. Он боялся, что в какой-то момент другие математики подтвердят критику его родителей.
Эти голоса, наконец, начали стихать, когда Оно получил назначение в Институт перспективных исследований в Принстоне, эхо достижения его отца четыре десятилетия назад. Это был первый раз, когда Оно было признано исключительно за его собственные идеи. «Эти ребята действительно слышали обо мне и знали некоторые из моих теорем, — говорит он. «Это был первый раз, когда я действительно осознал, что все остальное не имеет значения, если ты много работаешь, у тебя есть вера и немного удачи».
Позже, прорыв в функциях распределения, когда он был доцентом в Университете штата Пенсильвания, привел к международному признанию и стипендиям от Фонда Альфреда П. Слоана и Фонда Дэвида и Люсиль Паккард (см. »). В 1999 году Оно получило Президентскую премию за раннюю карьеру ученых и инженеров от президента Билла Клинтона. Его родители присутствовали на церемонии в Белом доме, после чего Такаши вручил Оно судьбоносное письмо от вдовы Рамануджана. Теперь, по его словам, он считает Оно законным владельцем письма. Он добавил: «Я так горжусь тобой».
Отношения Оно с родителями постепенно улучшаются. Его профессиональные успехи, в том числе назначения в Университете Висконсин-Мэдисон, а затем в Эмори, положили конец их критике, освободив место для новых способов связи. Его родители теперь посылают открытки на дни рождения и праздники, события, которые не отмечались, когда Оно росло. Оно, со своей стороны, лучше понял, почему они оказывали такое давление на своих детей.
В своих мемуарах он размышляет о традиционных японских представлениях о воспитании детей, которые его родители привезли с собой в Штаты, и о том, как расизм, с которым семья столкнулась в послевоенной Америке, еще больше сосредоточил их внимание на тяжелой работе и достижениях.
В 2014 году Такаши и Сатико отправились в Атланту на выпускной старшей школы дочери Оно, Аспен. Она и ее младший брат Сейдж сейчас учатся в Эмори. Они талантливые ученики, но Оно говорит о фигурном катании Аспена и плавании Сейджа (недавно он был назван лучшим пловцом-новичком UAA среди мужчин и национальным чемпионом NCAA, с гордостью говорит Оно). Оно воспитал их так, чтобы они следовали своим страстям и любили себя так же сильно, как любит их он, включая их несовершенства. По словам Оно, средний балл Аспен близок к идеальному 4,0, «поэтому я говорю ей, иди, получи четверку и узнай, что все в порядке».
В 2016 году Оно опубликовал мемуары « Мои поиски Рамануджана: как я научился считать » (Спрингер), в которых подробно описал свой извилистый жизненный путь и то, как он привел к индийскому математику.
(Книга посвящена его наставникам.) «Ему было полезно, — говорит его жена Эрика, — распаковать свой умственный туалет». Но Оно также написал это, чтобы помочь тем, кто, возможно, борется так же, как и он.
Оно любит рассказывать своим первокурсникам в Эмори, что за первые три года обучения в колледже у него почти не было пятерок по математике — рисуя смех, он добавляет: «Но поверьте мне, я вполне способен преподавать в этом классе».
«Они должны это услышать», — говорит Оно, особенно от такого успешного человека, как он. Он часто встречает учеников, которые, как он может сказать, находятся под сильным давлением родителей, чтобы получить высшие оценки, а затем выбрать профессию, которую предпочитает их семья. «На каждом уроке, который я провожу, мне приходится разговаривать с четырьмя или пятью детьми, которые не уверены в том, что они должны делать или кем должны быть», — говорит он. «И это шокирует, как часто это связано с «Ну, мои родители думают, что я должен это сделать».
Жизнь вне колледжа даже входит в программу курсов Оно. В течение многих лет последним вопросом на каждом выпускном экзамене, который он дает, был: «Что вы собираетесь сделать, чтобы сделать мир лучше?» Он настолько известен этим, что многие студенты заранее записывают и распечатывают свои ответы и приносят их, чтобы прикрепить к тесту.
В течение нескольких лет Оно обращался к родителям первокурсников во время семейных выходных Эмори, в которых рассказывал немного истории своей жизни. Прошлой осенью этот разговор явно опирался на его мемуары. (Санта также использовал историю своей жизни, чтобы помочь своим ученикам; в 2016 году он публично рассказал, что боролся с депрессией в молодости и продолжал рассказывать о своем собственном опыте, будучи президентом UBC, чтобы избавиться от стигматизации психических заболеваний на его кампусе и побуждать студентов обращаться за помощью, когда это необходимо.
)
В настоящее время Оно имеет семерых аспирантов, которые делят рабочее место по коридору от его офиса. Он часто бывает там, чтобы проверить, а также спросить одну о ее подготовке к марафону или серьезно сказать другой, что ей действительно следует подумать о Гавайях для своего медового месяца.
Но перед классной доской, решая задачу с одним из них, он спокоен и сосредоточен, формирует формулы с помощью быстрых вопросов и быстрой поддержки. Преданность Оно работе и идеям своих учеников эффективна и запоминается. «Когда вы работаете над чем-то изо дня в день, легко упустить из виду общую картину и волнение, и он может дать вам это», — сказал его бывший ученик Роберт Лемке Оливер 9.0021 Журнал Эмори
. «Я не был бы тем математиком, которым я являюсь сегодня, если бы у меня был почти любой другой советник». Оно любит «наблюдать за тем, как кто-то достигает чего-то, что, по их мнению, он никогда не сможет сделать».
Когда это случается, он с удовольствием говорит, что так им и сказал. — Никому не нравится это слышать, кроме как в этом случае. Он находит работу со студентами одновременно и радостью, и обязанностью, и чувствует, что обязан своим собственным наставникам — и Рамануджану — быть лучшим Харди, которым он может быть для следующего поколения.
В 2014 году Оно получил неожиданное электронное письмо от Мэтью Брауна, сценариста и режиссера фильма «Человек, который знал бесконечность », основанного на биографии Рамануджана Канигеля 1991 года. Команде Брауна требовалась помощь в обеспечении точности документов, которые собирались воспроизвести для биографического фильма. Впечатленный глубоким знанием Оно о работе и жизни Рамануджана, Браун пригласил Оно стать консультантом по математике в фильме.
Оно и актер Джереми Айронс, сыгравший Г. Х. Харди, на съемках фильма : Человек, который познал бесконечность . В октябре Айронс присоединился к Оно в Белом доме для показа фильма и панельной дискуссии по математическому образованию.
(Фото предоставлено Кеном Оно)На съемочной площадке в Англии Оно приступило к работе, проверяя и совершенствуя всю математику, которая появляется на экране. Он присутствовал во время репетиций и съемок, чтобы по мере необходимости объяснять математические концепции и помогать ведущим актерам, Деву Пателю и Джереми Айронсу, разрабатывать жесты и использовать интонации, которые подходят как персонажам, так и математике, обсуждаемой в фильме.
Оно даже смог помочь, когда координаторы фильма, ища образец почерка Джанаки Аммаля, спросили его, знает ли он что-нибудь и где-нибудь, на чем может быть подпись жены Рамануджана.
Когда он увидел, что история Рамануджана действительно вызвала отклик у Брауна и других, работающих над фильмом, Оно был в восторге. Он и продюсеры начали мозговой штурм, чтобы помочь The Man Who Knew Infinity оказать долгосрочное влияние. «Мы думали, что этому фильму не будет Бэтмен против Супермена , но для нас это важно», — говорит Оно.
«И поэтому мы решили, что фильм должен что-то значить».
Прошлой весной Оно, Pressman Film и IFC Films запустили инициативу Spirit of Ramanujan Math Talent Initiative. Проект основан на информационно-пропагандистской работе по математике, которую Оно проводил в течение многих лет, и его цель, по его словам, состоит в том, чтобы найти и поддержать «выдающихся аутсайдеров» — молодых людей, таких как Рамануджан, которые могут внести значительный вклад в математику, но имеют мало ресурсов. или наставники.
Онлайн-викторина The Spirit of Ramanujan для мобильных устройств по математике и логике направляет тех, кто набрал наибольшее количество баллов, к приложению. Американское математическое общество, Фонд Темплтона и другие организации также помогают продвигать эту инициативу, и во время ее первого раунда было подано более 8000 заявок.
Четыре победителя получили финансовую поддержку и связи с профессиональными математиками в своих областях. Десятиклассник Кендалл Кларк из Балтимора этим летом будет изучать прикладную математику с профессорами Университета Джона Хопкинса, а 13-летний Ишвар Картик каждую неделю работает с теоретиком чисел в кампусе Texas A&M в Катаре.
Оно обнаружило последнего победителя в декабре во время поездки в Кению. После того, как Оно закончил лекцию о своей недавней работе в Университете Найроби, молодой человек встал перед 500 зрителями, чтобы предложить исправление, основанное на доказательстве Ганса Радемахера 1930-х годов. Позже Оно встретился с задавшим вопросы, Мартином Ирунгу, и обнаружил, что он не аспирант, как думал Оно, а недавний выпускник средней школы. Не имея возможности оплачивать обучение в Найробийском университете, Ирунгу проводил свободное время в кампусе, изучая математические книги из библиотеки. «Он читал материал, который читал бы аспирант второго или третьего курса в ведущей школе», — говорит Оно.
Менее чем за 48 часов Оно удалось получить Ирунгу визу для поездки в Эмори. Он провел неделю в кампусе, работая с аспирантами Оно, и вернется на лето. Ирунгу также встретился с другими математиками со всей страны, приехавшими в город на конференцию. «В итоге я познакомил его с профессорами Гарварда, Массачусетского технологического института и Беркли, — говорит Оно, — и теперь они соревнуются за него».
Оно уверено, что инициатива Spirit of Ramanujan Math Talent будет продолжать выявлять таких же одаренных учеников. «Они там», — говорит он, и он сделает все возможное, чтобы найти их.
Именно в Лондоне, на съемках фильма «Человек, который познал бесконечность» , Оно поразило озарение, которое оказалось важным шагом вперед в доказательстве гипотезы о сумрачном самогоне. Он считает, что нахождение за пределами своего офиса и участие в другом творческом процессе имело значение — и стоять лицом к лицу с Рамануджаном (которого играет Пател) тоже не было больно.
С тех пор, как он гулял по пляжу с Гордоном, Оно проделал одну из лучших своих работ за пределами величественного белого каменного Центра математики и науки Эмори, будь то простая прогулка или подготовка к триатлону (он представлял сборную США в нескольких недавних чемпионатах мира по триатлону). чемпионаты).
Он также любит работать дома на диване в медитативном состоянии, обдумывая новые модели или идеи. По словам Эрики, это может выглядеть как сонливость. К счастью, у Оно есть носки с надписью «Не будите меня, я работаю», чтобы предотвратить неправильное толкование. Удовлетворенный вид тоже часто является подарком.
Прорыв Оно в 1999 году касался номеров разделов, или того, сколькими различными способами целое число может быть представлено в виде суммы положительных целых чисел.
Например, номер раздела 4, обычно обозначаемый как p (4) , равно 5, так как существует пять способов записать 4 в виде суммы натуральных чисел: 1+1+1
Рамануджан обнаружил закономерности в этих номерах разделов.
Например, он обнаружил, что для любого значения n номер раздела p (5 n +4) всегда делится на 5. Таким образом, когда n = 5, значение p (5х5+4) или p (29) равно 4,565, которое делится на 5. То же верно для любого значения n .
Рамануджан также обнаружил, что значение p (7 n +5) всегда делится на 7, а p (11 n +6) всегда делится на 1, не делится на 1. какой номер подключен к n . Никаких других подобных выражений, использующих другое простое число в качестве коэффициента n , нет в оставленной им работе. В неопубликованной записной книжке Рамануджан написал, что ему неизвестны какие-либо другие выражения с «столь же простыми свойствами» для функций распределения.
Оно обнаружило, что загадочное утверждение Рамануджана было верным — «простых» выражений вроде тех, которые нашел Рамануджан, не существует, но есть более сложные.
Опираясь на другие недавние достижения в области нумерации разделов и с помощью компьютерной программы для обработки чисел, Оно доказал, что для всех простых чисел от 5 до бесконечности существуют выражения вида p ( an + b ) , где полученные номера разделов делятся на простое число, представленное и .
Оно отмечает, что это часто «чудовища», такие как p (48037937 n +1122838) , которое всегда делится на 17. Только для простых чисел 5, 7 и 11 значения a равны простой делитель. Вероятно, это то, что Рамануджан имел в виду под выражением с «простыми свойствами», — говорит Оно.
С тех пор Оно добилось других значительных успехов в области номеров разделов, включая разработку первой точной формулы для расчета номера раздела для любого значения 9.0021 и . В 2011 году он представил эту формулу и связанные с ней паттерны стоячей толпе на специальной трехдневной конференции в Эмори.
Примечание. Эта статья первоначально была опубликована в журнале University of Chicago Magazine Spring/17 выпуск .
Факторы числа 89 — Найдите факторизацию простых чисел/Множители числа 89то есть 1 и 89, где 89 – самый большой коэффициент. Сумма всех множителей числа 89 равна 90. Его простые множители равны 1, 89, а (1, 89) являются парными множителями.
- Коэффициенты 89: 1 и 89
- Отрицательные коэффициенты 89: -1 и -89
- Простые множители числа 89: 89
- Факторизация числа 89: 89
- Сумма коэффициентов 89: 90
| 1. | Какие факторы 89? |
| 2. | Как рассчитать коэффициенты числа 89? |
| 3. | Коэффициенты 89 с помощью простой факторизации |
4. | Коэффициенты 89 в парах |
| 5. | Часто задаваемые вопросы о факторах 89 |
Какие множители числа 89?
Множители 89 — это числа, которые при попарном умножении дают произведение, равное 89. Множители 89 — это те числа, которые точно делят его и дают остаток как 0,
- Например, 89 ÷ 89 = 1
Вы получаете 1 в частном и 0 в остатке. Это означает, что 89 делится на 89. Следовательно, множители числа 89 равны 1 и 89.
Как рассчитать множители числа 89?
Мы можем использовать различные методы для нахождения множителей числа 89, такие как разложение на простые множители и метод деления. При простой факторизации мы выражаем 89 как произведение его простых множителей, а в методе деления мы видим, на какие числа 89 делится точно, не оставляя остатка.
Следовательно, множители числа 89 равны 1 и 89.
Изучите множители с помощью иллюстраций и интерактивных примеров
- Факторы числа 86 – множители числа 86 равны 1, 2, 43, 86
- Множители 96 – Множители 96 равны 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96
- Коэффициенты 72 — множители 72 равны 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
- Коэффициенты 76 – множители 76 равны 1, 2, 4, 19, 38, 76
- Коэффициенты 75 – множители 75 равны 1, 3, 5, 15, 25, 75
- Множители 37 – Множители 37 равны 1, 37
Множители 89 с помощью простой факторизации
Когда мы используем метод деления, чтобы найти множители 89.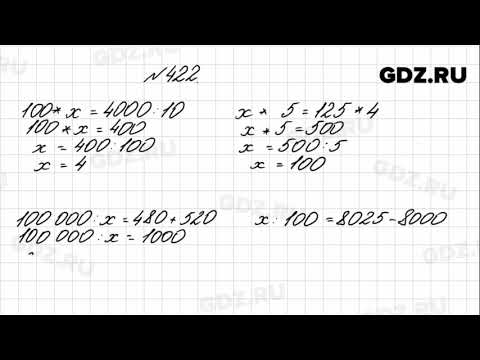
Деление показывает, что число 89 точно делится на 1 и 89.
Множители 89 могут быть представлены в виде методом деления вниз следующим образом:
Следовательно, множители 89 равны 1 и 89. Здесь 89 — простое число.
Факторы 89 в парах
- Пара чисел, которая дает 89при умножении называется парным коэффициентом 89 90 234.
- 1 × 89 и 89 × 1
- Следовательно, множители 89 в парах равны (1, 89) и (89, 1) .
- Когда мы умножаем два отрицательных числа, мы получаем положительную равнодействующую.
- Если умножить -1 на -89, то в результате получится 89, -1 × -89 = 89.
- 89 также имеет отрицательные парные множители (-1, -89)
Аналитический центр:
- Можете ли вы подумать, почему 89 — простое число?
- Подумай о числе, кратном 89.что также является коэффициентом 89
- Какими могут быть простые делители числа 89?
Важные примечания:
- Числа, которые мы умножаем, чтобы получить 89, являются делителями 89
- Факторы 89 равны 1 и 89
- Парные множители числа – это пара двух чисел, которые при умножении дают исходное число.
- Делители 89 в парах равны (1, 89) и (89, 1)
Коэффициенты 89 Решенные примеры
Пример 1: Можете ли вы определить, какое число при умножении на (-1) дает 89?
Решение:
Чтобы найти это, нам нужно разделить 89 на (-1) = 89/-1 = -89
Следовательно, – 89 при умножении на – 1 дает 89.Пример 2: Помогите Тиму найти положительные парные множители числа 89 из списка всех его множителей.
Решение:
Делители 89 – это числа, которые делят 89точно без остатка. Делители 89 равны 1 и 89.
Пары множителей – это пара двух таких чисел, которые при умножении дают 89. 90 142 Мы это знаем,
1 × 89 = 89 и 89 × 1 = 89
Следовательно, парные множители числа 89 – это (1, 89) и (89, 1).Пример 3: Сколько множителей есть для числа 89?
Решение:
Делители числа 89 равны 1, 89.
Следовательно, число 89 имеет 2 делителя.
Следовательно, число 89 имеет 2 делителя.перейти к слайдуперейти к слайдуперейти к слайду
Разбейте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о множителях 89
Что такое множители 89?
Множители числа 89 равны 1, 89, а его отрицательные множители равны -1, -89.
Какой наибольший общий делитель числа 89?а 45?
Делители числа 89 равны 1, 89, а числа 45 равны 1, 3, 5, 9, 15, 45. У чисел 89 и 45 есть только один общий делитель, равный 1. Это означает, что числа 89 и 45 взаимно просты .
Следовательно, наибольший общий делитель (НОД) чисел 89 и 45 равен 1.
Каковы общие делители чисел 89 и 11?
Поскольку делители числа 89 равны 1, 89, а делители числа 11 равны 1, 11. Следовательно, числа 89 и 11 имеют только один общий делитель, равный 1.