Математика быстрый счет в уме методика: Методика быстрого счета в уме без калькулятора

Методика “быстрого” счета

Отработка вычислительных навыков обучающихся на уроках математики с помощью приемов «быстрого» счета.

Кудинова И.К., учитель математики

МКОУ Лимановской СОШ

Панинского муниципального района

Воронежской области

«Приходилось ли тебе наблюдать, как люди с природными способностями к счёту бывают восприимчивы, можно сказать, ко всем наукам? Даже все те, кто туго соображает, если они обучаются этому и упражняются, то хотя бы они не извлекали из этого для себя никакой пользы, всё же становятся более восприимчивы, чем были раньше»

Платон

Важнейшей задачей образования является формирование универсальных учебных действий, обеспечивающих школьникам умение учиться, способность к саморазвитию и самосовершенствованию. Качество усвоения знаний определяется многообразием и характером видов универсальных действий. Формирование способности и готовности учащихся реализовывать универсальные учебные действия позволяет повысить эффективность процесса обучения. Все виды универсальных учебных действий рассматриваются в контексте содержания конкретных учебных предметов.

Важную роль в формировании универсальных учебных действий играет обучение школьников навыкам рациональных вычислений. Ни у кого не вызывает сомнения, что, развитие умения рациональных вычислений и преобразований, а также развитие навыков решения простейших задач “в уме” – важнейший элемент математической подготовки учащихся. Важность и необходимость таких упражнений доказывать не приходиться. Значение их велико в формировании вычислительных навыков, и совершенствовании знаний по нумерации, и в развитии личностных качеств ребенка. Создание определенной системы закрепления и повторения изученного материала дает учащимся возможность усвоения знаний на уровне автоматического навыка.

Знание упрощенных приемов устных вычислений остается необходимым даже при полной механизации всех наиболее трудоемких вычислительных процессов. Устные вычисления дают возможность не только быстро производить расчеты в уме, но и контролировать, оценивать, находить и исправлять ошибки. Кроме того, освоение вычислительных навыков развивает память и помогает школьникам полноценно усваивать предметы физико-математического цикла.

Очевидно, что приемы рационального счета  являются  необходимым элементом  вычислительной  культуры  в жизни каждого человека,  прежде всего силу своей практической значимости, а обучающимся она необходима практически на каждом уроке.

Вычислительная культура является фундаментом изучения математики и других учебных дисциплин, т. к. кроме того, что вычисления активизируют память, внимание, помогают рационально организовать деятельность и существенно влияют на развитие человека.

В повседневной жизни, на учебных занятиях, когда ценится каждая минута, очень важно  быстро и рационально провести устные и письменные вычисления, не допустив при этом ошибок и не используя при этом никаких дополнительных вычислительных средств.

Анализ результатов экзаменов в 9-х и 11-х классах показывает, что наибольшее количество ошибок учащиеся допускают при выполнении заданий на вычисления. Нередко даже высокомотивированные учащиеся к выходу на итоговую аттестацию утрачивают навыки устного счета. Они плохо и нерационально считают, все чаще прибегая к помощи технических средств-калькуляторов. Главная задача учителя – не только сохранить вычислительные навыки, но и научить применять нестандартные приемы устного счета, которые позволили бы значительно сократить время работы над заданием.

Рассмотрим конкретные примеры различных приемов быстрых рациональных вычислений.

РАЗЛИЧНЫЕ СПОСОБЫ СЛОЖЕНИЯ И ВЫЧИТАНИЯ

СЛОЖЕНИЕ

Основное правило для выполнения сложения в уме звучит так:

Чтобы прибавить к числу 9, прибавьте к нему 10 и отнимите 1;чтобы прибавить 8, прибавьте 10 и отнимите 2; чтобы прибавить 7, прибавьте10 и отнимите 3 и т. д. Например:

56+8=56+10-2=64;

65+9=65+10-1=74.

СЛОЖЕНИЕ В УМЕ ДВУЗНАЧНЫХ ЧИСЕЛ

Если цифра единиц в прибавляемом числе больше5, то число необходимо округлить в сторону увеличения, а затем вычесть ошибку округления из полученной суммы. Если же цифра единиц меньше, то прибавляем сначала десятки, а потом единицы. Например:

34+48=34+50-2=82;

27+31=27+30+1=58.

СЛОЖЕНИЕ ТРЕХЗНАЧНЫХ ЧИСЕЛ

Складываем слева на право, то есть сначала сотни, потом десятки, а затем единицы. Например:

359+523= 300+500+50+20+9+3=882;

456+298=400+200+50+90+6+8=754.

ВЫЧИТАНИЕ

Чтобы вычесть два числа в уме, нужно округлить вычитаемое, а затем подкорректируйте полученный ответ.

56-9=56-10+1=47;

436-87=436-100+13=349.

Умножение многозначных чисел на 9

1. Число десятков увеличим на 1 и вычтем из множимого

2. К результату приписываем дополнение цифры единиц множимого до 10

Пример:

576 · 9 = 5184 379 · 9 = 3411

576 – (57 + 1) = 576 – 58 = 518 . 379 – (37 + 1) = 341 .

4 1

Умножение на 99

1. Из числа вычитаем число его сотен, увеличенное на 1

2. Находим дополнение числа, образованного двумя последними цифрами до 100

3. Приписываем дополнение к предшествующему результату

Пример:

27 · 99 = 2673 (сотен – 0) 134 · 99 = 13266

27 – 1 = 26 134 – 2 = 132 (сотня – 1 + 1)

100 – 27 = 73 66

Умножение на 999 любого числа

1. Из умножаемого вычитаем число тысяч, увеличенное на 1

2. Находим дополнение до 1000

23 · 999 = 22977 ( тысяч – 0 + 1 = 1)

23 – 1 = 22

1000 – 23 = 977

124 · 999 = 123876 ( тысяч – 0 + 1 = 1)

124 – 1 = 123

1000 – 124 = 876

1324 · 999 = 1322676 (тысяча – 1 + 1 = 2)

1324 – 2 = 1322

1000 – 324 = 676

Умножение на 11, 22, 33, …99

Чтобы двузначное число, сумма цифр которого не превышает 10, умножить на 11, надо цифры этого числа раздвинуть и поставить между ними сумму этих цифр:

72 ×11= 7 (7+2) 2 = 792;

35 ×11 = 3 (3+5) 5 = 385.

Чтобы умножить 11 на двузначное число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить единицу, а вторую и последнюю (третью) оставить без изменения:

94 ×11 = 9 (9+4) 4 = 9 (13) 4 = (9+1) 34 = 1034;

59×11 = 5 (5+9) 9 = 5 (14) 9 = (5+1) 49 = 649.

Чтобы двузначное число умножить на 22, 33. …99, надо последнее число представить в виде произведения однозначного числа (от 1 до 9) на 11, т.е.

44= 4 × 11; 55 = 5×11 и т. д.

Затем произведение первых чисел умножить на 11.

48 × 22 =48 × 2 × (22 : 2) = 96 × 11 =1056;

24 × 22 = 24 × 2 × 11 = 48 × 11 = 528;

23 ×33 = 23 × 3× 11 = 69 × 11 = 759;

18 × 44 = 18 × 4 × 11 = 72 × 11 = 792;

16 × 55 = 16 × 5 × 11 = 80 × 11 = 880;

16 × 66 = 16 × 6 × 11 = 96 × 11 = 1056;

14 × 77 = 14 × 7 × 11 = 98 × 11 = 1078;

12 × 88 = 12 × 8 × 11 = 96 × 11 = 1056;

8 × 99 = 8 × 9 × 11 = 72 × 11 = 792.

Кроме того, можно применить закон об одновременном увеличении в равное число раз одного сомножителя и уменьшении другого.

Умножение на число, оканчивающееся на 5

Чтобы четное двузначное число умножить на число, оканчивающееся на 5, следует применить правило: если один из сомножителей увеличить в несколько раз, а другой – уменьшить во столько же раз, произведение не изменится.

44 × 5 = (44 : 2) × 5 × 2 = 22 × 10 = 220;

28 × 15 = (28 : 2) × 15 × 2 = 14 × 30 = 420;

32 × 25 = (32 : 2) × 25 × 2 = 16 × 50 = 800;

26 × 35 = (26 : 2) × 35 × 2 = 13 × 70 = 910;

36 × 45 = (36 : 2) × 45 × 2 = 18 × 90 = 1625;

34 × 55 = (34 : 2) × 55 × 2 = 17 × 110 = 1870;

18 × 65 = (18 : 2) × 65 × 2 = 9 × 130 = 1170;

12 × 75 = (12 : 2) × 75 × 2 = 6 × 150 = 900;

14 × 85 = (14 : 2) × 85 × 2 = 7 × 170 = 1190;

12 × 95 = (12 : 2) × 95 × 2 = 6 × 190 = 1140.

При умножении на 65, 75, 85, 95 числа следует брать небольшие, в пределах второго десятка. В противном случае вычисления усложнятся.

Умножение и деление на 25, 50, 75, 125, 250, 500

Для того, чтобы устно научиться умножать и делить на 25 и 75, надо хорошо знать признак делимости и таблицу умножения на 4.

На 4 делятся те, и только те числа, у которых две последние цифры числа выражают число, делящееся на 4.

Например:

124 делится на 4, так как 24 делится на 4;

1716 делится на 4, так как 16 делится на 4;

1800 делится на 4, так как 00 делится на 4

Правило. Чтобы число умножить на 25, надо это число разделить на 4 и умножить на 100.

Примеры:

484 × 25 = (484 : 4) × 25 × 4 = 121 × 100 = 12100

124 × 25 = 124 : 4 × 100 = 3100

Правило. Чтобы число разделить на 25, надо это число разделить на 100 и умножить на 4.

Примеры:

12100 : 25 = 12100 : 100 × 4 = 484

31100 : 25 = 31100 :100 × 4 = 1244

Правило. Чтобы число умножить на 75, надо это число разделить на 4 и умножить на 300.

Примеры:

32 × 75 = (32 :4) × 75 × 4 = 8 × 300 = 2400

48 × 75 = 48 : 4 × 300 = 3600

Правило. Чтобы число разделить на 75, надо это число разделить на 300 и умножить на 4.

Примеры:

2400 : 75 = 2400 : 300 × 4 = 32

3600 : 75 = 3600 : 300 × 4 = 48

Правило. Чтобы число умножить на 50, надо это число разделить на 2 и умножить на 100.

Примеры:

432× 50 = 432 :2 × 50 × 2 = 216 × 100 = 21600

848 × 50 = 848 : 2 × 100 = 42400

Правило. Чтобы число разделить на 50, надо это число разделить на 100 и умножить на 2.

Примеры:

21600 : 50 = 21600 : 100 × 2 = 432

42400 : 50 = 42400 : 100 × 2 = 848

Правило. Чтобы число умножить на 500, надо это число разделить на 2 и умножить на 1000.

Примеры:

428 × 500 = (428 :2) × 500 × 2 = 214 × 1000 = 214000

2436 × 500 = 2436 : 2 × 1000 = 1218000

Правило. Чтобы число разделить на 500, надо это число разделить на 1000 и умножить на 2.

Примеры:

214000 : 500 = 214000 : 1000 × 2 = 428

1218000 : 500 = 1218000 : 1000 × 2 = 2436

Прежде чем научиться умножать и делить на 125, надо хорошо знать таблицу умножения на 8 и признак делимости на 8.

Признак. На 8 делятся те и только те числа, у которых три последние цифры выражают число, делящееся на 8.

Примеры:

3168 делится на 8, так как 168 делится на 8;

5248 делится на 8, так как 248 делится на 8;

12328 делится на 8, так как 324 делится на 8.

Чтобы узнать, делится ли трехзначное число, оканчивающееся цифрами 2, 4, 6. 8. на 8, нужно к числу десятков прибавить половину цифр единиц. Если полученный результат будет делиться на 8, то исходное число делится на 8.

Примеры:

632 : 8, так как т.е. 64 : 8;

712 : 8, так как т.е. 72 : 8;

304 : 8, так как т.е. 32 : 8;

376 : 8, так как т.е. 40 : 8;

208 : 8, так как т.е. 24 : 8.

Правило. Чтобы число умножить на 125, надо это число разделить на 8 и умножить на 1000. Чтобы число разделить на 125, надо это число разделить на 1000 и умножить

на 8.

Примеры:

32 × 125 = (32 : 8) × 125 × 8 = 4 × 1000 = 4000;

72 × 125 = 72 : 8 × 1000 = 9000;

4000 : 125 = 4000 : 1000 × 8 = 32;

9000 : 125 = 9000 : 1000 × 8 = 72.

Правило. Чтобы число умножить на 250, надо это число разделить на 4 и умножить на 1000.

Примеры:

36 × 250 = (36 : 4) × 250 × 4 = 9 × 1000 = 9000;

44 × 250 = 44 : 4 × 1000 = 11000.

Правило. Чтобы число разделить на 250, надо это число разделить на 1000 и умножить на 4.

Примеры:

9000 : 250 = 9000 : 1000 ×4 = 36;

11000 : 250 = 11000 : 1000 ×4 = 44

Умножение и деление на 37

Прежде чем научиться устно умножать и делить на 37, надо хорошо знать таблицу умножения на три и признак делимости на три, который изучается в школьном курсе.

Правило. Чтобы умножить число на 37, надо это число разделить на 3 и умножить на 111.

Примеры:

24 × 37 = (24 : 3) × 37 × 3 = 8 × 111 = 888;

27 × 37 = (27 : 3) × 111 = 999.

Правило. Чтобы число разделить на 37, надо это число разделить на 111 и умножить на 3

Примеры:

999 : 37 = 999 :111 × 3 = 27;

888 : 37 = 888 :111 × 3 = 24.

Умножение на 111

Научившись умножать на 11, легко умножить на 111, 1111. и т. д. число, сумма цифр которого меньше 10.

Примеры:

24 × 111 = 2 (2+4) (2+4) 4 = 2664;

36 ×111 = 3 (3+6) (3+6) 6 = 3996;

17 × 1111 = 1 (1+7) (1+7) (1+7) 7 = 18887.

Вывод. Чтобы число умножить на 11, 111. и т. д., надо мысленно цифры этого числа раздвинуть на два, три и т. д. шагов, сложить цифры и записать между раздвинутыми цифрами.

Умножение двух рядом стоящих чисел

Примеры:

1) 12 ×13 = ? 1 × 1 = 1 1 × (2+3) = 5 2 × 3 = 6 156 2) 23 × 24 = ? 2 × 2 = 4 2 × (3+4) = 14 3 × 4 = 12 552 3) 32 × 33 = ? 3 × 3 = 9 3 × (2+3) = 15 2 × 3 = 6 1056 4) 75 × 76 = ? 7 × 7 = 49 7 × (5+6) = 77 5 × 6 = 30 5700

Проверка: ×12 13 36 12_ 156 Проверка: × 23 24 92 46_ 552 Проверка: × 32 33 96 96_ 1056 Проверка: × 75 76 450 525_ 5700

Вывод. При умножении двух рядом стоящих чисел надо сначала перемножить цифры десятков, затем цифру десятков умножить на сумму цифр единиц и, наконец, надо перемножить цифры единиц. Получим ответ (см. примеры)

Умножение пары чисел, у которых цифры десятков одинаковые, а сумма цифр единиц составляет 10

Пример:

24 × 26 = (24 – 4) × (26 + 4) + 4 × 6 = 20 × 30 + 24 = 624.

Числа 24 и 26 округляем до десятков, чтобы получить число сотен, и к числу сотен прибавляем произведение единиц.

18 × 12 = 2 × 1 сот. + 8 × 2 = 200 + 16 = 216;

16 × 14 = 2 × 1 × 100 + 6 × 4 = 200 + 24 = 224;

23 × 27 = 2 × 3 × 100 + 3 × 7 = 621;

34 × 36 = 3 × 4 сот. + 4 × 6 = 1224;

71 × 79 = 7 × 8 сот. + 1 × 9 = 5609;

82 × 88 = 8 × 9 сот. + 2 × 8 = 7216.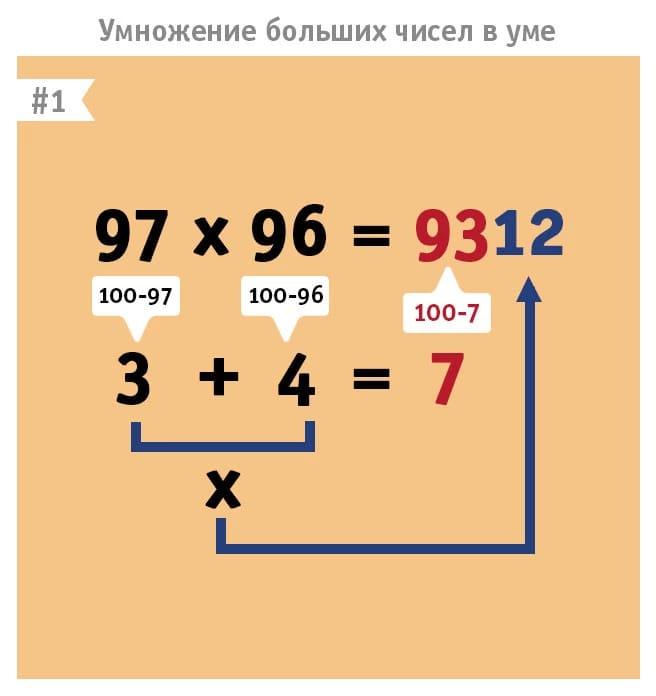

Можно решать устно и более сложные примеры:

108 × 102 = 10 × 11 сот. + 8 × 2 = 11016;

204 × 206 = 20 × 21 сот. +4 × 6 = 42024;

802 × 808 = 80 × 81 сот. +2 × 8 = 648016.

Проверка:

× 802

808

6416

6416__

648016

Умножение двузначных чисел, у которых сумма цифр десятков равна 10, а цифры единиц одинаковые.

Правило. При умножении двузначных чисел. у которых сумма цифр десятков равна 10, а цифры единиц одинаковые, надо перемножить цифры десятков. и прибавить цифру единиц, получим число сотен и к числу сотен прибавим произведение единиц.

Примеры:

72 × 32 = (7 × 3 + 2)сот. + 2 × 2 = 2304;

64 × 44 = (6 × 4 + 4) × 100 + 4 × 4 = 2816;

53 × 53 = (5 × 5 +3) × 100 + 3 × 3 = 2809;

18 × 98 = (1 × 9 + 8) × 100 + 8 × 8 = 1764;

24 × 84 = (2 × 8 + 4) ×100+ 4 × 4 = 2016;

63 × 43 = (6 × 4 +3) × 100 +3 × 3 = 2709;

35 × 75 = (3 × 7 + 5) × 100 +5 × 5 = 2625.

Умножение чисел, оканчивающихся на 1

Правило. При умножении чисел, оканчивающихся на 1, надо сначала перемножить цифры десятков и правее полученного произведения записать под этим числом сумму цифр десятков, а затем перемножить 1 на 1 и записать еще правее. Сложив столбиком, получим ответ.

Примеры:

1) 81 × 31 = ? 8 × 3 = 24 8 + 3 = 11 1 × 1 = 1 2511 81 × 31 = 2511

2) 21 × 31 = ? 2 × 3 = 6 2 +3 = 5 1 × 1 = 1 651 21 × 31 = 651

3) 91 × 71 = ? 9 × 7 = 63 9 + 7 = 16 1 × 1 = 1 6461 91 × 71 = 6461

Умножение двузначных чисел на 101, трехзначных – на 1001

Правило. Чтобы двузначное число умножить на 101, надо к этому числу приписать справа это же число.

Примеры: 32 × 101 = 3232

Проверка: × 32 101 32 32__ 3232

48 × 101 = 4848;

56 × 101 = 5656.

Правило. Чтобы трехзначное число умножить на 1001, надо к этому числу справа приписать это же число.

Примеры:

324 1001 = 324324

Проверка: 324 1001 324 324___ 324324

648 1001 = 648648;

999 1001 = 999999.

Приемы устных рациональных вычислений, используемые на уроках математики, способствуют повышению общего уровня математического развития;  развивают у учеников навык быстро выделять из известных им законов, формул, теорем те, которые следует применить для решения предложенных задач, расчетов и вычислений; содействуют развитию памяти, развивают способность зрительного восприятия математических фактов, совершенствуют пространственное воображение. 

Помимо этого, рациональный счет на уроках математики играет немаловажную роль в повышении у детей познавательного интереса к урокам математики, как одного из важнейших мотивов учебно-познавательной деятельности, развития личностных качеств ребенка. Формируя навыки устных рациональных вычислений, учитель тем самым воспитывает у учащихся навыки сознательного усвоения изучаемого материала, приучает ценить и экономить время, развивает желание поиска рациональных путей решения задачи. Иными словами формируются познавательные, включая логические, познавательные и знаково-символические универсальные учебные действия.

Цели и задачи школы кардинально меняются, осуществляется переход от знаниевой парадигмы к лично-ориентированному обучению. Потому важно не просто учить решать задачи по математике, а показывать действие основных математических законов в жизни, объяснять, как может учащийся применить полученные знания. И тогда у детей появится главное: желание и смысл учиться.

Список литературы

Минских Е.М. «От игры к знаниям», М., «Просвещение» 1982.

Кордемский Б.А., Ахадов А.А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986.

Совайленко ВК. Система обучения математике в 5-6 классах. Из опыта работы.- М.:Просвещение, 1991.

Катлер Э. Мак-Шейн Р. «Система быстрого счёта по Трахтенбергу» – М. Просвещение, 1967.

Хэндли Билл «Считать в уме как калькулятор» – Минск, Попурри, 2006.

Минаева С. С. «Вычисления на уроках и внеклассных занятиях по математике.» – М.: Просвещение, 1983. 

Сорокин А.С. «Техника счета (методы рациональных вычислений)», М, Знани», 1976

http://razvivajka.ru/ Тренировка устного счета

http://gzomrepus.ru/exercises/production/ Упражнения на продуктивность и быстрый устный счет

Как научиться считать в уме | Клуб любителей математики

Считать в уме, по мнению многих, в наше время уже неактуально, ведь калькулятор есть в каждом смартфоне, компьютере и ноутбуке. Однако калькулятор не будет сопровождать вас при каждом вашем шаге, а считать необходимо постоянно и много. Способность сосчитать в уме – умение весьма нужное даже в 21 веке. А тем более это нужно школьникам для решения примеров по математике из нелёгкой школьной программы. И им весьма полезно будет уметь считать быстро, не пребегая к электронным устройствам.

Опыт и постоянные тренировки играют важную роль в развитии любых способностей, но навык устного счета не состоит только лишь из опыта. Это могут доказать люди, умеющие считать в уме гораздо более сложные примеры: например, умножать и делить трех- и четырехзначные числа, находить суммы и разности огромных примеров.

Что необходимо знать и делать человеку, дабы повторить такое?

• Во-первых, концентрация или же умение ненадолго удерживать в памяти несколько вещей одновременно.

• Во-вторых, алгоритмы, специальные методы вычислений и математические уловки, значительно облегчающие процесс устного счёта.

• В-третьих, практика. Постоянные тренировки и постепенное усложнение решаемых задач позволят улучшить скорость и качество устного счета.

Важно отметить, что именно практика имеет наибольшее значение. Не обладая достаточным опытом, вы не сможете быстро применять удобные алгоритмы, подходящие под определённые ситуации. И помните, что максимальный эффект будет достигнут при оптимальном использовании всех трёх

составляющих. Тренировать сразу все аспекты этого навыка Вы можете в онлайн тренажере устного счёта.

Внимание и концентрация

Чтобы максимально быстро считать в уме, необходимо уметь концентрироваться на конкретном примере. Этот навык полезен не только для совершения математических операций, но и для решения любых жизненных задач. Существует несколько способов улучшить свою внимательность и способность к концентрации:

При счете в уме, важно ясно представлять себе решаемый пример – визуализировать его. Запоминать промежуточные результаты нужно не на слух, а так как они выглядят в записи, например, на бумаге. Тренировать подобное восприятие можно разными способами, и отчасти визуализация решения приходит с опытом.

Старайтесь всегда находить что-то интересное в рутине, превращая действие в игру. Так поступают и некоторые родители, желающие, чтобы их ребёнок выполнил какую-либо скучную работу.

Огромное количество людей всегда хотят «быть лучше» соперника. Именно поэтому состязательность является еще одним способом развить свою внимательность. В устном счете Вы можете найти себе соперника и пытаться его в этом превзойти.

Еще одним фактором, создающим азарт при счете, может стать борьба с самим собой при достижении определенного результата, то есть

личные рекорды. Их можно ставить, например, в скорости счета, в количестве решенных примеров и своей точности ответов.

Наконец, максимальная концентрация может быть достигнута при спонтанном увлечении процессом счета. Как пример, во время чтения Вы перестаёте думать об окружающих вас предметах, людях, ситуациях, полностью погружаетесь в книгу. Именно неподдельный интерес к чему-либо способен заставить вас приобрести наибольшую внимательность в этом деле.

Безусловно, все эти способы надо отрабатывать, практиковать. В этом могут помочь различные тренажеры зрительной памяти и улучшения внимательности.

Простые арифметические закономерности

Решение любой по сложности задачи всегда сводится к применению базовых принципов, и именно эти принципы и закономерности позволят вам быстро выполнять различного рода операции. Существует определенный набор таких правил и закономерностей, которые необходимо довести до автоматизма с помощью разных онлайн тренажеров по математике.

Вычитание 7, 8, 9. Чтобы вычесть 9 из любого числа, нужно вычесть из него 10 и прибавить 1. Чтобы вычесть 8 из любого числа, нужно вычесть из него 10 и прибавить 2. Чтобы вычесть 7 из любого числа, нужно вычесть из него 10 и прибавить 3. Если обычно вы считаете по-другому, то для лучшего результата вам необходимо привыкнуть к этому новому способу.

Таблица умножения. Для быстрого устного счета хорошо бы безупречно знать таблицу умножения, которая является основой счета. Если у Вас с этим еще проблемы, можете воспользоваться онлайн Тренажером таблицы умножения.

Умножение на 2. Для умножения на 2 некруглых чисел пробуйте округлять их до ближайших более удобных. Так 139×2 проще считать, если сначала умножить 140 на 2 (140×2=280), а потом вычесть 1×2=2 (именно 1 нужно прибавить к 139, чтобы получить 140). Итого: 140×2-1×2=280-2=278.

Деление на 2. Несмотря на то, что многим умножение и деление на 2 дается достаточно просто, в сложных случаях так же пытайтесь округлять числа. Например, чтобы разделить 198 на 2, нужно сначала разделить 200 (это 198+2) на 2 и отнять 2 деленое на 2. Итого: 198:2=200:2-2:2=100-1=99.

Деление и умножение на 4 и 8. Деление (или умножение) на 4 и на 8 являются двукратным или трехкратным делением (или умножением) на 2. Производить эти операции удобно последовательно. Например, 46×4=46×2×2=92×2=184.

Умножение на 5 и 25. Умножение на 5, и деление на 2 – практически одно и то же, поэтому всегда умножайте на 5, поделив число на 2 и умножив его на 10: 88×5=88:2×10=440. Умножение на 25 соответствует делению на 4 (с последующим умножением на 100). Так 120×25 = 120:4×100 = 30×100 = 3000.

Умножение на 9. Быстро умножить любое число на 9 можно следующим образом: сначала умножьте это число на 10, а затем вычтите из результата само число. Например: 89×9=890-89=801.

Умножение на 11. Чтобы умножить любое двузначное число на 11, нужно между первой и второй цифрой умножаемого числа вписать сумму первой и второй цифры. Например: 23×11= 2 (2+3) 3 = 253. Или если сумма чисел в центре дает результат больше 10: 29×11 = 2 (2+9) 9 = 2 (11) 9 = 319.

И наконец, полезно знать деление чисел, кратных 10 на числа, кратные двум: 1000 = 2×500 = 4×250 = 8×125 = 16×62,5.

Более сложные методики

Эффективность умножения в уме некоторых двузначных чисел может быть выше за счет меньшего количества действий, если использовать специальные алгоритмов. Ниже представлены три специальные методики, в том числе введение и использование опорного числа.

Квадрат суммы и квадрат разности

Для того чтобы возвести в квадрат двузначное число, можно воспользоваться формулами квадрата суммы или квадрата разности. Например:

23²= (20+3)² = 20² + 2×3×20 + 3² = 400+120+9 = 529

69² = (70-1)² = 70² – 70×2×1 + 1² = 4 900-140+1 = 4 761

Возведение в квадрат чисел, заканчивающихся на 5

Чтобы возвести в квадрат числа, заканчивающиеся на 5, необходимо число до последней пятерки, умножить на сумму этого же числа и единицы. К результату дописываем 25. Вот несколько примеров:

25² = (2×(2+1)) 25 = 625

85² = (8×(8+1)) 25 = 7 225

155² = (15×(15+1)) 25 = (15×16)25 = 24 025

Опорное число

Наиболее популярной методикой умножения больших чисел в уме является прием использования, так называемого, опорного числа. Опорное число при умножении – это число, к которому близко находятся оба множителя и на которое удобно умножать. А методика использования этого числа зависит от того, являются ли множители больше или меньше него самого.

Оба множителя меньше опорного

. Допустим, мы хотим умножить 48 на 47. Эти числа находятся достаточно близко к числу 50, а следовательно удобно использовать 50 в качестве опорного числа. Далее действуем так: из 47 вычетаем столько, сколько не хватает 48 до 50 (либо из 48 вычетаем столько, сколько не хватает 47 до 50), полученный результат умножаем на опорное число и прибавляем к нему произведение разностей опроного числа с каждым сомножителем. Наглядный пример:

(48–(50-47))×50 + (50-47)×(50-48) = 2250 + 6 = 2256

Оба множителя больше опорного. Действовать нужно точно так же, но не вычитать недостаток, а прибавлять избыток:

(51+(63-50))×50 + (63-50)×(51-50) = 3200 + 13 = 3213

Один множитель меньше, другой больше опорного

. Схема та же, но произведение недостатка и избытка нужно вычитать:

(45+(52-50))×50 – (52-50)×(50-45) = 2350 – 10 = 2340

В заключение

Как уже было сказано ранее, навык устного счета набирается из трех составляющих: это способность концентрироваться конкретном примере, грамотный подбор метода быстрого счета и, конечно, опыт. Запомните, даже зная наизусть все алгоритмы, упрощающие вам устный счет, вы не сможете сосчитать без пракики так же быстро, как если бы вы занимались этим каждый день уже несколько лет. Именно потоянные тренировки на разного рода тренажерах устного счета позволят вам отточить мастрство в этом деле и приобрести тот самый бесценный навык быстрого устного счета.

Онлайн тренажер устного счета 192 разнообразных режима тренировок: Уравнения, сравнения, отрицательные числа

Ментальная арифметика: как и зачем решать 10 примеров в секунду

Ментальная арифметика: как и зачем решать 10 примеров в секунду

Умение быстро считать в уме развивает внимание, скорость обработки информации и даже творческое мышление. Дает ли этот навык ребёнку конкурентное преимущество в будущем? Станет ли шагом к успешной жизни или просто отнимет драгоценное время? Екатерина Цыбуля, руководитель центра «Учусь на 5», логопед, тренер по ментальной арифметике, рассказывает, в чем польза такого обучения.

Екатерина Цыбуля, руководитель центра «Учусь на 5», логопед, тренер по ментальной арифметике

Ментальная арифметика — программа развития умственных и творческих способностей, основанная на системе устного счета. Освоив ее, ребенок сможет решать арифметические задачи в уме всего за несколько секунд. Методика рекомендована для детей от 4 до 12 лет. Однако современные развивающие центры готовы обучать и более взрослых людей, как правило, с одной оговоркой — чем позднее начнешь, тем больше усилий потребуется.

Ментальная арифметика зародилась в Японии в ХVI веке. На начальных этапах обучения используются специальные счеты — абак или соробан. Счеты состоят из рамки, разделительной полосы, вертикальных спиц, верхних («небесных») и нижних («земных») косточек. Одна «небесная» косточка равна пяти «земным». Количество спиц варьируется от 13 до 31. При работе ребенок использует только большой и указательный пальцы. Все движения доводятся до автоматизма. Через некоторое время ребенок совершает вычисления на воображаемом абаке, а задачи решаются с помощью образов.

Формула интеллекта: логика плюс интуиция

Известно, что левое полушарие отвечает за логику, рациональность и анализ, а правое — за образность, целостность, интуицию, фантазию и воображение. Современная система образования уделяет больше внимания точным наукам. Время на танцы, рисование или занятие музыкой выделяется по остаточному принципу. Но даже если родителям удается найти золотую середину, возникает вопрос — как развить взаимосвязь работы обоих полушарий, чтобы максимально раскрыть потенциал ребенка?

Программа обучения метальной арифметики направлена на формирование устойчивых нейронных связей левого и правого полушарий. По мнению педагогов, именно этот факт помогает людям выбирать наиболее эффективные решения и добиваться успеха в жизни.

Плюсы и минусы ментальной математики

Самый очевидный результат обучения — способность совершать арифметические действия с шестизначными числами за несколько секунд. Но сложно представить, зачем сегодня ребенку может понадобиться этот навык. Как утверждают педагоги по ментальной математике, быстрый счет в уме — это побочный эффект, а не цель. Основная задача обучения — добиться эффекта синергии от синхронной работы обоих полушарий мозга, который превосходит эффект от работы каждого полушария по-отдельности. Тогда вместе с математическими способностями в ребенке будут развиваться:

• усидчивость
• концентрация внимания
• фотографическая память
• воображение
• творческое мышление
• скорость обработки информации

Кроме возрастных ограничений, никаких противопоказаний к занятиям нет. Однако отзывы родителей говорят о том, что не все ученики наблюдают улучшение памяти и концентрации внимания, а у некоторых детей возникают проблемы с решением элементарных задач на логику.

Здесь стоит вспомнить простую истину о том, что каждый ребенок уникален. Менар — это одна из методик развития интеллекта, которая помогает выявить и раскрыть уникальные способности ребенка. Ребенок учится быстро усваивать новую информацию, формулировать мысли и делать выводы. Тем не менее, не стоит пренебрегать традиционными играми — шахматами, головоломками, ребусами. Поэтому, наблюдайте, пробуйте, анализируйте и выбирайте то, что подходит именно вам.

Как проходит обучение

Обучение состоит из 10 уровней, каждый из которых занимает до четырех месяцев. Полный курс длится 2−3 года. Занятия идут по два академических часа один раз в неделю, кроме этого дети должны потратить 15 минут на выполнение домашних заданий. Как правило, у каждого развивающего центра есть онлайн-платформы, которые позволяют более эффективно работать самостоятельно.

Самый главный инструмент — это абак. Также в процесс обучения включают настольные, подвижные игры, просмотр мультфильмов и физминутки. На первом этапе детей учат складывать и вычитать числа на абаке. В этот период тренируется мелкая моторика, пространственное и логическое мышление. Далее переходят на ментальную карту — картину с изображением абака. И на следующем этапе дети производят арифметические действия с помощью визуализации процесса. Таким образом, уже через год ребенок может делать вычисления в уме.

Как выбрать школу ментальной арифметики?

Результат обучения будет зависеть от трех участников процесса — ребенка, учителя и родителей. Но самое главное — правильно выбрать образовательный центр, где будут преподавать менар. Вот несколько простых правил:

• Запишитесь на пробное занятие. Оцените, насколько комфортно ребенку в новых условиях. Не упустите возможность пообщаться с другими родителями.
• Познакомьтесь с педагогом. Спросите, как готовят преподавателей ментальной арифметики? Контролирует ли головной офис методику преподавания, уровень знаний педагогов, проходят ли преподаватели аттестацию на профпригодность?
• Обратите внимание на количество учеников в группе. Только в небольших группах преподаватель может уделить необходимое время каждому ученику. Поэтому в младших группах занимаются 5−7 человек, в старших — 8−10.
• Сделайте анализ рынка. Стоимость обучения в пределах одного региона не может сильно отличаться. Слишком низкая цена может быть показателем недобросовестного подхода к подготовке персонала и разработке методики. Слишком высокая цена может быть связана с издержками, дорогой арендой или рекламой.

Самое главное — чтобы ребенку нравились. Ему должно быть интересно считать, несмотря на то что считать — может быть довольно скучным занятием. Если ребенку нравится, значит, преподаватель смог заинтересовать его. Кроме этого, чтобы оценить преподавателя, обычно спрашивают: через сколько появятся первые результаты? На какие способности влияет обучение? Что делают, чтобы ускорить обучение? Хороший педагог ответит на все вопросы.

Читайте также:

Ну и почерк! Почему детям всё-таки важно учиться красиво писать?

11 полезных советов для родителей от педагога по английскому языку

Зачем детям учить математику?

Фото: GRSI, Ann in the uk, NadyaEugene/Shutterstock.com

Быстрый счет в уме без калькулятора

Человек всегда стремился научиться легко и быстро производить операции с большими числами в уме. Несмотря на то, что сейчас почти у каждого есть возможность пользоваться таким благом цивилизации как калькулятор, многие люди все равно интересуются различными системами устных вычислений и хитрыми математическими приемами. Какую пользу они несут для детей и взрослых, и стоит ли их изучать?

Устный счет и его польза

У современного человека появилось немало новых повседневных задач, которые связаны с работой, учебой или иными видами деятельности. Чтобы эффективно справляться с ними, он должен обладать целым рядом определенных навыков. Одной из важнейших способностей можно назвать счет в уме, которому мы учимся еще в школе на уроках математики. В начальных классах малыши сначала осваивают сложение и вычитание небольших чисел, а затем более сложные операции – умножение и деление.

В первые годы учебы педагоги уделяют внимание развитию устного счета, учат считать без помощи калькулятора или иных подручных средств. Но в дальнейшем приоритеты школьной программы смещаются в сторону углубленного изучения каждой из дисциплин, и математика не является исключением. Постепенно ученики отказываются считать в уме, предпочитая производить операции с числами в столбик или пользоваться гаджетами. Отсутствие постоянной практики не дает детям полноценно развить свои навыки, а потому и во взрослом возрасте люди все чаще полагаются на умных помощников, а не на возможности собственного интеллекта.

Развитие технологий действительно сделало жизнь проще, но и у этого есть свои минусы. Чтобы добиться значительного успеха в любом начинании, человек постоянно должен самосовершенствоваться, работать над собой. Тренировка умения быстро считать в уме может стать отличным помощником для достижения этих целей, ведь повышение навыков работы с числами также является эффективным способом развития интеллекта. Конечно, речь идет не о базовых умениях, которые прививаются еще в детские годы, а о более углубленном изучении приемов быстрого счета без калькулятора. Поговорим о тех из них, которые известны уже давно, и о более новых, только набирающих популярность.

Примеры быстрого счета в уме без калькулятора

Ученые прошлого, чья жизнь и работа была неотрывно связана с точными науками, всегда стремились найти новые способы быстрого счета. В то время они отлично обходились без калькулятора. Благодаря их разработкам сегодня можно найти немало приемов, позволяющих считать с высокой скоростью даже большие числа. Рассмотрим несколько таких способов на примерах:

• умножение на 11. Чтобы быстро произвести данную операцию в уме, нужно умножить наше число на 10, а затем прибавить в нему это же число. К примеру, требуется произвести умножение 46 на 11. Число 46 мы умножаем на 10: 46*10=460. К этому новому значению прибавляем 46 и получаем следующее выражение: 460+46=506.
• деление на 5. Для решения такого выражения потребуется умножить делимое на 2, а затем перенести запятую на один знак влево. Рассмотрим этот способ на примере деления числа 643 на 5: 643*2=1286. Переносим запятую нашего нового числа на знак влево и получаем ответ: 128,6.
• умножение на полтора. Чтобы быстро произвести такое действие необходимо к нашему значению прибавить его половину. К примеру, нужно найти результат умножения 116 на 1,5. Делим 116 на 2, получается 58. Теперь к 116 прибавляем наше новое значение: 116+58=174.
• вычитание трехзначного числа из 1000. Для решения такого примера подойдет следующий способ: от числа 9 отнимаем каждую цифру вычитаемого, кроме последней – ее отнимаем от 10. Чтобы из 1000 вычесть 845 нужно произвести следующие действия: от 9 отнять 8, получается 1, от 9 отнять 4, получается 5, а от 10 отнять 5, получается 5. Последовательно записываем каждое новое значение и получаем верный ответ: 1000-845=155.

Несмотря на то, что перечисленные способы нельзя назвать кардинально новыми, их использование позволяет удивить окружающих своими интеллектуальными способностями. Особенно ярко данные приемы демонстрируют дети, которые участвуют в различных телевизионных программах в качестве гостей.

Удивительные люди

Основным плюсом математических хитростей является то, что освоить и научиться применять их на практике может даже ребенок. Малыши и подростки, которые в совершенстве овладели этими приемами, успешно выступают на телевидении, где удивляют зрителей умением складывать, вычитать, умножать и делить даже большие числа в уме. Но использование таких способов счета имеет и свои недостатки, главным из которых можно назвать невозможность применять один и тот же метод в различных случаях. Так правила умножения любого числа на 11 работают только в определенных условиях и не распространяются на те ситуации, где множителем выступает другое значение.

Именно поэтому в качестве альтернативы математическим хитростям многие люди находятся в поиске все новых и новых методов устных вычислений, которые удалось бы более широко применять на практике. Техникой, которая отвечает этим запросам и пользуется все большей популярностью с каждым годом, является ментальная арифметика. Поговорим о ее ключевых особенностях и о том, как она позволяет считать быстрее калькулятора даже маленькому ребенку.

Техника быстрого устного счета

Ментальная арифметика имеет совершенно другой подход, чем другие давно известные или более новые способы работы с числами. В ее основе лежат вычисления на абакусе – специальном инструменте, который представляет собой особые счеты. Обучение данной технике состоит из нескольких этапов. На первых занятиях студенты осваивают абакус и учатся складывать и вычитать на нем небольшие числа. Впоследствии им предстоит привыкнуть представлять эти счеты в своем воображении и научиться производить арифметические операции уже на них. Постепенно сложность тренировок повышается, и студенты также осваивают умножение и деление в уме.

В процессе тренировок удается добиться потрясающей скорости работы с числами. Однако, быстрый счет в уме – не главное и далеко не единственное преимущество ментальной арифметики. Ее важнейшая особенность – это разностороннее развитие интеллекта, благодаря которому удается совершенствовать память, концентрацию внимания, скорость реакции, а также логическое, аналитическое и творческое мышление. Все это делает занятия ментальной арифметикой эффективным способом саморазвития, который подходит и для детей, и для взрослых.

Теперь обучение ментальной арифметике доступно в режиме онлайн на платформе Amavit. Индивидуальные занятия с личным тренером, большое количество обучающих игр на платформе и специальное приложение с абакусом на смартфон сделают тренировки не только эффективными, но и интересными. Зарегистрируйтесь на сайте amavit.com, подберите удобный график занятий и начните совершенствовать навыки устного счета, которые пригодятся в любом возрасте.

Как освоить устный счёт школьникам и взрослым

Кроме отличных оценок по математике, умение считать в уме даёт массу преимуществ на протяжении всей жизни. Упражняясь в вычислениях без калькулятора, вы:

• Держите мозг в тонусе. Для эффективной работы интеллект, как и мускулатура, нуждается в постоянных тренировках. Счёт в уме развивает память, логическое мышление и концентрацию, повышает способность к обучению, помогает быстрее ориентироваться в ситуации и принимать правильные решения.
• Заботитесь о своём психическом здоровье. Исследования показывают ^{, что при устном счёте задействованы участки мозга, ответственные за депрессию и тревожность. Чем активнее работают эти зоны, тем меньше риск неврозов и чёрной тоски.}
• Страхуетесь от проколов в бытовых ситуациях. Способность быстро посчитать сдачу, размер чаевых, количество калорий или проценты по кредиту защищает вас от незапланированных трат, лишнего веса и мошенников.

Освоить приёмы быстрого счёта можно в любом возрасте. Не беда, если сначала вы будете немного «тормозить». Ежедневно практикуйте основные арифметические операции по 10–15 минут и уже через пару месяцев достигнете заметных результатов.

Как научиться складывать в уме

Суммируем однозначные числа

Начните тренировку с элементарного уровня — сложения однозначных чисел с переходом через десяток. Эту технику осваивают в первом классе, но почему-то часто забывают с возрастом.

• Предположим, вам нужно сложить 7 и 8.
• Посчитайте, сколько семёрке не хватает до десяти: 10 − 7 = 3.
• Разложите восьмёрку на сумму трёх и второй части: 8 = 3 + 5.
• Добавьте вторую часть к десяти: 10 + 5 = 15.

Тот же приём «опоры на десятку» используйте при суммировании однозначных чисел с двузначными, трёхзначными и так далее. Оттачивайте простейшее сложение, пока не научитесь совершать одну операцию за пару секунд.

Суммируем многозначные числа

Основной принцип — разбить слагаемые числа на разряды (тысячи, сотни, десятки, единицы) и суммировать между собой одинаковые, начиная с самых крупных.

Допустим, вы прибавляете 1 574 к 689.

• 1 574 раскладывается на четыре разряда: 1 000, 500, 70 и 4. 689 — на три: 600, 80 и 9.
• Теперь суммируем: тысячи с тысячами (1 000 + 0 = 1 000), сотни с сотнями (500 + 600 = 1 100), десятки с десятками (70 + 80 = 150), единицы с единицами (4 + 9 = 13).
• Группируем числа так, как нам удобно, и складываем то, что получилось: (1 000 + 1 100) + (150 + 13) = 2 100 + 163 = 2 263.

Основная сложность — удержать в голове все промежуточные результаты. Упражняясь в таком счёте, вы заодно тренируете память.

Как научиться вычитать в уме

Вычитаем однозначные числа

Снова возвращаемся в первый класс и оттачиваем навык вычитания однозначного числа с переходом через десяток.

Предположим, вы хотите отнять 8 от 35.

• Представьте 35 в виде суммы 30 + 5.
• Из 5 вычесть 8 нельзя, поэтому раскладываем 8 на сумму 5 + 3.
• Вычтем 5 из 35 и получим 30. Затем отнимем от 30 оставшуюся тройку: 30 − 3 = 27.

Вычитаем многозначные числа

В отличие от сложения, при вычитании многозначных чисел на разряды нужно разбивать только то, которое вы отнимаете.

Например, вас просят отнять 347 от 932.

• Число 347 состоит из трёх разрядных частей: 300 + 40 + 7.
• Сначала вычитаем сотни: 932 − 300 = 632.
• Переходим к десяткам: 632 − 40. Для удобства 40 можно представить в виде суммы 30 + 10. Сперва вычтем 30 и получим 632 − 30 = 602. Теперь отнимем от 602 оставшиеся 10 и получим 592.
• Осталось разобраться с единицами, используя всё ту же «опору на десятку». Сперва вычитаем из 592 двойку: 592 − 2 = 590. А затем то, что осталось от семёрки: 7 − 2 = 5. Получаем: 590 − 5 = 585.

Как научиться умножать в уме

Лайфхакер уже писал о том, как быстро освоить таблицу умножения.

Добавим, что наибольшие трудности и у детей, и у взрослых вызывает умножение 7 на 8. Есть простое правило, которое поможет вам никогда не ошибаться в этом вопросе. Просто запомните: «пять, шесть, семь, восемь» — 56 = 7 × 8.

А теперь перейдём к более сложным случаям.

Умножаем однозначные числа на многозначные

По сути, здесь всё элементарно. Разбиваем многозначное число на разряды, перемножаем каждый на однозначное число и суммируем результаты.

Разберём на конкретном примере: 759 × 8.

• Разбиваем 759 на разрядные части: 700, 50 и 9.
• Умножаем каждый разряд по отдельности: 700 × 8 = 5 600, 50 × 8 = 400, 9 × 8 = 72.
• Складываем результаты, разбивая их на разряды: 5 600 + 400 + 72 = 5 000 + (600 + 400) + 72 = 5 000 + 1 000 + 72 = 6 000 + 72 = 6 072.

Умножаем двузначные числа

Тут уже рука сама тянется к калькулятору или хотя бы к бумаге и ручке, чтобы воспользоваться старым добрым умножением в столбик. Хотя ничего сверхсложного в этой операции нет. Просто нужно немного потренировать краткосрочную память.

Попробуем умножить 47 на 32, разбив процесс на несколько шагов.

• 47 × 32 — это то же, что и 47 × (30 + 2) или 47 × 30 + 47 × 2.
• Сначала умножим 47 на 30. Проще некуда: 47 × 3 = 40 × 3 + 7 × 3 = 120 + 21 = 141. Приписываем справа нолик и получаем: 1 410.
• Поехали дальше: 47 × 2 = 40 × 2 + 7 × 2 = 80 + 14 = 94.
• Осталось сложить результаты: 1 410 + 94 = 1 500 + 4 = 1 504.

Этот принцип можно применять и к числам с большим количеством разрядов, но удержать в уме столько операций не каждому под силу.

Упрощаем умножение

Кроме общих правил, есть несколько лайфхаков, облегчающих умножение на определённые однозначные числа.

Умножение на 4

Можно умножить многозначное число на 2, а потом снова на 2.

Пример: 146 × 4 = (146 × 2) × 2 = (200 + 80 + 12) × 2 = 292 × 2 = 400 + 180 + 4 = 584.

Умножение на 5

Умножьте исходное число на 10, а потом разделите на 2.

Пример: 489 × 5 = 4 890 / 2 = 2 445.

Умножение

на 9

Умножьте на 10, а затем отнимите от результата исходное число.

Пример: 573 × 9 = 5 730 − 573 = 5 730 − (500 + 70 + 3) = 5 230 − (30 + 40) − 3 = 5 200 − 40 − 3 = 5 160 − 3 = 5 157.

Умножение на 11

Приём сводится к следующему: впереди и сзади подставляем первую и последнюю цифры исходного числа. А между ними последовательно суммируем все цифры.

При умножении на двузначное число всё выглядит крайне просто.

Пример: 36 × 11 = 3(3+6)6 = 396.

Если сумма переходит через десяток, в центре остаётся разряд единиц, а к первой цифре добавляем один.

Пример: 37 × 11 = 3(3+7)7 = 3(10)7 = 407.

Чуть сложнее с умножением на более крупные числа.

Пример: 543 × 11 = 5(5+4)(4+3)3 = 5 973.

Как научиться делить в уме

Это операция, обратная умножению, поэтому и успех во многом зависит от знания всё той же школьной таблицы. Остальное — дело практики.

Делим на однозначное число

Для этого разбиваем исходное многозначное число на удобные части, которые точно будут делиться на наше однозначное.

Попробуем разделить 2 436 на 7.

• Выделим из 2 436 наибольшую часть, которая нацело разделится на 7. В нашем случае это 2 100. Получаем (2 100 + 336) / 7.
• Продолжаем в том же духе, только теперь с числом 336. Очевидно, что на 7 разделится 280. А в остатке будет 56.
• Теперь делим каждую часть на 7: (2 100 + 280 + 56) / 7 = 300 + 40 + 8 = 348.

Делим на двузначное число

Это уже высший пилотаж, но мы всё равно попытаемся.
Предположим, вам надо поделить 1 128 на 24.

• Прикидываем, сколько раз 24 может поместиться в 1 128. Очевидно, что 1 128 примерно в два раза меньше, чем 24 × 100 (2 400). Поэтому для «пристрелки» возьмём множитель 50: 24 × 50 = 1 200.
• До 1 200 нашему делимому 1 128 не хватает 72. Сколько раз 24 поместится в 72? Правильно, 3. А значит, 1 128 = 24 × 50 − 24 × 3 = 24 × (50 − 3) = 24 × 47. Стало быть, 1128 / 24 = 47.

Мы взяли не самый трудный пример, но пользуясь методом «пристрелки» и дроблением на удобные части, вы научитесь совершать и более сложные операции.

Что поможет освоить устный счёт

Для упражнений придётся ежедневно придумывать новые и новые примеры, только если вы сами этого хотите. В противном случае воспользуйтесь другими доступными способами.

Настольные игры

Играя в те, где необходимо постоянно вычислять в уме, вы не просто учитесь быстро считать. А совмещаете полезное с приятным времяпрепровождением в кругу семьи или друзей.

Карточные забавы вроде «Уно» и всевозможные варианты математического домино позволяют школьникам играючи освоить простое сложение, вычитание, умножение и деление. Более сложные экономические стратегии а-ля «Монополия» развивают финансовое чутьё и оттачивают сложные навыки счёта.

Что купить

• «Уно»;
• «7 на 9»;
• «7 на 9 multi»;
• «Трафик Джем»;
• «Хекмек»;
• «Математическое домино»;
• «Умножариум»;
• «Код фараона»;
• «Суперфермер»;
• «Монополия».

Мобильные приложения

С ними вы сможете довести устный счёт до автоматизма. Большинство из них предлагают решить примеры на сложение, вычитание, умножение и деление по программе младших классов. Но вы удивитесь, насколько это непросто. Особенно если задачи нужно щёлкать на время, без ручки и бумаги.

Математика: устный счёт, таблица умножения

Охватывает задания на устный счёт, которые соответствуют 1–6 классам школьной программы, включая и задачи на проценты. Позволяет тренировать скорость и качество счёта, а также настраивать сложность. Например, от простой таблицы умножения можно перейти к умножению и делению двузначных и трёхзначных чисел.

Математика в уме

Ещё один простой и понятный тренажёр устного счёта с подробной статистикой и настраиваемой сложностью.

1 001 задача для счёта в уме

В приложении используются примеры из пособия по математике «1 001 задача для умственного счёта», которое ещё в XIX веке составил учёный и педагог Сергей Рачинский.

Математические хитрости

Приложение позволяет легко и ненавязчиво освоить основные математические приёмы, которые облегчают и ускоряют устный счёт. Каждый приём можно отработать в тренировочном режиме. А потом поиграть на скорость вычислений с собой или соперником.

Quick Brain

Цель игры — правильно решить как можно больше математических примеров за определённый промежуток времени. Тренирует знание таблицы умножения, сложение и вычитание. А ещё содержит популярный математический пазл «2 048».

Веб-сервисы

Регулярно заниматься интеллектуальной зарядкой с числами можно и на математических онлайн-тренажёрах. Выбирайте необходимый вам тип действия и уровень сложности — и вперёд, к новым интеллектуальным вершинам. Вот лишь несколько вариантов.

• Математика.Club — тренажёр устного счёта.
• Школа Аристова — тренажёр устного счёта (охватывает двузначные и трёхзначные числа).
• «Развивайка» — тренировка устного счёта в пределах ста.
• 7gy.ru — тренажёр по математике (вычисления в пределах ста).
• Chisloboy — онлайн-игра на развитие скорости счёта.
• kid-mama — тренажёры по математике для 0–6 классов.

Читайте также 🧠🎓😤

маленькие секреты репетитора — Колпаков Александр Николаевич

Умеете ли Вы быстро считать? Этот вопрос можно задать не только школьникам и родителям, но и начинающим репетиторам по математике 5 — 9 классов. Как-то, прочитывая старую литературу по занимательной математике, я наткнулся на сообщение о том, что до революции, когда не было калькуляторов и компьютеров школьники, по крайней мере, в школе Рачинского, умели возводить в квадрат числа до 100 в уме. Не столбиком, а именно в уме. Как они это делали? Казалось бы, процесс достаточно трудоемкий, однако при ближайшем рассмотрении выясняется, что освоить возведение в квадрат может любой, даже не слишком продвинутый в математике ученик. Ну, например, сколько будет 96 в квадрате? Конечно, можно взять калькулятор, набрать нужные кнопки и получить ответ. Можно взять листок бумаги и подсчитать это столбиком. А можно и в уме. Вот о методах быстрого счета, с которым репетитор по математике ежедневно сталкивается в практике своей работе, я и расскажу в этой статье.

Какие вычисления производит репетитор по математике в уме?

За свою многолетнюю историю репетиторства я никогда и ни на одно занятие не брал и не беру с собой калькулятор, предпочитая пользоваться, главным образом, устным счетом.

Для начала возьмем пример попроще. Например, сколько будет 11232-9889 ? Конечно, можно подсчитать это столбиком, каждый раз занимая и ставя точки по этому поводу над каждой цифрой, но ведь можно сосчитать и в уме. Представим себе числовую ось. Репетитор по математике может сделать для нее схематический рисунок:
Сколько не хватает числу 9889 до 10000? – 111. А на сколько 11232 больше, чем 10000? На 1232. А теперь складываем 1232 и 111 и получаем результат: 1232+111=1343.

А теперь разберем пример посложнее – умножение. Сколько будет 64×15? Техника быстрого счета позволяет репетитору по математике дать молниеносный ответ. Это будет 960. Стоит только увидеть число 15 в каком-нибудь примере, как сразу возникает возможность быстрого счета. Как умножить число на полтора, т.е. на 1,5? Для этого надо взять само это число, прибавить к нему половинку от него самого и получить результат. Если в примере фигурирует на 1,5, а 15, или 150, то надо приписать еще справа определенное количество нулей. Ну, например, 64 плюс половинка от этого числа, то есть 32 и ноль приписываем. То есть 64+32=96 96×10=960.

Аналогичный пример, но в этом случае можно подсчитать разными способами. 84×25. Можно рассматривать 25 как 2,5×10. Иными словами взять 84 два раза и прибавить к полученному результату 42. 84+84+42=210. И приписываем ноль. Итого получаем 2100. А можно и по-другому. 84×0,25×100. То есть разбиваем 25 на 0,25 и 100. Зачем нам это надо? Дело в том, что 0,25 это ¼ (одна четвертая). Иными словами 84 делим на 4, получается 21, и приписываем два ноля. То есть получается те же 2100.

Подобные способы использования обыкновенных дробей достаточно многочисленны, и при должном желании репетитор по математике, хорошо знающий свой предмет, может придумать еще несколько таких. Вот, пример, из реального занятия. Ученику 5-го класса следовало подсчитать, сколько будет 375 умножить на 48. Правильно то, репетитор по математике запрещает пользоваться калькулятором. Но произвести вычисления столбиком в 5 классе — это значит потратить уйму времени. Тем не менее, такое произведение можно найди в уме. Что такое 375? – Это 125×3. Число 125 – это одна восьмая, умноженная на тысячу. Следовательно, превращаем 375 в три восьмых и умножаем на 1000, так как одна восьмая – это 125 тысячных – 0,125).

Далее 48 делим на восемь и умножаем на 3. Итого получается 48:8×3=18. И приписываем три ноля. Получается 18000. Казалось бы, подобные вычисление не менее сложны, чем подсчет столбиком. Однако при постоянной практике быстрого счета «сокращенные» вычисления репетитор по математике может довести до автоматизма.

Работа с формулами сокращенного умножения

Формулы сокращенного умножения, изучающиеся в 7-м классе, позволяют репетитору облегчить устный счет. В этой статье я не буду подробно рассматривать все приемы, думаю, что им легко обучиться самостоятельно. Например, ученик, знакомый с формулой разности квадратов без труда умножит в уме 43 на 37. Я же остановлюсь на правиле, позволяющем возводить в квадрат числа, оканчивающиеся на пятерку. Например, 25 в квадрате, 35 в квадрате, 45 в квадрате, 95 в квадрате. Правило такое. Для этого, количество десятков возводимого в квадрат числа (например, 95) умножить на число, которое на единицу больше (то есть на 10 в случае 95) и приписать 25. Получается 9025.

Почему так получается комментировать не буду, думаю, ученик, знакомый с формулами сокращенного умножения без труда поймет это. Более того, в некоторых школах, учителя знакомят учеников с таким методом. Однако на занятиях у репетитора по математике этому приему внимание практически не уделяется. Едва ли где говорится, что это знание в некоторых случаях помогает возводить в квадрат числа. Берем таблицу квадратов, имеющуюся в учебниках 7-го, 8-го, 9-го классов. Среди чисел, перечисленных в ней, есть т.н. «опорные» числа. Это, во-первых, 10, 20, 30, 40, ….90 и во-вторых, 15, 25, 35… 95. Это те числа, возвести которые в квадрат очень просто.

Теперь берем число 96 и возводим его в квадрат. Для этого репетитор по математике возводит в квадрат 95 и прибавляет 95+96. Число 95 в квадрате дает 9025. Прибавляем 200 и отнимаем (5+4 – числа, дополняющие 95 и 96 до ста). Пишем результат – 9216. Аналогичным способом при соответствующей тренировке можно возводить в квадрат любое число из таблицы квадратов, вплоть до того, чтобы показывать фокусы быстрого счета перед одноклассниками. Для тех, кто всё еще побаивается столь больших чисел, репетитор по математике упрощает объяснение принципа. Как это делается? Берем 4 в квадрате. Это будет 16. Берем 5 в квадрате. Это будет 25. Берем 6 в квадрате. Это будет 36. Зная 4 в квадрате, результат следующего числа в квадрате получается прибавлением к предыдущему суммы возводимых в квадрат чисел. Например, 5 в квадрате = 4 в квадрате + 5+4 (т.е. 16+9). Или 7 в квадрате = 36 (6×6) + (6+7) = 49.

Это далеко не все способы быстрого счета, которые встречаются в практике репетитора.

Аркуров А.А. Репетитор по математике, Москва

Магия чисел. Быстрый счет. | Проекты

Тема:            Необычные способы счета.

 

Название:  Быстрый счет — удел компьютера или нужный инструмент для человека в этой жизни?

 

Цель исследования: Изучив способы быстрого счета, выявить, насколько эти способы важны человеку в этой жизни.

 

Задачи исследования:

• Изучить теоретический материал относительно темы
• Рассмотреть различные методы быстрого счета
• Выбрать наиболее простые способы для запоминания
• Выявить насколько устный счет важен человеку в жизни
• Провести опрос «зачем нужен устный счет и каковы причины отказа современных учеников от устного счета»
• Проанализировать полученные результаты
• Сделать выводы

Гипотеза: Для быстрого счета лучше использовать компьютер, так как вручную это занимает много времени.

 

Методы исследования:  изучение и обобщение, анализ,  опрос.

 

Этапы исследования:

Тизер:

https://www.powtoon.com/online-presentation/exzixmsDAd6/?mode=presentation#/

Теория:

Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.

Иногда мы сталкиваемся с людьми, способными складывать, умножать и делить сложные числа молниеносно. Такие люди не обладают сверхъестественными способностями, они просто знают формулы упрощенного счета и регулярно тренируют свой навык.

Как научиться быстро,считать в уме? Предложенные методы помогут вам развить феноменальный талант быстрого счета.

Устный счет — это математические вычисления, проведенные в голове человека без использования дополнительных устройств – калькулятора, компьютера, счет, и разных приспособлений

Благодаря несложным вычислениям в уме можно решать многие бытовые задачи, не говоря уже о рабочих моментах. К тому же, если вы научитесь быстро считать в уме, то это существенно улучшит ваш имидж. Особенно важно это тем, кто имеет престижную работу, которая связана с вычислением.

Приемы устного счета, которым может обучиться каждый желающий, помогут научиться организовывать себя во всевозможных жизненных ситуациях.

https://prezi.com/view/15L5ImEqgYLGbgZXAeyA/

От чего зависит возможность быстро считать в уме:

 Способность. Чтобы действительно научиться быстро считать в уме, нужно иметь предрасположенность к математике и уметь логически мыслить. Кроме того человек должен уметь концентрировать внимание и держать в краткосрочной памяти сразу несколько вещей. Не каждый это может делать.

Алгоритмы. Нужно знать специальные алгоритмы, а также уметь их быстро подобрать в нужный момент. При этом необходимо быстро сориентироваться и выбрать именно максимально эффективный алгоритм в зависимости от конкретной ситуации. Этому со временем можно научиться.

Тренировка и опыт. Только при многочисленных тренировках можно выработать навыки устного счета. Нужно ставить себе задачи и выполнять их. Постепенно их следует усложнять и упражняться. Это поможет быстро набраться опыта и улучшить качество устного счета.

 

Результат исследования:

Умение считать в уме играет большую роль. Компьютер не всегда находится под рукой и существует множество ситуаций, когда человек вынужден считать в уме. Это хорошо пригодиться в жизни каждого человека. При этом самым важным аспектом будет выступать хорошее знание таблицы умножения. Ее нужно повторять как можно чаще, чтобы не забывать, и применять ее на практике. Не стоит пользоваться калькулятором при вычислении легких значений. Умея хорошо считать в уме, можно быть уверенными в том, что в магазине вас не обманут. Это же поможет контролировать свои покупки, ведь вы быстро сможете посчитать, на какую сумму товара уже взяли. Многим умение быстро считать в уме пригодится и при устройстве на работу. Даже в организациях, в которых не занимаются непосредственно математическими расчетами, при собеседовании могут попросить высчитать какие-либо действия в уме. Если человек справляется, у него будет больше шансов на получение хорошей должности, ведь это будет говорить об аналитическом складе ума. Еще одним доказанным фактом выступает то, что люди, которые часто считают в уме, а не прибегают к калькулятору при каждой возможности, меньше подвергаются раннему слабоумию, а также старческому маразму.

Таким образом, если у вас есть возможность и желание научиться быстрому устному счету, обязательно воспользуйтесь этим. Это хорошо помогает в жизни и некоторых бытовых ситуациях. К тому же, учитывая удобные алгоритмы и небольшие хитрости, научиться этому можно довольно быстро. Надеемся, что наши советы помогут вам освоить приемы быстрого счета в уме. Следует помнить, что теория – это лишь 20 % успеха. Остальные 80% — ваше желание и практика.

После проведения опроса (https://docs.google.com/forms/d/1_glLUECYvooPBLDILW2Z28BA-EHtBKKOreDzaBTidag/edit ) мы выяснили, что только около 8% опрошенных  редко решают без калькулятора , а 57,7% хотят изучать  предложенные нами способы в школе.

Вывод:

• Существует множество способов быстрых вычислений
• Большинство учащихся понимают, что устный счет пригодится в школе, при изучении разных предметов, в будущей профессии.
• Люди разных профессий используют устный счет в своей работе.

 

 

 

Быстрый счет — удел компьютера или нужный инструмент

Использованная литература:

1. Время полезных советов.

2.«1001 задача для умственного счёта в школе С.А. Рачинского»

 

 

 

уловок с умственной математикой для скоростной математики

Уловки мысленной математики в этом посте научат вас, как выполнять мысленную математику с такой скоростью и легкостью, которую вы раньше считали невозможной. Вы сможете выполнять сложные вычисления без помощи калькулятора полностью в своей голове. Немного потренировавшись, вы быстро освоите эти математические уловки в уме, чтобы выполнять скоростную математику. Вы почувствуете себя чрезвычайно уверенным в цифрах, как никогда раньше.

Сначала мы рассмотрим некоторые из простых, но все же впечатляющих вещей в качестве введения.Затем мы рассмотрим математические уловки для сложения и вычитания. Мы рассмотрим приемы умножения для ментальной математики в следующем посте. Эти техники требуют, чтобы вы использовали только свой разум. Вам следует держаться подальше от ручки, бумаги или калькулятора, когда вы изучаете и применяете методы.

У каждой техники мысленной математики будет два примера. Первый пример виден всем, но вам нужно будет зарегистрироваться / войти в систему, чтобы увидеть, как работает второй пример каждой техники.

Прежде чем мы перейдем к умственным математическим трюкам для выполнения скоростной математики, давайте быстро поймем, что такое множимое и множитель. Возьмем, к примеру, задачу умножения 43 x 23. Здесь 43 – это множимое – число, на которое перемножается, а 23 – это множитель – число, которое умножает первое число.

Попробуйте умножить 423 x 11. Это может занять некоторое время, если вы не знаете техники. Давайте посмотрим на математическую технику умножения на 11:

.

1. Первое число множимого (умноженное число) записывается как число слева в ответе.

1. Каждое последующее число множимого добавляется к его соседнему справа.

1. Последнее число множимого становится числом в правой части ответа.

Теперь вы попробуйте умножить 534 x 11. Процедура получения этого ответа такая же, как и раньше, и вы можете найти ее ниже:

Попробуйте умножить 619 x 11. Если вы сказали 67109, значит, вы совершили ошибку новичка, не перенеся это число.Перенос чисел – обычное дело в математике скорости. Шаги по умножению на 11 такие же, как и раньше, но с одной небольшой разницей.

1. Первое число множимого (умноженное число) записывается как левое число ответа, как и раньше.

1. Каждое последующее число множимого прибавляется к своему соседу слева, как и раньше. Если в результате сложения получается две цифры, перенесите 1 (Примечание: двухзначное число не будет больше 19), поэтому вы всегда будете переносить 1.

1. Последнее число умножаемого становится числом в правой части ответа, как и раньше.

Теперь вы попробуйте умножить 348 x 11. Процедура получения этого ответа такая же, как и в предыдущем примере, и вы можете найти ее ниже:

Теперь вы, должно быть, спросите, а как насчет умножения чисел, отличных от 11. Прежде чем мы перейдем к этому, очень важно понять умственные математические приемы для сложения и вычитания, поскольку это служит основой для умножения.В следующем посте мы рассмотрим приемы умножения для ментальной математики.

Решение математики справа налево – вот что затрудняет выполнение мысленных вычислений в уме. Секрет умственной математики состоит в том, чтобы решать слева направо, а не наоборот. В школе нас учат решать справа налево, потому что так проще решать математику на бумаге. Но когда дело доходит до решения математики в уме, верно обратное. Когда вы решаете слева направо, вы начнете называть ответ еще до того, как завершите полный расчет.Сначала это может показаться странным, но вы обнаружите, что это наиболее естественный способ производить вычисления в уме. Немного попрактиковавшись, вы очень быстро научитесь решать математику слева направо.

Применение секретов умственных математических уловок к сложению

Давайте применим секрет умственных математических уловок, чтобы сложить два числа 9881 + 1234.

Правило простое. Добавляйте слева направо. По одной цифре за раз.

Причина, по которой сложение слева направо выполняется быстро, заключается в том, что вам нужно помнить меньшие числа в уме, когда вы пытаетесь сложить слева направо.Также вы сразу же начнете называть ответ с самого первого шага процесса.

Теперь вы попробуете и добавьте 5321 + 1234. Процедура получения этого ответа такая же, как и в предыдущем примере, и вы можете найти ее ниже:

Сложение путем округления

Иногда добавление может привести к переносу большого количества чисел. Самая сложная задача сложения математических вычислений, с которой вы когда-либо сталкивались, – это когда вам нужно переносить числа на всех этапах.В этом случае легче добавить его, сначала округлив число в большую сторону, а затем вычтя округленную сумму. Мы посмотрим, как это сделать, когда добавим 5492 + 8739.

1. Округлить число

1. Сложить слева направо

1. Вычтите округленную сумму

Теперь вы можете попробовать, добавив числа 9881 + 1234. Процедура получения этого ответа такая же, как и в предыдущем примере, и вы можете найти работу ниже:

Применение секретов умственных математических уловок для вычитания

Техника вычитания в уме не отличается от сложения.Вы просто вычитаете слева направо. Давайте применим секрет умственных математических уловок, чтобы вычесть два числа 8431 – 5741.

1. Правило простое. Вычтите слева направо. По одной цифре за раз. При необходимости заимствуйте номера.

Теперь вы попробуете и вычтите 5389 – 1234. Процедура получения этого ответа такая же, как и в предыдущем примере, и вы можете найти ее ниже:

Вычитание округлением в большую сторону

Вычитание слева направо легко и просто, когда нет заимствования.Иногда вычитание может привести к заимствованию большого количества чисел у своего соседа. В этом случае легче вычесть, округлив число в большую сторону и добавив сумму, округленную в большую сторону. Давайте посмотрим, как это сделать, вычтя 4530 – 3898

.

1. Округлить число

1. Вычесть слева направо

1. Сложите округленную сумму.

Округляя в большую сторону, вы получаете проблему сложения вместо проблемы вычитания.В мысленной математике немного проще выполнять сложение, а не вычитание.

У вас могут возникнуть проблемы с определением суммы округления. Есть простой способ узнать, сколько вы округлили. Но прежде чем мы углубимся в это, вы попробуете вычесть числа 7520–4998. Процедура получения этого ответа такая же, как и в предыдущем примере, и вы можете найти рабочий ниже:

Когда мы вычитали 4530 – 3898, мы округлили 3898 до 4000.Вы округлили до 102. Может быть сложно определить, сколько вы округлили в данном случае до 102. Вам нужно будет добавить это в конце (шаг 3 нашего предыдущего примера).

Чтобы узнать, сколько вы округлили, когда вы округлили 3898 до 4000, вам нужно использовать дополнения. От 102 до 898 (последние три цифры 3 898 ).

Так как же найти дополнение числа? Все очень просто. Возьмем, к примеру, 898. Дополнение к этому числу также будет состоять из трех цифр.Число (898) должно складываться с его дополнением (102), чтобы получить 1000. Первые две цифры прибавят к 9, а последняя цифра прибавит к 10.

Если заметили:

1. Сумма первой цифры числа (8) и первой цифры его дополнения (1) дает 9.
2. Аналогичным образом вторая цифра числа (9) и вторая цифра его дополнения (0) в сумме дают 9.
3. Сумма последней цифры числа (8) и ее дополнения (2) дает 10.

Таким образом, последняя цифра числа должна складываться с последней цифрой его дополнения, чтобы получить 10.Все остальные цифры должны складываться с соответствующей цифрой в дополнении, давая 9.

Хорошо, помня вышесказанное, быстро найдите дополнение:

47, 351, 4352

Дополнения: 53, 649, 5648.

Все числа складываются до его дополнения, чтобы получить 9, за исключением последней цифры, добавляемой к 10. Используйте дополнения, чтобы найти, сколько вы округлили, когда вы выполняете вычитание. Чтобы попрактиковаться в округлении с использованием дополнений, в учебном пособии есть больше упражнений на вычитание.

Вы можете загрузить некоторые практические пособия по методам, описанным в этом посте ниже.

Если вы хотите поднять свои математические навыки на новый уровень, вы действительно можете многому научиться из моего личного пути. Я не всегда хорошо разбирался в математике. Я ненавидел это, и у меня это получалось ужасно. Я снял видео, чтобы поделиться своим личным путешествием и секретом, который я узнал, навсегда изменившим мои представления о математике. Нажмите здесь, чтобы посмотреть видео сейчас.

Если у вас есть какие-либо вопросы или пояснения по этому сообщению, оставьте их в разделе комментариев ниже.Возможно, вы уже поняли эту технику, но потребуется практика, прежде чем она станет для вас второй натурой. Поначалу вам будет трудно запомнить все числа в своей голове, пока вы работаете над проблемой. Но ваша память улучшится с практикой. Когда вы обнаружите, что в повседневной жизни обращаетесь к калькулятору, сначала рассчитывайте слева направо, а затем дважды проверьте свой ответ с помощью калькулятора. По мере практики ваша скорость и способность выполнять вычисления в уме улучшатся.

Этот пост служит основой для других продвинутых математических трюков. После того, как вы попрактикуетесь и освоите уловки ментальной математики, описанные здесь, вы можете переходить к следующему посту, в котором рассказывается о трюках умножения для ментальной математики.

[конец сообщения]

Тестовые стратегии по ментальной математике показали

Дэвид Лемм

Ментальная арифметика может быть быстрее (не говоря уже о более впечатляющей), чем использование телефона – все, что нужно, – это несколько уловок.

«Рассчитывайте в уме слева направо, а не справа налево, как на бумаге», – говорит «математик» Артур Бенджамин, соавтор книги Secrets Of Mental Math (Three Rivers Press).«После этого просто нужно потренироваться».

Разрежьте проблему на мелкие кусочки

Даже самые сложные задачи в области ментальной арифметики обычно можно разделить на простые – все, что нужно, – это небольшое сложение или вычитание. «Вот очень простой, но практичный пример: легко рассчитать десятипроцентные чаевые. Как рассчитать 15-процентные чаевые?

Итак, возьмите десятипроцентные чаевые, разрежьте их пополам и прибавьте к исходному. Таким образом, если счет составляет 40 фунтов стерлингов, десять процентов от этой суммы составляют 4 фунта стерлингов, а половина – это дополнительные 2 фунта стерлингов.Таким образом, 15 процентов от 40 фунтов стерлингов = 6 фунтов стерлингов ». Тот же принцип применим к 17,5 процентам.

Обратите внимание на дополнения

Дополнение – это расстояние между числом и ближайшим удобным круглым числом, обычно заканчивающимся на нулей. «Итак, дополнение к 78 составляет 22 – это число, которое вы добавляете, чтобы получить 100, – говорит Бенджамин. – На бумаге 1234 минус 678 беспорядок. Но вы начинаете с чрезмерного вычитания: 1234 минус 700 равняется 534. Я вычитал слишком много, поэтому мне приходится снова добавлять дополнение.Насколько 700 было больше 678? 22. Вы превратили сложную задачу вычитания в задачу простого сложения: 534 плюс 22 равно 556.

Победить и разделить

«Если у вас есть семизначное число, разделенное на трехзначное число, ответ будет четырехзначным числом или, возможно, еще одним », – говорит Бенджамин. (Тот же трюк можно использовать при умножении – просто сложите вместо этого.) «Следовательно, если вы собираетесь вычислить 4 000 000 деленных на 600, ваш ответ будет состоять из четырех цифр.Затем упростите: четыре шестых – это две трети, что составляет примерно 0,667. Вы знаете длину, поэтому вы знаете, что ваш ответ будет около 7000 ». (Это 6 666 667.)

Совет быть квадратом

Вот трюк для быстрого вычисления квадратных чисел. Что 24 ² ? Это проще, чем кажется на первый взгляд: «Спуститесь с четырех до ближайшего простого числа: 20. Чтобы сбалансировать его, поднимитесь с четырех до 28. Итак, первое вычисление 20 умножить на 28. Дважды 28 = 56, поэтому сложите ноль и ответ 560.Вы близки. Чтобы получить окончательный результат, все, что вам нужно сделать, это сложить квадрат числа, которое вы увеличили или уменьшили – в данном случае это было четыре, чтобы получить ваш ответ: 576. Итак, чтобы подвести итог, 24 x 24 = (20 x 28) + (4 x 4), что составляет 576. “

По возможности используйте ярлыки

” Существуют определенные типы проблем, для которых есть ярлыки, на которые можно быстро получить ответ “, – говорит Бенджамин. число на 11, сложите сумму его цифр, а затем вставьте ее между исходными числами.«Чтобы сложить 53 умножить на 11, нужно сложить пять плюс три, и получится 583.» Чтобы возвести в квадрат любое двузначное число, оканчивающееся на пять, ответ всегда будет заканчиваться на 25. «Вы берете первую цифру и умножаете ее на следующую, более высокую цифру.

Например, 352: трижды четыре равно 12, и оно оканчивается на 25. Итак, ваш ответ – 1225 “.

Эта статья была первоначально опубликована в апреле 2014 года.

Уловки с умственной математикой | Блестящая вики по математике и науке

Квадратный корень:

А. Уловка при работе с квадратными корнями состоит в том, чтобы знать, в каком диапазоне находится квадратный корень. Поскольку возведение в квадрат чисел, заканчивающихся на 0, и чисел, заканчивающихся на 5, очень просты, ответ можно относительно легко вычислить в пределах диапазона 5.

B. Если известно, что число представляет собой полный квадрат, то конечную цифру можно определить, посмотрев на последнюю цифру числа. В частности, если число заканчивается на

• 0, то конечной цифрой будет 0;
• 1, то конечная цифра – 1 или 9;
• 4, то конечная цифра – 2 или 8;
• 5, то конечной цифрой будет 5;
• 6, то конечная цифра – 4 или 6;
• 9, то конечная цифра – 3 или 7.

C. Найдя последнюю цифру (или возможность между двумя цифрами), мысленно отрежьте две последние цифры и сосредоточьтесь на оставшихся цифрах.

D. Теперь попробуйте найти диапазон 5, в котором находится число (на шаге C). Сделав это, вы узнаете ответ, используя шаг B. Сначала найдите диапазон 10, затем выясните, если ответ находится в верхней половине диапазона (т. е. заканчивается на 5, 6, 7, 8 или 9) или если ответ находится в нижней половине диапазона (т.е.е. он заканчивается на 0, 1, 2, 3 или 4) возведением в квадрат среднего числа (числа в диапазоне, заканчивающемся на 5).

Кубических корней:

Каждая цифра единиц в совершенном кубе совпадает с цифрой единиц в кубе числа (за исключением цифр 2, 3, 7 и 8, которые заканчиваются на 8, 7, 3 и 2 соответственно). Используя эту схему, вы можете быстро определить цифру единиц данного корня куба. Затем изучите блок чисел слева от цифры сотен. Определите самый большой идеальный куб, который меньше этого блока, и извлеките из него кубический корень.Возьмите результат и поместите цифру единиц измерения, найденную ранее, в конец, чтобы получить результат.

Быстро вычислить 2269813 \ sqrt [3] {226981} 3226981.

---

Последняя цифра – 1. Следовательно, 2269813 \ sqrt [3] {226981} 3226981 оканчивается на 1.

Блок цифр слева от разряда сотен – 226. Самый большой совершенный куб меньше 226 – это 216, что составляет 6 кубов. Следовательно, 2269813 \ sqrt [3] {226981} 3226981 начинается с 6.

Делаем вывод, что 2269813 = 61.□ \ sqrt [3] {226981} = 61. \ _ \ square3226981 = 61. □

Быстро вычислить 1488773 \ sqrt [3] {148877} 3148877.

---

Здесь 7 находится в последней цифре, что означает 1488773 \ sqrt [3] {148877} 3148877 заканчивается на 3.

Блок цифр слева составляет 148. Так как 125 – это наибольший совершенный куб меньше 148, первая цифра равна 5.

Следовательно, 1488773 = 53. □ \ sqrt [3] {148877} = 53. \ _ \ square3148877 = 53. □

6 ментальных математических стратегий | Советы и уловки для студентов

Когда у них нет под рукой манипуляторов или рабочих документов, учащиеся должны чувствовать себя комфортно, выполняя основную математику в уме.

К счастью, любой ребенок может это сделать, если он знает правильные советы и уловки .

Вот шесть умственных математических стратегий, которым можно научить ваших учеников. Вы дадите им уверенность, что они отложат калькулятор и начнут решать проблемы самостоятельно!

Округление до десяти

Работа с партиями по 10 значительно упрощает сложение и вычитание, потому что не требуется заимствование или перенос. Студенты могут максимально использовать это, округляя суммы до ближайших 10.

Уловка состоит в том, чтобы сохранить «лишние» числа, использованные для округления, а затем вычесть их в конце. Смоделируйте это для своих учеников с помощью числовой речи. Например, если сумма 57 + 48, ваш мыслительный процесс может быть:

• Я округлю эти числа до 60 + 50, потому что их легче сложить.
• Но я должен иметь в виду, что я дал себе дополнительные 5 для округления (3, чтобы превратить 57 в 60, и дополнительные 2, чтобы превратить 48 в 50). Когда я доберусь, мне придется вычесть эти 5 из своего окончательного ответа.
• Моя округленная сумма: 60 ​​+ 40 = 110.
• Минус 5 = 105.

Работать слева направо

На бумаге мы учим студентов решать многозначные суммы справа налево, начиная с единиц и заимствуя / перегруппировывая по мере необходимости.

Но если они делают это мысленно, они могут работать наоборот и не беспокоиться о том, чтобы отслеживать заимствования и перегруппировку. Возьмем для примера 34 + 17:

• Сначала мы добавляем 3 и 4 в столбец десятков, что дает нам 40.
• Теперь мы складываем 4 и 7 в столбце единиц, что дает нам 11.
• Добавьте 11 к 40, и мы получим 51.

Используйте хаки умножения

Запоминание таблиц умножения является серьезным математическим препятствием для большинства учащихся начальной школы, но становится намного проще, когда они запоминают следующие «уловки»:

• Любое количество умноженное на 1 остается неизменным.
• К любому числу, умноженному на 10, добавляется ноль.
• Любое число до 9 умноженное на 11 – это одна и та же цифра, повторяемая дважды (например,грамм. 99).

Вместе эти приемы мгновенно дают учащимся 60 фактов умножения, которые могут быть вычислены автоматически – без запоминания.

Переместите десятичную дробь, чтобы легко найти процент

Вычислить 10% чаевых в ресторане – одна из самых цитируемых задач по математике. К счастью, для этого есть чит, который легко запомнить.

Все, что нужно студентам, – это переместить десятичную запятую на одну позицию назад, и результат будет ровно 10% от исходной суммы.Таким образом, 25 долларов превращаются в 2,50 доллара, а 7,50 доллара в 75 центов.

Как только они овладеют навыками, учащиеся могут использовать множество 10%, чтобы быстро вычислить и другие проценты. Им нужно только удвоить его, чтобы получить 20%, или уменьшить вдвое, чтобы получить 5%. Сложите эти два вместе, и у них будет 25%.

Розничная терапия внезапно становится намного проще!

Сделайте предположения

В повседневной жизни математические вычисления в уме редко должны быть точными на 100%. Если это так, мы все равно тянемся за калькулятором или листом бумаги.

Скажите своим ученикам, что можно подойти к более сложной математической задаче, «угадывая» ответ.

Это может означать, что нужно просто работать с высшими разрядами в сумме и использовать это для вычисления, что ответ будет «около» определенного числа. Затем они могут проверить ответ с помощью тренировки.

Разберитесь в проблеме

Глядя на некоторые из этих математических стратегий в уме, вы можете задаться вопросом, почему они, кажется, используют гораздо больше шагов, чем подход из учебника.Разве это не сбивает с толку, когда ученики размышляют над этим в уме?

На самом деле, наоборот . Вместо того, чтобы сразу переходить к окончательному решению, учащиеся добьются гораздо большего успеха, если они разделят большую проблему на ряд более мелких, а затем будут систематически их решать.

Помните, маловероятно, что этот процесс будет происходить естественным образом для всех. Лучший способ научить этому – моделировать числовую речь, когда вы сами решаете проблему.Подумайте вслух и четко привлеките внимание к каждому шагу, через который вы проходите, чтобы прийти к окончательному решению.

Совет: потренируйтесь в этом сами перед тем, как стать моделью в классе. Многие мыслительные движения, которые вы делаете, могут быть настолько интуитивными и быстрыми (в конце концов, вы же учитель математики), что вы даже не узнаете их, пока не замедлитесь и не начнете делать заметки!

Нужна дополнительная помощь, чтобы отточить умственную математику ваших учеников?

Наш ассортимент онлайн-программ обучения математике был разработан с педагогической точки зрения, чтобы отточить умственную математику и свободное владение фактами с помощью увлекательных мероприятий, таких как живые соревнования и динамичные игры.Подпишитесь на бесплатную пробную версию и узнайте, почему их любят 5 миллионов студентов по всему миру.

Отточите умственную математику своих учеников с помощью наших программ онлайн-обучения

Изучите программы

Mental Maths | Уловки | Проблемы

Содержание

20 января 2021 г.

Время чтения: 5 минут

Введение

Бывают моменты, когда нам нужно производить мгновенные арифметические вычисления.Например, предположим, что вы идете в магазин, чтобы купить футболку, которая предлагает вам 10% скидку. Очевидно, у вас не будет ручки и бумаги для арифметических расчетов окончательной цены, которую вы должны заплатить.

Это времена, когда нужно быстро рассчитывать, и это тоже без каких-либо ресурсов. В такие времена вам может помочь только ваш мозг. Поэтому очень важно, чтобы каждый разработал определенные приемы для умственной математики в такие моменты.

Кроме того, один из математических фактов в уме состоит в том, что между мысленным расчетом и математическим рассуждением существует положительная корреляция.Таким образом, если вы увеличите свои умственные математические способности, ваши математические и логические навыки рассуждений увеличатся автоматически.

Также читайте:

---

Загрузить PDF

Вот несколько дополнительных моментов, касающихся навыков ментальной математики. Чтобы просмотреть их, нажмите кнопку «Загрузить».

📥

Ментальная математика: как ее улучшить?

Загрузить

---

Что такое ментальная математика?

Как следует из названия, ментальная математика относится к группе навыков, которые позволяют людям выполнять арифметические вычисления «в уме» без использования калькуляторов или других ресурсов.Ментальная математика полезна в повседневной жизни, чтобы отвечать на различные вопросы, например:

• Какова окончательная цена продажи конкретного товара?

• Какое правильное количество сдачи я должен получить от кассира?

• В какое время уехать, чтобы вовремя добраться до того или иного места?

---

Важность развития умственных математических навыков

В детстве легко понять и развить уловки для умственной математики.Их важно развивать, потому что:

• Это помогает учащимся лучше понять основные математические концепции и концепции более высокого уровня.

• Регулярное использование и решение задач по математике помогает ребенку улучшить его / ее чувство чисел. Например, что лучше? Покупка коробки из 12 шоколада за 100 рупий или покупка плитки индивидуального шоколада за 100 рупий. 10.

• Это помогает студентам решать задачи более высокого уровня с большей скоростью.

• Стимулирует мозг и делает его острее. Это развивает у учащихся воображение, визуализацию и творческие способности.

• Повышает уверенность в себе и самооценку студента.

• Это похоже на упражнение для мозга, которое сохраняет его здоровье.

• Имеет множество практических применений.

• Регулярные попытки пройти тесты по математике подготовят вас к академическим и конкурсным экзаменам.

Глядя на вышеупомянутые причины, становится ясно, что очень важно развивать эти умственные математические уловки. Эти навыки не врожденные. Существуют различные методы и техники улучшения навыков, которые подводят нас к следующему вопросу.

---

Как улучшить умственную математику?

Вот некоторые из способов улучшения умственных математических способностей детей: –

Один из самых основных и важных математических фактов заключается в том, что вы изучаете математические понятия на практике.Все мы начинаем медленно, но очень важно поставить перед собой задачу быстрее выполнять арифметические вычисления без использования документов или калькуляторов.

Это возможно только в том случае, если мы регулярно практикуем эти вычисления в нашем мозгу, используя наши умственные способности.

Даже если вам нужно время, чтобы что-то посчитать, рекомендуется использовать ручку и бумагу вместо калькулятора. Это помогает в развитии умственных способностей ученика. Вы заметите, что ваш мозг начинает медленно и неуклонно развивать эти навыки, и вам даже не потребуется ручка и бумага.

Ученики достигли возраста обучения. Поэтому очень важно, как старейшинам, поддерживать их на каждом этапе. Они могут потерять уверенность в своих силах. Поэтому очень важно поддерживать их на каждом шагу.

Мысленные вычисления включают в себя построение техник, касающихся конкретных проблем, а не запоминание ответов. Существуют различные инструменты и игры для развития этих умственных стратегий, такие как карточки, онлайн-видео, математические головоломки и т. Д.

Математика – предмет практический.Это можно сделать проще, если учащиеся разовьют привычку сравнивать уравнения и визуализировать их с примерами из реальной жизни.

Узнайте, как выполнять мысленную математику. Каждый ученик начинает с ручки и бумаги. Затем они должны перейти к вычислениям на пальцах, и со временем у них разовьется привычка считать в уме.

Обучение бесполезно, если оно не делается от всей души. Поэтому важно, чтобы это было весело и увлекательно.Это помогает ребенку не сдаваться и преодолевать неудачи.

Вы также можете использовать приложения / веб-сайты, которые содержат множество ресурсов по ментальной математике, а также тесты по ментальной математике, которые помогут вам отточить свои умственные навыки.

---

Как выполнять умственные математические трюки?

Некоторые математические приемы в уме объясняются с помощью простых математических задач следующим образом: –

1. Уловка чисел, близких к кратным 10

Выполните вычисления, кратные 10, а затем сложите / вычтите требования.

Например,

Чтобы прибавить 9 к любому числу, сначала добавьте 10, а затем вычтите 1. Например, 9 + 7 = 10 + 7 – 1 = 16.

76 + 99 можно изменить на 75 + 100.

Еще один пример: 107 + 105 = 100 + 100 + 12 = 212

2. Уловка двойных плюс один

Преобразуйте разные числа в одно и то же, а затем добавьте / вычтите потребность. Например, 5 + 6 на единицу больше, чем 5 + 5 +1 = 11, или 9 + 8 равно 9 + 9-1 или 8 + 8 +1 = 17.

3. Выполните сложение, разбив числа по разрядам

Например, предположим, что у нас есть следующий вопрос: 220 + 364 + 44 + 18 = ??

200 + 300 = 500

20 + 60 +40 +10 = 130

4 + 4 +8 = 16

Повторите процесс:

500 + 100 = 600

30 + 10 = 40

А на месте единицы имеем 6.

Теперь выполняем, 600 + 40 + 6 = 646

4. Вычесть, прибавив

Это немного сложно, но регулярная практика упрощает все.Например, если вас просят найти, что такое 87–46, представьте это как «46 плюс какое число равно 87?» Другими словами, подумайте о 46 + ___ = 87. Ответ на вычитание будет таким же, как и на произведенное сложение, т.е. 41.

5. Отличный трюк

Чтобы найти 5 раз любое число, сначала умножьте это число на десять, а затем возьмите половину этого числа. Например, 5 × 58 можно найти, умножив 10 × 58 = 580 и взяв половину, т.е.е. 290. Мы можем использовать эту стратегию для создания других комбинаций, но для этого сначала нужно очень крепко владеть этими базовыми математическими концепциями.

6. Четыре и восемь чисел

Чтобы найти четырехкратное число, удвойте это число дважды. Например, что такое 4 × 72? Сначала найдите 72 x 2 = 144. Затем удвойте это, 144 x 2 = 288. Точно так же восемь умноженное на число просто означает удвоение три раза.Продолжая наш пример, если нам нужно найти 8 × 72, нам просто нужно еще раз удвоить 288, что даст 576.

7. Умножение по частям

Это довольно простая стратегия. Предположим, мы должны мысленно найти 3 × 74. Мы можем разбить его на части, например, 3 × 70 и 3 × 4, а затем сложить результаты. Получим 210 + 12 = 222.

---

Заключение

Регулярное использование и решение мысленных математических задач помогает ребенку улучшить свое чувство чисел и лучше понять основные математические концепции и концепции более высокого уровня.

Умственные математические навыки одинаково полезны как в повседневной, так и в академической жизни. Вы можете следовать вышеупомянутым советам, чтобы улучшить это. Вы даже можете продемонстрировать свои навыки быстрого расчета перед друзьями!

---

О компании Cuemath

Cuemath, удобная для учащихся платформа математики и кодирования, проводит регулярные онлайн-классы для преподавателей и развития навыков, а их приложение Mental Math для iOS и Android представляет собой универсальное решение для детей, развивающее несколько навыков.Ознакомьтесь со структурой Cuemath Fee и подпишитесь на бесплатную пробную версию.

---

Часто задаваемые вопросы (FAQ)

Что такое ментальная математика?

Под умственной математикой понимается группа навыков, которая позволяет людям выполнять арифметические вычисления «в уме» без использования калькуляторов или других ресурсов. t помогает учащимся лучше понять основы математики и концепции более высокого уровня

Как улучшить умственные математические навыки?

Регулярная практика и расчеты без использования калькуляторов помогут вам улучшить умственные математические навыки.Продолжайте заставлять себя выполнять сложные вычисления в уме. Существуют различные инструменты и игры для развития этих умственных стратегий, такие как карточки, онлайн-видео, математические головоломки и т. Д.

---

Внешние ссылки

Чтобы узнать больше о ментальной математике, посетите эти блоги:

4 забавных способа улучшить навыки умственной математики вашего ребенка

Понимание простых математических фактов может дать учащимся огромное преимущество в школе. Мысленно решая базовые задачи на сложение и вычитание, ребенок может повысить беглость математики, что позволит ему легче продвигаться к математике более высокого уровня.

Игра в простые, но увлекательные математические игры – это фантастический способ не только развить умственные математические способности вашего ребенка, но и идеальный способ улучшить числовые факты. Вот несколько наших любимых занятий.

Война умножения

С этой веселой карточной игрой ваш ребенок быстро овладеет фактами умножения! Перетасуйте колоду карт и раздайте их рубашкой вверх, давая каждому игроку равное количество карт. Присвойте карточкам с картинками значение 10, а тузам – значение 11.Каждый игрок переворачивает две карты лицом вверх, читает числовое предложение и дает ответ. Например, если ваш ребенок рисует 7 и 8, он говорит, что 7 × 8 = 56. Если вы возьмете 6 и 4, вы скажете, что 6 × 4 = 24. Поскольку его продукт больше, он выигрывает четыре карты и кладет их в конец своей стопки. Продолжайте игру, пока у одного игрока не закончатся карты.

Ментальная тайна

Попросите ребенка отсчитать пять маленьких предметов, таких как пенни, шарики или конфеты, и попросить его закрыть глаза.Затем спрячьте некоторые из пяти предметов, оставив остальные открытыми. Попросите ребенка подсчитать, сколько предметов он видит и сколько предметов закрыто. Практикуйте это задание, пока ваш ребенок не сможет быстро решить эти простые уравнения. Добавьте один дополнительный объект, как только ваш ребенок освоит этот уровень, чтобы увеличить сложность. Для детей постарше начните с 10-20 предметов.

101 и выход

Для игры вам понадобятся лист бумаги, карандаш и один кубик. Цель игры состоит в том, чтобы набрать как можно больше очков, не превышая 101.Игроки по очереди бросают кости. Во время броска вы можете принять число либо за единицу, либо за десятку. Например, если вы выбрасываете 5, это может быть равно 5 или 50. Игроки ведут текущий учет своего общего количества во время игры. Эта игра – отличный способ построить умственные математические стратегии, поскольку дети часто критически думают о том, какое число им нужно бросить следующим.

Математическая опасность

Дайте ребенку лист бумаги и назовите число. Дайте им одну минуту, чтобы найти как можно больше способов составить число, используя сложение, вычитание, умножение и деление.

Изучение базовых, но полезных математических стратегий может значительно повысить уверенность вашего ребенка в себе.

9 умственных математических приемов и игр для учащихся

Ментальная математика углубляет понимание учащимися основных математических понятий. Кроме того, знание того, что они могут заниматься мысленной математикой где угодно, не полагаясь на карандаши, бумагу или манипуляторы, дает учащимся чувство успеха и независимости. Освоив математические приемы и методы, учащиеся часто могут найти ответ на математическую задачу за то время, которое им потребовалось бы, чтобы вытащить калькулятор.

Вы знали?

На ранних этапах обучения математике использование математических манипуляторов (например, бобов или пластиковых счетчиков) помогает детям визуализировать и понимать взаимно однозначное соответствие и другие математические концепции. Как только дети усвоят эти концепции, они будут готовы начать изучение математики в уме.

Уловки с мысленной математикой

Помогите учащимся улучшить свои математические навыки с помощью этих математических приемов и стратегий. С помощью этих инструментов в своем математическом наборе ваши ученики смогут разбивать математические задачи на управляемые и решаемые части.

Разложение

Первый трюк, разложение, просто означает разбиение чисел на развернутую форму (например, десятки и единицы). Этот трюк полезен при обучении сложению двузначных чисел, поскольку дети могут раскладывать числа и складывать одинаковые числа. Например:

25 + 43 = (20 + 5) + (40 + 3) = (20 + 40) + (5 + 3).

Ученикам легко понять, что 20 + 40 = 60 и 5 + 3 = 8, в результате получается 68.

Разложение или разделение на части также можно использовать для вычитания, за исключением того, что самая большая цифра всегда должна оставаться нетронутой.Например:

57 – 24 = (57 – 20) – 4. Итак, 57 – 20 = 37, а 37 – 4 = 33.

Компенсация

Иногда учащимся полезно округлить одно или несколько чисел до числа, с которым легче работать. Например, если ученик складывает 29 + 53, ему может быть проще округлить 29 до 30, и тогда он легко увидит, что 30 + 53 = 83. Затем ему просто нужно убрать «лишнее». 1 (который он получил после округления 29), чтобы получить окончательный ответ 82.

Компенсацию также можно использовать с вычитанием. Например, при вычитании 53 – 29 ученик может округлить 29 до 30: 53 – 30 = 23. Затем ученик может сложить 1 из округления, чтобы получить ответ 24.

Сложение

Еще одна умственная математическая стратегия вычитания – это сложение. С помощью этой стратегии учащиеся составляют следующие десять. Затем они считают десятки, пока не достигнут числа, из которого они вычитают. Наконец, они вычисляют оставшиеся.

В качестве примера возьмем задачу 87 – 36. Ученик собирается сложить до 87, чтобы мысленно вычислить ответ.

Она может прибавить 4 к 36, чтобы получить 40. Затем она будет считать по десяткам, чтобы получить 80. Пока что ученица определила, что есть разница в 44 между 36 и 80. Теперь она складывает оставшиеся 7 единиц из 87 (44 + 7 = 51), чтобы вычислить, что 87-36 = 51.

пары

После того, как учащиеся выучат пары (2 + 2, 5 + 5, 8 + 8), они смогут использовать эту базу знаний для мысленной математики.Когда они сталкиваются с математической задачей, близкой к известному факту о двойниках, они могут просто сложить их и скорректировать.

Например, 6 + 7 близко к 6 + 6, которое, как известно ученику, равно 12. Затем все, что ему нужно сделать, – это добавить еще 1, чтобы получить ответ 13.

Ментальные математические игры

Покажите ученикам, что математика может быть интересной с помощью этих пяти активных игр, идеально подходящих для учеников младшего возраста.

Найди числа

Напишите на доске пять чисел (напр.грамм. 10, 2, 6, 5, 13). Затем попросите учащихся найти числа, соответствующие приведенным вами утверждениям, например:

• Сумма этих чисел составляет 16 (10, 6)
• Разница между этими числами 3 (13, 10)
• Сумма этих чисел составляет 13 (2, 6, 5)

При необходимости продолжайте вводить новые группы чисел.

Группы

Получите удовольствие от учеников в классах K-2, практикуя мысленную математику и навыки счета в этой активной игре.Скажите: «Соберитесь в группы по…», а затем укажите математический факт, например, 10–7 (группы по 3 человека), 4 + 2 (группы по 6 человек) или что-нибудь более сложное, например 29–17 (группы по 12 человек).

Встать / сесть

Прежде чем задавать ученикам мысленную математическую задачу, попросите их встать, если ответ больше определенного числа, или сесть, если ответ меньше. Например, попросите учащихся встать, если ответ больше 25, и сесть, если ответ меньше. Затем произнесите: «57-31.”

Повторите это с большим количеством фактов, суммы которых больше или меньше выбранного вами числа, или каждый раз меняйте номер стойки / сидения.

Номер дня

Каждое утро пишите на доске число. Попросите учащихся предложить математические факты, равные количеству дня. Например, если число 8, дети могут предложить 4 + 4, 5 + 3, 10-2, 18-10 или 6 + 2.

Предложите учащимся старшего возраста придумывать предложения по сложению, вычитанию, умножению и делению.