Главная
Математика дифференциалы: Недопустимое название | Математика | Fandom

Математика дифференциалы: Недопустимое название | Математика | Fandom

Содержание

Дифференциал, Свойства дифференциала | univer-nn.ru

Основные дифференциалы

Дифференциал функции обладает свойствами, аналогичными свойствам производной.
  1. Дифференциал постоянной равен нулю:dc = 0, с = const.
  2. Дифференциал суммы дифференцируемых функций равен сумме дифференциалов слагаемых:
    d(u+v)=du + dv
    Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны
    d(u+c) = du (c= const).
  3. Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой:
    d(uv) = udv + vdu.
    Следствие. Постоянный множитель можно выносить за знак дифференциала
    d(cu) = cdu (с = const).
  4. Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой
  5. Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной на дифференциал аргумента независимого от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.

Дифференциалы высших порядков.

Если х — независимая переменная и y = f(x) — дифференцируемая функция, то dx = f'(x)dx, т. е. дифференциал функции есть функция, зависящая от двух аргументов х и dx. Этот дифференциал будем называть также дифференциалом первого порядка (или первым дифференциалом).

Считая dx постоянной, получаем, что df(x) — функция одной переменной. Предположим, что функция у = f(x) имеет не только первую производную, но и n последовательных производных y» = f»(x), y’” = f”’(x).

Дифференциал от дифференциала функции у = f{x) называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y = d(dy), причем

Дифференциалом n-го порядка Смотрите пример вычисления дифференциалов первого и второго порядков
youtube.com/v/yxXZjmlY7bc?version=3″ />Помощь в решении задач по математике Вам окажут тут

Примеры работ

Материалы сайта

Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.

ДИФФЕРЕНЦИАЛ | Энциклопедия Кругосвет

Содержание статьи

ДИФФЕРЕНЦИАЛ – линейная часть приращения

функции. Пусть функция y = f(x) дифференцируема на отрезке [a,b]. Производная этой функции в некоторой точке x отрезка [a,b] определяется равенством

.

ДИФФЕРЕНЦИАЛ – линейная часть приращения функции. Пусть функция y = f(x) дифференцируема на отрезке [a,b]. Производная этой функции в некоторой точке x отрезка [a,b] определяется равенством

.

Отношение стремится к определенному числу f ў(x) и, следовательно, отличается от производной f ў(x) на величину бесконечно малую:

,

где a ® 0 при Dx ® 0.

Умножение всех членов последнего равенства на Dx дает

Dy = fў(x) Dx + aDx.

Так как, то приращение Dy функции состоит из двух слагаемых, из которых первое слагаемое есть (при f ў(x) № 0) так называемая главная часть приращения, линейная относительно Dx. Произведение f ў(x)Dx называют дифференциалом функции и обозначают через

dy или df(x):

dy = f ў(x)Dx

Можно найти дифференциал функции y = x. В этом случае yў = (x)ў = 1 и, следовательно,

Dy = dx = Dx. Таким образом, дифференциал dx независимой переменной x совпадает с ее приращением Dx.

Дифференциалы различных порядков.

Дифференциал функции y = f(x), где x – независимая переменная, есть dy = f ў(x)dx, некоторая функция от

x, но от x может зависеть только первый сомножитель f ў(x), второй же сомножитель (dx) является приращением независимой переменной x и от значения этой переменной не зависит. Так как dy есть функция от x, то можно определить дифференциал этой функции. Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y:

d(dy) = d2y = f ўў(x)(dx)2.

Дифференциалом

n-го порядка называется первый дифференциал от дифференциала n- 1–го порядка:

dny = d(dn–1y) = f(n)(x)dx(n).

В этом случае:

полный дифференциал df

Если функция зависит не от одного, а от нескольких аргументов xi (i изменяется от1 до n, I = 1,2,…n), f(x1, x2,…xn), то можно рассматривать приращение функции при изменении одного или нескольких (в том числе и всех) аргументов и аналогично функции одной переменной вводить понятие дифференциала как приращения каждого из меняющихся аргументов. Тогда можно записать полный дифференциал

df как линейную часть полного приращения функции при приращении всех ее аргументов

Здесь – частная производная по переменной xn .

Cм. также ПРОИЗВОДНАЯ.

Анна Чугайнова

Проверь себя!
Ответь на вопросы викторины «Математика»

Как звали математика, который в 19 лет решил задачу, не поддававшуюся усилиям лучших геометров со времен Евклида?

Для чего был изобретен интеграл и дифференциал, какое математическое действие лежит в их основе и их значение для естественных и технических наук?

В отличие от других ответчиков я начну с интеграла, а не с производной. Интеграл в жизни имеет конкретный физический смысл. Это площадь фигуры ограниченной осью абцисс Х и графиком функции. Далеко от жизни? Сейчас приблизим. Представим себе машину, которая едет. Отложим по оси Х время в пути, а по Y – скорость в каждый, конкретный момент времени, и начертим график скорости от времени. Если скорость постоянная – это будет горизонтальная прямая. Фигура ограниченная этой прямой и осью Х – будет прямоугольником. Ширина прямоугольника – время в пути, а высота – скорость машины. Ширина*высота=площадь. Но при этом время*скорость=расстояние. Т.е. расстояние равно площади! И пройденное расстояние – это интеграл скорости.

А теперь начинается магия математики. Как посчитать путь, который пройдет машина, если у неё непрерывно меняется скорость, и её график извилистая кривая? А очень просто. Ведь ничего не изменилось – надо только найти площадь фигуры на графике! Как мы будем искать эту площадь – не важно. Можно просто посчитать клеточки на бумаге (это будет численным интегрированием, которое всегда приблизительное). А если скорость описана функцией от времени – можно найти её интеграл и сразу получить точный ответ.

А диференцирование – это это действие обратное интегрированию. Если продиференцировать функцию расстояния от времени, которую получили интегрированием скорости – мы обратно получим скорость. Ту самую скорость, с которой меняется пройденный путь машины. Сейчас скорость большая, километровые столбы мелькают, и пройденный путь быстро растет, а когда скорость падает и пройденные километры набираются медленно. На графике пути от времени, скорость это наклон самого графика. Грфик идет вверх – скорость положительная, мы едем вперед и расстояние растет. График пошел вниз – скорость отрицательная, мы едем обратно, а расстояние до точки старта уменьшается. График горизонтальная линия (наклона нет) -скорость равна нулю, мы стоим и расстояние неизменно.

Немного решил дописать.

Вообще интеграл в изменяющихся физических процессах очень востребован. А любой процесс описывает какую-то жизненную ситуацию.

Это сколько воды натекло через трубу в пресловутый бассейн при переменном напоре. Сколько киловатт накрутил электросчетчик при переменной нагрузке на сеть. До какой температуры нагрелась вода в кастрюле, если в процессе нагрева мы регулировали мощность плиты.

Любой процесс изменяемый во времени можно интегрировать и получить полезный результат. То же касается и дифенциала, который показывает скорость изменения общего результата.

Практическая работа по математике “Дифференциал.

Применение дифференциала в приближенных вычислениях”

Практическая работа

Вариант 1

Вариант 2

1) Вычислить дифференциалы функций

;

2) Найти приближенное значение приращения функции

     при x = 2 и

 т. е.

Решение:

3) Найти приближенное значение функции у

= 5 при x = 2,01.

Решение:

2,01 = 2 + 0,01, т.е.  x = 2 и

dy = у

,  откуда

,

= 39 + 58=39 + 0,58 = 39,58

4) Найти приближенное значение приращения функции:

при x = 3 и

при x = 2 и

5) Найти приближенное значение функции:

при x = 2,01

при x = 3,02

6) Найти приближенные значения степеней:

7) Найти приближенные значения корней:

8) Найти приближенные значения дробей:

Дифференциал. Применение дифференциала в приближенных вычислениях

Открытое образование – Дифференциальное исчисление функций одной переменной

Курс «Дифференциальное исчисление функций одной переменной» является базовой составляющей в образовании современного инженера. Включает в себя следующие разделы: теория пределов; непрерывность функций, зависящих от одной переменной; производная и дифференциал функций одной переменной; применение дифференциального исчисления к исследованию функций одной переменной и построению их графиков. В курсе рассматриваются приложения дифференциального исчисления к решению инженерных, экономических и других задач.

В состав курса входят видео-лекции продолжительностью 6-10 минут, материалы для самостоятельного изучения пользователями, анимационные ролики с инфографикой.

Разделы курса завершаются тестами на понимание материала (15-20 вопросов).

Для полноценного освоения учебного материала по дисциплине студент должен использовать знания, полученные предварительно в объеме, предусмотренном программами общего среднего образования, а также знания и умения, приобретаемые в процессе изучения модуля “Аналитическая геометрия и линейная алгебра” дисциплины “Математика”.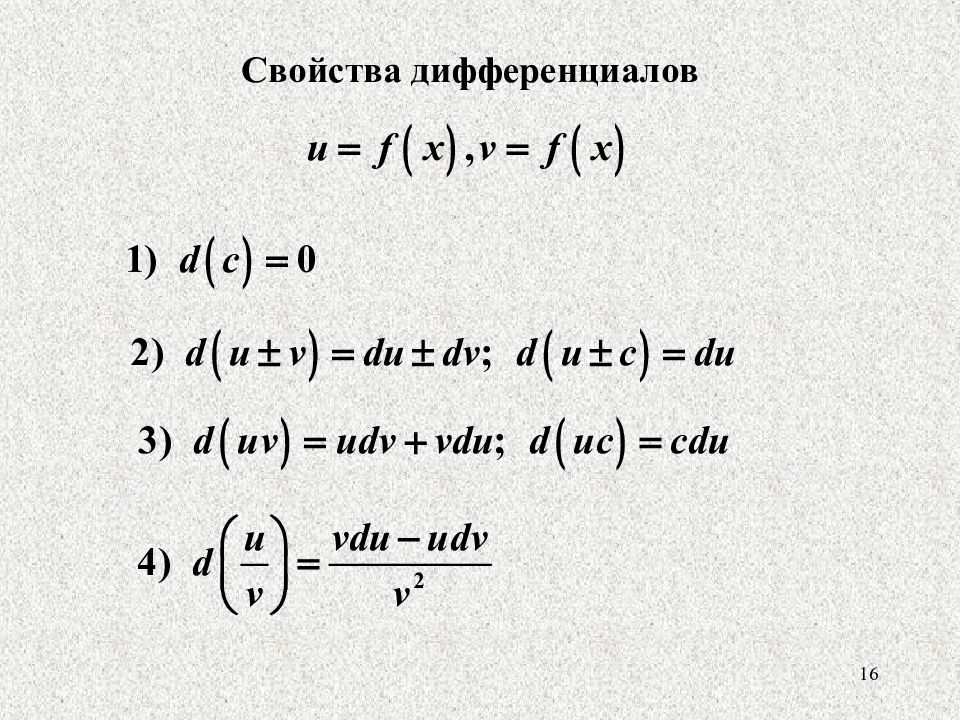 Кроме того, для иллюстрации методов применения дифференциального исчисления также необходимы знания по другим общеобразовательным и специальным дисциплинам, приобретаемым в процессе обучения.

Курс состоит из 9 разделов и 12 недель обучения: 

Неделя 1
Раздел I. Введение
Урок 1. О роли математики в инженерном образовании обучающихся
Урок 2. Математическая символика. Множества. Числовые множества. 
Урок 3. Ограниченные и неограниченные множества. Точные грани числового множе-ства
Урок 4. Теорема существования точной верхней грани у ограниченного сверху число-вого множества
Урок 5. Понятие числовой функции действительной переменной. Область определе-ния и область значений функции. Способы задания функции. 
Урок 6. Четные и нечетные функции
Урок 7. Периодические функции. Ограниченные и неограниченные функции
Урок 8. Монотонные функции. Обратная функция
Урок 9. Преобразование графиков функций. Графики основных элементарных функ-ций

Неделя 2
Раздел II. Числовые последовательности
Урок 1. Понятие числовой последовательности. Определение предела числовой по-следовательности. Примеры
Урок 2. Окрестность точки. Единственность предела числовой последовательности. Ограниченные последовательности
Урок 3. Ограниченность сходящейся последовательности. Арифметические операции над последовательностями. Бесконечно малые и бесконечно большие последова-тельности
Урок 4. Свойства бесконечно малых последовательностей. Бесконечно большие по-следовательности и их свойства
Урок 5. Арифметические операции над сходящимися последовательностями
Урок 6. Неопределенные выражения. Предельный переход в неравенствах
Урок 7. Монотонные последовательности. Точные грани последовательности. Суще-ствование предела у ограниченной монотонной последовательности (теорема Вейер-штрасса)
Урок 8. Число е
Урок 9. Принцип вложенных отрезков. Подпоследовательность числовой последова-тельности
Урок 10. Частичный, нижний и верхний пределы последовательности. Существование частичного предела у ограниченной последовательности. Теорема Больцано-Вейерштрасса. Фундаментальная последовательность
Урок 11. Критерий Коши существования предела последовательности

Неделя 3
Раздел III. Предел функции
Урок 1. Два определения предела функции в точке, их эквивалентность. Критерий Коши существования предела функции
Урок 2. Пределы функции в точке слева и справа (односторонние пределы)
Урок 3. Свойства функций, имеющих предел
Урок 4. Бесконечно малые и бесконечно большие функции. Их свойства
Урок 5. Асимптоты графика функции и способы их отыскания
Урок 6. Первый замечательный предел и его следствия
Урок 7. Второй замечательный предел и его следствия
Урок 8. Сравнение функций. Эквивалентные функции
Урок 9. Сравнение функций. Символы «о-малое» и «О-большое»
Урок 10. Асимптотическое представление функций

Неделя 4
Раздел IV. Непрерывность функции
Урок 1. Определение непрерывности функции в точке
Урок 2. Односторонняя непрерывность функции в точке. Точки разрыва, их класси-фикация
Урок 3. Свойства функций, непрерывных в точке
Урок 4. Свойства функций, непрерывных на отрезке. Первая и вторая теоремы Вей-ерштрасса
Урок 5. Свойства функций, непрерывных на отрезке.  Теоремы о нулях и о промежу-точных значениях непрерывной на отрезке функции
Урок 6. Непрерывность обратной функции
Урок 7. Непрерывность элементарных функций

Неделя 5
Раздел V. Производная и дифференциал функции
Урок 1. Определение производной функции в точке. Физический смысл производной
Урок 2. Физический смысл производной: продолжение. Вычисление производной си-нуса
Урок 3. Геометрический смысл производной
Урок 4. Дифференцируемость и дифференциал. Непрерывность дифференцируемой функции
Урок 5. Связь дифференциала и производной
Урок 6. Связь дифференциала и производной: примеры
Урок 7. Правила дифференцирования функции с постоянным множителем, суммы и разности функций
Урок 8. Правила дифференцирования произведения и частного функций
Урок 9. Теорема о производной обратной функции: формулировка и доказательство

Неделя 6
Урок 10. Теорема о производной обратной функции: примеры
Урок 11. Производная сложной функции: постановка задачи
Урок 12. Производная сложной функции: теорема. Инвариантность формы первого дифференциала
Урок 13. Производная сложной функции: примеры
Урок 14. Производная логарифма и экспоненты
Урок 15. Производная степенной функции. Производная тангенса и арктангенса
Урок 16. Таблица производных основных элементарных функций.
Урок 17. Применение дифференциала для приближенных вычислений значений функции

Неделя 7
Раздел VI.  Производные и дифференциалы высших порядков. Теоремы о дифференцируемых функциях
Урок 1. Производные высших порядков: определение
Урок 2. Производные высших порядков: примеры
Урок 3. Дифференциалы высших порядков
Урок 4. Неинвариантность формы высших дифференциалов
Урок 5. Правило Лейбница для нахождения производных высших порядков от произ-ведения функций: начало
Урок 6. Правило Лейбница для нахождения производных высших порядков от произ-ведения функций: доказательство. Метод индукции 
Урок 7. Правило Лейбница для нахождения производных высших порядков от произ-ведения функций: пример

Неделя 8
Урок 8. Дифференцирование функции, заданной в параметрическом виде: постановка задачи
Урок 9. Дифференцирование функции, заданной в параметрическом виде: вывод формулы
Урок 10. Основные теоремы о дифференцируемых функциях. Теорема Ферма: лемма о связи знака производной и монотонности в точке
Урок 11. Теорема Ферма: формулировка и доказательство
Урок 12. Основные теоремы о дифференцируемых функциях. Теорема Ролля о нулях производной
Урок 13. Основные теоремы о дифференцируемых функциях. Теорема Лагранжа (формула конечных приращений)
Урок 14. Основные теоремы о дифференцируемых функциях. Теорема Коши (обоб-щенная формула конечных приращений)

Неделя 9
Раздел VII. Правило Лопиталя.  Формула Тейлора
Урок 1. Правило Лопиталя раскрытия неопределенностей вида 0/0 
Урок 2. Правило Лопиталя. Неопределенность вида «0/0». Примеры
Урок 3. Правило Лопиталя. Неопределенность вида «бесконечность делить на беско-нечность»
Урок 4. Правило Лопиталя. Неопределенность вида «бесконечность делить на беско-нечность» при бесконечно больших аргументах
Урок 5. Правило Лопиталя. Другие виды неопределенностей

Неделя 10
Урок 6. Формула Тейлора для многочлена
Урок 7. Формула Тейлора с остаточным членом в форме Пеано
Урок 8. Разложения основных элементарных функций по формуле Тейлора
Урок 9. Разложения основных элементарных функций по формуле Тейлора: компози-ции функций
Урок 10. Вычисление пределов с помощью формулы Тейлора
Урок 11. Формула Тейлора с остаточным членом в форме Лагранжа.
Урок 12. Формула Тейлора с остаточным членом в форме Лагранжа: применение для приближённых вычислений значений функции

Неделя 11
Раздел VIII. Применение производной к исследованию функции. Поведение функции на интервале
Урок 1. Критерии постоянства и монотонности функции на интервале
Урок 2. Локальный экстремум функции. Необходимое условие локального экстрему-ма. Первое достаточное условие экстремума
Урок 3. Другие достаточные условия локального экстремума
Урок 4. Направление выпуклости и точки перегиба графика функции
Урок 5. Общая схема исследования функции одной переменной и построение ее гра-фика
Урок 6. Решение задач на исследование функций
Урок 7. Отыскание наибольшего и наименьшего значений функции на отрезке

Неделя 12
Раздел IX. Приложения дифференциального исчисления
Урок 1. Приложения дифференциального исчисления в горном деле. Задачи, приво-дящие к понятию производной
Урок 2. Приложения дифференциального исчисления в горном деле. Задачи, приво-дящие к понятию дифференциала
Урок 3. Приложения дифференциального исчисления к задачам экономики
Урок 4. Приложения дифференциального исчисления к теории информации
Урок 5. Приложения дифференциального исчисления к финансовой математике
Урок 6. Приложения дифференциального исчисления к логистической функции

В результате освоения курса студент:

●     знает основные определения и понятия дифференциального исчисления, основные теоремы дифференциального исчисления функций одной переменной;

●     находит пределы последовательностей и функций, производную и дифференциал функции, производные высших порядков;

●     классифицирует точки разрыва;

●     применяет теорему Лопиталя и формулу Тейлора для вычисления пределов;

●     знает основы построения графиков функций без производной и с применением производной;

●     понимает, как дифференцировать функции, зависящие от одной переменной;

●     понимает, в каких сферах человеческой деятельности применяется дифференциальное исчисление.

ОПК-1. Способен решать задачи профессиональной деятельности, применяя методы моделирования, математического анализа, естественнонаучные и общеинженерные знания

Производные, определение производных, дифференциалов, правила для дифференциалов

Определение производной

Если y = f(x), производная функции y или f(x) по отношению к x определяется как
13.1           
где h = Δx. Производная также обозначается как y’, df/dx от f'(x). Процесс взятия производной называется дифференцированием.

Общие правила дифференцирования

В нижеследующем u, v, w есть функции x; a, b, c, n – константы [ограниченные, если указано]; e = 2.71828… есть натуральная основа логарифмов; ln u – натуральный логарифм u [т.е. логарифм по основанию е] где предполагается, что u > 0 и все углы – в радианах.

Производные тригонометрических и обратных тригонометрических функций
Производные экспоненциальных и логарифмических функций

Производные гиперболических и обратных гиперболических функций


Высшие производные

Вторая, третья и более высокие производные определяется следующим образом.
13.43 Вторая производная = (d/dx).(dy/dx) = d2y/dx2 = f”(x) = y ”
13.44 Третья производная = (d/dx).(d2y/dx2) = d3/dx3 = f”'(x) = y”’
13.45 n-ая производная = (d/dx).(dn – 1/dxn – 1) = dn/dxn = f(n)(x) = y(n)

Правило Лейбница для высших производных произведения

Пусть Dp с оператором dp/dxp так, что DP u = dpu/dxp = p-ый дериватив u. Тогда
13.46       
где есть биномиальные коэффициенты.

Как особый случай, мы имеем
13.47        
13.48        

Дифференциалы

Пусть y = f(x) и Δy = f(x + Δx) – f(x). Тогда
13.49          Δy/Δx = [f(x + Δx) – f(x)]/Δx = f'(x) + ε = dy/dx + ε
где ε → 0 когда Δx → 0. Таким образом,
13.50          Δy = f'(x)Δx + εΔx
Если мы назовем Δx = dx дифференциалом x, тогда мы определяем дифференциал y как
13. 51        dy = f'(x)dx

Правила для дифференциалов

Правила для дифференциалов аналогичны правилам для производных. В качестве примера отметим, что

Частные производные

Пусть f(x, y) будет функцией двух переменных x и y. Тогда мы определяем частную производную f(x, y) по x, сохраняя у постоянным, как
13.58        
Подобно, частная производная f(x, y) по y, сохраняя x постоянным, будет
13.59       
Частные производные высших порядков могут быть определены следующим образом.
13.60        
13.61       
Результаты в 13.61 будут равны, если функция и ее частные производные являются непрерывными, т.е. в этом случае порядок дифференцирования не имеет значения.

Дифференциал f(x, y) определяется как
13.62          
где dx = Δx и dy = Δy.

Применение к функциям, имеющим более чем две переменные, в точности аналогично.

МатАн. Экзамен Экономического факультета МГУ. Дифференциалы функции « Математика, физика на «отлично»

МатАн.

Экзамен Экономического факультета МГУ. Дифференциалы функции

Продолжаем серию публикаций, посвященных экзамену по математическому анализу на Экономическом факультете МГУ им. М.В. Ломоносова. Сегодня мы обратимся к теме построения первого и второго дифференциалов функции, а также вспомним как необходимо записывать уравнение касательной плоскости, строить градиент, искать производную по направлению. А в конце найдем производную в точке неявно заданной функции.
С заданиями экзамена вы можете ознакомиться здесь


№9. Дана функция z = x2cos(xy2 + 3) и точка М(−3;1).

a) Постройте градиент функции в точке М
Градиентом функции мы называем вектор из значений частных производных в той или иной точке. Поэтому для записи градиента нам необходимо найти частные производные данной функции:

Z’x = 2x·cos(xy2 + 3) − x2·sin(xy2 + 3)·(xy2 + 3)’x = 2x·cos(xy2 + 3) − x2·sin(xy2 + 3)·y2

Z'(−3;1)x = −6·cos(0) − 9·sin(0)·1 = −6

Z’y = −x2·sin(xy2 + 3)·(2xy + 3)
Z'(−3;1)y = −9·sin(0)·(−3) = 0

grad Z(M) = (−6;0)

б) Вычислите производную функции Z в точке M вдоль вектора a (−1;4)

Производную по направлению мы вычислим по формуле: производная по направлению равна скалярному произведению градиента на единичный вектор направления. Для того, чтобы получить единичный вектор направления (сумма квадратов координат равна 1), поделим каждую координату на длину вектора, которая равна |a| = √(1 + 16) = 3:
a/|a| = (-1/√17; 4/√17)

Теперь произведение:

P = (-1/√17; 4/√17)·(−6;0) = 6/√17

в) Вычислите dZ

Дифференциал — это аналитическое выражение которое записывается по определённому правилу. Для дифференциала первого порядка это правило выглядит следующим образом:

dZ = Z’xdx + Z’ydy

Производные функции мы нашли в пункте а), поэтому просто подставим:

dZ = [2x·cos(xy2 + 3) − x2·sin(xy2 + 3)·y2]dx + [−x2·sin(xy2 + 3)·(2xy + 3)]dy

г) Вычислите d²z в точке М
Для дифференциала второго порядка мы прменяем следующее правило (учитывая равенство смешанных частных производных):

d2z = Z»xx(dx)2 + 2·Z»xydxdy + Z»yy(dy)2

Найдем вторые частные производные:

Z»xx = [2x·cos(xy2 + 3) − x2·sin(xy2 + 3)·y2]’x = 2cos(xy2 + 3) − 2x·sin(xy2 + 3)·y2 − 2x·sin(xy2 + 3)·y2 − x2·cos(xy2 + 3)·y2·y2 = (2 + x2·y4)·cos(xy2 + 3) − 4x·sin(xy2 + 3)·y2

Z»xx(M) = (2 + 9·1)·cos(0) − 4·(-3)·sin(0)·1 = 11

Z»yy = [−x2·sin(xy2 + 3)·(2xy + 3)]’y = 2yx·cos(xy2 + 3)·(−2yx3 −3x2) − 2x3·sin(xy2 + 3)

Z»yy(M) = −3·cos(0)·(63 + 92) + 63·sin(0) = −3·(216 + 81) = −891

Z»yx = [−x2·sin(xy2 + 3)·(2xy + 3)]’x = [sin(xy2 + 3)·(−2x3y − 3x2)]’x = cos(xy2 + 3)·(−2x3y − 3x2)·y2 + sin(xy2 + 3)·(−6x2y − 6x)

Z»yx(M) = cos(0)·(63 + 92) + sin(0)·(182 + 18) = 297

d2z = 11·(dx)2 + 594·dxdy − 891·(dy)2

д) Написать уравнение касательной плоскости к графику функции Z в точке М (−3;1)

Так как в данном случае мы работаем с функцией вида z = f(x,y), то по определению уравнение касательной плоскости имеет следующий вид:

h = Z(M) + Z’x·(x + 3) + Z’y·(y − 1) = 9·cos(0) + [2x·cos(xy2 + 3) − x2·sin(xy2 + 3)·y2]·(x + 3) + [−x2·sin(xy2 + 3)·(2xy + 3)]·(y − 1) = 9 − [6cos(0) − 9sin(0)]·(x + 3) + [9·sin(0)·(−3)]·(y − 1) = 9 − 6(x + 3) = − 6x − 9

е) Вычислить x'(1), где x = x(y) — это функция, задающая в некоторой окрестности точки М линию уровня функции Z, проходящую через эту точку.

Во-первых, в пункте д) мы уже вычисляли значение функции Z в точке М: Z(M) = 9. Поэтому уравнение линии уровня имеет вид:

9 = x2cos(xy2 + 3)

Продифференцируем обе части уравнения по переменной у, считая, что х — это функция от у:

9′y = [x2cos(xy2 + 3)]’x
0 = 2x·x’y·cos(xy2 + 3) − x2·sin(xy2 + 3)·(x’yy + x)

Так как по условию линия уровня проходит чрез точку M, то х = −3, y = 1:

0 = −6·x’y·cos(0) − 9·sin(0)·(x’y − 3)
0 = −6·x’y
x’y = 0

Удачи на экзамене!!

Понравилось это:

Нравится Загрузка…

Похожее

24.07.2012 – Posted by Маринка | Дифференциальное исчисление, Математика, Математический анализ | Математика, дифференциал, дифференциальное исчисление, математический анализ

Комментариев нет.

1. Дифференциал

Ранее в главе о дифференциации мы писали `dy / dx` и` f ‘(x) `, чтобы обозначать одно и то же. Мы использовали d / dx в качестве оператора .

Теперь мы видим другой способ записывать производную и думать о ней.

Мы будем использовать эту новую форму производной на протяжении всей главы, посвященной интеграции.

Определения

Дифференциалы – это бесконечно малые количества. Обычно мы пишем дифференциалы как dx, dy, dt (и так далее), где:

«dx» – бесконечно малое изменение «x»;

dy – бесконечно малое изменение y; и

«dt» – бесконечно малое изменение «t».

При сравнении небольших изменений величин, которые связаны друг с другом (например, в случае, когда `y` является некоторой функцией f` x`, мы говорим, что дифференциал `dy`, `y = f (x)` записывается:

`dy = f ‘(x) dx`

Примечание: Теперь мы рассматриваем dy / dx больше как дробь (где мы можем управлять частями отдельно), а не как оператор . 5- x.2−4x + 2`, тогда `f ‘(x) = 10x-4`.

Таким образом, дифференциал определяется по формуле:

`dy = (10x-4) dx`

Примечание

Мы могли бы использовать дифференциал для оценки реальное изменение значения функции (`Δy`), вызванное малым изменение в `x` (записывается как` Δx`). Много учебников сделать это, но это довольно глупо, поскольку мы можем легко найти точное изменение – зачем приближать его?

Мы представляем дифференциалы здесь как введение в обозначение, используемое в интеграции .

Каким образом dy, dx и Δ y и Δ x связаны?

“Дельта y” означает “изменение” y “, а” Delta x “означает” изменение “x”.

Мы узнали ранее в главе «Дифференциация», что наклон кривой в точке P определяется как «dy / dx».

Наклон пунктирной линии определяется соотношением `(Delta y) / (Delta x). `По мере того, как` Delta x` становится меньше, этот наклон становится ближе к фактическому наклону на P , что является «мгновенным» отношением `dy / dx`.

То есть

`lim_ (Delta x-> 0) (Delta y) / (Delta x) = dy / dx`

См. «Наклон касательной», чтобы узнать об этом подробнее.

Теперь мы перейдем к рассмотрению того, как дифференциал используется для выполнения противоположного процесса дифференциации, который сначала мы назовем антидифференцировкой , а позже интеграцией .

Дифференциал функции

Определение дифференциала функции

Рассмотрим функцию \ (y = f \ left (x \ right), \), которая непрерывна в интервале \ (\ left [{a, b} \ right]. \). Предположим, что в некоторой точке \ ({x_0 } \ in \ left [{a, b} \ right] \) независимая переменная увеличивается на \ (\ Delta x. \) приращение функции \ (\ Delta y \), соответствующее изменению независимой переменной \ (\ Delta x \) дается

\ [{\ Delta y = \ Delta f \ left ({{x_0}} \ right)} = {f \ left ({{x_0} + \ Delta x} \ right) – f \ left ({{x_0} } \верно). } \]

Для любой дифференцируемой функции приращение \ (\ Delta y \) может быть представлено как сумма двух членов:

\ [{\ Delta y} = {A \ Delta x + \ omicron \ left ({\ Delta x} \ right),} \]

, где первый член (называемый главной частью приращения) линейно зависит от приращения \ (\ Delta x, \), а второй член имеет более высокий порядок малости по отношению к \ (\ Delta x. \) Выражение \ (A \ Delta x \) называется дифференциалом функции и обозначается \ (dy \) или \ (df \ left ({{x_0}} \ right).2. \)

Обратите внимание, что в этом примере коэффициент \ (A \) равен значению производной от \ (S \) в точке \ ({x_0}: \)

\ [A = 2 {x_0}. \]

Оказывается, для любой дифференцируемой функции справедлива следующая теорема:

Коэффициент \ (A \) в главной части приращения функции в точке \ ({x_0} \) равен значению производной \ (f ‘\ left ({{x_0}} \ right ) \) в этой точке, то есть приращение \ (\ Delta y \) равно

\ [
{\ Delta y = A \ Delta x + \ omicron \ left ({\ Delta x} \ right)}
= {f ‘\ left ({{x_0}} \ right) \ Delta x + \ omicron \ left ({\ Delta x} \ right). }
\]

Разделив обе части уравнения на \ (\ Delta x \ ne 0 \), получим

\ [
{\ frac {{\ Delta y}} {{\ Delta x}} = A + \ frac {{\ omicron \ left ({\ Delta x} \ right)}} {{\ Delta x}} }
= {f ‘\ left ({{x_0}} \ right) + \ frac {{\ omicron \ left ({\ Delta x} \ right)}} {{\ Delta x}}.}
\]

В пределе как \ (\ Delta x \ to 0 \) получаем значение производной в точке \ ({x_0}: \)

\ [
{y ‘\ left ({{x_0}} \ right) = \ lim \ limits _ {\ Delta x \ to 0} \ frac {{\ Delta y}} {{\ Delta x}}}
= {A} = {f ‘\ left ({{x_0}} \ right).}
\]

Здесь мы учли, что для небольшого количества \ (\ omicron \ left ({\ Delta x} \ right) \) более высокого порядка малости, чем \ (\ Delta x, \), предел равен

\ [\ lim \ limits _ {\ Delta x \ to 0} \ frac {{\ omicron \ left ({\ Delta x} \ right)}} {{\ Delta x}} = 0. \]

Предполагая, что дифференциал независимой переменной \ (dx \) равен ее приращению \ (\ Delta x: \)

\ [dx = \ Delta x, \]

получаем из соотношения

\ [dy = A \ Delta x = y’dx \]

, что

\ [y ’= \ frac {{dy}} {{dx}}, \]

и. е. производная функции может быть представлена ​​как отношение двух дифференциалов.

Геометрическое значение дифференциала функции

На рисунке \ (2 \) схематично показано разделение приращения \ (\ Delta y \) на главную часть \ (A \ Delta x \) (дифференциал функции) и член более высокого порядка малости \ (\ omicron \ left ({\ Delta x} \ right). \)

Рис. 2.

Касательная \ (MN \), проведенная к кривой функции \ (y = f \ left (x \ right) \) в точке \ (M, \), как известно, имеет угол наклона \ (\ alpha, \), касательная к которой равна производной:

\ [\ tan \ alpha = f ’\ left ({{x_0}} \ right).\]

Когда независимая переменная изменяется на \ (\ Delta x \), тангенс увеличивается на \ (A \ Delta x. \). Это линейное приращение, образованное касательной, является просто дифференциалом функции. Оставшаяся часть полного приращения \ (\ Delta y \) (отрезок \ (N {M_1} \)) соответствует «нелинейной» добавке более высокого порядка малости по отношению к \ (\ Delta x. \)

Свойства дифференциала

Пусть \ (u \) и \ (v \) – функции переменной \ (x \). Дифференциал имеет следующие свойства:

  1. Из знака дифференциала можно вынести константу:
    \ (d \ left ({Cu} \ right) = Cdu, \)
    где \ (C \) – постоянное число.
  2. Дифференциал суммы (разности) двух функций равен сумме (разности) их дифференциалов:
    \ ({d \ left ({u \ pm v} \ right)} = {du \ pm dv.} \)
  3. Дифференциал константы равен нулю:
    \ (d \ left (C \ right) = 0. \)
  4. Дифференциал независимой переменной \ (x \) равен ее приращению:
    \ (dx = \ Delta x. \)
  5. Дифференциал линейной функции равен ее приращению:
    \ ({d \ left ({ax + b} \ right)} \) \ (= {\ Delta \ left ({ax + b} \ right)} \) \ (= {а \ Дельта х.{n – 1}} dx, \; \; \;} \ kern0pt
    {d \ left ({\ ln x} \ right) = \ frac {{dx}} {x}, \; \; \;} \ kern0pt
    {d \ left ({\ sin x} \ right) = \ cos x dx}
    \]

    и так далее.

    Формовая инвариантность дифференциала

    Рассмотрим композицию двух функций \ (y = f \ left (u \ right) \) и \ (u = g \ left (x \ right). \) Ее производную можно найти по цепному правилу:

    \ [{y’_x} = {y’_u} \ cdot {u’_x}, \]

    , где субиндекс обозначает переменную дифференцирования.

    Дифференциал «внешней» функции \ (y = f \ left (u \ right) \) можно записать как

    \ [dy = {y’_u} \, du.\]

    Дифференциал «внутренней» функции \ (u = g \ left (x \ right) \) может быть представлен аналогичным образом:

    \ [du = {u’_x} \, dx. \]

    Если подставить \ (du \) в последнюю формулу, получим

    \ [{dy = {y’_u} \, du} = {{y’_u} {u’_x} \, dx.} \]

    Поскольку \ ({y’_x} = {y’_u} \ cdot {u’_x}, \), то

    \ [dy = {y’_x} \, dx. \]

    Видно, что в случае составной функции мы получаем выражение для дифференциала в той же форме, что и для «простой» функции.Это свойство называется форм-инвариантностью дифференциала.

    Решенные проблемы

    Щелкните или коснитесь проблемы, чтобы увидеть решение.

    Пример 1

    Найти дифференциал функции \ (y = \ sin x – x \ cos x. 2} + 3x + 1 \) в точке \ (x = 1 \), когда \ (dx = 0,1.3} + 4x} \) при \ (x = 2. \)

    Пример 13

    Используйте дифференциал, чтобы аппроксимировать изменение \ (y = \ large {\ frac {1} {{\ sin x}}} \ normalsize \) при изменении \ (x \) с \ (\ large {\ frac {\ pi} {4}} \ normalsize \) в \ (\ large {\ frac {3 \ pi} {10}} \ normalsize. \)

    Пример 14

    Вычислить приращение и дифференциал функции \ (y = {\ large \ frac {{x + 2}} {{x + 1}} \ normalsize} \) в точке \ (x = 0 \), когда \ (\ Дельта x = 0,1. \)

    Пример 15

    Найдите дифференциал функции \ (y = \ ln \ tan 2x \) в \ (x = \ large {\ frac {\ pi} {8}} \ normalsize.{t + 1}} \ end {выровнен} \верно.. \]

    Найдите дифференциал функции в точке \ (\ left ({2, e} \ right). \)

    Пример 25

    Дана составная функция \ (y = \ ln u, \; u = \ cos x. \). Выразите дифференциал \ (y \) в инвариантной форме.

    Пример 1.

    Найти дифференциал функции \ (y = \ sin x – x \ cos x. \ prime}} \ right)}
    = {\ cos x} – {\ left ({\ cos x + x \ left ({ – \ sin x} \ right)} \ right)}
    = {\ cancel {\ cos x} – \ cancel {\ cos x}} + {x \ sin x} = {x \ sin x.2} dx.} \]

    Дробное комплексное преобразование для дробно-дифференциальных уравнений | Успехи в разностных уравнениях

    Пример 3.1 Рассмотрим следующее уравнение:

    {ρt1 / 21.128∂1 / 2u (t, z) ∂t1 / 2 + Dzβu (t, z) = 0, t∈J = [0 , 1] u (0, z) = 0, в окрестности z = 0,

    (14)

    где u (t, z) – неизвестная функция ρ∈ (0,1) и β∈ (0,1].

    Мы предлагаем показать, что уравнение (14) имеет единственное аналитическое решение, используя фиксированную точку Банаха. теорема.Принимая

    u (t, z) = μ (z) t + v (t, z) (v (t, z) = O (t2))

    в качестве формального решения, где μ (z) = O (zβ), из расчетов следует

    t1 / 2∂1 / 2u (t, z) ∂t1 / 2 = 1.128μ (z) t + t1 / 2vα (t, z), α = 1/2,

    и

    Dzβu (t, z) = Dzβ (μ (z) t + v (t, z)) = tDzβμ (z) + vβ (t, z).

    Следовательно, μ (z) удовлетворяет

    , что эквивалентно

    Dzβμ (z) = g (z, μ (z)),

    (15)

    где

    Теперь g (z, μ (z)) является отображением сжатия всякий раз, когда ρ∈ (0,1); поэтому, в силу теоремы Банаха о неподвижной точке, уравнениеУравнение (15) имеет единственное аналитическое решение в единичном круге и, следовательно, задача (14).

    Для вычисления индекса фрактальности для уравнения

    Dzβμ (z) + ρμ (z) = 0, μ (0) = 1,

    (16)

    мы предполагаем преобразование Z = zβ и решение может быть выражено в виде ряда в виде

    μ (Z) = ∑m = 0∞μmZm,

    (17)

    где мкм – константы. Подставляя (17) в уравнение. (16) дает

    ∂∂Z∑m = 0∞θβmμmZm + ρ∑m = 0∞μmZm = 0.

    (18)

    Поскольку

    θβm = Γ (1 + mβ) mΓ (1 + mβ − β),

    , то вычисление устанавливает соотношение

    Γ (1 + mβ) Γ (1 + mβ − β) μm + ρμm− 1 = 0

    с μ (0) = 1, и, следовательно, получаем

    Таким образом, имеем следующее решение:

    μ (Z) = ∑m = 0∞ (−ρ) mΓ (1 + mβ) Zm

    , что эквивалентно

    μ (z) = ∑m = 0∞ (−ρ) mΓ (1 + mβ) zmβ = Eβ (−ρzβ),

    , где Eβ – функция Миттаг-Леффлера. Последнее утверждение является точным решением задачи (16), а следовательно, и (14).

    Пример 3.2 Рассмотрим следующее уравнение:

    {t1 / 2 / 21.128∂1 / 2u (t, z) ∂t1 / 2 + 4z∂u (t, z) ∂z + Dzβu (t, z) = zβt, t∈J = [0,1], u (0, z) = 0, в окрестности z = 0,

    (19)

    где u (t, z) – неизвестная функция, а β∈ (0,1]. Таким же образом, как в примере 3.1, положим

    u (t, z) = μ (z) t + v (t , z) (v (t, z) = O (t2))

    как формальное решение, где μ (z) = O (zβ) и

    | μ ′ (z) −ν ′ (z) | < λ | μ (z) −ν (z) |, λ <18.

    Оценки подразумевают

    и

    Dzβu (t, z) = Dzβ (μ (z) t + v (t, z)) = tDzβμ (z) + vβ (t, z).

    Следовательно, μ (z) удовлетворяет

    μ (z) 2 + 4zμ ′ (z) + Dzβμ (z) −zβ = 0,

    , что эквивалентно

    Dzβμ (z) = G (z, μ (z), zμ ′ (z)),

    (20)

    , где

    G (z, μ (z), zμ ′ (z)) = zβ − 1 / 2μ (z) −4zμ ′ (z).

    Теперь, чтобы показать, что G (z, μ (z), zμ ′ (z)) является сжимающим отображением,

    Таким образом, ввиду теоремы Банаха о неподвижной точке, уравнениеУравнение (20) имеет единственное аналитическое решение в единичном круге и, следовательно, задача (19).

    Чтобы оценить индекс фрактальности для уравнения

    Dzβμ (z) + μ (z) 2 + 4zμ ′ (z) −zβ = 0, μ (0) = 1,

    (21)

    мы предполагаем преобразование Z = zβ и решение можно сформулировать, как в (17). Подставляя (17) в уравнение. (21) имеем

    ∂∂Z∑m = 0∞θβmμmZm + 12∑m = 0∞μmZm + 4∑m = 1∞mμmZm − Z = 0,

    (22)

    , где

    θβm = Γ (1 + mβ) mΓ (1 + mβ − β).

    Следовательно, вычисление накладывает соотношение

    (Γ (1 + mβ) Γ (1 + mβ − β) + 4m) μm + 12μm − 1 = 0

    с μ (0) = 1, и, следовательно, получаем

    где Bm через гамма-функцию. Если мы положим B: = maxm {Bm}, то решение приближается к

    μ (Z) ≃∑m = 0∞ (B) mΓ (1 + mβ) Zm,

    , что эквивалентно

    μ (z ) = ∑m = 0∞ (B) mΓ (1 + mβ) zmβ = Eβ (Bzβ).

    Последнее утверждение является точным решением задачи (21), а следовательно, и (19).

    Далее мы рассмотрим задачу Коши с помощью обобщенного дробно-дифференциального оператора (4).Мы покажем, что решение такой задачи может быть найдено в терминах функции Фокса-Райта [37]:

    где Aj> 0 для всех j = 1,…, p, Bj> 0 для всех j = 1, …, Q и 1 + ∑j = 1qBj − ∑j = 1pAj≥0 для подходящих значений | w | <1 и ai, bj - комплексные параметры.

    Пример 3.3 Рассмотрим задачу Коши в терминах дифференциального оператора (4)

    Dzα, μu (z) = F (z, u (z)),

    (23)

    , где F (z, u (z)) аналитична в и , а u (z) аналитична в единичном круге.Таким образом, F можно выразить как

    Пусть Z = zα (μ + 1). Тогда решение можно сформулировать следующим образом:

    где um – константы. Подставляя (24) в уравнение. Из (23) следует

    ∂∂Z∑m = 0∞Θα, μ, mumZm − ϕ∑m = 0∞umZm = 0.

    (25)

    Так как

    Θα, μ, m = (μ + 1) αΓ (mαμ + 1 + 1) mΓ (nαμ + 1 + 1 − α),

    , то расчет дает соотношение

    (μ + 1) αΓ (mαμ + 1 + 1) Γ (mαμ + 1 + 1 − α) um − ϕum − 1 = 0;

    , следовательно, получаем

    um = [ϕ (μ + 1) α] mΓ ((m − 1) αμ + 1 + 1 − α) Γ (mαμ + 1 + 1 − α) Γ ((m − 1 ) αμ + 1 + 1) Γ (mαμ + 1 + 1).

    Таким образом, имеем следующее решение:

    u (Z) = ∑m = 0∞ [ϕ (μ + 1) α] mΓ ((m − 1) αμ + 1 + 1 − α) Γ (mαμ + 1 + 1 − α) Γ ((m − 1) αμ + 1 + 1) Γ (mαμ + 1 + 1) Zm

    , что эквивалентно

    u (Z) = ∑m = 0∞ [ϕ (μ +1) α] mΓ (m + 1) Γ ((m − 1) αμ + 1 + 1 − α) Γ (mαμ + 1 + 1 − α) Γ ((m − 1) αμ + 1 + 1) Γ (mαμ + 1 + 1) Змм !.

    Поскольку ϕ – произвольная константа, мы предполагаем, что

    Таким образом, для подходящего α мы представляем

    или

    , где | z | <1.

    Производные инструменты, определение производных инструментов, дифференциалы, правила для дифференциалов

    Определение производного инструмента

    Если y = f (x), производная y или f (x) по x определяется как
    13.1
    где h = Δx. Производная также обозначается y ‘, df / dx функции f’ (x). Процесс получения производной называется дифференциация .

    Общие правила дифференциации

    Далее u, v, w являются функциями x; a, b, c, n постоянны [ограничены, если указано]; e = 2,71828 . .. естественное основание логарифмов; ln u – натуральный логарифм u [т.е. логарифм по основанию e], где предполагается, что u> 0 и все углы указаны в радианах.

    Производные тригонометрических и обратных тригонометрических функций
    Производные от экспоненциальных и логарифмических функций

    Производные гиперболических и обратных гиперболических функций


    Высшие производные

    Вторая, третья и более высокие производные определяются следующим образом.
    13,43 Вторая производная = (d / dx). (Dy / dx) = d 2 y / dx 2 = f ” (x) = y ”
    13.44 Третья производная = (d / dx). (D 2 y / dx 2 ) = d 3 / dx 3 = f ” ‘(x) = y’ ”
    13,45 n-я производная = (d / dx). (d n – 1 / dx n – 1 ) = d n / dx n = f (n) (x) = y (n)

    Правило Лейбница для высших производных продуктов

    Пусть D p обозначает оператор d p / dx p , так что D P u = d p u / dx p = p-я производная от u. Тогда
    13,46
    где – биномиальные коэффициенты.

    В качестве особых случаев имеем
    13,47
    13,48

    Дифференциалы

    Пусть y = f (x) и Δy = f (x + Δx) – f (x). Тогда
    13,49 Δy / Δx = [f (x + Δx) – f (x)] / Δx = f ‘(x) + ε = dy / dx + ε
    , где ε → 0 при Δx → 0. Таким образом,
    13,50 Δy = f ‘(x) Δx + εΔx
    Если мы назовем Δx = dx дифференциалом x, тогда мы определим дифференциал y как
    13,51 dy = f’ (x) dx

    Правила дифференциалов

    Правила для дифференциалов в точности аналогичны правилам для производных.В качестве примеров мы видим, что

    Частные производные

    Пусть f (x, y) – функция двух переменных x и y. Затем мы определяем частную производную f (x, y) по x, сохраняя y постоянным, равным
    13,58
    Аналогичным образом частная производная f (x, y) по y, сохраняя x постоянным, определяется как be
    13,59
    Частные производные более высокого порядка могут быть определены следующим образом.
    13,60
    13,61
    Результаты в 13.61 будет равным, если функция и ее частные производные непрерывны, т.е. в этом случае порядок дифференцирования не имеет значения.

    Дифференциал f (x, y) определяется как
    13,62
    , где dx = Δx и dy = Δy.

    Расширение на функции более чем двух переменных полностью аналогично.

    Бесплатный онлайн-калькулятор производной

    Дифференциалы

    Производная функции часто может использоваться для аппроксимации определенных значений функции с удивительной степенью точности.Для этого необходимо ввести понятие дифференциала независимой переменной и зависимой переменной.

    Определение производной функции y = f (x) , как вы помните, равно

    , который представляет наклон касательной к кривой в некоторой точке ( x, f (x) ). Если Δ x очень мало (Δ x ≠ 0), то наклон касательной примерно такой же, как наклон секущей линии через ( x, f (x) ). То есть

    Дифференциал независимой переменной x записывается как dx и совпадает с изменением в x , Δ x . То есть

    Дифференциал зависимой переменной y , записанный dy , определяется как

    Вывод, который следует сделать из предыдущего обсуждения, состоит в том, что дифференциал y (dy ) приблизительно равен точному изменению y (Δ y ) при условии, что изменение x (Δ x = dx ) относительно невелик.Чем меньше изменение в x , тем ближе dy будет к Δ y , что позволяет вам аппроксимировать значения функции, близкие к f (x) (рисунок).

    Рисунок 1 Аппроксимация функции дифференциалами.

    Пример 1: Найдите dy для y = x 3 + 5 x −1.

    Пример 2: Используйте дифференциалы, чтобы аппроксимировать изменение площади квадрата, если длина его стороны увеличивается с 6 см до 6.23 см.

    Пусть x = длина стороны квадрата. Площадь может быть выражена как функция от x , где y = x 2 . Дифференциал dy –

    Поскольку x увеличивается с 6 до 6,23, вы обнаруживаете, что Δ x = dx = 0,23 см; следовательно,

    Площадь квадрата увеличится примерно на 2,76 см 2 при увеличении длины его стороны с 6 до 6.23. Обратите внимание, что точное увеличение площади (Δ y ) составляет 2,8129 см 2 .

    Пример 3: Используйте дифференциалы, чтобы округлить значение до ближайшей тысячной.

    Поскольку вы применяете функцию, выберите удобное значение x , которое является идеальным кубом и относительно близко к 26,55, а именно x = 27. Дифференциал dy равен

    Потому что x уменьшается с 27 до 26.55, вы обнаружите, что Δ x = dx = −,45; следовательно,

    , что означает, что будет примерно на 1/60 меньше; следовательно,

    с точностью до тысячных.

    Обратите внимание, что значение калькулятора 2,983239874, которое округляется до того же ответа до ближайшей тысячной!

    Дифференциальные уравнения | Блестящая вики по математике и науке

    Дифференциальные уравнения часто встречаются в самых разных контекстах.

    Предположим, что ракета с массой mmm спускается так, что испытывает силу тяжести mgmgmg, и предположим, что она испытывает силу сопротивления, пропорциональную ее скорости силы bvbvbv при постоянном bbb. Затем второй закон Ньютона говорит нам, что если aaa – ускорение,

    F = ma = mg − bv ⟹ dvdt = g − bmv, F = ma = mg-bv \ подразумевает \ frac {dv} {dt} = g- \ frac {b} {m} v, F = ma = mg −bv⟹dtdv = g − mb v,

    , которое является дифференциальным уравнением в vvv. {- bt / m} + C, x (t) = bmg t + b2m2g e − bt / m + C,

    , где CCC – константа, зависящая от начального положения (x0) (x_0) (x0) ракеты, т.е.{kt}, P = P0 ekt,

    , где P0P_0P0 – начальный размер колонии.

    Многие химические реакции замедляются по мере их протекания из-за истощения реагентов. Например, скорость, с которой концентрация реагента AAA, обозначенного [A] [A] [A], уменьшается, часто пропорциональна количеству оставшегося реагента, то есть чем меньше реагента, реакция замедляется. Это дает уравнение

    d [A] dt = −k [A], \ frac {d [A]} {dt} = – k [A], dtd [A] = −k [A],

    , где стоит отрицательный знак, потому что скорость уменьшается.{-kt}, [A] = [A] 0 e − kt,

    где [A] 0 [A] _0 [A] 0 – начальная концентрация.

    Бизнес-расчет

    Дифференциальное уравнение – это уравнение, включающее производную функции. Они позволяют нам выразить простым уравнением взаимосвязь между величиной и скоростью ее изменения.

    Пример 1

    Банк платит 2% годовых по своему депозитному сертификату, но взимает ежегодную комиссию в размере 20 долларов.Напишите уравнение скорости изменения баланса \ (B ‘(t) \).

    Если баланс \ (B (t) \) состоит из долларовых единиц, то \ (B ‘(t) \) имеет долларовые единицы в год. Когда мы думаем о том, что меняет баланс счета, есть два фактора:

    1. проценты, увеличивающие остаток, и
    2. Комиссия, уменьшающая баланс.

    Учитывая процентную ставку, мы знаем, что каждый год баланс будет увеличиваться на 2%, но 2% чего? Каждый год это будет меняться, поскольку мы получаем проценты от любого текущего баланса.Мы можем представить сумму увеличения как 2% от баланса: \ (0,02B (t) \) долларов в год.

    В гонораре уже есть единицы долларов / год. Поскольку все теперь имеет одинаковые единицы измерения, мы можем сложить их вместе и создать уравнение: \ [B ‘(t) = 0,02B (t) -20. \]

    Результат – пример дифференциального уравнения. Обратите внимание, что это конкретное уравнение включает как производную , так и исходной функции, поэтому мы не можем просто найти \ (B (t) \), используя базовое интегрирование.3 – 4 \).

    Вы уже решили множество дифференциальных уравнений: каждый раз, когда вы находили первообразную функции \ (f (x) \), вы решали дифференциальное уравнение \ (y ‘= f (x) \), чтобы получить решение \ ( у \). Однако дифференциальное уравнение \ (y ‘= f (x) \) – это только начало. Другие приложения генерируют другие дифференциальные уравнения, как в приведенном выше примере банковского баланса.

    Проверка решений дифференциальных уравнений

    Независимо от того, легко или сложно решить дифференциальное уравнение, важно иметь возможность проверить, действительно ли возможное решение удовлетворяет дифференциальному уравнению.2} = 2, \] результат, который мы хотели проверить.

Разделимые дифференциальные уравнения

Дифференциальное уравнение называется разделяемым, если переменные могут быть разделены алгебраически так, что все \ (x \) и \ (dx \) составляют одну сторону уравнения, а все \ (y \) и \ (dy \) находятся по другую сторону уравнения. Другими словами, уравнение имеет вид \ (f (x) \, dx = g (y) \, dy \).

После разделения разделимые дифференциальные уравнения могут быть решены путем интегрирования обеих частей уравнения.2 + х + С. \]

Как и ожидалось, существует целое семейство решений этого дифференциального уравнения.

Задача начального значения (IVT)

Задача начального значения – это дифференциальное уравнение, которое предоставляет дополнительную информацию о начальном или начальном значении функции. Это позволяет нам затем найти константу и найти единственное решение.

Пример 4

Найдите решение \ (y ‘= \ frac {6x + 1} {2y} \), которое удовлетворяет \ (y (2) = 3 \).2 + х-5}. \]

Пример 5

Банк платит 2% годовых по своему депозитному сертификату, но взимает ежегодную комиссию в размере 20 долларов. Если вы изначально инвестируете 3000 долларов, сколько у вас будет через 10 лет?

Вы можете узнать это как пример из начала раздела, для которого мы составили уравнение \ (B ‘(t) = 0,02B (t) -20 \) или, проще говоря, \ [\ frac {dB } {dt} = 0,02B-20. \]

Мы можем разделить это уравнение, умножив его на \ (dt \) и разделив на все выражение справа: \ [\ frac {dB} {0.02B-20} = дт. \]

Интегрирование левой части этого уравнения требует подстановки. Пусть \ (u = 0,02B-20 \), поэтому \ (du = 0,02 \, дБ \). Делая замену, \ [\ begin {align *} \ int \ frac {дБ} {0,02B-20} = & \ int \ frac {du / 0,02} {u} \\ = & \ int \ frac {1} {u} \ frac {du} {0,02} \\ = & \ frac {1} {0.02} \ int \ frac {1} {u} \, du \\ = & \ frac {1} {0,02} \ ln | u | + C_1 \\ = & \ frac {1} {0,02} \ ln | 0,02B-20 | + C_1 \ конец {выравнивание *} \]

Проще интегрировать правую часть дифференциального уравнения: \ [\ int dt = t + C_2 \]

Вместе это дает нам общее решение дифференциального уравнения (на этом этапе мы также объединяем \ (C \)): \ [\ frac {1} {0.{0,02 (10)} + 1000 \ приблизительно \ $ 3442,81. \]

Стоит отметить, что это не совсем правильный ответ. Дифференциальные уравнения предполагают, что непрерывно, изменений, и маловероятно, что проценты начисляются непрерывно или плата извлекается непрерывно. Однако ответ, вероятно, близок к фактическому, а дифференциальные уравнения представляют собой относительно простую модель сложной ситуации.

Модели роста

Пример банковского счета продемонстрировал одну базовую модель роста: рост, пропорциональный существующему количеству.Банковские счета и население, как правило, растут таким образом, если это не сдерживается. Этот тип роста называется неограниченный рост .

Неограниченный рост

Если количество или популяция y растет со скоростью, пропорциональной размеру этого количества, его можно смоделировать с неограниченным ростом, который имеет дифференциальное уравнение: \ [y ‘= ry, \], где \ (r \) – постоянная величина.

Пример 6

Население ежегодно увеличивается на 8%. Если текущее население составляет 5000 человек, найдите уравнение для населения через \ (t \) лет.{0,08т}. \]

Обратите внимание, что решение уравнения неограниченного роста является экспоненциальным уравнением.

Когда продукт широко рекламируется, продажи будут расти очень быстро, но в конечном итоге рынок достигнет насыщения, и продажи замедлятся. В этом типе роста, называемом ограниченным ростом , популяция растет со скоростью, пропорциональной расстоянию от максимального значения.

Ограниченный рост

Если величина растет со скоростью, пропорциональной расстоянию от максимального значения \ (M \), ее можно смоделировать с ограниченным ростом, который имеет дифференциальное уравнение \ [y ‘= k (My), \] где \ (k \) – константа, а \ (M \) – максимальный размер \ (y \).

Пример 7

Представлен новый сотовый телефон. По оценкам компании, они продадут 200 тысяч телефонов. Через 1 месяц они продали 20 тысяч. Сколько они будут проданы через 9 месяцев?

В этом случае есть максимальное количество телефонов, которое они ожидают продать, так что \ (M = 200 \) тысяч. Моделируя продажи \ (y \) в тысячах телефонов, мы можем написать дифференциальное уравнение \ [y ‘= k (200-y). \]

Поскольку это был новый телефон, \ (y (0) = 0 \).{-0,105 (9)} + 200 \ приблизительно 122,26 \ text {тысяча телефонов}. \]

Ограниченный рост также обычно используется для моделей обучения, поскольку при изучении нового навыка люди обычно сначала учатся быстро, затем скорость их улучшения замедляется по мере приближения к мастерству.

Ранее мы использовали неограниченный рост для моделирования популяции, но часто население будет ограничено едой, пространством и другими ресурсами. Когда популяция растет как пропорционально ее размеру, так и по отношению к расстоянию от некоторого максимума, это называется логистическим ростом .Это приводит к дифференциальному уравнению \ (y ‘= ky (M-y) \), которое является точным, но не всегда удобным в использовании. Мы будем использовать небольшую модификацию. Поскольку решение этого дифференциального уравнения требует техники интегрирования, которую мы не изучили, приводится форма решения.

Логистический рост

Если количество растет со скоростью, пропорциональной его размеру и расстоянию от максимального значения, \ (M \), его можно смоделировать с помощью логистического роста , который имеет дифференциальное уравнение: \ [y ‘= ry \ слева (1- \ frac {y} {M} \ right).{-1.1404t} = & \ frac {\ frac {5} {3} -1} {49} \ приблизительно 0,01361 \\ t = & \ frac {\ ln (0,01361)} {- 1,1404} \ приблизительно 3,77 \ text {лет}. \ конец {выравнивание *} \]

Логистический рост также является хорошей моделью для нерекламируемых продаж. У нового продукта, который не рекламируется, продажи сначала будут расти медленно, а затем расти по мере распространения молвы и знакомства с продуктом. Продажи будут выравниваться по мере приближения к насыщению рынка.

.

Оставить комментарий