Математика для чайников. Глава 10. Линейная алгебра | Александр Шуравин.
Изображение взято из открытых источниковИзображение взято из открытых источников
Начало: Математика для чайников. Глава 1. Что такое математическая абстракция.
Предыдущая глава: Математика для чайников. Глава 9. Основы матанализа
В публикации Математика для чайников. Глава 4. Алгебра я уже кратко писал, что такое линейная алгебра. Напомню, что это про векторы, матрицы и прочее тому подобное, и этот раздел математики вам жизненно необходим если вы хотите стать программистом в области искусственного интеллекта и Data Science . Предметом изучения линейной алгебры являться различные объекты линейной природы, а именно:
· Векторы
· Матрицы и определители
· Системы линейных уравнений
· Тензоры и тензорное исчисление.
· Теория инвариантов.
Кроме программирования, линейная алгебра так же используется в экономике и физике (особенно в квантовой механике).
Теперь разберемся с понятиями линейной алгебры. И так, вектор . С точки зрения математики, это объект, который характеризуется величиной и направлением. А если сказать проще, то вектор – это стрелка. Проще всего, конечно, изобразить двумерный вектор:
Изображение взято из открытых источниковИзображение взято из открытых источников
Как видим, вектор характеризуется двумя точками: началом и концом. Вообще, различают векторы, которые:
· Жестко заданы в одном месте.
· Можно двигать вдоль линии, на которой вектор лежит.
· Можно двигать как вдоль линии, на которой он лежит, так переносить на другие линии, параллельный ей – так называемый параллельный перенос.
Нам особо интересный третий случай. Тогда начало вектора можно перенести в начало координат – в точку (0,0). Тогда точка конца вектора будет равна значению вектора. Или, если начало не в начале координат, тогда значение вектора можно получить, вычтя соответствующие координаты начала вектора из соответствующих координат конца вектора.
Таким образом, двумерный вектор – это два числа. Трехмерный (пространственный) вектор – это три числа. Но мерность вектора может быть и больше. Конечно, мы вряд ли сможем представить себе четырехмерное или даже пятимерное пространство, но как математический объект оно вполне себе может существовать.
Теперь о том, что можно сделать с векторами? Во-первых, их можно складывать. В координатах сложение векторов происходит поэлементно, первую координату складываем с первой, вторую со второй и так далее. Геометрический смысл сложения состоит в том, что мы конец первого вектора совмещаем с началом второго и проводим вектор из начала первого вектора в конец второго:
Изображение взято из открытых источниковИзображение взято из открытых источников
Что в геометрическом понимании, что в математическом, вообще без разницы, в какой последовательности складывать вектора. Поэтому здесь тоже действует алгебраический закон: «от перестановки слагаемых сумма не меняется», то есть:
Еще векторы можно умножать.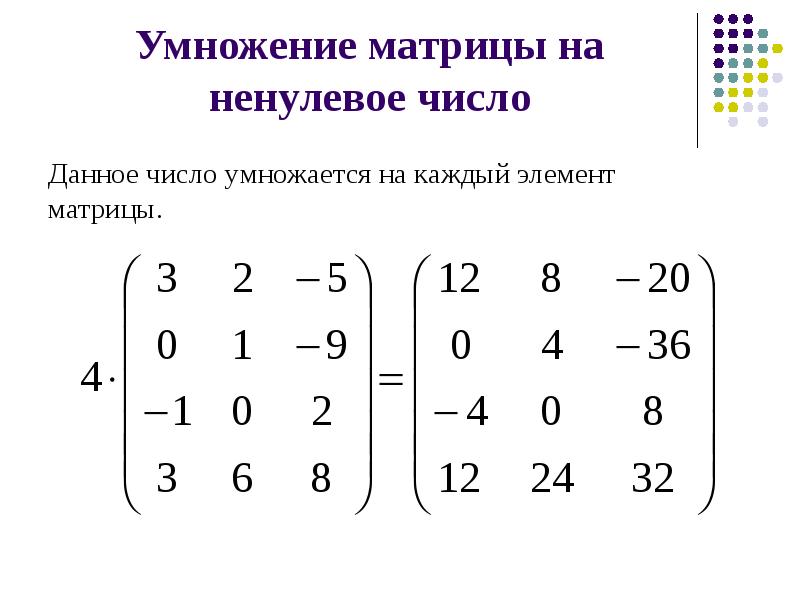 А вот тут интересней. Можно конечно, перемножить их координаты (векторное произведение). Но особого смысла в этом нет. А можно сложить поэлементные произведения и получить некоторое число (скалярное произведение):
А вот тут интересней. Можно конечно, перемножить их координаты (векторное произведение). Но особого смысла в этом нет. А можно сложить поэлементные произведения и получить некоторое число (скалярное произведение):
Смысл скалярного произведения состоит в том, что это косинус угла между векторами, умноженный на произведение их длин, то есть:
Таким образом, через скалярное произведение мы можем вычислить угол между векторами:
Где можно использовать понятие скалярное произведения векторов? Как я уже говорил, для определения угла между векторами, для определения длины вектора, проекции одного вектора на другой, нахождение перпендикуляра многих других операций, о которых я подробнее расскажу в будущих уроках. А сейчас поехали дальше.
Нетрудно заметить, что скалярное произведение так же подчиняется закону перестановки множителей, то есть:
Существует насколько обозначений произведения векторов. Это знак умножения (точка), просто без знака, и угловые скобки:
Последнее называется обозначение Дирака и используется в квантовой механике для обозначения состояния.
Перейдем к следующему объекту: матрица . Если вектор – это просто несколько чисел (в отличии от множества, тут порядок важен), то матрица – это уже таблица чисел. Вообще-то матрица необязательно состоит из чисел, там могут быть другие математические объекты, но для упрощения понимания пока думайте, что матрица – это таблица чисел. Эта таблица имеет размеры ( n , m ), где n – количество строк, m – количество столбцов. Запомните, в матрице сначала индексируются строки, а потом столбцы. Как правило, матрица обозначается заглавной латинской буквой, а ее элемент – строчной. Допустим, у нас есть матрица A , элемент ее строки i и столбца j будет обозначен как
Матрица может быть задана явно в виде таблицы, в таком случае она обозначается вот так:
Часто, запятую опускают (если индекс понятен и без запятой):
Что можно сделать с матрицами? Можно их поэлементно складывать (если размер матриц одинаков). Такая операция называется сложением матриц и так же подчиняется закону перестановки слагаемых:
Аналогично, матрицы можно вычитать и умножать на число.
Другая интересная операция с матрицами – это матричное умножение. Многим оно не очень понятно, многие в нем путаются и многих оно пугает. Но на самом деле ничего сложно в этом нет. Давайте вернемся к скалярному произведению векторов. Только на этот раз первый вектор будет строка, а второй – столбец:
Кстати, это так и называется вектор – строка и вектор столбец. По сути, вектор – это частный случай матрицы, которая состоит или из одной строки, или из одного столбца.
А что если вместо вектора строки мы возьмем матрицу? По сути, это будет несколько векторов-строк? Тогда для каждого вектора-строки мы посчитаем скалярное произведение. В нашем примере первая матрица содержит две строки:
В итоге нас получился вектор столбец из двух элементов. Ну или матрица из двух строк и одного столбца. Вообще, если мы умножаем матрицу на вектор-столбец, то у нас в итоге образуется матрица с количеством строк, как в этой матрице.
Аналогично, если мы умножаем одну строку на несколько столбцов, только теперь результаты будут уже в столбцы записывать, не в строки, и на выходе мы получим вектор-строку:
Теперь осталось разобраться с умножением матрицы на матрицу. Очевидно, что количество строк в первой матрице должно быть равно количеству столбцов во второй матрице. И тогда мы берем каждую сторожку первой матрицы и считаем скалярное произведение на каждый столбец второй матрицы, результат записывая в ячейку с номером строки из первой матрицы и соответствующим номером столбца из второй матрицы.
Очевидно, что количество строк в первой матрице должно быть равно количеству столбцов во второй матрице. И тогда мы берем каждую сторожку первой матрицы и считаем скалярное произведение на каждый столбец второй матрицы, результат записывая в ячейку с номером строки из первой матрицы и соответствующим номером столбца из второй матрицы.
Математически формулу умножения матриц можно записать так:
Пусть существует матрица A размером l x m :
И матрица B размером m x n :
Тогда матрица C , являющаяся произведением матрицы A и B :
Будет матрица из элементов, которые вычисляются по следующей формуле:
Если сказать по русский, то мы считаем скалярное произведение каждой строки на каждый столбце и результат пишем в точку их пересечения:
Изображение взято из открытых источниковИзображение взято из открытых источников
Может возникнуть вопрос, а для чего это вообще нужно, перемножать матрицы? Для ответа на этот вопрос рассмотрим систему линейных уравнений:
Ее можно представить в матричной форме:
Или:
Если бы это было уравнение из элементарной алгебры, то мы могли бы записать:
Но можно ли так же сделать в матричном виде? Существует ли деление матриц. На самом деле в матричном исчислении есть такое понятие, как обратная матрица. Она обозначается
На самом деле в матричном исчислении есть такое понятие, как обратная матрица. Она обозначается
Что же за штука такая, обратная матрица? Это такая матрица, что если ее умножить на исходную матрицу то получиться единичная матрица, то есть:
Единичная матрица обозначается буковкой E и состоит из единиц по диагонали, остальные нули, то есть:
То есть с нашей системой уравнений мы можем следить вот такой трюк:
Тогда получаем:
Нетрудно догадаться (или можете проверить сами), что умножая единичную матрицу на любую другую матрицу, мы получаем ту же самую матрицу. Тогда:
И все, система уравнений решена. Осталось только найти обратную матрицу. Существует даже метод нахождения такой обратной матрицу. Но его мы рассмотрим позже, когда будет изучать линейную алгебру более подробно. А на сегодня все.
Следующая глава: Математика для чайников. Глава 11. Почему делить на нуль нельзя или кое-что о пределах.
Может ли кто-нибудь порекомендовать некоторые учебники по матрице преобразования для чайников?
Я написал веб-программу, которую можно использовать для игры с матрицами преобразований. Он позволяет использовать как предустановленные типы, так и пользовательские.
Он позволяет использовать как предустановленные типы, так и пользовательские.
Играйте с ним онлайн или возьмите источник .
Должно быть легко играть с цифрами и мгновенно видеть, как это влияет на рисунок дома. Посмотрите на код, доступный в Интернете, чтобы определить, что он делает, и вы сможете понять, что происходит.
Если у вас возникли проблемы, поймите, что матрица 3×3 просто умножается на каждую вершину (координата X & Y) в форме дома. Умножение матрицы на вершину (теперь мы будем называть ее вектором) и матрица преобразования выглядят так…
1 0 0 1
0 1 0 * 2
0 0 1 0
Слева находится матрица идентичности (идемпотентная матрица, которая не влияет на вектор) и вектор 1, 2, 0 (предположим, что это соответствует положению X1 и Y2 в графике программы, упомянутой выше, и игнорирует конечный
Умножение матриц можно визуализировать следующим образом…
a b c x a * x + b * y + c * z
d e f + y = d * x + e * y + f * z
g h i z g * x + h * y + i * z
Итак, в нашем примере это было бы так. ..
..
1 0 0 1 1 * 1 + 0 * 2 + 0 * 0
0 1 0 * 2 = 0 * 1 + 1 * 2 + 0 * 0
0 0 1 0 0 * 1 + 0 * 2 + 1 * 0
Проделайте эту математику, и мы получим окончательный вектор…
1
2
0
Поскольку мы сказали, что наша матрица идентичности не должна изменять значения, мы можем видеть выше, что это так, поскольку результирующий вектор соответствует оригиналу.
Чтобы объяснить дальше, подумайте, когда вам нужно перевести вектор. Допустим, мы хотим перевести дом на 5 пикселя вдоль оси X. Мы хотим начать с матрицы идентичности, но измените верхнее правое число на 5 и сделайте дополнительное измерение в векторе 1 (вы кратко поймете, почему).
1 0 5 1 1 * 1 + 0 * 2 + 5 * 1
0 1 0 * 2 = 0 * 1 + 1 * 2 + 0 * 1
0 0 1 1 0 * 1 + 0 * 2 + 1 * 1
Мы снова делаем математику…
6
2
1
Мы видим, что первое число (X в наших координатах) было переведено вдоль оси X на 5 . Попробуйте это в программе, связанной выше.
Попробуйте это в программе, связанной выше.
Причина, по которой мы сделали третье значение 1 , заключается в том, что при выполнении математики учитывался перевод. Если бы это был 0 , он будет проигнорирован, так как любое число, умноженное на 0 , приведет к 0 .
Если у вас все еще возникают проблемы, посмотрите видео в Интернете ( например , это видео), которое может помочь объяснить это более наглядно.
3) Находим матрицу алгебраических дополнений
Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел: Именно у этих чисел, которые я обвел в кружок!
–
матрица
алгебраических дополнений соответствующих
элементов матрицы .
И всего-то лишь…
4) Находим транспонированную матрицу алгебраических дополнений .
Что такое транспонирование матрицы, и с чем это едят, смотрите в лекции
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
5) Ответ.
Вспоминаем нашу формулу Всё найдено!
Таким образом, обратная матрица:
Ответ лучше оставить в таком виде. НЕ НУЖНО делить каждый элемент матрицы на 2, так как получатся дробные числа. Более подробно данный нюанс рассмотрен в той же статьеДействия с матрицами.
Как проверить решение? Необходимо выполнить матричное умножение либо
Проверка:
Получена так называемая единичная матрица (с единицами по главной диагонали и нулями в остальных местах).
Таким образом, обратная матрица найдена правильно.
Переходим
к более распространенному на практике
случаю – матрице «три на три».
Пример:
Найти обратную матрицу для матрицы
Алгоритм точно такой же, как и для случая «два на два».
Обратную матрицу найдем по формуле: , где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
1) Находим определитель матрицы.
Здесь определитель раскрыт по первой строке.
Также не забываем, что , а значит, всё нормально – обратная матрица существует.
2) Находим матрицу миноров
Матрица миноров имеет размерность «три на три» , и нам нужно найти девять чисел.
Я подробно рассмотрю парочку миноров:
Рассмотрим следующий элемент матрицы: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:
Оставшиеся четыре числа записываем в определитель «два на два» Этот определитель «два на два» и является минором данного элемента. Его нужно вычислить: Всё, минор найден, записываем его в нашу матрицу миноров:
Как
Вы, наверное, догадались, необходимо
вычислить девять определителей «два
на два». Процесс, конечно, муторный, но
случай не самый тяжелый, бывает хуже.
Процесс, конечно, муторный, но
случай не самый тяжелый, бывает хуже.
Ну и для закрепления – нахождение еще одного минора в картинках: Остальные миноры попробуйте вычислить самостоятельно.
Окончательный результат: – матрица миноров соответствующих элементов матрицы .
То, что все миноры получились отрицательными – чистая случайность.
3) Находим матрицу алгебраических дополнений
В матрице миноров необходимо СМЕНИТЬ ЗНАКИ строго у следующих элементов: В данном случае: – матрица алгебраических дополнений соответствующих элементов матрицы .
4) Находим транспонированную матрицу алгебраических дополнений .
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
5) Ответ:
Проверка:
Таким образом, обратная матрица найдена правильно.
Как
оформить решение на чистовик? Примерный
образец чистового оформления задания
можно найти на странице Правило
Крамера. Метод обратной матрицы в
параграфе, где идет речь о матричном
методе решения системы линейных
уравнений. По существу, основная часть
упомянутой задачи – и есть нахождение
обратной матрицы.
Метод обратной матрицы в
параграфе, где идет речь о матричном
методе решения системы линейных
уравнений. По существу, основная часть
упомянутой задачи – и есть нахождение
обратной матрицы.
Нахождение обратной матрицы для матрицы «четыре на четыре» не рассматриваем, так как такое задание может дать только преподаватель-садист (чтобы студент вычислил 1 определитель «четыре на четыре» и 16 определителей «три на три»). В моей практике встретился только один такой случай, и заказчик контрольной работы заплатил за мои мучения довольно дорого =).
В ряде учебников, методических указаниях можно встретить несколько другой подход к нахождению обратной матрицы, но я Вам рекомендую пользоваться именно вышеизложенным алгоритмом решения. Почему? Потому-что вероятность запутаться в вычислениях и знаках – гораздо меньше.
Найден максимально быстрый способ умножения матриц
Американский математик Вирджиния Василевска-Уильямс (Virginia Vassilevska Williams) нашла максимально быстрый способ умножения квадратных матриц, основанный на известном алгоритме Копперсмита — Винограда

В информатике матричное умножение становится базовой операцией, часто встречающейся при решении даже тех вычислительных задач, которые, кажется, никакого отношения к матрицам не имеют. Для оценки его сложности вводят матричную экспоненту ω — такое минимальное число, что для любого ε > 0 и любого достаточно большого n количество арифметических операций, необходимых для вычисления произведения двух матриц размером n×n, не превосходит nω + ε.
Несложно показать, что классический алгоритм перемножения матриц (нахождение суммы произведений элементов из определённой строки матрицы А на соответствующие им элементы из столбца матрицы В) требует n
Недостатками такой методики называют бóльшую (по сравнению с классическим алгоритмом) сложность программирования и большой объём используемой памяти.
Публикация вычислений Штрассена инициировала активные поиски быстрых алгоритмов, и уже через несколько лет учёные заметно снизили оценку величины ω. График изменения ω приведён на рисунке ниже.
Рис. 1. Оценки ω, которые давали разные авторы (иллюстрация из кандидатской диссертации Вирджинии Уильямс).
В 1990 году американцы Дон Копперсмит и Шмуэль Виноград, развившие идеи Штрассена, добились ω < 2,376, после чего уменьшение оценки матричной экспоненты прекратилось. На протяжении двадцати лет алгоритм Копперсмита — Винограда оставался самым быстрым, но в реальных вычислительных задачах не использовался, так как он эффективен только на чрезвычайно больших матрицах.
Поскольку методу Копперсмита — Винограда свойственна рекурсивность (алгоритм выполняется двукратно), сами его авторы предлагали коллегам рассмотреть случаи с большей «глубиной» рекурсии и выяснить, не позволит ли это снизить ω.
Трёхкратное применение алгоритма не давало нужного эффекта, а задача по оценке ω на глубоких уровнях рекурсии оказалась довольно сложной, и некоторые математики поспешили признать значение 2,376 окончательным.
Г-жа Уильямс, однако, продолжила рассмотрение метода Копперсмита — Винограда и нашла несколько упрощённый способ расчёта ω. Испытывая его, она обнаружила, что восьмикратное применение алгоритма позволяет получить новое ограничение: ω < 2,3727.
Остаётся добавить, что истинным значением матричной экспоненты многие специалисты — скажем, те же Копперсмит и Виноград — считают двойку. Доказать это пока никому не удалось.
Норма матрицы
Рассмотрим произвольную матрицу A порядка m×n и связанную с нею линейное преобразование y=Ax, где x∈Vn, y∈Um. Введем в этих пространствах нормы векторов , .
Определим норму матрицы A равенством:
| (1) |
Из определения нормы матрицы следует:
| (2) |
Пусть для двух матриц A и B порядка m×n определены одни и те же векторные нормы. Тогда имеем соотношение:
Тогда имеем соотношение:
| (3) |
Кроме того справедливо равенство
| , | (4) |
где λ любое число.
Пусть для m×n матрицы A и n×k матрицы B определены матричные нормы , и пусть для m×k матрицы AB определена норма . Тогда
.
Вычислим норму матрицы A , введя в пространствах V и U конкретные векторные нормы.
1. Пусть в пространствах V и U введена векторная норма
Тогда
| (5) |
или
| , | (6) |
В (5) и (6) неравнетство превращается в равенство, если взять и , j=1,…,n, где l-то значение i, при котором
достигает своего максимума. Учитывая высшеизложенное, неравенство (6) и равенство (1), получим:
| (7) |
2. Введем в пространствах V и U векторную норму
Введем в пространствах V и U векторную норму
Тогда
или
| (8) |
Пусть достигается при j=l. Для вектора x, у которого только один элемент отлично от нуля, имеем:
Учитывая (1),(8) и (9) получим l-норму матрицы A:
| (10) |
Норму матрицы, определяемую с помощью формулы (1), называется операторной нормой, подчиненной данной норме векторов.
Отметим, что определение нормы матрицы (1) эквивалентно следующему определению:
| (11) |
Действительно, любой ненулевой вектор x∈V можно представить в виде произведения λx₁, где , . Тогда, учитывая, что , получим:
| (12) |
Примеры вычисления нормы матрицы
Вычислим m-норму и l-норму матрицы используя (7) и (10).
Геометрическая интерпретация нормы матрицы
Пусть в линейном пространстве V введена m-норма для всех векторов x∈V:
.
Найдем норму матрицы
.
Рассмотрим множество всех векторов, которые имеют норму 1. В двухмерном пространстве это те векторы конечные точки которых находятся на квадрате на рис. 1. Обозначим это множество символом X0.
Рис. 1
Рис. 2
На рисунке рис. 2 изображено пространство столбцов матрицы A. Каждому вектору x∈X0 соответствует вектор Ax в U. Конечные точки этих векторов находятся на пунктирном четырехугольнике ABCD. m-норма матрицы A – это модуль наибольшго координата наибольшего из векторов, конечная точка которого находится на четырехугольнике ABCD. На рис.2 это векторы и а модуль наибольшего координата 6. Используя (3), аналитически получим тот же результат.
Отметим, что норма матрицы показывает насколько максимально растягивается вектор x при отображении y=Ax. В нашем примере векторы х растягиваются максимально 6 раз.
– ACT Math
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. – относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Что такое матричная запись в математике?
Обозначение матриц
Матричная математика – один из самых важных инструментов, используемых в линейной алгебре, и, следовательно, один из ключевых моментов для изучения этого курса. Поскольку линейная алгебра занимается поиском решений систем линейных уравнений, матричная математика и изучение векторных пространств становятся инструментом для представления и упорядоченного решения таких систем упорядоченным и интуитивно понятным образом.
Поскольку линейная алгебра занимается поиском решений систем линейных уравнений, матричная математика и изучение векторных пространств становятся инструментом для представления и упорядоченного решения таких систем упорядоченным и интуитивно понятным образом.
Сегодняшний урок посвящен введению нового вида математической организации информации: матрицы (множественное число: матрицы). На нашем уроке мы познакомим вас с концепцией матрицы, как с ней можно работать математически, а затем будет небольшое введение, которое подготовит вас к следующим урокам этого курса, где вы узнаете, насколько полезны матрицы и методы их использования. решать с ними математические уравнения.
Что такое матрица?
В математике матрица – это упорядоченный список чисел, заключенный в прямоугольную скобку. Этот список также можно назвать прямоугольным массивом, и причина этого в том, что его элементы могут представлять различные члены коэффициентов или коэффициенты переменных в зависимости от их расположения в квадратной скобке.
Матрица обеспечивает упорядоченный способ отображения массива информации. Например:
Уравнение 1: Пример матрицыОбратите внимание, что прямоугольные скобки НЕ являются просто прямыми линиями, окружающими массив чисел, важно отметить это, поскольку существует другая операция, которую можно получить из матрицы, называемой определителем, которая, как оказалось, имеет обозначение, очень похожее на сама матрица, но вместо прямоугольных скобок у нее прямые линии по периметру.Просто помните, что если числа находятся внутри «квадрата», это матрица скобок, если числа находятся внутри двух длинных прямых линий, то это определитель. Мы поговорим о детерминанте матрицы 2×2 и матрицы 3×3, а также о свойствах определителей на уроках намного позже в этом курсе. А пока мы сосредоточимся на основах матричных обозначений, чтобы продолжить работу с ними.
Прежде чем мы узнаем определение матрицы, давайте поговорим об истории этого слова и о том, как имеет смысл иметь такое обозначение в математике: неудивительно, что термин «матрица» сам по себе умело использовался на протяжении всей истории не только среди математиков. популярная культура с разными коннотациями в зависимости от эпохи, но также в различных академических областях исследования от математики до различных областей науки.
популярная культура с разными коннотациями в зависимости от эпохи, но также в различных академических областях исследования от математики до различных областей науки.
Слово «матрица» от латинской этимологии означает «матка» и используется не только в математике, но и в таких областях, как биология, где этот термин используется для обозначения ткани на клетках живых организмов, где используются более специализированные материалы ( структуры с более высокими или более конкретными функциями). Вы также можете встретить термин «матрица», используемый в химическом анализе и экспериментах, где это слово описывает все остальное содержимое образца, которое не является конкретным материалом, представляющим интерес.В геологии матрица относится к компактному материалу без характерной формы, в который встроены четко определенные образцы горной породы или кристаллы.
Если мы обратим внимание на все эти употребления слова во всех областях естествознания, мы сможем найти образец, в котором в целом мы определяем матрицу как среду, в которой интересующая информация (будь то структуры или системы) размещается, фиксируется или содержатся и готовы к изучению или использованию. То же самое и с матричной алгеброй: в математике мы используем матричную запись для организации систем значений, поступающих из разных геометрических плоскостей.Это станет очевидным, когда мы продолжим наши уроки линейной алгебры, и поэтому мы просто упомянем это сейчас, чтобы вы могли начать понимать, что такое матрицы. На следующих уроках, где вы будете решать системы линейных уравнений с помощью построения графиков, а затем научитесь представлять линейную систему в виде матрицы, вы сможете непосредственно наблюдать то, о чем мы говорили о полезности и значении матриц как «ящики» информации.
То же самое и с матричной алгеброй: в математике мы используем матричную запись для организации систем значений, поступающих из разных геометрических плоскостей.Это станет очевидным, когда мы продолжим наши уроки линейной алгебры, и поэтому мы просто упомянем это сейчас, чтобы вы могли начать понимать, что такое матрицы. На следующих уроках, где вы будете решать системы линейных уравнений с помощью построения графиков, а затем научитесь представлять линейную систему в виде матрицы, вы сможете непосредственно наблюдать то, о чем мы говорили о полезности и значении матриц как «ящики» информации.
Размеры матрицы
Размеры матрицы определяют ее размер и в основном относятся к количеству строк и столбцов внутри матрицы.Например, если матрица имеет m строк и n столбцов, то мы говорим, что размеры матрицы равны m на n.
Рисунок 1: Объяснение размеров матрицы Таким образом, каждая запись в матрице называется элементом матрицы, который мы можем обозначать субиндексами. Например, если у нас есть матрица A размером m на n, тогда мы говорим, что матричный элемент a3,2a_ {3,2} a3,2 является записью в третьей строке и втором столбце.
Например, если у нас есть матрица A размером m на n, тогда мы говорим, что матричный элемент a3,2a_ {3,2} a3,2 является записью в третьей строке и втором столбце.
Давайте рассмотрим несколько следующих примеров:
Пример 1
Определите размеры следующих матриц:
Уравнение 3: Примеры матрицИтак, размеры для каждой матрицы:
- 3 x 3 = 3 строки и 3 столбца
- 1 x 3 = 1 строка и 3 столбца
- 3 x 2 = 3 строки и 2 столбца
- 2 x 3 = 2 строки и 3 столбца
- 4 x 1 = 4 строки и 1 столбец
- 3 x 6 = 3 строки и 6 столбцов
- 2 x 5 = 2 строки и 5 столбцов
Пример 2
Найдите элементы (или значения) матрицы, указанные ниже, из следующей матрицы:
Уравнение 4: Матрица 4 x 9- Элемент a1,1a_ {1,1} a1,1 = 3
- Элемент a2,3a_ {2,3} a2,3 = 8
- Элемент a4,6a_ {4,6} a4,6 = -72
- Элемент a4,9a_ {4,9} a4,9 = 99
- Значение a2,5a4,9 = 799 \ frac {a_ {2,5}} {a_ {4,9}} = \ frac {7} {99} a4,9 a2,5 = 997 = 0.
 {2} (a2,4) 2 = (6) 2 = 36
{2} (a2,4) 2 = (6) 2 = 36 - Значение 2 (a4,2) (a_ {4,2}) (a4,2) + 5 = 2 (25) + 5 = 55
- Значение a1,93 = 153 \ frac {a_ {1,9}} {3} = \ frac {15} {3} 3a1,9 = 315 = 5
- Значение a3,5 + a1,1a_ {3,5} + a_ {1,1} a3,5 + a1,1 = 1 + 3 = 4
Узнав, как размерность матрицы предоставляет информацию о характеристиках нотации массива, и зная, какие элементы в матрице, важно признать, что существует несколько различных типов матриц:
- Квадратные матрицы:
Когда матрица имеет одинаковое количество столбцов и строк, мы называем эту матрицу квадратной матрицей.Таким образом, квадратная матрица представляет собой матрицу размера mxn, в которой m = n, и, таким образом, ее обозначение в виде прямоугольника выглядит как квадратный прямоугольник, поскольку элементы внутри скобки матрицы имеют одинаковое количество с каждой стороны. Поскольку в этом случае m равно n, мы обычно называем размеры квадратных матриц просто nxn.
 Уравнение 2 показывает обозначение квадратной матрицы размером 3×3.
Уравнение 2 показывает обозначение квадратной матрицы размером 3×3. - Диагональные матрицы:
Хотя диагональные матрицы могут относиться к матрицам с любой комбинацией размеров, этот термин чаще используется, когда говорят о конкретных типах квадратных матриц.Причина этого в том, что диагональную матрицу легко идентифицировать по разнице между типом элементов, которые она имеет в своей главной диагонали, и остальной частью массива.
Основная диагональ матрицы – это диагональный массив чисел, который начинается с его самого верхнего левого угла и постепенно движется вниз к правой стороне, пока вы не дойдете до самой нижней возможной строки. Для квадратной матрицы основная диагональ идет от левого верхнего угла к правому нижнему углу. Если мы возьмем уравнение 2 в качестве предоставленной матрицы, главная диагональ этой матрицы будет содержать элементы: a1,1, a2,2a_ {1,1}, a_ {2,2} a1,1, a2,2 и a3 , 3a_ {3,3} a3,3.Для всех матриц главная диагональ – это массив элементов с субиндексами, где m равно n, и поэтому главная диагональ любой матрицы – это массив элементов, таких что: a1,1, a2,2, a3,3 .
 .. an, na_ {1,1}, a_ {2,2}, a_ {3,3} … a_ {n, n} a1,1, a2,2, a3,3 … an, n, где m = n.
.. an, na_ {1,1}, a_ {2,2}, a_ {3,3} … a_ {n, n} a1,1, a2,2, a3,3 … an, n, где m = n.Итак, диагональная матрица – это матрица, в которой только элементы внутри ее главной диагонали отличны от нуля.
- Матрица идентичности:
Матрица идентичности по определению являются квадратными матрицами, которые содержат только значения 1 на своей главной диагонали.Матрицы идентичности обозначаются как InI_ {n} In, где n представляет размерность матрицы nxn. Такие матрицы важны в нотации векторных матриц, поскольку они позволяют четко различать термины различных переменных в наборах векторов, записанных в виде матрицы, хотя мы продолжим эту тему более глубоко в последующих уроках, это важно для вас чтобы знать, что обозначение единичной матрицы обеспечивает основу для обозначения единичного вектора в линейной алгебре, и, таким образом, единичная матрица также может называться единичной матрицей.
Все единичные матрицы являются диагональными матрицами, и любые кратные из них тоже будут, потому что единственные значения, на которые влияет скалярное умножение, – это значения на главной диагонали (так как остальные из них – нули, любое число, умноженное на ноль, равно нулю, и поэтому нули не меняются).

- Нулевая матрица:
Нулевая матрица – это матрица, элементами которой являются только нули. Обозначение нулевой матрицы, вероятно, является самым простым, поскольку не имеет значения размеры рассматриваемой матрицы, поскольку все элементы внутри нее равны нулю, у вас есть нулевая матрица.Нулевые матрицы также могут называться нулевыми матрицами.
Все они будут подробно изучаться на уроках этого курса, поскольку они будут наиболее полезны с помощью различных операций или методов при решении линейных систем уравнений.
Пример 3
Определите, к какому типу матриц относится каждый из перечисленных в следующем списке, запишите их размеры и характеристики, которые позволили вам идентифицировать его:
Уравнение 5: различные типы матрицИ так, чтобы идентифицировать каждую из матриц выше:
- Это матрица 3 x 2, что означает, что она имеет три строки и два столбца, что легко заметить.

- Эта матрица является диагональной матрицей, поскольку она имеет разное количество строк и столбцов, мы называем эти типы матриц матрицами «прямоугольной диагонали». Размеры матрицы б) составляют 2 х 4.
- Это квадратная матрица размером 4 x 4 (4 строки и 4 столбца).
- Матрица d) является нулевой матрицей, поскольку все ее элементы нулевые.
- Matrix e) представляет собой матрицу столбцов с размерами 4 x 1 (все матрицы столбцов состоят из одного столбца и также известны как векторные матрицы).
- Эта матрица является единичной матрицей I3I_ {3} I3, что означает, что размер матрицы f) равен 3 или 3 x 3 (3 строки и 3 столбца).
Прежде чем мы завершим этот урок введением в правила, которые применяются к основным матричным операциям, мы хотели бы порекомендовать вам ознакомиться с этими заметками о матричной нотации и операциях, если вы хотите продолжить рассмотрение примеров того, что мы узнали на данный момент. этот курс. Еще одна приятная и понятная статья, которую вы можете посетить, – это статья о матричной нотации, где вы можете найти еще несколько примеров в упрощенной форме.
Еще одна приятная и понятная статья, которую вы можете посетить, – это статья о матричной нотации, где вы можете найти еще несколько примеров в упрощенной форме.
Матричные правила
В этом разделе у нас будет краткое введение в матричные правила для таких операций, как сложение и умножение. Эти типы операций будут подробно рассмотрены и с примерами позже в этом курсе линейной алгебры, но важно иметь базовое представление о том, как размер матрицы и сколько строк по сравнению с столбцами в матрице дает рекомендации о том, какие операции могут быть выполнены. с такой матрицей или нет.
- Сложение / вычитание:
Сложение (и, следовательно, вычитание) двух матриц – очень простая операция для вычисления.Правило состоит в том, что пока у вас есть две матрицы с одинаковым количеством строк и столбцов, вы можете складывать (или вычитать) их. Результирующая матрица будет иметь такое же количество строк и столбцов, что и две исходные матрицы, и операция просто выполняется путем добавления элементов с одинаковыми субиндексами из каждой матрицы и размещения результата в элементе с тем же субиндексом в результирующей матрице.
Рисунок 2: Матричное сложение Взгляните на рисунок 2, где вы можете соблюдать общее правило добавления матриц:
Взгляните на рисунок 2, где вы можете соблюдать общее правило добавления матриц: - Умножение: Рисунок 3: Правило умножения матриц
Чтобы перемножить две матрицы, первая матрица должна иметь такое же количество столбцов, что и вторая матрица, имеющая строки.Результатом этого умножения будет новая матрица с размерами, равными количеству строк в первой матрице на количество столбцов, найденных во второй матрице. Итак, это означает, что для двух матриц A = m1 × n1A = m_ {1} \ times n_ {1} A = m1 × n1 и B = m2 × n2B = m_ {2} \ times n_ {2} B = m2 × n2 для умножения, n1n_ {1} n1 должен быть равен m2m_ {2} m2, и результирующая матрица будет иметь размеры C = m1 × n2C = m_ {1} \ times n_ {2 } C = m1 × n2. Это можно увидеть на следующем рисунке:
Рисунок 4: Объяснение умножения матрицИтак, как вы, возможно, уже заметили, умножение матриц НЕ коммутативно: вы не можете изменить порядок умножаемых матриц и получить тот же результат, фактически, вы не сможете их умножить из-за того, что, Если они не являются квадратными матрицами, первая матрица не будет содержать такое же количество столбцов, как количество строк во второй, что делает умножение невозможным.

Это все для нашей сегодняшней темы, как видите, этот урок служит введением в алгебраические обозначения, которые мы будем использовать на протяжении большей части этого курса и любого курса линейной алгебры. Убедитесь, что вы понимаете примеры, чтобы подготовиться к следующему уроку.
Матрицы в ACT – Magoosh Blog
У многих студентов возникают незначительные приступы паники, когда они впервые сталкиваются с матрицами на тесте ACT по математике, но не бойтесь! Даже если матрицы кажутся вам совершенно чуждыми, быстрое прочтение этого блога успокоит ваши нервы.🙂
К счастью, матричные вопросы в тесте ACT встречаются довольно редко (вы можете не встретить ни одного из 60 вопросов в тесте ACT по математике!) И требуют только базовых навыков сложения и вычитания (или * кашляет * калькулятор TI-83 * кашель *) решить. Если вы можете сложить 5 и 6, все будет в порядке!
Основы матрицы ACT
Слово матрица относится к прямоугольному окну, заполненному числами, расположенными в строках и столбцах. Каждое число в матрице называется элементом .Когда дело доходит до матриц на тесте, вам действительно нужно знать основы:
Каждое число в матрице называется элементом .Когда дело доходит до матриц на тесте, вам действительно нужно знать основы:
Во-первых, матрицы называются по их размерам.
Матрицыбывают самых разных размеров. Сначала мы записываем размер матрицы с количеством строк, а затем с количеством столбцов.
Это, например, матрица 3 x 2. 3 строки и 2 столбца:
Скалярное умножение
Вы можете увидеть вопрос в ACT, который просит вас сделать то, что называется скалярным умножением.Это означает, что мы умножаем матрицу на обычное число. Каждая запись внутри матрицы просто умножается на это число.
Добавление матрицы
Вы также можете увидеть вопрос в ACT о сложении или вычитании матриц. Важное примечание: вы можете складывать или вычитать только две матрицы абсолютно одинаковых размеров. Мы складываем или вычитаем матрицы, складывая или вычитая соответствующие числа (числа, которые находятся в одном и том же «месте» на каждой матрице).
Обратите внимание, что размер матриц одинаков, и что каждый элемент в первой матрице добавляется к соответствующему элементу во второй матрице, чтобы получить соответствующий элемент в третьей матрице. -3 + -2 = -5.
С таким пониманием мы можем решить относительно x, написав простое уравнение: x + 9 = 11; х = 2.
Умножающие матрицы
Ладно, самое сложное я оставил напоследок. Вы можете умножать матрицы, только если количество столбцов в первой матрице равно количеству строк во второй матрице. Когда мы умножаем матрицы, матрица произведения будет иметь такое же количество строк, что и первая матрица, и такое же количество столбцов, как вторая. Например, произведение матрицы 2 x 3 и матрицы 3 x 2 будет матрицей 3 x 3 .
Чтобы найти запись в первом столбце, первой строке матрицы произведения, мы собираемся умножить каждое число в первой строке первой матрицы на соответствующее ему число в первом столбце второй матрицы и сложить произведения. все вместе.
Для записи во второй строке, втором столбце, мы сделаем то же самое со второй строкой первой матрицы и вторым столбцом второй матрицы:
Чтобы полностью заполнить эту матрицу, нам нужно будет выполнить 9 вычислений, но не волнуйтесь, ACT с большей вероятностью даст вам меньшие матрицы или матрицы с большим количеством нулей или попросит вас найти только одну запись в матрице .
Давайте рассмотрим вопрос о вычитании матриц.
Практический вопрос по матрице управляемого АСТ
Какова сумма x и y?
Чтобы ответить на этот вопрос, мы составим два уравнения для независимого решения относительно x и y.
16-2 = х и 3 – (-4) = у
14 = x и 7 = y
Их сумма 14 + 7 = 21.
Иногда для обозначения всей матрицы вводится переменная. Давайте посмотрим на пример:
Осторожно вычтите каждый соответствующий элемент.
Ответ
А теперь ответьте на практический вопрос самостоятельно!
Дополнительные практические вопросы по матрице ACT
Какое решение матриц?
(А)
(В)
(К)
(Г)
(R)
Ответ и объяснение
Правильный ответ (А).
Чтобы вычесть матрицы, вычтите каждый соответствующий элемент, как показано выше.Помните, что вычитание отрицательного числа становится сложением.
Практикуясь, вы увидите, что математика, используемая в вопросах матрицы ACT, редко бывает сложной – просто держите строки и столбцы выровненными, и вы не сможете не понять их правильно!
Популярные ресурсы
Между прочим, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT. Нажмите сюда, чтобы узнать больше!
О Майке MᶜGarry
Майк работал экспертом по GMAT в Magoosh, помогая создавать сотни видеоуроков и практических вопросов, чтобы помочь студентам GMAT добиться успеха.Он также был отмечен как «участник месяца» более двух лет в клубе GMAT. Майк имеет степень бакалавра гуманитарных наук. по физике (выпуск с отличием, ) и M.T.S. в «Религиях мира», оба из Гарварда. Помимо стандартизированного тестирования, у Майка более 20 лет опыта преподавания как в частных, так и в государственных школах, специализирующихся на математике и физике. В свободное время Майк любит разбивать футбольные мячи на орбите, и, несмотря на отсутствие очевидной черепно-мозговой недостаточности, он настаивает на том, чтобы болеть за Нью-Йорк Метс.Узнайте больше о GMAT через видеообъяснения Майка на YouTube и ресурсы, например «Что такое хороший результат GMAT?». и диагностический тест GMAT.Математика – Матричная алгебра – Мартин Бейкер
Матрица – это прямоугольный массив элементов, с которыми работают как с одним объектом. Элементами часто являются числа, но это может быть любой математический объект при условии, что он может быть добавлен и умножен с приемлемыми свойствами (это должна быть структура поля – подробности см. В рамке справа), например, мы можем иметь матрицу, элементы которой сложны. числа.
Применение матриц
Матрицы широко используются в приложениях по геометрии, физике и компьютерной графике. Например, на этой странице обсуждается, как их можно использовать для представления преобразований.
Связь с другими математическими величинами
Мы можем думать о матрице по-разному, например:
- В виде вектора со строками и столбцами.
- В случае тензора (тензор 2-го ранга – это матрица).
- Как представление системы линейных уравнений.
Матрицы являются векторным пространством, то есть имеют следующие операции:
| операция | обозначение | объяснение |
|---|---|---|
| дополнение | M [a + b] = M [a] + M [b] | сложение двух матриц выполняется путем сложения соответствующих элементов двух матриц. |
| скалярное умножение | M [s * a] = s * M [a] | скалярное произведение матриц получается путем умножения скалярного произведения на каждый из его членов по отдельности. |
Помимо векторного пространства, матрицы имеют дополнительную структуру, определяемую другим типом умножения, это позволяет нам перемножить две матрицы и получить третью матрицу (при соблюдении определенных условий относительно размеров). Этот тип умножения можно рассматривать как расширение «точечного» произведения векторов, это основной тип умножения матриц, и он обсуждается на этой странице.
Аксиомы
| аксиома | дополнение | скалярное умножение | умножение |
|---|---|---|---|
| ассоциативность | (a + b) + c = a + (b + c) | (s1 s2) a = s1 (s2 a) | (а * б) * с = а * (б * в) |
| коммутативность | а + Ь = Ь + а | не обязательно коммутативный | |
| распределенность | с * (b + c) = s * b + s * c (s1 + s2) * a = s1 * a + s2 * a | а * (Ь + с) = а * Ь + а * с (a + b) * c = a * c + b * c | |
| идентификатор | а + 0 = 0 + а = а | 1 * а = | а * 1 = 1 * а = |
| обратное | а + (- а) = 0 (-а) + а = 0 | а * а -1 = 1 а -1 * а = 1 если det [a] ≠ 0 |
В этой таблице приведены некоторые свойства матричных операций, обратите внимание, что умножение матриц не коммутативно.
Связь с векторами
Векторы сильно связаны с матрицами, их можно рассматривать как однонаправленную матрицу. Итак, можем ли мы создать матрицу из вектора, элементы которого сами являются векторами? Мы не можем этого сделать, потому что элементы вектора должны быть математической структурой, известной как «поле», а вектор сам по себе не является полем, потому что он не обязательно имеет коммутативное умножение и другие свойства, необходимые для поля.
Тем не менее, было бы неплохо, если бы мы могли построить матрицу из вектора (нарисованного в виде столбца), элементы которого сами являются векторами (нарисованными в виде строки):
Чтобы создать матрицу путем объединения векторных структур, нам нужно сделать две вещи с «внутренним вектором»:
- Нам нужно сделать транспонирование так, чтобы это была строка, а не столбец.
- Нам нужна операция умножения, которая сделает его полем.
Для этого мы создаем «двойник» вектора, это называется ковектором, как описано на этой странице.
Независимо от того, рассматриваем ли мы векторы как частный случай матриц или матрицы как векторы векторов, или если мы рассматриваем векторы и матрицы как разные типы, использование векторов и матриц вместе очень важно. Матрица – это способ преобразования одного вектора в другой вектор (и всего набора векторов в другой набор векторов).Это позволяет нам выразить линейное преобразование в виде одного уравнения:
| = |
|
Другая возможность состоит в том, что матрицы могут иметь матрицы в качестве элементов при условии, что все элементы имеют одинаковую размерность, в этом случае ее можно заменить одной большой матрицей.Например, если у нас есть матрица размера m × n, и каждый из ее элементов является матрицей p × q, то мы могли бы заменить ее одной матрицей (m * p) × (n * q).
Линейные функции
Матрица может представлять линейную карту или линейный оператор. Если у нас есть система одновременных линейных уравнений:
f1 (х, у) = а0 * х + а1 * у
f2 (х, у) = а2 * х + а3 * у
Это может быть представлено векторами и матрицами:
Чтобы найти x и y, нам нужно только инвертировать матрицу.
Дополнительная информация о матрицах
Для получения дополнительной информации о линейных преобразованиях с использованием матриц:
Как уже упоминалось, арифметика выполняется с использованием матриц как единого целого, способ выполнения этой арифметики объясняется здесь:
Существуют также другие функции, которые можно выполнять с матрицами, как описано здесь:
Матричное исчисление
Подробности см. Здесь
Матричная математика для Интернета – веб-API
Матрицы могут использоваться для представления преобразований объектов в пространстве и используются для выполнения многих ключевых типов вычислений при построении изображений и визуализации данных в Интернете.В этой статье рассказывается, как создавать матрицы и как использовать их с преобразованиями CSS и типом преобразования matrix3d .
Хотя в этой статье для упрощения пояснений используется CSS, матрицы – это основная концепция, используемая многими различными технологиями, включая WebGL, API WebXR (VR и AR) и шейдеры GLSL. Эта статья также доступна в виде комплекта материалов MDN. В живых примерах используется набор служебных функций, доступных в глобальном объекте с именем MDN .
Существует много типов матриц, но нас интересуют матрицы трехмерного преобразования.Эти матрицы состоят из набора из 16 значений, расположенных в сетке 4×4. В JavaScript матрицу легко представить в виде массива.
Начнем с рассмотрения единичной матрицы . Это специальная матрица преобразования, которая работает так же, как число 1 при скалярном умножении; так же, как n * 1 = n, умножение любой матрицы на единичную матрицу дает результирующую матрицу, значения которой соответствуют исходной матрице.
Идентификационная матрица в JavaScript выглядит так:
пусть identityMatrix = [
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1
];
Как выглядит умножение на единичную матрицу? Самый простой пример – умножить одну точку на единичную матрицу.Поскольку для трехмерной точки требуются только три значения (x, y и z), а матрица преобразования представляет собой матрицу значений 4×4, нам нужно добавить к точке четвертое измерение. Условно это измерение называется перспективой и обозначается буквой w. Для типичного положения установка w на 1 сделает математические вычисления более эффективными.
После добавления компонента w к точке обратите внимание, как аккуратно выстраиваются матрица и точка:
[1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1]
[4, 3, 2, 1]
Компонент w имеет несколько дополнительных применений, которые выходят за рамки данной статьи.Прочтите статью о проекции вида модели WebGL, чтобы узнать, как это может пригодиться.
Умножение матрицы и точки
В нашем примере кода мы определили функцию для умножения матрицы и точки – multiplyMatrixAndPoint () :
функция multiplyMatrixAndPoint (матрица, точка) {
пусть c0r0 = matrix [0], c1r0 = matrix [1], c2r0 = matrix [2], c3r0 = matrix [3];
пусть c0r1 = matrix [4], c1r1 = matrix [5], c2r1 = matrix [6], c3r1 = matrix [7];
пусть c0r2 = matrix [8], c1r2 = matrix [9], c2r2 = matrix [10], c3r2 = matrix [11];
пусть c0r3 = matrix [12], c1r3 = matrix [13], c2r3 = matrix [14], c3r3 = matrix [15];
пусть x = точка [0];
пусть y = point [1];
пусть z = point [2];
пусть w = точка [3];
пусть resultX = (x * c0r0) + (y * c0r1) + (z * c0r2) + (w * c0r3);
пусть resultY = (x * c1r0) + (y * c1r1) + (z * c1r2) + (w * c1r3);
пусть resultZ = (x * c2r0) + (y * c2r1) + (z * c2r2) + (w * c2r3);
пусть resultW = (x * c3r0) + (y * c3r1) + (z * c3r2) + (w * c3r3);
return [результатX, результатY, результатZ, результатW];
}
Теперь, используя функцию выше, мы можем умножить точку на матрицу.Используя единичную матрицу, он должен возвращать точку, идентичную исходной, поскольку точка (или любая другая матрица), умноженная на единичную матрицу, всегда равна самой себе:
пусть identityResult = multiplyMatrixAndPoint (identityMatrix, [4, 3, 2, 1]);
Возвращение той же точки не очень полезно, но есть другие типы матриц, которые могут выполнять полезные операции с точками. В следующих разделах будут продемонстрированы некоторые из этих матриц.
Умножение двух матриц
Помимо умножения матрицы и точки, вы также можете умножить две матрицы вместе.Вышеуказанная функция может быть повторно использована для помощи в этом процессе:
функция multiplyMatrices (matrixA, matrixB) {
пусть row0 = [matrixB [0], matrixB [1], matrixB [2], matrixB [3]];
пусть row1 = [matrixB [4], matrixB [5], matrixB [6], matrixB [7]];
пусть row2 = [matrixB [8], matrixB [9], matrixB [10], matrixB [11]];
пусть row3 = [matrixB [12], matrixB [13], matrixB [14], matrixB [15]];
пусть result0 = multiplyMatrixAndPoint (matrixA, row0);
пусть результат1 = multiplyMatrixAndPoint (matrixA, row1);
пусть результат2 = multiplyMatrixAndPoint (matrixA, row2);
пусть result3 = multiplyMatrixAndPoint (matrixA, row3);
возвращение [
результат0 [0], результат0 [1], результат0 [2], результат0 [3],
результат1 [0], результат1 [1], результат1 [2], результат1 [3],
результат2 [0], результат2 [1], результат2 [2], результат2 [3],
результат3 [0], результат3 [1], результат3 [2], результат3 [3]
];
}
Давайте посмотрим на эту функцию в действии:
пусть someMatrix = [
4, 0, 0, 0,
0, 3, 0, 0,
0, 0, 5, 0,
4, 8, 4, 1
]
пусть identityMatrix = [
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1
];
пусть someMatrixResult = multiplyMatrices (identityMatrix, someMatrix);
Важно : Эти матричные функции написаны для ясности объяснения, а не для управления скоростью или памятью.Эти функции создают множество новых массивов, что может быть особенно дорогостоящим для операций в реальном времени из-за сборки мусора. В реальном производственном коде лучше всего использовать оптимизированные функции. glMatrix – это пример библиотеки, ориентированной на скорость и производительность. В библиотеке glMatrix основное внимание уделяется целевым массивам, которые выделяются до цикла обновления.
Матрица преобразования основана на единичной матрице и используется в трехмерной графике для перемещения точки или объекта в одном или нескольких из трех направлений (x, y и / или z).Самый простой способ придумать перевод – это взять чашку кофе. Чашка для кофе должна стоять вертикально и ориентироваться таким же образом, чтобы кофе не проливался. Он может двигаться вверх по воздуху от стола и по воздуху в космосе.
На самом деле вы не можете пить кофе, используя только матрицу перевода, потому что, чтобы выпить его, вы должны иметь возможность наклонять или вращать чашку, чтобы налить кофе себе в рот. Мы рассмотрим тип матрицы (которая называется «матрица поворота »), которую вы используете для этого позже.
пусть x = 50;
пусть y = 100;
пусть z = 0;
пусть translationMatrix = [
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
х, у, z, 1
];
Поместите расстояния по трем осям в соответствующие позиции в матрице переноса, затем умножьте их на точку или матрицу, которые необходимо перемещать в трехмерном пространстве.
Действительно простой способ начать использовать матрицу – использовать преобразование CSS Lorem ipsum dolor sit amet, conctetur adipisicing elit ... Наконец, для каждого из примеров мы сгенерируем матрицу 4×4, а затем обновим стиль Посмотреть на JSFiddle Масштабная матрица создает что-то большее или меньшее в одном или нескольких из трех измерений: ширине, высоте и глубине.В типичных (декартовых) координатах. это вызывает растяжение или сжатие объекта в соответствующих направлениях. Величина изменения, применяемого к ширине, высоте и глубине, размещается по диагонали, начиная с верхнего левого угла и продвигаясь вниз к правому нижнему. Посмотреть на JSFiddle Матрица поворота используется для поворота точки или объекта.Матрицы поворота выглядят немного сложнее, чем матрицы масштабирования и преобразования. Они используют тригонометрические функции для вращения. Хотя в этом разделе мы не будем разбивать шаги на исчерпывающие детали (для этого ознакомьтесь с этой статьей о Wolfram MathWorld), возьмите этот пример для иллюстрации. Во-первых, вот код, который вращает точку вокруг начала координат без использования матриц. Можно закодировать этот тип шагов в матрицу и сделать это для каждого из измерений x, y и z. Ниже показано вращение против часовой стрелки вокруг оси Z в левой системе координат: Посмотреть на JSFiddle Вот набор функций, которые возвращают матрицы вращения для вращения вокруг каждой из трех осей.Одно большое замечание: перспектива не применяется, поэтому она может пока не казаться трехмерной. Плоскостность эквивалентна тому, когда камера действительно приближается к объекту на расстоянии – ощущение перспективы исчезает. Просмотр на JSFiddle Реальная мощность матриц исходит от компоновки матриц .Когда матрицы определенного класса перемножаются, они сохраняют историю преобразований и являются обратимыми. Это означает, что если матрица сдвига, поворота и масштабирования объединены вместе, когда порядок матриц изменяется на обратный и применяется повторно, то возвращаются исходные точки. Порядок умножения матриц имеет значение. При умножении чисел a * b = c и b * a = c истинны. Например, 3 * 4 = 12 и 4 * 3 = 12. В математике эти числа будут описаны как коммутативное .Матрицы , а не , гарантированно будут одинаковыми при переключении порядка, поэтому матрицы некоммутативны . Еще одна загвоздка в том, что умножение матриц в WebGL и CSS должно происходить в порядке, обратном интуитивно понятным операциям. Например, чтобы уменьшить что-либо на 80%, переместить его на 200 пикселей вниз, а затем повернуть вокруг начала координат на 90 градусов, это в псевдокоде будет выглядеть примерно так. Для составления наших матриц мы будем использовать функцию Посмотреть на JSFiddle Наконец, забавный шаг для демонстрации того, как работают матрицы, – это перевернуть шаги, чтобы вернуть матрицу к исходной единичной матрице. Матрицы важны, потому что они содержат небольшой набор чисел, который может описывать широкий диапазон преобразований в пространстве. Их можно легко использовать в программах.Различные координатные пространства могут быть описаны с помощью матриц, и некоторое умножение матриц переместит один набор данных из одного координатного пространства в другое координатное пространство. Матрицы эффективно запоминают каждую часть предыдущих преобразований, которые использовались для их создания. Для использования в WebGL видеокарта особенно хороша при умножении большого количества точек в пространстве на матрицы. Различные операции, такие как позиционирование точек, расчет освещения и постановка анимированных персонажей, полагаются на этот фундаментальный инструмент. Введение
в Матрицы / Размер матрицы (стр.
1 из 3) Разделы: Дополненные и коэффициенты
матрицы / Размер матрицы, Обозначение матрицы и
типы, Матрица равенства Дополненный
матрицы Матрицы невероятно
полезные вещи, которые возникают во многих различных прикладных областях.А пока вы
наверное, только простейшие манипуляции с матрицами, а потом
вы перейдете к следующей теме. Но не стоит удивляться, встретив
матрицы опять же, скажем, в физике или технике. (Множественное число «матрицы»
произносится как “МАЙ-тру-сиз”.) Матрицы изначально были
на основе систем
линейных уравнений. Запишите коэффициенты.
и значения ответов, включая все знаки «минус». Если там
– коэффициент «нет», тогда коэффициент равен «1». То есть, учитывая систему
(линейных) уравнений, вы можете связать с ним матрицу (сетку чисел
внутри скобок), который содержит только коэффициенты линейного
система. Это называется «расширенной матрицей»: сетка, содержащая
коэффициенты из левой части каждого уравнения были “дополнены”
с ответами из правой части каждого уравнения. Записи (то есть
значения в) матрице соответствуют x -, л –
и z -значения
в исходной системе, если исходная система устроена правильно
на первом месте. Иногда вам нужно переставить термины или вставить
нули в качестве заполнителей в вашей матрице. Мне сначала нужно переставить
система как: Тогда я могу написать
связанная матрица как: При формировании дополненной
матрица, используйте ноль для любой записи, где соответствующее место в системе
линейных уравнений пусто. Коэффициент
матрицы Если сформировать матрицу
только по значениям коэффициентов матрица будет выглядеть так: Это называется ”
матрица коэффициентов “.авторское право
Элизабет Стапель 2003-2011 Все права защищены Выше мы пошли от линейного
систему в расширенную матрицу. Вы можете пойти и другим путем. Помните, что матрицы
требуют, чтобы все переменные были выстроены аккуратно и аккуратно. И это
обычно, когда у вас есть три переменные, использовать x , л ,
и z ,
в этой последовательности.Таким образом, соответствующая линейная система должна быть: Размер
матрицы Матрицы часто упоминаются
по их размерам. Размер матрицы задается в виде измерения,
примерно так же, как комнату можно назвать «комнатой десять на двенадцать».
Размеры матрицы – это строки и столбцы, а не размер
ширина и длина. Например, рассмотрим следующую матрицу A : Начиная с A имеет три строк и четыре столбца ,
размер А это 3 4
(произносится как «три на четыре»). Ряды идут бок о бок;
колонны идут вверх и вниз. «Строка» и «столбец» – это
технические термины и не являются взаимозаменяемыми. Размеры матрицы всегда
задается сначала количеством строк, а затем количеством столбцов.
Следуя этому соглашению, следующая матрица B : … это 2
3. Если матрица
имеет такое же количество строк, что и столбцы, матрица называется “квадратной”.
матрица.Например, матрица коэффициентов сверху: … это 3
3 квадратная матрица. Верх
| 1 | 2 | 3 | Вернуться к указателю Далее
>> Цитируйте эту статью
как: Стапель, Елизавета.
«Введение в матрицы / размер матрицы.« Purplemath .
Доступно по номеру Math.js поддерживает многомерные матрицы и массивы. Матрицы могут быть
создаются, обрабатываются и используются в расчетах. Оба обычных JavaScript
массивы, а также матричный тип, реализованный math.js можно использовать
взаимозаменяемо во всех соответствующих функциях math.js. math.js поддерживает оба
плотные и разреженные матрицы. Math.js поддерживает два типа матриц: В большинстве случаев тип матричного вывода функций определяется
вход функции: массив Матрица может быть создана из массива с помощью функции Math.js поддерживает обычные массивы. Можно создать несколько размеров
путем вложения массивов друг в друга. Матрицы могут содержать разные типы значений: числа, комплексные числа,
единиц или строк.Различные типы можно смешивать в одной матрице. Существует ряд функций для создания матрицы определенного размера и
содержание: Функции Диапазоны могут быть созданы с помощью функции Все соответствующие функции math.js поддерживают матрицы и массивы. Math.js использует геометрические размеры: Размер матрицы можно вычислить с помощью функции Обратите внимание, что сами размеры не имеют значения.
При создании и печати двумерной матрицы первое измерение
обычно отображается как столбец , а второе измерение отображается как
строка . Например: Если у вас есть матрица, в которой первое измерение означает можно изменить с помощью их функции Наружные размеры матрицы можно сжать с помощью функции Подмножества матрицы могут быть извлечены или заменены с помощью функции Подмножество может быть определено с помощью индекса Обратите внимание, что математические приложения, такие как Matlab и Octave, работают по-разному,
поскольку они используют индексы на основе единицы. содержат функции Math.js поддерживает как плотные, так и разреженные матрицы. Разреженные матрицы эффективны для матриц, в основном содержащих нули.В этом случае они экономят много памяти, и вычисления могут быть намного быстрее, чем для плотных матриц. Math.js поддерживает два типа матриц: Тип матрицы можно выбрать при создании матрицы с помощью функций построения Все соответствующие функции в math.js поддерживают матрицы и массивы. Такие функции, как Полный список матричных функций доступен на странице справки по функциям. matrix3d () .Сначала мы создадим простой
Переместите меня с помощью матрицы
matrix3d .Имейте в виду, что хотя матрица состоит из 4 строк и 4 столбцов, она сворачивается в одну строку из 16 значений. В JavaScript матрицы всегда хранятся в одномерных списках.
function matrixArrayToCssMatrix (array) {
return 'matrix3d (' + array.join (',') + ')';
}
let moveMe = document.getElementById ('переместить меня');
let matrix3dRule = matrixArrayToCssMatrix (translationMatrix);
moveMe.style.transform = matrix3dRule;
пусть w = 1,5;
пусть h = 0,7;
пусть d = 1;
пусть scaleMatrix = [
ш, 0, 0, 0,
0, з, 0, 0,
0, 0, д, 0,
0, 0, 0, 1
];
пусть точка = [10, 2];
let distance = Math.sqrt (точка [0] * точка [0] + точка [1] * точка [1]);
пусть вращениеInRadians = Math.PI / 3;
пусть transformedPoint = [
Math.cos (вращениеInRadians) * расстояние,
Math.sin (вращениеInRadians) * расстояние
];
let sin = Math.sin;
пусть cos = Math.cos;
пусть a = Math.PI * 0,3;
пусть rotateZMatrix = [
cos (a), -sin (a), 0, 0,
грех (а), соз (а), 0, 0,
0, 0, 1, 0,
0, 0, 0, 1
];
function rotateAroundXAxis (a) {
возвращение [
1, 0, 0, 0,
0, cos (a), -sin (a), 0,
0, грех (а), соз (а), 0,
0, 0, 0, 1
];
}
function rotateAroundYAxis (a) {
возвращение [
соз (а), 0, грех (а), 0,
0, 1, 0, 0,
-sin (a), 0, cos (a), 0,
0, 0, 0, 1
];
}
function rotateAroundZAxis (a) {
возвращение [
cos (a), -sin (a), 0, 0,
грех (а), соз (а), 0, 0,
0, 0, 1, 0,
0, 0, 0, 1
];
}
трансформация = повернуть * перевести * масштаб
Составление нескольких преобразований
multiplyArrayOfMatrices () , которая является частью набора служебных функций, представленных в верхней части этой статьи.Он берет массив матриц и умножает их вместе, возвращая результат. В коде шейдера WebGL это встроено в язык, и можно использовать оператор * . Кроме того, в этом примере используются функции scale (), и translate () , которые возвращают матрицы, как определено выше.
пусть transformMatrix = MDN.multiplyArrayOfMatrices ([
rotateAroundZAxis (Math.PI * 0,5),
перевести (0, 200, 0),
шкала (0,8, 0,8, 0,8),
]);
пусть transformMatrix = MDN.multiplyArrayOfMatrices ([
шкала (1,25, 1,25, 1,25),
перевести (0, -200, 0),
rotateAroundZAxis (-Math.PI * 0,5),
rotateAroundZAxis (Math.PI * 0,5),
перевести (0, 200, 0),
шкала (0,8, 0,8, 0,8),
]);
Введение в матрицы / Размер матрицы
https://www.purplemath.com/modules/matrices.htm .
Дата обращения [Дата] [Месяц] 2016 г. обширная математическая библиотека для JavaScript и Node.js
Массивы и матрицы #
Массив , обычный массив JavaScript. Можно создать многомерный массив
вложенными массивами. Matrix , матричная реализация math.js. Матрица – это обернутый объект
вокруг обычного JavaScript Array , предоставляя служебные функции для упрощения
манипуляции с матрицей, такие как подмножество , размер , изменение размера , клон и другие. в качестве входных данных будет возвращать массив , матрицу в качестве входных данных.
вернет Matrix . В случае смешанного ввода возвращается Matrix .
Для функций, в которых тип вывода не может быть определен из
вход, выход определяется опцией конфигурации матрицы ,
который может быть строкой «Матрица» (по умолчанию) или «Массив» .
// создаем массив и матрицу
const array = [[2, 0], [-1, 3]] // Массив
const matrix = math.matrix ([[7, 1], [-2, 3]]) // Матрица
// выполняем вычисление для массива и матрицы
math.square (array) // Массив, [[4, 0], [1, 9]]
math.square (matrix) // Матрица, [[49, 1], [4, 9]]
// выполняем вычисления со смешанным массивом и вводом матрицы
math.add (array, matrix) // Матрица, [[9, 1], [-3, 6]]
математика.multiply (array, matrix) // Матрица, [[14, 2], [-13, 8]]
// создаем матрицу. Тип вывода функциональных определяется
// параметр конфигурации `matrix`
math.ones (2, 3) // Матрица, [[1, 1, 1], [1, 1, 1]]
Создание #
math.matrix . В
предоставленный массив может содержать вложенные массивы для создания многомерной матрицы. При вызове без аргументов пустая матрица будет
созданный.
// создание матриц
math.matrix () // Матрица, размер [0]
math.matrix ([0, 1, 2]) // Матрица, размер [3]
math.matrix ([[0, 1], [2, 3], [4, 5]]) // Матрица, размер [3, 2]
// создаем массивы
[] // Массив, размер [0]
[0, 1, 2] // Массив, размер [3]
[[0, 1], [2, 3], [4, 5]] // Массив, размер [3, 2]
// создаем матрицу со смешанными типами
const a = math.matrix ([2.3, 'привет', math.complex (3, -4), math.unit ('5,2 мм')])
a.subset (math.index (1)) // 'привет'
единиц , нулей , идентичность .
// нули создает матрицу, заполненную нулями
math.zeros (3) // Матрица, размер [3], [0, 0, 0]
математика.zeros (3, 2) // Матрица, размер [3, 2], [[0, 0], [0, 0], [0, 0]]
math.zeros (2, 2, 2) // Матрица, размер [2, 2, 2],
// [[[0, 0], [0, 0]], [[0, 0], [0, 0]]]
// единицы создают матрицу, заполненную единицами
math.ones (3) // Матрица, размер [3], [1, 1, 1]
math.multiply (math.ones (2, 2), 5) // Матрица, размер [2, 2], [[5, 5], [5, 5]]
// идентичность создает единичную матрицу
math.identity (3) // Матрица, размер [3, 3], [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
math.identity (2, 3) // Матрица, размер [2, 3], [[1, 0, 0], [0, 1, 0]]
единиц , нулей и identity также принимают один массив
или матрица, содержащая размеры для матрицы.Когда входом является массив,
функции выведут массив. Когда входом является матрица, выход будет
быть Матрицей. Обратите внимание, что в случае чисел в качестве аргументов вывод будет
определяется опцией , матрица , как описано в разделе
Массивы и матрицы.
// Массив на входе дает массив на выходе
math.ones ([2, 3]) // Массив, размер [3, 2], [[1, 1, 1], [1, 1, 1]]
math.ones (math.matrix ([2, 3])) // Матрица, размер [3, 2], [[1, 1, 1], [1, 1, 1]]
диапазон .Функция диапазон является
вызывается с параметрами start и end и, необязательно, с параметром step.
Начало диапазона включено, конец диапазона исключен.
math.range (0, 4) // [0, 1, 2, 3]
math.range (0, 8, 2) // [0, 2, 4, 6]
math.range (3, -1, -1) // [3, 2, 1, 0]
Расчеты №
// выполняем вычисление по матрице
const a = математика.matrix ([1, 4, 9, 16, 25]) // Матрица, [1, 4, 9, 16, 25]
math.sqrt (a) // Матрица, [1, 2, 3, 4, 5]
// выполняем вычисление в массиве
const b = [1, 2, 3, 4, 5]
math.factorial (b) // Массив, [1, 2, 6, 24, 120]
// умножаем массив на матрицу
const c = [[2, 0], [-1, 3]] // Массив
const d = math.matrix ([[7, 1], [-2, 3]]) // Матрица
math.multiply (c, d) // Матрица, [[14, 2], [-13, 8]]
// добавляем число в матрицу
математика.add (c, 2) // Массив, [[4, 2], [1, 5]]
// вычисляем определитель матрицы
math.det (c) // 6
math.det (d) // 23
Размер и размеры #
size .Функция размер возвращает Matrix или Array , в зависимости от параметра конфигурации matrix .
Кроме того, у матриц есть функция размером , которая всегда возвращает
массив.
// получаем размер скаляра
math.size (2.4) // Матрица, []
math.size (math.complex (3, 2)) // Матрица, []
math.size (math.unit ('5,3 мм')) // Матрица, []
// получаем размер одномерной матрицы (вектора) и строки
математика.size ([0, 1, 2, 3]) // Массив, [4]
math.size ('hello world') // Матрица, [11]
// получаем размер двумерной матрицы
const a = [[0, 1, 2, 3]] // Массив
const b = math.matrix ([[0, 1, 2], [3, 4, 5]]) // Матрица
math.size (a) // Массив, [1, 4]
math.size (b) // Матрица, [2, 3]
// матрицы имеют размер функции (всегда возвращает массив)
b.size () // Массив, [2, 3]
// получаем размер многомерной матрицы
const c = [[[0, 1, 2], [3, 4, 5]], [[6, 7, 8], [9, 10, 11]]]
математика.size (c) // Массив, [2, 2, 3]
console.table (math.zeros ([2, 4]))
// 0 0 0 0
// 0 0 0 0
x , а второе
означает y , это будет выглядеть запутанно, поскольку x печатается как столбец (вертикально) и y как ряд (горизонтально). Изменение размера #
Размер матриц resize . Эта функция называется
с массивом с новым размером в качестве первого аргумента и принимает необязательный
значение по умолчанию. По умолчанию для новых записей будет установлено значение 0 , но это возможно.
передать другое значение по умолчанию, например null , чтобы четко указать, что
записи не были заданы явно.
const a = math.matrix () // Матрица, размер [0], []
а.resize ([2, 3]) // Матрица, размер [2, 3], [[0, 0, 0], [0, 0, 0]]
a.resize ([2, 2, 2]) // Матрица, размер [2, 2, 2],
// [[[0, 0], [0, 0]], [[0, 0], [0, 0]]]
const b = math.matrix ()
b.resize ([3], 7) // Матрица, размер [3], [7, 7, 7]
b.resize ([5], 9) // Матрица, размер [5], [7, 7, 7, 9, 9]
b.resize ([2]) // Матрица, размер [2], [7, 7]
сжать . Когда
получение или установка подмножества в матрице, подмножество автоматически сжимается
или без сжатия.
// сжать матрицу
const a = [[[0, 1, 2]]]
math.squeeze (a) // [0, 1, 2]
math.squeeze ([[3]]) // 3
// подмножества автоматически сжимаются
const b = math.matrix ([[0, 1], [2, 3]])
b.subset (math.index (1, 0)) // 2
Получение или замена подмножеств #
subset .
Матрицы имеют функцию подмножества , которая применяется к самой матрице: Матрица.подмножество (индекс [, замена]) . И для матриц, и для массивов
статическая функция подмножества (матрица, индекс [, замена]) может использоваться.
Если параметр заменяет , функция заменяет подмножество
в матрице, и если нет, будет возвращено подмножество матрицы. . Индекс содержит одно значение
или набор значений для каждого измерения матрицы. Индекс может быть
создается с помощью функции , индекс .Матричные индексы в math.js отсчитываются от нуля, как и в большинстве языков программирования.
включая сам JavaScript.
// создаем матрицы
const a = [0, 1, 2, 3]
const b = [[0, 1], [2, 3]]
const c = math.zeros (2, 2)
const d = math.matrix ([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
const e = math.matrix ()
// получаем подмножество
math.subset (a, math.index (1)) // 1
математика.subset (a, math.index ([2, 3])) // Массив, [2, 3]
math.subset (a, math.index (math.range (0,4))) // Массив, [0, 1, 2, 3]
math.subset (b, math.index (1, 0)) // 2
math.subset (b, math.index (1, [0, 1])) // Массив, [2, 3]
math.subset (b, math.index ([0, 1], 0)) // Матрица, [[0], [2]]
// получаем подмножество
d.subset (math.index ([1, 2], [0, 1])) // Матрица, [[3, 4], [6, 7]]
d.subset (math.index (1, 2)) // 5
// заменяем подмножество. Подмножество будет применено к клону матрицы
математика.subset (b, math.index (1, 0), 9) // Массив, [[0, 1], [9, 3]]
math.subset (b, math.index (2, [0, 1]), [4, 5]) // Массив, [[0, 1], [2, 3], [4, 5]]
// заменяем подмножество. Подмножество будет применено к самой матрице
c.subset (math.index (0, 1), 1) // Матрица, [[0, 1], [0, 0]]
c.subset (math.index (1, [0, 1]), [2, 3]) // Матрица, [[0, 1], [2, 3]]
e.resize ([2, 3], 0) // Матрица, [[0, 0, 0], [0, 0, 0]]
e.subset (math.index (1, 2), 5) // Матрица, [[0, 0, 0], [0, 0, 5]]
Итерация #
Матрицы map и forEach для перебора всех элементов
(многомерная) матрица.Функция обратного вызова карты и forEach имеет
три параметра: значение (значение текущего итерационного элемента), индекс (массив со значением индекса для каждого измерения) и матрица (
матрица повторяется). Этот синтаксис аналогичен карте и для каждого функций собственных массивов JavaScript, за исключением того, что индекс – это не число, а
Массив с числами для каждого измерения.
const a = математ.матрица ([[0, 1], [2, 3], [4, 5]])
// Следующая итерация выведет в консоль следующее:
// значение: 0 индекс: [0, 0]
// значение: 1 индекс: [0, 1]
// значение: 2 индекс: [1, 0]
// значение: 3 индекс: [1, 1]
// значение: 4 индекс: [2, 0]
// значение: 5 индекс: [2, 1]
a.forEach (функция (значение, индекс, матрица) {
console.log ('значение:', значение, 'индекс:', индекс)
})
// Применяем преобразование к матрице
const b = a.map (функция (значение, индекс, матрица) {
вернуть math.multiply (math.sin (значение), math.exp (math.abs (значение)))
})
console.log (b.format (5)) // [[0, 2.2874], [6.7188, 2.8345], [-41.32, -142.32]]
// Создаем матрицу с совокупностью всех элементов
пусть count = 0
const cum = a.map (функция (значение, индекс, матрица) {
счетчик + = значение
счетчик возврата
})
console.log (cum.toString ()) // [[0, 1], [3, 6], [10, 15]]
Типы складов #
«плотная» , по умолчанию ) Обычная плотная матрица, поддерживающая многомерные матрицы. Это тип матрицы по умолчанию. 'разреженная' ): реализация двумерной разреженной матрицы. матрица , diag , identity , единиц и нулей .
// создаем разреженные матрицы
const m1 = math.matrix ([[0, 1], [0, 0]], 'разреженный')
const m2 = math.identity (1000, 1000, 'разреженный')
API №
math.add и math.subtract , math.sqrt , обрабатывают матрицы поэлементно. Существует набор функций, специально предназначенных для создания матриц или манипулирования ими, например: math.matrix и math.sparse , math.ones , math.zeros и math.identity для создания матрицы. math.subset и math.index для получения или замены части матрицы math.transpose и math.diag для управления матрицами.
