Числовые ряды – основные определения и свойства с примерами решений
Содержание:
- Числовые ряды. Сходимость числового ряда. Необходимый признак сходимости ряда
- Достаточные признаки сходимости рядов (радикальный и интегральный признаки Коши, признак сравнения, признак Д’Аламбера)
Числовые ряды. Сходимость числового ряда. Необходимый признак сходимости ряда
Пусть дана числовая последовательность Выражение вида
(1)
называется числовым рядом или просто рядом. Числа называются членами ряда, число с общим номером называется общим членом ряда. Суммы конечного числа первых членов ряда
называются частичными суммами ряда (1). Так как число членов ряда бесконечно, то частичные суммы образуют числовую последовательность
(2)
Ряд (1) называется сходящимся, если последовательность (2) его частичных сумм сходится к некоторому числу . В этом случае число называется суммой ряда (1).
В противном случае ряд (1) называется расходящимся. В случае сходимости ряда (1) его сумму записывают в виде символического равенства
.
Пример №109
Если в качестве последовательности мы рассмотрим бесконечную геометрическую прогрессию с первым членом, равным и знаменателем , то получим ряд
. (3)
При ряд (3) является сходящимся и его сумма равна . Например,
.
Пример №110
Рассмотрим ряд
Так как , то для -он частичной суммы ряда получаем выражение
.
После раскрытия скобок все слагаемые, кроме первого и последнего, взаимно уничтожаются, и в результате получаем . Отсюда следует, что . Итак, ряд сходится и его сумма равна 1.
Теорема 1 (необходимый признак сходимости ряда). Если числовой ряд (1) сходится, то предел его общего члена равен нулю:
.
Подчеркнем, что это только необходимое условие сходимости ряда, т.е. условие, при нарушении которого ряд не может сходиться. С помощью этого признака можно доказывать только расходимость ряда.
Пример №111
Исследуем на сходимость ряд
Имеем , поэтому данный ряд расходится.
Пример №112
Рассмотрим т.н. гармонический ряд
Очевидно, что для гармонического ряда выполнено необходимое условие сходимости, так-как . Тем не менее, в примере 6 будет показано, что гармонический ряд является расходящимся. Рассчитаем пока несколько его частичных сумм:
.
Видно, что они медленно растут, не стремясь к какому-то конкретному пределу .
Достаточные признаки сходимости рядов (радикальный и интегральный признаки Коши, признак сравнения, признак Д’Аламбера)
В дальнейшем будут рассматриваться числовые ряды , все члены которых положительны.
Теорема 34.2 (критерий сходимости ряда). Для того, чтобы ряд с положительными членами (1) сходился, необходимо и достаточно, чтобы последовательность его частичных сумм (2) была ограничена.
Указанный критерий имеет, скорее, теоретическое, нежели практическое значение.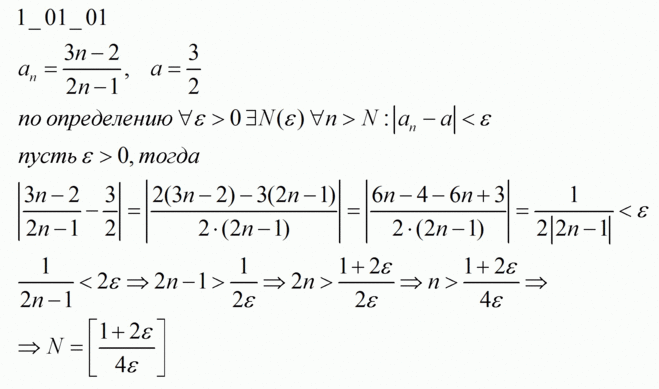
Поэтому необходимо уметь использовать достаточные признаки сходимости ряда: радикальный и интегральный признаки Коши, признак сравнения, признак Д’Аламбера.
Теорема 34.3 (радикальный признак Коши). Если для ряда с положительными членами (1) существует предел , то при ряд сходится, при – расходится, при вопрос о сходимости ряда остается открытым.
Пример №113
Исследуем сходимость ряда
Для этого применим радикальный признак Коши:
.
Следовательно ряд расходится.
Теорема 34.4 (интегральный признак Коши). Пусть задан ряд
, (4)
члены которого являются значениями непрерывной, положительной и монотонно убывающей функции при . Тогда ряд (4) будет сходящимся, если будет сходящимся несобственный интеграл , т.е. , и расходящимся, если этот интеграл будет расходящимся, т.е. .
Пример №114
Выясним, при каких сходится ряд
(5)
Положим .
Данная функция монотонно убывает, поскольку ее производная отрицательна. Поэтому по теореме 4 сходимость ряда (5) эквивалентна сходимости несобственного интеграла . Заметим, что
Видно, что этот интеграл сходится при и расходится при . Значит, и ряд (5) сходится при и расходится при . Так как при ряд (5) становится гармоническим
то, согласно интегральному признаку Коши, он является расходящимся рядом.
Теорема 5 (признак сравнения). Пусть даны два ряда с положительными членами:
(6)
(7)
причем члены первого ряда не превосходят соответствующих членов второго: . Тогда из сходимости большего ряда (7) следует сходимость меньшего ряда (6). Из расходимости меньшего ряда (6) следует расходимость большего ряда (7).
Замечание 1. Признак сравнения можно использовать и в том случае, когда неравенство выполняется не для всех членов рядов (34.6) и (34.7), а начиная с некоторого номера .
Замечание 2.
При исследовании рядов с помощью признака сравнения нужно знать, какие ряды сходящиеся и какие расходящиеся. Для сравнения удобно пользоваться рядами:
1) 2)
Пример №115
Исследуем сходимость ряда
Так как , и ряд – сходящийся как геометрическая прогрессия со знаменателем , то, согласно признака сравнения, исследуемый ряд тоже является сходящимся.
Теорема 6 (признак Д’Аламбера). Если для ряда с положительными членами существует предел
(8)
то ряд сходится в случае , расходится в случае и нуждается в дополнительном исследовании при .
Пример №116
Исследуем сходимость ряда
Для того, чтобы применить признак Д’ Аламбера, рассчитаем предел (8):
.
Следовательно, ряд является сходящимся.
Эта лекция взята из раздела о предмете высшая математика, там вы найдёте другие лекци по всем темам высшей математики:
| Высшая математика: полный курс лекций |
Другие темы которые вам помогут понять высшую математику:
| Методы определенного интегрирования |
| Приложения определенного интеграла |
| Степенные ряды |
| Дифференциальные уравнения |
Самая красивая теорема математики: тождество Эйлера / Хабр
Посмотрев лекцию профессора Робина Уилсона о тождестве Эйлера, я наконец смог понять, почему тождество Эйлера является самым красивым уравнением.
Чтобы поделиться моим восхищением это темой и укрепить собственные знания, я изложу заметки, сделанные во время лекции. А здесь вы можете купить его прекрасную книгу.
Что может быть более загадочным, чем взаимодействие мнимых чисел с вещественными, в результате дающее ничто? Такой вопрос задал читатель журнала Physics World в 2004 году, чтобы подчеркнуть красоту уравнения Эйлера «e в степени i, умноженного на пи равно минус единице».
Рисунок 1.0: тождество Эйлера — e в степени i, умноженного на пи, плюс единица равно нулю.
Ещё раньше, в 1988 году, математик Дэвид Уэллс, писавший статьи для американского математического журнала The Mathematical Intelligencer, составил список из 24 теорем математики и провёл опрос, попросив читателей своей статьи выбрать самую красивую теорему. И после того, как с большим отрывом в нём выиграло уравнение Эйлера, оно получило званием «самого красивого уравнения в математике».
Рисунок 2.0: обложка журнала The Mathematical Intelligencer
Рисунок 3.0: опрос Дэвида Уэллса из журнала
Леонарда Эйлера называют самым продуктивным математиком за всю историю. Других выдающихся математиков вдохновляли его работы. Один из лучших физиков в мире, Ричард Фейнман, в своих знаменитых лекциях по физике назвал уравнение Эйлера «самой примечательной формулой в математике». Ещё один потрясающий математик, Майкл Атья, назвал эту формулу “…математическим аналогом фразы Гамлета — «быть или не быть» — очень короткой, очень сжатой, и в то же время очень глубокой”.
Существует множество интересных фактов об уравнении Эйлера. Например, оно встречалось в некоторых эпизодах «Симпсонов».
Рисунок 4.0: в этой сцене уравнение Эйлера можно заметить на второй книге в самой правой стопке.
Рисунок 5.0: в этой сцене уравнение Эйлера написано на футболке второстепенного персонажа.
Также уравнение Эйлера стало ключевым пунктом в уголовном деле. В 2003 году аспирант Калифорнийского технологического института Билли Коттрелл писал краской на чужих спортивных автомобилях уравнение Эйлера. На суде он сказал: “Я знал теорему Эйлера с пяти лет, и её обязаны знать все“.
Рисунок 6.0: марка, выпущенная в 1983 году в Германии в память о двухсотлетии со смерти Эйлера.
Рисунок 7.0: марка, выпущенная Швейцарией в 1957 году в честь 250-й годовщины Эйлера.
Почему уравнение Эйлера так важно?
Вы имеете полное право задаться вопросом: почему Билли Коттрелл считал, что об уравнении Эйлера обязаны знать все? И был настолько в этом уверен, что начал писать его на чужих машинах? Ответ прост: Эйлер воспользовался тремя фундаментальными константами математики и применил математические операции умножения и возведения в степень, чтобы записать красивую формулу, дающую в результате ноль или минус один.
- Константа e связана со степенными функциями.
- Константа i является не вещественным, а мнимым числом, равным квадратному корню из минус единицы.
- Знаменитая константа π (пи) связана с окружностями.
Впервые тождество Эйлера появилось в 1748 году в его книге Introductio in analysin infinitorum. Позже другие люди увидели, что эта формула связана с тригонометрическими функциями синуса и косинуса, и эта связь удивительна, ведь степенная функция стремится к бесконечности, а тригонометрические функции колеблются в интервале от — 1 до -1.
e в степени i, умноженного на ϕ (фи) = cos ϕ + i * sin ϕ
Рисунок 8.0: экспоненциальная функция y=ex.
Рисунок 8.1: график тождества Эйлера.
Рисунок 8.
2: частоты, испускаемые LC-цепью.
Показанные выше уравнения и графы могут показаться абстрактными, но они важны для квантовой физики и вычислений обработки изображений, и при этом зависят от тождества Эйлера.
1: число для счёта
Число 1 (единица) является основой нашей системы исчисления. С неё мы начинаем счёт. Но как мы считаем? Чтобы считать, мы используем цифры 0–9 и систему разрядов, определяющую значение цифры.
Например, число 323 означает 3 сотни, 2 десятка и 3 единицы. Здесь число 3 исполняет две разные роли, которые зависят от его расположения.
323 = (3*100) + (2*10) + (3*1)
Существует и другая система исчисления, называемая двоичной. В этой системе вместо 10 используется основание 2. Она широко применяется в компьютерах и программировании. Например, в двоичной системе:
1001 = (23) + (02) + (01) + (20) = [9 в системе с основанием 10]
Кто создал системы исчисления? Как первые люди считали предметы или животных?
Как возникли наши системы исчисления? Как считали первые цивилизации? Мы точно знаем, что они не пользовались нашей разрядной системой.
Например 4000 лет назад древние египтяне использовали систему исчисления с разными символами. Однако они комбинировали символы, создавая новый символ, обозначающий числа.
Рисунок 11: показанные здесь иероглифы образуют число 4622; это одно из чисел, вырезанных на стене в храме в Карнаке (Египет).
Рисунок 12: иероглифы — это изображения, обозначающие слова, а в данном случае — числа.
В то же время, но в другом месте ещё один социум обнаружил способ подсчёта, но в нём тоже использовались символы. Кроме того, основанием их системы исчисления было 60, а не 10. Мы используем их метод счёта для определения времени; поэтому в минуте 60 секунд, а в часе 60 минут.
Рисунок 13: вавилонские числа из шестидесятиричной системы счисления (с основанием 60).
Тысячу лет спустя древние римляне изобрели римские числа. Для обозначения чисел они использовали буквы.
Римская нотация не считается разрядной системой, потому что для многих значений нашей системы счисления в ней использовались разные буквы. Именно по этой причине для счёта они использовали абакус.
Рисунок 14: романский абакус в шестнадцатеричной (с основанием 16) системе счисления
Рисунок 15: таблица преобразования из арабских в римские числа
Древние греки тоже не использовали разрядную систему счисления. Греческие математики обозначали числа буквами. У них были специальные буквы для чисел от 100 до 900. Многие люди в то время считали греческие числа запутанными.
Рисунок 15: таблица букв древних греков.
В то же самое время китайские математики начали использовать для расчётов небольшие бамбуковые палочки. Этот китайский способ счёта называют первой десятичной разрядной системой.
Рисунок 16: китайский способ счёта с числами-палочками.
Использовался как минимум с 400 года до нашей эры. Квадратная счётная доска использовалась примерно до 1500 года, когда её заменил абакус.
Однако самая уникальная система счёта использовалась индейцами майя. Их система счисления имела основание 20. Для обозначения чисел от 1 до 19 они использовали точки и линии. Чем же отличалась их система счисления? Для каждого числа они использовали изображения голов и отдельный символ нуля 0.
Рисунок 17: Система счисления майя с основанием 20, в которой числа обозначались головами
Рисунок 18: ещё один способ записи чисел майя.
Некоторые цивилизации использовали пробелы, чтобы, например, отличать число 101 от 11. Спустя какое-то время начало появляться особое число — ноль. К примеру, в пещере в индийском городе Гвалиор археологи обнаружили на стене число 270, в котором был ноль. Самое первое зафиксированное использование нуля можно увидеть в Бодлианской библиотеке.
Рисунок 19: вырезанный на стене храма в Гвалиоре круг обозначает ноль. Ему примерно 1500 лет.
Рисунок 20: чёрные точки в манускрипте Бакхшали обозначают нули; это самый старый письменный пример использования числа, ему примерно 1800 лет.
Примерно 1400 лет назад были записаны правила вычислений с нулём. Например, при сложении отрицательного числа и нуля получается то же отрицательное число. Деление на нуль не допускается, потому что если разделить на ноль, то мы получим число, которое может быть равно любому нужному нам числу, что должно быть запрещено.
Вскоре после этого многими людьми были опубликованы книги по арифметике, распространяющие использование индо-арабской записи чисел. Ниже показана эволюция индо-арабских чисел. В большинстве стран используется индо-арабская система чисел, но арабские страны до сих пор пользуются арабскими числами.
Рисунок 21: на этой схеме показана эволюция чисел, происходящих от чисел брахми и заканчивающаяся числами, которыми мы используем и сегодня.
Рисунок 22: классическая гравюра «Арифметика» из Margarita Philosophica
Пи (π): самое известное иррациональное число
Пи — самое популярное из известных нам иррациональных чисел. Пи можно найти двумя способами: вычислив соотношение длины окружности к её диаметру, или соотношение площади круга к квадрату его радиуса. Евклид доказал, что эти соотношения постоянны для всех окружностей, даже для луны, пенни, шины и т.д.
π = окружность / диаметр ИЛИ π = площадь круга / радиус²
Рисунок 22: анимированная связь между окружностью и диаметром в отношении пи.
Так как иррациональные числа наподобие пи бесконечны и не имеют повторений, мы никогда не закончим записывать пи.
Оно продолжается вечно. Есть люди, запомнившие множество десятичных разрядов пи (нынешний рекорд — 70 000 цифр! Источник: «Книга рекордов Гиннесса» ).
Рисунок 23: данные опроса 941 респондентов для определения процента людей, способных запомнить знаки пи после запятой.
Рисунок 24: На стене станции метро Karlsplatz в Вене записаны сотни разрядов пи.
На данный момент компьютеры смогли вычислить всего 2,7 триллиона разрядов пи. Может казаться, что это много, но на самом деле этот путь бесконечен.
Как я сказал выше, число пи нашёл Евклид. Но как поступали люди до Евклида, когда им нужно было найти площадь круга? Историки обнаружили вавилонскую глиняную табличку, в которой было записано отношение периметра шестиугольника к диаметру описанной вокруг него окружности. После вычислений полученное число оказалось равным 3.125. Это очень близко к пи.
Рисунок 24: вавилонская глиняная табличка с отношением периметра шестиугольника к длине описанной окружности.
Рисунок 25: Numberwarrior
Древние египтяне тоже близко подобрались к значению пи. Историки обнаружили документ, показывающий, как древние египтяне нашли число пи. Когда историки перевели документ, то нашли такую задачу:
Например, чтобы найти площадь поля диаметром 9 хета (1 хет = 52,35 метра), нужно выполнить следующее вычисление:Вычесть 1/9 диаметра, а именно 1. Остаток равен 8. Умножить его на 8, что даёт нам 64. Следовательно, площадь будет равна 64 setjat (единица измерения площади).
Другими словами, диаметр равен 2r, а 1/9 радиуса равно (1/9 • 2r). Тогда если мы вычтем это из исходного диаметра, то получим 2r — (1/9 • 2r) = 8/9(2r). Тогда площадь круга равна 256/81 r². То есть пи равно почти 3,16. Они обнаружили это значение пи примерно 4000 лет назад.
Рисунок 26: математический папирус Ахмеса.
Однако греческие математики нашли для вычисления пи способ получше.
Например, Архимед предпочитал работать с периметрами. Он начал рисовать окружности, описывающие многоугольники разного размера. Когда он чертил шестиугольник, то рисовал окружность с диаметром 1. Затем он видел что каждая сторона шестиугольника равна 1/2, а периметр шестиугольника равен 1/2 x 6 = 3. Затем он увеличивал количество сторон многоугольника, пока он не становился похожим на круг. Работая со 96-сторонним многоугольником и применив тот же способ, он получил 2 десятичных разряда пи после запятой: 3 и 10/71 = 3,14084. Спустя много лет китайский математик Лю Ху использовал 3072-сторонний многоугольник и получил число 3,14159 (5 верных десятичных разрядов числа пи после запятой). После этого ещё один китайский математик Цзу Чунчжи провёл ещё более впечатляющую работу. Он работал со 24000-сторонним многоугольником и получил 3,1415926 — семь верных десятичных разрядов пи после запятой.
Спустя тысячу лет немецкий математик Людольф Цейлен работал со 262-сторонним многоугольником и получил 35 десятичных разрядов пи.
Это число, названное Людольфовым, было высечено на его могильном камне.
В 1706 году англичанин Джон Мэчин, долгое время работавший профессором астрономии, использовал формулу сложения, чтобы доказать, что пи равно
Не беспокоясь о том, как откуда взялась эта формула, Мэчин начал постоянно ею пользоваться, а затем записал показанный ниже ряд. Это был самый большой на то время шаг в количестве разрядов пи.
Рисунок 29: Формула Мэчина для пи
Однако первое упоминание пи появилось в 1706 году. Преподаватель математики Уильям Джонс написал книгу и впервые предложил пи для измерения окружностей. Так пи впервые появилась в книгах!
Рисунок 30: Juliabloggers
В 1873 году Уильям Шэнкс воспользовался формулой Джона Мэчина и получил 707 десятичных разрядов пи. Эти цифры написаны в комнате пи парижского Дворца открытий.
Однако позже математики выяснили, что верными являются только 527 разрядов.
Рисунок 31: комната пи
С другой стороны, более интересный способ нахождения пи обнаружил Буффон. Его эксперимент основывался на случайном разбрасывании иголок для оценки пи. Он нарисовал на доске несколько параллельных линий на расстоянии D и взял иголки длиной L. Затем он случайным образом начал бросать иголки на доску и записывал долю иголок, пересекавших линию.
Рисунок 32.0: Science Friday
А после этого другой математик по имени Ладзарини подбросил иголку 3408 раз и получил шесть десятичных разрядов пи с соотношением 355/113. Однако если бы одна иголка не пересекла линию, он получил бы только 2 разряда пи.
Рисунок 32.1: бросание 1000 иголок для оценки приблизительного значения пи
e: история экспоненциального роста
e — это ещё одно знаменитое иррациональное число.
Дробная часть e тоже бесконечна, как и у пи. Мы используем число e для вычисления степенного (экспоненциального) роста. Другими словами, мы используем e, когда видим очень быстрый рост или уменьшение.
Один из величайших, а возможно и лучший математик Леонард Эйлер открыл число e в 1736 году и впервые упомянул это особое число в своей книге Mechanica.
Рисунок 33: источник
Чтобы разобраться в экспоненциальном росте, мы можем использовать историю об изобретателе шахмат. Когда он придумал эту игру, то показал её властителю Севера. Царю понравилась игра и он пообещал, что отдаст автору любую награду. Тогда изобретатель попросил нечто очень простое: 20 зерна на первую клетку шахматной доски, 21 зерна на вторую клетку доски, 22 зерна — на третью, и так далее. Каждый раз количество зерна удваивалось. Царь Севера подумал, что просьбу будет выполнить легко, но он ошибался, потому то на последнюю клетку нужно было бы положить 263 зёрен, что равно 9 223 372 036 854 775 808.
Это и есть экспоненциальный рост. Он начался с 1, постоянно удваивался, и через 64 шага вырос в огромное число!
Если бы изобретатель шахмат выбрал линейное уравнение, например 2n, то получил бы 2, 4, 6, 8, … 128… Следовательно, в дальней перспективе экспоненциальный рост часто намного превышает полиномиальный.
Кстати, 9 223 372 036 854 775 808–1 — это максимальное значение 64-битного целого числа со знаком.
Рисунок 34: источник: Wikipedia
Число e открыл Эйлер. Однако Якоб Бернулли тоже работал с числом e, когда вычислял сложный процент, чтобы заработать больше денег. Если вложить 100 долларов под 10% дохода, то как будет расти эта сумма? Во-первых, это зависит от того, как часто банк рассчитывает проценты. Например, если он рассчитывает один раз, то мы получим в конце года 110 долларов. Если мы передумаем и будем брать проценты каждые 6 месяцев, то в этом случае мы получим больше 110 долларов.
Дело в ттом, что процент, полученный за первые 6 месяцев, тоже получит свой процент. Общая сумма будет равна 110,25 долларов. Можно догадаться, что мы можем получить больше денег, если будем забирать деньги каждый квартал года. А если мы будем делать временной интервал всё короче, то окончательные суммы будут продолжать расти. Такой бесконечный сложный процент сделает нас богатыми! Однако наш общий доход стремится к ограниченному значению, связанному с e.
Бернулли не называл число 2,71828 именем e. Когда Эйлер работал с 2,71828, он возвёл экспоненциальную функцию e в степень x. Свои открытия он изложил в книге The Analysis of Infinite.
В 1798 году Томас Мальтус использовал экспоненциальную функцию в своём эссе, посвящённом пищевому дефициту будущего. Он создал линейный график, показывающий производство пищи и экспоненциальный график, показывающий население мира. Мальтус сделал вывод, что в дальней перспективе экспоненциальный рост победит, и мир ждёт серьёзный дефицит пищи.
Это явление назвали «мальтузианской катастрофой». Ньютон тоже использовал эту модель, чтобы показать, как охлаждается чашка чая.
Рисунок 35: закон Ньютона-Рихмана
Рисунок 36: мальтузианская катастрофа
Мнимость числа: i, квадратный корень -1
Долгое время для решения своих задач математикам было достаточно обычных чисел. Однако в какой-то момент для дальнейшего развития им потребовалось открыть нечто новое и загадочное. Например, итальянский математик Кардано пытался разделить число 10 на 2 части, произведение которых было бы равно 40. Чтобы решить эту задачу, он записал уравнение: x (10-x) = 40. Когда он решил это квадратное уравнение, то получил два решения: 5 плюс √-15 и 5 минус √-15, что в то время не имело никакого смысла. Этот результат был бессмысленным, потому что по определению квадратного корня ему нужно было найти число, квадрат которого был бы отрицательным.
Однако и положительное, и отрицательное числа в квадрате имеют положительное значение. Как бы то ни было, он нашёл своё уникальное число. Однако первым математиком, назвавшим √-1 (квадратный корень из минус единицы) мнимым числом i, был Эйлер.
Лейбниц дал такой комментарий о мнимом числе √-1:
Комплексные числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием.
Мы можем складывать, вычитать, умножать и делить мнимые числа. Сложение, вычитание и умножение просты, а деление немного сложнее. Вещественные и мнимые части складываются по отдельности. В случае умножения i2 будет равно -1.
После Эйлера математик Каспар Вессель представил мнимые числа геометрически с создал комплексную плоскость. Сегодня мы представляем каждое комплексное число a + bi как точку с координатами (a,b).
Рисунки 37 и 38: комплексные числа
В викторианскую эпоху многие относились к мнимым числам с подозрением.
Однако ирландский математик и астроном Уильям Роуэн Гамильтон покончил с этими сомнениями, определив комплексные числа применительно к кватернионам.
Самое красивое уравнение: тождество Эйлера
Тождество Эйлера связывает экспоненциальную функцию с функциями синуса и косинуса, значения которых колеблются от минус единицы до единицы. Чтобы найти связь с тригонометрическими функциями, мы можем представить их в виде бесконечного ряда, истинного для всех значений
Рисунок 39: открытие тождества Эйлера
Рисунок 40: тождество Эйлера
Эйлер никогда не записывал это тождество в явном виде, и мы не знаем, кто впервые записал его. Тем не менее, мы связываем его с именем Эйлера в знак почтения перед этим великим первопроходцем математики.
Натуральные числа: определение, примеры, свойства
Определение натурального числа
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и т. д.
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.
| Особенности натуральных чисел |
|---|
|
Какие операции возможны над натуральными числами
Записывайтесь на курсы обучения математике для учеников с 1 по 11 классы!
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Десятичная запись натурального числа
В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше.
Проговорим важные правила.
Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.
077, 0, 004, 0931 — это примеры неправильной записи натуральных чисел, потому что ноль расположен слева. Число не может начинаться с нуля. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.
Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».
Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое.
Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:
| 🍌🍌🍌 | 3 предмета («три») |
| 🍌🍌🍌🍌 | 4 предмета («четыре») |
| 🍌🍌🍌🍌🍌 | 5 предметов («пять») |
| 🍌🍌🍌🍌🍌🍌 | 6 предметов («шесть») |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 предметов («семь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 предметов («восемь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 предметов («девять») |
Основная функция натурального числа — указать количество предметов.
Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Однозначные, двузначные и трехзначные натуральные числа
Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.
Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.
По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.
Одна сотня — это множество, состоящее из десяти десятков.
Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.
Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.
Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначные натуральные числа состоят из двух и более знаков.
1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.
Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.
Сколько всего натуральных чисел?
Однозначных 9, двузначных 90, трехзначных 900 и т.д.
Свойства натуральных чисел
Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:
| множество натуральных чисел | бесконечно и начинается с единицы (1) |
| за каждым натуральным числом следует другое | оно больше предыдущего на 1 |
| результат деления натурального числа на единицу (1) | само натуральное число: 5 : 1 = 5 |
| результат деления натурального числа самого на себя | единица (1): 6 : 6 = 1 |
| переместительный закон сложения | от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4 |
| сочетательный закон сложения | результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4) |
| переместительный закон умножения | от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4 |
| сочетательный закон умножения | результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 × 8) |
| распределительный закон умножения относительно сложения | чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| распределительный закон умножения относительно вычитания | чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| распределительный закон деления относительно сложения | чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 + 8) : 3 = 9 : 3 + 8 : 3 |
| распределительный закон деления относительно вычитания | чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Разряды натурального числа и значение разряда
Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение.
Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Разряд — это позиция, место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел.
Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.
Десятичная система счисления
Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.
Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Вопрос для самопроверки
Сколько натуральных чисел можно отметить на координатном луче между точками с координатами:
0 и 15;
20 и 50;
100 и 130?
Базовая математика и предварительная алгебра для чайников, 2-е издание
Выбранный тип: Мягкая обложка
Количество:
24,99 $
Марк Зегарелли
ISBN: 978-1-119-29363-7
июнь 2016 г.
384 страницы
Электронная книга
От 15 долларов США
Печать
От 24,99 долл. США
Электронная книга 
com are delivered on the VitalSource platform. To download and read them, users must install the VitalSource Bookshelf Software.</li><li>E-books have DRM protection on them, which means only the person who purchases and downloads the e-book can access it.</li><li>E-books are non-returnable and non-refundable.</li><li>To learn more about our e-books, please refer to our <a href="https://www.wiley.com/wiley-ebooks" target="_blank">FAQ</a>.</li></ul>” data-original-title=”” title=””/>
15,00 $
Мягкая обложка
24,99 $
Загрузить рекламный проспект
Загрузить рекламный проспект
Загрузить флаер продукта для загрузки PDF в новой вкладке.
Это фиктивное описание.
Загрузить флаер продукта — загрузить PDF в новой вкладке. Это фиктивное описание.
Загрузить флаер продукта — загрузить PDF в новой вкладке. Это фиктивное описание.
Загрузить флаер продукта — загрузить PDF в новой вкладке. Это фиктивное описание.
Описание
Базовая математика и предварительная алгебра для чайников, 2-е издание (9781119293637) ранее публиковалось как Базовая математика и предварительная алгебра для чайников, 2-е издание (9781118791981). Хотя эта версия имеет новую обложку и дизайн для чайников, содержание такое же, как и в предыдущем выпуске, и его не следует рассматривать как новый или обновленный продукт.
Советы по упрощению сложных базовых математических и предалгебраических операций
Независимо от того, являетесь ли вы студентом, готовящимся к изучению алгебры, или родителем, который хочет или должен освежить в памяти базовую математику, это веселое и понятное руководство содержит инструменты, необходимые для того, чтобы освоиться.
От положительных, отрицательных и целых чисел до дробей, десятичных знаков и процентов вы приобретете необходимые математические навыки для решения более сложных тем, таких как мнимые числа, переменные и алгебраические уравнения.
- Объяснения и практические примеры, отражающие современные методы обучения
- Актуальный культурный язык и справочные материалы
- Стандарт для чайников Материалы, соответствующие текущим стандартам и дизайну
Базовая математика и предварительная алгебра для чайников устраняет страх при выполнении сложных операций и помогает подготовиться к алгебре!
Купить Набор из 1 предмета
Этот предмет: Базовая математика и предварительная алгебра для чайников, 2-е издание
Рабочая тетрадь по базовой математике и предварительной алгебре для чайников с онлайн-практикой, 3-е издание
(Мягкая обложка 24,99 доллара США)
Об авторе
Марк Зегарелли является автором многих успешных книг For Dummies по математике, логике и подготовке к экзаменам.
Он получил степень по английскому языку и математике в Университете Рутгерса и является основателем образовательного веб-сайта SimpleStep Learning (https://simplestep.co).
Разрешения
Запросить разрешение на повторное использование контента с этого сайта
Содержание
Введение 1
Часть 1: Начало работы с основами математики и предварительной алгеброй 5
ГЛАВА 1: Игра в числа 7
ГЛАВА 2:
Цифры 00 2 2 ГЛАВА 3: Большая четверка: сложение, вычитание, умножение и деление 29Часть 2. Работа с целыми числами 47
ГЛАВА 5: Вопрос о значениях: вычисление арифметических выражений 63
ГЛАВА 6: Что сказать? Превращение слов в числа 75
Глава 7: Разделимость 87
Глава 8: Сказочные факторы и чудесные мультипликации 95
Часть 3: Части целых: фракции, десятичные и перкс.
9: Обман с дробями 111
ГЛАВА 10: Расставание способов: фракции и операции Big Four 125
Глава 11: Dallying с десятичными десятичными. 1970003 ГЛАВА 15: Сколько у тебя есть? Вес и меры 205
ГЛАВА 16: Изображение Это: Основная геометрия 217
Глава 17: Взгляд верит: График как
Визуальный инструмент 239
Глава 18: Решение геометрии и измерения слов.
ГЛАВА 19: Расчет шансов: статистика и вероятность 259
ГЛАВА 20: Настройка с помощью теории базовых множеств 271
Часть 5: X-Files: Введение в Алгебру 279
Глава 21: Введите гр. X: Алгебра и алгебраические выражения 281
Глава 22: Гр. Глава 24: Десять маленьких математических демонов, которые сбивают людей с толку 323
: 50004 Десять важных чисел, которые необходимо знать 329
Индекс 337
Errata
| Глава | Page | Подробная информация | Дата | ПЕЧАТЬ |
|---|---|---|---|---|
| 3 | 33 | |||
| 3 | 33 | |||
| 3 | 33 | 01 марта 18 | ||
| 3 | 35 | Исправления Четвертый абзац, предшествующий отдельному уравнению. Измените 9 – 3 = 9 на 9 – 3 = 6 | 01 марта 18 | |
после шага 2 первое автономное уравнение. В первой строке уравнения измените 366 на 386.Dymocks – Математика для чайников
Дом / Книги
Фильтры
Фильтры
Сортировать по:
12 24 96
Фильтры
12 24 96
ПОИСК ПО КАТЕГОРИЯМ
Отделение
УТОЧНИТЬ РЕЗУЛЬТАТЫ
Доступность
Формат Очистить все фильтры
Ценовой диапазон
От: $
Кому: $
Дополнительные фильтры
Активные фильтры
Очистить всеМатематика для чайников
Основы исчисления для.
..
Марк Райан
Бумажная обложка
16,95 долларов США
Статистика для чайников, 2-е…
Дебора Дж. Рамси
Бумажная обложка
$32,95
Алгебра I Основы для…
Мэри Джейн Стерлинг
Бумажная обложка
16,95 долларов США
Базовая математика и предварительная алгебра…
Марк Зегарелли
Бумажная обложка
49,95 долларов США
Исчисление для чайников, 2-е…
Марк Райан
Бумажная обложка
$32,95
Основы алгебры II для.
..
Мэри Джейн Стерлинг
Бумажная обложка
16,95 долларов США
Основы геометрии для…
Марк Райан
Бумажная обложка
16,95 долларов США
Основы статистики для…
Дебора Дж. Рамси
Бумажная обложка
16,95 долларов США
Рабочая тетрадь для чайников…
Марк Райан
Бумажная обложка
41,95 доллара США
Базовая математика и предварительная алгебра для…
Марк Зегарелли
Бумажная обложка
41,95 доллара США
Алгебра I для чайников, 2.
..
Мэри Джейн Стерлинг
Бумажная обложка
41,95 доллара США
Базовая математика для чайников
Колин Беверидж
Бумажная обложка
$43,99
Основы предварительной алгебры для…
Зегарелли
Бумажная обложка
16,95 долларов США
Статистическая рабочая тетрадь для…
Дебора Дж. Рамси
Бумажная обложка
$32,95
Алгебра II для чайников, 2…
Мэри Джейн Стерлинг
Бумажная обложка
41,95 доллара США
Алгебра II для чайников
Мэри Джейн Стерлинг
Бумажная обложка
41,95 доллара США
Рабочая тетрадь для предварительного исчисления.
..
Мэри Джейн Стерлинг, Мишель…
Бумажная обложка
41,95 доллара США
Предварительное исчисление для чайников
Мэри Джейн Стерлинг, Эллейн…
Бумажная обложка
41,95 доллара США
Конечная математика для чайников
Мэри Джейн Стерлинг
Бумажная обложка
41,95 доллара США
Алгебра I Рабочая тетрадь для…
Мэри Джейн Стерлинг
Бумажная обложка
49,95 долларов США
Базовая математика и предварительная алгебра.
..
Марк Зегарелли
Бумажная обложка
41,95 доллара США
Алгебра I Рабочая тетрадь для…
Мэри Джейн Стерлинг
Бумажная обложка
41,95 доллара США
Геометрия для чайников, 3-я…
Марк Райан
Бумажная обложка
41,95 доллара США
Математика как и уровень для чайников
Колин Беверидж, Уайли
Бумажная обложка
$34,95
Математика 6 класс для чайников
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
9 математика – линейные системы |
учить математику восьмого класса |
решить для указанной переменной |
решить дифференциальное уравнение второго порядка учебник Matlab Рунге-кутта |
проблемы образца алгебры clep колледжа |
проблема возраста по математике (с решением и проверкой) |
алгебраические уравнения, содержащие дроби |
бесплатная математика 9 класса |
prentice hall предварительные практические тесты по алгебре |
онлайн-рабочие листы по биномам |
решить, используя примеры свойств четных корней с дробями |
двоичное шестнадцатеричное сложение и вычитание |
рабочие листы практики умножения решетки |
глава 5 раздел 7 алгебра гленко/макгроу-хилл ответы ключи
Я пытался найти учителя по этому предмету, но не смог найти его в своем районе. Доступные далеко и дорого.
Если бы вы разместили это сообщение до того, как наняли репетитора, вы могли бы сэкономить много денег! В любом случае, теперь вы не можете изменить это. Теперь, чтобы убедиться, что вы хорошо сдаете экзамены, я бы рекомендовал попробовать Algebrator. Это очень простое в использовании программное обеспечение. Он может решить для вас самые сложные проблемы, и, что еще круче, он даже может объяснить, как он это сделал! В какой-то момент, когда даже я с трудом понимал систему уравнений 3×3, квадратные неравенства и lcf. Но благодаря Algebrator теперь все хорошо.
