Издания | Библиотечно-издательский комплекс СФУ
- Издания(активная вкладка)
- Услуги
Все года изданияТекущий годПоследние 2 годаПоследние 5 летПоследние 10 лет
Все виды изданийУчебная литератураНаучная литератураЖурналыГазетыМатериалы конференций
Все темыЕстественные и точные наукиАстрономияБиологияГеографияГеодезия. КартографияГеологияГеофизикаИнформатикаКибернетикаМатематикаМеханикаОхрана окружающей среды. Экология человекаФизикаХимияТехнические и прикладные науки, отрасли производстваАвтоматика. Вычислительная техникаБиотехнологияВодное хозяйствоГорное делоЖилищно-коммунальное хозяйство. Домоводство. Бытовое обслуживаниеКосмические исследованияЛегкая промышленностьЛесная и деревообрабатывающая промышленностьМашиностроениеМедицина и здравоохранениеМеталлургияМетрологияОхрана трудаПатентное дело. Изобретательство. РационализаторствоПищевая промышленностьПолиграфия. Репрография.
ФотокинотехникаПриборостроениеПрочие отрасли экономикиРыбное хозяйство. АквакультураСвязьСельское и лесное хозяйствоСтандартизацияСтатистикаСтроительство. АрхитектураТранспортХимическая технология. Химическая промышленностьЭлектроника. РадиотехникаЭлектротехникаЭнергетикаЯдерная техникаОбщественные и гуманитарные наукиВнешняя торговляВнутренняя торговля. Туристско-экскурсионное обслуживаниеВоенное делоГосударство и право. Юридические наукиДемографияИскусство. ИскусствоведениеИстория. Исторические наукиКомплексное изучение отдельных стран и регионовКультура. КультурологияЛитература. Литературоведение. Устное народное творчествоМассовая коммуникация. Журналистика. Средства массовой информацииНародное образование. ПедагогикаНауковедениеОрганизация и управлениеПолитика и политические наукиПсихологияРелигия. АтеизмСоциологияФизическая культура и спортФилософияЭкономика и экономические наукиЯзыкознаниеХудожественная литератураХудожественные произведения
Все институтыВоенно-инженерный институтБазовая кафедра специальных радиотехнических системВоенная кафедраУчебно-военный центрГуманитарный институтКафедра ИТ в креативных и культурных индустрияхКафедра истории России, мировых и региональных цивилизацийКафедра культурологии и искусствоведенияКафедра рекламы и социально-культурной деятельностиКафедра философииЖелезногорский филиал СФУИнженерно-строительный институтКафедра автомобильных дорог и городских сооруженийКафедра инженерных систем, зданий и сооруженийКафедра проектирования зданий и экспертизы недвижимостиКафедра строительных конструкций и управляемых системКафедра строительных материалов и технологий строительстваИнститут архитектуры и дизайнаКафедра архитектурного проектированияКафедра градостроительстваКафедра дизайнаКафедра дизайна архитектурной средыКафедра изобразительного искусства и компьютерной графикиИнститут гастрономииБазовая кафедра высшей школы ресторанного менеджментаИнститут горного дела, геологии и геотехнологийКафедра геологии месторождений и методики разведкиКафедра геологии, минералогии и петрографииКафедра горных машин и комплексовКафедра инженерной графикиКафедра маркшейдерского делаКафедра открытых горных работКафедра подземной разработки месторожденийКафедра технической механикиКафедра технологии и техники разведкиКафедра шахтного и подземного строительстваКафедра электрификации горно-металлургического производстваИнститут инженерной физики и радиоэлектроникиБазовая кафедра “Радиоэлектронная техника информационных систем”Базовая кафедра инфокоммуникацийБазовая кафедра физики конденсированного состояния веществаБазовая кафедра фотоники и лазерных технологийКафедра нанофазных материалов и нанотехнологийКафедра общей физикиКафедра приборостроения и наноэлектроникиКафедра радиотехникиКафедра радиоэлектронных системКафедра современного естествознанияКафедра теоретической физики и волновых явленийКафедра теплофизикиКафедра экспериментальной физики и инновационных технологийКафедры физикиИнститут космических и информационных технологийБазовая кафедра “Интеллектуальные системы управления”Базовая кафедра “Информационные технологии на радиоэлектронном производстве”Базовая кафедра геоинформационных системКафедра высокопроизводительных вычисленийКафедра вычислительной техникиКафедра информатикиКафедра информационных системКафедра прикладной математики и компьютерной безопасностиКафедра разговорного иностранного языкаКафедра систем автоматики, автоматизированного управления и проектированияКафедра систем искусственного интеллектаИнститут математики и фундаментальной информатикиБазовая кафедра вычислительных и информационных технологийБазовая кафедра математического моделирования и процессов управленияКафедра алгебры и математической логикиКафедра высшей и прикладной математикиКафедра математического анализа и дифференциальных уравненийКафедра математического обеспечения дискретных устройств и системКафедры высшей математики №2афедра теории функцийИнститут нефти и газаБазовая кафедра пожарной и промышленной безопасностиБазовая кафедра проектирования объектов нефтегазового комплексаБазовая кафедра химии и технологии природных энергоносителей и углеродных материаловКафедра авиационных горюче-смазочных материаловКафедра бурения нефтяных и газовых скважинКафедра геологии нефти и газаКафедра геофизикиКафедра машин и оборудования нефтяных и газовых промысловКафедра разработки и эксплуатации нефтяных и газовых месторожденийКафедра технологических машин и оборудования нефтегазового комплексаКафедра топливообеспеченя и горюче-смазочных материаловИнститут педагогики, психологии и социологииКафедра информационных технологий обучения и непрерывного образованияКафедра общей и социальной педагогикиКафедра психологии развития и консультированияКафедра современных образовательных технологийКафедра социологииИнститут торговли и сферы услугБазовая кафедра таможенного делаКафедра бухгалтерского учета, анализа и аудитаКафедра гостиничного делаКафедра математических методов и информационных технологий в торговле и сфере услугКафедра технологии и организации общественного питанияКафедра товароведения и экспертизы товаровКафедра торгового дела и маркетингаОтделение среднего профессионального образования (ОСПО)Институт управления бизнес-процессамиБазовая кафедра Федеральной службы по финансовому мониторингу (Росфинмониторинг)Кафедра бизнес-информатики и моделирования бизнес-процессовКафедра маркетинга и международного администрированияКафедра менеджмент производственных и социальных технологийКафедра цифровых технологий управленияКафедра экономики и управления бизнес-процессамиКафедра экономической и финансовой безопасностиИнститут физ.
По релевантностиСначала новыеСначала старыеПо дате поступленияПо названиюПо автору
Текст в электронном виде
Экспертиза и управление недвижимостью.
Для курсового проектированияЭтноязыковые процессы у коренных народов
Теория отраслевых рынков
Электротехническое материаловедение. Лабораторный практикум
Общая и неорганическая химия. Лабораторный практикум
Высотные и большепролетные здания и сооружения
English for metallurgy and materials science students
Правовое регулирование труда и социального обеспечения сотрудников таможенных органов
Биоинжиниринг: белки и молекулярная динамика
English for Law Students
Горнопромышленная экология
Этнография народов Сибири
Матричная алгебра в экономике – презентация онлайн
1. Матричная алгебра в экономике
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ДОНЕЦКОЙ НАРОДНОЙ РЕСПУБЛИКИУЧРЕЖДЕНИЕ ДОПОЛНИТЕЛЬНОГО ОБРАЗОВАНИЯ
«ДОНЕЦКАЯ РЕСПУБЛИКА МАЛАЯ АКАЕМИЯ НАУК УЧАЩЕЙСЯ
МОЛОДЕЖИ»
Матричная
алгебра в
экономике
Работу выполнила:
Антошенко София Сергеевна,
учащаяся 10 класса
МУНИЦИПАЛЬНОГО ОБЩЕОБРАЗОВАТЕЛЬНОГО
УЧРЕЖДЕНИЯ « ШКОЛА № 10 ГОРОДА ТОРЕЗА»
Научный руководитель:
Толмачева Светлана Владимировна,
Учитель математики
МУНИЦИПАЛЬНОГО
ОБЩЕОБРАЗОВАТЕЛЬНОГО
УЧРЕЖДЕНИЯ « ШКОЛА № 10 ГОРОДА ТОРЕЗА»
2.
ВступлениеМногие не знают, чтотакое матрица, но еще
больше людей не знают,
как применять
матричный метод при
решении экономических
задач. Меня
заинтересовала эта тема,
поэтому я решила
посвятить свою работу
данному вопросу.
Немного из истории
Матрица представляет
собой математический объект, который
записывается в формате прямоугольной
таблицы с элементами внутри.
Впервые матрица появилась в
Древнем Китае и носила название
«волшебный квадрат». Чуть позже она
стала известна и арабским математикам.
В конце XVII века швейцарский ученый
Габриэль Крамер разработал свою
теорию, а в 1751 году опубликовал один из
методов решения систем линейных
уравнений «правило Крамера». Также в
этот период был создан «метод Гаусса».
Цель исследовательской работы: рассмотреть
матричную алгебру в экономике на примере решения задач
адаптированных к социально-экономическим реалиям жизни.
Предмет исследования: матрица.
Основными задачами моей исследовательской
работы являются:
•Научиться применять в экономике матричный аппарат.
•Показать взаимосвязь математики и экономики на примере задач
и упражнений.
Линейная алгебра
Линейная алгебра – это раздел математики, в рамках
которого изучаются самые разнообразные объекты
линейной природы. К числу таких объектов относят
линейные уравнения и пространства, отображения и
т.д.
Основным объектом линейной алгебры является
линейное пространство :
•множество векторов в пространстве;
•множество матриц одного типа с линейными
операциями, заданными на этих множествах.
6. Что такое матрицы и операции над ними?
Прямоугольная таблица А, содержащая m строк и n столбцов,называется матрицей порядка m на n. В развернутом виде
матрица А порядка выглядит следующим образом:
А=
a11 a12 a1n
a21 a22 …a2n
am1 am2 amn
Если m=n, то матрица называется квадратной, в противном
случае,– прямоугольной.
В квадратной матрице элементыобразуют ее главную диагональ.
Существуют основные операции над матрицами.
•Сложение (вычитание). Эта операция определена
для матриц происходит
сложение (вычитание) их соответствующих элементов. Так, пусть A aij m,n B bij m,n .
Тогда A B C cij
, где cij aij bij одинаковой размерности.
m ,n
Пример:
4 2
3 1
Найти сумму матриц A =
и
B
=
9 0
-3 4
4 2
A + B =
+
9
0
Задание
2 1
3 1 4 3
7 3
– 3 4 = 9 ( 3) 0 4 = 6 4
.
Решение:
Найти сумму и
разность
матриц и , если
Существуют основные операции над матрицами.
•Произведение матриц. Операция обозначается A B или просто AB
и определена для матриц, размерность которых удовлетворяет определенным
условиям. А именно, число столбцов первого множителя, т.е. матрицы A , равно число
строк второго множителя, т.е. матрицы В.
Пример:
4 2
3 1
Найти произведение матриц A =
и B =
9 0
-3 4
Решение:
3 1 4 x 3 2 x (-3)
-3 4
=
9 x 3 0 x (-3)
4 x 1 2 x 4
=
9 x1 0 x 4
.
4 2
A x B =
x
9
0
6 12
= 27 9
Существуют основные операции над матрицами.
•Транспонирование. Для того чтобы транспонировать матрицу A
T
необходимо сформировать новую матрицу, обозначается A , столбцами которой
являются соответствующие строки исходной.
m, n
, то
AT B bij n , m , где bij a ji
.
Так, если A aij
•Умножение на число. Для того, чтобы умножить матрицу A aij m,n на
число С необходимо на это число умножить все её элементы. Т.е. СA Сaij
m ,n
•Обращение матриц. Матрица B называется обратной к матрице A , если
AB BA E , где E является единичной матрицей. Матрица обратная к данной,
обычно, обозначается B A 1 . Обратная матрица определена только для квадратных
матриц.
Ранг матрицы
Рангом матрицы А называется наибольший из порядков ее миноров,
не равных нулю.
Обозначается ранг матрицы: r(A) или rang(A).
Существует два метода нахождения ранга матрицы:
1. Метод элементарных преобразований нахождения ранга матрицы
заключается в том, что матрицу A приводят к ступенчатому виду с
помощью элементарных преобразований; количество ненулевых
строк полученной ступенчатой матрицы есть искомый ранг
матрицы A.
2. Метод окаймляющих миноров.
Определитель матрицы
Определитель матрицы или детерминант матрицы – это
одна из основных численных характеристик квадратной
матрицы, применяемая при решении многих задач.
Определителем матрицы n×n будет число:
det(A) = Σ(-1)N(α1,α2,…,αn)·aα11·aα22·…·aαnn(α1,α2,…,αn)
где (α1,α2,…,αn) – перестановка чисел от 1 до n, N(α1,α2,…,αn) число инверсий в перестановке, суммирование идёт по всем
возможным перестановкам порядка n.
Определитель матриц A обычно обозначается det(A), |A|, или
∆(A) .
Метод Крамера
Метод Крамера предназначен для решения тех систем линейных
алгебраических уравнений (СЛАУ), у которых определитель матрицы
системы отличен от нуля. Естественно, при этом подразумевается, что
матрица системы квадратна (понятие определителя существует только
для квадратных матриц). Решение системы уравнений методом
Крамера проходит за три шага простого алгоритма:
1.Составить определитель матрицы системы (его называют также
определителем системы), и убедиться, что он не равен нулю, т.
е. Δ≠0.2.Для каждой переменной Xj необходимо составить определитель
Δ Xj , полученный из определителя Δ заменой j-го столбца столбцом
свободных членов заданной СЛАУ.
3.Найти значения неизвестных по формуле Xj =Δ Xj /Δ .
Метод Гаусса
Иногда он также называется методом исключения. Условно состоит из двух этапов.
Первый из них, – прямой ход, заключается в приведении, путем эквивалентных
преобразований, системы к, так называемому, треугольному виду:
второй этап – обратный ход, – в последовательном нахождении
переменных. Из последнего уравнения имеем
,
подставляя, теперь, это значение в предыдущее уравнение, определяем
и т.д., продвигаясь по системе снизу вверх последовательно
находим значения всех переменных.
Пример решения задания методом Крамера
Пример. Решить систему уравнений, используя правило Крамера.
Решение.
Найдем главный определитель системы по правилу треугольников. Имеем
.
•Определим вспомогательные определители.
,
,
.
•Найдем значения переменных.
.
•Выполним проверку:
.
Решение найдено верно.
Ответ:
Пример решения задания методом Гаусса
Пример. Решить систему уравнений, используя правило Гаусса.
Решение: Переставив первое и второе уравнения, получим систему
Приведем систему к треугольному виду.
•Выполним преобразования, связанные с первой строкой: Т.е.
.
Получим
•Выполним преобразования, связанные со второй строкой: Т.е.
.
Получим
.
Тогда из
3-го уравнения
2-го уравнения
1-го уравнения
Решение задач по экономике с помощью матриц
Типография производит печать продукции
трех видов: газеты, журналы, книги. Для их
производства используется сырье трех типов:
бумага 297×420 мм, краска для печати 1 л.,
бумвинил 1 м². Нормы расхода каждого из
них на одну продукцию и объем расхода
сырья на один день заданы таблицей:
Найти ежедневный объем выпуска каждого вида продукции.
Решение:
Пусть ежедневно типография выпускает x₁ газет, x₂ журналов и x₃ книг.
Тогда всоответствии с расходом материалов каждого вида имеем систему:
5x₁ + 25x₂ + 150x₃ = 23750
1,3x₁ + 2,1x₂ + 5,4x₃ = 1715
1,2x₃ = 120
∆ = -26,4
∆₁ = -13200
∆₂ = -6600
∆₃ = -2640
x₁ = -13200/(-26,4) = 500
x₂ = -6600/(-26,4) = 250
x₃ = -2640/(-26,4) = 100
Ответ: типография выпускает ежедневно 500 газет, 250 журналов и 100 книг.
Выводы
В своей работе я доказала, что матрицы могут быть применимы в
обыденной жизни, что алгебра матриц применима к решению большого
круга важных задач, она упрощает процедуру решения и облегчает
понимание процесса. И хотя в нашей работе этот метод к очень
упрощённым, утрированным экономическим решениям, стало ясно, что
он может быть использовать и в решении реальных задач экономики и
систематики.
Матричный язык, обозначения и матричные вычисления широко
используются в различных областях современной математики и ее
приложений. Матрицы являются основным математическим аппаратом
линейной алгебры и применяются при исследовании линейных
отображений векторных пространств, линейных и квадратичных форм,
систем линейных уравнений.
Я убедилась, что любую реальную ситуацию можно представить в виде
математической модели, а затем найти её решения.
Спасибо за
внимание !
Стиль вывода
|
Матрица, имеющая такое же количество строк, как и столбцов, называется квадратной матрицей, Приведенные ниже матрицы являются квадратными:
Матрица, содержащая только одну строку, называется матрицей-строкой. Вот несколько примеров:
[5 8], [6 -9 2] и [-4 0 0 0].
Наконец, матрица только из одного столбца, как в части (d) примера 1, является столбцом матрица.
В именах матриц принято использовать заглавные буквы. Обозначение нижнего индекса
используется для обозначения элементов матрицы следующим образом.
Используя эту нотацию, первая строка, первый элемент столбца обозначается как a11, второй ряд, элемент третьего столбца обозначен a23, а i -й ряд, j -й элемент столбца обозначается и и.д.
Две матрицы равны, если они имеют одинаковый размер и если каждая соответствующая элемент, позиция за позицией, равен. Используя это определение, матрицы
не равны (даже если они содержат одни и те же элементы и одинаковы размер), так как соответствующие элементы различаются.
Определение равенства двух матриц
Пример 3
Из определения равенства, данного выше, единственный способ, которым утверждение
может быть истинным, если 2 = x, 1 = y, p = -1 и q = 0.
Утверждение
никогда не может быть правдой, так как две матрицы имеют разные размеры. (Один 2 х 1 и другой 3 x 1.)
СЛОЖЕНИЕ МАТРИЦ
В начале этого раздела мы использовали матрицу
, где столбцы представляют количество коробок трех различных типов
vi тамины (A, E и K соответственно), а строки представляют два разных
производителей (Dexter и Sullivan соответственно).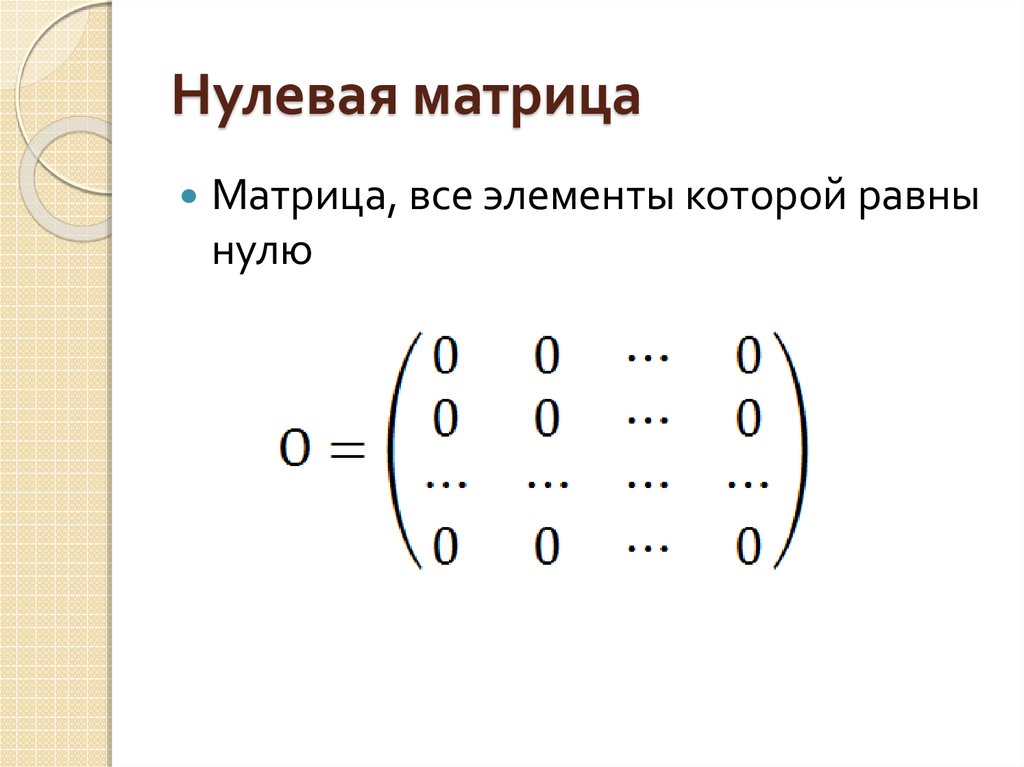
Например, элемент 7
представляет собой 7 коробок с таблетками витамина Е от Dexter и так далее. Предположим, другой
отгрузка от этих двух поставщиков описывается следующей матрицей.
Вот, например, из Салливана прибыло 8 коробок с таблетками витамина К.
количество коробок каждого вида таблеток, полученных от этих двух
поставки можно найти из этих двух матриц.
В первой партии от Dexter было получено 2 коробки таблеток витамина А, а во второй партии было получено 3 коробки таблеток витамина А.
Всего было получено 2 + 3 или 5 коробок этих таблеток. Соответствующие элементы могут быть
добавлено, чтобы найти общее количество полученных коробок с таблетками каждого типа.
Последняя матрица дает общее количество коробок с таблетками каждого типа, которые были
получили. Например, от Dexter было получено 15 коробок с таблетками витамина К.
Обобщение этого примера приводит к следующему определению.
ДОБАВЛЕНИЕ МАТРИЦЫ: Сумма двух м x n матриц A и B равна м
x n матрица A + B
в котором каждый элемент является суммой соответствующих элементов A и B.
ВНИМАНИЕ: Можно добавлять только матрицы одинакового размера.
Матрицы
разных размеров. Следовательно, суммы A + B не существует.
Матрица, содержащая только нулевые элементы, называется нулевой матрицей. Например, [0 0 0] — это нулевая матрица 1 X 3, а
— это нулевая матрица 2 X 3. Нулевая матрица может быть записана любого размера.
В главе 1 аддитивная обратная величина действительного числа а была определена как действительная число -a такое, что a + (-a) = 0 и = a + a = 0. Для заданной матрицы A можно найти матрицу -A такую, что A + (-A) = 0, где 0 – соответствующий нуль матрица и -A + A = 0. Например, если
, то элементы матрицы -A являются аддитивными обратными соответствующими
элементов A. (Помните, что каждый элемент A является действительным числом и, таким образом, имеет
аддитивная инверсия.)
Чтобы проверить, сначала проверьте, что A + (-A) равно 0, соответствующей нулевой матрице.
Затем проверьте, что -A +A также равно 0. Матрица -A является аддитивной обратной или отрицательной, матрицы A. Каждая матрица имеет уникальную аддитивную обратную.
ВЫЧИТАНИЕ МАТРИЦ
Вычитание действительных чисел было определено в главе L, говоря, что a – b = a +(-б). То же определение используется для вычитания матриц.
Если A и B матрицы одинакового размера, то
A – B = A + (-B)
Найдите каждую из следующих разностей.
Матрицы
имеют разные размеры и не могут быть вычтены.
Если матрицу A сложить с самой собой, каждый элемент в сумме будет в два раза больше, чем соответствующий элемент A. Например,
В последнем выражении число 2 перед матрицей называется скаляром чтобы отличить его от матрицы. Пример выше предполагает следующее определение умножения матрицы на скаляр.
УМНОЖЕНИЕ МАТРИЦЫ НА СКАЛЯР: Произведение скаляра k и a
матрица X — это матрица kX, каждый элемент которой в k раз больше соответствующего
элемент X.
Найти каждый продукт.
2: Матрицы – Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14509
- Кен Каттлер
- Университет Бригама Янга через Lyryx
- 2.1: Матричная арифметика
- Теперь вы решили системы уравнений, записав их в терминах расширенной матрицы, а затем выполняя операции над строками этой расширенной матрицы. Оказывается, матрицы важны не только для систем уравнений, но и во многих приложениях.
- 2.
2: Умножение матриц - Следующая важная матричная операция, которую мы рассмотрим, — это умножение матриц. Операция умножения матриц — одна из самых важных и полезных из матричных операций.
- 2.
- 2.3: ij-я запись произведения
- В предыдущих разделах мы использовали записи матрицы для описания действия сложения матриц и скалярного умножения. Мы также можем изучать умножение матриц, используя элементы матриц.
- 2.4: Свойства умножения матриц
- Как указывалось выше, иногда можно умножать матрицы в одном порядке, но не в другом порядке. Однако даже если определены и AB, и BA, они могут не совпадать. 9−1 \).
- 2.8: Элементарные матрицы
- Теперь обратим внимание на специальный тип матрицы, называемый элементарной матрицей.
- 2.9: Подробнее об обратных матрицах
- В этом разделе мы докажем три теоремы, которые прояснят концепцию обратных матриц.