Математика онлайн матрицы: Онлайн решение задач по математике. Матрицы. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Решение высшей математики онлайн

‹– Назад Над матрицами определена еще одна операция, называемая транспонированием.

Транспонированная матрица обозначается или . Операция транспонирования заключается в том, что строки и столбцы в исходной матрице меняются ролями. В транспонированной матрице первым столбцом служит первая строка исходной матрицы, вторым столбцом — вторая строка исходной матрицы и т.д. Например,

Читатель легко проверит, что

где — число. Доказательство. Пусть — матрица размеров , — матрица размеров . Тогда имеет размеры , — размеры . Число столбцов в совпадает с числом строк в , поэтому произведение на определено. Размеры этого произведения . Матрица имеет размеры , поэтому — матрица размеров . Итак, матрицы в правой и левой части равенства (14.

8) существуют и имеют одинаковые размеры.

Пусть , , , , . Нам нужно показать, что , , .

По определению транспонирования . По определению умножения матриц

(14.9)

С другой стороны, Поэтому Сравнивая полученный результат с (14.9), получаем .

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

матрицы и отображения» на Coursera

Новый курс «Линейная алгебра: матрицы и отображения» на Coursera от Новосибирского госуниверситета поможет изучить методы линейной алгебры, которая сейчас применятся широко: от криптографии и нейросетей до обработки видео. Лекции будут полезны как студентам физико-математических, технических и естественнонаучных направлений, так и экономистам, и социологам.

Зарегистрироваться на Coursera и начать обучение можно уже

сейчас.

Методы линейной алгебры применяются в решении систем линейных дифференциальных уравнений, при изучении течений жидкости и газа, в анализе больших массивов данных любой природы, в разработке протоколов контроля качества промышленной продукции, в нейронных сетях, в криптографии, в обработке видео, изображений или звука.

Многие исследования линейной алгебры актуальны для экономики, инженерных и естественнонаучных направлений из-за метода главных компонент — одного из наиболее популярных способов обработки больших массивов данных.

Авторами курса стали профессор кафедры алгебры и математической логики Механико-математического факультета НГУ

Павел Колесников и старший преподаватель кафедры алгебры и математической логики ММФ НГУ Тимур Насыбуллов.

— Онлайн-курс «Линейная алгебра: матрицы и отображения» может быть полезен тем, кто слушает регулярные курсы по высшей алгебре и/или аналитической геометрии и хочет получше понять некоторые разделы: наш курс предлагает взглянуть на ряд вопросов под несколько иным углом. Запущенный нами курс сможет дать более объемную картину классического раздела математики, который в последнее время становится основой для решения многочисленных практических задач в разных сферах жизни

, — сказал один из авторов курса Павел Колесников.

Курс состоит из пяти модулей: в них входят 45 видеолекций, внутрилекционные вопросы для закрепления пройденного материала, оцениваемые тесты по итогам освоения каждого модуля курса, итоговый тест и презентации к курсу.

Первый модуль посвящен векторному пространству, во втором модуле преподаватели расскажут о линейных отображениях. Третий модуль курса ознакомит с системами линейных уравнений и их приложениям в решении прикладных задач. В рамках четвертого модуля слушатели познакомятся с Жордановой формой, важной для решения многих теоретических задач. Последний, пятый модуль, посвящен симметрическим и ортогональным линейным операторам, и их приложениям, например, для решения оптимизационных задач.

— Курс по линейной алгебре был создан при грантовой поддержке Coursera. В декабре 2020 года был объявлен конкурс, во время которого анонсировали приоритетные для платформы направления, и для меня особенно отрадно, что в области линейной алгебры наши интересы совпали. Ведь, как мы знаем, в университете есть очень сильный Механико-математический факультет, и его преподаватели сумели подготовить действительно востребованный актуальный курс, который может быть полезен студентам и специалистам из совершенно разных сфер: от естественных наук до IT,

— уточнила Лилия Стяжкина, начальник отдела видеопроизводства НГУ.

Все материалы курса, включая оцениваемые задания, бесплатны для всех слушателей. Для студентов и преподавателей НГУ, ВКИ и СУНЦ, зарегистрированных в кампусной программе Coursera, сертификаты об успешном окончании курса также бесплатны. Если вы еще не зарегистрированы в программе – это легко исправить: подайте заявку в личном кабинете или напишите по адресу [email protected].

Калькулятор онлайн – Операции над матрицами: сложение, вычитание, умножение, деление, возведение в степень. Вычисление определителя матрицы, обратной матрицы, ранга матрицы

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.

Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Матрицы и операции над ними

Виды матриц

Определение 1.
Матрицей размера $m \times n $ называют прямоугольную числовую таблицу, состоящую из $mn$ чисел, которые расположены в $m$ строках и $n$ столбцах. Составляющие матрицу числа называют элементами этой матрицы.

Как правило, их обозначают строчной буквой с двумя индексами, например $a_{ij}$, где $i$ — номер строки ( $i=\overline{1,m} $ ), $j$ — номер столбца ( $j=\overline{1,n} $ ), в которых расположен этот элемент.

Матрицу записывают так:
$$ \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix} $$

Если по тексту ясно, в каких пределах изменяются индексы $i$ и $j$, то сокращённо матрицу можно записать так: $ \left(a_{ij} \right) $. Матрицу как единый объект обозначают прописной буквой: $A$, $B$ и т.д.

Элементами матриц могут быть не только действительные числа, но и комплексные, и даже другие математические объекты. Например, элементами матриц могут быть многочлены или матрицы.

Матрицу называют матрицей-строкой, если матрица имеет размер $1 \times n $, т. е. если у матрицы всего одна строка. Число элементов в матрице-строке называют её длиной.
$A=(a_1, \; …,\; a_n) $

Матрицу называют матрицей-столбцом, если матрица имеет размер $m \times 1 $, т.е. если у матрицы один столбец. Число элементов в матрице-столбце называют её высотой.
$A = \begin{pmatrix} a_{1} \\ \vdots \\ a_{m} \\ \end{pmatrix} $

Матрицу называют квадратной порядка $n$, если $ m=n$, т.е. когда матрица имеет столько же столбцов, сколько и строк :
$$ \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{pmatrix} $$ а если $m \neq n $ — прямоугольной.

У квадратных матриц выделяют последовательности элементов $ a_{11}, \; a_{22}, \; …, \; a_{nn} $ — главную диагональ, и \( a_{n1}, \; a_{n-1,2}, \; .

.., \; a_{1n} \) — побочную диагональ. Элементы главной диагонали называют диагональными. Понятия диагонального элемента и главной диагонали распространяют и на прямоугольные матрицы.

Если в квадратной матрице порядка $n$ все элементы, стоящие вне главной диагонали, равны нулю, т.е. если матрица имеет вид
$$ \begin{pmatrix} a_{11} & 0 & \cdots & 0 \\ 0 & a_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & a_{nn} \\ \end{pmatrix} $$,
то её называют диагональной к обозначают $ \text{diag} (a_{11}, \; …, \; a_{nn} ) $.
Если в диагональной матрице порядка $n$ на диагонали стоят единицы, то её называют единичной и обозначают обычно $E$ :
$$ E = \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\ \end{pmatrix} $$,

Матрицу размера $m \times n $, все элементы которой равны нулю, называют нулевой матрицей соответствующего размера и обозначают буквой $\Theta$ или цифрой 0.

Часто используют матрицы и других видов, например верхние треугольные матрицы
$$ \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ 0 & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & a_{nn} \\ \end{pmatrix} $$
у которых элементы, расположенные под главной диагональю, равны нулю, и нижние треугольные матрицы, у которых, наоборот, элементы над главной диагональю равны нулю:
$$ \begin{pmatrix} a_{11} & 0 & \cdots & 0 \\ a_{21} & a_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{pmatrix} $$

Ступенчатой матрицей (матрицей ступенчатого вида) называют матрицу размера $m \times n $, если для любой её строки выполнено следующее условие: под первым слева ненулевым элементом строки и предшествующими ему нулевыми элементами строки все элементы матрицы равны нулю.
Следующие матрицы имеют ступенчатый вид:
$ \begin{pmatrix} 0 & 2 & 3 & 0 \\ 0 & 0 & -1 & 1 \\ 0 & 0 & 0 & 3 \\ \end{pmatrix} $ $ \begin{pmatrix} 3 & 1 & 3 & 3 \\ 0 & 0 & 2 & 1 \\ 0 & 0 & 0 & 0 \\ \end{pmatrix} $ $ \begin{pmatrix} 1 & 1 & 3 & 3 \\ 0 & 3 & 0 & 1 \\ 0 & 0 & 1 & -1 \\ \end{pmatrix} $

Линейные операции над матрицами

Определение 2.
Две матрицы называют равными, если они имеют один и тот же размер и если у них совпадают соответствующие элементы.

Определение 3.
Суммой матриц $ A=(a_{ij}) $ и $ B=(b_{ij}) $ размера $m \times n $ называют матрицу $ C=(c_{ij}) $ того же размера с элементами $ c_{ij} = a_{ij} + b_{ij}, \; i=\overline{1,m} , \; j=\overline{1,n} $

В подробной записи:
$ A+B = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix} + $ $ \begin{pmatrix} b_{11} & b_{12} & \cdots & b_{1n} \\ b_{21} & b_{22} & \cdots & b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & \cdots & b_{mn} \\ \end{pmatrix} = $ $ \begin{pmatrix} a_{11}+b_{11} & a_{12}+b_{12} & \cdots & a_{1n}+b_{1n} \\ a_{21}+b_{21} & a_{22}+b_{22} & \cdots & a_{2n}+b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}+b_{m1} & a_{m2}+b_{m2} & \cdots & a_{mn}+b_{mn} \\ \end{pmatrix} = C $

Сумма определена только для матриц одного размера.

Определение 4.
Произведением матрицы $ A=(a_{ij}) $ размера $m \times n $ на число $ k \in \mathbb{R}$ называют матрицу $ C=(c_{ij}) $ размера $m \times n $ с элементами $ c_{ij} = k \cdot a_{ij} $.
Подробно это произведение выглядит так:
$ k \cdot \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix} = $ $ \begin{pmatrix} k \cdot a_{11} & k \cdot a_{12} & \cdots & k \cdot a_{1n} \\ k \cdot a_{21} & k \cdot a_{22} & \cdots & k \cdot a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ k \cdot a_{m1} & k \cdot a_{m2} & \cdots & k \cdot a_{mn} \\ \end{pmatrix} $

Замечание. Операции сложения и умножения на число для матриц аналогичны одноименным операциям над векторами. {n+m}\).

Элементарные преобразования матриц

Следующие три операции называют элементарными преобразованиями строк матрицы :

1. Умножение строки матрицы на число не равное нулю.

2. Перестановка двух строк матрицы.

3. Суммирование одной строки с другой строкой, умноженной на число.

Аналогичные операции над столбцами матрицы называют элементарными преобразованиями столбцов.

Каждое элементарное преобразование строк или столбцов матрицы имеет обратное элементарное преобразование, которое преобразованную матрицу превращает в исходную.

Теорема. С помощью элементарных преобразований строк любую матрицу можно привести к ступенчатому виду.

Определители

Определители n-го порядка

В теории определителей n-го порядка используются понятия перестановки, подстановки и их четности. Всякое расположение чисел $ 1,\; 2,\; 3,\; …,\; n $ в определенном порядке называют перестановкой из $n$ чисел.
Из $n$ чисел можно образовать $n!$ различных перестановок.
В общем случае перестановку записывают в виде матрицы-строки $ \alpha = (\alpha_1,\; \alpha_2,\; …,\; \alpha_n ) $
Перестановку $ (1,\; 2,\; 3,\; …,\; n) $ называют нормальной.

Два числа $\alpha_i$ и $\alpha_j$ в перестановке $ \alpha = (\alpha_1,\; …,\; \alpha_n ) $ образуют инверсию, если $\alpha_j > \alpha_i $ но при этом $\alpha_i$ стоит в перестановке правее $\alpha_j$ (т.е. $i>j$ ).
Общее количество инверсий в перестановке $\alpha $ обозначают $ |\alpha | $, и если это число четное, то перестановку называют четной, а если оно нечетное — нечетной.

Транспозицией перестановки называют такое её преобразование, при котором в ней меняются местами какие-либо два элемента, а другие остаются на своих местах.

Теорема. Любая транспозиция меняет четность перестановки.

Из двух перестановок $ ( \alpha_1,\; …,\; \alpha_n ) $ и $ ( \beta_1,\; …,\; \beta_n ) $ одних и тех же чисел можно составить новый объект
$$ \sigma = \begin{pmatrix} \beta_1 & \beta_2 & \cdots & \beta_n \\ \alpha_1 & \alpha_2 & \cdots & \alpha_n \end{pmatrix} , \tag{1} $$
который называют подстановкой n-й степени.

Подстановку называют четной, если перестановки, из которых она состоит, имеют одинаковую четность, и нечетной в противоположном случае.
Четность подстановки $ (1) $ совпадает с четностью числа $ |\beta|+|\alpha| $ — общего количества инверсий в строках подстановки, которое обозначают $ |\sigma| $.

Транспозицией подстановки называют любую перестановку её столбцов. Поскольку транспозиция подстановки вызывает транспозиции и в образующих её перестановках, то, согласно предыдущей теореме, очевидно, что транспозиция подстановки не меняет её четность.

Каждая подстановка вида $ (1) $ задает взаимно однозначное отображение множества чисел $ 1,\; 2,\; 3,\; …,\; n $ на себя, при котором $ \beta_1 $ отображается в $ \alpha_1 \; , \; \beta_2 $ — в $ \alpha_2$ и т.д.
В соответствии с интерпретацией подстановок как отображений две подстановки считают равными, если они отличаются только порядком записи своих столбцов.
Например, подстановки
$ \begin{pmatrix} 1 & 3 & 4 & 2 \\ 2 & 4 & 1 & 3 \\ \end{pmatrix} \;\; и \;\; \begin{pmatrix} 1 & 2 & 3 & 4 \\ 2 & 3 & 4 & 1 \\ \end{pmatrix} $
равны, так как вторая получается из первой перестановкой столбцов.

Соглашение о равенстве подстановок позволяет записать любую подстановку так, чтобы первая строка являлась нормальной перестановкой. Поэтому различных подстановок $n$-й степени имеется ровно $n!$

Определение. {|\sigma|} a_{1\alpha_1} a_{2\alpha_2} … a_{n\alpha_n} \tag{3} $$ которая берется по всевозможным подстановкам вида
$ \sigma = \begin{pmatrix} 1 & 2 & \cdots & n \\ \alpha_1 & \alpha_2 & \cdots & \alpha_n \end{pmatrix} $

Определитель матрицы $A$ часто называют просто определителем, или детерминантом, и обозначают
$ \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{vmatrix} $
или $ \det A$, называя $A$ матрицей этого определителя.

Свойства определителей
Поскольку определители соответствуют квадратным матрицам, в их теорию легко переносится матричная терминология (порядок, элементы, строки, столбцы, диагональ, диагональные элементы, виды матриц и определителей, транспонирование, элементарные преобразования строк и столбцов, линейные комбинации строк и столбцов и др. T \right| \)
Свойство 2. При перестановке двух строк (столбцов) определитель меняет свой знак на противоположный.
Свойство 3. Если все элементы $j$-го столбца определителя представлены в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все столбцы, кроме $j$-го, такие же, как и в данном определителе, а $j$-й столбец первого определителя состоит из первых слагаемых $j$-го столбца данного определителя, а второго — из вторых слагаемых :
$ \begin{vmatrix} a_{11} & \cdots & \alpha_{1j} + \beta_{1j} & \cdots & a_{1n} \\ a_{21} & \cdots & \alpha_{2j} + \beta_{2j} & \cdots & a_{2n} \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a_{n1} & \cdots & \alpha_{nj} + \beta_{nj} & \cdots & a_{nn} \end{vmatrix} = $ $ \begin{vmatrix} a_{11} & \cdots & \alpha_{1j} & \cdots & a_{1n} \\ a_{21} & \cdots & \alpha_{2j} & \cdots & a_{2n} \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a_{n1} & \cdots & \alpha_{nj} & \cdots & a_{nn} \end{vmatrix} + $ $ \begin{vmatrix} a_{11} & \cdots & \beta_{1j} & \cdots & a_{1n} \\ a_{21} & \cdots & \beta_{2j} & \cdots & a_{2n} \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a_{n1} & \cdots & \beta_{nj} & \cdots & a_{nn} \end{vmatrix} $ Аналогично для строки.
Свойство 4. Общий множитель элементов строки или столбца может быть вынесен за знак определителя.
Для умножения определителя на число достаточно умножить на это число элементы любой строки или любого столбца.
Свойство 5. Определитель равен нулю, если он имеет :
1) нулевую строку (столбец)
2) хотя бы две одинаковые строки (столбца)
3) хотя бы две строки (столбца), элементы которых пропорциональны
4) хотя бы одну строку (столбец), являющуюся линейной комбинацией других строк (столбцов).
Свойство 6. Определитель не изменится, если к любой его строке (столбцу) прибавить другую строку (столбцец), умноженную на число.
В матрице $A$ вычеркнем $i$-ю строку и $j$-й столбец, в которых стоит элемент $a_{ij}$. Из оставшихся элементов можно составить новую квадратную матрицу (n-1)-го порядка, сдвинув строки и столбцы после вычеркивания.
Определитель построенной матрицы обозначают через $ M_{ij} $ и называют минором (матрицы $A$ и её определителя $\Delta$ ), соответствующим элементу $a_{ij}$. {i+j} a_{ij} M_{ij} \tag{5} $$ ( разложение по $j$-му столбцу )
Разложения по строке (4) и столбцу (5) дают правила, в соответствии с которыми определитель n-го порядка сводится к n определителям (n-1)-го порядка, раскладывая которые получим n(n-1) определителей (n-2)-го порядка и т.д.
Эти вычисления получаются громоздкими, однако процесс упрощается, если среди элементов определителя имеется много нулей. Целесообразно раскладывать определитель по тому ряду (строке, столбцу), в котором больше нулей.
Если же в этом смысле некоторые ряды одинаковы, то удобнее выбирать тот из них, в котором элементы имеют большие значения по абсолютной величине, поскольку это упрощает выполнение арифметических вычислений.
Свойство 8. Определитель верхней (нижней) треугольной матрицы равен произведению элементов её главной диагонали, т.е.
$$ \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ 0 & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & a_{nn} \\ \end{vmatrix} = $$ $$ \begin{vmatrix} a_{11} & 0 & \cdots & 0 \\ a_{21} & a_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{vmatrix} = $$ $$ a_{11}a_{22}.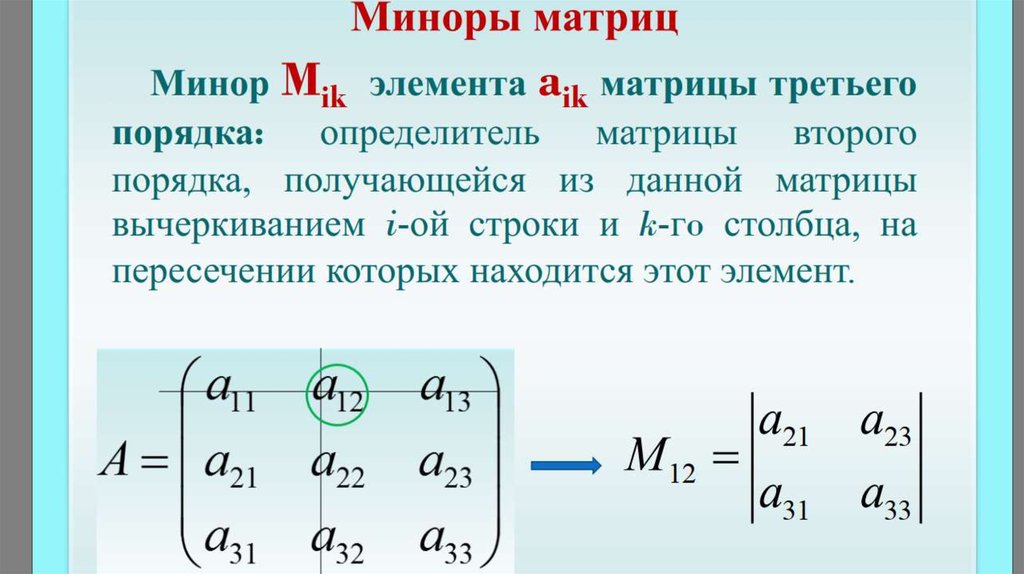 n a_{ii} $$
С помощью элементарных преобразований строк любая матрица приводится к ступенчатому виду. Квадратная матрица ступенчатого вида является частным случаем верхней треугольной матрицы, у которой диагональные элементы, начиная с некоторого, могут быть равны нулю. Определитель такой матрицы легко найти по свойству 8. В алгоритме приведения к ступенчатому виду используется перестановка строк, при которой определитель матрицы меняет знак. Изменение знака можно учесть, например, дополнительным умножением определителя или одной из строк на —1. Следовательно, квадратную матрицу всегда можно привести элементарными преобразованиями строк к верхнему треугольному виду с сохранением значения её определителя.
Свойство 9. Определитель произведения двух квадратных матриц A, B равен произведению их определителей, т.е. $ |АВ| = |A||B| $.
Свойство 10. Определитель обратной матрицы: $ \left| А^{-1} \right| = \frac{1}{|A|} $
Свойство 11. {1+3} a_{13} M_{13} = $$ $$ a_{11} \begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{vmatrix} – a_{12} \begin{vmatrix} a_{21} & a_{23} \\ a_{31} & a_{33} \end{vmatrix} + a_{13} \begin{vmatrix} a_{21} & a_{22} \\ a_{31} & a_{32} \end{vmatrix} = $$ $$ a_{11}a_{22}a_{33} – a_{11}a_{23}a_{32} – a_{12}a_{21}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} – a_{13}a_{22}a_{31} $$
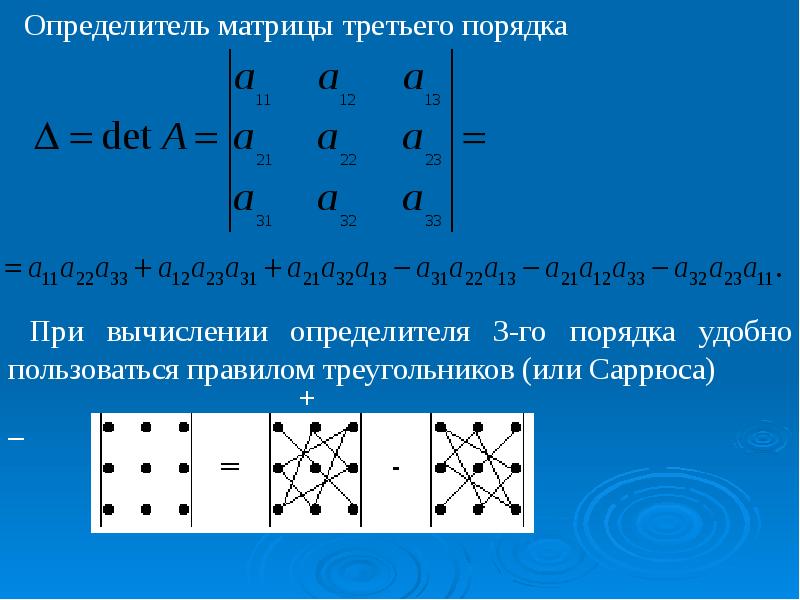
Чтобы запомнить, какие произведения элементов берутся со знаком $ “+” $, а какие со знаком $ “-” $ можно использовать следующее правило треугольников.
Произведения элементов, стоящих на зелёных точках складываются, а на синих – вычитаются :
Также для вычисления определителя 3-го порядка существует правило Саррюса.
Первый и второй столбцы матрицы записываются справа от основной матрицы.
Произведения элементов, стоящих на зелёных линиях складываются, а на синих – вычитаются :

Обратная матрица и её свойства
Определение. {-1}\), обратную к $A$, фактически надо решить матричное уравнение $AX=E$.
Отметим, что если над матрицей $A$ выполняется какое-либо элементарное преобразование строк, то это же преобразование осуществляется и над матрицей $AX$, поскольку любое элементарное преобразование строк матрицы эквивалентно умножению её слева на соответствующую матрицу специального вида. Таким образом, если в уравнении $AX=E$ над матрицами $A$ и $E$ одновременно выполнить какое-либо элементарное преобразование строк, т.е. домножить это равенство слева на некоторую матрицу специального вида, то в результате получится новое матричное уравнение $A_1X=B_1$. Оба эти матричные уравнения имеют одно и то же решение, так как любое элементарное преобразование строк имеет обратное элементарное преобразование строк.
Последовательность элементарных преобразований строк надо подобрать так, чтобы на s-м шаге матрица $A$ превратилась в единичную матрицу.
В результате этих s шагов получается уравнение $A_sX=B_s$, где $A_s=E$, т. {-1}\).

Ранг матрицы
Определение.
Рангом матрицы называют число, которое равно максимальному порядку среди её ненулевых миноров.
Для ранга матрицы $A$ используют обозначение $\text{rang}A$.
Если квадратная матрица порядка n невырождена, то её ранг равен её порядку n : ненулевым является единственный минор максимального порядка n, совпадающий с определителем матрицы.
В частности, ранг единичной матрицы $E$ порядка n равен n.
Если квадратная матрица вырождена, то её ранг меньше её порядка : единственный минор максимального порядка, равного порядку матрицы, является нулевым, и в этом случае ненулевые миноры имеют меньший порядок.
Ранг нулевой матрицы полагают равным нулю.
Ранг диагональной матрицы равен количеству её ненулевых диагональных элементов.
Непосредственно из определения ранга матрицы следует, что ранг имеет следующее свойство, полностью его характеризующее. T = \text{rang} A \)
Теорема. Ранг матрицы не меняется при элементарных преобразованиях её строк и столбцов.

Теорема о базисном миноре
Среди миноров матрицы могут быть как равные нулю, так и отличные от нуля.
Определение.
Минор $M$ матрицы $M$ называют базисным, если выполнены два условия:
1) он не равен нулю
2) его порядок равен рангу матрицы А
Матрица $A$ может иметь несколько базисных миноров. Строки и столбцы матрицы $A$, в которых расположен выбранный базисный минор, называют базисными.
Теорема о базисном миноре. Базисные строки (столбцы) матрицы $A$, соответствующие любому её базисному минору $M$, линейно независимы. Любые строки (столбцы) матрицы $A$, не входящие в $M$, являются линейными комбинациями базисных строк (столбцов).
Следствие. Для того чтобы квадратная матрица была невырожденной, необходимо и достаточно, чтобы её строки (столбцы) были линейно независимы.
Теорема. Линейно независимые строки (столбцы) матрицы, количество которых равно рангу матрицы, являются базисными строками (столбцами).
Теорема. Для любой матрицы её ранг равен максимальному количеству её линейно независимых строк (столбцов).
Следствие. Для любой матрицы максимальное число линейно независимых строк равно максимальному числу линейно независимых столбцов.

Вычисление ранга матрицы
Метод окаймляющих миноров
Минор $M’$ матрицы $A$ называют окаймляющим для минора $M$, если он получается из последнего добавлением одной новой строки и одного нового столбца матрицы $A$.
Ясно, что порядок окаймляющего минора $M’$ на единицу больше, чем порядок минора $M$.
Метод окаймляющих миноров позволяет найти один из базисных миноров матрицы и состоит в следующем.
Выбирается ненулевой минор первого порядка (ненулевой элемент матрицы). К очередному ненулевому минору последовательно добавляются такие строка и столбец, чтобы новый окаймляющий минор оказался ненулевым. Если этого сделать нельзя, то последний ненулевой минор является базисным (что утверждает следующая ниже теорема). Этот процесс рано или поздно закончится из-за ограниченных размеров матрицы.
Теорема. Если для некоторого минора матрицы все окаймляющие его миноры равны нулю, то он является базисным.
Метод элементарных преобразований
При элементарных преобразованиях строк (столбцов) матрицы её ранг не меняется. С помощью этих преобразований можно так упростить матрицу, чтобы ранг новой матрицы легко вычислялся.
Например с помощью элементарных преобразований строк любую матрицу можно привести к ступенчатому виду. Ранг же ступенчатой матрицы равен количеству ненулевых строк. Базисным в ней является минор, расположенный на пересечении ненулевых строк со столбцами, соответствующими первым слева ненулевым элементам в каждой из строк. Действительно, этот минор ненулевой, так как соответствующая матрица является верхней треугольной, а любое его окаймление содержит нулевую строку. Поэтому приведение матрицы к ступенчатому виду с помощью элементарных преобразований строк позволяет вычислить ранг матрицы.
Приведенные два метода существенно отличаются друг от друга.
При нахождении ранга конкретной матрицы методом окаймляющих миноров может потребоваться большое количество вычислений. Это связано с тем, что метод требует вычисления определителей, порядок которых может возрасти до минимального из размеров матрицы. Однако в результате будет найден не только ранг матрицы, но и один из её базисных миноров.
При нахождении ранга матрицы методом элементарных преобразований требуется гораздо меньше вычислений. Причем разница в объемах вычислений возрастает с ростом размеров матрицы и усложнением её вида. Но этот метод позволяет найти базисный минор лишь для матрицы ступенчатого вида, полученной в результате элементарных преобразований. Чтобы найти базисный минор исходной матрицы, нужны дополнительные вычисления с учетом уже известного ранга матрицы.
3 4 матрица
Вы искали 3 4 матрица? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 4 3 матрица, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «3 4 матрица».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 3 4 матрица,4 3 матрица,как найти определитель матрицы 3х4,как решить матрицу 3 на 4,как решить матрицу 4 на 3,матрица 4 на 3. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 3 4 матрица. Просто введите задачу в окошко и нажмите «решить» здесь (например, как найти определитель матрицы 3х4).
Где можно решить любую задачу по математике, а так же 3 4 матрица Онлайн?
Решить задачу 3 4 матрица вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Онлайн калькуляторы
Экзотические единицы длины
Следующий уникальный калькулятор служит для перевода экзотических единиц длины в…
Чей фунт тяжелее?
Следующий онлайн калькулятор о фунтах. Ранее он был очень популярен,…
Уровень жидкости в наклоненном цилиндрическом баке
Следующий онлайн калькулятор может вычислить уровень жидкости в цилиндрической таре…
Температурные шкалы
Следующий онлайн калькулятор переводит температуры между разными шкалами. Помните калькулятор…
Старинные русские деньги
Следующий калькулятор интересен тем, что он переводит древние российские денежные…
Соответствие размеров обуви
Следующий калькулятор будет очень полезен тем, кто решил купить или…
Системы измерения плоских углов
Следующий калькулятор работает очень просто, вам нужно ввести всего одно…
Рост в русской системе мер
Следующий онлайн калькулятор считает рост человека благодаря русской системе мер…
Размер экрана
Следующий онлайн калькулятор может вычислить габариты экрана телевизоров, компьютеров, проекторов,…
Размер снимка в пикселях и формат фотографии
Перед вами 2 калькулятора: один поможет вам подобрать формат снимков…
Перевод числа плиток в единицы площади и обратно
Следующие 2 калькуляторы переводят заданное число плиток в квадратные метры…
Перевод мер площади из метрической в английскую систему и обратно
Перед вами 2 онлайн-калькулятора. Они переводят меры площади из метрической…
Перевод мер длины из русской системы в метрическую и обратно
Следующий необычный калькулятор переводит меры длины из русской системы в…
Перевод мер длины из метрической в имперскую систему и обратно
Перед вами 2 калькулятора, которые предназначены для перевода мер длины…
Перевод кельвинов в градусы цельсия
Следующий простенький калькулятор переводит введенную вами toC из кельвинов в…
Перевод из фунтов в килограммы и обратно
Следующий калькулятор предназначен для перевода кг в фунты. Также есть…
Перевод из фунтов в дюймы
Следующий онлайн калькулятор переводит калибр древних артиллерийских орудий из фунтов…
Перевод из градусов Фаренгейта в градусы Цельсия
Давайте вспомним калькулятор, который переводит градусы Цельсия в градусы Фаренгейта:…
Перевод дробных чисел из одной системы счисления в другую
Как вы уже могли заметить на нашем сайте есть несколько…
Перевод градусов Цельсия в градусы Фаренгейта
Следующий уникальный калькулятор переводит градусы Цельсия в градусы Фаренгейта. Наверное,…
Перевод градусов минут и секунд в десятичные градусы и обратно
Следующий калькулятор умеет переводить значение угла, которое задано в градусах,…
Перевод градусов в радианы
Следующий калькулятор делает перевод единиц измерения углов из градусов, минут,…
Объем сегмента цилиндра
Следующий калькулятор делает расчет объема сегмента цилиндра. Давайте посмотрим каким…
Объем жидкости в наклоненном цилиндрическом баке
Следующий онлайн-калькулятор считает объем жидкости в бочке, которая имеет цилиндрическую…
Общее время наработки аппарата
Следующий калькулятор служит для детального подсчета суммарной работы аппарата. Вам…
Сочетание цветов
Перед вами отличный помощник для IT специалистов. С помощью данного…
О римских цифрах
Следующий калькулятор переводит числа, записанные римскими цифрами в простые десятичные…
Метров в секунду и километров в час
Следующий калькулятор переводит скорость из м/с в км/час. Часто при…
Конвертер единиц давления
Начнем с истории. В 17 веке итальянским ученым Торричелли было…
Калькулятор горловины для цилиндрического бака
Следующий онлайн-калькулятор рассчитывает параметры горловины для цилиндрического бочки. Все работает…
Математика онлайн – решение интегралов, производных, уравнений
Мы рады приветствовать Вас на нашем сайте. Данный сайт содержит онлайн калькуляторы для решения типовых задач по математическому анализу, линейной алгебре, элементарной математике и др.
На сайте представлено более 90 калькуляторов с помощью которых можно находить решение интегралов, производных, пределов, дифференциальных уравнений, строить графики функций, выполнять различные операции над матрицами: сложение, вычитание, умножение, транспонирование, возводить квадратную матрицу в степень, находить определитель, ранг, след, обратную матрицу, приводить матрицу к верхнетреугольному виду, а также находить ее собственные числа и вектора, получать решение алгебраических уравнений любой степени и любых систем линейных алгебраических уравнений (СЛАУ). Также на нашем сайте можно найти уравнение касательной, разложить функцию в ряд Тейлора, и многое другое.
Мы разрабатывали наши калькуляторы в течение нескольких лет, постоянно улучшая их внутренние алгоритмы, и теперь полностью уверены в том, что выдаваемое ими подробное решение во-первых полностью правильное, во-вторых соответствует требованиям, предъявляемым в ВУЗах России, Украины, Беларуси и стран СНГ.
Нам доверяют очень многие, каждый день мы получаем в свой адрес благодарности за данный проект. Всего с помощью нашего сайта решено уже более 1 000 000 задач. Ознакомьтесь со всеми преимуществами нашего пошагового решения.
ВНИМАНИЕ! Если Ваша задача нестандартная и получить ответ с помощью онлайн калькуляторов не удалось, мы всегда готовы оказать Вам помощь в учебе.
Определитель 4 порядка. Калькулятор
Определители четвертого и старших порядков возможно вычислять по упрощенным схемам, которые заключаются в разложении по элементам строк или столбцов или сведении к треугольному виду. Оба метода для наглядности будут рассмотрены на матрицах 4-го порядка.
Первый пример мы рассмотрим с подробными объяснениями всех промежуточных действий.
Пример 1. Вычислить определитель методом разложения.
Решение. Для упрощения вычислений разложим определитель четвертого порядка по элементам первой строки (содержит нулевой элемент). Они образуются умножением элементов на соответствующие им дополнения (образуются вычеркивания строк и столбцов на пересечении элемента, для которого исчисляются – выделено красным)

В результате вычисления сведутся к отысканию трех определителей третьего порядка, которые находим по правилу треугольников

Найденные значения подставляем в выходной детерминант
Результат легко проверить с помощью матричного калькулятора YukhymCALC . Для этого в калькуляторе выбираем пункт Матрицы-Определитель матрицы, размер матрицы устанавливаем 4*4.
Далее вводим же матрицу и осуществляем вычисления. Результатом расчетов будет следующий вывод данных
Результаты совпадают, следовательно вычисления проведены верно.
Пример 2. Вычислить определитель матрицы четвертого порядка.
Решение.
Как и в предыдущем задании осуществим вычисления методом разложения. Для этого выберем элементы первого столбца. Упрощенно определитель можно подать через сумму четырех детерминант третьего порядка в виде
Далее переходим к отысканию определителей по правилу треугольников

Вычисления не слишком сложные, главное не напутать со знаками и треугольниками. Найденные величины подставляем в главный определитель и суммируем
Результат проверяем матричным калькулятором YukhymCALC . Правильность расчетов подтверждается следующим рисунком
Метод возведения определителя к треугольному виду
Данный метод позволяет ряд определителей вычислить достаточно быстрый способ. Суть его заключается в объединении определителя к треугольному виду, при этом следует учитывать все множители на которые увеличиваем или уменьшаем строки и учете при конечных расчетах. Из данного определения Вы ничего для себя не поймете, поэтому лучше все показать на конкретных примерах.
Пример 3. Найти определитель матрицы сведением к треугольному виду
Решение.
Сначала осуществляем математические манипуляции, чтобы получить все нулевые элементы кроме первого в первом столбце. Для этого от второй строки вычитаем первый, умноженный на два. В результате получим
Далее есть два варианта: от третьей строки вычесть первый умноженный на три, или от третьего вычесть сумму первых двух строк. Последний вариант позволит получить сразу два нуля в строке, его и выбираем
Дальше целесообразнее от четвертой отнять удвоенную вторую строчку. В результате элементарных преобразований определитель примет вид
Осталось превратить в ноль один элемент в третьем столбце. Для этого от четвертой строки вычитаем удвоенную третью в предварительно записанном определителе
По свойству, определитель треугольной матрицы равен произведению диагональных элементов.

По желанию можно проверить результат матричным калькулятором.
В этом примере никаких умножений строк, в которых зануливали элементы мы не выполняли, поэтому полностью раскрыть метод на этом примере не получилось.
Рассмотрим более сложный.
Пример 4.
Найти определитель матрицы 4-го порядка
Решение.
Элементарными преобразованиями сводим определитель к треугольного вида. Для этого от каждой строки вычитаем первый. В результате преобразований получим следующий детерминант
Для удобства вычислений, меняем третью строчку со вторым местами..
По свойству определителей любая замена строк местами ведет к изменению знака определителя. Учитываем это в некотором множителе k=-1.
От третьей строки вычитаем второй, умноженный на минус три. После упрощений получим
Превращаем в ноль последний элемент во втором столбце, для этого вычитаем вторую строчку умноженный на 2.
Результат будет следующим
От удвоенного четвертой строки вычитаем третий. По свойству, умножения строки на постоянную а ведет к изменению определителя в а раз. Данное изменение фиксируем в множителе k=-1*2=-2.
Окончательное значение определителя будет равно произведению диагональных элементов разделенных (или нормированных) на множитель k, который отвечает за изменение детерминанта при элементарных преобразованиях. Выполняем вычисления
Проверка матричным калькулятором подтверждает правильность производимых вычислений.
Метод разложения определителя по элементам строк или столбцов достаточно быстрым при исчислении определителей больших размеров. Метод сведения к треугольного вида эффективен, если элементарные преобразования легко проследить и не приводят к большим произведений. В других случаях нужно пользоваться комбинацией этих методов, в последнее образовывать как можно больше нулевых элементов, а методом разложения по строкам или столбцам уменьшать количество выполненных операций. Это позволит без проблем вычислять определители третьего, четвертого и даже пятого порядка.
Обратное, умножение, сложение, вычитание, определитель, присоединенный
См. Также: Метод исключения Гаусса-Джордана, одновременные линейные уравнения, геометрическое линейное преобразование
Матрица представляет собой прямоугольный массив чисел.
Размер матрицы – это ее размерность, а именно количество строк и столбцов матрицы.
Для операций с матрицами используйте два калькулятора ниже.
Чтобы найти обратную матрицу, вы также можете использовать метод исключения Гаусса-Жордана.
Прочтите пояснения о матричных операциях ниже.
Калькулятор умножения, сложения и вычитания матриц
Введите размер матриц. (Строки × Столбцы).
Для умножения количество столбцов первой матрицы должно быть равно количеству строк второй матрицы, то есть (a × b) (b × c).
Для сложения и вычитания размеры двух матриц должны быть одинаковыми.
Максимальный размер матрицы для этой системы 9 × 9.

Сообщайте о любых ошибках на [адрес электронной почты] .
Матричный обратный, определяющий и сопряженный калькулятор
Чтобы матрица была обратимой, она должна быть квадратной.
Введите размер матрицы. (Строки × Столбцы).
Максимальный размер матрицы для этой системы 9 × 9.
Результат будет округлен до 3 десятичных знаков.

Сообщайте о любых ошибках на [адрес электронной почты] .

Матричные операции
Сложение и вычитание матриц
Если матрицы A и B одинакового размера,
сумма A & plus; B – это матрица, полученная путем добавления элементов B к соответствующим элементам A.
разница A-B – это матрица, полученная вычитанием записей B из соответствующих записей A.
Если A = a11a12… a1na21a22… a2n & vellip; & vellip; & dtdot; & vellip; am1am2… amn а также B = b11b12… a1nb21b22… a2n & vellip; & vellip; & dtdot; & vellip; bm1bm2… bmn
A & plus; B = a11 & plus; b11a12 & plus; b12… a1n & plus; b1na21 & plus; b21a22 & plus; b22… a2n & plus; b2n & vellip; & vellip; & dtdot; & vellip; am1 & plus; bm1am2 & plus; bm2… amn7 & plus;
A − B = a11 − b11a12 − b12… a1n − b1na21 − b21a22 − b22… a2n − b2n & vellip; & vellip; & dtdot; & vellip; am1 − bm1am2 − bm2… amn − bmn
Матрицы разных размеров нельзя складывать или вычитать.
Пример:
Если А = 120-3 а также В = 31–12
A и плюс; B = 120-3 и плюс; 31-12 = 43-1-1
A − B = 120-3−31-12 = -211-5
Умножение матриц
Если A – матрица размера m × r, а B – матрица размера r × n, продукт A⁢B – матрица размера m × n, чья запись из строки i и столбца j является суммой произведений соответствующих записей из строка i таблицы A и столбец j таблицы B.
Запись A⁢Bij в строке i и столбце j таблицы A⁢B равно
A⁢Bij = ai1⁢b1j & plus; ai2⁢b2j & plus;… & plus; air⁢brj
Матрицы A и B могут быть умножены только в том случае, если количество столбцов в A совпадает с количеством строк в B.
Пример:
А = 1210-32 а также В = 3101-12300-211
A⁢B = 1210-32⁢3101-12300-211 = 13723-10-72
Элемент в строке 1 и столбце 1 матрицы A⁢B получается путем суммирования произведения соответствующих записей строки 1 таблицы A и столбца 1 таблицы B, т. Е.
A⁢B11 = 13 & plus; 2−1 & plus; 10 = 1
Элемент в строке 1 и столбце 2 таблицы A⁢B получается путем суммирования произведения соответствующих записей строки 1 таблицы A и столбца 2 таблицы B, т.е.е.
A⁢B12 = 11 и плюс; 22 и плюс; 1-2 = 3
Элемент в строке 2 и столбце 1 матрицы A⁢B получается суммированием произведения соответствующих записей строки 2 таблицы A и столбца 1 таблицы B, т. Е.
A⁢B21 = 03 & plus; −3−1 & plus; 20 = 3
И так далее

Инверсия матрицы
Обратной к квадратной матрице A является матрица A − 1 такая, что A⁢A − 1 = I
Пример:
Если A = -325-4, тогда А − 1 = -2-1-2,5-1,5
потому что A⁢A − 1 = -325-4⁢-2-1-2.5-1,5 = 1001
Один из способов получить обратную квадратную матрицу A – использовать следующую формулу
A − 1 = adj & ApplyFunction; Det & ApplyFunction; A
Если определитель матрицы равен 0, матрица не имеет обратной, и она называется сингулярной матрицей .
Другой способ найти обратную матрицу – это добавить единичную матрицу в правую часть матрицы, а затем использовать метод исключения Гаусса-Жордана, чтобы привести матрицу к уменьшенной форме эшелона строк.
Запутались, есть вопросы? У нас есть ответы. С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в этой области.
Джимми Си
См. Также: Метод исключения Гаусса-Джордана, одновременные линейные уравнения, геометрическое линейное преобразование

Матрицы и системы кодирования линейных уравнений
Рассмотрим систему трех уравнений с тремя переменными из предыдущего раздела: $$ M = \ begin {array} {cl} x +2 \, y +3 \, z & = 1 \\ 2 \, x +6 \, y +5 \, z & = -2 \\ 3 \, x +5 \, y +10 \, z & = 6 \ конец {массив} \; \ текст {.} $$ Если мы посмотрим только на коэффициенты переменных, мы можем сформировать матрицу $$ \ left (\ begin {array} {ccc} 1 & 2 & 3 \\ 2 & 6 & 5 \\ 3 & 5 & 10 \ end {array} \ right) \, \ text {,} $$ где в первой строке перечислены коэффициенты при $ x \, $, $ \, y \, $ и $ z $ из первого уравнение по порядку. Во второй строке перечислены коэффициенты из второго уравнения в том же порядке, и третье уравнение перечисляет коэффициенты третьего уравнения снова в том же порядке.
Мы можем отслеживать этот порядок, перечисляя его следующим образом: $$ \ left (\ begin {array} {ccc} 1 & 2 & 3 \\ 2 & 6 & 5 \\ 3 & 5 & 10 \ end {array} \ right) \ cdot \ left (\ begin {array} {c} x \\ y \\ z \ end {array} \ right) \; \ text {.} $$ Здесь это означает, что элементы в первом столбце матрицы являются коэффициентами при $ x \, $, записи во втором столбце – это коэффициенты при $ y \, $, а записи в третьем столбце – коэффициенты при $ z \; $.
Обычный способ интерпретировать это – сказать, что матрица $ M $ “умножается” на столбец $ \ displaystyle {\ left (\ begin {array} {c} x \\ y \\ z \ end {array} \ right) \,} $, где «умножение» осуществляется путем умножения записей первой строки друг за другом на записи столбца, а затем добавление. Затем повторяется для второй строки $ M \, $, затем, наконец, третий ряд. Таким образом, первая операция дает $$ (1 \ cdot x) + (2 \ cdot y) + (3 \ cdot z) = x +2 \, y +3 \, z \; \ text {.} $$ Вторая операция дает $$ (2 \ cdot x) + (6 \ cdot y) + (5 \ cdot z) = 2 \, x +6 \, y +5 \, z \; \ text {.} $$ Третья операция дает $$ (3 \ cdot x) + (5 \ cdot y) + (10 \ cdot z) = 3 \, x +5 \, y +10 \, z \; \ text {.} $$
Запишем результат этого умножения как $$ \ left (\ begin {array} {c} x +2 \, y +3 \, z \\ 2 \, x +6 \, y +5 \, z \\ 3 \, x +5 \, y + 10 \, z \ end {array} \ right) \;\текст{.} $$ То есть посредством этого «умножения» мы восстанавливаем правые части нашей исходной системы уравнений – чтобы.Приравнивая элементы этой матрицы $ 3 \ times 1 $ к значения, которые наша система уравнений придает каждому из трех выражений, мы имеем $$ \ left (\ begin {array} {ccc} 1 & 2 & 3 \\ 2 & 6 & 5 \\ 3 & 5 & 10 \ end {array} \ right) \ cdot \ left (\ begin {array} {c} x \\ y \\ z \ end {array} \ right) = \ left (\ begin {array} {c} x +2 \, y +3 \, z \\ 2 \, x +6 \, y +5 \, z \\ 3 \, x +5 \, y + 10 \, z \ end {array} \ right) = \ left (\ begin {array} {c} 1 \\ -2 \\ 6 \ end {array} \ right) \; \ text {.} $$
Это можно сделать с любой системой конечного числа линейных уравнений с конечным числом переменных. – то есть полиномиальные уравнения, в которых каждое уравнение имеет степень $ 1 \; $.

Два примера систем линейных уравнений в матричной форме
Рассмотрим систему уравнений $$ \ begin {array} {rl} 3 \, u -v + x & = 12 \\ u +5 \, v -2 \, w -x & = -8 \ end {array} \; \ text { .} $$
В матричной форме имеем $$ \ left (\ begin {array} {cccc} 3 & -1 & 0 & 1 \\ 1 & 5 & -2 & -1 \ end {array} \ right) \ cdot \ left (\ begin {array} {c} u \\ v \\ w \\ x \ end {array} \ right) = \ left (\ begin {array} {c} 12 \\ -8 \ end {array} \ right) \; \ text {.} $$
Рассмотрим систему уравнений $$ \ begin {array} {rl} 5 \, a -3 \, b & = 9 \\ a +2 \, b & = -5 \\ 7 \, a + b & = -1 \\ 4 \, a -5 \, b & = 14 \ конец {массив} \; \ текст {.} $$
В матричной форме имеем $$ \ left (\ begin {array} {cc} 5 & -3 \\ 1 & 2 \\ 7 & 1 \\ 4 & -5 \ end {array} \ right) \ cdot \ left (\ begin {array} {c} a \\ b \ end {array} \ right) = \ left (\ begin {array} {c} 9 \\ -5 \\ -1 \\ 14 \ end {array} \ right) \; \ text {.} $$
Матричный калькулятор
– примеры, онлайн-калькулятор матриц
Калькулятор матриц
вычисляет результирующую матрицу, когда определенные арифметические операции применяются к двум данным матрицам.В математике матрица представляет собой сеточную функцию или прямоугольный массив, в котором числа расположены в упорядоченных строках и столбцах.
Что такое Матричный калькулятор?
Matrix Calculator – это онлайн-инструмент, который помогает выполнять различные матричные операции с матрицами 2 x 2, то есть сложение матриц, вычитание матриц и умножение матриц. Матрица с одинаковым количеством строк и столбцов называется квадратной матрицей. Чтобы использовать этот калькулятор матриц , введите числа в поле ввода.
Матричный калькулятор
* Используйте только 3 цифры.
Как пользоваться калькулятором матриц?
Выполните следующие действия, чтобы найти окончательную матрицу с помощью онлайн-калькулятора матриц:
Шаг 1: Зайдите в онлайн-калькулятор матриц Cuemath.
Шаг 2: Введите значение матриц 2 x 2 в поля ввода и выберите операцию, которую необходимо выполнить, из раскрывающегося списка.
Шаг 3: Нажмите кнопку «Рассчитать» , чтобы найти результирующую матрицу.
Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.
Как работает матричный калькулятор?
Размеры матрицы обычно представлены как m x n. Здесь m обозначает количество строк, а n обозначает количество столбцов в этой матрице. Таким образом, матрица 2 x 2 будет иметь 2 строки и 2 столбца. Вычитание, сложение и умножение могут выполняться с матрицами.Ниже приведены методы вычисления результата этих арифметических операций:
1. Сложение матриц – Если две матрицы имеют одинаковое количество строк и столбцов, то можно выполнить сложение. Чтобы добавить две матрицы, элементы каждой строки и столбца одной матрицы добавляются к соответствующим элементам другой матрицы.
A + B = \ (\ begin {bmatrix} a_ {11} & a_ {12} \\ a_ {21} & a_ {22} \ end {bmatrix} + \ begin {bmatrix} b_ {11} & b_ { 12} \\ b_ {21} & b_ {22} \ end {bmatrix} = \ begin {bmatrix} a_ {11} + b_ {11} & a_ {12} + b_ {12} \\ a_ {21} + b_ {21} & a_ {22} + b_ {22} \ end {bmatrix} \)
2. Вычитание матриц – Подобно сложению, мы можем вычесть две матрицы, только если они имеют одинаковое количество строк и столбцов. Мы вычитаем элементы каждой строки и столбца одной матрицы из соответствующих элементов предыдущей матрицы.
A – B = \ (\ begin {bmatrix} a_ {11} & a_ {12} \\ a_ {21} & a_ {22} \ end {bmatrix} – \ begin {bmatrix} b_ {11} & b_ { 12} \\ b_ {21} & b_ {22} \ end {bmatrix} = \ begin {bmatrix} a_ {11} – b_ {11} & a_ {12} – b_ {12} \\ a_ {21} – b_ {21} & a_ {22} – b_ {22} \ end {bmatrix} \)
3. Умножение матриц – Для умножения двух матриц количество столбцов в первой матрице должно быть равно количеству строк во второй матрице. Умножение матриц можно произвести следующим образом:
A x B = \ (\ begin {bmatrix} a_ {11} & a_ {12} \\ a_ {21} & a_ {22} \ end {bmatrix} \ times \ begin {bmatrix} b_ {11} & b_ {12} \\ b_ {21} & b_ {22} \ end {bmatrix} = \ begin {bmatrix} a_ {11} b_ {11} + a_ {12} b_ {21} & a_ {11} b_ {12 } + a_ {12} b_ {22} \\ a_ {21} b_ {11} + a_ {22} b_ {21} & a_ {21} b_ {12} + a_ {22} b_ {22} \ end { bmatrix} \)
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов.С Cuemath находите решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Решенные примеры на матрицах
Пример 1: Добавьте две матрицы \ (\ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} \) & \ (\ begin {bmatrix} 2 & 1 \\ 4 & 2 \ end {bmatrix} \) и проверьте это с помощью матричного калькулятора.
Раствор:
Матрица 1 + Матрица 2 = \ (\ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} + \ begin {bmatrix} 2 & 1 \\ 4 & 2 \ end {bmatrix} = \ begin { bmatrix} 3 и 3 \\ 7 и 6 \ end {bmatrix} \)
Пример 2: Вычтите две матрицы \ (\ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} \) & \ (\ begin {bmatrix} 2 & 1 \\ 4 & 2 \ end {bmatrix} \) и проверьте это с помощью матричного калькулятора.
Раствор:
Матрица 1 – Матрица 2 = \ (\ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} + \ begin {bmatrix} 2 & 1 \\ 4 & 2 \ end {bmatrix} = \ begin { bmatrix} -1 & 1 \\ -1 & 2 \ end {bmatrix} \)
Точно так же вы можете попробовать калькулятор матриц, чтобы сложить, вычесть и умножить следующие матрицы:
Матрицы = \ (\ begin {bmatrix} 2 & 1 \\ 4 & 2 \ end {bmatrix} \) & \ (\ begin {bmatrix} 3 & 3 \\ 7 & 6 \ end {bmatrix} \)
Матрицы = \ (\ begin {bmatrix} 5 & 8 \\ 10 & 16 \ end {bmatrix} \) & \ (\ begin {bmatrix} 8 & 2 \\ 1 & 3 \ end {bmatrix} \)
☛ Математические калькуляторы:
Калькулятор научных обозначений
– Примеры, факты
Калькулятор в научном представлении помогает выразить заданное число в экспоненциальном представлении.Научные обозначения дают нам возможность легко выражать очень большие или очень маленькие числа. Он использует десятичную форму, а также степень 10 для представления числа.
Что такое калькулятор в научной системе обозначений?
Калькулятор научной нотации – это онлайн-инструмент, который помогает вычислить научную нотацию данного числа, используя десятичные дроби и степени 10. Если число очень велико, показатель степени (или степень 10) положительный. Однако, если у нас небольшое число, степень 10 отрицательна.Чтобы использовать этот калькулятор в экспоненциальном представлении , введите значение в поле ввода.
Калькулятор в научной системе обозначений
Как пользоваться калькулятором в научном представлении?
Выполните следующие действия, чтобы рассчитать научное представление с помощью онлайн-калькулятора научного представления:
Шаг 1: Зайдите в онлайн-калькулятор научной записи Cuemath.
Шаг 2: Введите число в поле ввода калькулятора научной записи.
Шаг 3: Нажмите кнопку «Рассчитать» , чтобы найти экспоненциальное представление.
Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.
Как работает калькулятор в научном представлении?
Очень большое или маленькое число может быть выражено с использованием научных обозначений. Однако для использования научных обозначений необходимо соблюдать некоторые правила.Они даются следующим образом:
Правило 1: Предположим, у нас есть большое число больше 1. Затем мы перемещаем десятичную точку влево, и степень 10 становится положительной.
Правило 2: Предположим, у нас есть небольшое число, меньшее 1. Десятичная точка смещена вправо, а степень 10 отрицательна.
Ниже приведены шаги для представления числа в экспоненциальном представлении.
Десятичную точку необходимо перемещать до тех пор, пока слева от точки не останется только одна ненулевая цифра.Это число обозначается буквой c.
Теперь посчитайте количество разрядов, на которое была перемещена десятичная точка. Это представлено буквой n.
Если десятичная дробь была перемещена влево, n будет положительным. Это означает, что число большое.
Если десятичная дробь была перемещена вправо, n будет отрицательным. Это показывает, что количество невелико.
Теперь подставьте эти значения в формулу c × 10 ⁿ, чтобы получить научную запись.
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов.С Cuemath находите решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Решенные примеры в научной нотации
Пример 1: Найдите экспоненциальное представление для 0,00748 и проверьте его с помощью калькулятора экспоненциального представления.
Раствор:
Переместите десятичную запятую вправо от 0,00748 до 3 разрядов.
с = 7,48
n = -3 (поскольку десятичная дробь была перемещена вправо, следовательно, n отрицательное)
По формуле: c × 10 ⁿ
Следовательно, научная запись для 0.00748 – это 7,48 × 10 ^-3
Пример 2: Найдите экспоненциальное представление для 7485 и проверьте его с помощью калькулятора экспоненциального представления.
Раствор:
Переместите десятичную запятую влево от 7485 до 3 разрядов.
с = 7,485
n = 3 (поскольку десятичная дробь была перемещена влево, следовательно, n положительно)
По формуле: c × 10 ⁿ
Следовательно, 7485 в научном обозначении – 7.485 × 10 ³
Точно так же вы можете попробовать калькулятор в научном представлении, чтобы найти его для следующего:
☛ Математические калькуляторы:
Калькулятор квадратного корня
– Онлайн-калькулятор квадратного корня
Калькулятор
вычисляет квадратный корень из заданного числа. Квадратный корень определяется как значение, которое можно умножить само на себя, чтобы получить исходное число. Квадрат числа x будет числом y, которое удовлетворяет уравнению y ² = x.
Что такое калькулятор квадратного корня?
Калькулятор квадратного корня
– это онлайн-инструмент, используемый для вычисления квадратного корня для заданного числа, которое является положительным целым числом. Квадратный корень из числа также может быть выражен числом в степени 1/2. Чтобы использовать этот калькулятор квадратного корня , введите значения в поле ввода.
Калькулятор квадратного корня
* Используйте только 3 цифры.
Как пользоваться калькулятором квадратного корня?
Выполните следующие простые шаги, чтобы вычислить квадратный корень с помощью онлайн-калькулятора квадратного корня:
Шаг 1 : Зайдите в онлайн-калькулятор квадратного корня Cuemath.
Шаг 2 : Введите положительное число в поле ввода калькулятора квадратного корня.
Шаг 3 : Нажмите кнопку «Рассчитать» , чтобы найти квадратный корень из числа.
Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.
Как работает калькулятор квадратного корня?
Квадратный корень числа – это число, которое при умножении на само себя дает произведение как исходное число.«√» – это символ, который используется для представления квадратного корня из числа. Есть четыре способа найти квадратный корень из числа. Они перечислены ниже:
Метод повторного вычитания.
Метод простой факторизации.
Метод оценки.
Метод длинного деления.
Первые три метода очень полезны для определения квадратного корня из полного квадрата. Положительное число, которое можно записать как произведение числа само на себя, можно определить как полный квадрат.Однако метод деления в длину более трудоемок, его можно использовать для нахождения квадратного корня из любого числа. Такое число не обязательно должно быть точным квадратом. Если на месте единицы числа стоит 2, 3, 7 или 8, то полного квадратного корня не существует. Однако, если на месте единицы числа стоит 1, 4, 5, 6 или 9, тогда такое число может иметь точный квадратный корень. Формула квадратного корня равна
.
y = √x
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов.С Cuemath находите решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Решенные примеры на квадратный корень
Пример 1: Найдите квадратный корень из 64 и проверьте его с помощью калькулятора квадратного корня.
Раствор:
Использование метода простой факторизации
64 = 2 × 2 × 2 × 2 × 2 × 2
64 = 2 ² × 2 ² × 2 ²
64 = (2 × 2 × 2) ²
64 = 8 ²
√64 = 8
Следовательно, 8 – это квадратный корень 64.
Пример 2: Найдите квадратный корень из 25 и проверьте его с помощью калькулятора квадратного корня.
Раствор:
Использование метода простой факторизации
25 = 5 × 5
25 = 5 ²
√25 = 5
Следовательно, 5 – это квадратный корень 25.
Аналогичным образом, чтобы найти квадратный корень из числа, вы можете попробовать калькулятор квадратного корня для следующего:
☛ Математические калькуляторы:
Университет Ватерлоо Math Online
Векторы в евклидовом пространстве
В этом модуле мы рассмотрим основные свойства векторов в евклидовом пространстве.Этот параметр позволит нам использовать геометрические интерпретации для введения важных концепций покрытия, линейной независимости и базисов.
Системы линейных уравнений
Мы уже видели много случаев в линейной алгебре, когда требуется решить m уравнений с n неизвестными – например, при определении, находится ли вектор в диапазоне набора векторов, при определении того, находится ли набор векторов линейно независимы, или при вычислении формулы для перекрестного произведения.Мы увидим, что есть много других случаев, когда нам нужно это сделать.
Кроме того, такие проблемы возникают не только в линейной алгебре, но и во многих других областях математики, естественных наук, экономики, бизнеса и так далее. В реальных ситуациях мы легко могли бы иметь тысячи уравнений и тысячи переменных. Таким образом, важно изучить и понять теорию, лежащую в основе этого, а не просто запомнить метод решения небольших систем.
Матрицы и линейные отображения
В этом модуле мы будем рассматривать матрицы как объекты, а не просто как инструмент для решения систем линейных уравнений.При этом мы придем к идее линейных отображений.
Векторные пространства
В этом модуле мы расширим многое из того, что мы сделали с векторами в R ⁿ , на общие векторные пространства.В частности, мы рассмотрим остов, линейную независимость, подпространства и базисы. Затем мы будем использовать эту теорию, чтобы точно определить размерность и посмотреть на координаты вектора относительно базиса.
Инверсии и детерминанты
В этом модуле мы рассмотрим свойства обратимых матриц, как определить, является ли матрица обратимой с помощью определителя, а также некоторые способы использования обратимых матриц и определителей.
Диагонализация
Теперь мы рассмотрим одну из самых важных и полезных частей линейной алгебры – диагонализацию. В этом модуле нам нужно будет использовать материалы из каждого модуля.
Калькулятор умножения матриц 3×3
Как найти произведение матриц $ n \ times n $?
Многие операции с матрицами имеют смысл только в том случае, если матрицы имеют подходящие размеры. Другими словами, они должны быть одинакового размера, с одинаковым количеством строк и одинаковым количеством столбцов.
Когда мы имеем дело с умножением матриц, матрицы $ A = (a_ {ij}) _ {m \ times p} $ с $ m $ строками, $ p $ столбцами и $ B = (b_ {ij}) _ {r \ times n} $ с $ r $ строками, $ n $ столбцов можно умножать тогда и только тогда, когда $ p = r $. Это означает, что количество столбцов первой матрицы $ A $ должно быть равно количеству строк второй матрицы $ B $. Результатом этой матрицы является новая матрица, которая имеет то же количество строк, что и первая матрица, $ A $, и такое же количество столбцов, как вторая матрица, $ B $.Итак, соответствующее произведение $ C = A \ cdot B $ представляет собой матрицу размера $ m \ times n $. Элементами $ c_ {ij} $ этой матрицы являются $$ c_ {ij} = a_ {i1} b_ {1j} + a_ {i2} b_ {2j} \ ldots + a_ {ip} b_ {pj} \ quad \ mbox {for} \; i = 1, \ ldots , m, \; j = 1, \ ldots, n. $$ Например, умножение матриц $ 3 \ times 3 $ определяется по следующей формуле $$ \ begin {align} & \ left ( \ begin {array} {ccc} а_ {11} и а_ {12} и а_ {13} \\ а_ {21} и а_ {22} и а_ {23} \\ а_ {31} и а_ {32} и а_ {33} \\ \ end {массив} \ справа) \ cdot \левый( \ begin {array} {ccc} b_ {11} & b_ {12} & b_ {13} \\ b_ {21} & b_ {22} & b_ {23} \\ b_ {31} & b_ {32} & b_ {33} \\ \ end {массив} \ right) \\ & = \ left (\ begin {array} {ccc} a_ {11} b_ {11} + a_ {12} b_ {21} + a_ {13} b_ {31} и a_ {11} b_ {12} + a_ {12} b_ {22} + a_ {13} b_ {32} & a_ {11} b_ {13} + a_ {12} b_ {23} + a_ {13} b_ {33} \\ a_ {21} b_ {11} + a_ {22} b_ {21} + a_ {23} b_ {31} и a_ {21} b_ {12} + a_ {22} b_ {22} + a_ {23} b_ { 32} & a_ {21} b_ {13} + a_ {22} b_ {23} + a_ {23} b_ {33} \\ a_ {31} b_ {11} + a_ {32} b_ {21} + a_ {33} b_ {31} и a_ {31} b_ {12} + a_ {32} b_ {22} + a_ {33} b_ { 32} & a_ {31} b_ {13} + a_ {32} b_ {23} + a_ {33} b_ {33} \\ \ end {array} \ right) \ end {align} $$
Свойства умножения матриц
Умножение матриц, вообще говоря, не коммутативно, $ AB \ not BA $.В некоторых случаях продукт $ AB $ существует, а продукт $ BA $ не существует. Оба произведения $ AB $ и $ BA $ определены тогда и только тогда, когда матрицы $ A $ и $ B $ являются квадратными матрицами одинакового размера.
Если $ A = (a_ {ij}) _ {mn} $, $ B = (b_ {ij}) _ {np} $ и $ C = (c_ {ij}) _ {pk} $, то матричное умножение ассоциативно, т. е. $$ A (BC) = (AB) C $$
Если $ A = (a_ {ij}) _ {mn} $, $ B = (b_ {ij}) _ {np} $, $ C = (c_ {ij}) _ {np} $ и $ D = (d_ {ij}) _ {pq} $, тогда умножение матриц дистрибутивно относительно сложения матриц, т.е.е. $$ \ begin {align} A (B + C) & = AB + AC \\ (B + C) D & = BD + CD \ end {align} $$
Если $ A_ {n \ times n} $ – квадратная матрица, существует единичная матрица $ I_ {n \ times n} $ такая, что $$ AI = IA = A $$
Например, найдем продукт $ AB $ для $$ A = \ left ( \ begin {array} {ccc} 10 и 20 и 10 \\ 4 и 5 и 6 \\ 2 и 3 и 5 \\ \ end {массив} \ right) \ quad \ mbox {и} \ quad B = \ left ( \ begin {array} {ccc} 3 и 2 и 4 \\ 3 и 3 и 9 \\ 4 и 4 и 2 \\ \ end {массив} \ right) $$ Используя формулу умножения матриц $ 3 \ times 3 $, произведение $ AB $ представляет собой матрицу $$ \ begin {align} C & = \ left ( \ begin {array} {ccc} 10 \ cdot3 + 20 \ cdot3 + 10 \ cdot4 & 10 \ cdot2 + 20 \ cdot3 + 10 \ cdot4 & 10 \ cdot4 + 20 \ cdot9 + 10 \ cdot2 \\ 4 \ cdot3 + 5 \ cdot3 + 6 \ cdot4 & 4 \ cdot2 + 5 \ cdot3 + 6 \ cdot4 & 4 \ cdot4 + 5 \ cdot9 + 6 \ cdot2 \\ 2 \ cdot3 + 3 \ cdot3 + 5 \ cdot4 & 2 \ cdot2 + 3 \ cdot3 + 5 \ cdot4 & 2 \ cdot4 + 3 \ cdot9 + 5 \ cdot2 \\ \ end {массив} \ вправо) \\ & = \ влево ( \ begin {array} {ccc} 130 и 120 и 240 \\ 51 и 47 и 73 \\ 35 и 33 и 45 \\ \ end {массив} \ right) \ end {align} $$
Работа умножения матриц с пошаговыми инструкциями показывает полное пошаговое вычисление для нахождение произведения $ AB $ двух $ 3 \ times 3 $ матриц $ A $ и $ B $ с использованием формулы умножения матриц.