Решение уравнений средствами MathCad – Mathcad (мат.задачи)
Решение одного уравнения
Для простейших уравнений вида f(x) = 0 решение в Mathcad находится с помощью функции root. root( f(х1, x2, …), х1, a, b ) Возвращает значение х1, принадлежащее отрезку [a, b], при котором выражение или функция f(х) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр. Аргументы: f(х1, x2, …) – функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения. х1 – – имя переменной, которая используется в выражении. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня. a, b – необязательны, если используются, то должны быть вещественными числами, причем a < b. Если после многих итераций Mathcad не находит подходящего приближения, то появится сообщение (отсутствует сходимость). Эта ошибка может быть вызвана следующими причинами:
Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x) = 0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее будет root сходиться. Рекомендации по использованию функции root:
.
Рисунок 11.
Нахождение корней полинома Для нахождения корней выражения, имеющего вид vnxn + … + v2x2 + v1x + v0, лучше использовать функцию polyroots, нежели root. Polyroots(v) Возвращает корни полинома степени n. Коэффициенты полинома находятся в векторе v длины n + 1. Возвращает вектор длины n, состоящий из корней полинома. Аргументы: v – вектор, содержащий коэффициенты полинома. Рисунок 11 иллюстрирует решение уравнений средствами Mathcad. |
Методы нахождения корней полинома в алгоритме пеленгования UCA Root Rare в пакете Mathcad
Библиографическое описание: Коробков, М. А. Методы нахождения корней полинома в алгоритме пеленгования UCA Root Rare в пакете Mathcad / М. А. Коробков. — Текст : непосредственный // Молодой ученый. — 2014. — № 14 (73). — С. 54-56. — URL: https://moluch.ru/archive/73/12348/ (дата обращения: 05. 11.2022).
11.2022).
Рассмотрены два метода нахождения корней полинома, получаемого при выполнении алгоритма редукции ранга для пеленгования источников радиоизлучения UCA‑Root‑Rare. Продемонстрированы результаты численного моделирования. Приведён соответствующий листинг программ в пакете Mathcad.
Ключевые слова: UCA‑Root‑Rare, полином, Mathcad, polyroots, roots.
Введение. Определённый подкласс быстрых корреляционных алгоритмов оценивания координат источников излучения (ИИ), требует для своего применения выполнения поиска корней полиномов, степень, а соответственно и число корней, которых, в некоторых случаях, может быть более . В таких случаях, некоторые встроенные корни функции Mathcad не позволяют выполнить поиск решений.
Цель работы — используя свойства полинома, получаемого при выполнении алгоритма UCA‑Root‑Rare (Rare‑полином) [1], найти решения Rare‑полинома при помощи встроенных функций пакета Mathcad для произвольной степени полинома.
1.Алгоритм UCA‑Root‑Rare. Вычисление координат ИИ, в данном случае азимута, при помощи алгоритма UCA‑Root‑Rare, выполняется путём нахождения корней следующего полиномиального уравнения:
где — определитель матрицы,
(2)
матрица размера ,
(3)
диагональная матрица размера , оператор диагонализации элементов,
. (4)
— это матрица отражений или антидиагональная единичная матрица:
. (5)
Используя (1)‑(3) и (5) матрица для будет иметь следующий вид:
. (6)
(6)
Матрица — это матрица собственных векторов, соответствующих подпространству шума корреляционной матрицы данных в пространстве лучей [2].
Исследование уравнения (1) показывает, что степень полинома будет , а следовательно уже для число корней Rare‑полинома будет равным .
2. Встроенные функции пакета Mathcad.
2.А. Функция root.
Функция root используется для решения одного уравнения с одним неизвестным. Обращение к функции: root(f(x)), где — выражение, равное нулю; — аргумент, варьируя который, система ищет значение, обращающее функцию в нуль. Функция и аргумент должны быть скалярами, то есть результат вычисления функции — число, а не вектор или матрица. Функция
Функция и аргумент должны быть скалярами, то есть результат вычисления функции — число, а не вектор или матрица. Функция
2.А. Функция polyroots
Для нахождения корней полинома можно использовать функцию polyroots(K), которая определяет все корни полинома одновременно. Здесь — вектор коэффициентов полинома, начиная со свободного члена. Нулевые коэффициенты опускать нельзя. Если полином имеет корней (с учетом кратности), то вектор включает в себя коэффициент. Начальное приближение вводить не надо. Следует обратить внимание, что вектор должен содержать от до коэффициентов.
3. Получение оценок. Вэтом разделе рассматриваются оценки, получаемые при решении уравнения (1) при помощи функций polyroots и root.
Получение оценок. Вэтом разделе рассматриваются оценки, получаемые при решении уравнения (1) при помощи функций polyroots и root.
3.А. Получение решений при помощи функции polyroots.
Как говорилось ранее, функция polyroots работает только с полиномами, степень которых не превышает . Накладываемое функцией polyroots ограничение позволяет применять её для решения уравнения (1) в случае, если параметр размера матрицы не превышает , что будет соответствовать корням. Для применение функции
а) б)
Рис.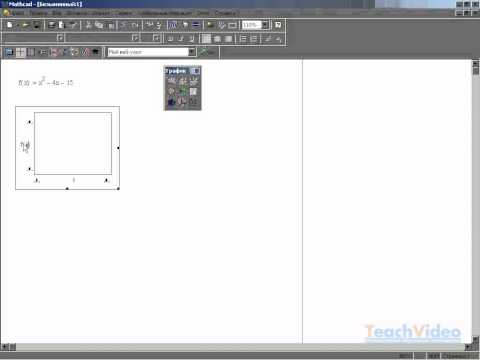
3.А. Получение решений при помощи функции root.
Исследование уравнения (1) показывает, что истинными оценками азимута будут являться только те корни, которые максимально близко расположены к единичной окружности. Следовательно, для поиска корней полинома степени большей, чем можно применить функцию root, ограничив область поиска значениями, лежащими на единичной окружности взяв их с некоторым шагом. Для комплексной плоскости этим значениям будет соответствовать некоторый угол , косинус которого будет соответствовать действительной части числа, а синус мнимой. Ниже приведён листинг программы в пакете Mathcad реализующий поиск корней Rare‑полинома произвольной степени при помощи функции
Листинг 1. Нахождение корней Rare‑полинома произвольной степени
где — это соответствующий полном уравнения (1). В случае, если заданы только коэффициенты полинома, то необходимо преобразовать функцию в выражение, используя, например, следующий листинг:
Листинг 2.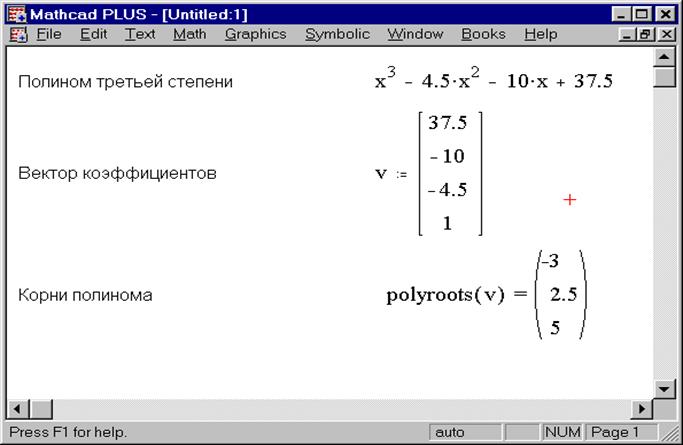 Преобразование коэффициентов полинома в выражение
Преобразование коэффициентов полинома в выражение
где — это переменная полинома, — вектор столбец из действительных частей коэффициентов полинома, — вектор столбец из мнимых частей полинома. После применения листинга 2 необходимо выполнить листинг 1. Соответствующее решение уравнения (1) показаны на рисунке 1 б).
Одним из свойств корней Rare‑полинома, является то, что все его корни обладают так называемым свойством взаимной сопряжённости, которое означает, что если — это корень полинома, то также будет корнем полинома [4]. Иными словами, корни симметричны относительно единичной окружности, что можно наблюдать на рисунке 1 а). Для корней вблизи центра окружности, их парные корни находятся за пределами области построения графика, и охватывают окружность с наружи таким же плотным кольцом, как и корни вблизи центра окружности.
Поиск корней по методу, приведённому в листингах 1 и 2, даёт только один корень. Учитывать корень нет необходимости, однако при желании это возможно сделать, просто выполнив операцию для каждого найденного решения.
Следует также обратить внимание, на то, что полученные решения по листингам 1 и 2 получаются несколько искажёнными, а кольцо вблизи центра окружности на рисунке 1 б) имеет деформацию, в отличие от аналогичного кольца на рисунке 1 а). Такое различие может быть вызвано как большой дискретностью шага поиска, так и отличием методов поиска решений функций polyroots иroot.
Литература:
1. Pesavento M., Böhme J. F. Direction of arrival estimation in uniform circular arrays composed of directional elements // Sensor Array and Multichannel Signal Processing Workshop. 2002. No 8. P. 503–507.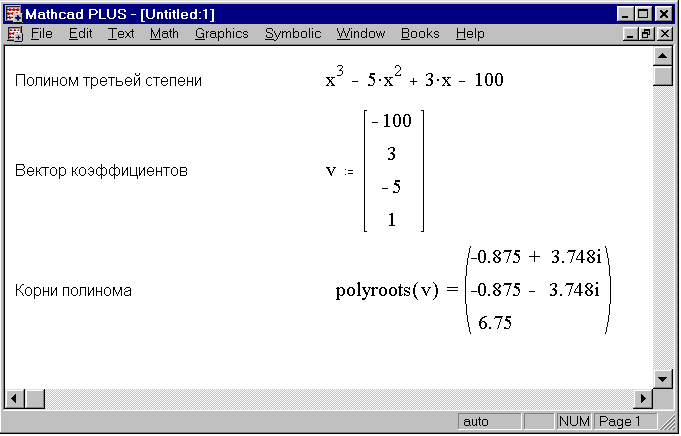
3. Макаров Е. Инженерные расчёты в Mathcad 15: Учебный курс — Спб.: Питер, 2011. — 400 с.: ил.
4. Li. H. Y., Xie J. L., He Z. S. A fast DOA estimation algorithm for uniform circular arrays in the presence of unknown mutual coupling // Progress In Electromagnetics Research C, 2011, Vol. 21, 257–271.
Основные термины (генерируются автоматически): UCA, функция, корень, полином, помощь функции, единичная окружность, начальное приближение, решение уравнения, корень полинома, центр окружности.
Три моих любимых рабочих листа — поиск корней в Mathcad
- 03.02.2017
Большинство расчетов, с которыми мы сталкиваемся каждый день, требуют от нас нахождения корней функции. Например, чтобы минимизировать функцию, нужно найти корень ее производной. Знаете ли вы, как Mathcad может помочь вам найти корни, которые вы ищете?
В сегодняшней статье я расскажу о трех рабочих листах, демонстрирующих некоторые встроенные функции Mathcad, предназначенные для поиска корней.
Функция
RootНа первом листе приведены примеры алгоритмического поиска корней с использованием функции Mathcad root . (Обратите внимание, что эта функция решает только одно уравнение с одним неизвестным.) Вы можете вызвать корневую функцию с двумя или четырьмя аргументами, в зависимости от того, хотите ли вы предоставить значение предположения для корня перед вызовом функции или значения в квадратных скобках для root внутри вызова функции.
Для функций с комплексными корнями можно также использовать комплексные приближенные значения, чтобы найти комплексный корень функции.
Пример использования функции root
Функция
Polyroots удобнее находить все корни сразу, используя функцию polyroots . Эта функция возвращает вектор, содержащий корни многочлена. Входными данными для поликорней является один вектор действительных или комплексных чисел, содержащий коэффициенты многочлена. Коэффициенты перечислены от низшей степени к высшей, включая все 0 коэффициентов.
Коэффициенты перечислены от низшей степени к высшей, включая все 0 коэффициентов.
Пример определения вектора коэффициентов и нахождения вектора корней.
Если корни многочлена неразличимы, вы можете прочитать раздел «Повторяющиеся и парные корни» на листе, чтобы увидеть, как Mathcad справляется с этой ситуацией.
Поиск символьного корня
Я уверен, вы знаете, что Mathcad имеет два типа математических машин: числовые и символьные. Вы можете использовать символьный процессор в Mathcad для символьного поиска корней. Это может быть более точным, чем численное нахождение корня, а также может дать больше информации о решении.
Простой пример поиска символьного корня
Вы можете присвоить символьное решение переменной или функции, сделав его доступным для использования на рабочем листе. Когда существует более одного решения, например, в приведенном выше квадратном уравнении, решение хранится в векторе, где каждый элемент представляет собой одну часть общего решения.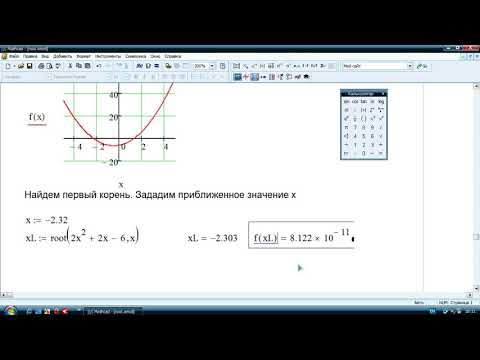
Также обратите внимание, что, поскольку выражение содержит несколько переменных, вы должны ввести запятую после «решить», а затем переменную, x , для которого вы решаете.
Вы можете найти эти три рабочих листа и множество других подробных примеров в коллекции рабочих листов PTC Mathcad — Education в интернет-магазине PTC.
Решение уравнений » MathCadHelp.com » Номер 1 в заданиях MathCad
В этой главе описывается, как решать уравнения, начиная от одного уравнения
с одним неизвестным и заканчивая системами из пятидесяти уравнений с пятьюдесятью неизвестными. Описанные здесь методы генерируют числовые решения. «Символическое вычисление» описывает различные методы символического решения уравнений.
Следующие секции составляют
Решение одного уравнения
Как использовать функцию корня Mathcad для численного решения одного уравнения с одним неизвестным.
Системы уравнений
Как использовать «блоки решения» для решения систем из n уравнений с n неизвестными.
Эффективное использование решателя
Примеры эффективного решения систем уравнений для различных значений параметра.
Решение одного уравнения
Чтобы решить одно уравнение с одним неизвестным, используйте функцию корня. Эта функция принимает выражение и одну из переменных выражения. Затем он изменяет эту переменную до тех пор, пока выражение не станет равным нулю. После этого функция возвращает значение, при котором выражение становится равным нулю.
Возвращает значение z, при котором выражение или функцияj(z) равно 0. Оба аргумента этой функции должны быть скалярными. Функция возвращает скаляр
Первый аргумент — это либо функция, определенная в другом месте листа, либо выражение. Он должен возвращать скалярное значение.
Второй аргумент — это имя переменной, которое появляется в выражении. Именно эту переменную Mathcad будет изменять, чтобы выражение стремилось к нулю. Вы должны присвоить номер этой переменной, прежде чем использовать корневую функцию. Mathcad использует это как начальное значение при поиске решения.
Mathcad использует это как начальное значение при поиске решения.
Например, чтобы определить a как решение уравнения <Вставьте уравнение здесь>, выполните следующие действия: 9.0007
• Определите предполагаемое значение для x. Введите x: 3. Ваш выбор значения приближения определяет, какой корень Mathcad возвращает. используйте корневую функцию.
• Для выражений с несколькими корнями, например, x2 – 1 = 0, ваше предполагаемое значение определяет, какой корень будет возвращен Mathcad. На рис. 15-1 показан пример, в котором корневая функция возвращает несколько разных значений, каждое из которых зависит от начального предполагаемого значения.
• Mathcad найдет комплексные корни так же, как и действительные корни. Чтобы найти сложный корень, вы должны начать с комплексного значения для начального предположения.
• Решение уравнения формы f(x) = g(x) эквивалентно использованию корневой функции следующим образом:
решение уравнения
Корневая функция может решить только одно уравнение с одним неизвестным. Чтобы решить несколько уравнений одновременно, используйте технику, описанную в следующем разделе “Системы уравнений”. Чтобы решить уравнение с помощью символов или найти точный числовой ответ с точки зрения элементарных функций, выберите “Решить для переменной” в меню “Символические” или используйте ключевое слово решения. См. главу 17, «Вычисление символов 9».0007
Чтобы решить несколько уравнений одновременно, используйте технику, описанную в следующем разделе “Системы уравнений”. Чтобы решить уравнение с помощью символов или найти точный числовой ответ с точки зрения элементарных функций, выберите “Решить для переменной” в меню “Символические” или используйте ключевое слово решения. См. главу 17, «Вычисление символов 9».0007
Использование графика и корневой функции для поиска корней выражения.
Что делать, если функция корня не сходится
Mathcad вычисляет функцию корня, используя метод секущих. Предположительное значение, которое вы указываете для x, становится отправной точкой для последовательных приближений к корневому значению. Когда величина j(x), оцененная в предложенном корне, меньше значения предопределенной переменной TOL, корневая функция возвращает результат.
Если после многих приближений Mathcad все еще не может найти приемлемый ответ, он помечает корневую функцию сообщением об ошибке, указывающим на ее неспособность сходиться к результату. Эта ошибка может быть вызвана любой из следующих причин:
Эта ошибка может быть вызвана любой из следующих причин:
• Выражение не имеет корней.
• Корни выражения далеки от первоначального предположения.
• Выражение имеет локальные максимумы или минимумы между начальным предположением и корнями.
• Выражение имеет разрывы между начальным предположением и корнями.
• Выражение имеет комплексный корень, но первоначальная догадка была реальной (или наоборот).
Чтобы найти причину ошибки, попробуйте построить выражение. Это поможет определить, пересекает ли выражение ось X, и если да, то примерно, где это происходит. Как правило, чем ближе ваше первоначальное предположение к точке пересечения выражения с осью X, тем быстрее корневая функция будет сходиться к приемлемому результату.
Советы по использованию корневой функции
Вот несколько советов по максимальному использованию корневой функции:
• Чтобы изменить точность корневой функции, измените значение встроенной переменной TaL. Если вы увеличите TaL, корневая функция будет сходиться быстрее, но ответ будет менее точным. Если вы уменьшите TaL, корневая функция будет сходиться медленнее, но ответ будет более точным. Чтобы изменить TaL в указанной точке рабочего листа, включите определение, например TOL := 0,01 . Чтобы изменить TaL для всего листа, выберите «Параметры» в меню «Математика», перейдите на вкладку «Встроенные переменные» и замените число в текстовом поле рядом с «TaL». После того, как вы нажмете «ОК», выберите «Рассчитать рабочий лист» в меню «Математика», чтобы обновить весь рабочий лист, используя новое значение TaL.
Если вы увеличите TaL, корневая функция будет сходиться быстрее, но ответ будет менее точным. Если вы уменьшите TaL, корневая функция будет сходиться медленнее, но ответ будет более точным. Чтобы изменить TaL в указанной точке рабочего листа, включите определение, например TOL := 0,01 . Чтобы изменить TaL для всего листа, выберите «Параметры» в меню «Математика», перейдите на вкладку «Встроенные переменные» и замените число в текстовом поле рядом с «TaL». После того, как вы нажмете «ОК», выберите «Рассчитать рабочий лист» в меню «Математика», чтобы обновить весь рабочий лист, используя новое значение TaL.
• Если выражение имеет несколько корней, попробуйте найти их с разными значениями предположений. Построение графика функции – это хороший способ определить, сколько существует корней, где они находятся и какие первоначальные догадки могут их найти. На рис. 15-1 показан пример этого. Если два корня расположены близко друг к другу, возможно, вам придется сократить TaL, чтобы различить
между ними.
• Если fix) имеет небольшой наклон около корня, то root(f(x), x) может сходиться к значению r, которое относительно далеко от фактического корня. В таких случаях, даже если It( r)1 < TO L , r может быть далеко от точки, где f( r) = O. Чтобы найти более точный корень, уменьшите значение TaL. Или попробуйте найти root(g(x),x), где
Советы по использованию корневой функции
• Для выраженияfix) с известным корнем a, нахождение дополнительных корней fix) эквивалентно поиску корней hex) = (f(x))/(x – a ). Разделение известных корней подобным образом . эффективен для разрешения двух корней, которые могут быть расположены близко друг к другу. Часто проще искать корни шестнадцатеричного числа, как определено здесь, чем пытаться найти другие корни для исправления) с различными предположениями
Многократное решение уравнения
Предположим, вы хотите решить уравнение много раз, варьируя один из параметров в уравнении. Например, предположим, что вы хотите решить уравнение eX = a · x2 для нескольких различных значений параметра a. Самый простой способ сделать это — определить функцию:
Самый простой способ сделать это — определить функцию:
Повторное решение уравнения
Чтобы решить уравнение для определенного значения a, укажите как a, так и предполагаемое значение x в качестве аргументов для этой функции. Затем оцените помазание, набрав f (a, x) =.
На рис. 15-2 показан пример использования такой функции для поиска нескольких решений корневой функции. Обратите внимание, что поскольку предполагаемое значение x передается в саму функцию, нет необходимости определять его где-либо еще на листе.
Определение пользовательской функции с корневой функцией.
Нахождение корней многочлена
Чтобы найти корни выражения, имеющего форму:
Нахождение корней многочлена
, вы можете использовать функцию поликорней, а не функцию корня. В отличие от корня, для поликорня не требуется приблизительное значение. Более того, многокорень возвращает сразу все корни, действительные или сложные. На Рисунке 15-3 и Рисунке 15-4 показаны примеры.



 Другой вариант заключается в замене уравнения f(x) = 0 на g(x) = 0
Другой вариант заключается в замене уравнения f(x) = 0 на g(x) = 0 В отличие от функции root, функция polyroots не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные.
В отличие от функции root, функция polyroots не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные.