1.3.5. Программирование MathCAD 12 руководство
Основными инструментами работы в Mathcad являются математические выражения, переменные и функции. Нередко записать формулу, использующую ту или иную внутреннюю логику (например, возвращение различных значений в зависимости от условий), в одну строку не удается. Назначение программных модулей как раз и заключается в определении выражений, переменных и функций в несколько строк, часто с применением специфических программных операторов.
Принцип программирования в Mathcad
При помощи элементов программирования можно определять переменные и функции (как показано в листинге 1.19).
Листинг 1.19. Функция условия, определенная с помощью программы
Традиционное программирование, упрощенный вариант которого применен в Mathcad и осуществляется при помощи панели инструментов
Programming (Программирование), имеет ряд существенных преимуществ, которые в ряде случаев делают документ более простым и читаемым:
- возможность применения циклов и условных операторов;
- простота создания функций и переменных, требующих нескольких простых шагов;
- возможность создания функций, содержащих закрытый для остального документа код, включая преимущества использования локальных переменных и обработку исключительных ситуаций.

Как видно из листинга 1.19, программный модуль обозначается в Mathcad вертикальной чертой, справа от которой последовательно записываются операторы языка программирования. Чтобы начать создание программного модуля, следует (в случае листинга 1.19 после символа присваивания) нажать на панели
Programming (Программирование) кнопку Add One (Добавить линию). Затем, если приблизительно известно, сколько строк кода будет содержать программа, можно создать нужное количество линий повторными нажатиями кнопки
Add Line (Добавить линию) (рис. 1.18).
Рис. 1.18. Начало создания программного модуля
В появившиеся местозаполнители введите желаемый программный код, используя программные операторы. В рассматриваемом примере в каждый местозаполнитель вводится строка, например, в средний — “positive” (рис. 1.19). Затем нажимается кнопка
If (Если) на панели Programming (Программирование) и в возникший местозаполнитель вводится выражение
х>0. После того как программный модуль полностью определен, и ни один местозаполнитель не остался пустым, функция может использоваться обычным образом, как в численных, так и в символьных расчетах.
ВНИМАНИЕ!
Не вводите с клавиатуры имена программных операторов. Для их вставки можно применять лишь сочетания клавиш, которые приведены в тексте всплывающей подсказки (рис. 1.18 и 1.19).
Рис. 1.19. Вставка программного оператора
Добавление строк программного кода
Вставить строку программного кода в уже созданную программу можно в любой момент с помощью той же самой кнопки
Add Line (Добавить линию). Для этого следует предварительно поместить на нужное место внутри программного модуля линии ввода. Например, расположение линии ввода на строке, показанной на рис. 1.18, приведет к появлению новой линии с местозаполнителем перед этой строкой. Если передвинуть вертикальную линию ввода из начала строки (как это показано на рис. 1.20) в ее конец, то новая линия появится после строки. Если выделить строку не целиком, а лишь некоторую ее часть (рис. 1.20), то это повлияет на положение в программе новой строки кода (результат нажатия кнопки
Add Line показан на рис.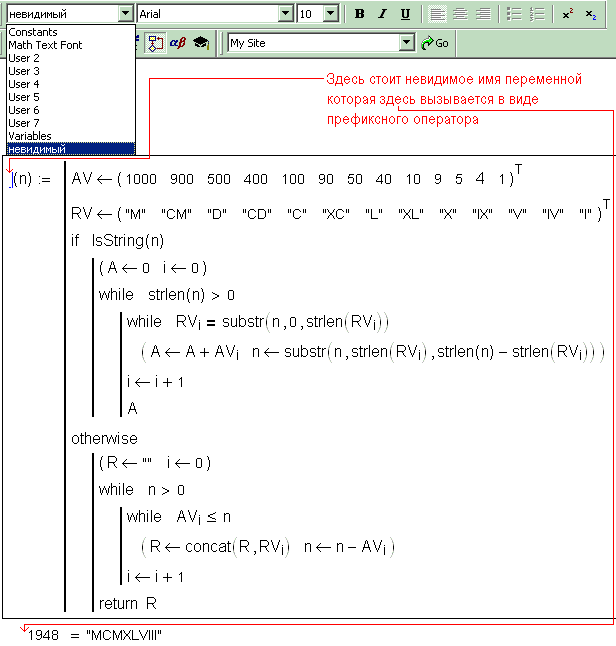
СОВЕТ
Не забывайте, что для желаемого размещения линий ввода внутри формулы можно использовать не только мышь и клавиши со стрелками, но и пробел. С помощью последовательных нажатий пробела линии ввода “захватывают” разные части формулы.
Рис. 1.20. Положение линий ввода влияет на положение создаваемой строки программы
Зачем может потребоваться вставка новой линии в положение, показанное на рис. 1.21? Новая вертикальная черта с двумя линиями выделяет фрагмент программы, который относится к условию х>0, находящемуся в его заголовке. Пример возможного дальнейшего программирования показан в листинге 1.20.
Рис. 1.21. Результат вставки новой линии в программу (из положения рис. 1.20)
Листинг 1.20. Пример усовершенствования программы
В режиме выполнения программы, а это происходит при любой попытке вычислить f (х), выполняется последовательно каждая строка кода. Например, в предпоследней строке листинга 1.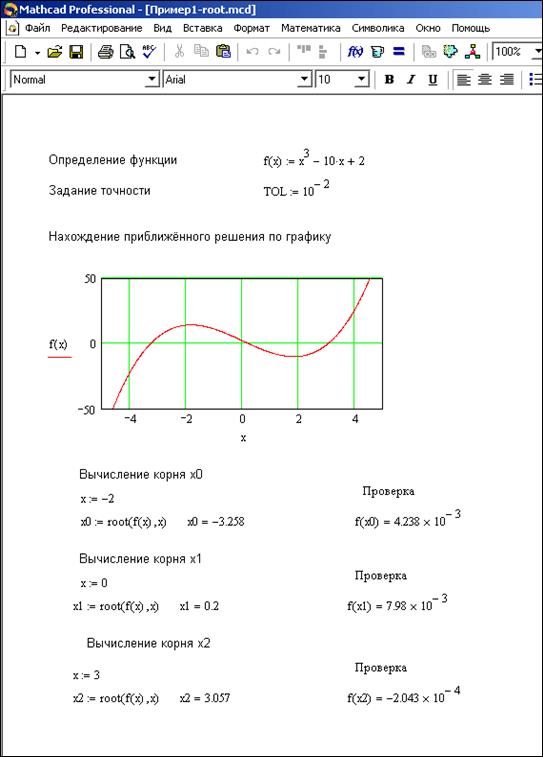
1. Поскольку х=1, то условие х<0 не выполнено, и в первой строке ничего не происходит.
2. Условие второй строки х>о выполнено, поэтому выполняются обе следующие строки, объединенные короткой вертикальной чертой в общий фрагмент.
3. Функции f(x) присваивается значение f (x)=”positive”.
4. Условие х>1000 не выполнено, поэтому значение “big positive” не присваивается f (х), она так и остается равной строке “positive”.
5. Последняя строка не выполняется, т. к. одно из условий (х>0) оказалось истинным, и оператор otherwise (т. е., “иначе”) не понадобился.
Таким образом, основной принцип создания программных модулей заключается в правильном расположении строк кода. Ориентироваться в их действии довольно легко, т. к. фрагменты кода одного уровня сгруппированы в программе с помощью вертикальных черт.
Локальное присваивание (<—)
Язык программирования Mathcad не был бы эффективным, если бы не позволял создавать внутри программных модулей локальные переменные, которые “не видны” извне, из других частей документа.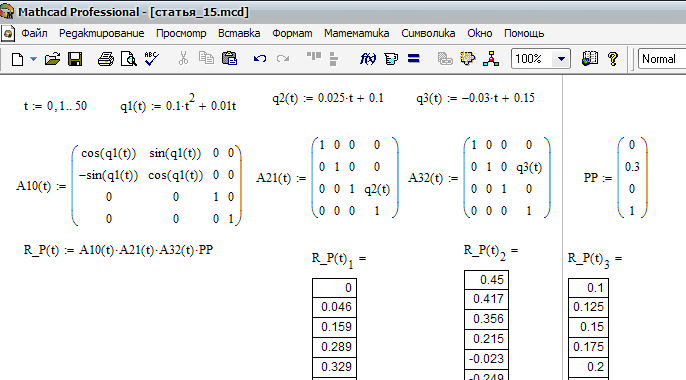
ВНИМАНИЕ!
Ни оператор присваивания :=, ни оператор вывода = в пределах программ применять не разрешается.
В Mathcad 12 переменным, которые впервые появляются в программных модулях, по умолчанию присваивается значение 0. В прежних версиях программы использование переменных в программах без предварительного присваивания им значений приводило к генерации ошибки (как в расчетах на рабочей области документов Mathcad).
Локальное присваивание иллюстрируется листингом 1.21. Переменная z существует только внутри программы, выделенной вертикальной чертой. Из других мест документа получить ее значение невозможно. На этом же листинге вы видите пример применения оператора цикла for.
Листинг 1.21. Локальное присваивание в программе
Лекция№10 – Программирование в системе MathCAD
Функции являются важнейшим инструментом математики.
В разделе 1.9 технология работы с пользовательскими функциями, которые можно описать с помощью одного выражения.
Язык программирования MathCAD содержит все элементы языка высокого уровня, необходимые для математических расчетов. Будучи дополненным сотнями встроенных функций и операторов системы, возможностями численного и символьного расчета различных величин, он по эффективности не уступает профессиональным системам программирования. Кроме того, у него есть одно очень крупное преимущество: язык программирования MathCAD предельно прост (а по изящности и наглядности в оформлении алгоритмов вообще не имеет аналогов).
Как правило, при использовании функций, встроенных в систему MathCAD, пользователи не задумываются о том, на основании каких методов и решений достигается цель, поставленная перед функцией.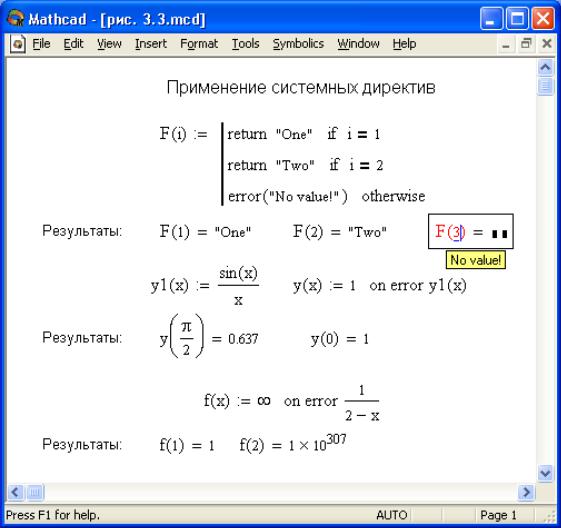
При программировании пользовательских функций будем придерживаться «созвучного» порядка, т.е. идти от спецификации к программированию.
4.1. Спецификации функций
Спецификация функции состоит из ее заголовка и описания назначения – выходного значения или результата работы функции. Для примера можно обратиться к мастеру функций и более внимательно посмотреть на предоставляемые им для его функций описания. На рис. 4.1 открыта страница со спецификацией функции
Рис. 4.1. Спецификация функции, предоставляемая мастером функций
Заголовок содержит имя функции (rnorm) и список формальных параметров (m, mu, sigma). Каждая пользовательская программа-функция MathCAD должна иметь оригинальное имя, используя которое будет осуществляться обращение к этой программе-функции. Через это же имя (и только через это имя ) «возвращается» в рабочий документ результат выполнения программы-функции.
Каждая пользовательская программа-функция MathCAD должна иметь оригинальное имя, используя которое будет осуществляться обращение к этой программе-функции. Через это же имя (и только через это имя ) «возвращается» в рабочий документ результат выполнения программы-функции.
Через формальные параметры «внутрь» программы-функции «передаются» данные, необходимые для выполнения вычислений внутри программы. В качестве формальных параметров могут использоваться имена простых переменных, массивов и функций. Формальные параметры отделяются друг от друга запятой.
При описании назначения функции необходимо сказать, что возвращает функция в качестве своего результата (в описываемой функции rnorm возвращает вектор нормально распределенных случайных значений). При этомобязательно нужно пояснить роль каждого из формальных параметров, перечисленных в заголовке (m – количество значений, mu – среднее значение, sigma – стандартное отклонение).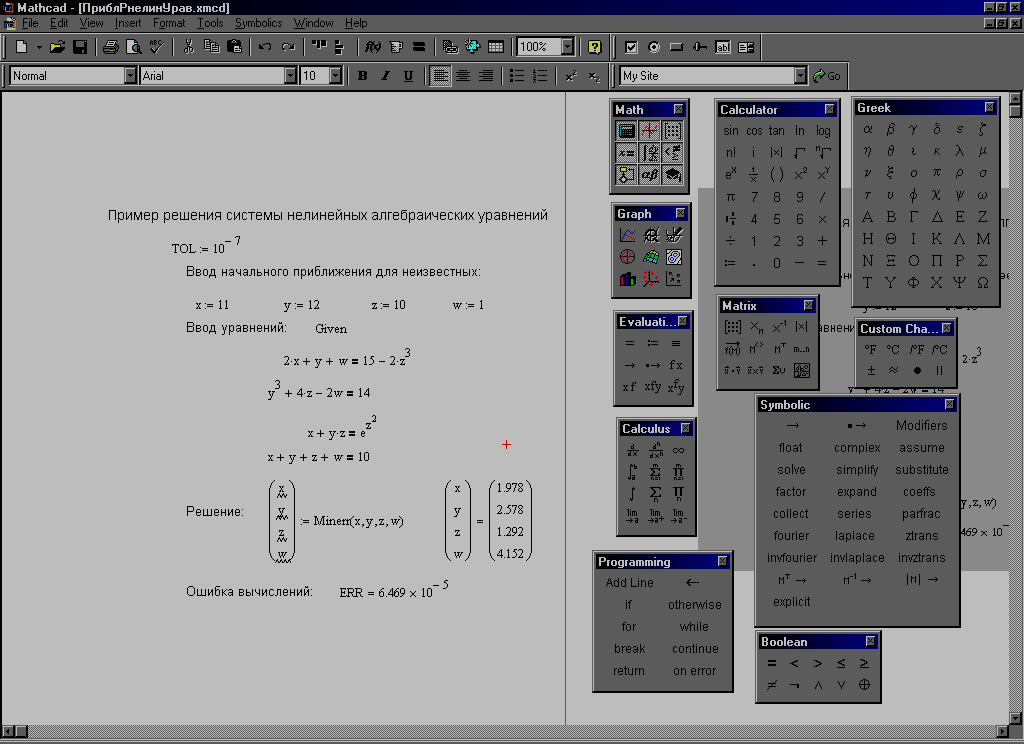 Желательно сказать об ограничениях, т.е. невозможность расчета при … каких-либо условиях.
Желательно сказать об ограничениях, т.е. невозможность расчета при … каких-либо условиях.
Для написания программ-функций в системе MathCAD предусмотрена специальная панель программироваия –Programming (Программирование), содержащая все операторы и элементы языка. Общий вид панели Programmingпредставлен на рис. 4.2. Операторы в программу вставляются только с помощью кнопок этой панели.
Назначение основных команд, представленных на панели:
Add Line – добавление новой строки в программу или создание заготовки программы из двух строк, если программы еще не существует; ← – присвоение значения локальной переменной; if – условный оператор. otherwise – используется сразу после оператора if и позволяет выполнить определенные действия при невыполнении условия в операторе if ; for – оператор создания цикла со счетчиком; while – оператор создания цикла, выполнение которого продолжается до тех пор, пока выполняется указанное условие. continue – продолжить вычисления в цикле; break – прервать вычисления в цикле; return – оператор возврата; on error – оператор перехода при возникновении ошибки.
|
Рис.4.2. Вид панели инструментов Programming (Программирование)
Чтобы написать программу, прежде всего для нее должен быть создан специальный, обособленный от остального документа, программный блок-тело функции.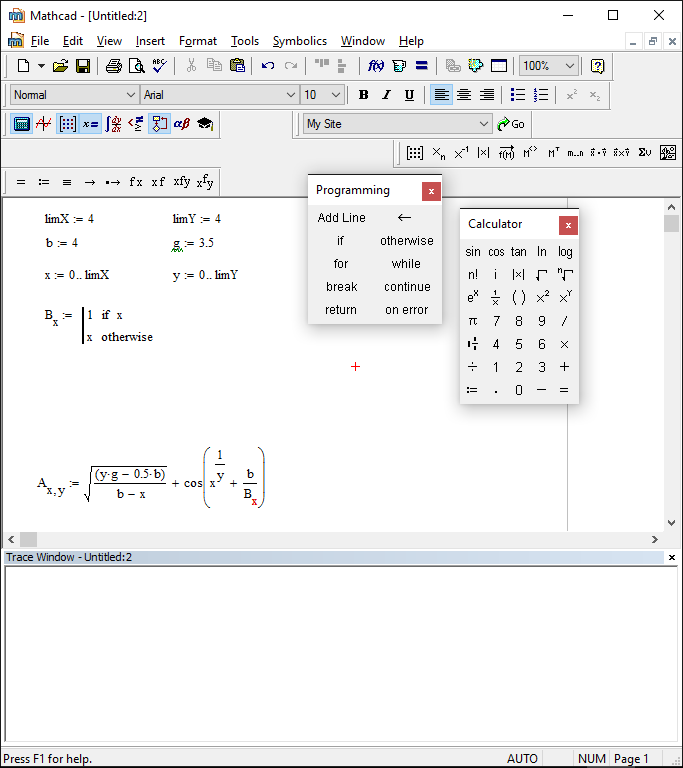 Выглядит он как черная вертикальная линия с маркерами, в которые заносятся те или иные выражения и операторы алгоритма. Чтобы построить единичный элемент программного блока, нажмите кнопку команды Add Line (Добавить линию) панели Programming (Программирование).
Выглядит он как черная вертикальная линия с маркерами, в которые заносятся те или иные выражения и операторы алгоритма. Чтобы построить единичный элемент программного блока, нажмите кнопку команды Add Line (Добавить линию) панели Programming (Программирование).
Присваивание значений в программах имеет ряд особенностей. Важнейшим из них является то, что присвоение величин используемым алгоритмом функциям и переменным может быть произведено как в самой программе, так и выше нее. Данные два подхода весьма существенно разнятся:
Если значение переменной или функции присваивается в программе посредством оператора «←» , то такая переменная или функция будет являться локальной. То есть она будет видимой только в рамках программы. Как-то повлиять на объекты вне программы она не сможет (равно, как извне к ней нельзя будет получить доступ).
Если переменная или функция задается выше программы с помощью оператора «:=», то она в программе будет обладать глобальной видимостью.
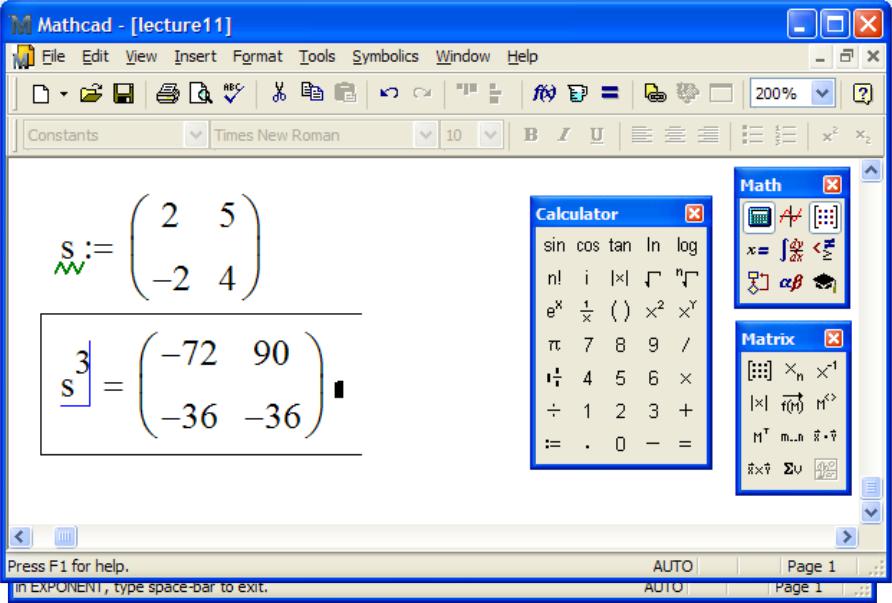 То есть такая переменная или функция будет доступна любому нижележащему объекту, в том числе и коду программ. Однако программа может только прочитать значение глобальной переменной или вызвать глобальную функцию. Изменить каким-либо образом значение глобальной переменной или функции программа не может. Это очень важно учитывать при написании алгоритмов.
То есть такая переменная или функция будет доступна любому нижележащему объекту, в том числе и коду программ. Однако программа может только прочитать значение глобальной переменной или вызвать глобальную функцию. Изменить каким-либо образом значение глобальной переменной или функции программа не может. Это очень важно учитывать при написании алгоритмов.Если программа должна осуществлять какую-то модификацию объекта, то результат своей работы она должнавозвращать.
Все программы составляемые в пакете MathCAD с точки зрения любого языуа программирования (например, Turbo Pascal) представляют собой подпрограммы – функции, которые могут возвращать в качестве результата число, вектор или матрицу.
Перед тем как использовать программу-функцию нужно ее описать. Описание программы-функции размещается в рабочем документе перед вызовом программы-функции и включает в себя заголовок функции и тело функции, соединенные в единое целое с помощью операции присваивания («:=»).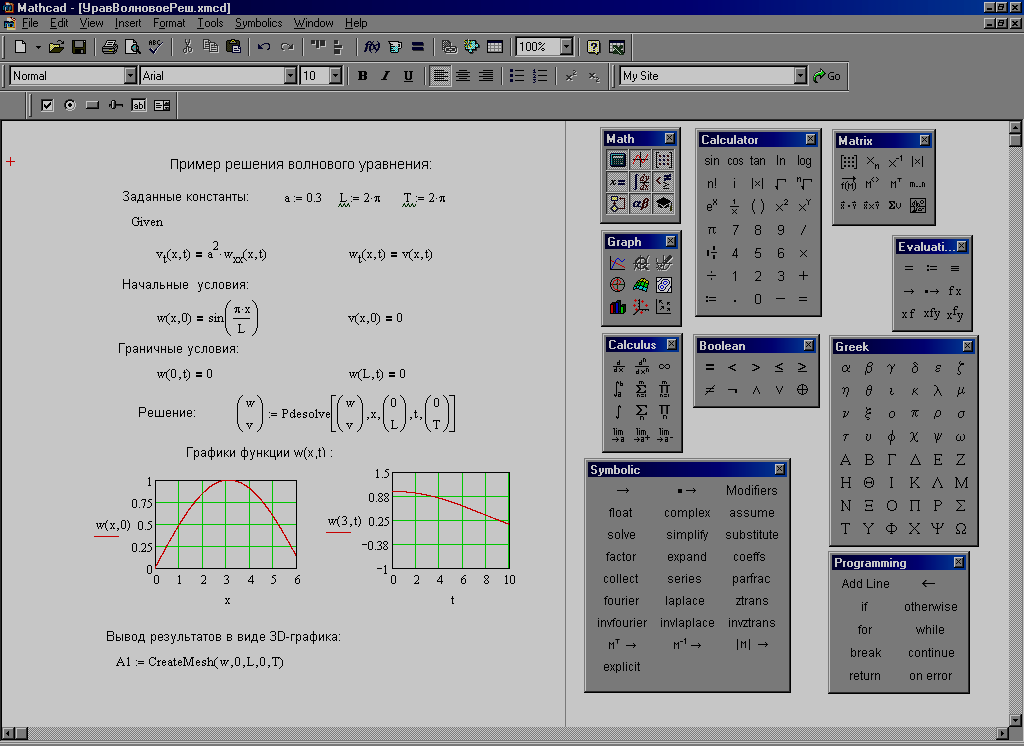
Заметим, что если программа используется для вычисления одного значения, то в своем заголовке она не содержит списка формальных параметров и называется программой-скаляром.
Программа-функция может не иметь формальных параметров и тогда, когда данные передаются через имена переменных, определенных выше описания программы-функции. Эти переменные будут являться глобальными для данной функции.
Технология создания программы-функции в рабочем документе MathCAD состоит из следующих шагов:
Ввести заголовок функции.
Ввести знак присваивания «:=».
Выполнить команду Add line, расположенную на панели Programming (Программирование). Появившейся на экране шаблон с вертикальной чертой и полями для ввода операторов будут составлять заготовку для тела программы-функции.

Вписать операторы в шаблон-заготовку. Тело программы-функции может включать любое число операторов: локальных операторов присваивания, условных операторов и операторов цикла, а также вызов других программ-функций.
Самое нижнее поле всегда предназначено для определения возвращаемого программой значения.
Пример 1. Требуется подготовить описание функции и вычислить значения этой функции приx = 4.15 и g = 1.854.
Решение. Заметим, что при вычислении y можно обойтись без описания и использования пользовательской функции и тем более без программирования, как это показано на рис. 8.4, a. Использование функции следует из требования к задаче для простоты изложения. Для нахождения значения функции «внутрь» программы-функции следует передать значения x и g, необходимые для выполнения вычислений внутри программы.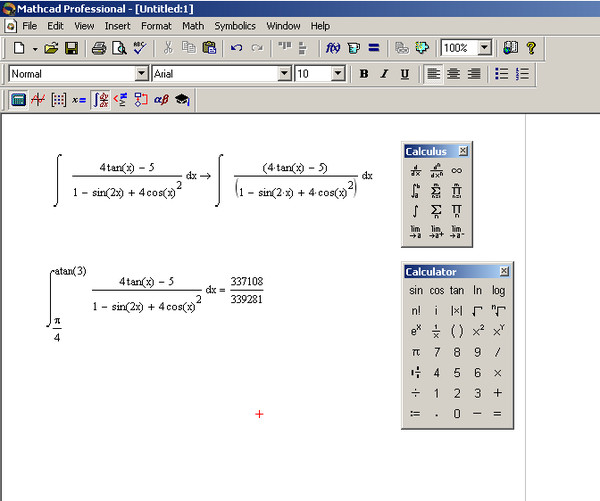 Поэтому переменные x и g следует включить в список формальных параметров заголовка создаваемой функции. Назовем эту функцию – y. Тогда подготовка описания функции, и ее выполнение в соответствии с описанной технологией могут быть выполнены, как это представлено на рис. 8.3.
Поэтому переменные x и g следует включить в список формальных параметров заголовка создаваемой функции. Назовем эту функцию – y. Тогда подготовка описания функции, и ее выполнение в соответствии с описанной технологией могут быть выполнены, как это представлено на рис. 8.3.
(1-2) |
(3) | (4-5)
|
(6) |
Рис.4.3. Пошаговое создание и выполнение программы-функции
В данном примере введена вспомогательная локальная переменная t для вычисления значения функции. И эта переменная расположена в последней строчке программного блока. В пункте (6) приведена операция вычисления функции для фактических значений. На рис. 4.4, b, c приведены другие варианты решения поставленной задачи.
И эта переменная расположена в последней строчке программного блока. В пункте (6) приведена операция вычисления функции для фактических значений. На рис. 4.4, b, c приведены другие варианты решения поставленной задачи.
Рис. 4.4. Демонстрация элементов программирования простых выражений
В примере, представленном на рис. 4.4, в первой колонке a для вычисления значения используется базовый набор средств без элементов программирования. Во второйb и третьей c колонках производятся точно такие же вычисления, но с использованием элементов программирования. Обе программы (b и c) можно считать эквивалентными, так как возвращают они одно и то же значение, которое располагается в последней строчке программируемой части. В (bи c) мы имеем дело с программой – скаляром, так как они используются для вычисления одного значения и не имеют формальных параметров.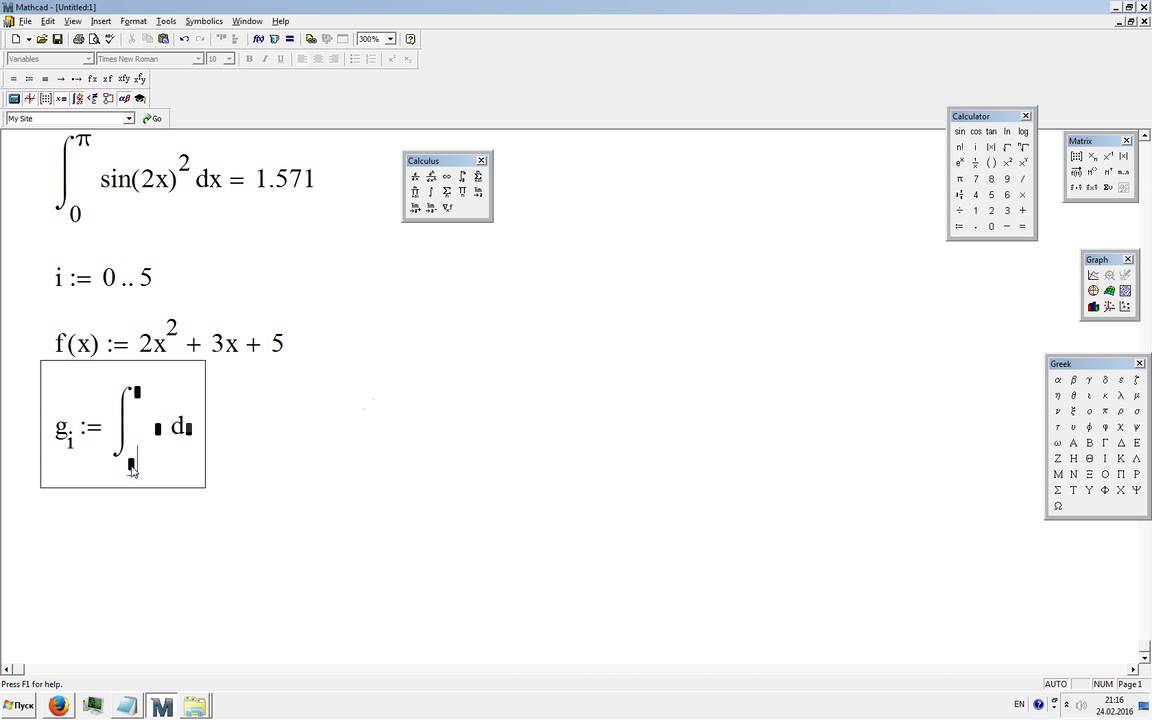
Внутри программ (b и c) используются глобальные переменные g и x из документа. Значения этих переменных определены заранее. Обе программы из примера, представленного на рис. 4.4, в своей программируемой части содержат операторы присваивания с использованием локальных переменных. Переменные, созданные внутри программы с таким видом присваивания, являются внутренними, и доступ к ним может осуществляться только в самой программе.
Впрограммной части используются глобальные переменные обычнотолько как операнды в выражениях.
Присвоить глобальным переменным значения внутри программы можно только локальным образом. После выхода из программы эти переменные сохраняют свои «глобальные» значения.
Использование «обычного» оператора присваивания «:=» в теле программы-функции приводит к синтаксической ошибке.
Последняя строка программы не должна содержать управляющих операторов. Эта строка задает значение, возвращаемое программой, т.е. получает результат вычислений и может содержать имя локальной переменной результата (рис. 4.4, c) или выражение, вычисляющее результат (рис. 4.4, b).
Обычно программа содержит больше чем две строки, поэтому рекомендуется сразу задавать блок из 5-6 маркеров.
Добавление недостающих полей для ввода дополнительных операторов производится с помощью кнопки Add lineпанели программирования. При этом поле ввода добавляется внизу выделенного к этому моменту оператора.
Для удаления того или иного оператора или поля ввода из тела программы-функции, нужно заключить его выделить и нажать клавишу <Delete> .
Программный блок можно создать и внутри уже заданного блока (вложенный блок).
 Для этого следует использовать один из стандартных способов: поставить курсор в маркер соответствующего оператора программирования и выполнить Add line.
Для этого следует использовать один из стандартных способов: поставить курсор в маркер соответствующего оператора программирования и выполнить Add line.Иногда при написании программы бывает нужным добавить строку к уже созданному блоку. Чтобы это сделать, поставьте курсор в ту строку блока, выше или ниже которой должна быть введена строка, и нажмите клавишу <Пробел>. При этом строка будет выделена и можно будет произвести добавление одним из стандартных способов.
Положение вставляемого маркера определяется положением вертикальной черты курсора. Если она находится слева от выделенного выражения, то маркер будет добавлен выше выделенной строки, если справа – то ниже.
Чтобы развернуть курсор в нужную сторону, нажмите клавишу <Insert>.
Чтобы добавить строку к целому блоку, его следует выделить, дважды нажав клавишу <Пробел>.
В том случае, если программа содержит блоки различных уровней, то для добавления строки, например, к первому блоку, нажмите клавишу <Пробел> несколько раз: при каждом нажатии будут выделяться блоки более низкого уровня.
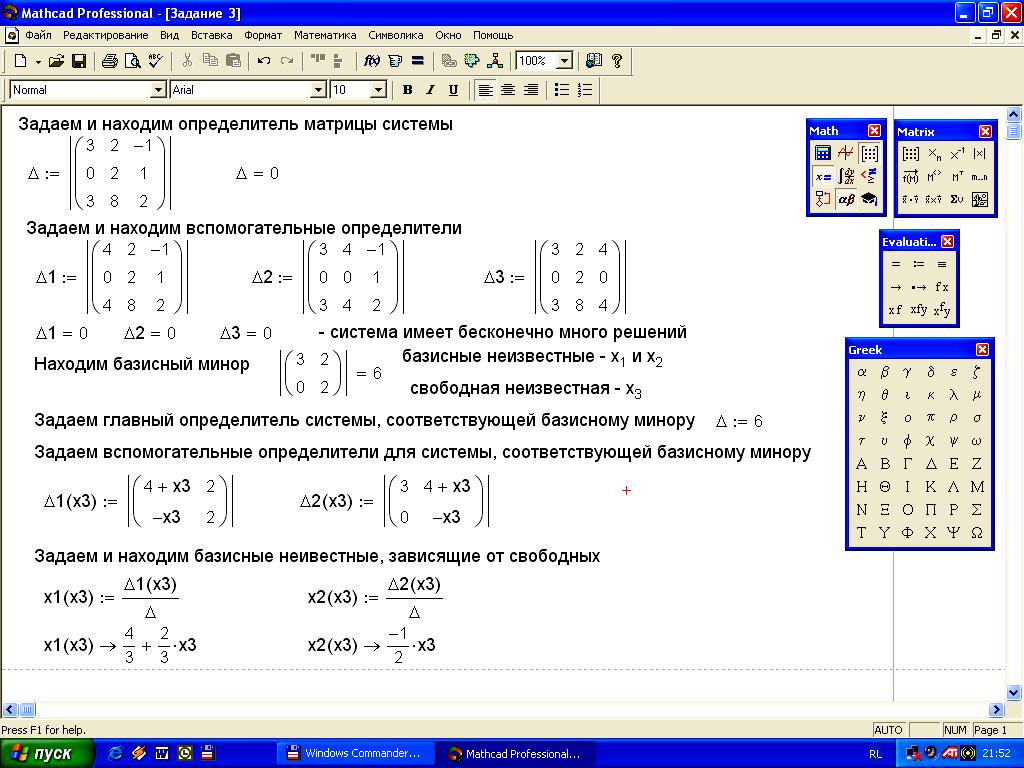
Пример 2. Требуется найти действительные корни квадратного уравнения , гдеa, b, c – любые действительные числа и . Известно, что в зависимости от знака дискриминантадействительные корни уравнения могут быть получены по формуле:
Решение. Опишем вычисление корней в виде программы-функции.
Спецификацию для этой функции можно записать следующим образом. Функция R(a,b,с) возвращает значения действительных корней квадратного уравнения или сообщает о том, что уравнение не имеет корней.
Здесьa, b, с – коэффициенты уравнения.
Очевидно, что в данном случае мы имеем дело с ветвящимся процессом.
Программирование ветвящихся процессов требует проверки некоторых условий, в зависимости от которых выбирается вычислительная формула. Для реализации таких вычислений на панели программирования предусмотрен оператор if (если).
При включении оператора if в блок программирования появляется шаблон с двумя полями ввода – справа и слева от оператора:
if .
В поле ввода справа от оператора записывается условие. Для ввода условий следует использовать панельBoolean (Логические), где есть кнопки для проверки условий ( = > < ≥ ≤ ≠ ).

В поле ввода слева нужно ввести строку программы (или несколько строк), которая будет выполняться, если введенное условие истинно.
Если невыполнение условия должно привести к выполнению какой-либо другой строки (или нескольких строк), то можно в строке, следующей за оператором if , вставить оператор otherwise (иначе). В поле ввода слева от этого оператора надо ввести строку, которая будет выполняться только в том случае, если условие ложно.
Чаще всего оператор if используется для задания разрывных или кусочно-непрерывных функций.
Описание функции и примеры ее вызова представлены на рис. 4.5.
Рис. 4.5. Описание функции R(a,b,x), предназначенной для вычисления корней квадратного уравнения
Пример 3.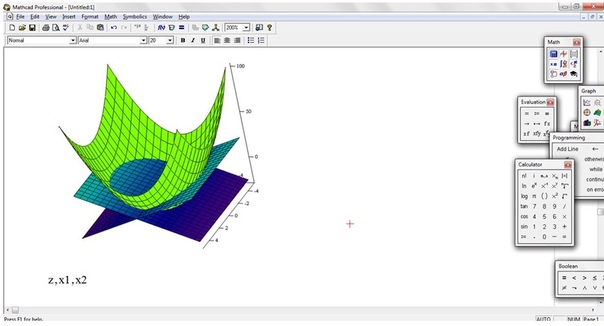 Требуется подготовить описание программы-функции и построить ее график на интервале [–2, 4] .
Требуется подготовить описание программы-функции и построить ее график на интервале [–2, 4] .
Решение. Из анализа аналитического выражения функции y видно, что функция является кусочно-непрерывной на числовой оси и алгоритм вычислений содержит три ветви. Вычисление значения y зависит от местоположения переменной x на числовой оси.
Для нахождения значения функции целесообразно ввести один формальный параметр, соответствующий переменной x.Спецификацию для этой функции можно записать следующим образом:
Функция f(x) возвращает значение функции, определенной в соответствии с условием примера 3. Здесь х – аргумент для вычисления.
В описании функции требуется проверить три условия. В зависимости от результатов проверки этих условий применяется соответствующая условию вычислительная формула.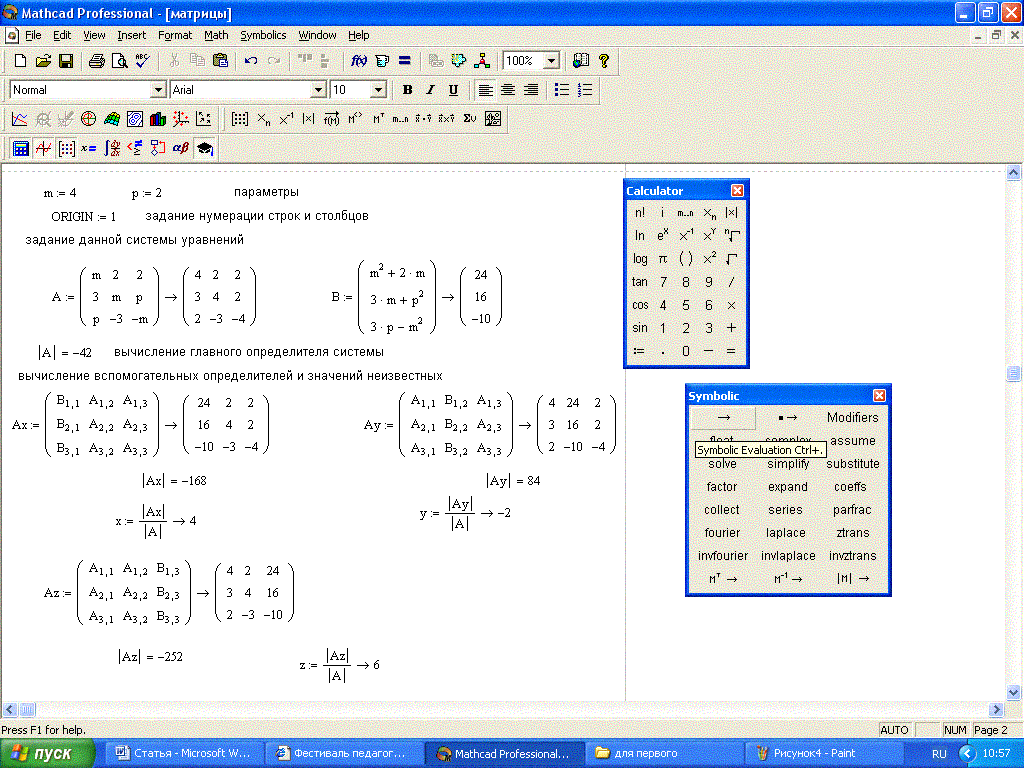 Поэтому при программировании можно с проверкой каждого из условий связать условный оператор if, как это показано на рис. 8.6. А можно ограничиться проверкой двух условий и оператором otherwise, учитывая тот факт, что функция задана на всей числовой оси, и исключение двух условий оставляет выполнение третьего условия. На рис. 8.7 представлен второй вариант функции-программы.
Поэтому при программировании можно с проверкой каждого из условий связать условный оператор if, как это показано на рис. 8.6. А можно ограничиться проверкой двух условий и оператором otherwise, учитывая тот факт, что функция задана на всей числовой оси, и исключение двух условий оставляет выполнение третьего условия. На рис. 8.7 представлен второй вариант функции-программы.
Рис. 4.6. Демонстрация элементов программирования ветвящихся процессов
Рис. 4.7. Демонстрация элементов программирования ветвящихся процессов
На рис. 4.8 представлены примеры программ-функций, реализующих вычисления, содержащие ветвящиеся процессы.
Рис. 4.8. Примеры программирования функций с проверкой условий. Здесь x – глобальная переменная
Пример 4. Требуется найти максимальный и минимальный элементы в заданном массиве.
Решение. Задача поиска наибольшего/наименьшего значений в заданном массиве относится к типовым циклическим алгоритмам .
Спецификацию для этой функции можно записать следующим образом:
Функция Fun(P) возвращает наибольшее и наименьшее значение в массиве Р.
Для создания циклов в MathCAD предусмотрено два оператора: for и while. Поскольку количество повторений цикла заранее известно и связано с числом элементов заданного массива, в данном решении целесообразно использовать оператор for.
После вставки оператораfor в строку программы его сопровождают три поля ввода, как это показано на рис. 4.9.
Рис. 4.9. Шаблон оператора цикла for
В поле ввода после слова for следует указать имя переменной-счетчика.
 Это может быть любое имя, которое не использовалось ранее в программе. Внутри цикла можно использовать эту переменную в любых выражениях, нельзя только присваивать ей никакого значения.
Это может быть любое имя, которое не использовалось ранее в программе. Внутри цикла можно использовать эту переменную в любых выражениях, нельзя только присваивать ей никакого значения.В поле ввода после знака € следует указать диапазон значений, которые будет принимать переменная-счетчик. Вместо диапазона в данном поле ввода можно указать имя некоторого массива (вектора или матрицы). В таком случае переменная-счетчик будет последовательно принимать значения всех элементов этого массива. Количество повторов цикла будет равно количеству элементов массива.
В поле ввода под словом for следует ввести тело цикла
Обозначим имя переменной-счетчика, которая используется в операторе for – буквой t. Для описания алгоритма воспользуемся тем, что в операторе цикла для переменной-счетчика можно указать в качестве диапазона имя массива. Как сказано выше, в таком случае переменная t будет последовательно принимать значения всех элементов указанного вfor массива (в нашем случае – это массив Р). Для обозначения максимального и минимального значений в программу введем две вспомогательные переменные Pmax и PMin. Тогда описание функции может быть представлено в виде, как это показано на рис. 4.10.
Как сказано выше, в таком случае переменная t будет последовательно принимать значения всех элементов указанного вfor массива (в нашем случае – это массив Р). Для обозначения максимального и минимального значений в программу введем две вспомогательные переменные Pmax и PMin. Тогда описание функции может быть представлено в виде, как это показано на рис. 4.10.
Отметим, что в данном случае в качестве результата работы функции нужно вернуть два значения, а специфика функции в MathCAD такова, что она позволяет вернуть только одно значение, но при этом сказано, что функция в качестве результата может вернуть, в том числе, вектор и матрицу. Поэтому при формировании результата мы определим его как вектор из двух значений.
Справа от программы-функции, представленной на рис. 4.10, написаны операторы, предназначенные для создания вектора с именем U из шести элементов. Для этого введена вспомогательная переменная i, задающая диапазон изменения индекса массива, а значения элементов массива U формируются с помощью функции rnd – датчика случайных чисел. Параметр 20 в ней определяет диапазон принимаемых значений.
Для этого введена вспомогательная переменная i, задающая диапазон изменения индекса массива, а значения элементов массива U формируются с помощью функции rnd – датчика случайных чисел. Параметр 20 в ней определяет диапазон принимаемых значений.
На рис. 4.11, a представлен второй вариант программы-функции, в котором в качестве диапазона значений для переменной-счетчика цикла for берется диапазон изменения индекса массива. Поэтому в список формальных параметров в заголовок функции вносится еще один параметр n, который указывает верхнюю границу изменения индекса.
Рис. 4.10. Описание и использование функции Fun(P)
а) |
b) |
Рис.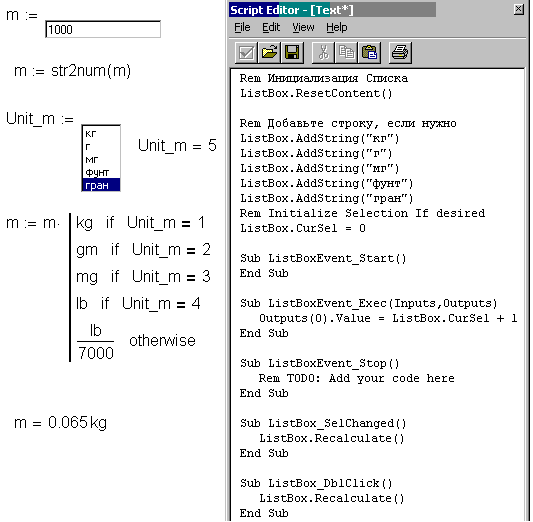 4.11. Описание и использование функции Fun(P)
4.11. Описание и использование функции Fun(P)
Пример 5. Требуется определить функцию, предназначенную для вычисления приближенного значения квадратного корня из числа N по формуле Ньютона:
,
где – заданное начальное приближение корня.
Решение.
Спецификацию для этой функции можно записать следующим образом:
Функция Fun(N,,x0) возвращает значение квадратного корня из числа N с заданной точностью вычислением – и заданным начальным приближением корня – x0.
Анализ блок-схемы показывает, что в представленном циклическом процессе количество повторений цикла заранее неизвестно и напрямую зависит от точности вычислений. Поэтому пользоваться оператором for не является целесообразным.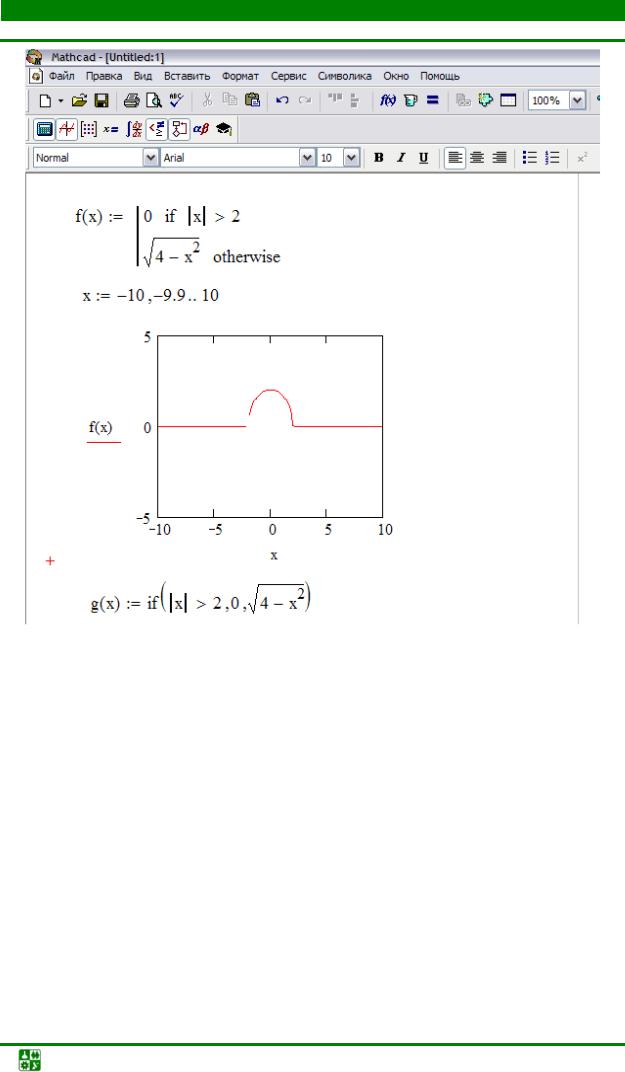 Для таких циклических процессов предусмотрен оператор цикла while.
Для таких циклических процессов предусмотрен оператор цикла while.
После вставки этого оператора в строку программы его сопровождают два поля ввода, как это показано на рис. 4.12.
Рис. 4.12. Шаблон оператора цикла while
В поле ввода ниже слова while следует ввести тело цикла – одна или несколько строк программы, выполнение которых нужно повторить несколько раз.
В поле ввода справа от слова while следует ввести условие. Оно будет проверяться после каждого выполнения тела цикла и в тот момент, когда условие перестанет выполняться, повторение тела цикла прекратится.
Из описания оператора цикла следует, что условие повторения цикла записывается cправа от слова while, а повторяемая часть цикла должна располагаться ниже конструкции while, а в описанной блок-схеме один из повторяемых операторов, а именно оператор, в котором вычисляется значение х, располагается до блока с условием повторения. Чтобы согласовать действия в блок-схеме с действиями оператора, сделаем перестановку — поставим определение переменной х после блока-условия. А для проверки условия введем вспомогательную переменную R, и для того, чтобы на начальном этапе пройти внутрь цикла для вычислений, определим начальное значение этой переменной значением, большим, чем указанная точность, например, значением, равным 1. И тогда функция может быть представлена в виде, как это показано на рис. 8.13.
Чтобы согласовать действия в блок-схеме с действиями оператора, сделаем перестановку — поставим определение переменной х после блока-условия. А для проверки условия введем вспомогательную переменную R, и для того, чтобы на начальном этапе пройти внутрь цикла для вычислений, определим начальное значение этой переменной значением, большим, чем указанная точность, например, значением, равным 1. И тогда функция может быть представлена в виде, как это показано на рис. 8.13.
Рис. 4.13. Описание и использование функции, предназначенной для извлечения квадратного корня
Пример 6. Требуется определить функцию, которая будет изменять значения элементов матрицы, имеющейnстрок и m столбцов следующим образом: заменить все неотрицательные элементы нулем, а отрицательные – единицей.
Решение. Алгоритм решения задача подробно рассмотрен в главе 1, блок-схема алгоритма представлена на рис. 1.11. Поэтому остановимся только на спецификации программы-функции, и ее описании. Спецификацию для этой функцииможно записать следующим образом:
1.11. Поэтому остановимся только на спецификации программы-функции, и ее описании. Спецификацию для этой функцииможно записать следующим образом:
Функция Fun(а,n,m) возвращает преобразованную матрицу а(nxm) по правилу: все неотрицательные элементы заменяются нулем, а отрицательные – единицей.
Анализ алгоритма показывает, что в данном случае мы имеем дело с двумя вложенными циклами, в которых переменныеi и j могут играть роль переменных-счетчиков операторов цикла типа for. Очевидно, что в качестве диапазона значений для этих переменных берется диапазон изменения индекса массива. На рис. 4.14 приведено определение функции. Описанная функция вызывается для изменения матрицы D, причем, измененная матрица заносится в матрицу T.
Рис. 4.14. Описание и использование функции, предназначенной для преобразования матрицы
Подготовить спецификацию функции.
Разработать алгоритм решения.
Установить, какие переменные помимо формальных параметров (локальные, глобальные переменные) понадобятся для реализации алгоритма.
Описать алгоритм словами или в виде блок-схемы.
Описать алгоритм в виде программы-функции на языке MathCAD.
Программирование в Mathcad 15, 14, 13. Программы, циклы, условные операторы
В статье рассмотрены основы программирования в mathcad версии 15 и более старших. Приведены полезные примеры для инженерных расчетов
Цикл “FOR” в mathcad 15
Для примера рассмотрим пример заполнения матрицы-вектора в автоматическом режиме. Предположим, что нам нужно заполнить матрицу случайными числами. Размер матрицы 10 элементов. Заполнение в ручную такой матрицы безусловно отнимет массу времени
В свободном поле mathcad введите имя вашей будущей матрицы M. Поставте знак присвоить “:=” и затем на английской раскладке нажмите комбинацию Alt (правый) + “]”. В место привычного маркера возникнет вертикальная черная черта с двумя маркерами. Удерживая клавишу Alt введите еще несколько раз символ “]” так, чтобы увеличить число свободных маркеров.
Можно также воспользоваться кнопкой “Add Line” на панели Programming. В этих маркерах записываются строки кода
Поставте знак присвоить “:=” и затем на английской раскладке нажмите комбинацию Alt (правый) + “]”. В место привычного маркера возникнет вертикальная черная черта с двумя маркерами. Удерживая клавишу Alt введите еще несколько раз символ “]” так, чтобы увеличить число свободных маркеров.
Можно также воспользоваться кнопкой “Add Line” на панели Programming. В этих маркерах записываются строки кода
Поместите курсор в первый маркер и на панели Programming нажмите кнопку с надписью “for”. Вы увидите заготовку для формирования цикла FOR с маркером для ввода “тела цикла”, который несколько отстоит от основных маркеров
Рис. 2. Запись безусловного цикла FORТеперь нужно ввести переменную-счетчик (пусть это будет “i”), которая будет менять свое значение от 1 до 10. Диапазон от 1 до 10 задается с помощью ранжированной переменной, которую можно найти на панели Matrix
Рис. 3. Настройка параметров цикла for в mathcad 15 Цикл for в этом примере будет перебирать значения счетчика i от 1 до 10 c шагом 1. При каждом значении i элементу матрицы с соответсвующим индексом будет присваиваться случайное число с помощью стандартной функции rnd(m). Функция rnd присваивает переменной значение в диапазоне от 0 до “m”
При каждом значении i элементу матрицы с соответсвующим индексом будет присваиваться случайное число с помощью стандартной функции rnd(m). Функция rnd присваивает переменной значение в диапазоне от 0 до “m”
Операция присваивания осуществляется при помощи операции Local difinition с панели Programming. Опрерация присваивания отображена в виде стрелочки “←”. Чтобы присвоить какое либо значение элементу матрицы нужно указать соответсвующий индекс матрицы. Это делается с помощью кнопки Subscript на панели Matrix.
Операция присваиваивания должна осуществляться в “теле цикла”. То есть, все действия, которые должны повторяться по мере работы счетчика циклы, должны находиться в соответсвующих маркерах. После завершения работы цикла в последний маркер тела программы нужно ввести имя матрицы, над заполнением которой мы работали. В нашем случае это M. См. рисунок 4
Рис. 4. Синтаксис программы по заполнению матрицы-вектора случайными числами в mathcad 15 Теперь можно посмотреть на результат. Введем имя матрицы M и поставим знак равно “=”. Мы сразу же увидим содержимое матрицы-вектора, который был заполнен с помощью нашей программы. Теперь меняя количество итераций в цикле for мы можем изменять размерность матрицы-вектора. Можн также поменять и закон заполнения матрицы-вектора.
Введем имя матрицы M и поставим знак равно “=”. Мы сразу же увидим содержимое матрицы-вектора, который был заполнен с помощью нашей программы. Теперь меняя количество итераций в цикле for мы можем изменять размерность матрицы-вектора. Можн также поменять и закон заполнения матрицы-вектора.
Можно изменить программу таким образом, чтобы заполнить квадратную матрицу. Для этого нам нужно ввести еще один счетчик и еще один цикл for с индексом j. Таким образом один цикл будет выполняться внутри другого, формируя столбцы и строки матрицы
Рис. 6. Программа для заполнения квадратной матрицы в mathcad 15Программы в mathcad могут использовать значения переменных, находящихся вне тела программы. Например, на рисунке ниже видно, как можно конечные значения счетчиков цикла связать со значениями переменных из вне
Рис. 7. Программа для заполнения квадратной матрицы в mathcad 15Условные операторы “IF” в mathcad 15
Чтобы посмотреть, как работает условный оператор “if” в mathcad 15 рассмотрим простой пример.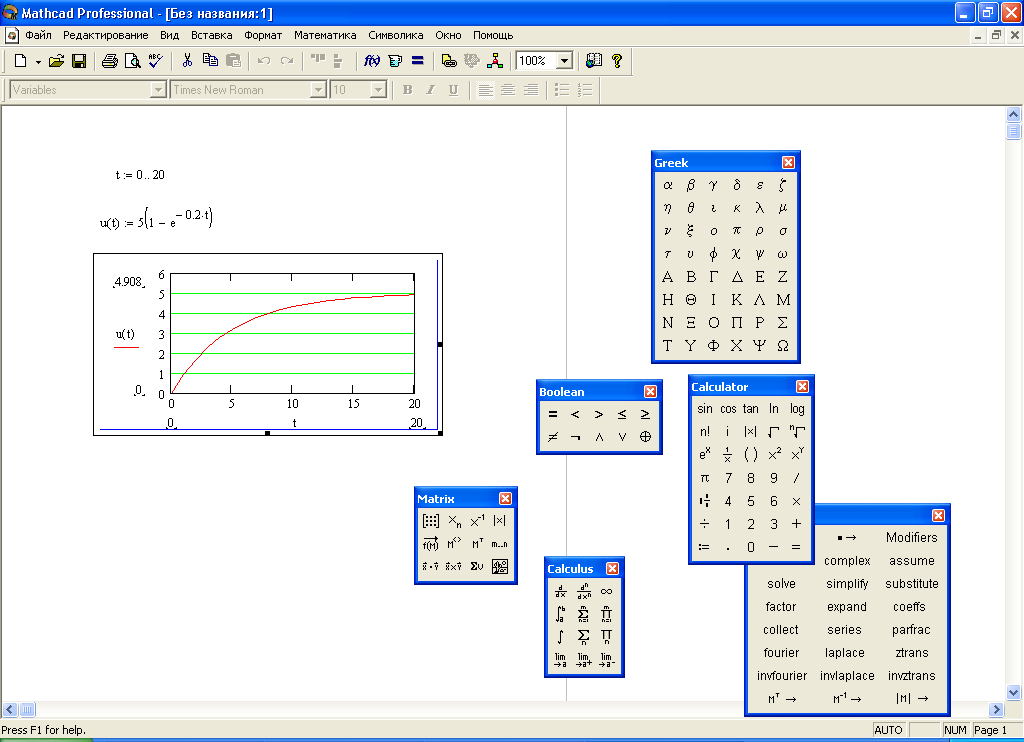 Заполним квадратную матрицу G размером 5 х 5 элементов случайными числами и затем обнулим все элементы, которые меньше 10
Заполним квадратную матрицу G размером 5 х 5 элементов случайными числами и затем обнулим все элементы, которые меньше 10
На рисунке 8 приведен уже знакомый код заполнения матрицы случайными числами
Рис. 8. Программа для заполнения квадратной матрицы случайными числамиДля обнуления элементов, значение которых меньше 10, запишем второй участок кода с использованием условного оператора “If”. Для проверки каждого элемента на выполнение этого условия нам опять потребуется два вложенных цикла “for” с счетчиками i и j. См. рис. 9. Обратите внимание, в теле второго цикла оставлено два свободных маркера
Рис. 9. Заготовка для применения условного оператораРезультат работы программы для удобства будет записываться в матрицу P. Поместите курсор в первый свободный маркер и нажмите на кнопку с надписью “if” на панели Programming. Вы увидите заготовку для записи условного оператора
Рис.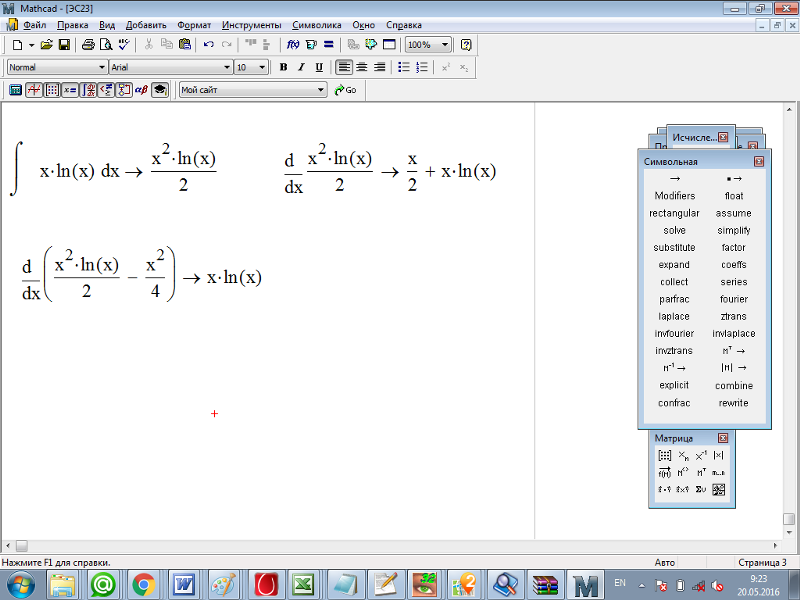 10. Заготовка для условного оператора
10. Заготовка для условного оператораВ этой заготовке выполним обнуление элемента матрицы G если значение этого элемента менее 10. Присвоение элементу матрицы значение нуля осуществляется символом “←” . Буквально логика данной операции следующая: “присвоить элементу матрицы P с текущим индексом i и j значение 0 если елемент матрицы G с тем же индексом меньше 10”
Рис. 11. Ввод условного оператора в mathcad 15Теперь запишем второе условие, по которому все элементы матрицы G, которые больше либо равны 10 попадают в матрицу P без изменеий на те же “мееста”. Буквально логика данной операции следующая: “присвоить элементу матрицы P с текущим индексом i и j значение елемента матрицы G с тем же индексом если значение элемента больше либо равно 10”. Сразу же после текста программы можно вывести результат. См. рис. 12.
Рис. 12. Ввод условного оператора в mathcad 15Теперь можно наглядно увидеть, как изменилась матрица после ее обработки условными операторами
Рис. 13. Результат работы условного оператора
13. Результат работы условного оператораЦикл “WHILE” в mathcad 15
Цикл While является условным циклом. То есть повторение его тела осуществляется до тех пор пока верно условие.
Рассмотрим простой пример заполнения матрицы-столбца с использованием цикла while. В качестве условия работы цикла будем проверять верно ли равенство m < 7. Переменную m будем изменять в теле цикла, так что бы в какой то момент условие не выполнилось и цикл завершился. Также в тело цикла введем закон изменения значений элементов нашей матрицы-столбца. На рис. 14 приведен синтаксис цикла while.
Рис. 14. Цикл WHILE в mathcadВ теле цикла могут находиться абсолютно любые команды и операторы: арифметические вычисления, открытие, анализ, обработка и запись данных в файл, запуск скриптов и приложений и т.д. Одним словом программирование это очень полезный и весьма универсальный инструмент, который позволяет реализовать любую идею в инженерной деятельности
Обратите внимание на то, что если в процессе выполнения программы условие запуска цикла “while” всегда оказывается верным, то цикл не завершится.
Произойдет так называемое “зацикливание” программы и придется прерывать процесс счета вручную и искать ошибку
7. Программирование в Mathcad
Впакете Mathcad существует богатый набор средств для решения различных математических задач, встроено огромное количество функций из различных разделов математики. Однако написать функции для всех практических задач, которые могут стоять перед пользователями пакета, невозможно. Для расширения возможностей разработчики пакета встроили достаточно простой и оригинальный язык программирования. В любом месте документа Mathcad можно вставить код программы на встроенном языке программирования. Это можно сделать при помощи «горячих клавиш» или команд из панели инструментов Programming (Программирование).
Для визуализации панели програм-
мирования необходимо нажать на кнопку из панели математических инструментов или по-
дать команду View \Toolbars \Programming. На данной панели имеется десять команд. Щелчок по одной из этих команд создает в текущей
На данной панели имеется десять команд. Щелчок по одной из этих команд создает в текущей
позиции заготовку для соответствующей программной конструкции. При частом использовании команд программирования удобнее запомнить комбинации «горячих клавиш» и команды генерировать при помощи клавиатуры.
Примечание. При составлении программ ключевые слова команд вручную писать нельзя. Заготовку команды можно получить только при помощи щелчка мыши по соответствующей кнопке или при помощи комбинаций клавиш.
Приведем значение «горячих клавиш», использующих при программировании на Mathcadе.
Команда | Горячая клавиша | Команда | Горячая клавиша |
Add Line | ] | ← | { |
if | } | otherwise | CTR+Shift+] |
for | Ctrl+Shift+’ | while | Ctrl+] |
break | Ctrl+Shift+[ | continue | Ctrl+[ |
return | Ctrl+Shift+\ | On error | Ctrl+’ |
Предполагается, что читатель уже знаком с основными идеями программирования, изучив один из стандартных языков про-
118
граммирования: QBasic, Visual Basic, Fortran, Pascal, C++, Java, Ruby или любой другой язык программирования. Данный практикум адресован пользователям, решающим инженерные и научные задачи, для которых программирование не является основным видом деятельности. Для таких пользователей языки программирования C++ и Java противопоказаны, так как ориентированы на профессиональных специалистов. Инженерам, использующим программирование не ежедневно, для решения большинства задач достаточно и одиннадцати команд из панели программирования Mathcad.
Данный практикум адресован пользователям, решающим инженерные и научные задачи, для которых программирование не является основным видом деятельности. Для таких пользователей языки программирования C++ и Java противопоказаны, так как ориентированы на профессиональных специалистов. Инженерам, использующим программирование не ежедневно, для решения большинства задач достаточно и одиннадцати команд из панели программирования Mathcad.
Сразу же отметим недостатки программирования в среде Mathcad. Одним из главных недостатков является неразвитость отладчика программ. Ошибки, возникающие при выполнении программ, отображаются, но подробной информации о типе ошибки, значении локальных и глобальных переменных в момент останова программы оперативно получить нельзя. Отлаживать программы уже средней сложности в Mathcad не доставляет особой радости. Поэтому сложные инженерные, научные и экономические задачи удобнее и быстрее, с точки зрения автора, выполнять в рамках визуального алгоритмического языка Visual Basic [3] или последних версий языка Fortran.
Рассмотрим все команды из панели программирования Math-
cad.
1. Add Line – добавить строку в текущую позицию программы. При вводе данной команды появляется или расширяется на одну строку вертикальная линия, объединяющая отдельные операторы в блок с одним входом и одним выходом, который выполняется как один оператор.
Позиция, куда вставится строка, определяется положением курсора. Чтоб вставить новую строку в середину программы, нужно выделить (пробелами) строку перед позицией, куда будет вставлена пустая строка. Удалить лишнюю строку можно с помощью кнопки backspace на клавиатуре.
Для того чтобы начать ввод подпрограммы, необходимо набрать имя программы и в скобках через запятую перечислить формальные параметры подпрограммы, ввести нужное количество раз команду Add Line. Программа выводит последнюю переменную, обрабатываемую программой перед выходом. Вместо
119
имени подпрограммы можно указать имя переменной, куда необходимо вывести результат работы подпрограммы.
2. ← – оператор присваивания значения локальной переменной. При выходе из блока программы значения локальных переменных оказываются недоступны для других участков Mathcad файла.
В Mathcad имеются два оператора присваивания: для глобальных переменных (обозначается двумя символами «:=») и для локальных переменных «←». Глобальные переменные доступны в любом месте программы после объявления данной переменной, а локальные – только в текущем блоке.
Для пояснения действия локального и глобального оператора присваивания рассмотрим пример простейшей программы на
Mathcad.
Напишем программу для решения квадратного уравнения ax2+bx+c=0. В программе при помощи операторов глобального присваивания задаются значения глобальных переменных a, b и c. Для сравнения введем еще локальную переменную k и присвоим ей значение 4. Далее вычисляем значение корней квадратного уравнения при помощи программы, состоящей из одного блока операторов. В программе применяются три оператора локального присваивания и возвращается значения вектора x, состоящего из двух чисел. После выполнения программы выводим значение всех переменных, используемых в программе. При этом значение всех локальных переменных D, x и k, заданных вне блока, программа не видит, поэтому вместо знака = выводится оператор глобального присваивания «:=». В этом случае значение переменной не выводится, а вместо него отображается красный прямоугольный маркер.
После выполнения программы выводим значение всех переменных, используемых в программе. При этом значение всех локальных переменных D, x и k, заданных вне блока, программа не видит, поэтому вместо знака = выводится оператор глобального присваивания «:=». В этом случае значение переменной не выводится, а вместо него отображается красный прямоугольный маркер.
Начало программы.
a :=1 b := −4 c := 3 k ← 4 ORIGIN :=1
x1 |
| = | D | ←b2 −4 a c | |||||
|
|
|
|
|
|
|
|
| |
x2 |
|
| x | ← | −b − | D | |||
|
|
|
|
|
|
|
| ||
|
|
| 1 |
|
| 2 a |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| x | ← | −b + | D | |||
|
|
|
|
|
|
| |||
|
|
| 2 |
|
| 2 a |
|
|
|
|
|
| x |
|
|
|
|
| |
D := | x := | k := |
|
|
| ||||
|
|
|
| ||||||
x1 =1 x2 = 3 a =1 b = −4 c = 3.
Конец программы.
3. Оператор if предназначен для организации разветвляющихся вычислительных процессов. Чтобы ввести оператор if в программу, необходимо мышкой щелкнуть по кнопке if из панели программирования или использовать горячую клавишу – }.
При этом в программу вставляется заготовка для оператора if: if .
Общий вид простого оператора if: D if L, L – логическое выражение;
D – оператор, выполняемый в случае, если условие L принимает значение «истина».
Оператор работает следующим образом:
•вычисляется логическое условие L;
•если L – истина, то выполняется оператор D, в ином случае он не выполняется;
•выполнение программы продолжается со следующего,
после if, оператора.
Как мы видим, данный оператор if идентичен аналогичному оператору из других высокоуровневых языков программирования. Единственное отличие заключаются в синтаксисе.
Для формирования сложных условий можно использовать панель инструментов Boolean, содержатся знаки логического равенства, неравенства и логических операций. В частности, «V» означает логическое «или», а «Λ» — логическое «и».
В частности, «V» означает логическое «или», а «Λ» — логическое «и».
121
Таким образом, чтобы сформулировать условие, что переменная х находится в диапазоне (–3;4), необходимо написать: x > –3 Λ x < 4.
При формулировании сложных логических условий для расстановки приоритетов можно использовать скобки.
Пример. Построить график следующей функции:
28 −6x, | x (−∞;3) | |
| +1, | x [3;−1] . |
f (x) = x2 | ||
|
| x (1,∞) |
2, |
| |
Решение.
f (x) := 28 −6 x if x > 3
x2 +1 if x ≤ 3 x ≥ −1
2if x < −1
Всложных подпрограммах
часто используется блочный оператор if: if L
D1
Dn
Где D1, …, Dn – действия, выполняемые в случае, если логическое условие L истинно.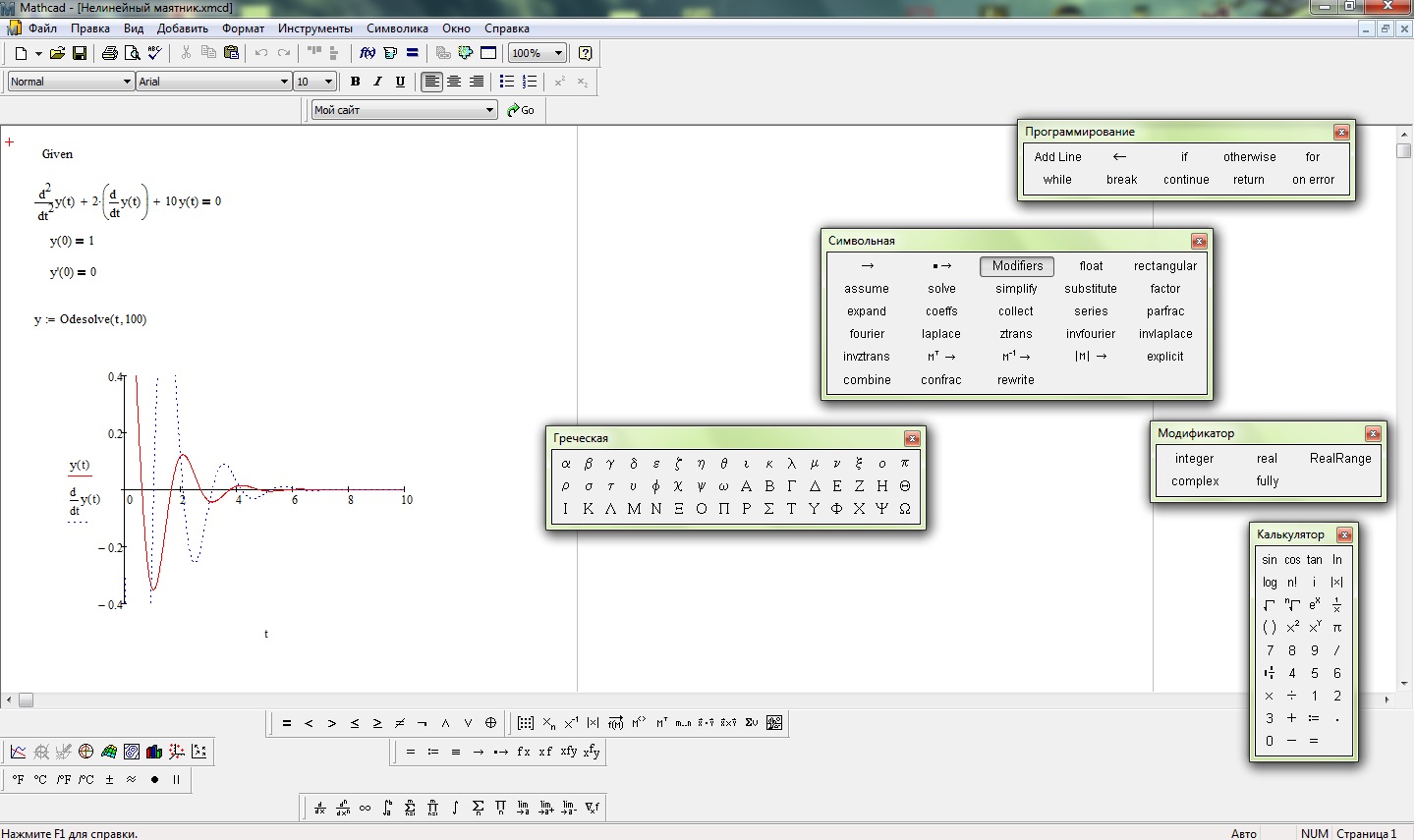
Для того чтобы вставить подобную конструкцию, нам необходимо, на панели инструментов Programming, выбрать if , затем установить курсор на место ввода слева от оператора if и n раз нажать на Add Line.
Приведем пример программы с подобным оператором. Усовершенствуем программу для решения квадратного уравнения ax2+bx+c=0.
Начало программы.
x1 |
| = | ORIGIN :=1 a :=1 b := −1 c := 4 | |||
|
| D ←b | 2 | −4 | a c | |
x2 |
|
|
| |||
|
|
| if D ≥ 0 |
| ||
x1 ← −b2− a D x2 ← −b2+ a D
if D < 0
x1 ←”действительных корней нет” x2 ←”действительных корней нет”
x
x1 =”действительных корней нет” x2 =”действительных корней нет”
Конец программы.
В данном случае при дискриминанте меньше 0 программа выдает сообщение «действительных корней нет!».
Кроме оператора if, программа Mathcad может содержать и оператор otherwise.
4. Оператор otherwise применяется в случае, когда используется условие с двумя вариантами действия, то есть, если условие истинно, нужно выполнить одно действие (или действия), а если ложно, то другое.
Общий вид такого оператора следующий:
D1 if L
D2 otherwise
В случае если условие L истинно, выполняются действия D1, иначе выполняются действия D2. То есть otherwise аналогичен оператору else в Бейсике, Фортране и других высокоуровневых языках.
Рассмотрим пример программы, использующей операторы if и otherwise. В данном случае проверяются условия, при которых логарифм не существует (x<0 или y<0 или y=1). Если они выпол-
123
нены, выдается сообщение «error», в противном случае вычисля-
ется logyx. |
|
|
|
f _ log(x, y) := |
| “error” | if x ≤ 0 y ≤ 0 y =1 |
| |||
|
| log(x, y) | otherwise |
f _ log(−4,5) =”error” |
| ||
f _ log(8,2) = 3 |
|
|
|
Когда в блоке otherwise несколько строк, нужно установить курсор в место ввода слева от оператора otherwise и нажать Add Line необходимое количество раз.
Вернемся к программе, вычисляющей корни уравнения ax2+bx+c=0, и запишем ее с помощью операторов if и otherwise. Начало программы.
ORIGIN :=1 a :=1 b := 2 c := 2
x1 | = |
| D ←b | 2 | −4 a c |
|
|
| |||
|
|
|
| ||||||||
|
|
|
|
| |||||||
x2 |
|
| if D ≥ 0 |
|
|
| |||||
|
|
|
| x | ← |
| −b − | D | |||
|
|
|
|
| |||||||
|
|
|
|
|
|
| |||||
|
|
|
| 1 |
|
|
| 2 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
| x | ← | −b + | D | ||||
|
|
|
|
|
| ||||||
|
|
|
| 2 |
|
|
| 2 a |
|
|
|
|
|
| otherwise |
|
|
| |||||
|
|
|
| x1 ←”действительных корней нет” | |||||||
|
|
|
| ||||||||
|
|
|
| x2 ←”действительных корней нет” | |||||||
|
|
| x |
|
|
|
|
|
|
| |
x1 = −2 |
| x2 = −1 |
|
|
| ||||||
Конец программы.
5. Оператор for используется для создания циклических вычислительных процессов. В документе Mathcad простейшие циклы могут быть заменены ранжированными векторами. Для более сложных циклов необходимо составлять программу.
Чтобы вставить оператор for в программу, необходимо мышкой щелкнуть по кнопке for из панели программирования или использовать «горячую» клавишу «Ctrl+Shift+’». При этом в программу вставляется заготовка для оператора for:
for
Общий вид оператора выбора for: for i k1..kn
D
Или
for i (k1 k2 k3 … kn)
D
Где i – счетчик цикла. Переменная, которая меняется в диапазоне от k1 до kn. Диапазон изменения счетчика цикла вводится с помощью ранжированной переменной или с помощью вектора.
D –действия, которые выполняются в цикле (тело цикла). Ниже приведен пример, в котором диапазон изменения счетчика цикла n задан с помощью вектора. Вектор вставляется с по-
мощью панели инструментов Matrix.
sum := s ← 0
for n (1 2 5 7 10 11 13 16 17 19)
s ← s + 1n
sum = 2.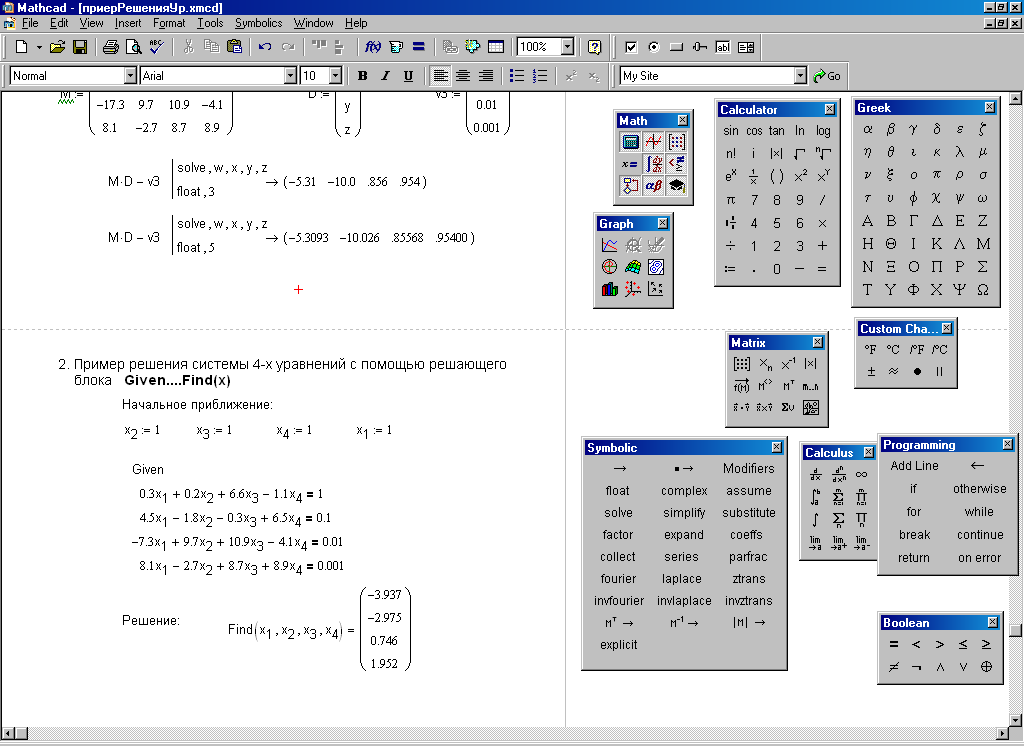 285.
285.
Данная программа вычисляет сумму
Sum=1+1/2+1/5+1/7+1/10+1/11+1/13+1/16+1/17+1/19.
Если тело цикла оператора for состоит из нескольких строк, то необходимо установить курсор на позицию для ввода тела цикла и соответствующее количество раз нажать на Add Line.
Как и в обычных программах, циклы и условные операторы могут быть вложенными. Mathcad, впрочем, сам следит за вложенностью циклов и сделать ошибку во вложенности просто не позволит.
Пример. Написать функцию FA, создающую матрицу A, состоящую из M строк и N столбцов следующего вида:
125
1 | 2 | 4 | 8 | 16 |
| |
| 0 | 1 | 2 | 4 | 8 |
|
|
| |||||
| 0 | 0 | 1 | 2 | 4 |
|
|
| |||||
| 0 | 0 | 0 | 1 | 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запишем подпрограмму, выводящую эту матрицу с помощью двух вложенных циклов:
FA(M , N ) := |
| for | i 0. |
| ||||
|
| |||||||
|
|
|
| for | j 0..N −1 |
| ||
|
|
|
|
| Ai , j | ← 1 | if | i = j |
|
|
|
|
| ||||
|
|
|
|
| Ai , j | ← 0 | if | i > j |
|
|
|
|
| Ai , j ← 2 Ai, j−1 | if i < j | ||
|
|
| A |
|
|
|
|
|
1 | 2 | 4 | 8 | 16 |
|
| ||
| 0 | 1 | 2 | 4 | 8 |
|
|
|
FA(4,5) = |
|
|
| |||||
| 0 | 0 | 1 | 2 | 4 |
|
|
|
|
|
|
| |||||
| 0 | 0 | 0 | 1 | 2 |
|
|
|
Обозначим i – | строку матрицы, j – столбец матрицы. | |||||||
Тогда главная диагональ задается уравнением «i=j», элементы матрицы, расположенные выше главной диагонали, уравнением «i<j», а элементы матрицы, расположенные ниже главной диагонали, – усравнением «i<j».
Каждый элемент, расположенный выше главной диагонали, вычисляется как удвоенное произведение элемента, стоящего в этой же строке в предыдущем столбце: Ai j=2* Ai j–1.
Для проверки работы функции подали команду: FA(4,5)=. 6. Оператор цикла while используется тогда, когда цикл дол-
жен выполняться не заданное количество раз, а до тех пор, пока не будет выполнено определенное в цикле условие.
Чтобы вставить оператор while в программу, необходимо мышкой щелкнуть по кнопке while из панели программирования или использовать горячую клавишу – «Ctrl+]». При этом в программу вставляется заготовка для оператора while:
while
Общий вид оператора While: while L
D,
где L – условие, при выполнении которого выполняется цикл (условие цикла). В данном случае, действие D (тело цикла) выполняется до тех пор, пока условие L истинно. Если логическое условие L изначально ложно, то операторы, составляющие тело цикла, не будут выполняться, а управление передается на оператор следующий за оператором while.
В данном случае, действие D (тело цикла) выполняется до тех пор, пока условие L истинно. Если логическое условие L изначально ложно, то операторы, составляющие тело цикла, не будут выполняться, а управление передается на оператор следующий за оператором while.
Если в теле цикла выполняемых действий должно быть несколько, то необходимо установить курсор на позицию для ввода тела цикла и соответствующее количество раз нажать на Add Line.
Следует заметить, что если условие L истинно всегда, то программа будет работать бесконечно (зациклится). Именно поэтому с циклом while необходимо быть очень осторожным и тщательно проверять условие выхода из цикла, прежде чем выполнять программу.
Если программа все-таки повисла, то чтобы прервать ее выполнение, необходимо нажать клавишу «Esc» и в появившемся окне нажать на кнопку OK.
Приведем пример программы, использующей цикл while.
s ← 0 |
|
|
| ||
n ←1 |
|
|
| ||
| 1 |
|
| ||
while |
|
| > tol | ||
n | |||||
|
|
|
| ||
s ← s + 1n n ← n +1
s
= 2.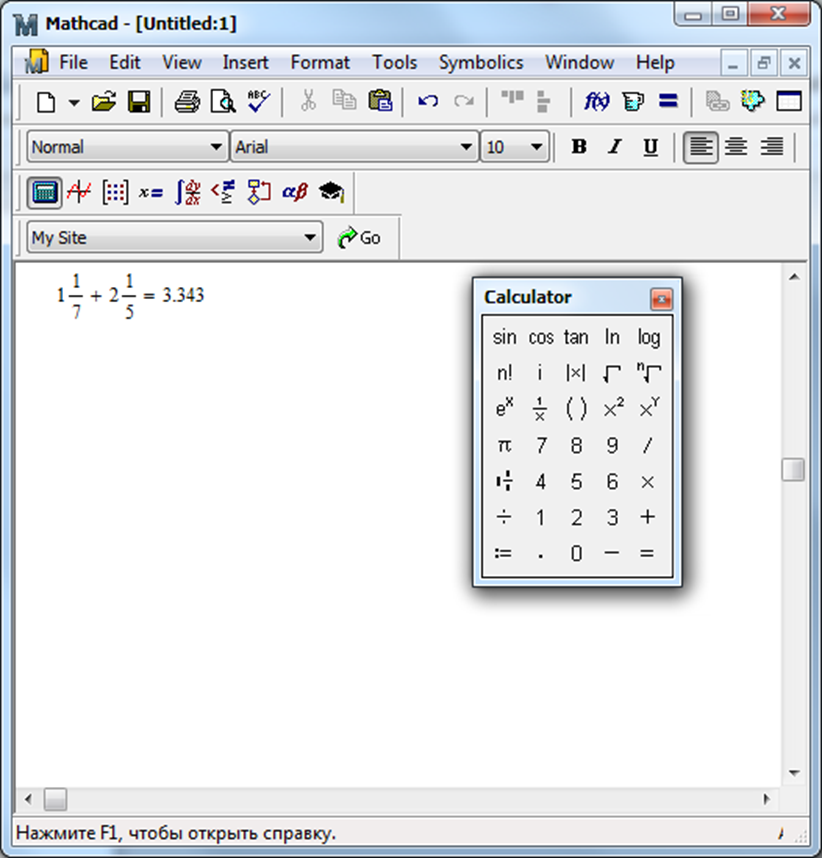 829.
829.
Вданной программе с указанной точностью (tol) вычисляется сумма s=1+1/2+1/3+1/4+1/5+1/6+1/7…
7. Оператор break обеспечивает экстренный выход из цикла. Программа при этом продолжает выполнять следующую после цикла строку. Данный оператор часто применяется, чтобы избежать «зацикливания» программы.
Вкачестве примера применения оператора break рассмотрим
∞ |
| 12n −1 |
|
|
|
задачу вычисления суммы числового ряда S = ∑ |
|
| . | В | |
n | 3 | ||||
n=1 | + 2n +1 |
|
| ||
приведенной ниже программе, суммирование членов ряда прекращается, когда достигается точность, указанная параметром tol или если число итераций цикла превышает 10000.
f (n) := | 12 n −1 |
| |
n3 + 2 n +1 | |||
| |||
sum(tol) := s ← 0 n ←1
while f (n) > tol s ← s + f (n)
break if n >10000 n ← n +1
s sum(0.000011) =8.726 .
В данном случае оператор break исключается возможность зацикливания программы для расходящегося ряда.
8. Оператор continue возвращает управление в первую строку цикла. Как только этот оператор встречается в программе, выполнение текущей итерации прерывается и выполняется переход на следующую итерацию цикла. Выход из цикла не производится.
Данный оператор, как и оператор break, не содержит параметров.
Пример: Найти сумму N первых членов ряда:
N |
| 1 |
|
S = ∑ |
| . | |
2n | 3 | ||
n=1 | −16 |
|
В программе, при помощи оператора continue, происходит обход слагаемого в котором знаменатель дроби равен нулю.
sum(N ) := |
| s ← 0 | |
| |||
|
| for n 1..N | |
|
|
| a ← 2 n3 −16 |
|
|
| |
|
|
| continue if a = 0 |
|
|
| s ← s + 1 |
|
|
| a |
|
| s | |
sum(100) = −0.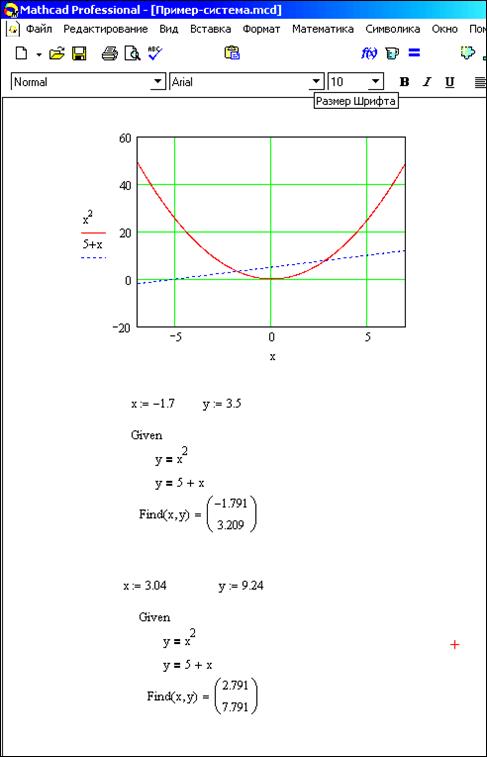 024.
024.
9. Оператор return прерывает выполнение программы. В качестве результата работы программы возвращается значение, указанное в позиции для ввода, после оператора return.
При выборе на панели инструментов пункта return вставляется строка.
Пример. Подсчитать с указанной точностью tol сумму ряда:
∞ |
|
| 12n |
|
S = ∑ |
|
| . | |
n | 2 | + 2n +16 | ||
n=1 |
|
|
Если ряд получается расходящийся, программа выдаст сообщение «расходится». Ряд будет считаться расходящимся, если число итераций цикла превысило 1000000 раз.
f 1(n) := | 12n | |||||||
n2 + 2n +16 |
|
|
|
|
| |||
sum1(N ) := |
| s ← 0 | ||||||
| ||||||||
|
| n ←1 | ||||||
|
| while |
| f 1(n) |
| > tol | ||
|
|
|
| |||||
|
|
| s ← s + f 1(n) | |||||
|
|
| ||||||
|
|
| return ” ряд расходится” if n >100000 | |||||
|
|
| n ← n +1 | |||||
|
| s | ||||||
129
sum1(0.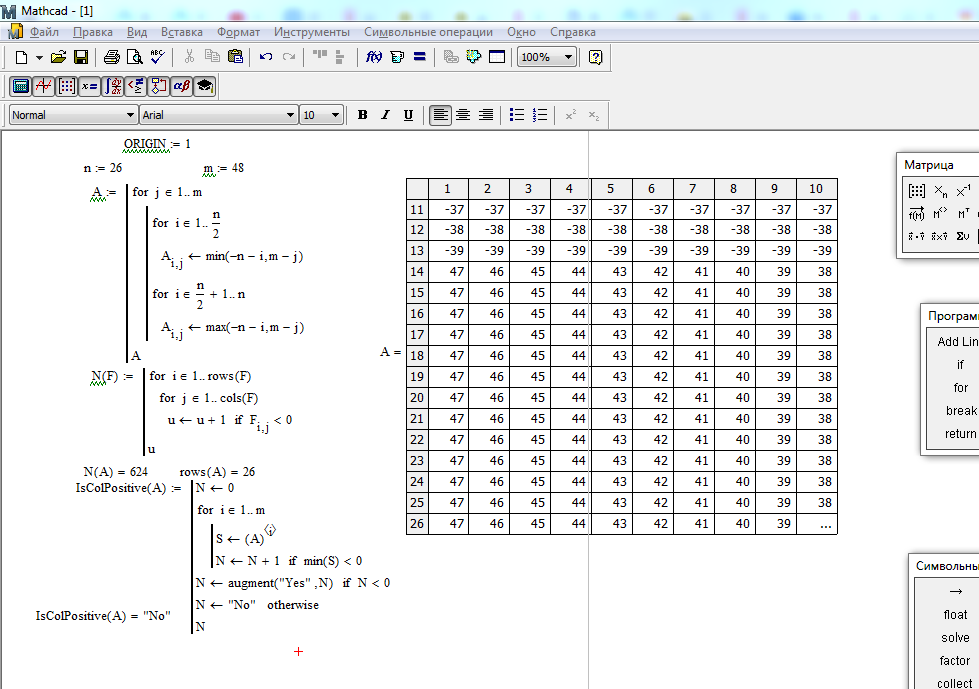 01) =” ряд расходится”.
01) =” ряд расходится”.
10. Оператор on error отвечает за обработку ошибок. При выборе данного оператора в программу вставляется заготовка следующего вида:
Общий вид оператора on error: D1 on error D2 .
Если при вычислении выражения D1 произошла ошибка, будет вычислено значение D2.
Данный оператор имеет смысл использовать, если при выполнении программы возможна ошибка в каком-то определенном месте, например деление на ноль.
Приведем пример программы, вычисляющей десятичный логарифм числа xy.
Если логарифм не существует, выдается сообщение об ошибке: «аргумент логарифма <0».
|
|
|
f (x, y) := |
| z ← x y |
| ||
|
| “аргумент логарифма < 0” on error log(z) |
f (0,5) =”аргумент логарифма < 0″; | ||
f (10,1) =1. | ||
Оператор on error можно применять в комплексе встроенной функцией error().
f (x, y) := z ← x y
error(“аргумент логарифма < 0”) on error log(z)
В данном случае сообщение об ошибке будет показываться в стандартном для Mathcad виде. При ошибке текст вызова функции выделяется красным цветом, а при подведении мыши к этому вызову внизу отображается запрограммированный в функции error текст.
16. Тема 4. Создание программных фрагментов в MathCad. Краткие теоретические сведения
Система MathCad позволяет создавать программные фрагменты для вычисления алгоритмов, которые нельзя реализовать базовым набором средств и методов Mathcad.
Программный фрагмент можно использовать в операторе «=» или в правой части оператора «:=». Слева в операторе «:=» может находиться либо переменная, либо пользовательская функция.
Программный фрагмент состоит из строк программы, каждая из которых может содержать операторы программы.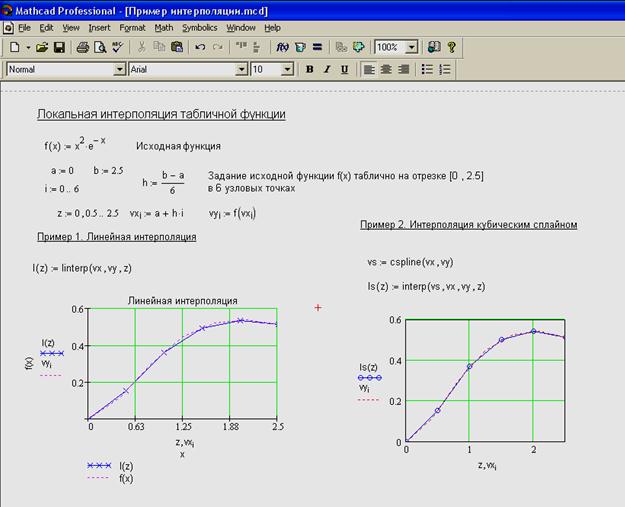
Для создания программного фрагмента используется панель программирования, Кнопки которой имеют следующее назначение:
Add Line – Создание и расширение программного фрагмента; – Оператор внутреннего локального присваивания. IF – Оператор условия. FOr – Оператор цикла с заданным числом повторений. WHile – оператор цикла с предусловием. Оtherwise – Оператор “иначе”, обычно используется совместно с If для выполнения действий в случаи невыполнения условия. Break – Оператор прерывания работы программного фрагмента. Сontinue – Оператор продолжения работы цикла после прерывания. |
Ниже приведен общий вид операторов программного фрагмента, рассмотрены правила их выполнения.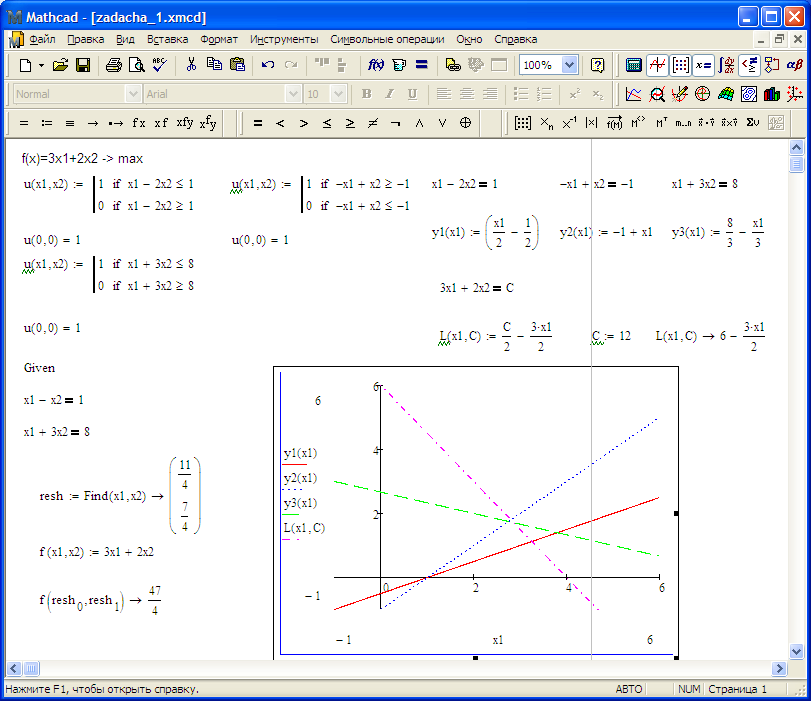
Общий вид оператора If:
Выражение if условие
Порядок выполнения: если логическое выражение, стоящее в Условии, истинно, то вычисляется Выражение, стоящее слева от оператора if.
Общий вид For :
For Var Î Nmin .. Nmax.
Nmin.. Nmax – Диапазон изменения переменной цикла, организуется по правилам формирования дискретных переменных.
Порядок выполнения: переменную цикла Var изменяет свое значение в пределах от Nmin До Nmax с шагом 1 или -1, при каждом новом значении переменной цикла выполняется рабочая часть цикла.
Общий вид WHile:
While условие
Рабочая часть цикла записывается на месте шаблона
Порядок выполнения: рабочая часть цикла выполняется до тех пор, пока логическое выражение, стоящее в условии, истинно.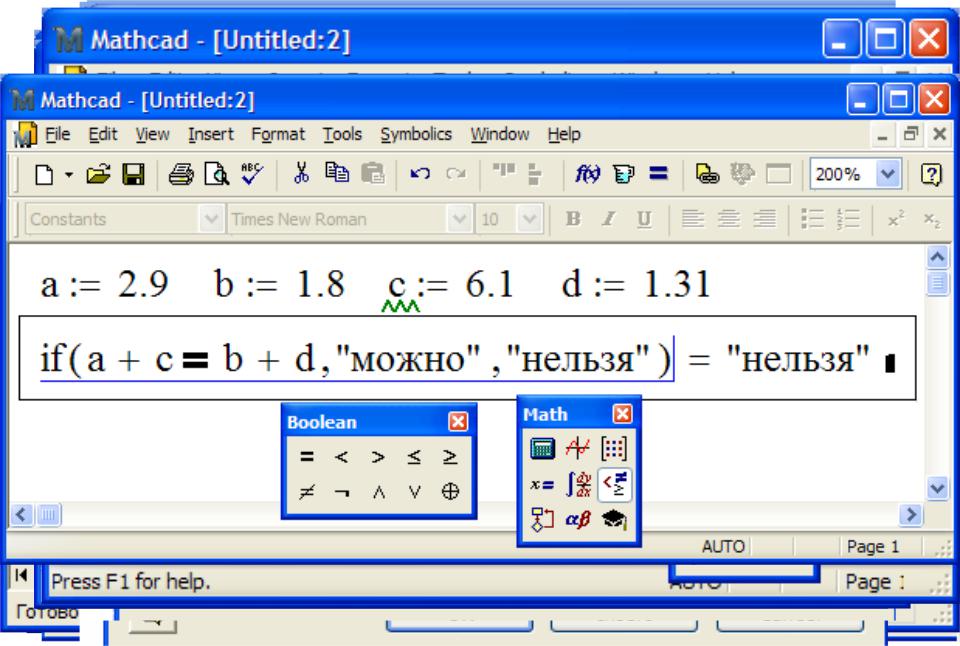
Результаты работы программного фрагмента передаются следующим образом: во внешнюю вычислительную область из программного фрагмента передается значение последнего выражения, вычисленного в программном фрагменте или значение переменной, имя которой записано в последней строке программы.
На рисунке 2.4.1 приведены примеры программных фрагментов. Из примера 1 видно, что программный фрагмент, реализующий линейный алгоритм, может заканчиваться оператором «=», а может быть присвоен переменной, например, k. Программный фрагмент может участвовать при создании пользовательской функции, например, y(x), которая затем вычисляется при конкретном значении ее аргумента, например, 3. Внутренние переменные программного фрагмента являются неопределенными вне его, например, переменная z, которая использовалась в программном фрагменте, не имеет конкретного числового значения вне его.
Пример1 | Пример2 |
Рисунок 2. |
Пример 2 демонстрирует программирование разветвляющихся и циклических алгоритмов. Для реализации разветвляющихся алгоритмов формируется пользовательская функция a(b), которая вычисляется по разным аналитическим зависимостям при различных значениях аргумента. Показана возможность вычисления этой функции в разных точках: при b равном -4, 9 и 15. Программирование циклических алгоритмов продемонстрировано на двух задачах. При решении задачи поиска суммы целых чисел от 1 до 5 применяется программный фрагмент с циклом for, результат получается с помощью оператора «=». Во второй части примера решается задача поиска суммы целых четных чисел от 0 до 10 с помощью оператора цикла while. Результат вычисления присваивается переменной h, хотя внутри цикла для накопления суммы используется переменная s.
| < Предыдущая | Следующая > |
|---|
Обзор mathcad.
 лучший помощник в вычислениях.
лучший помощник в вычислениях.Mathcad Express — бесплатный математический редактор, про который мало кто знает
Прежде всего, приветствую первых посетителей моего блога. Это моя первая статья на Хабре и я надеюсь, что смогу рассказать вам здесь много полезного.
РТС Mathcad – это характерный пример математического ПО, предназначенного для осуществления, как численных, так и аналитических расчетов по формулам и визуализации их результатов в виде графиков.
На протяжении последних лет Mathcad стал очень популярным, и его, на мой взгляд, по праву можно считать математическим пакетом №1 в мире.
Сначала несколько фактов о Mathcad, конечно, известных большинству читателей, т.к. Mathcad у нас уже не один десяток лет используется в ВУЗовском обучении, научных и инженерных расчетах. Скорее всего, вы использовали «старую» версию Mathcad (последняя – за номером 15), мало изменившуюся еще с прошлого века.
В наши дни она вполне успешно сосуществует с более молодым семейством Mathcad, которое носит имя Mathcad Prime. Таким образом, разработчики несколько лет назад полностью переписали код программы, но заботиться о 100%-й совместимости не стали. Поэтому сейчас они благополучно поддерживают оба семейства – и «старый» Mathcad, и «новый» Mathcad Prime.
Таким образом, разработчики несколько лет назад полностью переписали код программы, но заботиться о 100%-й совместимости не стали. Поэтому сейчас они благополучно поддерживают оба семейства – и «старый» Mathcad, и «новый» Mathcad Prime.
Дальше и в этой статье, и в моем блоге, будем говорить именно о Mathcad Prime.
Сразу скажу, что русскоязычный дистрибутив, полнофункциональную 30-дневную версию Mathcad Prime вы можете скачать с сайта русского реселлера РТС. Если вы уже собрались попробовать ее в работе, мой совет – не торопитесь в Мастере установки согласиться с включением тестового 30-дневного периода.
Обратите внимание
Дело в том, что Mathcad Prime, наряду с мощной полнофункциональной версией (окно которой вы видите сверху) имеет бесплатную ограниченную версию, которая называется Mathcad Express. Особенность Mathcad Express заключается в том, что большинство функций в этой версии выключено и являются недоступными.
Тем не менее, в программе Mathcad Express остается довольно богатый функционал, достаточный, по крайней мере, для того, чтобы изучать математику в школе и на 1-м курсе технического ВУЗа.
Формулы можно вводить в документы либо с клавиатуры (если подходящие символы на ней есть), либо при помощи меню Математика. Давайте ради примера посчитаем интеграл от функции cos(x).
Для этого выбираем символ интеграла, а потом — в соответствующие местозаполнители вводим (с клавиатуры) пределы интегрирования и подынтегральную функцию cos(x).
Остается нажать клавишу «равно», чтобы сразу получить ответ.
Надо хорошо себе представлять, что происходит, когда мы вводим знак равенства.
А именно, запускается соответствующий численный алгоритм вычисления интеграла: интервал интегрирования разбивается на некоторое число отрезков, в определенных точках которых вычисляется массив значений подынтегральной функции, который потом пересчитывается в соответствующую аппроксимацию интегральной суммы.
Таким образом, большая часть расчетов скрыта и происходит «за кадром», а на экран выводится лишь конечный результат.
Ключевые инструменты Mathcad – это операторы и функции. Например, в наших расчетах мы использовали оператор интегрирования и функцию косинуса. Для выбора нужной встроенной функции удобно использовать меню Функции.
Например, в наших расчетах мы использовали оператор интегрирования и функцию косинуса. Для выбора нужной встроенной функции удобно использовать меню Функции.
Давайте теперь определим пользовательскую функцию f(t), которая будет зависеть от переменной t. Будем использовать предназначенный для этого в Mathcad оператор присваивания (двоеточие со знаком равно).
Мы определили функцию f(t), как наш интеграл от cos(x) с переменным верхним пределом t. После того, как мы определили функцию f(t), можно посчитать ее значения в точках (для чего достаточно ввести аргумент и нажать клавишу «равно», чтобы вывести в документ ответ).
Для ввода константы, например π, используется или меню Символы, или меню Константы.
Важно
В качестве аргумента можно использовать не только скалярную, но и векторную переменную. Определить ее можно так:Тогда и результатом вычисления функции будет соответствующий вектор. Наконец, одна из важных возможностей Mathcad Express – это возможность построения в документе графиков.
Давайте выделим место в документе и вставим в это место XY-график (т.е. декартов график) нашей функции f(x).
Обозначаем на оси абсцисс имя переменной z (чтобы не путать с уже использованными ранее x и t), а на оси ординат – имя функции f(z), функцию, которую, как вы помните, мы определили, как интеграл от косинуса, равный конечно, sin(z). В итоге, получаем график этой функции.
Скажу еще, что в Mathcad Express (возможно, по недосмотру разработчика) остаются доступными матричные операции. Поэтому Mathcad Express — довольно мощный инструмент для решения задач линейной алгебры.
Переходя по документу вверх и вниз, мы можем просматривать свои расчеты, а управлять ими можно при помощи меню Расчет. По умолчанию, включена опция автоматического расчета (по мере ввода формул в документ, эти формулы сразу рассчитываются). Если эту опцию отключить, то для того чтобы рассчитать документ вручную, достаточно нажить кнопку Рассчитать.
Давайте я на этом остановлюсь, полагая, что задача знакомства читателя с Mathcad Express решена, и в следующих статьях блога, когда речь пойдет, собственно, о математике, я смогу использовать расчеты в Mathcad, не углубляясь в его интерфейс.
В заключение, адресую заинтересовавшегося читателя к своему видеокурсу по математическому анализу, который в формате МООС прошел на портале ИНТУИТ в 2014 году. Все лабораторные работы выполнены в Mathcad Prime и скачать их можно здесь. Все эти материалы на сайте Nerepetitor.
ru бесплатные, регистрация не требуется.
PS. К своему удивлению столкнувшись с несколькими негативными комментариями, отмечу и несколько недостатков Mathcad (опять-таки, с моей точки зрения):
- имеется только Windows версия
- ресурсоемкий, работает медленнее«прошлых» Mathcad
- интерфейс мог бы быть и более удобным
- нельзя сохранить документ в прошлой версии (напр. из 3-й в формате 2-ю)
- документы из «прошлых» Mathcad не всегда удается импортировать в Prime
Источник: https://habr.com/company/nerepetitor/blog/247999/
Урок 18. Символьные вычисления в Mathcad
Mathcad представляет из себя WYSIWYG-редактор, в котором можно размещать математические и текстовые области. До этого урока в математических областях мы проводили только численные расчеты.
До этого урока в математических областях мы проводили только численные расчеты.
Однако расчеты в Mathcad могут быть и символьными (аналитическими) – это позволяет совершать операции дифференцирования, интегрирования, вычисления пределов, разложение в ряд и т.д.
и записать результат вычисления в привычном виде.
Если Вы только начинаете работу с символьными вычислениями, лучше проводите их в отдельных файлах. Если Вы используете одинаковые имена переменных для символьных и численных вычислений, то они могут взаимодействовать и мешать друг другу. Вы можете вставлять результаты из одного файла в другой.
В этом уроке мы будем в основном использовать те инструменты, которые уже изучили, но с той большой разницей, что вычисления будут символьными.
Оператор «Аналитическое преобразование»
Мы уже знаем пять различных знаков «равно» в Mathcad:
Добавим в этот список еще один знак – аналитическое преобразование:
Этот оператор достаточно важен, поэтому будет полезным запомнить его сочетание клавиш.
Совет
Там, где это возможно, аналитическое преобразование дает точный результат, без округления. Примеры:
Если параметры известны, аналитическое преобразование вставит их в результат:
Интегрирование
В качестве первого примера возьмем интеграл: вкладка Математика –> Операторы и символы –> Операторы –> Математический анализ –> Интеграл:
Введите в местозаполнители следующее:
Аналитическое преобразование даст:
Это вычисление динамично – если Вы меняете функцию, результат также меняется. Чтобы найти определенный интеграл, введите в местозаполнители пределы интегрирования:
Таким же образом можно вычислить результат численно:
Mathcad может брать достаточно сложные интегралы, где численное вычисление не работает:
Mathcad может брать двойные и тройные интегралы:
Дифференцирование
Введите оператор дифференцирования, затем переменную, затем функцию:
Пример:
Чтобы найти производную более высокого порядка, введите в дополнительный местозаполнитель за переменной в знаменателе (щелкните по оператору, чтобы увидеть этот местозаполнитель):
Таким же образом можно найти частную производную:
Пределы
Для вычисления предела введите оператор со вкладки Математика –> Операторы и символы –> Операторы –> Математический анализ, введите в местозаполнители точку и функцию и вычислите символьно:
Оператор предела содержит четвертый местозаполнитель (щелкните по оператору, чтобы увидеть его). Используйте этот местозаполнитель, чтобы вычислять предел слева (с [-]) или предел (с [+]). Мы проиллюстрируем все три предела на примере функции тангенса:
Используйте этот местозаполнитель, чтобы вычислять предел слева (с [-]) или предел (с [+]). Мы проиллюстрируем все три предела на примере функции тангенса:
Резюме
В этом уроке мы познакомились с символьными вычислениями.
- Символьные вычисления дают точный результат (там, где возможно). При этом используется оператор аналитического преобразования с сочетанием клавиш [Ctrl+.].
- Проводите символьные вычисления в отдельных файлах; если необходимо, вставляйте результат в изначальный документ.
- Оператор интегрирования можно использовать как символьно, так и численно.
- Оператор дифференцирования может вычислить производную любого порядка. Этот оператор производит символьные и численные вычисления.
- Результат интегрирования и дифференцирования можно использовать в качестве функции.
- Оператор предела вычисляет обычный предел, предел справа и предел слева. Предел можно вычислить только символьно.
Источник: http://sapr-journal. ru/uroki-mathcad/urok-18-simvolnye-vychisleniya-v-mathcad/
ru/uroki-mathcad/urok-18-simvolnye-vychisleniya-v-mathcad/
Mathcad – описание продукта и расширений
Mathcad позволяет создавать корпоративные и отраслевые средства сертифицированных расчётов в различных отраслях науки и техники, обеспечивающие единую методологию для всех организаций, входящих в корпорацию или отрасль.
Что такое Mathcad?
Mathcad – это приложение для математических и инженерных вычислений, промышленный стандарт проведения, распространения и хранения расчетов. Mathcad – продукт компании PTC – мирового лидера разработки систем САПР, PDM и PLM. Mathcad является универсальной системой, т.е. может использоваться в любой области науки и техники – везде, где применяются математические методы.
Документы Mathcad представляют расчеты в виде, очень близком к стандартному математическому языку, что упрощает постановку и решение задач.
Mathcad содержит текстовый и формульный редактор, вычислитель, средства научной и деловой графики, а также огромную базу справочной информации, как математической, так и инженерной.
Обратите внимание
Редактор формул обеспечивает естественный «многоэтажный» набор формул в привычной математической нотации (деление, умножение, квадратный корень, интеграл, сумма и т.д.). Мощные средства построения графиков и диаграмм сочетают простоту использования и эффектные способы визуализации данных и подготовки отчетов.
Вычислительные средства Mathcad обеспечивают расчеты по сложным математическим формулам, включая численные методы и аналитические преобразования.
Mathcad имеет большой набор встроенных математических функций, позволяет вычислять ряды, суммы, произведения, интегралы, производные, работать с комплексными числами, решать линейные и нелинейные уравнения, а также дифференциальные уравнения и системы, проводить минимизацию и максимизацию функций, выполнять векторные и матричные операции, статистический анализ и т.д. Автоматически ведётся контроль размерностей и пересчёт в разных системах измерения (СИ, СГС и др.).
Mathcad – промышленный стандарт
Mathcad является мировым стандартом для инженерных вычислений.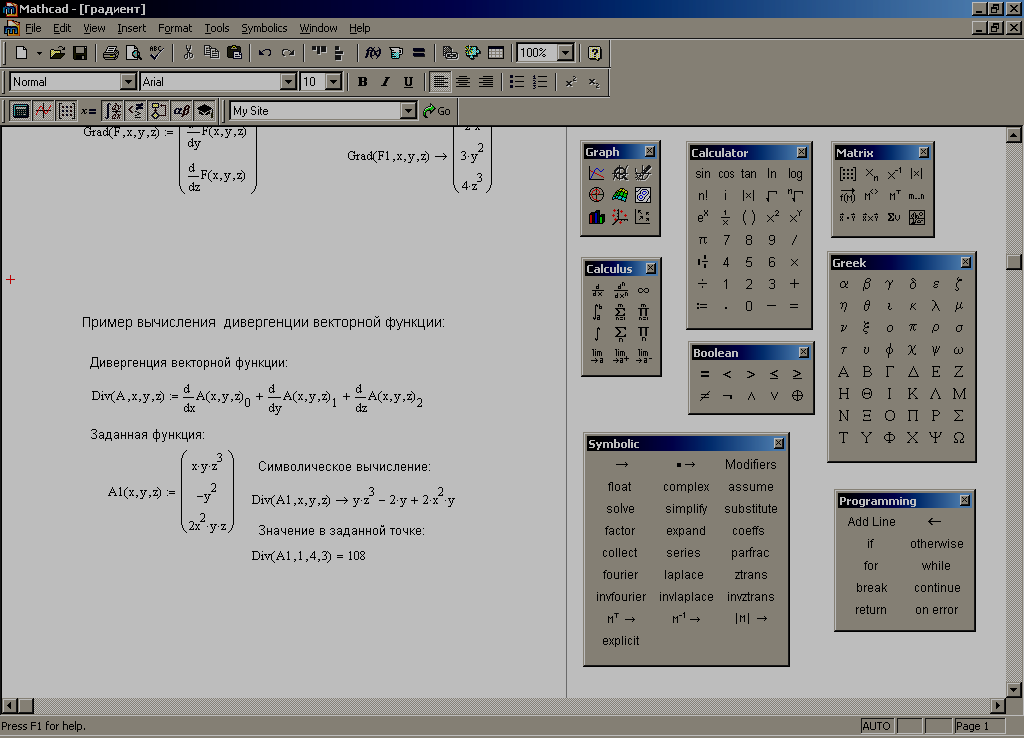 На данный момент его используют более 250 000 инженеров по всему миру.
На данный момент его используют более 250 000 инженеров по всему миру.
С помощью простого и понятного интерфейса в виде «волшебной» электронной доски инженеры могут комбинировать текст, «живые» вычисления и графики на одном рабочем листе.
Mathcad обеспечивает непревзойденный диапазон вычислительных возможностей, включая более 400 встроенных функций и автоматизированное управление единицами измерения.
Mathcad обеспечивает уникальную, интуитивную инженерную среду, которая позволяет быстро осуществлять важные инженерные вычисления, в том числе и разработку технического задания, анализ исходных данных, выбор методов решения, уравнений, обоснование допущений, а также обмениваться этими вычислениями.
Текущие версии Mathcad
Приобретая Mathcad сейчас, вы, фактически, получите две программы:
- Mathcad Prime 3.0 – новая редакция программы;
- Mathcad 15 – традиционная редакция (будет поддерживаться PTC до выхода версии Mathcad Prime 4.
 0 + еще два года).
0 + еще два года).
Программы имеют примерно схожий функционал, но существенно различаются строением интерфейса (в частности, Mathcad Prime содержит ленту и располагает расширенными средствами представления расчетов).
В чем отличие Mathcad от другого математического ПО?
Mathcad – это первое и единственное решение для ведения инженерных вычислений, которое одновременно позволяет вести сами вычисления и документировать их, существенно снижая риск появления дорогостоящих ошибок.
В отличие от классического инструмента программирования или электронных таблиц интерфейс Mathcad отображает на дисплее естественную математическую нотацию, понятную даже людям, далеким от компьютеров.
Так как рабочие листы содержат вычисления в реальном времени, то одно единственное нажатие клавиши, изменяющее входные данные или вид уравнения, немедленно возвращает обновленный результат.
В случае изменения значения переменной происходит немедленный пересчет результата и обновление двумерных или трехмерных графиков, что избавляет от необходимости пересчета вручную. Результаты вычислений сохраняются в рабочих листах, которые могут использоваться повторно и легко преобразуются в целый ряд форматов.
В новой версии Mathcad Prime 3.
Важно
0 появилась долгожданная возможность внешнего программирования: теперь вы можете создать программу на C++ или Fortran-е за пределами Mathcad (например, в Microsoft Visual Studio).
Внутри Mathcad эта программа будет работать, как пользовательская функция, причем передать в нее и из нее параметры можно в той же форме, что и для обычной встроенной функции Mathcad.
Mathcad интегрируется с другими продуктами
Формат файлов XML и поддержка стандартных интерфейсов облегчают совместное использование рабочих листов, методов или числовых значений с другими пользователями и системами, включая управление документооборотом, автоматизированным проектированием (CAD) и решениями по управлению сведениями об изделии (PDM). Mathcad бесшовно интегрируется с другими продуктами PTC: Creo® (ранее Pro/ENGINEER®) – лидер рынка ПО для трехмерного автоматизированного проектирования (CAD), автоматизированного управления (CAM) и автоматизированного конструирования (CAE).
Мощная взаимная интеграция обеспечивает уникальные возможности высокопроизводительной инженерии.
Mathcad может использоваться для прогнозирования поведения проектируемой конструкции, а результаты могут быть использованы для определения параметров и размеров в объектах Creo.
Параметры и размеры моделей Creo также могут быть возвращены в Mathcad для дальнейшего анализа конструкции. Кроме того, рабочие листы Mathcad могут храниться и обрабатываться в системе PTC Windchill.
Это гарантирует, что все критически важные инженерные вычисления будут централизованно архивироваться и могут повторно использоваться в будущих совместных проектах. Mathcad легко интегрируется с огромным количеством баз данных и ПО сторонних производителей, включая Microsoft Excel®, MATLAB® от MathWorks и др.
Почему в ведущих компаниях Mathcad используется в качестве стандартной программы?
Mathcad позволяет инженерам заниматься проектированием, выполнять вычисления и документировать работу в легко читаемом формате, удобном для совместного и повторного использования.
Все это улучшает проверку, сертификацию, публикацию и совместную работу на всех этапах разработки.
Результатом является ускорение разработки изделий, повышение их качества, лучшее соответствие стандартам и интеграция Mathcad в существующие инженерные приложения.
В новой версии Mathcad Prime 3.
Совет
0 рабочие формулы можно размещать в пределах текста, что позволяет добиться идеальной читаемости и целостности документа и использовать один и тот же файл для проведения вычислений, хранения, распространения и подготовки отчетов.
Семейство продуктов Mathcad позволяет компаниям автоматизировать инженерные вычисления и их документирование, а также быстрее создавать более качественные продукты. Mathcad используется более чем в 90% компаний из списка Fortune 1000, представляющих множество промышленных вертикалей.
Пакеты расширений Mathcad
Пакеты расширений представляют собой набор дополнительных функций, встроенных автоматически в Mathcad Prime. Доступ к ним находятся в главном меню программы, в меню “Функции”. Всего для расширения возможностей Mathcad по отдельным научным дисциплинам компания PTC предлагает четыре пакета расширений Mathcad.
Пакет расширений Mathcad для обработки данных
Дает возможность инженерам в Mathcad легко импортировать, анализировать структуры данных и их взаимозависимость, и управлять ими.
Пакет расширений Mathcad для обработки сигналов
Предлагает более 70 встроенных функций обработки сигналов для обработки аналоговых и цифровых сигналов, их анализа и визуализации.
Пакет расширений Mathcad для обработки изображений
Реализует алгоритмы сглаживания, повышения четкости, определения границ, размывания и расширения для цветных и черно-белых изображений. Применим в медицине, астрономии, метеорологии, геофизике, геологии, эхолокации и в целом ряде других областей.
Пакет расширений Mathcad для работы с вейвлетами
Реализует современный подход вейвлетного анализа сигналов, изображений и временных рядов. Пакет будет полезен инженерам, которым требуется сжатие очень больших объемов данных (например, дактилоскопических данных или кодов магнитного резонанса).
Обучение и внедрение, проводимые компанией PTS
Mathcad – широко распространенное приложение, на основе которого изучают технические науки студенты во многих университетах мира. Опыт компании PTS позволит максимально быстро внедрить Mathcad и другие продукты PTS в работу вашего предприятия или учебного заведения.
Компания PTS сертифицирована для проведения обучения по программам и методике компании PTC. Обучение проводится как по стандартным курсам PTC, так и по адаптированным в соответствии с потребностями конкретных заказчиков.
Все курсы переведены на русский язык компанией PTS и соответствуют актуальным версиям. Курсы обычно проводятся на территории заказчика.
По окончании обучения слушатели, успешно освоившие курс, получают стандартный сертификат компании PTC.
Руководитель направления Mathcad в PTS – к.ф.-м.н. Дмитрий Кирьянов, имеющий 15-летний опыт работы с Mathcad, автор нескольких десятков курсов и книг, опубликованных в России и США. Некоторые из ресурсов доступны онлайн и помогут вам, если вы планируете самостоятельное обучение работе в Mathcad.
Источник: http://pts-russia.com/products/mathcad/mathcad-info
Чем расчеты в Mathcad лучше работы с электронными таблицами Excel
Разработчики Mathcad постоянно совершенствуют данное программное средство, чтобы сделать его лучше для пользователей. Самым последним обновлением стала программа Mathcad Prime 3.0. Благодаря ей конструкторы получили возможность быстро и удобно обрабатывать огромные объемы числовых значений, использовать новые возможности разработки и конструирования объектов.
Любое другое программное средство, предназначенное для формирования электронных таблиц, создания презентаций или редактирования текста отличается сложным процессом сбора данных и их непосредственного применения.
Все те же операции можно сделать гораздо быстрее и эффективнее, если воспользоваться средствами Mathcad, его программные компоненты позволяют без труда заполнить соответствующие формулы, картинки или данные любого другого типа.
Обратите внимание
Как результат, существенно упрощается не только сбор данных, но и процессы верификации, а также повторного использования заданной информации.
Именно поэтому мы постараемся разобраться с тем, какими же преимуществами обладает Mathcad перед другими программными средствами.
Наглядность расчетов
Одной из главных особенностей проведения расчетов средствами Mathcad является то, что используемые формулы всегда находятся на виду у конструктора. Именно поэтому математические данные, никогда не теряют наглядности. Благодаря такому расположению элементов можно довольно быстро отыскать промахи и проблемы в расчетах.
Напротив формульных значений располагаются таблицы, которые отображают лишь результат подсчетов, но при необходимости уравнение всегда можно увидеть, если кликнуть мышкой по определенному значению в таблице. Именно формулы помогают пользователю программы на интуитивном уровне разобраться с порядком проведения вычислений, которые нередко показаны в виде непонятных скриптов.
Наименования параметров
Расчеты типа Mathcad применяют такие наименования параметров и переменных, которые являются вполне привычными для инженеров. Аналогичные имена можно встретить в технической литературе и нормативных документах.
Что же касается других программных средств, предназначенных для создания электронных таблиц, то там используется совершенно иной метод: наименование переменных представляют собой прямые ссылки на ячейки с пояснениями.
Как правило, при огромных объемах подобных ссылок пользователю бывает очень трудно разобраться с источниками.
Физические единицы измерения
Если в процессе работы с Mathcad конструктор по той или иной причине не применяет правильные единицы измерения, ему не удастся провести расчет.
Более того, любую ошибку, связанную с некорректным внесением данных, всегда можно изменить, что автоматически повлечет за собой исправление результатов расчетов. В Mathcad имеется специальный программный компонент, отвечающий за проверку правильности использования единиц измерения.
Это значит, что вы не сможете принудить программу сложить или вычесть физические величины, которые отличаются друг от друга по смыслу и назначению.
Однако в электронных таблицах конструктор может вносить в ячейки самые разные данные и единицы измерения. Отображаясь в поле ячейки, данная информация не будет оказывать практически никакого влияния на результат вычислений. Получается, что никакого автоматического контроля над ошибками пользователя не будет.
Документирование
Еще одной изюминкой Mathcad является работа программы по принципу «Что видишь, то и получаешь». Благодаря нему пользователь в итоге получает документированное вычисление на максимально профессиональном уровне.
Интересно, что конструктор в процессе работы может не только производить требуемые расчеты, но и проверять тексты на грамотность, дополнять их сносками на достоверные источники, личными записями о применяемых методиках.
Для того чтобы выставить акцент на ту или иную часть документа, что бывает особенно актуально в некоторых случаях, можно воспользоваться средствами форматирования. Проявляется грамотный тандем текстовых и математических элементов.
Применение шаблонов
Для стандартизации документов и файлов Mathcad использует шаблоны, которые содержат всю необходимую информацию для создания пояснительной документации в соответствии с корпоративными требованиями заказчиков.
Работая с шаблоном, конструктор получает доступ к форматированию, профильным формулам и выражениям, а также пользовательской системе единиц измерения.
Это избавляет инженера от необходимости вводить те или иные данные вручную.
Совместная работа Mathcad и Microsoft Excel
Если вам нравится работать с таблицами Microsoft Excel, тогда вам непременно придется по вкусу информация о том, что еще одним преимуществом работы с Mathcad является интеграция программы с данным программным компонентом. Сделано это таким образом, что он в виде отдельной таблицы входит в состав нового документа Mathcad. Таким образом, пропадает необходимость в преобразовании данных.
Источник: https://archicad-autocad.com/uroki-mathcad/chem-rascheti-v-mathcad-luchshe-raboti-s-elektronnimi-tablitsami-excel.html
История создания и развития программы.
Вскоре после окончания второй мировой войны потребность в автоматизации математических расчетов привела к созданию компьютеров (computer — в буквальном переводе “счетная машина”). Но широкого применения первые поколения таких машин на электронных лампах не получили.
Они были дороги и громоздки, а потому доступны лишь специалистам. С развитием микроэлектроники появились специализированные, предназначенные для математических расчетов миниатюрные компьютеры личного пользования — программируемые калькуляторы [I].
Они широко применяются и сейчас.
Однако в последние годы массовое распространение получили куда более мощные, быстрые и универсальные персональные компьютеры (ПК), имеющие превосходные графические возможности и используемые практически во всех сферах науки, производства, бизнеса и образования.
Само по себе появление компьютеров не упрощало математические расчеты, а лишь позволяло резко повысить скорость их выполнения и сложность решаемых задач.
Пользователям ПК, прежде чем начинать такие расчеты, нужно было изучать сами компьютеры, языки программирования и довольно сложные методы вычислений, применять и подстраивать под свои цели программы для решения расчетных задач на языках Бейсик или Паскаль.
Поневоле ученому и инженеру, физику, химику и математику приходилось становиться программистом, к сожалению, порою довольно посредственным.
Важно
Широкую известность и заслуженную популярность еще в середине 80-х годов приобрели интегрированные системы для автоматизации математических расчетов класса MathCAD, разработанные фирмой MathSoft (США).
По сей день они остаются единственными математическими системами, в которых описание решения математических задач дается с помощью привычных математических формул и знаков. Такой же вид имеют и результаты вычислений. Так что системы MathCAD вполне оправдывают аббревиатуру CAD (Computer Aided Design), говорящую о принадлежности к наиболее сложным и продвинутым системам автоматического проектирования — САПР. Можно сказать, что MathCAD — своего рода САПР в математике.
Возможности программы Mathcad.
Решение дифференциальных уравнений, в том числе и численными методами Построение двумерных и трёхмерных графиков функций (в разных системах координат, контурные, векторные и т. д.
) Использование греческого алфавита как в уравнениях, так и в тексте Выполнение вычислений в символьном режиме Выполнение операций с векторами и матрицами Символьное решение систем уравнений Аппроксимация кривых Выполнение подпрограмм Поиск корней многочленов и функций Проведение статистических расчётов и работа с распределением вероятностей Поиск собственных чисел и векторов Вычисления с единицами измерения Интеграция с САПР системами, использование результатов вычислений в качестве управляющих параметров
Документирование всех вычислений в процессе их проведения.
Описание Mathcad и его отличительные черты.
Mathcad универсальная программа позволяющая производить математические расчеты любой сложности, данная программа применима для расчетов в любой области, в том числе и радиотехнических расчетах. Отличительной особенностью данной программы является высокая визуализация процесса ввода данных в программу.
Решение уравнений и различных задач в программе Mathcad не составляет большого труда даже для неопытного пользователя. Уровень визуализации процессов на столько высок, что процесс работы в Mathcad очень схож с работой стандартного редактора формул в программе Word.
В среде Mathcad доступны более сотни операторов и логических функций, предназначенных для численного и символьного решения математических задач различной сложности. MathCAD — математически ориентированные системы.
Помимо собственно вычислений они позволяют с блеском решать задачи, которые с трудом поддаются популярным текстовым редакторам или электронным таблицам.
С их помощью можно не только качественно подготовить тексты статей, книг, диссертаций, научных отчетов, дипломных и курсовых проектов, они, кроме того, облегчают набор самых сложных математических формул и дают возможность представле ния результатов, в графическом виде.
Совет
Система MathCAD предоставляет собой мощное, удобное и наглядное средство описания алгоритмов решения математических задач. Система MathCAD настолько гибка и универсальна, что может оказать неоценимую помощь в решении математических задач как школьнику, постигающему азы математики, так и академику, работающему со сложнейшими научными проблемами.
Разработчики Mathcad сделали ставку на расширение системы в соответствии с потребностями пользователя.
Для этого предназначены дополнительные библиотеки и пакеты расширения, которые можно приобрести отдельно и которые имеют дополнительные функции, встраиваемые в систему при установке, а также электронные книги с описанием методов решения специфических задач, с примерами действующих алгоритмов и документов, которые можно использовать непосредственно в собственных расчетах. Текстовый редактор служит для ввода и редактирования текстов. Тексты являются комментариями, и входящие в них математические выражения не выполняются. Текст может состоять из слов, математических символов, выражений и формул. Формульный процессор обеспечивает естественный «многоэтажный» набор формул в привычной математической нотации (деление, умножение, квадратный корень, интеграл, сумма и т.д.). Последняя версия Mathcad полностью поддерживает буквы кириллицы в комментариях, формулах и на графиках.
Вычислитель обеспечивает вычисление по сложным математическим формулам, имеет большой набор встроенных математических функций, позволяет вычислять ряды, суммы, произведения, интегралы, производные, работать с комплексными числами, решать линейные и нелинейные уравнения, а также дифференциальные уравнения и системы, проводить минимизацию и максимизацию функций, выполнять векторные и матричные операции, статистический анализ и т.д.
Mathcad относится к системам компьютерной алгебры, то есть средств автоматизации математических расчетов. В этом классе программного обеспечения существует много аналогов различной направленности и принципа построения. Наиболее часто Mathcad сравнивают с такими программными комплексами, как Maple, Mathematica, MATLAB, а также с их аналогами MuPAD, Scilab, Maxima и др.
Впрочем, объективное сравнение осложняется в связи с разным назначением программ и идеологией их использования. Возможности Mathematica ориентированы на пользователей — профессиональных математиков. Тоже самое можно сказать и о Maple.
Maple изначально создавался для численного решения математических задач, он ориентирован на решение задач именно прикладной, а не теоретической математики, когда нужно получить результат без углубления в математическую суть задачи. Однако, последние версии приближают вычислительную мощность Mathcad к Maple.
Основное отличие Mathcad от аналогичных программ — это графический, а не текстовый режим ввода выражений. Для набора команд, функций, формул можно использовать как клавиатуру, так и кнопки на многочисленных специальных панелях инструментов. В любом случае — формулы будут иметь привычный, аналогичный книжному, вид. То есть особой подготовки для набора формул не нужно.
Обратите внимание
Вычисления с введенными формулами осуществляются по желанию пользователя или мгновенно, одновременно с набором, либо по команде. Обычные формулы вычисляются слева направо и сверху вниз (подобно чтению текста). Любые переменные, формулы, параметры можно изменять, наблюдая воочию соответствующие изменения результата.
Это дает возможность организации действительности интерактивных вычислительных документов.
В среде Mathcad фактически нет графиков функций в математическом понимании термина, а есть визуализация данных, находящихся в векторах и матрицах (то есть осуществляется построение как линий так и поверхностей по точкам с интерполяцией), хотя пользователь может об этом и не знать, поскольку у него есть возможность использования непосредственно функций одной или двух переменных для построения графиков или поверхностей соответственно. Так или иначе, механизм визуализации Mathcad значительно уступает таковому у Maple, где достаточно иметь только вид функции, чтобы построить график или поверхность любого уровня сложности. Однако следует помнить об основной области применения Mathcad — для задач инженерного характера и создание учебных интерактивных документов, возможностей визуализации вполне достаточно. Опытные пользователи Mathcad демонстрируют возможность визуализации сложнейших математических конструкций, но объективно это уже выходит за рамки назначения пакета.
Новая версия продукта – это Mathcad Prime 1.0, который отличается ещё более удобным современным интерфейсом, мощным математическим аппаратом и многим другим. Так же, благодаря версии Prime, Mathad теперь полностью русифицирован.
Вывод.
Mathcad является одной из лучших программ в своей области. Всё больше дорабатываясь с каждой последующей версией, сейчас она представляет собой незаменимый инструмент для людей, имеющих дело с расчётами и вычислениями.
Так же Mathcad нашла применение в различных областях науки.
Она позволяет производить символьные и аналитические вычисления, производит операции с матрицами, системами уравнений, функциями, а так же строить графики и диаграммы по полученным результатам.
Источник: http://good-sale.ru/node/100220
MathCAD — это просто! Часть 1. Знакомство
MathCAD — замечательный математический пакет, верный помощник и для студента, и для инженера, и для ученого. И для представителей многих других профессий тоже — ведь в мире существует огромное число различных задач, решить которые можно с помощью математики.
Делать это с помощью MathCAD намного проще, чем решать, вооружившись листком бумаги и ручкой, и даже проще, чем программировать собственные вычислительные алгоритмы.
Именно поэтому стоит изучить работу в MathCAD — эта программа придумана для облегчения жизни, которую все так и норовят усложнить.
Почему именно MathCAD?Математических пакетов в мире существует множество: Maple, Mathematica, Matlab: И вроде бы MathCAD — не самый крупный по объему, а значит, и не самый из них.
Почему же стоит выбрать именно MactCAD? Во-первых, стоит сказать, что MathCAD — самая простая из перечисленных выше программ для того, кто владеет математикой и представляет себе, чего именно он хочет с ее помощью добиться.
Все математические формулы и преобразования в MathCAD’е записываются точно так же, как в классических учебниках по матанализу и диффурам, а большинство задач можно решить, не прибегая к программированию. Во-вторых, MathCAD — довольно универсальная среда, одинаково хорошо умеющая и считать численные выражения, и преобразовывать символьные, и строить графики.
Кроме того, эта программа имеет довольно неплохие возможности по оформлению готовой работы прямо в ней — вы можете вставлять пояснения, таблицы, а о графиках я уже и так упоминал. Прямо из MathCAD вы сможете экспортировать свою работу в HTML и вывесить на сайте, напечатать ее или переслать коллегам по электронной почте.
Благодаря тому, что MathCAD имеет простой (по сравнению с другими математическими пакетами) пользовательский интерфейс, а также благодаря универсальности функционала этой среды практически любой пользователь, нуждающийся в услугах , сможет работать с MathCAD’ом. Ну и, наконец, третье — это скорость работы MathCAD.
Лично я начинал работать с этой программой на стареньком Pentium-200 с 64 Мб оперативной памяти. И при этом MathCAD (конечно, более старой версии, чем та, которой я пользуюсь сейчас) работал весьма и весьма шустро. В общем, думаю, причины, по которым стоит выбрать именно MathCAD, вполне ясны и понятны. Теперь давайте обговорим другой вопрос, не менее важный: где именно можно добыть эту волшебную программу?
Где взять MathCAD?Думаю, не открою для вас Америки, если скажу, что очень многие программы можно найти в магазинах, ларьках и павильонах на рынках, где торгуют компакт-дисками. На мой взгляд, это самый оптимальный способ приобретения MathCAD.
Почему? Потому, что скачивать из интернета дистрибутив программы для большинства отечественных пользователей будет довольно-таки затруднительно: весит он более 200 мегабайт, так что и тем, кто сидит на dial-up, и тем, кто платит за трафик из своего кармана, выходит накладно.
Кроме того, зачастую на дисках, где встречается MathCAD, есть и к нему — для большинства пользователей этой программы вещь просто необходимая, потому что доходы им не позволяют купить лицензионную версию пакета.
Важно
Я, конечно, ни в коем случае не призываю вас пользоваться взломанной версией и заниматься, таким образом, пиратством, но просто хочу отметить, что студентам, инженерам и профессорам в нашей стране иначе с MathCAD’ом работать довольно затруднительно.
Тем не менее, если есть необходимость скачать программу, во всемирной паутине нетрудно найти дистрибутив ее пробной версии. Лежит он по адресу сайт . Можно попробовать также поискать на разных форумах ссылки на выложенные на какой-нибудь сервис типа RapidShare образы дисков с MathCAD’ом, но я не думаю, что это будет лучше, чем скачивать пробную версию с официального сайта программы.
Теперь еще, думаю, стоит уточнить, какую именно версию следует устанавливать, потому что на дисках версии встречаются самые разные, буквально с первой по последнюю. На мой взгляд, все зависит от того, насколько у вас мощный компьютер: если ему уже лет пять, то стоит поискать что-нибудь вроде MathCAD 2000, а если ему три года и меньше, то подойдет и последняя версия, 14-я.
Большинству пользователей различия между разными версиями MathCAD будут практически незаметны невооруженным глазом, а потому особенно стараться, добывая, устанавливая и героически запуская именно 14-ю версию MathCAD’а, на мой взгляд, не стоит.
При написании статей я буду использовать 13-ю версию MathCAD’а, а потому, если в вашей версии что-то не будет работать — пишите, разберемся.
Знакомимся с интерфейсомНесмотря на то, что интерфейс у программы MathCAD предельно простой, у того, кто сталкивается с ней впервые, он может вызвать замешательство. Поэтому давайте посмотрим на то, что, собственно, в этом интерфейсе содержится. Взгляните на скриншот главного окна MathCAD.
Там вы увидите рабочую область (в ней расположены формулы и график) и различные панели инструментов. На самом деле, при первой загрузке программы панели видны далеко не все — хотя они все сразу обычно и не нужны. Да и рабочая область при первой загрузке пустая.
Но то, что она пустая, легко можно поправить — щелкните мышкой в любом ее месте и начните печатать.
Совет
Обратите внимание, что, в отличие от текстовых редакторов, электронных таблиц и прочих привычных большинству пользователю программ, MathCAD никак не ограничивает размещение объектов в рабочей области — вы можете перемещать текст, формулы, графики мышкой в любое удобное для вас место и, таким образом, компоновать все так, чтобы было максимально удобно работать. Правда, когда это все нужно скомпоновать красиво, могут возникнуть некоторые трудности, но об этом мы с вами поговорим как-нибудь потом. Для того, чтобы эффективно работать с программой, нужно, тем не менее, сделать видимыми некоторые панели инструментов, которые скрыты по умолчанию. Зайдите в меню View, затем в подменю Toolbars и поставьте флажки напротив всех названий панелей инструментов. Конечно, как я уже говорил, все сразу при работе они будут нужны очень редко, и лучше сразу все их не отображать, чтобы они не заполонили рабочую область, как на втором скриншоте. Однако сейчас мы с вами будем с ними знакомиться, а потому лучше, чтобы они были на виду. Название панели подписано сверху над кнопками, которые она содержит.
. Calculator — панель, содержащая цифры, математические знаки и стандартные математические функции (квадратный корень, синус и косинус, логарифм с экспонентой и т.д.). Одна из самых полезных и нужных особенно часто панелей. . Graph — панель, используемая при работе с графиками.
Графики в MathCAD’е нужны довольно часто (большая часть людей — визуалы и информацию на графике воспринимают лучше, чем по формулам), и панель для работы с графиками бывает нужна тоже довольно-таки часто. . Matrix — панель для работы с матрицами и векторами.
С ее помощью можно задавать матрицы и матричные преобразования (вычисление обратной матрицы, транспонирование, вычисление детерминанта), вычислять произведения векторов, работать с ранжированными переменными. . Evaluation — панель с операторами присваивания значений и вывода результатов расчетов.
Тоже довольно часто нужна, а потому полезна на экране. . Calculus — панель с дифференциальными и интегральными операторами. Содержит в себе операторы взятия производной и интеграла, вычисления суммы, произведения, предела. . Boolean — панель, содержащая булевские операторы, нужные при работе с логическими выражениями. .
Greek — панель, позволяющая внедрить одним щелчком мыши в текст или формулу символы греческого алфавита, как заглавные, так и строчные. . Symbolic — панель для символьных вычислений. Панель очень большая по размерам и нужная сравнительно редко, однако от этого не менее полезная. .
Modifier — чем-то сходная с предыдущей панелью панель символьных модификаторов. О ней мы позже поговорим еще подробнее, как, впрочем, и о самих символьных вычислениях.
. Custom Characters — панель с разными специальными символами, не используемыми непосредственно при вычислениях: знаками градуса, плюс- минус, приближенно равно и т.д.
Как видите, панелей в MathCAD’е существует великое множество, и есть опасность в них запутаться. Однако выручают подсказки, которые появляются при наведении курсора мыши на кнопки, расположенные на панели.
На мой взгляд, обилие панелей в MathCAD’е — скорее благо, нежели зло, а если они начинают мешать, то лучше всего их просто перегруппировать таким образом, чтобы они мешать перестали.
Перемещать панели можно с помощью мышки, а закрывать, естественно, с помощью крестика в правом верхнем углу. Также панель можно стягивать и растягивать за края, меняя, таким образом, ее форму.
Обратите внимание
Некоторые панели, небольшие по размеру, можно перетянуть на верхний край окна к стандартным панелям инструментов или аналогичным образом на нижний край окна. Можно сделать так, чтобы панель разместилась сверху автоматически — для этого нужно дважды по ней кликнуть.
В итоге можно добиться того, чтобы панели на заслоняли друг друга и не мешали работать. Пример того, как разместить их таким образом, показан на третьем скриншоте.
Что ж, пока что для знакомства, на мой взгляд, достаточно. В следующий раз мы с вами уже приступим непосредственно к вычислениям.
Компьютерная газета
Источник: https://mathcadworld.wordpress.com/2010/10/15/mathcad-introduction/
MathCad – система компьютерной алгебры из класса САПР
Практически любая инженерная или физическая задача предполагает под собой большое количество математических расчетов.
Долгое время это было рутиной и занимало огромное количество времени, а если быть более точным, то примерно 80%.
С изобретением компьютера, а позже и специальных задач, проведение подобных расчетов значительно упростилось. Сегодня одной из самых популярных и простых в использовании считается MathCad.
История создания
Первая версия вышла в 1986 году и на то время была незаменимым помощником инженеров. Уже тогда, помимо простых и сложных алгебраических вычислений, была возможность построения 2d графики. Чуть позже программу научили строить и 3d графику. Впрочем, развитие очень сильно тормозили слабые вычислительные возможность ЭВМ.
Ален Раздов – человек, который придумал и написал первую версию программы, прекрасно понимал, что нужно большинству пользователей и к 5-ой версии реализовал, то что в будущем стало одним из главных преимущества MathCad. Это была возможность подключать собственные функции к программе.
Нужную функцию можно было написать на языке С, откомпилировать и прикрепить к программе через DLL-механизм. Для того, чтобы было понятнее, что же в этом такого классного можно привести пример.
Каждый день на работе инженер сталкивается с большим количеством просчетов. Наверняка определенные куски вычислений повторяются из раза в раз.
Да, MathCad уже дал возможность даже копировать уже написанные формулы и просто изменять входящие значения, но при этом расчеты все равно оставались визуально большими.
Программа дала возможность скрыть всю эту алгебраическую часть через создание функции. В дальнейшем это все заменяется всего лишь одной строчкой. Удобство и комфорт.
Говоря об удобстве, нельзя не упомянуть замечательный дружеский интерфейс. Функции, которые чаще всего используются, выведены на отдельную панель, которую, к слову, можно изменять под себя. Второй момент это использования принципа “получаешь то, что видишь”.
Важно
То есть, работая в программе, вы визуально наблюдаете все так же, как если бы писали все на бумаге. Это же является преимуществом, когда нужно распечатать документ. По факту, можно скачать MathCad и уже через 30 минут изучения, начать полноценно в нем работать.
Во всемирной сети, вы также можете mathcad скачать торрент на большой скорости.
Подробно рассматривать ранние версии программы особого смысла нет, а поэтому сразу же перейдем к 2006 году, когда компанию Mathsoft, созданную Аланом Раздовым, купила корпорация PTC. Уже совместными усилиями они начали разрабатывать MathCad 14.
Особенности MathCad 14
Главное, что следует отметить, это изменение ядра программы. Используемые ранее подмножества Maple заменили на алгебраическое ядро MuPad. Это повысило точность и качество расчетов, что несомненно является плюсом, но добавило проблем пользователям.
Дело в том, что некоторые файлы, созданные в ранних версиях теперь могли попросту не открываться в 14-ой. А если и открывались, то не было уверенности, что все правильно работает.
Поэтому люди, которые долгое время уже работали с MathCad, очень неохотно переходили на новую версию.
Изменений в программе было много, например, введение полной поддержки всех шрифтов Unicode или орфографическая проверка на 15 языках мира, но все это мелочи.
Что действительно важно для пользователя, так это введение тандема операторов «… := … = …». Теперь можно было присвоить переменной выражение и тут же получить решение.
Казалось бы, это вообще не существенно, но это еще один шаг в сторону стандартной и обычной записи расчетов и уход от программной и машинной записи.
Также добавлены три новых алгоритма решения дифференциальных уравнений и несколько новых функций в символьный процессор.
Нельзя сказать, что MathCad 14 скачать хотели очень многие, но решающим для некоторых стала интеграция с пакетом Pro/ENGINEER.
Совет
Это дало колоссальные возможности в комплексе инженерно-конструкторских работ. Теперь строить модель по расчетам или вести расчеты с учетом геометрии модели стало значительно проще и легче.
Даже те, кто не особо любил одну или вторую программу перешли на эту связку, просто из-за экономии времени.
MathCad 15
MathCad 15 скачать можно было уже в 2010 году. Были доработаны ряд функций и продолжилась интеграция с различными базами данных, таких как KnovelMath и Truenumbers. То есть корпорация PTC продолжала делать программу как можно более удобной и расширять возможности.
Самое главное, что можно отметить в отличии MathCad 15 от предыдущей версии – это расширение функционала по расчетам для планирования экспериментов. И конечно, добавили поддержку новых на то время Windows 7 и Excel 2007.
MathCad Prime
Следующим значимым этапом в развитии программы после покупки MathSoft корпорацией PTC и замены алгебраического ядра стал выход MathCad Prime.
Можно сказать, что это совершенно новая программа, просто написанная с учетом предыдущего опыта полученного от создания “цифровых версий”.
MathCad Prime действительно писался полностью с нуля, имеет обновленный пакет функций в том числе и для планирования экспериментов. Без проблем работает на Windows 7 и поддерживает работу с MS Excel.
Также MathCad стал более “живой”. Простой новый интерфейс и текстовые примечания к расчетам очень быстро сделали ее любимой программой высших учебных заведений и небольших компаний. Сложно найти современного студента-инженера, который пренебрегает этой программой.
В ней возможно легко и быстро сделать как прочностные расчеты, так и решать задачи в основе которых лежит дискретная математика. При этом, если возникают ошибки, а они возникают, то достаточно исправить несколько переменных и не приходиться все заново пересчитывать. Все за тебя меняет программа.
Такой подход значительно облегчает и решение проектировочных задач, в которых присутствует несколько кругов итерации.
MathCad Prime 3.0
Сегодня самой свежей версией является MathCad Prime 3.0, которая представлена публике 16 октября 2013 года. Сами разработчики выделяют следующие особенности и возможности:
- Глобальное определение переменных. Это значит, что вы можете задать значение переменной в любом месте рабочего листа, не заботясь о последовательности просчетов. Если же схема расчетов не стандартна и программа ее не определяет, то можно воспользоваться программными функциями “if” и “then”.
- Математика и текст едины. После проведения всех расчетов вам не потребуется оформлять их и доводить до презентабельного вида в какой-то другой программе. В MathCad встроен хороший текстовый редактор, которые позволяет добавлять различные заметки, пояснения и записи. На выходе вы получите документ, который не стыдно распечатать и отнести преподавателю на проверку.
- Создание шаблонов. Когда вы часто пользуетесь программой и занимаетесь одним направлением, то достаточно удобно будет создавать шаблоны, которые уже включают в себя определенный набор формул, текст и т.д. Это освобождает от надобности каждый раз проделывать одну и ту же работу, переходя к другой задаче.
- Форматирование. Как уже упоминалось выше, в MathCad встроен текстовый редактор с достаточным набором возможностей. Но с помощью него можно редактировать и форматировать формулы.
- Интеграция функций. Несмотря на то, что в MathCad встроено более 3-х тысяч функций, охватить абсолютно все дисциплины невозможно. Поэтому создана возможность программировать и добавлять собственные функции для дальнейшего удобного использования.
- Интеграция с Excel. Чаще всего большой объем данных после разнообразных замеров или подобного сохраняют в таблицах Excel. Но многих не устраивает функционал построения графиков, которые дает это программное обеспечение. MathCad без труда распознает такие таблицы и дает возможность как их экспорта так и импорта.
- Символьные расчеты и формулы. Не всегда есть возможность, а иногда и желание проводить все расчет численно. MathCad дает возможность посчитать все посимвольно, ввести начальные данные и только в конце получить силовое значение.
- Графические инструменты. Нужно построить сложный пространственный график? Вам нужно всего лишь скачать Маткад и сделать это с помощью него легко и быстро.
С покупкой Mathsoft корпорацией PTC изменился и маркетинг. Не всем нужна полная версия программы. Поэтому было принято разделить MathCad на разные пакеты.
Есть возможность самую облегченную и урезанную версию Маткад скачать бесплатно.
Далее идет разделение на индивидуальную версию, многопользовательскую и специальную учебную, которая идет по очень заниженной цене, не требует определенных подтверждений и запросов от учебных заведений.
Обратите внимание
Также разработан специальный веб-интерфейс для которого не нужно покупать или устанавливать саму программу. Впрочем, это не будет лишним, так как с купленной лицензией веб-интерфейс дает более высокий уровень доступа.
Важно
Если вы хотите скачать Маткад русская версия, который у нас также имеется, то это можно сделать здесь.
MathCad Prime 4.0
Можно ли доверять сложные инженерные расчеты электронным таблицам? Ни за что. Поэтому инженеры выбирают приложение PTC Mathcad в качестве инструмента для расчетов. Весной 2017 года компания PTC выпустила самую ожидаемую пользователями версию программного обеспечения Mathcad Prime 4.
0, которая упрощает работу с вашими расчетами и их защиту, позволяя безопасно предоставлять их другим участникам. Основные нововведения в программе коснулись прежде всего безопасности, производительности и удобства использования.
Новая версия позволяет организовывать большие сложные документы и взаимодействовать с ними, предлагает функцию защиты и блокировки областей, чтобы вы могли управлять уровнем доступа, а также теперь можно внедрять содержимое, созданное в других приложениях, в документы PTC Mathcad.
Хотите попробовать – нажмите скачать MathCad Prime 4 беспалано. Так почему же стоит выбирать новый Маткад Прайм:
- Защищенная передача конструкторского замысла и проектных знаний.
- Понятное построение расчетов с использованием стандартного математического представления.
- Создание документов профессионального уровня с использованием активных математических формул, графиков, текста и изображений.
- Адаптация стандартных расчетов.
- Повышение производительности за счет полной поддержки единиц вычисления на всем протяжении расчетов.
- Ускорение обучения и внедрения за счет мгновенного доступа к электронным обучающим материалам.
С покупкой Mathsoft корпорацией PTC изменился и маркетинг. Не всем нужна полная версия программы. Поэтому было принято разделить MathCad на разные пакеты.
Есть возможность самую облегченную и урезанную версию Маткад скачать бесплатно.
Далее идет разделение на индивидуальную версию, многопользовательскую и специальную учебную, которая идет по очень заниженной цене, не требует определенных подтверждений и запросов от учебных заведений.
Обратите внимание
Также разработан специальный веб-интерфейс для которого не нужно покупать или устанавливать саму программу. Впрочем, это не будет лишним, так как с купленной лицензией веб-интерфейс дает более высокий уровень доступа.
Важно
Если вы хотите скачать Маткад русская версия, который у нас также имеется, то это можно сделать здесь.
Источник: http://photoshop-archicad.com/mathcad/mathcad.html
В 11. системы математических вычислений mathcad, mathlab. назначение, возможности, примеры применения.
Системы математических вычислений — программы (или математические системы), которые можно использовать для различных вычислений и вычерчивания графиков (Mathematica, Derive, Statistica, MathCAD, MathLAB и др.). В этих системах процесс вычислений сильно автоматизирован, что позволяет экономить время и больше внимания уделять физическому смыслу получаемого результата. Выбор системы зависит от характера решаемых задач, от вкуса, от практики.
Система MathCAD -разработка фирмы MathSoft. Примерно каждый год появляется новая версия этой системы. В настоящий момент известна версия Mathcad 12.
Назначение системы:MathCAD — это интегрированная система программирования, ориентированная на проведение математических и инженерно-технических расчетов. MathCAD содержит текстовый редактор, вычислитель, символьный процессор и графический процессор.
Фактически документы MathCadпредставляют собой программу, написанную на визуально-ориентированном языке программирования Язык программирования MathCad ориентирован на математические вычисления и потому практически не отличается от обычного языка математических статей, отчетов и книг.
Входной язык MathCad относится к интерпретируемому типу. Это значит, что, когда система опознает какой-либо объект, она немедленно исполняет указанные в блоке операции.
Визуально-ориентированный язык общения системы MathCad надо отличать от языка реализации системы, т.е. обычного языка программирования высокого уровня, на котором написана система. Языком реализации системы MathCad является один из самых мощных языков высокого уровня – С++.
По существу входной язык системы – промежуточное звено между скрытым от пользователя языком документа и языком реализации системы. По мере того как пользователь создает (средствами текстового, формульного, символьного и графического редакторов) в окне редактирования объекты (тексты, формулы, таблицы и графики), система сама составляет программу на некотором промежуточном языке связи. Эта программа хранится в оперативной памяти до тех пор, пока не будет записана на диск в виде файла с расширением .mcd. Однако от пользователя не требуется знание языков программирования (реализации и связи), достаточно освоить приближенный к естественному математическому языку входной язык системы.
К основным объектам входного языка системы MathCAD можно отнести: алфавит, константы, переменные, операторы, функции.
МАТЛАБ (MATLAB) – система компьютерной математики, которая в настоящее время широко применяется исследователями для решения прикладных и теоретических задач на ЭВМ. Название МАТЛАБ происходит от словосочетания “матричная лаборатория (matrixlaboratory), что первоначально соответствовало основному назначению системы – матричным вычислениям. Впоследствии, с развитием системы, в неё были добавлены функции и вычислительные алгоритмы из многих других областей математики. Но основной подход к элементарным операциям, когда число рассматривается как частный случай матрицы, сохранился. В настоящее время МАТЛАБ представляет собой развитую систему, включающую в себя в качестве составных частей инструменты для решения задач из разных областей математики, таких как линейная алгебра, численные методы, динамические системы и т. д.
Пользователю предлагается несколько вариантов использования системы. Основным режимом является режим командной строки, при котором команды, набираемые пользователем на клавиатуре в ответ на приглашение системы, выполняются в диалоговом режиме с немедленной выдачей результата. В этом режиме легко получить решение таких задач, как вычисление определителей, обращение и перемножение матриц, решение систем линейных алгебраических уравнений и др. Для выполнения этих и других операций необходимо вызвать соответствующую функцию системы, передав ей входные параметры и, возможно, сохранить результат для последующего использования.
Ядро МАТЛАБ содержит более тысячи функций. Помимо них доступно большое количество внешних функций, описанных в расширениях системы. В добавление к ним пользователь может создавать свои собственные функции, используя для этого специально предусмотренный язык программирования. Таким образом, МАТЛАБ является расширяемой системой, и это одно из важных её достоинств.
Помимо режима командной строки, являющегося основным режимом работы, некоторые расширения МАТЛАБ предлагают собственные диалоговые средства. Примером такого расширения является PDETool – графический интерфейс, предназначенный для решения дифференциальных уравнений в частных производных. Помимо функций, доступных из командной строки, он также предоставляет пользователю графическую среду, работающую в отдельном окне.
Выше упоминалось о том, что в МАТЛАБ имеется язык программирования. С его помощью можно создавать и реализовывать собственные алгоритмы, используя все доступные функции системы и все основные приёмы программирования, имеющиеся в других языках, такие как подпрограммы, циклы, ветвления, рекурсии и другие. Запись алгоритма на языке программирования МАТЛАБ сохраняется в файле в текстовом формате, либо в специальном внутреннем представлении.
Современные версии МАТЛАБ имеют развитые средства интеграции с другими языками программирования. Непосредственно из МАТЛАБ-программы можно создавать и использовать объекты Java; для написания S-функций (системных функций МАТЛАБ-Simulink) можно использовать языки высокого уровня C, C++, Ada, Fortran; кроме того функции системы МАТЛАБ можно экспортировать в dll и вызывать из других программ. Также можно использовать вычислительные возможности системы, передавая запросы удалённому компьютеру по сети.
На сегодняшний день система МАТЛАБ считается одной из наиболее мощных и развитых систем компьютерной математики.
Статьи к прочтению:
Introduction to MATLAB
Похожие статьи:
Назначение системы smartmath
Система SmartMath и ее возможности Назначение системы SmartMath Начиная с версии 4. 0 система MathCAD обзавелась новым средством оптимизации вычислений —…
Вычисление значений математических выражений
Для вычисления значений различных математических выражений в Pascal существуют различные арифметические функции: Функция Математическое обозначение…
примеров программирования »MathCadHelp.com» Номер 1 в MathCad Assignments
-
Facebook
-
Твиттер
-
Google+
-
Реддит
-
LinkedIn
Среда программирования Mathcad, имеющая всего десять кнопок на палитре программирования, проста в использовании. Тем не менее, за этой простотой скрываются удивительные возможности программирования.В сочетании с богатой числовой и символьной функциональностью Mathcad и вместе с абстрактными структурами данных, предоставляемыми вложенными массивами Mathcad, эти десять операторов позволяют писать сложные программы в Mathcad.
Следующие рисунки иллюстрируют лишь некоторые из возможностей. Поэкспериментируя с программированием в Mathcad, вы откроете для себя множество новых приложений. Дополнительные примеры программирования см. В разделе «Программирование» в QuickSheets Resource Center.А в Mathcad Professional Центр ресурсов включает специальный раздел «Казначейское руководство по программированию», который включает подробные примеры и приложения, чтобы показать вам, как получить больше от программ Mathcad.
Программа для поиска чисел, общих для двух векторов.
Использование сита Эратосфена для поиска простых чисел.
Степень случайной матрицы переходов.
Сглаживание матрицы
Связанные проекты MathCad
- Программирование
- Управление выполнением программы
- Программы в программах
- Условные операторы
- Ограничения символьной обработки
- Галерея анимаций
- Преимущества использования READPRN и WRITEPRN
- Поиск информации в электронной книге
Программирование с помощью PTC Mathcad Prime
Мы все понимаем, насколько важны расчеты и испытания для инженерных проектов.Иногда для получения правильных результатов требуется множество итераций. Однако выполнение этих тестов вручную требует множества проб и ошибок. Когда вы используете бумагу или программное обеспечение для элементарной математики, вы не можете запрограммировать свои вычисления так, чтобы они выполняли за вас нелинейные инструкции или регистрировали ошибки.
Все это и многое другое можно делать в PTC Mathcad. И вам не нужно знать Java, Python или какой-либо другой распространенный язык программирования. Фактически, вам совсем не нужен опыт написания кода. Твоих математических и инженерных знаний более чем достаточно.
Любой инженер с PTC Mathcad может включить логику программирования и:
- Условная оценка ветвей принятия решений
- Добавление контуров в инженерный анализ
- Добавьте точки останова или перехватите ошибки для устранения неполадок
- Экономия часов проб и ошибок по сравнению с традиционными методами
PTC Mathcad проведет вас через весь процесс создания программ. Пока вы знаете базовую логику проблемы, которую хотите решить, вы просто выбираете программные конструкции из меню и заполняете пустые поля.
Лучшая часть? Даже язык программирования в PTC Mathcad использует естественную математическую нотацию. Вот простой пример.
Начните с меню программирования в PTC Mathcad. Обратите внимание на простые варианты сборки с помощью мыши.
Используйте эти операторы для построения функции пузырьковой диаграммы. При программировании в PTC Mathcad можно пропустить матрицу и 18 команд построения графика. Просто настройте всю последовательность в несколько строк кода. В приведенном ниже примере устанавливается матрица, а затем методично строится каждое число, прежде чем вернуться назад, чтобы захватить и построить следующее число.После того, как последнее число в матрице нанесено на график, программа автоматически завершается.
Введите пример данных:
Создайте то, что нужно для участка:
Затем используйте первый столбец как значения x, а второй столбец как значения y на графиках XP:
Программирование в PTC Mathcad предназначено для инженеров. Он включает в себя естественную математическую нотацию, а код аккуратно вписывается во все ваши другие уравнения, таблицы, текст и графики.Вы можете скачать 30-дневную пробную версию сегодня и начать работу. Никаких книг, уроков или предыдущего опыта не требуется.
Совет: программирование также помещает больше ваших вычислений и тестового кода в меньшее количество областей, так что вам будет легче скрыть и защитить свою интеллектуальную собственность.
Простое программирование математических программ в Mathcad Prime
Программирование – слово, которое пугает многих.Раньше, когда я думал о программировании своего математического программного обеспечения, я думал о сложном, чувствительном синтаксисе, который не является интуитивно понятным и трудным для расшифровки для всех, кроме эксперта. Так было до тех пор, пока я не попробовал программировать Mathcad.
Начало работы Программирование математических программ
Mathcad требует только понимания фундаментальных концепций циклического или условного оператора. Давайте рассмотрим те:
For (цикл) – оператор потока управления для указания итерации, который позволяет выполнять код повторно.Сделайте _____ _____ раз.
While (цикл) – оператор потока управления, который позволяет выполнять код повторно на основе заданного логического условия. Повторяйте _____, пока _____ не станет ложным.
If-else-else if (conditional) – особенности программы, которые выполняют различные действия в зависимости от того, истинно или ложно логическое условие. Если _____ верно, сделайте _____, иначе сделайте _____. Если у вас несколько уровней или логических условий, вы можете ввести оператор else if.Если _____ верно, сделайте _____ иначе, если _____ верно, сделайте _____ иначе, сделайте _____.
Сами по себе концепции довольно просты. Вы говорите алгоритму выполнить вычисление определенное количество раз или до тех пор, пока не будет выполнено определенное условие (цикл), и / или вы указываете, какое действие предпринять (условное).
Как программировать Mathcad
Предположим, вы остановились и спросили дорогу. Женщина или джентльмен могут сказать вам: «Просто продолжайте ехать по этой дороге, пока не доберетесь до Гудзон-авеню.и возьми направо. Это цикл while. Этот человек говорит вам что-то сделать, продолжайте ехать по этой дороге , пока не будет выполнено условие, , пока не дойдете до Hudson Ave , а затем в этот момент примите меры, поверните направо .
Когда вы запускаете программу, просто подумайте логически, как вам нужно объяснить компьютеру, как действовать во всех сценариях, с которыми он может столкнуться. Возможно, вам нужно перебрать две независимые переменные и проверить каждую их комбинацию с помощью оператора if-else if-else.
В Mathcad вам просто нужно вставить эти структуры из раскрывающегося меню программирования на вкладке Math
Команды программирования Mathcad
И Mathcad создаст основу для ввода логических условий.
Среда программирования
В качестве заполнителей вы можете использовать переменные и функции, которые вы ранее определили в своем рабочем листе, и ввести локальные переменные в программу, например, счетчик.Лучше всего то, что вы можете делать все это с помощью фирменной естественной математической записи Mathcad.
Дополнительную подробную пошаговую демонстрацию см. В руководстве по программированию в PTC University. Возможно, вам потребуется создать учетную запись, если у вас ее еще нет, но после входа в систему вы получите доступ к еще нескольким бесплатным руководствам по PTC Mathcad.
Среда программирования с результирующим графиком в Mathcad
Начало работы с Mathcad
PTC Mathcad – это программное обеспечение для инженерной математики, которое помогает выполнять (и даже программировать), анализировать и совместно использовать все наиболее важные вычисления.Инженеры из новаторских компаний используют его, и теперь вы можете попробовать свою собственную бесплатную версию и посмотреть, что это мощное математическое программное обеспечение может сделать для вас. Загрузите PTC Mathcad Express прямо сейчас.
Написание программ в MathCAD – онлайн-скачать видео на ppt
Презентация на тему: «Написание программ в MathCAD» – стенограмма презентации:
ins [data-ad-slot = “4502451947”] {display: none! important;}} @media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = “4502451947”]) {display: none! important;}} @media (max-width: 800px) {# place_14 {width: 250px;}} @media (max-width: 500 пикселей) {# place_14 {width: 120px;}} ]]> 1 Написание программ в MathCAD
PH Численные методы Написание программ в MathCAD
2 Написание программ в MathCAD
Многое может обойтись без программирования Некоторым алгоритмам требуются программы Итерационные, повторяются до решения Может упростить другие задачи Скрыть детали внутри программы
3 Золотое правило программирования
Применимо ко всему программированию K.I.S.S. принцип Keep It Simple Stupid
4 Программа MathCAD Все программы MathCAD являются функциями
Выражение на нескольких строках Строки, выполняемые по порядку Локальные переменные Значение последней строки – результат
5 Простая программа MathCAD # 1
Общее подвыражение, вычисленное 3 раза в функции Можно переписать с помощью программы
6 fExample (a, b) в виде двухстрочной программы
1-я строка вычисляет sqrt и присваивает локальной переменной ‘r’ Вторая строка вычисляет выражение и возвращает ответ
7 Внимательно следите за окном выбора
Программы MathCAD # 1 Палитра программирования на панели инструментов Выберите ключевые слова из палитры, НЕ НАБИРАЙТЕ Добавить строку для добавления строк в программу Внимательно следите за окном выбора
8 MathCAD Программы # 2 Назначения являются локальными для программы
Назначения в использовании программы Может использовать весь спектр функций MathCAD в программе Последняя строка является результатом программы Используйте векторы и массивы для возврата нескольких результатов
9 Программы MathCAD Интерактивная справка
Справка | Дополнительные разделы ресурсного центра | Казначейское руководство по программированию | Программирование в MathCAD Учебные таблицы Quicksheets | Примеры справочных материалов по программированию
10 Преобразование прямоугольной формы в полярную # 1
Уравнения для r и q при заданных x и y Хотите, чтобы одна функция возвращала оба значения Используйте вектор
11 Преобразование прямоугольной формы в полярную
Функция возвращает вектор с 2 элементами Элемент 0 r Элемент 1 q NB.Можно использовать atan2 (x, y) Нет ошибки для x = 0
12 MathCAD Программы Структуры
если в противном случае для, while Отступ и вертикальные полосы Наблюдать за прямоугольником выделения <Пробел> для увеличения (больше строк) <Вставить> для смены сторон Нет GOTO Считается опасным
13 MathCAD программирует оператор if
Лучше, чем функция if () для сложных случаев.В противном случае оператор для отлова необработанных случаев.
14 Оператор If в программах
Модель ракетного двигателя Тяга = 0 для t <0 Тяга = 100 для t> 0 и t <5 Тяга = 80 для t> 5 и t <20 Тяга = 0 для t> 20
15 Запрограммированный оператор if
Примечание. Используется для сравнения иначе, чтобы уловить все случаи.
16 Функция fThrust ()
17 Программы MathCAD – цикл for.
Расширение цикла показано отступом. Создан массив «Результат». Примечание. Синтаксис строки «for» Используйте, если заранее знаете, сколько итераций
18 Использование программы fOnes ()
19 Цикл while Выполнение операторов, пока выполняется условие
Используется, когда вы заранее не знаете, сколько раз будет выполняться цикл.Цикл при поиске Цикл, пока ошибка слишком велика Цикл, пока система стабильна
20 Пример цикла while Найти первый член вектора Vec, превышающий пороговое значение, t Записано как функция j – это индекс, в то время как цикл возвращает индекс и значение в виде вектора.
21 год Использование нашей функции Thresh
Vv – тестовый вектор Функция возвращает индекс и значение
22 Более длинные циклы Используйте «Добавить строку» в теле цикла, чтобы расширить область действия цикла.
Линии добавлены на вертикальную полосу. Клавиша
23 Более длинные петли
24 MathCAD Программы Пример гистограммы № 1
Без программирования Рассчитать количество и ширину интервалов Создать массив интервалов Создать гистограмму Эти шаги необходимо записать для каждой гистограммы
25 MathCAD Программы Пример # 2 гистограммы
Как программа Возвращает вектор с двумя элементами Bin Histogram Min, Max, i local Записано как функция
26 Программы MathCAD, использующие функцию Hist ()
То же, что и любую другую функцию
27 Расчет ряда Фиббоначи
28 год Пример программы Рассеяние фотонов # 1
Фотон входит в коробку Проходит случайное расстояние Разброс под случайным углом Повторите с шага 2, пока фотон не покинет коробку Записать прогулку для потомков
29 Программа рассеяния фотонов для создания прогулки
30 Пример программы Photon Scattering # 2
Сохранение координат x-y как двухэлементных векторов V Функции записи для Pathlength () ScatterAngle (q) InBox (V) NewPos (V, P, q) Протестируйте эти функции !!!
31 год Функция Photon Scattering PathLength
s связана с 1 / средний путь x заполнитель фиктивный rnd (1) дает случайное число 0-1 См. Также функцию rexp (NPts, 1 / s)
32 Photon Scattering ScatterAngle (q)
Изотропное рассеяние – равномерное Все углы между –p p С анизотропией разбираться позже
33 Функция Photon Scattering InBox (V)
Принимает вектор в качестве аргумента Аргумент «Распаковка» с нижними индексами Использует умножение для формирования И возвращает 1, если в поле, 0 в противном случае
34 Photon Scattering NewPos (V, P, q)
Arguments OldPosition V Pathlength P Angle q Возвращает новую позицию как вектор
35 год Программа рассеяния фотонов для создания прогулки
36 Рассеяние фотонов с помощью программы
37 Выводы по рассеянию фотонов
8-строчная программа + функции Записывает всю прогулку Извлечь информацию из вектора результатов Легко расширить трехмерное рассеяние Анизотропия Изменить угол разброса (q)
Программирование с помощью Mathcad Prime – Скачать PDF бесплатно
Быстрый старт для настольной версии
Краткое руководство для настольной версии Что такое GeoGebra? Программное обеспечение для динамической математики в одном удобном пакете Для обучения и преподавания на всех уровнях образования Объединяет интерактивную 2D и 3D геометрию, алгебру,
Дополнительная информацияПовторить действие с таблицей Excel №1
Повторить действие с таблицей Excel № 1 Мелисса Эблинг 11/9/06 Указания: Пожалуйста, следуйте всем указаниям в этом пакете.Это задание будет состоять из вашего отслеживания десяти различных акций за период
. Дополнительная информацияВведение в электронные таблицы Excel
Введение в электронные таблицы Excel Каковы цели этого документа? Цели документа: 1. Ознакомить вас с тем, что такое электронная таблица, как она работает и каковы ее возможности; 2. Использование
Дополнительная информацияБазовые знания Excel 2007
Меню ленты Система меню ленты с вкладками для различных команд Excel.Эта ленточная система заменяет традиционные меню, используемые в Excel 2003. Над лентой в верхнем левом углу находится Microsoft
. Дополнительная информацияИнструкции по установке RIT
Руководство пользователя RIT Сборка 1.00 Инструкции по установке RIT Содержание Введение … 2 Введение в Excel VBA (для разработчиков) … 3 Команды API для RIT … 11 Инициализация RIT API … 12 Алгоритмический
Дополнительная информацияЦели задания:
Задачи назначения: Сводная таблица регрессии Упражнение № 1 – Простая линейная регрессия Часто взаимосвязь между двумя переменными, Y и X, может быть адекватно представлена простым линейным уравнением модели
. Дополнительная информацияMicrosoft Word 2007 Модуль 1
Microsoft Word 2007, модуль 1 http: // pds.hccfl.edu/pds Microsoft Word 2007: модуль 1 июля 2007 г. 2007 Общественный колледж Хиллсборо – профессиональное развитие и веб-службы Общественный колледж Хиллсборо
Дополнительная информацияРуководство по построению пользовательских вопросов
Учебное пособие по построителю пользовательских вопросов Pearson Education, 2011 (21.01.2011) Page 1 КОНТАКТНАЯ ИНФОРМАЦИЯ Общая информация MyMathLab: www.mymathlab.com MyStatLab: www.mystatlab.com MathXL: www.mathxl.com
Дополнительная информацияЗнакомство с TI-Nspire CX
Введение в TI-Nspire CX Обзор упражнения: В этом упражнении вы познакомитесь с компоновкой TI-Nspire CX. Шаг 1. Найдите сенсорную панель. Тачпад используется для перемещения курсора
Дополнительная информацияТаблица – Введение
CSCA0102 ИТ и бизнес-приложения Глава 6 Электронная таблица – Введение Электронная таблица Электронная таблица (или программа для работы с электронными таблицами) – это программное обеспечение, которое позволяет использовать числовые данные и выполнять автоматическое выполнение
Дополнительная информацияКраткое руководство для ProcessModel
Краткое руководство для ProcessModel www.blueorange.org.uk ProcessModel Jump-Start Tutorial Это руководство содержит пошаговые инструкции по созданию модели процесса, запуску моделирования и просмотру
Дополнительная информацияРуководство пользователя EzyScript
Версия 1.4 Z Option 417 Oakbend Suite 200 Льюисвилл, Техас 75067 www.zoption.com (877) 653-7215 (972) 315-8800 факс: (972) 315-8804 EzyScript Руководство пользователя Инструмент создания сценариев транзакций и таблиц SAP
Дополнительная информацияFlash MX Image Animation
Flash MX Image Animation Introduction (Подготовка рабочей области) Определения свойств фильма: перейдите на панель «Свойства» в нижней части окна, чтобы выбрать частоту кадров, ширину, высоту и цвет фона
Дополнительная информацияКраткий обзор F9 1
Краткий обзор F9 1 Содержание I.Краткий обзор F9 … 3 1. Начало работы … 3 2. Быстрый пробный баланс … 7 3. Более динамичный табличный отчет … 10 II. Основная формула F9 … 14 Формула GL …
Дополнительная информацияGeoGebra. 10 уроков. Геррит Столс
GeoGebra в 10 уроках Геррит Столс Выражение признательности GeoGebra – это программное обеспечение для динамической математики с открытым исходным кодом (бесплатное) для изучения и преподавания математики в школах. Его разработал Маркус Хоэнвартер
. Дополнительная информацияКрутые хитрости и инструменты для умной доски
Крутые приемы и инструменты Smart Board Отображение двух страниц и закрепление Вы можете легко переключаться между отображением двух страниц и одной страницы с помощью кнопки двух страниц на панели инструментов.В режиме двух страниц вы можете закрепить один
Дополнительная информацияФормы PDF Acrobat – Часть 2
Формы PDF Acrobat – Часть 2 Поля форм PDF В этом уроке вам будет предоставлен файл с именем Форма запроса информации, который можно использовать в Word 2003 или Word 2007. Этот урок проведет вас через
Дополнительная информацияСоздание журнала успеваемости в Excel
Создание журнала успеваемости в электронной таблице 1 Создание журнала успеваемости в Excel Электронные таблицы – отличный инструмент для создания журналов успеваемости.Приложив немного усилий, вы можете создать индивидуальный журнал успеваемости, в котором будет указано
Дополнительная информацияИнтерактивные таблицы Excel:
Интерактивные таблицы Excel: создание инструментов визуализации для улучшения вашего ориентированного на учащихся класса математики и естественных наук Скотт А. Синекс Департамент физических наук и инженерии Prince George
Дополнительная информацияНачало Microsoft Project
НАЧАЛО ПРОЕКТА Microsoft НАЧАЛО ПРОЕКТА МАЙКРОСОФТ…1 ЧТО ТАКОЕ ПРОЕКТ? ДЛЯ ЧЕГО ИСПОЛЬЗУЕТСЯ? … 1 ОКНА ПРОЕКТА … 1 Виды и таблицы … 1 ЭТАП 1: ПЛАНИРОВАНИЕ И НАСТРОЙКА ПРОЕКТА … 2 ПЛАНИРОВАНИЕ И
Дополнительная информацияMicrosoft Office PowerPoint 2013
Microsoft Office PowerPoint 2013 Навигация в среде PowerPoint 2013 Лента: на ленте вы получите доступ к большинству команд, которые вы будете использовать для создания и разработки презентации.
Дополнительная информацияExcel 2007: учебное руководство по основам
Excel 2007: Руководство по основам обучения Знакомство с Excel На первый взгляд новый интерфейс Excel 2007 может показаться немного тревожным: толстые полосы, называемые лентами, заменяют каскадные текстовые меню и панели задач. Это
Дополнительная информацияЛекция 2 Основы Mathcad
Лекция операторов 2 Основы Mathcad + Сложение, – Вычитание, * Умножение, / Деление, ^ Степень () Указание порядка вычисления Порядок операций () ^ высший уровень, первый приоритет * / следующий приоритет
Дополнительная информацияОКНА WORDPAD TUTORIAL 7
WORDPAD TUTORIAL WINDOWS 7 Панель быстрого доступа Вкладка «Главная» Треугольники = Дополнительные команды Группы на вкладке «Главная» Правое поле абзаца Левое поле абзаца и отступ абзацев Линейка Наведите указатель мыши на
Дополнительная информацияЦелевая группа по технологиям / EXCEL
Рабочая группа по технологиям EXCEL Основная терминология Электронная таблица Электронная таблица – это электронный документ, в котором хранятся различные типы данных.Есть вертикальные столбцы и горизонтальные строки. Ячейка – это место, где
Дополнительная информацияУчебное пособие по Microsoft Excel 2010
1 Учебное пособие по Microsoft Excel 2010 Excel – это программа для работы с электронными таблицами в системе Microsoft Office. Вы можете использовать Excel для создания и форматирования книг (набора электронных таблиц) для анализа данных и
Дополнительная информацияПостроение: настройка графика
Построение графика: настройка графиков данных: общие советы Как сделать график данных активным Внутри графического слоя может быть активным только один график данных.График данных должен быть активным, прежде чем вы сможете использовать Data Selector
. Дополнительная информацияКак создать веб-сайт SharePoint Руководство по SharePoint для начинающих: 1. Введение 2. Доступ к сайту SharePoint 3. Редактирование домашней страницы 4. Работа с текстом 5. Вставка изображений 6. Создание таблиц
Дополнительная информацияШаг 2. Заголовки и подзаголовки
Шаг 2: Заголовки и подзаголовки В этом PDF-файле объясняется Шаг 2 пошаговых инструкций, которые помогут вам правильно отформатировать ETD в соответствии с требованиями форматирования UCF.Шаг 2 показывает вам, как установить
Дополнительная информацияExcel 2007: руководство для начинающих
Excel 2007 Руководство для начинающих Введение для начинающих Целью этого документа является ознакомление с некоторыми основными методами использования Excel для ввода данных, выполнения расчетов и создания простых диаграмм на основе
. Дополнительная информацияФормулы и графики Excel
Использование основных формул Формула может представлять собой комбинацию значений (чисел или ссылок на ячейки), математических операторов и выражений.Excel требует, чтобы каждая формула начиналась со знака равенства (=). Excel также имеет
Дополнительная информацияОсновы MathCAD
Основы MathCADВВЕДЕНИЕ В MathCAD
MathCAD – одна из нескольких конкурирующих программ, используемых в качестве инструмента автоматизированного проектирования для ученых, инженеров, инженеров-технологов и инженеров. Некоторые из этих конкурирующих программ включают Mathmatica, Matlab, TK Problem Solver и Maple.Некоторые могут рассматривать в качестве конкурентов электронные таблицы, такие как Excel, StarCalc или Gnumeric. Однако позже в этом курсе мы увидим, что MathCAD довольно хорошо работает с компонентами электронных таблиц, особенно с MS Excel. Фактически, часть этого курса посвящена совместному использованию MathCAD и Excel, обеспечивая очень мощный инструмент для проектирования / расчета.
Подобно портативному калькулятору, MathCAD НЕ является инструментом, который сделает вашу работу за вас; и это не инструмент, который заменит плохие математические навыки.Последний момент особенно важен. Чтобы эффективно применять MathCAD, необходимо разбираться в математике в целом, а также в специфике своей дисциплины. Можно даже утверждать, что дальнейшее использование MathCAD на других курсах и на работе значительно улучшит математические навыки.
MathCAD избавит вас от утомительного выполнения многих математических операций. Благодаря встроенному символьному механизму это включает символьную алгебру и символьное исчисление.Например, хотя решение двух уравнений с двумя неизвестными посредством ручного вычисления является очень простым процессом, использование блока «Решить» в MathCAD позволяет выполнить такое решение за секунды.
Как и любое другое программное обеспечение, MathCAD прост в использовании, если вы его знаете. Однако в нем есть свои нюансы, с которыми вам необходимо ознакомиться. Таким образом, для его эффективного и действенного использования требуется практика. Но ни один курс не может научить вас всем аспектам MathCAD или любой другой важной части программного обеспечения в этом отношении.Несомненно, наиболее важным аспектом любого программного обеспечения для изучения является его справочная / учебная утилита. MathCAD имеет исключительную справочную функцию.
Использование справки MathCAD
MathCAD предоставляет широкий набор функций справки. К ним относятся:- Справка MathCAD
Это стандартный диалог справки Windows, который вы найдете в любом программном пакете. Этот диалог включает вкладки «Содержание», «Указатель» и «Поиск».Откройте диалоговое окно справки, нажав клавишу « F1 » или выбрав «Справка»> «Справка MathCAD» в строке меню.
- Содержание Вкладка представляет информационные темы в виде Оглавления, как в любой книге.
- Указатель Вкладка оформлена в виде указателя, который находится на обратной стороне любой книги.
- Поиск позволяет искать тему на основе ввода ключевого слова.
В конце концов, все три метода поиска информации заканчиваются одним и тем же результатом. То, что вы используете, – это скорее вопрос предпочтений.
Доступ к учебным пособиям из пункта меню «Справка». Все темы учебника будут вам полезны в течение всего квартала. Но в первую неделю вам следует ознакомиться с «Учебниками по началу работы» (за исключением символических праймеров). Эти учебники охватывают большую часть того, чем мы занимаемся в первую неделю занятий.
Функция quicksheet – одна из самых приятных функций в арсенале инструментов справки MathCAD.Короче говоря, это живые рабочие листы MathCAD, содержащие примеры функций MathCAD, возможностей построения графиков и программирования. Вы также можете изменить или добавить в Quicksheet. Хотя вы не можете сохранить эти изменения в исходном файле Quicksheet, вы можете сохранить файл под другим именем. Вы также можете скопировать / вставить уравнения из быстрой таблицы на свой рабочий лист.
Еще одна уникальная особенность MathCAD – наличие справочных таблиц. Это просто таблицы различных физических свойств, таких как удельный вес выбранных жидкостей, фундаментальные константы и т. Д.Хотя это ни в коем случае не исчерпывающий ресурс, они исключительно подходят для ряда приложений.
Еще одна особенность MathCAD – электронная книга или электронная книга. MathCAD поставляется с несколькими электронными книгами, которые установлены по умолчанию. Дополнительные электронные книги доступны на веб-сайте MathCAD. Большинство из них бесплатны, но некоторые необходимо покупать. Электронные книги, как правило, посвящены определенной теме. Например, одна из установленных по умолчанию электронных книг – «Механика материалов». Это электронное приложение к популярному тексту материалов, написанному Гиром и Тимошенко.
- Сотрудничество MathCAD (форум пользователей)
Структура рабочего листа
Фраза «Блокнот инженера» часто используется для описания MathCAD.Это подходящее описание. MathCAD позволяет вам писать уравнения для разработки полных решений проблем, как если бы вы это делали на бумаге. По большей части вы можете размещать уравнения, определения переменных, графики и текст в любом месте на странице, где захотите. Вот почему я часто называю MathCAD «электронной таблицей произвольной формы». Однако существует минимальный набор правил относительно такого размещения и есть синтаксис, который необходимо понимать применительно к математическим операциям.
Основные математические операции
От базовой арифметики до уравнений в частных производных MathCAD использует стандартную номенклатуру для всех математических операций.MathCAD также следует стандартной иерархии операций. А пока давайте сосредоточимся на арифметических операциях и определениях переменных.- Круглые скобки – используйте открывающие / закрывающие круглые скобки (Shift-9 и Shift-0) для круглых скобок. Не пытайтесь использовать квадратные или фигурные скобки. MathCAD при необходимости изменит скобки, если вы используете вложенные наборы.
- Возведение в степень – используйте символ пряника (Shift-6) для возведения в степень
- Умножение – используйте звездочку (Shift-8) в качестве оператора умножения.Оператор отображается в виде выпуклой точки. (например: вводится как 5 * 6 =)
- Деление – используйте косую черту в качестве оператора деления. Оператор отображается в виде стандартной дроби. (например: вводится как 5/6 =)
- Дополнение – Вы можете использовать знак плюса на цифровой клавиатуре или в верхнем ряду клавиш (Shift- =)
- Вычитание – вы можете использовать знак минус на цифровой клавиатуре или в верхнем ряду клавиш.
-
Переменные, присвоение переменных и вычисление уравнений.
Конечно, чтобы в полной мере использовать MathCAD, нужно уметь определять переменную, использовать ее в уравнении или функции, а затем оценивать эту функцию.Очевидно, это делается со знаком равенства, но существует шесть различных форм знака равенства в зависимости от того, определяете ли вы переменную или оцениваете функцию. Ниже объясняется каждая из этих форм.Присвоение равно (:) – Используйте эту версию знака равенства, чтобы присвоить значение локальной переменной или определить уравнение или функцию. Используйте ключ двоеточия. Например, нажатие клавиш для присвоения значения пяти переменной «x» будет x: 5. Значение «x» доступно только для функций, следующих за объявлением.
Глобальное присвоение равно (~) – Используйте эту версию знака равенства, чтобы присвоить значение глобальной переменной. Для этого используйте клавишу тильды (~). Эта клавиша обычно находится сразу под клавишей Escape. Эта версия знака равенства позволяет назначенной переменной быть доступной для всех уравнений на листе, даже если объявление переменной происходит после объявления уравнения. Хотя это звучит неплохо, это может затруднить устранение неполадок на сложном листе.Я рекомендую вам использовать этот метод объявления переменных только для объявления констант. Клавиши, используемые для присвоения значения 13 переменной ‘y’, имеют вид y ~ 13.
Вычислить равно (=) – Эта форма знака равенства используется для фактического вычисления уравнения или функции. Он НЕ используется для присвоения значения. Оператор оценки равенства – это просто стандартный знак равенства на клавиатуре. Например, предположим, что переменная «z» представляет собой сумму переменных «x» и «y», обе из которых были определены выше.. Мы можем ввести это, нажав клавиши z: x + y, что приведет к уравнению:
Чтобы оценить результат, просто введите z =
Логическое равенство (Ctl- =) – Логическое равенство фактически является логическим оператором. Он не используется для присвоения значений и не используется для оценки функции. Он используется как оператор сравнения и задает вопрос: «Равна ли переменная ‘x’ ‘y’?». Если выражение истинно, оно возвращает единицу, если выражение ложно, оно возвращает ноль.Логический оператор равенства используется в основном в программировании, но мы также будем использовать его при решении систем уравнений. Сочетание клавиш для логического оператора равенства – Ctl- =. Например, мы ранее присвоили значение пять переменной x и значение 13 переменной y. Очевидно, мы знаем, что «x» не равно «y». В терминах логического выражения мы можем записать и оценить следующим образом:
Вышеупомянутое выражение просто сравнивает значение «x» со значением «y», определяет, что они не равны, таким образом возвращает значение нуля (ложь).
Локальное присвоение ({) – Эта версия знака равенства идентична двоеточию равенства, за исключением того, что она используется в рамках программы MathCAD. Имеет вид:
Локальное назначение не имеет абсолютно никакой цели вне рамок программирования. Мы обсудим это в следующей лекции по программированию MathCAD.
Символьная оценка (Ctl-.) – В то время как описанный выше знак равенства дает приблизительное решение, символьная оценка дает точное решение с использованием символьного механизма MathCAD.Чаще всего он используется для вычисления выражений символьного исчисления. В качестве примера оцените частное 17/51 приблизительно и точно следующим образом:
Приближенное решение с использованием оценки равно.
Точное решение с использованием символьной оценки
На первый взгляд кажется, что символическая оценка просто уменьшает дробь. В случае простой арифметики это, по сути, верно. Но на самом деле символический двигатель делает гораздо больше. Чтобы не усложнять задачу, символьный движок предоставляет точное решение, сохраняя все числа в их рациональной форме (то есть: 1/3 вместо 0.3333) или выразив решение с помощью символа (например: p вместо 3,14159). Например, натуральный логарифм 5 – это иррациональное число. Его нельзя выразить рациональной дробью, приблизительное и точное решение:
Примерное решение
Точное решение
Определение переменных
При определении переменных важно не переопределять встроенную переменную или переопределять ранее определенную пользовательскую переменную. Еще одна важная проблема, связанная с переменными, заключается в том, что MathCAD чувствителен к регистру.Следующие переменные, хотя они могут показаться вам и мне одинаковыми, уникальны для MathCAD просто из-за использования заглавных букв.Обратите внимание на зеленую волнистую линию под последним определением. Это указывает на переопределение переменной. В этом случае «галлоны в минуту» в нижнем регистре – это единица измерения MathCAD галлонов в минуту. НИКОГДА не переопределяйте переменную MathCAD или модуль , если вы точно не знаете, что делаете и каковы последствия вашего действия.Как мы обсудим позже, это, вероятно, приведет к переопределению ряда других модулей, что приведет к ошибочным результатам, которые трудно устранить. Обратите внимание на эту маленькую закорючку. Это сэкономит ваше время.
Встроенные константы
MathCAD имеет ряд встроенных констант. Это:Infinity (Ctl-Shift-z) – При алгебраическом использовании бесконечность имеет значение 1×10 307 и -1×10 307 .
При символическом использовании это трактуется как истинная бесконечность.
или же Алгебраическое определение
или же Символическое определение
Пи (Ctl-Shift-p) –
Ускорение свободного падения (g) – Хотя MathCAD действительно определяет ускорение свободного падения, он не определяет гравитационную постоянную. В системе единиц СИ гравитационная постоянная равна единице. Однако в английской системе единиц гравитационная постоянная g c равна
. 32.174 (фут-фунт м ) / (фунт f -сек 2 ).
База Напериана (д) – Это значение «е», используемое при работе с натуральными логарифмами.
Процент (%) – Процент всегда является десятичным числом. Таким образом, символ процента фактически умножает предыдущее число на 0,01. Например,
Speed of Light (c) – Маленькая буква c обозначает скорость света в вакууме
Комплексные числа (i) – Квадратный корень из отрицательного числа обозначается буквой «i» или буквой «j».Я рекомендую вам выбрать наиболее удобную для вас номенклатуру и придерживаться ее. Чтобы ввести комплексное число, просто введите коэффициент, за которым следует буква «i» или «j» (в зависимости от того, что вы предпочитаете).
ВАЖНО: введенные строчные буквы «i» или «j» НЕ представляют собой квадратный корень из отрицательного числа. Вы ДОЛЖНЫ ставить перед буквой «i» или «j» цифру один. Например, приведенные ниже выражения – это два разных числа, несмотря на то, что они имеют одинаковый внешний вид.
Корень квадратный из отрицательного
Переменной i присвоено значение три
Греческие буквы
Как мы все знаем, использование греческих букв в технике довольно распространено. Греческие буквы доступны через палитру «Греческий», которая, в свою очередь, доступна из палитры «Математика». Если ваша математическая палитра не отображается, включите ее в строке меню, выбрав «Вид»> «Панели инструментов»> «Математика». Если вы знаете взаимосвязь между греческим алфавитом и набором римских символов, вы можете просто ввести латинскую букву, а затем нажать Ctrl-G, чтобы преобразовать ее в соответствующую греческую букву.Будьте очень осторожны при использовании заглавных греческих букв, которые выглядят как заглавные латинские буквы. Например, заглавная буква «А» и заглавная буква альфа показаны ниже.
Заглавная буква римская ‘А’
Заглавная буква греческого альфа
Хотя они выглядят практически одинаково, это две разные переменные. Это может вызвать значительные трудности при устранении неполадок или даже при простом использовании рабочего листа. Также обратите внимание, что заглавная римская буква «A» помечена как ранее определенная переменная (помните зеленую волнистую линию?).В этом случае MathCAD использует его в качестве инженерной единицы для усилителя. Вероятно, использовать A в качестве переменной – не лучшая идея. С другой стороны, вместо этого можно было бы использовать заглавную альфа, но вам нужно помнить, что символ, который выглядит как заглавная римская буква «А», на самом деле является заглавной греческой альфой. Думаю, вы видите проблему.
Написание собственных уравнений и функций
Прежде чем мы на самом деле напишем уравнения и функции, давайте обсудим еще два пункта. Первый касается использования индексов при определении переменных.MathCAD использует два разных типа индексов: литеральные индексы и индексы массива. Литеральный нижний индекс очень полезен для различения похожих переменных. Вы можете указать нижний индекс, просто нажав клавишу точки (.) При определении переменной. Например, давайте определим переменную ex sub see (x c ) и установим ее равной 10. Нажатие клавиш при этом будет x.c: 10.Индексы массивов будут рассмотрены через пару недель, когда мы обратимся к матрицам и векторам.
Последний пункт – использование клавиши пробела. Пробел полезен для управления синим курсором, окружающим разработку уравнения. Несомненно, наиболее частое использование – это перемещение курсора из знаменателя дроби или из экспоненты. Например, предположим, что вы хотите написать формулу, умножив десять на одну треть, а затем прибавив 20. Дробь, одна треть, вводится нажатием клавиш 1/3. Однако, прежде чем нажимать клавиши +20, вы должны вывести курсор из знаменателя, иначе +20 окажется в знаменателе дроби, а не в качестве независимого члена, который вам нужен.Введите уравнение, нажав следующие клавиши: 1/3 {sp} + 20 = где {sp} обозначает пробел. Следует также отметить, что повторные нажатия клавиши пробела циклически перемещают синий курсор Math по рассматриваемому уравнению.
А теперь давайте применим наши навыки на практике. Заимствуя из курса статики, продублируйте определение следующих переменных и следующее выражение.
Попробуйте воспроизвести приведенное выше уравнение в стороне.Обратите внимание, что символ квадратного корня можно найти на палитре калькулятора или вы можете использовать горячую клавишу, косую черту (\). Если ваше заполненное уравнение станет красным, это означает, что произошла ошибка. При нажатии на уравнение появится всплывающая всплывающая подсказка, сообщающая вам, в чем проблема. Если вы не понимаете сообщение, нажмите функциональную клавишу F1 для получения контекстно-зависимой справки. Нажатия клавиш для приведенного выше уравнения:
S Ctl-g M. 0.5 {sp} * (R.3)
Примечание. {Sp} – это пробел
. Ctl-g – это последовательность клавиш, в которой удерживается клавиша управления при одновременном нажатии и отпускании клавиши «g».
Часто более желательно определить уравнение как функцию. Пользовательские функции определяются так же просто, как уравнение. Например, уравнение параболы можно определить как:
Поскольку переменная ‘b’ не определена, уравнение генерирует ошибку. Но если бы кто-то определил его как функцию ‘f’ в переменной ‘b’, мы бы записали его следующим образом:
Теперь мы можем оценить функцию в дискретных точках, просто подставив число или определенную переменную в качестве аргумента функции.
Функции также могут быть определены в нескольких переменных.
Обратите внимание, что переменная ‘c’ помечена как предопределенная переменная; снова обратите внимание на зеленую волнистую линию. Маленькая буква «c» зарезервирована MathCAD как скорость света. Если ваши расчеты прямо или косвенно не включают скорость света, вероятно, можно использовать эту переменную. Но поймите, что у вас больше нет доступа к этой константе для оставшейся части рабочего листа.
Встроенные функции
MathCAD имеет множество встроенных функций, больше, чем кто-либо, вероятно, когда-либо воспользуется.Определенно больше, чем у нас есть время, чтобы обсудить. Вот почему функция справки MathCAD так важна. Если вам нужно что-то сделать, воспользуйтесь служебными программами, чтобы узнать, как это сделать.
Доступ к функциям можно получить, щелкнув значок f (x) в строке меню. В появившемся диалоговом окне на правой панели отображается полный список функций. Не пугайтесь существующих функций. Эта программа предназначена для использования в самых разных дисциплинах.Мы будем использовать только небольшую часть доступных функций.
Функции, которые нам нужно решить сегодня, включают тригонометрические функции, логарифмические функции и функции округления / усечения. Имея дело с тригонометрическими функциями, важно понимать, что MathCAD ожидает углы в радианах. Все функции arc возвращают углы в радианах. Если мы хотим использовать градусное измерение, мы должны явно указать это. Например, синтаксис функции синуса – sin (x), где x – угловое измерение в радианах.Чтобы использовать градусные меры, умножьте аргумент на единицу «град». Ниже приведены некоторые примеры.
При использовании функций дуги результатом является угловая величина в радианах. | ||||||||||||||||||||||||||||||||||||||||||
Если вы нажмете на указанное выше выражение, вы увидите заполнитель, маленький черный квадрат, сразу справа от результата. В этот заполнитель вы вводите единицу измерения. Если вы хотите отображать указанное выше в градусах, введите «градус» в поле-заполнитель.
Логарифмические функции включают в себя функции с основанием Напериана, основанием 10 и основанием «n».
Функции пола и потолка работают очень хорошо, если нужно определить целое число объектов.Например, при проектировании бетонной балки выполняется расчет для определения количества арматурных хомутов. Очевидно, что количество хомутов должно быть целым, но расчет дает десятичное число. Использование функции потолка позволяет MathCAD возвращать целое число хомутов, которое затем можно использовать в последующих вычислениях для определения расстояния хомутов.
Базовые единицы
Единицы можно рассматривать как переменную и применяются как таковые. Другими словами, если кто-то хочет объявить значение ‘x’ равным пяти футам, можно определить это, используя нажатия клавиш x: 5 * ft.
MathCAD может обрабатывать преобразование единиц измерения без явного указания коэффициента преобразования.Например, определите переменную t как 10 секунд, а переменную v как частное от x и t.
В приведенном выше примере отображаются футы в секунду. Если кто-то желает получить решение в разных единицах, можно заменить любую эквивалентную единицу таким же образом, как мы преобразовали радианы в градусы (как обсуждалось выше).
MathCAD неплохо справляется с отображением результирующих единиц вычисления.Однако бывают случаи, когда полученные единицы сводятся к чему-то более фундаментальному. В этих обстоятельствах вам нужно будет заменить желаемое устройство. Например, в термодинамике базовый расчет теплопередачи утверждает, что энергия равна массе объекта, умноженной на удельную теплоемкость этого объекта, умноженную на изменение температуры. Предположим, что объект имеет массу 30 слизней, удельную теплоемкость 12 британских тепловых единиц / (фунт R) с изменением температуры на 30 градусов по Ренкину.Результирующее энергосодержание должно быть в БТЕ. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Обратите внимание, что результат не отображается в BTU. Результат отображается в наборе единиц, размерно эквивалентных BTU. Чтобы отобразить правильную единицу, щелкните результат и вручную вставьте единицу BTU в заполнитель. | ||||||||||||||||||||||||||||||||||||||||||||||||||||
Примечание о температуре в MathCAD
MathCAD не может обрабатывать температуры, выраженные в градусах Фаренгейта или в градусах Цельсия.Вы можете использовать только температуры, выраженные в градусах Ренкина (R) или в Кельвинах (K). Это связано с тем, что преобразование из Ренкина в Фаренгейта и из Кельвина в Цельсия связано с дополнительным компонентом.
Ренкин = Фаренгейт + 459,69
Кельвина = Цельсия + 273,17
Фаренгейт = 1,8 (Цельсия) +32
Однако преобразование между Рэнкином и Кельвином является мультипликативным, поэтому преобразование единиц измерения выполняется легко.
Ренкина = 1,8 Кельвина
Однако все это не проблема.В дисциплинах термодинамики и теплопередачи большинство расчетов связано с разницей температур. Поскольку шкала Ренкина и шкала Фаренгейта на самом деле являются одними и теми же шкалами, только обозначены по-разному, разница температур в один градус, выраженная в шкале Ренкина, равна разнице температур в один градус, выраженной в градусах Фаренгейта. Это также верно для шкал Кельвина и Цельсия. Самая распространенная проблема, с которой сталкивается учащийся при работе с температурой, – это понимание этой концепции. Предположим, у вас есть тело, которое начинается при температуре 120 F и заканчивается при температуре 150 F.Очевидно, это изменение температуры на 150–120 = 30 градусов по Фаренгейту. Но каково изменение температуры в градусах Ренкина? Просто преобразуйте температуру Фаренгейта в температуру Ренкина, добавив 460, а затем вычтите две температуры следующим образом.
(150 + 460) – (120 + 460) = 610 – 580 = 30
рэндов
Изменение температуры по шкале Фаренгейта такое же, как и по шкале Ренкина. Опять же, в этом есть смысл. Это одинаковые весы с разными надписями.
Те расчеты, которые учитывают текущую температуру тела, а не изменение температуры, всегда основаны на абсолютной температуре, выраженной в единицах Ренкина или Кельвина.Таким образом, проблема, связанная с Farenheit или Celcius, не имеет значения.
Заметка о единицах массы и силы в MathCAD
Нет ничего особенного в использовании единиц массы и силы в MathCAD. Однако использование соответствующих единиц для массы и силы кажется проблемой для многих студентов, особенно в английской системе. Типичные единицы массы и силы в английской системе и системе СИ показаны ниже
.
Английский SI
Масса пули кг (масса-килограмм)
фунт (фунт-масса)
Сила фунт-сила (фунт-сила) Н (Ньютон)
кгс (килограмм-сила)
К настоящему времени мы все знаем закон Ньютона, сила – это продукт массы и ускорения.Применение закона Ньютона довольно просто при использовании системы единиц СИ. Многие не знают, как применить закон Ньютона в английской системе единиц, когда масса выражается в единицах массы или фунта.
Например, в системе СИ закон Нетвона требует, чтобы масса выражалась в килограммах, ускорение свободного падения составляет 9,807 м / с 2 , а результирующая сила выражается в ньютонах. | ||||||||||||||||||||||||||||||||||||||||||||||||
В системе дюйм-фунт закон Ньютона требует, чтобы масса выражалась в слитках.Слизняк – это старая английская единица массы. Он равен (фунт f s 2 ) / фут. Результирующая сила измеряется в фунтах силы. В MathCAD фунт-сила выражается в фунтах-силах. Следует отметить, что обе единицы массы. фунт-масса и снаряд до сих пор используются в машиностроении и инженерных технологиях. Нужно знать и то, и другое. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Однако более распространенной единицей массы в системе дюйм-фунт является фунт-масса.В MathCAD единицей фунта-массы является просто фунт. Но чтобы использовать фунт-массу в законе Ньютона, нужно немного изменить закон Ньютона, введя гравитационную постоянную. Многие люди не понимают, что ускорение свободного падения НЕ является постоянной величиной. На самом деле он немного меняется по поверхности земли. Однако гравитационная постоянная – постоянная величина. Он присваивается переменной g c и имеет значение 32,174 (фут-фунт м ) / (фунт f -с 2 ).Таким образом, закон Ньютона модифицируется, как показано, и результирующая сила выражается в фунтах силы. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Хотя все это верно и очень важно понимать, многое из этого становится неактуальным при работе в MathCAD.Это потому, что MathCAD выполняет все преобразования единиц измерения за вас. Например, можно показать, что одна пуля равна 32,174 фунтам массы. Поскольку MathCAD выполняет все преобразования единиц измерения, нет необходимости явно писать закон Ньютона с использованием гравитационной постоянной при работе с массой в фунтах-массах. Рассмотрим следующий пример. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
При использовании единиц измерения в MathCAD программа всегда будет поддерживать целостность размеров, даже если вы ошиблись при указании единицы измерения.Это часто приводит к появлению каких-то странных (бессмысленных?) Дисплеев устройств. Например, рассмотрим следующее уравнение для определения выходной мощности двигателя с учетом развиваемого крутящего момента и скорости вращения. В показанном уравнении крутящий момент выражается в единицах силы фут-фунт, а число оборотов в минуту выражается в единицах в минуту (1 / мин). Единицей измерения мощности в MathCAD является л.с. С точки зрения размеров, лошадиные силы – это сила на фунт-фут в единицу времени. Найдите выходную мощность двигателя, если развиваемый крутящий момент составляет 1000 фут-фунт-сила, а скорость вращения составляет 3600 об / мин.
Просто определите переменные крутящий момент и обороты, как показано | |||||||||||||||||||||||||||||||||||||||||||||||
Напишите уравнение для мощности | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Покажите решение.Выглядит правильно, не так ли? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Повторно отобразите решение и введите единицу измерения «hp» в поле единицы измерения. Обратите внимание на результат. Что именно это означает? Короче говоря, это значит, что кто-то ошибся. В этом конкретном случае причина, по которой единица отображается так, как показано, заключается в том, что мы неправильно определили крутящий момент.Обратите внимание, что крутящий момент был неправильно определен в единицах массы фут-фунт. Предполагается, что крутящий момент определяется как сила на фунт-фут. Эта ошибка в сочетании с тем фактом, что хорспауэр – это сила в фут-фунт в единицу времени, вынуждает MathCAD вставлять «корректирующую» единицу для сохранения целостности размеров относительно того, как были определены исходные данные. Это легко исправить. Просто определите крутящий момент с правильной единицей измерения фут-фунт-сила. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если такая ситуация возникает, когда вы делаете домашнее задание, интерпретируйте ее так, какова она есть, ВЫ ЧТО-ТО ДЕЛАЛИ НЕПРАВИЛЬНО.Таким образом, исправьте ошибку, прежде чем сдавать задание. Я не вижу смысла в отправке заведомо неверного задания. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Введите переменную, а затем оценку равно (например: m =). Если единица измерения определена, вы получите что-то, как показано слева. Это очевидное свидетельство того, что переменная является встроенной единицей или была ранее определена вами. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Второй способ – это фактическое определение переменной.Если под переменной появляется зеленая волнистая линия, переменная уже используется. В зависимости от того, является ли переменная встроенной переменной MathCAD или пользовательской переменной, вы должны принять решение о выборе новой переменной или переопределении существующей. Почти всегда можно переопределить пользовательскую переменную. Очень редко вы хотите переопределить встроенную переменную или единицу MathCAD. Это может иметь негативные последствия, которые ОЧЕНЬ сложно устранить. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ВНИМАНИЕ: Следует понимать, что способность MathCAD идентифицировать переопределение переменной появилась в первом обновлении пакета обновления для MathCAD 11.В исходном выпуске версии 11 и во всех предыдущих версиях MathCAD не извивался :). Кроме того, этот параметр может быть отключен пользователем (Инструменты> Настройки> Предупреждения). В этом случае не полагайтесь на эту функцию, если вы не знаете, что она доступна (то есть: правильная версия MathCAD и функция включена). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Структура рабочего листа
Рабочий лист MathCAD состоит из трех областей: математической, текстовой и графической.Как можно понять из названий, математическая область содержит только математические формулы, текстовая область содержит только текст, а область графика содержит только график.
По умолчанию, когда вы начинаете вводить текст на листе, MathCAD автоматически создает математическую область. Ниже приведены некоторые примеры.
Если первый вводимый вами символ – это альфа-символ, MathCAD предполагает, что вы вводите имя переменной. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если первый вводимый вами символ – это число, MathCAD интерпретирует его как число. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если первый вводимый вами символ – это число, за которым следует строка буквенных символов, MathCAD интерпретирует это как число, умноженное на переменную. Знак умножения не очевиден, но подразумевается.Нажмите на запись, чтобы увидеть подразумеваемый знак умножения. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Текстовая область – это область, содержащая чистый текст.Весь текст, который вы читали, находится в текстовой области. Самый простой способ начать текстовую область – просто начать печатать. Как только вы начнете печатать, MathCAD создаст математическую область. Но как только вы нажимаете клавишу пробела, регион преобразуется в текстовую область. Однако с этим неявным методом создания текстовой области возникают некоторые трудности. Большинство знаков препинания – это сочетания клавиш в MathCAD для ввода определенных функций. Таким образом, если вы начинаете текстовую область с числа или знака препинания (например, апострофов) или если вы должны ввести знак препинания перед нажатием клавиши пробела, MathCAD интерпретирует нажатие клавиши как желание ввести какой-либо тип функции. или формула.В таких случаях ЗАПУСТИТЕ текстовую область, нажав клавишу двойных кавычек. Вы можете отличить математическую область от текстовой двумя способами. Самым надежным считается внешний вид курсора. В математической области курсор имеет синий цвет и окружает математическую запись или ее часть с двух сторон от нее. Текстовый курсор представляет собой вертикальную красную линию. Второй способ – распознать разницу в стиле и размере шрифта между математической областью и текстовой областью. Однако пользователь может изменять стили и размеры шрифтов как для математических, так и для текстовых областей.Другими словами, шрифты в обоих регионах могут быть идентичными. Однако по умолчанию это не так. Все числа и формулы, вводимые в текстовой области, являются текстовыми строками. Это не живые формулы. Однако MathCAD позволяет вводить математическую область внутри текстовой области. Фактически, этот метод широко используется в этом листе, а также в других листах лекций, используемых в оставшейся части этого курса. Чтобы ввести математическую область внутри текстовой области, перейдите в пункт меню «Вставка»> «Математическая область».Например, я могу определить переменную: и формула: Обратите внимание, что и «x», и «y» доступны, даже если они определены внутри текстовой области. Это отличная функция, позволяющая писать хорошо работающие отчеты. Другими словами, вам не нужно делать непонятную ссылку на переменную или функцию в тексте, который вы пишете, а затем разбивать текст, чтобы ввести переменную или формулу в отдельной области Math.Вы можете просто ввести математическую область внутри текстовой области. У вас будет много возможностей попрактиковаться в этом при выполнении первого домашнего задания. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Область графика – это просто область, в которую вводится график.Графики вводятся из меню вставки. MathCAD позволяет создавать графики различных типов. Однако мы сосредоточимся только на создании стандартного графика X-Y. График также можно ввести, нажав клавишу @ (Shift-2). Простой график создается путем простой вставки графика, ввода функции в местозаполнитель центральной оси Y и последующего помещения зависимой переменной в местозаполнитель центральной оси x. Остальные четыре заполнителя предназначены для определения пределов осей x и y.Если вы их не заполните, MathCAD построит график функции для значения x от -10 до 10. Мы обсудим построение графиков более подробно в следующей лекции. А пока давайте определим и построим график функции: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Макет страницы
К настоящему времени очевидно, что MathCAD имеет возможности обработки текстов. Хотя эти возможности не такие широкие, как у MS Word, et. др., их более чем достаточно для создания красивого документа. Я позволю вам самостоятельно изучить возможности форматирования текста и абзацев.Поговорим о форматировании страниц.
В MathCAD единственные параметры форматирования страницы, которые у вас есть, – это ширина поля, ориентация страницы, размер страницы и разрывы страниц. Для правильной документации (например, домашнего задания) вам необходимо знать это, чтобы ваша статья выглядела профессионально.
Чтобы установить поля, размер бумаги и ориентацию страницы, перейдите в пункт меню «Файл»> «Параметры страницы». Установите параметры по своему усмотрению.
Как и в MS Word, разрывы страниц бывают двух видов: жесткие и мягкие.Непосредственно над этим текстом находится горизонтальная сплошная линия (не отображается, если вы читаете это на распечатке или в виде HTML-страницы). Чуть выше, над графиком, находится горизонтальная пунктирная линия (также не видна на распечатке или странице HTML). Пунктирная линия представляет собой мягкий разрыв страницы. За исключением возможности изменять поля страницы, вы не можете перемещать или каким-либо иным образом контролировать расположение мягкого разрыва страницы. Однако вы можете вставить, удалить или переместить жесткий разрыв страницы. Сплошная линия непосредственно выше – это такой разрыв страницы.Чтобы вставить разрыв, поместите курсор в то место, где вы хотите разрыв, и выберите «Разрыв страницы» в меню «Вставить». Чтобы переместить или удалить разрыв страницы, используйте мышь и щелкните разрыв, удерживая нажатой клавишу «Shift». Разрыв будет выделен парой пунктирных линий. Используйте мышь, чтобы перетащить разрыв. Чтобы удалить, щелкните разрыв, удерживая клавишу Shift, и выберите «Вырезать» в меню редактирования. Выполняя домашнее задание, убедитесь, что вы правильно используете разрывы страниц, чтобы домашнее задание отображалось логично. Нет причин, чтобы разрыв страницы пересекал уравнение! Вам будут выставлены оценки за представление домашнего задания.
При вычислении рабочего листа MathCAD чувствителен к относительному расположению формул и переменных. Как и в случае с электронной таблицей, MathCAD выполняет вычисления слева направо и сверху вниз. Это означает, что вы должны убедиться, что ваши формулы и определения переменных правильно расположены. Обычно это просто перетаскивание соответствующей математической области в соответствующее место. С другой стороны, бывают случаи, когда вы хотите, чтобы формулы выстраивались либо по горизонтали, либо по вертикали. Для этого используйте две кнопки выравнивания на панели значков.MathCAD предупредит вас, если выравниваемые области перекрываются. Если они это сделают, вам, возможно, придется внести некоторые незначительные изменения в расположение регионов перед автоматическим выравниванием.
Вы также можете вставить «Область» MathCAD. Просто выберите «Вставить»> «Область» в меню «Вставка». Такая область чрезвычайно полезна для сокрытия расчетов. При желании зону можно свернуть и заблокировать. С помощью мыши щелкните правой кнопкой мыши стрелку вверху и слева. Контекстное меню позволяет свернуть область (если она развернута) или развернуть область (если она свернута).Он также позволяет заблокироватьобласть с паролем. НЕ ПОТЕРЯЙТЕ ПАРОЛЬ. Невозможно разблокировать область, если пароль утерян.
ПРИМЕЧАНИЕ. Эта область не отображается при просмотре как HTML-страница; он будет отображаться как обычный абзац. Разграничение области печатается на распечатке, но при желании может быть скрыто.
Mathcad: отраслевой пример | Программное обеспечение Hearne
Mathcad и экономические дебаты
Mathcad в анализе экономических данных
Доцент Стив Кин из Университета Западного Сиднея в последние годы оказал большое влияние на экономические дискуссии.Вся его работа была сделана с использованием Mathcad.
Вы можете использовать уравнения Mathcad для решения практически любой математической задачи, которую только можете придумать, символически или численно. Комбинируя уравнения, текст и графику на одном листе, Mathcad упрощает отслеживание самых сложных вычислений. Это упрощает и упрощает документирование и публикацию вашей работы.
«Я использую Mathcad двумя основными способами, – объяснил доктор Кин, – для статистического анализа и представления данных, а также для построения динамических моделей.«Доктор Кин издает ежемесячный информационный бюллетень Debtwatch, который предупреждает об опасностях чрезмерного частного долга. Информационный бюллетень написан на Mathcad и использует очень гибкий язык программирования Mathcad для импорта данных из широкого круга статистических источников. Затем доктор Кин позволяет использовать возможности Mathcad для построения графиков, чтобы сделать эту информацию наглядной. Debtwatch теперь стал очень влиятельным в австралийских экономических дебатах, и здесь важны мощность и гибкость Mathcad.Никакая другая программа не могла позволить так быстро перейти от анализа к аргументу.
Он также использует Mathcad для моделирования динамических систем, таких как модель создания кредитных денег, которая выходит далеко за рамки учебной модели «денежного мультипликатора». Здесь бесценно сочетание в Mathcad естественного отображения математики, логического и числового программирования ». Используя программирование Mathcad и символьный механизм, я смог ввести матрицу, которая записывает потоки между банковскими счетами таким образом, что бухгалтер признал бы – это, по сути, двойная бухгалтерия.Затем из этого очень естественного интерфейса я автоматически получаю набор дифференциальных уравнений для моделирования с помощью блока Odesolve. Программы, которые достигают этого, невероятно просты, но в то же время очень мощны ».
«Это сочетание аналитических возможностей и очень естественного выражения математической логики делает Mathcad таким непревзойденным. Я ожидаю, что я мог бы сделать все это в любом количестве других программ, но программировать было бы гораздо труднее, позднее было бы труднее интерпретировать, а представление результатов потребовало бы экспорта в другую программу для правильного форматирования текста, графиков и уравнений.В Mathcad я могу делать все это в одном месте ».« Я также считаю, что великолепный редактор уравнений Mathcad позволяет мне разработать логику математического аргумента в Mathcad быстрее и точнее, чем я когда-либо мог бы на бумаге, а затем практически мгновенно проверить идею. Другой такой программы просто нет. Если бы я обнаружил, что потерпел крушение на пустынном острове – или что-то вроде компьютерного эквивалента, когда мне пришлось бы выбирать только одну программу из всех известных мне, – тогда Mathcad был бы им ».

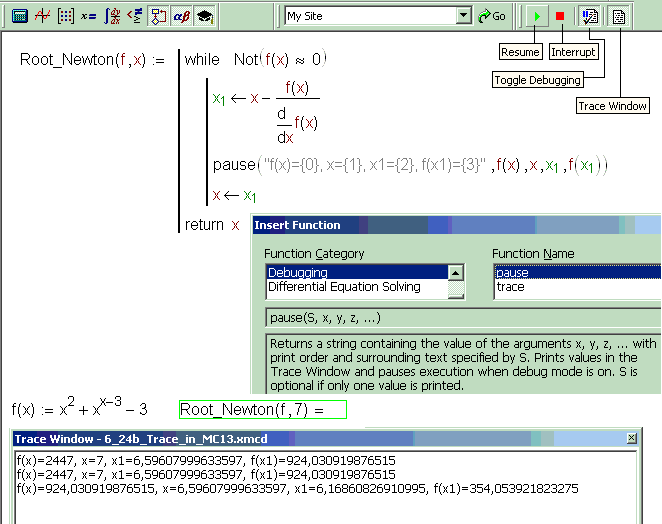 Позволяет в зависимости от условия выполнять или не выполнять те или иные действия;
Позволяет в зависимости от условия выполнять или не выполнять те или иные действия;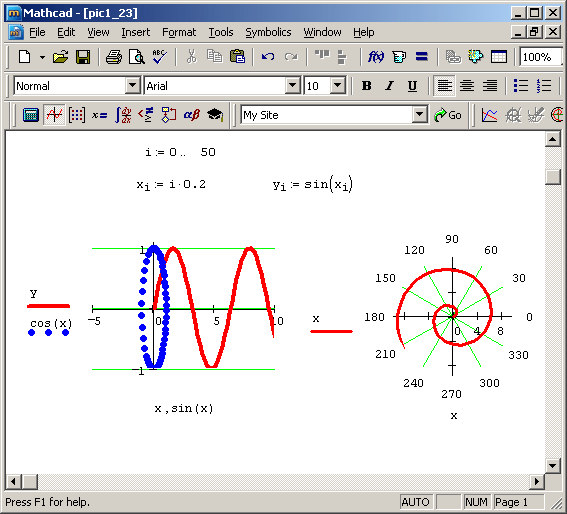
 .M −1
.M −1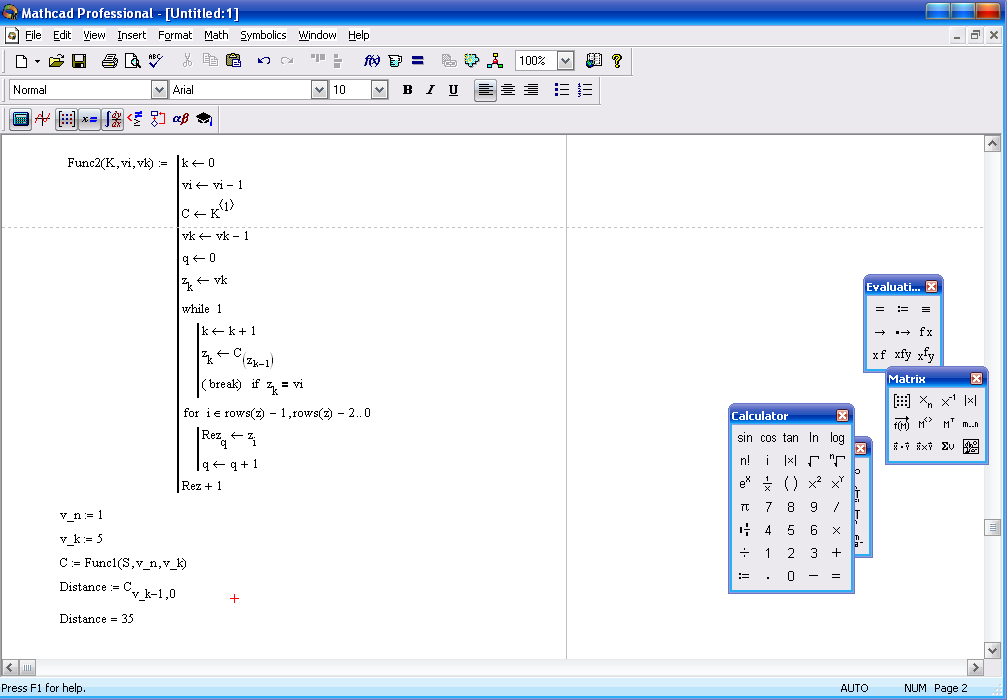

 4.1 – Примеры программных фрагментов
4.1 – Примеры программных фрагментов