Вычисление тройных интегралов: теория и примеры
Тройные интегралы – это аналог двойного интеграла для функции трёх переменных, заданной как f(M) = f(x, y, z).
Записывается тройной интеграл так:
.
Здесь V – пространственная (трёхмерная) фигура, ограниченная плоскостями, выражения которых (равенства) даны в задании вычисления тройного интеграла. V называют также замкнутой ограниченной областью трёхмерного пространства.
Вычислить тройной интеграл – значит найти число, равное объёму тела V или, что то же самое – области V.
Практически каждый может понять смысл вычисления тройного интеграла “на своей шкуре”.
Точнее – “под шкурой”, а ещё точнее – по своим органам дыхания – лёгким.
 Теперь будем максимально увеличивать число таких
маленьких областей, а наибольший диаметр Δvi –
наоборот, уменьшать. Можем составить интегральную сумму вида
Теперь будем максимально увеличивать число таких
маленьких областей, а наибольший диаметр Δvi –
наоборот, уменьшать. Можем составить интегральную сумму вида.
Если функция f(M) = f(x, y, z) непрерывна, то будет существовать предел интегральных сумм вида, указанного выше. Этот предел и называется тройным интегралом.
В этом случае функция f(M) = f(x, y, z) называется интегрируемой в области V; V – областью интегрирования; x, y, z – переменными интегрирования, dv (или dx dy dz) – элементом объёма.
Как и в случае двойных интегралов, вычисление тройных интегралов сводится к вычислению интегралов
меньшей кратности.
Рассмотрим трёхмерную область V. Снизу и сверху (то есть по высоте)
эта область ограничена поверхностями z = z1(x, y) и
z = z2(x, y).
С боковых сторон (то есть по ширине) область ограничена поверхностями y = y1(x) и
y = y2(x). И, наконец,
по глубине (если Вы смотрите на область в направлении оси
Чтобы применять переход к интегралам меньшей кратности, требуется, чтобы трёхмерная область
V была правильной. Она правильна тогда, когда прямая, параллельная оси
Oz, пересекает границу области V не более чем в двух точках. Правильными
трёхмерными областями являются, например, прямоугольный параллелепипед, эллипсоид, тетраэдр. На рисунке ниже –
прямоугольный параллелепипед, который встретится нам в первом примере на решение задач.
Чтобы наглядно представить отличие правильности от
неправильности, добавим, что поверхности области по высоте у правильной области не должны быть вогнуты вовнутрь. На
рисунке ниже – пример неправильной области
Мы будем рассматривать только правильные области.
Итак, область V – правильная. Тогда для любой функции f(x, y, z), непрерывной в области V, справедлива формула
Эта формула позволяет свести вычисление тройного интеграла к последовательному вычислению
внутреннего определённого интеграла по переменной
Переходя от двойного интеграла к повторному, получаем следующую формулу для вычисления тройного интеграла:
Таким образом, для вычисления тройного интеграла требуется последовательно вычислить три
определённых интеграла.
Вычисляются эти интегралы от самого внутреннего (по переменной z) к самому внешнему (по переменной x). Для удобства восприятия последовательности вычислений три “вложенных” интеграла можно записать так:
.
Из этой записи уже однозначно видно, что:
- сначала нужно интегрировать функцию f(x, y, z) по переменной z, а в качестве пределов интегрирования взять уравнения z = z1(x, y) и z = z2(x, y) поверхностей ограничивающих область V снизу и сверху;
- получившийся на предыдущем шаге результат интегрировать по переменной y, а в качестве пределов
интегрирования взять уравнения
- получившийся на предыдущем шаге результат интегрировать по переменной x, а в качестве пределов
интегрирования взять уравнения x = a и x = b
поверхностей, ограничивающих область V по глубине.

Пример 1. Пусть от тройного интеграла можно перейти к повторному интегралу
–
последовательности трёх определённых интегралов. Вычислить этот повторный интеграл.
Решение. Вычисление повторного интеграла всегда начинается с последнего интеграла:
.
Вычислим второй интеграл – по переменной y:
.
Теперь вычисляем самый внешний интеграл – по переменной x:
.
Ответ: данный повторный интеграл и соответствующий ему тройной интеграл равен 10.
Пример 2. Вычислить тройной интеграл
,
где V – параллелепипед, ограниченный плоскостями

Решение. Пределы интегрирования для всех трёх определённых интегралов однозначно заданы уравнениями поверхностей, ограничивающих параллелепипед. Поэтому сразу сводим данный тройной интеграл к последовательности трёх определённых интегралов:
.
Вычисляем самый внутренний интеграл – по переменной z, считая икс и игрек константами. Получаем:
.
.
Теперь вычисляем самый внешний интеграл – по переменной x:
Ответ: данный тройной интеграл равен -2.
Пример 3. Вычислить тройной интеграл
,
где V – пирамида, ограниченная плоскостью
x + y + z = 1
и координатными плоскостями
x = 0, y = 0,
z = 0. Область
Область
Решение. Расставим сначала пределы интегрирования. Для интеграла по переменной z нижний предел интегрирования задан однозначно: z = 0. Чтобы получить верхний предел, выразим z из x + y + z = 1. Получаем 1 − x − y. Для интеграла по переменной y нижний предел интегрирования задан однозначно: y = 0. Для получения верхнего предела выразим y из x + y + z = 1, считая при этом, что z = 0 (так как линия расположена в плоскости xOy). Получаем: 1 − x.
Сводим данный тройной интеграл к последовательности трёх определённых интегралов:
.
Вычисляем самый внутренний интеграл – по переменной z, считая икс и игрек константами. Получаем:
Получаем:
.
Вычисляем средний интеграл – по переменной y. Получаем:
Наконец, вычисляем самый внешний интеграл – по переменной x:
Ответ: данный тройной интеграл равен 1/8.
Вычислить тройной интеграл самостоятельно, а затем посмотреть решение
Бывает, что студенты, у которых не вызывает особых трудностей непосредственное вычисление
интегралов, не могут освоиться в расстановке пределов интегрирования при переходе от тройного интеграла к
последовательности трёх определённых интегралов. В этом деле действительно требуется некоторая натренированность.
В первом примере область интегрирования V представляла собой параллелепипед,
с которым всё понятно: со всех сторон его ограничивают плоскости, а значит, пределы интегрирования однозначно
заданы уравнениями плоскостей. Во втором примере – пирамида: здесь уже требовалось чуть больше подумать и выразить
один из пределов из уравнения. А если область V ограничивают не плоские
поверхности? Нужно, конечно, определённым образом осмотреть область V.
Во втором примере – пирамида: здесь уже требовалось чуть больше подумать и выразить
один из пределов из уравнения. А если область V ограничивают не плоские
поверхности? Нужно, конечно, определённым образом осмотреть область V.
Начнём с примера “пострашнее”, чтобы почувствовать “обстановку, приближенную к боевой”.
Пример 5. Расставить пределы интегрирования при переходе от тройного интеграла, в котором область V – эллипсоид
.
Решение. Пусть центр эллипсоида – начало координат, как показано на рисунке выше. Посмотрим на эллипсоид снизу. Снизу его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена ниже плоскости xOy. Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение со знаком минус будет нижним пределом интегрирования по переменной z:
.
Теперь посмотрим на эллипсоид сверху. Здесь его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена выше оси xOy. Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение будет верхним пределом интегрирования по переменной z:
.
Проекцией эллипсоида на плоскость xOy является эллипсоид. Его уравнение:
.
Чтобы получить нижний предел интегрирования по переменной y, нужно выразить y из уравнения эллипсоида и взять полученное выражение со знаком минус:
.
Для верхнего предела интегрирования по переменной y то же выражение со знаком плюс:
.
Что касается интегрирования по переменной x, то область V
ограничена по глубине плоскостями. Следовательно, пределы интегрирования по переменной x можно
представить как координаты задней и передней границ области. В случае эллипсоида ими будут взятые с отрицательным
и положительным знаками величины длин полуоси
a: x1 = − a и
x2 = a.
Следовательно, пределы интегрирования по переменной x можно
представить как координаты задней и передней границ области. В случае эллипсоида ими будут взятые с отрицательным
и положительным знаками величины длин полуоси
a: x1 = − a и
x2 = a.
Таким образом, последовательность интегралов для вычисления объёма эллипсоида следующая:
,
где “игрек первое”, “игрек второе”, “зет первое” и “зет второе” – полученные выше выражения. Если у Вас есть желание и отвага вычислить этот интеграл и, таким образом, объём эллипсоида, то вот ответ: 4πabc/3.
Следующие примеры – не такие страшные, как только что рассмотренный. При этом они предполагают
не только расстановку пределов интегрирования, но и вычисление самого тройного интеграла. Проверьте,
чему вы научились, следя за решением “страшного” примера. Думать при расстановке пределов всё равно
придётся.
Думать при расстановке пределов всё равно
придётся.
Пример 6. Вычислить тройной интеграл
,
если область интегрирования ограничена плоскостями x + y = 1, x + 2y = 4, y = 0, y = 1, z = 1, z = 5.
Решение. “Курортный” пример по сравнению с примером 5, так как пределы интегрирования по “игрек” и “зет” определены однозначно. Но придётся разобраться с пределами интегрирования по “иксу”. Проекцией области интегрирования на плоскость xOy является трапеция ABCD.
В этом примере выгоднее проецировать трапецию на ось Oy, иначе, чтобы вычислить тройной
интеграл, на придётся разделить фигуру на три части. В примере 4 мы начинали осмотр области интегрирования
снизу, и это обычный порядок. Но в этом примере мы начинаем осмотр сбоку или, если так проще, положили
фигуру набок и считаем, что смотрим на неё снизу. Можем найти пределы интегирования по “иксу”
чисто алгебраически. Для этого выразим “икс” из первого и второго уравнений, данных в условии примера.
Из первого уравения получаем нижний предел 1 − y, из
второго – верхний 4 − 2y. Сведём данный тройной
интеграл к последовательности трёх определённых интегралов:
Можем найти пределы интегирования по “иксу”
чисто алгебраически. Для этого выразим “икс” из первого и второго уравнений, данных в условии примера.
Из первого уравения получаем нижний предел 1 − y, из
второго – верхний 4 − 2y. Сведём данный тройной
интеграл к последовательности трёх определённых интегралов:
.
Внимание! В этом примере самый внешний интеграл – не по переменной “икс”, а по переменной “игрек”, а “средний” – по переменной “икс”! Здесь мы применили смену порядка интегрирования, с которой ознакомились при изучении двойного интеграла. Это связано с тем, что, как уже говорилось, мы начали осмотр области интегрирования не снизу, а сбоку, то есть спроецировали её не на ось Ox, на на ось Oy.
Вычисляем самый внутренний интеграл – по переменной z, считая икс и игрек константами. Получаем:
.
Вычисляем средний интеграл – по переменной x. Получаем:
Получаем:
.
Наконец, вычисляем самый внешний интеграл – по переменной y:
Ответ: данный тройной интеграл равен 43.
Пример 7. Вычислить тройной интеграл
,
если область интегрирования ограничена поверхностями x = 0, y = 0, z = 2, x + y + z = 4.
Решение. Область V (пирамида MNRP) является правильной. Проекцией области V на плоскость xOy является треугольник AOB.
Нижние пределы интегрирования по всем переменным заданы в условии примера.
Найдём верхний предел интегирования по “иксу”. Для этого выразим “икс” из четвёртого уравнения,
считая “игрек” равным нулю, а “зет” равным двум. Получаем x = 2.
Найдём верхний предел интегирования по “игреку”. Для этого выразим “игрек” из того же четвёртого
уравнения, считая “зет” равным двум, а “икс” – переменной величиной. Получаем
y = 2 − x. И, наконец,
найдём верхний предел интегрирования по переменной “зет”. Для этого выразим “зет” из того же
четвёртого уравнения, считая “игрек” и “зет” переменными величинами. Получаем
z = 4 − x − y.
Для этого выразим “игрек” из того же четвёртого
уравнения, считая “зет” равным двум, а “икс” – переменной величиной. Получаем
y = 2 − x. И, наконец,
найдём верхний предел интегрирования по переменной “зет”. Для этого выразим “зет” из того же
четвёртого уравнения, считая “игрек” и “зет” переменными величинами. Получаем
z = 4 − x − y.
Сведём данный тройной интеграл к последовательности трёх определённых интегралов:
.
Вычисляем самый внутренний интеграл – по переменной z, считая икс и игрек константами. Получаем:
.
Вычисляем средний интеграл – по переменной y. Получаем:
.
Вычисляем самый внешний интеграл – по переменной x и окончательно находим данный тройной интеграл:
Ответ: данный тройной интеграл равен 2.
Если проекцией области интегрирования на какую-либо из координатных плоскостей является круг или часть круга, то тройной интеграл проще вычислисть, перейдя к цилиндрическим координатам. Цилиндрическая система координат является обобщением полярной системы координат на пространство. В системе цилиндрических координат точка M характеризуется тремя величинами (r, φ, z), где r – расстояние от начала координат до проекции N точки M на плоскость xOy, φ – угол между вектором ON и положительным направлением оси Ox, z – аппликата точки M (рисунок ниже).
Прямоугольные координаты x, y, z с цилиндрическими координатами r, φ, z связывают формулы
x = rcosφ,
y = rsinφ,
z = z.
Для того, чтобы в тройном интеграле перейти к цилиндрическим координатам, нужно подынтегральную функцию выразить в виде функции переменных r, φ, z:
.
То есть переход от прямогольных координат к цилиндрическим осуществляется следующим образом:
.
Тройной интеграл в цилиндрических координатах вычисляется так же как и в декартовых прямоугольных координатах, путём преобразования в последовательность трёх определённых интегралов:
Если область интегрирования в тройном интеграле представляет собой шар или часть шара,
то проще вычислить тройной интеграл в сферических координатах. В сферических координатах точку M
характеризуют три величины (ρ, φ, θ), где ρ – расстояние от точки
M до начала координат 0, φ – угол между вектором ON и положительным
направлением оси Ox (N – проекция точки M на плоскость xOy),
θ – угол между вектором OM и положительным направлением оси Oz.
Сферические координаты связаны с прямоугольными декартовыми координатами соотношениями
x = ρsinθcosφ,
y = ρsinθsinφ,
z = ρcosθ.
Элемент объёма в сферических координатах выражается следующим образом:
.
Таким образом, переход от прямоугольных декартовых координат в тройном интеграле к сферическим координатам осуществляется по формуле:
Чтобы вычислить тройной интеграл в сферических координатах, нужно поступить так же, как при вычислениях в прямоугольных декартовых и цилиндрических координатах – перейти к повторным интегралам (последовательности трёх определённых интегралов):
Пример 9. Вычислить тройной интеграл
переходом к сферическим координатам, где V –
область, ограниченная неравенствами и
.
Решение. Снизу область интегрирования ограничена конической поверхностью , а сверху – сферой . Так как область интегирования представляет собой часть шара, перейдём к сферическим координатам. Перепишем подынтегральную функцию:
Учитывая, что , получаем
Расставим пределы интегрирования и перепишем последний полученный интеграл в виде трёх повторных интегралов. По рисунку видно, что , , . Поэтому
Итак, тройной интеграл вычислен. Так как все три интеграла – независисмые друг от друга, мы смогли интегрировать каждый отдельно и результаты перемножить.
Вычисление объёма тела. Объём области V равен тройному интегралу по этой области, если подынтегральная функция равна 1:
.
Вычисление массы неоднородного тела. Массу неоднородного тела с плотностью
ρ = ρ(x, y, z)
можно вычислить по формуле:
Массу неоднородного тела с плотностью
ρ = ρ(x, y, z)
можно вычислить по формуле:
.
Статические моменты материального тела. Статические моменты относительно плоскостей xOy, xOz, yOz материального тела с плотностью ρ = ρ(x, y, z) можно вычислить по формулам:
Моменты инерции материального тела. Моменты инерции относительно плоскостей xOy, xOz, yOz материального тела с плотностью ρ = ρ(x, y, z) можно вычислить по формулам:
Моменты инерции относительно осей Ox, Oy, Oz определяются по формулам:
Центр тяжести материального тела. Координаты центра массы
C(xc, yc, zc)
материального тела с плотностью ρ = ρ(x, y, z)
определяются по формулам:
Координаты центра массы
C(xc, yc, zc)
материального тела с плотностью ρ = ρ(x, y, z)
определяются по формулам:
Кратные и криволинейные интегралы
Поделиться с друзьями
∫∫∫ Тройной интеграл – Калькулятор Он-лайн
Введите подинтегральную функцию, для которой надо найти тройной интеграл
Найдём решение тройного интеграла от функции f(x, y, z).
Введите вверхние и нижние пределы для области интегрирования и
подинтегральную функцию для тройного интеграла.
Если подинтегральной функции нету, то укажите 1.
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция – арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция – арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- exp(x)
- Функция – экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - sin(x)
- Функция – Синус от x
- cos(x)
- Функция – Косинус от x
- sinh(x)
- Функция – Синус гиперболический от x
- cosh(x)
- Функция – Косинус гиперболический от x
- sqrt(x)
- Функция – квадратный корень из x
- sqr(x) или x^2
- Функция – Квадрат x
- ctg(x)
- Функция – Котангенс от x
- arcctg(x)
- Функция – Арккотангенс от x
- arcctgh(x)
- Функция – Гиперболический арккотангенс от x
- tg(x)
- Функция – Тангенс от x
- tgh(x)
- Функция – Тангенс гиперболический от x
- cbrt(x)
- Функция – кубический корень из x
- gamma(x)
- Гамма-функция
- LambertW(x)
- Функция Ламберта
- x! или factorial(x)
- Факториал от x
- Действительные числа
- вводить в виде 7.
 3
3- – возведение в степень
- x + 7
- – сложение
- x – 6
- – вычитание
- 15/7
- – дробь
Другие функции:
- asec(x)
- Функция – арксеканс от x
- acsc(x)
- Функция – арккосеканс от x
- sec(x)
- Функция – секанс от x
- csc(x)
- Функция – косеканс от x
- floor(x)
- Функция – округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция – округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция – Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция – гиперболический арксеканс от x
- csch(x)
- Функция – гиперболический косеканс от x
- sech(x)
- Функция – гиперболический секанс от x
- acsch(x)
- Функция – гиперболический арккосеканс от x
Постоянные:
- pi
- Число “Пи”, которое примерно равно ~3.
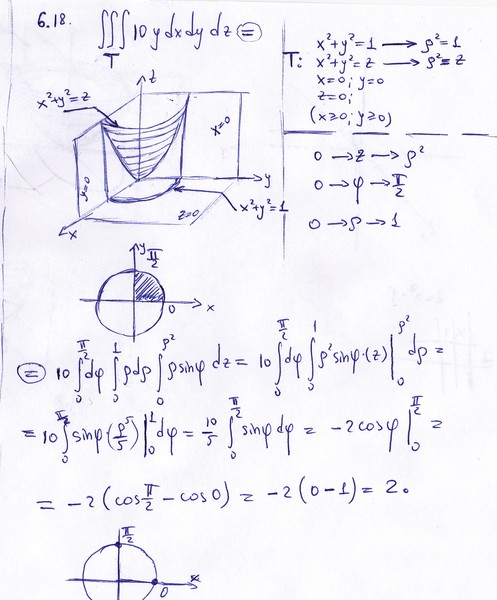 14159..
14159.. - e
- Число e – основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности – знак для бесконечности
Тройной интеграл, формулы и примеры
Понятие тройного интеграла вводиться аналогично понятию двойного интеграла.
Пусть функция определена в ограниченной замкнутой области , которая принадлежит трехмерному пространству с определенной декартовой системой координат . Разобьем заданную область на частей , которые не имеют общих внутренних точек и объемы которых равны соответственно . В каждой такой элементарной области возьмем произвольную точку и составим сумму , называемую интегральной суммой для функции по области .
Пусть – наибольшее из расстояний между точка элементарной области . Если существует предел , который не зависит ни от способа разбиения области на элементарные области , ни от выбора в них точек , то этот предел называется тройным интегралом по области и обозначается
Если существует предел , который не зависит ни от способа разбиения области на элементарные области , ни от выбора в них точек , то этот предел называется тройным интегралом по области и обозначается
Пусть – замкнутая пространственная область, которая ограничена снизу и сверху поверхностями и соответственно (), а з боку – цилиндрической поверхностью с образующими, параллельными оси (рис. 1).
Переменные и изменяются в плоской области , которая является проекцией пространственной области на координатную плоскость .
В прямоугольной декартовой системе координат элемент объему вычисляется по формуле . Для указанной области тройной интеграл равен:
Внутренний интеграл вычисляется по переменной , а переменные и в этом случае считаются постоянными. Результатом интегрирования есть функция переменных и – . Итак, вычисление тройного интеграла сводится к вычислению двойного интеграла .
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Лекции Тройной интеграл
Скачать с Depositfiles
Тройной интеграл.
Контрольные вопросы.
Тройной интеграл, его свойства.
Вычисление тройного интеграла в декартовых координатах.
Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических координатах.
Вычисление тройного интеграла в сферических координатах.
Пусть функция u = f(x,y,z) определена в ограниченной замкнутой области V пространства R3. Разобьём область V произвольным образом наn элементарных замкнутых областей V1, … , Vn, имеющих объемы V1, …, Vn соответственно. Обозначим d – наибольший из диаметров областей V1, … , Vn. В каждой области Vk выберем произвольную точку Pk (xk , yk , zk) и составим интегральную сумму функции f(x, y, z)
В каждой области Vk выберем произвольную точку Pk (xk , yk , zk) и составим интегральную сумму функции f(x, y, z)
S =
Определение. Тройным интегралом от функции f(x, y, z) по области V называется предел интегральной суммы , если он существует.
Таким образом,
(1)
Замечание. Интегральная сумма S зависит от способа разбиения области V и выбора точек Pk (k=1, …, n). Однако, если существует предел, то он не зависит от способа разбиения области V и выбора точек Pk . Если сравнить определения двойного и тройного интегралов, то легко увидеть в них полную аналогию.
Достаточное условие существования тройного интеграла. Тройной интеграл (13) существует, если функция f(x, y, z) ограничена в V и непрерывна в V, за исключением конечного числа кусочно-гладких поверхностей, расположенных в V .
В дальнейшем будем считать, что все рассматриваемые тройные интегралы существуют.
Некоторые свойства тройного интеграла.
1) Если С – числовая константа, то
3) Аддитивность по области. Если область V разбита на области V1 и V2, то
.
4) Объем тела V равен
(2)
Вычисление тройного интеграла в декартовых координатах.
Пусть D проекция тела V на плоскость xOy, поверхности z=φ1(x, y), z=φ2(x, y) ограничивают тело V снизу и сверху соответственно. Это значит, что
V = {(x, y, z): (x, y)D, φ1(x, y) ≤ z ≤ φ2(x, y)} .
Такое тело назовем z-цилиндрическим. Тройной интеграл (1) по z-цилиндрическому телу V вычисляется переходом к повторному интегралу, состоящему из двойного и определенного интегралов:
(3)
В этом повторном интеграле сначала вычисляется внутренний определенный интеграл по переменной z, при этом x, y считаются постоянными.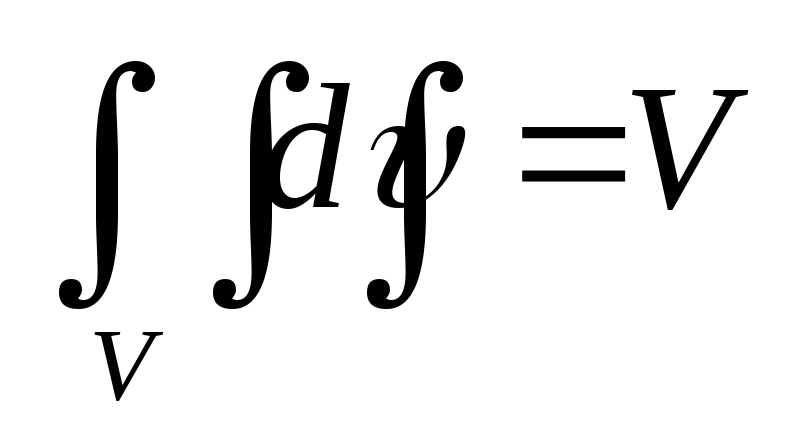 Затем вычисляется двойной интеграл от полученной функции по области D.
Затем вычисляется двойной интеграл от полученной функции по области D.
Если V x-цилиндрическое или y-цилиндрическое тело, то верны соответственно формулы
В первой формуле D проекция тела V на координатную плоскость yOz, а во второй на плоскость xOz
Примеры. 1) Вычислить объем тела V, ограниченного поверхностями z = 0, x2 + y2 = 4, z = x2 + y2 .
Решение. Вычислим объём при помощи тройного интеграла по формуле (2)
Перейдем к повторному интегралу по формуле (3).
Пусть D круг x2 + y2 ≤ 4, φ1(x, y) = 0, φ2(x, y)= x2 + y2 . Тогда по формуле (3) получим
Тогда по формуле (3) получим
Для вычисления этого интеграла перейдем к полярным координатам. При этом круг D преобразуется во множество
Dr ={ (r, φ) : 0 ≤ φ < 2π , 0 ≤ r ≤ 2 }.
2) Тело V ограничено поверхностями z=y, z= –y, x=0 , x=2, y=1. Вычислить
Плоскости z = y, z = –y ограничивают тело соответственно снизу и сверху, плоскости x=0 , x=2 ограничивают тело соответственно сзади и спереди, а плоскость y=1 ограничивает справа. V – z-цилиндрическое тело, его проекцией D на плоскость хОу является прямоугольник ОАВС. Положим φ1(x, y) = –y, φ2(x, y)= y и применим формулу (3):
Тройные интегралы
Имеют те же свойства, что и двойные интегралы (линейность, аддитивность, формулы среднего значения и т. д.)
д.)
I. Вычисление тройных интегралов с помощью повторного интегрирования
1. Предположим, что функция f(x, y, z) непрерывна в рассматриваемой области T.
Пусть сначала T = [a, b; c, d; e, f] – прямоугольный параллелепипед, проектирующийся на плоскость yz в прямоугольник R = [c, d; e, f]. Тогда
Заменяя в (1) двойной интеграл повторным, получим
Вычисление тройного интеграла сводится к последовательному вычислению трёх определённых интегралов.
Если первые два интеграла в (2) объединить в двойной, то будем иметь
где P = [a, b; c, d] – проекция параллелепипеда T на плоскость xy.
Заметим, что в этих случаях можно менять роли переменных.
2. Пусть область T заключена между плоскостями x = a и x = b, причём каждое сечение области T плоскостью x=const, a ≤ x ≤ b представляет собой квадрируемую фигуру G(x)(рис. 1). Тогда
1). Тогда
3. Пусть теперь тело T представляет собой “цилиндрический брус”, ограниченный снизу и сверху, соответственно, поверхностями z = z1(x, y) и z = z2(x, y), проектирующиеся на плоскость xy в некоторую квадрируемую фигуру G (рис.2), z1(x, y) и z2(x, y) – непрерывны в G. Тогда
Отметим, что наряду с указанными формулами имеют место и им подобные, получающиеся перестановкой переменных x, y и z.
II. Замена переменных в тройном интеграле состоит в переходе от переменных x, y, z к новым переменным u, v, w по формулам
Если выполняются условия
то имеет место формула
Формулы (6) называют криволинейными координатами (u, v, w) в области T. Рассмотрим примеры криволинейных координат.
1. Цилиндрические координаты представляют соединение полярных координат в плоскости xy с обычной декартовой аппликатой z (рис. 3).
3).
Пусть M(x, y, z) – произвольная точка в пространстве xyz, P – проекция точки M на плоскость xy. Точка M однозначно определяется тройкой чисел (r,φ,z), где (r,φ) – полярные координаты точки P, z – аппликата точки M. Формулы, связывающие их с декартовыми, имеют вид
2. Сферические координаты. Пусть M(x, y) – произвольная точка в пространстве xyz, P – проекция точки M на плоскость xy. Точка M однозначно задаётся тройкой чисел (r,θ,φ), где r – расстояние точки M до точки 0, θ – угол между лучами OM и OZ, φ – полярный угол точки P на плоскости xy. Тройка чисел (r,θ,φ) называется сферическими координатами точки M.
Они связаны с прямоугольными формулами
Якобиан отображения
Иногда используются обобщённые сферические координаты.
Объём V кубируемой области T (кубического тела) в пространстве xyz выражается формулой
Переходя в этом равенстве к новым переменным по формулам (6), получим выражение объёма области T в криволинейных координатах
Пусть T – материальное тело (кубируемая область) с плотностью
Тогда
Пример1. 2}}\) вырезанная цилиндром, проектируется в область
2}}\) вырезанная цилиндром, проектируется в область
Перейдём в интеграле к цилиндрическим координатам по формулам (8). При этом уравнение окружности x? + y? – ax = 0 преобразуется в кривую
Таким образом
Пример 2. Вычислить интеграл
Решение. Перейдём в интеграле к сферическим координатам по формулам (9). Тогда область интегрирования можно задать неравенствами
Вычисление тройного интеграла. Теорема о переходе от тройного интеграла к повторному / Тройной интеграл / 3dstroyproekt.ru
Будем называть ограниченную замкнутую область $\mathbf { \textit { V } } \textbf { простой правильной } $, если выполняются два условия : проекция $\mathbf { \textit { V } } $ на какую-либо координатную плоскость, например, на плоскость $\mathbf { \textit { Оху } } $ – простая область $\mathbf { \textit { D } } $, и любая прямая, перпендикулярная этой плоскости и проходящая через внутреннюю точку $\mathbf { \textit { V } } $, пересекает границу $\mathbf { \textit { V } } $ в двух точках. { \large\frac { \pi } { 2 } \normalsize } }\right] } = { \frac { 1 } { 7 } \cdot \frac { \pi } { 2 } } = { \frac { \pi } { { 14 } } . } $
{ \large\frac { \pi } { 2 } \normalsize } }\right] } = { \frac { 1 } { 7 } \cdot \frac { \pi } { 2 } } = { \frac { \pi } { { 14 } } . } $
CA MAT Analyze для Zowe CLI
Подключаемый модуль CA MAT Analyze для Zowe CLI позволяет расширить интерфейс командной строки (CLI) Zowe для взаимодействия с CA Mainframe Application Tuner (CA MAT).
Как разработчик приложений, вы можете использовать ресурсы CA MAT прямо со своего компьютера и инструменты интегрированной среды разработки (IDE), используя знакомый интерфейс командной строки. Подключаемый модуль CA MAT Analyze для Zowe CLI позволяет управлять профилями монитора CA MAT, вызывать мониторы для измерения приложений мэйнфрейма и получать доступ к данным анализа с помощью Zowe CLI.
Этот плагин совместим с Zowe CLI и отмечен значком Zowe Conformance Program. Лицензированные пользователи CA MAT имеют право на поддержку этого подключаемого модуля. Этот плагин не требует подписки CA Brightside для загрузки или использования. Этот плагин не требует подписки CA Brightside для загрузки или использования. |
Как разработчик приложения вы можете использовать плагин CA MAT Analyze для Zowe CLI для выполнения следующих задач:
-
Управление профилями монитора
.Создавайте и вызывайте профили монитора, просматривайте списки доступных профилей и извлекайте историю измерений. -
Анализировать данные измерений
. Получите доступ к данным измерений из CA Mainframe Application Tuner, которые доступны вам в интерфейсе командной строки в виде аналитических представлений CA MAT. -
Устранение проблем с производительностью в исходном коде
. Если список исходных программ зарегистрирован в CA MAT, пользователи IDE Visual Studio Code (VS Code) могут получать сведения о гистограмме и отображать определенные местоположения исходной программы, связанные с наиболее ресурсоемкими программными модулями и CSECT.Когда вы запрашиваете данные измерения гистограммы из терминала командной строки VS Code, подключаемый модуль CA MAT Analyze для Zowe CLI передает список исходного кода на ваш локальный компьютер и направляет вас непосредственно к определенной строке и номеру столбца исходного кода. , что позволяет сразу же изучить оператор программы и определить возможные возможности настройки. Чтобы использовать опцию получения листинга, вам необходимо указать в вашем профиле MAT локальный каталог, в который подключаемый модуль загружает листинги программ.
Команда для проверки подключаемого модуля CA MAT Analyze для Zowe CLI:
Вы можете настроить профиль CA MAT, чтобы не вводить сведения о подключении при каждой команде.Профиль содержит тип протокола, хост и порт, которые вы определили для сервера CA MAT REST API, а также имя пользователя и пароль мэйнфрейма. Профиль CA MAT также содержит параметр$ плагины zowe проверяют @ broadcom / mat-analysis-for-zowe-cli
zowediscoverable
, который указывает, хотите ли вы использовать Zowe API Mediation Layer для обработки команд для этого профиля. Установите–zowediscoverable true
, только если вы настроили свойства уровня передачи Zowe API в настройках сервера CA MAT REST API.Вы можете создать несколько профилей и при необходимости переключаться между ними.Создайте профиль, используя следующую команду:
профили zowe создают профиль mat matprofile --prtпротокол
--hnимя хоста
--ptномер порта
--пользовательимя пользователя
- пароль пароля --zowediscoverabletrue
илиложь
- Создайте профиль MAT с именем matprofile, используя конфигурацию CA MAT и детали REST API, с сервером CA MAT REST API, интегрированным с посредническим слоем Zowe API:
профили zowe создать mat-profile matprofile --prt http --hn localhost --pt 1234 --user johndoe --pass qwerty --zowediscoverable true
- Создайте профиль MAT под названием ‘matprofile’, используя вашу конфигурацию CA MAT и детали сервера CA MAT REST API без интеграции с Zowe API Mediation Layer, и определите каталог ‘c: \ listings’ для мгновенного хранения списков программ. анализ из вашей VS Code IDE:
профили zowe создают mat-profile matprofile --prt http --hn localhost --pt 1234 --user johndoe --pass qwerty --zowediscoverable false --listingDir 'c: \ listings'
zowe profiles create
с теми же значениями параметров профиля, за которыми следует– -overwrite
|– вариант потока
.Для получения дополнительной информации введите следующую команду:профилей zowe create mat-profile –help
. Выпуски· hybridgroup / gocv · GitHub версии
· hybridgroup / gocv · GitHub- все
- обновление до OpenCV 4.5.3
- make task и build tag для статической сборки OpenCV / GoCV в Linux
- добавить задачи Makefile для установки OpenCV на Nvidia Jetson
- добавить gotest для более красочного вывода тестов запуск тестов из контейнеров
- сборка
- корректирующий выходной формат для отчета о покрытии кода
- обеспечить соблюдение правила, что весь код Go правильно отформатирован
- удалить кодеков
- ядро
- добавить функции NewPointVectorFromMat () и NewPoint2fVectorFromMat ()
- Исправьте возможную гонку MatProfile, приказав удалить перед освобождением.
- cuda
- добавить основные функции для GpuMat, такие как Cols (), Rows () и Type ()
- начальная реализация функции Flip
- документы
- обновить ДОРОЖНУЮ КАРТУ на основе последних вкладов
- примеры
- правильный список примеров и исправление комментария
- функции 2d
- отслеживание
- highgui
- Добавить функцию CreateTrackbarWithValue в тип окна.
- imgcodec
- оптимизировать IMEncode, избегая множественных копий данных.
- imgproc
- Добавить функцию CircleWithParams
- Добавить функцию DilateWithParams () (# 827)
- Добавить функцию EllipseWithParams
- Добавить функцию FillPolyWithParams
- Добавить функцию PointPolygonTest
- Добавить функцию RectangleWithParams
- фото
- добавить функции MergeMertens, AlignMTB и Denoising (# 848)
- xphoto
- Добавить Xphoto contrib (# 844)
- все
- ядро
- добавить Append () в PointsVector / PointVector
- добавить резюме :: RNG
- добавить реализацию для Point2fVector
- добавить функции rand
- добавить тестовое покрытие для PointsVector
- создает новые оболочки PointVector / PointVector, чтобы избежать повторяющегося копирования памяти для кажущихся невинных операций с фрагментами изображения.Путевая точка
- тестовое покрытие для Point2f
- используйте PointVector для всего, что мы можем, чтобы ускорить конвейер при передаче векторов Point
- используйте enum вместо int для метода инвертирования
- cuda
- добавление HoughLinesDetector и HoughSegmentDetector
- добавление тестов для CannyEdgeDetector
- некоторый рефакторинг API
- добавление файлов докеров для OpenCV 4.5.2 с CUDA 11.2
- добавить GaussianFilter
- правильная подпись и тест на порог
- орудие SobelFilter
- переместить функции модуля арифметики в правильное место
- переименовать файлы, чтобы избавиться от такого количества файлов
- добавить реализацию функции abs
- DNN
- докер
- сделать все имена / теги Dockerfiles более согласованными
- документы
- добавить функции CUDA, которые необходимо реализовать, в ROADMAP
- удалить недопустимые разделы и добавить некоторые недостающие функции из ROADMAP
- imgproc
- Добавить функцию FindContoursWithParams
- Добавить ToImageYUV и ToImageYUVWithParams
- марка
- добавить задачу make для отображения журнала изменений для следующего выпуска
- wechat_qrcode
- отключить модуль в Windows из-за ошибки компоновщика
- все
- ядро
- добавить инициализаторы матрицы: глаз, единицы, нули (# 758)
- добавить создание многомерного мата
- добавить конструктор ndim mat
- добавлены аккумуляторы
- добавлена норма звонка с двумя матами (# 600)
- хранит ссылку на байт [], поддерживающий Mat.(# 755)
- удалить защиту для DataPtrUint8, так как любой мат можно обработать как Uint8
- добавить функцию Mat IsContinuous () и убедиться, что любые указатели данных Mat, используемые для создания срезов Go, применяются только к непрерывным матам.
- исправить размер буфера для строк Go для 32-разрядных операционных систем
- сборка
- калибр3d
- правильно закрыть мат после теста
- DNN
- добавить ReadNetFromONNX и ReadNetFromONNXBytes (# 760)
- увеличить тестовое покрытие
- докер
- dockerfiles для opencv gpu builds
- документы
- исправленные ссылки на CUDA и OpenVINO
- список всех нереализованных функций в фотомодуле
- заменить GoDocs на pkg docs
- обновить ДОРОЖНУЮ КАРТУ на основе последних публикаций
- imgproc
- добавить тестовое покрытие для GetTextSizeWithBaseline ()
- закрывает все маты даже те, которые основаны на срезах памяти
- закрыть Mat, чтобы избежать утечки памяти в ToImage ()
- рефакторинг функций ToImage и ImageToMatXX
- openvino
- исправить репозиторий dldt в make-файле для openvino
- ос
- добавление пакета gcc-c ++ в rpm deps
- фото
- добавить функцию SeamlessClone
- профиль
- добавить созданные маты в Split и ForwardLayers в профиль (# 780)
- все
- обновление для opencv выпуска 4.5,0
- сборка
- добавить зависимости файлов, необходимые для тестов DNN
- добавить подробный вывод для тестов на CircleCI
- также запускает модульные тесты несвободных алгоритмов. YMMV.
- исправить сборку с помощью cuda
- удалите Travis и переключитесь на CircleCI, используя сборки на основе Docker
- обновляет CI-сборки до Go 1.15
- ядро
- добавить метод mixChannels () в Mat (# 746)
- Добавить в помощник GoStrings
- поддерживает метод ConvertToWithParams
- DNN
- Добавить функцию NMSBoxes (# 736)
- Добавлена возможность загрузки файла Torch.Протестированные функции для извлечения 128d векторов
- исправлено использование неправильного типа для неподключенного уровня
- использовать ddepth по умолчанию для преобразования в blob из изображения в соответствии с рекомендациями @berak
- докер
- используйте отдельный файл докеров для opencv, чтобы избежать массивной перестройки
- документы
- добавить недавние изменения в ROADMAP, а также добавить функции cuda, которые все еще нуждаются в реализации
- отобразить значок CircleCI в README
- незначительные улучшения в документации CUDA в файлах README
- функции 2d
- добавить FlannBasedMatcher
- добавить совпадения (# 720)
- исправить утечку памяти в SIFT
- highgui
- imgproc
- Добавить параметр для возврата базовой линии с помощью GetTextSizeWithBaseline
- объект
- Добавить QRCode DetectAndDecodeMulti
- видео
- Добавьте свойства захвата видео и установите предпочтительный сервер API (# 739) Требуется исправление
- , как описано в выпуске golang / go № 32479 .
- все
- обновить Makefile и README
- изменить константы и соответствующие сигнатуры функций, чтобы они имели правильные типы (# 689)
- заменить терминологию основной ветви версией
- обновление до OpenCV 4.4,0
- калибр3d
- добавить FindHomography ()
- добавить функцию EstimateAffinePartial2D ()
- добавить GetAffineTransform () и GetAffineTransform2f ()
- добавить UndistortPoints (), FisheyeUndistortPoints () и EstimateNewCameraMatrixForUndistortRectify ()
- ядро
- документы
- добавить недавние публикации в ROADMAP
- создать CODE_OF_CONDUCT.md
- год обновления авторских прав
- функции 2d
- закрыть мат вернул из алгоритма SIFT
- исправить проблему 707 с помощью DrawKeyPoints Срок действия патента
- SIFT истек, поэтому он является частью основных модулей OpenCV
- imgproc
- изменить структуру, чтобы удалить предупреждение о расширении указателя поля в старом стиле GNU
- сборка
- обновить Makefile и README Обновление
- для использования go1.14
- калибр3d
- ядро
- исправить утечку памяти в Mat.Size () и Mat.Split () (# 580)
- cuda
- добавить поддержку сборки
- добавить серверную часть cuda / цель
- добавить поддержку для:
- cv :: cuda :: CannyEdgeDetector
- cv :: cuda :: CascadeClassifier Class
- cv :: cuda :: HOG Class
- удалить оператор взлома регистра
- DNN
- Избегайте параллельных тестовых прогонов
- удалить попытку преобразования изображения в градациях серого, в котором используется настройка среднего значения
- докер
- docker file последнее изменение команды (# 505)
- документы
- добавить недавние публикации в ROADMAP
- imgproc
- добавить функцию ErodeWithParams
- добавить функцию getGaussianKernel
- добавить тип Go Point2f и обновить GetPerspectiveTransform () (# 589)
- добавить привязку PhaseCorrelate (# 626)
- добавлена функция полилинии
- не освобождает данные контуров до тех пор, пока не будут нарисованы необходимые контуры
- Threshold () должен вернуть значение (# 620)
- марка
- добавлена поддержка Raspberry Pi Zero в make-файл
- opencv
- openvino
- окна
- добавить флаг cmake для типа счетчика статистики распределителя, чтобы избежать проблемы opencv # 16398
- bgsegm
- Добавить BackgroundSubtractorCNT
- калибр3d
- Добавлена функция устранения искажений (# 520)
- ядро
- сложение функций (разложение по сингулярным числам, умножение между матрицами, транспонирование матрицы) (# 559)
- Добавить новые функции (# 578)
- добавить метод setIdentity () в Mat
- добавить метод String (# 552)
- MatType: добавить недостающие константы
- DNN
- Добавление GetLayerNames ()
- учитывает битовую глубину входного изображения, чтобы установить ожидаемый результат при преобразовании изображения в blob
- doc
- изменить opencv версии 3.от x до 4.x
- докер
- imgcodecs
- Исправить ошибку декодирования изображения webp (# 523)
imgcodecs: оптимизировать копию данных, используемых для метода IMDecode
- Исправить ошибку декодирования изображения webp (# 523)
- imgproc
- Добавить GetRectSubPix
- Добавлен ClipLine
- Добавлен InvertAffineTransform
- Добавлена функция LinearPolar (# 524)
- правильный параметр размера ksize, используемый для модульного теста MedianBlur
- Добавить / вставить текст с типом линии (# 527)
- FitEllipse
- В функциях FillPoly и DrawContours удалите обертку func (), чтобы избежать освобождения памяти перед вызовом функций opencv.(# 543)
- объект
- opencv
- обновление до версии OpenCV 4.2.0
- openvino
- тест
- Допускается неточный результат в SolvePoly
- Терпеть неточность в TestHoughLines
- сборка
- добавлен go clean –cache для очистки цели, см. Проблему 458
- ядро
- Добавить функцию KMeans
- добавлена функция MeanWithMask для матов (# 487)
- Исправить возможную утечку ресурсов
- cuda
- добавил cudaoptflow
- добавил NewGpuMatFromMat, который создает GpuMat из Mat
- Поддержка деформации изображения CUDA (# 494)
- DNN
- добавить BlobFromImages (# 467)
- добавить ImagesFromBlob (# 468)
- документы
- обновить ДОРОЖНУЮ КАРТУ со всеми последними вкладами.Спасибо!
- примеры
- Распознавание лиц по URL-адресу изображения с помощью IMDecode (# 499)
- лучший формат
- imgproc
- Добавить calcBackProject
- Добавить СравнитьHist
- Добавить DistanceTransform и Watershed
- Добавить GrabCut
- Добавить интеграл
- Добавить морфологиюExWithParams
- opencv
- openvino
- обновления, необходимые для 2019 R3
- видео
- Добавлен ToCodec для преобразования строки FOURCC в числовое представление (# 485)
- сборка
- Используйте Go 1.12.x для сборки
- Обновление до OpenCV 4.1.0
- cuda
- Начальная реализация cuda
- документы
- Исправьте команду для установки xquartz через brew / cask
- функции 2d
- Добавить поддержку SimpleBlobDetectorParams (# 434)
- Добавлен FastFeatureDetectorWithParams
- imgproc
- Добавлен вызов функции в cv :: morphologyDefaultBorderValue
- тест
- Увеличить тестовое покрытие для FP16BlobFromImage ()
- видео
- Добавлен calcOpticalFlowPyrLKWithParams
- Добавление конструктора MOG2 / KNN с опциями
AAF ContabilidadeAvancada Aula22a31 EugenioMontoto MatProfI | PDF | Capital Próprio (Finanças)
Вы читаете бесплатный превью
Страницы с 11 по 54 не показаны в этом предварительном просмотре.
Вы читаете бесплатный превью
Страницы с 62 по 76 не показаны в этом предварительном просмотре.
Вы читаете бесплатный превью
Страницы с 88 по 101 не показаны в этом предварительном просмотре.
Вы читаете бесплатный превью
Страницы со 109 по 111 не показаны в этом предварительном просмотре.
Вы читаете бесплатный превью
Page 117 не отображается в этом предварительном просмотре.
Вы читаете бесплатный превью
Страницы с 124 по 128 не показаны в этом предварительном просмотре.
Вы читаете бесплатный превью
Страницы с 135 по 138 не показаны в этом предварительном просмотре.
Вы читаете бесплатный превью
Страницы с 142 по 150 не показаны в этом предварительном просмотре.
Вы читаете бесплатный превью
Страницы с 154 по 163 не показаны в этом предварительном просмотре.
Вы читаете бесплатный превью
Страницы с 168 по 177 не показаны в этом предварительном просмотре.
Вы читаете бесплатный превью
Страницы с 183 по 185 не показаны при предварительном просмотре.
Камилла, автор сайта Visit Åland R.F.
КОЛЬЦО ANMÄLAN STÄNGD 24000 FÖR INFO
Обычный
0
21
ложь
ложь
ложь
SV-FI
X-NONE
X-NONE
LatentStyleCount = “371”>
< w: LsdException Locked = "false" SemiHidden = "true" UnhideWhenUsed = "true"
Name = »Маркер списка 2 ″ />
< w: LsdException Locked = "false" SemiHidden = "true" UnhideWhenUsed = "true"
Name = »Основной текст 2 ″ />
< w: LsdException Locked = "false" SemiHidden = "true" UnhideWhenUsed = "true"
Name = »Нет List »/>
< w: LsdException Locked = "false" SemiHidden = "true" UnhideWhenUsed = "true"
Name = “Table Professional” />
/ * Определения стилей * /
таблица.MsoNormalTable
{mso-style-name: «Обычная таблица»;
МСО-стиль-строка-размер-полосы: 0;
мсо-стиль-кольбанд-размер: 0;
МСО-стиль-ношоу: да;
МСО-стиль-приоритет: 99;
родительский-стиль MSO: ””;
mso-padding-alt: 0cm 5.4pt 0cm 5.4pt;
МСО-пара-маржа-верх: 0 см;
МСО-пара-поле-право: 0 см;
МСО-пара-маржа-низ: 8.0pt;
МСО-пара-маржа-левый: 0 см;
высота строки: 107%;
МСО-пагинация: вдова-сирота;
размер шрифта: 11.0pt; Семейство шрифтов
: «Calibri», «без засечек»;
mso-ascii-font-family: Calibri;
МСО-ascii-тема-шрифт: второстепенный латинский;
мсо-ханси-шрифтов: Calibri;
МСО-ханси-тема-шрифт: второстепенный латинский;
mso-bidi-font-family: «Times New Roman»;
МСО-биди-тема-шрифт: второстепенный-биди;
mso-fareast-language: EN-US;}
Välkommen på Visit Ålands årsmöte 2014
Boka in fredagen den 11 апреля vid Käringsund Resort & Conference med start kl.16!
Vi samlas i Eckerö för vårt årsmöte och kickoff for den kommande säsongen. Mötet inleds med information om verksamheten 2014 samt arbetet med ett online bokningssystem och den nya hemsidan.
Här hittar du;
verksamhetsberättelsen
mötesagenda
valberedningens förslag
följebrev till stadgeändringen
для стадиона
визит-aland-stadgar-2010
кл.15.30 Автобусное сообщение с автобусного маршрута Mariehamns
Kl.16.00 Посетите Åland informerar
Kl.17.00 Kaffeservering и регистрация до mötet
Kl.17.45 Programmet fortsätter. Tid for frågor och diskussion
Kl.18.15 Посетите Ålands årsmöte
KL.19.00 Middagsbuffé med underhållning
Kl.22.30 Возвращение на автобусе до Мариехамна
Vi avslutar kvällen med en gemensam middagsbuffé till ett självkostnadspris på 36 € / чел. drycker som faktureras efter mötet. Kaffeserveringen & busstransporten är kostnadsfri.
Verksamhetsberättelsen 2013, mötesagendan, valberedningens förslag samt förslag på stadgeändring skickas ut per post den 2 апреля.
Din bindande anmälan för deltagandet, transporten och middagen behöver vi senast måndagen den 7 апреля.
Hjärtligt välkommen!
КОЛЬЦО ANMÄLAN STÄNGD 24000 FÖR INFO
Без названия – Мотилал Освал
Декларация главного исполнительного директора
Сертификат аудитора о Корпорации
к
к отчету независимых аудиторов
Бухгалтерский баланс Бухгалтерский балансIN Примечание Как
Отчет о движении денежных средств Отчет о движении денежных средств
Примечания к финансовой отчетности (продолжение
Примечания к финансовой отчетности (продолжение
Примечания к финансовой отчетности (продолжение
Примечания к финансовой отчетности (продолжение
Примечания к финансовой отчетности (продолжение
Примечания к финансовой отчетности (продолжение
Примечания к финансовой отчетности (продолжение
Примечания к финансовой отчетности (продолжение
Примечания к Финансовый отчет (продолжение
Примечания к финансовому отчету (продолжение
Примечания к финансовому отчету (продолжение
Аудиторский отчет Совету директоров Di
)Консолидированный баланс Consolida
Консолидированный отчет о движении денежных средствCon
Примечания к Consoli от Financial Sta
Примечания к Consolidated Financial Sta
Примечания к Consolidated Financial Sta
Примечания к Consolidated Financial Sta
Примечания к консолидированной финансовой отчетности
Примечания к консолидированной финансовой отчетности
Примечания к консолидированной финансовой отчетности
Примечания к консолидированной финансовой отчетности Стр. 111 и 112:
Примечания к консолидированной финансовой отчетности
Примечания к консолидированной финансовой отчетности
Примечания к консолидированной финансовой отчетности
Примечания к консолидированной финансовой отчетности
Примечания к консолидированной финансовой отчетности
9002 8Примечания к консолидированной финансовой отчетности
Примечания к консолидированной финансовой отчетности
Примечания к консолидированной финансовой отчетности
Основные финансовые показатели дочерней компании
Примечания
Christina m подкасты | Айви.FM
Кристина М. Грир, доктор философии, доцент кафедры политологии и американистики Фордхэмского университета (кампус Линкольн-центра). В 2018 году она была научным сотрудником Института политики и исследований в области бедности МакСилвера Серебряной школы социальной работы Нью-Йоркского университета. Ее основные исследовательские и педагогические интересы – это расовая и этническая политика, американские городские центры, президентская политика, кампании и выборы. Ее дополнительные исследовательские интересы также включают транспорт, мэров и государственную политику в городских центрах.В своей предыдущей работе она сравнивала преступную деятельность и политические реакции в Бостоне и Балтиморе, а также в Балтиморе и Сент-Луисе. Книга профессора Грира Black Ethnics: Race, Immigration, and the Pursuit of the American Dream (Oxford University Press, 2013) исследует все более этнически разнообразное чернокожее население США из Африки и Карибского бассейна и получила награду WEB du Bois Best Книжная премия в 2014 году, присужденная Национальной конференцией черных политологов. Профессор Грир в настоящее время работает над рукописью, в которой подробно описывается политический вклад Барбары Джордан, Фанни Лу Хамер и Стейси Абрамс.Недавно она была соредактором «Черная политика в переходный период», в которой исследуются джентрификация, пригороды и иммиграция чернокожих в Америку. Она является членом правления Музея многоквартирных домов в Нью-Йорке, Центра общественных изменений, а также членом Консультативного совета Университета Тафтса. Она также является ярым сторонником FIERCE в Нью-Йорке и Project South в Атланте, Джорджия, и бывшим членом правления BAJI (Черный альянс за справедливую иммиграцию), Альянса райдеров Нью-Йорка и Совета по социальным услугам.Она часто выступает политическим комментатором в нескольких СМИ, в первую очередь MSNBC, WNYC и NY1, и ее часто цитируют в таких СМИ, как NYTimes, Wall Street Journal и AP. Она является соведущей подкаста FAQ-NYC, ориентированного на Нью-Йорк, и соведущей подкаста, ориентированного на чернокожих, Что в нем для нас, редактором политики на thegrio.com, продюсером и ведущей The Aftermath и The Претендент на Ozy.com, а также их главный редактор, часто является автором и рассказчиком образовательной серии TedEd, а также ведет еженедельную колонку в The Amsterdam News, одной из старейших черных газет в США.С. Грир получила степень бакалавра в университете Тафтса, а также степень магистра, магистра философии и доктора философии. Кандидат политических наук Колумбийского университета. Лиз Миле, родом из Нью-Джерси, начала выступать в Нью-Йорке в 16 лет. В 18 лет она была представлена в журнале The New Yorker Magazine, в 22 года появилась в шоу Comedy Central «Live at Gotham». Недавно она появилась в шоу Comedy Central «This Week at the Comedy Cellar», «Подожди, погоди, не говори мне» NPR, «Coming To The Stage» Hulu, «Gotham Comedy Live» на канале AXS TV и была представлена в мартовском номере 2015 мира бегунов.У нее есть несколько вирусных видео на Youtube, Instagram и Tiktok, включая шутки «Феминистские сексуальные позы», «F * ck Finland» и «Лондонские копы лучше, чем американские копы». Она регулярно гастролирует по всему миру и выпустила три альбома на Spotify, itunes и выпустила свой первый специальный выпуск «Self Help Me» в мае 2020 года бесплатно на YouTube. Ее первая книга «Почему кошки – засранцы» будет доступна повсюду 30 марта 2021 года. Она написала и спродюсировала первый сезон своего анимационного веб-сериала «Поврежденный», озвученный такими великими комиксами, как Маз Джобрани, Хари Кондаболу, Тед Александро, Джермейн Фаулер, Дин. Эдвардс, округ Колумбия Бенни, Джо Мачи и многие другие.Она также была сопродюсером и одной из главных ролей в 40 эпизодах веб-сериала «Apt C3» с коллегой по комиксам Кармен Линч и модным фотографом Крисом Вонгсаватом. Еженедельно выходит ее подкаст «2 не доктора». ДЖЕКИ ФАБУЛОУС – писатель, продюсер, спикер и главный комик, который использует комедию, чтобы одновременно развлекать, воодушевлять и расширять возможности аудитории. Пережив свою долю любви, трагедий, уроков и неловких моментов, Джеки направляет всю эту энергию в веселые декорации и вдохновляющие выступления.Она больше, чем просто забавная леди, она призвана вдохновлять женщин всего мира и помогать им находить смешное в своих недостатках. Когда Джеки не в туре, вы обнаружите, что она выступает с потрясающими речами и секционными выступлениями на корпоративных мероприятиях и конференциях или в качестве полуфиналистки 14-го сезона шоу «Америка есть талант». В своей прошлой жизни она была юристом, и она понимает тяжелое положение работающей женщины. Ее подписные выступления и готовящаяся к выпуску книга из ее веселой серии «Найди свою сказку» оставят у зрителей чувство воодушевления, воодушевления и вдохновения для преодоления взлетов и падений в жизни и работе.Ее разнообразный стиль комедии позволил ей работать с легендами комедии, такими как Розанна Барр и Ванда Сайкс, а также с OWN Network, NBC, CBS и FOX, чтобы назвать некоторых. Всегда в гостях у Марины Франклин – One Hour Comedy Special: Single Black Female (Amazon Prime, CW Network), Trainwreck, Louie Season V, The Jim Gaffigan Show, Conan O’Brien, Stephen Colbert, HBO’s Crashing и The Breaks with Michelle Wolf
Сидан кунде инте хиты |
стратегии
Klockan 12.30 – 13.30 и 18.00 – 19.00 день 16 марта 2021 г. Лидер бьюдера Эстра Скараборг (Östra Skaraborg) до получения информации для ознакомления с арбететом мед ден нья стратегин. Mötena kommer att hållas digitalt.
Var med och få information om Hur och när du kan delta i arbetet med att ta fram vår nya Strategin. В рамках апрельской коммерции Det att genomföras en mängd digitala workshops på olika teman och for olika målgrupper.
Лидер Östra Skaraborg söker efter ny personal då vår administratör Jenny går hem på mammaledighet.Vill du veta mer om tjänsten kontakta Verksamhetsledare Jesper Uvesten.
Почта: [email protected]
Телефон: 0702-46 00 99
Onsdag den 19 Oktober kommer verksamhetsledare Jesper Uvesten att finnas på plats i Habo.
Mellan 09.00 och ca 16.00 kommer Jesper att sitta på biblioteket i Habo. Vill ni prata projekt är det bara att komma förbi, vill ni boka ett möte ring 0702-460099.
Leader Östra Skaraborg har haft sina två första beslutsmöten, 21 июня в Sventorps bygdegård и 28 июня в Hotell Bellevue i Hjo.På mötena velondlades 15 projekt som alla var på plats for att föredra sin projektidé för styrelsen. Av de 15 projekten var det 12 som blev beviljade stödmedel.
Genom beviljandet av dessa 12 projekt har Leader Östra Skaraborg nu beslutat att fördela 6 743 439 SEK i projektmedel for att utveckla vårt område.
Pressmeddelandet du når via länken innehåller информация и контакты до 12 beviljade projekten:
Pressmeddelande_LÖS_juli_2016
För frågor, intervjuer, bilder eller annat som gäller Leader Östra Skaraborgs verksamhet tveka inte att kontakta Leader Östra Skaraborgs verksamhetsledare Jesper Uvesten eller ordförande Niclas Fällström.Для получения информации об этом конкретном проекте, vänligen vänd er i första hand direkt till respektive projekt
Йеспер Увестен Никлас Феллстрём
Verksamhetsledare Ordförande 0702-46 00 99070-674 50 65 [email protected] [email protected]
Okategoriserade
Välkomna till vår nya hemsida! -Hemsidan kommer att löpande uppdaterats med nya projekt och annat som är intressant for dig som är intresserad av Leader Östra Skaraborg.
