матричная таблица – это… Что такое матричная таблица?
- матричная таблица
Robots: matrix table
Универсальный русско-английский словарь. Академик.ру. 2011.
- матричная таблетка
- матричная телекамера
Смотреть что такое “матричная таблица” в других словарях:
Таблица обозначений абстрактной алгебры — В абстрактной алгебре повсеместно используются символы для упрощения и сокращения текста, а также стандартные обозначения для некоторых групп. Ниже приведён список наиболее часто встречающихся алгебраических обозначений, соответствующие команды в … Википедия
КОНТИНГЕНТНОСТИ ТАБЛИЦА — англ. concontingency, table of; нем. Kontingenztdbelle. Матричная таблица, необходимая для упорядочивания объектов (элементов выборки исследования по двум признакам).

КОНТИНГЕНТНОСТИ ТАБЛИЦА — англ. concontingency, table of; нем. Kontingenztdbelle. Матричная таблица, необходимая для упорядочивания объектов (элементов выборки исследования по двум признакам) … Толковый словарь по социологии
ГОСТ 21879-88: Телевидение вещательное. Термины и определения — Терминология ГОСТ 21879 88: Телевидение вещательное. Термины и определения оригинал документа: 150. 2 T импульс Телевизионный измерительный сигнал, имеющий форму синусквадратичной функции за один ее период между нулевыми значениями и длительность … Словарь-справочник терминов нормативно-технической документации
Математика гармонии — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/22 ноября 2012. Пока процесс обсуждени … Википедия
Компания — (Company) Содержание Содержание Юридические формы компании Понятие организации и предпринимательства.
 Основные признаки и классификации компаний Признаки фирмы Основные концепции организации Контрактная концепция фирмы Стратегическая концепция… … Энциклопедия инвестора
Основные признаки и классификации компаний Признаки фирмы Основные концепции организации Контрактная концепция фирмы Стратегическая концепция… … Энциклопедия инвестораФирма — (Firm) Определение фирмы, признаки и классификация фирм Определение фирмы, признаки и классификация фирм, концепции фирмы Содержание Содержание Фирма Юридические формы Понятие фирмы и предпринимательства. Основные признаки и классификации фирм… … Энциклопедия инвестора
Матрица — I Матрица (нем. Matrize, от латинского matrix матка, источник, начало) в полиграфии, 1) сменный элемент литейной формы с углублённым (иногда фотографическим) изображением буквы или знака, используемый при отливке типографских… … Большая советская энциклопедия
Белки — I Белки (протеины) органические соединения, структурной основой которых служит полипептидная цепь, состоящая из аминокислотных остатков, соединенных пептидными связями ( СО Nh3 ) в определенной последовательности.
 Белки являются главными… … Медицинская энциклопедия
Белки являются главными… … Медицинская энциклопедияВекторная авторегрессия — (VAR, Vector AutoRegression) модель динамики нескольких временных рядов, в которой текущие значения этих рядов зависят от прошлых значений этих же временных рядов. Модель предложена Кристофером Симсом как альтернатива системам одновременных… … Википедия
Матрица
7.5. Матричная диаграмма. Системное решение проблем
7.5. Матричная диаграмма
Матричная диаграмма позволяет идентифицировать взаимоотношения между отдельными факторами, которые имеют вид причинно-следственных связей. Преимущество матричной диаграммы по сравнению с другими методами анализа заключается в ее способности дать графическую интерпретацию степени интенсивности этих взаимоотношений.
Матричную диаграмму можно использовать как для идентификации проблем и причин, так и для определения приоритетов.
В зависимости от числа рассматриваемых переменных и формы матрицы существует несколько типов матричных диаграмм (рис. 7.3).
Для построения матричной диаграммы специалисты рекомендуют выполнить ряд действий.[22]
1. Выберите переменные, для которых проводится анализ потенциальных связей.
2. Выберите формат матрицы, основываясь на числе переменных и числе ожидаемых связей. (Эту работу можно упростить, если воспользоваться табл. 7.1.)
Таблица 7.1
Вспомогательная таблица для построения матричной диаграммы
3. Внесите переменные в матричную диаграмму.
4. Обозначьте имеющиеся связи, используя символы весов, приведенные на рис. 7.4. Не поддавайтесь искушению сразу расставить в клетках рабочей матрицы вместо этих символов соответствующие числовые значения весов. Это может ухудшить читаемость диаграммы.
5. Для каждого столбца и каждой строки матричной диаграммы сложите веса в соответствии с указанными символами. Полученные суммарные значения весов следует поместить в соответствующие клетки матричной диаграммы.
Полученные суммарные значения весов следует поместить в соответствующие клетки матричной диаграммы.
6. Переменные, для которых получаются большие суммарные веса, играют большую роль в данной задаче. Их стоит рассмотреть дальше.
Пример заполнения матрицы для сети пунктов кинопроката кассет приведен на рис. 7.5.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРесКомитет 1540 — Вопросы и ответы
Вопросы и ответы
- Что такое резолюция 1540 (2004) и в чем ее значение?
- Какие требования предъявляет резолюция 1540 (2004) к государствам?
- Почему резолюция 1540 (2004) имеет отношение к государствам, не обладающим оружием массового уничтожения?
- В чем состоит особая ценность резолюции 1540 (2004), когда большинство государств уже несет международные обязательства в области нераспространения, например в рамках Договора о нераспространении, Конвенции о химическом оружии и Конвенции о биологическом оружии?
- Как соотносится резолюция 1540 (2004) с контртеррористическими усилиями?
- Что такое Комитет 1540 и как функционируют Комитет и его эксперты?
- Является ли Комитет 1540 комитетом по санкциям? Проводит ли Комитет 1540 какие-либо расследования или разбирательства?
- Каковы взаимоотношения между Комитетом 1540 и другими комитетами Совета Безопасности в области борьбы с терроризмом?
- Какую роль в осуществлении резолюции играют международные, региональные и субрегиональные организации и какую связь поддерживает с ними Комитет?
- Каким образом Комитет поощряет осуществление резолюции государствами?
- Что такое матричная таблица Комитета 1540, и что означают используемые в ней символы «Х» и «?»?
- На какие контрольные списки можно ссылаться при осуществлении экспортного контроля?
- Как часто государства должны докладывать Комитету?
- На какое содействие можно рассчитывать?
- Каков механизм поиска предложений в ответ на запросы об оказании содействия?
- Какова взаимосвязь между наращиванием потенциала в контексте резолюции 1540 и развитием?
1.
 Что такое резолюция 1540 (2004) и в чем ее значение?
Что такое резолюция 1540 (2004) и в чем ее значение?Совет Безопасности принял резолюцию 1540 (2004) в соответствии с главой VII Устава Организации Объединенных Наций и подтвердил в ней, что распространение ядерного, химического и биологического оружия, а также средств его доставки представляет угрозу для международного мира и безопасности. Эта резолюция имеет значимый характер в качестве обязывающего документа, согласно которому незаконный оборот ядерного, химического и биологического оружия, средств его доставки и относящихся к ним материалов является новым аспектом распространения и в котором признается наличие взаимосвязи между распространением и риском приобретения такого оружия и относящихся к нему материалов негосударственными субъектами, включая террористов. В то время, как другие международно-правовые документы прежде всего регулируют деятельность государств, в резолюции 1540 (2004) рассматривается угроза, создаваемая негосударственными субъектами, и прямо предусматривается, что государства должны воздерживаться от оказания в любой форме поддержки деятельности таких субъектов, связанной с распространением, и принимать меры для предотвращения их участия в такой незаконной деятельности.
ˆ Наверх ˆ
2. Какие требования предъявляет резолюция 1540 (2004) к государствам?
В резолюции 1540 (2004) предусматривается, что все государства воздерживаются от оказания в любой форме поддержки негосударственным субъектам, которые пытаются разрабатывать, приобретать, производить, обладать, перевозить, передавать или применять ядерное, химическое или биологическое оружие и средства его доставки.
Кроме того, в ней предусмотрено, что все государства в соответствии со своими национальными процедурами принимают и эффективно применяют соответствующие законы, запрещающие любому негосударственному субъекту производить, приобретать, обладать, разрабатывать, перевозить, передавать или применять ядерное, химическое или биологическое оружие и средства его доставки, в особенности в террористических целях, равно как и попытки участвовать в любых из вышеупомянутых действий, участвовать в них в качестве сообщника, оказывать им помощь или финансирование.
В резолюции предусматривается также, что все государства принимают и применяют эффективные меры в целях установления национального контроля для предотвращения распространения ядерного, химического или биологического оружия и средств его доставки, в том числе посредством установления надлежащего контроля над относящимися к ним материалами в сфере обеспечения учета, сохранности и физической защиты, принятия мер пограничного контроля и правоприменительных мер, контроля за экспортом и трансграничным перемещением, и с этой целью должны:
- разрабатывать и осуществлять надлежащие эффективные меры по обеспечению учета и сохранности таких предметов при производстве, применении, хранении или транспортировке;
- разрабатывать и осуществлять надлежащие эффективные меры физической защиты;
- разрабатывать и осуществлять надлежащие эффективные меры пограничного контроля и правоприменительные меры в целях выявления, пресечения, предотвращения и противодействия, в том числе путем международного сотрудничества, когда это необходимо, незаконному обороту и посредничеству в отношении таких предметов в соответствии с национальными системами правового регулирования и законодательством и совместимые с международным правом;
- устанавливать, совершенствовать, пересматривать и поддерживать надлежащий эффективный контроль на национальном уровне за экспортом и трансграничным перемещением таких предметов, включая надлежащие законы и нормативные акты по контролю за экспортом, транзитом, трансграничным перемещением и реэкспортом, и меры контроля за предоставлением средств и услуг, относящихся к такому экспорту и трансграничному перемещению, таких как финансирование и транспортировка, которые способствовали бы распространению, а также устанавливать меры контроля за конечным пользователем; и устанавливать и применять надлежащие меры уголовной и гражданской ответственности за нарушение таких законов и нормативных актов в области экспортного контроля.

ˆ Наверх ˆ
3. Почему резолюция 1540 (2004) имеет отношение к государствам, не обладающим оружием массового уничтожения?
Резолюция 1540 (2004) касается всех государств, поскольку распространение ядерного, химического и биологического оружия и средств его доставки представляет собой угрозу международному миру и безопасности, которая затрагивает все государства. В случае применения или угрозы применения оружия массового уничтожения ни один член международного сообщества не будет застрахован от глобальных последствий.
Кроме того, физические или юридические лица, которые участвуют в деятельности по распространению, в том числе в террористической деятельности и/или незаконном обороте, или поддерживают такую деятельность, не признают национальных границ и действуют на различных территориях. Во многих государствах существуют отрасли или структуры, обладающие и/или осуществляющие торговлю соответствующими материалами, которые могут также использоваться в программах, касающихся оружия массового уничтожения (материалы двойного назначения). Кроме того, территории государств могут использоваться негосударственными субъектами для транзита и/или трансграничного перемещения. Это требует активного участия и сотрудничества всех государств в усилиях международного сообщества по нераспространению.
Кроме того, территории государств могут использоваться негосударственными субъектами для транзита и/или трансграничного перемещения. Это требует активного участия и сотрудничества всех государств в усилиях международного сообщества по нераспространению.
ˆ Наверх ˆ
4. В чем состоит особая ценность резолюции 1540 (2004), когда большинство государств уже несет международные обязательства в области нераспространения, например в рамках Договора о нераспространении, Конвенции о химическом оружии и Конвенции о биологическом и токсинном оружии?
Резолюция 1540 (2004) дополняет соответствующие многосторонние договоры и конвенций, поскольку она требует от всех государств выполнения изложенных в ней обязанностей, независимо от статуса этих государств в отношении таких договоров и соглашений. В силу предусмотренного в ней комплексного подхода резолюция 1540 (2004) нацелена на предотвращение распространения оружия массового уничтожения и средств его доставки, а также незаконного оборота связанных с таким оружием материалов, особенно в том, что касается деятельности негосударственных субъектов. Резолюция 1540 (2004) имеет особое значение на практическом уровне. Так, например, осуществление резолюции 1540 (2004) позволяет государствам лучше интегрировать свой национальный потенциал, в частности в сфере сотрудничества между правоохранительными и пограничными органами, чтобы предотвращать распространение и незаконный оборот оружия массового уничтожения, дополняя таким образом свои договорные обязательства.
Резолюция 1540 (2004) имеет особое значение на практическом уровне. Так, например, осуществление резолюции 1540 (2004) позволяет государствам лучше интегрировать свой национальный потенциал, в частности в сфере сотрудничества между правоохранительными и пограничными органами, чтобы предотвращать распространение и незаконный оборот оружия массового уничтожения, дополняя таким образом свои договорные обязательства.
ˆ Наверх ˆ
5. Как соотносится резолюция 1540 (2004) с контртеррористическими усилиями?
Главная цель резолюции 1540 (2004) заключается в том, чтобы предотвратить распространение оружия массового уничтожения и средств его доставки и запретить с этой целью любому негосударственному субъекту осуществлять любую деятельность, связанную с распространением, в особенности в террористических целях. В резолюции не делается упор исключительно на террористов, а используется довольно широкое понятие «негосударственного субъекта», которое определяется как «физическое лицо или организация, не имеющие законных полномочий от какого-либо государства на осуществление деятельности, подпадающей под действие» этой резолюции. Цель резолюции заключается в предотвращении приобретения или применения оружия массового уничтожения и средств его доставки любым негосударственным субъектом и в сдерживании незаконного оборота связанных с оружием материалов. Резолюция не ставит вопрос о борьбе с терроризмом напрямую, а охватывает широкий круг мероприятий по нераспространению, которые имеют иной характер, но дополняют усилия по борьбе с терроризмом, поскольку их цель заключается в снижении риска распространения, которое может привести к применению оружия массового уничтожения в террористических целях. Невзирая на сформулированный в резолюции 1540 (2004) уникальный мандат в области нераспространения мандат, который отличается от мандатов для принятия других мер по борьбе с терроризмом, Комитет 1540 неразрывно связан с другими контртеррористическими комитетами Организации Объединенных Наций и их работой.
Цель резолюции заключается в предотвращении приобретения или применения оружия массового уничтожения и средств его доставки любым негосударственным субъектом и в сдерживании незаконного оборота связанных с оружием материалов. Резолюция не ставит вопрос о борьбе с терроризмом напрямую, а охватывает широкий круг мероприятий по нераспространению, которые имеют иной характер, но дополняют усилия по борьбе с терроризмом, поскольку их цель заключается в снижении риска распространения, которое может привести к применению оружия массового уничтожения в террористических целях. Невзирая на сформулированный в резолюции 1540 (2004) уникальный мандат в области нераспространения мандат, который отличается от мандатов для принятия других мер по борьбе с терроризмом, Комитет 1540 неразрывно связан с другими контртеррористическими комитетами Организации Объединенных Наций и их работой.
Усилия по борьбе с терроризмом, со своей стороны, включают содействие принятию государствами законодательных и правоприменительных мер, рекомендуемых комитетами Совета Безопасности, занимающимися вопросами борьбы с терроризмом, и охватывающих широкий спектр деятельности террористов, которые применяют любое доступное оружие или иные смертоносные средства. Такие контртеррористические меры способствуют усилению безопасности го-сударств и таким образом дополняют усилия Комитета 1540 по повышению степени защиты государств от рисков, вытекающих из любого распространения связанных с оружием массового уничтожения предметов.
Такие контртеррористические меры способствуют усилению безопасности го-сударств и таким образом дополняют усилия Комитета 1540 по повышению степени защиты государств от рисков, вытекающих из любого распространения связанных с оружием массового уничтожения предметов.
ˆ Наверх ˆ
6. Что такое Комитет 1540 (2004) и как функционируют Комитет и его эксперты?
Комитет 1540 является вспомогательным органом Совета Безопасности и состоит из всех 15 действующих членов Совета. Мандат и сфера деятельности Комитета 1540 вытекают из резолюции 1540 (2004) и последующих резолюций, в частности резолюций 1673 (2006), 1810 (2008), 1977 (2011) и 2325 (2016), а также программ работы, которые Председатель Комитета 1540 представляет Председателю Совета Безопасности. В девятой Программе работы, которая охватывала период с января 2010 года по 31 января 2011 года, было предусмотрено, что Комитет должен был учредить и впоследствии поддерживать рабочие группы по следующим вопросам:
- мониторинг и национальное осуществление;
- помощь;
- cотрудничество с международными организациями, в том числе с комитетами Совета Безопасности, учрежденными резолюциями 1267 (1999) и 1373 (2001);
- транспарентность и работа со средствами массовой информации.

Рабочие группы открыты для участия всех членов Комитета, учрежденного резолюцией 1540 (2004).
Комитету 1540 оказывает помощь группа экспертов. Эксперты и их координатор назначаются Генеральным секретарем после утверждения их кандидатур Комитетом. В соответствии с резолюцией 2055 (2012) может быть назначено до девяти экспертов. Комитету 1540 и его группе экспертов оказывают поддержку Департамент по политическим вопросам Организации Объединенных Наций (ДПВ) и Управление Организации Объединенных Наций по вопросам разоружения (УВРООН).
ˆ Наверх ˆ
7. Является ли Комитет 1540 (2004) комитетом по санкциям? Проводит ли Комитет 1540 какие-либо расследования или разбирательства?
Комитет 1540 не является комитетом по санкциям. Он не занимается проведением каких-либо расследований или судебным преследованием за совершение предполагаемых нарушений обязанностей по нераспространению. Комитет 1540 и его группа экспертов решительно настроены на сотрудничество с международным сообществом в целях содействия осуществлению резолюции 1540 (2004) всеми государствами.
ˆ Наверх ˆ
8. Каковы взаимоотношения между Комитетом 1540 и другими комитетами Совета Безопасности в области борьбы с терроризмом?
Этот вопрос касается трех вспомогательных органов Совета Безопасности: Комитета по организации «Аль-Каида» и связанным с ней лицам и организациям, Контртеррористического комитета (КТК) и Комитета 1540, которые были учреждены, соответственно, резолюциями 1267 (1999), 1373 (2001) и 1540 (2004). Эти комитеты имеют различные мандаты и структуры (сравнительную таблицу см. http://www.un.org/en/sc/1540/documents/table-cooperation-areas 14nov2012.
pdf).
Совет Безопасности настоятельно рекомендует этим комитетам поддерживать сотрудничество в их соответствующих сферах деятельности, поскольку они являются частью общей структуры Организации Объединенных Наций по борьбе с терроризмом. В частности, в резолюциях 1810 (2008), 1977 (2011) и 2325 (2016) подтверждается необходимость укрепления постоянного сотрудничества между Комитетом 1540 и этими другими вспомогательными органами, в том числе «посредством активизации информационного обмена, скоординированной организации страновых визитов в рамках их соответствующих мандатов, оказания технической помощи и решения других вопросов, касающихся всех трех комитетов».
Комитеты проводят периодические совместные брифинги для Совета Безопасности, которые дают государствам возможность комментировать работу комитетов и сотрудничество между ними.
Комитет 1540 учредил рабочую группу, которая, в частности, занимается вопросами сотрудничества с комитетами Совета Безопасности, учрежденными резолюциями 1267 (1999) и 1373 (2001).
ˆ Наверх ˆ
9. Какую роль в осуществлении резолюции играют международные, региональные и субрегиональные организации и какую связь поддерживает с ними Комитет?
Международные, региональные и субрегиональные организации, особенно организации, занимающиеся вопросами разоружения и нераспространения оружия массового уничтожения, могут играть жизненно важную роль в оказании своим государствам-членам помощи в осуществлении резолюции 1540 (2004) в рамках своих соответствующих программ. В числе таких организаций следует отметить Международное агентство по атомной энергии (МАГАТЭ), Организацию по запрещению химического оружия (ОЗХО) и Группу имплементационной поддержки Конвенции о запрещении биологического и токсинного оружия (ГИП-КБТО). К числу других относятся Всемирная организация здравоохранения (ВОЗ), Всемирная таможенная организация (ВТО) и Международная организация уголовной полиции (Интерпол).
К числу других относятся Всемирная организация здравоохранения (ВОЗ), Всемирная таможенная организация (ВТО) и Международная организация уголовной полиции (Интерпол).
Например, МАГАТЭ оказывает государствам содействие в создании и поддержании эффективных национальных режимов обеспечения ядерной безопасности, содействует обеспечению во всем мире безопасности ядерных и других радиоактивных материалов в процессе их использования, хранения и транспортировки. Кроме того, МАГАТЭ содействует применению соответствующих международных документов, таких как Конвенция о физической защите ядерного материала и поправка к ней, принятая в 2005 году, а также Кодекс поведения МАГАТЭ по обеспечению безопасности и сохранности радиоактивных источников.
Комитет 1540 наладил рабочие отношения с различными международными и региональными организациями и будет продолжать углублять эти отношения, в том числе путем создания дополнительных формальных и неформальных механизмов сотрудничества для содействия обмену информацией об эффективной практике и извлеченных уроках, разработки и внедрения стандартов, а также определения потребностей в помощи и выявления программ оказания помощи.
В соответствии со своей программой работы рабочая группа Комитета 1540 по вопросам сотрудничества с международными организациями, в том числе комитетами Совета Безопасности, учрежденными резолюциями 1267 (1999) и 1373 (2001), взаимодействует с соответствующими организациями по линии брифингов и поездок экспертов.
ˆ Наверх ˆ
10. Каким образом Комитет поощряет осуществление резолюции государствами?
Комитет стремится содействовать осуществлению резолюции путем диалога, информационно-пропагандистской деятельности, оказания помощи и поддержания сотрудничества. В рамках этих усилий он использует ряд инструментов, в том числе матрицу Комитета 1540, стандартную форму заявки на оказание помощи, практикумы и мероприятия, имеющие отношение к осуществлению этой резолюции, и свой веб-сайт, на котором размещается соответствующая информация (см. перечень информационно-пропагандистских мероприятий).
Информационно-пропагандистские мероприятия обеспечивают участвующим государствам возможность для обмена национальным опытом и информацией о различных подходах в деле осуществления резолюции 1540 (2004). Эти мероприятия также способствуют укреплению сотрудничества между отдельными государствами и Комитетом 1540 по линии двусторонних консультаций и обсуждений дальнейших действий, таких как добровольные национальные планы действий по осуществлению резолюции 1977 (2011) в целях содействия наращиванию потенциала на национальном и региональном уровнях.
Эти мероприятия также способствуют укреплению сотрудничества между отдельными государствами и Комитетом 1540 по линии двусторонних консультаций и обсуждений дальнейших действий, таких как добровольные национальные планы действий по осуществлению резолюции 1977 (2011) в целях содействия наращиванию потенциала на национальном и региональном уровнях.
Комитет рекомендует государствам провести обзор своего действующего законодательства и практики и рассмотреть шаги для устранения любых пробелов.
ˆ Наверх ˆ
11. Что такое матричная таблица Комитета 1540 (2004), и что означают используемые в ней символы «Х» и «?»?
Матрица 1540 представляет собой инструмент, используемый Комитетом 1540 для того, чтобы фиксировать меры, которые государства приняли или планируют принять для выполнения обязанностей по резолюции. Информация, приведенная в матрице, поступает от государств и межправительственных организаций. Матрица охватывает требования резолюции и может помочь государствам в выявлении тех сфер, в которых необходимо принять дополнительные меры. Матрица используется Комитетом 1540 и его экспертами в качестве основы для диалога и оказания помощи.
Матрица используется Комитетом 1540 и его экспертами в качестве основы для диалога и оказания помощи.
Знак «X», проставленный в любом поле данных, означает, что государство приняло соответствующую меру и представило конкретные указания на применимые нормативно-правовые основы или решения исполнительной власти. Он не означает подтверждения Комитетом 1540 того, что государство выполнило соответствующие обязанности. Знак «?», проставленный в любом поле данных, означает, что имеются вопросы относительно применимости или наличия соответствующих законов.
Пробел в любом поле данных означает лишь, что соответствующее государство не представило информацию Комитету или что он не смог обнаружить такую информацию.
ˆ Наверх ˆ
12. На какие контрольные списки можно ссылаться при осуществлении экспортного контроля?
Комитет не утверждает никаких контрольных списков и не требует от государств их принятия. Каждое государство может принимать такие списки материалов, веществ и технологий, которые оно считает целесообразными. Комитет признает, что в рамках ряда международных конвенций, межправительственных организаций и многосторонних или региональных соглашений или договоренностей уже приняты и находятся в открытом доступе списки товаров двойного назначения.
Каждое государство может принимать такие списки материалов, веществ и технологий, которые оно считает целесообразными. Комитет признает, что в рамках ряда международных конвенций, межправительственных организаций и многосторонних или региональных соглашений или договоренностей уже приняты и находятся в открытом доступе списки товаров двойного назначения.
ˆ Наверх ˆ
13. Как часто государства должны докладывать Комитету?
Государствам было предложено представить Комитету первый доклад о шагах, которые они предприняли или предполагают предпринять для выполнения этой резолюции. В последующих резолюциях к государствам, которые еще не представили первый доклад, был обращен призыв сделать это без промедления, а государствам, которые уже представили доклады, было рекомендовано представлять дополнительную информацию в любое время или по просьбе Комитета 1540. По состоянию на 1 января 2017 года 172 государства и одна региональная организация представили первые доклады Комитету, а 108 из них представили дополнительную информацию (см. страницу «Национальные доклады» на веб-сайте Комитета). От государств не требуется принятие всех соответствующих законов и мер до представления доклада Комитету 1540. Кроме того,
государства могут включать в свои доклады просьбу об оказании помощи для содействия осуществлению резолюции 1540 (2004).
страницу «Национальные доклады» на веб-сайте Комитета). От государств не требуется принятие всех соответствующих законов и мер до представления доклада Комитету 1540. Кроме того,
государства могут включать в свои доклады просьбу об оказании помощи для содействия осуществлению резолюции 1540 (2004).
ˆ Наверх ˆ
14. На какое содействие можно рассчитывать?
В пункте 7 постановляющей части резолюции 1540 (2004) Совет Безопасности признал, что «некоторым государствам может потребоваться содействие в выполнении» этой резолюции, и предложил государствам оказывать такое содействие в ответ на конкретные запросы. Комитет 1540 предоставляет государствам техническую экспертную помощь в подготовке их докладов Комитету, подготовке заявок на оказание помощи и в планировании деятельности по осуществлению, но только в той мере, в какой это позволяют его ресурсы или получаемые им добровольные взносы. Вместе с тем существуют многие другие источники помощи, которыми государства могут воспользоваться для осуществления резолюции.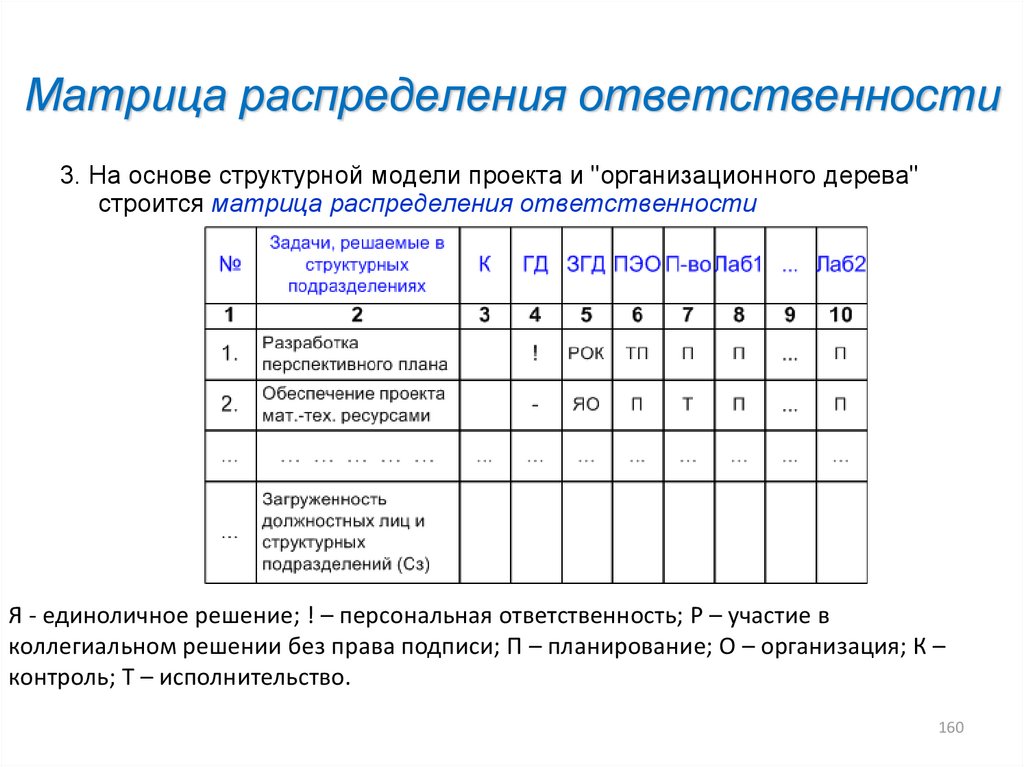 Во многих случаях государства опираются на программы помощи, которые существовали до принятия резолюции, например, программы МАГАТЭ и ОЗХО, программы, предлагаемые отдельными государствами, и даже программы помощи, осуществляемые частными фондами и неправительственными организациями, которые непосредственно занимаются вопросами тех или иных обязанностей по резолюции. Кроме того, некоторые структуры разработали новые программы помощи, специально предназначенные для осуществления резолюции. На веб-сайте Комитета 1540 имеется дополнительная информация о предложениях других государств об оказании помощи и о программах помощи, осуществляемых международными организациями или иными структурами.
Во многих случаях государства опираются на программы помощи, которые существовали до принятия резолюции, например, программы МАГАТЭ и ОЗХО, программы, предлагаемые отдельными государствами, и даже программы помощи, осуществляемые частными фондами и неправительственными организациями, которые непосредственно занимаются вопросами тех или иных обязанностей по резолюции. Кроме того, некоторые структуры разработали новые программы помощи, специально предназначенные для осуществления резолюции. На веб-сайте Комитета 1540 имеется дополнительная информация о предложениях других государств об оказании помощи и о программах помощи, осуществляемых международными организациями или иными структурами.
ˆ Наверх ˆ
15. Каков механизм поиска предложений в ответ на запросы об оказании содействия?
В пункте 7 постановляющей части резолюции 1540 (2004) Совет Безопасности призывает государства оказывать содействие «в ответ на конкретные запросы» от других государств. В настоящее время государства уведомляют Комитет 1540 о своих запросах или предложениях в официальном сообщении на имя Председателя Комитета 1540 или включают их в доклады Комитету 1540. Кроме того, Комитет 1540 учитывает, что ряд государств и международных структур осуществляют несколько соответствующих программ оказания помощи. Комитет 1540 выступает также в качестве «координационного центра» для заявок и предложений, размещая предложения на своем веб-сайте и направляя заявки на оказание помощи непосредственно тем структурам, которые предлагают помощь, а также размещая на веб-сайте выдержки из заявок. В рамках своей информационно-пропагандистской деятельности Комитет 1540 также рекомендует государствам направлять заявки, причем формулировать их как можно более конкретно, и разработал для этой цели стандартную форму заявки на оказание помощи.
В настоящее время государства уведомляют Комитет 1540 о своих запросах или предложениях в официальном сообщении на имя Председателя Комитета 1540 или включают их в доклады Комитету 1540. Кроме того, Комитет 1540 учитывает, что ряд государств и международных структур осуществляют несколько соответствующих программ оказания помощи. Комитет 1540 выступает также в качестве «координационного центра» для заявок и предложений, размещая предложения на своем веб-сайте и направляя заявки на оказание помощи непосредственно тем структурам, которые предлагают помощь, а также размещая на веб-сайте выдержки из заявок. В рамках своей информационно-пропагандистской деятельности Комитет 1540 также рекомендует государствам направлять заявки, причем формулировать их как можно более конкретно, и разработал для этой цели стандартную форму заявки на оказание помощи.
После принятия резолюций 1810 (2008), 1977 (2011) и 2325 (2016) Комитет 1540 в официальном и неофициальном порядке неизменно выступает с настоятельными призывами активно участвовать в подборе совпадающих предложений и просьб об оказании помощи, «используя такие инструменты, как стандартные формы просьбы об оказании помощи», планы действий и другую информацию, получаемую Комитетом 1540 (соответственно, пункты 11c, 15 и 20 постановляющей части). Рабочая группа Комитета 1540 по оказанию помощи постоянно проводит обзор своих процедур, чтобы сделать обработку, анализ и сопоставление заявок и предложений как можно более действенными и эффективными.
Рабочая группа Комитета 1540 по оказанию помощи постоянно проводит обзор своих процедур, чтобы сделать обработку, анализ и сопоставление заявок и предложений как можно более действенными и эффективными.
ˆ Наверх ˆ
16. Какова взаимосвязь между наращиванием потенциала в контексте резолюции 1540 (2004) и развитием?
Помимо предлагаемой другими государствами помощи в содействии осуществлению резолюции 1540 (2004) многие государства заинтересованы в наращивании потенциала в сферах, которые они считают приоритетными, в частности в сфере развития. В докладе по итогам проведенного в 2009 году всеобъемлющего обзора хода осуществления резолюции говорится, что Комитет 1540 должен рассмотреть возможность совмещения деятельности по выполнению обязанностей, изложенных в резолюции 1540 (2004), с деятельностью по достижению более широких национальных целей. Помощь, которую могут предоставлять государства и международные организации в целях осуществления резолюции 1540 (2004), может дополнять или поддерживать наращивание потенциала, например, в сфере обеспечения пограничного и таможенного контроля, обеспечения технической и физической безопасности транспорта и оказания услуг в сфере общественного здравоохранения. Кроме того, проекты по осуществлению резолюции 1540 (2004) могут быть встроены в существующие программы развития, нацеленные на укрепление национальной инфраструктуры, в том числе после конфликтов или стихийных бедствий.
Кроме того, проекты по осуществлению резолюции 1540 (2004) могут быть встроены в существующие программы развития, нацеленные на укрепление национальной инфраструктуры, в том числе после конфликтов или стихийных бедствий.
ˆ Наверх ˆ
Проект “Матричная алгебра в экономике”
В процессе работы над индивидуальным проектом по математике “Матричная алгебра в экономике” учеником 11 класса гимназии были рассмотрены матричные методы в экономике на примерах решения задач экономического содержания. В работе доступно объясняется, что такое “математическая матрица” и как ее применять.
Подробнее о проекте:
В ученической исследовательской работе по математике “Матричная алгебра в экономике” автор проводит анализ учебно-методической литературы о математических матрицах, на примере задач показывает связь математики и экономики, учится применять в экономике математический аппарат и показывает роль математических методов в экономике (реальные задачи из разных сфер жизнедеятельности человека).
Готовый творческий и исследовательский проект по математике “Матричная алгебра в экономике” наглядно демонстрирует взаимосвязь математики и экономики, определяет роль математических методов в анализе экономических процессов, объектов и явлений.
Оглавление
Введение
1. Немного истории.
2. Матрицы и операции над ними.
3. Решение с помощью матриц экономических задач.
Заключение
Используемая литература
Приложение
Введение
На современном этапе экономические взаимоотношения между субъектами образуют экономические системы со сложной структурой, большим количеством элементов и связей между ними, которые являются причиной почти всех особенностей экономических задач.
Современные экономические условия в нашей жизни стали намного сложнее. Принимать важные стратегические решения для общества и частных лиц стало труднее. Именно в моменты преодоления всех этих препятствий, появляется большой интерес к математическим методам, которые можно было бы применять в экономике, то есть к таким математическим методам, которые смогли бы выработать лучшую стратегию на решение действующих проблем и на долгосрочные проекты.
 Таким видом выхода из сложившейся ситуации стало решение задач в экономике при помощи матричных методов.
Таким видом выхода из сложившейся ситуации стало решение задач в экономике при помощи матричных методов.На внедрение и развитие математических методов в решении экономических задач, большое влияние оказало создание и развитие современной вычислительной техники. Вычислительная техника нового поколения позволила применять на практике множество новых методов, которые были описаны ранее только в теории или объяснялись на простых примерах.
Но никакая вычислительная техника не способна заменить человека и поэтому, люди должны уметь эффективно использовать теоретические знания в области математики в экономике, а именно, уметь правильно решать экономические задачи при помощи матричных методов.
Понятие матрицы и основанный на нем раздел математики – матричная алгебра – имеют чрезвычайно важное значение для экономистов. Объясняется это тем, что значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное – компактной матричной форме.
Также матрицы позволяют с минимальными затратами труда и времени обрабатывать огромный и весьма разнообразный статистический материал, различные исходные данные, характеризующие уровень, структуру, особенности социально-экономического комплекса.
В современных условиях особенно актуально использование матриц для формирования баз данных, ведь вся информация обрабатывается и хранится в форме матриц.
Матрицы можно эффективно использовать не только в науке, но и применять их на практике в крупных предприятиях для решения современных экономических задач. Матричный метод позволяет упростить работу человека, уменьшить количество критериев и альтернатив для выбора и получать выгодные варианты решения для выхода из различных экономических ситуаций.
В данной работе содержится информация о самих матрицах, операциях над ними и на примерах показано, как можно решать экономические задачи при помощи матриц.
Актуальность. Математика и экономика – две на первый взгляд далекие друг от друга науки. Однако, взаимосвязь между этими науками, роль математических методов в анализе экономических процессов, объектов и явлений были отмечены учеными ещё в XVII веке.
Однако, взаимосвязь между этими науками, роль математических методов в анализе экономических процессов, объектов и явлений были отмечены учеными ещё в XVII веке.
В XX веке происходило бурное проникновение математических методов в самые разные науки, в том числе и в экономику. В настоящее время этот процесс ещё более активизировался, благодаря развитию вычислительной техники. Поэтому современному экономисту необходима основательная математическая подготовка. И в число наиболее важных математических дисциплин для экономиста входит линейная алгебра, а именно матричная алгебра. В этом я вижу актуальность выбранной темы.
Цель. Рассмотреть матричные методы в экономике на примерах решения задач экономического содержания.
Задачи:
- На примере задач показать связь математики и экономики
- Научиться применять в экономике математический аппарат
- Показать роль математических методов в экономике (реальные задачи из разных сфер жизнедеятельности человека)
Гипотеза Используются ли в экономике те математические знания, которыми мы владеем
Предмет исследования: Матричные методы.
Объект исследования: Математические понятия и законы, экономические модели.
Методы исследования: Теоретическое изучение материала, образцы решения экономических задач.
Немного истории
Впервые матрица появилась в Древнем Китае и носила название «волшебный квадрат». Чуть позже она стала известна и арабским математикам. В конце XVII века швейцарский ученый Габриэль Крамер разработал свою теорию, а в 1751 году опубликовал один из методов решения систем линейных уравнений «правило Крамера».
В это же время был предложен другой метод решения систем линейных уравнений, который тоже носит имя своего изобретателя, это «метод Гаусса». Заметим, что «правило Крамера» работает только для систем с ненулевым детерминантом (определителем системы), тогда как «метод Гаусса» работает для любой системы линейных уравнений.
Огромный вклад в развитие теории матриц в середине XIX внесли такие известные ученые как Уильям Гамильтон и Артур Кэли. Наряду с ними развивали данную теорию немецкие математики Карл Вейерштрасс и Фердинанд Георг Фробениус, а также, французский математик Мари Энмон Камиль Жордан. В 1850 году Джеймс Сильвестр ввел современное понятие матрицы. Под влиянием работ этих великих ученых в математике появился новый раздел, который был назван матричной алгеброй.
Наряду с ними развивали данную теорию немецкие математики Карл Вейерштрасс и Фердинанд Георг Фробениус, а также, французский математик Мари Энмон Камиль Жордан. В 1850 году Джеймс Сильвестр ввел современное понятие матрицы. Под влиянием работ этих великих ученых в математике появился новый раздел, который был назван матричной алгеброй.
Матрицы и операции над ними
Матрица – это прямоугольная таблица, представляющая собой совокупность строк и столбцов. Размерностью матрицы называется величина m×n, где m-число строк, n-число столбцов.
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате, решение систем линейных уравнений сводится к операциям над матрицами. А множество экономических задач можно свести к системам линейных уравнений.
Операции с матрицами не слишком громоздки и не требуют чрезмерно кропотливой работы; напротив, матричную алгебру во многих случаях ценят именно за краткость, простоту и ясность. С помощью матричной алгебры можно выразить в математической форме многие задачи, как большие, так и малые, независимо от их размерности.
С помощью матричной алгебры можно выразить в математической форме многие задачи, как большие, так и малые, независимо от их размерности.
Основные операции с матрицами рассмотрены в Приложении.
Решение с помощью матриц экономических задач
Для наглядности перейдём к рассмотрению задач.
1. С помощью матриц удобно записывать некоторые экономические зависимости. Одним из примеров может послужить таблица распределения ресурсов по различным отраслям экономики.
Таблица: Распределение ресурсов
| Ресурсы | Промышленность | Сельское хозяйство | Торговля |
| Трудовые ресурсы | 4,8 | 6,7 | 7,1 |
| Водные ресурсы | 3,1 | 2,5 | 5,8 |
| Электроэнергия | 5,6 | 4,3 | 3,4 |
Так, например, элемент матрицы а22 = 2,5 показывает, сколько водных ресурсов потребляет сельское хозяйство, а элемент матрицы а13 = 7,1 показывает, сколько трудовых ресурсов потребляет торговля.
2. Рассмотрим такую ситуацию. Некоторая фирма занимается реализацией четырех видов товаров в трех районах. Данные об уровне продаж товаров по районам образуют матрицу.
Величина aij, которая находится в i-й строке и j-м столбце матрицы A, обозначает количество j-го товара, проданное в i-м районе. Таким образом, строки матрицы соответствуют районам, а столбцы – видам товаров. Обозначим через ci, i= 1, 2, 3, 4 цены на реализуемые товары. Они образуют матрицу-столбец.
Если хотим найти суммарный объем продаж в первом районе, то мы должны вычислить следующее выражение:
a11c1 + a12c2 + a13c3 + a14c4,
которое является скалярным произведением первой строки матрицы A на столбец цен C. И строчка, и столбец являются арифметическими 4-х мерными векторами. Про выражение (a11c1 + a12c2 + a13c3 + a14c4) говорят, что оно получено при умножении первой строки матрицы A на столбец C.
Производя такое умножение на столбец C второй и третьей строк, получаем еще две величины, которые представляют собой суммарные продажи во втором и третьем районах. Эти две величины вместе с ранее найденной величиной образуют вектор суммарных продаж.
Эти две величины вместе с ранее найденной величиной образуют вектор суммарных продаж.
В этом примере фактически применено действие умножения матриц.
3. В таблице приведены данные о дневной производительности 5 предприятий, выпускающих 4 вида продукции с потреблением 3-х видов сырья, а также продолжительность работы каждого предприятия в году и цена каждого вида сырья.
Требуется определить:
- годовую производительность каждого предприятия по каждому виду изделий;
- годовую потребность каждого предприятия по каждому виду сырья;
- годовую сумму кредитования каждого предприятия для закупки сырья, необходимого для выпуска продукции указанных видов и количеств.
Решение. Нужно составить матрицы, характеризующие весь интересующий нас экономический спектр производства, а затем при помощи соответствующих операций над ними получить решение данной задачи.
Каждый столбец этой матрицы соответствует дневной производительности отдельного предприятия по каждому виду продукции. Следовательно, годовая производительность j-го предприятия по каждому виду продукции получается умножением j-гo столбца матрицы А на количество рабочих дней в году для этого предприятия (j = 1, 2, 3, 4, 5). Таким образом, годовая производительность каждого предприятия по каждому из изделий описывается матрицей.
Следовательно, годовая производительность j-го предприятия по каждому виду продукции получается умножением j-гo столбца матрицы А на количество рабочих дней в году для этого предприятия (j = 1, 2, 3, 4, 5). Таким образом, годовая производительность каждого предприятия по каждому из изделий описывается матрицей.
Матрица затрат сырья на единицу изделия (эти показатели по условию одинаковы для всех предприятий) имеет вид
Дневной расход по типам сырья на предприятиях описывается произведением матрицы В на матрицу А:
где i-я строка соответствует номеру типа сырья, а j-й столбец — номеру предприятия согласно табл. 16.2 (i = 1, 2, 3; j = 1, 2, 3, 4, 5). Ответ на второй вопрос задачи получим по аналогии с матрицей Агод умножением столбцов матрицы ВА на соответствующие количества рабочих дней в году для предприятий — это годовая потребность каждого предприятия в каждом виде сырья:
Введем вектор стоимости сырья.
Тогда стоимость общего годового запаса сырья для каждого предприятия получается умножением вектора на матрицу ВAгод:
Следовательно, суммы кредитования предприятий для закупки сырья определяются соответствующими компонентами вектора .
4. Множество экономических задач можно свести к системам линейных уравнений. Для наглядного примера рассмотрим следующую задачу.
Предположим, что кривая спроса на автомобили для некоторого периода времени может быть описана уравнением
x1 = 12000 – 0,2×2,
где x1 – цена автомобиля (в долларах), а x2 – их количество.
Предполагаем также, что уравнение кривой предложения имеет вид:
x1 = 300 + 0,1×2
Объединим уравнения в систему.
Эту систему, конечно, легко решить непосредственно, например методом подстановки. Но мы перейдем от системы к матричному уравнению.
AX = B
Напрашивается решение этого уравнения в виде:
X = B/A
Но операции деления матриц нет. Но есть операция вычисления обратной матрицы. Подумаем, как мы решаем уравнение 5X = 7? Мы пишем, не особенно задумываясь, X = 7/5. а как записать ответ, не пользуясь делением? Это возможно: X = 5-1•7 или 7•5-1.
Обратная матрица A-1 должна обладать свойством A-1A = E, где E – единичная матрица.
Умножим слева на A-1 обе части матричного уравнения AX = В и получим равенство
A-1AX = A-1B.
Но так как A-1A =E, а EX = X, то мы приходим к равенству
X = A-1B.
Это означает, что равновесная цена на автомобили X = 4200 долларов, а объем продаж X = 39000 штук.
Подобные задачи удобно решать методом Гаусса – методом последовательного исключения переменных, который заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Преобразования Гаусса можно проводить не только с уравнениями системы, но и с матрицей их коэффициентов.
Заключение
Из вышеизложенного следует, что матрицы позволяют в достаточно простой и понятной форме записывать различные экономические процессы и закономерности, дают возможность решать сложные задачи.
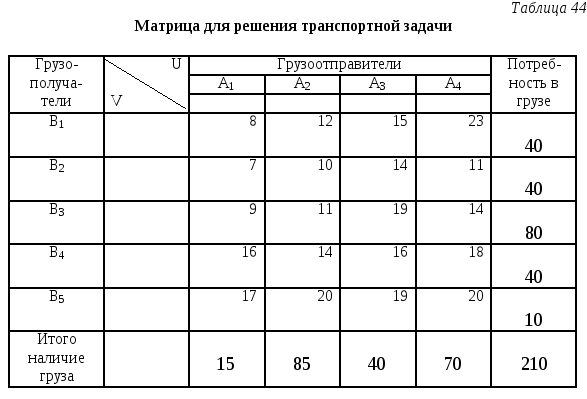
Проанализировав применение матричной алгебры в экономике, можно прийти к выводу, что использование матриц имеет свои достоинства и недостатки.
Недостатки заключаются в том, что матричная алгебра не обеспечивает реальных рекомендаций по разработке специфических стратегий; по матрицам невозможно определить сферы бизнеса, которые готовы стать победителями.
Достоинства же применения матриц в том, что они используют широкий набор стратегически значимых переменных; указывают направление движения ресурсов; позволяют с минимальными затратами труда и времени обрабатывать огромный и весьма разнообразный статистический материал, различные исходные данные, характеризующие уровень, структуру, особенности социально-экономического комплекса.
При наличии отрицательных моментов применения матричной алгебры положительная часть значительно обширнее.
Из выше рассмотренного можно сделать вывод, что роль матриц в экономике очень и очень велика. Ведь благодаря их использованию можно гораздо быстрее, чем с использованием какого-либо другого математического аппарата, и проще решить многие экономические задачи, что чрезвычайно важно для экономистов.
Используемая литература
- Коршунова Н.И., Плясунов В.С. Математика в экономике. – М.:«Вита-Пресс», 1996.
- Сирл С., Госман У. Матричная алгебра в экономике. – М.:Статистика, 1974.
- Немцова А.В., Попова С.В. ПРИМЕНЕНИЕ СРЕДСТВ МАТРИЧНОЙ АЛГЕБРЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ ЭКОНОМИЧЕСКОГО СОДЕРЖАНИЯ // Современные наукоемкие технологии. – 2014. – № 5-2.
- Ахмедханова А.И., Кожемякина В.А., Мамаев И.И. ПРИМЕНЕНИЕ МАТРИЦ В ЭКОНОМИКЕ // Международный студенческий научный вестник. – 2015. – № 3-4.;
- Авдеев Д.Д., Турченко В.В. ПРИМЕНЕНИЕ МАТРИЦ В ЭКОНОМИКЕ // Научное обозрение. Педагогические науки. – 2019. – № 4-3.
Приложение. Операции над матрицами
Линейные операции над матрицами.
Определение 1. Матрицей называется прямоугольная таблица:
A = = (aij)
Число m ее строк и число n ее столбцов называют размерами матрицы А. Про матрицу А говорят, что она размером m×n. Обозначим Mm×n множество матриц размером m×n (m строк и n столбцов).
Обозначим Mm×n множество матриц размером m×n (m строк и n столбцов).
Определение 2. Пусть A=(aij) и B=(bij) – две матрицы размером m×n.
Суммой матриц A и B называется матрица C=(cij) є Mm×n , такая, что cij = aij+bij для всех i и j.
Действие сложения определено для матриц одинакового размера
C=A +B=
Произведением матрицы A на число α называется матрица αA с элементами (αaij).
αA=
Операции сложения матриц и умножения матрицы на число называют линейными операциями.
Пример 1.
+ =
Если страница Вам понравилась, поделитесь в социальных сетях:
Организационные структуры
Организационная структура является фактором среды предприятия, который может оказывать влияние на доступность ресурсов и на выполнение проектов. Организационные структуры варьируются от функциональных до проектных, при этом между ними существует множество матричных структур.
 В таблице 2-1 показаны связанные с проектом ключевые характеристики главных типов организационных структур.
В таблице 2-1 показаны связанные с проектом ключевые характеристики главных типов организационных структур. | Таблица 2-1. Влияние организационных структур на проекты |
Классическая функциональная организация, показанная на рисунке 2-1, является иерархией, в которой у каждого сотрудника есть один явный вышестоящий начальник. Штатные сотрудники сгруппированы на верхнем уровне по специальностям, таким как производство, маркетинг, технические специальности и бухгалтерский учет. Далее специальности могут подразделяться на функциональные подразделения, такие как машиностроение и электротехника. Каждый отдел в функциональной организации будет выполнять свою работу по проекту независимо от других отделов.
| Рис. 2-1. Функциональная организация |
Матричные организации, как показано на рис.
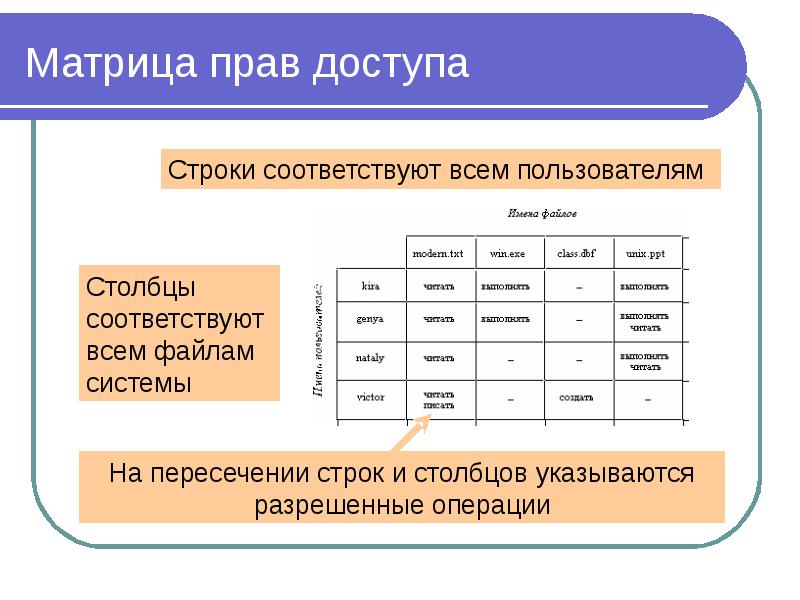 с 2-2 по 2-4, отражают сочетание функциональных и проектных характеристик. Матричные организации можно классифицировать на слабые, сбалансированные и сильные в зависимости от относительного уровня полномочий и влияния функциональных руководителей и руководителей проекта.
с 2-2 по 2-4, отражают сочетание функциональных и проектных характеристик. Матричные организации можно классифицировать на слабые, сбалансированные и сильные в зависимости от относительного уровня полномочий и влияния функциональных руководителей и руководителей проекта.Слабые матричные организации сохраняют многие из характеристик функциональной организации, а роль руководителя проекта больше напоминает роль координатора или диспетчера. Диспетчер проекта работает как помощник персонала и координатор коммуникаций. Диспетчер не может лично принимать решения или обеспечивать их исполнение. Координаторы проектов могут принимать некоторые решения, они наделены определенными полномочиями и подчиняются руководителю высшего уровня.
| Рис. 2-2. Слабая матричная организация |
| Рис. 2-3. Сбалансированная матричная организация |
| Рис. 2-4. Сильная матричная организация |
| Рис. 2-5. Проектная организация |
| Рис. 2-6. Комбинированная организация |
Многие организационные структуры имеют стратегический уровень, средний уровень управления и операционный уровень. Руководитель проекта может взаимодействовать со всеми тремя уровнями в зависимости от таких факторов, как:
- стратегическое значение проекта,
- способность заинтересованных сторон оказывать влияние на проект,
- степень зрелости в управлении проектами,
- системы управления проектами,
- организационные коммуникации.
Данное взаимодействие определяет характеристики проекта, такие как:
- уровень полномочий руководителя проекта,
- доступность и управление ресурсами,
- сторона, контролирующая бюджет проекта,
- роль руководителя проекта,
- состав команды проекта.
Разработка комплексных таблично-матричных легенд для геоэкологических карт (Design of Complex Geoecological Map Legends in Matrix Table Format) by Polina Lemenkova :: SSRN
Actual Problems of Ecology in XXI Century. Proc. Int’l Conference. Vladimir State University n. a. Alexander and Nikolay Stoletovs. Ed. E. P. Gracheva. Russia, Vladimir: Arkaim, pp. 198–202. ISBN: 978-5-93767-119-6, 2015
5 Pages Posted: 6 Mar 2019
Date Written: November 27, 2015
Abstract
Russian Abstract: При использовании ГИС в экологическом картографировании возникает задача формализации картографической легенды, содержащей существенную часть атрибутивной информации на основе классификаций изображаемых объектов. Синтетические карты сопровождаются сложными легендами. Тем не менее, единогласно принятых рекомендаций и оптимальных решений по разработке картографической легенды на данный момент не существует. Настоящая работа восполняет этот пробел в методике экологического картографирования.
English Abstract: The formalization of the legends is necessary for effective use of GIS for the environmental mapping. The legend contains an important part of the attribute information helping to read the map and classify objects. Complex maps usually have complex legends. However, nowadays there is a lack in accepted manuals or optimal solutions on creation of GIS legends. This work fills this gap in this part of the methodology of GIS mapping.
Note: Downloadable document is in Russian.
Keywords: GIS mapping, environmental mapping, environmental monitoring, environmental managmenet, environmental assessment
JEL Classification: Q00, Q01, Q23, Q24, Q25, Q55, Q56
Suggested Citation: Suggested Citation
Lemenkova, Polina and Lemenkova, Polina, Разработка комплексных таблично-матричных легенд для геоэкологических карт (Design of Complex Geoecological Map Legends in Matrix Table Format) (November 27, 2015). Actual Problems of Ecology in XXI Century. Proc. Int’l Conference. Vladimir State University n. a. Alexander and Nikolay Stoletovs. Ed. E. P. Gracheva. Russia, Vladimir: Arkaim, pp. 198–202. ISBN: 978-5-93767-119-6, 2015, Available at SSRN: https://ssrn.com/abstract=3334956Матричная форма таблиц Толле — метод начальных параметров
Оборудование, материаловедение, механика и …
Статьи Чертежи Таблицы О сайте Реклама МАТРИЧНАЯ ФОРМА ТАБЛИЦ ТОЛЛЕ — МЕТОД НАЧАЛЬНЫ ПАРАМЕТРОВ. Начальными параметрами здесь будут угол поворота 01 и момент (внешний или инерционный) на одном из кон-1 цов вала. Матрица жесткости или податливости и матрица масш (моментов инерции) будут матрицами второго порядка. Чтобы строить эти матрицы, рассмотрим систему, состоящую из двух дисков с моментами инерции и /3, соединенных валом с податливостью (рис. 58). Концы вала — свободны. Матрица-столбец начальных параметров на правом конце ) (до перехода через диск 1 ) буди [c.240]Смотреть главы в:
Теория колебаний -> Матричная форма таблиц Толле — метод начальных параметров
СтатьиЧертежиТаблицы
Матричная форма
Матричные ФПУ
Матричные методы
Матричный метод начальных параметров
Метод начальных параметро
Метод начальных параметров
Метод начальных параметров в матричной форме
Параметры начальные
Параметры форма
Таблица Толле
Таблицы параметров
Толле
Толле метод
© 2021 Mash-xxl.info Реклама на сайте
Создание визуального элемента матрицы в Power BI – Power BI
- 11 минут на чтение
В этой статье
ПРИМЕНЯЕТСЯ К: ✔️ Power BI Desktop ✔️ Служба Power BI
Визуал матрицы похож на таблицу. Таблица поддерживает два измерения, а данные являются плоскими, что означает, что повторяющиеся значения отображаются, а не агрегируются.Матрица упрощает осмысленное отображение данных в нескольких измерениях – она поддерживает ступенчатый макет. Матрица автоматически объединяет данные и позволяет выполнять детализацию.
Вы можете создавать визуальные элементы матрицы в отчетах Power BI Desktop и перекрестно выделять элементы в матрице с другими визуальными элементами на этой странице отчета. Например, вы можете выбрать строки, столбцы и даже отдельные ячейки и выделить их крестиком. Кроме того, отдельные ячейки и несколько выбранных ячеек можно скопировать и вставить в другие приложения.
С матрицей связано множество функций, и мы рассмотрим их в следующих разделах этой статьи.
Примечание
Для совместного использования отчета с коллегой по Power BI необходимо, чтобы у вас обоих были отдельные лицензии Power BI Pro или чтобы отчет был сохранен в емкости Premium.
Понимание того, как Power BI вычисляет итоги
Прежде чем переходить к использованию визуального элемента матрицы, важно узнать, как Power BI вычисляет итоговые и промежуточные значения в таблицах и матрицах.Для строк итогов и промежуточных итогов Power BI оценивает меру по всем строкам в базовых данных – это не просто сложение значений в видимых или отображаемых строках. Это означает, что в итоговой строке вы можете получить другие значения, чем вы ожидали.
Обратите внимание на следующие визуальные элементы матрицы.
В этом примере каждая строка в крайнем правом визуальном элементе матрицы показывает Сумма для каждой комбинации продавец / дата. Однако, поскольку продавец появляется на несколько дат, числа могут появляться более одного раза.Таким образом, точная сумма из базовых данных и простое добавление видимых значений не равнозначны. Это обычная закономерность, когда сумма, которую вы суммируете, находится на стороне «один» отношения «один ко многим».
Когда вы смотрите на итоги и промежуточные итоги, помните, что эти значения основаны на базовых данных. Они основаны не только на видимых ценностях.
Развертывание и сворачивание заголовков строк
Есть два способа раскрыть заголовки строк. Первый – через контекстное меню.Вы увидите варианты расширения выбранного заголовка строки, всего уровня или всего до самого последнего уровня иерархии. У вас есть аналогичные варианты для сворачивания заголовков строк.
Вы также можете добавить кнопки +/- к заголовкам строк через панель форматирования под карточкой Заголовки строк . По умолчанию значки будут соответствовать форматированию заголовка строки, но вы можете настроить цвета и размеры значков отдельно, если хотите.
Когда значки включены, они работают аналогично значкам сводной таблицы в Excel.
Состояние раскрытия матрицы сохранится вместе с отчетом. Матрицу можно прикрепить к панели управления развернутой или свернутой. Когда эта плитка панели мониторинга выбрана и отчет открывается, состояние раскрытия все еще можно изменить в отчете.
Примечание
Если вы создаете отчет на основе многомерной модели служб Analysis Services, есть некоторые особые соображения по развертыванию / свертыванию, если модель использует функцию элемента по умолчанию.Дополнительные сведения см. В разделе Работа с многомерными моделями в Power BI
.Использование действий детализации с визуалом матрицы
С помощью визуального элемента «Матрица» вы можете выполнять всевозможные интересные действия по детализации, которые раньше были недоступны. Это включает возможность детализации с использованием строк, столбцов и даже отдельных разделов и ячеек. Давайте посмотрим, как работает каждый из них.
Развернуть заголовки строк
На панели «Визуализации», когда вы добавляете несколько полей в раздел Строки лунки Поля , вы активируете действия детализации для строк визуального элемента матрицы.Это похоже на создание иерархии, которая затем позволяет выполнять детализацию (а затем резервное копирование) по этой иерархии и анализировать данные на каждом уровне.
На следующем изображении раздел строк содержит этап продаж и размер возможности , создавая группировку (или иерархию) в строках, которые мы можем детализировать, чтобы увидеть подробности.
Когда визуал имеет группировку, созданную в разделе рядов , сам визуал отображает сверло и развернуть значки в верхнем левом углу визуала.
Подобно поведению детализации и развертывания в других визуальных элементах, выбор этих кнопок позволяет нам углубиться (или выполнить резервное копирование) по иерархии. В этом случае мы можем развернуться от этапа продаж до Размер возможности , как показано на следующем изображении, где был выбран значок перехода вниз на один уровень (вилы).
Помимо использования этих значков, вы можете выбрать любой из этих заголовков строк и развернуть их, выбрав из появившегося меню.
Обратите внимание, что в появившемся меню есть несколько опций, которые дают разные результаты:
Выбор Drill Down расширяет матрицу для , что уровень строки , исключая все остальные заголовки строк, кроме заголовка строки, который был выбран. На следующем изображении выбрано Proposal > Drill Down . Обратите внимание, что другие строки верхнего уровня больше не отображаются в матрице. Этот способ детализации – полезная функция, и становится особенно крутой, когда мы переходим к разделу перекрестного выделения.
Щелкните значок Drill up , чтобы вернуться к предыдущему виду верхнего уровня. Если затем выбрать Предложение > Показать следующий уровень , вы получите список всех элементов следующего уровня по возрастанию (в данном случае поле Размер возможности ) без категоризации иерархии более высокого уровня.
Выберите значок Развернуть в верхнем левом углу, чтобы матрица отображала все категории верхнего уровня, затем выберите Предложение > Развернуть до следующего уровня , чтобы увидеть все значения для обоих уровней иерархии – Этап продаж и Размер возможности .
Вы также можете использовать пункт меню Expand для дальнейшего управления отображением. Например, выберите Предложение > Разверните > Выбор . Power BI отображает одну итоговую строку для каждой стадии продаж и всех вариантов размера возможной сделки для предложения .
Развернуть заголовки столбцов
Подобно возможности детализации по строкам, вы также можете детализировать столбцы.На следующем изображении два поля в лунке поля Columns создают иерархию, аналогичную той, которую мы использовали для строк ранее в этой статье. В полевой скважине Columns у нас есть Region и Segment . Как только второе поле было добавлено в Столбцы , новое раскрывающееся меню, отображаемое на визуальном элементе, в настоящее время показывает строк .
Чтобы развернуть столбцы, выберите Столбцы из меню Детализация по , которое можно найти в верхнем левом углу матрицы.Выберите регион East и выберите Drill Down .
Когда вы выбираете Drill Down , отображается следующий уровень иерархии столбцов для Region> East , который в данном случае равен Opportunity count . Другой регион скрыт.
Остальные пункты меню работают со столбцами так же, как и со строками (см. Предыдущий раздел, Развернуть заголовки строк ). Вы можете Показать следующий уровень и Развернуть до следующего уровня со столбцами так же, как вы можете со строками.
Примечание
Значки детализации и детализации в верхнем левом углу визуального элемента матрицы применяются только к строкам. Чтобы развернуть столбцы, необходимо использовать контекстное меню.
Пошаговый макет с матричными визуальными элементами
Визуальный элемент матрицы автоматически делает отступы для подкатегорий в иерархии под каждым родительским элементом, что называется ступенчатым макетом.
В исходной версии матричного визуала подкатегории отображались в совершенно другом столбце, занимая гораздо больше места в визуале.На следующем изображении показана таблица в исходном матричном визуале; обратите внимание на подкатегории в отдельном столбце.
На следующем изображении вы видите матричный визуал с пошаговой компоновкой в действии. Обратите внимание, что подкатегории категории «Компьютеры » (аксессуары для компьютеров, настольные компьютеры, ноутбуки, мониторы и т. Д.) Имеют небольшой отступ, что обеспечивает более четкое и сжатое изображение.
Вы можете легко настроить ступенчатую компоновку. При выбранном визуальном элементе матрицы в разделе Формат (значок валика) на панели Визуализации разверните раздел заголовков строк.У вас есть два варианта: переключатель ступенчатого макета (который включает или выключает) и отступ ступенчатого макета (указывает размер отступа в пикселях).
Если вы отключите пошаговый макет, Power BI покажет подкатегории в другом столбце, а не с отступом под родительской категорией.
Промежуточные и общие итоги с визуальными элементами матрицы
Вы можете включить или выключить промежуточные итоги в визуальных элементах матрицы как для строк, так и для столбцов. На следующем изображении вы можете видеть, что промежуточные итоги строк установлены на на и настроены на отображение внизу.
Когда вы включаете Промежуточные итоги и добавляете метку, Power BI также добавляет строку и ту же метку для общего итогового значения. Чтобы отформатировать общий итог, выберите вариант формата для Всего .
Если вы хотите отключить промежуточные итоги и общую сумму, в разделе формата на панели визуализаций разверните карточку Промежуточные итоги . Установите ползунок промежуточных итогов строк на Выкл. . При этом промежуточные итоги не отображаются.
Тот же процесс применяется для промежуточных итогов столбцов.
Добавить условные значки
Добавьте визуальные подсказки в таблицу или матрицу с помощью условных значков .
В разделе форматирования на панели «Визуализации» разверните карточку Условное форматирование . Установите ползунок Icons на на и выберите Advanced controls .
Настройте условия, значки и цвета для вашей матрицы и выберите OK .В этом примере мы использовали красный флаг для низких значений, фиолетовый кружок для высоких значений и желтый треугольник для всего, что находится между ними.
Перекрестное выделение с помощью матричных визуальных элементов
С помощью визуального элемента матрицы вы можете выбрать любые элементы в матрице в качестве основы для перекрестного выделения. Выберите столбец в матрице, и Power BI выделит столбец, как и любые другие визуальные элементы на странице отчета. Этот тип перекрестного выделения был общей чертой других визуальных элементов и выбора точек данных, поэтому теперь визуальный элемент матрицы предлагает ту же функцию.
Кроме того, использование Ctrl + Click также работает для перекрестного выделения. Например, на следующем изображении набор подкатегорий был выбран из матричного визуала. Обратите внимание, как элементы, которые не были выбраны из визуального элемента, становятся серыми, и как другие визуальные элементы на странице отражают выбор, сделанный в визуальном элементе матрицы.
Копирование значений из Power BI для использования в других приложениях
Ваша матрица или таблица может иметь содержимое, которое вы хотели бы использовать в других приложениях: Dynamics CRM, Excel и других отчетах Power BI.Щелкнув правой кнопкой мыши Power BI, вы можете скопировать одну или несколько ячеек в буфер обмена. Затем вставьте их в другое приложение.
Чтобы скопировать значение отдельной ячейки, выберите ячейку, щелкните правой кнопкой мыши и выберите Копировать значение . Имея значение неформатированной ячейки в буфере обмена, теперь вы можете вставить его в другое приложение.
Чтобы скопировать более одной ячейки, выберите диапазон ячеек или используйте CTRL, чтобы выбрать одну или несколько ячеек. Выбор копирования гарантирует, что меры будут отформатированы в соответствии с правилами форматирования столбца, в отличие от неформатированной команды Копировать значение .
Копия будет включать заголовки столбцов и строк.
Чтобы сделать копию самого визуального элемента, содержащего только выбранные ячейки, выберите одну или несколько ячеек с помощью CTRL, щелкните правой кнопкой мыши и выберите Копировать визуал
Копия будет другой матричной визуализацией, но будет содержать только ваши скопированные данные.
Установка значения матрицы в качестве настраиваемого URL-адреса
Если у вас есть столбец или показатель, содержащий URL-адреса веб-сайтов, вы можете использовать условное форматирование, чтобы применить эти URL-адреса к полям в качестве активных ссылок. Вы найдете эту опцию под карточкой Условное форматирование на панели форматирования.
Включите Web URL и выберите поле, которое будет использоваться в качестве URL-адреса для столбца. После применения значения в этом поле (столбце) становятся активными ссылками.Наведите указатель мыши, чтобы увидеть ссылку, и выберите, чтобы перейти на эту страницу.
Дополнительные сведения см. В разделе Условное форматирование таблицы
Цвета затенения и шрифта с визуальными элементами матрицы
С помощью визуального элемента матрицы вы можете применить условное форматирование (цвета, заливку и гистограммы) к фону ячеек в матрице, а также применить условное форматирование к тексту и самим значениям.
Чтобы применить условное форматирование, выберите визуальный элемент матрицы и откройте панель Формат .Разверните карту условного форматирования и для Цвет фона , Цвет шрифта или Строки данных , поверните ползунок на На . При включении одного из этих параметров отображается ссылка на Расширенные элементы управления , которая позволяет настраивать цвета и значения для цветового форматирования.
Выберите Дополнительные элементы управления , чтобы отобразить диалоговое окно, в котором можно вносить изменения. В этом примере показан диалог для Панели данных .
Рваная иерархия
Рваная иерархия содержит уровни без данных. Хорошим примером является матрица сотрудников компании. В компании много уровней, от генерального директора до ниже. Генеральный директор является высшим уровнем в иерархии и не подчиняется никаким другим сотрудникам. С другой стороны, любой другой сотрудник компании может подчиняться цепочке менеджеров, которые подчиняются вице-президенту, который подчиняется генеральному директору. В зависимости от своего уровня в иерархии и того, как организован их отдел, сотрудники могут иметь данные для одного, двух, пяти или десяти уровней иерархии.И для любого конкретного сотрудника могут отсутствовать данные для определенных уровней иерархии.
В настоящее время нет способа скрыть пустые строки или идентичные родительские и дочерние значения. И вы не можете контролировать, какие уровни иерархии можно, а какие нельзя расширять. Тем не менее, есть несколько шагов, которые вы можете предпринять, чтобы сделать внешний вид более привлекательным.
Отключить ступенчатую раскладку. На панели «Формат» выберите Заголовки строк > Отключить ступенчатый макет .Все пустые значения для уровня иерархии теперь будут отображаться в одной строке.
Отключить промежуточные итоги для строк и столбцов матрицы. На панели Формат выберите Формат > Промежуточные итоги .
Рекомендации и устранение неисправностей
- Если текстовые данные в ячейках или заголовках вашей матрицы содержат символы новой строки, эти символы будут игнорироваться, если вы не включите параметр «Перенос слов» на соответствующей карточке панели форматирования элемента.
Следующие шаги
Визуальный элемент Power Apps для Power BI
Типы визуализации в Power BI
Как преобразовать таблицу lxmx в матрицу
Как преобразовать таблицу lxmx в матрицу Возврат к Main Index page Перейти вернуться к примечаниям к лекции 12Практические соображения в формулирование матричная демографическая модель:
Преобразование л x м x график в Лесли матрица.
Стоит ли переделывать л x м x расписание? Когда ответ будет положительным, а когда – отрицательным?ДА : Если мы заинтересованы в анализе некоторых опубликованных данных, что уже существуют в л x м x формат (возможно, для сравнения с данными, которые мы собрали, или для сравнение с другим набором собственных данных или из литературы)
НЕТ : если мы были начать полевые исследования с нуля и запланировать их использование в матрице формат (тогда мы рассчитали бы P i и m i прямо из наших данных)
Сначала посмотрим на график жизненного цикла:
Фиг.12.1. Жизнь
график цикла для популяции с возрастной классификацией по частоте пульса
постбридинг
перепись.
Термины предназначены для отображения данных, используемых для
расчет параметров из l x m x Таблица ниже.
Давайте посмотрим на полностью возрастную жизненный цикл для которого кто-то составил таблицу л x м x набор данных.Формат l x m x является традиционный тот, из которого можно вычислить многие из одних и тех же “выходов”, таких как репродуктивный ценности и стабильное возрастное распределение. Формат матрицы, однако, позволяет нам делать все, что мы можем сделать с l x m x стол и многое другое. Вот пример l x m x стол:
Таблица 12.1. л x м x расписание используется для построения графика жизненного цикла, подобного изображенному на рис. 12.4.
- х
l x м x
________________________
2 0,315 1
3 0,2205 3
4
0
0
________________________________
[Обратите внимание, что л x м x таблицы иногда будут иметь неявный ноль для последней строки. я показывать нули, чтобы подчеркнуть, что мы часто будем использовать нулевой столбец в нашей матрице]
От непрерывного x до дискретного i : Обратите внимание, что мы переходим от непрерывного возраста ( x ) к дискретному возрасту возрастной класс ( и ).Вернемся к рис. 12.2 напомнить себе о различиях между непрерывным возрастом (в нижнем индексе x ) и дискретный возрастной класс (с индексами и ).
Удобрения : Удобно, хотя м x = м i . Пытаться в логика. Первогодние особи ( i = 1) размножаются на конце их первого года, когда им исполнился 1 год ( x = 1). сходным образом м i = м x для всех старших возрастных категорий.Давайте использовать только что разработанные эквиваленты. повернуть л x м x данные в таблице 12.1 в P i и F i , которые мы используем в матрице Лесли. P 1 = л 1 / л ø = 0,45 / 1,0 = 0,45Выживаемость : для после размножения перепись п. и = л x = i / л x-1 .
С этими двумя эквивалентностями мы можем обратиться любой л x м x график в соответствующие P i и F i термины, необходимые для графа жизненного цикла и матрицы в матричной анализ.
P 2 = л 2 / l 1 = 0.315 / 0,45 = 0,70
P 3 = л 3 / l 2 = 0,2205 / 0,315 = 0,70
P 4 = л 4 / л 3 = 0 / 0,2205 = 0
F 1 = P 1 * м 1 = 0,45 * 0 = 0
F 2 = P 2 * м 2 = 0.70 * 1 = 0,70
F 3 = P 3 * м 3 = 0,7 * 3 = 2,1
F 4 = P 4 * м 4 = 0 * 0 = 0
Теперь давайте построим матрицу из данных, которые мы имеют.| Ф 1 | Ф. 2 | Ф. 3 | Ф. 4 |
| P 1 | |||
| П 2 | |||
| П 3 |
Верхний ряд (удобрения) и субдиагональный (выживание) : Обратите внимание, что для анализа , строго классифицированного по возрасту , оплодотворение буду быть в верхнем ряду, а годовые коэффициенты выживаемости – в поддиагонали. Все остальные ячейки пусты (ноль). Как мы увидим в Мудреце Рябчик пример, однако, жизненный цикл, классифицированный как стадия , может иметь ненулевой ячеек в других местах (они почти всегда будут удобрения в верхнем ряду).
Подставляя значения сверху, получаем
следующий
числовые значения:
| 0 | 0.70 | 2,10 | 0 |
| 0,45 | |||
| 0.70 | |||
| 0,70 |
Теперь мы можем скрутить матрицу с помощью матрицы демографический анализ упаковка.
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§ §§§§§§§§§§§§§§§§
Возврат к началу страницы
GitHub – miter / advmlthreatmatrix: Матрица состязательных угроз
Мы рады объявить о новом интерактивном выпуске матрицы угроз AdvML под новым брендом: ATLAS – Состязательная среда угроз для систем искусственного интеллекта!
Посетите наш новый веб-сайт https: // atlas.mitre.org для новой интерактивной матрицы, новых тематических исследований и специализированного навигатора ATLAS!
- Состязательная ML 101
- Матрица угроз состязательного машинного обучения
- Примеры из практики
- Авторы
- Обратная связь и участие
- Свяжитесь с нами
Цель этого проекта – позиционировать атаки на системы машинного обучения (ML) в структуре в стиле ATT & CK, чтобы аналитики безопасности могли ориентироваться этим новым и грядущим угрозам.
Если вы новичок в том, как можно атаковать системы машинного обучения, мы предлагаем начать с этого простого Adversarial ML 101, предназначенного для аналитиков безопасности.
Или, если вы хотите погрузиться в подробности, перейдите к Матрице угроз состязательного машинного обучения.
Зачем разрабатывать матрицу угроз состязательного машинного обучения?
- За последние три года у таких крупных компаний, как Google, Amazon, Microsoft и Tesla, системы машинного обучения обманывали, обходили стороной или вводили в заблуждение.
- Эта тенденция будет только расти: согласно отчету Gartner.К 2022 году 30% кибератак будут связаны с отравлением данных, кражей моделей или примерами состязательных действий.
- Промышленность недостаточно подготовлена. При опросе 28 организаций, охватывающих как небольшие, так и крупные организации, 25 организаций не знали, как защитить свои системы машинного обучения.
В отличие от традиционных уязвимостей кибербезопасности, которые привязаны к конкретным программным и аппаратным системам, состязательные уязвимости машинного обучения допускаются внутренними ограничениями, лежащими в основе алгоритмов машинного обучения.Данные могут быть использованы в качестве оружия новыми способами, что требует расширения способов моделирования поведения киберпреступников, чтобы отразить новые векторы угроз и быстро развивающийся жизненный цикл состязательных атак с машинным обучением.
Эта матрица угроз возникла в результате партнерства с 12 отраслевыми и академическими исследовательскими группами с целью дать аналитикам по безопасности возможность сориентироваться в этих новых и грядущих угрозах. Фреймворк содержит тщательно подобранный набор уязвимостей и действий злоумышленников, которые Microsoft и MITER проверили на эффективность против производственных систем машинного обучения. .Мы использовали ATT & CK в качестве шаблона, поскольку аналитики безопасности уже знакомы с использованием этого типа матрицы.
Мы рекомендуем покопаться в Матрице угроз состязательного машинного обучения.
Чтобы увидеть Матрицу в действии, мы рекомендуем ознакомиться с тематическими исследованиями
Авторы
| Организация | Авторы |
|---|---|
| Microsoft | Рам Шанкар Шива Кумар, Хайрам Андерсон, Сьюзи Шапперле, Блейк Стром, Мэдлин Кармайкл, Мэтт Суонн, Марк Руссинович, Ник Биде, Кэти Ву, Энди Комиссионеру, Шарон Ся, Марио Гертцель, Джеффри Сновер, Дерек Адам, Дипак Манохарта Бхау , Питер Ваксман, Абхишек Гупта, Энн Джонсон, Эндрю Паверд, Пит Брайан, Роберто Родригес, Уилл Пирс |
| MITER | Микель Родригес, Кристина Лиагати, Кейт Манвилл, Майкл Крамдик, Джош Харгесс, Вирджиния Адамс, Шири Бенделак, Генри Конклин, Поомати Дураисами, Дэвид Джангрейв, Эмили Холт, Кайл Джексон, Николь Лейп, Сара Лири, Элиза Мейс, Кристофер Мобли Смит, Джеймс Танис, Майкл Трит, Дэвид Уиллмс, Лили Вонг |
| Bosch | Маноджкумар Пармар |
| IBM | Пин-Ю Чен |
| NVIDIA | Дэвид Ребер мл., Кейт Козо, Кристофер Коттрелл, Дэниел Рорер |
| Airbus | Адам Уэджбери |
| PricewaterhouseCoopers | Майкл Монтесилло |
| Глубокий инстинкт | Надав Маман, Шимон Ноам Орен, Ишай Розенберг |
| Two Six Labs | Дэвид Слейтер |
| Университет Торонто | Аделин Трэверс, Джонас Гуан, Николас Паперно, |
| Кардиффский университет | Пит Бурнап |
| Институт программной инженерии / Университет Карнеги-Меллона | Натан М.VanHoudnos |
| Берривильский институт машинного обучения | Гэри МакГроу, Гарольд Фигероа, Виктор Шепардсон, Ричи Бонетт |
| Цитадель AI | Кенни Сонг |
| McAfee | Кристиан Бик |
| Неаффилированные | Кен Луу |
| Группа муравьев | Генри Сюэф |
| Palo Alto Networks | Мэй Ван, Стефан Ахлейтнер, Ю Фу, Аджая Неупане, Лей Сю |
Обратная связь и участие
Матрица угроз состязательного машинного обучения – это первая попытка собрать базу знаний о том, как можно атаковать системы машинного обучения.Нам нужна ваша помощь, чтобы сделать его целостным и заполнить недостающие пробелы!
Исправления и улучшения
- Для немедленных исправлений отправьте запрос на вытягивание с предлагаемыми изменениями! Мы рады сделать эту систему лучше вместе с вами!
- Чтобы получить больше практических отзывов, мы сотрудничаем с AI Village от Defcon, чтобы открыть фреймворк для всех членов сообщества, чтобы они могли получать отзывы и улучшать его. В настоящее время думают, что этот семинар должен быть Январь / февраль 2021 г.Пожалуйста, зарегистрируйтесь здесь.
Принять участие в тематических исследованиях
Мы особенно рады новым тематическим исследованиям! Мы с нетерпением ждем вкладов как промышленных, так и академических исследователей. Прежде чем отправлять тематическое исследование, учтите, что атака:
- Использует одну или несколько уязвимостей, которые ставят под угрозу конфиденциальность, целостность или доступность системы машинного обучения.
- Атака была направлена на производственную, коммерческую систему ML. Это может быть MLaaS, например Amazon, Microsoft Azure, Google Cloud AI, IBM Watson и т. Д., Или системы машинного обучения, встроенные в клиент / край.
- У вас есть разрешение поделиться информацией / опубликовать это исследование. Пожалуйста, следуйте соответствующим каналам, прежде чем сообщать о новой атаке, и убедитесь, что вы практикуете ответственное раскрытие информации.
Вы можете отправить электронное письмо по адресу: [email protected] со сводкой инцидента и сопоставлением матрицы угроз состязательного машинного обучения.
Присоединяйтесь к нашему списку рассылки
- Мы приглашаем всех присоединиться к нашей группе Google здесь, чтобы обсудить Матрицу угроз состязательного машинного обучения.
- Примечание. Группы Google обычно используют вашу личную электронную почту по умолчанию. Если вы предпочитаете заходить на этот форум, используя свой корпоративный адрес электронной почты (в отличие от Gmail), вы можете создать учетную запись Google, используя свой корпоративный адрес электронной почты, прежде чем присоединиться к группе.
- Также большинство почтовых клиентов направляют электронные письма из групп Google в папку «Другое» / «Спам» / «Форумы». Итак, вы можете создать правило в своем почтовом клиенте, чтобы эти электронные письма попадали в ваш почтовый ящик.
Свяжитесь с нами
Для исправлений и улучшений или для участия в тематическом исследовании см. Обратная связь.
Элегантная таблица корреляции с использованием пакета xtable R – Easy Guides – Wiki
Анализ корреляционной матрицы – важный метод поиска зависимости между переменными. Здесь объясняется вычисление корреляционной матрицы и рисование коррелограммы . Цель этой статьи – показать вам, как получить нижнюю часть и верхнюю треугольную часть корреляционной матрицы . Мы также будем использовать пакет xtable R для отображения красивой корреляционной таблицы в форматах html или latex.
Корреляционный матричный анализ
Следующий код R вычисляет корреляционную матрицу с использованием данных mtcars. Нажмите здесь, что прочитать подробнее.
мкр mpg cyl disp hp drat wt qsec против am gear carb
миль на галлон 1,00 -0,85 -0,85 -0,78 0,68 -0,87 0,42 0,66 0,60 0,48 -0,55
цилиндр -0,85 1,00 0,90 0,83 -0,70 0,78 -0,59 -0,81 -0,52 -0,49 0,53
disp -0,85 0,90 1,00 0,79 -0,71 0,89 -0,43 -0,71 -0,59 -0,56 0.39
л.с. -0,78 0,83 0,79 1,00 -0,45 0,66 -0,71 -0,72 -0,24 -0,13 0,75
драт 0,68 -0,70 -0,71 -0,45 1,00 -0,71 0,09 0,44 0,71 0,70 -0,09
вес -0,87 0,78 0,89 0,66 -0,71 1,00 -0,17 -0,55 -0,69 -0,58 0,43
qsec 0,42 -0,59 -0,43 -0,71 0,09 -0,17 1,00 0,74 -0,23 -0,21 -0,66
по сравнению с 0,66 -0,81 -0,71 -0,72 0,44 -0,55 0,74 1,00 0,17 0,21 -0,57
am 0,60 -0,52 -0,59 -0,24 0,71 -0,69 -0,23 0,17 1,00 0,79 0,06
шестерня 0,48 -0,49 -0,56 -0,13 0,70 -0,58 -0,21 0,21 0,79 1,00 0,27
карб -0.55 0,53 0,39 0,75 -0,09 0,43 -0,66 -0,57 0,06 0,27 1,00 Результатом является таблица коэффициентов корреляции между всеми возможными парами переменных.
Нижняя и верхняя треугольная часть корреляционной матрицы
Чтобы получить нижнюю или верхнюю часть корреляционной матрицы , можно использовать функцию R lower.tri () или upper.tri () . Форматы функций:
lower.tri (x, diag = FALSE)
верхний.tri (x, diag = FALSE) – x : это матрица корреляции – diag : если ИСТИНА, диагональ не включается в результат.
Две указанные выше функции возвращают матрицу логических значений, которая имеет тот же размер, что и корреляционная матрица . Записи ИСТИНА в нижнем или верхнем треугольнике:
верх. Три (mcor) [, 1] [, 2] [, 3] [, 4] [, 5] [, 6] [, 7] [, 8] [, 9] [, 10] [, 11] »
[1,] FALSE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[2,] FALSE FALSE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[3,] FALSE FALSE FALSE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[4,] FALSE FALSE FALSE FALSE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
[5,] FALSE FALSE FALSE FALSE TRUE TRUE TRUE TRUE TRUE TRUE
[6,] FALSE FALSE FALSE FALSE FALSE FALSE TRUE TRUE TRUE TRUE TRUE
[7,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE TRUE TRUE TRUE
[8,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE TRUE TRUE
[9,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE TRUE
[10,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE
[11,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE # Скрыть верхний треугольник
верх mpg cyl disp hp drat wt qsec против am gear carb
миль на галлон 1
цил -0.85 1
disp -0,85 0,9 1
л.с. -0,78 0,83 0,79 1
драфт 0,68 -0,7 -0,71 -0,45 1
вес -0,87 0,78 0,89 0,66 -0,71 1
мкс 0,42 -0,59 -0,43 -0,71 0,09 -0,17 1
по сравнению с 0,66 -0,81 -0,71 -0,72 0,44 -0,55 0,74 1
утра 0,6 -0,52 -0,59 -0,24 0,71 -0.69 -0,23 0,17 1
шестерня 0,48 -0,49 -0,56 -0,13 0,7 -0,58 -0,21 0,21 0,79 1
карбюратор -0,55 0,53 0,39 0,75 -0,09 0,43 -0,66 -0,57 0,06 0,27 1 # Скрыть нижний треугольник
нижняя mpg cyl disp hp drat wt qsec против am gear carb
миль на галлон -0,85 -0,85 -0,78 0,68 -0,87 0,42 0,66 0,6 0,48 -0,55
цилиндр 0,9 0,83 -0,7 0,78 -0,59 -0,81 -0,52 -0,49 0,53
disp 0,79 -0,71 0,89 -0,43 -0.71 -0,59 -0,56 0,39
л.с. -0,45 0,66 -0,71 -0,72 -0,24 -0,13 0,75
драт -0,71 0,09 0,44 0,71 0,7 -0,09
вес -0,17 -0,55 -0,69 -0,58 0,43
qsec 0,74 -0,23 -0,21 -0,66
и 0,17 0,21 -0,57
утра 0,79 0,06
шестерня 0.27
карбюратор Объединить матрицу коэффициентов корреляции и уровней значимости
Пользовательская функция corstars () используется для объединения коэффициентов корреляции и уровня значимости . R-код функции приведен в конце этой статьи. Требуется 2 пакета:
Прежде чем продолжить выполнение следующих упражнений, вы должны сначала скопировать и вставить исходный код функции corstars (), которую вы можете найти в конце этой статьи.
corstars (mtcars [, 1: 7], result = "html") | миль на галлон | цилиндр | дисп | л. с. | тряпка | вес | |
|---|---|---|---|---|---|---|
| миль на галлон | ||||||
| цилиндр | -0,85 **** | |||||
| дисп | -0.85 **** | 0,90 **** | ||||
| л. с. | -0,78 **** | 0,83 **** | 0,79 **** | |||
| тряпка | 0,68 **** | -0,70 **** | -0,71 **** | -0,45 ** | ||
| вес | -0,87 **** | 0,78 **** | 0.89 **** | 0,66 **** | -0,71 **** | |
| qsec | 0,42 * | -0,59 *** | -0,43 * | -0,71 **** | 0,09 | -0,17 |
п
Код функции corstars (код адаптирован из кода, размещенного на этом форуме и в этом блоге):
# x - матрица, содержащая данные
# method: метод корреляции. "pearson" "или" spearman "" поддерживается
# removeTriangle: удалить верхний или нижний треугольник
# результат: если "html" или "latex"
# результаты будут отображаться в формате html или latex
корстарс Таблицаvs.Матричные визуализации в Power BI
Опубликовано Jon
На первый взгляд визуализации таблиц и матриц в Power BI выглядят одинаково. Оба отображают данные в табличном формате, который напоминает пользователю Excel. Однако понимание разницы между визуализацией таблицы и матрицы в Power BI важно для эффективного отображения данных.
Основное отличие состоит в том, что в таблицах данные отображаются только в двух измерениях.Пользователь имеет возможность вводить поля данных как значения и отображать их в виде столбца. Матричные визуализации предоставляют пользователю больше возможностей для отображения данных в виде таблицы. У пользователя есть возможность указать строки и столбцы, а также расположить данные по слоям, чтобы воспользоваться функциональностью детализации Power BI. На изображении ниже показаны данные, отображаемые в многослойном формате в матрице.
Матричная визуализация слева – изображение получено из MicrosoftBenefits в матрицу над таблицами
- Матричные визуализации также предоставляют возможность автоматического вычисления промежуточных итогов для числовых столбцов.
- Matrix обеспечивают более надежную детализацию для конечного пользователя.
Легкая аналогия, которую следует иметь в виду, заключается в том, что таблица в Power BI – это, по сути, просто столбцы Excel. Помимо просмотра данных, здесь не так много функций. Визуальный элемент матрицы в Power BI лучше, чем сводная таблица. Сводная таблица намного надежнее, и Excel знает, что нужно рассматривать сводную таблицу как динамический объект, а не как статические столбцы.
Лучше всего использовать матричную визуализацию, потому что она намного надежнее таблицы.Даже если дополнительные функции не используются, использование матричной визуализации по сравнению с табличной визуализацией не оказывает значительного влияния на производительность.
Для получения дополнительных сведений о Power BI ознакомьтесь с другими публикациями в нашем блоге здесь! Вы также можете узнать больше о таблицах и матрицах в Power BI на веб-сайте Microsoft здесь.
Матрица графомат– Высокопроизводительные IBCS-таблицы для ваших отчетов –
Высокопроизводительные столы
матрица graphomate в виде кросс-таблицы, включая рассчитанные абсолютные отклоненияГрафоматическая матрица – это наш новый компонент таблицы.Таблицы вездесущи, без них не обходится ни один отчет. Microsoft Excel по-прежнему остается любимым инструментом сборщиков данных. Однако часто после первых пробных запусков с компонентами таблиц в интерфейсных инструментах бизнес-аналитики наступает разочарование: хотя доступ к данным теперь возможен без особого перебора чисел, предлагаемые варианты форматирования очень ограничены.
Обзор преимуществ графоматической матрицы
- форматирование на основе данных
- собственный язык форматирования
- отображение иерархий в строках И столбцах
- плавная прокрутка
- отсутствие ограничений данных благодаря современной технологии
- IBCS-совместимый
Матрица графомат доступна для
Примечание. Таблицы graphomate для SAP Web Intelligence по-прежнему доступны.Степень переноса матрицы на последний интерфейсный инструмент все еще обсуждается.
Здесь можно найти руководства пользователя для графоматической матрицы в соответствующих интерфейсных инструментах.
У нашей матрицы есть что предложить!
Здесь мы и начинаем: всеобъемлющие – даже условные – параметры форматирования для каждой ячейки, строки или столбца, всегда обеспечивающие высокий уровень производительности! Благодаря нашему собственному языку форматирования – Cell Formatting Language (CFL), основанному на JavaScript – вы можете полностью настроить внешний вид матрицы.
Вы хотите выделить отдельные ячейки в зависимости от их значения? Выделить итоги или строки? Использовать таблицу в качестве тепловой карты? Установить размер шрифта каждой ячейки в зависимости от значения? Использовать сложные числовые форматы?
Графоматическая матрица реализует все эти требования к дизайну таблиц!
графоматическая матрица с тепловой картой; реализация с использованием языка форматирования ячеекgraphomate воплощает в жизнь вашу индивидуальную таблицу
Если у вас есть особые требования, сообщите нам, и мы предоставим сценарий, который точно соответствует вашим потребностям.Если вы хотите написать код самостоятельно, мы поможем вам запрограммировать CFL с помощью простого веб-редактора. Он поддерживает автозаполнение и подсветку синтаксиса. Примеры кода, такие как микропироги или тепловая карта, помогут вам познакомиться с CFL.
Матрица graphomate заменяет таблицы graphomate , продукт, который мы предлагаем с 2014 года. Хотя таблицы graphomate предлагали возможность отображать требования IBCS в таблицу с помощью нескольких щелчков мышью, наши клиенты запрашивали те же функции и даже больше вариантов форматирования для очень больших таблицы.
матрица graphomate со сценариями в заголовках столбцов и диаграммах в ячейкахПоскольку наша первая цель – удовлетворить наших клиентов, мы много работали над разработкой графоматической матрицы. Высокая производительность сочетается с максимально возможной гибкостью. Фиксированные заголовки строк и столбцов и плавная прокрутка – это только две замечательные особенности.
Матрица graphomate также предлагает популярные функции для удовлетворения требований IBCS, уже знакомых по таблицам graphomate, включая
- отклонений в виде столбиковой или игольчатой диаграммы
- сценариев в столбцах и
- диаграмм в ячейках
, которые можно легко и гибко реализовать.
Кроме того, матрица graphomate позволяет просматривать как иерархическое, так и табличное (кросс-таблицы). Особенно последнее было востребовано многими покупателями. Кроме того, иерархии также могут использоваться в столбцах, а другие столбцы могут быть дополнены вашими собственными вычислениями, такими как возможные отклонения.
Проверьте это: графоматрица – звезда среди таблиц!
Indesign: Использование и стилизация таблиц для матриц
Часто в дизайн-проектах нас просят создать матрицы или таблицы данных для сравнения записей в легко читаемом формате.Есть довольно много способов добиться этого, но я хотел бы поделиться с вами табличным методом и, надеюсь, преобразовать тех из вас, кто создает свои матрицы со сложной компоновкой графических элементов. Размещение ваших матриц внутри таблицы не только семантическое, это дает вам большую гибкость, когда дело доходит до изменения стиля, и экономит массу времени при вводе данных – особенно если вы работаете с другими людьми над проектом, которым может потребоваться редактирование, перемешивание или добавить в свою матрицу. Кроме того, в качестве небольшого примечания, они, скорее всего, получатся более аккуратными и точными, чем любой другой метод, что для меня просто необходимо!
Для этого примера давайте создадим обеденную матрицу выше.Мы собираемся сравнить список из 5 популярных (но уже придуманных!) Ресторанов, как в путеводителе для посетителей или в чем-то подобном, и сравнить некоторые важные статистические данные между ними.
Планирование
Во-первых, давайте спланируем. Определитесь с точками данных, которые вы хотите включить в свою матрицу – правильное планирование может немного упростить этот процесс, поэтому всегда начинайте с бумаги. В этом примере я остановился на 10 столбцах информации, 5 ресторанах и 1 строке заголовков.
Теперь мы создадим текстовое поле с теми же размерами, что и ваша окончательная матрица, и вставим новую таблицу. Таблица -> Вставить таблицу Заполните детали, для этого примера нам понадобится 10 столбцов, 5 строк и одна строка заголовка .
Получим нам это:
У вас останется очень простой стол. С этого момента мне нравится произвольно упорядочивать свои столбцы в их окончательной конфигурации и начинать вставку моих данных. Таким образом, мы фокусируемся на отображении содержимого таблицы с самого начала, чтобы в дальнейшем у нас не возникало проблем с компоновкой.
* Совет. Вы можете установить размеры нескольких столбцов, выбрав их и вставив значение в поле ширины столбца, показанное здесь.
В этом примере я хочу, чтобы контрольные столбцы были одинаковой ширины – 0,25 дюйма .
В этом процессе некоторые заголовки были переопределены, мы исправим это позже.
Укладка каркаса – Укладка
Следующий шаг – начать стилизацию нашей таблицы. Я подхожу к этому, чтобы начать в широком смысле и постепенно перейти к стилизации мельчайших деталей – так же, как фокусировка изображения.Начните с создания нового стиля таблицы и применения его к матрице, удалив большую часть форматирования, например обводки и заливки строк и столбцов (если они есть).
Затем давайте назначим чередующийся шаблон заливки на вкладке Заливки , как указано выше. В этом примере неплохо выглядел бы чередующийся узор, поэтому я выбрал Every Other Row и заранее сделал два градиента, которые я выбрал для каждого соответственно. Обратите внимание, что строки заголовков не подпадают под это действие, и нам придется назначить для них особый стиль ячейки.Ниже представлена наша таблица, так что давайте сделаем это дальше.
Стилизация строки заголовка
Создайте новый стиль ячейки и назовите его Заголовок – по умолчанию , так как это будет наш базовый стиль для строки заголовка. В разделе «Текст» мне нравится добавлять несколько точек заполнения к каждой ячейке, и я выровняю текст по нижнему краю, через секунду вы поймете, почему.
Затем я заполню его синим цветом и удалю все штрихи, которые, по моему мнению, принадлежат стилю по умолчанию.
Сейчас мы заметим, что моя матрица имеет темно-синий фон и черный текст – очевидно, плохое начало, поэтому давайте создадим новый стиль абзаца для наших заголовков и сделаем их жирным и белым.Затем давайте назначим этот стиль нашему заголовку – стиль ячейки по умолчанию в поле: Общие -> Стили абзаца
Затем в своем стиле таблицы для этой матрицы назначьте новый стиль Заголовок – по умолчанию полю строк заголовка. в: Общие -> Стили ячеек
Ниже представлена наша таблица с новым стилем заголовка. Выглядит лучше! Теперь нам просто нужно выяснить, как обрабатывать этот вытесненный текст в небольших столбцах.
Вертикальный текст в заголовке
Давайте продублируем наш заголовок – стиль по умолчанию и назовем только что созданный заголовок стиля ячейки – вертикальный .Нам нужно повернуть этот текст, поэтому в Text -> Text Rotation присвойте ему значение 270 градусов, и установите вертикальное выравнивание по центру.
Теперь нам просто нужно назначить этот стиль нужным заголовкам столбцов и увеличить высоту строки заголовка, чтобы она соответствовала, см. Ниже.
** Совет. Причина, по которой мы назначили наш заголовок – стиль по умолчанию для выравнивания текста по нижнему краю, заключается в том, что наши заголовки, ну… выравниваются по нижнему краю!
Гладить или не гладить (хе-хе)
Наши заголовки выглядят неплохо! Давайте сделаем еще один небольшой шаг и разберемся с этой пограничной ситуацией.Давайте удалим их, создав новый стиль ячеек и назовем его Ячейка – по умолчанию . Давайте добавим ему отступы и установим вертикальное выравнивание на середину, на Strokes и Fills
обеспечим выделение всех четырех краев и удалим любую обводку, которая может быть применена.
Затем в нашем стиле таблицы назначьте поле Cell – Default style: General -> Body Rows
Наша матрица должна теперь выглядеть примерно так:
Добавление вертикальных штрихов
Наконец, давайте добавим несколько штрихов к столбцам контрольного списка, чтобы помочь глазу перемещаться по ним.для этого нам нужно настроить стиль Header – Vertical так, чтобы слева и справа были белые штрихи. Для этого откройте стиль ячейки и в разделе «Обводки и заливки» убедитесь, что у вас выделены только левая и правая штрихи и создайте сплошную белую обводку размером 1 пункт.
Затем нам нужно продублировать наш стиль Cell – Default и переименовать его в Cell – Vertical . Выполните те же шаги, что и выше, чтобы установить сплошную белую обводку толщиной 1pt слева и справа и назначить этот стиль их столбцам.Наша таблица теперь выглядит так:
Последние штрихи
Чтобы закончить матрицу, давайте просто добавим еще одну белую обводку внизу каждой строки таблицы. Выберите стиль Cell – Default и нарисуйте белый сплошной штрих толщиной 1pt внизу. Обратите внимание, как ваш стиль Cell – Vertical подхватывает изменение обводки от стиля по умолчанию? Как мило!
Мы закончили.


 Основные признаки и классификации компаний Признаки фирмы Основные концепции организации Контрактная концепция фирмы Стратегическая концепция… … Энциклопедия инвестора
Основные признаки и классификации компаний Признаки фирмы Основные концепции организации Контрактная концепция фирмы Стратегическая концепция… … Энциклопедия инвестора Белки являются главными… … Медицинская энциклопедия
Белки являются главными… … Медицинская энциклопедия