Умножение матриц NumPy: начните за 5 минут
NumPy — популярная библиотека Python, которая предлагает ряд мощных математических функций. Библиотека широко используется в количественных областях, таких как наука о данных, машинное обучение и глубокое обучение. Мы можем использовать NumPy для выполнения сложных математических вычислений, таких как умножение матриц.
Умножение матриц может помочь нам быстро приблизиться к очень сложным вычислениям. Он может помочь нам в теории сетей, линейных системах уравнений, моделировании населения и многом другом. В этом руководстве мы рассмотрим некоторые основные вычисления с умножением матриц NumPy.
Содержание
- Что такое NumPy?
- Установка и импорт NumPy
- Что такое матрица NumPy?
- Методы умножения матриц NumPy
- Скалярное умножение или скалярное произведение с numpy.dot
- Матричный продукт с numpy.matmul
- Поэлементное умножение матриц с помощью numpy.multiply
- Подведение итогов и следующие шаги
Что такое NumPy?
NumPy — это библиотека Python с открытым исходным кодом, которую мы можем использовать для выполнения высокоуровневых математических операций с массивами, матрицами, линейной алгеброй, анализом Фурье и т.
Д. Библиотека NumPy очень популярна в научных вычислениях, науках о данных и машинном обучении. NumPy совместим с популярными библиотеками данных, такими как pandas, matplotlib и Scikit-learn. Это намного быстрее, чем списки Python, потому что он объединяет более быстрые коды, такие как C и C ++, в Python. Он также разбивает наши задачи на несколько частей и обрабатывает каждую часть одновременно.
Установка и импорт NumPy
Прежде чем мы начнем, убедитесь, что у нас установлен NumPy. Если у вас уже есть Python, вы можете установить NumPy с помощью одной из следующих команд:
conda install numpy
или
pip install numpy
Чтобы импортировать NumPy в наш код Python, мы можем использовать следующую команду:
import numpy as np
Что такое матрица NumPy?
Матрица — это двумерный массив. Каждый элемент в массиве имеет два индекса. Давайте посмотрим на пример в NumPy:
import numpy as np
A = [[6, 7],
[8, 9]]
print(np.
array(A) [0,0])
array(A) [0,0])В приведенном выше коде, мы имеем матрицу A [[6, 7], [8, 9]]. Мы запрашиваем элемент, указанный в (0,0), и наш результат возвращается 6. Когда мы хотим определить форму нашей матрицы, мы используем количество строк по количеству столбцов. Это означает, что матрица A имеет форму 2×2.
Теперь давайте взглянем на несколько различных методов умножения матриц NumPy.
Методы умножения матриц NumPy
Есть три основных способа выполнить умножение матрицы NumPy:
- np.dot(array a, array b): возвращает скалярное произведение или скалярное произведение двух массивов
- np.matmul(array a, array b): возвращает матричное произведение двух массивов
- np.multiply(array a, array b): возвращает поэлементное матричное умножение двух массивов
Давайте подробнее рассмотрим каждый из трех методов:
Скалярное умножение или скалярное произведение с numpy.dot
Скалярное умножение — это простая форма умножения матриц, это просто число, как 1, 2или 3.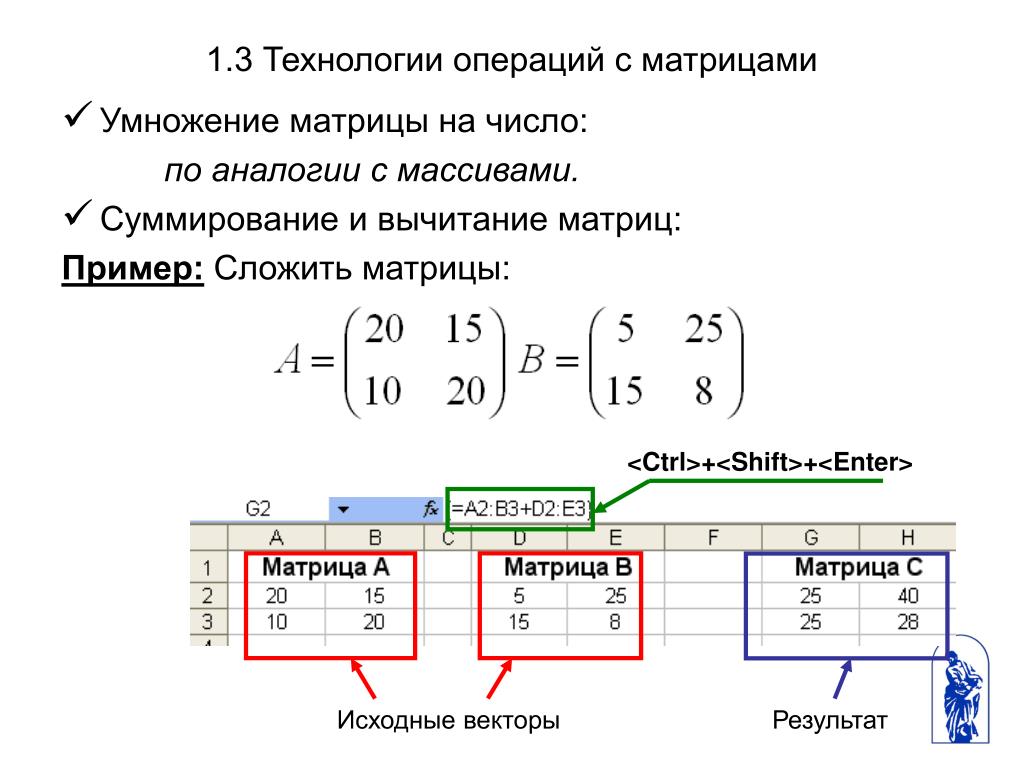
При скалярном умножении мы умножаем скаляр на матрицу. Каждый элемент в матрице умножается на скаляр, в результате чего выходные данные имеют ту же форму, что и исходная матрица.
При скалярном умножении порядок не имеет значения. Мы получим один и тот же результат независимо от того, умножаем ли мы скаляр на матрицу или матрицу на скаляр.
Давайте посмотрим на пример:
import numpy as np
A = 5
B = [[6, 7],
[8, 9]]
print(np.dot(A,B))
Теперь давайте умножим двумерную матрицу на другую двумерную матрицу. При умножении двух матриц порядок имеет значение. Это означает, что матрица A, умноженная на матрицу B, не то же самое, что матрица B, умноженная на матрицу A.
Прежде чем мы начнем, давайте посмотрим на визуальное представление того, как выполняется умножение.
import numpy as np
A = [[6, 7],
[8, 9]]
B = [[1, 3],
[5, 7]]
print(np.dot(A,B))
print(«———-«)
print(np.
dot(B,A))Примечание. Важно отметить, что мы можем перемножить две матрицы только в том случае, если количество столбцов в первой матрице равно количеству строк во второй матрице.
Матричный продукт с numpy.matmul
matmul()Функция дает нам матрицу произведение двух 2-й массивов. С помощью этого метода мы не можем использовать скалярные значения для нашего ввода. Если один из наших аргументов представляет собой одномерный массив, функция преобразует его в матрицу, добавляя 1 к его измерению. Он удаляется после завершения умножения.
Если один из наших аргументов больше 2-d, функция рассматривает его как стек матриц в последних двух индексах. Этот matmul()метод отлично подходит для случаев, когда мы не уверены в размерах наших матриц.
Давайте посмотрим на несколько примеров:
Умножение двумерного массива на другой двумерный массив
import numpy as np
A = [[2, 4],
[6, 8]]
B = [[1, 3],
[5, 7]]
print(np.
matmul(A,B))Умножение двумерного массива на одномерный массив
import numpy as np
A = [[5, 0],
[0, 5]]
B = [5, 2]
print(np.matmul(A,B))
Один массив с размерами больше 2-х
import numpy as np
A = np.arange(8).reshape(2, 2, 2)
B = np.arange(4).reshape(2, 2)
print(np.matmul(A,B))
Поэлементное умножение матриц с помощью numpy.multiply
numpy.multiply()Метод принимает две матрицы в качестве входных данных и выполняет поэлементное умножение на них. Поэлементное умножение, или произведение Адамара, умножает каждый элемент первой матрицы на эквивалентный элемент во второй матрице. При использовании этого метода обе матрицы должны иметь одинаковые размеры.
Давайте посмотрим на пример:
import numpy as np
A = np.array([[1, 3, 5, 7, 9], [2, 4, 6, 8, 10]])
B = np.array([[1, 2, 3, 4, 5], [5, 4, 3, 2, 1]])
print(np.
multiply(A,B))Мы можем передать в numpy.multiply()метод определенные строки, столбцы или подматрицы. Размеры строк, столбцов или подматриц, которые мы передаем в качестве наших операндов, должны быть одинаковыми. Давайте посмотрим на пример:
import numpy as np
A = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]])
B = np.array([[11, 12, 13, 14, 15], [16, 17, 18, 19, 20]])
print(np.multiply(A[ 0,:], B[ 1,: ]))
print(«———-«)
print(np.multiply(A[ 1,:], B[ 0,:]))
Подведение итогов и следующие шаги
Поздравляем с вашими первыми шагами в умножении матриц NumPy! Это сложная, но важная часть линейной алгебры. Это помогает нам лучше понять различные аспекты науки о данных, машинного обучения, глубокого обучения и других распространенных областей. Еще многое предстоит узнать о NumPy и матрицах. Вот некоторые рекомендуемые темы для обсуждения:
- Транспонирование матрицы NumPy
- Массивы NumPy (ndarray)
- NumPy векторизация
Понять матричное умножение – Русские Блоги
Большинство людей прошли курс «линейной алгебры» в средней школе или в младших классах колледжа.
Этот курс фактически представляет собой обучающую матрицу.
Когда я впервые узнал, это было довольно просто: добавление матриц – это просто сложение чисел в одной позиции.
Матричное вычитание аналогично.
Умножение матрицы на константу означает, что все позиции умножаются на это число.
Однако, когда матрица умножается на матрицу, все иначе.
Как рассчитывается этот результат?
Учебник сообщает вам, что правило расчета состоит в том, что каждое число (2 и 1) в первой строке первой матрицы умножается на число (1 и 1) в первом столбце второй матрицы, а затем складываются продукты. (2 x 1 + 1 x 1), получите значение 3 в верхнем левом углу матрицы результатов.
Другими словами, значение на пересечении m-й строки и n-го столбца результирующей матрицы равно сумме произведения каждого значения в соответствующей позиции в m-й строке первой матрицы и n-м столбце второй матрицы.
Как могло быть такое странное правило?
Я никогда не понимал смысла этого правила, ведущего к курсу «Линейной алгебры».
Когда я был аспирантом, я обнаружил, что линейная алгебра является основой векторных вычислений, а многие важные математические модели используют векторные вычисления, поэтому я не могу создавать сложные модели. Это всегда меня немного расстраивало.
Несколько дней назад, вдохновленный статьей, я наконец понял, что такое умножение матриц. Ключ – одно предложение, суть матрицы – линейное уравнение, и два имеют взаимно однозначное соответствие. С точки зрения линейных уравнений нетрудно понять умножение матриц.
Ниже приводится набор линейных уравнений.
Первоначальная цель матрицы заключалась в том, чтобы предоставить сокращенную форму для системы линейных уравнений.
Честно говоря, из вышесказанного уже видны правила умножения матриц: сумма 2 и 1 в первой строке матрицы коэффициентов и произведение x и y равно 3. Однако это не строгое доказательство, это просто правило записи для преобразования линейного уравнения в матрицу.
Следующее – строгое доказательство.
Есть три набора неизвестных x, y и t. Связь между x и y следующая.
Связь между x и t следующая.
С помощью этих двух наборов уравнений мы можем найти связь между y и t. С точки зрения матрицы очевидно, что вам нужно только подставить вторую матрицу в первую матрицу.
С точки зрения уравнения, вторую систему уравнений также можно подставить в первую систему уравнений.
Приведенные выше уравнения можно представить в следующей форме.
При сравнении последнего матричного уравнения с предыдущим матричным уравнением будет получено следующее соотношение.
Таким образом, правила вычисления матричного умножения доказаны.
————
Редактировать ∑Pluto
Источник: блог Жуань Ифэна
Более захватывающим:
☞Анекдоты о теореме Тейлора
☞Цю Чэнтун: к разговору о дифференциальной геометрии
☞Как Лейбниц пришел к исчислению? (Один)
☞Физический смысл линейной корреляции и ранга
☞Как вы думаете, какая формула самая уродливая в истории математики?
☞Дао Чжэсюань о том, что такое хорошая математика
☞Тянь Юаньдун: Использование математики (Часть 2)
☞Вы никогда не думали, что математик такой мошенник, который жестоко докажет, что не согласен.
☞Пять лучших докторских диссертаций в мире
☞Какие совпадения в математике заставляют людей сиять?
☞Достоинства алгоритма! У дипломированного профессора Цинхуа была украдена машина в США, и полиция не смогла ничего сделать, чтобы вернуть ее с помощью «жадного алгоритма».
☞Странные статьи по академической истории: как с помощью математики поймать льва
☞Размышление профессора НТУ: самый тяжелый урок, который мы не преподали студентам
☞Пособие для выпускников Технологического института Массачусетса (MIT) – Как стать выпускником
☞ Поделитесь математикой, здравым смыслом и удачей – лекция, прочитанная инвестиционным мастером Джеймсом Симмонсом в Массачусетском технологическом институте в 2010 году.
Красота математики алгоритмов Публичный аккаунт WeChat приветствует пожертвования
Рукописи связаны с математикой, физикой, алгоритмами, компьютерами, программированием и другими смежными областями. После принятия мы предложим вознаграждение.
Электронная почта для участия: [email protected]
Интеллектуальная рекомендация
Несколько вопросов о справочных указателях 2018-06-15
Указатель по умолчанию под дугой является сильная ссылка: __ SICK & __ слабое и __ небезопасное сравнение ссылка:__strong & __weak & __ Unsafe_unreted…
Pytorch использует больше средств GPU
Использование нескольких графических процессоров в Pytorch требует инициализации заявленной модели после Декларационной модели, такой как: Затем, после запуска файла Python The Model Training, все GPU…
Как долго это так долго? Как логистические роботы не побежали на тысячи домохозяйств?
В заключенных ЦЕС Группа «Немецкая континентальная группа демонстрирует свои последние логистические роботы» – собака доставки пакетов Anymal. Для этого результат Круг медиа и технологичес…
Примечания к практическому изучению машинного обучения — алгоритм априори
Анализ ассоциаций – это задача поиска интересных взаимосвязей в крупномасштабных наборах данных.
Spring (4) Фреймворк заключительной главы третьей интеграции
Spring_day04 (интеграция трех основных фреймворков) 1. Три фреймворка (принцип интеграции) Бэкэнд веб-проекта разделен на три слоя. 2. Направляющий пакет (42) hibernate: hibernate/lib/required hiberna…
Вам также может понравиться
Первое понимание юнит-теста серии Python
Среду модульного тестирования unittest можно применять не только для модульного тестирования, но и для разработки и выполнения веб-автоматизированных тестовых примеров.Конструктура тестирования может …
Принцип непоследовательной загрузки изображений в процессе загрузки изображений в виде списка.
// Основная раскладка интерфейса // Вложенный макет // Основная функция MainActivity // Создать новый класс бина // Создать адаптер // Инструменты…
SpringBoot + mysql + развертывание проекта docker
Подготовка доменного имени и сервера Alibaba Cloud доменное имя: Вы можете приобрести необходимые доменные имена у основных поставщиков облачных услуг.
Я приобрел доменное имя Alibaba Cloud. В облако …
Строить IPA-сервер с нуля. Реализация LDAP + Kerberos домена Проверка (Open Firewall, Command Version)
Рисунок метод конфигурации, пожалуйста, обратитесь к статье 1, экспериментальная среда: Физика хост-хост две виртуальные машины. Физический IP хост: 192.168.9.6/24 GW: 192.168.9.254 DNS: 8.8.8.8 Вирту…
Вызов клиента Центра конфигурации Apollo
Вызов клиента Центра конфигурации Apollo введение Центр конфигурации Создать проект Опубликовать пространство имен Создайте файл конфигурации локального кеша код проекта springboot Предыдущая запись: …
Матричное умножение. Медленное достижение мифической цели
В недавней работе был установлен новый рекорд скорости по умножению двух матриц. Она также знаменует и конец эпохи для метода, который ученые применяли для исследований на протяжении десятилетий.
Математики стремятся к достижению мифической цели — второй степени (exponent two), то есть к умножению пары матриц n х n всего за n2 шагов.
Исследователи подбираются все ближе к своей цели, но получится ли у них когда-нибудь достичь ее?
Для специалистов в области Computer Science и математиков сама идея о «второй степени» связана с представлениями о совершенном мире.
«Трудно разграничить научное мышление и беспочвенные мечтания», — признается Крис Уманс из Калифорнийского технологического института. «Я хочу, чтобы степень была равна двум, потому что это красиво».
С точки зрения необходимого количества шагов «вторая степень» — это идеальная скорость выполнения одной из самых фундаментальных математических операций — матричного умножения. Если вторая степень достижима, то матричное умножение получится выполнять максимально быстро, насколько это физически возможно. Если это не так, то мы застряли в мире, который не соответствует нашим мечтам.
Матрицы представляют собой массивы чисел. Когда две матрицы согласованы (число столбцов в первом сомножителе равно числу строк во втором), их можно перемножить, чтобы получить третью.
Поэтому наименьшее возможное количество шагов для умножения пар матриц это n2, то есть количество шагов, необходимое просто для записи ответа. Отсюда и название «вторая степень».
И хотя никто точно не знает, можно ли этого достичь, исследователи продолжают продвигаться в этом направлении.
Статья, опубликованная в октябре, подбирается к цели еще ближе и описывает самый быстрый на данный момент метод умножения двух матриц. Результат, который получили Джош Алман, докторант Гарвардского университета, и Вирджиния Василевска Уильямс из Массачусетского технологического института, уменьшает степень предыдущего лучшего показателя примерно на одну стотысячную. Это действительно большое достижение в данной области, добытое кропотливым трудом.
Чтобы получше разобраться в этом процессе и понять, как его можно усовершенствовать, давайте начнем с пары матриц 2 х 2, A и B. При вычислении каждого элемента их произведения вы используете соответствующую строку из A и соответствующий столбец из B. Чтобы получить верхний правый элемент, умножьте первое число в первой строке A на первое число во втором столбце B, затем умножьте второе число в первой строке A на второе число во втором столбце B и сложите эти два произведения.
Самуэль Веласко / Quanta Magazine
Эта операция известна как получение «скалярного произведения» строки со столбцом (иногда называется «внутренним произведением»). Чтобы вычислить другие элементы в произведении матриц, повторите процедуру с соответствующими строками и столбцами.
В целом, классический метод умножения матриц 2 х 2 состоит из восьми умножений и нескольких сложений. Как правило, этот способ умножения двух матриц размера n х n требует n
С увеличением размера матриц количество умножений, необходимых для нахождения их произведения, растет намного быстрее, чем количество сложений.
Чтобы найти произведение матриц 2 х 2 требуется всего восемь промежуточных умножений, а чтобы найти произведение матриц 4 х 4 их требуется уже 64. Однако количество сложений, необходимых для получения суммы этих матриц, не так значительно отличается. Обычно количество сложений равно количеству элементов в матрице, то есть четыре для матриц 2 х 2 и 16 для матриц 4 х 4. Эта разница между сложением и умножением позволяет понять, почему исследователи измеряют скорость умножения матриц исключительно с точки зрения количества требуемых умножений.
«Умножения — это наше всё, — утверждает Уманс, — Показатель степени в итоге полностью зависит только от количества умножений. Сложения в некотором смысле исчезают».
На протяжении веков люди считали, что n3 — это самый быстрый способ умножения матриц. По имеющимся сведениям, в 1969 году Фолькер Штрассен намеревался доказать, что невозможно умножить матрицы 2 х 2, используя менее восьми умножений. Видимо, он все-таки не смог найти доказательства, а через некоторое время и понял почему: на самом деле, существует способ сделать это с помощью семи умножений!
Штрассен придумал сложный набор соотношений, которые позволили заменить одно из этих восьми умножений 14 дополнительными сложениями.
Может показаться, что разница совершенно незначительна, но она оправдывает себя, так как умножение вносит больший вклад, чем сложение. Найдя способ избавиться от одного умножения для маленьких матриц 2 х 2, Штрассен открыл возможность, которую он мог использовать при умножении бOльших матриц.
«Это крошечное изменение приводит к огромным улучшениям в работе с большими матрицами», — говорит Уильямс.
Вирджиния Василевска Уильямс из Массачусетского технологического института и Джош Алман из Гарвардского университета открыли самый быстрый способ перемножения двух матриц за n2.3728596 шагов. Джаред Чарни; Ричард Т.К. Хоук
Предположим, вы хотите перемножить пару матриц 8 х 8. Один из способов сделать это — разбить каждую большую матрицу на четыре матрицы размером 4 х 4 так, чтобы каждая имела по четыре элемента. Поскольку элементы матрицы также могут являться матрицами, вы можете считать исходные матрицы парой матриц 2 х 2, каждый из четырех элементов которых сам по себе является матрицей 4 х 4.
Смысл этого многократного разбиения больших матриц на более мелкие заключается в том, что можно снова и снова применять алгоритм Штрассена к меньшим матрицам и с помощью его метода сокращать количество шагов на каждом этапе. В целом алгоритм Штрассена увеличил скорость умножения матриц с n3 до n2.81 мультипликативных шагов.
Следующий важный шаг в развитии идеи произошел в конце 1970-х, когда появился принципиально новый подход к решению этой задачи. Он подразумевает перевод матричного умножения в другую вычислительную задачу линейной алгебры с использованием объектов, называемых тензорами. Тензоры, используемые в этой задаче, представляют собой трехмерные массивы чисел, состоящие из множества различных частей, каждая из которых выглядит как небольшая задача на умножение матриц.
Умножение матриц и эта задача, связанная с тензорами, в определенном смысле эквивалентны друг другу, но для решения последней исследователи уже имели более быстрые процедуры.
Таким образом, перед ними встала задача определить «обменный курс» между ними: Матрицы какого размера можно перемножить при тех же вычислительных затратах, которые требуются для решения тензорной задачи?
«Это очень распространенная в теоретической информатике концепция: преобразовывать задачи и проводить аналогию между ними, чтобы показать, что они одинаково простые или сложные», — сказал Алман.
В 1981 году Арнольд Шёнхаге использовал этот подход, чтобы доказать, что умножение матриц возможно выполнить за n2.522 шагов. Позднее Штрассен назвал этот подход «лазерным методом» (laser method).
За последние несколько десятилетий каждое улучшение в процессе умножения матриц происходило за счет усовершенствования лазерного метода, поскольку исследователи находили все более эффективные способы трансформации задачи. В своем новом доказательстве Алман и Уильямс стирают различие между 2 задачами и показывают, что уменьшить число умножений возможно.
«В целом Джош и Вирджиния нашли способ применить машинные вычисления в рамках лазерного метода и получили лучшие на настоящий момент результаты», — сказал Генри Кон из Microsoft Research.
В их статье теоретическое ограничение скорости умножения матриц улучшено до n2.3728596.
Также благодаря этому исследованию Уильямс может вернуть себе корону в области матричного умножения, которую она по праву получила в 2012 году (n2.372873), а затем уступила в 2014 году Франсуа Ле Галлю (n2.3728639).
Но, несмотря на все эти гонки и победы, становится ясно, что в случае с этим подходом действует закон убывающей доходности, или убывающей отдачи. Скорее всего, усовершенствование Алмана и Уильямс почти полностью исчерпало возможности лазерного метода, но так и не позволило достичь конечной теоретической цели.
«Маловероятно, что получится приблизиться ко второй степени, используя это семейство методов», — отметил Уманс.
Для этого потребуется открытие новых методов и стойкая вера в то, что это вообще возможно.
Уильямс вспоминает один из разговоров со Штрассеном об этом: «Я спросила его, считает ли он, что возможно получить вторую степень для матричного умножения, и он ответил: «Нет, нет, нет, никогда!».
ИИ DeepMind находит новый способ умножения чисел и ускорения работы компьютеров
Мэтью Спаркс
Умножение чисел — фундаментальная задача для компьютеров
Дмитрий Викарчук/Shutterstock
способ умножения чисел, первый такой прогресс за более чем 50 лет. Находка может повысить скорость некоторых вычислений до 20%, поскольку целый ряд программного обеспечения полагается на выполнение задачи в больших масштабах.
Умножение матриц — когда две сетки чисел перемножаются вместе — является фундаментальной вычислительной задачей, в той или иной степени используемой практически во всех программах, но особенно в графике, искусственном интеллекте и научном моделировании. Даже небольшое улучшение эффективности этих алгоритмов может привести к значительному приросту производительности или значительной экономии энергии.
Самое большое число в мире Агниджо Банерджи из New Scientist Прямой эфир в октябре этого года
На протяжении веков считалось, что наиболее эффективный способ умножения матриц будет пропорционален количеству умножаемых элементов, а это означает, что задача становится пропорционально сложнее для все больших и больших матриц.
Но математик Фолькер Штрассен в 1969 году доказал, что умножение матрицы из двух строк из двух чисел на другую матрицу того же размера не обязательно требует восьми умножений и что с помощью хитрого трюка ее можно уменьшить. до семи. Этот подход, называемый алгоритмом Штрассена, требует некоторого дополнительного сложения, но это приемлемо, поскольку сложения в компьютере занимают гораздо меньше времени, чем умножения.
Алгоритм считается наиболее эффективным подходом к большинству размеров матриц уже более 50 лет, хотя были обнаружены некоторые небольшие улучшения, которые нелегко адаптировать к компьютерному коду.
Но ИИ DeepMind теперь обнаружил более быструю технику, которая отлично работает на современном оборудовании. Новый ИИ компании, AlphaTensor, начал работу, не зная никаких решений, и столкнулся с проблемой создания работающего алгоритма, который выполнял бы задачу с минимальным количеством шагов.
Он нашел алгоритм умножения двух матриц из четырех строк по четыре числа, используя всего 47 умножений, что превосходит 49 умножений Штрассена. Он также разработал улучшенные методы умножения матриц других размеров, всего 70.
AlphaTensor обнаружила тысячи функциональных алгоритмов для каждого размера матрицы, в том числе 14 000 только для матриц 4×4. Но только небольшое меньшинство было лучше, чем состояние искусства. Исследование основано на AlphaZero, игровой модели DeepMind, на разработку которой ушло два года.
Подробнее: ИИ DeepMind, сворачивающий белки, решает самую большую проблему биологии
Хусейн Фавзи из DeepMind говорит, что результаты математически обоснованы, но далеки от интуитивного понимания человеком.
«Мы действительно не знаем, почему система придумала это, по сути», — говорит он. «Почему это лучший способ умножения матриц? Неясно.”
«Каким-то образом нейронные сети интуитивно понимают, что выглядит хорошо, а что плохо. Честно говоря, я не могу вам точно сказать, как это работает. Я думаю, что здесь предстоит проделать некоторую теоретическую работу о том, как именно глубокое обучение справляется с такими вещами», — говорит Фаузи.
DeepMind обнаружил, что алгоритмы могут повысить скорость вычислений на 10–20 % на определенном оборудовании, таком как графический процессор Nvidia V100 (GPU) и тензорный процессор Google (TPU) v2, но нет гарантии, что эти прирост также будет заметен на обычных устройствах, таких как смартфон или ноутбук.
Джеймс Найт из Университета Сассекса, Великобритания, говорит, что ряд программ, работающих на суперкомпьютерах и мощном оборудовании, таких как исследования ИИ и моделирование погоды, по сути являются крупномасштабным умножением матриц.
«Если бы такой подход действительно был там реализован, то это могло бы стать своего рода универсальным ускорением», — говорит он. «Если бы Nvidia реализовала это в своей библиотеке CUDA [инструмент, который позволяет графическим процессорам работать вместе], я бы сказал, что это снизит некоторый процент большинства рабочих нагрузок глубокого обучения».
Читать далее: ИИ переводит математические задачи в код, чтобы упростить их решение
Одед Лахиш из Биркбека, Лондонский университет, говорит, что новые алгоритмы могут повысить эффективность широкого спектра программного обеспечения, потому что умножение матриц является очень распространенной проблемой, и, вероятно, последуют другие алгоритмы.
«Я полагаю, что мы увидим результаты, сгенерированные ИИ, для других задач аналогичного характера, хотя и редко таких центральных, как умножение матриц.
У такой технологии есть существенная мотивация, поскольку меньшее количество операций в алгоритме означает не только более быстрые результаты, но и меньше затрат энергии», — говорит он. Если задачу можно выполнить немного эффективнее, то ее можно выполнить на менее мощном, менее энергоемком оборудовании или на том же оборудовании за меньшее время и с меньшим потреблением энергии.
Но успехи DeepMind не обязательно означают, что программисты-люди остались без работы. «Должны ли программисты беспокоиться? Может быть, в далеком будущем. Автоматическая оптимизация применялась в индустрии проектирования микрочипов на протяжении десятилетий, и это еще один важный инструмент в арсенале программиста», — говорит Лахиш.
Ссылка на журнал: Nature , DOI: 10.1038/s41586-022-05172-4
Дополнительные сведения по этим темам:
- математика
- Глубокий разум
- ИИ
Игровой искусственный интеллект DeepMind только что побил 50-летний рекорд в компьютерных науках
Искусственный интеллект
Новая версия AlphaZero открыла более быстрый способ матричного умножения — ключевой вычислительной проблемы, затрагивающей тысячи повседневных компьютеров задачи.
Автор:
- Уилл Дуглас Страница Heavenarchive
5 октября 2022 г.
Ms Tech | EnvatoDeepMind использовала свою настольную игру AI AlphaZero, чтобы найти более быстрый способ решения фундаментальной математической задачи в области компьютерных наук, побив рекорд, который стоял более 50 лет.
Задача, умножение матриц, является ключевым типом вычислений, лежащим в основе многих различных приложений, от отображения изображений на экране до моделирования сложной физики. Это также имеет фундаментальное значение для самого машинного обучения. Ускорение этого вычисления могло бы оказать большое влияние на тысячи повседневных компьютерных задач, сократив расходы и сэкономив энергию.
«Это действительно удивительный результат», — говорит Франсуа Ле Галль, математик из Университета Нагоя в Японии, который не участвовал в работе. «Матричное умножение используется повсеместно в технике», — говорит он.
«Все, что вы хотите решить численно, вы обычно используете матрицы».
Несмотря на повсеместное распространение вычислений, они до сих пор недостаточно изучены. Матрица — это просто сетка чисел, представляющая все, что вы хотите. Умножение двух матриц вместе обычно включает умножение строк одной на столбцы другой. Базовая техника решения задачи преподается в средней школе. «Это похоже на азбуку вычислений», — говорит Пушмит Кохли, руководитель группы искусственного интеллекта DeepMind для науки.
Но все усложняется, когда вы пытаетесь найти более быстрый метод. «Никто не знает лучшего алгоритма для ее решения», — говорит Ле Галл. «Это одна из самых больших открытых проблем в информатике».
Это потому, что существует больше способов перемножения двух матриц, чем атомов во Вселенной (10 в степени 33, для некоторых случаев, которые изучали исследователи). «Количество возможных действий почти бесконечно», — говорит Томас Хьюберт, инженер DeepMind.
Хитрость заключалась в том, чтобы превратить задачу в своеобразную трехмерную настольную игру под названием TensorGame.
Доска представляет собой задачу на умножение, которую нужно решить, и каждый ход представляет собой следующий шаг в решении этой задачи. Таким образом, серия ходов, сделанных в игре, представляет собой алгоритм.
Исследователи обучили новую версию AlphaZero, названную AlphaTensor, играть в эту игру. Вместо того, чтобы изучать лучшие серии ходов в го или шахматах, AlphaTensor изучил лучшие серии шагов при умножении матриц. Его награждали за победу в игре за минимальное количество ходов.
«Мы превратили это в игру, наш любимый вид фреймворка, — говорит Хьюберт, один из ведущих исследователей AlphaZero.
Исследователи описывают свою работу в статье, опубликованной сегодня в журнале Nature. Главный результат заключается в том, что AlphaTensor открыл способ умножения двух матриц четыре на четыре, который работает быстрее, чем метод, разработанный в 1969 году немецким математиком Фолькером Штрассеном, который с тех пор никто не мог улучшить. Базовый метод средней школы состоит из 64 шагов; Дубли Штрассена 49шаги.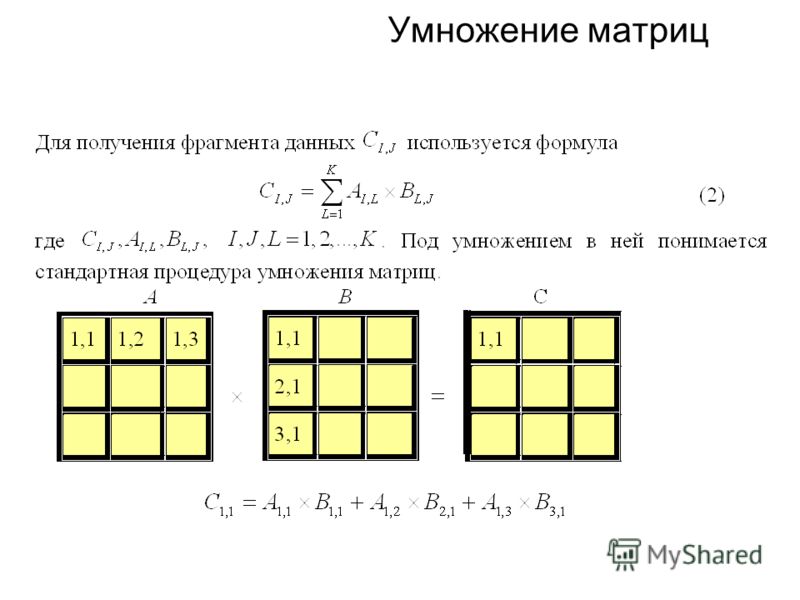
AlphaTensor нашел способ сделать это за 47 шагов.
В целом, AlphaTensor превосходит лучшие существующие алгоритмы для более чем 70 различных размеров матриц. Он сократил количество шагов, необходимых для умножения двух матриц 9 на 9, с 511 до 498, а количество шагов, необходимых для умножения двух матриц 11 на 11, с 919 до 896. Во многих других случаях AlphaTensor заново открыл лучший из существующих алгоритмов. .
Исследователи были удивлены тем, сколько различных правильных алгоритмов AlphaTensor нашел для каждого размера матрицы. «Удивительно, что существует по меньшей мере 14 000 способов умножения матриц четыре на четыре», — говорит Хусейн Фаузи, научный сотрудник DeepMind.
После поиска самых быстрых алгоритмов в теории команда DeepMind захотела узнать, какие из них окажутся быстрыми на практике. Разные алгоритмы могут лучше работать на разном оборудовании, потому что компьютерные чипы часто разрабатываются для определенных типов вычислений. Команда DeepMind использовала AlphaTensor для поиска алгоритмов, адаптированных для графического процессора Nvidia V100 и процессоров Google TPU, двух наиболее распространенных чипов, используемых для обучения нейронных сетей.
Алгоритмы, которые они нашли, были на 10-20% быстрее при умножении матриц, чем те, которые обычно используются с этими чипами.
Вирджиния Уильямс, специалист по информатике из Лаборатории компьютерных наук и искусственного интеллекта Массачусетского технологического института, воодушевлена результатами. Она отмечает, что в течение некоторого времени люди использовали вычислительные подходы для поиска новых алгоритмов умножения матриц, и многие из существующих самых быстрых алгоритмов были разработаны таким образом. Но никто не смог улучшить долгосрочные результаты, как Штрассен.
«Этот новый метод делает что-то совершенно отличное от того, что делали другие», — говорит Уильямс. «Было бы неплохо выяснить, действительно ли этот новый метод включает в себя все предыдущие, или вы можете объединить их и получить что-то еще лучше».
Теперь DeepMind планирует использовать AlphaTensor для поиска других типов алгоритмов. «Это новый способ изучения информатики, — говорит Кохли.
Уилл Дуглас Хэвен
Глубокое погружение
Искусственный интеллект
Что GPT-3 «знает» обо мне?
Крупноязыковые модели обучаются на массивах персональных данных, собранных в Интернете. Так что я хотел знать: Что это имеет на меня?
Оставайтесь на связи
Иллюстрация Роуз Вонг
Откройте для себя специальные предложения, главные новости, предстоящие события и многое другое.
Введите адрес электронной почты
Политика конфиденциальностиСпасибо за отправку вашего электронного письма!
Ознакомьтесь с другими информационными бюллетенями
Похоже, что-то пошло не так.
У нас возникли проблемы с сохранением ваших настроек.
Попробуйте обновить эту страницу и обновить их один раз
больше времени. Если вы продолжаете получать это сообщение,
свяжитесь с нами по адресу
customer-service@technologyreview.
com со списком информационных бюллетеней, которые вы хотели бы получать.
Открытие новых алгоритмов с помощью AlphaTensor
Первое расширение AlphaZero для математики открывает новые возможности для исследований
Алгоритмы помогали математикам выполнять фундаментальные операции на протяжении тысячелетий. Древние египтяне создали алгоритм умножения двух чисел без использования таблицы умножения, а греческий математик Евклид описал алгоритм вычисления наибольшего общего делителя, который используется до сих пор.
Во времена Золотого века ислама персидский математик Мухаммад ибн Муса аль-Хорезми разработал новые алгоритмы для решения линейных и квадратных уравнений. Фактически, имя аль-Хорезми, переведенное на латынь как Algoritmi , привело к появлению термина алгоритм. Но, несмотря на знакомство с алгоритмами сегодня, которые используются во всем обществе от школьной алгебры до передовых научных исследований, процесс открытия новых алгоритмов невероятно сложен и является примером удивительных мыслительных способностей человеческого разума.
В нашей статье, опубликованной сегодня в журнале Nature , , мы представляем AlphaTensor , первую систему искусственного интеллекта (ИИ) для обнаружения новых, эффективных и доказуемо правильных алгоритмов для фундаментальных задач, таких как умножение матриц. Это проливает свет на 50-летний открытый вопрос в математике о поиске самого быстрого способа умножения двух матриц.
Этот документ является ступенькой в миссии DeepMind по развитию науки и раскрытию наиболее фундаментальных проблем с использованием ИИ. Наша система AlphaTensor основана на AlphaZero, агенте, который продемонстрировал сверхчеловеческую производительность в настольных играх, таких как шахматы, го и сёги, и эта работа впервые показывает путь AlphaZero от игр до решения нерешенных математических задач.
Умножение матриц
Умножение матриц — одна из самых простых операций в алгебре, которую обычно преподают на уроках математики в средней школе. Но за пределами классной комнаты эта скромная математическая операция имеет огромное влияние в современном цифровом мире и повсеместно используется в современных вычислениях.
Эта операция используется для обработки изображений на смартфонах, распознавания речевых команд, создания графики для компьютерных игр, запуска симуляций для прогнозирования погоды, сжатия данных и видео для публикации в Интернете и многого другого. Компании по всему миру тратят много времени и денег на разработку вычислительного оборудования для эффективного умножения матриц. Таким образом, даже незначительные улучшения эффективности матричного умножения могут иметь широкое значение.
На протяжении веков математики считали, что стандартный алгоритм умножения матриц является наилучшим с точки зрения эффективности. Но в 1969 году немецкий математик Фолькер Штрассен шокировал математическое сообщество, показав, что существуют более совершенные алгоритмы.
Стандартный алгоритм по сравнению с алгоритмом Штрассена, который использует на одно скалярное умножение меньше (7 вместо 8) для умножения матриц 2×2. Умножения имеют гораздо большее значение, чем сложения для общей эффективности.
Изучая очень маленькие матрицы (размер 2×2), он обнаружил оригинальный способ объединения элементов матриц для получения более быстрого алгоритма. Несмотря на десятилетия исследований, последовавших за прорывом Штрассена, более масштабные версии этой проблемы остались нерешенными — вплоть до того, что неизвестно, насколько эффективно можно перемножать две матрицы размером всего 3×3.
В нашей статье мы рассмотрели, как современные методы искусственного интеллекта могут способствовать автоматическому обнаружению новых алгоритмов умножения матриц. Основываясь на прогрессе человеческой интуиции, AlphaTensor открыл алгоритмы, которые более эффективны, чем современные, для многих размеров матриц. Наши алгоритмы, разработанные искусственным интеллектом, превосходят алгоритмы, разработанные человеком, что является важным шагом вперед в области алгоритмических открытий.
Процесс и прогресс автоматизации алгоритмического поиска
Во-первых, мы превратили задачу поиска эффективных алгоритмов умножения матриц в игру для одного игрока.
В этой игре доска представляет собой трехмерный тензор (массив чисел), отражающий, насколько далек от правильного текущий алгоритм. С помощью набора разрешенных ходов, соответствующих инструкциям алгоритма, игрок пытается изменить тензор и обнулить его элементы. Когда игроку удается это сделать, это приводит к доказуемо правильному алгоритму умножения матриц для любой пары матриц, а его эффективность определяется количеством шагов, предпринятых для обнуления тензора.
Эта игра невероятно сложна — количество возможных алгоритмов для рассмотрения намного превышает количество атомов во Вселенной, даже для небольших случаев матричного умножения. По сравнению с игрой в го, которая десятилетиями оставалась проблемой для ИИ, количество возможных ходов на каждом шаге нашей игры на 30 порядков больше (выше 10 33 для одной из рассматриваемых нами настроек).
По сути, чтобы хорошо играть в эту игру, нужно найти мельчайшую иголку в гигантском стоге сена возможностей. Чтобы решить проблемы этой области, которая значительно отличается от традиционных игр, мы разработали несколько важных компонентов, включая новую архитектуру нейронной сети, которая включает в себя индуктивные смещения для конкретных задач, процедуру для создания полезных синтетических данных и рецепт использования симметрии проблема.
Затем мы обучили агента AlphaTensor, используя обучение с подкреплением, играть в игру, начав без каких-либо знаний о существующих алгоритмах умножения матриц. Благодаря обучению AlphaTensor со временем постепенно совершенствуется, заново открывая исторические алгоритмы быстрого умножения матриц, такие как алгоритм Штрассена, в конечном итоге превосходя область человеческой интуиции и открывая алгоритмы быстрее, чем были известны ранее.
Однопользовательская игра от AlphaTensor, цель которой — найти правильный алгоритм умножения матриц. Состояние игры представляет собой кубический массив чисел (показанный серым цветом для 0, синим для 1 и зеленым для -1), представляющим оставшуюся работу, которую необходимо выполнить. Например, если традиционный алгоритм, которому обучают в школе, умножает матрицу 4×5 на 5×5, используя 100 умножений, и это число было уменьшено до 80 благодаря человеческой изобретательности, AlphaTensor нашел алгоритмы, которые выполняют ту же операцию, используя всего 76 умножений.
Помимо этого примера, алгоритм AlphaTensor улучшает двухуровневый алгоритм Штрассена в конечном поле впервые с момента его открытия 50 лет назад. Эти алгоритмы умножения малых матриц можно использовать в качестве примитивов для умножения гораздо больших матриц произвольного размера.
Кроме того, AlphaTensor также обнаруживает разнообразный набор алгоритмов с самой современной сложностью — до тысяч алгоритмов умножения матриц для каждого размера, показывая, что пространство алгоритмов умножения матриц богаче, чем считалось ранее.
Алгоритмы в этом богатом пространстве имеют разные математические и практические свойства. Используя это разнообразие, мы адаптировали AlphaTensor специально для поиска алгоритмов, которые быстро работают на данном оборудовании, таком как графический процессор Nvidia V100 и Google TPU v2. Эти алгоритмы умножают большие матрицы на 10-20% быстрее, чем обычно используемые алгоритмы на том же оборудовании, что демонстрирует гибкость AlphaTensor в оптимизации произвольных целей.
Изучение влияния на будущие исследования и приложения
С математической точки зрения наши результаты могут направить дальнейшие исследования в области теории сложности, целью которых является определение самых быстрых алгоритмов для решения вычислительных задач. Исследуя пространство возможных алгоритмов более эффективно, чем предыдущие подходы, AlphaTensor помогает лучше понять богатство алгоритмов умножения матриц. Понимание этого пространства может открыть новые результаты для определения асимптотической сложности матричного умножения, одной из самых фундаментальных открытых проблем в информатике.
Поскольку умножение матриц является основным компонентом многих вычислительных задач, охватывающих компьютерную графику, цифровую связь, обучение нейронных сетей и научные вычисления, алгоритмы, открытые AlphaTensor, могут сделать вычисления в этих областях значительно более эффективными.
Гибкость AlphaTensor для рассмотрения любых целей может также стимулировать появление новых приложений для разработки алгоритмов, которые оптимизируют такие показатели, как потребление энергии и числовая стабильность, помогая предотвратить лавинообразное увеличение небольших ошибок округления в процессе работы алгоритма.
Хотя здесь мы сосредоточились на конкретной проблеме матричного умножения, мы надеемся, что наша статья вдохновит других на использование ИИ для руководства алгоритмическими открытиями для других фундаментальных вычислительных задач. Наше исследование также показывает, что AlphaZero — это мощный алгоритм, который может быть расширен далеко за пределы области традиционных игр для решения открытых математических задач. Опираясь на наши исследования, мы надеемся стимулировать большую работу — применение ИИ, чтобы помочь обществу решить некоторые из наиболее важных проблем в математике и других науках.
Примечания
Дополнительную информацию можно найти в репозитории AlphaTensor на GitHub.