Матричный метод и метод крамера: Решить систему линейных уравнений тремя методами: методом Крамера, методом обратной матрицы, методом Гаусса. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

5.2. Матричный метод решения систем линейных уравнений

Пусть дана система линейных уравнений снеизвестными:

где

Будем предполагать, что основная матрица невырожденная. Тогда, по теореме 3.1, существует обратная матрицаПомножив матричное уравнениена матрицуслева, воспользовавшись определением 3.2, а также утверждением 8) теоремы 1.1, получим формулу, на которой основан матричный метод решения систем линейных уравнений:

Замечание. Отметим, что матричный метод решения систем линейных уравнений в отличие от метода Гаусса имеет ограниченное применение: этим методом могут быть решены только такие системы линейных уравнений, у которых, во-первых, число неизвестных равно числу уравнений, а во-вторых, основная матрица невырожденная.

Пример. Решить систему линейных уравнений матричным методом.

Задана система трёх линейных уравнений с тремя неизвестными где

Основная матрица системы уравнений невырожденная, поскольку её определитель отличен от нуля:

Обратную матрицу составим одним из методов, описанных в пункте 3.

По формуле матричного метода решения систем линейных уравнений получим

5.3. Метод Крамера

Данный метод так же, как и матричный, применим только для систем линейных уравнений, у которых число неизвестных совпадает с числом уравнений. Метод Крамера основан на одноимённой теореме:

Теорема 5.2. Система линейных уравнений снеизвестными

основная матрица которой невырожденная, имеет единственное решение, которое может быть получено по формулам

где определитель матрицы, полученной из основной матрицысистемы уравнений заменой еёго столбца столбцом свободных членов.

Пример. Найдём решение системы линейных уравнений, рассмотренной в предыдущем примере, методом Крамера. Основная матрица системы уравнений невырожденная, поскольку Вычислим определители

По формулам, представленным в теореме 5.2, вычислим значения неизвестных:

6. Исследование систем линейных уравнений.

Базисное решение

Исследовать систему линейных уравнений – означает определить, какой является эта система – совместной или несовместной, и в случае её совместности выяснить, определённая эта система или неопределённая.

Условие совместности системы линейных уравнений даёт следующая теорема

Теорема 6.1 (Кронекера–Капелли).

Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу её расширенной матрицы:

Для совместной системы линейных уравнений вопрос о её определённости или неопределённости решается с применением следующих теорем.

Теорема 6.2. Если ранг основной матрицы совместной системы равен числу неизвестных, то система является определённой

Теорема 6.3. Если ранг основной матрицы совместной системы меньше числа неизвестных, то система является неопределённой.

Таким образом, из сформулированных теорем вытекает способ исследования систем линейных алгебраических уравнений. Пусть n – количество неизвестных, Тогда:

при система несовместна;
при система совместна, причём, если, система определённая; если же, система неопределённая.

Определение 6.1. Базисным решением неопределённой системы линейных уравнений называют такое её решение, в котором все свободные неизвестные равны нулю.

Пример. Исследовать систему линейных уравнений. В случае неопределённости системы найти её базисное решение.

Вычислим ранги основной и расширенной матрицданной системы уравнений, для чего приведём расширенную (а вместе с тем и основную) матрицу системы к ступенчатому виду:

Вторую строку матрицы сложим с её первой строкой, умноженной на третью строку – с первой строкой, умноженной наа четвёртую строку – с первой, умноженной наполучим матрицу

К третьей строке этой матрицы прибавим вторую строку, умноженную на а к четвёртой строке – первую, умноженную наВ результате получим матрицу

удаляя из которой третью и четвёртую строки получим ступенчатую матрицу

Таким образом, Следовательно, данная система линейных уравнений совместна, а поскольку величина ранга меньше числа неизвестных, система является неопределённой.Полученной в результате элементарных преобразований ступенчатой матрице соответствует система уравнений

Неизвестные иявляются главными, а неизвестныеисвободными. Придавая свободным неизвестным нулевые значения, получим базисное решение данной системы линейных уравнений:

НОУ ИНТУИТ | Лекция | Матричная запись системы. Метод Гаусса. Метод Крамера. Матричный способ

< Лекция 10 || Лекция 5: 12345

Аннотация: В лекции рассмотрено использование ранее изученных методов для поиска решений системы линейных уравнений

Ключевые слова: определитель, Алгебраическим дополнением, алгебраические, коэффициенты, равенство, свободными членами, определителем системы, переменная, бесконечное множество, вывод, множитель, коэффициентами системы, система линейных уравнений, обратный, матричная форма, матрица, детерминант, совместность, расширенная матрица, выражение

Правило Крамера

Основные задачи изучения системы (3.1), “лекции 3” :

Выяснить, является ли система (3.1) совместной или несовместной.
Если система (3.1) совместна, то выяснить, является ли она определенной и найти решения.

Далее рассмотрим, в частности, систему трех уравнений первой степени с тремя неизвестными.

( 4.2)

Составим из коэффициентов при неизвестных системы (4.2) определитель этой системы

Умножим обе части первого уравнения почленно на алгебраическое дополнение А₁₁ элемента а₁₁, второе уравнение – на алгебраическое дополнение А₂₁ элемента а₂₁, а третье – на алгебраическое дополнение А₃₁ элемента а₃₁.

Сложим все три полученных уравнения, умножив предварительно на соответствующие алгебраические дополнения, получим

( 4.3)

Коэффициенты при y и z в силу свойства определителя (см. “лекц. 1” , теорема 2) равны нулю, а коэффициент при х на основании тех же свойств (см. “лекц. 1” , теорема 1) равен , т.е. , поэтому равенство (4.3) примет вид:

( 4.4)

( 4.

Заметим, что определитель получается из определителя путем замены коэффициентов а₁₁, а₂₁, а₃₁ при неизвестном х свободными членами или замены первого столбца коэффициентов при искомом х столбцом свободных членов. Аналогично получаются другие равенства:

( 4.6)

Определители и получают из определителя системы заменой второго и третьего столбцов коэффициентов при y и z столбцом свободных членов.

Рассмотрим следующие случаи.

. Тогда из равенств (4. 4) и (4.5) находим решение системы (2) как
( 4.7)
которые называют формулами Крамера.
. Тогда по крайней мере один из , или отличен от нуля и система (4.2) не имеет решения (система несовместна), что можно показать. Пусть, например, . Тогда равенство из (4.4) получаем или , что невозможно.
и . Тогда система (4.2) либо не имеет решения, либо имеет бесконечное множество решений.

Пример 1. Решить систему

Решение. Вычислим все определители.

Так как , то данная система имеет единственное решение, которое найдем по формулам Крамера (4.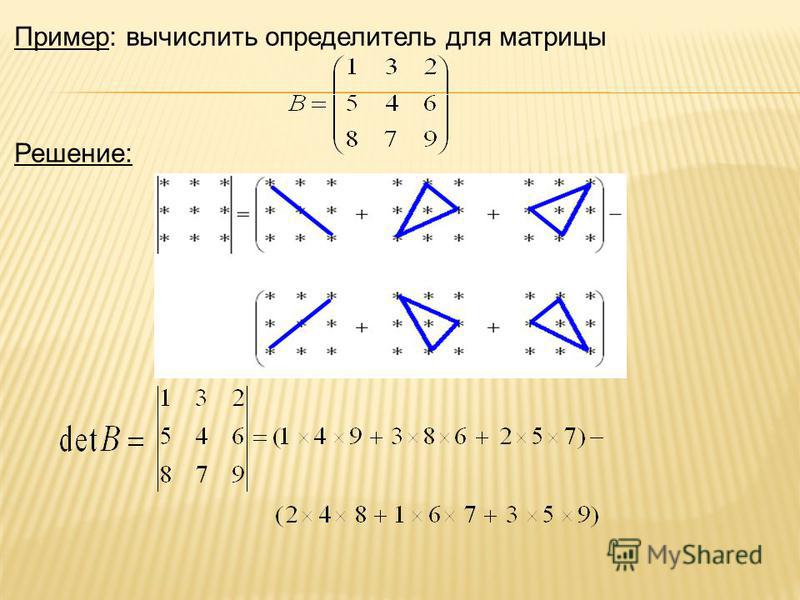 7):

т.е. (2, 0, -1) – искомое решение системы.

Пример 2. Решить систему

Решение. Вычислим определители

т.е. система решений не имеет (случай 2)

Пример 3. Решить систему

Решение. Нетрудно убедиться в том, что и . Данная система не имеет решений, так как первое и третье уравнения противоречивы. Если умножить первое уравнение на 3 и вычесть из полученного уравнение третье, то придем к ложному равенству 0 = 3.

Пример 4. Решить систему

Решение. Нетрудно убедиться в том, что и . Так как второе уравнение получается из первого умножением на 2, то данная система равносильна системе двух уравнений относительно трех неизвестных

Так как

то можно найти решение последней системы

в которой переменная z является свободной, и, следовательно, исходная система имеет бесконечное множество решений, которое можно найти либо по формулам Крамера, либо методом исключений. В результате получим (-5z/11; (7z+11)/11; z), где z может принимать произвольные значения.

Дальше >>

< Лекция 10 || Лекция 5: 12345

определителей и правило Крамера | безграничная алгебра |

Матрицы

Определители квадратных матриц 2 на 2

Определитель квадратной матрицы

2×22\times 22×2

— это математическая конструкция, используемая при решении задач, которая находится по специальной формуле.

Цели обучения

Потренируйтесь находить определитель матрицы

2×22\times 22×2

Основные выводы

Ключевые моменты

Ключевые термины

определитель : Уникальная скалярная функция над квадратными матрицами, которая является дистрибутивной при умножении матриц, полилинейна в строках и столбцах и принимает значение 1 для единичной матрицы. Его аббревиатура «
det⁡\detdet
».

Что такое определитель?

Матрица часто используется для представления коэффициентов в системе линейных уравнений, и определитель может использоваться для решения этих уравнений. Использование определителей в исчислении включает определитель Якоби в правиле замены переменных для интегралов функций многих переменных. Детерминанты также используются для определения характеристического многочлена матрицы, что важно для задач на собственные значения в линейной алгебре. В аналитической геометрии определители выражают знаковые

ннн

-мерные объемы

ннн

-мерные параллелепипеды. Иногда определители используются просто как компактная запись для выражений, которые в противном случае было бы громоздко записывать.

Можно доказать, что любая матрица имеет единственную обратную, если ее определитель отличен от нуля. Также можно доказать различные другие теоремы, в том числе то, что определитель произведения матриц всегда равен произведению определителей; и определитель эрмитовой матрицы всегда действителен.

Определитель матрицы

[A][A][A]

обозначается

det⁡(A)\det(A)det(A)

det⁡ A\det\ Ad эт A

, или

∣A∣\left | А \право |∣А∣

. В случае, когда элементы матрицы выписаны полностью, определитель обозначается путем окружения элементов матрицы вертикальными чертами вместо скобок или круглых скобок матрицы.

Например, определитель матрицы

[abde]\begin{bmatrix} a & b \\ d & e \end{bmatrix}[adbe]

пишется

∣abde∣\begin{vmatrix} a & b \\ d & e \end{vmatrix}∣

∣adbe∣

∣

Определитель матрицы 2 на 2

В линейной алгебре определитель — это значение, связанное с квадратной матрицей. Его можно вычислить из элементов матрицы с помощью определенного арифметического выражения, показанного ниже:

Для

2×22 \times 22×2

Матрица,

[abcd] \ begin {bmatrix} a & b \\ c & d \ end {bmatrix} [ac bd]

Определитель

∣abcd∣ begin {vmatrix} a & b\\ c & d \end{vmatrix}∣

∣acbd∣

∣

определяется как

ad-bcad-bcad-bc

Пример 1. Найдите определитель следующей матрицы:

[4−275]\displaystyle \begin{bmatrix} 4 & -2 \\ 7 & 5 \end{bmatrix}[47−25]

Определитель

∣4−275∣\begin{vmatrix} 4 & -2\\ 7 & 5 \end{vmatrix}∣

∣47−25∣

∣

равен: 9000 5

( 4⋅5)−(−2⋅7)=20−(−14)=34\displaystyle \начать{выравнивать} (4 \cdot 5) – (-2 \cdot 7)&= 20 – (-14)\\ &=34 \end{align}(4⋅5)−(−2⋅7)=20−(−14)=34

Кофакторы, миноры и дополнительные детерминанты

Кофактор записи

(i,j)(i,j)(i,j)

матрицы

AAA

— минор этой матрицы со знаком.

Цели обучения

Объясните, как использовать минорные матрицы и матрицы кофакторов для вычисления определителей

Ключевые выводы

Ключевые точки

Ключевые термины

кофактор : Знаковый минор записи матрицы.
младший : Определитель некоторой меньшей квадратной матрицы, вырезанной из матрицы
AAA
путем удаления одной или нескольких ее строк или столбцов.

Кофактор и минор: определения

Кофактор

В линейной алгебре кофактор (иногда называемый дополнением) описывает конкретную конструкцию, которая полезна для вычисления как определителя, так и обратной квадратной матрицы. В частности, кофактор записи

(i,j)(i,j)(i,j)

матрицы, также известной как

(i,j)(i,j)(i,j) Кофактор

этой матрицы является минорным знаком этой записи.

Кофактор 9{i+j}M_{ij}Cij=(−1)i+jMij

Незначительный

Чтобы узнать, что такое знаковый минор, нам нужно знать, что такое минор матрицы. В линейной алгебре минор матрицы

AAA

является определителем некоторой меньшей квадратной матрицы, вырезанной из

AAA

путем удаления одной или нескольких ее строк или столбцов. Миноры, полученные удалением всего одной строки и одного столбца из квадратных матриц (первые миноры), необходимы для вычисления матрицы кофакторов.

Пусть

AAA

будет

m×nm \times nm×n

матрицей и

kkk

целым числом с 9 0005

k≤nk \leq nk≤n

. A

k×kk \times kk×k

младшая из

AAA

является определителем матрицы

k×kk \times kk×k

, полученной из 900 05

AAA

, удалив

m-km-km-k

строк и

n-kn-kn-k

столбцов.

Вычисление определителя

Определитель любой матрицы можно найти, используя ее знаковые миноры. Определитель — это сумма миноров со знаком любой строки или столбца матрицы, масштабированных по элементам в этой строке или столбце.

Расчет миноров

Следующие шаги используются, чтобы найти определитель данного минора матрицы A:

Выберите запись
aija_{ij}aij
из матрицы.
Вычеркните записи, лежащие в соответствующей строке
iii
и столбце
jjj
.
Переписать матрицу без отмеченных элементов.
Получите определитель этой новой матрицы.

MijM_{ij}Mij

называется второстепенным для записи

aija_{ij}aij

Примечание: если

i+ji+ji+j

четное число, то кофактор совпадает с его минором:

Cij=MijC_{ij}=M_{ij}Cij=Mij

. В противном случае он равен аддитивной величине, обратной своему минору:

Cij=-MijC_{ij}=-M_{ij}Cij=-Mij

Вычисление определителя

Мы найдем определитель следующей матрицы A, вычислив определители ее сомножителей для третьего, самого правого столбца, а затем умножив их на элементы этого столбца.

[147305−1911]\displaystyle \begin{bmatrix} 1 и 4 и 7\\ 3 & 0 & 5\\ -1& 9&11\\ \end{bmatrix}⎣

⎡13−14097511⎦

⎤

В качестве примера вычислим определитель минора

M23M_{23}M23 9 0005

, которая является определителем матрицы

2×22 \times 22×2

, образованной удалением

222

-й строки и

333

-го столбца. Черная точка представляет элемент, который мы удаляем.

∣14∙∙∙∙−19∙∣=∣14−19∣=(9−(−4))=13\displaystyle \начать{выравнивать} \begin{vmatrix} 1 & 4 & \bullet\\ \bullet& \bullet& \bullet\\ -1& 9&\bullet \end{vmatrix} &= \begin{vmatrix} 1 & 4\\ -1&9 \end{vmatrix}\\ &=(9-(-4))\\&=13 \end{align}∣

∣1∙−14∙9∙∙∙∣

∣=∣

∣1−149∣

∣=(9− (−4))=13

Поскольку

i+j=5i+j=5 i+j=5

является нечетным числом, кофактор является аддитивным, обратным его минору:

−(13 )=−13-(13)=-13−(13)=−13

Умножаем это число на

a23=5a_{23}=5a23=5

, что дает

−65-65−65

Тот же процесс выполняется для нахождения определителей

C13C_{13}C13

C33C_{33}C33

, которые затем умножаются на

900 02 а13а_{13}а13

a33a_{33}a33

соответственно. Затем определитель находится путем суммирования всех этих значений:

det⁡A=a_13det⁡C_13+a_23det⁡C_23+a_33det⁡C_33=7⋅27−5⋅13+11⋅−12=−8\begin {align} \ det{A} &= a\text{\textunderscore}{13}\det{C\text{\textunderscore}{13}}+a\text{\textunderscore}{23}\det{C\text{\textunderscore {23}}+a\text{\textunderscore}{33}\det{C\text{\textunderscore}{33}} \\ &= 7\cdot27-5\cdot13+11\cdot-12 \\& =-8 \end{align}detA=a_13detC_13+a_23detC_23+a_33detC_33=7⋅27−5⋅13+11⋅−12=−8