вычисление матриц
вычисление матрицВы искали вычисление матриц? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление матрицы, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «вычисление матриц».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычисление матриц,вычисление матрицы,вычисление определителей онлайн,вычисление определителя 4 порядка онлайн,вычисление определителя 4 порядка онлайн с решением,вычисление определителя калькулятор онлайн,вычисление определителя матрицы,вычисление определителя матрицы калькулятор,вычисление определителя матрицы онлайн,вычисление определителя онлайн,вычисление определителя онлайн калькулятор,вычислите определитель 3 порядка,вычислите определитель матрицы онлайн,вычислитель определитель матрицы онлайн,вычислитель определителя онлайн,вычислить матрица,вычислить онлайн определитель 4 порядка,вычислить онлайн определитель второго порядка,вычислить определитель 2 порядка онлайн,вычислить определитель 4 го порядка онлайн,вычислить определитель 4 порядка калькулятор,вычислить определитель 4 порядка калькулятор онлайн,вычислить определитель 4 порядка онлайн,вычислить определитель 4 порядка онлайн калькулятор,вычислить определитель 4 порядка онлайн с подробным решением,вычислить определитель второго порядка онлайн,вычислить определитель второго порядка онлайн с решением,вычислить определитель используя свойства определителя онлайн,вычислить определитель калькулятор,вычислить определитель матрицы 4х4,вычислить определитель матрицы 4х4 онлайн с решением,вычислить определитель матрицы калькулятор,вычислить определитель матрицы калькулятор онлайн,вычислить определитель матрицы онлайн,вычислить определитель матрицы онлайн калькулятор,вычислить определитель матрицы онлайн с решением,вычислить определитель матрицы онлайн с решением подробно,вычислить определитель методом понижения порядка онлайн,вычислить определитель онлайн,вычислить определитель онлайн 4 порядка,вычислить определитель онлайн калькулятор,вычислить определитель онлайн с подробным решением,вычислить определитель онлайн с подробным решением онлайн,вычислить определитель с подробным решением онлайн,вычислить определитель третьего порядка,вычислить определитель четвертого порядка онлайн,вычислить определитель четвертого порядка онлайн с подробным решением,вычислить определитель четвертого порядка онлайн с решением,вычислить определитель четвертого порядка с решением онлайн,вычислить определить,вычислить определить онлайн,вычислить определить онлайн 4 на 4,детерминант матрицы 4 на 4,детерминант матрицы калькулятор,детерминант матрицы онлайн,детерминант матрицы онлайн калькулятор,детерминант онлайн,задачи определитель матрицы,используя свойства определителя вычислить определитель онлайн,как вычислить матрицу,как вычислить определитель 4 порядка онлайн с решением подробно,как вычислить определитель матрицы 4х4,как найти определитель матрицы,как найти определитель матрицы 4х4,как найти определитель матрицы 4х4 онлайн,как найти определитель матрицы 5х5,как посчитать матрицу 4 на 4,калькулятор визначників,калькулятор визначників онлайн,калькулятор вычисления определителя матрицы,калькулятор вычислить определитель,калькулятор вычислить определитель 4 порядка,калькулятор вычислить определитель 4 порядка онлайн,калькулятор вычислить определитель матрицы,калькулятор детерминант матрицы,калькулятор детерминанта матрицы,калькулятор для определителей,калькулятор матриц 4 порядка,калькулятор матриц матричный метод,калькулятор матриц матричным методом,калькулятор матриц онлайн определитель,калькулятор матриц онлайн определитель с решением,калькулятор матриц онлайн с решением определитель,калькулятор матриц определителей,калькулятор матриц определитель,калькулятор матриц определитель онлайн,калькулятор матрица определитель,калькулятор матрицы 4 порядка,калькулятор матрицы вычислить определитель,калькулятор матрицы вычислить определитель матрицы,калькулятор матрицы детерминант,калькулятор матрицы онлайн найти определитель,калькулятор матрицы определитель онлайн калькулятор с подробным решением,калькулятор матричный метод,калькулятор матричный метод онлайн,калькулятор матричный способ,калькулятор найти определитель матрицы,калькулятор онлайн вычисление определителя,калькулятор онлайн вычислить определитель матрицы,калькулятор онлайн вычислить определитель матрицы онлайн с решением,калькулятор онлайн матриц определитель,калькулятор онлайн матрица определитель,калькулятор онлайн матричный метод,калькулятор онлайн метод матричный,калькулятор онлайн найти определитель,калькулятор онлайн найти определитель матрицы,калькулятор онлайн обчислити визначник,калькулятор онлайн определителей,калькулятор онлайн определители,калькулятор онлайн определителя,калькулятор определения,калькулятор определителей,калькулятор определителей 4 порядка,калькулятор определителей матриц,калькулятор определителей матриц онлайн,калькулятор определителей матрицы,калькулятор определителей онлайн,калькулятор определители,калькулятор определители онлайн,калькулятор определитель,калькулятор определитель 4 порядка,калькулятор определитель матриц,калькулятор определитель матриц онлайн,калькулятор определитель матрицы,калькулятор определитель матрицы 4 порядка,калькулятор определитель третьего порядка онлайн с решением,калькулятор определителя,калькулятор определителя 4 порядка,калькулятор определителя 4 порядка онлайн,калькулятор определителя матрицы,калькулятор определителя матрицы онлайн,калькулятор определителя онлайн,калькулятор систем матриц,калькулятор союзной матрицы,линейная алгебра онлайн калькулятор,матрица 3 на 3 онлайн,матрица 4 порядка онлайн,матрица вычисление,матрица вычислить,матрица калькулятор онлайн определитель,матрица калькулятор определитель,матрица метод треугольника онлайн,матрица нахождение определителя,матрица онлайн калькулятор определитель,матрица онлайн определитель,матрица определитель калькулятор,матрица определитель калькулятор онлайн,матрица определитель онлайн,матрица определитель онлайн калькулятор,матрица четвертого порядка онлайн,матрицы onlinemschool,матрицы вычисление,матрицы калькулятор найти определитель матрицы,матрицы онлайн калькулятор найти определитель,матрицы определитель 4 порядка онлайн,матрицы считать,матричный калькулятор матричный способ,матричный калькулятор метод,матричный калькулятор онлайн матричный метод,матричный калькулятор онлайн метод матричный,матричный калькулятор определитель,матричный метод калькулятор,матричный метод калькулятор онлайн с подробным решением,матричный метод онлайн калькулятор с подробным решением,матричный способ калькулятор,матричный способ калькулятор онлайн,матричный способ онлайн калькулятор,метод матричный калькулятор,метод матричный онлайн калькулятор,метод матричный онлайн калькулятор с подробным решением,метод треугольника матрица онлайн,метод треугольника матрицы онлайн,метод элементарных преобразований матрицы онлайн калькулятор,модуль матрицы,найти детерминант матрицы онлайн,найти определитель калькулятор онлайн,найти определитель матрицы 3х3 онлайн,найти определитель матрицы 4х4,найти определитель матрицы 4х4 онлайн,найти определитель матрицы 4х4 онлайн с решением,найти определитель матрицы калькулятор онлайн,найти определитель матрицы онлайн,найти определитель матрицы онлайн 4х4,найти определитель матрицы онлайн калькулятор,найти определитель матрицы онлайн с подробным решением,найти определитель матрицы онлайн с решением,найти определитель матрицы с решением онлайн,найти определитель онлайн,найти определитель онлайн калькулятор,найти определить матрицы,нахождение детерминанта матрицы,нахождение определителя матрица,нахождение определителя матрицы 4 порядка онлайн,нахождение определителя матрицы онлайн,нахождение определителя матрицы онлайн с решением,нахождение определителя онлайн,обчислити визначник калькулятор онлайн,обчислити визначник онлайн калькулятор,онлайн вычисление определителей,онлайн вычисление определителя 4 порядка,онлайн вычисления определителя матрицы,онлайн вычислитель определителя,онлайн вычислить определитель четвертого порядка,онлайн детерминант,онлайн калькулятор визначників,онлайн калькулятор вычисление определителя,онлайн калькулятор вычислить определитель,онлайн калькулятор вычислить определитель 4 порядка,онлайн калькулятор вычислить определитель матрицы,онлайн калькулятор детерминант матрицы,онлайн калькулятор матриц определителей,онлайн калькулятор матриц определитель,онлайн калькулятор матриц определитель с решением,онлайн калькулятор матриц с решением определитель,онлайн калькулятор матрица определитель,онлайн калькулятор матрицы вычислить определитель,онлайн калькулятор матрицы детерминант,онлайн калькулятор матрицы найти определитель,онлайн калькулятор матричный метод,онлайн калькулятор матричный способ,онлайн калькулятор метод матричный,онлайн калькулятор метод саррюса,онлайн калькулятор найти определитель,онлайн калькулятор найти определитель матрицы,онлайн калькулятор обчислити визначник,онлайн калькулятор определение матрицы,онлайн калькулятор определителей,онлайн калькулятор определителей матриц,онлайн калькулятор определители,онлайн калькулятор определитель,онлайн калькулятор определитель 4 порядка,онлайн калькулятор определитель второго порядка,онлайн калькулятор определитель матриц,онлайн калькулятор определитель матрица,онлайн калькулятор определитель матрицы,онлайн калькулятор определитель матрицы 4 порядка,онлайн калькулятор определитель матрицы с подробным решением,онлайн калькулятор определитель матрицы с решением,онлайн калькулятор определителя,онлайн калькулятор определителя 4 порядка,онлайн калькулятор определителя матрицы,онлайн калькулятор присоединенная матрица,онлайн калькулятор решение определителей,онлайн матрица 3 на 3,онлайн определение определителя матрицы,онлайн определители,онлайн определители матриц,онлайн определитель 2 порядка,онлайн определитель 4 порядка,онлайн определитель матрицы 4 порядка,онлайн определитель матрицы 4х4,онлайн определитель матрицы с решением,онлайн определитель четвертого порядка,онлайн определить,онлайн подсчет определителя матрицы,онлайн расчет определителя матрицы,онлайн решение матриц 4 порядка,онлайн решение матриц методом,онлайн решение матрицы 3 на 3,онлайн решение матрицы определитель,онлайн решение определителей,онлайн решение определителей 4 порядка,онлайн решение определители,онлайн решение определитель,онлайн решение определитель матрицы,онлайн решение определителя,онлайн решение определителя 4 порядка,онлайн решить определитель,онлайн решить определитель 4 порядка,онлайн считать определитель,определение матрицы онлайн калькулятор,определение онлайн,определение определителя матрицы онлайн,определители 4 порядка онлайн,определители вычислить,определители калькулятор,определители калькулятор онлайн,определители матриц онлайн,определители онлайн,определители онлайн калькулятор,определители онлайн решение,определители решение онлайн,определитель 2 порядка онлайн,определитель 4 го порядка калькулятор онлайн,определитель 4 го порядка онлайн,определитель 4 порядка калькулятор,определитель 4 порядка калькулятор онлайн,определитель 4 порядка матрицы онлайн,определитель 4 порядка онлайн,определитель 4 порядка онлайн калькулятор,определитель 4 порядка онлайн с решением,определитель 4 порядка онлайн с решением подробно,определитель 4 порядка решить онлайн,определитель 5 порядка онлайн,определитель второго порядка онлайн калькулятор,определитель как считать,определитель калькулятор,определитель калькулятор матриц,определитель калькулятор онлайн,определитель матриц калькулятор,определитель матриц онлайн калькулятор,определитель матрица калькулятор онлайн,определитель матрица онлайн калькулятор,определитель матрицы 3х3 онлайн,определитель матрицы 4 порядка калькулятор,определитель матрицы 4 порядка онлайн,определитель матрицы 4 порядка онлайн калькулятор,определитель матрицы 4х4,определитель матрицы 4х4 найти,определитель матрицы 4х4 онлайн,определитель матрицы 4х4 формула,определитель матрицы 5х5,определитель матрицы калькулятор,определитель матрицы онлайн,определитель матрицы онлайн 4 порядка,определитель матрицы онлайн 4х4,определитель матрицы онлайн калькулятор,определитель матрицы онлайн калькулятор с подробным решением,определитель матрицы онлайн калькулятор с решением,определитель матрицы онлайн по строке,определитель матрицы онлайн решение,определитель матрицы онлайн с буквами,определитель матрицы онлайн с решением,определитель матрицы по строке онлайн,определитель матрицы рассчитать,определитель матрицы рассчитать онлайн,определитель матрицы решение онлайн,определитель матрицы с буквами онлайн,определитель матрицы с решением онлайн,определитель матрицы с решением онлайн калькулятор,определитель матрицы считать онлайн,определитель онлайн,определитель онлайн 2 порядка,определитель онлайн калькулятор,определитель онлайн решение,определитель онлайн решить,определитель посчитать,определитель решение матрицы онлайн,определитель решение онлайн,определитель решить,определитель решить онлайн,определитель считать,определитель считать онлайн,определитель третьего порядка онлайн калькулятор,определитель четвертого порядка калькулятор онлайн,определитель четвертого порядка онлайн,определить вычислить онлайн,определить матрицы калькулятор,определить матрицы онлайн,определить онлайн,определить онлайн матрицы,определить посчитать онлайн,подсчет определителя матрицы онлайн,поиск определителя матрицы онлайн,получить нули в строке матрицы онлайн калькулятор,посчитать детерминант матрицы онлайн,посчитать онлайн определитель,посчитать онлайн определитель 4 порядка,посчитать определитель,посчитать определитель 4 порядка онлайн,посчитать определитель матрицы,посчитать определитель матрицы онлайн,посчитать определитель онлайн,посчитать определить онлайн,приведение матрицы к диагональному виду онлайн,привести к диагональному виду матрицу онлайн,привести матрицу к диагональному виду онлайн,рассчитать определитель матрицы,рассчитать определитель матрицы онлайн,рассчитать определитель онлайн,расчет матрицы,расчет определителя матрицы онлайн,решение матриц 4 порядка онлайн,решение матриц 4х4,решение матриц методом онлайн,решение матриц онлайн 4 порядка,решение матриц онлайн методом,решение матрицы онлайн 3 на 3,решение матрицы онлайн определитель,решение матрицы определитель онлайн,решение онлайн матриц 4 порядка,решение онлайн определитель,решение онлайн определитель матрицы,решение онлайн определителя,решение определителей 4 порядка онлайн,решение определителей онлайн,решение определители онлайн,решение определитель матрицы онлайн,решение определитель онлайн,решение определителя 4 порядка онлайн,решение определителя онлайн,решить онлайн определитель,решить онлайн определитель 4 порядка,решить определитель 4 порядка онлайн,решить определитель онлайн,сделать линейные преобразования найти определитель,считать онлайн определитель,считать онлайн определитель матрицы,считать определитель,считать определитель матрицы онлайн,считать определитель онлайн,теорема лапласа онлайн калькулятор,упростить и вычислить определитель.
Решить задачу вычисление матриц вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Вычисление определителя матрицы в EXCEL. Примеры и описание
Вычислим определитель (детерминант) матрицы с помощью функции
МОПРЕД()
или англ. MDETERM, разложением по строке/столбцу (для 3 х 3) и по определению (до 6 порядка).
Определитель матрицы (det) можно вычислить только для квадратных матриц, т.е. у которых количество строк равно количеству столбцов.
Для вычисления определителя в MS EXCEL есть специальная функция МОПРЕД() . В аргументе функции необходимо указать ссылку на диапазон ячеек (массив), содержащий элементы матрицы (см. файл примера ).
Массив может быть задан не только как интервал ячеек, например A7:B8 , но и как массив констант , например =МОПРЕД({5;4:3;2}) . Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.
Ссылка на массив также может быть указана как ссылка на
именованный диапазон
.
Для матриц порядка 2 можно определитель можно вычислить без использования функции МОПРЕД() . Например, для вышеуказанной матрицы выражение =A7*B8-B7*A8 вернет тот же результат.
Для матрицы порядка 3, например размещенной в диапазоне A16:C18 , выражение усложняется =A16*(B17*C18-C17*B18)-B16*(A17*C18-C17*A18)+C16*(A17*B18-B17*A18) (разложение по строке).
В файле примера для матрицы 3 х 3 определитель также вычислен через разложение по столбцу и по правилу Саррюса.
Свойства определителя
Теперь о некоторых свойствах определителя (см. файл примера ):
- Определитель транспонированной матрицы равен определителю исходной матрицы
- Если в матрице все элементы хотя бы одной из строк (или столбцов) нулевые, определитель такой матрицы равен нулю
- Если переставить местами две любые строки (столбца), то определитель полученной матрицы будет противоположен исходному (то есть, изменится знак)
- Если все элементы одной из строк (столбца) умножить на одно и тоже число k, то определитель полученной матрицы будет равен определителю исходной матрицы, умноженному на k
- Если матрица содержит строки (столбцы), являющиеся линейной комбинацией других строк (столбцов), то определитель =0
- det(А)=1/det(А -1 ), где А -1 –
матрица обратная
матрице А (А – квадратная невырожденная матрица).
Вычисление определителя матрицы по определению (до 6 порядка включительно)
СОВЕТ : Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция МОПРЕД() .
Как было показано выше для вычисления матриц порядка 2 и 3 существуют достаточно простые формулы и правила. Для вычисления определителя матриц более высокого порядка (без использования функции МОПРЕД() ) придется вспомнить определение:
Определителем квадратной матрицы порядка
n
х
n
является сумма, содержащая
n!
слагаемых (
=ФАКТР(n)
). Каждое слагаемое представляет собой произведение
n
элементов матрицы, причем в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы
А
.
Перед
k-ым
слагаемым появляется коэффициент
(-1)
, если элементы матрицы
А
в произведении упорядочены по номеру строки, а количество инверсий в
k-ой
перестановке множества номеров столбцов нечетно.
где ( α 1 , α 2 ,…, α n ) – перестановка чисел от 1 до n , N( α 1 , α 2 ,…, α n ) – число инверсий в перестановке , суммирование идёт по всем возможным перестановкам порядка n .
Попытаемся разобраться в этом непростом определении на примере матрицы 3х3.
Для матрицы 3 х 3, согласно определения, число слагаемых равно 3!=6, а каждое слагаемое состоит из произведения 3-х элементов матрицы. Ниже приведены все 6 слагаемых, необходимых для вычисления определителя матрицы 3х3:
- а21*а12*а33
- а21*а32*а13
- а11*а32*а23
- а11*а22*а33
- а31*а22*а13
- а31*а12*а23
а21, а12 и т.
д. – это элементы матрицы. Теперь поясним, как были сформированы индексы у элементов, т.е. почему, например, есть слагаемое а11*а22*а33, а нет а11*а22*а13.
Посмотрим на формулу выше (см. определение). Предположим, что второй индекс у каждого элемента матрицы (от 1 до n) соответствует номеру столбца матрицы (хотя это может быть номер строки (это не важно т.к. определители матрицы и ее транспонированной матрицы равны). Таким образом, второй индекс у первого элемента в произведении всегда равен 1, у второго – 2, у третьего 3. Тогда первые индексы у элементов соответствуют номеру строки и, в соответствии с определением, должны определяться из перестановок чисел от 1 до 3, т.е. из перестановок множества (1, 2, 3).
Теперь понятно, почему среди слагаемых нет а11*а22*а13, т.к. согласно определения ( в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы
А ),
а в нашем слагаемом нет элемента из строки 3.
Примечание : Перестановкой из n чисел множества (без повторов) называется любое упорядочивание данного множества, отличающиеся друг от друга лишь порядком входящих в них элементов. Например, дано множество их 3-х чисел: 1, 2, 3. Из этих чисел можно составить 6 разных перестановок: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 1, 2), (3, 2, 1). См. статью Перестановки без повторений: Комбинаторика в MS EXCEL
Число перестановок множества из 3-х чисел =3!=6 (что, конечно, равно числу слагаемых в выражении для расчета определителя, т.к. каждому слагаемому соответствует своя перестановка). Для матрицы 3х3 все перестановки приведены в примечании выше. Можно убедиться, что в каждом слагаемом первые индексы у элементов равны соответствующим числам в перестановке. Например, для слагаемого а21*а12*а33 использована перестановка (2, 1, 3).
СОВЕТ : Для матрицы 4 порядка существует 4! перестановок, т.е. 26, что соответствует 26 слагаемым, каждое из которых является произведением различных 4-х элементов матрицы. Все 26 перестановок можно найти в статье Перебор всех возможных Перестановок в MS EXCEL .
Теперь, когда разобрались со слагаемыми, определим множитель перед каждым слагаемым (он может быть +1 или -1). Множитель определяется через четность числа инверсий соответствующей перестановки.
Примечание : Об инверсиях перестановок (и четности числа инверсий) можно почитать, например, в статье Перестановки без повторений: Комбинаторика в MS EXCEL
Например, первому слагаемому соответствует перестановка (2, 1, 3), у которой 1 инверсия (нечетное число) и, соответственно, -1 в степени 1 равно -1. Второму слагаемому соответствует перестановка (2, 3, 1), у которой 2 инверсии (четное число) и, соответственно, -1 в степени 2 равно 1 и т.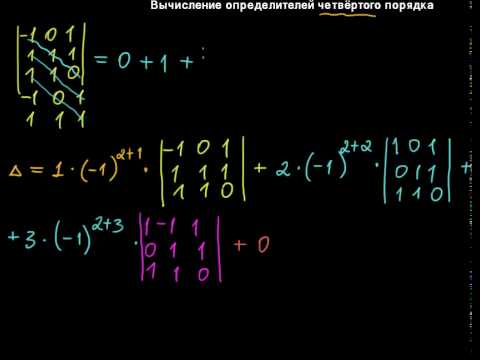
д.
Сложив все слагаемые: (-1)*(а21*а12*а33)+(+1)*(а21*а32*а13)+(-1)*(а11*а32*а23)+(+1)*(а11*а22*а33)+(-1)*(а31*а22*а13)+(+1)*(а31*а12*а23) получим значение определителя.
В файле примера на листе 4+, и зменяя порядок матрицы с помощью элемента управления Счетчик , можно вычислить определитель матрицы до 6 порядка включительно.
Следует учитывать, что при вычислении матрицы 6-го порядка в выражении используется уже 720 слагаемых (6!). Для 7-го порядка пришлось бы сделать таблицу для 5040 перестановок и, соответственно, вычислить 5040 слагаемых! Т.е. без использования МОПРЕД() не обойтись (ну, или можно вычислить определитель вручную методом Гаусса).
линейная алгебра – Помогите найти определитель матрицы 4×4?
Извините за отсутствие обозначений, но работать будет легко, если вы знаете, что делаете. Хорошо, моя проблема в том, что в книге говорится, что это можно сделать, расширив любой столбец или строку, но единственный способ получить то, что делает книга в их практическом примере, – это выбрать строку, которую они выбрали.
2 = 1$. Это должно быть умножено на определитель минора. Теперь, найдя определитель, я сделал:
3 раза $$ \begin{pmatrix} 0 и 3 \\ 0 и -6 \\ \end{pматрица} $$ давая $ 3 (0-0) = 0 $ затем:
0 раз $$ \begin{pmatrix} -8 и 3\\ 5 и -6\\ \end{pматрица} $$
дает 0(48-15)=0
Тогда: 4 раза $$ \begin{pmatrix} -8 и 0 \\ 5 и 0 \\ \end{pматрица} $$ давая $ 4 (0-0) = 0 $ складывая определители получаем $0+0+0=0$ Итак, det M1 $= 0(1) = 0$
93 = -1$$$ \begin{pmatrix} 0 & 0 & -4 \\ -5 & 0 & 3 \\ 0 & 0 & -6 \\ \end{pматрица} $$
о* $$ \begin{pmatrix} 0 и 3 \\ 0 и -6 \\ \end{pматрица} $$ давая $ 0 (0-0) = 0 $
, очевидно, что следующая матрица будет выглядеть так же, как верхний член во втором столбце равен нулю, поэтому определитель для этого будет равен $ 0 $. Теперь, наконец,
4 раза $$ \begin{pmatrix} -8 и 0 \\ 5 и 0 \\ \end{pматрица} $$ давая 4 (0-0) = 0 94 = 1$
$$ \begin{pmatrix} 0 и 3 и -4 \\ -5&-8&3\ 0 и 5 и -6 \\ \end{pматрица} $$
для определителя:
0 раз $$ \begin{pmatrix} -8 и 3\ 5 и -6 \\ \end{pматрица} $$ что дает $0(48-15)=0$
-3 раза $$ \begin{pmatrix} -5&3\\ 0 и -6 \\ \end{pматрица} $$
, что дает $-3(30-0)= -90$
отсюда продолжать избыточно, потому что после окончательного вычисления для этого минора я получаю -100 и в результате получаю det M3 = -190 и получаю определитель нулей для следующего определителя M4.
что дает: $ 0 (5) + 0 (-7) + (-90) (2) + (0) (2) $ дает
Det Ax $= -380.$ В книге написано, что это 20$, и когда я сделал это на калькуляторе, получилось 20, но проблема в том, что и книга, и калькулятор расширяются по строке с наибольшим количеством нулей, но теоретически говоря, НЕЗАВИСИМО КАКАЯ строка или столбце, который вы решили расширить, вы должны получить тот же ответ. Так что же это? Мои вычисления неверны или мое предположение о том, что вы можете расширяться по любой строке или столбцу, неверно? Разве это не важно, только если определитель не равен нулю? или точное значение имеет значение в более сложных случаях?
Определитель матрицы – 2×2, 3×3, 4×4…
Каталин Дэвид
Определение
Определитель квадратной матрицы A — это целое число, полученное с помощью ряда методов с использованием элементов матрицы.
Обозначение
Пусть $ А = \begin{pmatrix} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \end{pmatrix}$
$дет(А) = \влево|А\вправо| “=” \begin{vmatrix} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \end{vmatrix}$
Свойства определителя
- Если в матрице есть строка или столбец, все элементы которых равны 0 , то определитель матрицы равен 0 .
Пример 12
$\begin{vmatrix} 1 и 4 и 2\\ 0 и 0 и 0\\ 3 и 9 и 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 и 4 и 0\\ 4 и 2 и 0\\ 3 и 9 и 0 \end{vmatrix}=0$ - Если матрица имеет две равные строки или два равных столбца , то его определитель равен 0 .
Пример 13
$\begin{vmatrix} 1 и 4 и 2\\ 1 и 4 и 2\\ 3 и 9 и 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 и 4 и 1\\ 4 и 2 и 4\\ 3 и 9 и 3 \end{vmatrix}=0$ - Если матрица имеет две пропорциональные строки или два пропорциональных столбца , то ее определитель равен 0 .
Пример 14
$\begin{vmatrix} 1 и 4 и 2\\ 2 и 8 и 4\\ 3 и 9& 5 \end{vmatrix}= 0$ (первые две строки пропорциональны)
или
$\begin{vmatrix} 8 и 4 и 7\\ 4 и 2 и 3\\ 18 и 9 и 8 \end{vmatrix}=0$ (первые два столбца пропорциональны) - Если строка или столбец есть сумма или разность других строк, соответственно столбцов , то определитель равен 0 .
Пример 15
$\begin{vmatrix} 1 и 4 и 2\\ 7 и 2 и 3\\ 8 и 6 и 5 \end{vmatrix}= 0$ $R_{1} +R_{2} =R_{3}$ или$ \begin{vmatrix} 9 и 12 и 3\\ 1 и 8 и 7\\ 5 и 7 и 2 \end{vmatrix}=0$ $C_{1}+C_{3}=C_{2}$
- В определителе мы можем отдельно выносить целые числа из строк и столбцов.
Пример 16
В определителе
$\begin{vmatrix} 3 и 9 и 12\\ 5 и 1 и 8 \\ 7 и 4 и 2 \end{vmatrix}$, мы множим 3 из строки 1 $(R_{1})$ и получаем:
$3 \cdot \begin{vmatrix} 1 и 3 и 4\\ 5 и 1 и 8\\ 7 и 4 и 2 \end{vmatrix}$, то мы выносим 2 из столбца 3 $(C_{3})$:
$6\cточка \begin{vmatrix} 1 и 3 и 2\\ 5 и 1 и 4\\ 7 и 4 и 1 \end{vmatrix}$ - В определителе мы можем прибавлять или вычитать строки или столбцы к другим строкам, соответственно столбцам, и значение определителя остается прежним.
Пример 17
$\begin{vmatrix} 1 и 5\\ 3 и 8 \end{vmatrix}$ $\xlongequal{R_{1}+R_{2}} \begin{vmatrix} 4 и 13\\ 3 и 8 \end{vmatrix}$
Пример 18
$\begin{vmatrix} 1 и 5\\ 3 и 8 \end{vmatrix}$ $\xlongequal{C_{1}+C_{2}} \begin{vmatrix} 6 и 5\\ 11 и 8 \end{vmatrix}$ - В определителе мы можем складывать или вычитать несколько строк или столбцов.
Пример 19
$\begin{vmatrix} 1 и 5\\ 3 и 8 \end{vmatrix}$ $\xlongequal{2R_{1}+3R_{2}} \begin{vmatrix} 11 и 34\\ 3 и 8 \end{vmatrix}$Пример 20
$\begin{vmatrix} 1 и 5\\ 3 и 8 \end{vmatrix}$ $\xlongequal{5C_{1}-C_{2}} \begin{vmatrix} 0 и 5\\ 7 и 8 \end{vmatrix}$ - Определитель матрицы равен определителю ее транспонирования.
- Определитель произведения двух квадратных матриц равен произведению определителей данных матриц.
Минор матрицы
Определитель, полученный путем удаления некоторых строк и столбцов в квадратной матрице, называется минором этой матрицы.
Пример 21
$A=\begin{pmatrix}
1 и 4 и 2 \\
5 и 3 и 7 \\
6 и 2 и 1
\end{pmatrix}$
Один из миноров матрицы A равен $\begin{vmatrix} 1 и 4\\ 5 и 3 \end{vmatrix}$ (получено удалением строки 3 и столбца 3 из матрицы A)
Другой несовершеннолетний $\begin{vmatrix} 1 и 2 \\ 6 и 1 \end{vmatrix}$ (получено удалением строки 2 и столбца 2 из матрицы A)
Пример 22
$B=\begin{pmatrix}
2 и 5 и 1 и 3\\
4 и 1 и 7 и 9\\
6 и 8 и 3 и 2\\
7 и 8 и 1 и 4
\end{pматрица}
$
Один из миноров матрицы B равен $ \begin{vmatrix} 1 и 7 и 9\\ 8 и 3 и 2\\ 8 и 1 и 4 \end{vmatrix}$ (получено удалением строки 1 и столбца 1 из матрицы B)
Еще один несовершеннолетний $\begin{vmatrix} 1 и 7 \\ 8 и 3 \end{vmatrix}$ (получено удалением строк 1 и 4 и столбцов 1 и 4 из матрицы B)
Позволять
$A= \begin{pmatrix}
а_{1,1} и а_{1,2} и а_{1,3} и .
& . & a_{1,n}\\
а_{2,1} и а_{2,2} и а_{2,3} и . & . & а_{2,n}\\
а_{3,1} и а_{3,2} и а_{3,3} и . & . & а_{3,n}\\
. & . & . & . & .& .\\
a_{n,1} & a_{n,2} & a_{n,3} & . & . & Анна}
\end{pmatrix}$
Мы можем связать минор $\Delta_{i,j}$ (полученный удалением строки i и столбца j) с любым элементом $a_{i,j}$ матрицы A.
Пример 23
$ A = \begin{pmatrix}
4 и 7\\
2 и 9
\end{pmatrix}$
Нам нужно определить минор, связанный с 2. Так как этот элемент находится в строке 2, столбце 1, то 2 равно $a_{2,1}$.
Мы должны исключить строку 2 и столбец 1 из матрицы A, в результате чего получается
Минор числа 2 равен $\Delta_{2,1} = 7$.
Пример 24
$B=\begin{pmatrix}
1 и 4 и 2 \\
5 и 3 и 7 \\
6 и 2 и 1
\end{pmatrix}$
Нам нужно определить минор, связанный с 7. Так как этот элемент находится в строке 2, столбце 3, то 7 равен $a_{2,3}$.
Мы должны исключить строку 2 и столбец 3 из матрицы B, в результате чего получится
Минор числа 7 равен $\Delta_{2,3}= \begin{vmatrix} 1 и 4\\ 6 и 2 \end{vmatrix}$
Пример 25
$C=\begin{pmatrix}
2 и 5 и 1 и 3\\
4 и 1 и 7 и 9\\
6 и 8 и 3 и 2\\
7 и 8 и 1 и 4
\end{pmatrix}$
Нам нужно определить минор, связанный с 5.
Поскольку этот элемент находится в строке 1 столбца 2, то 5 равно $a_{1,2}$.
Мы должны исключить строку 1 и столбец 2 из матрицы C, в результате чего получится
Минор числа 5 равен $\Delta_{1,2}= \begin{vmatrix} 4 и 7 и 9\\ 6 и 3 и 2\\ 7 и 1 и 4\\ \end{vmatrix}$ 9{7}\cdot\Delta_{2,5}= -\Delta_{2,5} $ соответствует элементу $ a_{2.5}$
Приказ определителя
Порядок определителя равен количеству его строк и столбцов.
Пример 26
$\begin{vmatrix}
1 и 4\\
6 и 2\\
\end{vmatrix}$ (у него 2 строки и 2 столбца, поэтому его порядок равен 2)
Пример 27
$\begin{vmatrix}
4 и 7 и 9\\
6 и 3 и 2\\
7 и 1 и 4\\
\end{vmatrix}$ (у него 3 строки и 3 столбца, поэтому его порядок равен 3)
Вычисление определителя матрицы
Определитель матрицы равен сумме произведений элементов любой строки или столбца и их сомножителей.
$\слева| А\право| “=”
\begin{vmatrix}
а_{1,1} и а_{1,2} и а_{1,3} и .
& . & a_{1,n}\\
а_{2,1} и а_{2,2} и а_{2,3} и . & . & а_{2,n}\\
а_{3,1} и а_{3,2} и а_{3,3} и . & . & а_{3,n}\\
. & . & . & . & .& .\\
a_{n,1} & a_{n,2} & a_{n,3} & . & . & Анна}\\
\end{vmatrix}$
9{3}\cdot\Delta_{1,2}=a_{1,1}\cdot\Delta_{1,1}-a_{1,2}\cdot\Delta_{1,2}$
Однако $ \Delta_{1,1}= a_{2,2} $ и $ \Delta_{1,2}=a_{2,1}$
$ \ влево | А\право| =a_{1.1} \cdot a_{2,2}- a_{1.2} \cdot a_{2,1}$
$\цвет{красный}{ \begin{vmatrix} а и б\\ CD \end{vmatrix} =a \cdot d – b \cdot c}$
Пример 28
$\begin{vmatrix}
2 и 5\\
3 и 8
\end{vmatrix} =2 \cdot 8 – 3 \cdot 5 = 16 -15 =1$
Пример 29{4}\cdot\Delta_{1,3}=$ $a_{1,1}\cdot\Delta_{1,1}-a_{1.2}\cdot\Delta_{1,2}+a_{1.3}\cdot\Delta_{1,3}$
$\Дельта_{1,1}= \begin{vmatrix} а_{2,2} и а_{2,3}\\ а_{3,2} и а_{3,3} \end{vmatrix} = а_{2,2}\cdot а_{3,3}-a_{2,3}\cdot а_{3,2}$
$\Дельта_{1,2}= \begin{vmatrix} а_{2,1} и а_{2,3}\\ а_{3,1} и а_{3,3} \end{vmatrix} = а_{2,1}\cdot а_{3,3}-a_{2,3}\cdot а_{3,1}$
$\Дельта_{1,3}= \begin{vmatrix} а_{2,1} и а_{2,2}\\ а_{3,1} и а_{3,2} \end{vmatrix} = а_{2,1}\cdot а_{3,2}-a_{2,2}\cdot а_{3,1}$
$\влево| А\право| =a_{1,1}\cdot( a_{2,2}\cdot a_{3,3}-a_{2,3}\cdot a_{3,2})-a_{1,2}\cdot( a_{2,1}\cdot a_{3,3}-a_{2,3}\cdot a_{3,1})+$ $a_{1,3}\cdot(a_{2,1}\cdot а_{3,2}-а_{2,2}\cdot а_{3,1})=$
$a_{1,1}\cdot a_{2,2}\cdot a_{3,3}-a_{1,1}\cdot a_{2,3}\cdot a_{3,2}-a_{1 ,2}\cdot a_{2.
1}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3,1}+$ $a_{1,3}\ cdot a_{2,1}\cdot a_{3,2}-a_{1,3}\cdot a_{2,2}\cdot a_{3,1}=$
$\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3, 1}+a_{1,3}\cdot a_{2,1}\cdot a_{3,2}-}$
$\color{red}{(a_{1,1}\cdot a_{2,3}\cdot a_{3,2}+a_{1,2}\cdot a_{2,1}\cdot a_{3 ,3}+a_{1,3}\cdot a_{2,2}\cdot a_{3,1})}$
Чтобы быстрее достичь последнего отношения, мы можем использовать следующий метод.
Сначала перепишем первые две строки под определителем следующим образом.
$\begin{vmatrix}
\color{red}{a_{1,1}} & a_{1,2} & a_{1,3}\\
\color{red}{a_{2,1}} & \color{red}{a_{2,2}} & a_{2,3}\\
\color{red}{a_{3,1}} & \color{red}{a_{3,2}} & \color{red}{a_{3,3}}
\end{vmatrix}$
$\hspace{2мм}\begin{массив}{ccc}
a_{1,1} & \color{red}{a_{1,2}} & \color{red}{a_{1,3}}\\
a_{2,1} & a_{2,2} & \color{red}{a_{2,3}}\\
\end{массив}$
Мы умножаем элементы на каждой из трех красных диагоналей (главная диагональ и нижние) и суммируем результаты:
$\color{red}{a_{1,1}\cdot a_{2,2}\ cdot a_{3,3}+ a_{2,1}\cdot a_{3,2}\cdot a_{1,3}+a_{3,1}\cdot a_{1,2}\cdot a_{2 ,3}}$
$\begin{vmatrix}
\color{red}{a_{1,1}} & \color{red}{a_{1,2}} & \color{blue}{a_{1,3}}\\
\color{red}{a_{2,1}} & \color{blue}{a_{2,2}} & \color{blue}{a_{2,3}}\\
\color{blue}{a_{3,1}} & \color{blue}{a_{3,2}} & \color{blue}{a_{3,3}}
\end{vmatrix}$
$\hпробел{2мм}
\begin{массив}{ccc}
\color{blue}{a_{1,1}} & \color{blue}{a_{1,2}} & \color{red}{a_{1,3}}\\
\color{blue}{a_{2,1}} & \color{red}{a_{2,2}} & \color{red}{a_{2,3}}\\
\end{массив}$
Мы умножаем элементы на каждой из трех синих диагоналей (второстепенная диагональ и нижняя) и суммируем результаты:
$\color{синий}{a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1, 1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1}}$
Если мы вычтем два отношения, мы получим формулу определителя:
$\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+ a_{2,1}\cdot a_{3,2}\cdot a_{1, 3}+a_{3,1}\cdot a_{1,2}\cdot a_{2,3}-}$ $\color{red}{(a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1 ,1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1})}$
Пример 30
$A=\begin{pmatrix}
1 и 4 и 3 \\
2 и 1 и 5\\
3 и 2 и 1\\
\end{pmatrix}$
$\begin{vmatrix}
1 и 4 и 3 \\
2 и 1 и 5\\
3 и 2 и 1\\
\end{vmatrix}$
$\hspace{2мм}\begin{массив}{ccc}
1 и 4 и 3\\
2 и 1 и 5\\
\end{массив}$
$ = 1\cdot1\cdot1 + 2\cdot2\cdot3 + 3\cdot4\cdot5 – (3\cdot1\cdot3 + 5\cdot2\cdot1 + 1\cdot4\cdot2) =$ $1 + 12 + 60 -(9 + 10 + 8)=73-27=46$
Пример 31
$A=\begin{pmatrix}
3 и 5 и 1 \\
1 и 4 и 2\\
7 и 1 и 9\\
\end{pmatrix}$
$\begin{vmatrix}
3 и 5 и 1 \\
1 и 4 и 2\\
7 и 1 и 9\\
\end{vmatrix}$
$\hspace{2mm}\begin{массив}{ccc}
3 и 5 и 1\\
1 и 4 и 2\\
\end{массив} $
$= 3\cdot4\cdot9 + 1\cdot1\cdot1 + 7\cdot5\cdot2 – (1\cdot4\cdot7 + 2\cdot1\cdot3 + 9\cdot5\cdot1) =$ 108$ + 1 + 70 -(28 + 6 + 45)=79-79=100$
Существуют определители, элементами которых являются буквы.
Их легче вычислить, используя свойства определителей. Например, мы вычисляем определитель матрицы, в которой есть одни и те же элементы в любой строке или столбце, но переупорядоченные.
$\begin{vmatrix} а и б и в \\ такси\\ б и в и а \end{vmatrix}$ $ \xlongequal{C_{1}+C_{2}+C_{3}} \begin{vmatrix} а + б + с и б и с\\ с + а + б & а & б \\ б + в + а и в и а \end{vmatrix} = (а + б + с) \cdot \begin{vmatrix} 1 и б и в\\ 1 и а и б\\ 1 и с и а \end{vmatrix}$ 9{2} \end{vmatrix}= $
$\begin{vmatrix} а-в и б-в \\ (а-с) (а+с) и (б-с)(б+с) \end{vmatrix}=$ $(а-в)(б-в)\begin{vmatrix} 1 и 1\\ а+с и б+с \end{vmatrix}=$
$=(a-c)(b-c)[(b+c)-(a+c)]=$ $(a-c)(b-c)(b+c-a-c)=(a-c)(b-c)(b-a)$
Вычисление определителя 4×4
Для вычисления определителей 4×4 используем общую формулу.
Перед применением формулы с использованием свойств определителей:
- Проверяем, выполняется ли какое-либо из условий, чтобы значение определителя было равно 0.
- Мы проверяем, можем ли мы выделить любую строку или столбец.
- Проверяем, является ли определитель матрицей Вандермонда и имеет ли он те же элементы, но переупорядоченные, в любой строке или столбце.
В любом из этих случаев воспользуемся соответствующими методами вычисления определителей 3×3. Мы модифицируем строку или столбец, чтобы заполнить его 0, за исключением одного элемента. Определитель будет равен произведению этого элемента и его кофактора. В этом случае кофактор представляет собой детерминант 3×3, который рассчитывается по специальной формуле.
Пример 33
$\begin{vmatrix}
1 и 3 и 9 и 2\\
5 и 8 и 4 и 3\\
0 и 0 и 0 и 0\\
2 и 3 и 1 и 8
\end{vmatrix}$
Заметим, что все элементы в строке 3 равны 0, поэтому определитель равен 0.
Пример 34
$\begin{vmatrix}
1 и 3 и 1 и 2\\
5 и 8 и 5 и 3\\
0 и 4 и 0 и 0\\
2 и 3 и 2 и 8
\end{vmatrix}$
Заметим, что $C_{1}$ и $C_{3}$ равны, поэтому определитель равен 0.
Пример 35
$\begin{vmatrix}
1 и 3 и 9 и 2\\
5 и 8 и 4 и 3\\
10 и 16 и 18 и 4\\
2 и 3 и 1 и 8
\end{vmatrix}$
Заметим, что строки 2 и 3 пропорциональны, поэтому определитель равен 0.
Пример 36
$\begin{vmatrix}
\цвет{красный}{4} & 3 & 2 & 2\\
0 и 1 и -3 и 3\\
0 и -1 и 3 и 3\\
0 и 3 и 1 и 1
\end{vmatrix}$
Поскольку в столбце 1 есть только один элемент, отличный от 0, мы применяем общую формулу, используя этот столбец. Кофакторы, соответствующие элементам, равным 0, не нужно вычислять, потому что произведение их и этих элементов будет равно 0.
=
$=4(1\cdot3\cdot1 +(-1)\cdot1\cdot3+3\cdot(-3)\cdot3$ $-(3\cdot3\cdot3+3\cdot1\cdot1 +1\cdot( -3)\cdot(-1)))$ $=4(3-3-27-(27+3+3))=4\cdot(-60)=-240$
Пример 37
$\begin{vmatrix}
4 и 3 и 2 и 2\\
0 и 1 и 0 и -2\\
1 и -1 и 3 и 3\\
2 и 3 и 1 и 1
\end{vmatrix}$
Чтобы изменить строки так, чтобы в них было больше нулей, мы оперируем столбцами и наоборот.
Мы выбираем строку или столбец, содержащие элемент 1, потому что мы можем получить любое число путем умножения.
Мы замечаем, что в строке 2 уже есть два элемента, равных 0. Мы делаем только один другой 0, чтобы вычислить только сомножитель 1.
$\begin{vmatrix}
4 и 3 и 2 и 2\\
0 и 1 и 0 и -2\\
1 и -1 и 3 и 3\\
2 и 3 и 1 и 1
\end{vmatrix}
\xlongequal{C_{4}+2C_{2}}$
$\begin{vmatrix}
4 и 3 и 2 и 8\\
0 & \цвет{красный}{1} & 0 & 0\\
1 и -1 и 3 и 1\\
2 и 3 и 1 и 7
\end{vmatrix}=$
$=$
9{2+2}\cdot
\begin{vmatrix}
4 и 2 и 8\\
1 и 3 и 1\\
2 и 1 и 7
\end{vmatrix}=$
$=4\cdot3\cdot7 + 1\cdot1\cdot8 + 2\cdot2\cdot1$ $-(8\cdot3\cdot2 + 1\cdot1\cdot4 + 7\cdot2\cdot1) = $
84$ + 8 + 4- 48-4-14=30$
Пример 38
$\begin{vmatrix}
1 и -2 и 3 и 2\\
2 и 3 и 1 и -1\\
3 и 3 и 3 и 3\\
-1 и 4 и 2 и 1\\
\end{vmatrix}$
Мы можем разложить 3 из строки 3:
$3\cdot
\begin{vmatrix}
1 и -2 и 3 и 2\\
2 и 3 и 1 и -1\\
1 и 1 и 1 и 1\\
-1 и 4 и 2 и 1\\
\end{vmatrix}$
9{3+4}\cdot$ $=(-1)\cdot
\begin{vmatrix}
-1 и -4 и 1\\
3 и 4 и 2 \\
-2 и 3 и 1\\
\end{vmatrix}$
$=-((-1)\cdot 4\cdot 1 +3 \cdot 3\cdot1 + (-2)\cdot (-4)\cdot 2$ $- (1\cdot 4 \cdot (-2) + 2\cdot 3\cdot (-1) + 1\cdot (-4)\cdot3))$ $=-(-4 + 9 + 16 + 8 + 6 + 12) =-47 $
Пример 39
$\begin{vmatrix}
2 и 5 и 1 и 4\\
4 и 1 и 6 и 3\\
5 и 3 и 7 и 2\\
1 и 0 и 2 и 4
\end{vmatrix}$
В этом примере мы можем использовать последнюю строку (которая содержит 1) и можем сделать нули в первом столбце.
9{4+1}\cdot
\begin{vmatrix}
5 и -3 и -4\\
1 и -2 и -13\\
3 и -3 и -18
\end{vmatrix}=$
$(-1)\cdot
\begin{vmatrix}
5 и -3 и -4\\
1 и -2 и -13\\
3 и -3 и -18
\end{vmatrix}$
Мы умножаем -1 из столбца 2 и -1 из столбца 3.
$ (-1)\cdot(-1)\cdot(-1)\cdot
\begin{vmatrix}
5 и 3 и 4\\
1 и 2 и 13\\
3 и 3 и 18
\end{vmatrix}=$
$(-1)\cdot
\begin{vmatrix}
5 и 3 и 4\\
1 и 2 и 13\\
3 и 3 и 18
\end{vmatrix}=$
$-[5\cdot 2\cdot 18 + 1\cdot 3\cdot 4+ 3\cdot 3\cdot 13 – (4\cdot 2\cdot 3\cdot + 13\cdot 3\cdot 5 + 18\cdot 3 \cdot 1)]=$
$-(180+12+117-24-195-54)=36$
Пример 40
$\begin{vmatrix}
4 и 7 и 2 и 3\\
1 и 3 и 1 и 2\\
2 и 5 и 3 и 4\\
1 и 4 и 2 и 3
\end{vmatrix}$
В столбце 3 стоит 1, поэтому мы обнулим строку 2.
$\begin{vmatrix} 4 и 7 и 2 и 3\\ 1 и 3 и 1 и 2\\ 2 и 5 и 3 и 4\\ 1 и 4 и 2 и 3 \end{vmatrix}$ $\xlongequal{C_{1}-C_{3}, C_{2}-3C_{3},C_{4}-2C_{3}} \begin{vmatrix} 2 и 1 и 2 и -1\\ 0 и 0 и \цвет{красный}{1} и 0 \\ -1 и -4 и 3 и -2\\ -1 и -2 и 2 и -1 \end{vmatrix}=$ $=1\cdot(-1)^{2+5}\cdot \begin{vmatrix} 2 и 1 и -1\\ -1 и -4 и -2\\ -1 и -2 и -1 \end{vmatrix}$
Мы умножаем -1 из строки 2 и -1 из строки 3.