Обратная матрица методом Гаусса | Численные методы на Python
Для получения матрицы будем исходить из того, что она является решением уравнения , где – единичная матрица. Представим искомую матрицу как набор векторов-столбцов img а единичную матрицу как набор единичных векторов img Матричное уравнение в соответствии с правилами умножения матриц возможно заменить не связанной между собой системой уравнений img Каждое из этих уравнений может быть решено методом Гаусса. Заметим то обстоятельство, что все СЛАУ имеют одну и ту же матрицу коэффициентов, поэтому
Суть метода Гаусса-Жордана заключается в том, что если с единичной матрицей провести элементарные преобразования, которыми невырожденная квадратная матрица приводится к , то получится обратная матрица .
Для отображения всех элементарных преобразований, совершающихся над матрицей , на единичную матрицу , удобно “склеить” две матрицы в одну. Если матрицы и имели размер , то склеенная матрица будет иметь размер .
Прямой ход
Пусть матрица имеет размер . Тогда на первом этапе будет совершено шагов. На каждом шаге необходимо совершить три действия.
- Поменять местами строки и , в случае если . Этот шаг необходим для исключения ситуации нахождения на главной диагонали 0.
- Преобразовать элемент, стоящий на главной диагонали к 1. Для этого необохдимо домножить всю строку на .
- Обнулить все нижележащие элементы столбца.
 Для этого вычтем из каждой нижележащей строки c индексом результат умножения элемента c текущей строкой. Напомним, что в результате шага 2 первый элемент 1, поэтому первым элементом вычитаемой строки будет являться значение первого элемента строки , что и даст 0 в элементе
Для этого вычтем из каждой нижележащей строки c индексом результат умножения элемента c текущей строкой. Напомним, что в результате шага 2 первый элемент 1, поэтому первым элементом вычитаемой строки будет являться значение первого элемента строки , что и даст 0 в элементе
Обратный ход
Теперь необходимо преобразовать матрицу так, чтобы все элементы n-ого столбца выше стали равны нулю. Для этого прибавляем к n-1 строке соответсвующие элементы n-ой строки, умноженные на . К n-2 строке прибавляем соответсвующие элементы (n-1)-ой строки, умноженные на и т.д. Аналогичные действия необходимо совершить над оставшимися строками.
Реализация
Приведем реализацию функции inverse, принимающей в качестве аргумента исходную матрицу коэффициентов, и возвращающую матрицу, обратную к исходной. Склеим матрицу коэффициентов с единичной матрицей с помощью функции hstack
m = np.hstack((matrix_origin,
np.matrix(np.
diag([1.0 for i in range(matrix_origin.shape[0])]))))
Прямой ход
for k in range(n):
swap_row = pick_nonzero_row(m, k)
if swap_row != k:
m[k, :], m[swap_row, :] = m[swap_row, :], np.copy(m[k, :])
if m[k, k] != 1:
m[k, :] *= 1 / m[k, k]
for row in range(k + 1, n):
m[row, :] -= m[k, :] * m[row, k]
Для проверки первгого условия реализуем вспомогательную функцию pick_non_zero_row, возвращающую индекс первой строки, в которой элемент интересующего нас столбца не равен нулю
def pick_nonzero_row(m, k):
while k < m.shape[0] and not m[k, k]:
k += 1
return k
Обратный ход
for k in range(n - 1, 0, -1):
for row in range(k - 1, -1, -1):
if m[row, k]:
m[row, :] -= m[k, :] * m[row, k]
Возвратим преобразованную единичную матрицу, т. е. вторую часть “склееного” массива, воспользовавшись функцией hsplit
е. вторую часть “склееного” массива, воспользовавшись функцией hsplit
return np.hsplit(m, n // 2)[1]
Страница не найдена — ПриМат
© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Денис Стехун (8), Валентин Малявко (8), Елизавета Савицкая (8), Игорь Любинский (8), Юлия Стерлянко (8), Александр Базан (7), Анна Чалапчий (7), Константин Берков (7), Олег Шпинарев (7), Максим Швандт (6), Людмила Рыбальченко (6), Кирилл Волков (6), Татьяна Корнилова (6), Влад Радзивил (6), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2),
Глава 11.
 Метод Гаусса – Контрольные работы по математике и другим предметам!
Метод Гаусса – Контрольные работы по математике и другим предметам!
Метод Гаусса (или метод последовательного исключения неизвестных) состоит в том, что посредством последовательного исключения неизвестных данная система
(1.11.1) |
Превращается в ступенчатую (в частности, треугольную) систему
(1.11.2) |
Последняя система равносильна данной, но решать ее намного проще. Переход системы (1.11.1) к равносильной ей системе (1.11.2) называется Прямым ходом метода Гаусса, а нахождение переменных из системы (1.11.2) – Обратным ходом.
Рассмотрим этот метод на конкретных примерах.
Пример
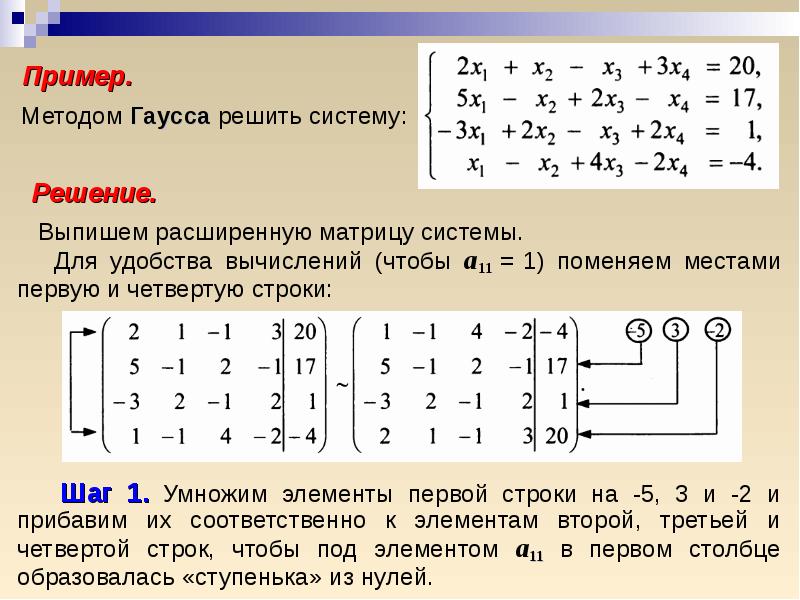
Решить систему методом Гаусса:
Решение
Исключим x1 из 2–го т 3–го уравнений. Для этого 1–е уравнение умножим на (–2) и прибавим его ко 2–му, а затем 1–е уравнение умножим на (–3) и прибавим его к 3–му уравнению:
Новая система равносильна данной. Исключим из 3–го уравнения x2 для чего 2–е уравнение вычтем из 3–го:
Исключим из 3–го уравнения x2 для чего 2–е уравнение вычтем из 3–го:
Из последней системы находим x3 = –1, x2 = (56 + x3)/11 = (56 – 1)/11 = 55/11 = 5, x1 = –22 +4×2 – 3×3 = –22 + 4×5 – 3×(–1) = 1.
Пример
Решить систему методом Гаусса:
Решение
Умножим 2–е уравнение на (–2), а 1–е – на 3 и сложим, а затем 2–е уравнение умножим на (–5), а 3–е – на 3 и тоже сложим. Получим Исключим x2 из 3–го уравнения, умножив 2–е уравнение на (–2) и прибавив его к 3–му уравнению:
Последнее уравнение превратилось в неверное равенство. Это говорит о том, что система несовместна, т. е. решений не имеет.
Пример
Решить систему методом Гаусса:
Решение
Исключим x1 из 2–го и 3–го уравнений. Для этого умножим 1–е уравнение на (–1) и прибавляем его ко 2–му, далее умножим 1–е же на (–4) и прибавляем к 3–му уравнению:
Так 2–е и 3–е уравнения одинаковы, одно из них отбрасываем:
Число уравнений – два – меньше числа неизвестных – три. Такая система имеет бесчисленное множество решений. Пусть x3 = 13k, где k – произвольное число. Тогда x2 = (16/13)x3 = 16k, x1 = 3×2 – 5×3 = –17k.
Такая система имеет бесчисленное множество решений. Пусть x3 = 13k, где k – произвольное число. Тогда x2 = (16/13)x3 = 16k, x1 = 3×2 – 5×3 = –17k.
Преобразования Гаусса удобно проводить не с самой системой уравнений, а с матрицей ее коэффициентов. Введем матрицу
(1.11.3) |
Называемую Расширенной матрицей системы (1.8.1) размера M´(N+1), так как матрица А дополнена столбцом свободных членов.
Пример
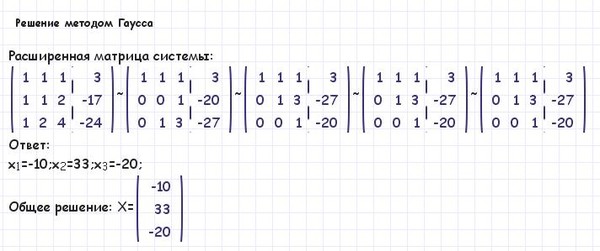
Найти решение системы уравнений методом Гаусса.
Решение
Составим расширенную матрицу этой системы, после чего выполним соответствующие шаги прямого хода Гаусса.
Шаг 1. Умножим первую строку матрицы AB на –2 и прибавим ее ко второй и третьей строке. Затем умножим первую строку матрицы AB на –3 и прибавим ее к четвертой строке. Получим
.
Поскольку две последние строки являются линейно зависимыми, то одну из них можно отбросить.
Шаг 2. Умножим вторую строку полученной матрицы на –7/5 и прибавим ее к третьей строке. Получим
.
Заключительный вид расширенной матрицы соответствует совместной системе трех уравнений с четырьмя неизвестными, ранг которой меньше числа неизвестных. Полагая X4 свободной переменной, получаем
Из этой системы получаем обратным ходом метода Гаусса
.
Данная система уравнений имеет бесчисленное множество решений, так как X4 может принимать любые значения.
Отметим Достоинства метода Гаусса по сравнению с методом обратной матрицы и методом Крамера:
– метод является значительно Менее трудоемким;
– метод дает возможность однозначно Установить, совместна система или нет, а в случае
Совместности, найти ее решения;
– метод дает возможность Найти максимальное число линейно независимых уравнений, т. е. определить ранг матрицы системы.
| < Предыдущая | Следующая > |
|---|
Метод Гаусса и Крамера
Матрицы
Метод Гаусса
Формулы Крамера
Матрица Определение
Прямоугольная таблица из m , n чисел, содержащая m – строк и n – столбцов, вида:
называется матрицей размера m n
Числа, из которых составлена матрица, называются элементами матрицы.
Положение элемента а i j в матрице характеризуются двойным индексом:
первый i – номер строки;
второй j – номер столбца, на пересечении которых стоит элемент.
Сокращенно матрицы обозначают заглавными буквами: А, В, С…
Коротко можно записывать так:
Иоганн Карл Фридрих Гаусс (30 апреля 1777, Брауншвейг — 23 февраля 1855, Гёттинген)
Метод Гаусса
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Система т линейных уравнений с п неизвестными имеет вид:
x 1 , x 2 , …, x n – неизвестные.
a i j – коэффициенты при неизвестных.
b i – свободные члены (или правые части)
Типы уравнений
Система линейных уравнений называется совместной , если она имеет решение, и несовместной , если она не имеет решения.
Совместная система называется определенной , если она имеет единственное решение и неопределенной , если она имеет бесчисленное множество решений.
Две совместные системы называются равносильными , если они имеют одно и то же множество решений.
Элементарные преобразования
К элементарным преобразованиям системы отнесем следующее:
- перемена местами двух любых уравнений;
- умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;
- прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.
Общий случай
Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:
Дана система:
1-ый шаг метода Гаусса
На первом шаге исключим неизвестное х 1 из всех уравнений системы (1), кроме первого. Пусть коэффициент . Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а 11 . Получим уравнение:
Пусть коэффициент . Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а 11 . Получим уравнение:
где
Исключим х 1 из второго и третьего уравнений системы (1). Для этого вычтем из них уравнение (2), умноженное на коэффициент при х 1 (соответственно а 21 и а 31 ).
Система примет вид:
Верхний индекс (1) указывает, что речь идет о коэффициентах первой преобразованной системы.
(1)
(2)
(3)
2-ой шаг метода Гаусса
На втором шаге исключим неизвестное х 2 из третьего уравнения системы (3) . Пусть коэффициент . Выберем его за ведущий элемент и разделим на него второе уравнение системы (3) , получим уравнение:
где
Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на Получим уравнение:
Предполагая, что находим
(4)
В результате преобразований система приняла вид:
Система вида (5) называется треугольной .
Процесс приведения системы (1) к треугольному виду (5) (шаги 1 и 2 ) называют прямым ходом метода Гаусса .
Нахождение неизвестных из треугольной системы называют обратным ходом метода Гаусса.
Для этого найденное значение х 3 подставляют во второе уравнение системы (5) и находят х 2 . Затем х 2 и х 3 подставляют в первое уравнение и находят х 1 .
(5)
Если в ходе преобразований системы получается противоречивое уравнение вида 0 = b , где b 0, то это означает, что система несовместна и решений не имеет.
В случае совместной системы после преобразований по методу Гаусса, составляющих прямой ход метода, система т линейных уравнений с п неизвестными будет приведена или к треугольному или к ступенчатому виду.
Треугольная система имеет вид:
Такая система имеет единственное
решение, которое находится в
результате проведения обратного хода метода Гаусса.
Ступенчатая система имеет вид:
Такая система имеет бесчисленное
множество решений.
Рассмотрим на примере
- Покажем последовательность решения системы из трех уравнений методом Гаусса
- Поделим первое уравнение на 2, затем вычтем его из второго (a 21 =1, поэтому домножение не требуется) и из третьего, умножив предварительно на a 31 =3
- Поделим второе уравнение полученной системы на 2, а затем вычтем его из третьего, умножив предварительно на 4,5 (коэффициент при x 2 )
Тогда
x 3 =-42/(-14)=3;
x 2 =8-2×3=2
x 1 =8-0,5×2-2×3=1
Метод Крамера
Метод Крамера—способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы. Создан Габриэлем Крамером в 1751 году.
Габриэль Крамер (31 июля 1704, Женева, Швейцария—4 января 1752, Баньоль-сюр-Сез, Франция)
Рассмотрим систему линейных уравнений с квадратной матрицей A , т. е. такую, у которой число уравнений совпадает с числом неизвестных:
е. такую, у которой число уравнений совпадает с числом неизвестных:
Теорема. Cистема
a 11 x 1 +a 12 x 2 +…+a 1n x n =b 1
a 21 x 1 +a 22 x 2 +…+a 2n x n =b 2
… …
a n1 x 1 +a n2 x 2 +…+a nn x n =b n
- a 11 x 1 +a 12 x 2 +…+a 1n x n =b 1 a 21 x 1 +a 22 x 2 +…+a 2n x n =b 2 … … a n1 x 1 +a n2 x 2 +…+a nn x n =b n
- a 11 x 1 +a 12 x 2 +…+a 1n x n =b 1 a 21 x 1 +a 22 x 2 +…+a 2n x n =b 2 … … a n1 x 1 +a n2 x 2 +…+a nn x n =b n
- a 11 x 1 +a 12 x 2 +…+a 1n x n =b 1 a 21 x 1 +a 22 x 2 +…+a 2n x n =b 2 … … a n1 x 1 +a n2 x 2 +…+a nn x n =b n
Имеет единственное решение тогда и только тогда, когда определитель матрицы этой системы отличен от нуля:
a 11 a 12 … a 1n
a 21 a 22 … a 2n
… …
a n1 a n2 … a nn
- a 11 a 12 … a 1n a 21 a 22 … a 2n … … a n1 a n2 … a nn
≠ 0
В этом случае решение можно вычислить по формуле Крамера
Для получения значения x k в числитель ставится определитель, получающийся из det(A) заменой его k- го столбца на столбец правых частей
- Пример.
 Решить систему уравнений :
Решить систему уравнений :
Решение.
Найдите оставшиеся компоненты решения.
- Формулы Крамера не представляют практического значения в случае систем с числовыми коэффициентами: вычислять по ним решения конкретных систем линейных уравнений неэффективно, поскольку они требуют вычисления (n+1)-го определителя порядка n , в то время как метод Гаусса фактически эквивалентен вычислению одного определителя порядка n . Тем не менее, теоретическое значение формул Крамера заключается в том, что они дают явное представление решения системы через ее коэффициенты. Например, с их помощью легко может быть доказан результат
- Решение системы линейных уравнений с квадратной матрицей A является непрерывной функцией коэффициентов этой системы при условии, что det A не равно 0 .
Найдите оставшиеся компоненты решения.
- Кроме того, формулы Крамера начинают конкурировать по вычислительной эффективности с методом Гаусса в случае систем, зависящих от параметра.

- зависящей от параметра , определить предел отношения компонент решения:
Решение.
- В этом примере определитель матрицы системы равен . По теореме Крамера система совместна при . Для случая применением метода Гаусса убеждаемся, что система несовместна. Тем не менее, указанный предел существует. Формулы Крамера дают значения компонент решения в виде
и, хотя при каждая из них имеет бесконечный предел, их отношение стремится к пределу конечному.
Ответ.
Приведенный пример поясняет также каким образом система линейных уравнений, непрерывно зависящая от параметра, становится несовместной: при стремлении параметра к какому-то критическому значению (обращающему в нуль определитель матрицы системы) хотя бы одна из компонент решения «уходит на бесконечность».
Использованные источники
- В.С. Щипачев, Высшая математика
- Ильин В. А., Позняк Э. Г. Линейная алгебра: Учебник для вузов.

- Волков Е.А. Численные методы.
- В.Е. Шнейдер и др., Краткий курс высшей математики,том I.
Метод Гаусса – Энциклопедия по машиностроению XXL
Для решения систем ЛАУ в большинстве проектных процедур анализа используют метод Гаусса или его разновидности. Вычисления по методу Гаусса состоят из прямого и обратного ходов. При прямом ходе из уравнений последовательно исключают неизвестные, т. е. исходную систему приводят к виду, в котором матрица коэффициентов становится треугольной. Такое приведение основано на /г-кратном применении формулы пересчета коэффициентов [c.229]Методы разреженных матриц. Если выполнять вычисления, пользуясь (5.4), для всех элементов матрицы коэффициентов, то экономичность метода Гаусса характеризуется кубической зависимостью затрат машинного времени Т от порядка системы уравнений п. Это приводит к ограничению области целесообразного применения метода Гаусса значениями п в несколько десятков.
 Однако во многих практических задачах п имеет порядок сотен или тысяч. Применение метода Гаусса к таким задачам оказывается эффективным, если учитывать свойство разреженности матрицы коэффициентов в системе решаемых уравнений (5.3).
[c.230]
Однако во многих практических задачах п имеет порядок сотен или тысяч. Применение метода Гаусса к таким задачам оказывается эффективным, если учитывать свойство разреженности матрицы коэффициентов в системе решаемых уравнений (5.3).
[c.230]Следует различать исходную и итоговую разреженность матрицы. Исходная разреженность определяется числом ненулевых элементов, имеющихся в матрице до начала выполнения исключений неизвестных по методу Гаусса, Такие нулевые элементы называют первичными. Однако в процессе вычислений по (5.4) некоторые коэффициенты Uij, бывшие нулевыми, могут стать ненулевыми. Такие коэффициенты называют вторичными ненулевыми элементами. Итоговая разреженность определяется суммарным числом первичных и вторичных ненулевых элементов, и эффективность учета разреженности матрицы тем выше, чем больше итоговая разреженность. [c.230]
Для решения систем ЛАУ с трехдиагональными матрицами коэффициентов используют разновидность метода Гаусса, называемую методом прогонки. Нетрудно заметить, что в трехдиагональных матрицах при исключении очередной неизвестной vt- из системы уравнений пересчет по (5.4) следует производить только в отношении диагонального элемента ац и свободного члена t-ro уравнения hi. Обозначим преобразованные по (5.4) значения ац и bi через Г( и qi соответственно. Тогда прямой ход по методу Гаусса сводится к расчету коэффициентов г,- и qi, i = 2,
[c.231]
Нетрудно заметить, что в трехдиагональных матрицах при исключении очередной неизвестной vt- из системы уравнений пересчет по (5.4) следует производить только в отношении диагонального элемента ац и свободного члена t-ro уравнения hi. Обозначим преобразованные по (5.4) значения ац и bi через Г( и qi соответственно. Тогда прямой ход по методу Гаусса сводится к расчету коэффициентов г,- и qi, i = 2,
[c.231]
Для решения системы линейных алгебраических уравнений (ЛАУ) вида AV=B выбирают либо метод Гаусса, либо итерационные методы. [c.233]
На точность решения задачи оказывают влияние задаваемые пользователем в исходных данных значения допустимых погрешностей si или б2, а также обусловленность модели. Однако задаваемые значения ei или ег могут вообще оказаться недостижимыми или из-за несходимости, или из-за слишком медленной сходимости вычислительного процесса. Поэтому если создаваемый ППП ориентирован на решение систем уравнений с широким диапазоном значений Ц, то нужно принимать специальные меры по обеспечению точности решения. При реализации метода Гаусса
[c.234]
При реализации метода Гаусса
[c.234]
Надежность применения метода определяется не только фактом принципиальной сходимости к корню, но и тем, каковы затраты времени Т на получение решения с требуемой точностью. Ненадежность итерационных методов проявляется либо при неудачном выборе начального приближения к корню (метод Ньютона), либо при плохой обусловленности задачи (методы релаксационные и простых итераций), либо при повышенных требованиях к точности решения (метод простых итераций), либо при высокой размерности задач (метод Гаусса при неучете разреженности). Поэтому при создании узкоспециализированных программ необходимы предварительный анализ особенностей ММ заданного класса задач (значений п, Ц, допустимых погрешностей) и соответствующий выбор конкретного метода. При создании ППП с широким спектром решаемых задач необходима реализация средств автоматической адаптации метода решения к конкретным условиям.
 Такая адаптация в современных ППП чаще всего применяется в рамках методов установления или продолжения решения по параметру.
[c.235]
Такая адаптация в современных ППП чаще всего применяется в рамках методов установления или продолжения решения по параметру.
[c.235]Прямой ход метода Гаусса состоит из L этапов. На t-м этапе исключаются переменные V,-, при этом пересчет коэффициентов по формуле Гаусса производится только в под- [c.244]
Для решения полученных систем алгебраических уравнений можно использовать метод Гаусса (метод последовательного исключения неизвестных). [c.58]
Блок-схема программы решений систем (25) и (26) совместно с ключами представлена на рис. 66, где решение системы (25) методом Гаусса Фз – если Re > О, то переход к Ф , если же Rf работы программы, — решение системы (26) методом Гаусса. [c.58]
| Рис. 5.25. Пример поиска по методу Гаусса-Зейделя |
 Однако уже при и > 3 это единственный метод (из исследуемых здесь), который позволяет получать решение за приемлемое время при дискретно изменяющихся параметрах.
[c.172]
Однако уже при и > 3 это единственный метод (из исследуемых здесь), который позволяет получать решение за приемлемое время при дискретно изменяющихся параметрах.
[c.172]Метод крутого восхождения. При использовании этого метода в отличие от градиентного корректировка направления производится не после каждого следующего шага, а по достижении в некоторой точке х на данном направлении частного экстремума целевой функции (рис. 6.9) аналогично методу Гаусса — Зайделя. Важной особенностью процедуры крутого восхождения является также регулярное проведение статистического анализа промежуточных результатов на пути к оптимуму. [c.130]
Среди точных методов, очень важных в теоретическом плане, много таких (метод обратной матрицы, метод Крамера и некоторые другие), которые не могут быть рекомендованы для вычислительной практики, так как они требуют для своей реализации очень большого объема вычислений и при некоторых неблагоприятных обстоятельствах могут приводить к большим ошибкам округления. Из точных методов, с вычислительной точки зрения наиболее удобен метод Гаусса или метод исключения неизвестных. Отметим следующие достоинства этого метода.
[c.89]
Из точных методов, с вычислительной точки зрения наиболее удобен метод Гаусса или метод исключения неизвестных. Отметим следующие достоинства этого метода.
[c.89]
Метод Гаусса легко реализуется на ЭВМ, так как сводится к некоторому числу простых однотипных операций. Он не требует памяти вычислительной машины кроме той, в которой хранятся коэффициенты матрицы и правые части системы. [c.89]
Реализацию метода Гаусса можно организовать таким образом, что ошибка округления будет минимальной из всех возможных (метод главного элемента). Число операций, потребных для реализации этого метода, также минимально, [c.89]
Метод Гаусса легко обобщается на одновременное решение нескольких систем, отличающихся столбцами свободных членов, а также на отыскание матрицы, обратной к А. Одновременно с решением системы уравнений может быть вычислен определитель матрицы А.
 [c.89]
[c.89]Итак, прямой ход метода Гаусса с выбором главного элемента по строке состоит из следующих операций, выполняемых над k-ш уравнением всех систем сразу (fe = 1, 2,. .., п). [c.90]
Из всех уравнений, следующих за fe-м, исключим неизвестное с номером S, для чего из уравнения с номером г г k) вычтем й-е уравнение, умноженное на Ors – После перечисленных действий системы превращаются в треугольные для всех k. Произведение всех главных элементов может только знаком отличаться от определителя матрицы А. Обратный ход метода заключается в том, что с помощью й-го уравнения k п, п — 1, гг — 2,. .., 2) исключается неизвестное, соответствующее главному элементу-этого уравнения из всех уравнений с номером, меньшим чем к. После окончания обратного хода на местах, где были расположены правые части, теперь будет располагаться решение рассматриваемых систем. Можно показать, что если взять п правых частей, в совокупности образующих единичную матрицу, то и ответов будет п столбцов, и они в совокупности будут образовывать матрицу обратную к А. Таким образом, метод Гаусса может быть использован для отыскания обратной матрицы.
[c.90]
Таким образом, метод Гаусса может быть использован для отыскания обратной матрицы.
[c.90]
Обычно эти системы уравнений решают методом Гаусса последовательного исключения неизвестных. Этот метод удобен в данном случае тем, что для ленточных матриц допускает существенную экономию арифметических операций и позволяет одновременно решать системы уравнений для нескольких правых частей. [c.168]
Метод Гаусса. Рассмотрим решение системы линейных алгебраических уравнений [c.24]
Простейшим прямым методом является метод исключения Гаусса, требующий примерно (2/3) арифметических действий. Метод Гаусса основан на приведении матрицы А к треугольной, у которой все элементы, расположенные ниже главной диагонали, равны нулю. [c.25]
Метод Гаусса широко используют в случае матрицы А общего вида. Для уравнений со специальными матрицами существуют более экономичные методы. Один из них — метод прогонки — применяют для решения системы с трехдиагональными матрицами А. Он изложен в предыдущем параграфе. Метод прогонки — частный случай метода Гаусса исключения неизвестных при решении системы (1.55). В прямом ходе метода прогонки уравнения приводятся к виду (1.57), в результате матрица системы будет треугольной. Обратный ход метода прогонки такой же, как и в методе Гаусса.
[c.26]
Он изложен в предыдущем параграфе. Метод прогонки — частный случай метода Гаусса исключения неизвестных при решении системы (1.55). В прямом ходе метода прогонки уравнения приводятся к виду (1.57), в результате матрица системы будет треугольной. Обратный ход метода прогонки такой же, как и в методе Гаусса.
[c.26]
В заключение отметим, что число операций в методе прогонки 8N, в то время как в методе Гаусса оно— для мат- [c.94]
Процедуру поиска оптимальных параметров при использовании метода Гаусса—Зейделя выполняют следующим образом. [c.152]
Для того, чтобы быть уверенным в том, что в результате применения метода Гаусса—Зейделя или метода наискорейшего спуска получен глобальный, а не локальный минимум целевой функции, приходится неоднократно повторять процедуру поиска, начиная его из различных начальных точек в пространстве параметров. [c.154]
Разреженной называют ту матрицу, в которой преобладают элементы, равные нулю. Разреженность S оценивается отношением числа нулевых элементов к общему числу элементов матрицы. Анализ показывает, что в математических моделях большинства поректируемых объектов число ненулевых элементов пропорционально первой степени п. Поэтому если учитывать разреженность матрицы, то Тм можно сделать линейной функцией п и суш,ественно расширить пределы эффективного применения метода Гаусса. Учет разреженности при этом заключается в том, что арифметические действия по (5.4) не производят, если выполняется хотя бы одно из условий aik=0 или а = 0.
[c.230]
Разреженность S оценивается отношением числа нулевых элементов к общему числу элементов матрицы. Анализ показывает, что в математических моделях большинства поректируемых объектов число ненулевых элементов пропорционально первой степени п. Поэтому если учитывать разреженность матрицы, то Тм можно сделать линейной функцией п и суш,ественно расширить пределы эффективного применения метода Гаусса. Учет разреженности при этом заключается в том, что арифметические действия по (5.4) не производят, если выполняется хотя бы одно из условий aik=0 или а = 0.
[c.230]
Для метода Гаусса Я=1, и если не учитывать разреженность матрицы коэффициентов А, то 7 2(rtV3 + 2n). Неучет разреженности ограничивает целесообразность применения метода Гаусса решением задач только невысокой размерности. При п>50 учет разреженности становится необходимым. Для метода Гаусса при учете разреженности и оптимальном упорядочении строк и столбцов матрицы А в задачах проектирования технических объектов имеем
[c. 233]
233]
Для решения систем ЛАУ итерационными методами с учетом разреженности матрицы коэффициентов имеем Я>1, а y—2Qn, где Q = 1—S—насыщенность матрицы. Так как Q = Kln, где К — среднее арифметическое для числа ненулевых элементов в одной строке матрицы А то у= 2К. Так, для моделей переключательных электрон ных схем получаем по результатам статистических иссле дований у ж 7,8, т. е. одна итерация выполняется быстрее чем по методу Гаусса. Однако из-за того, что И 1, ите рационные методы по показателю Г практически всегда проигрывают методу Гаусса. [c.233]
Экономичность метода решения систем АУ определяется также затратами оперативной памяти. При неучете разреженности только на хранение матрицы Якоби нужно п ячеек памяти. Поэтому если для одного слова используется 8 байт, то при п=100 для хранения требуется 80 кбайт, а при п = 500 — уже 2 Мбайт. Итак, подтверждается вывод о необходимости учета разреженности при решении задач с п>п р, где Ппр зависит от характеристик используемой ЭВМ и, как правило, составляет несколько десятков. В задачах анализа распределенных моделей, в которых п может превышать 10 , экономичность метода по затратам машинной памяти становится одной из важнейших характеристик. В таких случаях применяют либо релаксационные методы, либо метод Ньютона с использованием на каждой итерации метода Гаусса, но в рамках рассматриваемого ниже диакоптического подхода.
[c.234]
В задачах анализа распределенных моделей, в которых п может превышать 10 , экономичность метода по затратам машинной памяти становится одной из важнейших характеристик. В таких случаях применяют либо релаксационные методы, либо метод Ньютона с использованием на каждой итерации метода Гаусса, но в рамках рассматриваемого ниже диакоптического подхода.
[c.234]
Для решения систем линейных алгебраических уравнений (ЛАУ) AV = B применяют диакоптический вариант метода Гаусса, основанный на приведении матрицы коэффициентов к блочно-диагональному виду с окаймлением (БДО). При анализе электронных схем этот вариант называют методом подсхем. Б методе подсхем исходную схему разбивают на фрагменты (подсхемы). Фазовые переменные (например, узловые потенциалы) делят на внутренние переменные фрагментов и граничные переменные. Вектор фазовых переменных [c.243]
Прямые методы оценки н а пр а в л е н и й. Наиболее простым является метод покоординатного спуска (метод Гаусса —Зейдел я). Направление поиска выбирают поочередно вдоль всех координатных осей, т. е. вектор Р в (6.43) состоит из нулевых элементов за исключением одного, равного единице.
[c.284]
Наиболее простым является метод покоординатного спуска (метод Гаусса —Зейдел я). Направление поиска выбирают поочередно вдоль всех координатных осей, т. е. вектор Р в (6.43) состоит из нулевых элементов за исключением одного, равного единице.
[c.284]
Решение системы (2.12) обычно производится методом Гаусса для ряда значений частоты о). Получешпле [c.52]
На рис. 82 показана зависимость Sh (т) для различнйх значений параметра W, рассчитанная при помощи соотношения (6. 7. 30). Величина интеграла / (х) была определена путем численного интегрирования по методу Гаусса [97]. Из рис. 82 видно, что при X XI значение потока целевого компонента на межфазной поверхности стремится к квазистационарному для всех значений параметра W. Влияние конвективной диффузии на величину потока становится заметным лишь после достаточного времени контакта между жидкостью и газовым пузырьком. При этом величина вклада конвективной диффузии в массоперенос зависит от значения W. [c.276]
[c.276]
При равном числе элементов быстродействие программы метода Гаусса -Зейцеля (кривая – it = 2,5 с, 10 мин кривая 2 – / = 5 с, [c.137]
Методы покоординатного поиска. Типичными представителями группы многоэтапных методов поисковой оптимизации являются метод Гаусса—Зейделя и созданный на его основе метод Пауэлла [30]. В соответствии с методом Гаусса-Зейделя поиск на каждом этапе ведется по одному параметру при зафиксированных значениях всех остальных. Пример поиска по методу Гаусса-Зейделя в пространстве двух параметров показан на рис. 5.25. В примере сначала фиксируется значение параметра х, =х, ив этом сечении определяется значение параметрах , дающее лучшее значение Q. Затем фиксируется параметр Хг на уровне Х2 и находится значение первого параметра х”, соответствующее лучшему значению Q в сечении Х2 =Х2 = onst. В дальнейшем действия по. поиску экстремума Q повторяются в той же последовательности. [c.161]
Элементы линейной алгебры для школьников
Главная / Математика / Элементы линейной алгебры для школьников / Тест 2 Упражнение 1:Номер 1
ЕслиА- исходная матрица коэффициентов,В- столбец свободных членов,Х- столбец неизвестных,то система линейных алгебраических уравнений (СЛАУ) в матричном виде запишется как
Ответ:
 (1) АХ=В 
 (2) ВХ=А 
 (3) АВ=Х 
 (4) ХА=В 
Номер 2
В системе линейных алгебраических уравнений АХ=В Х- этоОтвет:
 (1) матрица коэффициентов  
 (2) столбец свободных членов 
 (3) столбец неизвестных 
Номер 3
В системе линейных алгебраических уравнений АХ=В А - этоОтвет:
 (1) матрица неизвестных  
 (2) матрица коэффициентов 
 (3) матрица свободных членов 
Упражнение 2:
Номер 1
Согласно методу Гаусса для решения СЛАУ ее матрицу коэффициентов необходимо привести к
Ответ:
 (1) треугольному виду 
 (2) диагональной матрице 
 (3) единичной матрице 
Номер 2
На первом шаге метода Гаусса решения СЛАУ
Ответ:
 (1) обнуляются элементы первого столбца матрицы коэффициентов 
 (2) обнуляются элементы первой строки матрицы коэффициентов 
 (3) обнуляются диагональные элементы матрицы коэффициентов 
Номер 3
В результате прямого хода метода Гаусса исходная матрица коэффициентов преобразуется к
Ответ:
 (1) треугольному виду 
 (2) единичной матрице 
 (3) диагональной матрице  
Упражнение 3:
Номер 1
При программной реализации метода Гаусса решения СЛАУ матрица коэффициентов хранится в
Ответ:
 (1) одномерном массиве 
 (2) двумерном массиве 
 (3) n-мерном массиве 
Номер 2
Исходная матрица коэффициентов и приписанный к ней справа столбец свободных коэффициентов называется
Ответ:
 (1) расширенной матрицей системы 
 (2) основной матрицей системы 
 (3) главной матрицей системы 
Номер 3
При программной реализации метода Гаусса решения СЛАУ вектор неизвестных хранится в
Ответ:
 (1) двумерном массиве 
 (2) n-мерном массиве 
 (3) одномерном массиве 
Упражнение 4:
Номер 1
Время работы прямого хода метода Гаусса решения СЛАУ с m строк и n столбцов асимптотически составляет Ответ:
 (1) O(mn2) 
 (2) O(n2) 
 (3) O(m2) 
Номер 2
Время работы обратного хода метода Гаусса решения СЛАУ с m строк и n столбцов асимптотически составляет Ответ:
 (1) O(m2)  
 (2) O(mn2)  
 (3) O(n2) 
Номер 3
При программной реализации метода Гаусса решения СЛАУ возникают проблемы
Ответ:
 (1) точности вычислений 
 (2) трудоемкости 
 (3) переполнения стека 
Упражнение 5:
Номер 1
Особенностью битовой СЛАУ является то, что
Ответ:
 (1) все коэффициенты матрицы системы являются 0 и 1 
 (2) она решается элементарно 
 (3) все коэффициенты матрицы системы являются единицами 
Номер 2
Метод Гаусса
Ответ:
 (1) применим к решению битовой СЛАУ без ограничений 
 (2) не применим к решению битовой СЛАУ  
 (3) применим к решению битовой СЛАУ, но с существенными ограничениями 
Номер 3
Особенностью решения битовой СЛАУ методом Гаусса является
Ответ:
 (1) отсутствие в вычислениях вещественных чисел 
 (2) отсутствие проблемы округления и точности вычислений  
 (3) отсутствие риска переполнения стека  
Упражнение 6:
Номер 1
Если в перестановке числоiрасположено левее числа j, ноi>j, то такая ситуация называется
Ответ:
 (1) инверсией 
 (2) аномалией  
 (3) прямым порядком  
Номер 2
Перестановка, в которой четное число инверсий, называется
Ответ:
 (1) четной  
 (2) нечетной 
 (3) позитивной 
 (4) негативной 
Номер 3
Число четных перестановок
Ответ:
 (1) равно числу нечетных 
 (2) больше числа нечетных  
 (3) меньше числа нечетных 
Упражнение 7:
Номер 1
Одна транспозиция в перестановке
Ответ:
 (1) меняет четность перестановки на противоположную  
 (2) не изменяет четность перестановки 
 (3) всегда приводит кк четной перестановке 
 (4) всегда приводит к нечетной перстановке 
Номер 2
Определитель матрицы - это
Ответ:
 (1) число 
 (2) матрица 
 (3) вектор 
Номер 3
Определитель существует
Ответ:
 (1) у произвольной матрицы 
 (2) только у квадратной матрицы 
 (3) только у вектора 
Упражнение 8:
Номер 1
Если в определителе есть нулевая строка (столбец),то он равен
Ответ:
 (1) 0 
 (2) 1 
 (3) -1  
Номер 2
Если в определителе поменять местами любые две строки, то он
Ответ:
 (1) сменит четность 
 (2) сменит знак 
 (3) будет равен 1  
Номер 3
Если в определителе поменять местами любые два столбца, то он
Ответ:
 (1) сменит четность 
 (2) сменит знак 
 (3) будет равен 1  
Упражнение 9:
Номер 1
Если элементы одного из стобцов (строки) определителя умножить на отличное от нуля действительное число, то
Ответ:
 (1) определитель изменится на это число 
 (2) определитель изменится в это число раз  
 (3) определитель не изменится  
Номер 2
Если в определителе две строки (столбца) равны, то
Ответ:
 (1) определитель равен 1 
 (2) определитель равен -1  
 (3) определитель равен 0  
Номер 3
Если в определителе к элементам строки (столбца) прибавить одно и то же отличное от нуля действительно число, то
Ответ:
 (1) определитель не изменится 
 (2) определитель изменится в это число раз 
 (3) определитель изменится на это число 
Упражнение 10:
Номер 1
Если в определителе две строки (столбца) линейно зависимы, то определитель равен
Ответ:
 (1) -1 
 (2) 0  
 (3) -1 
Номер 2
Если в определителе есть нулевая строка, то он равен
Ответ:
 (1) -1 
 (2) 0 
 (3) 1 
Номер 3
Определитель диагональной или треугольной матрицы равен
Ответ:
 (1) произведению элементов главной диагонали 
 (2) произведению ненулевых элементов 
 (3) произведению элементов первой строки 
Упражнение 11:
Номер 1
Для вычисления определителя произвольной матрицы с помощью метода Гаусса используется
Ответ:
 (1) только обратный ход 
 (2) только прямой ход 
 (3) прямой и обратный ходы 
Номер 2
Матрица называется вырожденной, если
Ответ:
 (1) ее определитель не равен 0 
 (2) ее определитель равен 1 
 (3) ее определеитель равен 0 
 (4) ее определеитель не равен 1 
Номер 3
Матрица называется невырожденной, если
Ответ:
 (1) ее определиетль не равен 0 
 (2) ее определитель не равен 1 
 (3) ее определеитель не равен -1 
Упражнение 12:
Номер 1
Определитель матрицы
\mathbf{A}=
\left( \begin{array}{cc}
1 & 2 \\
3 & 4
\end{array} \right)
равен
Ответ:
 (1) 1  
 (2) -2 
 (3) 2 
Номер 2
Определитель матрицы
\mathbf{A}=
\left( \begin{array}{ccc}
1 & 4 & 5 & \\
0 & 2 & 6 & \\
0 & 0 & 3 &
\end{array} \right)
равен
Ответ:
 (1) 0 
 (2) 6 
 (3) 12 
Номер 3
Определитель матрицы
\mathbf{A}=
\left( \begin{array}{ccc}
1 & 2 & 5 & \\
2 & 4 & 6 & \\
3 & 6 & 7 &
\end{array} \right)
равен
Ответ:
 (1) 0 
 (2) 28 
 (3) 35 
Оценка многоматричных гауссовских графов
J R Stat Soc Series B Stat Methodol. Авторская рукопись; доступно в PMC 1 ноября 2019 г.
Авторская рукопись; доступно в PMC 1 ноября 2019 г.
Опубликован в окончательной редакции как:
PMCID: PMC6261498
NIHMSID: NIHMS969429
Yunzhang Zhu
† Департамент статистики Государственного университета Огайо
Lexin Li
‡ Отдел биостатистики Калифорнийского университета в Беркли
† Статистический факультет Университета штата Огайо
‡ Отдел биостатистики Калифорнийского университета в Беркли
1 Адрес для переписки: Лексин Ли, Отдел биостатистики, Калифорнийский университет в Беркли, Беркли, Калифорния, 94720 U.S.A. ude.yelekreb@ilnixel См. Другие статьи в PMC, в которых цитируется опубликованная статья.Abstract
Матричные данные, в которых единицей выборки является матрица, состоящая из строк и столбцов измерений, появляются во многих научных и бизнес-приложениях. Матричная гауссовская графическая модель – полезный инструмент для характеристики структуры условной зависимости строк и столбцов. В этой статье мы используем невыпуклые штрафы для оценки нескольких графов на основе матричнозначных данных при нормальном матричном распределении.Мы предлагаем высокоэффективный алгоритм невыпуклой оптимизации, который можно масштабировать для графов с сотнями узлов. Мы устанавливаем асимптотические свойства оценки, которая требует менее строгих условий и имеет более точную границу вероятности ошибки, чем существующие результаты. Мы демонстрируем эффективность предлагаемого нами метода как с помощью моделирования, так и с помощью реальных анализов функциональной магнитно-резонансной томографии.
В этой статье мы используем невыпуклые штрафы для оценки нескольких графов на основе матричнозначных данных при нормальном матричном распределении.Мы предлагаем высокоэффективный алгоритм невыпуклой оптимизации, который можно масштабировать для графов с сотнями узлов. Мы устанавливаем асимптотические свойства оценки, которая требует менее строгих условий и имеет более точную границу вероятности ошибки, чем существующие результаты. Мы демонстрируем эффективность предлагаемого нами метода как с помощью моделирования, так и с помощью реальных анализов функциональной магнитно-резонансной томографии.
Ключевые слова: Условная независимость, Гауссова графическая модель, Матричное нормальное распределение, Невыпуклые штрафы, Функциональная магнитно-резонансная томография в состоянии покоя, Разрезанность
1 Введение
Гауссовская графическая модель широко используется для описания отношения условной зависимости, которое кодируется в матрице частичной корреляции среди набора взаимодействующих переменных. Было предложено большое количество статистических методов для оценки разреженной гауссовской графической модели (Meinshausen, Bühlmann, 2006; Yuan, Lin, 2007; Friedman et al., 2008; Ravikumar et al., 2011; Cai et al., 2011). , среди прочего). Существуют также расширения от оценки одного графика до нескольких графиков по группам (Guo et al., 2011; Danaher et al., 2014; Zhu et al., 2014; Lee and Liu, 2015; Cai et al., 2016) . Все эти методы предполагают, что вектор взаимодействующих переменных имеет нормальное распределение.В последние годы быстро появляются матричные данные, где каждая единица выборки представляет собой матрицу, состоящую из строк и столбцов измерений. Соответственно, нормальное матричное распределение становится все более популярным при моделировании таких матричнозначных наблюдений (Zhou, 2014). В рамках этого распределения недавно была разработана оценка разреженных графических моделей, цель которой – охарактеризовать зависимость строк и столбцов матричных данных (Инь и Ли, 2012; Ленг и Тан, 2012; Цилигкаридис и др.
Было предложено большое количество статистических методов для оценки разреженной гауссовской графической модели (Meinshausen, Bühlmann, 2006; Yuan, Lin, 2007; Friedman et al., 2008; Ravikumar et al., 2011; Cai et al., 2011). , среди прочего). Существуют также расширения от оценки одного графика до нескольких графиков по группам (Guo et al., 2011; Danaher et al., 2014; Zhu et al., 2014; Lee and Liu, 2015; Cai et al., 2016) . Все эти методы предполагают, что вектор взаимодействующих переменных имеет нормальное распределение.В последние годы быстро появляются матричные данные, где каждая единица выборки представляет собой матрицу, состоящую из строк и столбцов измерений. Соответственно, нормальное матричное распределение становится все более популярным при моделировании таких матричнозначных наблюдений (Zhou, 2014). В рамках этого распределения недавно была разработана оценка разреженных графических моделей, цель которой – охарактеризовать зависимость строк и столбцов матричных данных (Инь и Ли, 2012; Ленг и Тан, 2012; Цилигкаридис и др. , 2013). В этой статье мы стремимся к оценке нескольких графов для матричных данных при нормальном распределении матрицы.
, 2013). В этой статье мы стремимся к оценке нескольких графов для матричных данных при нормальном распределении матрицы.
Нашей мотивацией является анализ связности мозга на основе функциональной магнитно-резонансной томографии (фМРТ) в состоянии покоя. Между тем, наше предложение в равной степени применимо ко многим другим анализам сетевых данных. Функциональная связность мозга выявляет синхронизацию систем мозга через корреляции в нейрофизиологических показателях активности мозга. При измерении в состоянии покоя он отображает внутреннюю функциональную архитектуру мозга (Varoquaux and Craddock, 2013).Анализ связности мозга сейчас находится на переднем плане исследований в области нейробиологии. Накопленные данные свидетельствуют о том, что сеть связи изменяется при наличии многочисленных неврологических расстройств, и такие изменения содержат полезные сведения о патологиях болезней (Fox and Greicius, 2010). В типичном исследовании функциональной связи данные фМРТ собираются для нескольких субъектов из группы заболевания и нормального контроля. Для каждого отдельного субъекта наблюдаемые данные фМРТ принимают форму области по времени , матрицы , где количество областей мозга обычно составляет порядка 10 2 , а количество временных точек составляет от 150 до 200.На основе этой матрицы оценивается корреляционная матрица регион за регионом для описания графа связности мозга, по одному для каждой диагностической группы отдельно . На этом графике узлы представляют области мозга, а связи измеряют зависимость между областями мозга, где частичная корреляция является обычно используемой мерой корреляции (Fornito et al., 2013). Затем анализ связности мозга превращается в задачу оценки матриц частичной корреляции в рамках гауссовских графических моделей для нескольких групп.
Для каждого отдельного субъекта наблюдаемые данные фМРТ принимают форму области по времени , матрицы , где количество областей мозга обычно составляет порядка 10 2 , а количество временных точек составляет от 150 до 200.На основе этой матрицы оценивается корреляционная матрица регион за регионом для описания графа связности мозга, по одному для каждой диагностической группы отдельно . На этом графике узлы представляют области мозга, а связи измеряют зависимость между областями мозга, где частичная корреляция является обычно используемой мерой корреляции (Fornito et al., 2013). Затем анализ связности мозга превращается в задачу оценки матриц частичной корреляции в рамках гауссовских графических моделей для нескольких групп.
Наше предложение объединяет матричное нормальное распределение, оценку матриц множественной частичной корреляции и невыпуклые штрафы. Такая интеграция отличает наше предложение от существующих решений. Для матричнозначных данных прямое применение существующих методов оценки графической модели с предположением о векторном нормальном распределении, по сути, требует, чтобы столбцы матричных данных были независимыми, что, очевидно, неверно. Например, для фМРТ столбцы соответствуют временным рядам многократно измеряемой активности мозга и сильно коррелированы.Отбеливание может помочь уменьшить корреляцию между столбцами. В Разделе 5 мы сравниваем и показываем, что наш метод существенно превосходит два современных метода многографической оценки на основе векторных нормалей: Lee and Liu (2015) и Cai et al. (2016), обоим способствовало отбеливание. Среди немногих решений по оценке графической модели при матричном нормальном распределении (Инь и Ли, 2012; Ленг и Тан, 2012; Чжоу, 2014) ни одно не решает задачи оценки нескольких графиков в разных популяциях, а вместо этого сосредоточено только на одном графике.Наше предложение также отличается от двух недавних методов оценки нескольких графиков Qiu et al. (2016) и Хан и др. (2016), как в целях исследования, так и в подходах к оценке. В частности, Qiu et al. (2016) стремились оценить график в любом заданном месте, например, по возрасту, тогда как Han et al. (2016) стремились зафиксировать и обобщить общность, лежащую в основе набора отдельных графиков.
Например, для фМРТ столбцы соответствуют временным рядам многократно измеряемой активности мозга и сильно коррелированы.Отбеливание может помочь уменьшить корреляцию между столбцами. В Разделе 5 мы сравниваем и показываем, что наш метод существенно превосходит два современных метода многографической оценки на основе векторных нормалей: Lee and Liu (2015) и Cai et al. (2016), обоим способствовало отбеливание. Среди немногих решений по оценке графической модели при матричном нормальном распределении (Инь и Ли, 2012; Ленг и Тан, 2012; Чжоу, 2014) ни одно не решает задачи оценки нескольких графиков в разных популяциях, а вместо этого сосредоточено только на одном графике.Наше предложение также отличается от двух недавних методов оценки нескольких графиков Qiu et al. (2016) и Хан и др. (2016), как в целях исследования, так и в подходах к оценке. В частности, Qiu et al. (2016) стремились оценить график в любом заданном месте, например, по возрасту, тогда как Han et al. (2016) стремились зафиксировать и обобщить общность, лежащую в основе набора отдельных графиков. Напротив, наша цель состоит в том, чтобы одновременно оценить несколько графиков, по одному от каждой из данной группы субъектов. Кроме того, Qiu et al.(2016) предложили двухэтапную процедуру, которая сначала получала сглаженную оценку выборочной ковариационной матрицы посредством сглаживания ядра, а затем подключалась к ограниченному методу минимизации ℓ 1 Cai et al. (2011) для оценки матрицы точности. Han et al. (2016) впервые получили оценку всех отдельных графиков, снова используя Cai et al. (2011), а затем включили в целевую функцию, которая минимизирует расстояние Хэмминга между целевым медианным графиком и отдельными графиками.Для нашего предложения мы используем функцию потерь, основанную на правдоподобии, плюс комбинацию штрафа за невыпуклую разреженность и штрафа за невыпуклую разреженность группы, чтобы вызвать как разреженность, так и сходство между множественными матрицами частичной корреляции. Мы выбрали функцию потерь, чтобы обеспечить как теоретические свойства, так и положительную определенность оценки.
Напротив, наша цель состоит в том, чтобы одновременно оценить несколько графиков, по одному от каждой из данной группы субъектов. Кроме того, Qiu et al.(2016) предложили двухэтапную процедуру, которая сначала получала сглаженную оценку выборочной ковариационной матрицы посредством сглаживания ядра, а затем подключалась к ограниченному методу минимизации ℓ 1 Cai et al. (2011) для оценки матрицы точности. Han et al. (2016) впервые получили оценку всех отдельных графиков, снова используя Cai et al. (2011), а затем включили в целевую функцию, которая минимизирует расстояние Хэмминга между целевым медианным графиком и отдельными графиками.Для нашего предложения мы используем функцию потерь, основанную на правдоподобии, плюс комбинацию штрафа за невыпуклую разреженность и штрафа за невыпуклую разреженность группы, чтобы вызвать как разреженность, так и сходство между множественными матрицами частичной корреляции. Мы выбрали функцию потерь, чтобы обеспечить как теоретические свойства, так и положительную определенность оценки.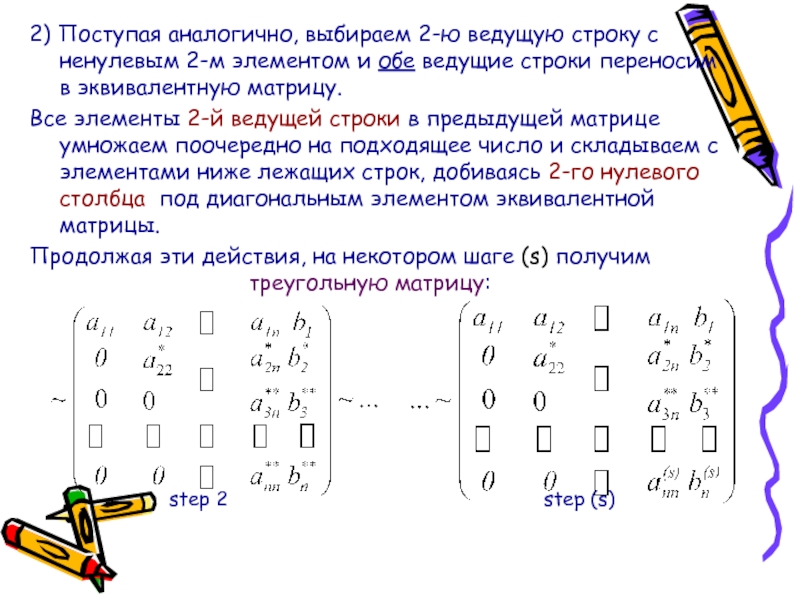 Между тем, наш выбор функции штрафа мотивирован убеждением, что истинный график является приблизительно разреженным, и разница графиков между несколькими группами также приблизительно разрежена.Другими словами, эти графики могут демонстрировать разные шаблоны подключения, но также рекомендуется быть похожими друг на друга. Более того, невыпуклые штрафы в многомерных моделях часто превосходят его выпуклые аналоги как в теории, так и на практике (Fan and Li, 2001a; Zhang, 2010; Shen et al., 2012). В контексте графической модели с векторным нормальным распределением было показано, что невыпуклые штрафы обеспечивают более точные и сжатые графические оценки (Fan et al., 2009; Шен и др., 2012).
Между тем, наш выбор функции штрафа мотивирован убеждением, что истинный график является приблизительно разреженным, и разница графиков между несколькими группами также приблизительно разрежена.Другими словами, эти графики могут демонстрировать разные шаблоны подключения, но также рекомендуется быть похожими друг на друга. Более того, невыпуклые штрафы в многомерных моделях часто превосходят его выпуклые аналоги как в теории, так и на практике (Fan and Li, 2001a; Zhang, 2010; Shen et al., 2012). В контексте графической модели с векторным нормальным распределением было показано, что невыпуклые штрафы обеспечивают более точные и сжатые графические оценки (Fan et al., 2009; Шен и др., 2012).
Новизна нашего предложения заключается как в вычислительном, так и в теоретическом вкладе. С точки зрения вычислений, осознавая, что невыпуклая оптимизация является более сложной задачей, чем выпуклая оптимизация, мы предлагаем высокоэффективный и масштабируемый алгоритм посредством комбинации двух современных методов оптимизации, алгоритма минимизации-максимизации (MM, Hunter and Lange, 2004) и метода переменного направления. множителей (ADMM, Boyd et al., 2011). Предлагаемый алгоритм является быстрым, обеспечивая сопоставимое время вычислений с его выпуклым аналогом.Это также намного быстрее, чем конкурирующие методы Ли и Лю (2015) и Цай и др. (2016). Кроме того, наш метод достаточно хорошо масштабируется и может работать для графов с числом узлов до сотен. Примечательно, что этот диапазон охватывает типичный размер сети связи мозга при нейровизуализационном анализе.
множителей (ADMM, Boyd et al., 2011). Предлагаемый алгоритм является быстрым, обеспечивая сопоставимое время вычислений с его выпуклым аналогом.Это также намного быстрее, чем конкурирующие методы Ли и Лю (2015) и Цай и др. (2016). Кроме того, наш метод достаточно хорошо масштабируется и может работать для графов с числом узлов до сотен. Примечательно, что этот диапазон охватывает типичный размер сети связи мозга при нейровизуализационном анализе.
Теоретически мы изучаем асимптотические свойства предложенной задачи оптимизации и устанавливаем точные теоретические результаты. Мы сосредотачиваемся на двух сценариях: наложение только штрафа за разреженность и наложение только штрафа за разреженность группы.Такое исследование пролило бы новый взгляд на связь и различие двух типов штрафов, а также облегчило бы прямое сравнение с существующими теоретическими результатами.
В частности, первый сценарий соответствует выполнению оценки разреженного графа для нескольких групп отдельно . В контексте оценки одного графа при векторном нормальном распределении теоретический анализ правильной идентификации разреженной структуры был исследован в Ravikumar et al.(2011); Fan et al. (2014); Ло и Уэйн-райт (2014). По сравнению с Ravikumar et al. (2011), которые использовали выпуклый штраф ℓ 1 и, таким образом, требовали непредставимого условия, наш результат разреженности не требует этого довольно строгого условия из-за использования невыпуклого штрафа. По сравнению с Fan et al. (2014), мы получаем более точную границу вероятности ошибки и улучшенное условие минимальной мощности сигнала. Более того, нам не нужна последовательная начальная оценка, поскольку Fan et al.(2014) сделали. По сравнению с Loh and Wainwright (2014) наш результат напрямую сопоставим. Но мы разрабатываем новую технику доказательства, которую можно легко обобщить на несколько графов. В контексте оценки одного графа при матричном нормальном распределении Ленг и Танг (2012) предоставили оценку и гарантию поиска разреженности; однако их результаты были установлены для некоторого неизвестного локального минимизатора их функции оптимизации.
В контексте оценки одного графа при векторном нормальном распределении теоретический анализ правильной идентификации разреженной структуры был исследован в Ravikumar et al.(2011); Fan et al. (2014); Ло и Уэйн-райт (2014). По сравнению с Ravikumar et al. (2011), которые использовали выпуклый штраф ℓ 1 и, таким образом, требовали непредставимого условия, наш результат разреженности не требует этого довольно строгого условия из-за использования невыпуклого штрафа. По сравнению с Fan et al. (2014), мы получаем более точную границу вероятности ошибки и улучшенное условие минимальной мощности сигнала. Более того, нам не нужна последовательная начальная оценка, поскольку Fan et al.(2014) сделали. По сравнению с Loh and Wainwright (2014) наш результат напрямую сопоставим. Но мы разрабатываем новую технику доказательства, которую можно легко обобщить на несколько графов. В контексте оценки одного графа при матричном нормальном распределении Ленг и Танг (2012) предоставили оценку и гарантию поиска разреженности; однако их результаты были установлены для некоторого неизвестного локального минимизатора их функции оптимизации. Напротив, мы получаем теоретические свойства для фактического локального оптимума, вычисленного с помощью алгоритма оптимизации.Кроме того, Zhou (2014) изучал ошибку оценки, а мы сосредоточились на реконструкции модели разреженности графической зависимости.
Напротив, мы получаем теоретические свойства для фактического локального оптимума, вычисленного с помощью алгоритма оптимизации.Кроме того, Zhou (2014) изучал ошибку оценки, а мы сосредоточились на реконструкции модели разреженности графической зависимости.
Второй сценарий соответствует оценке нескольких графов совместно. Оба Danaher et al. (2014) и Zhu et al. (2014) изучали оценку множественных графов со штрафами типа слияния. Однако Danaher et al. (2014) не предоставили никаких теоретических результатов по восстановлению графов, тогда как Zhu et al. (2014) получили разреженность глобального, но не локального решения их функции оптимизации.И Ли и Лю (2015), и Кай и др. (2016) предоставили теоретическую гарантию восстановления структуры с несколькими графами, но ни один из них не предоставил гарантии положительной определенности для результирующей оценки.
Остальная часть статьи организована следующим образом. В разделе 2 представлена модель и целевая функция со штрафом. В разделе 3 разработан алгоритм оптимизации. В разделе 4 исследуются асимптотические свойства. Раздел 5 представляет моделирование, а Раздел 6 анализ данных фМРТ. Раздел 7 завершает статью обсуждением.Все технические доказательства помещены в дополнительное онлайн-приложение.
В разделе 3 разработан алгоритм оптимизации. В разделе 4 исследуются асимптотические свойства. Раздел 5 представляет моделирование, а Раздел 6 анализ данных фМРТ. Раздел 7 завершает статью обсуждением.Все технические доказательства помещены в дополнительное онлайн-приложение.
2 Модель
2.1 Оптимизация с учетом штрафов
Предположим наблюдаемые данные, X ki , i = 1,…, n k , k = 1,…, K , из K гетерогенных популяций, с n k наблюдений из k -й группы. Каждое наблюдение X ki представляет собой матрицу p × q , где p обозначает пространственное измерение, а q – временное измерение.Мы предполагаем, что X ki следует нормальному матричному распределению, т.е.
Xk1,…, Xknki.id ~ N (Mk, ∑kS⊗∑kT), k = 1, ⋯, K,
, где M k = E [ X ki ], Σ kS ∈ IR p × p и Σ kT ∈ IR p × p обозначают матрицы пространственной и временной ковариации, соответственно, и ⊗ – произведение Кронекера. Это предположение о нормальном матричном распределении часто применялось во многих приложениях, связанных с матричнозначными наблюдениями (Yin and Li, 2012; Ленг и Tang, 2012). Это также научно правдоподобно в контексте нейровизуализационного анализа. Например, стандартное программное обеспечение для обработки нейровизуализации, такое как SPM (Friston et al., 2007) и FSL (Smith et al., 2004), принимает структуру, которая предполагает, что данные обычно распределяются по вокселю (местоположению) с коэффициентом шума и авторегрессионная структура, которая имеет тот же дух, что и нормальная формулировка матрицы.Мы обсудим возможное ослабление этого предположения в разделе 7.
Это предположение о нормальном матричном распределении часто применялось во многих приложениях, связанных с матричнозначными наблюдениями (Yin and Li, 2012; Ленг и Tang, 2012). Это также научно правдоподобно в контексте нейровизуализационного анализа. Например, стандартное программное обеспечение для обработки нейровизуализации, такое как SPM (Friston et al., 2007) и FSL (Smith et al., 2004), принимает структуру, которая предполагает, что данные обычно распределяются по вокселю (местоположению) с коэффициентом шума и авторегрессионная структура, которая имеет тот же дух, что и нормальная формулировка матрицы.Мы обсудим возможное ослабление этого предположения в разделе 7.
Наш основной интерес представляет пространственная частичная корреляционная матрица,
Ωk = Diag (∑kS) −1 / 2∑kS − 1Diag (∑kS) −1 / 2, k = 1, ⋯, K.
При нормальном распределении нулевой частный коэффициент корреляции подразумевает условную независимость двух узлов с учетом всех остальных на графике. k = DiagScale {∑i = 1nk (Xki − X¯k) (Xki − X¯k) T}, k = 1, ⋯, K,
k = DiagScale {∑i = 1nk (Xki − X¯k) (Xki − X¯k) T}, k = 1, ⋯, K,
, где DiagScale ( C ) = Diag ( C ) −1/2 C Diag ( C ) −1/2 для любой квадратной матрицы C .То есть мы включаем в (1) набор согласованных оценок корреляции. Оценка Γ̂ k была изучена Чжоу (2014), и ее скорость сходимости была установлена в многомерном режиме, что облегчило бы наше последующее асимптотическое исследование. Однако прямое решение (1) может столкнуться с некоторыми проблемами. Во-первых, количество неизвестных параметров в
{Ωk} k = 1K может намного превышать размер выборки, вызывая проблему с инверсией Γ̂ k .Во-вторых, нас обычно интересует поиск пар узлов, которые условно независимы от остальных. Однако минимизация (1) не дала бы точных нулевых оценок в
{Ωk} k = 1K, что затрудняет интерпретацию. В-третьих, часто желательно поощрять схожесть оценочных графиков для разных групп, полагая, что различия графической структуры обычно сосредоточиваются на некоторых локальных областях узлов. Например, при анализе связности мозга связи между областями мозга обычно редки (Zhang et al.k) −log det (Ωk)} + ∑k = 1Knk∑i ≠ jpλ1k (| ωkij |) + nmin∑i ≠ jpλ2 (ω1ij2 + ⋯ ωKij2)
В-третьих, часто желательно поощрять схожесть оценочных графиков для разных групп, полагая, что различия графической структуры обычно сосредоточиваются на некоторых локальных областях узлов. Например, при анализе связности мозга связи между областями мозга обычно редки (Zhang et al.k) −log det (Ωk)} + ∑k = 1Knk∑i ≠ jpλ1k (| ωkij |) + nmin∑i ≠ jpλ2 (ω1ij2 + ⋯ ωKij2)
(2)
, где λ max ( Ω k ) обозначает наибольшее собственное значение Ω k , n min = min 1≤ k ≤ K n k , a, R > 0, λ 1 k ; k = 1, ⋯, K и λ 2 – параметры настройки, а функция штрафа p λ (·): ℝ + → ℝ + удовлетворяет следующему условия:
p λ ( x ) неубывающая и дифференцируемая на ℝ + и p λ (0) = 0;
limx → 0 + pλ ′ (x) = λ;
p λ ( x ) + x 2 / b выпукло для некоторой константы b > 0;
pλ ′ (x) = 0 для | x | > aλ для некоторой константы a ≥ b /2.

Сделаем несколько замечаний. Во-первых, условие a ≥ b /2 обеспечивает существование p λ ( x ), а различные варианты a, b соответствуют различным невыпуклым штрафам. Например, a > 2, b = 2 / ( a – 1) приводит к штрафной функции Фан и Ли (2001a), а a = b /2, b > 0 по сравнению с Чжаном (2010). Здесь также могут использоваться другие типы невыпуклого штрафа, например.g., усеченный штраф 1 (Shen et al., 2012) или штраф ℓ q с q <1. Во-вторых, наша функция штрафа состоит из двух частей, штрафа за разреженность. который поощряет разреженность в каждой отдельной матрице частичной корреляции и штраф за разреженность группы, который поощряет общие модели разреженности в различных матрицах частичной корреляции. В-третьих, наша штрафная функция, как правило, невыпуклая, и использование невыпуклого штрафа дает несколько преимуществ. Это приводит к почти несмещенной оценке параметров, упрощает перекрестную проверку для настройки параметров и может обеспечить лучшую гарантию разреженности при менее строгих предположениях (Fan et al., 2009; Shen et al., 2012).
Это приводит к почти несмещенной оценке параметров, упрощает перекрестную проверку для настройки параметров и может обеспечить лучшую гарантию разреженности при менее строгих предположениях (Fan et al., 2009; Shen et al., 2012).
2.2 Настройка параметров
Настройка параметров всегда является сложной задачей для многомерных моделей, и мы предлагаем следующий подход перекрестной проверки для настройки параметров в (2). Руководствуясь нашим теоретическим анализом в разделе 4, мы позволили λ11 = λ1log (p∨q) n1q, ⋯, λ1K = λ1log (p∨q) nKq, где p ∨ q = max ( p, q ), и пусть λ = ( λ 1 , λ 2 ) T .k − l (λ)} – p].
Оптимальный параметр настройки для каждого раздела данных выбирается как λ ★ = arg min λ CV ( λ ), который затем используется для получения окончательной оценки с перекрестной проверкой. ( Ом̂ 1 ,, Ом̂ K ). Минимизация CV ( λ ) осуществляется с помощью простого поиска по сетке в области параметров настройки. Следуя как общей практике невыпуклых штрафов, так и нашему собственному теоретическому анализу, мы решили не настраивать a и b на p λ (·), а вместо этого устанавливаем b = 2 a и . равно некоторой постоянной, деленной на λ 1 .Мы также решили не настраивать R , поскольку наш метод не чувствителен к значению R , если оно достаточно велико. Мы также сделаем несколько замечаний, сравнивая настройку на основе перекрестной проверки при выпуклом и невыпуклом штрафах. При сравнении степени согласия двух выбранных моделей, по сути, сравнивается функция правдоподобия, оцененная с помощью ограниченной оценки максимального правдоподобия (MLE), то есть MLE по выбранной поддержке параметров.
( Ом̂ 1 ,, Ом̂ K ). Минимизация CV ( λ ) осуществляется с помощью простого поиска по сетке в области параметров настройки. Следуя как общей практике невыпуклых штрафов, так и нашему собственному теоретическому анализу, мы решили не настраивать a и b на p λ (·), а вместо этого устанавливаем b = 2 a и . равно некоторой постоянной, деленной на λ 1 .Мы также решили не настраивать R , поскольку наш метод не чувствителен к значению R , если оно достаточно велико. Мы также сделаем несколько замечаний, сравнивая настройку на основе перекрестной проверки при выпуклом и невыпуклом штрафах. При сравнении степени согласия двух выбранных моделей, по сути, сравнивается функция правдоподобия, оцененная с помощью ограниченной оценки максимального правдоподобия (MLE), то есть MLE по выбранной поддержке параметров. Так как выпуклый штраф, такой как ℓ 1 , не приводит к ограниченному MLE; скорее, он сжимает MLE для достижения оптимального компромисса смещения и дисперсии, оценка перекрестной проверки выпуклой штрафной оценки не подходит для сравнения моделей.Напротив, невыпуклая штрафная оценка почти идентична ограниченной MLE с учетом выбранной поддержки (Fan and Li, 2001a; Zhang, 2010; Shen et al., 2012). Таким образом, невыпуклый штраф лучше подходит для настройки перекрестной проверки для идентификации разреженности. При оценке графической модели с выпуклым штрафом перекрестная проверка и более традиционный байесовский информационный критерий показали плохие результаты (Liu et al., 2010). Далее мы численно сравниваем две штрафные функции в разделе 5.
Так как выпуклый штраф, такой как ℓ 1 , не приводит к ограниченному MLE; скорее, он сжимает MLE для достижения оптимального компромисса смещения и дисперсии, оценка перекрестной проверки выпуклой штрафной оценки не подходит для сравнения моделей.Напротив, невыпуклая штрафная оценка почти идентична ограниченной MLE с учетом выбранной поддержки (Fan and Li, 2001a; Zhang, 2010; Shen et al., 2012). Таким образом, невыпуклый штраф лучше подходит для настройки перекрестной проверки для идентификации разреженности. При оценке графической модели с выпуклым штрафом перекрестная проверка и более традиционный байесовский информационный критерий показали плохие результаты (Liu et al., 2010). Далее мы численно сравниваем две штрафные функции в разделе 5.
3 Вычисления
Невыпуклая оптимизация в целом более сложна, чем выпуклая оптимизация. В этом разделе мы разрабатываем высокоэффективный и масштабируемый алгоритм оптимизации невыпуклой минимизации (2). Алгоритм состоит из двух основных компонентов: алгоритм минимизации-максимизации, который оптимизирует (2) посредством последовательности выпуклых релаксаций (Hunter, Lange, 2004), и метод множителей с переменным направлением, который оптимизирует каждую выпуклую релаксацию (Boyd et al. , 2011). Сначала мы резюмируем нашу процедуру оптимизации, а затем подробно обсуждаем каждый отдельный компонент. Мы завершаем этот раздел обсуждением общих вычислительных затрат.
, 2011). Сначала мы резюмируем нашу процедуру оптимизации, а затем подробно обсуждаем каждый отдельный компонент. Мы завершаем этот раздел обсуждением общих вычислительных затрат.
3.1 Последовательная выпуклая релаксация с помощью алгоритма MM
Алгоритм MM обычно используется для приближенного решения невыпуклой оптимизации. Его основная идея – разложить целевую функцию на разность двух выпуклых функций. В нашей настройке мы линеаризуем невыпуклый штраф на основе предыдущей итерации x ( t ) , т.е.K (t + 1)) на шаге ( t + 1) и повторять t до сходимости.
3.2 Метод переменного направления умножителей
Для решения каждой релаксации (3) мы предлагаем алгоритм ADMM. В частности, мы вводим K новых переменных Δ k = ( δ kll ′ ) 1≤ l, l ′ ≤ p , так что Δ k = Ом k и K связанных двойных переменных Θ k = ( θ kll ′ ) 1≤ l, l ′ ≤ p , k = 1, ⋯, K . k) −log detΩ)) + ρ2‖Ω − ∆k (m) + Θk (m) ‖22},
k) −log detΩ)) + ρ2‖Ω − ∆k (m) + Θk (m) ‖22},
(4a)
(δkll ′ (m + 1)) k = 1K = arg minδ∈ℝK { ρ2∑k = 1K (δk − ωkll ′ (m + 1) −θkll ′ (m)) 2 + ∑k = 1Kbkll ′ (t) | δk | + cll ′ (t) ‖δ‖2}, Θk (m +1) = Θk (m) + Ωk (m + 1) −Δk (m + 1),
(4b)
Первое обновление (4a) может быть эффективно выполнено согласно следующей лемме.
Лемма 1
Рассмотрим следующую задачу оптимизации ,
минимизироватьΩ⪰0, λmax (Ω) ≤Rtrace (ΩΔ) −log detΩ + c2‖Ω‖F2
Пусть Δ = UDU ⊤ – собственное разложение Δ . Решение вышеуказанной проблемы дает
где Q – диагональная матрица с диагональными элементами
Qii = arg min0 Второе обновление (4b) имеет аналитическое решение согласно следующей лемме. Рассмотрим следующую общую задачу минимизации , минимизировать x∈ℝK12∑k = 1K (xk − ak) 2 + ∑k = 1Kbk | xk | + ν∑k = 1Kxk2. Его решение дает x ★ = {1 − ν [∑k = 1K (Sbk (ak)) 2] −1/2} + {Sb1 (a1), ⋯, SbK (aK)}, где S b ( a ) = Sign ( a ) (| a | – b ) + – это функция мягкого определения порога . Доказательства лемм 1 и 2 приведены в Приложении. Сделаем несколько замечаний относительно общих вычислений нашего алгоритма. Во-первых, вычислительная сложность за итерацию для выполнения шага ADMM составляет O ( Kp 3 ). Такая кубическая зависимость от p по существу неизбежна, если нужно получить положительно определенную матричную оценку. Если положительная определенность не требуется, существуют некоторые альтернативные функции потерь, такие как потеря псевдоядности, и возможны более быстрые алгоритмы.Мы выбрали вероятность потери отчасти из-за требования положительной определенности, а отчасти потому, что она более поддается теоретическому анализу. Наш асимптотический анализ фокусируется на двух сценариях. При этом мы также уточняем наш теоретический вклад. Для отдельного сценария оценки графа с λ 2 = 0 мы предоставляем новый результат разреженности, который обеспечивает более точную границу ошибки, требует менее строгих условий и выполняется для фактического локального оптимума алгоритма оценки. Для сценария совместной оценки нескольких графов с λ 1 = 0 мы устанавливаем разреженность для фактического локального, а не глобального минимизатора, и гарантируем как восстановление структуры нескольких графов, так и симметрию и положительную определенность.Более того, мы разрабатываем новую технику доказательства, которая допускает прямое обобщение от случая одного графа к случаю нескольких графов. Этот метод доказательства является новым в литературе и потенциально полезен также для теоретического анализа других моделей. Сначала мы рассмотрим случай, когда мы накладываем только штраф за разреженность и устанавливаем λ 2 = 0 в (2). Позволять
Ak0 = {(i, j): ωkij0 ≠ 0} обозначают носитель истинной частичной корреляционной матрицы.
Ωk0 = (ωkij0), i, j = 1,…, p, k = 1, ⋯, K .kΩ) −log det (Ω)}, (5) , что по сути является MLE над
{Ak0} k = 1К. Кроме того, пусть n min = min 1≤ k ≤ K n k и n max = max 1≤ k ≤ K n к . Сделаем следующие предположения. A1 Пусть
Γk0 = Diag (∑kS) −1 / 2∑kSDiag (∑kS) −1/2 обозначают истинную корреляционную матрицу. Предположим, что для всех k = 1, ⋯, K , c0−1 <λmin (Γk0) ≤λmax (Γk0) выполняется для некоторого положительного действительного числа c 0 . A2 Пусть
c1 = maxk‖Γk0‖∞, ∞,
c2 = maxk‖Ik‖∞, ∞, где
Ik = 12 [Ωk0] −1⊗s [Ωk0] −1 – это информационная матрица Фишера в группе k , а
‖A‖∞, ∞ = max1≤j≤p∑k = 1n | Ajk | – это операторная норма матрицы ℓ ∞ / ℓ ∞ A . Позволять
s0 = max1≤k≤Kmax1≤j≤p∑i = 1pI ((i, j) ∈Ak0), где I – индикаторная функция. Предположим, что 2c1c2c3 (1 + 2c12c2) s0log (p∨q) nkq≤1, k = 1, ⋯, K, , где c 3 – некоторая абсолютная постоянная. Предположение (A1) – это часто применяемое условие при анализе теоретических свойств многих типов оценщиков матрицы точности; см., например, Fan et al. (2009); Cai et al. (2016). Предположение (A2) ограничивает масштабирование измеренного уровня разреженности графика на с 0 в зависимости от размера выборки n и размера графика p . Подобное масштабирование использовалось Fan et al. Эта теорема показывает, что оракул является единственным минимизатором (2) при λ 2 = 0. То есть, когда максимальная степень узла с 0 не растет слишком быстро, как ( n , p ) стремится к бесконечности, при некотором выборе параметров настройки решение (2) может восстановить истинную структуру графов K с вероятностью, стремящейся к единице.Этот результат верен, когда минимальный сигнал удовлетворяет условию (6). Если мы дополнительно предположим, что c i , i = 1, 2, 3, являются постоянными, то условие минимального сигнала (6) примерно требует, чтобы мин (i, j) ∈Ak0 | ωkij0 | ≥O (log (p∨q) nkq), k = 1, ⋯, K. (7) Сравнение (7) с условием минимальной мощности сигнала в Fan et al. (2014), их состояние является субоптимальным с точки зрения зависимости от разреженности столбца / строки с 0 , поскольку для этого требуется
min (i, j) ∈Au | ωij0 |> O (s02logpn).Напротив, нам требуется только
min (i, j) ∈Au | ωij0 |> O (logpn). Наш результат сопоставим с результатом Loh and Wainwright (2014). Однако в их доказательстве использовалась техника прямого двойственного свидетеля, тогда как наше доказательство состоит из двух этапов: сначала устанавливается скорость сходимости для оценки оракула, а затем доказывается, что оценка оракула является единственным локальным минимумом. Преимущество нашего двухэтапного доказательства состоит в том, что его легко обобщить на случай множественных матриц частичной корреляции, когда дополнительно накладывается штраф за разреженность группы.Наконец, в отличие от Ленг и Танг (2012), которые установили свойство оракула для некоторого неизвестного локального минимизатора их целевой функции, мы получаем результат для нашего фактического локального минимизатора. Далее мы рассмотрим случай, когда мы накладываем только штраф за разреженность группы и устанавливаем λ 1 = 0 в (2). В этом случае невозможно восстановить оценщик оракула, если только
A10 = ⋯ = AK0, поскольку оценки графа, полученные с использованием только штрафа за разреженность группы, будут идентичны для всех групп.kΩ) −log det (Ω)}, , который, по сути, является MLE по совокупности соединений A и . Мы также немного модифицируем предположение (A2) и вводим следующее предположение. (A3) Пусть
s∼0 = max1≤j≤p∑i = 1pI ((i, j) ∈Au). Предположим, что 2c1c2c3 (1 + 2c12c2) s∼0log (p∨q) nkq≤1, k = 1, ⋯, K. Допущение (A3) напрямую сопоставимо с (A2). В (A3) s̃ 0 – это уровень разреженности соединения всех K графиков, тогда как s 0 в (A2) – максимальный уровень разреженности всех графиков. При предположениях (A1) и (A3) и условии, что min (i, j) ∈Au∑k = 1K (ωkij0) 2> 2c2c3klog (p∨q) nminq + (1 + c12c2) c3 (c0 + 2c1−1) 2nmaxnminKlog (p∨q) nminq, ( 8) для k = 1,…, K, существуют λ 2 и такое, что оракул Ω̂ k, A u , k = 1, ⋯, K – уникальный минимизатор (2) , когда R = 2a, b = 2 a, а λ 1 = 0, с вероятностью не менее 1−6K (p∨q) 2, при n, p → ∞. Эта теорема говорит, что если размер объединения опор
Ak0 не слишком велик, оценка оракула является единственным локальным оптимумом (2) при λ 1 = 0 и может восстановить истинную структуру графа с вероятностью, стремящейся к единице. Опять же, если мы будем рассматривать c i , i = 1, 2, 3, как константы, то условие (8) станет мин (i, j) ∈Au∑k = 1K (ωkij0) 2> O (nmaxnminKlog (p∨q) nminq). (9) Сравнение двух условий минимальной мощности сигнала (7) и (9) дает некоторые полезные сведения о двух штрафах.Отмечено, что ни одно состояние не сильнее и не слабее другого. Когда размеры выборки n 1 , ⋯, n K хорошо сбалансированы, а модели разреженности одинаковы для всех групп, добавление штрафа за разреженность группы должно облегчить восстановление графа. Это можно увидеть, проверив крайний случай, когда n 1 = ⋯ = n K = ñ и образцы разреженности идентичны. Мы генерируем данные из матрицы нормального распределения. Мы рассматриваем три структуры пространственной зависимости: цепной граф, хаб-граф и случайный граф, как показано на. Три типа графиков, используемых в наших исследованиях моделирования Мы сравниваем наш метод с некоторыми конкурирующими альтернативными решениями. Первый – это матричный гауссовский метод оценки нескольких графов с использованием выпуклого штрафа, т. Цепной график. Приведены среднее значение и стандартное отклонение (в скобках) критериев точности на основе 100 повторений данных. Лемма 2

3.3 Общие вычислительные затраты
 Во-вторых, хотя невыпуклая оптимизация в целом является более сложной задачей, наш невыпуклый алгоритм обеспечивает сопоставимое время вычислений с его выпуклым аналогом, как мы сообщаем в разделе 5. Это связано с быстрой сходимостью шага, который устраняет невыпуклость, т. Е. Шага ММ выпуклых релаксаций. Наше численное исследование показывает, что шаг ММ обычно сходится всего за несколько итераций.Следовательно, в основной вычислительной стоимости алгоритма преобладает выпуклый шаг оптимизации ADMM. В-третьих, наш алгоритм оптимизации достаточно хорошо масштабируется и может обрабатывать сети с количеством узлов до нескольких сотен. Примечательно, что при функциональном анализе связности типичный размер региональной сети мозга составляет от десятков до нескольких сотен. Таким образом, наш метод хорошо подходит для приложений, связанных с мозгом. Наконец, отметим, что некоторые шаги в нашем алгоритме можно распараллелить для дальнейшего ускорения вычислений.
Во-вторых, хотя невыпуклая оптимизация в целом является более сложной задачей, наш невыпуклый алгоритм обеспечивает сопоставимое время вычислений с его выпуклым аналогом, как мы сообщаем в разделе 5. Это связано с быстрой сходимостью шага, который устраняет невыпуклость, т. Е. Шага ММ выпуклых релаксаций. Наше численное исследование показывает, что шаг ММ обычно сходится всего за несколько итераций.Следовательно, в основной вычислительной стоимости алгоритма преобладает выпуклый шаг оптимизации ADMM. В-третьих, наш алгоритм оптимизации достаточно хорошо масштабируется и может обрабатывать сети с количеством узлов до нескольких сотен. Примечательно, что при функциональном анализе связности типичный размер региональной сети мозга составляет от десятков до нескольких сотен. Таким образом, наш метод хорошо подходит для приложений, связанных с мозгом. Наконец, отметим, что некоторые шаги в нашем алгоритме можно распараллелить для дальнейшего ускорения вычислений. 4 Асимптотика
 Сначала мы исследуем случай, когда есть только штраф за разреженность, т.е. когда λ 2 = 0. Затем мы исследуем случай, когда есть только штраф за разреженность группы, т.е. когда λ 1 = 0 Рассмотрение этих случаев позволяет по-новому взглянуть на связь и различие двух типов штрафных функций. Между тем, это позволяет прямое сравнение с существующими теоретическими результатами в гауссовских графических моделях.Мы также отмечаем, что мы не преследовали сценарий, в котором оба значения λ 1 и λ 2 не равны нулю, по двум причинам. Хотя, несомненно, представляет интерес изучение теоретических свойств при наличии обоих штрафов, такая характеристика, естественно, потребует явного количественного определения сходства между истинными графами. Подобные знания почти наверняка неизвестны в реальности, что делает асимптотический результат менее актуальным на практике. Более того, отсутствуют инструменты для преодоления некоторых технических трудностей при анализе условий KKT, когда используются как разреженные, так и групповые штрафы.
Сначала мы исследуем случай, когда есть только штраф за разреженность, т.е. когда λ 2 = 0. Затем мы исследуем случай, когда есть только штраф за разреженность группы, т.е. когда λ 1 = 0 Рассмотрение этих случаев позволяет по-новому взглянуть на связь и различие двух типов штрафных функций. Между тем, это позволяет прямое сравнение с существующими теоретическими результатами в гауссовских графических моделях.Мы также отмечаем, что мы не преследовали сценарий, в котором оба значения λ 1 и λ 2 не равны нулю, по двум причинам. Хотя, несомненно, представляет интерес изучение теоретических свойств при наличии обоих штрафов, такая характеристика, естественно, потребует явного количественного определения сходства между истинными графами. Подобные знания почти наверняка неизвестны в реальности, что делает асимптотический результат менее актуальным на практике. Более того, отсутствуют инструменты для преодоления некоторых технических трудностей при анализе условий KKT, когда используются как разреженные, так и групповые штрафы. Даже для векторной нормали работы такого типа не существует. Мы откладываем это стремление как потенциальное исследование в будущем.
Даже для векторной нормали работы такого типа не существует. Мы откладываем это стремление как потенциальное исследование в будущем.
4.1 Штраф за разреженность только при
λ 2 = 0
 (2009); Ло и Уэйнрайт (2014). Также следует отметить, что величины c 0 , c 1 , c 2 и s 0 могут расти вместе с размером выборки, пространственным измерением и временным измерением. .k, Ak0 – это уникальный минимизатор задачи (2) , когда R = 2a, b = 2 a, а λ 2 = 0, с вероятностью не менее 1−6K (p∨q) 2, при n, p → ∞.
(2009); Ло и Уэйнрайт (2014). Также следует отметить, что величины c 0 , c 1 , c 2 и s 0 могут расти вместе с размером выборки, пространственным измерением и временным измерением. .k, Ak0 – это уникальный минимизатор задачи (2) , когда R = 2a, b = 2 a, а λ 2 = 0, с вероятностью не менее 1−6K (p∨q) 2, при n, p → ∞.

4.2 Штраф за разреженность группы только с
λ 1 = 0 Легко с 0 ≤ с 0 ; и когда образец разреженности значительно отличается в разных группах, s ~ 0 может быть намного больше, чем s 0 . В этом смысле штраф за разреженность группы наиболее эффективен, когда модели разреженности одинаковы в разных группах. При (A1) и (A3) имеем следующий результат.
Легко с 0 ≤ с 0 ; и когда образец разреженности значительно отличается в разных группах, s ~ 0 может быть намного больше, чем s 0 . В этом смысле штраф за разреженность группы наиболее эффективен, когда модели разреженности одинаковы в разных группах. При (A1) и (A3) имеем следующий результат. Теорема 2

 В этом случае условие использования штрафа за разреженность группы сводится к
min (i, j) ∈Au∑k = 1K (ωkij0) 2K≥O (log (p∨q) n∼q), что явно менее жестко, чем условие (7), необходимое для использования штрафа за разреженность, поскольку
min (i, j) ∈Au∑k = 1K (ωkij0) 2K≥minkmin (i, j) ∈Ak0 | ωkij0 |.С другой стороны, если размеры выборки сильно несбалансированы или модели разреженности заметно различаются в разных группах, то использование штрафа за разреженность потребует менее строгих условий. По сравнению с некоторым существующим векторным анализом нескольких графов, наш результат относится к фактическому локальному минимизатору, а не к глобальному минимизатору, как в Zhu et al. (2014). Более того, мы гарантируем как восстановление структуры нескольких графов, так и положительную определенность оценки, в то время как Lee and Liu (2015); Cai et al.k − I) 2}, k = 1, ⋯, K.
В этом случае условие использования штрафа за разреженность группы сводится к
min (i, j) ∈Au∑k = 1K (ωkij0) 2K≥O (log (p∨q) n∼q), что явно менее жестко, чем условие (7), необходимое для использования штрафа за разреженность, поскольку
min (i, j) ∈Au∑k = 1K (ωkij0) 2K≥minkmin (i, j) ∈Ak0 | ωkij0 |.С другой стороны, если размеры выборки сильно несбалансированы или модели разреженности заметно различаются в разных группах, то использование штрафа за разреженность потребует менее строгих условий. По сравнению с некоторым существующим векторным анализом нескольких графов, наш результат относится к фактическому локальному минимизатору, а не к глобальному минимизатору, как в Zhu et al. (2014). Более того, мы гарантируем как восстановление структуры нескольких графов, так и положительную определенность оценки, в то время как Lee and Liu (2015); Cai et al.k − I) 2}, k = 1, ⋯, K. Мы фиксируем структуру временной зависимости как модель авторегрессии первого порядка. Мы сосредотачиваемся на оценке двухгруппового графа, то есть с K = 2, хотя наш метод может быть одинаково применен к более чем двум группам. Сначала мы генерируем граф, следуя одной из трех структур в одной группе, затем строим граф для другой группы, случайным образом добавляя несколько ребер к первому графу.Мы варьируем количество субъектов в каждой группе n k = {10, 20}, пространственное измерение p = {100, 200} и временное измерение q = {50, 100}. В интересах экономии места мы сообщаем результаты, когда n k = 10, в дополнительном онлайн-приложении.
Мы фиксируем структуру временной зависимости как модель авторегрессии первого порядка. Мы сосредотачиваемся на оценке двухгруппового графа, то есть с K = 2, хотя наш метод может быть одинаково применен к более чем двум группам. Сначала мы генерируем граф, следуя одной из трех структур в одной группе, затем строим граф для другой группы, случайным образом добавляя несколько ребер к первому графу.Мы варьируем количество субъектов в каждой группе n k = {10, 20}, пространственное измерение p = {100, 200} и временное измерение q = {50, 100}. В интересах экономии места мы сообщаем результаты, когда n k = 10, в дополнительном онлайн-приложении. 5.2 Сравнение
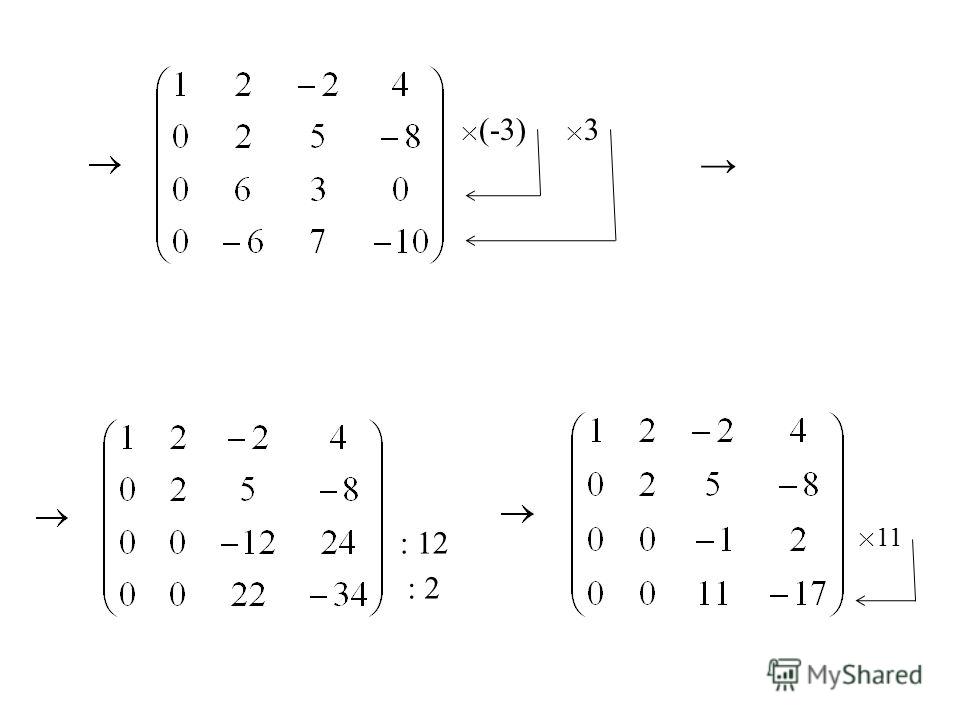 е.е., сочетание штрафа ℓ 1 и группы ℓ 1 . Ко второй категории относятся два современных метода оценки векторных гауссовских мультиграфов, Lee and Liu (2015) и Cai et al. (2016). Оба оценивают несколько графов, имеющих общую структуру, и оба используют выпуклый штраф. Поскольку оба метода были разработаны для векторных, а не для матричных данных, мы сначала применяем отбеливание, чтобы уменьшить временные корреляции между столбцами матричных данных, а затем применяем Lee and Liu (2015) и Cai et al.(2016). Все настройки параметров выполняются с помощью 5-кратной перекрестной проверки. чтобы суммировать результаты на основе 100 репликаций данных для трех структур пространственного графа в. Таким образом, предлагаемый нами метод явно превосходит альтернативные решения с точки зрения как идентификации разреженности, так и точности оценки графов.
е.е., сочетание штрафа ℓ 1 и группы ℓ 1 . Ко второй категории относятся два современных метода оценки векторных гауссовских мультиграфов, Lee and Liu (2015) и Cai et al. (2016). Оба оценивают несколько графов, имеющих общую структуру, и оба используют выпуклый штраф. Поскольку оба метода были разработаны для векторных, а не для матричных данных, мы сначала применяем отбеливание, чтобы уменьшить временные корреляции между столбцами матричных данных, а затем применяем Lee and Liu (2015) и Cai et al.(2016). Все настройки параметров выполняются с помощью 5-кратной перекрестной проверки. чтобы суммировать результаты на основе 100 репликаций данных для трех структур пространственного графа в. Таким образом, предлагаемый нами метод явно превосходит альтернативные решения с точки зрения как идентификации разреженности, так и точности оценки графов. Таблица 1
 Также сообщается среднее время работы (в секундах).Критерии оценки включают частоту ложноположительных результатов (FP), частоту ложноотрицательных результатов (FN), потерю энтропии (EL k ) и квадратичную потерю (QL k ). Мы сравниваем предложенный метод оценки на основе невыпуклых множественных графов (обозначенный как Nonconvex) с его выпуклым аналогом (обозначенным как Convex), методом Ли и Лю (2015) (обозначенным как Lee & Liu) и методом Cai et al. . (2016) (обозначен как Cai et al.).
Также сообщается среднее время работы (в секундах).Критерии оценки включают частоту ложноположительных результатов (FP), частоту ложноотрицательных результатов (FN), потерю энтропии (EL k ) и квадратичную потерю (QL k ). Мы сравниваем предложенный метод оценки на основе невыпуклых множественных графов (обозначенный как Nonconvex) с его выпуклым аналогом (обозначенным как Convex), методом Ли и Лю (2015) (обозначенным как Lee & Liu) и методом Cai et al. . (2016) (обозначен как Cai et al.). n k p q Метод FP FN EL 1 EL 1 EL EL1178 QL 2 Время 20 100 100 Невыпуклый 0.  003 (0,005)
003 (0,005) 0,000 (0,000) 0,093 (0,015) 0,105 (0,015) 0,230 (0,036) 0,265 (0,038) 116 Конвекс () 0,059 0,059 0,000 (0,000) 4,030 (2,160) 3,520 (1,700) 7,850 (4,410) 7,080 (3,640) 85 Ли и Лю 0,413 (0,058) 912. 000
000 1,475 (0,043) 0.960 (0,059) 3,991 (0,121) 2,562 (0,181) 1050 Cai et al. 0,005 (0,005) 6e-04 (0,002) 14,40 (1,100) 16,90 (2,000) 48,00 (5,000) 55,50 (9,300) 631 50 Невыпуклый 0,001 (0,003) 0,000 (0,000) 0,194 (0,028) 0,216 (0,027) 0.484 (0,072) 0,547 (0,069) 159 Выпуклая 0,053 (0,045) 0,000 (0,000) 6,500 (3,350) 5,460 (2,440) 916 (7,41223) 131216 131223 11,70 (5,800) 102 Ли и Лю 0,382 (0,008) 0,000 (0,000) 1,835 (0,070) 1,253 (0,070) 5,063 (0,218) 0,23 3,4 1096 Cai et al. 7e-04 (7e-04) 0,000 (0,000) 7,200 (0,750) 9,300 (1,500) 22,10 (2,300) 28,30 (4,700) 608 200 100 Невыпуклый 0,000 (0,001) 0,000 (0,000) 0,192 (0,023) 0,196 (0,018) 0,475 (0,023) 0,412 (0,023) 912 912 474 Выпуклый 0.032 (0,032) 0,000 (0,000) 11,40 (5,020) 9,110 (3,780) 22,70 (10,40) 18,70 (8,130) 398 0,0012 Ли и Лю 912 0,000 (0,000) 2,800 (0,059) 1,600 (0,044) 7.200 (0,170) 4.000 (0,120) 9308 Cai et al. 1e-04 (2e-04) 0,000 (0,000) 13,50 (1.200) 19.10 (2,400) 41,20 (3,800) 54,20 (7,800) 7875 50 Невыпуклый 0,000 (0,000) 0,000 (0,000) 0,390 (0,039) 0,384 (0,034) 0,972 (0,099) 912 930 912 (0,099) 0,912 Выпуклый 0,023 (0,027) 0,000 (0,000) 16,70 (6,510) 13,10 (4,550) 34.10 (14,50) 27,20 (10,400) 672 Ли и Лю 0,212 (0,031) 0,000 (0,000) 3,400 (0,088) 1,900 (0,180) 912,900 (0,22023) 5.000 (0,520) 11770 Cai et al. 0,001 (0,001) 0,000 (0,000) 8.200 (0,680) 10,50 (1,800) 23,70 (1,700) 29,00 (4,300) 7281 Таблица .Настройка такая же, как.
| n k | p | q | Метод | FP | FN | EL 1 | EL 1 | EL | QL 2Время | |
|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 100 | 100 | Невыпуклый | 0,005 (0,005) | 0,000 (0,000) | 0.121 (0,016) | 0,146 (0,016) | 0,328 (0,044) | 0,457 (0,054) | 195 |
| Выпуклый | 0,143 (0,045) | 0,001 (0,002) | 2,230 (1,11216 | ) 2,230 3,010 (1,430) | 4,850 (2,730) | 6,540 (3,510) | 178 | |||
| Ли и Лю | 0,471 (0,030) | 0,000 (0,000) | 0,950 (0,034) | 2,600 (0,120) | 3.700 (0,150) | 1107 | ||||
| Cai et al. | 0,006 (0,006) | 0,030 (0,008) | 10,50 (1,000) | 6,900 (0,660) | 40,80 (5,700) | 23,90 (3,700) | 605 | |||
| 50 | Невыпуклый | 0,029 (0,008) | 0,001 (0,002) | 0,276 (0,034) | 0,409 (0,094) | 0,736 (0,094) | 112,200 (0,094) | 112.200 (0,216) | ||
| Выпуклый | 0.304 (0,061) | 0,001 (0,002) | 1,690 (0,854) | 2,050 (0,883) | 3,720 (1,990) | 4,510 (2,190) | 153 | |||
| Ли и Лю | (0,01123)3e-04 (8e-04) | 1,300 (0,048) | 1,800 (0,068) | 3,800 (0,160) | 5.200 (0,280) | 1145 | ||||
| Cai et al. | 0,005 (0,005) | 0,026 (0,009) | 8,100 (0,800) | 6.100 (0,600) | 29,20 (3,900) | 22,00 (3,600) | 580 | |||
| 200 | 100 | Невыпуклый | 0,022 (0,001) | 0 (0,001) | 0,284 (0,021) | 0,459 (0,077) | 0,776 (0,057) 930 (0,31223) 930 (0,31255) 930 1206 | |||
| Выпуклый | 0,333 (0,016) | 0,001 (0,001) | 1,610 (0,073) | 2,510 (0.075) | 3,78 (0,18) | 6,120 (0,193) | 1082 | |||
| Ли и Лю | 0,204 (0,033) | 0,002 (0,001) | 3,000 (0,057) | 41216 | 4000 8.000 (0.180) | 10.90 (0.310) | 9600 | |||
| Cai et al. | 0,007 (0,010) | 0,079 (0,006) | 14,60 (0,800) | 13,10 (0,780) | 60,00 (6,000) | 96,20 (11,60) | 8310 | |||
| 50 | Невыпуклый | 0.020 (0,003) | 0,020 (0,006) | 0,700 (0,058) | 1,810 (0,169) | 1,850 (0,157) | 6,480 (0,638) | 1303 | ||
| Convex | () | 0,29 0,2 0,009 (0,002) | 3,400 (0,645) | 5,030 (0,873) | 7,900 (1,470) | 11,90 (2,090) | 1071 | |||
| Lee & Liu | 0,334 (0,024) 0,00616 9123 | 3,800 (0,088) | 6.000 (0,140) | 10,70 (0,290) | 22,70 (1,400) | 11904 | ||||
| Cai et al. | 0,004 (0,004) | 0,077 (0,008) | 11,10 (0,880) | 13,20 (0,980) | 38,50 (3,700) | 98,60 (14,10) | 7959 | |||
По сравнению с методом Ли и Лю (2015), опять же, наше предложение работает намного лучше как с точки зрения идентификации разреженности, так и с точки зрения точности оценки графов. В частности, метод Ли и Лю (2015) дает гораздо более высокую частоту ложных срабатываний, чем наш подход, в то время как ложноотрицательные показатели этих двух сопоставимы. Кроме того, ошибка оценки нашего метода в 3-10 раз меньше, чем у Ли и Лю (2015). По сравнению с методом Cai et al. (2016), наше предложение работает примерно так же с точки зрения идентификации разреженности, но существенно улучшает оценку графов.Собственно, ошибка оценки графика Cai et al. (2016) является худшим среди всех решений, и в некоторых ситуациях его ошибка оценки в 1000 раз выше, чем у предлагаемого нами метода. Поскольку и Ли и Лю (2015), и Кай и др. (2016) полагались на некоторые выпуклые штрафы, эти результаты частично отражают конфликт между согласованностью выбора и точностью оценки, что нередко при использовании выпуклого штрафа (Shen et al., 2012). Более того, он показывает преимущество прямой работы с матричными данными, а не с векторными данными после отбеливания.
5.3 Вычисления
Мы также подробно исследуем вычислительную стоимость предлагаемого нами решения. Все вычисления производились на одноядерном процессоре Xeon E5-2690 v3 с частотой 2,6 ГГц и 128 ГБ памяти. Сначала мы сообщаем и сравниваем время работы различных методов для примеров моделирования в разделе 5.2. В последнем столбце до записывается среднее время работы в секундах, округленное до целых чисел. Видно, что предлагаемый нами метод медленнее, чем его выпуклый аналог, но незначительно, и два времени работы сравнимы.Например, для цепного графа с n k = 20, p = 200, q = 100 среднее время работы нашего метода составляет 474 секунды, а для выпуклого решения – 398 секунд. Это связано с тем, что шаг выпуклой релаксации нашей невыпуклой целевой функции ММ обычно сходится всего за несколько итераций. Следовательно, в основной вычислительной стоимости нашего алгоритма преобладает выпуклый шаг оптимизации ADMM. С другой стороны, мы наблюдали замедление времени бега в 4–50 раз для двух других конкурирующих методов Lee and Liu (2015) и Cai et al.(2016). Для вышеупомянутой установки среднее время для Ли и Лю (2015) составляет 9 308 секунд, а для Цая и др. (2016) составляет 7875 секунд. Отчасти это связано с тем, что эти две альтернативы используют метод внутренней точки при оптимизации, который значительно замедляется при увеличении размера графа. В качестве дополнительной иллюстрации мы также указываем время вычислений, когда количество сетевых узлов постепенно увеличивается с p = 25 до p = 500 в дополнительном онлайн-приложении.Наш метод оказался сравнимым с выпуклым решением с точки зрения времени выполнения, но он намного быстрее, чем Lee and Liu (2015) и Cai et al. (2016), особенно когда размер графика p велик.
6 Анализ данных
6.1 Исследование расстройства аутистического спектра
Расстройство аутистического спектра (РАС) является все более распространенным расстройством психического развития, и его предполагаемая распространенность составляла 1 на каждые 68 американских детей по данным Центров по контролю и профилактике заболеваний в 2014 г.Для него характерны такие симптомы, как социальные трудности, дефицит общения, стереотипное поведение и задержка когнитивных функций (Rudie et al., 2013). Мы проанализировали набор данных фМРТ в состоянии покоя из исследования обмена данными визуализации мозга при аутизме (ABIDE) (Di Martino et al., 2014). Визуализацию выполняли на магнитотрио сканерах Siemens с параметрами сканирования: размер вокселя = 3 × 3 × 4 мм, толщина среза = 4 мм, количество срезов = 34, время повторения = 3 с и время эхо = 28 мс. Во время получения изображений всех испытуемых просили лежать неподвижно, бодрствовать и держать глаза открытыми на белом фоне с черным крестиком центральной фиксации.После удаления изображений с низким качеством или существенными пропущенными значениями мы сосредоточились на наборе данных из 795 субъектов, среди которых 362 имеют РАС, а 433 являются нормальными контрольными объектами. См. Основную демографическую информацию об изучаемых предметах. Все фМРТ-сканирования были предварительно обработаны с помощью стандартного конвейера, включая коррекцию времени среза, коррекцию движения, шумоподавление путем регрессии параметров движения и временного режима белого вещества и спинномозговой жидкости, пространственное сглаживание, полосовую фильтрацию и регистрацию.Затем каждое изображение мозга было разделено на 116 интересующих областей с использованием атласа анатомической автоматической маркировки (AAL) (Tzourio-Mazoyer et al., 2002). Затем временные ряды вокселей в одной и той же области были усреднены, в результате чего была получена матрица пространственно-временных данных для каждого отдельного субъекта с пространственным размером p = 116 и временным размером q = 146. Мы также комментируем, что: Помимо простого усреднения, существуют альтернативные подходы к суммированию данных вокселей в каждой области (Канг и др., 2016). Предлагаемый нами метод в равной степени применим к данным с другой сводкой.
Таблица 4
Демографическая информация набора данных ASD и набора данных ADHD.
| Группа | Исследование РАС | Исследование СДВГ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Случай | Контроль | Случай | Контроль | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Размер выборки | 362 | 433 | 96 | 91 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16,27 ± 6,893 | 11,38 ± 2,757 | 12,38 ± 3,112 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Муж. Научный интерес состоит в том, чтобы понять, чем функциональная связность мозга различается между субъектами с РАС и нормальным контролем. Мы применили к этим данным наш метод оценки невыпуклых штрафов с несколькими графами и настроили параметры с помощью 5-кратной перекрестной проверки.Быстрый анализ графика квантиль-квантиль (здесь не показан) показал, что нормальность приблизительно сохраняется для этих данных. сообщает результаты. Чтобы облегчить графическое представление, мы наносим на график только верхние 2% идентифицированных ссылок для групп аутизма и нормального контроля. Серые ссылки являются общими для обеих групп, а красные ссылки уникальны для каждой группы. Наши результаты в целом согласуются с литературой по РАС. Например, мы наблюдали снижение связи между двумя полушариями, как показано красными связями в контрольной группе между левой и правой половиной графика (Vissers et al., 2012). Мы также обнаружили некоторые области мозга с разными паттернами связи между двумя группами субъектов, такие как нижняя лобная извилина и веретенообразная извилина, которые также были отмечены в предыдущих исследованиях (Rudie et al., 2013; Di Martino et al., 2014; Tyszka et al., 2014). Предполагаемые сети связи для данных ABIDE. Левая панель предназначена для группы ASD, а правая панель – для обычного управления. Показаны верхние 2% ссылок, где серые ссылки являются общими для обеих групп, а красные ссылки уникальны для каждой группы. 6.2 Исследование синдрома дефицита внимания и гиперактивностиСиндром дефицита внимания и гиперактивности (СДВГ) является одним из наиболее часто диагностируемых расстройств нервного развития с дебютом у детей и имеет оценочную распространенность в детстве от 5 до 10% во всем мире (Pelham et al., 2007). Симптомы включают трудности с сосредоточением и вниманием, трудности с контролем поведения и чрезмерную активность. Эти симптомы могут сохраняться в подростковом и взрослом возрасте, приводя к пожизненным нарушениям (Biederman et al., 2000). Мы проанализировали набор данных фМРТ в состоянии покоя из Глобального конкурса ADHD-200. Изображения фМРТ получали на сканерах Siemens allegra 3T в Нью-Йоркском университете с параметрами сканирования: размер вокселя = 3 × 3 × 4 мм, толщина среза = 4 мм, количество срезов = 33, время повторения = 2 с и время эхо = 15 мс. . Во время съемки всех испытуемых просили бодрствовать и ни о чем не думать под черным экраном. Для каждого субъекта были получены одно или два сканирования фМРТ, и для каждого сканирования кураторы данных давали оценку контроля качества (удовлетворительно или сомнительно).Мы использовали только сканы, прошедшие контроль качества. Если оба сканирования объекта прошли контроль качества, мы произвольно выбрали первое сканирование. Если ни одно сканирование не прошло контроль качества, мы исключили этот объект из дальнейшего анализа. В результате получено 187 субъектов, 96 из которых являются комбинированными субъектами с СДВГ, а 91 типично разрабатывает контрольную группу. См. Демографическую информацию. Все сканированные изображения были предварительно обработаны с использованием конвейера Athena, включая коррекцию синхронизации срезов, коррекцию движения, шумоподавление, пространственное сглаживание, полосовую фильтрацию и регистрацию.Затем каждое изображение было разделено с использованием атласа AAL, и полученные данные представляют собой пространственно-временную матрицу с пространственным размером p = 116 и временным размером q = 172. Цель нашего исследования – оценить и сравнить функциональная сеть связи между ADHD и контрольными группами. Мы применили наш метод, настроенный на 5-кратную перекрестную проверку. График квантиль-квантиль показал, что данные примерно нормальные. показывает результаты первых 2% идентифицированных ссылок для двух групп.Мы обнаружили ряд областей мозга, которые демонстрируют различные паттерны связи между группами СДВГ и контрольной группой, включая лобную извилину, поясную извилину, мозжечок и червь мозжечка. Такие находки в целом согласуются с литературой по СДВГ. В частности, префронтальная кора отвечает за многие психические функции более высокого порядка, включая те, которые регулируют внимание и поведение, и обычно считается, что СДВГ связан с изменениями в префронтальной коре (Arnsten and Li, 2005).Поясная извилина связана с когнитивным процессом, и есть доказательства дисфункции передней части поясной извилины у пациентов с СДВГ (Bush et al., 2005). Мозжечок отвечает за моторный контроль и когнитивные функции, такие как внимание и речь, а также сообщалось о дисфункции мозжечка и аномалии червя мозжечка у пациентов с СДВГ (Toplak et al., 2006; Goetz et al., 2014). Предполагаемые сети связи для данных ADHD. Левая панель предназначена для группы СДВГ, а правая панель – для нормального контроля.Показаны верхние 2% ссылок, где серые ссылки являются общими для обеих групп, а красные ссылки уникальны для каждой группы. 7 ОбсуждениеВ этой статье мы предложили невыпуклый штрафной метод для одновременной оценки нескольких графов из матричнозначных данных. Мы разработали эффективный алгоритм оптимизации и получили четкие теоретические результаты. Численный анализ продемонстрировал явные преимущества нашего метода по сравнению с некоторыми альтернативными решениями. Мы выступаем за невыпуклый штраф, поскольку он дает почти несмещенную оценку, лучше подходит для настройки перекрестной проверки и может обеспечить лучшую теоретическую гарантию при менее строгих предположениях. Между тем мы осознаем его потенциальные ограничения. С точки зрения точности прогнозирования и оценки невыпуклый штраф имеет тенденцию работать лучше, когда сигнал в данных является разреженным и имеет относительно большую величину. С другой стороны, выпуклый штраф имеет тенденцию работать лучше, если сигнал не является разреженным и если имеется много небольших сигналов.Это явление постоянно наблюдается в контексте выбора многомерной линейной модели и оценки графа (Fan et al., 2009; Zhang, 2010; Shen et al., 2012). Мы также поясняем, что предложенная формулировка оптимизации со штрафами в (2) в общем случае является невыпуклой задачей. Однако (2) может быть выпуклым для частных случаев, когда λ 1 = 0 или λ 2 = 0 при некотором выборе параметров, например, R = 2a, b = 2 a .Выпуклость позволяет нам установить желаемые теоретические свойства для этих частных случаев. Это стратегия, обычно используемая в многомерном теоретическом анализе. Например, для выбора переменных обычно только показано, что существуют некоторые значения параметров настройки, при которых решение является согласованным с выбором или приобретает свойство оракула (Fan and Li, 2001b; Zhang, 2010; Shen et al., 2013) . Ключевым предположением в нашем предложении является матричное нормальное распределение. Такое предположение широко используется и является научно правдоподобным в контексте анализа связи мозга.С другой стороны, мы признаем, что это предположение не всегда может быть верным. Есть два возможных способа ослабить это предположение. Первый – рассмотреть другую функцию потерь; например, функция потерь D-следа (Zhang and Zou, 2012) или функция потерь псевдоядия (Lee and Hastie, 2015). Функция штрафа, разработанная в нашем решении, может быть объединена с этими альтернативными функциями потерь. Мы выбрали функцию потерь, основанную на правдоподобии, потому что она более поддается теоретическому анализу благодаря свойству сильной выпуклости отрицательной функции потерь логарифмической вероятности и потому, что она дает положительно определенную оценку для матрицы точности.Второй тип релаксации возник в результате недавних разработок, расширяющих векторную гауссовскую графическую модель до полупараметрической модели (Liu et al., 2012) или полностью непараметрической модели (Lee et al., 2016). Параллельное распространение этих методов на матричные данные необходимо для будущих исследований. В этой статье мы в первую очередь сосредоточились на оценке графа , которая представляет собой другую проблему, чем вывод графа , хотя и то, и другое может фактически дать разреженное представление структуры графа.Мы понимаем, что вывод на основе графов – очень сложная проблема, и в настоящее время это активная область исследований, которая привлекает все большее внимание (Janková and van de Geer, 2015; Xia and Li, 2017). Альтернативным решением является оценка байесовского графа (Peterson et al., 2015; Zhu et al., 2016), которая может автоматически давать действительный вывод для всех параметров при условии, что априорное значение задано надлежащим образом. Однако основной проблемой для класса байесовских решений является вычисление и масштабируемость до больших графов.Метод выборки, используемый в байесовском анализе, в вычислительном отношении намного дороже, чем оптимизация в частотном решении. Для гауссовой графической модели каждая итерация цепи Маркова методом Монте-Карло (MCMC) требует O ( p 3 ) операций, а количество шагов MCMC, необходимых для микширования, обычно намного больше, чем количество шагов ADMM в нашем оптимизация. Оценка масштабируемого байесовского графа – важное направление будущего. Таблица 2График концентратора.Настройка такая же, как.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Для этого вычтем из каждой нижележащей строки c индексом результат умножения элемента c текущей строкой. Напомним, что в результате шага 2 первый элемент 1, поэтому первым элементом вычитаемой строки будет являться значение первого элемента строки , что и даст 0 в элементе
Для этого вычтем из каждой нижележащей строки c индексом результат умножения элемента c текущей строкой. Напомним, что в результате шага 2 первый элемент 1, поэтому первым элементом вычитаемой строки будет являться значение первого элемента строки , что и даст 0 в элементе
 Решить систему уравнений :
Решить систему уравнений :

