Матрица гаусса онлайн: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Метод Гаусса онлайн

Назначение сервиса. Онлайн-калькулятор предназначен для решения системы линейных уравнений методом Гаусса, а также методом Гаусса-Жордано (чем они отличаются). Результат решения сохраняется в формате Word и Excel.

Шаг №1
Шаг №2
Видеоинструкция
Оформление Word
Также решают

Инструкция. Для получения онлайн решения необходимо выбрать количество переменных: 2345678 и количество строк 23456

Вместе с этим калькулятором также используют следующие:
По координатам вершин треугольника найти площадь, уравнения сторон, уравнение медианы, уравнение биссектрисы

По координатам вершин пирамиды найти

Построение графика функции методом дифференциального исчисления

Экстремум функции двух переменных

Вычисление пределов

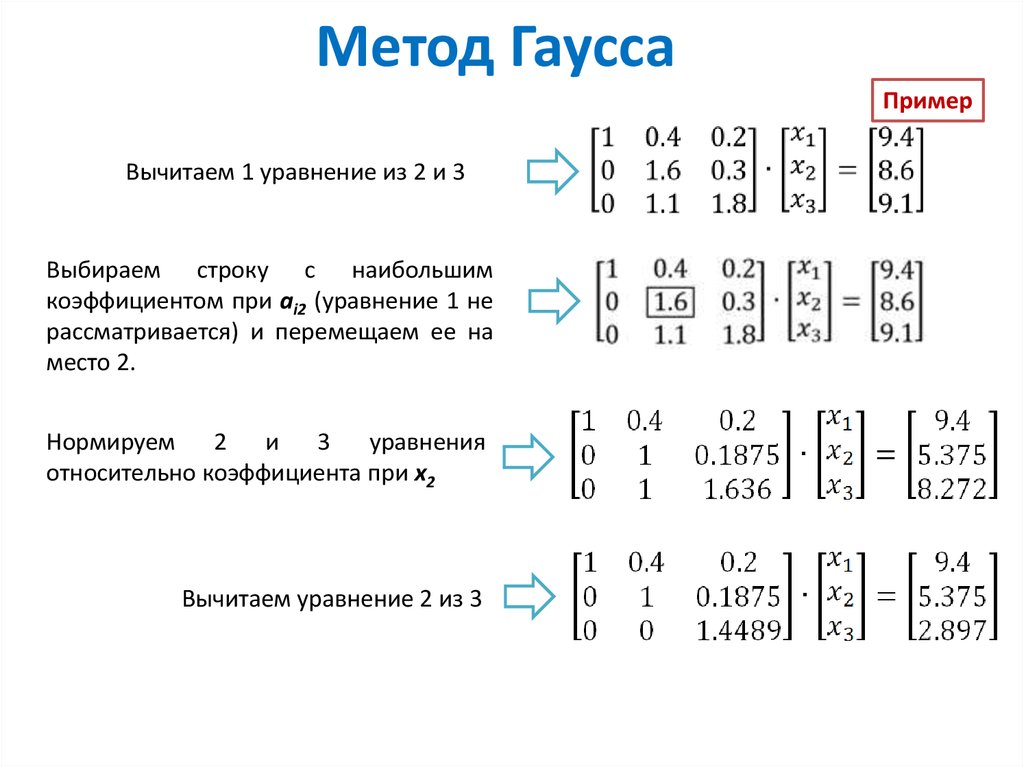
Смысл метода: последовательно исключаем переменную за переменной, пока в одной из строк не будет однозначно определена переменная x_i. Идею можно проиллюстрировать на простом примере:
x₁ - x₂ = 3
-x₁ + 2x₂ = 1
=========== (складываем строки)
-x₂ + 2x₂= 3 + 1 = 4 или x₂ = 4
Откуда, x₁ = 7

Суть метода можно понять, проанализировав пример решения.

Пример.
2x₁-x₂=0
-x₁+x₂+4x₃=13
x₁+2x₂+3x₃=14

Решение.
Запишем систему в виде расширенной матрицы:

2	-1	0
-1	1	4
1	2	3

Далее умножаем 2-ую строку на (2) и добавляем к первой:

0	1	8
-1	1	4
1	2	3

Добавим 3-ую строку к 2-ой:

0	1	8
0	3	7
1	2	3

Умножим первую строчку на (3), 2-ую строку умножаем на (-1).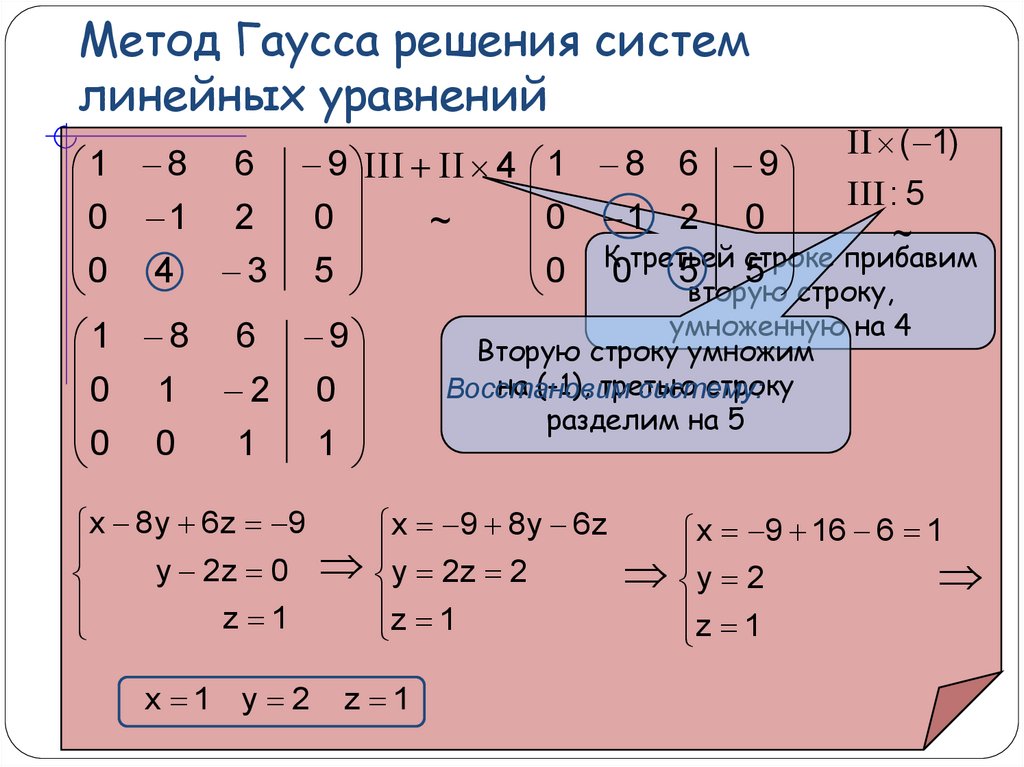

Следующее действие: складываем первую и вторую строки:

0	0	17
0	3	7
1	2	3

Теперь исходную систему можно записать как:
x₃ = 51/17
x₂ = [27 - 7x₃]/3
x₁ = [14 - (2x₂

+ 3x₃)]
Из 1-ой строки выражаем x₃: 51/17 = 3
Из 2-ой строки выражаем x₂: (27 - 7*3)/3 = 2
Из 3-ой строки выражаем x₁: (14 - 2*2 - 3*3) = 1

Вывод: метод Гаусса является достаточно простым методом при небольшом количестве переменных и позволяет найти точное значение переменных. Процесс отыскания переменных можно упростить, если каждый раз сортировать столбцы по возрастанию.

Как решить систему уравнений. Руководство к онлайн сервису

Построить график функции Точки разрыва функции Построение графика методом дифференциального исчисления Упростить выражение

Примеры решенийРанг матрицыМетод КрамераУмножение матриц Определитель матрицы Метод обратной матрицы Обратная матрица Метод Гаусса онлайн LU разложение матрицы Производная онлайн

В указанных онлайн-калькуляторах решение сохраняется в формате Word со всеми выкладками. Также доступна проверка решений в Excel.

Прямые методы

Решение СЛАУ методом Гаусса. Этот сервис также используется для исследования системы алгебраических уравнений с помощью теоремы Кронекера-Капелли.

Решение СЛАУ методом Крамера происходит через нахождение определителей матрицы.
Метод обратной матрицы. Также смотрите онлайн-калькулятор по нахождению матричных уравнений (A*X = B, X*A = B, и других).

Исследование системы линейных уравнений

Базисные решения системы линейных уравнений.
Исследование системы линейных уравнений на совместность и определенность.
Решение системы линейных однородных уравнений позволяет найти нетривиальное и фундаментальное решения.
Координаты вектора в базисе. В естественном базисе заданы векторы a=(1,1,0)^T, b=(1,-1,1)^T, c=(-3,5,-6)^T, d=(4,-4,5)^T. Показать, что векторы образуют базис.

Итерационные методы

Решения СЛАУ методом простой итерации.
Решения СЛАУ методом Зейделя.
Решения системы методом декомпозиции (LU-разложение).

см. также раздел Высшая математика онлайн: онлайн-сервисы по аналитической геометрии, линейной алгебре, теории вероятности и другим.

Методы нахождения определителей

Определитель матрицы разложением по строкам и столбцам через миноры.
Определитель матрицы методом треугольников
Определитель матрицы методом понижения порядка
Определитель методом приведения к треугольному виду (методом Гаусса)
Определитель матрицы методом декомпозиции

При изучении данной темы могут понадобится следующие онлайн-калькуляторы:

Ранг матрицы
Обратная матрица через алгебраические дополнения .Определение миноров матрицы, алгебраических дополнений, транспонированной матрицы
Обратная матрица методом Жордано-Гаусса
Умножение матриц
Преобразование матрицы до треугольной

LU разложение матрицы

Калькулятор по аналитической геометрии и векторной алгебре

Помощь в решении
Поиск
Поддержать проект

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Я создал онлайн-калькулятор для конечных полей и линейной алгебры

Демонстрация моего нового калькулятора, умножающего матрицы в \(\mathbb{F}_4\)

TL;DR: Вот он: matrixer.davidaugustat.com

Все знакомы с так называемыми действительными числами, означающие числа, которые мы используем в нашей повседневной жизни, такие как 3, -4, 0,5 или \(\pi\). Будучи студентом информатики, я посещаю математический класс в университете, где мы используем не только действительные числа, но и другие алгебраические поля, так называемые конечные поля.

В отличие от действительных чисел, конечные поля имеют только конечный набор чисел. При выполнении математических операций \(+, -, \cdot\) или \(/\) над элементами из этого ограниченного набора чисел “вырваться” из него невозможно, т.е. тот же набор.

Маленький пример

Поле \(\mathbb{F}_5\) состоит из 5 элементов: \(0, 1, 2, 3\) и \(4\).
В этом поле, например. \(3+4 = 2\) и \(2\cdot 3 = 1\) являются допустимыми выражениями. Очевидно, что в реальных числах это не имело бы никакого смысла, но в \(\mathbb{F}_5\) имеет смысл.

Но как я вычислил эти числа?
На самом деле это не так сложно для одиночных вычислений. Все, что вам нужно сделать, это вычислить, как с действительными числами, но затем

разделить результат на \(5\) и взять остаток .

Например, \(3+4\) равно \(7\) в \(\mathbb{R}\). \(7/5 = 1\), Остаток: \(2\). Поэтому \(3+4 = 2\) в \(\mathbb{F}_5\).

То же самое для умножения: \(2\cdot 3\) равно \(6\) в \(\mathbb{R}\). \(6/5 = 1\), Остаток: \(1\). Поэтому \(2\cdot 3 = 1\) в \(\mathbb{F}_5\).

Если мы проделаем это для всех элементов \(\mathbb{F}_5\), мы получим следующие таблицы для сложения и умножения:

\[\begin{массив}{c|ccccc} + & 0 & 1 & 2 & 3 & 4 \\ \hline 0 и 0 и 1 и 2 и 3 и 4 \\ 1 и 1 и 2 и 3 и 4 и 0 \\ 2 и 2 и 3 и 4 и 0 и 1 \\ 3 и 3 и 4 и 0 и 1 и 2 \\ 4 и 4 и 0 и 1 и 2 и 3 \конец{массив}\] \[\begin{массив}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 и 0 и 0 и 0 и 0 и 0 \\ 1 и 0 и 1 и 2 и 3 и 4 \\ 2 и 0 и 2 и 4 и 1 и 3 \\ 3 и 0 и 3 и 1 и 4 и 2 \\ 4 и 0 и 4 и 3 и 2 и 1 \конец{массив}\]

В целом

Для любого другого конечного поля, число элементов которого является простым числом (\(\mathbb{F}_2, \mathbb{F}_3, \mathbb{F}_5, \mathbb{F}_7, \dots\)) работает точно так же. Единственная разница в том, что вы делите не на \(5\), а на соответствующее количество элементов в поле.

в \(\mathbb{F}_3\) есть три элемента \(0, 1\) и \(2\).
\(1+2 = 3\) в \(\mathbb{R}\). \(3/3 = 1\), Остаток: \(0\). Поэтому \(1+2 = 0\) в \(\mathbb{F}_3\).

Как я уже сказал, эти правила применимы только к конечным полям, число элементов которых является простым числом. Это означает, что вы не можете вычислять так в \(\mathbb{F}_4\), так как \(\mathbb{F}_4\) имеет 4 элемента и \(4\) не является простым числом.

Но почему я не могу этого сделать?
Ответ таков: \(\mathbb{F}_4\) больше не было бы полем, если бы вы вычисляли таким образом. В алгебраическом поле каждый элемент (кроме \(0\)) должен иметь мультипликативный обратный элемент по определению. Мультипликативный обратный элемент \(y\) элемента \(x\) определяется как \(x \cdot y = 1\).
Другими словами: для каждого элемента в поле должен существовать элемент, так что элемент, умноженный на другой элемент, равен \(1\).

Если мы посмотрим на \(\mathbb{F}_4\), то быстро обнаружим, что оно не соответствует этому критерию, если вычисляется как поле простых чисел. В качестве контрпримера возьмем элемент \(2\):

\[\начать{выравнивать*} 2\cточка 0 = 0 \\ 2\cdot 1 = 2 \\ 2\cточка 2 = 0 \\ 2\cdot 3 = 2 \конец{выравнивание*}\]

Как видите, элемента нет, так что \(2\cdot y = 1\). Следовательно, \(\mathbb{F}_4\) не является полем, если мы определяем его таким образом.

Однако, если количество элементов в поле является простым числом, существует мультипликативный обратный элемент для для каждого элемента. Доказательство этого было бы слишком сложным для этой статьи, поэтому я не буду его включать.

Вот где вступают в игру расширенные поля

Тем не менее, можно определить поле с 4 элементами. Такое поле называется расширенным полем , и с ним гораздо сложнее производить расчеты, поскольку его элементы и правила несколько необычны.

Фактическое поле \(\mathbb{F}_4\) содержит элементы \(0, 1, \alpha\) и \(\alpha + 1\). Да, верно, \(\alpha + 1\) — это не математическое выражение, а элемент \(\mathbb{F}_4\).

Подробно объяснять как считать с этими элементами не буду, но вот таблицы:

\[\begin{массив}{c|ccccc} + & 0 & 1 & \alpha & \alpha+1\\ \hline 0 и 0 и 1 и \альфа и \альфа+1 \\ 1 и 1 и 0 и \альфа+1 и \альфа\\ \альфа & \альфа & \альфа+1 & 0 & 1 \\ \альфа+1 & \альфа+1 & \альфа & 1 & 0 \конец{массив}\] \[\begin{массив}{c|ccccc} \cdot & 0 & 1 & \alpha & \alpha+1\\ \hline 0 и 0 и 0 и 0 и 0 \\ 1 и 0 и 1 и \альфа и \альфа+1 \\ \альфа и 0 и \альфа и \альфа+1 и 1 \\ \alpha+1 & 0 & \alpha+1 & 1 & \alpha \конец{массив}\] 92\). Расчет с ними вызывает головную боль и занимает много времени.

В университете мы довольно часто используем эти конечные поля, а также занимаемся линейной алгеброй, используя конечные поля. Желаю вам удачи в умножении этих матриц без ошибок:

\[\begin{pmatrix} 1 & \альфа & \альфа+1 \\ 0 и \альфа+1 и 1 \\ \альфа & 0 & \альфа+1 \end{pматрица} \cdot \begin{pматрица} 1 и 1 \\ \альфа+1 и \альфа\\ 0 и \альфа+1 \end{pmatrix}\]

Matrixer

Как вы, вероятно, заметили, вычисления с конечными полями не так-то просто выполнить вручную. Однако, поскольку мне очень нравится программировать, я решил просто написать калькулятор, который может делать эти вычисления за меня.

Все еще помните матрицы сверху? Мой калькулятор под названием «Matrixer» может сделать это менее чем за 20 миллисекунд:

Не верите мне? Вот ссылка на этот точный расчет.

Matrixer может не только перемножать матрицы, но и делать следующие вещи:

Базовые вычисления с числами (сложение, вычитание, умножение, деление и возведение в степень)
Вычислить мультипликативный обратный элемент (\(x\cdot y = 1\))
Вычислить аддитивный обратный элемент (\(x+y = 0\))
Матрицы сложения и вычитания
Транспонировать матрицы (поменять местами строки и столбцы)
Умножение матрицы на вектор
Сложение, умножение и вычитание векторов
Решить систему однородных уравнений
Преобразовать матрицу в сокращенную ступенчатую форму строки

Все эти вычисления можно выполнять с вещественными числами, а также с конечными полями \(\mathbb{F}_2, \mathbb{F}_3, \mathbb{F}_4, \mathbb{F}_5, \ mathbb{F}_7, \mathbb{F}_8, \mathbb{F}_9, \mathbb{F}_{11}, \mathbb{F}_{13}, \mathbb{F}_{17}\ ) и \(\mathbb{F}_{19}\).

Интерфейс 93)+(2/3)

является допустимым вводом.

Матрицы: Заключены в фигурные скобки, строки разделены точкой с запятой, а столбцы — запятой.
Например, {1, 2, 3; 4, 5, 6} представляет следующую матрицу:

\[\begin{pматрица} 1 и 2 и 3 \\ 4 и 5 и 6 \конец{pmatrix}\]

Векторы: Заключено в квадратные скобки, строки разделены запятой.
Например, [1, 2, 3] представляет следующий вектор:

\[\begin{pматрица} 1\\ 2\\ 3 \конец{pmatrix}\] 92\)

j это \(\йота\) (йота)

Это означает, что приведенный выше расчет при вводе выглядит так:
{1, a, a+1; 0, а+1, 1; а, 0, а+1} * {1, 1; а+1, а; 0, a+1}

Более подробные инструкции по вводу выражений можно найти на самом сайте.

О коде

Весь калькулятор написан на языке JavaScript, работающем на интерфейсе в браузере пользователя. Это означает, что веб-сайт хорошо масштабируется, поскольку на сервере не выполняется код, а пользователю отправляются только статические файлы.

Одним из недостатков этого является то, что Matrixer работает не во всех браузерах. До сих пор я обнаружил, что этот веб-сайт не работает в Internet Explorer 11. Ничего не происходит, когда я нажимаю кнопку «Рассчитать». Тем не менее, в любом другом браузере, который у меня был под рукой (Chrome, Firefox, Edge), калькулятор работал безупречно.

На сегодняшний день полный исходный код составляет около 7000 строк (включая комментарии и пустые строки). Сюда входят файлы JavaScript, HTML и CSS.

Я решил сделать весь проект открытым исходным кодом, и вы можете найти полный исходный код в этом репозитории GitHub. Он выпущен под лицензией GNU GPL V3.0, что означает, что вы можете повторно использовать этот код для своих собственных проектов, если вы указываете мое имя и публикуете свой код под той же лицензией.

И все!

Взгляните на мой калькулятор здесь, если вы еще этого не сделали, а также взгляните на код, если хотите. Если что-то не работает или кажется неправильным, просто свяжитесь со мной, и я постараюсь решить проблему.

‎App Store: Калькулятор Матрицы

Description

Matrix Calculator

This App Covers:

Matrix Addition Calculator
Matrix Subtraction Calculator
2×2 Matrix Multiplication Calculator
3×3 Matrix Multiplication Calculator
Matrix Determinant Calculator
3×3 Inverse Matrix Calculator
2×2 Inverse Matrix Calculator
2×2 Matrix Addition & Калькулятор вычитания
Матричный калькулятор сложения и вычитания 4×4
4×4 Калькулятор умноженного матрикса
4×4 Калькулятор обратного матрикса
Калькулятор квадратного матричного матрикса
Калькулятор матрикса. калькулятор умножения
обратный калькулятор
обратная матрица
обратная матрица
калькулятор rref
генератор матриц
обратная матрица
онлайн-калькулятор матриц
обратимая матрица
обратная матрица 3×3
расширенный калькулятор матриц
калькулятор матриц онлайн
обратная матрица 3×3
калькулятор определителя матрицы
обратная матрица 2×2
обратная матрица 2×2
калькулятор преобразования матрицы
обратная матрица 3×3
инвертор матриц
формула матрицы
онлайн-решатель матриц
обратный калькулятор матрица
калькулятор собственных значений
2×2 обратная матрица
найти обратную матрицу
инвертировать матрицу
3×3 обратная матрица
калькулятор умножения матриц
расчет матрицы
калькулятор обратный 5 матрице 3×3 матричный калькулятор
мультипликативный обратный калькулятор
определительный калькулятор 3×3
обратный матричный калькулятор 3×3
найти обратную матрицу
калькулятор матрицы
онлайн-решатель матриц
обратная матрица 3×3
обратная 3×3 калькулятор матриц
калькулятор алгебры матриц
калькулятор решений матриц
онлайн-калькулятор матриц
калькулятор решения матриц
калькулятор матриц rref
поиск обратной матрицы
обратная матрица онлайн
Калькулятор сложных матриц
Калькулятор матриц 3х3
Калькулятор матриц
Формула обратной матрицы
Калькулятор с матрицей
онлайн матрица
калькулятор ранга матрицы
калькулятор операций с матрицами
метод обращения матриц
калькулятор сопряженных матриц
обратная матрица 3×3
калькулятор решения матриц
калькулятор определителя 4×4
обратная матрица 3×3
вычислить обратную матрицу
метод обратной матрицы онлайн Калькулятор матриц 3×3
Решатель математических матриц
Калькулятор матрицы кофакторов
Калькулятор произведения матриц
Обратная матрица 3×3
найти обратную матрицу 3×3
инвертировать матрицу
матричные компьютеры
обратная матрица 2 на 2
определитель определителя
решить матрицы онлайн
найти обратный калькулятор
онлайн обратная матрица
графический калькулятор
найти обратную матрицу калькулятор
найти обратную матрицы 3×3
научный калькулятор
калькулятор собственных векторов
генератор матриц онлайн
калькулятор сокращения строк матрицы
калькулятор диагонализации
Калькулятор матрицы перехода
Обратная матрица 2×2
Решение матрицы онлайн
Калькулятор определительной матрицы
Калькулятор диагонализации матрицы
Математический калькулятор

Поддерживаемые операции с матрицами:
– Обратная матрица.
– Определитель матрицы.
– Матричное скалярное умножение.
– Добавление матрицы.
– Вычитание матриц.
– Умножение матриц.
– Матричная транспозиция.

Приложение может работать с:
– целыми числами (-2, -1, 0, 1, 2 и т.д.).
– Десятичные дроби (1,5, 3,14 и т.д.).
– Простые дроби (1/2, 3/4, 7/3 и т. д.).
– Комплексные числа (i, 1+i, 1/2-2i, 0,5+2/3i и т. д.).

Проверьте результаты матриц 2×2, 3×3, 4×4, nxn или матриц сложения, вычитания, умножения, определителя, обратной или транспонированной матрицы или выполните такие вычисления с помощью этих формул и калькуляторов. Основная цель этих матричных инструментов — помочь студентам, специалистам и исследователям быстро выполнить такие расчеты или проверить результаты таких расчетов для анализа, определения и решения линейных функций и уравнений. Эти матричные формулы и калькуляторы могут дать ответы на многие сложные алгоритмы обработки цифровой информации, изображений и видео.

7 сентября 2021 г.

Версия 1.5

Исправления ошибок, обновление библиотеки и повышение производительности.

Разработчик Sunnykumar Mavani указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.

Данные, используемые для отслеживания вас

Следующие данные могут использоваться для отслеживания вас в приложениях и на веб-сайтах, принадлежащих другим компаниям:

Покупки
Расположение
Пользовательский контент
Идентификаторы
Данные об использовании
Диагностика
Другие данные

Данные, связанные с вами

Следующие данные могут быть собраны и связаны с вашей личностью:

Покупки
Расположение
Пользовательский контент
Идентификаторы
Данные об использовании
Диагностика
Другие данные

Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста.