Матрица и действия с ними: Матрицы и действия над ними. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Матрицы и действия над ними.

Ответ:

Матрица – прямоугольная таблица чисел, расположенных в n строках и m столбцах. A = (i,j) где i – номер строки, j – номер столбца.

Размерность матрицы – число строк и число столбцов в данной матрице.

Квадратная матрица – матрица, когда у нее число строк и число столбцов равны.

Главная диагональ – диагональ, идущая из верхнего левого до правого нижнего угла.

Побочная диагональ – диагональ, идущая из верхнего правого до нижнего левого угла.

Матрица, у которой все элементы нули называют нулевой матрицей. А = ( 0 0 )

Диагональная матрица – матрица, у которой элементы расположенные вне главной диагонали нули.

Умножение матрицы на число подчиняется следующим законам:

-ассоциативный закон относительно числового множества
-распределительный (дистрибутивный) закон относительного множества
– дистрибутивный закон относительно суммы числовых множителей

Единичная матрица – диагональная матрица, в которой элементы главной диагонали равны 1.

Действия над матрицами.

Умножение матрицы на число.

Любую матрицу можно умножить на число.

Для этого каждый элемент матрицы умножается на число.

Сложение матриц.

Свойства сложения матриц:

– переместительный(коммуникативный) закон
– сочетательный (ассоциативный) закон
– где Q-нулевая матрица соответствующего размера

Любые две матрицы одних и тех же размеров можно сложить. Получится матрица в точности тех же размеров.

Пусть

А = и

В = , то A+B=

Умножение матриц.

Свойства произведения матриц:

– ассоциативность
– ассоциативность по умножению

– умножение на единичную матрицу

Матрицу А можно умножать на матрицу В, если количество столбцов А равно количеству строк В.

Пусть , то возможно только если . При этом в результате получится матрица C размерами .

Пусть , то

Так произведение BA существует и равно .

следовательно, умножение матриц некоммутативно, т.е. зависит от порядка сомножителя.

Свойства транспонирования:
1. 3)
2. 4)
Транспонирование матрицы.

Транспонирование – это операция над матрицами, когда ее строки становятся столбцами с теми же номерами.

Пусть , то транспонированная матрица .

Ответ:

Квадратная матрица A n-го порядка характеризуется неким числом называемым определителем.

Обозначается: detA

Если порядок матрице равен единице, то определитель такой матрицы равен этому элементу: A=(6), то detA=6.

Вычисление определителя 2-ого порядка:

Пусть , то

Минором некоторого элемента определителя – определитель, получаемый из данного определителя вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.

Так, минором элемента будет .

Алгебраическим дополнением некоторого элемента определителя – минор этого элемента, умноженный на .

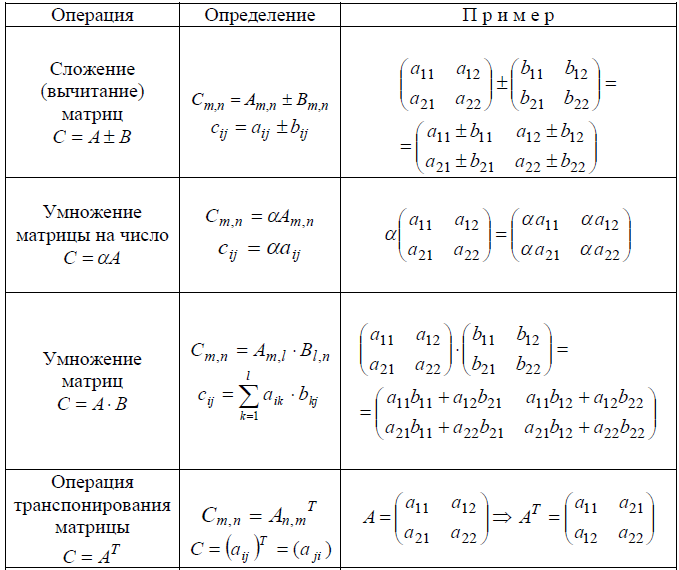
Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.

Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник/ / Линейная алгебра. (Вектора, матрицы) / / Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.

Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.

Матрицы (и соответственно математический раздел – матричная алгебра) имеют важное значение в прикладной математике, так как позволяют записать в достаточно простой форме значительную часть математических моделей объектов и процессов. Термин “матрица” появился в 1850 году. Впервые упоминались матрицы еще в древнем Китае, позднее у арабских математиков.

Матрицей A=A_mn порядка m*n называется прямоугольная таблица чисел, содержащая m – строк и n – столбцов

Элементы матрицы a_ij, у которых i=j, называются диагональными и образуют главную диагональ.

Для квадратной матрицы (m=n) главную диагональ образуют элементы a₁₁, a₂₂,…, a_nn .

Равенство матриц.

A=B, если порядки матриц A и B одинаковы и a_ij=b_ij (i=1,2,…,m; j=1,2,…,n)

Действия над матрицами.

1. Сложение матриц – поэлементная операция

2. Вычитание матриц – поэлементная операция

3. Произведение матрицы на число – поэлементная операция

4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

A_mk*B_kn=C_mn причем каждый элемент с_ijматрицы C_mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т. е.

Покажем операцию умножения матриц на примере

5. Возведение в степень

m>1 целое положительное число. А – квадратная матрица (m=n) т.е. актуально только для квадратных матриц

6. Транспонирование матрицы А. Транспонированную матрицу обозначают A^T или A’

Строки и столбцы поменялись местами

Пример

Свойства опрераций над матрицами

A+B=B+A

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(A’)’=A

(λA)’=λ(A)’

(A+B)’=A’+B’

(AB)’=B’A’

Виды матриц

1. Прямоугольные: m и n – произвольные положительные целые числа

2. Квадратные: m=n

3. Матрица строка: m=1. Например, (1 3 5 7 ) – во многих практических задачах такая матрица называется вектором

4. Матрица столбец: n=1. Например

5. Диагональная матрица: m=n и a_ij=0, если i≠j. Например

6. Единичная матрица: m=n и

7. Нулевая матрица: a_ij=0, i=1,2,…,m

j=1,2,…,n

8. Треугольная матрица: все элементы ниже главной диагонали равны 0.

Пример.

9. Симметрическая матрица: m=n и a_ij=a_ji(т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно A’=A

Например,

10. Кососимметрическая матрица: m=n и a_ij=-a_ji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы).

Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем a_ii=-a_ii)

Пример.

Ясно, A’=-A

11. Эрмитова матрица: m=n и a_ii=-ã_ii (ã_ji– комплексно – сопряженное к a_ji, т.е. если A=3+2i, то комплексно – сопряженное Ã=3-2i)

Пример

Дополнительная информация от TehTab.ru:

Использование матрицы для заданий

О стратегиях матриц

Стратегия матриц позволяет использовать переменные в одном определении задания для автоматического создания нескольких запусков заданий на основе комбинаций переменных. Например, вы можете использовать матричную стратегию для тестирования своего кода в нескольких версиях языка или в нескольких операционных системах.

Использование матричной стратегии

Используйте заданий. .strategy.matrix для определения матрицы различных конфигураций заданий. В вашей матрице определите одну или несколько переменных, за которыми следует массив значений. Например, следующая матрица имеет переменную с именем версия со значением [10, 12, 14] и переменная с именем os со значением [ubuntu-latest, windows-latest] :

  пример_матрицы:
    стратегия:
      матрица:
        версия: [10, 12, 14]
        ОС: [ubuntu-последняя, Windows-последняя]

Задание будет выполняться для каждой возможной комбинации переменных. В этом примере рабочий процесс будет выполнять шесть заданий, по одному для каждой комбинации переменных os и версии .

По умолчанию GitHub максимизирует количество заданий, выполняемых параллельно, в зависимости от доступности исполнителя. Порядок переменных в матрице определяет порядок создания заданий. Первая переменная, которую вы определите, будет первым заданием, созданным в ходе вашего рабочего процесса. Например, приведенная выше матрица создаст задания в следующем порядке:

{версия: 10, os: ubuntu-latest}
{версия: 10, ОС: последняя версия Windows}
{версия: 12, ОС: ubuntu-последняя}
{версия: 12, ОС: последняя версия Windows}
{версия: 14, ОС: ubuntu-последняя}
{версия: 14, ОС: последняя версия Windows}

Матрица создает не более 256 заданий за один запуск рабочего процесса. Это ограничение распространяется как на исполнителей, размещенных на GitHub, так и на собственных.

Определяемые вами переменные становятся свойствами в контексте матрицы , и вы можете ссылаться на свойство в других областях файла рабочего процесса. В этом примере вы можете использовать matrix.version и matrix.os для доступа к текущему значению версии и os , которое использует задание. Дополнительные сведения см. в разделе «Контексты».

Пример: Использование одномерной матрицы

Вы можете указать одну переменную для создания одномерной матрицы.

Например, следующий рабочий процесс определяет переменную версии со значениями [10, 12, 14] . Рабочий процесс запустит три задания, по одному для каждого значения переменной. Каждое задание будет иметь доступ к значение версии через контекст matrix.version и передать значение как node-version в действие action/setup-node .

 рабочих мест:
  пример_матрицы:
    стратегия:
      матрица:
        версия: [10, 12, 14]
    шаги:
      - использует: action/setup-node@v3
        с:
          версия узла: ${{ matrix.version }}

Пример: использование многомерной матрицы

Можно указать несколько переменных для создания многомерной матрицы. Задание будет выполняться для каждой возможной комбинации переменных.

Например, в следующем рабочем процессе указаны две переменные:

Две операционные системы, указанные в переменной os
Три версии Node.js, указанные в переменной версии

Рабочий процесс будет выполнять шесть заданий, по одному для каждой комбинации переменных os и версии . Каждое задание установит значение run-on на текущее значение os и передаст текущее значение .значение версии для действия action/setup-node .

 рабочих мест:
  пример_матрицы:
    стратегия:
      матрица:
        ОС: [убунту-22.04, убунту-20.04]
        версия: [10, 12, 14]
    запуски: ${{ matrix.os }}
    шаги:
      - использует: action/setup-node@v3
        с:
          версия узла: ${{ matrix.version }}

Пример: использование контекстов для создания матриц

Вы можете использовать контексты для создания матриц. Дополнительные сведения о контекстах см. в разделе «Контексты».

Например, следующий рабочий процесс запускается по событию relay_dispatch и использует информацию из полезной нагрузки события для построения матрицы. Когда событие отправки репозитория создается с полезной нагрузкой, подобной приведенной ниже, переменная matrix version будет иметь значение [12, 14, 16] . Дополнительные сведения о триггере relay_dispatch см. в разделе «События, запускающие рабочие процессы».

 {
  "тип_события": "тест",
  "client_payload": {
    "версии": [12, 14, 16]
  }
}

 по:
  репозиторий_отправка:
    типы:
      - контрольная работа
 
вакансии:
  пример_матрицы:
    запуски: ubuntu-последняя
    стратегия:
      матрица:
        версия: ${{ github.event.client_payload.versions }}
    шаги:
      - использует: action/setup-node@v3
        с:
          версия узла: ${{ matrix.version }}

Расширение или добавление конфигураций матриц

Используйте задания . .strategy.matrix.include , чтобы расширить существующие конфигурации матриц или добавить новые конфигурации. Значение включают список объектов.

Для каждого объекта в списке include пары ключ:значение в объекте будут добавлены к каждой из комбинаций матриц, если ни одна из пар ключ:значение не перезапишет какие-либо исходные значения матрицы. Если объект не может быть добавлен ни к одной из комбинаций матриц, вместо нее будет создана новая комбинация матриц. Обратите внимание, что исходные значения матрицы не будут перезаписаны, но добавленные значения матрицы могут быть перезаписаны.

Например, эта матрица:

 стратегия:
  матрица:
    фрукты: [яблоко, груша]
    животное: [кошка, собака]
    включать:
      - цвет: зеленый
      - цвет: розовый
        животное: кошка
      - фрукты: яблоко
        форма: круг
      - фрукты: банан
      - фрукты: банан
        животное: кошка

приведет к шести заданиям со следующими комбинациями матриц:

{фрукт: яблоко, животное: кошка, цвет: розовый, форма: круг}
{фрукт: яблоко, животное: собака, цвет: зеленый, форма: круг}
{фрукт: груша, животное: кошка, цвет: розовый}
{фрукт: груша, животное: собака, цвет: зеленый}
{фрукты: банан}
{фрукт: банан, животное: кошка}

, следуя следующей логике:

{цвет: зеленый} добавляется ко всем исходным комбинациям матриц, поскольку его можно добавлять без перезаписи какой-либо части исходных комбинаций.
{цвет: розовый, животное: кошка} добавляет цвет:розовый только к исходным матричным комбинациям, которые включают животное: кошка . Это перезаписывает цвет : зеленый , который был добавлен предыдущей записью include .
{фрукт: яблоко, форма: круг} добавляет форма: круг только к исходным матричным комбинациям, которые включают фрукт: яблоко .
{фрукт: банан} не может быть добавлен ни к какой исходной комбинации матриц без перезаписи значения, поэтому он добавляется как дополнительная комбинация матриц.
{фрукт: банан, животное: кошка} нельзя добавить ни к какой исходной комбинации матриц без перезаписи значения, поэтому она добавляется как дополнительная комбинация матриц. Он не добавляется к матричной комбинации {фрукты: банан} , потому что эта комбинация не была одной из исходных матричных комбинаций.

Пример: расширение конфигураций

Например, следующий рабочий процесс будет выполнять шесть заданий, по одному для каждой комбинации os и узел . При запуске задания для os со значением windows-latest и node со значением 16 в задание будет включена дополнительная переменная с именем npm со значением 6 .

 рабочих мест:
  пример_матрицы:
    стратегия:
      матрица:
        ОС: [Windows-последняя, Ubuntu-последняя]
        узел: [12, 14, 16]
        включать:
          - ОС: windows-последняя
            узел: 16
            нпм: 6
    запуски: ${{ matrix.os }}
    шаги:
      - использует: action/setup-node@v3
        с:
          версия узла: ${{ matrix.node }}
      - если: ${{ matrix.npm }}
        выполнить: npm install -g npm@${{ matrix.npm }}
      - запустить: npm --версия

Пример: Добавление конфигураций

Например, эта матрица будет запускать 10 заданий, по одному для каждой комбинации os и версии в матрице, а также задание для os со значением windows-latest и версия значение 17 .

 рабочих мест:
  пример_матрицы:
    стратегия:
      матрица:
        os: [macos-последние, windows-последние, ubuntu-последние]
        версия: [12, 14, 16]
        включать:
          - ОС: windows-последняя
            версия: 17

Если вы не укажете какие-либо матричные переменные, все конфигурации под включают . Например, следующий рабочий процесс будет запускать два задания, по одному для каждой записи , включая . Это позволяет вам воспользоваться матричной стратегией, не имея полностью заполненной матрицы.

 рабочих мест:
  include_only:
    запуски: ubuntu-последняя
    стратегия:
      матрица:
        включать:
          - сайт: "производство"
            центр обработки данных: "site-a"
          - сайт: "постановка"
            центр обработки данных: "site-b"

Исключение конфигураций матрицы

Чтобы удалить определенные конфигурации, определенные в матрице, используйте задания ..strategy. matrix.exclude . Исключенная конфигурация должна иметь только частичное совпадение, чтобы ее можно было исключить. Например, следующий рабочий процесс будет выполнять девять заданий: одно задание для каждой из 12 конфигураций, минус одно исключенное задание, соответствующее {os: macos-latest, version: 12, environment: production} , и два исключенных задания. что соответствует {ОС: последняя версия Windows, версия: 16} .

 стратегия:
  матрица:
    os: [macos-последние, windows-последние]
    версия: [12, 14, 16]
    среда: [постановка, производство]
    исключать:
      - os: macos-последняя
        версия: 12
        среда: производство
      - ОС: windows-последняя
        версия: 16
запуски: ${{ matrix.os }}

Примечание: Все включают комбинаций, обрабатываются после исключают . Это позволяет использовать включая , чтобы добавить обратные комбинации, которые ранее были исключены.

Обработка сбоев

Вы можете управлять обработкой сбоев заданий с помощью заданий ..strategy.fail-fast и заданий..continue-on-error .

jobs..strategy.fail-fast применяется ко всей матрице. Если для jobs..strategy.fail-fast установлено значение true , GitHub отменит все выполняемые и поставленные в очередь задания в матрице, если какое-либо задание в матрице завершится неудачно. Это свойство по умолчанию равно верно .

заданий..continue-on-error относится к одному заданию. Если заданий..continue-on-error равно true , другие задания в матрице будут продолжать выполняться, даже если задание с заданиями..continue-on-error: true завершится ошибкой.

Вы можете использовать заданий..strategy.fail-fast и заданий..continue-on-error вместе. Например, следующий рабочий процесс запустит четыре задания. За каждую работу продолжение при ошибке определяется значением matrix.experimental . Если какое-либо из заданий с continue-on-error: false завершится ошибкой, все задания, которые выполняются или находятся в очереди, будут отменены. Если задание с continue-on-error: true завершится ошибкой, это не повлияет на другие задания.

 рабочих мест:
  контрольная работа:
    запуски: ubuntu-последняя
    продолжение при ошибке: ${{ matrix.experimental }}
    стратегия:
      безотказный: правда
      матрица:
        версия: [6, 7, 8]
        экспериментальный: [ложь]
        включать:
          - версия: 9экспериментальный: правда

Определение максимального количества одновременных заданий

По умолчанию GitHub максимизирует количество заданий, выполняемых параллельно, в зависимости от доступности исполнителя. Чтобы установить максимальное количество заданий, которые могут выполняться одновременно при использовании стратегии заданий matrix , используйте заданий. .strategy.max-parallel .

Например, следующий рабочий процесс будет запускать максимум два задания одновременно, даже если есть исполнители, доступные для запуска всех шести заданий одновременно.

 рабочих мест:
  пример_матрицы:
    стратегия:
      макс-параллельно: 2
      матрица:
        версия: [10, 12, 14]
        ОС: [ubuntu-последняя, Windows-последняя]

Как использовать матрицу действий

У каждой компании есть уникальные методы работы, которые помогают обеспечить эффективность, общение и сотрудничество в рамках всей организации. В Hive мы быстро выросли из организации, состоящей из 15 человек, в компанию из более чем 40 за последние 18 месяцев, и нам пришлось адаптировать наши уникальные методы работы, чтобы лучше адаптироваться к нашей растущей команде. Один из самых эффективных способов сделать это — использовать то, что мы назвали «Матрица действий». Эта матрица — живой, дышащий документ, в котором отслеживается все, что делает наша организация.

В заключение скажу, что матрица — это инструмент для отслеживания трех типов действий: повторяющихся действий, триггеров и проектов. Повторяющееся действие — это действие, которое происходит с определенной периодичностью (ежегодно, ежемесячно и т. д.), и некоторыми примерами этого являются ежегодное планирование праздничных вечеринок или двухгодичные обзоры производительности. Триггеры — это именно то, на что они похожи — что-то происходит, что запускает действие. Примером этого является то, что когда сотрудник начинает работать в компании, запускается ряд адаптационных действий, чтобы помочь ему быстрее освоиться в организации. Наконец, проекты — это более крупные элементы подъема, которые обычно предполагают сотрудничество между отделами. Примером этого является внедрение нового программного обеспечения для управления проектами или управления персоналом.

Изучив различные типы действий, происходящих в вашей организации, вы можете определить четыре вещи: что это за действие или задание на самом деле, триггер, продолжительность и кто его выполняет. Оттуда вы можете построить Матрицу действий всего, что делается в команде или организации. Вот как это будет выглядеть, когда вы начнете:

Этот перечень обязанностей и ответственности необходим для организации, особенно в эту новую эру удаленной работы. Мы уверены, что когда вы внедрите матрицу, произойдут три вещи: вы перестанете работать с тенями, вы перестанете приносить песок на пляж и сможете легко найти пустое пространство. Идея о том, что вы перестанете выполнять теневую работу, означает, что вы перестанете дублировать работу. Вы также перестанете выполнять работу, похожую на «приносить песок на пляж», когда кто-то выполняет работу, которая уже сделана или в которой нет необходимости. Наконец, вы сможете найти пробелы, т. е. что люди не делают, что нам действительно нужно решить? Оттуда вы можете создавать новые «Работы» в матрице и выяснять, сколько времени, по вашему мнению, люди должны тратить на них, как долго они должны выполняться и кто будет этим заниматься.

Вы можете подумать: это то, что вы ДЕЙСТВИТЕЛЬНО используете в Hive? Ответ положительный, и мы используем Hive, чтобы отслеживать все это. Каждое действие индивидуально выстраивается в карточке действия, назначается человеку, помещается в проект с указанием срока выполнения и периодичностью. Вы можете увидеть примерную схему того, как эти элементы выглядят вместе на изображении ниже. Мы обнаружили, что табличное представление Hive лучше всего подходит для просмотра матрицы, поскольку оно дает вам взгляд на действия, подобный Excel, в истинной матричной форме. При этом вы можете использовать гибкие представления проектов Hive, чтобы просматривать все действия в представлении Ганта, Канбана, календаря или портфолио. Как только ваши действия скомпилированы и назначены, вы получаете кристально четкое представление обо всем, что происходит в вашей организации в любой момент.

Что делает для нас матрица? Во-первых, это помогает нам лучше понять соотношение свободного и повторяющегося времени каждого.